Автоматика и телемеханика, № 12, 2020
© 2020 г. А.И. КИБЗУН, д-р физ.-мат. наук (kibzun@mail.ru),
С.В. ИВАНОВ, канд. физ.-мат. наук (sergeyivanov89@mail.ru)
(Московский авиационный институт
(национальный исследовательский университет))
ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ МНОЖЕСТВ ПОГЛОЩЕНИЯ
С ПОМОЩЬЮ СТАТИСТИЧЕСКИХ МЕТОДОВ1
Рассматривается задача о построении доверительного множества по-
глощения, представляющего собой множество начальных позиций систе-
мы, обеспечивающих с заданной вероятностью непревышение функци-
ей потерь в терминальный момент времени некоторого фиксированного
уровня. Предполагается, что зависимость состояния системы в терми-
нальный момент времени от начальной позиции описывается известной
случайной функцией. Предлагается подход к построению внешних и внут-
ренних аппроксимаций доверительного множества поглощения. На пер-
вом этапе строятся детерминированные внутренняя и внешняя аппрокси-
мации. Затем полученные аппроксимации уточняются для некоторого ко-
нечного множества начальных позиций системы с помощью выборочных
оценок. Получены оценки объема выборки, достаточного для построе-
ния указанных аппроксимаций. Данная оценка улучшается для случая
звездчатой функции потерь. Предлагается алгоритм построения аппрок-
симаций доверительного множества поглощения в двумерном случае. По-
лученные аппроксимации применяются в задаче планирования производ-
ства.
Ключевые слова: стохастическое программирование, доверительное мно-
жество поглощения, функция вероятности, функция квантили.
DOI: 10.31857/S0005231020120053
1. Введение
Качество функционирования стохастической системы при заданном на-
чальном состоянии системы может оцениваться вероятностью непревышения
потерями фиксированного предельно допустимого уровня в терминальный
момент времени. Представляет интерес множество начальных состояний си-
стемы, при которых с заданной вероятностью потери, возникающие в ходе
функционирования системы, в терминальный момент времени не будут пре-
вышать заданный предельно допустимый уровень. Данное множество назы-
вается доверительным множеством поглощения.
Описанная задача аналогична задаче построения множеств уровня функ-
ции вероятности в задачах стохастического программирования. Свойства
1 Работа Кибзуна А.И. выполнена при финансовой поддержке Российского фонда фун-
даментальных исследований (проект № 18-07-00617 А). Работа Иванова С.В. выполнена
при финансовой поддержке Российского фонда фундаментальных исследований (проект
№ 19-07-00436 А).
82
функции вероятности изучаются в [1, 2]. С точки зрения построения мно-
жеств уровня наиболее важными свойствами функции вероятности является
выпуклость и квазивыпуклость, при наличии которых множества уровня яв-
ляются выпуклыми. Достаточные условия выпуклости, квазивыпуклости и
логарифмической выпуклости функции вероятности изучаются в [3-8].
Для аппроксимации множеств уровня функции вероятности может быть
использован подход, основанный на использовании p-эффективных точек,
представляющих собой многомерное обобщение квантили распределения. Ал-
горитм для поиска p-эффективных точек дискретного случайного вектора
предложен в [9]. Аппроксимации множеств уровня с помощью p-эффектив-
ных точек, предназначенные для решения задач стохастического програм-
мирования, предлагаются в [10, 11]. Обзор подобных методов решения задач
стохастического программирования приведен в [12].
Другим подходом к аппроксимации доверительного множества поглоще-
ния является использование выборочных методов, когда функция вероятно-
сти оценивается с помощью выборки. Данный подход известен и как метод
Монте-Карло. Основой для построения таких оценок является равномерный
закон больших чисел [13, 14], позволяющий оценить объем выборки, доста-
точный для оценивания максимального отклонения частоты от вероятности
по некоторому классу событий. В дальнейшем данные идеи применялись
в [15-17] для оценивания объема выборки, достаточного для аппроксимации
задач оптимизации функции математического ожидания. В [18] проведено
исследование скорости сходимости для задач стохастического программиро-
вания с вероятностными ограничениями.
Данная статья является дальнейшим развитием [19], где был предложен
основанный на доверительном методе [1] подход к построению внутренней ап-
проксимации доверительного множества поглощения. В статье предлагается
подход, сочетающий детерминированные и выборочные методы. На первом
этапе строятся детерминированные аппроксимации. Внутренняя аппрокси-
мация строится с помощью методов, предложенных в [19], а внешняя ап-
проксимация с помощью α-ядра вероятностной меры [1, 20]. На втором
этапе полученные аппроксимации улучшаются с помощью выборочных оце-
нок. Выводятся оценки достаточного для аппроксимации объема выборки.
Приводится описание класса задач, для которых объем выборки может быть
уменьшен. Рассматривается численный пример.
2. Постановка задачи
Пусть зависимость терминального состояния системы от начального со-
стояния y ∈ Y ⊂ Rs и от реализации x ∈ X ⊂ Rm случайного вектора X опи-
сывается функцией z : Y × X → Z. Считается, что данная зависимость из-
вестна. Поиск функции z не является предметом статьи. Конечно, ее вид
существенно зависит от того, какого класса изучаемая система. Будем счи-
тать, что множества Y , Z и X замкнуты. Данное предположение не огра-
ничивает общности, поскольку можно от исходных множеств перейти к их
замыканиями. Случайный вектор X определен на вероятностном простран-
стве (X , L(X ), P0), где L(X ) лебегово пополнение борелевской σ-алгебры
83
подмножеств X . Будем считать, что для всех x ∈ X выполнено равенство
X(x) = x, т.е. пространство элементарных событий отождествляется с про-
странством реализаций случайного вектора X. Предполагается, что функция
x → z(y,x) является измеримой при всех y ∈ Y .
Пусть борелевская функцияΦ: Z → R описывает потери, возникающие
при известном терминальном состоянии системы. Определим функцию по-
терь Φ: Y × X → R в терминальный момент времени:
Φ(y, x) ≜Φ(z(y, x)).
Введем функцию вероятности
Pϕ(y) ≜ P0{Φ(y,X) ≤ ϕ},
где ϕ ∈ R заданный максимально допустимый уровень потерь.
Рассматривается задача построения доверительного множества поглоще-
ния, определяемого по правилу
Yϕ,α ≜ {y ∈ Y | Pϕ(y) ≥ α},
где α ∈ (0, 1)
заданное значение вероятности непревышения максималь-
но допустимого уровня потерь. Из приведенного определения следует, что
доверительное множество поглощения можно рассматривать как множество
уровня функции вероятности.
3. Построение внешней и внутренней аппроксимации доверительного
множества поглощения
Определим функцию квантили
ϕα(y) ≜ min{ϕ ∈ R | Pϕ(y) ≥ α}.
Приведем утверждение, известное как лемма Розенблатта.
Лемма 1 [1]. Пусть α ∈ (0,1), ϕ ∈ R, функция x → Φ(y,x) измерима для
всех y ∈ Y . Тогда
{y ∈ Y | Pϕ(y) ≥ α} = {y ∈ Y | ϕα(y) ≤ ϕ}.
Согласно приведенной лемме Розенблатта доверительное множество погло-
щения можно определить с помощью функции квантили:
(1)
Yϕ,α = {y ∈ Y | ϕα
(y) ≤ ϕ}.
Для построения внешней аппроксимации доверительного множества по-
глощения будем использовать понятие α-ядра вероятностной меры.
Определение 1
[1]. Множество
⋂
{
}
Kα =
x | c⊤x ≤ bα(c)
,
∥c∥=1
где bα(c)
α-квантиль случайной величины c⊤X, называется α-ядром ве-
роятностной меры, порожденной распределением случайного вектора X.
84
Иными словами, α-ядро является пересечением замкнутых полупро-
странств вероятностной меры не менее α.
Введем обозначения:
ψ(S, y) ≜ sup Φ(y, x),
x∈S
Yϕ(S) ≜ {y ∈ Y | ψ(S,y) ≤ ϕ} ,
где S ⊂ X некоторое множество реализаций случайного вектора X.
Сформулируем утверждение о внешней аппроксимации доверительного
множество поглощения.
Лемма 2. Пусть функция x → Φ(y,x) квазивыпукла и полунепрерывна
снизу при всех значениях y ∈ Y . Тогда для любого множества ∅ = Kα ⊂ Kα
(2)
Yϕ,α ⊂ Yϕ(Kα) ⊂ Yϕ(Kα
).
Доказательство. Пусть y ∈ Yϕ,α. Тогда из (1) следует, что
(3)
ϕα
(y) ≤ ϕ.
Как доказано в [1, лемма 3.15], для всех y ∈ Y справедлива оценка
(4)
ψ(Kα, y) ≤ ϕα
(y),
если выполнены условия сформулированной леммы 2. Из полученных нера-
венств (3) и (4) следует, что
ψ(Kα, y) ≤ ϕ,
а значит, y ∈ Yϕ(Kα). Таким образом, выполнено включение Yϕ,α ⊂ Yϕ(Kα).
Проверим включение Yϕ(Kα) ⊂ Yϕ(Kα). Пусть y ∈ Yϕ(Kα). Это значит,
что ψ(Kα, y) ≤ ϕ. По построению ψ(Kα, y) ≤ ψ(Kα, y). Поэтому ψ(Kα, y) ≤ ϕ.
Таким образом, y ∈ Yϕ(Kα). Лемма 2 доказана.
(
)
m
В [21] доказано, что Kα = ∅ при α ∈
,1
. Лемма 2 предлагает способ
m+1
построения внешней аппроксимации в том случае, когда возможно постро-
ить хотя бы внутреннюю аппроксимацию α-ядра вероятностной меры. Для
построения внутренней аппроксимации α-ядра достаточно найти в нем хотя
бы одну точку. Если удается найти несколько точек, принадлежащих α-ядру,
то в силу его выпуклости выпуклая комбинация данных точек также являет-
ся его внутренней аппроксимацией. Если α-ядро данной вероятностной меры
пусто, то в качестве внешней аппроксимации доверительного множества по-
глощения можно взять тривиальную аппроксимацию в виде множества Y .
Перейдем к построению внутренней аппроксимации доверительного мно-
жества поглощения. Пусть S некоторое доверительное множество с вероят-
ностной мерой не менее α, т.е. S ∈ Fα, где Fα семейство всех доверительных
множеств с мерой не менее α. В [1, теорема 3.9] доказано, что для всех y ∈ Y
и S ∈ Fα выполнено неравенство
ψ(S, y) ≥ ϕα(y).
85
Поэтому при выполнении неравенства
ψ(S, y) ≤ ϕ
справедливо, что
ϕα(y) ≤ ϕ.
Из полученного неравенства следует, что
Yϕ(S) ⊂ Yϕ,α.
Дальнейшие способы улучшения внутренней аппроксимации доверитель-
ного множества поглощения приводятся в [19]. Предлагается использовать
параметризованное семейство множеств St, t ∈ T , таких что P0(St) ≥ α, на-
пример семейство прямоугольников, повернутых относительно начала коор-
динат. В этом случае внутренняя аппроксимация доверительного множества
поглощения принимает вид
⋃
Yϕ(St) ⊂ Yϕ,α.
t∈T
4. Улучшение аппроксимации доверительного множества поглощения
с помощью выборочных методов
Пусть построены (например, с помощью методов, описанных в разделе 3)
внутренняя и внешняя аппроксимации доверительного множества поглоще-
ния:
Yϕ,α ⊂ Yϕ,α ⊂ Yϕ,α.
Чтобы выяснить, какие из точек множества Yϕ,α \ Yϕ,α содержатся в дове-
рительном множестве поглощения, построим выборочную оценку функции
вероятности.
Пусть задана последовательность независимых случайных векторов {Xn},
n ∈ N, распределения которых совпадают с распределением случайного век-
тора X. Будем считать, что последовательность случайных векторов {Xn}
задана на вероятностном пространстве (X∞, F, P). Построим оценку функ-
ции вероятности как частоту события {Φ(y, X) ≤ ϕ}:
∑
1
P(n)ϕ(y) ≜
χ(-∞,ϕ](Φ(y,Xk)),
n
k=1
где
{
1, если a ∈ A,
χA(a) =
0, если a ∈ A.
86
Выборочная аппроксимация доверительного множества поглощения имеет
вид
{
}
Y(n)ϕ,α ≜ y ∈ Yϕ,α \ Yϕ,α | P(n)ϕ(y) ≥ α
∪Yϕ,α.
Множество Yϕ,α является случайным. Этот объект следует рассматривать
как функцию, которая каждой реализации выборки ставит в соответствие
некоторое числовое множество.
В общем случае множество Yϕ,α не является ни внутренней, ни внешней
аппроксимацией множества Yϕ,α. Однако, как будет показано далее, с высо-
кой вероятностью множество Y(n)ϕ,α+ε, где ε > 0, целиком содержится в множе-
стве Yϕ,α, а множество Y(n)ϕ,α-ε является его внешней аппроксимацией. Пусть
Y конечное подмножество Yϕ,α \ Yϕ,α, состоящее из
Y | точек. Количество
элементов в данном множестве связано с требуемой точностью построения
доверительного множества поглощения и должно обеспечивать достаточную
мелкость разбиения множества Y . Выясним, при каком объеме выборки n
можно с вероятностью β ∈ (0, 1) гарантировать включения Y(n)ϕ,α+ε
Y ⊂Yϕ,α
и Yϕ,α
Y ⊂ Y(n)ϕ,α-ε. Данные включения гарантируют, что все точки из мно-
жеств
Y , в которых значение выборочной оценки вероятности не менее α + ε,
содержатся в доверительном множестве поглощения, а во всех точка
Y из
доверительного множества поглощения значение выборочной оценки веро-
ятности не менее α - ε. Второе условие эквивалентно тому, что все точки
из множеств
Y , в которых значение выборочной оценки вероятности менее
α - ε, содержатся в дополнении доверительного множества поглощения.
Теорема 1. Пусть β ∈ (0,1), ε > 0,
Y
конечное подмножество
Yϕ,α \ Yϕ,α. Тогда при
ln
Y | - ln(1 - β)
(5)
n≥
2ε2
выполнено неравенство
({
}
{
})
(n)
(6)
P Y(n)
ϕ,α+ε
∩
Y ⊂Yϕ,α
∩ Yϕ,α ∩Y
⊂Yϕ
,α-ε
≥ β.
Доказательство. События, состоящие в том, что Y(n)ϕ,α+ε
Y ⊂Yϕ,α и
Yϕ,α
Y ⊂ Y(n)ϕ,α-ε, можно представить в виде
{
}
⋃
{
}
Y(n)
∩
Y ⊂Yϕ,α
=
P(n)ϕ(y) ≥ α + ε
,
ϕ,α+ε
y
Y \Yϕ,α
{
}
⋃
{
}
Yϕ,α
Y ⊂Y(n)
=
P(n)ϕ(y) < α - ε
,
ϕ,α-ε
y
Y ∩Yϕ,α
который гарантирует измеримость события, рассматриваемого в неравен-
стве (6).
87
Случайная величина n
ϕ (y) определяет число успехов в серии из n опы-
тов с вероятностью успеха Pϕ(y), а значит, распределена по биномиальному
закону. Известно из [22], что для биномиально распределенной случайной ве-
личины выполнены неравенства
{
}
(7)
P P(n)ϕ(y) - Pϕ(y) ≥ ε
≤e-2nε2,
{
}
(8)
P P(n)ϕ(y) - Pϕ(y) ≤ -ε
≤e-2nε2.
Из неравенства (7) следует, что
{
}
⋃
{
}
P Y(n)
∩
Y ⊂Yϕ,α
=P
P(n)ϕ(y) ≥ α + ε
≤
ϕ,α+ε
y
Y \Yϕ,α
{
}
(9)
≤
Y \ Yϕ,α| max P P(n)ϕ(y) ≥ α + ε
≤
y
Y \Yϕ,α
{
}
≤
Y \ Yϕ,α| max P P(n)ϕ(y) ≥ Pϕ(y) + ε
≤
Y \ Yϕ,α|e-2nε2.
y
Y \Yϕ,α
Из неравенства (8) следует, что
{
}
⋃
{
}
P Yϕ,α
Y ⊂Y(n)
=P
P(n)ϕ(y) < α - ε
≤
ϕ,α-ε
y
Y ∩Yϕ,α
{
}
(10)
≤
Y ∩ Yϕ,α| max P P(n)ϕ(y) ≤ α - ε
≤
y
Y ∩Yϕ,α
{
}
≤
Y ∩ Yϕ,α| max P P(n)ϕ(y) ≤ Pϕ(y) - ε
≤
Y ∩ Yϕ,α|e-2nε2.
y
Y ∩Yϕ,α
Складывая неравенства (9) и (10), получаем
({
}
{
})
(n)
P Y(n)
∩
Y ⊂Yϕ,α
∪ Yϕ,α ∩Y
⊂Yϕ
≤
ϕ,α+ε
,α+ε
{
}
{
}
(n)
≤P Y(n)
∩
Y ⊂Yϕ,α
+P Yϕ,α ∩Y
⊂Yϕ
≤
ϕ,α+ε
,α+ε
≤
Y \Yϕ,α|e-2nε2 +
Y ∩Yϕ,α|e-2nε2 =
Y |e-2nε2 .
Чтобы обеспечить выполнение неравенства (6), эквивалентного неравен-
ству
({
}
{
})
(n)
1-P Y(n)
∩
Y ⊂Yϕ,α
∪ Yϕ,α ∩Y
⊂Yϕ
≥ β,
ϕ,α+ε
,α-ε
88
достаточно выполнения условия
(11)
1-
Y |e-2nε2
≥ β.
Выражая из полученного неравенства (11) n, получаем неравенство (5). Тео-
рема 1 доказана.
В общем случае сделать заключение о том, принадлежат ли точки, не
входящие в конечное множеств
Y , доверительному множеству поглощения,
не представляется возможным. Однако в том случае, когда функция веро-
ятности является квазивогнутой, можно построить выпуклую внутреннюю
аппроксимацию доверительного множества Yϕ,α.
Следствие. Пусть множество Y выпукло, а функция вероятности
y → Pϕ(y) квазивогнута. Тогда в условиях теоремы 1 при выполнении нера-
венства (5) справедливо неравенство
({
(
)
}
{
})
(n)
(12)
P Conv Y(n)
ϕ,α+ε
∩
Y
⊂Yϕ,α
∩ Yϕ,α ∩Y
⊂Yϕ
,α-ε
≥ β.
Доказательство. Поскольку функция y → Pϕ(y) является квазиво-
гнутой, все ее верхние множества уровня вида
{y ∈ Y | Pϕ(y) ≥ δ},
где δ ∈ [0, 1], к которым относится и множество Yϕ,α, выпуклы. Поэтому вы-
пуклая оболочка любых элементов множества Yϕ,α также содержится в нем,
а значит,
{
}
{
(
)
}
(n)
(13)
Y(n)
∩
Y ⊂Yϕ,α
⊂ Conv Yϕ
∩
Y
⊂Yϕ,α
ϕ,α+ε
,α+ε
Из того что выпуклая оболочка элементов множества содержит эти элементы
и из (13) следует равенство
{
}
{
(
)
}
(n)
Y(n)
∩
Y ⊂Yϕ,α
= Conv Yϕ
∩
Y
⊂Yϕ,α
,
ϕ,α+ε
,α+ε
обеспечивающее измеримость события, вероятность которого рассматривает-
ся в (12). Из теоремы 1 следует, что при выполнении неравенства (5)
({
(
)
}
{
})
(n)
P Conv Y(n)
∩
Y
⊂Yϕ,α
∩ Yϕ,α ∩Y
⊂Yϕ
=
ϕ,α+ε
,α-ε
({
}
{
})
(n)
=P Y(n)
ϕ,α+ε
∩
Y ⊂Yϕ,α
∩ Yϕ,α ∩Y
⊂Yϕ
,α-ε
≥ β.
Следствие доказано.
5. Уменьшение объема выборки с помощью учета ядра вероятностной меры
Пусть выполнены условия леммы 2. Тогда в качестве внешней аппрокси-
мации доверительного множества поглощения можно взять множество
Yϕ,α = Yϕ(Kα),
89
где Kα ⊂ Kα. В силу определения множества Yϕ(Kα) для всех x ∈ Kα вы-
полнено неравенство Φ(y, x) ≤ ϕ, а значит,
Kα ⊂ {Φ(y,X) ≤ ϕ} .
Поэтому
Pϕ(y) = γ + (1 - γ)P0 {Φ(y,X) ≤ ϕ | X ∈ Kα} ,
где γ = P0(Kα). Таким образом, для оценивания функции вероятности Pϕ(y)
можно использовать выборку, закон распределения которой совпадает с
условным законом распределения случайного вектора X относительно собы-
тия {X ∈ Kα}. Последовательность независимых случайных векторов, рас-
пределенных по указанному закону, обозначим через {Xn}, n ∈ N. Используя
данную выборку, можно построить оценку функции вероятности
∑
(
)
P(n)ϕ(y) ≜ γ +
χ(-∞,ϕ] Φ(y,Xk)
n
k=1
и оценку доверительного множества поглощения
{
}
Y(n)ϕ,α ≜ y ∈ Yϕ,α \ Yϕ,α
P(n)ϕ(y) ≥ α
∪Yϕ,α.
Сформулируем теорему 2, аналогичную теореме 1, для уточненной оценки
доверительного множества поглощения.
Теорема 2. Пусть выполнены условия леммы 2, β ∈(0,1), ε>0
Y
конечное подмножество Yϕ,α \ Yϕ,α. Тогда при
ln
Y | - ln(1 - β)
(14)
n≥
(1 - γ)2
2ε2
выполнено неравенство
({
}
{
})
(15)
P
Y(n)ϕ,α+ε
Y ⊂Yϕ,α
∩ Yϕ,α
Y
Y(n)
≥ β.
ϕ,α-ε
Доказательство. Введем обозначения
{
}
Pϕ,Kα (y) ≜ P0 Φ(y,X) ≤ ϕ | X ∈ Kα
,
∑
(
)
1
P(n)ϕ(y) ≜
χ(-∞,ϕ] Φ(y,Xk)
n
k=1
Справедливы включения
{
}
⋃
{
}
Y(n)
∩
Y ⊂Yϕ,α
=
P(n)ϕ(y) ≥ α + ε
=
ϕ,α+ε
y
Y \Yϕ,α
90
⋃
{
}
=
γ+(1-γ
P(n)ϕ(y) ≥ α + ε
⊂
y
Y \Yϕ,α
⋃
{
}
⊂
γ+(1-γ
P(n)ϕ(y) ≥ γ + (1 - γ)P
ϕ,Kα
(y) + ε
=
y
Y \Yϕ,α
{
}
⋃
ε
=
P(n)ϕ(y) ≥ Pϕ,K
(y) +
α
1-γ
y
Y \Yϕ,α
Аналогично получаем, что
{
}
⋃
{
}
Yϕ,α
Y
Y(n)
=
P(n)ϕ(y) < α - ε
⊂
ϕ,α-ε
y
Y ∩Yϕ,α
{
}
⋃
ε
⊂
P(n)ϕ(y) ≤ Pϕ,K
(y) -
α
1-γ
y
Y ∩Yϕ,α
Учитывая, что случайная величина
ϕ (y) распределена по биномиаль-
ному закону, для которой выполнены неравенства, аналогичные (7) и (8), из
полученных включений следует, что
}
({
{
})
P
Y(n)ϕ,α+ε
Y ⊂Yϕ,α
∪
Yϕ,α
Y ⊂Y(n)
≤
ϕ,α+ε
{
}
{
}
≤P
Y(n)ϕ,α+ε
Y ⊂Yϕ,α
+P
Yϕ,α
Y ⊂Y(n)
≤
ϕ,α+ε
2nε2
(1-γ)2
≤
Y \Yϕ,α|e-(1-γ)2 +
Y ∩Yϕ,α|e
=
Y |e
(1-γ)2 .
Решая неравенство
2nε2
1-
Y |e- (1-γ)2 ≥ β,
гарантирующее выполнение утверждения теоремы 2, получаем значения n,
удовлетворяющие неравенству (14).
Теорема 2 доказана.
6. Уменьшение объема выборки для звездчатой
функции потерь
Дальнейшее улучшение оценки объема выборки проведем для случая, ко-
гда функция потерь (y, x) → Φ(y, x) является звездчатой по y при всех x.
Таковыми, например, являются системы с линейной по y функцией потерь
c⊤(x)y, если y ≥ 0, c(x) ≥ 0.
91
Определение 2. Функция f с действительными значениями, опреде-
ленная на выпуклом множестве Y , таком что 0 ∈ Y , называется звездча-
той, если функция
µ → f(µy)
является неубывающей по µ ∈ [0, 1] для всех y, являющихся внутренними
точками множества Y .
Будем считать, что Y ⊂ R2 компактное множество. Пусть
D = max∥y∥.
y∈Y
Построим конечное множеств
Y следующим образом:
{
iD
2(j - 1)π
(16)
Y = yij ≜ (ri cosθj,ri sinθj) | ri =
, θj =
,
M
N
}
i = 1,M, j = 1,N
∩ Y,
где N, M выбранные натуральные константы.
Из леммы 2 следует, что вероятность
({
}
{
})
(n)
P Y(n)
∩
Y ⊂Yϕ,α
∩ Yϕ,α ∩Y
⊂Yϕ
≥β
ϕ,α+ε
,α-ε
при
ln(MN) - ln(1 - β)
n≥
2ε2
Однако данную оценку можно существенно улучшить.
Теорема 3. Пустьβ∈(0,1),ε>0
Y - множество, определенное в (16).
Тогда при
ln(2N) - ln(1 - β)
(17)
n≥
2ε2
выполнено неравенство
({
}
{
})
(n)
(18)
P Y(n)
∩
Y ⊂Yϕ,α
∩ Yϕ,α ∩Y
⊂Yϕ
≥ β.
ϕ,α+ε
,α-ε
Доказательство. Из того что функция потерь является звездчатой,
следует, что
(19)
Pϕ(yij) ≥ Pϕ(yi+1,j
),
(20)
P(n)ϕ(yij) ≥ P(n)ϕ(yi+1,j)
92
для всех i = 1, M - 1 и при всех реализациях выборки. Пусть
i1(j) ≜ max{i | Pϕ(yij) < ϕ - ε},
i2(j) ≜ min{i | Pϕ(yij) ≥ ϕ + ε}.
Если указанный минимум или максимум не достигается при некотором j,
положим по определению i1(j) = 0 или i2(j) = 0. Пусть
{
}
{
}
Y ≜ yi1(j),j | j = 1,N,i1(j) = 0
∪ yi2(j),j | j = 1,N,i2(j) = 0
Заметим, что
Y | ≤ 2N.
В силу отмеченных свойств монотонности (19) и (20) справедливо равен-
ство событий
{
}
{
}
(n)
Y(n)
ϕ,α+ε
∩
Y ⊂Yϕ,α
∩ Yϕ,α ∩Y
⊂Yϕ
,α-ε
=
(21)
{
}
{
}
(n)
= Y(n)
∩
Y ⊂Yϕ,α
∩ Yϕ,α ∩Y
⊂Yϕ
ϕ,α+ε
,α-ε
Применяя теорему 1 для конечного множеств
Y , получаем, что при
ln(2N) - ln(1 - β)
n≥
2ε2
выполнено неравенство
({
}
{
})
(n)
(22)
P Y(n)
∩
Y ⊂Yϕ,α
∩ Yϕ,α ∩Y
⊂Yϕ
≥ β.
ϕ,α+ε
,α-ε
Из равенства (21) и неравенства (22) следует утверждение теоремы 3.
Если дополнительно к условиям теоремы 3 выполнены условия теоремы 2,
то при
ln(2N) - ln(1 - β)
n≥
(1 - γ)2
2ε2
выполнено неравенство (15), а если при этом функция вероятности y → Pϕ(y)
квазивыпукла, то более того
({
(
)
}
{
})
(n)
P Conv
Y(n)
∩
Y
⊂Yϕ,α
∩ Yϕ,α
Y ⊂Y
≥ β.
ϕ,α+ε
ϕ,α-ε
Для решения задачи построения доверительного множества поглощения в
рассматриваемом случае может быть использован следующий алгоритм.
Алгоритм 1.
1. Сгенерировать
⌈
⌉
ln
Y | - ln(1 - β)
n=
(1 - γ)2
2ε2
93
реализаций случайный величины, распределенной по условному закону рас-
пределения случайного вектора X относительно события X ∈ Kα. (⌈z⌉ обо-
значает минимальное целое число не менее z.)
2. Присвоить j := 1.
3. Пока j ≤ N:
а) найти с помощью метода дихотомии максимальный r ∈ R, такой
что
ϕ
((r cos(θj), r sin(θj ))) ≥ α + ε, и минимальный
r ∈ R, такой что
ϕ
((rcos(θj), rsin(θj ))) < α - ε.
б) включить точки (r cos(θj ), r sin(θj )) для r ≤ r во внутреннюю аппрок-
симацию доверительного множества поглощения, а для r ≤ r во внешнюю
аппроксимацию.
в) j := j + 1.
Замечание 1. Если построение ядра вероятностной меры Kα и даже
его непустой внутренней аппроксимации Kα является затруднительным, то
можно считать, что Kα = ∅, γ = 0. В этом случае на шаге 1 алгоритма 1
вместо условного закона распределения рассматривается безусловный закон
распределения случайного вектора X.
Замечание 2. Аналогичный алгоритм можно предложить и в простран-
ствах большей размерности, но при этом придется отказаться от построения
равномерной сетки.
7. Пример
Рассмотрим простейшую модель экономической системы производства и
потребления. Предположим, что для производства продукции двух видов мо-
жет быть закуплено сырье трех типов. Через v ≜ (v1, v2, v3)⊤ обозначим век-
тор, в котором vi объем закупаемого сырья i-го типа, i ∈ {1, 2, 3}. Цены на
каждый из видов сырья образуют вектор c ≜ (c1, c2, c3)⊤. Технологию произ-
водства описывает матрица B ≜ (bij ), i ∈ {1, 2}, j ∈ {1, 2, 3}, в которой вели-
чина bij показывает количество i-го вида продукции, получаемого из едини-
цы сырья j-го типа. Спрос на продукцию складывается из двух компонент.
Первая компонента соответствует спросу, возникающему вследствие заранее
подписанных договоров на поставку продукции, и поэтому является детер-
минированной. Для компоненты спроса введем обозначение
{
}
y = (y1,y2)⊤ ∈ Y = y ∈ R2
|0≤y1 ≤ y1, 0≤y2 ≤ y2
Вторая компонента X = (X1, X2)⊤ случайна, ее реализации обозначены че-
рез x = (x1, x2)⊤. Случайность спроса связана с непредсказуемостью поведе-
ния потребителей продукции. Необходимо удовлетворить весь возникающий
спрос. Тогда потери, связанные с функционированием системы, описываются
функцией
{
}
Φ(y, x) = min c⊤v | Bv ≥ x + y, v ≥ 0
v∈R3
94
Требуется определить, при каких значениях y ∈ Y потери при функцио-
нировании системы не превысят величину ϕ с вероятностью α, т.е. построить
доверительное множество поглощения.
Переходя к двойственной задаче, получаем, что
{
}
Φ(y, x) = max (x + y)⊤λ | B⊤λ ≤ c, λ ≥ 0
λ∈R2
Через λj, j = 1, J, обозначим вершины множества
{
}
Λ ≜ λ ∈ R2 | B⊤λ ≤ c, λ ≥ 0
Тогда функцию потерь можно записать в виде
{
}
Φ(y, x) = max (x + y)⊤λj
j=1,J
Заметим, что полученная функция является выпуклой по совокупности ар-
гументов и звездчатой по y.
Решим задачу для следующих модельных данных:
c = (8;17;11)⊤, ϕ = 100,
y1 = 20,
y2 = 20,
(
)
1
2
1
B=
1
3
2
Пусть компоненты случайного вектора X независимы и распределены по нор-
мальному закону X1 ∼ N (5, 1), X2 ∼ N (6, 4).
Множество Λ содержит пять вершин:
λ1 = (0;0)⊤, λ2 = (0;5,5)⊤, λ3 = (1;5)⊤, λ4 = (7;1)⊤, λ5 = (8;0)⊤.
Для построения детерминированных аппроксимаций доверительного мно-
жества поглощения введем случайный вектор
X≜ (X1,X2)⊤, распределен-
ный по стандартному нормальному закону. Реализации этого случайного век-
тора будем обозначать через x ≜ (x1, x2). Случайный векторX свяжем с век-
тором X соотношениями
X1 = 5 +X1, X2 = 6 + 2X2.
Тогда можно ввести функцию потерь
(
)
Φ(y, x) ≜ Φ y, (5 + x1, 6 + 2x2)⊤
,
значения которой совпадают с исходной функцией потерь. Для вероятностной
меры, порожденной двумерным стандартным нормальным распределением,
известно, что α-ядро является шаром радиуса, равного квантили стандартно-
го нормального распределения уровня α, а доверительный шар имеет радиус,
равный квадратному корню из квантили уровня α распределения χ2(2).
95
y2
12
10
8
6
4
2
0
1
2
3
4
5
6
y1
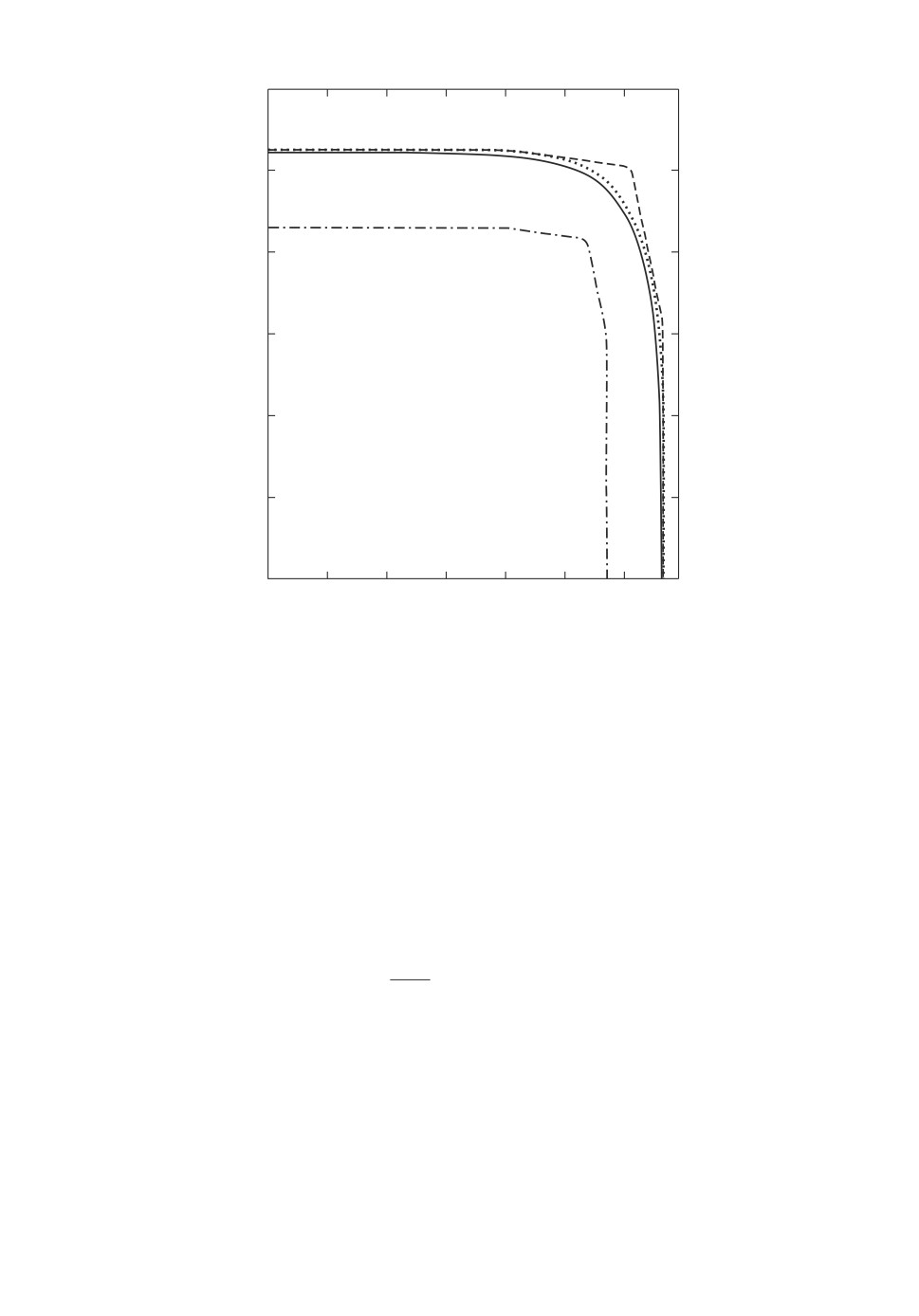
Рис. 1. Аппроксимации доверительного множества поглощения при α = 0,8.
Вычисления были проведены для уровней α = 0,8 и α = 0,9. Их результаты
представлены на рис. 1 и 2.
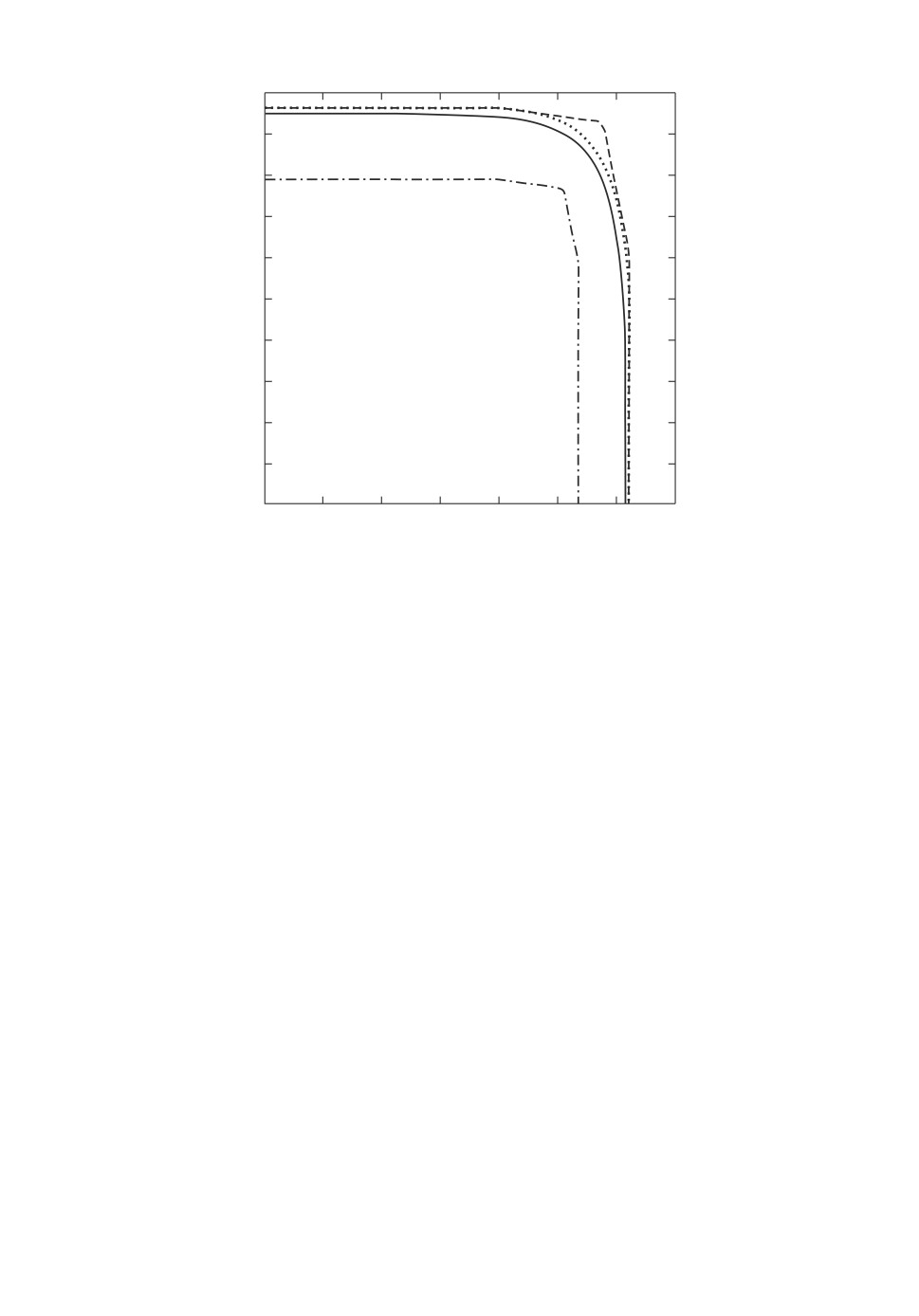
Штриховой линией обозначена граница внешней аппроксимации довери-
тельного множества поглощения, полученной с помощью ядра вероятностной
меры. Штрихпунктирной линией обозначена граница внутренней аппрокси-
мации доверительного множества поглощения, полученной с помощью дове-
рительного шара.
Статистическая аппроксимация строилась для уровня доверительной ве-
роятности β = 0,99 при ε = 0,01. Для построения аппроксимаций доверитель-
ного множества поглощения использовался алгоритм 1 при N = 400, но в силу
того что множество Y целиком содержится в первой координатной четверти,
рассматривались значения j = 1,Ń ,Ń = 101, что позволило уменьшить объ-
ем используемой выборки. Если не учитывать вероятностную меру α-ядра,
то для аппроксимации задачи необходим объем выборки n = 49568. Если ис-
пользовать условное распределение, то при α = 0,8 требуется объем выборки
n = 24411, а при α = 0,9 ее объем можно уменьшить до n = 9593.
На рис. 1 и 2 сплошной линией изображена внутренняя статистическая
аппроксимация доверительного множества поглощения, а отмеченные точ-
ки с вероятностью β являются внешними по отношению к доверительному
множеству поглощения. Полученные внешняя и внутренняя аппроксимации
близки друг к другу, что подтверждает эффективность разработанного ме-
96
y2
10
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
y1
Рис. 2. Аппроксимации доверительного множества поглощения при α = 0,9.
тода построения статистических аппроксимаций доверительного множества
поглощения.
Заметим, что в сравнении с предложенным в статье методом решения за-
дачи непосредственное статистическое оценивание значений функции веро-
ятности в большом количестве точек из множества Y приводит к гораздо
большему объему вычислений. Для получения аналогичных по точности ре-
зультатов в каждой точке конечного подмножеств
Y множества Y необхо-
димо провести около 2300 вычислений. При N = 100, M = 100 это приводит
к необходимости моделирования 23 · 106 реализаций случайных факторов.
8. Заключение
В статье разработан статистический подход к построению внутренней и
внешней статистических аппроксимаций доверительного множества погло-
щения. Получены теоретические оценки достаточного объема выборки для
построения аппроксимаций некоторого конечного множества начальных по-
зиций системы. Отметим, что данный объем выборки одновременно гаранти-
рует с заданной вероятностью то, что два построенных множества являются
внутренней и внешней аппроксимациями заданного конечного подмножества
истинного доверительного множества поглощения. Предложены условия, при
которых можно построить внутреннюю аппроксимацию самого доверитель-
ного множества поглощения, а не его конечного подмножества. На численном
примере показано, что указанные аппроксимации строятся при приемлемом
объеме выборки. При этом обеспечивается близость внутренней и внешней
97
аппроксимаций друг к другу. Конечно, для ряда задач достаточный объем
выборки может быть уменьшен. Описание классов таких задач может яв-
ляться предметом дальнейших исследований.
СПИСОК ЛИТЕРАТУРЫ
1.
Кибзун А.И., Кан Ю.С. Задачи стохастического программирования с вероят-
ностными критериями. М.: Физматлит, 2009.
2.
Prékopa A. Stochastic Programming. Dordrecht-Boston: Kluwer, 1995.
3.
Тамм Э. О квазивыпуклости функций вероятности и квантили // Изв. АН
ЭССР, физ.-мат. 1976. Т. 25. № 2. С. 141-144.
4.
Кан Ю.С., Кибзун А.И. Свойства выпуклости функций вероятности и квантили
в задачах оптимизации // АиТ. 1996. № 3. С. 82-102.
Kan Yu.S., Kibzun A.I. Convexity Properties of Probability Functions and Quantiles
in Optimization Problems // Autom. Remote Control. 1996. V. 57. No. 3. P. 368-383.
5.
Van Ackooij W. Eventual Convexity of Chance Constrained Feasible Sets // Opti-
mization (J. Math. Programm. Oper. Res.). 2015. V. 64. No. 5. P. 1263-1284.
6.
Prékopa A. On Logarithmic Concave Measures and Functions // Acta Sci. Math.
(Szeged). 1973. V. 34. P. 335-343.
7.
Borell C. Convex Set Functions in d-Space // Period. Math. Hung. 1975. V. 6. No. 2.
P. 111-136.
8.
Норкин В.И., Роенко Н.В. α-вогнутые функции и меры и их приложения //
Кибернетика и системный анализ. 1991. № 6. С. 77-88.
Norkin V.I., Roenko N.V. α-Concave Functions and Measures and Their Applica-
tions // Cybern. Syst. Anal. 1991. V. 27. No. 6. P. 860-869.
9.
Lejeune M., Noyan N. Mathematical Programming Approaches for Generating p-Ef-
ficient Points // Eur. J. Oper. Res. 2010. V. 207 P. 590-600.
10.
Dentcheva D., Prékopa A., Ruszczynski A. On Convex Probabilistic Programming
with Discrete Distributions // Nonlinear Anal.-Theor. 2001. V. 47. No. 3. P. 1997-
2009.
11.
Van Ackooij W., Berge V, de Oliveira W., Sagastizábal C. Probabilistic Optimization
via Approximate p-Efficient Points and Bundle Methods // Comput. Oper. Res. 2017.
V. 77. P. 177-193.
12.
Lejeune M.A., Prékopa A. Relaxations for Probabilistically Constrained Stochastic
Programming Problems: Review and Extensions // Ann. Oper. Res. 2018 (online
13.
Вапник В.Н., Червоненкис А.Я. Теория распознавания образов (статистические
проблемы обучения). М.: Наука, 1974.
14.
Вапник В.Н., Червоненкис А.Я. О равномерной сходимости частот появления
событий к их вероятностям // Теория вероятн. и ее примен. 1971. Т. 16. № 2.
С. 264-279.
15.
Shapiro A. Monte Carlo Sampling Methods. / Ruszczynski A., Shapiro A. (eds.)
Handbooks in OR Handbooks in Operations Research and Management Science &
MS. V. 10. P. 353-425. North-Holland, Dordrecht, The Netherlands, 2003.
16.
Shapiro A., Dentcheva D., Ruszczynski A. Lectures on Stochastic Programming.
Modeling and Theory. Philadelphia: Society for Industrial and Applied Mathematics
(SIAM), 2014.
98
17. Kleywegt A.J., Shapiro A., Homem-De-Mello T. The Sample Average Approximation
Method for Stochastic Discrete Optimization // SIAM J. Optim. 2001. V. 12. No. 2.
P. 479-502.
18. Luedtke J. Ahmed S. A Sample Approximation Approach for Optimization with
Probabilistic Constraints // SIAM J. Optim. 2008. V. 19. No. 2. P. 674-699.
19. Кибзун А.И., Иванов С.В., Степанова А.С. Построение доверительного множе-
ства поглощения в задачах анализа статических стохастических систем // АиТ.
2020. № 4. С. 21-36.
Kibzun A.I., Ivanov S.V., Stepanova A.S. Construction of Confidence Absorbing Set
for Analysis of Static Stochastic Systems // Autom. Remote Control. 2020. V. 81.
No. 4. P. 589-601.
20. Васильева С.Н., Кан Ю.С. Аппроксимация вероятностных ограничений в зада-
чах стохастического программирования с использованием ядра вероятностной
меры // АиТ. 2019. № 11. С. 93-107.
Vasil’eva S.N., Kan Yu.S. Approximation of Probabilistic Constraints in Stochas-
tic Programming Problems with a Probability Measure Kernel // Autom. Remote
Control. 2019. V. 80. No. 11. P. 2005-2016.
21. Васильева С.Н., Кан Ю.С. Метод линеаризации для решения задачи квантиль-
ной оптимизации с функцией потерь, зависящей от вектора малых случайных
параметров // АиТ. 2017. № 7. С. 95-109.
Vasil’eva S.N., Kan Yu.S. Linearization Method for Solving Quantile Optimization
Problems with Loss Function Depending on a Vector of Small Random Parameters //
Autom. Remote Control. 2017. V. 78. No. 7. P. 1251-1263.
22. Ширяев А.Н. Вероятность. М.: МЦНМО, 2017.
Статья представлена к публикации членом редколлегии Б.М. Миллером.
Поступила в редакцию 02.03.2020
После доработки 18.05.2020
Принята к публикации 09.07.2020
99