Автоматика и телемеханика, № 12, 2020
Линейные системы
© 2020 г. ДАТ ВО КУОК (cuoi.di.em89@gmail.com),
А.А. БОБЦОВ, д-р техн. наук (bobtsov@mail.ru)
(Университет ИТМО, Санкт-Петербург)
АДАПТИВНЫЙ НАБЛЮДАТЕЛЬ ПЕРЕМЕННЫХ СОСТОЯНИЯ
ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ С ПАРАМЕТРАМИ,
ЗАДАННЫМИ НЕ ТОЧНО1
Рассматривается задача синтеза адаптивного наблюдателя переменных
состояния для линейных нестационарных систем. Допускается, что часть
параметров нестационарного объекта могут быть неизвестными числами,
умноженными на известные функции времени. Предлагаемый подход ба-
зируется на идентификационных методах адаптации. Другими словами,
основная идея заключается в преобразовании математической модели в
виде линейного нестационарного дифференциального уравнения к ста-
тической линейной регрессионной модели, содержащей неизвестные па-
раметры. При этом в качестве неизвестных параметров упомянутой ре-
грессионной модели, выступают как неизвестные параметры объекта, так
и начальные условия переменных состояния. Далее, с использованием
стандартных градиентных методов или других подходов параметриче-
ской идентификации осуществляется оценивание неизвестных парамет-
ров регрессионной модели и строится наблюдатель. Представленные ре-
зультаты компьютерного моделирования иллюстрируют достижение за-
данной цели синтеза наблюдателя переменных состояния.
Ключевые слова: линейные нестационарные системы, наблюдатели пере-
менных состояния, идентификация параметров.
DOI: 10.31857/S0005231020120065
1. Введение
В статье рассматривается новый метод синтеза наблюдателей переменных
состояния для линейных нестационарных систем. Хотя данная проблематика
не является новой, она до сих пор активно исследуется. Однако, с точки
зрения авторов, на текущий момент универсальных подходов практически не
существует. На сегодняшний день в современной научной литературе хорошо
зарекомендовал себя универсальный подход, предусматривающий решение
матричного дифференциального уравнения Риккати (см, например, [1, 2]).
Суть этого подхода заключается в следующем. Рассматривается линейная
нестационарная система вида
v = M (t)v + U,
w = Lv,
1 Данная статья выполнена при финансовой поддержке Министерства науки и высшего
образования РФ, паспорт госзадания № 2019-0898.
100
для которой синтезируется наблюдатель
v = Mv + U - HLT(Lv - w),
где v(t) ∈ Rn - неизмеряемый вектор переменных состояния, v(t) - текущая
оценка v(t), w(t) - измеряемый выход, матрица H(t) является решением диф-
ференциального матричного уравнения Риккати
H
= HMT + MH - HLTLH + Q.
Хорошо известно (см., например, [1, 2]), что данный наблюдатель обес-
печивает асимптотическую сходимость, если система является равномерно
наблюдаемой, т.е. существуют положительные числа T0, δ1 и δ2, такие что
для любого момента времени t выполняется неравенство
∫
δ1I ≤
XT(t,τ)LTLX(t,τ)dτ ≤ δ2I,
t
где X(·, ·) - переходная матрица системы.
Однако реализация подобных наблюдателей имеет ряд недостатков. Преж-
де всего, это вычисление матрицы H, требующее решения онлайн n диффе-
ренциальных уравнений с квадратичными членами, которые могут быть чув-
ствительны к численным методам. Еще одним существенным недостатком яв-
ляется необходимость точного знания всех параметров объекта управления.
В данной статье предлагается новый подход, позволяющий синтезировать на-
блюдателей для систем, в которых некоторые параметры являются частично
неизвестными.
2. Постановка задачи
Рассмотрим линейный нестационарный полностью управляемый и наблю-
даемый одноканальный объект управления вида
(1)
x(t) = A(t)x(t) + b(t)u(t),
(2)
y(t) = cT
(t)x(t),
где x(t) ∈ Rn - неизмеряемый вектор переменных состояния; A(t), b(t) и c(t) -
нестационарные матрицы с частично известными коэффициентами; y(t)
и u(t) - соответственно измеряемые выход и сигнал управления.
Ставится задача синтеза наблюдателя переменных состояния
(3)
x (t) = f(y, u),
обеспечивающего для системы (1), (2) достижение целевого условия
(4)
lim
x(t) = 0,
t→∞
где x(t) = x(t) - x(t).
Решение задачи синтеза наблюдателя (3) для полностью управляемого и
наблюдаемого объекта (1), (2), обеспечивающего выполнение (4), будет обес-
печиваться при выполнении следующих предположений.
101
Предположение 1. Матрица A(t) имеет структуру
A(t) = A0 (t) + g(t)cT (t),
где A0(t) - нестационарная матрица с известными параметрами; g(t) - вектор
неизвестных параметров, элементы которого заданы в виде
gi(t) = aisi(t),
где ai - неизвестное число, но si(t) - известная функция.
Предположение 2. Векторы b(t) и c(t) имеют вид
(5)
b (t) = βb0
(t),
(6)
c(t) = σc0
(t),
где b0(t) и c0(t) - известные функции; β > 0 и σ > 0 - неизвестные числа.
Замечание 1. Следует отметить, что структуры (5), (6) можно было бы
обобщить до уровня
bi(t) = βib0i(t),
ci(t) = σic0i(t),
где βi, σi - неизвестные числа и βib0i(t), c0i(t) - известные функции. Однако в
этом случае задача идентификации существенно усложняется из-за большо-
го количества настраиваемых параметров, а содержательная идея подхода
синтеза наблюдателя переменных состояния может исчезнуть за большим
числом математических манипуляций.
3. Синтез адаптивного наблюдателя
Рассмотрим новый метод синтеза наблюдателя для объекта управления
(1), (2). Для синтеза наблюдателя будем использовать идеи, опубликованные
в [3, 4]. Рассмотрим уравнение (1) при структурных предположениях
A(t) = A0 (t) + g(t)cT (t) ,
b (t) = βb0 (t) .
Тогда (1) примет вид
(
)
(7)
x=
A0 + gcT
x+βb0u=A0x+gy+βb0
(t)u.
Для системы (7) введем в рассмотрение новый вектор ξ = col{x, a, β}, где
a = col{a1,...,an} - вектор неизвестных постоянных параметров. Тогда (7)
можно записать в виде
A0
yΩ b0u
x
(8)
˙ξ = F (t)ξ =
0
0
0
a
,
0
0
0
β
(9)
y=rTξ,
[
]
где матрица Ω = diag{s1 (t) , . . . , sn (t)} и rT =
cT
0
0
102
Введем в рассмотрение новую переменную z(t), являющуюся решением
уравнения
(10)
Ż = F (t)z.
Рассмотрим вектор ошибок
(11)
e(t) = z (t) - ξ (t) .
Дифференцируя (11), получаем
(12)
ė(t) = F (t)e(t).
Сформируем фундаментальную матрицу решения уравнения (12)
Φ(t) = F (t)Φ (t),
где для простоты выберем Φ (0) = I.
Хорошо известно (см, например, [5]), что
e(t) = Φ (t) θ,
где θ = z (0) - ξ (0) .
Тогда из уравнения (11) следует
ξ (t) = z (t) - e (t) = z (t) - Φ (t) θ,
откуда легко видеть, что задача оценивания вектора ξ (t) может быть сведена
к идентификации вектора неизвестных параметров θ, т.е.
(13)
ξ (t) = z (t) - Φ (t)θ,
гдеθ - оценка θ.
Для идентификации вектора неизвестных параметров θ воспользуемся вы-
ражением (9). Подставляя в (9) слагаемое ξ (t) = z (t) - e (t), получаем
(14)
y (t) = rT (z (t) - e (t)) = rTz (t) - rTΦ (t) θ = σψ1 (t) - σψT2
(t) θ,
[
]
[
]
где ψ1 =
c0(t)T
0
0
z и ψ2 =
c0(t)T
0
0
Φ - соответственно скаляр и
вектор, полученные из уравнений
[
]
[
]
σψ1 = rTz =
σc0(t)T
0
0
z=σ
c0(t)T
0
0
z,
[
]
σψT2 = rTΦ = σ
c0(t)T
0
0
Φ.
Из (14) получаем классическую регрессионную модель вида
(15)
y=ψT
η,
где ψ = col{ψ1, -ψ2} - вектор известных функций и η = col{σ, σθ} - вектор
неизвестных постоянных параметров.
103
Для идентификации вектора неизвестных параметров η можно воспользо-
ваться стандартными процедурами, например градиентным алгоритмом вида
(16)
η = -kψψT
η+kψy,
где k > 0 - коэффициент настройки.
Из η = col{σ, σθ} следует, что для вычисления вектора θ необходимо вос-
пользоваться уравнением
(17)
θ =1 col(η2,..., ηn+1
).
η1
Из (17) следует, что для вычисленияθ требуется осуществлять деление на
функцию η1, которая может пересекать ноль. Данная проблема не является
тривиальной, но ее можно избежать, например используя алгоритм, опуб-
ликованный в [6]. Однако заметим, что если число σ известно, то данная
проблема существенно упрощается.
Утверждение. Рассмотрим систему (8), (9), полученную путем рас-
ширения объекта (1), (2). Пусть для оценивания вектора переменных со-
стояния ξ (t) используется уравнение (13) с настройкой вектора неизвест-
ных параметров вида (16), (17) при предположении, что вектор ψ удовле-
творяет условиям незатухающего возбуждения (см., подробнее, [7-9]). То-
гда
lim
ξ (t) - ξ (t) = 0.
t→∞
Доказательство. Рассмотрим вектор
ξ
ξ-ξ.
Поскольку
ξ (t) = z (t) - e (t) = z (t) - Φ (t) θ,
ξ (t) = z (t) - Φ (t) θ,
то дл
ξ имеем
ξ
ξ - ξ = -Φθ+ Φθ = -Φθ,
гдеθ =θ - θ.
Поскольку в рамках утверждения допускается, что вектор ψ удовлетворя-
ет условиям незатухающего возбуждения, то гарантируется экспоненциаль-
ная сходимость η к η = col{σ, σθ} . Так как η сходится экспоненциально к η,
то из уравнения (17) следует асимптотическая сходимостьθ к θ, откуда имеем
lim
Φθ = 0.
t→∞
104
Из последнего выражения следует
lim
ξ (t) - ξ (t) = 0,
t→∞
что и требовалось доказать.
Замечание 2. Следует отметить, что выбор в качестве Φ(0) единичной
матрицы не вносит никаких принципиальных изменений в алгоритм вычисле-
ния переменной ξ (t) и, как следствие, вектора x (t) . Разница будет состоять
в изменении уравнения
θ = z (0) - ξ (0)
на аналогичное уравнение вида
θ = Φ-1(0)(z (0) - ξ (0)),
что в свою очередь повлияет только на качество переходных процессов, но
не на сходимость оценк
ξ (t) к истинному значению ξ (t).
Замечание 3. Хорошо известно, что в случае градиентного алгоритма
настройки (16) вектор η экспоненциально сходится к η при условии незату-
хающего возбуждения. Более того, алгоритм (16) не дает возможности су-
щественного ускорения процессов идентификации за счет выбора коэффи-
циента настройки k > 0. Поэтому для обеспечения высокого быстродействия
оценивания параметров целесообразно воспользоваться другими подходами,
например методом DREM (см., например, [7]).
4. Пример
Для иллюстрации работоспособности предлагаемой схемы синтеза наблю-
дателя, а также для наибольшей прозрачности предлагаемого подхода рас-
смотрим пример. Пусть система (1), (2) имеет вид
[
]
[
][
]
[
]
x1
a1
1
x1
0
(18)
=
+
u,
x2
0
sin 2t
x2
1
(19)
y = 5x1,
где a1 - неизвестный постоянный параметр.
Легко видеть, что с помощью представленных далее простых манипуляций
система (18) может быть приведена к виду (8). Для этого рассмотрим новый
вектор переменных состояния ξ = [x1 x2 a1]T. Тогда легко видеть, что
модель (18), (19) можно записать в виде
(20)
ξ,
где
0
1
0,2y
0
F (t) =
0 sin2t
0
, G =
1
, rT = [5
0
0].
0
0
0
0
105
Далее рассмотрим динамическую систему, полностью эквивалентную (20),
Ż (t) = F (t) z (t) + G (t) u (t) .
Сформируем матрицу Φ(t) с единичными начальными условиями
Φ(t) = F (t)Φ (t)
и регрессионное уравнение для поиска вектора неизвестных параметров
(21)
y (t) = rT (t) z (t) - rT
(t) Φ (t) θ.
Из уравнения (21) получаем
(22)
q=ωT
θ,
где q = rT (t) z (t) - y(t) и вектор ωT = rT (t) Φ (t).
Для обеспечения быстродействия оценивания параметров и монотонности
их переходных процессов воспользуемся методом DREM (см., например, [7]).
Следуя [7], пропустим известные элементы регрессионной модели (22) через
блоки запаздывания [H (·)] (t) = (·) (t - τ), где τ ∈ R+. Тогда для (22) имеем
(23)
qfi = ωT
θ.
fi
Сформулируем на основе исходной регрессионной модели (22) и новой от-
фильтрованной регрессионной модели (23) расширенную модель
(24)
qe = Ae
θ,
где
q
ωT
θ1
qf1
ωTf
θ2
1
qe =
,
Ae =
,
θ=
.
qfn-1
ωTf
θn
n-1
Умножая (24) на алгебраическое дополнение Ae, получаем
Y = adjAeqe = Δθ,
откуда имеем скалярную модель вида
Yi = Δθi,
где Δ = det{Ae} - определитель матрицы Ae.
Оценку θi будем вычислять по формуле
(25)
dθi/dt = -kiΔ(Δθi - Yi
),
где ki - положительное число, увеличивая которое можно добиваться ускоре-
ния процессов сходимости неизвестных параметров к истинным значениям.
106
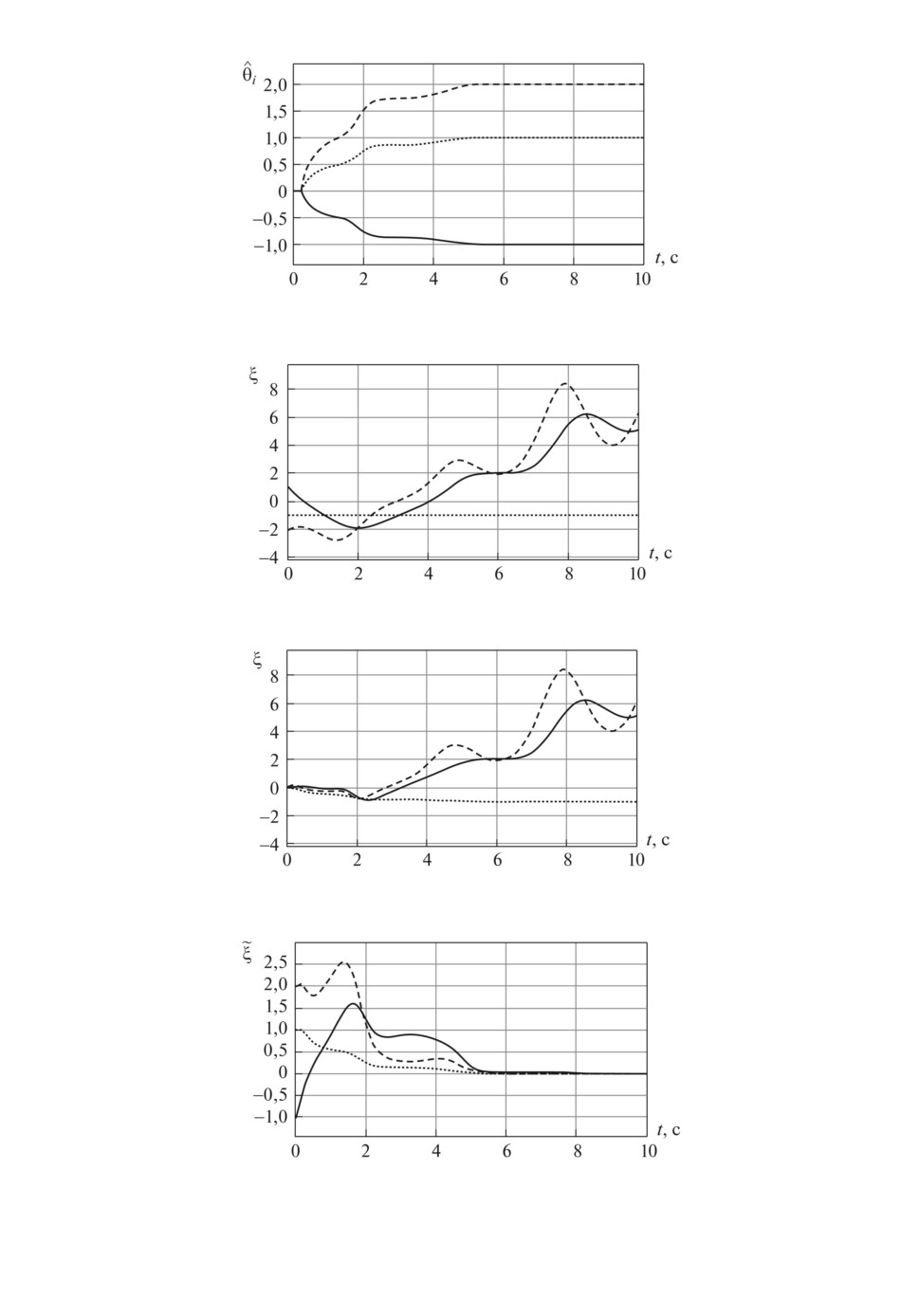
Рис. 1. Графики переходных процессов для
θi при ki = 10 (θ1 - сплошная
линия;
θ2 - штриховая линия;
θ3 - точечная линия).
Рис. 2. Графики переменных вектора ξ при ki = 10 (x1 - сплошная линия;
x2 - штриховая линия; a1 - точечная линия).
Рис. 3. Графики оценок переменных вектора
ξ при ki = 10 (x1 - сплошная
линия; x2 - штриховая линия; â1 - точечная линия).
Рис. 4. Графики оценок сигналов
ξ =
ξ- ξ при ki = 10 (x1 - сплошная
линия; x2 - штриховая линия; ã1 - точечная линия).
107
Рис. 5. Графики переходных процессов для
θi при ki = 1000 (θ1 - сплош-
ная линия;
θ2 - штриховая линия;
θ3 - точечная линия).
Рис. 6. Графики переменных вектора ξ при ki = 1000 (x1 - сплошная
линия; x2 - штриховая линия; a1 - точечная линия).
Рис. 7. Графики оценок переменных вектора
ξ при ki = 1000 (x1 - сплош-
ная линия; x2 - штриховая линия; â1 - точечная линия).
Рис. 8. Графики оценок сигналов
ξ=
ξ - ξ при ki = 1000 (x1 - сплошная
линия; x2 - штриховая линия; ã1 - точечная линия).
108
Для формирования оценок вектора ξ подставим полученные значения оце-
ниваемых параметров в уравнение
(26)
ξ (t) = z (t) - Ф (t)θ
Замечание 4. Легко показать, что для ошибки оценивания параметра
θi =θi - θi справедливо
˜
θi = -kiΔ2
θi,
oткуда легко видеть, что за счет увеличения числа ki можно добиваться уве-
личения скорости сходимостиθi к нулю.
При моделировании адаптивного наблюдателя (25), (26) были выбраны:
τ = 0,1, z (0) = 0, u = 1. На рис. 1-4 и 5-8 соответственно представлены гра-
фики переходных процессов дляθi, ξ
ξ,
ξ
ξ - ξ при ki = 10 и ki = 1000.
Из графиков переходных процессов можно видеть, что предлагаемый подход
синтеза адаптивного наблюдателя обеспечивает достижение целевого усло-
вия (4), демонстрируя улучшение быстродействия за счет увеличения коэф-
фициента ki.
5. Заключение
В статье предложен новый метод синтеза наблюдателя переменных состоя-
ния для линейной, полностью управляемой и наблюдаемой нестационарной
системы (1), (2). Допуская, что параметры системы (1), (2) могут быть неиз-
вестными, был синтезирован наблюдатель переменных состояния (13)-(17),
обеспечивающий асимптотическую сходимость настраиваемых оценок к ис-
тинным значениям. Данная задача была решена в некотором классе струк-
турных ограничений, представленных в предположениях 1 и 2. Для синтеза
наблюдателя был использован новый подход, предусматривающий преобра-
зование исходной модели объекта управления к линейной регрессионной мо-
дели вида (14), (15). Представленные в статье результаты компьютерного
моделирования иллюстрируют работоспособность предложенного подхода и
демонстрируют хорошее качество переходных процессов.
В качестве перспектив развития рассмотренного подхода видится его рас-
ширение на класс многоканальных объектов управления. Рассмотрим много-
канальный объект вида
(27)
x(t) = A(t)x(t) + B(t)u(t) ,
(28)
y (t) = C (t) x (t) ,
где x(t) ∈ Rn - неизмеряемый вектор переменных состояния; A (t), B (t) и
C (t) - нестационарные матрицы соответствующих размеров; y(t) ∈ Rny и
u(t) ∈ Rnu - соответственно измеряемые выход и сигнал управления.
Действуя по аналогии с одноканальным случаем, будем предполагать (см.
предположения 1 и 2), что
A (t) = A0 (t) + Gs (t) C (t) , B (t) = βB0 (t) , C (t) = σC0(t)
109
и квадратная матрица Gs(t) = diag{g1(t), . . . , gn(t)} с элементами gi(t) =
= aisi(t). Тогда, следуя (13)-(17), с несущественными изменениями может
быть построен наблюдатель переменных состояния для объекта (27), (28).
Также дальнейшее развитие данного подхода может быть связано с услож-
нением предположений на структуру матрицы A(t) и на системы, подвержен-
ные влиянию внешних возмущающих воздействий.
СПИСОК ЛИТЕРАТУРЫ
1. Rugh W.J. Linear system theory. Prentice Upper Saddle River: Prentice Hall, 1996.
2. Rueda-Escobedo J., Ushirobira R., Efimov D., Moreno J. Gramian-Based Uniform
Convergent Observer for Stable LTV Systems with Delayed Measurements // Int. J.
3. Ortega R., Bobtsov A., Pyrkin A., Aranovskiy S. A Parameter Estimation Approach
to State Observation of Nonlinear Systems // Syst. Control Lett. 2015. V. 85. No. 11.
P. 8-94.
4. Ortega R., Bobtsov A., Dochain D., Nikolaev N. State Observers for Reaction Sys-
tems with Improved Convergence Rates // J. Process Control. 2019. V. 83. No. 11.
P. 53-62.
5. Демидович Б.П. Лекции по математической теории устойчивости. М.: Наука,
1967.
6. Bobtsov A.A., Miroshnik I.V. A Dynamic Adaptation Algorithm for Time-varying
Systems // Autom. Remote Control. 1999. V. 60. No. 12. 1773-1781.
7. Aranovskiy S., Bobtsov A., Ortega R., Pyrkin A. Performance Enhancement of Pa-
rameter Estimators via Dynamic Regressor Extension and Mixing // IEEE Trans.
Automat. Control. 2016. V. 62. No. 7. P. 3546-3550.
8. Мирошник И.В., Никифоров В.О., Фрадков А.Л. Нелинейное и адаптивное
управление сложными динамическими системами. СПб.: Наука, 2000.
9. Sastry S., Bodson M. Adaptive Control: Stability, Convergence and Robustness. Mi-
neola: Dover, 2011.
Статья представлена к публикации членом редколлегии С.А. Красновой.
Поступила в редакцию 12.04.2020
После доработки 02.07.2020
Принята к публикации 09.07.2020
110