Автоматика и телемеханика, № 12, 2020

Стохастические системы

(Институт проблем управления им. В.А. Трапезникова РАН, Москва),

А.В. ЛЕБЕДЕВ, д-р физ.-мат. наук (avlebed@yandex.ru)

(Московский государственный университет им. М.В. Ломоносова)

СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ДВУМЯ

ВХОДЯЩИМИ ПОТОКАМИ, АБСОЛЮТНЫМ ПРИОРИТЕТОМ

И СТОХАСТИЧЕСКИМ СБРОСОМ

Рассматривается однолинейная система массового обслуживания с на-

копителем неограниченной емкости, в которую с различными интенсивно-

стями поступают два пуассоновских потока заявок. Заявки первого типа

имеют абсолютный приоритет относительно заявок второго типа. Кроме

того, в момент окончания обслуживания приоритетная заявка с некото-

рой вероятностью может сбросить все неприоритетные заявки, находящи-

еся в очереди. Обcлуживание заявок обоих типов имеет экспоненциальное

распределение с разными параметрами. Представлены выражения для

вычисления стационарных вероятностей системы, вероятности обслужи-

вания неприоритетной заявки в терминах производящей функции и фор-

мула для среднего числа заявок второго типа.

Ключевые слова: система массового обслуживания, абсолютный приори-

тет, обобщенное обновление, стохастический сброс заявок.

DOI: 10.31857/S0005231020120077

1. Введение

Рассмотрим систему массового обслуживания (СМО) с двумя входящими

потоками, заявки первого потока имеют абсолютный приоритет относительно

заявок второго потока, причем в момент окончания обслуживания приори-

тетная заявка может с некоторой вероятностью сбросить все неприоритетные

заявки.

Подобное явление, когда заявка при уходе сбрасывает другие заявки из

накопителя, называется обновлением (renovation). Класс систем с обновлени-

ем возник в результате развития идей СМО с отрицательными заявками [1].

Разница в том, что отрицательные заявки представляют собой отдельный

тип заявок и “убивают” или выталкивают куда-то обычные заявки при своем

поступлении, а не уходе, причем сами не требуют обслуживания. Системам с

отрицательными заявками посвящена обширная литература, подробный об-

зор которой можно найти, например, в [2], начиная с самых ранних работ на

эту тему, или в [3], где обсуждаются более свежие публикации. В свою оче-

редь упомянем лишь некоторые статьи, отражающие различные направления

исследований. Так, в [4, 5] изучаются системы с отрицательными заявками и

111

ограниченным временем пребывания, в [6-10] представлены системы с отри-

цательными заявками и повторными обращениями, ряд работ [11-16] посвя-

щен изучению подобных систем в дискретном времени, кроме того известны

статьи, в которых рассматриваются системы с групповыми поступлениями

заявок, причем некоторые из них предполагают коррелированные входные

потоки [16-20], также стоит отметить ряд публикаций, освещающих характе-

ристики так называемых СМО с доходами [21-25], при этом выделенные ка-

тегории не исключают взаимных пересечений и наложений дополнительных

условий, так, например, в [6, 13, 16, 18, 20, 26] исследуемые системы подразу-

мевают еще и прогулки или отдых (vacations) приборов на периодах простоя.

Отметим также ряд последних зарубежных работ [27-29], где можно найти

соответствующую библиографию.

Одной из первых статей, посвященных системам с обновлением, была [30],

где стационарное распределение вероятностей было получено в терминах про-

изводящей функции. В более поздних публикациях [31-33] был предложен

другой метод нахождения искомых вероятностей и найдены некоторые вре-

менные характеристики. При этом было введено понятие обобщенного обнов-

ления, когда из накопителя сбрасываются не все заявки, а случайное число

с заданным распределением.

Заметим, что обобщенное обновление можно рассматривать как механизм

активного управления очередью (Active Queue Management, AQM). Такие ме-

ханизмы предполагают принятие решения об отказе заявке в обслуживании

в зависимости от состояния системы, с целью ограничения числа заявок в

очереди. Простейшей, но часто оптимальной оказывается пороговая страте-

гия управления [34, 35]. В других случаях широко используются различные

стохастические алгоритмы, например RED (Random Early Detection), соглас-

но которому вероятность отказа линейно возрастает на определенном проме-

жутке числа заявок. Обычно решение принимается в момент прихода заявки,

однако ничто не мешает его принимать и в момент ухода заявки (в отношении

имеющихся или будущих заявок). Следуя такому подходу, в [36] проведено

сравнение обобщенного обновления с RED-подобными алгоритмами. Основ-

ные результаты исследований по AQM можно найти в [37, 38].

Рассматриваемая в настоящей статье модель со стохастическим сбросом

также может рассматриваться как вариант AQM. В частности, модель эф-

фективно ограничивает число заявок 2-го типа, при любой интенсивности их

поступления система остается эргодической, что может быть важно в случае

DDoS-атак (Distributed Denial of Service attack) (см. далее).

Классическая система с двумя типами заявок и абсолютным приоритетом

была введена в [39]. Там, в частности, были выведены условие эргодично-

сти, вероятность простоя, среднее и дисперсия числа неприоритетных заявок

и др. Отметим, что понятие обновления может быть обобщено на системы

с приоритетами многими способами. Авторы будут придерживаться направ-

ления, заданного публикациями [40, 41], где предполагалось, что приоритет-

ные заявки (1-го типа) при уходе с некоторой вероятностью сбрасывают все

неприоритетные заявки (2-го типа). Таким образом, заявки 1-го типа отча-

сти играют роль отрицательных заявок в отношении заявок 2-го типа, но с

указанными выше различиями.

112

Практический интерес к перечисленным системам массового обслужива-

ния объясняется следующим. Во-первых, с помощью такого рода моделей

возможно проанализировать поведение компьютерных и телекоммуникаци-

онных систем в условиях потери данных, которые могут быть вызваны все-

возможными причинами, начиная с банальных поломок, оптимизации рабо-

ты подобным образом и заканчивая нетерпеливостью пользователей таких

систем [40]. Также механизм сброса может применяться с целью регулирова-

ния интенсивности потока данных и политики дифференцированного обслу-

живания пользователей [42, 43]. Все названные варианты могут действовать

в рамках различных стратегий AQM.

Кроме того, речь может идти и об анализе (мониторинге) угроз информа-

ционной безопасности, поскольку безопасность сети является довольно важ-

ной проблемой как с теоретической точки зрения, так и с точки зрения ин-

женерных приложений. Существует множество типов сетевых атак (вирусы,

черви, трояны, DDoS-атаки), которые могут вызывать значительные сбои и

создавать серьезные проблемы в работе компьютерных сетей. Большинство

исследований в этой области концентрируется на способах обнаружения атак

и ответных действиях, а работ, посвященных аналитическому изучению дан-

ной проблемы не так много, несмотря на то что это могло бы поспособство-

вать увеличению знаний о поведении вредоносных программ и соответствен-

но улучшить качество оценки их влияния на систему [44-47].

Таким образом, анализируемая авторами СМО может моделировать функ-

ционирование какой-либо информационной системы, которая подвергается

различного рода атакам с целью нарушения ее деятельности или получения

несанкционированного доступа к данным. В систему поступает обычный для

нее пользовательский поток запросов (заявки 2-го типа) и периодически при-

ходит условная “вирусная” заявка (заявка 1-го типа). В случае пассивной ата-

ки вредоносная заявка просто покидает систему. Либо эту ситуацию можно

расценить как то, что система безопасности угрозу распознала и обработа-

ла, не дав ей навредить. В противном случае, когда система безопасности не

справилась с угрозой либо атака оказалась активной, эта вредоносная заявка

сбрасывает весь поток “хороших” заявок.

Исследование рассматриваемой в статье системы было начато в [41], но

тогда удалось получить некоторые результаты¹ только для специального слу-

чая детерминированного сброса при уходе заявки (с вероятностью единица),

в том числе вывести формулу вероятности простоя. В [40] рассматривалась

аналогичная система с относительным приоритетом, однако она оказалась бо-

лее сложной для теоретического анализа. Заметим, что при малом среднем

времени обслуживания заявки 2-го типа характеристики систем с абсолют-

ным и относительным приоритетом должны быть близкими.

Поскольку терминология обновления систем с приоритетами пока не при-

нята, будем называть рассматриваемую модель системой со стохастическим

сбросом.

Отметим, что данная система является промежуточной между классиче-

ской системой с абсолютным приоритетом без сброса [39] и системой с детер-

¹ При этом в (4) и (17) были допущены логические ошибки.

113

минированным сбросом [41], поэтому можно ожидать, что ее характеристики

также окажутся промежуточными, а характеристики в крайних случаях мо-

гут быть получены соответствующими предельными переходами. Теоретиче-

ский и численный анализ подтверждают это предположение.

Итак, статья организована следующим образом: во втором разделе описа-

на математическая модель СМО и представлены формулы для распределения

числа заявок в системе, в третьем разделе описывается способ вычисления

вероятности простоя системы, в четвертом основное внимание уделено вы-

числению среднего числа заявок 2-го типа, в пятом нахождению вероятно-

сти обслуживания заявки 2-го типа, а в шестом разделе приведен численный

пример.

2. Математическая модель

В однолинейную систему массового обслуживания с накопителем неогра-

ниченной емкости поступают заявки двух типов. Входящие в систему потоки

являются пуассоновскими с интенсивностью λ₁ для заявок 1-го типа и ин-

тенсивностью λ₂ для заявок 2-го типа. Времена обслуживания заявок име-

ют экспоненциальное распределение с параметрами µ₁ и µ₂ соответственно.

Заявки 1-го типа имеют абсолютный приоритет по сравнению с заявками

2-го типа, т.е. при наличии в очереди заявок обоих потоков на обслужива-

ние выбирается приоритетная заявка, а неприоритетная заявка может быть

выбрана на обслуживание только в том случае, когда в очереди нет заявок

1-го типа. Кроме того, если в момент поступления приоритетной заявки на

обслуживании находится заявка 2-го типа, то ее обслуживание немедлен-

но прерывается и она возвращается в начало очереди, а заявка 1-го типа

поступает на прибор. Заявки одного потока обслуживаются в порядке по-

ступления. Более того, приоритетная заявка, находящаяся на приборе, мо-

жет в момент окончания обслуживания либо с вероятностью p просто поки-

нуть систему, либо с вероятностью q еще и сбросить все заявки второго типа

из накопителя, p + q = 1.

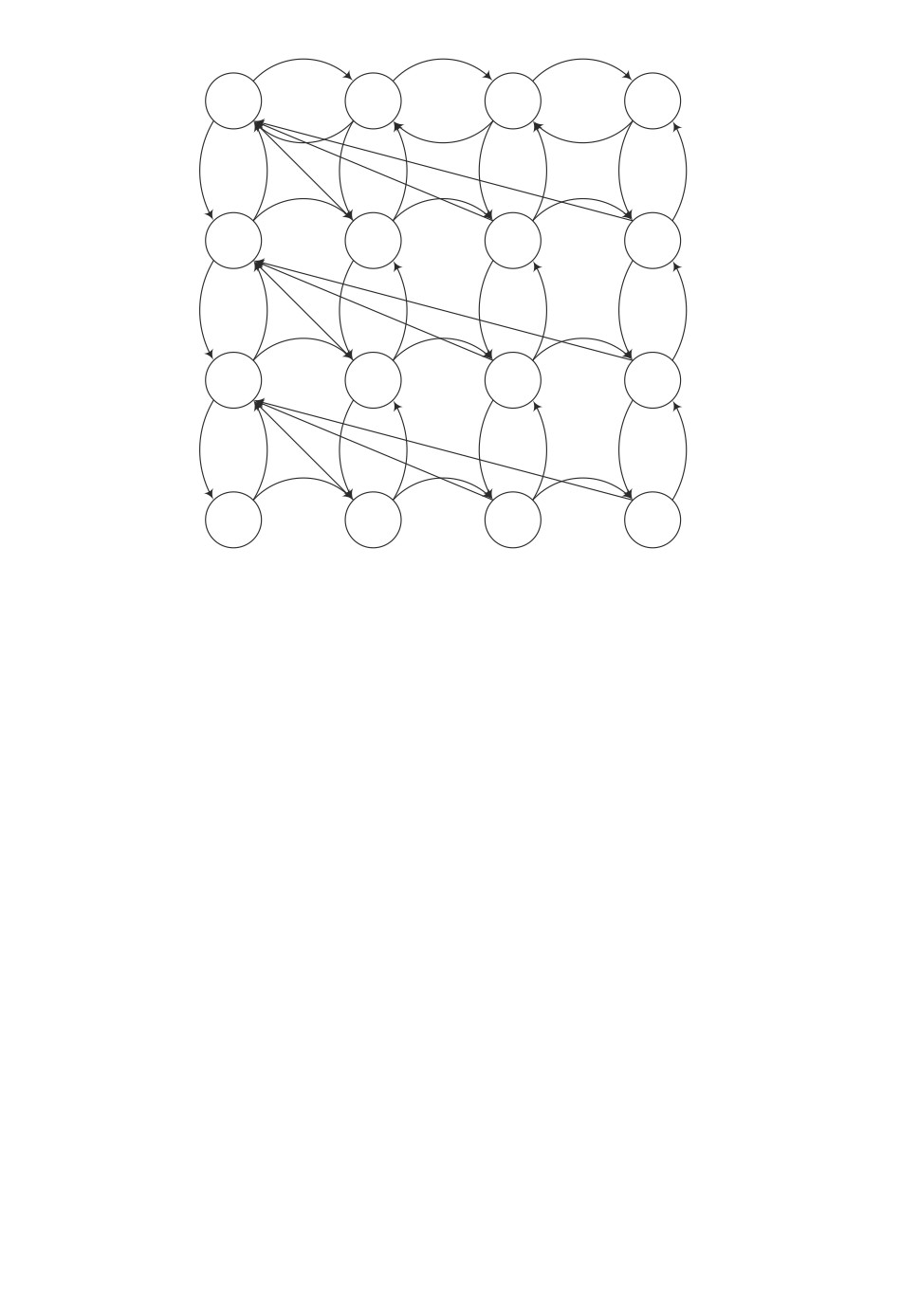
Функционирование представленной СМО можно описать марковским про-

цессом X(t) = {ν₁(t), ν₂(t)}, где ν₁(t) и ν₂(t) число заявок первого (i) и вто-

рого (j) типов, с дискретным множеством состояний X = {(i, j), i ≥ 0, j ≥ 0}

(рис. 1).

Зададимся вопросом об эргодичности системы. Поскольку заявки 2-го ти-

па никак не влияют на заявки 1-го типа, то поведение ν₁(t) будет таким

же, как в соответствующей системе M|M|1, с условием эргодичности ρ₁ < 1,

ρ_i = λ_i/µ_i, i = 1,2. При этом поскольку время от времени происходит пол-

ный сброс заявок 2-го типа (через промежутки времени с конечным сред-

ним), то ν₂(t) не может стремиться к бесконечности, независимо от ρ₂. Таким

образом, условием эргодичности системы оказывается ρ₁ < 1, в чем имеется

качественное различие с классической системой [39], где условием эргодич-

ности было ρ₁ + ρ₂ < 1. Далее будем считать условие ρ₁ < 1 выполненным

по умолчанию.

Обозначим через p_i,j, i ≥ 0, j ≥ 0 стационарную вероятность того, что в

системе находится i приоритетных заявок и j неприоритетных заявок. Ста-

114

l₂

0,0

0,1

0,2

0,3

m₂

qm₁

l₁

m₁

qm₁

l₁

pm₁

l₁

pm₁

l₁

pm₁

l₂

1,0

1,1

1,2

1,3

qm₁

l₁

m₁

qm₁

l₁

pm₁

l₁

pm₁

l₁

pm₁

l₂

2,0

2,1

2,2

2,3

qm₁

l₁

m₁

qm₁

l₁

pm₁

l₁

pm₁

l₁

pm₁

l₂

3,0

3,1

3,2

3,3

Рис. 1. Диаграмма интенсивностей переходов.

ционарное распределение существует и удовлетворяет системе уравнений рав-

новесия:

∑

(1)

(λ₁ + λ₂)p_0,0 = µ₁pp_1,0 + µ₂p_0,1 + µ₁q

p_1,j,

j=0

∑

(2)

(λ₁ + λ₂ + µ₁)p_i,0 = λ₁p_i-1,0 + µ₁pp_i+1,0 + µ₁q

p_i+1,j

i ≥ 1,

j=0

(3)

(λ₁ + λ₂ + µ₂)p_0,j = µ₁pp_1,j + λ₂p_0,j-1 + µ₂p_0,j+1

j ≥ 1,

(4)

(λ₁ + λ₂ + µ₁)p_i,j = µ₁pp_i+1,j + λ₁p_i-1,j + λ₂p_i,j-1

i, j ≥ 1.

Введем обозначения для маргинальных вероятностей:

∑

p_i,· =

p_i,j,

p_·,j =

p_i,j,

i, j ≥ 0.

j=0

i=0

Поскольку заявки 2-го типа никак не влияют на приоритетные заявки, то

распределение числа приоритетных заявок будет соответствовать распреде-

лению числа заявок в СМО типа M|M|1, т.е.

p_i,· = (1 - ρ₁)ρⁱ¹, i ≥ 0,

причем должно выполняться условие эргодичности ρ₁ < 1.

115

Далее введем обозначение для производящей функции

∑∑

(5)

B(u, v) =

p_i,juⁱv^j.

i=0 j=0

Тогда справедливо, что

∑

B(u, 0) =

p_i,0uⁱ,

i=0

∑

B(0, v) =

p_0,jv^j,

j=0

∑∑

∑

1-ρ₁

B(u, 1) =

p_i,juⁱ =

p_i,·uⁱ =

1-ρ₁u

i=0 j=0

i=0

∑∑

∑

B(1, v) =

p_i,jv^j =

p_·,jv^j.

i=0 j=0

j=0

Теперь найдем выражение для производящей функции. Для этого умножим

уравнения (1)-(4) на uⁱv^j и просуммируем по всем возможным значениям i

и j, т.е.

∑

(λ₁ + λ₂ + µ₁)B(u, v) - µ₁p_0,0 + (µ₂ - µ₁)

p_0,jv^j =

j=1

∑

= µ₁pp_1,0 + µ₂p_0,1 + µ₁q

p_1,ju + λ₁

p_i-1,0uⁱ + µ₁p

p_i+1,0uⁱ +

j=0

i=1

∑∑

∑

+µ₁q

p_i+1,juⁱ + µ₁p

p_1,jv^j

+λ₂

p_0,j-1v^j

+µ₂

p_0,j+1v^j +

i=1 j=0

j=1

∑∑

+µ₁p

p_i+1,juⁱv^j

+λ₁

p_i-1,juⁱv^j

+λ₂

p_i,j-1uⁱv^j.

i=1 j=1

После преобразований получим, что

(6)

B(u, v) =

(

)

µ1v(u - p) - µ2u(v - 1)

B(0, v) + µ₁qv(B(u, 1) - p_0,·) + µ₂p_0,0u(v - 1)

λ₁uv(1 - u) + λ₂uv(1 - v) + µ₁v(u - p)

Тогда распределение числа заявок, не обладающих приоритетом, описывает-

ся выражением



1 ∂^jB(1,v)

p_·,j =



∂v^j

v=0

116

l₂(1 - v) + m₁(1 - p)

u₂

-m₁p

Рис. 2. Иллюстрация к утверждению, что 0 < u₂(v) < 1.

а распределение числа заявок первого и второго типов определяется форму-

лой



∂^i+jB(u,v)



p_i,j =



i!j!

∂uⁱ∂v^j

u=v=0

Далее найдем нули знаменателя (6), т.е. получим корни квадратного трех-

члена относительно переменной u

√

λ₁ + λ₂(1 - v) + µ₁ ±

(λ₁ + λ₂(1 - v) + µ₁)² - 4λ₁µ₁p

(7)

u_1,2 = u_1,2(v) =

2λ₁

Докажем, что 0 < u₂(v) < 1 с учетом того, что ρ₁ = λ₁/µ₁ < 1. Для этого

рассмотрим поведение функции λ₁u(1 - u) + λ₂u(1 - v) + µ₁(u - p) из зна-

менателя (6). При u = 0 получаем -µ₁p < 0, при u = 1 имеем λ₂(1 - v) +

+µ₁(1 - p) > 0, 0 < p < 1. Поскольку графиком функции является парабола,

ветви которой направлены вниз (рис. 2), можем сделать вывод, что корень

квадратного трехчлена, лежащий в интервале от 0 до 1, существует, кроме

того, он будет являться меньшим корнем этого трехчлена.

В силу того что производящая функция B(u, v) является непрерывной

функцией при u, v ∈ [0, 1], при подстановке (u₂, v), 0 < u₂ < 1, в выраже-

ние (6) одновременно со знаменателем в ноль должен обращаться и числи-

тель. Следовательно, имеем

(

)

µ₁v(u₂ -p)-µ₂u₂(v -1)

B(0, v) + µ₁qv(B(u₂, 1) - p_0,·) + µ₂p_0,0u₂(v - 1) = 0,

где, напомним,

1-ρ₁

B(u₂, 1) =

p_0,· = (1 - ρ₁).

1-ρ₁u₂

Таким образом, выражение для B(0, v) примет вид

µ₁qρ₁u₂(ρ₁ - 1)v + (1 - ρ₁u₂)µ₂u₂(1 - v)p_0,0

(8)

B(0, v) =

(1 - ρ₁u₂)(µ₁v(u₂ - p) - µ₂u₂(v - 1))

и для полного решения задачи остается только найти вероятность простоя

системы p_0,0.

117

3. Вероятность простоя системы

Рассмотрим знаменатель выражения (8). Поскольку v ∈ [0, 1], то в край-

них точках отрезка выражение принимает значение µ₂u₂ > 0 при v = 0 и при

v=1

значение µ₁v(u₂ - p), определим его знак. В силу того что из знаме-

нателя (6)

λ₁u₂(1 - u₂) + λ₂u₂(1 - v) + µ₁(u₂ - p) = 0,

где λ₁u₂(1 - u₂) > 0 и λ₂u₂(1 - v) > 0, можем заключить, что µ₁(u₂ - p) < 0.

Это означает, что существует такое v^∗ ∈ (0, 1), при котором знаменатель (8)

обращается в ноль, а значит, и числитель (8) должен обращаться в ноль:

µ₁qρ₁u₂(v^∗)(ρ₁ - 1)v^∗ + (1 - ρ₁u₂(v^∗))µ₂u₂(v^∗)(1 - v^∗)p_0,0 = 0,

откуда с учетом 0 < u₂(v) < 1 получаем, что

∗

λ₁q(1 - ρ₁)v

(9)

p_0,0 =

µ₂(1 - ρ₁u₂(v^∗))(1 - v^∗)

Зная p_0,0, можем вычислить все стационарные вероятности и характери-

стики системы.

Теперь покажем, что поведение p_0,0 на обеих границах отрезка p ∈ [0, 1]

соответствует результатам, полученным ранее в [39, 41].

Случай 1. Пусть p → 0, тогда необходимо доказать, что

p_0,0 → p^(0)0,0 =λ1(1-ρ1)z2 ,

v^∗ → z₂,u₂ → 0,

µ₂

1-z₂

где выражение для z₂ имеет вид [41]:

√

λ₁ + λ₂ + µ₁ -

(λ₁ + λ₂ + µ₁)² - 4λ₂µ₂

(10)

z₂ =

2λ₂

При p → 0 для любого значения v выполняется u₂ → 0. Поэтому чтобы най-

ти v^∗, получим асимптотическое разложение выражения для u₂ с помощью

формулы Тейлора при p → 0

µ₁

(11)

u₂ =

p + o(p),

λ₁ + λ₂(1 - v) + µ₁

тогда

λ₁ + λ₂(1 - v)

(12)

p-u₂ =

p + o(p).

λ₁ + λ₂(1 - v) + µ₁

Далее приравниваем знаменатель в (8) к нулю и получаем

µ₂u₂

(13)

1-v

µ₁(p - u₂)

118

В правую часть полученного равенства подставляем асимптотические выра-

жения (11) и (12), откуда

µ₂

(14)

+ o(1),

1-v

λ₁ + λ₂(1 - v)

в результате после перехода к пределу при p → 0 получаем уравнение

λ₂v² - (λ₁ + λ₂ + µ₂)v + µ₂ = 0,

которое в точности соответствует уравнению из [41] для вычисления 0<z₂ <1.

Таким образом, из v^∗ → z₂, u₂ → 0 сходимость p_0,0 к p^(0)0,0 следует автомати-

чески.

Случай 2. Положим ρ₁ + ρ₂ < 1. Пусть p → 1, тогда необходимо доказать,

что

p_0,0 → p^(1)0,0 = 1 - ρ₁ - ρ₂, v^∗ → 1,u₂ → 1,

где выражение для p^(1)0,0 из [39]. Из того что p → 1 следует, что v^∗ → 1 и u₂ → 1.

Введем обозначение ε = 1 - v, тогда ε → 0, q → 0. Далее, воспользовавшись

аналогичным образом асимптотическим разложением u₂ с помощью форму-

лы Тейлора, можем записать, что

λ₂

µ₁

u₂ = 1 -

ε-

q + o(ε) + o(q).

µ₁ - λ₁

Тогда

λ₂

λ₁

p-u₂ =

ε+

q + o(ε) + o(q).

µ₁ - λ₁

Из равенства (13) при v → 1, u₂ → 1, p → 1 получаем, что

1-v∼

µ₁ (p - u₂),

µ₂

т.е. при ε, q → 0

(

)

µ₁

λ₂

λ₁

ε∼

ε+

µ₂

µ₁ - λ₁

следовательно,

λ₁µ₁

ε∼

µ₁µ₁ - λ₁µ₂ - λ₂µ₁

Тогда

λ₁q

µ₁µ₂ - λ₁µ₂ - λ₂µ₁

p_0,0 ∼

→

=1-ρ₁ -ρ₂ =p^(1)0,0,

µ₂ε

µ₁µ₂

что соответствует классическому результату [39].

119

4. Среднее число заявок 2-го типа в системе

Среднее число неприоритетных заявок в системе равно



∑



∂B(1,v)

N₂ =

jp_·,j =



∂v

j=0

v=1

После соответствующих преобразований получим



∂B(1,v)

∂B(0,v)

λ₂µ₁ + λ₁µ₂ - µ₁µ₂(1 - p_0,0)



∂v

µ²¹q

v=1

где



∂B(0,v)



∂v

v=1

′

(1)λ₁q(1 - ρ₁) + λ₁u₂(1)q(1 - ρ₁) + µ₂u₂(1)(1 - ρ₁u₂(1))p_0,0

µ₁(1 - ρ₁u₂(1))(p - u₂(1))

′

λ₁u₂(1)q(1 - ρ₁)[µ₁(p - u₂(1)) + µ₂u₂(1) - u₂(1)µ₁]

µ²¹(1 - ρ₁u₂(1))(p - u₂(1))²

′

(1)λ²¹u₂(1)q(1 - ρ₁)

µ²¹(1 - ρ₁u₂(1))²(p - u₂(1))

√

λ₁ + µ₁ -

(λ₁ + µ₁)² - 4λ₁µ₁p

u₂(1) =

2λ₁



(

)



λ₂(λ₁ + µ₁)



√

-λ₂

u^′2(1) =∂u2(v)∂v

2λ₁

(λ₁ + µ₁)² - 4λ₁µ₁p

v=1

Среднее время пребывания в системе неприоритетной заявки можно вы-

числить с помощью формулы Литтла, т.е. справедливо, что

N₂ = λ₂v₂,

где v₂

среднее время пребывания заявки 2-го типа в системе, тогда

N₂

v₂ =

=w₂ +

λ₂

µ₂

откуда среднее время пребывания неприоритетной заявки в очереди равно

w₂ = v₂ -

µ₂

Среднее число приоритетных заявок в системе, среднее время пребыва-

ния приоритетных заявок в очереди и в системе определяется с помощью

известных формул для СМО M|M|1 из-за отсутствия влияния на них заявок

второго типа.

120

5. Вероятность обслуживания заявки 2-го типа

Теперь определим вероятность обслуживания неприоритетной заявки. От-

метим, что это непростая задача, поскольку судьба заявки зависит не только

от состояния системы в момент ее поступления, но и от дальнейшего развития

событий.

Для этого введем величину s_i,j - вероятность того, что заявка второго

типа будет обслужена, если перед ней в очереди (с учетом заявки на приборе)

находится i приоритетных и j неприоритетных заявок.

Возможны следующие ситуации (рис. 3):

1) если в системе перед неприоритетной заявкой находятся i заявок первого

и j заявок второго типа, то с вероятностью λ₁/(λ₁ + µ₁) в систему может

поступить новая приоритетная заявка и занять место перед рассматри-

ваемой неприоритетной (не обязательно непосредственно перед ней), т.е.

приоритетных заявок станет (i + 1), либо с вероятностью µ₁/(λ₁ + µ₁) мо-

жет обслужиться заявка первого типа и при этом с вероятностью p просто

покинет систему, не сбрасывая неприоритетные заявки, тогда перед заяв-

кой второго типа станет (i - 1) приоритетных заявок (рис. 3,а);

2) если в системе перед неприоритетной заявкой находятся только j заявок

второго типа, то с вероятностью λ₁/(λ₁ + µ₂) в систему может поступить

приоритетная заявка и занять место перед рассматриваемой неприоритет-

ной, либо с вероятностью µ₂/(λ₁ + µ₂) может обслужиться заявка второго

типа (рис. 3,б );

3) если в системе перед неприоритетной заявкой нет других заявок, то с ве-

роятностью λ₁/(λ₁ + µ₂) в систему может поступить приоритетная заявка

и занять место перед рассматриваемой неприоритетной, либо с вероятно-

стью µ₂/(λ₁ + µ₂) заявка второго типа успеет успешно обслужиться.

Заметим, что поступления новых неприоритетных заявок в систему никак не

влияют на обслуживание неприоритетных заявок, уже находящихся в систе-

m₁p

------

l₁ + m₁

i - 1, j

i, j

i + 1, j

l₁

------

l₁ + m₁

m₂

------

l₁ + m₂

0, i - 1

0, j

1, j

l₁

------

l₁ + m₂

Рис. 3. Возможные изменения состояний СМО в условиях ожидания неприо-

ритетной заявки.

121

ме, поэтому эти события нигде не учитываются. Составим систему уравнений

λ₁

µ₁p

(15)

s_i,j =

s_i+1,j +

s_i-1,j

i ≥ 1,j ≥ 0,

λ₁ + µ₁

λ₁

µ₂

(16)

s_0,j =

s_1,j +

s_0,j-1,

j ≥ 1,

λ₁ + µ₂

λ₁

µ₂

(17)

s_0,0 =

s_1,0 +

λ₁ + µ₂

Будем искать решение (15) в виде

(18)

s_i,j = γⁱs_0,j

i ≥ 1,j ≥ 0,

тогда при подстановке (18) в (15) при i = 1 можем записать, что

λ₁

µ₁p

γ=

γ² +

λ₁ + µ₁

т.е. получаем квадратное уравнение относительно переменной γ

λ₁γ² - (λ₁ + µ₁)γ + µ₁p = 0.

Решением уравнения является

√

λ₁ + µ₁ ±

(λ₁ + µ₁)² - 4λ₁µ₁p

γ_1,2 =

2λ₁

Выбираем корень, лежащий в интервале от 0 до 1, т.е. γ₂. Таким образом,

получаем, что

(19)

s_i,j = γⁱ²s_0,j

j ≥ 0.

Теперь подставляем полученное решение для s_i,j в (16), откуда можем выра-

зить s_0,j в виде:

µ₂

s_0,j =

s_0,j-1, j ≥ 1.

λ₁(1 - γ₂) + µ₂

Далее подставим (19) при i = 1 и j = 0 в (17), что позволит выразить веро-

ятность s_0,0 в явном виде:

µ₂

s_0,0 =

λ₁(1 - γ₂) + µ₂

Следовательно,

(20)

s_0,j = δ^j+1

j ≥ 0,

где

µ₂

δ=

λ₁(1 - γ₂) + µ₂

122

Таким образом, получаем формулу для искомых вероятностей

s_i,j = γⁱ²δ^j+1, i,j ≥ 0.

Теперь, определив величины s_i,j, можем выразить вероятность обслуживания

неприоритетной заявки

∑∑

p^(serv) =

p_i,js_i,j = δ

p_i,jγⁱ²δ^j = δB(γ₂,δ),

i=0 j=0

где B(γ₂, δ) определяется выражением для производящей функции (5).

Заметим, что при p → 1 имеем γ₂ → 1, δ → 1 и p^(serv) → 1, что согласуется

с p^(serv) = 1 в классической системе [39]. С другой стороны, при p → 0 имеем

γ₂ → 0, δ → µ₂/(λ₁ + µ₂) и

(

)

µ₂

p^(serv) →

B 0,

λ₁ + µ₂

что представляет собой правильный результат в специальном случае q = 1

(детерминированного сброса), рассмотренном в [41].

6. Численный пример

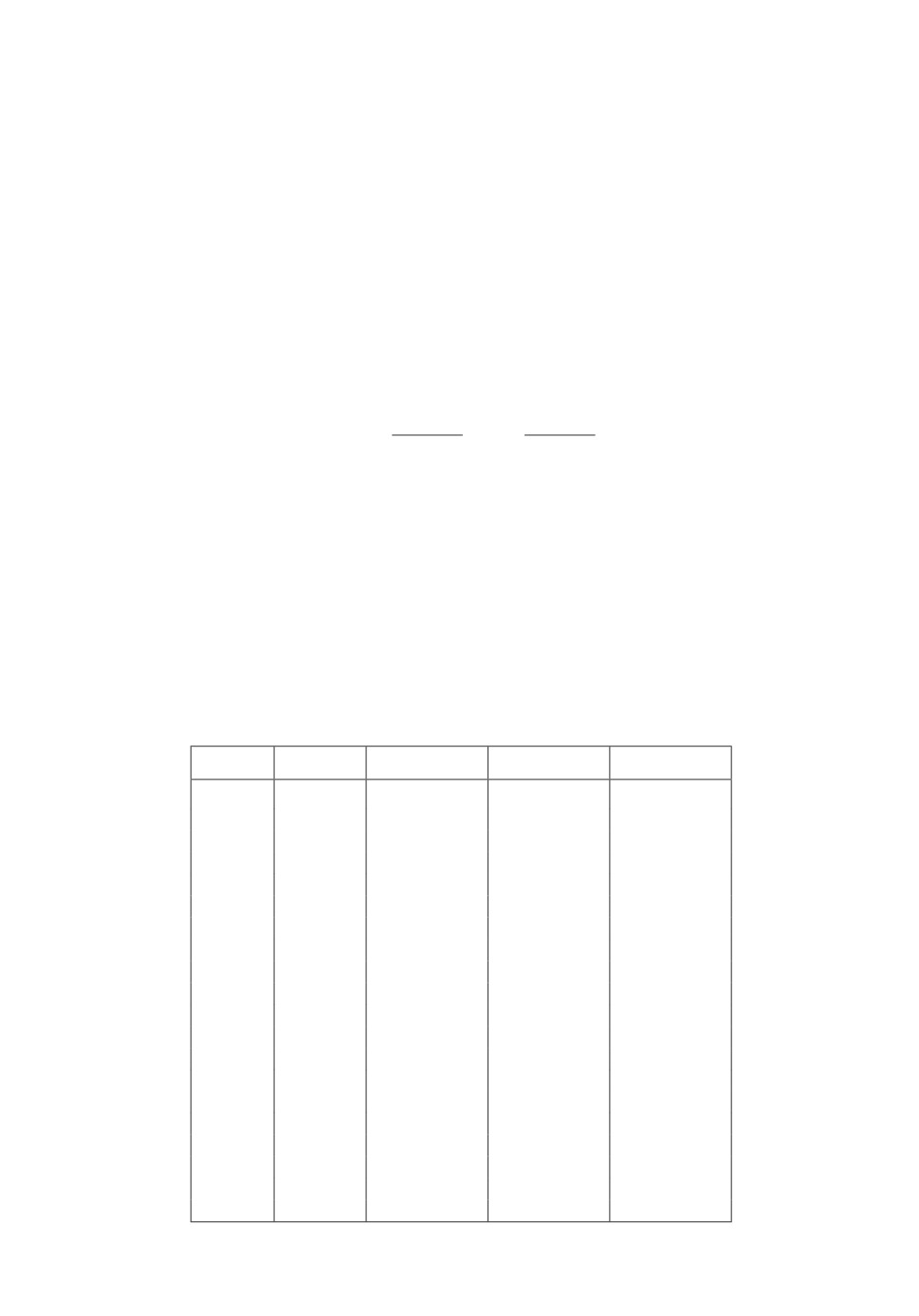
Проиллюстрируем поведение среднего числа неприоритетных заявок в си-

стеме и вероятности их обслуживания, а также вероятности простоя в зави-

симости от значения вероятности p. Положим λ₁ = 1, λ₂ = 2, µ₁ = 3, µ₂ = 4.

Значения p_0,0, N₂ и p^(serv) в зависимости от вероятности p;

λ₁ = 1, λ₂ = 2, µ₁ = 3, µ₂ = 4

№ п/п

p_0,0

N₂

p^(serv)

0,00001

0,42692456

0,72138505

0,44783943

0,0001

0,42691639

0,72142797

0,44785372

0,001

0,42683463

0,72185751

0,44799666

0,01

0,42601289

0,72618609

0,44943427

0,05

0,42226759

0,74618419

0,45601022

0,1

0,41735867

0,77308223

0,46468915

0,2

0,40668331

0,83441279

0,48380588

0,3

0,39464575

0,90860175

0,50577935

0,4

0,38089405

1,00059049

0,53145181

0,5

0,36491803

1,11839002

0,56207704

0,6

0,34593336

1,27603001

0,59963204

0,7

0,32262946

1,50090229

0,64748988

0,8

0,29251571

1,85620264

0,71212093

0,9

0,24962267

2,53878264

0,80873235

0,95

0,21798769

3,23966558

0,88200599

0,97

0,20130170

3,70732327

0,92074722

0,99

0,18016569

4,43379884

0,96939467

0,999

0,16814903

4,93317210

0,99666168

0,9999

0,16681649

4,99318955

0,99966287

0,99999

0,16668166

4,99931765

0,99996625

123

0,45

0,40

0,35

0,30

0,25

0,20

0,15

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

5,5

4,5

3,5

2,5

1,5

0,5

0,1

0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9

1,0

Рис. 4. Зависимости: а вероятности простоя системы от вероятности p; б

среднего числа неприоритетных заявок в системе от вероятности p; λ₁ = 1,

λ₂ = 2, µ₁ = 3, µ₂ = 4.

1,0

0,9

0,8

0,7

0,6

0,5

0,4

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

Рис. 5. Зависимость вероятности обслуживания неприоритетной заявки p^(serv)

от вероятности p; λ₁ = 1, λ₂ = 2, µ₁ = 3, µ₂ = 4.

Как видно из графиков (рис. 4) и таблицы среднее число неприоритетных

заявок в системе с увеличением p растет, а сама вероятность p_0,0 при этом

убывает. Причем заметим, что вероятность простоя в классической СМО без

возможности сброса неприоритетных заявок, вычисляемая по формуле из [39]

p^(1)0,0 = 1 - ρ₁ - ρ₂, ρ_i = λ_i/µ_i, i = 1,2,

124

равна 0,16667 (или 1/6), а среднее число неприоритетных заявок в той же

классической системе, описываемое формулой из [39]

(

)

λ₂(µ₁(µ₁ - λ₁) + λ₁µ₂)

ρ₂

µ₂ρ₁

N⁽¹⁾² =

(µ₁ - λ₁)(µ₁µ₂ - λ₁µ₂ - λ₂µ₁)

1-ρ₁ -ρ₂

µ₁(1 - ρ₁)

в точности равно 5. Таким образом, значения N₂ и p_0,0 с приближением веро-

ятности сброса заявок второго типа q к нулю стремятся к соответствующим

значениям N⁽¹⁾² и p^(1)0,0 для классической системы с отсутствием возможности

такого сброса, чего и следовало ожидать. С другой стороны, из [41] известна

вероятность простоя при p = 0, которая оказывается равна p^(0)0,0 ≈ 0,426925,

что также согласуется с таблицей. Что касается вероятности обслуживания

заявок второго типа p^(serv), то она, что естественно, с ростом p стремится к

единице (рис. 5).

7. Заключение

В статье рассмотрена СМО с абсолютным приоритетом заявок первого

типа над заявками второго типа и стохастическим сбросом. Представлены

выражения для вычисления стационарных вероятностей системы, вероятно-

сти простоя, вероятности обслуживания неприоритетной заявки (в терминах

производящей функции), а также формула для среднего числа заявок второ-

го типа. Проведено сравнение с ранее известными результатами для крайних

случаев и показано, что они получаются соответствующими предельными пе-

реходами.

СПИСОК ЛИТЕРАТУРЫ

1. Gelenbe E., Glynn P., Sigman K. Queues with Negative Arrivals // J. Appl. Prob.

1991. V. 28. No. 1. P. 245-250.

2. Do T.V. Bibliography on G-networks, Negative Customers and Applications //

Math. Comput. Model. 2011. V. 53. P. 205-212.

3. Caglayan M. G-Networks and their Applications to Machine Learning, Energy Packet

Networks and Routing: Introduction to the Special Issue // Prob. Eng. Inform. Sci.

2017. V. 31. No. 4. P. 381-395.

4. Малинковский Ю.В., Бородин Н.Н. Сети массового обслуживания с конечным

числом потоков отрицательных заявок и с ограниченным временем пребыва-

ния // Пробл. физики, математики и техники. 2017. № 1. С. 64-68.

5. Малинковский Ю.В. Стационарное распределение вероятностей состояний G-се-

тей с ограниченным временем пребывания // АиТ. 2017. № 10. С. 155-167.

Malinkovskii Y.V. Stationary Probability Distribution for States of G-Networks with

Constrained Sojourn Time // Autom. Remote Control. 2017. V. 78. No. 10. P. 1857-

1866.

6. Dimitriou I. A Mixed Priority Retrial Queue with Negative Arrivals, Unreliable

Server and Multiple Vacations // Appl. Math. Model. 2013. V. 37. P. 1295-1309.

7. Rajkumar M. An (s, S) Retrial Inventory System with Impatient and Negative Cus-

tomers // Int. J. Math. Oper. Res. 2014. V. 6. P. 106-122.

125

Farkhadov M., Fedorova E. Asymptotic Analysis of Retrial Queue M|M|1 with Nega-

tive Calls Under Heavy Load Condition // Distributed Comput. Commun. Networks.

2017. P. 470-475.

Farkhadov M., Fedorova E. Retrial Queue M|M|1 with Negative Calls Under Heavy

Load Condition // Commun. Comput. Inform. Sci. 2017. V. 700. P. 406-416.

10.

Zidani N., Spiteri P., Djellab N. Numerical Solution for the Performance Charac-

teristics of the M|M|C|K Retrial Queue with Negative Customers and Exponential

Abandonments by Using Value Extrapolation Method // RAIRO-Oper. Res. 2019.

V. 53. P. 767-786.

11.

Kyung C. Chae, Hyun M. Park, Won S. Yang. A GI|Geo|1 Queue with Negative

and Positive Customers // Appl. Math. Model. 2010. V. 34. P. 1662-1671.

12.

Wang J., Huang Y., Dai Z. A Discrete-Time On-Off Source Queueing System with

Negative Customers // Comput. Ind. Eng. 2011. V. 61. P. 1226-1232.

13.

Gao Sh., Wang J., Zhang D. Discrete-Time GI^X |Geo|1|N Queue with Negative

Customers and Multiple Working Vacations // J. Korean Stat. Soc. 2013. V. 42.

P. 515-528.

14.

Wang J., Huang Y., Do T. A Single-Server Discrete-Time Queue with Correlated

Positive and Negative Customer Arrivals // Appl. Math. Model. 2013. V. 37.

P. 6212-6224.

15.

Lee D.H., Kim K. Analysis of Repairable Geo|G|1 Queues with Negative Cus-

tomers // Appl. Math. Model. 2014. Article ID 350621, 10 P.

16.

Senthil Vadivu A., Arumuganathan R., Senthil Kumar M. Analysis of Discrete-Time

Queues with Correlated Arrivals, Negative Customers and Server Interruption //

RAIRO-Oper. Res. 2016. V. 50. P. 67-81.

17.

Klimenok V.I., Dudin A.N. A BMAP |P H|N Queue with Negative Customers and

Partial Protection of Service // Commun. Statist. Simulat. Comput. 2012. V. 41.

No. 7. P. 1062-1082.

18.

Rajadurai P., Chandrasekaran M., Saravanarajan M.C. Steady State Analysis of

Batch Arrival Feedback Retrial Queue with Two Phases of Service, Negative Cus-

tomers, Bernoulli Vacation and Server Breakdown // Int. J. Math. Oper. Res. 2015.

V. 7. P. 519-546.

19.

Singh C.J., Jain M., Kaur S., Meena R.K. Retrial Bulk Queue with State Dependent

Arrival and Negative Customers // Proc. Sixth Int. Conf. on Soft Computing for

Problem Solving. Advances in Intelligent Systems and Computing. 2017. V. 547.

P. 290-301.

20.

Ayyappan G., Thamizhselvi P. Transient Analysis of M[X1], M[X2]/G₁, G₂/1 Retrial

Queueing System with Priority Services, Working Vacations and Vacation Interrup-

tion, Emergency Vacation, Negative Arrival and Delayed Repair // Int. J. Appl.

Comput. Math. 2018. V. 4. Article number: 77. 35 P.

21.

Маталыцкий М.А. Прогнозирование ожидаемых доходов в марковских сетях с

положительными и отрицательными заявками // АиТ. 2017. № 5. С. 56-70.

Matalytski M.A. Forecasting Anticipated Incomes in the Markov Networks with

Positive and Negative Customers // Autom. Remote Control. 2017. V. 78. No. 5.

P. 815-825.

22.

Lee D.H. Optimal Pricing Strategies and Customers’ Equilibrium Behavior in an

Unobservable M|M|1 Queueing System with Negative Customers and Repair //

Math. Probl. Eng. 2017. Article ID 8910819. 11 P.

23.

Matalytski M. Finding Expected Revenues in G-network with Multiple Classes of

Positive and Negative Customers Probability in the Engineering and Informational

Sciences // Prob. Eng. Inform. Sci. 2019. V. 33. No. 1. P. 105-120.

126

24.

Matalytski M. Analysis of the Network with Multiple Classes of Positive and Negative

Customers at a Transient Regime // Prob. Eng. Inform. Sci. 2019. V. 33, No. 2.

P. 172-185.

25.

Sun K., Wang J. Equilibrium Joining Strategies in the Single Server Queues with

Negative Customers // Int. J. Comput. Math. 2019. V. 96. No. 6. P. 1169-1191.

26.

Xu Xiu-li, Wang Xian-ying, Song Xiao-feng, Li Xiao-qing. Fluid Model Modulated

by an M|M|1 Working Vacation Queue with Negative Customer // Acta. Math.

Appl. Sin.-E. 2018. V. 34. No. 2. P. 404-415.

27.

Chin C.H., Koh S.K., Tan Y.F., Pooi A.H., Goh Y.K. Stationary Queue Length

Distribution of A Continuous-Time Queueing System with Negative Arrival // J.

Phy. Conf. 2018. V. 1132. Article ID 012057.

28.

Peng Y. The MAP/G/1 G-queue with Unreliable Server and Multiple Vacations //

Informatica. 2019. V. 43. No. 4. P. 545-550.

29.

Gupta U., Kumar N., Barbhuiya F. A Queueing System with Batch Renewal Input

and Negative Arrivals // 2020. arXiv:2002.08209v1.

30.

Kreinin A. Queueing Systems with Renovation // J. Appl. Math. Stoch. Anal. 1997.

V. 10. No. 4. P. 431-443.

31.

Бочаров П.П., Зарядов И.С. Стационарное распределение вероятностей в систе-

мах массового обслуживания с обновлением // Вест. Росс. ун-та дружбы наро-

дов. Сер. “Математика. Информатика. Физика”. 2007. № 1-2. С. 14-23.

32.

Зарядов И.С., Печинкин А.В. Стационарные временные характеристики систе-

мы GI|M|n|∞ с некоторыми вариантами дисциплины обобщенного обновле-

ния // АиТ. 2009. № 12. С. 161-174;

Zaryadov I.S., Pechinkin A.V. Stationary Time Characteristics of the GI|M|n|∞

System with Some Variants of the Generalized Renovation Discipline // Autom.

Remote Control. 2009. V. 70. No. 12. P. 2085-2097.

33.

Зарядов И.С. Система массового обслуживания GI|M|n|∞ с обобщенным обнов-

лением // АиТ. 2010. № 4. P 130-139.

Zaryadov I.S. The GI|M|n|∞ Queuing System with Generalized Renovation // Au-

tom. Remote Control. 2010. V. 71. No. 4. P. 663-671.

34.

Гришунина Ю.Б. Оптимальное управление очередью в системе M|G|1|∞ с воз-

можностью ограничения приема заявок // АиТ. 2015. № 3. С. 79-93.

Grishunina Y.B. Optimal Control of Queue in the M|G|1|∞ System with Possibility

of Customer Admission Restriction // Autom. Remote Control. 2015. V. 76. No. 3.

P. 433-445.

35.

Агаларов Я.М., Шоргин В.С. Об одной задаче максимизации дохода СМО типа

G|M|1 с пороговым управлением очередью // Информатика и ее применения.

2017. Т. 11. Вып. 4. С. 55-64.

36.

Konovalov M.G., Razumchik R.V. Comparison of Two Active Queue Management

Schemes through the M|D|1|N Queue // Inform. Appl. 2018. V. 12. No. 4. P. 9-15.

37.

Adams R. Active Queue Management: A Survey // IEEE Commun. Surveys Tuto-

rials. 2013. V. 15. No. 3. P. 1425-1476.

38.

Anup Sh., Ashok B. A Survey on Active Queue Management Techniques // Int. J.

Eng. Comput. Sci. 2016. V. 5. P. 18993-18997.

39.

White H., Christie Lee S. Queuing with Preemptive Priorities or with Breakdown //

Oper. Res. 1958. V. 6. No. 1. P. 79-95.

40.

Зарядов И.С., Горбунова А.В. Анализ характеристик системы массового обслу-

живания с двумя входящими потоками, относительным приоритетом и сбро-

сом // Современные информационные технологии и ИТ-образование. 2014. № 10.

С. 388-393.

127

41. Zaryadov I.S., Gorbunova A.V. The Analysis of Queueing System with Two Input

Flows and Stochastic Drop Mechanism // Bulletin of Peoples’ Friendship University

of Russia. Series “Mathematics. Informatics. Physics”. 2015. No. 2. P. 33-37.

42. Зарядов И.С., Королькова А.В. Применение модели с обобщенным обновлением

к анализу характеристик систем активного управления очередями типа Random

Early Detection (RED) // T-Comm - Телекоммуникации и транспорт. 2011. № 7.

С. 84-88.

43. Chydzinski A., Mrozowski P. Queues with Dropping Functions and General Arrival

Processes // PLoS ONE. 2016. V. 11. Article ID 0150702.

44. Wang Y., Lin Ch., Li Q.-L., Fang Y. A Queueing Analysis for the Denial of Ser-

vice (DoS) Attacks in Computer Networks // Computer Networks. 2007. V. 51.

P. 3564-3573.

45. Imamverdiyev Y., Nabiyev B. Queuing Model for Information Security Monitoring

Systems // PIT. 2016. V. 07. No. 1. P. 28-32.

46. Kammas P., Komninos T., Stamatiou Y.C. Queuing Theory Based Models for

Studying Intrusion Evolution and Elimination in Computer Networks // Fourth Int.

Conf. on Information Assurance and Security. 2008. P. 167-171.

47. Ariba Y., Gouaisbaut F., Rahme S., Labit Y. Traffic Monitoring in Transmission

Control Protocol/Active Queue Management Networks through a Time-Delay Ob-

server // IET Control Theory A. 2012. V. 6. No. 2. P. 506-517.

Статья представлена к публикации членом редколлегии В.М. Вишневским.

Поступила в редакцию 26.12.2019

После доработки 27.05.2020

Принята к публикации 09.07.2020

128