Автоматика и телемеханика, № 12, 2020

М.С. СТЕПАНОВ, канд. техн. наук (mihstep@yandex.ru)

(Московский технический университет связи и информатики)

МЕТОДЫ ОЦЕНКИ НЕОБХОДИМОГО ОБЪЕМА РЕСУРСА

МУЛЬТИСЕРВИСНЫХ УЗЛОВ ДОСТУПА

Построена и исследована математическая модель распределения ре-

сурса передачи информации мультисервисного узла доступа. В модели

рассматривается произвольное число потоков мультимедийного трафи-

ка, которые различаются интенсивностью поступления заявок, величи-

ной ресурса, используемого для обслуживания одной заявки, и временем

занятия ресурса. Интервалы времени между поступлением заявок име-

ют экспоненциальное распределение с параметром, зависящим от числа

заявок рассматриваемого потока, находящихся на обслуживании. Постро-

ен рекурсивный алгоритм оценки характеристик. Установлены соотно-

шения между интегральными и потоковыми характеристиками качества

обслуживания заявок. Построен эффективный алгоритм оценки объема

ресурса, требуемого для обслуживания заданных потоков трафика с необ-

ходимым качеством. Эффективность расчетной процедуры достигается

в результате организации рекурсии по объему ресурса и использования

нормированных значений вероятностей состояний. Рассмотрено решение

задачи оценки необходимого объема ресурса для модели мультисервис-

ного узла, допускающего использование механизмов резервирования ре-

сурса и его динамического распределения при обслуживании эластичного

трафика. Приведены численные примеры, иллюстрирующие особенности

реализации построенных расчетных процедур.

Ключевые слова: мультисервисный узел доступа, марковские модели, си-

стема уравнений равновесия, рекурсивные алгоритмы, резервирование,

эластичный трафик.

DOI: 10.31857/S0005231020120089

1. Введение

Одной из основных задач моделирования сетей и систем связи является

разработка научно обоснованных средств оценки необходимого объема ре-

сурса передачи информации [1-8]. Результаты моделирования также играют

существенную роль в обосновании действий оператора, направленных на по-

вышение эффективности работы сети и улучшение качества обслуживания

пользователей [5-8]. К таким действиям относятся: дифференцированное об-

служивание пользователей, резервирование ресурса, динамическое распреде-

ление ресурса и т.д. Особенно важно найти решение перечисленных задач

для мультисервисных узлов доступа, реализующих функцию концентрации

возникающих информационных потоков. Оцениваемый ресурс определим че-

рез величину скорости передачи информационного потока, необходимой для

129

обеспечения заказанного сервиса. В сетях фиксированной связи использова-

ние этого определения не вызывает особых затруднений [9-13]. В сетях бес-

проводной связи битовая скорость является функцией технологии и условий

передачи информации, в частности расстояния до базовой станции, играющей

роль мультисервисного узла доступа [14-16]. На уровне поступления заявок

распределение ресурса для обоих видов связи исследуется схожими метода-

ми, поэтому для простоты далее будем предполагать, что рассматривается

фиксированная связь. Разработка методов оценки объема ресурса включа-

ет в себя решение ряда задач, возникающих из-за необходимости учета спе-

цифики формирования и обслуживания мультисервисных информационных

потоков. Обсудим их и дадим им более точную формулировку.

В мультисервисных сетях по определению рассматривается процесс сов-

местного обслуживания нескольких потоков трафика. Наличие большого чис-

ла потоков с разными характеристиками усложняет задачу планирования

необходимого объема ресурса из-за неопределенности в выборе нормативных

показателей. Для этих целей обычно рассматривают значения интегральных

характеристик. В их числе: максимальная доля потерянных заявок, доля по-

терянного трафика и т.д. При этом качество обслуживания отдельных пото-

ков не оценивается. Возникающие трудности можно устранить, если найти

зависимость между интегральными характеристиками и характеристиками

обслуживания отдельных потоков. Решение этой задачи служит основанием

для выбора и использования метрики при оценке достаточности ресурса.

Следующая задача относится к построению эффективного алгоритма

оценки величины ресурса. Эффективность в данном контексте означает до-

стижение минимальных затрат вычислительных ресурсов на реализацию ал-

горитма и его стабильность. Все эти требования необходимы для примене-

ния алгоритма в программно-аналитических продуктах типа калькуляторов

сетевой инфраструктуры. Этого результата можно добиться, если организо-

вать рекурсию по объему ресурса и при проведении вычислений использовать

только нормированные значения вероятностей состояний.

Результаты исследований [5-8] показывают, что совместное занятие ресур-

са несколькими информационными потоками, с одной стороны, может при-

вести к его перераспределению и ухудшению качества обслуживания отдель-

ных потоков, а с другой стороны, может быть использовано для повышения

эффективности его занятия, например при пересылке эластичного трафика.

Отмеченные положительные и отрицательные стороны совместного обслу-

живания трафика должны быть учтены при построении модели мультисер-

висного узла доступа и в дальнейшем приняты во внимание при разработке

методов оценки необходимого объема ресурса.

Решения перечисленных задач будут рассмотрены в настоящей работе на

примере модели мультисервисного узла доступа, в которой интервалы вре-

мени между поступлением заявок зависят от числа заявок рассматриваемого

потока, находящихся на обслуживании. Помимо базового варианта модели

будут рассмотрены ее обобщения, допускающие использование механизмов

резервирования ресурса и его динамического распределения при пересыл-

ке эластичного трафика. Решение отдельных задач исследовалось в более

ранних публикациях в основном для модели с пуассоновскими потоками зая-

130

вок. Так, рекурсивные алгоритмы оценки характеристик рассматривались в

[1-4], вопросы планирования ресурса исследовались в [9-13], использование

механизмов резервирования анализировались в [5, 8, 16], особенности обслу-

живания эластичного трафика изучались в [8, 10, 11], совместная передача

трафика реального времени и данных представлена в [8, 11,4-18]. Здесь эти

результаты будут получены в более общей постановке и более эффективными

средствами.

Работа имеет следующую структуру. В разделах 2 и 3 построены соот-

ветственно функциональная и математическая модели мультисервисного уз-

ла доступа. В следующем разделе сформулированы определения основных

характеристик качества обслуживания поступающих потоков заявок. Рекур-

сивный алгоритм их оценки рассмотрен в разделе 5. Там же установлены со-

отношения между интегральными и потоковыми характеристиками качества

обслуживания заявок, которые упрощают выбор метрики при решении задач

планирования ресурса узла доступа. Эффективный алгоритм оценки требуе-

мого числа каналов передачи информации построен в разделе 6. Эффектив-

ность расчетной процедуры достигается в результате организации рекурсии

по объему ресурса и использовании нормированных значений вероятностей

состояний. В разделе 7 решение задачи оценки необходимого числа каналов

рассмотрено для модели мультисервисного узла, допускающего использова-

ние механизмов резервирования ресурса и его динамического распределения

при пересылке эластичного трафика.

2. Функциональная модель

Мультисервисный узел доступа реализует функции агрегации и передачи

данных от разнообразных источников информационной нагрузки. К тако-

вым можно отнести абонентские терминалы, мультимедийные компьютеры,

видеооборудование и т.д. По запросу пользователя устанавливается вирту-

альное соединение (ВС) и осуществляется передача данных в виде последова-

тельности пакетов. В большинстве случаев эта последовательность представ-

ляет локально периодический поток. За периодом генерации пакетов, обычно

происходящей с максимальной для рассматриваемого источника скоростью,

следует период времени, когда пакеты не поступают. Такая структура пото-

ка позволяет реализовать принцип статистического мультиплексирования и

уменьшить потребности в ресурсе передачи информации. Виртуальное соеди-

нение выполняет пересылку информационных потоков, относящихся к неко-

торому конечному набору сервисов. Сюда входят передача речи и разных

форм видео, обмен файлами и т.д. Будем предполагать, если это не огова-

ривается особо, что рассматриваются коммуникационные сервисы реального

времени, требующие для своего обслуживания фиксированную скорость пе-

редачи информации.

Важными составными частями мультисервисного узла доступа являются:

процедура контроля доступа (CAC Call Admission Control), буфер и вы-

сокоскоростная линия концентрации трафика. Процедура CAC может быть

реализована с использованием протокола RSVP (Resource reSerVation Pro-

tocol) в рамках архитектуры управления ресурсами IntServ (Integrated Ser-

131

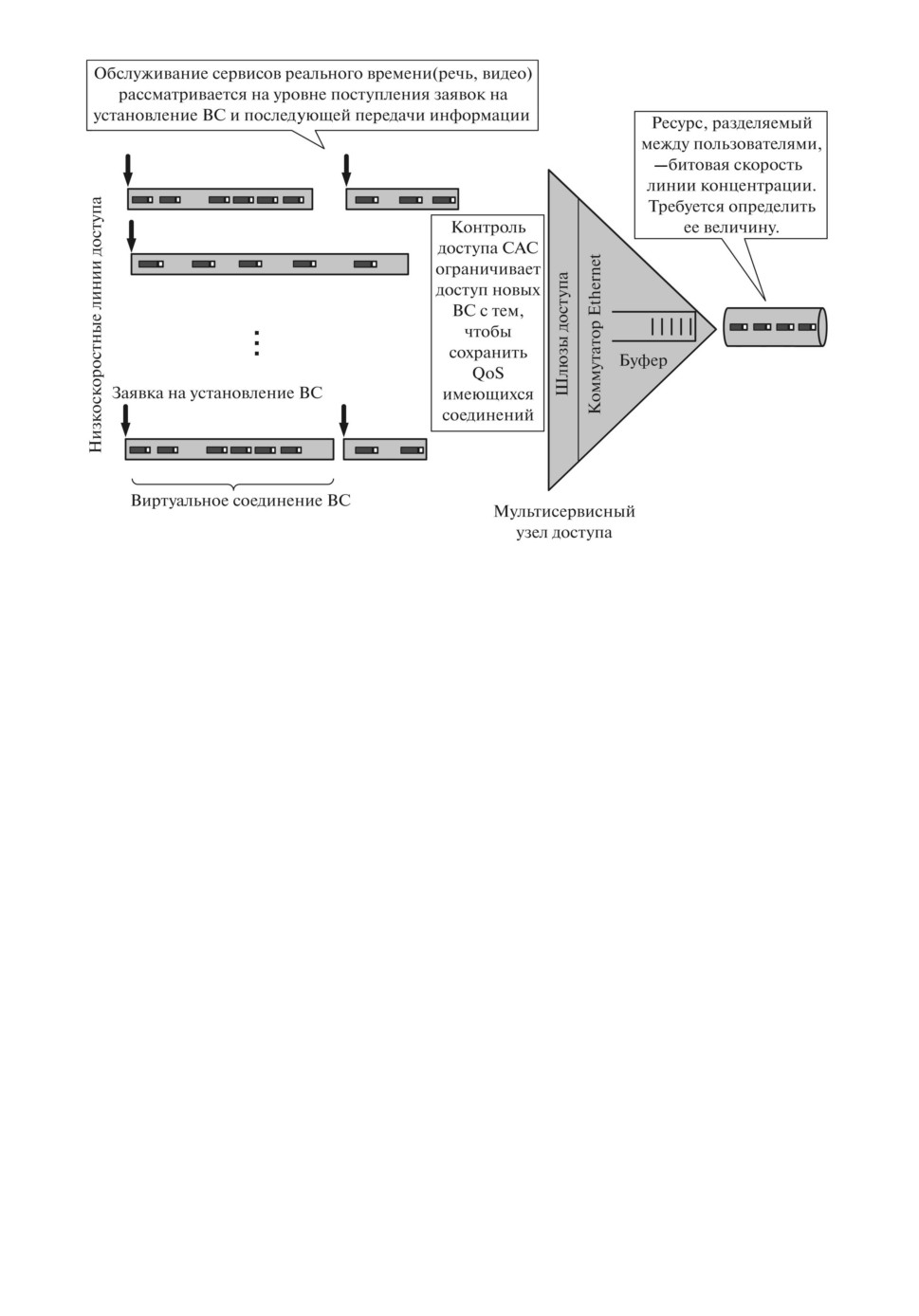
Рис. 1. Функциональная модель мультисервисного узла доступа.

vices). Формализованное описание CAC основано на введении дескриптора

трафика, который задает потребность в ресурсе передачи информации у по-

ступившей заявки, и сравнимого дескриптора, оценивающего свободный ре-

сурс [19]. Решение о приеме заявки принимается после сравнения значений

обоих показателей. В качестве дескриптора трафика можно взять значение

пиковой интенсивности поступления информации в потоке, ассоциированном

с обслуживанием заявки. Это решение отличается простотой, однако суще-

ственно переоценивает потребности в ресурсе, не учитывает возможности ста-

тистического мультиплексирования трафика на уровне пакетов и поэтому

неэффективно. Эти недостатки отчасти устраняет использование в качестве

дескриптора понятия эффективной скорости передачи информации [20]. Ее

величина лежит между средней и пиковой скоростями передачи информации

анализируемого потока и учитывает свойство статистического мультиплекси-

рования. Заявка принимается, если сумма значений используемого ресурса r_o

и ресурса, требуемого для обслуживания поступившей заявки r_n, не превос-

ходит имеющегося ресурса C. Таким образом, для приема заявки необходимо

выполнение неравенства: r_o + r_n < C. Буфер получает пакеты из установлен-

ных соединений и передает их один за другим по линии. Он служит интер-

фейсом между поступающими потоками пакетов и высокоскоростной линией

и сглаживает всплески информационной нагрузки. Функциональная модель

мультисервисного узла доступа показана на рис. 1.

Построенная функциональная модель мультисервисного узла в упрощен-

ной форме описывает процесс занятия и использования ресурса передачи

информации. Она освобождена от конкретики технологий и протоколов. Их

132

влияние переводится с микро- на макроуровень в форме параметров, завися-

щих от состояния сети и действия разного рода механизмов, управляющих

процессом обслуживания абонентов. Она служит своего рода интерфейсом

между исследуемой системой связи и моделью, с помощью которой далее бу-

дут найдены показатели качества обслуживания заявок, используемые для

оценки требуемой по нагрузке скорости линии. Отметим, что могут приме-

няться и более сложные модели формализованного описания условий приема

заявок в соответствии с процедурой CAC. Часть из них, основанная на при-

менении процедуры резервирования ресурса, будет рассмотрена в разделе 7.

3. Математическая модель

Обозначим через C скорость передачи информации, выраженную в би-

тах в секунду, обеспечиваемую линией концентрации абонентского трафика

(см. рис. 1). Назовем единицей ресурса u минимальное требование к скорости

от поступающих заявок (скорость одного виртуального канала). Предполо-

жим, что значение C нацело делится на u, и обозначим через v =^Cu скорость

передачи линии, выраженную в виртуальных каналах. Линия использует-

ся для обслуживания n потоков заявок на передачу трафика сервисов ре-

ального времени. Интервал времени между последовательным поступлени-

ем заявок k-го потока имеет экспоненциальное распределение с параметром

λ_k(i_k) = α_k + i_kβ_k, k = 1,... ,n, где i_k

число заявок k-го потока, находя-

щихся на обслуживании. Для допуска заявки k-го потока требуются b_k вир-

туальных каналов, которые резервируются на случайное время, имеющее экс-

поненциальное распределение с параметром µ_k, и используются для передачи

информационного потока, ассоциированного с рассматриваемой заявкой.

В литературе [4, 6-8] рассмотренная модель входного потока заявок носит

название поток BPP (Bernoulli-Poisson-Pascal) по трем известным частным

случаям. Для потока Бернулли λ_k(i_k) = (s_k - i_k)ζ_k, где s_k число пользо-

вателей, создающих k-й поток заявок, а ζ_k параметр экспоненциального

распределения времени между последовательными поступлениями заявок от

одного пользователя. Для пуассоновского потока λ_k(i_k) = λ_k и значение λ_k

не зависит от числа абонентов, находящихся на обслуживании. Для потока

Паскаля λ_k(i_k) = (s_k + i_k)ζ_k, где s_k положительное целое число и ζ_k > 0.

Наличие двух параметров в модели входного потока дает возможность с

большей точностью аппроксимировать поступление заявок. Процесс поступ-

ления заявок зависит от числа пользователей, находящихся на обслуживании.

Тем самым учитывается зависимость поступления заявок от загрузки линии

связи. Рассмотренную модель рекомендуется использовать в тех ситуациях,

когда необходимо выделить небольшие группы так называемых тяжелых

абонентов, создающих существенный объем потенциального трафика. Необ-

ходимость учета этой особенности формирования входного потока особенно

актуальна для перспективных сетей подвижной связи. Эти системы рабо-

тают в диапазоне высоких частот. Здесь размеры соты невелики, и число

активных абонентов влияет на величину интенсивности поступающего пото-

ка заявок. Аналогичная ситуация наблюдается в местах городской застройки

при обслуживании небольших территорий (офисы, отдельные здания), где

133

используются малые соты (фемтосоты, пикосоты, метросоты и т.д.) с пре-

дельно малым (до нескольких десятков) числом абонентов. В дальнейшем,

не теряя общности изложения материала, ограничимся рассмотрением мо-

дели входного потока Бернулли. По аналогии с моносервисным случаем эта

модель называется мультисервисной моделью Энгсета.

4. Характеристики обслуживания заявок

Достаточность ресурса линии оценим долей потерянных заявок, а эффек-

тивность его использования средним числом занятых единиц ресурса. Для

оценки этих характеристик достаточно знать долю времени пребывания ли-

нии в состоянии с известным числом заявок каждого потока, находящихся

на обслуживании. Выбор характеристик определяет состояние модели в виде

вектора (i₁, . . . , i_n), где i_k число обслуживаемых заявок k-го потока. Значе-

∑_n

ния i_k ограничены пропускной способностью линии

i_kb_k ≤ v и числом

k=1

абонентов в каждой группе i_k ≤ s_k, k = 1, . . . , n. Векторы (i₁, . . . , i_n), удовле-

творяющие приведенным неравенствам, определяют пространство S состоя-

ний модели.

Динамика изменения состояний модели во времени описывается случай-

ным марковским процессом r(t) = (i₁(t), . . . , i_n(t)), где i_k(t) число заявок

k-го потока, находящихся в момент t на обслуживании. Пусть U_k множе-

ство состояний (i₁, . . . , i_n) ∈ S, удовлетворяющих условию i₁b₁ + . . . + i_nb_n+

+b_k > v. В каждом из состояний U_k поступившая заявка k-го потока полу-

чает отказ. Обозначим через p(i₁, . . . , i_n) стационарную вероятность состоя-

ния (i₁, . . . , i_n). Она имеет интерпретацию доли времени пребывания r(t) в

(i₁, . . . , i_n), что позволяет использовать p(i₁, . . . , i_n) для оценки характери-

стик модели.

Из обратимости марковского процесса r(t) следует свойство мультиплика-

тивности. Для всех (i₁, . . . , i_n) ∈ S

∏

(s₁ - j)γ

(s_n - j)γinn

(1)

p(i₁, . . . , i_n) =

× j=0

···^j=0

i₁!

i_n!

где γ_k = ζ_k/µ_k среднее число заявок, поступающих от одного абонента k-го

потока за среднее время обслуживания заявки 1/µ_k. Далее это время будет

принято за единицу и отдельно в модели не рассматривается, а N норми-

ровочная константа

∏

(s₁ - j)γi11

(s_n - j)γinn

∑

j=0

N =

···

i₁!

i_n!

(i₁,...,in)∈S

Мультипликативное соотношение и алгоритмы, полученные на его основе,

не зависят от вида функции распределения времени обслуживания заявки

и функции распределения времени между поступлением заявок от одного

134

абонента [21

23]. Требуется только, чтобы соответствующие времена не за-

висели друг от друга. Это существенно расширяет область применения полу-

ченных расчетных выражений.

Качество обслуживания заявок k-го потока оценим долей времени недо-

ступности ресурса передачи π_t,k; долей потерянных заявок π_c,k; сред-

ним числом потенциальных соединений a_k =sk γ^k (среднее число соедине-_1+γ

ний в отсутствие потерь); средним числом занятых единиц ресурса m_k;

средним числом обслуживаемых заявок y_k = m_k/b_k; долей потерянных

соединений π_ℓ,k = (a_k - y_k)/a_k и интенсивностью входного потока заявок

Λ_k = (s_k - y_k)γ_k:

∑

(2)

π_t,k =

p(i₁, . . . , i_n

);

(i₁,...,in)∈Uk

∑

p(i₁, . . . , i_n)(s_k - i_k)

π_c,k =

(i₁,...,in)∈Uk∑

;

p(i₁, . . . , i_n)(s_k - i_k)

(i₁,...,in)∈S

∑

m_k =

p(i₁, . . . , i_n)i_kb_k.

(i₁,...,in)∈S

Из формулы Литтла следует y_k = Λ_k(1 - π_c,k). Из определений характери-

стик получаем π_c,k = π_ℓ,k (1 + γ_k)/(1 + π_ℓ,k γ_k). Если для k-го потока заявок

известно значение одной из введенных ранее характеристик y_k, m_k, π_c,k, π_ℓ,k,

Λ_k и величины входных параметров s_k, a_k (или s_k, γ_k), то, используя приве-

денные выше выражения, можно найти значения оставшихся характеристик.

Величина a_k определяет потенциальное число соединений и будет далее ис-

пользоваться при описании входных параметров модели в процессе прове-

дения вычислений. Предположим, что в результате измерений или расчетов

стали известны значения π_c,k, s_k, a_k. Величины оставшихся характеристик

могут быть найдены из выражений:

a_k

π_c,k(s_k - a_k)

a_ks_k(1 - π_c,k)

(3)

γ_k =

;

π_ℓ,k =

;

y_k =

;

s_k - a_k

s_k - a_kπ_c,k

a_kb_ks_k(1 - π_c,k)

a_ks_k

m_k =

;

Λ_k =

s_k - a_kπ_c,k

5. Оценка характеристик и их свойства

Алгоритм оценки характеристик модели основан на использовании пока-

зателей пребывания r(t) во множестве агрегированных состояний модели S_i,

i = 0,1,...,v, в которое включены состояния (i₁,...,i_n) ∈ S, удовлетворяю-

щие условию i₁ b₁ + . . . + i_n b_n = i. Пусть p(i) вероятность занятости i еди-

ниц ресурса, а y_k(i)

среднее число заявок k-го потока, находящихся на

обслуживании в ситуации, когда заняты i единиц ресурса

∑

(4)

p(i) =

p(i₁, . . . , i_n), y_k(i) =

p(i₁, . . . , i_n) i_k.

(i₁,...,in)∈Si

135

Используя p(i) и y_k(i), можно оценить все введенные ранее характеристики

модели. Из определений π_t,k и π_c,k следует

∑

(

)

p(i) s_k - y_k(i)

∑

(5)

π_t,k =

p(i); π_c,k

= i=v-bk+1v

∑(

)

i=v-b_k +1

p(i) s_k - y_k(i)

i=0

Значения y_k, m_k, π_ℓ,k, Λ_k находятся с помощью полученных ранее фор-

мул (3) их косвенной оценки через значения π_t,k, π_c,k и величины s_k, a_k. По-

строим рекурсивный алгоритм оценки p(i) и y_k(i), i = 0, 1, . . . , v. Из обрати-

мости r(t) для (i₁, . . . , i_n) ∈ S следует соотношение детального баланса

(

)

p(i₁, . . . , i_k - 1, . . . , i_n)

s_k - i_k + 1

γ_k = p(i₁,... ,i_k,... ,i_n)i_k.

Просуммируем полученное выражение по всем (i₁, . . . , i_n) ∈ S_i. Используя

определения S_i, p(i), y_k(i), находим искомую рекурсию

(6)

Y_k(i) = P(i - b_k)s_k γ_k - Y_k(i - b_k)γ_k

k = 1,...,n;

∑

P (i) =

b_k Y_k(i).

k=1

Положим значение¹ P (0) = 1. По определению Y_k(0) = 0, k = 1, . . . , n. Выра-

зим значения Y_k(i), k = 1, . . . , n, P (i) через P (0), используя рекурсию (6) и по-

следовательно увеличивая i от 1 до v. Находим величину нормировочной кон-

∑_v

станты N =

P (i), нормированные значения вероятностей p(i) = P (i)/N

i=0

и вспомогательных функций y_k(i) = Y_k(i)/N , i = 0, 1, . . . , v. Рассчитываем

значения характеристик с помощью (5), определения и формулы (3). При

реализации рекурсии для больших значений v может теряться точность вы-

числений. Это происходит из-за наличия отрицательного слагаемого в (6).

В данной ситуации для расчета характеристик рекомендуется использовать

алгоритм свертки [7].

Воспользуемся разработанными алгоритмами для анализа зависимости ха-

рактеристик качества обслуживания заявок от параметров возникающих ин-

формационных потоков и условий допуска заявок к занятию ресурса. Обо-

∑_n

значим через ρ =¹

a_kb_k потенциальную загрузку одного виртуального

k=1

канала (в.к.). Будем предполагать, что b_k занумерованы в порядке возраста-

ния их значений. Рассмотрим модель узла для следующих значений входных

параметров: v = 100; n = 4; b₁ = 1; b₂ = 5; b₃ = 10; b₄ = 20. Величины v и b_k

выражены в виртуальных каналах. Примем, что a_k = vρ/nb_k, s_k = ⌊a_k⌋ + 10,

k = 1,2,3,4. Отсюда следует, что γ_k =ak и потенциальная загрузка ресур-_s

k-ak

са a_kb_k у всех потоков одинакова и равна vρ/n. На рис. 2 показана зависи-

мость π^′c,k = π_c,k/b_k от увеличения ρ.

В ситуации, когда ρ ≈ 1, выполняется соотношение π_c,i/b_i ≈ π_c,j/b_j . Кро-

ме этого, если ρ < 1 и b_i > b_j, то π_c,i/b_i > π_c,j/b_j , если ρ > 1 и b_i > b_j, то

¹ Здесь и далее прописные буквы используются для обозначения ненормированных ве-

личин вероятностей и характеристик, а строчные для нормированных.

136

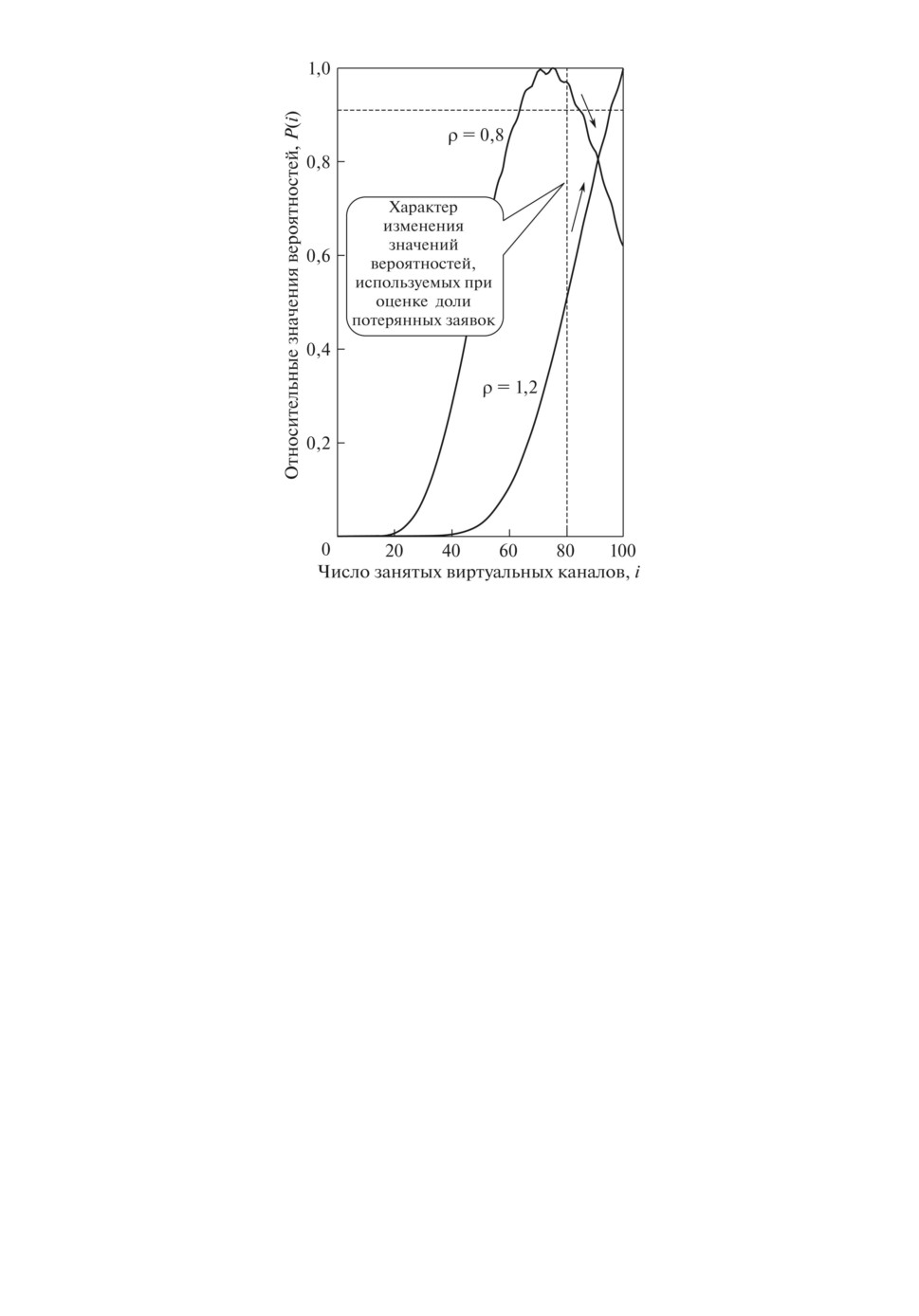
Рис. 4. Зависимость относительных значений P (i) от i

при ρ = 0,8 и ρ = 1,2.

но с числом абонентов, формирующих k-й поток, равным s_k - 1, т.е. на еди-

ницу меньшим, чем в анализируемой модели. Отмеченное изменение числа

абонентов не сказывается сильно на свойствах и величине π_c,k. По этой при-

чине зависимость поведения π_c,k от ρ можно исследовать на примере зави-

симости π_t,k от ρ. По определению π_t,k = p(v) + p(v - 1) + . . . + p(v - b_k + 1).

В этой сумме представлены b_k значений вероятностей состояний с максималь-

ным занятым ресурсом. Зависимость P (i), отнормированных по максималь-

ному значению P (i), показана на рис. 3 (ρ = 1) и рис. 4 (ρ = 0,8 и ρ = 1,2).

Из результатов расчетов видно, что в области ρ ≈ 1 величины P (i), участ-

вующие в определении π_t,k, примерно равны, а для ρ, больших или меньших

единицы, выполняются свойства монотонного убывания (для ρ < 1) и воз-

растания (для ρ > 1). Эти свойства и определяют характер поведения π^′c,k,

отмеченный на рис. 2.

Рассмотрим, какие практические приложения имеет полученный резуль-

тат. При обслуживании потоков мультисервисного трафика возникают про-

блемы с выбором метрик для оценки достаточности ресурса. Трудности свя-

заны с тем, что обычно нормируются интегральные характеристики каче-

ства обслуживания заявок, например, такие, как максимальная доля потерь

заявок, а какие при этом величины потерь у отдельных потоков, остается

неясным. Воспользуемся отмеченными выше свойствами совместного обслу-

живания заявок и покажем, что существуют простые соотношения, которые

могут помочь решить сформулированную проблему.

138

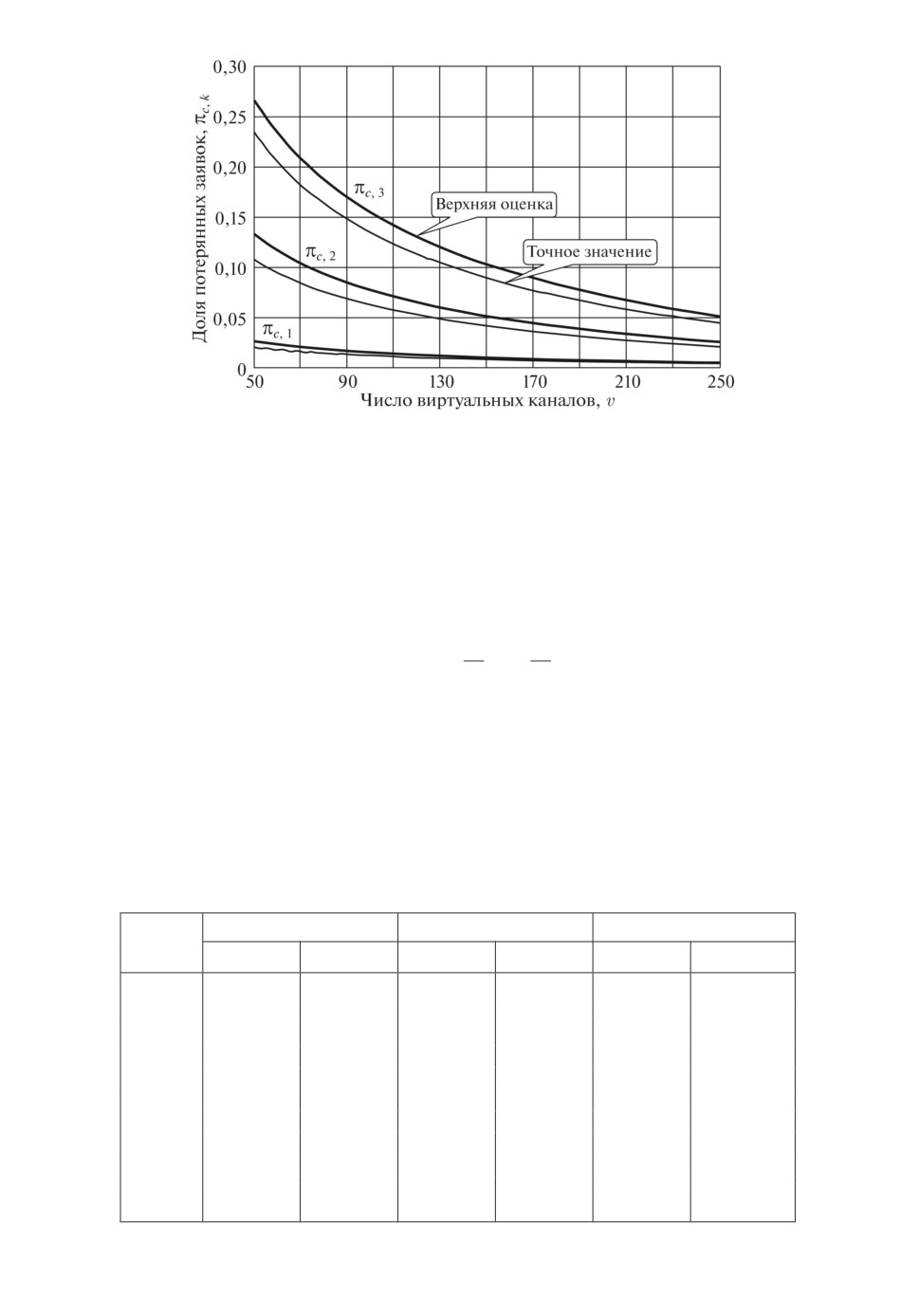
Рис. 5. Точные и приближенные значения потерь в зависимости от v.

Обычно в задачах планирования ρ ≲ 1. Примем далее это допущение.

Предположим, что достаточность ресурса планируется исходя из ограниче-

ния на максимальную долю потерянных заявок maxπc,k = πc,n ≤ π. Из свой-

ства пропорциональности для ρ ≲ 1 находим оценки сверху для потерь заявок

всех потоков

b_k

(7)

π_c,k ≲ π_c,n

=π

b_k .

b_n

На рис. 5 показаны результаты анализа погрешности приближенного рас-

чета потерь при заданном значении максимальной доли потерянных заявок.

Исходные данные те же, что были использованы при вычислении данных,

представленных на рис. 3, за исключением v, которое менялось от 50 до 300.

Нагрузка на канал ρ = 0,8. Приближенные значения π_c,k найдены из соотно-

Анализ погрешности приближенного расчета потерь исходя из известного

значения максимальной доли потерянных заявок

π₁

π₂

π₃

ед.рес.

Точно Прибл.

Точно

Прибл.

0,032887

0,034599

0,170260

0,172995

0,348522

0,345990

0,029118

0,029235

0,144857

0,146175

0,293293

0,292350

100

0,026561

0,026081

0,129868

0,130405

0,260794

0,260809

125

0,024229

0,023859

0,118881

0,119296

0,238268

0,238592

150

0,022739

0,022160

0,111309

0,110798

0,222043

0,221596

175

0,021829

0,020960

0,105821

0,104798

0,209939

0,209596

200

0,020937

0,019936

0,101177

0,099679

0,200654

0,199357

225

0,019929

0,019057

0,096631

0,095287

0,191666

0,190574

250

0,019425

0,018426

0,093898

0,092132

0,185390

0,184264

275

0,018968

0,017774

0,091270

0,088869

0,179780

0,177738

300

0,018323

0,017197

0,088150

0,085986

0,173754

0,171971

139

шений (7) и выделены на рисунке жирной линией. Полученные приближен-

ные значения потерь отличаются высокой точностью особенно для больших

значений ресурса передачи информации.

Особенно высокую точность оценки (7) имеют в области ρ ≈ 1. Соответ-

ствующие результаты приведены в таблице для тех же значений параметров,

что использовались для рис. 5.

6. Эффективный алгоритм оценки объема ресурса

Рассмотрим использование рекурсии (6) для оценки v скорости линии кон-

центрации мультисервисного трафика, требуемой для обслуживания задан-

ных потоков трафика с требуемым качеством. Предложенный трафик ха-

рактеризуется величинами a_k, b_k, s_k, фиксированными на время решения

задачи. Достаточность ресурса оценивается из достижения требуемых зна-

чений π = maxπc,k. Понятно, что сформулированная задача может быть ре-

шена методом перебора. Этот подход имеет два существенных недостатка.

Во-первых, для каждого промежуточного значения объема ресурса r вы-

числяются все ненормированные вероятности состояний P (i), i = 0, 1, . . . , r,

которые затем нормируются. Хотя для оценки π достаточно знать только

b = maxbk нормированных вероятностей состояний с максимальным занятым

ресурсом. Тем самым значительно увеличивается объем вычислительной ра-

боты при определении v. Во-вторых, реализация рекурсии (6) может приве-

сти к вычислительным сложностям из-за применения в (6) относительных

значений P (i), выраженных через P (0). Значение p(0) быстро стремится к

нулю с ростом v. Эта характеристика (6) затрудняет реализацию рекурсии

в программно-аналитических продуктах типа калькуляторов сетевой инфра-

структуры.

Построим алгоритм оценки v, свободный от перечисленных недостатков.

Рекурсия будет вестись по объему имеющегося ресурса r, и при ее реализации

будут использоваться только b нормированных вероятностей состояний моде-

ли с максимальным числом занятых каналов. Обозначим через r переменное

значение ресурса линии, а через p_r(i), y_k,r(i) обозначим зависимость от r для

вероятностей состояний p(i) и вспомогательных функций y_k(i). Аналогично

через y_k(r) и π_c,k(r) обозначим зависимость от r для среднего числа обслу-

живаемых заявок y_k и доли потерянных заявок π_c,k. Реализация алгоритма

включает в себя следующие шаги.

1. Положим p₀(0) = 1. Из (4) следуют соотношения y_k,0(0) = 0, k = 1, . . . , n.

2. Для каждого фиксированного r = 1, 2, . . . находим min(b, r + 1) норми-

рованных вероятностей p_r(i), i = r, r - 1, . . . , max(r - b + 1, 0) и зна-

чений вспомогательных функций y_k,r(i), k = 1, . . . , n, i = r, r - 1, . . . ,

max(r - b + 1, 0) с максимальным занятым ресурсом. Для этого использу-

ются аналогичные вероятности и вспомогательные функции, полученные

на предыдущем шаге. Вначале находится нормировочная константа

∑{

}

p_r-1(r - b_k)s_k - y_k,r-1(r - b_k) b_k γ_k = 1 + S_r-1,

k=1

140

затем нормированные значения вероятностей

S_r-1

p_r(r) =

i=r;

1+S_r-1

p_r-1(i)

p_r(i) =

i = r-1, r-2, ... ,max(r - b + 1,0)

1+S_r-1

и вспомогательных функций

y_k,r-1(i)

y_k,r(i) =

k = 1,...,n; i = r, r-1, ... ,max(r - b + 1,0);

1+S_r-1

y_k(r - 1)

y_k(r) =

+ y_k,r(r), k = 1,... ,n.

1+S_r-1

3. Далее рассчитывается значение функционала, используемого для оцен-

ки достаточности ресурса. В рассматриваемом случае таковым является

π = maxπc,k. Выражение для потерь заявок k-го потока для объема ресур-

са r находится с использованием соотношения (5) и имеет вид

(

)

p_r(i)s_k - y_k,r(i)

π_c,k(r) =i=r-bk+1

s_k - y_k(r)

Величина π сравнивается с его нормативным значением, и если требуемый

уровень потерь не достигнут, то число виртуальных каналов увеличивает-

ся на единицу и расчеты повторяются начиная с п. 2.

Для расчета характеристик и выполнения следующего шага достаточно

знать b вероятностей состояний и соответствующее число значений вспомо-

гательных функций с максимальным числом занятых каналов. Количество

используемых параметров не зависит от объема ресурса. При проведении вы-

числений не возникает проблем с переполнением или исчезновением порядка,

поскольку расчеты выполняются только с нормированными значениями ве-

роятностей состояний модели с максимальным числом занятых каналов. По

условиям анализа модели они имеют наибольшие относительные значения.

По сравнению с традиционным методом оптимизированный алгоритм сокра-

щает расчетную работу при оценке требуемого числа каналов мультисервис-

ного узла доступа примерно в v/(2 +^bn ) раз.

7. Оценка ресурса в условиях дифференцированного обслуживания

В исследуемой модели мультисервисного узла доступа все потоки имеют

одинаковые условия использования ресурса передачи информации. Встро-

им в модель узла процедуры дифференцированного обслуживания потоков

трафика и воспользуемся появляющимися возможностями для решения сле-

дующих двух задач. Первая из них связана с устранением отрицательных

последствий неконтролируемого перераспределения ресурса в пользу отдель-

ных потоков. Вторая относится к анализу процедур управления ресурсом,

141

направленных на повышения эффективности его занятия. Рассмотрим, как

в этих условиях решается задача оценки объема ресурса, необходимого по

нагрузке и качеству обслуживания пользователей услуг связи, а также как

происходит выбор параметров управления ресурсом.

Начнем с первой задачи. Необходимость ее решения возникает при сов-

местной передаче неоднородного трафика в единой транспортной среде. За-

явки с малыми требованиями к ресурсу вытесняют из процесса обслуживания

заявки, имеющие существенные требования к скорости передачи. Самый про-

стой способ выравнивания показателей обслуживания или в предоставлении

преимущества в занятии ресурса заключается в использовании механизмов

его резервирования для выделенной группы потоков. Интерес представля-

ют те способы, которые допускают возможность относительно простой реа-

лизации и оценки эффективности применения. Этими качествами обладает

процедура резервирования, основанная на фильтрации поступающих потоков

заявок, зависящей от номера потока и степени загрузки ресурса.

Вернемся к математическому описанию модели мультисервисного узла

доступа, изложенному в разделе 3, и внесем в него изменения, относящие-

ся к реализации процедуры резервирования. Обозначим через ϕ_k(i) веро-

ятностную функцию, которая будет применяться для фильтрации процес-

са доступа поступающих заявок к ресурсу в зависимости от значений k

номера потока и i общего числа занятых единиц ресурса. Заявка k-го по-

тока, поступившая в момент занятости i единиц ресурса, принимается к

обслуживанию с вероятностью 1 - ϕ_k(i), а с противоположной вероятно-

стью ϕ_k(i) заявка получает отказ и не возобновляется. В остальном схема

функционирования узла не меняется. Сохраним для параметров и харак-

теристик обобщенной модели те же обозначения, что были использованы

в разделе 3.

Динамика изменения состояний (i₁, . . . , i_n) описывается многомерным

марковским процессом r(t) = (i₁(t), . . . , i_n(t)) с компонентами, введенными

в разделе 4, и изменениями в пространстве состояний S, вытекающими из

применения функций ϕ_k(i). Значения p(i₁, . . . , i_n) стационарных вероятно-

стей r(t) связаны системой уравнений равновесия, имеющей вид

(

)

∑

(

)

(8)

P (i₁, . . . , i_n)

(s_k - i_k)ζ_k

1 - ϕ_k(i)

+ ik µk I(i_k > 0)

k=1

∑

(

)

= P(i₁,...,i_k - 1,...,i_n)(s_k - i_k + 1)ζ_k

1 - ϕ_k(i - b_k)

I(i_k > 0) +

k=1

∑

+ P(i₁,...,i_k + 1,...,i_n)(i_k + 1)µk I(i_k + 1 ≤ s_k,i + b_k ≤ v),

k=1

(i₁, . . . , i_n) ∈ S.

В (8) для состояния (i₁, . . . , i_n) ∈ S значение i определяет величину занятого

ресурса i = i₁b₁ + . . . + i_nb_n, а I(·) индикаторная функция события. Най-

денные значения P (i₁, . . . , i_n) необходимо нормировать.

142

Характеристики качества обслуживания заявок определяются по анало-

гии с (2). Приведем несколько определений:

∑

(9)

π_t,k =

p(i₁, . . . , i_n) ϕ_k

(i);

(i₁,...,in)∈S

∑

m_k =

p(i₁, . . . , i_n) i_k b_k; y_k = m_k/b_k;

(i₁,...,in)∈S

∑

p(i₁, . . . , i_n) (s_k - i_k) ϕ_k(i)

(i₁,...,in)∈S

π_c,k =

∑

;

π_ℓ,k = (a_k - y_k)/a_k.

p(i₁, . . . , i_n) (s_k - i_k)

(i₁,...,in)∈S

Для оценки объема ресурса и выбора параметров его резервирования необхо-

димо решить систему уравнений (8). Сделать это можно итерационным мето-

дом Гаусса-Зейделя. Для оценки характеристик можно также использовать

и достаточно обоснованные приближенные методы.

Результаты расчетов показывают, что при совместной передаче неоднород-

ного трафика в единой транспортной среде заявки с малыми требованиями

к ресурсу имеют существенно меньшие потери и ограничивают тем самым

допуск к ресурсу для других заявок. Наличие механизма резервирования да-

ет возможность выравнять потери заявок при обслуживании неоднородного

трафика, а также создать условия для использования определенного объема

ресурса только заявками выделенной группы потоков. Покажем это. Для ре-

шения первой задачи достаточно выбрать значения функций фильтрации из

соотношений (предполагается, что b_k занумерованы в порядке возрастания

значений):

(10)

ϕk(i) = 1, i = v - bn + 1, v - bn

+ 2, . . . , v; k = 1, . . . , n.

В этой ситуации доли времени занятости ресурса для всех потоков будут

одинаковыми, поскольку выполняется соотношение

∑

(11)

π_t,k =

p(i₁, . . . , i_n)ϕ_k(i) =

p(i), k = 1, . . . , n.

(i₁,...,in)∈S

i=v-bn+1

Допустим, ставится задача предоставить в эксклюзивное пользование z вир-

туальных каналов потокам заявок с номерами 2, 3, . . . , n. В этой ситуации

функцию фильтрации заявок выберем из соотношений

ϕk(i) = 1, i = v - b1 - z + 1, v - b1 - z + 2, . . . , v; k = 1;

(12)

ϕk(i) = 1, i = v - bk + 1, v - bk + 2, . . . , v; k = 2, 3, . . . , n.

В результате такого выбора функций блокировки заявки потоков с номе-

рами k ≥ 2 используют все доступные каналы узла. Причем z каналов из v

имеющихся могут использоваться только этими потоками. Заявки 1-го по-

тока не могут занять более v - z каналов. Увеличивая значение z, можно

143

Рис. 6. Оценка величин ресурса и уровня резервирования, обеспечивающих

заданные характеристики обслуживания заявок мультисервисного узла до-

ступа.

уменьшить потери потоков с номерами k ≥ 2 до требуемых величин. Правда,

этот результат достигается за счет ухудшения качества обслуживания заявок

1-го потока. По этой причине наряду с использованием резервирования для

выравнивания потерь заявок необходимо также увеличивать и общий объем

ресурса с тем, чтобы качество обслуживания всех потоков было в пределах

нормы.

Рассмотрим такую постановку задачи. Предположим, что требуется най-

ти значения v и z такие, чтобы потери ¾легкого¿ трафика (1-й поток) были

менее π₁, а потери ¾тяжелого¿ трафика (потоки с номерами k ≥ 2) ме-

нее π₂. Для решения задачи поступим следующим образом. После выравни-

вания потерь только ¾тяжелых¿ заявок с использованием правила (10) для

них определяется число z резервируемых каналов, обеспечивающее требуе-

мое соотношение потерь для всех потоков трафика. Если значение z с такими

свойствами не находится, то v увеличивается на единицу и расчеты повто-

ряются. Поскольку можно ожидать, что с ростом v при фиксированном z

потери уменьшаются, а с увеличением z при фиксированном v потери ¾лег-

кого¿ трафика увеличиваются, ¾тяжелого¿ падают, то всегда можно найти

требуемое решение. Иллюстрацией этого подхода служат данные, приведен-

ные на рис. 6, где показаны зависимости потерь заявок π_t,k от увеличения v

и z.

Характеристики найдены для следующих значений входных парамет-

ров: v = 200; n = 3; b₁ = 1; µ₁ = 1; b₂ = 5; µ₂ = 1; b₃ = 10; µ₃ = 1. Величи-

ны v, b_k и z выражены в виртуальных каналах. Примем, что a_k = vρ/nb_k,

s_k = ⌊a_k⌋ + 10, k = 1,2,3. Здесь ρ

потенциальная нагрузка одного в.к.,

ζ_k =−ks_ka_k .Требуемыеуровнипотерьπ1^=0,01;π2^{=0,001.Цифрой1обо-}

значена доля потерь по времени для 1-го потока, цифрой 2 для 2-го и

3-го потоков (значения потерь равны в соответствии с (10)). Начальное зна-

чение объема ресурса v = 200. Последовательное увеличение v, использова-

ние процедуры резервирования и проверка условия попадания значений по-

терь в требуемый коридор π_t,1 ≤ 0,01; π_t,2 = π_t,3 ≤ 0,001 приводят к следую-

144

щим значениям: v = 374, z = 19. При данном выборе объема ресурса и пара-

метров резервирования выполняются соотношения: π_t,1 = 0,007929 ≤ 0,01 и

π_t,2 = π_t,3 = 0,000969 ≤ 0,001.

В заключение отметим следующее. Если функция внутренней блокировки

равна единице, то осуществляется процедура ¾жесткого¿ контроля за допус-

ком заявок. Она дает возможность создать условия для их дифференциро-

ванного обслуживания. Однако это происходит за счет некоторого уменьше-

ния коэффициента использования канала. Отрицательные последствия этого

эффекта можно ослабить, если выполнить допуск заявок с вероятностью,

меньшей единицы. В этом случае можно увеличить коэффициент исполь-

зования канала за счет некоторого изменения условий дифференцированно-

го обслуживания заявок. Понятно, что в такой постановке выбор значений

функции внутренней блокировки зависит от экономических условий обслу-

живания заявок. Исследование этой проблемы в данной работе не рассмат-

ривается.

Теперь обратимся к решению второй из сформулированных в начале раз-

дела задач. Информационные потоки, обладающие свойством эластичности²,

можно передавать с большей скоростью, используя для этих целей ресурс,

оставшийся свободным от обслуживания трафика реального времени. Вер-

немся к математическому описанию модели мультисервисного узла доступа,

изложенному в разделе 3, и внесем в нее изменения, относящиеся к ускорен-

ной передаче данных.

Предположим, что свойством эластичности обладает дополнительный

(n + 1)-й поток и его параметры не зависят от номера потока. Заявки на пере-

дачу данных (файлов) поступают от конечной группы абонентов. Обозначим

через s их число. Заявки от одного абонента поступают через случайное вре-

мя, имеющее экспоненциальное распределение с параметром ζ. Для простоты

предположим, что для обслуживания заявки требуется как минимум один

виртуальный канал. Время обслуживания заявки одним каналом имеет экс-

поненциальное распределение с параметром µ. Таким образом, объем файла

имеет экспоненциальное распределение со средним значением F = u/µ, вы-

раженным в битах.

Построим процедуру динамического распределения ресурса при организа-

ции пересылки файлов. Допустим, что на обслуживании находятся d заявок

на передачу данных и для этого используются (v - i) виртуальных каналов,

оставшихся свободными от обслуживания трафика реального времени. Пусть

g = ⌊^v-id⌋ целая часть от деления (v - i) на d. Разделим d заявок на две

группы d = d₁ + d₂, где d₁ = v - i - g d, а d₂ = (g + 1) d - (v - i). Для обслу-

живания заявок из групп d₁ и d₂ используются соответственно (g + 1) и g

виртуальных каналов. При выбранном распределении ресурса все (v - i) сво-

бодных каналов занимаются на обслуживание d принятых заявок на передачу

данных, а время до освобождения первой из d заявок имеет экспоненциальное

распределение с параметром (v - i)µ. Понятно, что в рассматриваемых усло-

виях скорость передачи каждого файла возрастает с появлением свободных

² К ним относятся передача файлов и других подобных им данных, допускающая

небольшую задержку без потери качества обслуживания.

145

каналов и, наоборот, уменьшается при их сокращении, не становясь при этом

меньше скорости, обеспечиваемой одним виртуальным каналом. В остальном

схема функционирования узла не меняется. Сохраним для параметров и ха-

рактеристик обобщенной модели те же обозначения, что были использованы

в разделе 3.

Пусть i_k(t)

число заявок k-го потока на передачу трафика реального

времени, обслуживаемых в момент времени t, а d(t) число заявок на переда-

чу файлов, обслуживаемых в момент времени t. Динами(а изменения состо)

ний модели описывается марковским процессом r(t) =

i₁(t),... ,i_n(t),d(t)

определенным на пространстве состояний S и состоящем из векторов

(i₁, . . . , i_n, d) с компонентами

{

⌊v⌋};

i₁ = 0,1,... ,min s₁,

b₁

{

⌊v-i₁b₁ -...-i_n-1b_n-1⌋};...;

i_n = 0,1,... ,min s_n,

b_n

d = 0,1,... ,v - i1 b₁ - ... - in b_n.

Значения p(i₁, . . . , i_n, d) стационарных вероятностей r(t) связаны системой

уравнений равновесия, имеющей вид

∑((

)

(13)

P (i₁, . . . , i_n, d)

(s_k - i_k)ζ_kI(i + d + b_k ≤ v) + i_k µ_k I(i_k > 0)

k=1

)

+ (s - d)ζI(i + d + 1 ≤ v) + (v - i)µI(d > 0)

∑

= P(i₁,...,i_k - 1,...,i_n,d)(s_k - i_k + 1)ζk I(i_k > 0) +

k=1

∑

+ P(i₁,...,i_k + 1,...,i_n,d)(i_k + 1)µk I(i_k + 1 ≤ s_k,i + d + b_k ≤ v) +

k=1

+ P(i₁,...,i_n,d - 1)(s - d + 1)ζ I(d > 0) +

+ P(i₁,...,i_n,d + 1)(v - i)µI(d + 1 ≤ s,i + d + 1 ≤ v),

(i₁, . . . , i_n, d) ∈ S.

В (13) для состояния (i₁, . . . , i_n, d) ∈ S значение i определяет величину ре-

сурса, занятого трафиком сервисов реального времени, i = i₁b₁ + . . . + i_nb_n,

а I(·)

индикаторная функция события. Найденные значения P (i₁, . . . , i_n)

необходимо нормировать.

Характеристики качества обслуживания заявок на передачу трафика ре-

ального времени определяются по аналогии с (2). Показатели обслуживания

эластичного трафика оценим долей времени недоступности ресурса переда-

чи π_t; долей потерянных заявок π_c; средним числом обслуживаемых заявок y;

146

средним временем доставки файла t_d; средним числом виртуальных каналов,

используемых для передачи одного файла b_f :

∑

(14)

π_t =

p(i₁, . . . , i_n

, d);

(i₁,...,in,d)∈S|i+d+1>v

∑

p(i₁, . . . , i_n, d)(s - d)

(i₁,...,in,d)∈S|i+d+1>v

π_c =

∑

;

p(i₁, . . . , i_n, d)(s - d)

(i₁,...,in,d)∈S

∑

p(i₁, . . . , i_n, d)d; t_d =

;

(s - y)ζ(1 - π_c)

(i₁,...,in,d)∈S

∑

b_f =

p(i₁, . . . , i_n, d)(v - i) =

t_dµ

(i₁,...,in,d)∈S|d>0

Для определения объема необходимого ресурса и оценки введенных пока-

зателей эффективности использования каналов при обслуживании эластич-

ного трафика необходимо решить систему уравнений (13). Сделать это мож-

но итерационным методом Гаусса-Зейделя. Для оценки характеристик мож-

но также применять приближенные алгоритмы. Построим соответствующую

процедуру. Воспользуемся тем, что требуемый объем ресурса соответству-

ет области малых потерь заявок. В этой ситуации совместное обслуживание

трафика реального времени и эластичного трафика данных обладает свой-

ствами, упрощающими оценку характеристик. Рассмотрим момент поступле-

ния заявки на передачу файла. Обозначим через i число каналов, занятых в

этот момент на обслуживание трафика реального времени. Оставшиеся v - i

каналов используются для передачи файлов. Применим технику декомпози-

ции и оценим по отдельности процесс обслуживания трафика реального вре-

мени и данных. Пусть p(i) вероятность занятости i каналов на передачу

трафика реального времени в условиях, когда трафик данных не поступа-

ет, i = 0, 1, . . . , v. Величины p(i) находятся из рекурсивных соотношений (6).

Предположим теперь, что в модели рассматривается обслуживание только

заявок на передачу файлов. Обозначим через y(v - i) и t_d(v - i) соответ-

ственно среднее число заявок на передачу файлов и среднее время передачи

файла при числе виртуальных каналов, равном (v - i). Несложно показать,

что значения введенных характеристик рассчитываются из выражений:

∑

y(v - i)

(15)

y(v - i) =

p_d(d)d; t_d(v - i) =

∑

d=0

p_d(d)(s - d)ζ

d=0

где вероятности p_d(d) находятся из рекурсивных соотношений

p_d(d + 1)(v - i)µ = p_d(d)(s - d)ζ, d = 0,1,... ,v - i - 1

147

0,5

0,4

0,3

Оценка

0,2

Точное

значение

Точное

значение

0,1

Оценка

0,8

0,7

0,6

0,5

0,4

0,3 0,2

0,8

0,7

0,6

0,5

0,4

0,3 0,2

Нагрузка на канал, r

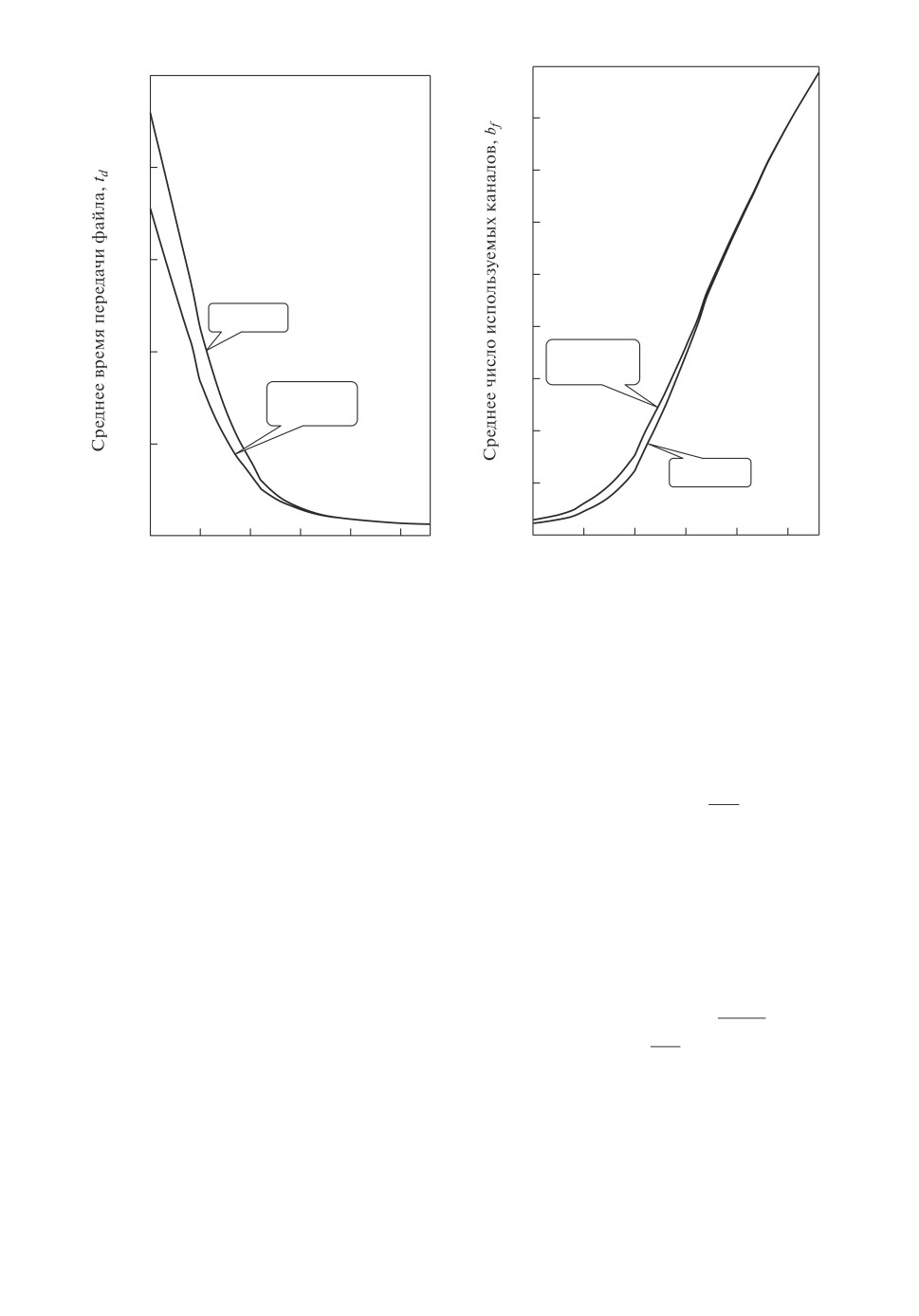
Рис. 7. Точная и приближенная

Рис. 8. Точная и приближенная

оценки t_d.

оценки b_f .

с последующей их нормировкой. Обозначим получаемые оценки характери-

стик передачи эластичного трафика теми же символами, что применялись в

исследуемой модели. Для их расчета используются соотношения

∑

(16)

y = p(i)y(v - i),

t_d =

p(i)t_d(v - i),

b_f =

t_dµ

i=0

Оценим погрешность приближенного алгоритма расчета характеристик

передачи эластичного трафика. Рассмотрим процесс совместного обслужи-

вания трафика реального времени и эластичных данных для модели узла

доступа со следующими фиксированными значениями входных параметров:

v = 100; n = 2; b₁ = 5; µ₁ = 1; b₂ = 10; µ₂ = 1. Величины v, b₁ и b₂ выражены в

виртуальных каналах. Примем, что a₁ = vρ/3b₁, a₂ = vρ/3b₂, s_k = ⌊a_k⌋ + 10,

k = 1,2. Здесь ρ потенциальная нагрузка одного в.к., а ζ_k =ak

. Пара-

s_k-a_k

метры эластичного трафика a = vρ/3, s = ⌊a⌋ + 10, ζ =^as-a , µ = 1. Точные

и приближенные значения t_d и b_f в зависимости от величины ρ приведены

соответственно на рис. 7 и рис. 8. Точные величины характеристик находи-

лись в результате решения системы уравнений (13) итерационным методом

Гаусса-Зейделя, а приближенные с использованием выражений (16).

Анализ погрешности вычислений позволяет сделать вывод о хорошей точ-

ности расчетов особенно в области малых потерь, характерных для решения

задач планирования требуемого объема ресурса. Сформулируем последова-

148

Рис. 9. Оценка требуемого объема ресурса при передаче эластичного трафика.

тельность действий, которую можно использовать для решения этой задачи.

Предположим, что заданы параметры трафика реального времени n, s_k, ζ_k,

b_k, µ_k и эластичных данных s, ζ, µ. Требуется определить число каналов v,

обеспечивающее выполнение ограничений на долю потерянных заявок

(17)

max(π₁, . . . , π_n, π_c

)<π

и среднее время передачи файла

(18)

t_d

≤ t.

Если вести передачу эластичного трафика на условиях трафика реально-

го времени, то это приведет к увеличению доли потерянных заявок и даст

возможность получить обоснованную оценку числа каналов v₁ в смысле вы-

полнения неравенства (17). Для решения этой задачи используется либо ре-

курсия (6), либо алгоритм, рассмотренный в разделе 6. Далее при последо-

вательном увеличении v₁ определяется величина ресурса v, обеспечивающая

выполнение неравенства (18). Приведем пример реализации сформулирован-

ного алгоритма.

Рассмотрим потоки трафика со следующими значениями входных па-

раметров: n = 2; b₁ = 3; b₂ = 5, µ₁ = 1, µ₂ = 1. Величины v, b₁ и b₂ вы-

ражены в виртуальных каналах. Примем, что a₁ = 75ρ/3b₁, a₂ = 75ρ/3b₂,

s_k = ⌊a_k⌋ + 10, k = 1,2. Здесь ρ

потенциальная нагрузка одного в.к.,

ζ_k =−ks_ka_k .Параметрыэластичноготрафикаa=75ρ/3,s=⌊a⌋+10,ζ

s-a

µ = 1. Контрольные значения параметров π = 0,03, t = 0,2. После выполне-

ния 1-го этапа получаем v₁ = 99. Результаты реализации 2-го этапа пред-

ставлены на рис. 9, где показана зависимость t_d от v. Приведены данные

приближенного вычисления t_d с использованием (16) и точные величины, по-

лученные с помощью решения (13). Для t = 0,2 приближенный расчет дает

ответ v = 112, а точный v = 110. Результаты вычислений отличаются хоро-

шей точностью, приемлемой для практических приложений.

149

В заключение отметим следующее. Выбор экспоненциального распределе-

ния для описания времени обслуживания заявок упрощает моделирование

мультисервисного узла доступа. Если положить равными нулю трафик ре-

ального времени или эластичный трафик, то расчетные формулы и алгорит-

мы перестанут зависеть от функции распределения времени обслуживания

заявок [10, 21]. Это свойство дает основание ожидать слабую зависимость

полученных результатов от выбора соответствующей функции и для модели

совместного обслуживания заявок. Отмеченное свойство нуждается в чис-

ленном анализе средствами имитационного моделирования и здесь не иссле-

дуется.

8. Заключение

Построена и исследована математическая модель распределения ресурса

передачи информации мультисервисного узла доступа. В модели рассматри-

вается произвольное число потоков мультимедийного трафика, которые раз-

личаются интенсивностью поступления заявок, величиной ресурса, исполь-

зуемого для обслуживания одной заявки, и временем занятия ресурса. Интер-

валы времени между поступлением заявок имеют экспоненциальное распре-

деление с параметром, зависящим от числа заявок рассматриваемого пото-

ка, находящихся на обслуживании. Построен рекурсивный алгоритм оценки

характеристик. Установлены соотношения между интегральными и потоко-

выми характеристиками качества обслуживания заявок, которые упрощают

выбор метрики при решении задач планирования ресурса узла доступа. По-

строен эффективный алгоритм оценки объема ресурса, требуемого для обслу-

живания заданных потоков трафика с необходимым качеством. Эффектив-

ность расчетной процедуры достигается в результате организации рекурсии

по объему ресурса и использовании нормированных значений вероятностей

состояний. Рассмотрено решение задачи оценки необходимого объема ресурса

для модели мультисервисного узла, допускающего использование механизмов

резервирования ресурса и его динамического распределения при обслужива-

нии эластичного трафика. Приведены численные примеры, иллюстрирующие

особенности реализации построенных расчетных процедур. Построенную мо-

дель и методы ее расчета можно обобщить на случаи, когда поступление

заявок носит групповой характер.

СПИСОК ЛИТЕРАТУРЫ

1. Fortet R., Grandjean Ch. Congestion in a Loss System When Some Calls Want Sev-

eral Devices Simultaneously // Electr. Communicat. 1964. V. 39. No. 4. P. 513-526.

2. Kaufman J.S. Blocking in a shared resource environment // IEEE Transact. Com-

municat. 1981. V. 29. No. 1. P. 1474-1481.

3. Roberts J.W. A service system with heterogenous user requirements application to

multi-service telecommunications systems / Performance of Data Communication

Systems and their Applications. Pujolle G. (ed.). North Holland, 1981. P. 423-431.

4. Delbrouck L.E.N. On the Steady-State Distribution in a Service Facility Carrying

Mixtures of Traffic with Different Peakedness Factor and Capacity Requirements //

IEEE Transactions on Communications. 1983. V. COM-31. P. 1209-1211.

150

Broadband network traffic. Performance evaluation and design of broadband multi-

service networks. Final report of action COST 242 / James Roberts (ed). Lecture

notes in computer sciences. Springer, 1996.

Ross K.W. Multiservice loss models for broadband telecommunication networks. Lon-

don: Springer, 1995.

Iversen V.B. Teletraffic Engineering and Network Planning. Technical University of

Denmark, May. 2010.

Степанов С.Н. Теория телетрафика: концепции, модели, приложения. М.: Го-

рячая линия - Телеком, 2015.

Степанов С.Н., Степанов М.С. Планирование ресурса передачи информации

соединительных линий мультисервисных иерархических сетей доступа // АиТ.

2018. № 8. С. 66-80.

Stepanov S.N., Stepanov M.S. Planning the Resource of Information Transmission for

Connection Lines of Multiservice Hierarchical Access Networks // Autom. Remote

Control. 2018. V. 79. No. 8. P. 1422-1433.

10.

Bonald T., Virtamo J. A recursive formula for multirate systems with elastic traf-

fic // IEEE Communicat. Lett. 2005. V. 9. No. 8. P. 753-755.

11.

Степанов С.Н., Степанов М.С. Планирование ресурса передачи при совмест-

ном обслуживании мультисервисного трафика реального времени и эластичного

трафика данных // АиТ. 2017. № 11. C. 79-93.

Stepanov S.N., Stepanov M.S. Planning Transmission Resource at Joint Servicing of

the Multiservice Real Time and Elastic Data Traffics // Autom. Remote Control.

2017. V. 78. No. 11. P. 2004-2015.

12.

Iversen V.B., Stepanov S.N. The optimal dimensioning of multi-service links //

Proc. COST-285 Mid-term Symposium. Munchen, September 8-10, 2005. Chapter 7

(pp. 151-178) in A. Nejat Ince & Ercan Topuz (editors): Modeling and simulation

tools for emerging telecommunication networks. Springer, 2006.

13.

Berezner S.A., Krzesinski A.E. An Efficient Stable Recursion to Compute Multiser-

vice Blocking Probabilities // Performance Evaluation. 2001. V. 43. P. 151-164.

14.

Begishev V., Petrov V., Samuylov A., Moltchanov D., Andreev S., Koucheryavy Y.,

Samouylov K. Resource Allocation and Sharing for Heterogeneous Data Collection

over Conventional 3GPP LTE and Emerging NB-IoT Technologies // Comput. Com-

municat. 2018. V. 120. No. 2. P. 93-101.

15.

Shorgin S., Samouylov K., Gaidamaka Y., Chukarin A., Buturlin I., Begishev V.

Modeling Radio Resource Allocation Scheme with Fixed Transmission Zones for

Multiservice M2M Communications in Wireless IoT Infrastructure // Lecture Notes

Comput. Scie., Springer, Cham. 2015. V. 9012. P. 473-483.

16.

Степанов С.Н., Степанов М.С. Эффективный алгоритм оценки требуемого

объема ресурса беспроводных систем связи при совместном обслуживании гете-

рогенного трафика устройств интернета вещей // АиТ. 2019. № 11. C. 108-126.

Stepanov S.N., Stepanov M.S. Efficient Algorithm for Evaluating the Required Vol-

ume of Resource in Wireless Communication Systems under Joint Servicing of Het-

erogeneous Traffic for the Internet of Things // Autom. Remote Control. 2019. V. 80.

No. 11. P. 2017-2032.

17.

Степанов С.Н. Модель совместного обслуживания трафика сервисов реального

времени и данных. I // АиТ. 2011. № 4. С. 121-132.

Stepanov S.N. Model of Joint Servicing of Real-Time Service Traffic and Data Traf-

fic. I // Autom. Remote Control. 2011. V. 72. No. 4. P. 787-797.

151

18. Степанов С.Н. Модель совместного обслуживания трафика сервисов реального

времени и данных. II // АиТ. 2011. № 5. С. 139-147.

Stepanov S.N. Model of Joint Servicing of Real-Time Service Traffic and Data Traf-

fic. II // Autom. Remote Control. 2011. V. 72. No. 5. P. 1028-1035.

19. Evans J., Filsfils C. Deploying IP and MPLS QOS for Multiservice Networks. Theory

and Practice / The Morgan Kaufmann Series in Networking. Elsevier Ltd, 2007.

20. Kelly F.P. Notes on effective bandwidths. In: F. Kelly, S. Zachary and I. Ziedi-

nis (Eds.), Stochastic Networks: Theory and Applications Telecommunications Net-

works. Volume 4 of Royal Statistical Society Lecture Notes Series, Oxford. 1996.

P. 141-168. Oxford University Press.

21. Bonald T., Feuillet M. Network Performance Analysis. United Kingdom, London:

Wiley, 2011.

22. Bonald T., Comte C. The multi-source model for dimensioning data networks //

Computer Networks, 2016 (10.1016/j.comnet.2016.03.019. hal-01314992).

23. Башарин Г.П. Лекции по математической теории телетрафика: Учеб. пособие.

Изд. 3-е исправ. и доп. М.: Изд-во РУДН, 2009.

Статья представлена к публикации членом редколлегии А.И. Ляховым.

Поступила в редакцию 17.03.2000

После доработки 15.05.2020

Принята к публикации 09.07.2020

152