Автоматика и телемеханика, № 2, 2020

(Дальневосточный федеральный университет, Владивосток;

Институт проблем морских технологий ДВО РАН, Владивосток),

А.В. ЗУЕВ, канд. техн. наук (zuev@dvo.ru)

(Институт проблем морских технологий ДВО РАН, Владивосток;

Университет Иннополис, Иннополис),

А.Е. ШУМСКИЙ, д-р техн. наук (a.e.shumsky@yandex.con)

(Дальневосточный федеральный университет, Владивосток)

ДИАГНОСТИРОВАНИЕ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ:

ПОДХОД НА ОСНОВЕ СКОЛЬЗЯЩИХ НАБЛЮДАТЕЛЕЙ¹

Рассматривается задача функционального диагностирования техниче-

ских систем, описываемых линейными динамическими моделями, в при-

сутствии возмущений. Для решения задач обнаружения, поиска и иден-

тификации дефектов используется метод на основе скользящих наблюда-

телей. Предлагаются модификации этого метода, позволяющие ослабить

ограничения на его реализацию по сравнению с известными результатами

и добиться уменьшения сложности средств диагностирования.

Ключевые слова: линейные системы, диагностирование, идентификация

дефектов, скользящие наблюдатели.

DOI: 10.31857/S0005231020020026

1. Введение и постановка задачи

Работа посвящена решению задачи функционального диагностирования

(ФД) технических систем в рамках концепции аналитической избыточности.

Согласно этой концепции ФД осуществляется путем проверки соотношений,

существующих между входами и выходами системы, измеренными на конеч-

ном интервале времени. Процесс ФД включает в себя генерацию невязки как

результата рассогласования между поведением системы и ее эталонной моде-

ли и принятием решений путем оценки полученной невязки.

Задача ФД интенсивно исследуется уже более 30 лет, см., например, об-

зоры [1-3] и книги [4-7]. Были изучены различные модели технических си-

стем — линейные, полиномиальные, нелинейные, сингулярные, гибридные;

разработано несколько методов диагностирования — диагностические наблю-

датели, фильтры Калмана, соотношения паритета, идентификация. Одним

из методов идентификации является метод, основанный на наблюдателях,

использующих особенности скользящих режимов, детально рассмотренных

в [8]; для простоты будем далее называть такие наблюдатели скользящими.

¹ Работа выполнена при финансовой поддержке Российского научного фонда, проект

№ 16-19-00046-П (разработан метод построения скользящих наблюдателей) и грантом Пре-

зидента РФ МК-1987.2018.8 (выполнен синтез наблюдателей для идентификации дефек-

тов).

Скользящие наблюдатели используются для решения задачи идентифи-

кации дефектов, в линейных [9-11], нелинейных [12-14] и сингулярных си-

стемах [15], для оценивания неизмеряемых компонент вектора состояния и

внешних возмущений в нелинейных системах [16, 17], для обеспечения отка-

зоустойчивого управления [18], в ряде практических приложений [19-22].

В настоящей работе по аналогии с [9, 10] рассматриваются линейные систе-

мы, для которых решается задача идентификации дефектов в присутствии

возмущений, но при наложении менее жестких, нежели в [9, 10, 13], ограни-

чений на класс рассматриваемых систем. Кроме того, предлагаемый подход

позволяет добиться уменьшения сложности средств диагностирования.

Рассматривается класс систем, описываемых линейной динамической мо-

делью

x(t) = F x(t) + Gu(t) + Dd(t) + Lρ(t),

(1.1)

y(t) = Hx(t),

где x(t) ∈ Rⁿ, u(t) ∈ R^m, y(t) ∈ R^l — векторы состояния, управления и вы-

хода, F , G, H, D и L — постоянные матрицы соответствующих размеров,

d(t) ∈ R^q — функция, описывающая дефекты: при их отсутствии d(t) = 0,

после появления дефекта d(t) становится неизвестной ограниченной функци-

ей времени, ρ(t) ∈ R^p — возмущение, предполагается, что ρ(t) — неизвестная

ограниченная функция времени.

Коротко напомним некоторые положения и результаты из [10, 13], исполь-

зуемые в настоящей работе.

В [10] предполагается, что система (1.1) при ρ(t) = 0 удовлетворяет сле-

дующим условиям: 1) q ≤ l < n, 2) rank (HD) = q, 3) инвариантные нули

тройки (F, D, H) лежат в C_-. Известно, что в этих предположениях суще-

(

)

z₁

ствует преобразование координат

= Tx для некоторой невырожден-

z₂

ной матрицы T такое, что в новых координатах система описывается урав-

нениями

Ż₁(t) = F₁₁z₁(t) + F₁₂z₂(t) + G₁u(t),

Ż₂(t) = F₂₁z₁(t) + F₂₂z₂(t) + G₂u(t) + D₂d(t),

y(t) = z₂(t),

где z₁(t) ∈ R^n-l, z₂(t) ∈ R^l и матрица F₁₁ устойчива. Характерной особенно-

стью преобразованной системы является то, что rank (D₂) = q, функция d(t)

входит только во вторую подсистему, а ее вектор выхода совпадает с векто-

ром состояния этой подсистемы; это существенно используется в дальнейшем

решении.

Для оценки функции d(t) строится скользящий наблюдатель

z₁(t) = F₁₁z₁(t) + F₁₂z₂(t) + G₁u(t) - F₁₂e_y(t),

z₂(t) = F₂₁z₁(t) + F₂₂z₂(t) + G₂u(t) - (F₂₂ - F∗22)e_y(t) + v(t),

ŷ(t) = z₂(t),

где e_y(t) = ŷ(t) - y(t), F∗22 — некоторая устойчивая матрица, разрывная функ-

ция v(t) определяется соотношением

⎧

⎨

P₂e_y(t)

-g∥D₂∥

если e_y(t) = 0,

v(t) =

∥P₂e_y(t)∥

⎩

в противном случае,

где P₂ ∈ R^l×l — матрица Ляпунова для F∗22, скаляр g выбирается из усло-

вия g > ∥d(t)∥. В [10] обосновывается, что разрывная функция v(t) может

быть заменена непрерывной аппроксимирующей функцией

P₂e_y(t)

(1.2)

v_δ(t) = -g∥D₂∥

∥P₂e_y(t)∥ + δ

где δ — малое положительное число. Тогда, поскольку rank (D₂) = q, функ-

ция d(t) может быть оценена с высокой степенью точности в виде

P₂e_y(t)

d(t) = -g∥D₂∥(D^T2D₂)-1D^T

² ∥P₂e_y(t)∥ + δ

В отличие от [10] в [13] задача идентификации дефекта решается при

наличии возмущений, когда ρ(t) = 0, в предположениях q = 1, p < l < n и

rank (HL) = rank (L), что позволяет представить систему (1.1) в виде

Ż₁(t) = F₁₁z₁(t) + F₁₂z₂(t) + G₁u(t) + D₁d(t),

w₁(t) = H₁₁z₁(t),

Ż₂(t) = F₂₁z₁(t) + F₂₂z₂(t) + G₂u(t) + D₂d(t) + L₂ρ(t),

w₂(t) = H₂₂z₂(t),

(

)

(

)

z₁

w₁

где z₁(t) ∈ R^n-q, z₂(t) ∈ R^q,

= Tx,

= Sy для некоторых невы-

z₂

w₂

рожденных матриц T и S. Далее при некоторых дополнительных предполо-

жениях строится два скользящих наблюдателя и на основе первого из них

производится оценка скалярной функции d(t).

Отметим, что в простейшем случае условие rank (HL) = rank (L) означает,

что возмущение входит в уравнения тех переменных системы (1.1), значения

которых измеряются.

В настоящей работе по аналогии с [13] задача идентификации дефекта ре-

шается при наличии возмущений с условием q ≤ l < n, однако предположение

rank (HL) = rank (L) не делается. Кроме того, строится только один скользя-

щий наблюдатель, причем пониженной размерности, позволяющий оценить

векторную функцию d(t).

Следует также отметить работу [23], в основе которой (как и в настоящей

работе) лежит идея использования редуцированной (имеющей меньшую раз-

мерность) модели исходной системы, которая, однако, реализуется в настоя-

щей работе и в [23] различными способами. Кроме того, в отличие от настоя-

щей работы, где решается задача идентификации дефекта, в [23] скользящий

наблюдатель применяется для оценки величины возмущения, которое далее

используется в строящемся диагностическом наблюдателе для компенсации

этого возмущения с целью повышения робастности процесса диагностирова-

ния.

Рассмотрим вначале задачу идентификации дефекта для скалярной функ-

ции d(t).

2. Построение редуцированной модели

Решение поставленной задачи опирается на редуцированную модель си-

стемы (1.1), которая в общем случае описывается уравнением

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗y(t) + D_∗d(t) + L_∗ρ(t),

(2.1)

y_∗(t) = H_∗x_∗(t),

где x_∗(t) ∈ R^k — вектор состояния модели, F_∗, G_∗, J_∗, H_∗, D_∗ и L_∗ — матри-

цы соответствующих размеров, подлежащие определению. Как обычно, пред-

полагается, что при отсутствии возмущений и дефектов и после окончания

переходного процесса, вызванного возможным рассогласованием начальных

состояний системы (1.1) и модели (2.1), выполняются равенства x_∗(t) = Φx(t)

и y_∗(t) = R_∗y(t) для некоторых матриц Φ и R_∗. Известно [1, 24, 25], что эти

матрицы удовлетворяют условиям

(2.2)

ΦF = F_∗Φ + J_∗H, R_∗H = H_∗Φ, ΦG = G_∗, ΦD = D_∗, ΦL = L_∗.

Рассмотрим метод построения модели (2.1) минимальной размерности, не

чувствительной к возмущениям, на основе которой может быть построен

скользящий наблюдатель. Для анализа возможности построения такой мо-

дели введем матрицу L₀ максимального ранга такую, что L₀L = 0. Извест-

но [24, 25], что условие нечувствительности к возмущениям имеет вид ΦL = 0;

тогда из максимальности ранга матрицы L₀ следует Φ = T L₀ для некото-

рой матрицы T . Заменим матрицу Φ в выражении R_∗H = H_∗Φ на T L₀:

R_∗H = H_∗TL₀ и перепишем его в виде

(

)

(R_∗

-H_∗T)

= 0.

L₀

Это уравнение имеет нетривиальное решение, когда между строками матриц

H и L₀ имеется линейная зависимость, откуда следует, что критерием его

нетривиального решения является условие

(

)

(2.3)

rank

< rank(H) + rank(L₀

L₀

Аналогично уравнение ΦF = F_∗Φ + J_∗H после указанной подстановки

приводится к виду

⎛

⎞

L₀F

⎜

⎟

-F_∗T

-J_∗)⎝ L0

⎠ = 0,

а условием его нетривиального решения является неравенство

⎛

⎞

L₀F

(

)

⎜

⎟

L₀

(2.4)

rank

⎝ L0

⎠ < rank(L0F) + rank

Условия (2.3) и (2.4) являются необходимыми, т.е. их выполнение не гаран-

тирует возможности построения модели, не чувствительной к возмущениям,

поскольку в уравнения, на основе которых они получены, входит неизвестная

матрица T . Если хотя бы одно из условий (2.3), (2.4) не выполняется, модели,

не чувствительной к возмущениям, не существует. Ниже предполагается, что

эти условия выполняются, т.е. явные препятствия для построения модели с

указанным свойством отсутствуют.

Отметим также, что простые достаточные условия возможности построе-

ния модели, не чувствительной к возмущениям, имеют вид HL = 0 и F L = 0,

что следует из уравнений (2.6), приведенных ниже, но эти условия достаточно

редко выполняются на практике.

Для упрощения процедуры построения модели матрицы F_∗ и H_∗ ищутся

в канонической форме следующего вида:

⎛

⎞

⎜

⎟

F∗ =

⎝

⎠,

(2.5)

H_∗ = ( 1 0

0 )

Используя (2.5), получим из (2.2) уравнения для строк матриц Φ и J_∗:

(2.6)

Φ₁ = R_∗H, Φ_iF = Φi+1 + J_∗iH, i = 1,... ,k - 1, Φ_kF = J_∗k

где Φ_i и J_∗i — i-е строки матриц Φ и J_∗, i = 1, . . . , k, k — размерность моде-

ли (2.1). Уравнения (2.6) могут быть приведены к одному уравнению. Дей-

ствительно, из (2.6) при i = 1 следует Φ₁F = Φ₂ + J∗1H; умножая обе части

этого равенства на матрицу F справа и заменяя Φ₂F на Φ₃ + J∗2H, получаем

R_∗HF² = Φ₃ + J∗1HF + J∗2H. Продолжая аналогично, приходим к выраже-

нию

R_∗HF^k = J∗1HFk-1 + J∗2HFk-2 + ... + J_∗kH.

Запишем его в виде

(2.7)

( R_∗

-J∗1

-J∗2

-J_∗k )V(k)

= 0,

где

⎛

⎞

HF^k

⎟

V(k) =^⎝ HFk-1

⎠.

Можно показать [24, 25], что условие нечувствительности к возмущениям

ΦL = 0 может быть представлено в форме

(2.8)

( R_∗

-J∗1

-J∗2

-J_∗k )B(k)

= 0,

где

⎛

⎞

HL HFL HF²L ... HFk-1L

⎜₀

⎟

HL HFL ... HFk-2L

⎜

⎟

B(k) =

⎠^.

⎝

Так как строка ( R_∗

-J∗1

-J∗2

-J_∗k ) удовлетворяет условию (2.7), из

(2.7) и (2.8) получаем

(2.9)

( R_∗

-J∗1

-J∗2

-J_∗k )(V(k) B(k)

) = 0.

Уравнение (2.9) имеет нетривиальное решение, если

rank (V(k) B(k)) < l(k + 1).

Из последнего условия определяется минимальная размерность k, при кото-

рой уравнение (2.9) имеет решение, находится решение уравнения (2.9), из

(2.6) определяются строки матрицы Φ и принимается G_∗ := ΦG и D_∗ := ΦD.

В результате модель (2.1) принимает вид

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗y(t) + D_∗d(t),

(2.10)

y_∗(t) = H_∗x_∗(t) = R_∗y(t).

3. Построение скользящего наблюдателя

По аналогии с [13] скользящий наблюдатель ищется в виде

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗y(t) + D_∗v(t) - Ke_y(t),

(3.1)

ŷ∗(t) = H∗ x∗(t),

где матрица K выбирается так, чтобы F₀ = F_∗ - KH_∗ стала устойчивой мат-

рицей,

⎧

⎨

Qe_y(t)

-g

если e_y(t) = 0,

(3.2)

v(t) =

∥Qe_y (t)∥

⎩

в противном случае,

e_y(t) = ŷ_∗(t) - y_∗(t) = ŷ_∗(t) - R_∗y(t) — ошибка по выходу; правила выбора

матрицы Q и положительного скаляра g обсуждаются ниже. Отметим, что,

поскольку матрицы F_∗ и H_∗ ищутся в каноническом виде (2.3), матрица K

всегда существует.

Введем ошибку по состоянию e(t) = x_∗(t) - x_∗(t); нетрудно видеть, что

e_y(t) = H_∗e(t). Используя (2.10) и (3.1), запишем уравнение динамики ошиб-

ки e(t) :

(3.3)

ė(t) = F_∗e(t) + D_∗(v(t) - d(t)) - Ke_y(t) = F₀e(t) + D_∗

(v(t) - d(t)).

По аналогии с [13] предполагается, что существуют матрица Q и симмет-

рическая положительно определенная матрица P такие, что

(3.4)

PD_∗ =HT∗Q^T.

Скаляр g выбирается из условия g > ∥d(t)∥. Так как матрица F₀ устойчива, то

для произвольной симметрической положительно определенной (СПО) мат-

рицы W существует такая СПО матрица P , что F^T0P + P F₀ = -W .

Теорема 1. При указанном выборе матрицы Q и скаляра g наблюдатель

(3.1) сходится асимптотически, т.е.

lim e(t) = 0.

t→∞

Доказательство. Рассмотрим функцию Ляпунова

V (t) = e^T(t)P e(t)

и с учетом выражений (3.2)-(3.4) найдем ее производную по времени:

V (t) = (F₀e(t) + D_∗(v(t) - d(t)))^TP e(t) + e^T(t)P (F₀e(t) + D_∗(v(t) - d(t))) =

= e^T(t)(FT0 P + PF₀)e(t) + (D_∗(v(t) - d(t)))^TPe(t) + e^T(t)PD_∗(v(t) - d(t)) =

= -e^T(t)We(t) + 2e^T(t)PD_∗(v(t) - d(t)) =

= -e^T(t)We(t) + 2e^T(t)HT∗Q^Tv(t) - 2e^T(t)H^T∗ Q^Td(t) =

Qe_y(t)

= -e^T(t)We(t) - 2ge^T(t)HT∗Q^T

- 2(QH_∗e(t))^Td(t) =

∥Qe_y(t)∥

QH_∗e(t)

= -e^T(t)We(t) - 2g(QH_∗e(t))^T

- 2(QH_∗e(t))^Td(t) ≤

∥QH_∗e(t)∥

≤ -e^T(t)We(t) - 2g∥QH_∗e(t)∥ + 2∥QH_∗e(t)∥∥d(t)∥ =

= -e^T(t)We(t) - 2(g - ∥d(t)∥)∥QH_∗e(t)∥ < 0;

в последнем неравенстве учтено, что W — СПО матрица и g > ∥d(t)∥. Полу-

ченный результат доказывает теорему.

Поскольку в скользящем режиме ė(t) = 0 и e(t) = 0, то из уравнения (3.3)

следует 0 = D_∗(v(t) - d(t)) и функция d(t) может быть оценена в виде

Qe_y(t)

d(t) = -g

∥Qe_y (t)∥ + δ

где δ — малая положительная константа; напомним, что согласно [10] раз-

рывная функция v(t) заменяется непрерывной функцией v_δ(t) (1.2). Следует

отметить, что полученное выражение зависит только от ошибки по выходу

e_y(t) = ŷ_∗(t) - R_∗y(t).

В случае, когда в измерениях присутствуют шумы, главный резуль-

тат остается прежним, только ужесточаются требования к величине ска-

ляра g для обеспечения скользящего режима. Действительно, пусть y(t) =

= Hx(t) + ρ_s(t), где ρ_s(t) — функция, описывающая шумы измерений. То-

гда e_y(t) = H_∗e(t) - R_∗ρ_s(t), правая часть

(3.3) дополняется слагаемым

(KR_∗ + J_∗)ρ_s(t), а последние элементы выражения для^V (t) принимают вид

V (t) ≤ -e^T(t)W e(t) - 2g∥QH_∗e(t)∥ + 2∥QH_∗e(t)∥∥d(t)∥+

+2∥P (KR_∗ + J_∗))∥∥e(t)∥∥ρ_s(t)∥ ≤

∥P (KR_∗ + J_∗)∥

≤ -e^T(t)We(t) - 2(g - ∥d(t)∥ - ∥ρ_s(t)∥

)∥QH_∗∥∥e(t)∥.

∥QH_∗∥

Ясно, что^V (t) < 0 при

∥P (KR_∗ + J_∗)∥

(3.5)

g > ∥d(t)∥ + ∥ρ_s(t)∥

∥QH_∗∥

что гарантирует существование скользящего режима. Ясно, что оценка функ-

ции d(t) в этом случае будет произведена с погрешностью, не превосходящей

величины ∥ρ_s(t)∥∥P (KR_∗ + J_∗)∥.

Отметим, что в [12] для решения задачи идентификации дефектов при

наличии возмущений требуется выполнение условия Im(L) ∩ Im(D) = {0},

которое в простейших случаях означает, что дефект и возмущение действуют

на разные части системы. В предлагаемом подходе оно заменено на ΦL = 0.

Обсуждение связи между этими условиями требует специального анализа.

Отметим также, что предложенный подход может быть использован для

оценки величины возмущения ρ(t) на основе редуцированной модели (2.1),

не чувствительной к дефекту. Для построения такой модели используется

подход, описанный в разделе 2, с заменой L в матрице B(k) на D. Оценен-

ное таким образом возмущение ρ(t) предлагается использовать в дополни-

тельном диагностическом наблюдателе, чувствительном как к дефекту, так

и возмущениям. Такой наблюдатель может быть построен известными ме-

тодами [1, 24]. Введение в него оценки функции ρ(t) позволяет существенно

повысить степень робастности процесса диагностирования и уменьшить ве-

роятности ошибочных решений.

4. Случай векторной функции d(t)

В случае, когда d(t) — векторная функция, редуцированная модель (2.1)

также должна иметь векторный выход y_∗(t), что в общем случае предполагает

ее максимально возможную размерность. Для построения такой модели опи-

санную выше процедуру предлагается модифицировать следующим образом.

Матрица F_∗ модели также ищется в канонической форме (2.5), но канони-

ческая форма матрицы H_∗ и первое уравнение в (2.6) не используются. Это

связано с тем, что форма матрицы H_∗ в (2.5) соответствует скалярному вы-

ходу y_∗(t), а первое уравнение накладывает ограничение на первую строку

матрицы Φ и, следовательно, на остальные строки, поскольку они связаны с

первой соотношениями (2.6). В результате уравнение (2.7) изменяется:

( Φ₁

-J∗1

-J∗2

-J_∗k )

∗

= 0,

где

⎛

⎞

F^k

⎜

⎟

∗

⎝^H

Fk-1

⎠.

Аналогичным образом модифицируются уравнения (2.8) и (2.9):

( Φ₁

-J∗1

-J∗2

-J_∗k )B∗k) = 0,

(4.1)

( Φ₁

-J∗1

-J∗2

-J_∗k )(

∗

B∗k)

) = 0,

где

⎛

⎞

L FL F²L ... Fk-1L

⎜₀

⎟

HL HFL ... HFk-2L

⎜

⎟

B∗k) =

⎠^.

⎝

В отличие от скалярного случая ищется не минимальное, а максималь-

ное значение k, при котором уравнение (4.1) имеет решение. Требование

максимальности связано с тем, что для построения матрицы R_∗ со свой-

ством rank (R_∗) ≥ rank (D_∗) необходима модель максимальной размерности.

Из уравнения (4.1) находятся матрицы Φ₁, J∗1, . . . , J_∗k, после чего из со-

отношений (2.6) определяются строки Φ₂, . . . , Φ_k матрицы Φ и принима-

ется G_∗ := ΦG и D_∗ := ΦD. Для определения матриц R_∗ и H_∗ уравнение

R_∗H = H_∗Φ записывается в виде

(

)

(R_∗

-H_∗)

= 0,

откуда и находятся искомые матрицы. Это уравнение имеет нетривиальное

решение, когда между строками матриц H и Φ имеется линейная зависи-

мость, откуда следует, что критерием его нетривиального решения является

условие

(

)

rank

< rank(H) + rank(Φ),

проверяющее наличие такой зависимости. Предполагается, что пара

(F_∗, H_∗) наблюдаема, в этом случае существует такая матрица K, что

F₀ = F_∗ - KH_∗ — устойчивая матрица [13]. В остальном процедура построе-

ния скользящего наблюдателя и оценки функции d(t) совпадает с рассмот-

ренной в разделе 3.

Если s = rank (R_∗) ≥ rank (D_∗), задача идентификации векторной функ-

ции d(t) может быть решена описанным выше методом, в противном случае

удается оценить только s компонент этой функции.

5. Идентификация дефектов в датчиках

Рассмотрим случай, когда дефекты возникают в датчиках, для чего скор-

ректируем модель (1.1): положим d(t) = 0 и добавим в уравнение для изме-

рений слагаемое D_sd_s(t) :

y(t) = Hx(t) + D_sd_s(t),

где, как и для дефектов в динамике, d_s(t) либо равно нулю при отсутствии

дефектов, либо становится неизвестной ограниченной функцией времени при

их появлении. Остановимся на случае, когда d_s(t) — скаляр, вариант вектор-

ной функции может быть рассмотрен по аналогии с разделом 4.

Аналогичная задача в отсутствие возмущений изучалась в [10]; как и вы-

ше, предлагаемое решение основывается на редуцированной модели (2.1), не

чувствительной к возмущениям, которая в рассматриваемом случае прини-

мает вид

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗Hx(t),

(5.1)

y_∗(t) = H_∗x_∗(t) + D_∗sd_s(t),

где D_∗s = R_∗D_s. Для обеспечения существования скользящего режима необ-

ходимо положить R_∗D_s = 0, так как только в этом случае e_y(t) = H_∗e(t), где

e_y(t) = ŷ_∗(t) - y_∗(t) — ошибка по выходу, e(t) = x_∗(t) - x_∗(t) — ошибка по со-

стоянию.

В отличие от раздела 3 скользящий наблюдатель ищется в несколько ином

виде:

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗y(t) - J_∗D_sv(t) - Ke_y(t),

(5.2)

ŷ∗(t) = H∗ x∗(t);

предполагается, что J_∗D_s = 0, матрица K выбирается так, чтобы F₀ = F_∗ -

- KH_∗ стала устойчивой матрицей,

⎧

⎨

Qe_y(t)

если e_y(t) = 0,

v(t) =

g_s ∥Qe_y(t)∥,

⎩

в противном случае,

правила выбора матрицы Q и положительного скаляра g_s обсуждаются ниже.

Используя (5.1) и (5.2), запишем уравнение динамики ошибки e(t):

ė(t) = F_∗e(t) + J_∗y(t) - J_∗Hx(t) - J_∗D_sv(t) - Ke_y(t) =

(5.3)

= F_∗e(t) - KH_∗e(t) + J_∗D_sd_s(t) - J_∗D_sv(t) =

= F₀e(t) - J_∗D_s(v(t) - d_s(t)),

где F₀ = F_∗ - KH_∗ — устойчивая матрица. По аналогии с [13] предполагается,

что существуют матрица Q и СПО матрица P такие, что

(5.4)

PJ_∗D_s = HT∗Q^T.

Скаляр g_s выбирается из условия g_s > ∥d_s(t)∥.

По аналогии с теоремой 1 может быть доказана

Теорема 2. При указанном выборе матрицы Q и скаляра g_s наблюда-

тель (5.2) сходится асимптотически.

Поскольку в скользящем режиме ė(t) = 0 и e(t) = 0, то из уравнения (5.3)

следует 0 = J_∗D_s(v(t) - d_s(t)), и функция d_s(t) может быть оценена в виде

Qe_y(t)

d_s(t) = g_s

∥Qe_y (t)∥ + δ

где δ — малая положительная константа.

При наличии шума в измерениях проверяемого датчика как-либо отстро-

иться от него не представляется возможным, можно оценить только сумму

d_s(t) + ρ_s(t); если же зашумлены другие измерения, следует применить под-

ход, описанный в разделе 3, что выливается в увеличение величины скаля-

ра g_s по аналогии с (3.5).

6. Практический пример

Рассмотрим модель следящего электропривода, разомкнутая цепь которо-

го без учета вязкого трения описывается следующей моделью [26]:

x₁(t) =

1 x₂(t),

i_p

(6.1)

x₂(t) =

K_M x₃(t) + ρ(t) + d₂(t),

J_H

K_ω

K_U

x₃(t) = -

x₂(t) -

x₃(t) +

u(t) + d₃(t),

где x₁ — угол поворота выходного вала редуктора, x₂ — угловая скорость вра-

щения вала электродвигателя, x₃ — ток электродвигателя, i_p — передаточное

отношение редуктора, J_H — момент инерции ротора двигателя и вращающих-

ся частей редуктора, приведенный к ротору, K_M — моментный коэффициент

электродвигателя, K_ω — коэффициент противо-э.д.с., R — активное сопротив-

ление обмотки якоря электродвигателя, L — индуктивность якорной обмотки

электродвигателя, K_U — коэффициент усиления усилителя мощности.

Рассматривается следующее множество дефектов: первый d_s(t) = x₁(t) —₍

)

ошибка в показаниях датчика положения; второй d₂(t) =KM

x₃(t)

-KMJ_H

J_H

J (t)

соответствует изменению номинального момента инерции нагрузки навели-

R(t)

чин

J (t), третий d₃(t) = -

x₃(t) — изменению активного сопротивления

^M (t)

цепи якоря электродвигателя на величину^R(t). Возмущение ρ(t) = -

J_H

J(t)

обусловлено наличием внешнего нагрузочного момента

^M (t), приведенного

к валу двигателя. Из вида модели ясно, что второй дефект неотличим от

возмущения, поэтому отдельно ниже он не рассматривается.

Обозначим:

K_M

K_ω

K_U

k₁ =

k₂ =

k₃ = -

k₄ = -

k₅ =

i_p

J_H

Полагая, что измеряемыми являются переменные x₁ и x₃, рассматриваемую

систему опишем следующими матрицами:

⎛

⎞

⎛

⎞

k₁

(

)

F =^⎝ 0

k₂

⎠,G= ⎝₀

⎠,H=

k₃

k₄

k₅

⎛

⎞

⎛

⎞

⎛

⎞

(

)

D_s =

D₂ =^⎝ 1

⎠,D3 = ⎝ 0

⎠,L= ⎝₁

⎠_.

Отметим, поскольку HL = 0, то условие rank (HL) = rank (L), необходимое

для применения подхода, предложенного в [13], здесь не выполняется.

Построим модель, инвариантную к возмущению. Примем k = 1 и найдем

матрицы V⁽¹⁾ и B⁽¹⁾ :

⎛

⎞

k₁

^⎛ 0

k₃

k₄

⎟

V(1) =^⎝

⎠, B⁽¹⁾ =^⎝

⎠.

Так как rank (V⁽¹⁾, B⁽¹⁾) = 3 < 2(1 + 1) = 4, уравнение (2.9) имеет решение с

матрицами

R_∗ = (k₃

- k₁), J_∗ = (0

- k₁k₄),

откуда Φ = (k₃ 0

- k₁) и G_∗ = -k₁k₅. Модель (2.8) принимает вид

x_∗(t) = -k₁k₄y₂(t) - k₁k₅u(t),

y_∗(t) = x_∗(t),

где x_∗ = k₃x₁ - k₁x₃.

Так как ΦD₂ = 0 и ΦD₃ = D∗3 = -k₁, построенная модель чувствительна

к третьему дефекту, рассмотрим его.

Из канонической формы

(2.5) получаем H_∗ = 1; примем K := b > 0.

Из (3.4) следует, что можно принять Q := -k₁ и P := 1; в результате сколь-

зящий наблюдатель описывается уравнениями

x_∗(t) = -k₁k₄y₂(t) - k₁k₅u(t) - be_y(t) - k₁v(t),

(6.2)

ŷ∗(t) = x∗(t),

где e_y(t) = ŷ_∗(t) - (k₃y₁(t) - k₁y₂(t)),

⎧

⎨

k₁e_y(t)

, если e_y(t) = 0,

v(t) =

∥k₁e_y(t)∥

⎩

в противном случае,

g > ∥d₃(t)∥. Оценка функции d₃(t) дается выражением

k₁e_y(t)

(6.3)

d₃(t) = g

∥k₁e_y(t)∥ + δ

Для рассмотрения дефекта в датчике предположим для простоты, что

возмущение ρ(t) отсутствует, но измерения в этом датчике подвержены воз-

мущению ρ_s(t), т.е. y₁(t) = H₁x(t) + d_s(t) + ρ_s(t). Поскольку для модели (6.1)

R_∗D_s = k₃ = 0, условие существования скользящего режима не выполняется,

для идентификации дефекта d_s(t) необходимо использовать другую модель.

Можно показать, что этому требованию удовлетворяет модель

x∗1(t) = x∗2(t) + k₅u(t) + k₀H₁x(t),

x∗2(t) = (k²⁴ + k₂k₃)y₂(t) + k₄k₅u(t),

y∗1(t) = x∗1(t) = y₂(t),

где x∗1 = x₃, x∗2 = -k₀x₁ + x₂ + x₃, k₀ = k₃k₄/k₁. Здесь R_∗ = (0 1) и J_∗ =

(

)

k₀

, что дает R_∗D_s = 0 и J_∗D_s = (k₀ 0).

k²⁴ + k₂k₃

Из канонической формы

(2.3) получаем H_∗ = (1 0); примем K :=

:= (0,2 0,01)^T. Так как J_∗D_s = (k₀ 0), а для принятых при моделировании

значений параметров привода k₀ = 10⁵, из (5.4) следует, что можно принять

(

)

10-9

P :=

и Q := 10-9k₀; в результате скользящий наблюдатель

10-7

описывается уравнениями

x∗1(t) = x∗2(t) + k₅u(t) + k₀y₁(t) - k₀v(t) - 0,2e_y(t),

(6.4)

x∗2(t) = (k²⁴ + k₂k₃)y₂(t) + k₄k₅u(t) - 0,01e_y(t),

ŷ∗1(t) = x∗1(t),

где e_y(t) = ŷ_∗(t) - y₂(t),

⎧

⎨

10-9k₀e_y(t)

v(t) =

g_s ∥10-9k₀e_y(t)∥,еслиey(t)=0,

⎩

в противном случае,

ds(t)

t, c

Рис. 4. Оценка функции

d_s(t).

ds(t)

0,3

0,2

0,1

0,2

0,3

t, c

Рис. 5. Ошибка оценки функции d_s(t) + ρ_s(t).

Проведем моделирование системы (6.1) с наблюдателями (6.2) и (6.4). При

моделировании задавались следующие параметры рассматриваемого следя-

щего электропривода: J_H = 0,0001 Kgm², K_ω = 0,02 Vc, K_U = 100, R = 0,4 Ω,

L = 0,004H, K_M = 0,02Nm/A, i_p = 100. Для обеспечения заданных показате-

лей качества управления в прямой цепи электропривода использовалось ти-

повое последовательное корректирующие устройство с передаточной функ-

цией W (s) =(0,089s+1)(0,0011s+1)(0,001s+1)(0,001s+1) . При этом в качестве входного воздействия

на электропривод подавалось следующее желаемое значение угла поворота

выходного вала редуктора: xref1 (t) = sin(t).

При моделировании возмущение ρ(t) имитировалось действием внешне-

го нагрузочного момента величиной

^M (t) = 0,1 sin(0,8t) Nm на интервале

t = 1 ÷ 10c; дефекты имитировались следующим образом: d_s(t) — введени-

ем постоянной ошибки x₁(t) = 0,006 рад в датчик положения выходного ва-

ла редуктора на интервале t = 2 ÷ 6 c, d₃(t) — изменением активного сопро-

тивления якоря на величину^R(t) = 0,2 sin(πt/4 - π) на интервале t = 4 ÷ 8 c.

Предполагается, что в датчике присутствует погрешность ρ_s(t), имитируе-

мая белым шумом. При моделировании для наблюдателя (6.2) принималось

g = 10, b = 10 и δ = 10-6, для наблюдателя (6.4) — g_s = 0,01 и δ = 10-6.

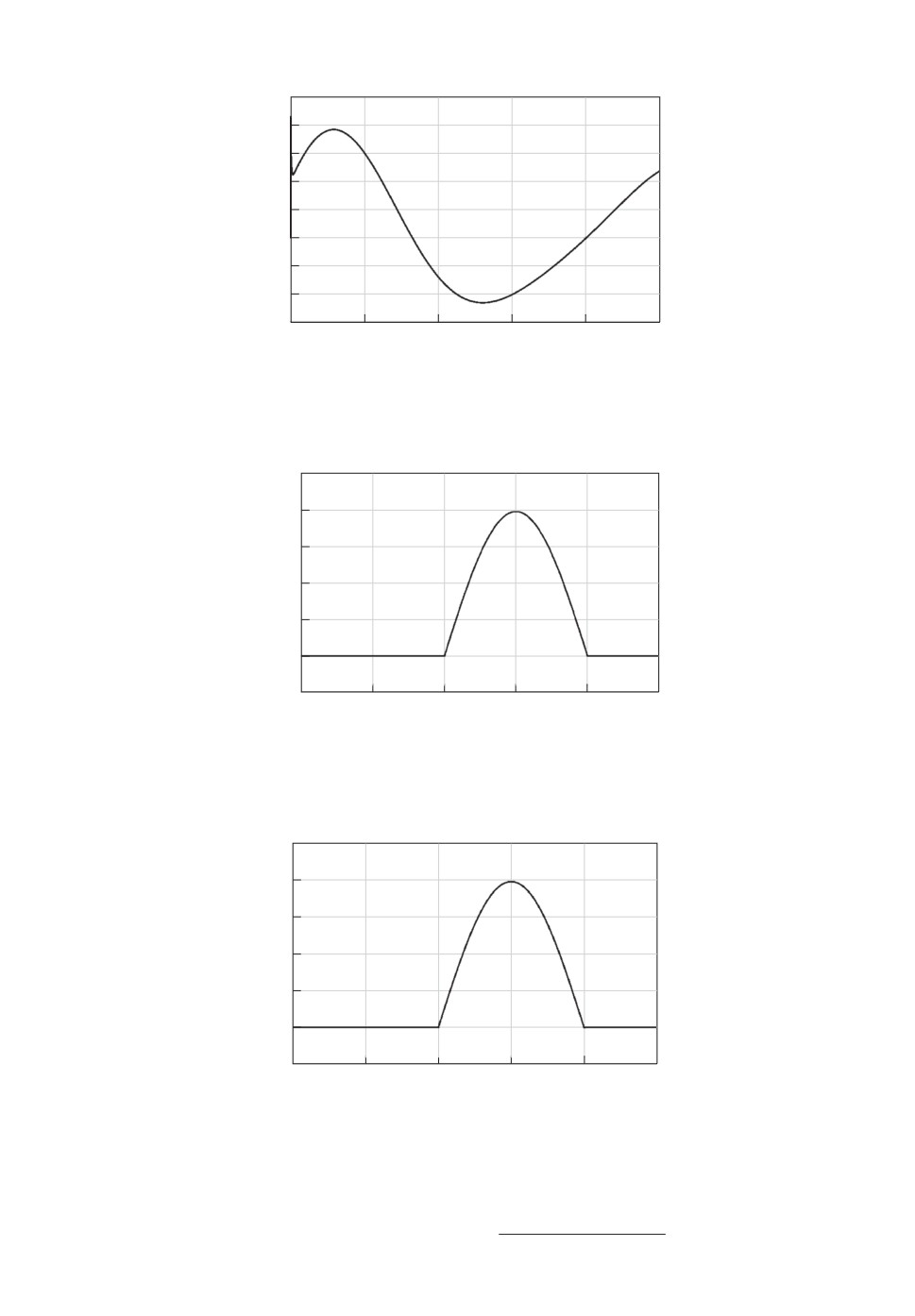
На рис. 1 приведен график функции u(t) при моделировании. На рис. 2

и 3 представлены результаты моделирования с наблюдателем (6.2): графики

оценк

d₃(t), совпадающей с функцией v_δ(t), и ошибки этой оценки; на рис. 4

и 5 — с наблюдателем (6.4) (“scale” здесь — это масштаб): графики оцен-

ки сумм

d_s(t) = d_s + ρ_s(t), совпадающей с функцией v_δ(t), и ошибки этой

оценки. Из этих рисунков видно, что максимальное значение ошибки иден-

тификации в установившемся режиме не превышает для функции d_s(t) 3,3%,

для функции d₃(t) — 1%.

Из этих рисунков видно, что построенные наблюдатели позволили обес-

печить своевременное обнаружение возникающих ошибок в сигналах, посту-

пающих с датчика положения электропривода, а также изменение величины

активного сопротивления обмотки якоря электродвигателя. Поскольку на ин-

тервалах 0 ÷ 2 c и 8 ÷ 10 c значения оценок равны нулю, ясно, что построен-

ные наблюдатели не чувствительны к возмущению ρ(t).

Следует отметить, что при моделировании и при практической реализации

наблюдателя в нем возникает не идеальный, а реальный скользящий режим;

параметры реального скользящего режима в работе не рассматриваются.

7. Заключение

В работе для решения задач обнаружения и идентификации дефектов ис-

пользован метод на основе скользящих наблюдателей. Предложенная моди-

фикация этого метода позволила ослабить ограничения, накладываемые на

условия его реализации, для решения указанных задач при наличии возму-

щений и уменьшить сложность средств диагностирования по сравнению с

известными результатами. Теоретические результаты иллюстированы при-

мером диагностирования реальной технической системы.

СПИСОК ЛИТЕРАТУРЫ

1. Frank P. Fault diagnosis in dynamic systems using analytical and knowledge-based

redundancy. A survey and some new results // Automatica. 1990. V. 26. P. 459-474.

2. Gertler J. Residual generation in model-based fault diagnosis // Theory Advanced

Technol. 1993. V. 9. P. 259-285.

3. Samy I., Postlethwaite I., Gu D. Survey and application of sensor fault detection

and isolation schemes // Control Engineer. Practic. 2011. V. 19. P. 658-674.

4. Blanke M., Kinnaert M., Lunze J., Staroswiecki M. Diagnosis and Fault-Tolerant

Control. Berlin: Springer-Verlag, 2005.

5. Ding S. Data-driven design of fault diagnosis and fault-tolerant control systems.

London: Springer-Verlag, 2014.

6. Russell E., Chiang L., Chiang L. Fault Detection and Diagnosis in Industrial

Systems. Berlin: Springer, 2001.

7. Simani S., Fantuzzi C., Patton R. Model-based Fault Diagnosis in Dynamic Systems

Using Identification. Berlin: Springer-Verlag, 2002.

Уткин В.И. Скользящие режимы и их применение в системах с переменной

структурой. М.: Наука, 1974.

Edwards C., Spurgeon S. On the development of discontinuous observers // Int. J.

Control. 1994. V. 59. P. 1211-1229.

10.

Edwards C., Spurgeon S., Patton R. Sliding mode observers for fault detection and

isolation // Automatica. 2000. V. 36. P. 541-553.

11.

Filaretov V., Zhirabok A., Protcenko A., Zuev A. Fault identification in nonlinear

dynamic systems // Proc. 5 Int. Conf. Syst. Control. Marrakesh, Morocco, 2016.

P. 273-277.

12.

Yan X., Edwards C. Nonlinear robust fault reconstruction and estimation using a

sliding modes observer // Automatica. 2007. V. 43. P. 1605-1614.

13.

He J., Zhang C. Fault Reconstruction based on sliding mode observer for nonlinear

systems // Math. Probl. in Engineer. 2012. P. 1-22.

14.

Brahim A., Dhahri S., Hmida F., Sellami A. Simultaneous actuator and sensor

faults reconstruction based on robust sliding mode observer for a class of nonlinear

systems // Asian J. Contr. 2017. V. 19. P. 362-371.

15.

Chan J., Tan C., Trinh H. Robust fault reconstruction for a class of infinitely

unobservable descriptor systems // Int. J. Syst. Sci. 2017. P. 1-10.

16.

Краснова С.А., Кузнецов С.И. Оценивание на скользящих режимах неконтроли-

руемых возмущений в нелинейных динамических системах // АиТ. 2005. № 10.

С. 54-69.

Krasnova S.A., Kuzntsov S.I. Uncontrollable perturbation of nonlinear dynamic

systems: estimation on moving modes // Autom. Remote Control. 2005. V. 66.

No. 10. P. 1580-1593.

17.

Krasnova S., Utkin V. Prelimit implementation of states and disturbances observer

on sliding modes // Proc. Int. Workshop Recent Advances Sliding Modes (RASM

2015). Istanbul, Turkey, 2015. P. 1-6.

18.

Alwi H., Edwards C. Fault tolerant control using sliding modes with on-line control

allocation // Automatica. 2008. V. 44. P. 1859-1866.

19.

Chandra K., Alwi H., Edwards C. Fault reconstruction for a quadrotor using an

LPV sliding mode observer // Proc. 9 IFAC Symp. Safeprocess. Paris, France, 2015.

P. 374-379.

20.

Meziane H., Labarre C., Lefteriu S., Defoort M., Djemai M. Fault detection and

isolation for a multi-cellular converter based on sliding mode observer // Proc.

9 IFAC Symp. Safeprocess. Paris, France, 2015. P. 164-170.

21.

Mohamed M., Yan X-G., Spurgeon S., Jiang B. Robust sliding mode observer design

for interconnected systems with application to multimachine power systems // Proc.

IEEE CDC, Conf. Decision Control. Las Vegas, USA, 2016. P. 6246-6251.

22.

Zhang K., Jiang B., Yan X., Mao Z. Sliding mode observer based incipient sensor

fault detection with application to high-speed railway traction device // ISA

Transact. 2016. P. 1-28.

23.

Zhirabok A., Shumsky A., Zuev A. Fault diagnosis in linear systems via sliding mode

observers // Int. J. Control. 2019. DOI: 10.1080/00207179.2019.1590738.

24.

Жирабок А.Н., Шумский А.Е., Павлов С.В. Диагностирование линейных дина-

мических систем непараметрическим методом // АиТ. 2017. № 7. С. 3-21.

Zhirabok A., Shumsky A., Pavlov S. Diagnosis of linear dynamic systems by the

nonparametric method // Autom. Remote Control. 2017. V. 78. No. 7. P. 1173-

1188.