Автоматика и телемеханика, № 2, 2020

(Санкт-Петербургский государственный университет)

ОБ ОДНОМ МЕТОДЕ РЕШЕНИЯ ЛОКАЛЬНОЙ КРАЕВОЙ ЗАДАЧИ

ДЛЯ НЕЛИНЕЙНОЙ УПРАВЛЯЕМОЙ СИСТЕМЫ

Предложен достаточно удобный для численной реализации алгоритм

построения синтезирующей управляющей функции, гарантирующей пе-

ревод широкого класса нелинейных стационарных систем обыкновенных

дифференциальных уравнений из начального состояния в заданное ко-

нечное состояние фазового пространства c учетом ограничений на управ-

ление. Получен конструктивный критерий, гарантирующий указанный

перевод. Эффективность алгоритма иллюстрируется при численном мо-

делировании решения конкретной практической задачи.

Ключевые слова: управляемость, краевые условия, стабилизация.

DOI: 10.31857/S000523102002004X

1. Введение

При создании автономных интеллектуальных систем управления различ-

ными техническими объектами (роботами-манипуляторами, летательными

аппаратами, автономными подводными аппаратами и др.) и их моделиро-

вании на различных этапах проектирования важную роль приобретают во-

просы, связанные с формированием управляющих функций, обеспечивающих

перевод управляемого объекта из начального состояния в заданное конечное

состояние. Математическими моделями интеллектуальных систем управле-

ния многих технических объектов являются сложные нелинейные управляе-

мые системы обыкновенных дифференциальных уравнений. Процесс форми-

рования управляющего воздействия сводится к задаче нахождения управ-

ляющих функций, при которых соответствующие функции фазовых коорди-

нат удовлетворяют заданным краевым условиям. Такой класс задач назы-

вают краевыми задачами, и он является одной из важных и сложных про-

блем математической теории управления. Впервые полное решение этих за-

дач для линейных нестационарных систем в классе управляющих функций,

суммируемых с квадратом, было выполнено в [1]. В последующие десятиле-

тия появились работы, направленные на исследование локальных и глобаль-

ных краевых задач для линейных и нелинейных управляемых систем специ-

ального вида [2-15]. Исследование краевых задач ведется по трем основным

направлениям. Первое связано с нахождением необходимых и достаточных

условий, наложенных на правую часть управляемых систем и гарантирую-

щих перевод систем управления в заданную точку фазового пространства,

см. [1, 2, 4, 5, 7, 8, 11-15]. Второе включает исследование множества конеч-

ных состояний, в которые возможен перевод управляемой системы из некото-

рого начального состояния см. [4, 6, 9-11, 14, 15]. Третье направление касает-

ся разработки точных или приближенных методов построения управляющих

функций и соответствующих им траекторий, соединяющих заданные точки

в фазовом пространстве [1, 3, 11-15]. В настоящее время проблема краевых

задач достаточно подробно изучена для линейных и нелинейных управляе-

мых систем специального вида. Однако теория решения граничных задач

для нелинейных управляемых систем общего вида ввиду их сложности еще

недостаточно разработана.

Главное отличие результатов данной статьи от известных ранее состоит в

том, что в ней для достаточно широкого класса нелинейных стационарных

управляемых систем обыкновенных дифференциальных уравнений разрабо-

тан удобный для численной реализации и устойчивый к погрешностям вычис-

лений алгоритм решения локальных краевых задач в классе синтезирующих

управлений, а также найдено конструктивное легко проверяемое необходимое

и достаточное условие, гарантирующие реализацию полученного в работе ал-

горитма в классе синтезирующих управлений. Это условие совпадает с кри-

терием управляемости Р. Калмана в случае линейных стационарных систем.

Поставленная цель достигнута сведением решения исходной задачи к реше-

нию задачи стабилизации линейной нестационарной системы специального

вида и последующему решению задачи Коши для вспомогательной системы

обыкновенных дифференциальных уравнений.

2. Постановка задачи

Объектом исследования является управляемая система обыкновенных

дифференциальных уравнений:

(2.1)

x = f(x,u),

где x = (x₁, . . . , x_n)^T, x ∈ Rⁿ; u ∈ R^r, u = (u₁, . . . , u_r)^T, t ∈ [0, 1], r ≤ n;

(2.2)

f ∈ C4n(Rⁿ × R^r; Rⁿ), f = (f₁,...,f_n)^T,

(2.3)

f (0, 0) = 0,

rank S = n, S = (B, AB, A²B, . . . , An-1B),

(2.4)

∂f

(0, 0), A =

(0, 0),

∂u

∂x

(2.5)

∥u∥ < N.

Пусть заданы состояния

(2.6)

x(0) = 0, x(1) = x,

x=(x₁,...,x_n)^T,

где x — заданный вектор фазового пространства.

Определение 1. Будем говорить, что пара функций x(t), u(t,x) при-

надлежит множеству Γ, если для нее выполнены условия:

(2.7)

x(t) ∈ C¹([0, 1]; Rⁿ), u(t, x) ∈ C¹([0, 1) × Rⁿ; R^r

Задача. Найти пару функций (x(t),u(t,x)) ∈ Γ, удовлетворяющую си-

стеме (2.1) и условиям (2.6), а также условию

(2.8)

u(t, x) ≡ 0, ∀t ∈ [0, 1] при

x = 0.

Указанную пару x(t), u(t, x) будем называть решением задачи (2.1), (2.6).

Определение 2. Будем говорить, что задача (2.1), (2.6) локально раз-

решима, если существует ε > 0 такое, что для всех x таких, что ∥x∥ < ε

существует решение задачи (2.1), (2.6).

Теорема. Пусть для правой части системы (2.1) выполнены условия

(2.2), (2.3). Тогда для локальной разрешимости задачи (2.1), (2.6) необходи-

мо и достаточно, чтобы было выполнено условие (2.4). При этом соответ-

ствующее решение задачи (2.1), (2.6) может быть получено после решения

задачи стабилизации линейной нестационарной системы с экспоненциаль-

ными коэффициентами и последующим решением задачи Коши для вспомо-

гательной системы обыкновенных дифференциальных уравнений.

Главная идея доказательства теоремы состоит в том, что посредством пре-

образований зависимых и независимых переменных решение исходной задачи

сводится к решению задачи стабилизации нелинейной вспомогательной систе-

мы обыкновенных дифференциальных уравнений специального вида при по-

стоянно действующих возмущениях. Для ее решения находится синтезирую-

щее управление, обеспечивающее экспоненциальное убывание фундаменталь-

ной матрицы линейной части вспомогательной системы. На заключительном

этапе осуществляется переход к исходным переменным.

3. Построение вспомогательной системы

Функцию x(t), входящую в решение задачи (2.1), (2.6), ищем в виде

(3.1)

x_i(t) = a_i(t) + x_i

i = 1,...,n.

При новых переменных система (2.1) и граничные условия (2.6) примут вид

(3.2)

a = f(x + a,u),

(3.3)

a(0) = -x, a(1) = 0.

В соответствии с (2.3), (2.7), (2.8) пару функций a(t, x) ∈ C1([0, 1]; Rn),

u(t, a(t, x)) = u(t, a(t, x) + x) ∈ C¹([0, 1) × Rⁿ; R^r),

u(t, a(t, 0)) ≡ 0, a(t, 0) ≡ 0

∀t ∈ [0,1], удовлетворяющую системе (3.2) и условиям (3.3), будем называть

решением задачи (3.2), (3.3). Рассмотрим задачу: найти пару a(t, x) ∈ C¹[0, 1],

u(t, a) ∈ C¹([0, 1) × Rⁿ; R^r), u(t, a(t, 0)) ≡ 0, a(t, 0) ≡ 0 ∀t ∈ [0,1], удовлетво-

ряющую системе (3.2) и условиям

(3.4)

a(0) = -x, a(t) → 0 при t → 1.

Замечание 1. Переходя к пределу в решении задачи (2.2), (2.4) при

t → 1, получим решение задачи (3.2), (3.3).

Сделаем в системе (3.2) преобразование независимой переменной t по фор-

муле

(3.5)

t=1-e^-ατ

τ ∈ [0,+∞),

где α > 0 — некоторое фиксированное число, подлежащее определению. Тогда

при новой независимой переменной τ система (3.2) и условия (3.4) примут вид

(3.6)

= αe^-ατ

f(x + c,d),

dτ

(3.7)

c(0) = -x, c(τ) → 0 при τ → ∞,

(3.8) c(τ, x) = a(t(τ), x), d(τ, c) = u(t(τ), c(τ, x)), c(τ, 0) ≡ 0, d(τ, c(τ, 0)) ≡ 0,

τ ∈ [0,+∞); c = (c₁,...,c_n)^T, d = (d₁,...,d_r)^T.

Пару функций c(τ, x) ∈ C¹([0, ∞); Rⁿ), d(τ, c) ∈ C¹([0, ∞) × Rⁿ; R^r), удовле-

творяющую системе (3.6) и условиям (3.7), (3.8) будем называть решением

задачи (3.6), (3.7). Имея решение задачи (3.6), (3.7), с помощью формул (3.5),

(3.8) можно получить решение задачи (3.2), (3.4). Введем обозначения

c= x + θ_ic,

d = θ_id, θ_i ∈ [0,1], i = 1,...,n,

∑

|k| =

k_i,

|m| =

m_i, k! = k₁!... k_n!, m! = m₁!... m_r!

i=1

Используя свойство (2.2) и разложение правой части системы (2.1) в ряд

Тейлора в окрестности точки (x, 0), систему (3.6) можно записать в виде

∑

dc_i

∂f_i

= αe^-ατ f_i(x,0) + αe-ατ

(x,0)c_j

+ αe^-ατ

(x,0)d_j +

dτ

∂x_j

∂u_j

j=1

⎡

∑∑

∂²fi

∂²f_i

αe^-ατ ⎣

(x,0)c_jc_k + 2

(x,0)c_jd_k +

∂xj∂x

∂x_j∂u_k

j=1 k=1

⎤

∑∑

∂²f_i

(3.9)

(x,0)d_jd_k⎦

+...

∂u

j∂uk

j=1 k=1

∑

∂|k|+|m|f_i

...+ αe^-ατ

k₁

(x,0)ck11c22 × ...

k!m!_∂x

|k|+|m|=4n-2

∂xk22 . . . ∂xnn ∂u11 ∂u22 . . . ∂ur

...... × ckndm11d22 × ... × drr +

∑

∂|k|+|m|f_i

+ αe^-ατ

d)ck11 c22 × . . .

k!m!∂xk1

|k|+|m|=4n-1

∂xk22 . . . ∂xnn ∂u11 ∂u22 . . . ∂ur

... × cknn d11d22 × ... × drr, i = 1,...,n.

Ограничим область изменения c(τ) неравенством

(3.10)

∥c(τ)∥ < C₁

τ ∈ [0,∞).

Сделаем множество преобразований сдвигов функций c_i(τ), i = 1, . . . , n. Глав-

ная их цель состоит в том, чтобы в правой части системы, полученной в

результате этих преобразований, все слагаемые, не содержащие в явном ви-

де степеней компонент c и d, в области (2.5), (3.10) удовлетворяли оценке

O(e-4nατ ∥x∥) при τ → ∞, ∥x∥ → 0. На первом этапе выполним замену c_i(τ),

i = 1,...,n по формуле

(3.11)

c_i(τ) = c(1)i - e^-ατ f_i

(x,0), i = 1,... ,n.

Пусть

∂|k|+|m|f_i

D|k|+|m|f_i ≡

i = 1,...,n.

∂xk11 ∂x22 . . . ∂xnn ∂u11 ∂u22 . . . ∂ur

После подстановки (3.11) в левую и правую части системы (3.9) с учетом

введенного обозначения получим систему

∑

dc(1)i

∂f_i

= -αe-2ατ

(x,0)f_j(x,0) +

dτ

∂x_j

j=1

∑∑

∂²f

(x,0)e-3ατ f_j(x,0)f_k(x,0) +

∂x

j∂xk

j=1 k=1

⎛

⎞

∑

∑∑

∂f_i

∂²f_i

+ α^⎝e^-ατ

(x,0)c(1)j

- e-2ατ

(x,0)f_k(x,0)c(1)j⎠+

∂x_j

∂x_j∂x_k

j=1

j=1 k=1

⎛

⎞

∑

∑∑

∂f_i

∂²f_i

+ α ^⎝e^-ατ

(x,0)d_k -

(x,0)e-2ατfj(x,0)dk⎠ +

∂u

∂u_k∂x_j

j=1

j=1 k=1

∑∑

∑

∂²f_i

αe^-ατ

(x,0)c(1)jc(1)k

+ αe^-ατ

(x,0)d_kc(2)j +

∂x_j∂x_k

∂x_j∂u_k

j=1 k=1

∑∑

∂²f_i

(3.12)

αe^-ατ

(x,0)d_kd_j

+...

∂u

j∂uk

j=1 k=1

∑

... + αe^-ατ

D|k|+|m|f_i(x,0)(c⁽¹⁾¹ - e^-ατ f₁(x,0))k1 ×

k!m!

|k|+|m|=4n-2

× (c⁽¹⁾² - e^-ατ f₂(x, 0))k2 × . . . × (c(1)n - e^-ατ f_n(x, 0))kn dm11 d22 ×

∑

+ αe^-ατ

D|k|+|m| f_i(c

d)(c⁽¹⁾¹ - e^-ατ f₁(x, 0))k1 ×

... × dmrr

k!m!

|k|+|m|=4n-1

× (c⁽¹⁾² - e^-ατ f₂(x, 0))k2 × . . . × (c(1)n - e^-ατ f_n(x, 0))kn dm11 d22 × . . . × drr ,

i = 1,...n.

Из (3.7), (3.11) следует

(3.13)

c(1)i(0) = -x_i + f_i(x,0), i = 1,... ,n.

Нетрудно видеть, что в правой части системы (3.12) слагаемые, не содержа-

щие в явном виде степеней компонент векторов c и d, в области (2.5), (3.10)

удовлетворяют условию O(e-2ατ ∥x∥), τ → ∞, x → 0. На втором этапе сдела-

ем замену

∑

∂f_i

c(1)i(τ) = c(2)i(τ)+1e-2ατ

(x,0)f_j(x,0) = c(2)i(τ)+e-2ατ φ(2)i(x),

∂x_j

j=1

(3.14)

∑

∂f_i

φ(2)i(x) =1

(x,0)f_j(x,0), φ(2)i(0) = 0, i = 1,... ,n.

∂x_j

j=1

В результате в новых переменных начальные условия (3.13) примут вид

(3.15)

c(2)i(0) = -x_i + f_i(x,0) - φ(2)i(x), φ(2)i

(0) = 0, i = 1, . . . , n.

Нетрудно видеть, что в отличие от предыдущей замены в правой части полу-

ченной системы слагаемые, не содержащие в явном виде степеней компонент

векторов c и d, в области (2.5), (3.10) удовлетворяют условию O(e-3ατ ∥x∥),

τ → ∞, ∥x∥ → 0, i = 1,...,n. Используя (3.11)-(3.15) и индуктивный переход

на k-м шаге, получим искомое преобразование вида

(3.16)

c(k-1)i(τ) = c(k)i + e^-kατ φ(k)i(x), φ(k)i

(0) = 0, i = 1, . . . , n.

Если применить преобразования (3.16) 4n - 1 раз, объединить слагаемые в

полученной системе, линейные по компонентам вектора c(4n-1) и содержащие

коэффициенты e^-iατ , i = 1, . . . , n, а также слагаемые, линейные по компонен-

там вектора d и содержащие коэффициенты e^-iατ , i = 1, . . . , 2n, то согласно

(3.12)-(3.16) будем иметь систему и начальные данные, которые в векторной

форме можно записать следующим образом:

dc(4n-1)

= Pc(4n-1) + Qd + R₁(c(4n-1),d, x,τ) + R₂(c(4n-1),d, x,τ) +

dτ

+ R₃(c(4n-1),d,τ) + R₄(x,c(4n-1),d,τ),

(3.17)

R₁ = (R¹¹,... ,Rn1)^T, R₂ = (R¹²,... ,Rn2)^T,

R₃ = (R¹³,... ,Rn3)^T, R₄ = (R¹⁴,... ,Rn4)^T.

Функции Ri4 состоят из суммы слагаемых, не содержащих степеней компо-

нент векторов c(4n-1) и d; Ri1 содержат все слагаемые, которые линейно зави-

сят от компонент вектора c(4n-1)c коэффициентами e^-iατ , i ≥ n + 1, а также

слагаемые, входящие в последнюю сумму правой части полученной системы,

которые не содержат степеней компонент вектора d и с суммой степеней ком-

понент вектора c(4n-1), равной единице; Ri2 содержат все слагаемые, которые

линейно зависят от компонент вектора d с множителями e^-iατ , i ≥ 2n + 1,

а также слагаемые входящие в последнюю сумму правой части полученной

системы, которые не содержат степеней компонент вектора c(4n-1) и с суммой

степеней компонент вектора d, равной единице. В Ri3 содержатся все слагае-

мые, нелинейные по компонентам векторов c(4n-1) и d.

(

)

P(x) = αe^-ατ P₁(x) + e^-ατP₂(x) + ... + e-(n-1)ατPn-1(x) ,

∂f

P₁(x) =

(x,0), P₁(0) = A;

∂x

(3.18)

(

)

Q(x) = αe^-ατ Q₁(x) + e^-ατ Q₂(x) + ... + e-(2n-1)ατ Q2n-1(x) ,

∂f

Q₁(x) =

(x,0), Q₁(0) = B;

∂u

c(4n-1)(0) = -x + f(x,0) - φ⁽²⁾(x) - φ⁽³⁾(x) - ... - φ(4n-1)(x),

(3.19)

(

)_T

φ(i) = φ(i)1,... ,φ(i)n

i = 1,...,4n - 1, φ(i)(0) = 0.

4. Алгоритм решения задачи

1. Построение вспомогательной системы (3.17).

2. Используя метод Н.Н. Красовского, решаем задачу стабилизации линей-

ной части системы (3.17) с матрицами (3.18):

dc(4n-1)

= Pc(4n-1) + Qd.

dτ

В результате получаем управление d(τ) в виде обратной связи

(4.1)

d(τ) = M(τ)c(4n-1).

3. Решаем задачу Коши для системы (3.17), замкнутой управлением (4.1) с

начальными данными (2.19). Подстановка полученного решения в (4.1) дает

пару функций c(4n-1)(τ), d(τ).

4. После перехода в c(4n-1)(τ), d(τ) к исходным зависимым и независимым

переменным по формулам (3.16), (3.14), (3.11), (3.8), (3.5), (3.1) на основании

замечания 1 получим искомые функции x(t), u(t, x).

5. Решение задачи управления однозвенным манипулятором

В качестве иллюстрации предложенного метода рассмотрим решение за-

дачи управления однозвенным манипулятором с учетом нестационарных воз-

мущений. В соответствии с [13] система уравнений, описывающая движение

манипулятора, имеет вид

(5.1)

x₁ = x₂,

x₂ = -a₁x₂ - a₂ sin x₁

+ u + μt,

где x₁ — угол отклонения манипулятора от вертикальной оси,(x2 — ск)рость

отклонения угла, a₁ = αL-2m-11, m₁ = m₀ +M3 , a₂ = gL-1

m₀ +M2

m-11,

g — ускорение свободного падения, α — коэффициент трения, m₀ — масса

переносимого груза, L — длина манипулятора, M — масса манипулятора,

x = (x₁,x₂)^T. Рассмотрим краевые условия

(5.2)

x(0) = x, x(1) = 0, x = (x₁, x₂)^T,

x=(x₁,x₂)^T.

Система (3.6) и условия (3.7) для задачи (5.1), (5.2) имеют вид

dc₁

dc₂

(5.3)

= αe^-ατ c₂,

= αe^-ατ (-a₂ sin c₁ - a₁c₂ + d + μ(1 - e^-ατ

)),

dτ

(5.4)

c₁(0) = x₁, c₂(0) = 0, c₂

(τ) → 0

при τ → ∞, i = 1, 2.

Для решения задачи (5.3), (5.4) достаточно выполнить одно преобразование

функции c₂(τ) :

(5.5)

c₂(τ) = c⁽¹⁾²(τ) - μe^-ατ .

В результате получаем новую функцию c⁽¹⁾²(τ).

dc₁

= αe^-ατ c⁽¹⁾² - αμe-2ατ ,

dτ

(5.6)

dc⁽¹⁾²

= -αe^-ατ a₂ sin c₁ -αe^-ατ a₁c⁽¹⁾² -αe-2ατ a₁μ+αe^-ατ d-αμe-2ατ .

dτ

Линейная часть системы (5.6) может быть записана в форме

= αe^-ατ P c + αe^-ατ Qd,

c = (c₁,c⁽¹⁾²)^T,

dτ



(5.7)



₀



P =^

-a₂,

-a₁

,

₁

^.

После решения задачи стабилизации системы (5.7) и перехода к исходным

переменным по формулам (5.5), (3.5), (3.8) получаем закон управления

6α + 4α² + 2 - (1 - t)²a₂α

-3 - 3α + α(1 - t)a₁

u(t, x) = -

x₁ +

x₂ +

α²(1 - t)²

α(1 - t)

(5.8)

-3 - 3α + α(1 - t)a₁

+μ

Далее решаем задачу Коши для системы (5.1), замкнутой управлением (5.8)

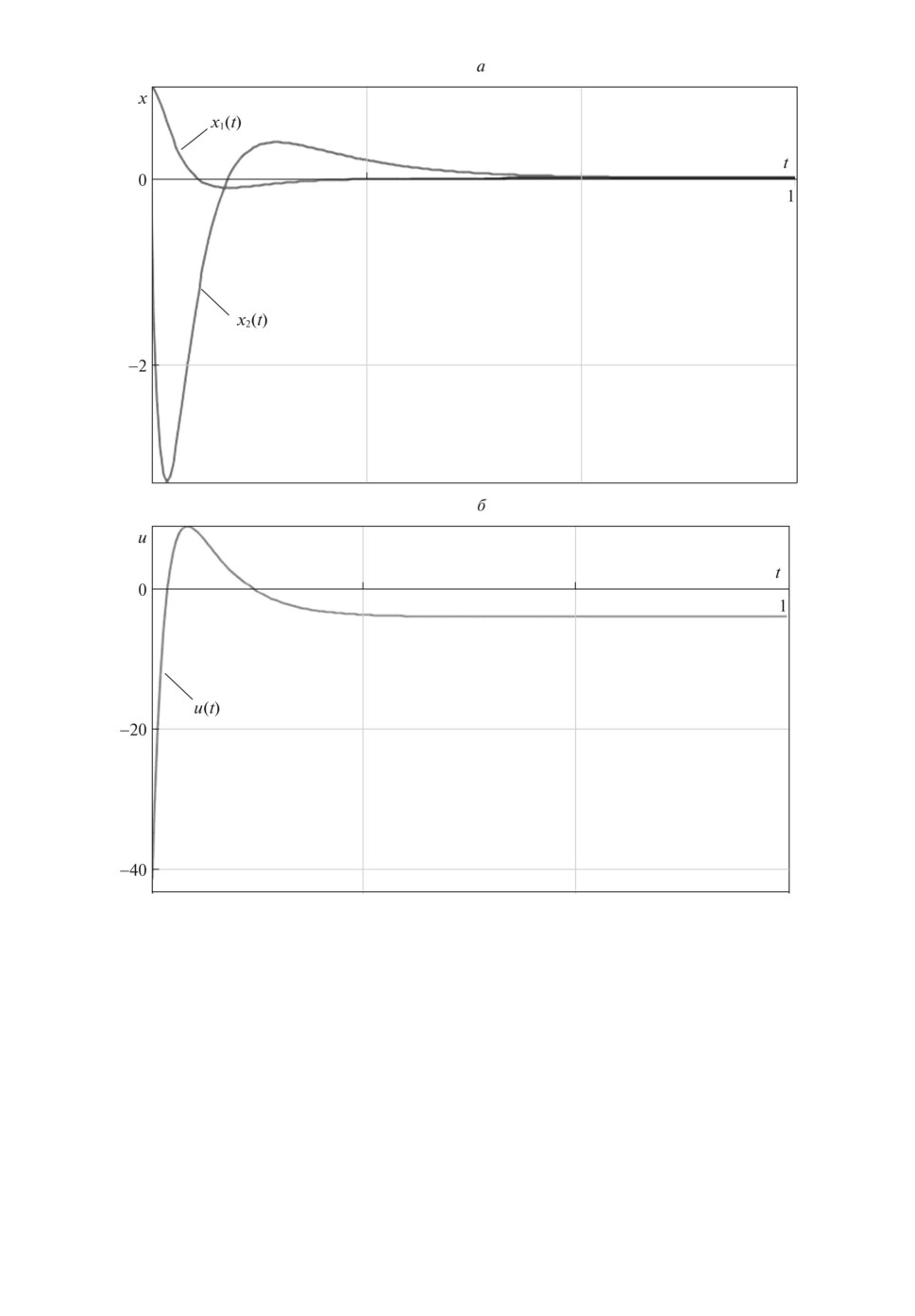
с начальными данными (5.2). В процессе численного моделирования пола-

галось x₁ = 1 рад, α = 0,1, α = 0,25, L = 10 м, M = 20 кг, m₀ = 1 кг, μ = 0,1,

t ∈ [0, 0,9). На рисунке а и б представлены графики изменения соответствую-

щих функций фазовых координат x₁(t), x₂(t) и управления u(t).

Замечание 2. При μ = 0, x = 0 из (5.1), (5.8) получаем u(t,x(t,0)) ≡

≡ 0 ∀t ∈ [0,1].

Рисунок.

6. Заключение

Анализ приведенного в разделе 4 алгоритма позволяет утверждать, что

наиболее трудоемкая часть процедуры построения решения поставленной за-

дачи, а именно построение вспомогательной системы, нахождение матрицы

обратной связи вспомогательного стабилизирующего управления и переход к

исходным переменным, может быть выполнена в аналитическом виде с ис-

пользованием методов компьютерной алгебры. С другой стороны, результаты

решения задачи управления роботом-манипулятором показывают, что пред-

ложенный в работе метод может быть применен при решении конкретных

практических задач с использованием персональных ЭВМ.

ПРИЛОЖЕНИЕ

Доказательство теоремы. Достаточность. Из процедуры нахож-

дения искомой управляющей функции u(t, x) и соответствующей функции

фазовых координат x(t), подробно изложенной в [11], следует, что пара

x(t), u(t, x), является решением задачи (2.1), (2.6).

Необходимость. Пусть условие (2.4) не выполнено и предположим против-

ное, что существует ε > 0 такое, что для всех x ∈ Rⁿ : ∥x∥ < ε существует ре-

шение задачи (2.1), (2.6). Тогда для x существует решение задачи (3.6), (3.7).

Согласно (2.2) систему (3.6) можно записать в виде

∑

dc_i

∂f_i

= αe^-ατ f_i(x,0) + αe-ατ

(x,0)c_j

+ αe^-ατ

(x,0)d_j +

dτ

∂x_j

∂u_j

j=1

⎡

∑∑

∂²fi

∂²f_i

(Π.1)

αe^-ατ ⎣

(c,˜)cj ck + 2

d)c_j d_k +

∂xj∂x

∂x_j∂u_k

j=1 k=1

⎤

∑∑

∂²f_i

d)d_j d_k⎦,

i = 1,...,n.

∂u

j∂uk

j=1 k=1

Из условий (2.2), (2.3) следует

∑

∑∑

∂f_i

∂²f_i

f_i(x,0) =

(0, 0)x_j +

(x,0)x_j x_k,

x= θ_ix,

θi ∈ [0, 1],

∂x

∂x_j∂x_k

j=1

k=1 j=1

∑

∂f_i

∂²f_i

(Π.2)

(x,0) =

(0, 0) +

(x,0)x_k,

= θ_ix,

∈ [0, 1],

∂x_j

∂x_j∂x_k

k=1

∑

∂f_i

∂²f_i

x₌

(x,0) =

(0, 0) +

(x,0)xk,

ix,

i ∈[0,1], i=1,...,n.

∂u_j

∂u_j∂x_k

k=1

С учетом (П.2) систему (П.1) можно записать в форме

∑

∑∑

dc_i

∂f_i

∂²f_i

= αe^-ατ

(0, 0)x_j

+ αe^-ατ

(x,0)x_j x_k +

dτ

∂x

∂x_jx_k

j=1

j=1 k=1

∑

∑∑

∂f_i

∂²f_i

+ αe^-ατ

(0, 0)c_j

+ αe^-ατ

(x,0)x_kc_j +

∂x

∂x_j∂x_k

j=1

j=1 k=1

∑

∑∑

∂f_i

∂²f_i

+ αe^-ατ

(0, 0)d_j

+ αe^-ατ

(x,0)x_kd_j +

(Π.3)

∂u

∂x_k∂u_j

j=1

j=1 k=1

⎡

∑∑

∂²fi

∂²f_i

αe^-ατ ⎣

(c,˜)cj ck + 2

d)c_j d_k +

∂xj∂x

∂x_j∂u_k

k=1 j=1

⎤

∑∑

∂²f_i

d)d_j d_k⎦

i = 1,...,n.

∂u

j∂uk

k=1 j=1

Запишем систему (П.3) в векторном виде

= αe^-ατ (Ac + Bd + Ax) + αe^-ατ (R1(x) +R2(c, x) +R3(d, x) +R4(c, d, x)),

dτ

(Π.4)

R₁ = (R11,... ,Rn1)^T,

R₂ = (R12,... ,Rn2)^T,

R₃ = (R13,... ,Rn3)^T,

R₄ = (R14,... ,Rn4)^T,

∑∑

∂²fi

∂²f_i

˜i2 =

(x,0)x_j x_k,

(x,0)c_j x_k,

∂xj∂x

∂x_k∂x_j

k=1 j=1

(Π.5)

∑∑

∂²fi

(˜,0)xkdj,

∂u

j∂xk

j=1 k=1

⎡

∑∑

∂²fi

∂²f_i

(c,˜)cj ck + 2

d)c_j d_k +

∂x

j∂x

∂x_j∂u_k

j=1 k=1

(Π.6)

⎤

∑∑

∂²fi

(c,˜)dj dk⎦ .

∂u

j∂uk

j=1 k=1

Из равенств (П.5), (П.6) следует, что при ∥x∥ < ε в области (2.5), (3.10) спра-

ведливы оценки



^R

≤L

1 ∥x∥2 ,

^R

≤L

2 ∥c∥ ∥x∥ ,

^R

≤L

3 ∥d∥ ∥x∥ ,

(Π.7)



^R

≤L

4(∥c∥² + ∥d∥²),

L_i > 0, i = 1,... ,4.

Пусть rank S = k, 0 < k < n. Обозначим через b_i i-й столбец матрицы B.

Введем в рассмотрение матрицу

{

}

S₄ = b₁,Ab₁,... ,Ak1-¹b₁,b₂,Ab₂,... ,Ak2-¹b₂,... ,b_r,... ,Akr-¹br,lk+1,... ,ln

Здесь k_j , j = 1, . . ., r, - максимальное количество столбцов вида b_j, . . . , Akj -¹b_j

таких, что векторы b₁, Ab₁, . . . , Ak1-¹b₁, b₂, Ab₂, . . . , Ak2-¹b₂, . . . , b_r, Ab_r,

...,Akr-¹b_r линейно независимы, векторы l_j, j = k + 1,...,n выбраны так,

чтобы

(Π.8)

rank S₄

= n.

Используя (П.8), выполним в системе (П.4) замену переменной c по формуле

(Π.9)

c=S₄

Согласно [1] в новых переменных система (П.4) и условия (2.7) примут вид

(

)

(

)

(

)

A₁

A₂

B₁

A₁

A₂

= αe^-ατ

y + αe^-ατ

d + αe^-ατ

dτ

O₁

A₃

O₂

O₁

A₃

(Π.10)

+ αe^-ατ S-14 R₁(S₄ y) + αe^-ατ S-14 R₂(S₄y, S₄ y) +

+ αe^-ατ S-14 R₃(d, S₄ y) + αe^-ατ S-14 R₄(S₄y, d, S₄ y),

y = S-14x,

(Π.11)

y(0) = -y, y(τ) → 0 при τ → ∞ ∀ y : ∥S₄y∥ < ε.

В правой части (П.10) A₁, A₂, A₃, B₁ — матрицы с постоянными коэффициен-

тами соответственно размерностей k × k, k × n - k, n - k × n - k, k × r. Бло-

ки O₁, O₂ являются матрицами с нулевыми элементами соответственно раз-

мерностей n - k × k, n - k × r. Представим векторы y(τ), y в виде y(τ) =

= (y(τ), y(τ))^T, y(τ) = (y1(τ), . . . , yk(τ))T,

y(τ) = (yk+1(τ), . . . , y_n(τ))^T, y=

= (y, y)^T,

y=(y1,... , y_k)^T,

y=(yk+1,...,y_n)^T

. Введем в рассмотрение си-

стему, состоящую из последних n - k уравнений системы (П.10), предполо-

жив дополнительно, что в ее правую часть подставлены известные функ-

ции y(τ), d(τ). Не умоляя общности, можно положить

y = (0,...,0, yk+1,..., yk+1)^T,

= αe^-ατ A₃ y + αe^-ατ A₃ y +

(Π.12)

dτ

[

]

+ αe^-ατ

S-14

R₁(S₄y) +R2(S₄y,S₄y) +R3(d,S₄y) +R4(S₄y,d,S₄ y) ,

гд

S-14 — матрица, состоящая из последних n - k строк матрицы S-14. Тогда

из (П.11) вытекают условия

(Π.13)

y(0) = -y,

(τ) → 0

при τ → ∞.

Покажем, что решения системы (П.12), начинающиеся в достаточно ма-

лой окрестности начала координат, не удовлетворяют условию (П.13).

Очевидно, что Φ(τ) = e-e-ατ A³ eA3

— фундаментальная матрица системы

= αe^-ατ A₃ y, нормированная в нуле. Решение системы (П.12) с началь-

dτ

ными данными (П.13) имеет вид

∫τ

y(τ) = -e-e-ατ A³ eA3 y + e-e-ατ A³ ee-αtA³ αe^-αtA₃ ydt +

∫τ

[

(Π.14)

+e-e-ατA³ ee-αtA³αe^-α

S-14

R₁(S₄y) +

]

+ R₂(S₄y,S₄y) +R3(d,S₄y) +R4(S₄y,S₄y) dt, τ ∈ [0,∞).

 учеом ограничения (2.5) и условий (2.2), (3.8), (П.9), (П.11) в области

S-14 y

≤εимеемоценки

(Π.15)

∥y(τ, y)∥ ≤ L₁ ∥y∥,

∥d(τ, y(τ, y))∥ ≤ L₂

∥y∥ .

После вычисления первого интеграла в правой части равенства (П.14) полу-

чаем

∫τ

[

y(τ) = -y + e-e-ατ A³ ee-αtA³ αe^-αt

S-14

R₁(S₄y) +R2(S₄y,S₄y) +

]

R₃(d,S₄y) +R4(S₄y,S₄y) dt, τ ∈ [0,∞).

Отсюда



∫τ



[



˜



^ατ A₃



^αtA₃



y(τ)≥



y-

e-e-

 αe^-αt

ee-



S-14

^R

1(S4 y)+



]



^R

2(S4y, S4 y)+

^R

3(d, S4y)+

^R

4(S4y, S4 y) dt, τ ∈ [0, ∞).

Используя (П.7), (П.9), ( П.15), из последнего неравенства получаем



˜

˜

(Π.16)

y(τ)

_≥



y-L3

y

τ ∈ [0,∞).

В (П.16) константа L₃ > 0 зависит от области ∥S₄ y∥ < ε. Зафиксируем^y в

области ∥S₄ y∥ < ε так, чтобы



(

)_T



˜

(Π.17)

y<

∥S₄y∥ < ε,

0, . . . , 0,yk+1, . . . ,yn

y > 0.

L₃

Из (П.16) следует, что все траектории системы (П.12), начинающиеся в об-

ласти (П.17), не удовлетворяют условию (П.13). Указанное обстоятельство

противоречит утверждению о существовании ε > 0, которое фигурирует в

формулировке теоремы. В случае, когда k = 0, доказательство аналогично.

Необходимость доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Kaлман Р., Фалб П., Арбиб М. Очерки по математической теории систем / Под

ред. Э.Л. Напельбаума. М.: Мир, 1971.

2. Walсzak S. A note on the controllability of nonlinear systems // Math. Syst. Theory

1984. V. 17. No. 4. P. 351-356.

3. Комаров В.А. Синтез ограниченных управлений для линейных неавтономных

систем // АиТ. 1984. № 10. С. 44-50.

Komarov V.A. Design of Constrained Control Signals for Nonlinear Non-autonomous

Systems // Autom. Remote Control. 1984. V. 45. No. 10. P. 1280-1286.

4. Крищенко А.П. Исследование управляемости и множеств достижимости нели-

нейных систем управления // АиТ. 1984. № 6. С. 30-36.

Krishchenko A.P. Controllability and Attainability sets of Nonlinear Control

Systems // Autom. Remote Control. 1984. V. 45. No. 6. P. 707-713.

5. Dirk A. Controllability for polynomial systems // Lect. Notes Contr. Inf. Sci. 1984.

No. 63. P. 542-545.

6. Комаров В.А. Оценка множества достижимости для линейных систем // Изв.

АН СССР. Сер. Мат. 1984. № 1. С. 83-87.

7. Balachandran K. Global and local controllability of nonlinear systems // JEEE.

Proc. 1985. No. 1. P. 14-17.

8. Benzaid Z. Global null controllability of perturbed systems // JEE. Trans. Autom.

Control. 1987. No. 7. P. 623-625.

9. Попова С.Н. К свойству локальной достижимости линейной управляемой систе-

мы // Дифференц. уравнения. 2003. Т. 39. № 1. С. 50-56.

10. Бердышев Ю.И. О построении области достижимости в одной нелинейной зада-

че // Изв. РАН. Теория и системы управл. 2006. № 4. С. 22-26.

11. Kvitko A., Yakusheva D. On one boundary problem for nonlinear stationary

controlled System // Int. J. Control. 2019. V. 92. No. 4. P. 828-839.

DOI: 10.1080/00207179.2017.1370727

12. Coron J.M. Control and Nonlinearity

// Amer. Math. Soc. Math. Surveys

Monographs. 2007. V. 136.

13. Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория кон-

струирования систем управления. М.: Высш. шк., 1998.

14. Balachandran K., Govindaraj V. Numerical controllability of fractional dynamical

systems // Optimization. 2014. V. 63. No. 8. P. 1267-1279.

15. Красовский Н.Н. Теория управления движением. М.: Наука, 1968.

Статья представлена к публикации членом редколлегии М.М. Хрусталевым.

Поступила в редакцию 16.07.2018

После доработки 23.06.2019

Принята к публикации 18.07.2019