Автоматика и телемеханика, № 2, 2020
© 2020 г. И.Б. ФУРТАТ, д-р техн. наук (cainenash@mail.ru)
(Институт проблем машиноведения РАН, Санкт-Петербург;
Университет ИТМО, Санкт-Петербург)
ДИВЕРГЕНТНЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ
ДИНАМИЧЕСКИХ СИСТЕМ1
Предложен метод исследования устойчивости динамических систем с
использованием свойств потока и дивергенции вектора фазовой скорости.
Установлена связь между методом функций Ляпунова и предложенным
методом. На базе полученных результатов приведен синтез закона управ-
ления с обратной связью по состоянию для стабилизации динамических
систем, который сводится к решению дифференциального неравенства
относительно искомой функции управления. Рассмотрены примеры, ил-
люстрирующие применимость предложенного метода и существующих.
Ключевые слова: динамическая система, устойчивость, поток векторного
поля, дивергенция, управление.
DOI: 10.31857/S0005231020020051
1. Введение
Динамическими моделями описывается множество процессов в окружаю-
щем макро- и микромире. Одним из важных вопросов эволюции таких систем
является исследование сходимости решений данных моделей. Однако найти
явное решение дифференциального уравнения не всегда представляется воз-
можным, а численные решения могут значительно отличаться от истинно-
го [1].
Хорошо известно, что метод функций Ляпунова позволяет исследовать
устойчивость решений дифференциальных уравнений, не решая их. Впервые
это показано А.М. Ляпуновым в конце XIX в. в его докторской диссертации
(позже опубликованной в [2]) применительно к задачам астрономии и движе-
ния жидкости. Последующее развитие метода функций Ляпунова для иссле-
дования устойчивости и неустойчивости различных динамических систем, а
также приложения полученных результатов в авиации, технике, механике и
т.д. можно найти в следующих классических трудах [3-7]. В зависимости от
решаемых задач функция Ляпунова также интерпретируется как потенци-
альная функция (potential function) [8], функция энергии (energy function) [9]
или функция хранения (storage function) [10]. Однако основное ограничение в
использовании аппарата функций Ляпунова состоит в поиске данных функ-
ций.
1 Результаты раздела 2 получены при поддержке Российского фонда фундаменталь-
ных исследований (проект № 17-08-01266). Результаты раздела 3 получены при поддержке
Российского научного фонда (проект № 18-79-10104).
62
Методы исследования устойчивости динамических систем на базе свойств
дивергенции вектора фазовой скорости объекта являются альтернативны-
ми методу функций Ляпунова. Одними из первых основополагающих ра-
бот в направлении получения дивергентных условий устойчивости были тру-
ды [11-13]. В [14] получены фундаментальные результаты, посвященные раз-
витию дивергентного метода для многомерных систем. Вопросы исследова-
ния устойчивости с использованием свойств индекса Пуанкаре и дивергенции
векторных полей многомерных систем рассмотрены в [15, 16].
Результаты, предложенные в настоящей статье, будут тесно связаны с
работами В.П. Жукова и А. Рантцера (A. Rantzer). Несмотря на то что
в западной литературе нередко первенство в исследовании устойчивости
с помощью дивергенции вектора фазовой скорости отдается А. Рантцеру
[17, 18], в отечественной литературе подобные идеи были опубликованы ра-
нее А.А. Шестаковым, А.Н. Степановым в [14] и В.П. Жуковым в [19]. В [19]
исследуется неустойчивость решения нелинейного дифференциального урав-
нения с помощью дивергенции векторного поля. Затем в течение примерно
30 лет по исследованию неустойчивости различного вида динамических си-
стем В.Н. Жуковым опубликован цикл работ, с частью которых можно сво-
бодно ознакомиться на сайте журнала “Автоматики и телемеханики”. В [20]
приведено необходимое условие устойчивости нелинейных систем в виде непо-
ложительности дивергенции векторного поля фазовой скорости. В [14, 21]
для исследования неустойчивости нелинейных динамических систем вво-
дится вспомогательная скалярная функция. Отметим, что введение данной
функции для исследования свойств устойчивости и неустойчиовсти по Ляпу-
нову особой точки системы дифференциальных уравнений рассматривалось
еще ранее в [22], но без использования дивергентных подходов. Позже в [17]
А. Рантцер использовал также вспомогательную скалярную функцию, кото-
рую назвал функцией плотности (density function). В [14, 23] получены усло-
вия устойчивости для систем второго порядка. Затем А. Рантцер в [17, 18] об-
суждает сходимость почти всех решений нелинейных динамических систем
произвольного порядка и рассматривает вопросы синтеза закона управле-
ния. Подход в [17, 18] отличается от подходов в [14, 23] тем, что для иссле-
дования устойчивости в [17, 18] используется функция плотности, которая
подобна обратной вспомогательной функции в [14, 23], за исключением их
свойств в точке равновесия динамической системы. В настоящее время под-
ход из [17, 18] распространен на различного рода системы [24-27]. В [28] пред-
ложен совершенно другой способ исследования устойчивости динамических
систем с использованием свойств потока вектора фазовой скорости через за-
мкнутую выпуклую поверхность и установлена связь дивергентного метода
со вторым методом Ляпунова.
Однако результатам [18, 20, 23, 28] присущи следующие особенности:
1) необходимое условие [20] — достаточно усиленное;
2) метод [23] обоснован только для систем второго порядка;
3) основной результат [18, теорема 1] гарантирует сходимость почти всех
решений системы. Для того чтобы определить устойчивость системы с ис-
63
пользованием [18, теорема 1], дополнительно накладывается условие неполо-
жительности дивергенции вектора фазовой скорости [18, см. утверждение 2];
4) условия устойчивости в [28] требуют существования преобразования
координат, которое приводит исходную систему к диагональному виду. Для
нелинейных систем поиск такого преобразования является трудно решаемой
задачей.
В настоящей статье предложен новый метод устойчивости динамических
систем с использованием свойств потока и дивергенции вектора фазовой ско-
рости. Получены необходимые условия устойчивости. Установлена связь ме-
тода функций Ляпунова с предложенным методом исследования устойчиво-
сти на базе потока и дивергенции вектора фазовой скорости. Предложены
достаточное условие устойчивости и метод синтеза закона управления. Ста-
тья сопровождается примерами, иллюстрирующими применимость предло-
женного метода и результатов статьи [18].
2. Основной результат
Рассмотрим динамическую систему
(1)
x = f(x),
где x = [x1, . . . , xn]T
— вектор состояния, f = [f1, . . . , fn]T : D → Rn
—
непрерывно-дифференцируемая функция, определенная в области D ⊂ Rn.
Множество D содержит начало координат и f(0) = 0. Для простоты поло-
жим, что область притяжения DA точки x = 0 совпадает с областью D. Одна-
ко все полученные результаты будут справедливы, если DA ⊂ D или DA = Rn.
Обозначим черезD границу области D.
В статье будем использовать следующие обозначения: grad{W (x)} =
[
]T
∂W
=
,...,∂W∂x
— градиент скалярной функции W (x), div{h(x)} = ∂h1 + . . .∂x
∂x1
n
1
... + ∂xn∂ n — дивергенция векторного поля h(x) = [h1(x),... ,h(x)n]T, |·| — ев-
клидова норма соответствующего вектора. Под устойчивостью будем пони-
мать устойчивость нулевого положения равновесия системы по Ляпунову [29].
Сформулируем необходимое условие устойчивости (1).
Теорема 1. Пусть x = 0 — асимптотически устойчивая точка рав-
новесия системы
(1). Тогда существует положительно определенная
непрерывно-дифференцируемая функция S(x), такая что S(x) → ∞ при
x →D, |grad{S(x)}| = 0 для любых x ∈ D \ {0} и для которой выполнено од-
но из следующих условий:
1) функция div{∫grad{S(x)}|f(x)} интегрируема в области V = {x ∈ D :
S(x) ≤ C} ⊂ D иV div{|grad{S(x)}|f(x)}dV < 0 для всех C > 0;
2) функция div{|grad{S-1(x)}|f(x)} интегрируема в области Vinv = {x ∈ D :∫
S-1(x) ≥ C} ⊂ D иVinv div{|grad{S-1(x)}|f(x)}dVinv > 0 для всех C > 0.
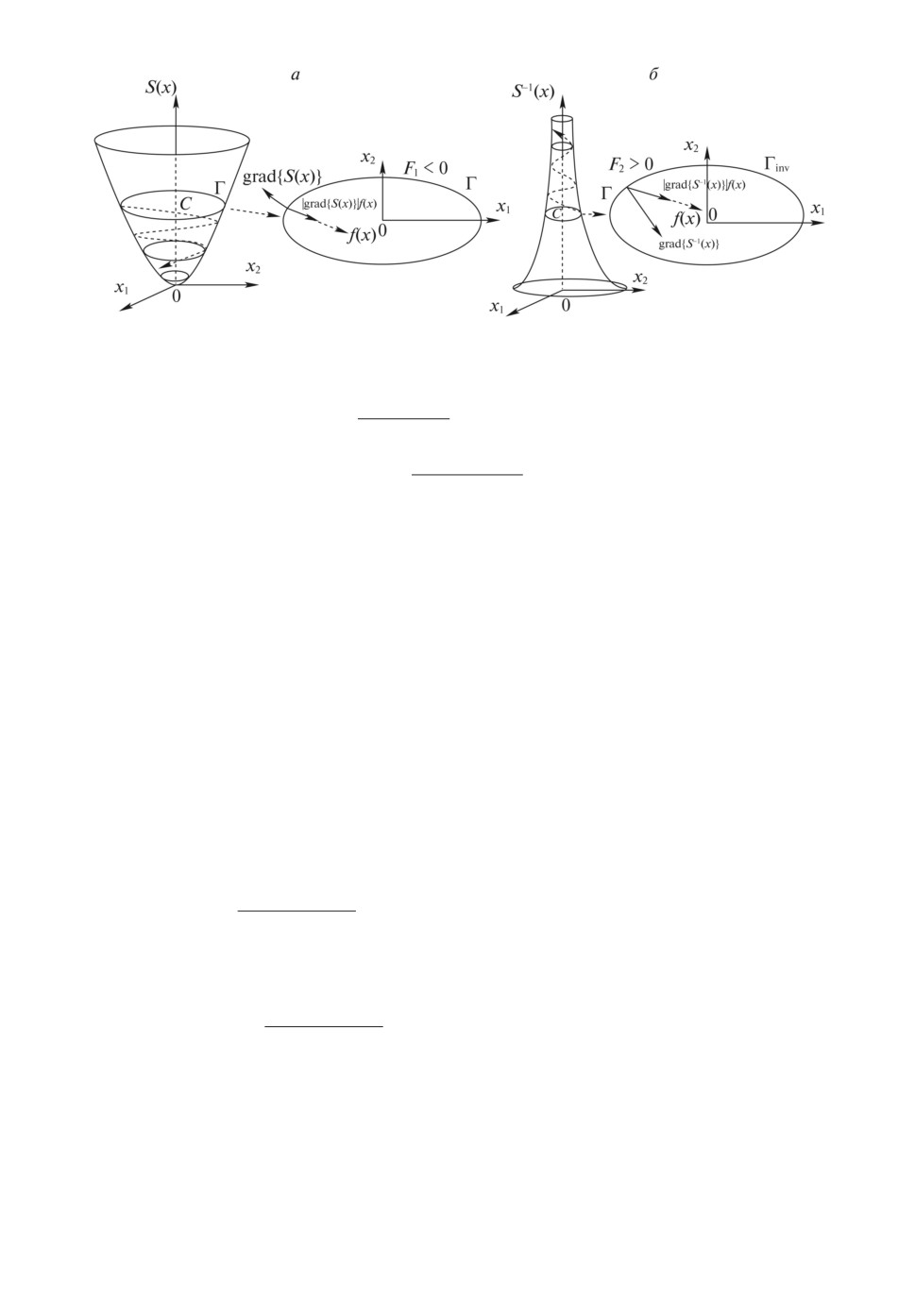
Рассмотрим геометрическую интерпретацию двух случаев в зависимости
от вида функции S(x) или S-1(x) в теореме 1. Обозначим через F1 поток век-
торного поля |grad{S(x)}|f(x) через поверхность Γ = {x ∈ D : S(x) = C} с еди-
64
Рис. 1. Геометрическая иллюстрация теоремы 1.
1
ничным вектором нормали
grad{S(x)} и через F2 — поток вектор-
|grad{S(x)}|
ного поля |grad{S-1(x)}|f(x) через поверхность Γinv = {x ∈ D : S-1(x) = C}
1
с единичным вектором нормали
grad{S-1(x)}. На рис. 1 проил-
|grad{S-1(x)}|
люстрирована геометрическая интерпретация обоих случаев при x ∈ R2, где
схематически изображены функции S(x) и S-1(x) (на рис. 1,а и 1,б слева) и
потоки F1 и F2 векторных полей |grad{S(x)}|f(x) и |grad{S-1(x)}|f(x) через
соответствующие поверхности уровней Γ и Γinv (на рис. 1,а и 1,б справа).
Если система (1) устойчива, то поток векторного поля F1 (F2) через поверх-
ность Γ (Γinv) принимает отрицательное (положительное) значение.
Доказательство. Согласно [29, теорема 4.17] если x = 0 — асимптоти-
чески устойчивая точка равновесия системы (1), то существует непрерывно-
дифференцируемая положительно определенная функция S(x), такая что
S(x) → ∞ при x →D, grad{S(x)}Tf(x) < 0 для любых x ∈ D \ {0} и
grad{S(x)}Tf(x)
= 0. Заметим, что если D = Rn, то функция S(x) яв-
x=0
ляется радиально неограниченной. Рассмотрим далее два случая по отдель-
ности, которые соответствуют функциям S(x) и S-1(x).
1. Если grad{S(x)}Tf(x) < 0, то и
1
grad{S(x)}T|grad{S(x)}|f(x) < 0.
|grad{S(x)}|
Значит, будет справедливо следующее выражение
∮
1
F1 =
grad{S(x)}T|grad{S(x)}|f(x)dΓ < 0.
Γ |grad{S(x)}|
Воспользовавшись формулой Гаусса-Остроградского (в литературе ее так-
же можно найти в виде divergence theore
∫
theorem (теорема Гаусса)), получим F1 =V div{|grad{S(x)}|f(x)}dV < 0.
2. Если grad{S-1(x)}Tf(x) < 0, то
grad{S-1(x)}Tf(x) = -S-2(x)grad{S(x)}Tf(x) > 0.
65
С другой стороны,
1
grad{S-1(x)}Tf(x) =
grad{S-1(x)}T|grad{S-1(x)}|f(x).
|grad{S-1(x)}|
Значит, будет выполнено следующее соотношение
∮
1
F2 =
grad{S-1(x)}T|grad{S-1(x)}|f(x)dΓinv > 0.
Γinv |grad{S-1(x)}|
Воспользовавшись формулой Гаусса-Остроградского, получим, что
∫
F2 =
div{|grad{S-1(x)}|f(x)}dVinv > 0.
Vinv
Теорема 1 доказана.
Подынтегральные выражения в теореме 1 явно зависят от функции S(x),
которая связана с поверхностью интегрирования. Сформулируем следствие,
которое позволит ослабить данное требование.
Следствие. Пусть x = 0 — асимптотически устойчивая точка рав-
новесия системы
(1). Тогда существуют положительно определенные
непрерывно-дифференцируемые функции φ(x) и S(x), такие что φ(x) → ∞
и S(x) → ∞ при x →D, |grad{S(x)}| = 0 для любых x ∈ D \ {0} и для кото-
рых выполнено одно из следующих условий:
1) функция di
∫
S(x) ≤ C} ⊂ D иV div{ρ(x)f(x)}dV < 0 для всех C > 0, где ρ(x) =
= φ(x)|grad{S(x)}|;
2) функция div{ρ-1(x)f(x)} интегрируема в области Vinv = {x ∈ D :∫
S-1(x) ≥ C}⊂D иVinv div{ρ-1(x)f(x)}dVinv > 0 для всех C > 0, где ρ-1(x) =
= φ-1(x)|grad{S-1(x)}|.
Доказательство. Следуя доказательству теоремы 1, рассмотрим два
случая.
1. Если grad{S(x)}Tf(x) < 0, то и φ(x)grad{S(x)}Tf(x) < 0. Следователь-
но, дальнейшее доказательство аналогично доказательству в теореме 1, рас-
сматривая только поток векторного поля φ(x)|grad{S(x)}|f(x) через поверх-
ность Γ.
2. Если grad{S(x)}Tf(x) < 0, то и φ-1(x)grad{S(x)}Tf(x) < 0. Значит,
дальнейшее доказательство аналогично доказательству теоремы 1, но с уче-
том потока векторного поля φ-1(x)|grad{S-1(x)}|f(x) через поверхность Γinv.
Следствие доказано.
Замечание. Если функция ρ(x) выбрана так, что div{ρ(x)f(x)} и
div{ρ-1(x)f(x)} интегрируемы, а также div{ρ(x)f(x)}<0 и div{ρ-1(x)f(x)}>∫
>0 для любых x∈D\{0}, то соответствующие условияV div{ρ(x)f(x)}dV <∫
<0 иV
div{ρ-1(x)f(x)}dVinv > 0, представленные в следствии, будут вы-
inv
полнены. В [18] для сходимости почти всех решений (1) требуется интегри-
руемость div{ρ-1(x)f(x)} и выполнение условия div{ρ-1(x)f(x)} > 0, что яв-
ляется частным требованием в следствии.
66
Теперь сформулируем достаточное условие устойчивости.
Теорема 2. Пусть задана положительно определенная непрерывно-
дифференцируемая функция ρ(x), определенная в области D. Тогда точка
x = 0 устойчива (асимптотически устойчива), если выполнено одно из сле-
дующих условий:
1) div{ρ(x)f(x)} ≤ ρ(x)div{f(x)} (div{ρ(x)f(x)} < ρ(x)div{f(x)})
для любых x ∈ D \ {0} и div{ρ(x)f(x)}
= 0;
x=0
2) div{ρ-1(x)f(x)} ≥ 0 (div{ρ-1(x)f(x)} > 0)
[
]
и div{f(x)} ≤ 0 для любых x ∈ D \ {0} и lim
ρ2(x)div{ρ-1(x)f(x)}
= 0;
|x|→0
3) div{ρ(x)f(x)} ≤ β(x)ρ2(x)div{ρ-1(x)f(x)}
(div{ρ(x)f(x)} < β(x)ρ2(x)div{ρ-1(x)f(x)}),
где β(x) > 1 и div{f(x)} ≤ 0 или только β(x) = 1 для любых x ∈ D \ {0},
[
]
а также div{ρ(x)f(x)}
= 0 и lim
ρ(x)div{ρ-1(x)f(x)}
= 0.
x=0
|x|→0
Доказательство. Приведем доказательство устойчивости для каждо-
го случая в отдельности. Доказательство асимптотической устойчивости ана-
логично.
1. Из соотношения div{ρ(x)f(x)} = grad{ρ(x)}Tf(x) + div{f(x)}ρ(x) сле-
дует, что если div{ρ(x)f(x)} ≤ div{f(x)}ρ(x), то и grad{ρ(x)}f() ≤ 0 в обла-
сти D \ {0}. По условию ρ(0) = 0. Поэтому если div{ρ(x)f(x)}
= 0, то и
x=0
grad{ρ(x)}f(x)
= 0. Значит, согласно теореме Ляпунова [29] система (1)
x=0
устойчива.
2. Из выражения div{ρ-1(x)f(x)} = grad{ρ-1(x)}Tf(x) + div{f(x)}ρ-1(x)
следует, что grad{ρ(x)}Tf(x) = ρ(x)div{f(x)} - ρ2(x)div{ρ-1(x)f(x)}. Если
div{ρ-1(x)f(x[} ≥ 0 и div{f(x)} ≤ 0,]то grad{ρ(x)}Tf(x)[ 0 в области D]\{0}.
Если lim|x|→0
ρ2(x)div{ρ-1(x)f(x)}
= 0, то и lim|x|→0
grad{ρ(x)}f(x)
= 0.
Значит, система (1) устойчива.
3. Условие 3 состоит в объединении результатов условий 1 и 2. Сумми-
руя β(x)grad{ρ(x)}Tf(x) = β(x)ρ(x)div{f(x)} - β(x)ρ2(x)div{ρ-1(x)f(x)} и
grad{ρ(x)}Tf(x) = div{ρ(x)f(x)} - div{f(x)}ρ(x), получим
(1 + β(x))grad{ρ(x)}Tf(x) =
= div{ρ(x)f(x)} - β(x)ρ2(x)div{ρ-1(x)f(x)} + (β(x) - 1)ρ(x)div{f(x)}.
Если
div{ρ(x)f(x)} ≤ β(x)ρ2(x)div{ρ-1(x)f(x)}
при β(x) = 1 или β(x) > 1 и div{f(x)} ≤ 0, то
grad{ρ(x)}Tf(x) ≤ 0 в области D \ {0}.
67
Если
[
]
div{ρ(x)f(x)}
= 0 и lim
ρ2(x)div{ρ-1(x)f(x)}
= 0,
x=0
|x|→0
то и
[
]
lim
grad{ρ(x)}f(x)
= 0.
|x|→0
Значит, система (1) устойчива. Теорема 2 доказана.
Во введении отмечалось, что результат [23] применим только для систем
второго порядка. Далее рассмотрим иллюстрацию полученных результатов
для систем третьего порядка и сравним полученные результаты с [18].
Пример 1. Рассмотрим систему
x1 = x2 - 2x1x23,
(2)
x2 = -x1 - 2x2x23,
x3 = -2x33,
которая имеет точку равновесия (0, 0, 0).
Выберем ρ(x) = |x|2α, где α — натуральное число. Проверим сначала усло-
вия следствия. Так как div{ρ(x)f(x)} = -|x|2α(4α + 10)x23 < 0 для любых α и
x3 = 0, а также div{ρ-1(x)f(x)} = (4α - 10)x23|x|-2α > 0 для α ≥ 3 и x3 = 0,
то условия следствия будут выполнены. Поскольку функция div{ρ-1(x)f(x)}
интегрируема в области {x ∈ Rn : |x| ≥ 1}, то будут выполнены условия тео-
ремы 1 [18] о сходимости почти всех решений (2).
Проверим теперь условия теоремы
2. Соотношение div{ρ(x)f(x)}-
−ρ(x)div{f(x)} = -4αx23|x|2α < 0 выполнено для любых α и x3 = 0. В свою
очередь div{f(x)} = -10x23 < 0 и функция div{ρ-1(x)f(x)} > 0 для лю-
бых α ≥ 3 и x3 = 0 (данный вывод можно также получить при исполь-
зовании утверждения 2 в [18]). Пусть β(x) = β ≥ 1. Тогда div{ρ(x)f(x)}-
-βρ2(x)div{ρ-1(x)f(x)} = -(4α + 10 + 4βα - 10β)x23|x|2α < 0 при α >5(β-1)2(β+1)
и x3 = 0. Все три случая дали одинаковые результаты. Значит, систе-
ма (2) асимптотически устойчива с любыми начальными условиями, когда
x3(0) = 0. Если начальные условия содержат x3(0) = 0, то система (2) устой-
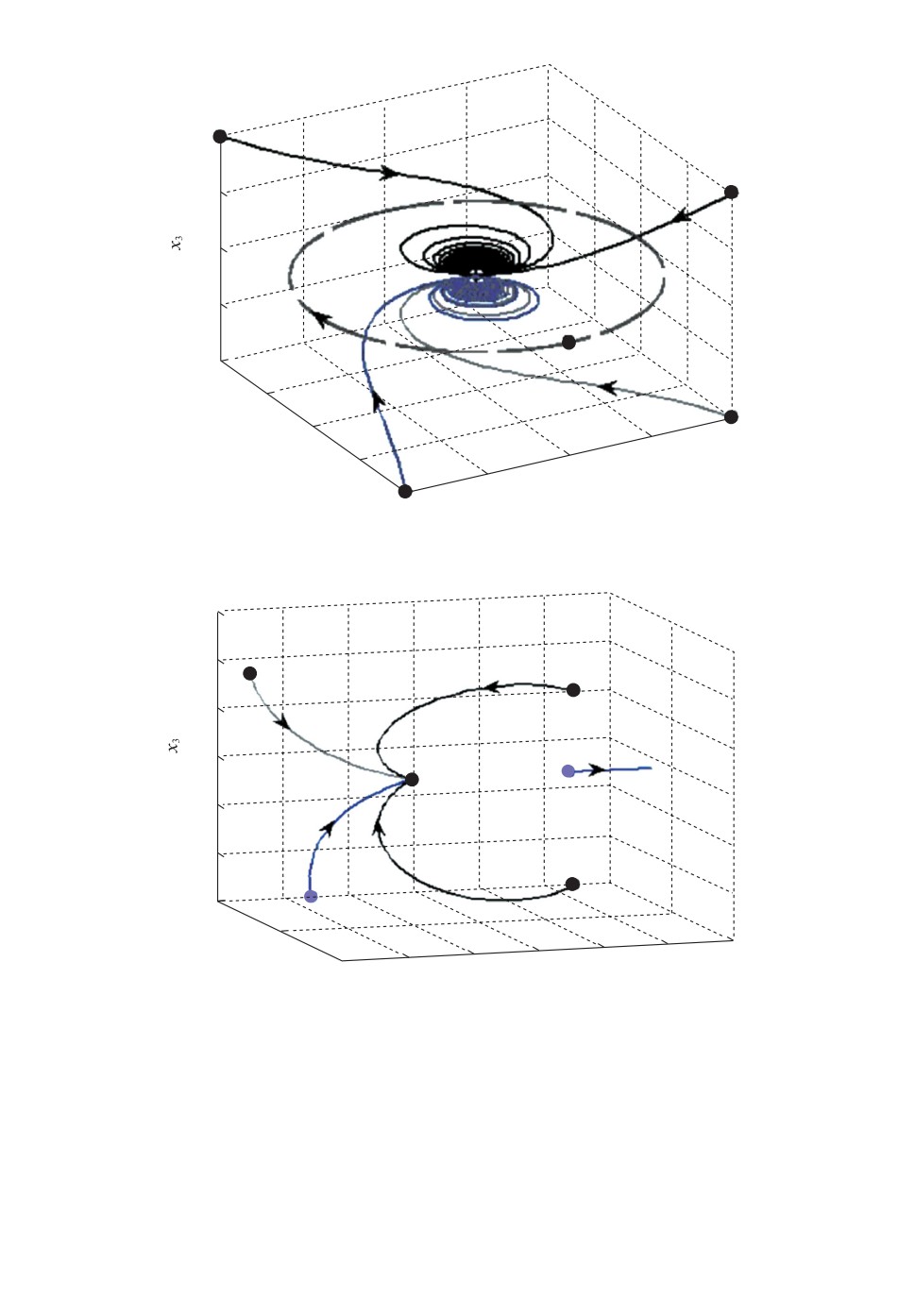
чива. Фазовые траектории системы (2) изображены на рис. 2, где цикл полу-
чен для начального условия с x3 = 0, спирали — при x3 = 0.
Таким образом, следствие и теорема 2, как и результаты [18], дали поло-
жительные ответы об устойчивости (2). Дополнительно условия теоремы 2
позволили установить, когда система (2) устойчива и когда асимптотически
устойчива.
Пример 2. Рассмотрим систему
x1 = -x1 + x21 - x22 - x23,
(3)
x2 = -x2 + 2x1x2,
x3 = -x3 + 2x1x3,
68
1,0
0,5
0
0,5
1,0
1,0
0,5
x2 0
1,0
0,5
0,5
0
x1
0,5
1,0
Рис.
2. Фазовые траектории системы (2).
1,5
1,0
0,5
0
0,5
1,0
1,5
2
0
x2
1,5
2,0
0,5
1,0
2
0,5
0
1,0
x1
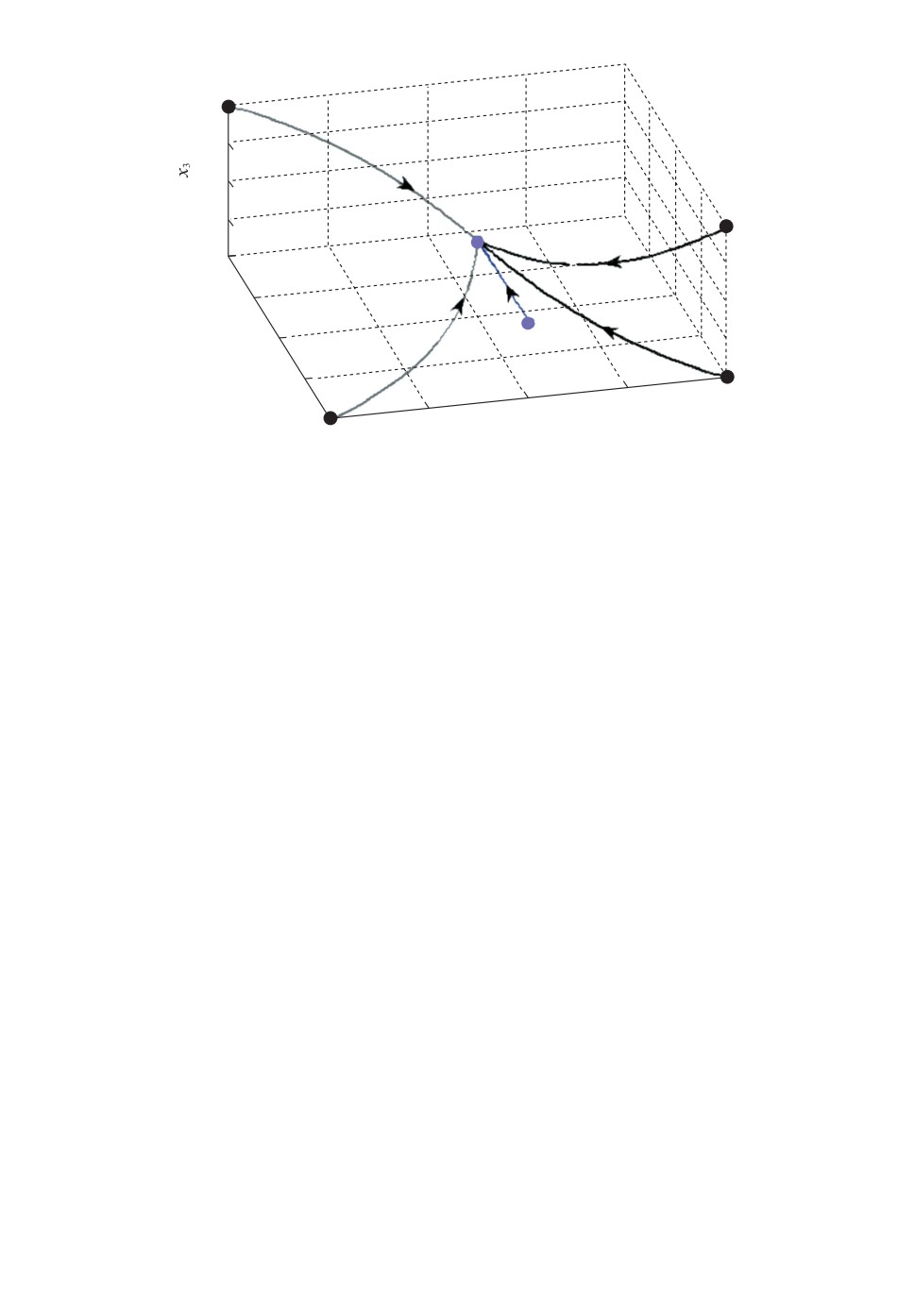
Рис.
3. Фазовые траектории системы (3).
которая имеет две точки равновесия (0, 0, 0) и (1, 0, 0). Все траектории си-
стемы сходятся к точке (0, 0, 0), за исключением тех, которые начинают-
ся на полуоси x1 ≥ 1, x2 = 0 и x3 = 0 (см. рис. 3). Выберем ρ(x) = |x|2α.
Тогда div{ρ-1(x)f(x)} = |x|-2α[2α - 3 + 2x1(3 - α)] > 0 при α = 3. Функ-
ция div{f(x)} = -3 + 6x1 не удовлетворяет условию div{f(x)} ≤ 0 при
x1 > 0,5. Соотношения div{ρ(x)f(x)} ≤ ρ(x)div{f(x)} и div{ρ(x)f(x)} ≤
69
1,0
0,5
0
0,5
1,0
1,0
0,5
0
x2
0,5
1,0
0,5
0
0,5
x1
1,0
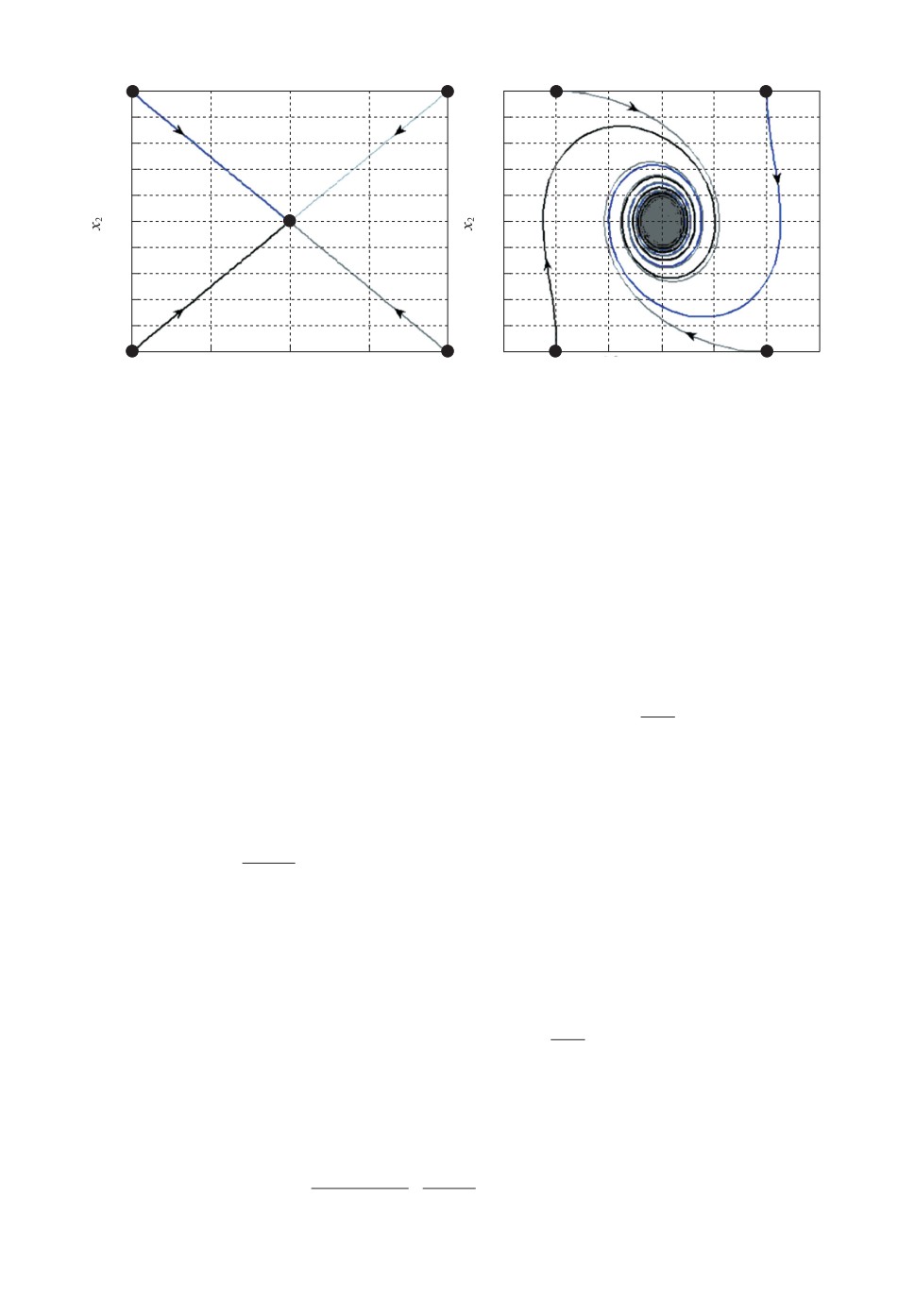
Рис. 4. Фазовый траектории системы (4) с двумя точками равновесия.
≤ β(x)ρ2(x)div{ρ-1(x)f(x)} тоже не выполнены. В результате в данном при-
мере выполнены условия следствия (и условия теоремы 1 из [18]), но не вы-
полнены условия теоремы 2 (и условия утверждения 2 из [18]).
Пример 3. Рассмотрим систему
x1 = -4x1x22 - x31,
(4)
x2 = 4x21x2 - x32 - 8x2x23,
x3 = -x33 + 8x22x3
с точкой равновесия (0, 0, 0). Фазовые траектории (4) изображены на рис. 4
для различных начальных условий.
Выберем ρ(x) = |x|2α и проверим сначала условия следствия. Вычислив
div{ρ(x)f(x)} = |x|2α-2[(-2α + 1)x41 + (-2α + 1)x42 + (-2α - 11)x43 + 2x21x22 -∫
-10x21x23 - 10x22x23], получим, чтоV div{ρ(x)f(x)}dV < 0 для любых C и α.
Для div{ρ-1(x)f(x)} = |x|-2α-2[(2α + 1)x41 + (2α + 1)x42 + (2α - 11)x43 + 2x21x22-∫
-10x21x23 - 10x22x23] условиеVinv div{ρ-1(x)f(x)}dVinv > 0 выполнено для лю-
бых C и α ≥ 3. Следовательно, условия следствия выполнены (условия тео-
ремы 1 из [18] выполнены только при α ≥ 8).
Проверим теперь условия теоремы
2. Соотношение div{ρ(x)f(x)}-
−ρ(x)div{f(x)} = -2α|x|2α-2(x41 + x42 + x43) < 0 выполнено для любых α и
x = 0. Функция div{f(x)} = x21 + x22 - 11x23 не является знакоопределенной,
значит, независимо от выбора ρ-1(x) утверждением
2
в [18] и вторым
случаем теоремы 2 здесь воспользоваться нельзя. Условие div{ρ(x)f(x)}-
-βρ2(x)div{ρ-1(x)f(x)} < 0 в теореме 2 выполнено при β = 1 и x = 0.
Таким образом, для системы (4) выполнены условия следствия и теоре-
мы 2, откуда следует, что (0, 0, 0) — асимптотически устойчивая точка рав-
новесия. Согласно [18] можем только заключить, что почти все решения (4)
70
сходятся к (0, 0, 0) поскольку не выполнены условия утверждения 2 из [18], а
выполнены только условия теоремы 1 из [18].
3. Синтез закона управления
Рассмотрим динамическую систему, аффинную по управлению,
(5)
x = ξ(x) + g(x)u(x),
где u(x) — сигнал управления, функции ξ(x), g(x) и u(x) — непрерывно-диф-
ференцируемые в области D, ξ(0) = 0 и g(0) = 0 и система (5) является управ-
ляемой в области D. Сформулируем следующий результат.
Теорема 3. Пусть задана положительно определенная непрерывно-
дифференцируемая функция ρ(x) при x ∈ D. Если закон управления u(x) вы-
бран так, что выполнено одно из следующих условий:
1) div{ρ(x)(ξ(x) + g(x)u(x))} ≤ ρ(x)div{ξ(x) + g(x)u(x)}
(div{ρ(x)(ξ(x) + g(x)u(x))} < ρ(x)div{ξ(x) + g(x)u(x)})
для любых x ∈ D \ {0} и div{ρ(x)(ξ(x) + g(x)u(x))}
= 0;
x=0
2) div{ρ-1(x)(ξ(x) + g(x)u(x))} ≥ 0 (div{ρ-1(x)(ξ(x) + g(x)u(x))} > 0)
[
]
для любых x ∈ D \ {0} и lim
ρ2(x)div{ρ-1(x)(ξ(x) + g(x)u(x))}
= 0;
|x|→0
3) div{ρ(x)(ξ(x) + g(x)u(x))} ≤ β(x)ρ2(x)div{ρ-1(x)(ξ(x) + g(x)u(x))}, β ≥ 1
(div{ρ(x)(ξ(x) + g(x)u(x))} < β(x)ρ2(x)div{ρ-1(x)(ξ(x) + g(x)u(x))}),
где β(x) > 1 и div{ξ(x) + g(x)u(x)} ≤ 0 или только β(x) = 1
для любых x ∈ D \ {0}, а также div{ρ(x)(ξ(x) + g(x)u(x))}
=0 и
x=0
[
]
lim
ρ(x)div{ρ-1(x)(ξ(x) + g(x)u(x))}
= 0,
|x|→0
то замкнутая система будет устойчивой (асимптотически устойчивой).
Поскольку система (5) является управляемой в области D, то доказатель-
ство теоремы 3 непосредственно следует из доказательства теоремы 2 с уче-
том замены f(x) = ξ(x) + g(x)u(x).
Отметим, что при синтезе закона управления с использованием функции
Ляпунова V (x) требуется выбрать u так, чтобы было выполнено алгебраиче-
ское неравенство grad{V }(f + gu) < 0. Согласно теореме 3 u необходимо вы-
брать так, чтобы было выполнено дифференциальное неравенство, что дает
новое условие поиска закона управления.
Пример 4. Рассмотрим систему
x1 = dx2 - x1x22,
(6)
x2 = u,
71
а
б
1,0
1,0
0,8
0,8
0,6
0,6
0,4
0,4
0,2
0,2
0
0
0,2
0,2
0,4
0,4
0,6
0,6
0,8
0,8
1,0
1,0
1,0
0,5
0
0,5
1,0
1,5
1,0
0,5
0
0,5
1,0
1,5
x1
x1
Рис. 5. Фазовые траектории в замкнутой системе при d = 0 (а) и при d = 1,
β = 2 (б).
где d принимает значения 0 и 1. Требуется разработать закон управления u,
который бы обеспечил асимптотическую устойчивость (6) в окрестности точ-
ки (0, 0). Очевидно, что при u = 0 система (6) не является асимптотически
устойчивой при любом значении d. Выберем ρ(x) = |x|2α, α — натуральное
число, и воспользуемся третьим случаем теоремы 3.
1. Пусть d = 0. Вычислим
div{ρ(x)(ξ(x) + g(x)u(x))} - β(x)ρ2(x)div{ρ-1(x)(ξ(x) + g(x)u(x))} =
(
)
∂u
= -2α(1 + β)x21x22 + 2α(1 + β)ux2 + (1 - β)
-x22 +
(x21 + x22).
∂x2
Выбрав u = -x32, получим, что
div{ρ(x)(ξ(x) + g(x)u(x))} - β(x)ρ2(x)div{ρ-1(x)(ξ(x) + g(x)u(x))} < 0
при β ≥ 1, α >2(β-1)β+1 и x2 = 0, а также div{ξ(x) + g(x)u(x)} ≤ 0. Фазовые
траектории замкнутой системы изображены на рис. 5,а.
2. Пусть d = 1. Вычислим
div{ρ(x)(ξ(x) + g(x)u(x))} - β(x)ρ2(x)div{ρ-1(x)(ξ(x) + g(x)u(x))} =
= 2α(1 + β)x1x2 - 2α(1 + β)x21x22 +
(
)
∂u
+ 2α(1 + β)ux2 + (1 - β)
-x22 +
(x21 + x22).
∂x2
Выбрав u = -x1 - (β - 1)x32, получим, что
div{ρ(x)(ξ(x) + g(x)u(x))} - β(x)ρ2(x)div{ρ-1(x)(ξ(x) + g(x)u(x))} < 0
{
}
(β-1)(3β-2)
3β-2
при β ≥ 1 и α > max
,
, а также div{ξ(x) + g(x)u(x)} ≤ 0.
2(β+1)
2(β+1)
Фазовые траектории замкнутой системы изображены на рис. 5,б при β = 2.
72
4. Заключение
Предложен метод исследования устойчивости динамических систем с ис-
пользованием свойств потока и дивергенции вектора фазовой скорости. Для
исследования устойчивости требуется существование определенного вида по-
верхности интегрирования или вспомогательной скалярной функции. Сфор-
мулированы отдельно необходимые и достаточные условия устойчивости.
Дальнейшие результаты могут быть связаны с распространением полученно-
го метода на другие виды систем, например неавтономные системы, системы
с запаздыванием и т.д.
Полученные результаты применены к синтезу закона управления с об-
ратной связью для динамических систем. Показано, что для выбора зако-
на управления требуется разрешить дифференциальное неравенство отно-
сительно сигнала управления, в то время как при использовании аппарата
функций Ляпунова требуется разрешить алгебраическое неравенство. Про-
должением работ по синтезу новых алгоритмов управления с использовани-
ем дивергентных методов может являться модификация некоторых эффек-
тивных схем управления, разработанных на базе метода функций Ляпунова.
К таким методам управления можно отнести метод инвариантных эллипсо-
идов [30], метод скоростного градиента [31] и др.
СПИСОК ЛИТЕРАТУРЫ
1.
Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория кон-
струирования систем управления. М.: Высш. школа, 2003.
2.
Ляпунов А.М. Общая задача об устойчивости движения. М.; Л.: ГИТТЛ, 1950.
3.
Четаев Н.Г. Устойчивость движения. М.: 1955.
4.
Летов А.М. Устойчивость нелинейных регулируемых систем. М.: Физматгиз,
1962.
5.
Малкин И. Теория устойчивости движения. М.: Наука, 1966.
6.
Зубов В.И. Устойчивость движения. Методы Ляпунова и их применение. М.:
Высш. шк., 1984.
7.
Румянцев В.В., Озиранер А.С. Устойчивость и стабилизация движения по от-
ношению к части переменных. М.: Наука, 1987.
8.
Yuan R., Ma Y.-A., Yuan B., Ao P. Lyapunov Function as Potential Function:
A Dynamical Equivalence // Chin. Phys. B. 2014. V. 23. No. 1. P. 010505.
9.
Bikdash M.U., Layton R.A. An Energy-Based Lyapunov Function for Physical
Systems // IFAC Proc. 2000. V. 33. No. 2. P. 81-86.
10.
Willems J.C. Dissipative Dynamical Systems. Part I: General Theory. Part II: Linear
Systems with Quadratic Supply Rates // Arch. Rational Mech. Anal. 1972. V. 45.
No. 5. P. 321-393.
11.
Zaremba S.K. Divergence of Vector Fields and Differential Equations // Amer. J.
Math. 1954. V. LXXV. P. 220-234.
12.
Fronteau J. Le théorèm de Liouville et le problèm général de la stabilité. Genève:
CERN, 1965.
13.
Brauchli H.I. Index, divergenz und Stabilität in Autonomen equations. Zürich:
Abhandlung Verlag, 1968.
73
14.
Шестаков А.А., Степанов А.Н. Индексные и дивергентные признаки устой-
чивости особой точки автономной системы дифференциальных уравнений //
Дифференц. уравнения. 1979. Т. 15. № 4. С. 650-661.
15.
Масина О.Н., Дружинина О.В. Моделирование и анализ устойчивости некото-
рых классов систем управления. М.: ВЦ РАН, 2011.
16.
Дружинина О.В. Индекс, дивергенция и функции Ляпунова в качественной
теории динамических систем. М.: Изд. группа URSS, 2013.
17.
Rantzer A., Parrilo P.A. On Convexity in Stabilization of Nonlinear Systems //
Proc. 39th IEEE Conf. on Decision and Control. Sydney, Australia. 2000. P. 2942-
2946.
18.
Rantzer A. A Dual to Lyapunov’s Stability Theorem // Syst. & Control Lett. 2001.
V. 42. P. 161-168.
19.
Жуков В.П. Об одном методе качественного исследования устойчивости нели-
нейных систем // АиТ. 1978. № 6. С. 11-15.
Zhukov V.P. On One Method for Qualitative Study of Nonlinear System Stability //
Autom. Remote Control. 1978. V. 39. No. 6. P. 785-788.
20.
Жуков В.П. К методу источников для исследования устойчивости нелинейных
систем // АиТ. 1979. № 3. С. 12-17.
Zhukov V.P. On the Method of Sources for Studying the Stability of Nonlinear
Systems // Autom. Remote Control. 1979. V. 40. No. 3. P. 330-335.
21.
Жуков В.П. Необходимые и достаточные условия неустойчивости нелинейных
автономных динамических систем // АиТ. 1990. № 12. С. 59-65.
Zhukov V.P. Necessary and Sufficient Conditions for Instability of Nonlinear
Autonomous Dynamic Systems // Autom. Remote Control. 1990. V. 51. No. 12.
P. 1652-1657.
22.
Красносельский М.А., Перов А.И., Поволоцкий А.И., Забрейко П.П. Векторные
поля на плоскости. М.: Физматлит, 1963.
23.
Жуков В.П. Дивергентные условия асимптотической устойчивости нелинейных
динамических систем второго порядка // АиТ. 1999. № 7. С. 34-43.
Zhukov V.P. On the Divergence Conditions for the Asymptotic Stability of Second-
Order Nonlinear Dynamical Systems // Autom. Remote Control. 1999. V. 60. No. 7.
P. 934-940.
24.
Monzon P. On Necessary Conditions for Almost Global Stability // IEEE Trans.
Autom. Control. 2003. V. 48. No. 4. P. 631-634.
25.
Loizou S.G., Jadbabaie A. Density Functions for Navigation-Function-Based
Systems // IEEE Trans. Autom. Control. 2008. V. 53. No. 2. P. 612-617.
26.
Castañeda
Á., Robledo G. Differentiability of Palmer’s Linearization Theorem and
Converse Result for Density Functions // J. Diff. Equat. 2015. V. 259. No. 9.
P. 4634-4650.
27.
Karabacak
Ö., Wisniewski R., Leth J. On the Almost Global Stability of Invariant
Sets // Proc. 2018 Eur. Control Conf. (ECC 2018). Limassol, Cyprus. 2018. P. 1648-
1653.
28.
Фуртат И.Б. Исследование устойчивости динамических систем с использова-
нием свойств потока вектора фазовой скорости через замкнутую выпуклую по-
верхность // Науч.-техн. вестн. информ. технологий, механики и оптики. 2013.
Т. 83. № 1. С. 23-27.
29.
Халил Х.К. Нелинейные системы. М.; Ижевск: Ин-т компьют. исслед., 2009.
74
30. Поляк Б.Т., Топунов М.В. Подавление ограниченных внешних возмущений:
управление по выходу // АиТ. 2008. № 5. C. 72-90.
Polyak B.T., Topunov M.V. Suppression of Bounded Exogenous Disturbances:
Output Feedback // Autom. Remote Control. 2008. V. 69. No. 5. P. 801-818.
31. Фрадков А.Л. Схема скоростного градиента и ее применение в задачах адаптив-
ного управления // АиТ. 1979. № 9. С. 90-101.
Fradkov A.L. A Scheme of Speed Gradient and its Application in Problems of
Adaptive Control // Autom. Remote Control. 1980. V. 40. No. 9. P. 1333-1342.
Статья представлена к публикации членом редколлегии Л.Б. Рапопортом.
Поступила в редакцию 21.05.2019
После доработки 02.07.2019
Принята к публикации 18.07.2019
75