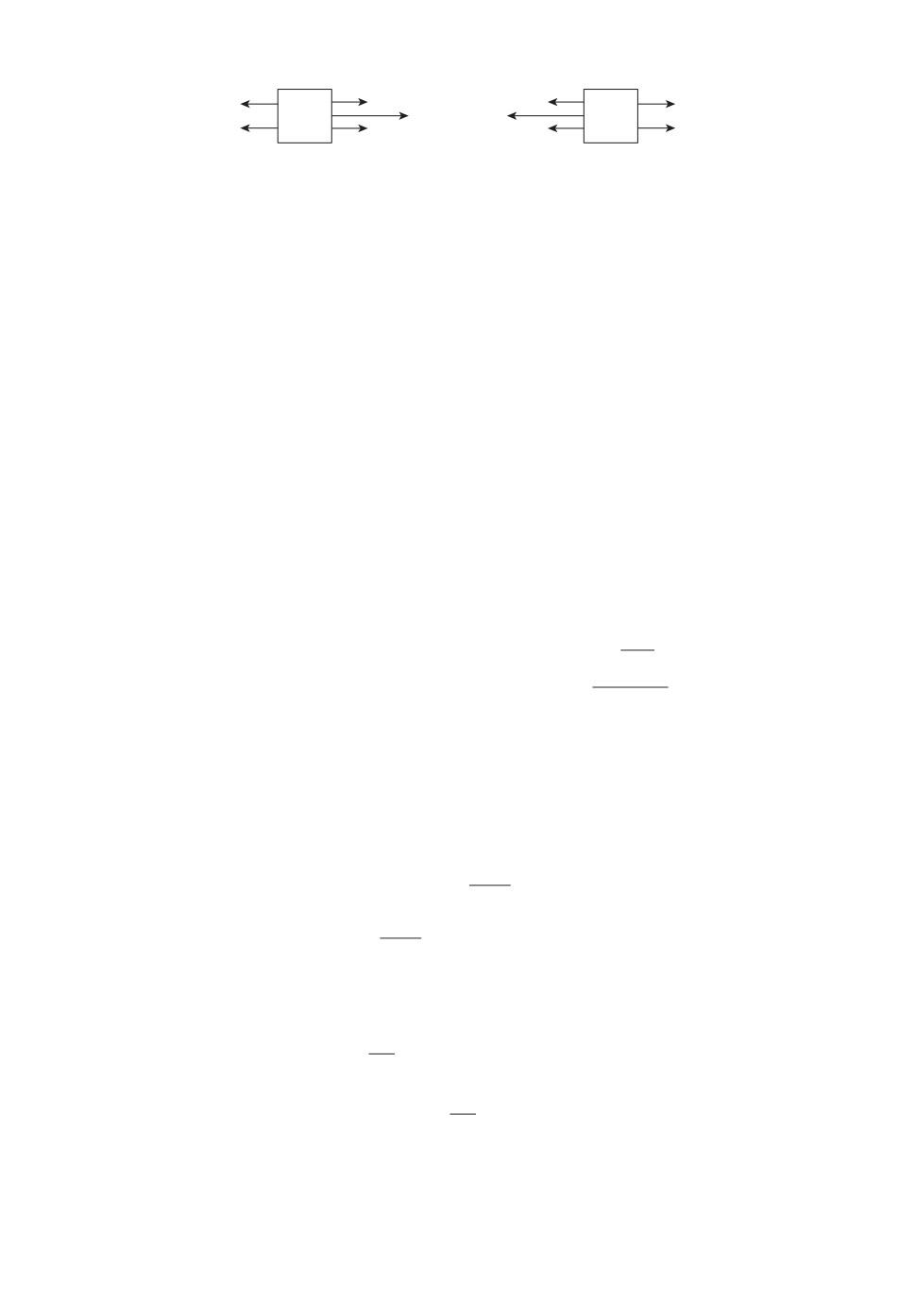Автоматика и телемеханика, № 2, 2020
Управление в технических системах
© 2020 г. А.А. ТИХОНОВ, д-р физ.-мат. наук (a.tikhonov@spbu.ru)
(Санкт-Петербургский государственный университет;
Санкт-Петербургский горный университет)
МЕТОД УПРАВЛЕНИЯ ДЛЯ УГЛОВОЙ СТАБИЛИЗАЦИИ
ЭЛЕКТРОДИНАМИЧЕСКОЙ ТРОСОВОЙ СИСТЕМЫ1
Рассматривается проблема стабилизации электродинамической тросо-
вой системы (ЭДТС) на круговой околоземной орбите в положении, когда
трос вытянут вдоль местной вертикали. Для решения этой задачи предло-
жена оригинальная схема построения ЭДТС, включающая отрицательно
заряженный коллектор на нижнем конце троса и положительно заряжен-
ный коллектор на верхнем конце троса. Величина заряда на отрицательно
заряженном коллекторе контролируется электронными эмиттерами. Ана-
литически и численно показано, что момент сил Лоренца, действующий
на ЭДТС благодаря заряженным коллекторам на концах троса, значи-
тельно расширяет область устойчивости вертикального положения троса.
Кроме того, управление зарядом на отрицательно заряженном коллекто-
ре в соответствии с текущим угловым движением троса позволяет создать
такую управляющую составляющую лоренцева момента, которая имеет
диссипативный характер. Одновременная работа восстанавливающих и
диссипативно-подобных составляющих управляющего лоренцева момен-
та позволяет обеспечить асимптотическую устойчивость вертикального
положения троса без необходимости отключать электрический ток, про-
текающий вдоль троса. Предложенный метод управления может быть ис-
пользован для стабилизации ЭДТС с целью повышения эффективности
ее работы по удалению космического мусора.
Ключевые слова: электродинамическая тросовая система, стабилизация,
геомагнитное поле, лоренцев момент, электродинамическое управление.
DOI: 10.31857/S0005231020020075
1. Введение
Среди разнообразия космических тросовых систем [1, 2] принято выделять
в отдельную категорию системы с тросами, проводящими электрический ток.
Ток, протекающий по изолированному тросу, следует рассматривать как ток,
протекающий по псевдоцепи, включающей околоземную плазму и замыкаю-
щейся через ионосферные токи, текущие вдоль силовых линий геомагнитного
поля [1]. В результате взаимодействия тока с геомагнитным полем возбужда-
ются амперовы и лоренцевы силы, оказывающие влияние на динамику про-
водящего троса [1]. Поэтому космические системы с проводящими тросами
1 Работа выполнена при финансовой поддержке Российского фонда фундаментальных
исследований (проект № 17-01-00672-а).
91
называют электродинамическими тросовыми системами (ЭДТС). В настоя-
щее время ЭДТС рассматриваются как весьма перспективные для решения
ряда задач по освоению космического пространства [3, 4]. В частности, актив-
но исследуются возможности использования ЭДТС для удаления с орбиты
отработавших искусственных спутников Земли (ИСЗ) или для уборки косми-
ческого мусора. В этом случае трос используется как электродинамический
тормоз орбитального движения, работающий на основе тормозящего влия-
ния амперовых сил [5-13]. При этом наибольшей эффективностью отличает-
ся проводящий трос, функционирующий в режиме проводника с током, ори-
ентированного в околоземном пространстве по местной вертикали [1, 5, 14].
Данная ориентация троса является устойчивой в центральном ньютоновском
гравитационном поле [1, 15]. Вместе с тем, установлено, что под действи-
ем момента сил Ампера вертикальная ориентация троса разрушается [1, 16].
Проблема неустойчивости ЭДТС известна [10, 14, 17]. Решению этой пробле-
мы посвящен ряд работ [13, 18, 19]. Среди возможных подходов к ее решению
наиболее известным является подход, предлагающий использование тех или
иных вариантов управления силой тока, протекающего по тросу [14, 18, 20],
включая периодическое прерывание тока или изменение его направления.
Однако в большинстве случаев ЭДТС должна функционировать в условиях,
предполагающих непрерывное протекание тока вдоль троса в одном направ-
лении, например для создания упомянутой выше силы тяги с целью удаления
космического мусора или для работы ЭДТС в режиме генератора мощности.
Поэтому периодическое выключение тока, протекающего по тросу, или пере-
ключение направления тока снижает эффективность ЭДТС и ограничивает
возможности их использования.
В данной работе рассматривается принципиально другой способ обеспече-
ния вертикального положения проводящего троса, основанный не на управле-
нии силой тока, протекающего по тросу, а на разделении разноименных заря-
дов по концам троса и использовании момента лоренцевых сил [21, 22], влия-
ние которого при определенных условиях является ориентирующим [23-30].
В [31] показано, что лоренцев момент может быть использован в качестве
восстанавливающей составляющей управляющего момента в системе стаби-
лизации проводящего троса в околоземном пространстве вдоль местной вер-
тикали. При этом усложнение конструкции ЭДТС не является существен-
ным, поскольку не предполагает введения в ее состав принципиально новых
устройств по сравнению с теми, которые обычно используются в ЭДТС.
Если же дополнительно ввести в состав ЭДТС блок управления, позволяю-
щий измерять текущее отклонение троса от вертикали и скорость изменения
угла отклонения, а также управлять электронным эмиттером, установлен-
ным на отрицательно заряженном коллекторе ЭДТС, изменяя заряд этого
коллектора в соответствии с данными измерений, то можно, как установ-
лено в данной работе, создать дополнительный момент диссипативного ха-
рактера [32]. Показано, что несмотря на неполную диссипацию, создаваемую
предложенным устройством, одновременное включение восстанавливающего
и диссипативного моментов позволяет решить задачу стабилизации ЭДТС в
вертикальном положении.
92
2. Конструкция троса
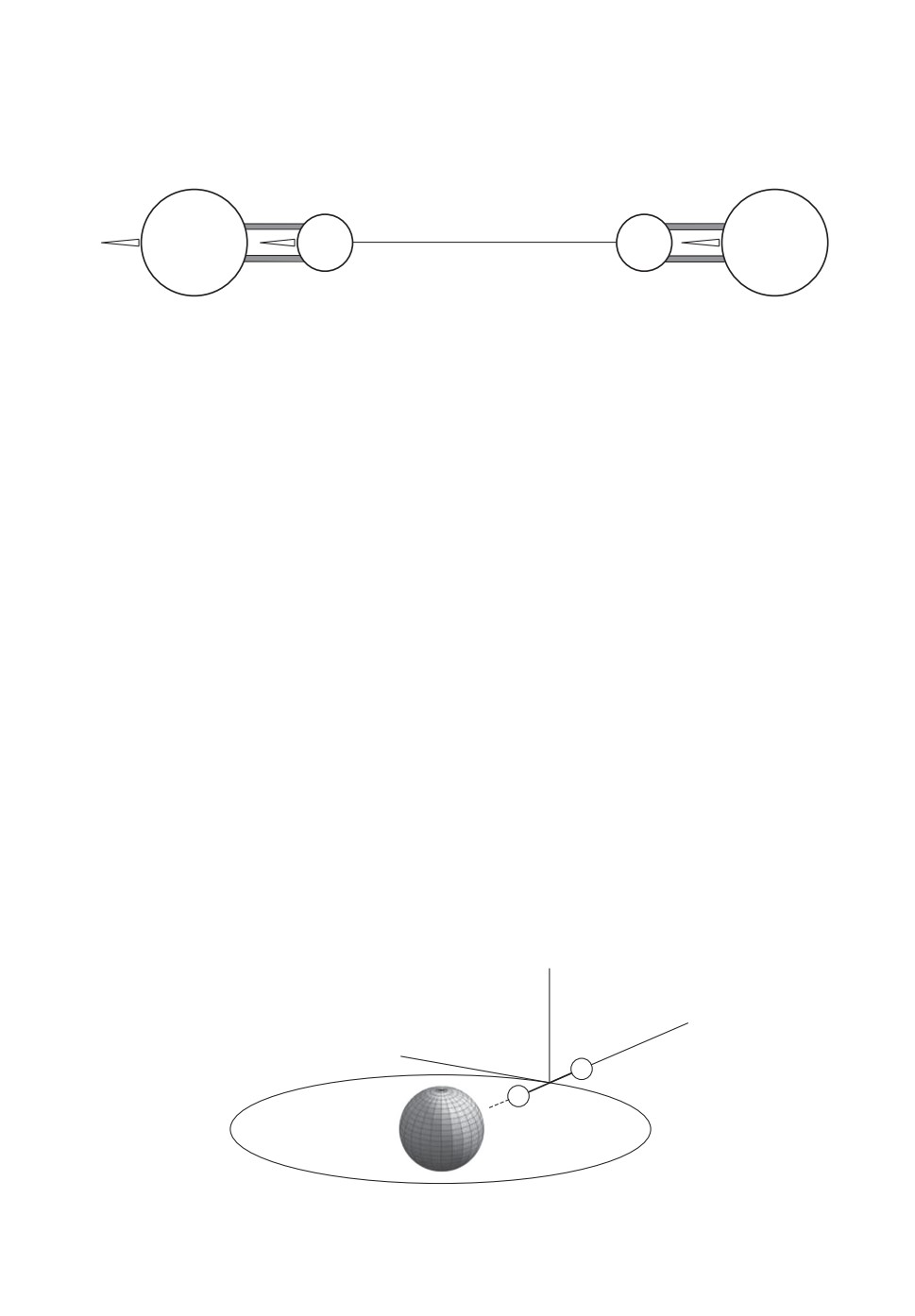
Конструктивная схема рассматриваемого электродинамического троса по-
казана на рис. 1.
2
2
5
3
3
3
+
4
6
2
2
1
7
Рис. 1. Конструктивная схема электродинамического троса.
Поверхность 1, находящаяся на нижнем конце троса (ближе к Земле) полу-
чает отрицательный заряд, поддерживаемый электронным эмиттером 3 (на-
пример, холловским ионным источником) со стороны концевого тела 4. Ана-
логичные электронные эмиттеры 3, установленные на поверхности 1, позво-
ляют управлять величиной заряда на поверхности 1, сбрасывая часть заряда
с поверхности 1 в окружающее пространство. С помощью электроизолирую-
щих креплений 2 поверхность 1 соединена с концевым телом 4 проводяще-
го троса 5. На противоположном конце троса тело 6 аналогичным образом
соединено с положительно заряженной поверхностью 7. Положительный за-
ряд на поверхности 7 поддерживается с помощью электронного эмиттера 3,
передающего отрицательный заряд на концевое тело 6.
3. Постановка задачи
Рассматривается электроизолированный проводящий трос, вдоль которого
течет ток. Трос находится на околоземной круговой орбите в гравитационном
и магнитном полях Земли и функционирует в режиме, близком к состоянию
обычного тяжелого троса, находящегося в натянутом состоянии вдоль мест-
ной вертикали благодаря градиенту гравитационного поля Земли (рис. 2).
Далее будем называть этот режим движения троса номинальным. В но-
минальном режиме работы ЭДТС, предназначенной для торможения кос-
мического объекта, направление силы тока совпадает с направлением оси Cz
C
Рис. 2. Орбитальная система координат.
93
натянутого троса, а ось Cz коллинеарна оси Cζ, направленной вдоль радиуса-
−-→
вектораR =OEC = Rζ0 центра масс троса относительно центра Земли OE.
В ограниченной спутниковой постановке задачи орбита точки C предполага-
ется круговой и лежащей в плоскости геомагнитного экватора. Оси Cξ и Cη,
направленные соответственно по касательной к орбите в сторону движения
точки C и по нормали к плоскости орбиты, образуют вместе с осью Cζ орби-
тальную систему координат Cξηζ. В инерциальном пространстве орбиталь-
ная система координат поворачивается с угловой скоростью ω0 = ω0η0.
К концам троса присоединены устройства для сбора электрических заря-
дов. Пренебрегая их размерами по сравнению с длиной троса и считая трос
натянутым, будем моделировать систему тонким прямолинейным тросом с
массой m0 и с точечными массами m1 и m2 на концах и для краткости назы-
вать ее связкой. Координаты масс mk обозначим через zk (k = 1, 2). Коорди-
наты центров зарядов qk также будем считать совпадающими с zk. Поскольку
координата центра масс ЭДТС
z2
∫
1
m0(z1 + z2) + 2m1z1 + 2m2z2
zC =
z dm =
m0 + m1 + m2
2(m0 + m1 + m2)
z1
равна нулю в силу выбора начала координат, то с учетом равенства z2-z1 = l,
где l - длина троса, получаем
l(m0 + 2m2)
l(m0 + 2m1)
(1)
z1 = -
,
z2 =
2(m0 + m1 + m2)
2(m0 + m1 + m2)
Сформулированная постановка задачи является максимально упрощенной с
целью выполнения предварительного аналитического исследования, рассчи-
танного в первую очередь на апробацию нового метода стабилизации ЭДТС, а
не на всесторонний учет разнообразных динамических факторов, усложняю-
щих функционирование системы, но не изменяющих принципа ее работы.
4. Силы натяжения троса
Рассматриваемая конструктивная схема ЭДТС предполагает наличие раз-
ноименно заряженных коллекторов на концах связки и соответствующих сил
кулонова притяжения коллекторов. Поэтому анализ вопроса о реализуемости
принятой модели ЭДТС в виде связки, пребывающей в натянутом состоянии,
является необходимым пунктом исследования, обсуждаемым в данном раз-
деле.
Отличие рассматриваемого троса от обычного тяжелого троса, находяще-
гося в натянутом состоянии вдоль местной вертикали благодаря градиенту
гравитационного поля Земли, заключается в наличии лоренцевых и кулоно-
вых сил, действующих на заряженные коллекторы, а также в наличии ам-
перовых сил, распределенных по всей длине троса. В номинальном режиме
движения связки сила Ампера ортогональна к тросу, а силами, определяю-
щими натяжение троса, являются гравитационные, лоренцевы и кулоновы
94
q1
q2
FL1
Fq1
Fq2
FL2
T1
T2
FG1
Ie1
FG2
Ie2
m1
m2
Рис. 3. Силы, действующие на концевые тела тросовой системы.
силы. Рассмотрим вопрос о силе натяжения троса и ее наибольшем значе-
нии, предполагая, что трос находится в номинальном движении (ось Cz троса
совпадает с осью Cζ местной вертикали), а геомагнитное поле моделируется
прямым магнитным диполем [15] с магнитной индукциейB = -g01(RE /r)3η0,
где g01 = -29556,8 нТл — гауссов коэффициент, RE — средний радиус Земли,
r — расстояние от центра Земли до данной точки пространства. В этом слу-
чае расстояния от центра Земли до концевых масс m1 и m2 соответственно
равны
(2)
R1 = R + z1, R2 = R + z2.
Скорости концевых точек, находящихся на расстояниях Rk от центра Земли и
обладающих зарядами qk, вычисленные в движении относительно геомагнит-
ного поля, равны vk = Rk(ω0 - ωE)ξ0. Поскольку эти скорости ортогональны
векторуB, то лоренцевы сил
FLk = qkvk ×Bk, действующие на коллекторы
с зарядами qk, направлены вдоль троса. ЗдесьBk =B(Rk) (k = 1, 2). Также
вдоль троса направлены гравитационные силы FGk =μmk, где μ — гравита-
R2
k
ционная постоянная Земли, кулоновы силы Fqk =k0q1q2
, k0 = 9,0 · 109 —
(R2-R1)2
постоянная закона Кулона, переносные силы инерции Iek, действующие на
концевые массы и заряды, и силы натяжения троса Tk (k = 1, 2), приложен-
ные к концевым точкам (рис. 3).
В равновесном положении концевых точек имеют место следующие равен-
ства проекций активных сил и переносных сил инерции на местную верти-
каль:
μm1
T1 + Fq1 + m1ω20R1 -
- |q1|v1B1 = 0,
R2
1
μm2
-T2 - Fq2 -
+ m2ω20R2 + q2v2B2 = 0.
R2
2
Отсюда находим силы натяжения троса, приложенные к концевым точкам:
(
)
μ
T1 = m1
-ω2R1
+ |q1|v1B1 - Fq1,
0
R2
1
(3)
(
)
μ
T2 = m2
ω20R2 -
+q2v2B2 - Fq2.
R2
2
Для отыскания натяжения троса в произвольной его точке рассмотрим
бесконечно малый элемент троса длиной dr и массой dm0. Силы, действую-
щие на этот элемент, показаны на рис. 4.
95
T(r)
T(r + dr)
dFG
dIe
dr
Рис. 4. Силы, действующие на элемент троса.
— постоянная ли-
l
нейная плотность троса. Из условий равновесия элемента троса получаем
уравнение
T (r + dr) - T (r) + dIe - dFG = 0.
Отсюда
(
)
μ
dT (r) =
- ω20r γ dr.
r2
Интегрируя это уравнение, находим
(
)
μ
ω20r2
(4)
T (r) = γ
-
-
+ const,
r
2
причем постоянная интегрирования может быть найдена с помощью любого
из равенств (3), задающих натяжение троса на концах. Воспользовавшись
первым из равенств (3), получим
(
)
(
)
μ
ω20r2
μ
ω20R21
T (r) = γ
-
-
+γ
+
+
r
2
R1
2
(5)
(
)
μ
+m1
-ω2
0
R1
+ |q1| v1B1 - Fq1.
R2
1
(
)
Посколькуd2T(r)
=γ
-2μ
-ω2
< 0, то T(r) достигает максимума при
dr2
r3
0
ω20 =μr3 . Но ω0 = const. Поэтому последнее равенство достигается при неко-
тором конкретном значении r = R0. На основании (5) имеем
(
)
)
2
γμ
3
R0
1
(R1
(6)
T (r)max = T (R0) =
-
+
+
+
R0
2
R1
2
R0
)
((
)2
μm1
R0
R1
+
-
+
R2
R1
R0
0
)
(√ μ
R3E
k0|q1|q2
+ |q1|
-ωE
(-g01)
-
R30
R21
(R2 - R1)2
Для отыскания величины R0, входящей в (6), составим уравнение равнове-
сия сил, растягивающих трос, в точке r = R0. Поскольку кулоновы силы,
приложенные к концевым точкам, равны по величине и противоположны по
96
направлению, то в точке O уравновешиваются гравитационные, лоренцевы
силы и силы инерции. Следовательно,
⎛
⎞
⎛
⎞
∫
∫
m2
γ dr
ω20 ⎝m1R1 + m2R2 +
γr dr⎠ - μ ⎝m1
+
+
⎠+FL2 - FL1 = 0.
R21
R2
r2
2
R1
R1
После интегрирования и подстановки явных выражений для лоренцевых сил
получаем следующее квадратное уравнение относительно ω0:
(
)
1
(7) ω20 m1R1 + m2R2 +
m0(R1 + R2)
+
2
)
(m1
m2
m0
+ (ω0 - ωE)(q2R2B(R2) - |q1|R1B(R1)) - μ
+
+
= 0.
R21
R22
R1R2
Решив это уравнение, найдем угловую скорость обращения радиуса-век-
тораR0 точки O, которую можно назвать центром, движущимся по орби-
те, или орбитальным центром [33]. В рассматриваемой постановке задачи
B(R1) = -g01RE
, B(R2) = -g01 RE
и уравнение (7) принимает вид
R31
R3
2
(
)
)
1
(q2
|q1|
(8) ω20 m1R1 + m2R2 +
m0(R1 + R2)
+ ω0(-g01)R3
-
-
2
E R22
R2
1
)
)
(q2
|q1|
(m1
m2
m0
- ωE(-g01)R3
-
-μ
+
+
= 0.
E R22
R21
R21
R22
R1R2
После отыскания ω0, вычисляем R0 и подставляем в (6).
Пример 1. Рассматривается связка с тросом длиной l = 2 · 104 м и по-
гонной плотностью γ = 2 · 10-3 кг/м, с концевыми массами m1 = 104 кг, m2 =
= 1,02 · 104 кг, концевыми зарядами q1 = -10-3 Кл, q2 = 10-3 Кл. Центр масс
системы движется по круговой околоземной орбите с радиусом R = 7 · 106 м.
На основании формул
(1),
(2) находим R1 = 6,990098814 · 106 м, R2 =
= 7,010098814 · 106 м. Из уравнения (8) находим ω0 = 1,078014368 · 10-3 c-1 и
затем по формуле R0 = (μ/ω20)1/3 получаем R0 = 6,999985732 · 106 м. Подста-
новка этого значения в формулу (6) позволяет найти Tmax = 352,425 Н. Нако-
нец, по формулам (3) находим натяжения тросов на концах: T1 = 352,084 Н,
T2 = 352,069 Н.
С учетом сказанного в начале данного раздела полученные результаты
следует рассматривать не только как оценочные сверху для сил натяжения
троса, но и свидетельствующие о реализуемости модели натянутой связки
при выбранных параметрах ЭДТС.
5. Уравнения вращательного движения связки
Как уже упоминалось выше в разделе 3, ЭДТС в развернутом состоянии
моделируется тонкой нитью с точечными массами на концах и для краткости
97
z
y
C
x
Рис. 5. Сопутствующая система координат.
называется связкой. Нить не оказывает сопротивления деформациям сжа-
тия. В рабочем состоянии нить остается натянутой во все время движения.
При этом она сохраняет прямолинейную форму и считается нерастяжимой.
В системе главных центральных осей инерции C xyz (ортыi1,i2,⃗i3) тензор
инерции связки имеет вид J = diag (A, A, C0), где
m0
A=
(z21 + z1z2 + z22) + m1z21 + m2z22,
3
а C0 пренебрежимо мало по сравнению с A.
Поскольку рассматривается симметричная относительно продольной оси
конструкция троса, то для устранения неопределенности в выборе осей x и y
представляется целесообразным ввести в рассмотрение сопутствующие оси
(оси Резаля) Cxyz с ортамиi,j,k так, что ось Cz (с ортом⃗i3 =k), как и
ранее, направлена вдоль натянутого троса, а трехгранник Cxyz не участвует
в повороте троса вокруг оси Cz на угол ϕ. Взаимную ориентацию осей си-
стем координат Cξηζ и Cxyz зададим с помощью матрицы направляющих
косинусов
⎛
⎞
α1
α2
α3
(9)
A=⎝β1 β2 β3⎠
γ1
γ2
γ3
так, что
ξ0 = α1i1 + α2i2 + α3i3,
η0 = β1i1 + β2i2 + β3i3,
ζ0 = γ1i1 + γ2i2 + γ3i3.
Наряду с направляющими косинусами будем также использовать углы ϑ
и ψ, однозначно определяющие положение сопутствующего трехгранника от-
носительно орбитальной системы координат (рис. 5).
98
Зависимость элементов матрицы A от углов ϑ и ψ определяется равен-
ствами
α1 = cos ψ, α2 = - sin ψ cos ϑ, α3 = sin ψ sinϑ,
(10)
β1 = sin ψ, β2 = cos ψ cos ϑ,
β3 = - cos ψ sinϑ,
γ1 = 0,
γ2 = sin ϑ,
γ3 = cos ϑ.
Кинематическими характеристиками вращательного движения связки яв-
ляются: абсолютная угловая скорость ω, угловая скорость сопутствующего
трехгранника относительно орбитальной системы координат ω1 = pi+qj+rk,
угловая скорость связки относительно сопутствующего трехгранника ϕ˙k, уг-
ловая скорость связки относительно орбитальной системы координат ω′ =
=ω1 +ϕ˙k.
Эти величины связаны соотношением ω = ω′ + ω0, которое в проекциях на
оси Cxyz имеет вид
(11)
ωx = p + ω0β1, ωy = q + ω0β2, ωz = r +ϕ˙ + ω0β3.
Кроме того, справедливы равенства
(12)
p =ϑ, q =ψ sin ϑ, r =
ψ
cos ϑ.
Оси Резаля остаются главными центральными осями инерции ЭДТС во
все время движения. Поэтому динамические уравнения вращательного дви-
жения ЭДТС в проекциях на оси Резаля получим проектированием на x, y, z
векторного уравнения
(
)
dK
(13)
+ (ω1 + ω0) × K =M
,
dt
xyz
представляющего собой теорему об изменении кинетического моментаK =
= Aωxi+Aωy⃗j под действием главного моментаM внешних сил относительно
центра масс.
6. Моменты сил, действующих на связку
В центральном ньютоновском гравитационном поле на связку действует
гравитационный момент
MG [15]. В данной задаче с учетом принятых обо-
значений проекции гравитационного момента на оси Cxyz имеют вид
(14)
MGx = 3ω20A(-γ2γ3), MGy = 3ω20Aγ1γ3, MGz
= 0.
Для вычисления главного момента сил Лоренца, действующих на заряды q1
и q2 в магнитном поле с индукциейB, воспользуемся простейшей аппрокси-
мацией этого момента [22], учитывающей точечный характер зарядов:
(15)
ML
P ×T
99
P = (q1z1 + q2z2)k,
T = A⊤(vC × B), vC = R(ω0 - ωE) ξ0, где ωE — угло-
вая скорость суточного вращения Земли. В условиях моделирования гео-
магнитного поля прямым магнитным диполем
B= -g01(RE/R)3η0, где
g01 = -29556,8нТл — гауссов коэффициент, RE — средний радиус Земли. По-
этому
MLx = R3ER-2g01(ω0 - ωE)(q1z1 + q2z2)γ2,
(16)
MLy = -R3ER-2g01(ω0 - ωE)(q1z1 + q2z2)γ1, MLz = 0.
Главный момент сил Ампера вычислим по формуле [1]
∫z2
(17)
MA =
ρ × (Ik × B
) dz,
z1
где ρ — радиус-вектор, проведенный из точки C в точку троса с текущей
координатой z, I — величина силы тока в проводнике. Принимая I = const,
в результате интегрирования (17) получаем
1
MAx =
Ig01(RE/R)3(z22 - z21)β1,
2
(18)
1
MAy =
Ig01(RE/R)3(z22 - z21)β2, MAz = 0.
2
7. ЭДТС без системы управления
7.1. Положения равновесия связки
В качестве дифференциальных уравнений вращательного движения связ-
ки относительно центра масс будем использовать динамические уравнения
Эйлера, вытекающие из (13),
⎧
⎨A˙ωx-Aωyωz=MGx+MLx+MAx,
(19)
A ωy + Aωzωx = MGy + MLy + MAy,
⎩
ωz = ωz0 = const
и кинематические уравнения Пуассона
α1 + ωyα3 - ωzα2 = -ω0γ1,
(x→y→z)
(20)
β1 + ωyβ3 - ωzβ2 = 0,
1→2→3
γ1 + ωyγ3 - ωzγ2 = ω0α1.
Для отыскания равновесных положений связки в орбитальной системе ко-
ординат будем рассматривать направляющие косинусы как неизвестные по-
стоянные величины, а проекции относительной угловой скорости p, q, r будем
100
полагать равными нулю в уравнениях (11), (19), (20). Динамические уравне-
ния примут вид
⎧
R3E
⎪
⎪Aω20β2β3 = 3ω20Aγ2γ3 -
g01(ω0 - ωE)(q1z1 + q2z2)γ2 -
⎪
R2
⎪
⎪
Ig01R3E
⎨
-
(z22 - z21)β1,
2R3
(21)
⎪
R3E
⎪
Aω20β1β3 = 3ω20Aγ1γ3 -
g01(ω0 - ωE)(q1z1 + q2z2)γ1 +
⎪
⎪
R2
⎪
Ig01R3E
⎩
+
(z22 - z21)β2.
2R3
Из (20), (21) следует, что номинальный режим движения связки, соответст-
вующий значению γ3 = 1, имеет место лишь при условии
(22)
z21 = z22.
В дальнейшем будем считать, что это условие выполнено. Ввиду однородно-
сти троса условие (22) выполняется при z1 = -z2, m1 = m2. В этом случае
A = (m0/3 + 2m2)z22.
Для решения вопроса о существовании других возможных положений рав-
новесия связки в орбитальной системе координат перейдем в уравнениях (21)
от направляющих косинусов к углам ϑ и ψ (рис. 5) по формулам (10). Полу-
чим систему уравнений
Ig01R3E
Aω20 sin ϑ sin ψ cos ψ = -
(z22 - z21) cos ψ cos ϑ,
2R3
Ig01R3E
(23)
Aω20 sin ϑ cos ϑ cos2 ψ =
(z22 - z21) sin ψ - -3Aω20 sin ϑ cos ϑ +
2R3
R3E
+
g01(ω0 - ωE)(q1z1 + q2z2)sin ϑ.
R2
Из (23) следует, что кроме номинального режима движения ϑ = 0, тео-
ретически возможны также и другие (“наклонные”) положения равновесия
связки в орбитальной системе координат, определяемые из условий:
(24)
1) sin ψ = 0, 4Aω20 cos ϑ1 = -L, или
2) cos ψ = 0, 3Aω20 cos ϑ2
= -L,
где
R3E
L=-
g01(ω0 - ωE)(q1z1 + q2z2).
R2
Поскольку L > 0, то возможным “наклонным” положениям равновесия связ-
ки могут отвечать лишь значения ϑ1 и ϑ2 из промежутка (π/2, π). Эти поло-
жения соответствуют “перевернутому” состоянию троса (если при этом он мо-
жет пребывать в натянутом состоянии), не обеспечивающему номинального
режима функционирования ЭДТС, и поэтому не рассматриваются в рамках
данной работы.
101
7.2. Устойчивость номинального режима движения
Рассмотрим вопрос об устойчивости номинального режима движения связ-
ки. Для этого обратимся к исходным уравнениям Эйлера (19) и, вводя обо-
значение a = Ig01(RE /R)3(z22 - z21)/2, перепишем первые два из них в виде
{
Aωx - Aωyωz = -3Aω20γ2γ3 - Lγ2 + aβ1,
(25)
Aωy + Aωxωz = 3Aω20γ1γ3 + Lγ1 + aβ2.
Несложно проверить, что имеет место равенство
[
]
d
A
3
(ω2x + ω2y) -
Aω20γ23 - Lγ3 - Aω0(ωxβ1 + ωyβ2)
=
dt
2
2
= a(ωxβ1 + ωyβ2 - ω0(β21 + β22)),
где производная в левой части равенства вычисляется в силу (25). Переходя
от абсолютных угловых скоростей ωx, ωy к относительным угловым скоро-
стям p, q по формулам (11), перепишем это равенство в виде
]
d
[A
A
3
(p2 + q2) -
ω20(β21 + β22) -
Aω20γ2
3
- Lγ3
= a(pβ1 + qβ2).
dt
2
2
2
Затем, вводя новую переменную Δ = 1 - γ3, представляющую собой отклоне-
ние связки от номинального режима движения γ3 = 1, перепишем последнее
соотношение в виде
d
[
]
A(p2 + q2) + (3Aω20 + L)α23 + (4Aω20 + L)β23 + LΔ2
= 2a(pβ1 + qβ2).
dt
Отсюда следует, что если учесть условие (22), то a = 0 и получаем первый
интеграл
V (α3, β3, Δ, p, q) = A(p2 + q2) + (3Aω20 + L)α23+
(26)
+ (4Aω20 + L)β23 + LΔ2 = h = const.
Поскольку выбором q1z1 + q2z2 > 0 всегда можно обеспечить выполнение
неравенства L > 0, то функция V (α3, β3, Δ, p, q) будет положительно опре-
деленной. Принимая ее в качестве функции Ляпунова, приходим к выво-
ду об устойчивости номинального режима движения связки по отклонениям
α3,β3,Δ и угловым скоростям p,q на основании теоремы Ляпунова об устой-
чивости. Для оценки амплитуды возмущенных колебаний ЭДТС в окрестно-
сти устойчивого номинального режима движения имеем неравенства
(27)
α23 ≤ h/(3Aω20 + L), β23 ≤ h/(4Aω20 + L), Δ2
≤ h/L,
вытекающие из (26). Из (27) следует, что при
(28)
h<L
102
положительно заряженный конец троса остается выше отрицательно заря-
женного конца троса, как и должно быть в номинальном режиме движения.
Заметим что условие “непереворачиваемости” троса (28) накладывает ограни-
чение p2 + q2 < L/A на начальную угловую скорость связки. Заметим также,
что увеличение параметра L > 0, обусловленного наличием лоренцева момен-
та, расширяет область устойчивости номинального режима движения связки.
Тем самым подтверждается стабилизирующий эффект лоренцева момента,
возбуждаемого за счет зарядов на концах троса. Соответствующие результа-
ты численного счета, иллюстрирующие этот вывод, приведены в [31].
Однако для решения задачи стабилизации номинального режима движе-
ния троса требуется обеспечить не только восстанавливающий, но и диссипа-
тивный момент. Рассмотрим возможности использования лоренцева момента
для создания управляющего воздействия, имеющего диссипативный харак-
тер.
8. ЭДТС с системой управления
8.1. Синтез управляющего момента
Из (15) следует, что формирование управляющего лоренцева момента опи-
рается на возможность создания управляемого вектор
P. Для модели линей-
ного относительного угловой скорости диссипативного момента [34] задача
может быть сведена к подбору такой неотрицательной диагональной матрицы
D=diag(D1,D2,D3), для которой выполняется равенство P1k
T = -Dω1,
эквивалентное системе
⎧
⎨P1Ty=D1ω1x,
(29)
P1Tx = -D2ω1y,
⎩
0=D3ω1z.
Поскольку Tx = 0 в силу выбора системы координат xyz, то из (29) сле-
дует, что D2 = 0 и остается только управление по каналу “x”, которое мож-
но подобрать с помощью подходящего выбора D1. Например, можно взять
D1 = d1|Ty|, где d1 > 0. Тогда
P1 = d1ω1xsign(Ty) = d1ω1xsign(sin ϑ).
Принимая во внимание, чт
P1 имеет положительную проекцию на ось z
(см. (15)), замечаем, что полученное выражение для P1 имеет смысл лишь
при ω1x =ϑ > 0. Поэтому можно предложить такое управление векторо
P1:
{⃗P
ϑ>0,
1 = d1 ϑsign(sinϑ)k,
(30)
ϑ≤0.
P1 = 0,
Для доказательства работоспособности предложенного управления преж-
де всего следует решить вопрос о возможности реализации вектор
P1 в со-
ответствии с формулой (30). Будем рассматривать заряды q1 и q2 как со-
держащие постоянные части q10 и q20 и переменные (управляемые) q1 и q2.
103
Тогда
P = (q10z1 + q20z2)k + (q1z1 + q2z2)k.
Пуст
P1 = (q1z1 + q2z2)k. Вводя коэффициент kq так, что q1 = -kq q2, на ос-
новании (1) получим
lq2(kq(m0 + 2m2) + m0 + 2m1)k
(31)
P1 =
2(m0 + m1 + m2)
Приравнивая (30) и (31), получим следующий закон изменения kq:
⎧
]
⎪
1
[ 2d1
(m0 + m1 + m2)ϑsign(sin ϑ) - m0 - 2m1 ,
ϑ>0,
⎨kq =
m0 + 2m2
lq2
(32)
⎪
m0 + 2m1
⎩kq = -
,
ϑ≤0
m0 + 2m2
или, что то же,
]
1
(33)
kq =
[d1 (m0+m1+m2)(
ϑ|+ϑ)sign(sin ϑ)-m0 -2m1
⇌kq.
m0 +2m2
lq2
Из (32) следует, что в процессе колебаний ЭДТС коэффициент kq =
= kq(ϑ, ϑ) может принимать не только положительные, но и отрицательные
значения. Поэтому во избежание ситуации, когда заряд нижнего коллектора
q1 = -kq q2 + q10 должен будет стать положительным, следует потребовать,
чтобы выполнялось неравенство
kq(ϑ,ϑ) >q10 ⇌ kqmin.
q2
С другой стороны, заряд нижнего коллектора не должен быть слишком
большим по модулю, чтобы не возникло риска “схлопывания” тросовой си-
стемы под действием сил кулонова притяжения. Поэтому исходя из априор-
ных оценок величин зарядов ЭДТС, основанных на вычислении сил натя-
жения троса (формулы (3), (7)), следует выбрать некоторое допустимое зна-
чение q1min, чтобы затем на основании неравенства q1min < q1 = -kq q2 + q10
получить верхнюю границу для коэффициента kq:
kq(ϑ,ϑ) <q10 -q1min ⇌ kqmax.
q2
Введем в рассмотрение функцию S(kq) = (kq - kqmin)(kq - kqmax). Тогда,
если S(kq) < 0, работает управление с функциейkq. Если S(kq) > 0, то нужно
выбирать из двух вариантов: если kq(ϑ,ϑ) < kqmin, следует взять
1
kqmin =
kqmin(1 - sign(kq - kqmin)),
2
104
если kq(ϑ,ϑ) > kqmax, то следует взять
1
kqmax =
kqmax(1 - sign(kqmax -kq)).
2
В результате получаем, что удовлетворяющее вышеуказанным требованиям
выражение коэффициента kq может быть кратко записано в виде
1
(34) kq =
kq(1 - sign(S(kq))) +1(sign(S(kq)) + 1)×
2
4
[
]
× kqmax(1 - sign(kqmax -kq)) + kqmin(1 - sign(kq - kqmin))
Найденный закон изменения kq позволяет получить управляющий момент
MLD = d1ϑ˙sign(sin ϑ)k
T,
проекция которого на ось x равна
(35)
MLDx = -d1ϑ˙|sin ϑ|R3ER-2(-g01)(ω0 - ωE
),
где
{
d1 > 0,
ϑ>0,
(36)
d1 = 0,
ϑ≤0.
Если ввести обозначение D = d1R3ER-2(-g01)(ω0 - ωE), то можно перепи-
сать (35) кратко в виде
1
(37)
MLDx = -
D(|p| + p)|γ2
|.
2
8.2. Исследование режима стабилизации ЭДТС
С учетом предложенного управления (37) дифференциальные уравнения
Эйлера (25) примут вид
⎧
1
⎨
A ωx - Aωyωz = -3Aω20γ2γ3 - Lγ2 + aβ1 -
D(|p| + p)|γ2|,
(38)
2
⎩
A ωy + Aωxωz = 3Aω20γ1γ3 + Lγ1 + aβ2.
Докажем, что справедлива следующая
Теорема 1. При выполнении условия a = 0 управление (37) обеспечива-
ет асимптотическую устойчивость номинального режима движения связ-
ки.
Доказательство теоремы 1. Заметим вначале, что имеет место ра-
венство
105
[
]
d
A
3
(ω2x + ω2y) -
Aω20γ23 - Lγ3 - Aω0(ωxβ1 + ωyβ2)
=
dt
2
2
D
= a(ωxβ1 + ωyβ2 - ω0(β21 + β22)) -
p (|p| + p)|γ2|,
2
где производная в левой части равенства вычисляется в силу (38). Переходя
от абсолютных угловых скоростей ωx, ωy к относительным угловым скоро-
стям p, q по формулам (11), перепишем это равенство в виде
]
d
[A
A
3
(p2 + q2) -
ω20(β21 + β22) -
Aω20γ2
- Lγ3
=
3
dt
2
2
2
D
= a(pβ1 + qβ2) -
p (|p| + p)|γ2|.
2
Вводя новую переменную Δ = 1 - γ3, представляющую собой отклонение
связки от номинального режима движения γ3 = 1, перепишем последнее со-
отношение в виде
dV (α3, β3, Δ, p, q)
= 2a(pβ1 + qβ2) - Dp (|p| + p)|γ2|,
dt
где
V (α3, β3, Δ, p, q) = A(p2 + q2) + (3Aω20 + L)α23 + (4Aω20 + L)β23 + LΔ2.
Отсюда следует, что если учесть условие (22), то a = 0 и для функции
V (α3, β3, Δ, p, q) получаем следующее дифференциальное уравнение:
√
dV (α3, β3, Δ, p, q)
(39)
= -Dω0p (|p| + p) α23 + β23.
dt
Поскольку выбором q1z1 + q2z2 > 0 всегда можно обеспечить выполнение
неравенства L > 0, то функция V (α3, β3, Δ, p, q) является положительно опре-
деленной. Ее производная в силу (38) является знакопостоянной отрицатель-
ной. Из (39) следует, что указанная производная может обратиться в ноль в
следующих двух случаях:
1) p = 0,
2) α3 = β3 = 0.
Рассмотрим каждый из них и докажем от противного отсутствие соответ-
ствующих им ненулевых решений системы (38).
1. Случай p = 0.
Из (12) следует, что в этом случае ϑ = const = ϑ0, q =ψ sin ϑ0, r =ψ cos ϑ0
и (38) принимает вид
{
ω0β˙1 - (q + ω0β2)(r + ω0β3) = -3ω20γ2γ3 - LA-1γ2,
˙q + ω0β˙2 + ω0β1(r + ω0β3) = 0.
106
На основании (10) перепишем эту систему в углах ψ и ϑ = ϑ0:
⎧
⎪sin ϑ0(2ω0 ψ˙ cos ψ sin ϑ0 -ψ2 cos ϑ0 +
⎨
(40)
+ ω20 cos2 ψ cosϑ0 + 3ω20 cosϑ0 + LA-1) = 0,
⎪
⎩
sin ϑ0
ψ - ω20 sinψ cosψ) = 0.
В силу предположения (от противного) о существовании ненулевого решения
поделим первое из уравнений (40) на sin ϑ0 cos ϑ0, второе уравнение — на
sin ϑ0, а затем заменим второе уравнение этой системы на соответствующий
ему первый интеграл:
⎧
L
⎨
ψ2 - 2ω0ψ˙ cos ψ tan ϑ0 - ω20 cos2 ψ - 3ω20 -
= 0,
(41)
A cos ϑ0
⎩
ψ2 + ω20 cos2 ψ = C2 = const ≥ 0.
Разрешив полученные уравнения относительно
ψ, приходим к системе
⎧
√
⎪
os2 ψ
L
⎨ψ˙ = ω0 cosψ tanϑ0 ± ω2 c
+ 3ω20 +
,
0 cos2 ϑ0
A cos ϑ0
(42)
⎪
√
⎩ψ˙ = ±C2 - ω20 cos2 ψ.
Несложно проверить, что она является совместной тогда и только тогда, ко-
гда выполняется равенство
cos4 ψ
1
ω4
+ g0ω20 cos2 ψ +
(g0 - C2)2 = 0,
0 cos2 ϑ0
4
все три слагаемых в котором неотрицательны. Следовательно, данное равен-
ство эквивалентно системе уравнений
(43)
cos ψ = 0, g0 = C2.
Проверим, является ли (43) решением системы (41). Предположив, что (43)
является решением, приходим к равенству C2 = 0, откуда следует, что g0 = 0.
Последнее равносильно равенству 3Aω20 cos ϑ0 + L = 0, которое совпадает со
вторым вариантом из (24) и соответствует нереализуемому наклонному поло-
жению равновесия связки. Полученное противоречие доказывает отсутствие
ненулевых решений в первом случае. Перейдем к рассмотрению второго воз-
можного случая.
2. Случай α3 = β3 = 0.
Этот случай, очевидно, равносилен γ3 = 1. С физической точки зрения
это означает, что ϑ = 0 и, следовательно, p = 0. Проверим, реализуются ли
равенства
(44)
p = 0, γ3
=1
107
на нетривиальных решениях системы (41). Предположив, что равенства (44)
могут реализоваться на нетривиальных решениях, приходим к системе урав-
ненийβ1 = β2r,β2 = -β1r, откуда следует, что β1β˙1 + β2β˙2 = 0. Проинтегри-
ровав последнее равенство, получаем β21 + β22 = const. Поскольку β3 = 0, то
может реализоваться только случай β21 + β22 = 1. Отсутствие других решений
завершает рассмотрение случая 2. Таким образом, выполняются условия тео-
ремы Барбашина - Красовского [35] и положение равновесия ϑ = 0 является
асимптотически устойчивым. Теорема 1 доказана. Тем самым подтвержда-
ется возможность стабилизации номинального режима движения связки с
помощью предложенного управления.
Аналогичная гантелеобразная система двух заряженных ИСЗ рассматри-
валась в [36]. Однако, в [36] отсутствовал ток и вызванный им амперов мо-
мент, а идея изменения величин зарядов ИСЗ использовалась не для гене-
рации диссипативного момента, а лишь для изменения восстанавливающего
момента в рамках консервативной механической системы, допускающей инте-
грал энергии. Рассмотрение задачи велось в плоской постановке для изучения
колебаний в плоскости орбиты.
9. Результаты компьютерного моделирования
В процессе работы было предпринято компьютерное моделирование и вы-
полнена серия численных экспериментов. В данном разделе приводится при-
мер связки с “плохими” с точки зрения процесса стабилизации значениями
параметров, значительно отличающимися от тех, которые использовались в
примере 1.
Пример 2. Рассматривается связка с тросом длиной l = 200м и погонной
плотностью γ = 2 · 10-3 кг/м, с концевыми массами m1 = 29,4 кг, m2 = 30 кг,
имеющими значения z-координаты -100,5 м и 99,5 м соответственно. Центр
связки движется по орбите с радиусом R = 7 · 106 м. По тросу протекает ток
силой 1А. В работе системы стабилизации троса принимают участие следую-
щие заряды: постоянная часть положительного заряда на верхнем коллекторе
q20 = 5 · 10-5 Кл, постоянная часть отрицательного заряда на нижнем кол-
лекторе q10 = -5 · 10-5 Кл. В процессе работы системы стабилизации троса
заряд на нижнем коллекторе может возрастать по абсолютной величине. Для
предотвращения возможных нежелательных динамических эффектов такого
возрастания значение указанного заряда ограничивается в соответствии с вы-
шеописанным алгоритмом управления величиной q1min = -9 · 10-5 Кл. При
таком значении q1min минимальное значение натяжения троса, как показы-
вает проверка по формулам (3), остается положительным. Оно достигается
на нижнем конце троса и равно T1 = 0,01 Н. Коэффициент d1 принимается
равным 0,01. В начальный момент времени трос был отклонен от местной
вертикали на угол 60◦ в плоскости (η, ζ) и отпущен без относительной угло-
вой скорости.
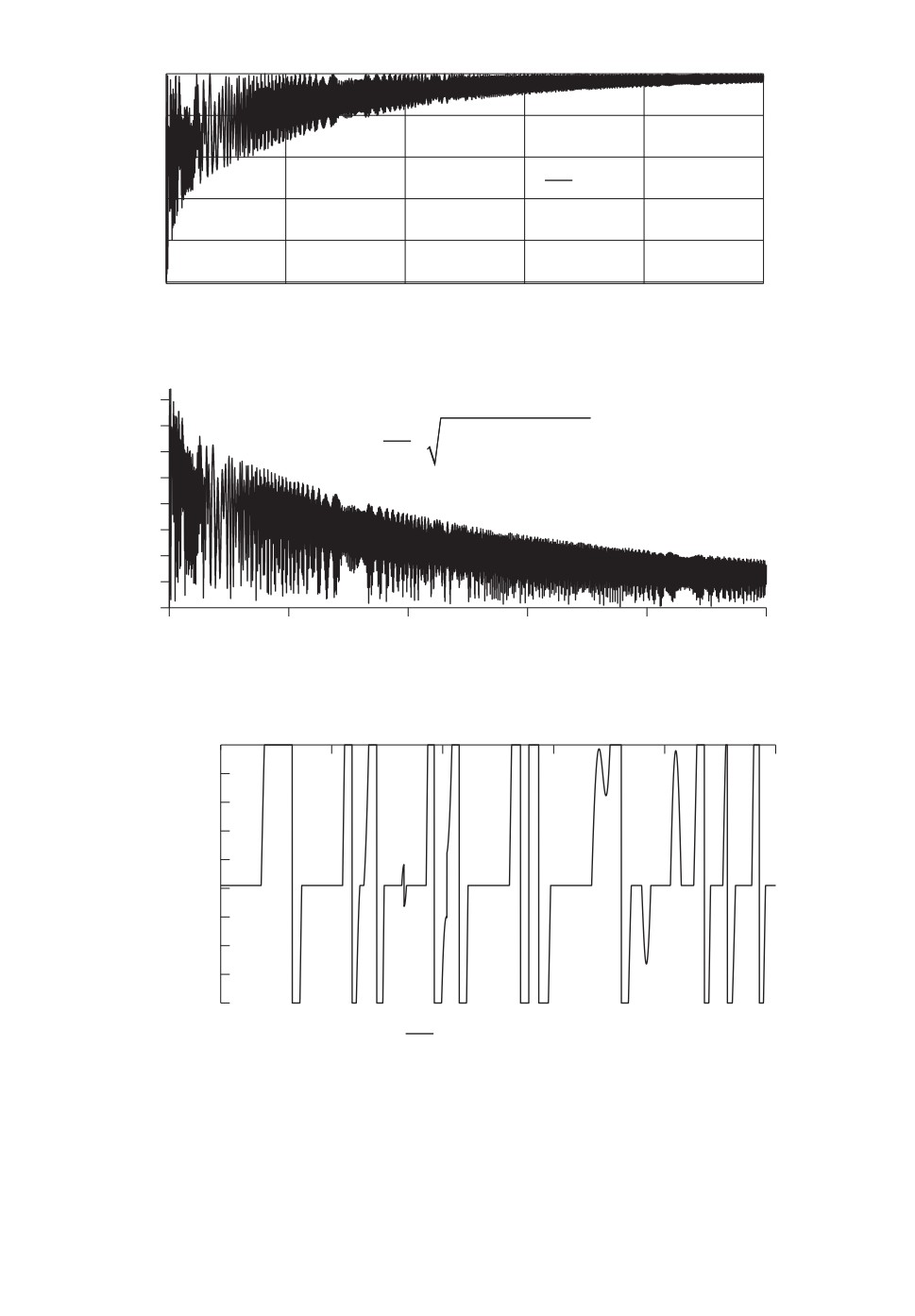
Результаты численного интегрирования представлены на рис. 6-9, где по
оси абсцисс на всех рисунках отложен безразмерный угол — аргумент ши-
роты u = ω0t. Основным параметром ориентации троса является направляю-
108
1,0
0,9
0,8
3(u)
0,7
0,6
0,5
0
10 000
20 000
30 000
40 000
50 000
Рис. 6. Процесс стабилизации троса.
1,6
1,4
2
2
p(u) + q(u)
1,2
1,0
0,8
0,6
0,4
0,2
0
10 000
20 000
30 000
40 000
50 000
Рис. 7. Затухание угловой скорости (рад/с) троса.
10
20
30
40
50
0
0,00001
0,00002
0,00003
0,00004
0,00005
0,00006
0,00007
0,00008
0,00009
q1(u)
Рис. 8. Изменение заряда (Кл) на нижнем коллекторе.
щий косинус γ3, стремящийся к целевому значению γ3 = 1 (рис. 6). Из рис. 6
видно, что если выберем допустимое отклонение 0,2 для γ3, то с момента вре-
мени u = 7000 амплитуда колебаний связки будет находиться в допустимых
пределах и будет продолжать уменьшаться.
109
a
1,0
0,9
MGra(u)
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
10 000
20 000
30 000
40 000
50 000
б
0,0040
0,0035
MAmp(u)
0,0030
0,0025
0
10 000
20 000
30 000
40 000
50 000
в
0,0012
MLor(u)
0,0010
0,0008
0,0006
0,0004
0,0002
0
10 000
20 000
30 000
40 000
50 000
0,0009
г
0,0008
0,0007
0,0006
MDis(u)
0,0005
0,0004
0,0003
0,0002
0,0001
0
10 000
20 000
30 000
40 000
50 000
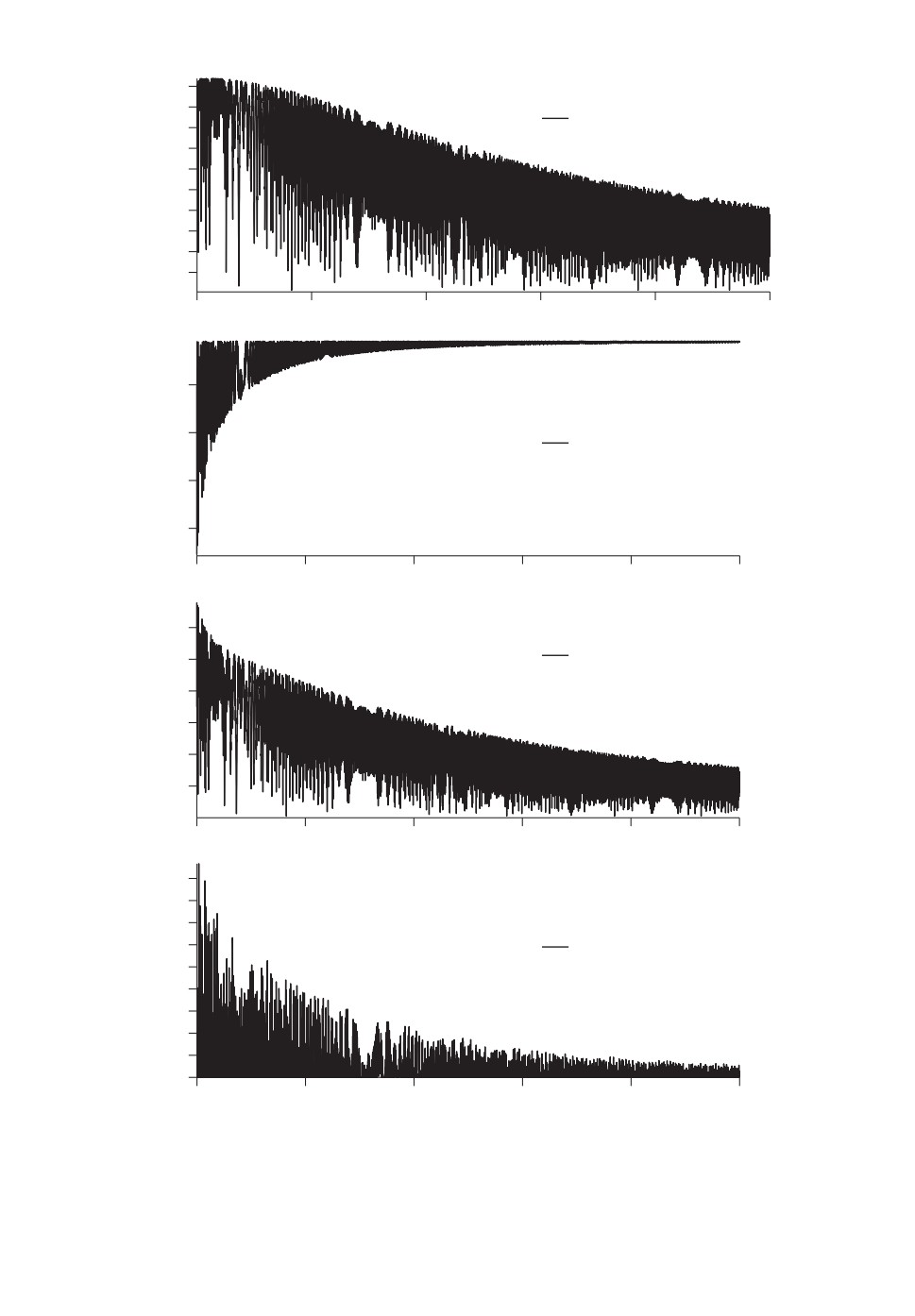
Рис. 9. a - Гравитационный момент (Нм), б -aмперов момент (Нм), в - лорен-
цев момент (Нм), г - активный демпфирующий момент (Нм).
110
a
1,0
0,8
0,6
0,4
0,2
0
1000
2000
3000
4000
5000
6
000
0,2
0,4
0,6
3(u)
0,8
6
б
5
2
2
4
p u
q u
3
2
1
0
1000
2000
3000
4000
5000
6000
7000
Рис. 10. а - Неуправляемая дестабилизация вертикального положения троса,
б - неуправляемая дестабилизация угловой скорости (рад/с) троса.
Относительная угловая скорость (в рад/с) троса стремится к нулю (рис. 7).
Величины зарядов коллекторов варьируются в соответствии с законом
управления и уравнением (34). Изменение заряда q1 = -kq q2 + q10 на отри-
цательно заряженном коллекторе показано на рис. 8. Для ясности рисунка
график построен для небольшого диапазона изменения времени.
На рис. 9,а-9,г показаны графики изменения моментов, действующих на
ЭДТС.
Замечание 1. В данном примере с целью приближения к реальным
условиям значения масс m1 и m2 выбраны разными. Это приводит к тому,
что условие (22) не выполняется, строго вертикальное положение равнове-
сия троса отсутствует, а система стабилизации работает в условиях, когда
дестабилизирующий амперов момент можно рассматривать как постоянно
действующее возмущение.
Выполнено также моделирование динамики обычного тяжелого троса с
массами m1 и m2 на концах, но не несущего зарядов на коллекторах и, со-
ответственно, не управляемого. Значения прочих параметров и начальные
условия движения ЭДТС совпадают с теми, которые были выбраны в при-
мере 2. Дестабилизация такого троса показана на рис. 10.
10. Заключение
Рассмотрена задача угловой стабилизации ЭДТС в вертикальном поло-
жении троса. Аналитические исследования и компьютерное моделирование
111
показали, что лоренцев момент, действующий на ЭДТС благодаря заряжен-
ным коллекторам на концах троса, существенно расширяет область устой-
чивости вертикального положения троса. Кроме того, показана возможность
генерировать управляющий момент диссипативного характера путем актив-
ного управления величиной заряда на нижнем коллекторе в соответствии с
условиями, определяемыми текущей ориентацией троса. Если при этом пара-
метры троса выбраны в соответствии с условиями, учитывающими влияние
возмущающих моментов, то достигается асимптотическая устойчивость ори-
ентации троса вдоль местной вертикали без необходимости выключения тока,
протекающего по тросу. Таким образом, предложенное устройство и метод
управления могут быть использованы для стабилизации космической тросо-
вой системы в околоземном пространстве с целью повышения эффективности
ее функционирования в процессе уборки космического мусора.
СПИСОК ЛИТЕРАТУРЫ
1.
Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М.: Наука,
1990.
2.
Муницына М.А. Относительные равновесия системы “гантель-груз” с односто-
ронними связями на круговой кеплеровой орбите // АиТ. 2007. № 9. С. 9-15.
Munitsina M.A. Relative Equilibrium on the Circular Keplerian Orbit of the
“Dumbbells-Load” System with Unilateral Connections // Autom. Remote Control.
2007. V. 68. No. 9. P. 1476-1482.
3.
Кульков В.М., Егоров Ю.Г., Тузиков С.А. Исследование конфигурации и фор-
мирование проектного облика развернутой электродинамической тросовой си-
стемы в составе орбитальных космических аппаратов // Изв. РАН. Энергетика.
2018. № 3. С. 119-130.
4.
Воеводин П.С., Заболотнов Ю.М. Моделирование и анализ колебаний электро-
динамической тросовой системы на орбите спутника Земли // Мат. моделиро-
вание. 2017. № 6. С. 21-34.
5.
Forward R.L. Electrodynamic drag terminator tether, Appendix K of high strength-
to-weight tapered Hoytether for LEO to GEO payload transport // Final Report on
NASA SBIR Phase I Contract NAS8-40690. 10 July 1996.
6.
Forward R.L., Hoyt R.P., Uphoff C. Application of the Terminator Tether
electrodynamic drag technology to the deorbit of constellation spacecraft // 34 Joint
Propulsion Conf. Exhibit. Paper AIAA 98-3491. Cleveland, OH. 1998.
7.
Forward R.L., Hoyt R.P. Terminator Tether: a spacecraft deorbit device //
J. Spacecraft Rockets. 2000. V. 37. P. 187-196.
8.
Cosmo M.L., Lorenzini E.C. Tethers in Space Handbook, 3-rd ed. Smithsonian
Astrophysical Observatory, Cambridge, MA, USA, 1997.
9.
Vannaroni G., Dobrowolny M., De Venuto F. Deorbiting with electrodynamic
tethers: comparison between different tether configurations // Space Debris. 2001.
V. 1. P. 159-172.
10.
Iess L., Bruno C., Ulivieri C., et al. Satellite de-orbiting by means of electrodynamic
tethers. Part I: general concepts and requirements // Acta Astronautica. 2002. V. 50.
No. 7. P. 399-406.
11.
Iess L., Bruno C., Ulivieri C., Vannaroni G. Satellite de-orbiting by means of
electrodynamic tethers. Part II: System configuration and performance // Acta
Astronautica. 2002. V. 50. No. 7. P. 407-416.
112
12.
Ishige Y., Kawamoto S., Kibe S. Study on electrodynamic tether system for space
debris removal // Acta Astronautica. 2004. V. 55. No. 11. P. 917-929.
13.
Yamaigiwa Y., Hiragi E., Kishimoto T. Dynamic behavior of electrodynamic tether
deorbit system on elliptical orbit and its control by Lorentz force // Aerospace Sci.
Technol. 2005. V. 9. P. 366-373.
14.
Zhong R., Zhu Z.H. Libration dynamics and stability of electrodynamic tethers
in satellite deorbit // Celestial Mechan. Dynam. Astronom. 2013. V. 116. No. 3.
P. 279-298.
15.
Белецкий В.В. Движение искусственного спутника относительно центра масс.
М.: Наука, 1965.
16.
Levin E.M. Dynamic Analysis of Space Tether Missions - Advances in the
Astronautical Sciences / San Diego, California, American Astronautical Society.
V. 126. 2007.
17.
Pelaez J., Lorenzini E.C., Lopez-Rebollal O., Ruiz M. A new kind of dynamic
instability in electrodynamic tethers / AAS 00-190, AAS/AIAA Space Flight
Meeting. 2000.
18.
Corsi J., Iess L. Stability and control of electrodynamic tether for de-orbiting
applications // Acta Astronautica. 2001. V. 48. No. 5-12. P. 491-501.
19.
Larsen M.B., Blanke M. Passivity-based control of a rigid electrodynamic tether //
J. Guidance, Control, Dynam. 2011. V. 34. P. 118-127.
20.
Yang Y., Cai H. Extended time-delay autosynchronization method for libration
control of electrodynamic tether using Lorentz force // Acta Astronautica. 2019.
V. 159. P. 179-188.
21.
Петров К.Г., Тихонов A.A. Момент сил Лоренца, действующих на заряженный
спутник в магнитном поле Земли. Ч.1: Напряженность магнитного поля Земли в
орбитальной системе координат // Вестн. CПб. ун-та. Сер.1. 1999. Вып. 1. No. 1.
С. 92-100.
22.
Петров К.Г., Тихонов A.A. Момент сил Лоренца, действующих на заряжен-
ный спутник в магнитном поле Земли. Ч.2: Вычисление момента и оценки его
составляющих // Вестн. CПб. ун-та. Сер.1. 1999. Вып. 3. No. 15. С. 81-91.
23.
Тихонов A.A. Метод полупассивной стабилизации космического аппарата в гео-
магнитном поле // Космические исслед. 2003. Т. 41. № 1. С. 69-79.
24.
Тихонов A.A. О вековой эволюции ротационного движения заряженного ИСЗ
на регрессирующей орбите // Космические исслед. 2005. Т. 43. № 2. С. 111-125.
25.
Антипов К.А., Тихонов A.A. Параметрическое управление в задаче о стаби-
лизации космического аппарата в магнитном поле Земли // АиТ. 2007. № 8.
С. 44-56.
Antipov K.A., Tikhonov A.A. Parametric Control in the Problem of Spacecraft
Stabilization in the Geomagnetic Field // Autom. Remote Control. 2007. V. 68.
No. 8. P. 1333-1345.
26.
Тихонов А.А., Спасич Д.Т., Антипов К.А., Саблина М.В. Оптимизация элек-
тродинамического метода стабилизации ИСЗ // АиТ. 2011. № 9. С. 112-121.
27.
Александров А.Ю., Тихонов А.А. Одноосная электродинамическая стабилиза-
ция искусственного спутника Земли в орбитальной системе координат // АиТ.
2013. № 8. С. 22-31.
Aleksandrov A.Yu., Tikhonov A.A. Monoaxial electrodynamic stabilization of Earth
satellite in the orbital coordinate system // Autom. Remote Control. 2013. V. 74.
P. 1249-1256. DOI: 10.1134/S000511791308002X
113
28. Антипов К.А., Тихонов A.A. Электродинамическое управление в задаче о ста-
билизации космического аппарата в геомагнитном поле // Космические исслед.
2014. Т. 52. № 6. С. 512-520.
29. Antipov K.A., Tikhonov A.A. On satellite electrodynamic attitude stabilization //
Aerospace Sci. Technology. 2014. V. 33. P. 92-99.
30. Aleksandrov A.Yu., Antipov K.A., Platonov A.V., Tikhonov A.A. Electrodynamic
attitude stabilization of a satellite in the Konig frame // Nonlinear Dynam. 2015.
V. 82. P. 1493-1505.
31. Tikhonov A.A., Shcherbakova L.F. On Equilibrium Positions and Stabilization of
Electrodynamic Tether System in the Orbital Frame // AIP Conf. Proc. 2018.
V. 1959. No. 040023.
32. Шамолин М.В. Сопоставление интегрируемых по Якоби случаев плоского и про-
странственного движения тела в среде при струйном обтекании // Прикладная
математика и механика. 2005. Т. 69. № 6. С. 1003-1010.
33. Woo P., Misra A.K. Mechanics of very long tethered systems // Acta Astronautica.
2013. V. 87. P. 153-162.
34. Shamolin M.V. Some questions of the qualitative theory of ordinary differential
equations and dynamics of a rigid body interacting with a medium // J. Math.
Sci. 2002. V. 110. No. 2. P. 2528-2557.
35. Барбашин Е.А. Функции Ляпунова. М.: Наука, 1970.
36. Yamakawa H., Hachiyama S., Bando M. Attitude dynamics of a pendulum-shaped
charged satellite // Acta Astronautica. 2012. V. 70. P. 77-84.
Статья представлена к публикации членом редколлегии В.М. Глумовым.
Поступила в редакцию 01.06.2019
После доработки 29.10.2019
Принята к публикации 28.11.2019
114