Автоматика и телемеханика, № 2, 2020

Интеллектуальные системы управления,

анализ данных

(Самарский национальный исследовательский

университет им. акад. С.П. Королева)

РЕФЛЕКСИВНЫЕ ИГРЫ В ЛИНЕЙНЫХ МОДЕЛЯХ ДУОПОЛИИ

ШТАКЕЛЬБЕРГА ПРИ НЕСОВПАДЕНИИ РАНГОВ РЕФЛЕКСИИ

Рассматривается проблема определения равновесий на рынке олигопо-

лии при наличии лидера (лидеров) по Штакельбергу с учетом рефлексив-

ного поведения агентов рынка в случае несовпадения рангов рефлексии

при различных предельных и постоянных издержках агентов. Разработа-

на модель рефлексивной игры для рынка дуополии, позволившая полу-

чить формулы расчета информационных равновесий при несовпадении

рангов рефлексии агентов и при различных предельных и постоянных

издержках агентов. Показано, что опережение (запаздывание) рефлек-

сии одного агента по сравнению с контрагентом влияет на интенсивность

конкуренции на рынке олигополии и на неравномерность распределения

выигрыша между агентами в пользу рефлексивного лидера.

Ключевые слова: олигополия, лидер по Штакельбергу, рефлексивная иг-

ра, равновесие по Нэшу.

DOI: 10.31857/S0005231020020099

1. Введение

В условиях олигополии [1] прибыль каждого продавца (агента) является

функцией не только его действия в виде выбранного объема выпуска, но и

действий остальных агентов, называемых окружением. Поэтому олигополия

моделируется в форме игры [2]. Максимизирующие полезность (прибыль)

каждого агента действия, т.е. наилучшие ответы, формализуемые в виде

функций реакций, приводят к формированию равновесия Нэша [3] как реше-

ния соответствующей игры. Несмотря на то, что функции полезности агентов

считаются известными всем агентам, при моделировании олигополии имеет

место фундаментальная проблема несовершенства информированности аген-

та о действиях окружения. Проблема заложена в самой концепции наилуч-

ших ответов и заключается в априорной неосведомленности каждого агента о

том, на основе какого предположения окружение выбирает действия: предпо-

ложения о неизменности действий агента, предположения о наилучшем отве-

те агента на действия окружения, предположения о наилучшем ответе агента

на наилучший ответ окружения и т.д.

134

Классический подход к разрешению этой проблемы сводился к выдвиже-

нию некоторой гипотезы о поведении окружения, причем считалось, что фак-

тические действия агентов совпадают с предположениями об этих действи-

ях. Поэтому вектор действий агентов, являющийся решением игры по Нэшу,

расценивался как реальное результирующее равновесие рынка. Исторически

первой стала гипотеза А. Курно [4] об игнорировании влияния выпуска окру-

жения на выбор данного агента. В дальнейшем в модели выбора действий

агента считались заданными предположительные вариации [5], выражающие

предполагаемое агентом ответное изменение выпуска контрагента, оптимизи-

рующее критерий последнего при выбранном действии первого. В частности,

модель олигополии, в которой один из агентов (лидер) информирован о том,

что окружение игнорирует его действия в соответствии с гипотезой Курно,

рассмотрена Г. Штакельбергом [6] в виде так называемого лидерства по Шта-

кельбергу.

В русле классического подхода к проблеме несовершенства информиро-

ванности агента современные исследователи, как правило, рассматривают

линейную модель олигополии, т.е. вводят гипотезу о линейных функциях ры-

ночного спроса и издержек агентов. Сформировался обширный корпус иссле-

дований таких равновесий в случае симметричной информированности аген-

тов для линейной модели олигополии [7-13], а также для нелинейной модели

олигополии, см. [14-18], в том числе обзоры [19, 20]. Линейные модели оли-

гополии, как правило, незначительно уступая в адекватности нелинейным,

существенно превосходят последние в результативности, позволяя получить

аналитические решения. Исследования рынка олигополии с лидерством по

Штакельбергу [21-24], как правило, базируются на априори заданных пози-

циях лидера и ведомого. Кроме того, постановка проблемы сравнительно-

го анализа позиций лидера и ведомого [25, 26] определила направление ис-

следований состояний рынка олигополии в случае неединственности лидеров

[27-29].

Другой подход разрешения проблемы несовершенства информированно-

сти базируется на анализе мыслительного процесса (рефлексии) агентов,

формализуемого в виде представлений о стратегиях окружения, выдвигае-

мых каждым из агентов. Соответственно набору возможных представлений

решение игры по Нэшу формирует набор векторов действий агентов, расце-

ниваемых как возможные равновесия рынка. С учетом рефлексивной моде-

ли асимметрии человеческого восприятия Лефевра [30-32] под рефлексией

в дальнейшем понимается процесс выдвижения агентом гипотез о возмож-

ных действиях окружения или так называемая рефлексия второго рода. От-

метим, что далее рассматривается стратегическая рефлексия, при которой

агент предполагает действия окружения, а не его информированность, в от-

личие от модели игры с неполной информированностью [33, 34]. Рефлексив-

ный анализ оперирует также понятием глубины рефлексии, мерой которой

является ранг — порядковый номер представления в следующей бесконеч-

ной последовательности: 1) представление агента о стратегиях окружения;

2) представление агента о представлениях окружения о стратегии агента;

3) представление агента о представлениях окружения о представлении аген-

та о стратегиях окружения и т.д. Исследования рефлексивных моделей на-

135

правлены в первую очередь на оценку оптимальной глубины стратегической

рефлексии [35-38].

Модель рефлексивной игры является инструментом описания информи-

рованности агентов, с помощью которого множество представлений агентов

(о стратегиях окружения или о представлениях окружения в зависимости

от моделируемого ранга рефлексии) как экзогенно заданная информирован-

ность сводится к множеству возможных игр с полной информированностью.

Затем в каждой из этих игр находится решение игры агента с представляе-

мыми (фантомными) агентами окружения. Поэтому решением рефлексивной

игры является не реальное, а информационное равновесие — вектор действий

реальных и фантомных (существующих во мнении реальных) агентов, при ко-

тором агент максимизирует полезность исходя из своей информированности

об окружении, т.е. если бы окружение выбирало те действия, которые пред-

ставляет этот агент. Решения всех возможных игр агента с фантомами обра-

зуют набор информационных равновесий, используемый для последующего

сравнения с параметрами реальных рынков с целью оценки ранга рефлексии

реальных агентов.

В модели олигополии рефлексивный анализ был впервые применен [6] (как

было отмечено в [39]) в дуополии Штакельберга как «борьба за лидерство»,

при которой оба агента предполагают, что их контрагенты действуют как

ведомые; поскольку эти предположения одновременно не могут быть реаль-

ностью, то они являются представлениями агентов, а соответствующая игра,

приводящая к неравновесию Штакельберга, является рефлексивной. Рефлек-

сивные игры агентов рынка олигополии исследованы в модели Курно - Шта-

кельберга для первых двух рангов стратегической рефлексии [40-42], анали-

зировались информационные равновесия при информационной рефлексии о

значениях экзогенного параметра функции полезности [43], а также о пара-

метрах функций издержек окружения [44]. Проводился [45] сравнительный

анализ эффективности равновесий по Курно и Штакельбергу; рассматрива-

лись [46] динамические рефлексивные игры в модели Штакельберга и ана-

лизировалось временное влияние информационного преимущества на эффек-

тивность агентов. Оценивалась эффективность лидерства по Штакельбергу

по сравнению с представлением агента о рынке как о совершенной конкурен-

ции [47]. В модели олигополии с нелинейными функциями издержек агентов

исследовалось [48-50] взаимодействие ведомых агентов и лидеров по Шта-

кельбергу, имеющих различные ранги рефлексии. В модели дуополии с ли-

нейными функциями спроса и издержек при одинаковых предельных и по-

стоянных издержках агентов найдены [51] информационные равновесия при

наличии лидеров по Штакельбергу произвольного уровня в случае совпа-

дающих рангов рефлексии. Однако актуальной задачей, требующей даль-

нейшего исследования, представляется анализ равновесий на рынке дуопо-

лии при различных предельных и постоянных издержках агентов в случае

несовпадения рангов рефлексии агентов, когда один из агентов имеет опе-

режающее рефлексивное представление («рефлексивный лидер»), а другой,

соответственно, запаздывает («рефлексивный последователь»). В такой по-

становке оценка оптимальной глубины стратегической рефлексии произво-

136

дится путем сравнительного анализа эффективности опережения рефлексии

одних агентов относительно других.

2. Методология

Рассмотрим следующую линейную модель рынка олигополии. Пусть аген-

ты выбирают действия исходя из максимума своих функций полезности (при-

были)

(1)

Π_i (Q,Q_i) = P (Q)Q_i - C_i (Q_i), Q_i

≥ 0, i ∈ N = {1, . . . , n} ,

при линейной модели спроса

(2)

P (Q) = a - bQ, a,b > 0,

где совокупный выпуск равен

∑

(3)

Q= Q_i,

i∈N

и линейных функциях издержек

(4)

C_i(Q_i) = d_i + c_iQ_i, c_i,d_i > 0, c_i

< a, i ∈ N,

где Q_i, Π_i — выпуск и прибыль i-го агента; N — множество агентов рынка;

n — количество агентов; P, Q — равновесная цена и суммарный объем рын-

ка; c_i, d_i — коэффициенты функций издержек агентов, d_i интерпретируется

как постоянные издержки, c_i — предельные издержки; a, b — коэффициенты

функции рыночного спроса.

Модель выбора оптимального действия агента определяет неотрицатель-

ное действие Q^∗i, максимизирующее прибыль i-го агента, зависящую также

от суммарного действия всех агентов Q (символом «^∗» обозначено оптималь-

ное действие). Модели выбора действий агентов при (1)-(4) записываются в

следующем виде:

(5)

Q^∗i = arg maxΠi (Q,Qi) = arg max{(a - bQ) Qi - di - ciQi

}, i∈N.

Q_i≥0

Равновесие Нэша [3] в системе (5) представляет собой вектор оптималь-

ных действий агентов при выбранных действиях окружения. Поскольку оп-

тимальные по модели (5) действия должны удовлетворять условию первого

порядка [52], то равновесие Нэша определяется из решения следующей систе-

мы уравнений (так называемых уравнений реакций):

∂Πi (Q_i,ρ_ij)

(6)

= 0, i, j ∈ N,

∂Q_i

где ρ_ij = Q^′

— предположительная вариация в уравнении реакции i-го аген-

jQ_i

та, т.е. предполагаемое изменение выпуска j-го агента в ответ на единичный

137

прирост выпуска i-го агента. Поскольку согласно модели (5) оптимумы аген-

тов зависят не только от собственного действия i-го агента Q_i, но и от дей-

ствий окружения через Q, то последняя зависимость представлена в систе-

ме (6) как функция полезности Π_i (Q_i, ρ_o→j) от вектора предположительных

вариаций, характеризующих влияние действий окружения на изменение Q.

Вектор предположительных вариаций i-го агента ρ_i = {ρ_ij , j ∈ N} форма-

лизует априори неизвестную ему информацию о принципах действия окру-

жения, поэтому система (6) имеет множество решений, зависящих от вектора

ρ = {ρ_ij,i,j ∈ N} как от параметра. Для нахождения множества возможных

векторов ρ используем рефлексивный анализ, т.е. будем считать предположи-

тельные вариации некоторыми функциями предположений агентов о страте-

гиях окружения.

При анализе рефлексии примем следующие гипотезы: 1) агенты выбира-

ют действия одновременно, однократно и независимо; 2) агент выбирает дей-

ствия, максимизирующие его функцию полезности исходя из доступной ему

информации о действиях окружения; 3) в момент выбора действий агенты

располагают информацией о функциях полезности всех агентов (функциях

рыночного спроса и издержек агентов), о количестве агентов, а также о том,

что окружение имеет равный с ними уровень информированности; 4) агенты

на каждом ранге рефлексии могут иметь представления о наилучших страте-

гиях окружения, а также о представлениях окружения, т.е. для всех агентов

рассматривается стратегическая рефлексия второго рода¹.

Рефлексивные представления, т.е. мнения агентов о стратегиях окруже-

ния, обусловливают стратификацию агентов по уровням лидерства следую-

щим образом: агент, вычисляя свою оптимальную реакцию, подставляет в

соответствующее уравнение системы (6) некоторые предположительные ва-

риации действий окружения, которые выбираются исходя из представлений

агента — нулевые вариации соответствуют представлению об окружении как

о ведомых, поэтому данный агент становится лидером первого уровня; нену-

левые вариации соответствуют представлению об окружении как о лидерах,

следовательно, агент становится лидером более высокого уровня. На вто-

ром ранге рефлексии агент анализирует возможные представления окруже-

ния о своей стратегии, аналогичные вышеуказанным (ведомый или лидер), и

рассчитывает предположительные вариации окружения исходя из того, что

окружение само является лидером более высокого уровня. Вследствие этого

уровень лидерства агента становится еще выше по сравнению с первым ран-

гом рефлексии. Отметим, что используемое далее понятие ранга рефлексии

соответствует известному подходу [54]², адаптированному применительно к

задаче олигополии, в которой классически сложилась бинарная система пред-

¹ Напомним, что согласно принятой терминологии [53] рефлексия первого рода — это

мнение агента о собственных представлениях о реальности; рефлексия второго рода — это

мнение агента о действиях или представлениях окружения; стратегическая рефлексия —

это мнение агента о действиях (стратегиях или принципах принятия решений) окружения.

² Напомним краткую характеристику этого подхода: «Агент имеет нулевой ранг ре-

флексии, если он знает только матрицу платежей. Агент обладает первым рангом рефлек-

сии, если он считает, что его противники имеют нулевой ранг рефлексии, т.е. знают только

матрицу платежей. Вообще агент с k-м рангом рефлексии предполагает, что его противни-

ки имеют (k - 1)-й ранг рефлексии».

138

ставлений агентов вида «ведомый-лидер». Используемый далее термин «уро-

вень лидерства» является расширением классического понятия лидерства по

Штакельбергу [6], соответствующего первому рангу рефлексии («я думаю,

что окружение является ведомыми») на случай углубления рефлексии («я ду-

маю, что окружение думает, что я ведомый» и т.д.).

Возникающую в результате представляемую иерархию агентов запишем в

виде множества

(7)

G = (M₀,M₁,...,M_l

где l — количество уровней лидерства агентов; M_m (m = 0, . . . , l) — множе-

ства агентов; M₀ - множество ведомых агентов; M_m (m = 1, . . . , l) — множе-

ство лидеров m-го уровня. Множество (7) есть разбиение множества агентов,

удовлетворяющее ограничениям

M_m ∩ M_j = ∅, m = j, M₀ ∪ M₁ ∪ ··· ∪ M_l = N = {1,... ,n}.

В силу гипотезы 4 агент имеет какие-либо представления о стратегиях

окружения и его представлениях, что позволяет ему на каждом ранге ре-

флексии построить конкретное множество вида (7). В частности, структура

множества (7) определяется следующим образом: если на первом ранге ре-

флексии агент представляет, что окружение выбирает стратегию ведомого,

то последнее относится к множеству M₀; если в этом случае агент думает,

что окружение является «классическим» лидером по Штакельбергу, то он

относит окружение к множеству лидеров первого уровня M₁. Соответствен-

но, если на втором ранге рефлексии агент представляет, что окружение ду-

мает о нем как о ведомом, т.е. само является лидером первого уровня, то

оно относится к множеству M₁; если в этом случае агент представляет, что

окружение думает о нем как о лидере по Штакельбергу, т.е. оно является ли-

дером второго уровня, то окружение относится к множеству M₂. Аналогично

окружение стратифицируется на последующих рангах рефлексии. Поэтому

между рангом рефлексии агента и уровнем лидерства окружения имеет ме-

сто следующее соотношение: уровень лидерства окружения либо равен рангу

рефлексии агента, если в представлении фигурирует термин «лидер», либо на

единицу меньше ранга рефлексии агента, если в представлении фигурирует

термин «ведомый».

С учетом терминологии, введенной в [50], F-стратегией (стратегией ведо-

мого агента) считается выбор агентом действия по (5) без учета действий

окружения согласно гипотезе Курно [4], в результате данный агент имеет

в множестве (7) уровень M₀; L-стратегия (стратегия лидера по Штакель-

бергу [6]) — это выбор действия по модели (5) в предположении, что окру-

жение придерживается F -стратегии, в результате агент имеет уровень M₁.

Формально эти стратегии можно записать следующим образом: если η₀-й

агент выбирает F -стратегию, то в η₀-м уравнении системы (6) полагается

ρη0j = 0∀j ∈ N\η0; если η1-й агент выбирает L-стратегию, то в η1-м уравне-

нии системы (6) ρη1j вычисляется дифференцированием по Qη₁ остальных

(N - 1) уравнений (6), в которых полагается ρ_ij = 0∀j ∈ N\i. В частности,

для модели (5) без учета рефлексивных представлений эти стратегии имеют

139

классический вид [39] функций реакций ведомого агента Курно и лидера по

Штакельбергу:

a-c_i

Q_j

a-c_i

Q_j

Q^∗Fi =

;

Q^∗Li =

i, j ∈ N.

1,5b

1,5

Последовательность представлений i-го агента, упорядоченная по возрас-

танию последовательности рангов рефлексии, записывается в виде множества

{

}

(8)

Gi =

Grij , j ∈ N\i, r ∈ Z

i∈N,

где G^rij — представляемая i-м агентом стратегия окружения на r-м ранге

рефлексии; в нижнем индексе первый символ обозначает рефлексирующего

агента, второй символ — номер агента окружения; r — ранг рефлексии; Z —

множество целых чисел. Представляемая стратегия окружения может быть

двух типов (F или L) и записывается либо в виде G^rij = F ∨ G^rij = L, либо в

виде обусловленных этими стратегиями уровней лидерства окружения G^rij =

= (M₀) ∨ G^rij = (M₁).

Для применения классического информационного регламента Штакель-

берга [6], определяющего равновесие при полной информированности, мно-

жество возможных рефлексивных представлений агентов (8) на r-м ранге

рефлексии необходимо свести к набору множеств уровней лидерства (7) на

первом ранге рефлексии. Тем самым рефлексивная игра сводится к множе-

ству игр с полной информированностью вида

(9)

Γ=

N,{Q_i,i ∈ N} ,{Π_i,i ∈ N} ,G¹

где G¹ — система представлений всех агентов о принципах выбора действий

окружением на первом ранге рефлексии в виде (7).

Определение 1. Информационное равновесие в игре двух агентов (9)₍₎

есть вектор действий агентов Q^∗i,Q^∗j,i,j ∈ N , полученный из решения

задачи (6).

В дальнейшем информационное равновесие описывается парой (ψ^∗, Q^∗),

где Q^∗ = Q^∗i + Q^∗j, i, j ∈ N — сумма равновесных действий агентов, ψ^∗ =Q∗Q ,_i

i, j ∈ N — показатель структуры равновесных действий.

Определение 2. Показатель структуры выигрыша в игре двух аген-

тов

(9) при информационном равновесии есть величина Ψ^∗ =Πj (Qj),

Π_i(Q^∗i)

i, j ∈ N.

Определение 3. Рефлексивным лидером называется j-й агент, ранг

рефлексии которого больше ранга рефлексии i-го агента, называемого рефлек-

сивным последователем, на целое число γ, которое называется параметром

опережения, если γ > 0 (запаздывания, если γ < 0), т.е. r_j = r_i + γ, γ ∈ Z.

В случае γ < 0 рефлексивные позиции лидера и последователя меняются

местами, однако представляется целесообразным сохранить введенную тер-

минологию для идентичности понятийного аппарата при анализе рефлексии

140

с различными типами несовпадения рангов, как при опережении, так и при

запаздывании.

Поставим задачу нахождения всех информационных равновесий в игре (9)

на произвольном ранге рефлексии i-го агента при произвольном значении

параметра опережения γ ранга рефлексии j-го агента.

В дальнейшем будем придерживаться следующей логики. Решение иг-

ры (9) в виде равновесного по Нэшу вектора действий Q^∗i, i ∈ N может быть

получено из системы уравнений (6), для чего должен быть задан вектор пред-

положительных вариаций ρ = {ρ_ij, i, j ∈ N}. Этот вектор согласно опреде-

лению предположительной вариации (ρ_ij = Q^′

) вычисляется дифференци-

jQ_i

рованием уравнений системы (6), соответствующих окружению i-го агента.

Поскольку i-й агент на первом ранге рефлексии может выдвигать предполо-

жение о двух стратегиях окружения (F или L), т.е. относить окружение либо

к множеству M₀, либо к множеству M₁, то в уравнениях (6) для окружения

может быть либо ρ_ji = 0∀j ∈ M₀, либо ρ_ji = -¹² ∀j ∈ M₁. На втором ранге ре-

флексии i-й агент также может выдвигать предположение о двух стратегиях

окружения (F или L), но это означает, что, по мнению агента, окружение от-

носит его либо к множеству M₀, либо к множеству M₁. На последующих ран-

гах рефлексии интерпретация предположений еще более усложняется, поэто-

му первый этап решения игры (9) состоит в редукции предположений агентов

на r-м ранге рефлексии к предположениям на первом ранге, когда вектор ρ

можно вычислить непосредственно. На втором этапе решения игры (9) опре-

деляется зависимость ρ_ij от предположений i-го агента, сведенных к первому

рангу рефлексии, как функция ранга рефлексии этого агента, т.е. вычисля-

ется вектор ρ. На третьем этапе путем решения системы (6) вычисляется

вектор Q^∗i, i ∈ N как функция ранга рефлексии i-го агента r и параметра

опережения (запаздывания) γ.

3. Результаты

Как было показано [50], представление агента о стратегиях окружения при

гипотезах 1-4 может быть либо L-стратегией, либо F -стратегией. Поэтому

запишем в виде (7) совокупность представлений двух агентов на r-м ранге

рефлексии:

Grt=1 = (M₀ = (i, j)) , Grt=2 = (M₁ = (i, j)) ,

(10)

Grt=3 = (M₀ = (i) ∧ M₁ = (j)) , Grt=4 = (M₀ = (j) ∧ M₁ = (i)) ,

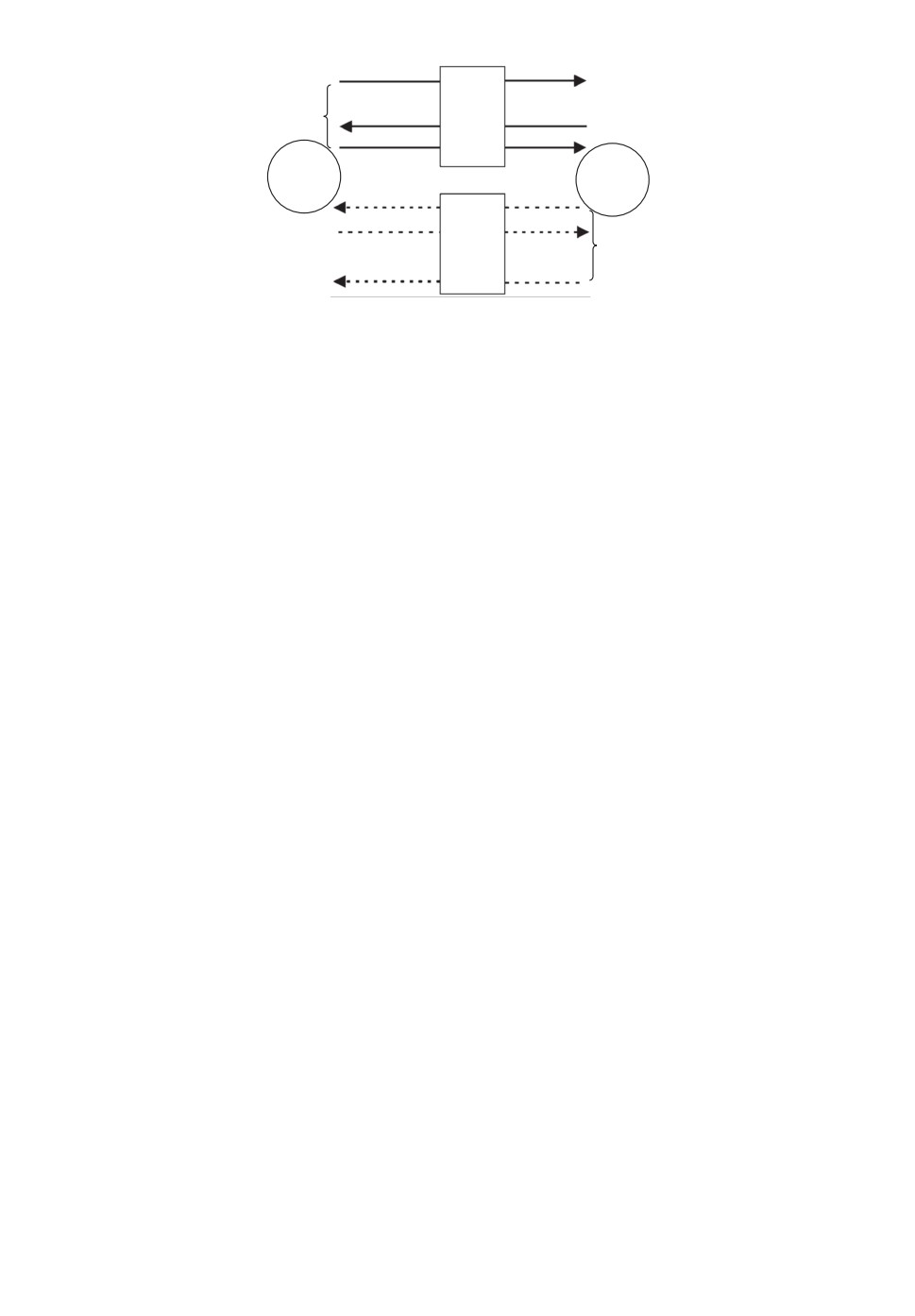
где t = 1, 2, 3, 4 — номер игрового случая (рис. 1-4), определяющего игру (9)

соответствующего вида. На рис. 1-4 использована следующая символика: ◦ —

агент; □ — представляемая агентом стратегия окружения; → — представления

i-го агента; -- → — представления j-го агента; ■■■ — непоказанные стрел-

ки; { — последовательность представлений (8) каждого агента до r-го ранга

рефлексии включительно.

В соответствии с (10) возможно четыре игровых случая, схематично изоб-

раженных на рис. 1-4: идентичность представлений агентов друг о друге как

о ведомых агентах (рис. 1); идентичность представлений агентов друг о друге

141

r +

Рис. 1. Схема игры при идентичности представлений агентов друг о друге как

о последователях.

r +

Рис. 2. Схема игры при идентичности представлений агентов друг о друге как

о лидерах.

r +

Рис. 3. Схема игры при контрадикторности представлений агентов: i-й агент

считает контрагента лидером, j-й агент считает контрагента последователем.

как о лидерах по Штакельбергу (рис. 2); контрадикторность представлений

агентов, когда рефлексивный последователь представляет рефлексивного ли-

дера лидером по Штакельбергу, а последний считает контрагента ведомым

(рис. 3); контрадикторность представлений агентов, когда рефлексивный по-

следователь представляет рефлексивного лидера ведомым, а последний счи-

тает контрагента лидером по Штакельбергу (рис. 4). Отметим, что непосред-

ственное сравнение этих случаев с возможными в реальности ситуациями

142

r +

Рис. 4. Схема игры при контрадикторности представлений агентов: i-й агент

считает контрагента последователем, j-й агент считает контрагента лидером.

допустимо только при γ = 0: случаи идентичности представлений не соответ-

ствуют реальности (как «борьба за лидерство»), а случаи контрадикторности

представлений реалистичны, поскольку агент, которого окружение представ-

ляет лидером по Штакельбергу, считает контрагента ведомым, а последний,

соответственно, представляет контрагента лидером по Штакельбергу. При

γ > 0 соответствие представлений реальности устанавливается посредством

анализа информационных равновесий.

Определим виды рефлексивной игры двух агентов с представлениями (10)

в указанных случаях в виде следующего утверждения.

Утверждение 1. Рефлексивная игра двух агентов (9) в случае несов-

падения рангов рефлексии на величину γ при различных представлениях на

r-м ранге рефлексии описывается следующей системой разбиений типа (7)

на первом ранге рефлексии:

G1t=1 = (M_r,Mr+γ) , M_r = (i), Mr+γ = (j)

(11a)

при G^rij = (M₀ = (j)) ∧ Gr+γji = (M₀ = (i)) ,

G1t=2 = (Mr+1,Mr+γ+1) , Mr+1 = (i), Mr+γ+1 = (j)

(11b)

при G^rij = (M₁ = (j)) ∧ Gr+γji = (M₁ = (i)) ,

G1t=3 = (Mr+1,Mr+γ) , Mr+1 = (i), Mr+γ = (j)

(11c)

при G^rij = (M₁ = (j)) ∧ Gr+γji = (M₀ = (i)),

G1t=4 = (M_r,Mr+γ+1) , M_r = (i), Mr+γ+1 = (j)

(11d)

при G^rij = (M₀ = (j)) ∧ Gr+γji = (M₁ = (i)),

i, j ∈ N, r, γ ∈ Z.

Формализация (11) системы представлений агентов на первом ранге ре-

флексии при различных видах (10) представлений агентов на r-м ранге ре-

флексии позволяет найти информационные равновесия в игре (9). Для этого

на базе соответствующих множеств G¹ формируются функции наилучших

143

ответов агентов в виде системы (6), решение которой зависит от вектора

предположительных вариаций на r-м ранге рефлексии.

Утверждение 2. Предположительная вариация на произвольном ран-

ге рефлексии в уравнении реакции i-го агента, такого что M_r = (i), в систе-

ме уравнений (6) вычисляется по формуле

r_i

(12)

ρ^rij = -

r_i + 1

Утверждение 3. Информационное равновесие в рефлексивной игре (9)

на произвольном ранге рефлексии для двух агентов с различными предель-

ными издержками вычисляется по формулам

(

)

r_i+γ

α_i

2-_r

-α_j

i+γ+1

Q^∗i (r_i,γ) =

(

)(

)

r_i+γ

2-ri

2-_r

-1

r_i+1

+γ+1

(13)

(

)

r_i

α_j

2-_r

-α_i

i+1

Q^∗j (r_i,γ) =

(

)(

)

i, j ∈ N,

r_i+γ

2-ri

2-_r

-1

r_i+1

+γ+1

(

)

(

)

r_i+γ

α_i

1-_r

+α_j

1-ri

i+γ+1

r_i+1

Q^∗ (r_i,γ) =

(

)(

)

r_i+γ

2-ri

2-_r

-1

r_i+1

+γ+1

(14)

(

)

α_j

2-ri

-1

r_i+1

ψ^∗ (r_i,γ) =αi

i, j ∈ N,

2-ri+^γr

i+γ+1

- α^jα_i

где

a-c_i

α_i =

i∈N.

Формулы (13) представляют собой равновесные по Нэшу действия аген-

тов в игре (9). Формулы (13), (14) выражают информационное равновесие

как функцию ранга рефлексии r_i рефлексивного последователя и параметр

опережения γ рефлексивного лидера Q^∗ (r_i, γ), ψ^∗ (r_i, γ), что позволяет ана-

лизировать влияние этих показателей на структуру равновесия в игре в виде

следующего утверждения.

Рассмотрим пример применения формул (13) в случае классической иг-

ры Штакельберга, для которой r_i = 0, γ = 1 ⇒ r_j = 1. В этом случае из (13)

i-αj

следует, что Q^∗i (0, 1) =² α

, Q∗j (0,1) = 2αj-αi2, а если агенты имеют иден-

тичные параметры функций издержек c = c_i, i ∈ N, т.е. α = α_i, i ∈ N, то

Q^∗i (0,1) =α4, Q^∗j (0,1) =α2, что совпадает с известным результатом для рав-

новесия Штакельберга [55]: Q^F =a-c4b , Q^L =a-c2b .

144

Утверждение 4. В информационном равновесии рефлексивной игры (9)

двух агентов на произвольном ранге рефлексии структура равновесных дей-

ствий неравномерна и зависит от параметра опережения и ранга рефлексии

⎧

α_j

⎨

> 1, при

> ω (r_i),

α_i

ψ^∗

^⎩ < 1, приαj < ω (r_i), i,j ∈ N,

α_i

⎧

α_j

⎨

> 0, при

> ζ (r_i),

∂ψ^∗

α_i

(15)

∂γ ⎩<0,приαj<ζ(ri) , i,j ∈ N,

α_i

⎧

α_j

⎪

> 0, при

ζ (r_i) ,

⎪

α_i

⎨

∂ψ^∗

< 0, при

< ζ (r_i), i,j ∈ N,

∂r_i ⎪

α_i

⎪

α_j

⎩<0,приζ(ri) <

ζ (r_i) ∧ δ₁ > |δ₂| ,

α_i

где

r_i+γ

3-_r

r_i + γ

i+γ+1

ω=

ζ =

ζ =2-

r_i + γ + 1

(

)

α_j

1 -αjα_iζ

δ₁ =

ζ-

δ₂ =

α_i (r_i + 1)²

α_i

(r_i + γ + 1)²

Структура действий в информационном равновесии рефлексивной игры

двух агентов согласно формулам (15) в общем случае зависит от ранга ре-

флексии и параметра опережения через функции ω (r_i), ζ (r_i)

ζ (r_i). Однако

для практически важного частного случая существенного превышения пара-

метра обратной функции спроса a над предельными издержками агентов c_i,

c_j можно выявить однозначный характер зависимости ψ^∗ (r_i,γ).

Утверждение 5. В информационном равновесии рефлексивной игры (9)

двух агентов на произвольном ранге рефлексии при условии a ≫ max {c_i, c_j },

c_i,c_j > 0, i,j ∈ N неравномерность действий растет с увеличением пара-

метра опережения рефлексии и убывает с увеличением ранга рефлексии:

{

∗

> 1, если γ ≥ 1,

∂ψ

∂ψ^∗

(15а)

ψ^∗

> 0,

< 0.

< 1, если γ ≤ -1, |γ| < r_i,

∂γ

∂r_i

Результат игры (9) оценивается не только по параметрам информацион-

ного равновесия (14), но и по распределению выигрыша (прибыли) между

агентами, определенному в виде следующего утверждения.

Утверждение 6. Показатель структуры выигрыша равен

(a - bQ^∗ - c_j ) ψ^∗Q^∗ - (1 + ψ^∗) d_j

(16)

Ψ^∗ =

i, j ∈ N,

(a - bQ^∗ - c_i) Q^∗ - (1 + ψ^∗) d_i

145

Q*(r_i)

1450

1400

1350

1300

1250

r_i

t = 1,

= 1

t = 1,

= 3; t = 2,

= 1

t = 1,

= 5; t = 2,

= 3

t = 2,

= 5

t = 3,4,

= 1

t = 3,4,

= 3

t = 3,4,

= 5

Рис. 5. Суммарное действие агентов (млрд мин) в зависимости от ранга ре-

флексии.

*(r_i)

4,0

3,5

3,0

2,5

2,0

1,5

1,0

0,5

r_i

t = 1,

= 1

t = 1,

= 3

t = 1,

= 5

t = 2,

= 1

t = 2,

= 3

t = 2,

= 5

t = 3,

= 1

t = 3,

= 3

t = 3,

= 5

t = 4,

= 1

t = 4,

= 3

t = 4,

= 5

Рис. 6. Показатель структуры равновесных действий агентов в зависимости

от ранга рефлексии.

а при условиях P (Q^∗) ≫ max{c_i,c_j} ∧ P (Q^∗)Q^∗ ≫ max{d_i,d_j}, i,j ∈ N, ра-

вен Ψ^∗ ≈ ψ^∗.

Формула (16) определяет полезности агентов в равновесии Нэша в относи-

тельной форме; абсолютные равновесные значения полезностей вычисляются

на основе равновесных действий (13) через функции полезности агентов (1).

Рассмотрим модельный пример расчета информационных равновесий

рынка дуополии на основе данных для двух агентов (i = 1, j = 2), получен-

ных [53] для телекоммуникационного рынка России. Коэффициенты регрес-

146

Q*( )

1450

1400

1350

1300

t = 1,4, r_i= 5

t = 1,4, r_i= 7

t = 2,3, r_i= 5

t = 2,3, r_i= 7

Рис. 7. Суммарное действие агентов (млрд мин) в зависимости от параметра

опережения рефлексии.

*( )

2,2

1,8

1,4

1,0

0,6

0,2

t = 1,4, r_i= 5

t = 1,4, r_i= 7

t = 2,3, r_i= 5

t = 2,3, r_i= 7

Рис. 8. Показатель структуры равновесных действий агентов в зависимости

от параметра опережения рефлексии.

сионных моделей функции спроса (2) и функций издержек агентов (4) при-

ведены в табл. 1.

На рис. 5, 6 показаны параметры информационных равновесий (суммар-

ного действия агентов и показателя структуры равновесных действий) для

различных игровых случаев (t = 1, 2, 3, 4) в зависимости от ранга рефлексии

i-го агента, рассчитанные по формулам (14).

Таблица 1. Коэффициенты функции спроса, функций издержек агентов

Коэффициенты

Коэффициенты функций издержек

функции спроса

Агент 1

Агент 2

руб руб/млн мин тыс. руб/ мин млрд руб тыс. руб/ мин млрд руб

1,85

0,0000001

0,0004

63,4

0,0003

58,6

147

На рис. 7, 8 показаны параметры информационных равновесий (суммар-

ного действия агентов и показателя структуры равновесных действий) для

различных игровых случаев (t = 1, 2, 3, 4) в зависимости от параметра опе-

режения рефлексии γ при значениях ранга рефлексии i-го агента r_i = 5, 7,

рассчитанные по формулам (14).

4. Обсуждение

Структуры игры (11) показывают, что 1) на r-м ранге рефлексивный по-

следователь имеет статус лидера по Штакельбергу r-го уровня, если в его

представлении контрагент ведомый, и (r + 1)-го уровня, если в его пред-

ставлении контрагент — лидер; 2) рефлексивный лидер имеет статус, превы-

шающий на величину γ статус рефлексивного последователя в случаях 1, 2

идентичности представлений агентов; 3) статус рефлексивного лидера вы-

ше статуса рефлексивного последователя на величину (γ - ε) в случаях 3, 4

контрадикторности представлений агентов, где ε характеризует степень кон-

традикторности представлений, ε = m_i - m_j, в частности ε = 1 - 0 = 1 в слу-

чае 3, ε = 0 - 1 = -1 в случае 4.

Формулы информационных равновесий (14) позволяют оценить степень

близости равновесия к конкурентному состоянию [56], поскольку чем боль-

ше величина Q^∗, тем ниже равновесная рыночная цена, следовательно, тем

сильнее конкуренция агентов. Показатель структуры равновесных действий

ψ^∗ характеризует эффективность опережения рефлексивного представления

для рефлексивного лидера: с ростом ψ^∗ увеличивается дифференциация рын-

ка в пользу рефлексивного лидера.

Формулы (15) определяют зависимость структуры равновесных действий

и тенденций изменения этой структуры от соотношения параметров α для

рефлексивного лидера (α_j ) и рефлексивного последователя (α_i). В практиче-

ски реализуемом случае (15а) a ≫ c_i, c_j , i, j ∈ N, т.е. когда параметр обрат-

ной функции спроса a, интерпретируемый как максимальная цена спроса,

существенно превышает предельные издержки агентов [57], сумма действий

всегда перераспределяется в пользу рефлексивного лидера (ψ^∗ > 1), неравно-

мерность распределения действий в пользу рефлексивного лидера возрастает

> 0) и убывает с ростом ранга рефлек-

сии (∂ψ∗ < 0)._∂r

Анализ результатов численного эксперимента приводит к следующим вы-

водам.

Из анализа рис. 5, во-первых, следует, что суммарное действие (суммар-

ный выпуск) агентов возрастает, следовательно, равновесная рыночная цена

снижается, с увеличением ранга рефлексии r_i и параметра опережения ре-

флексии γ, что свидетельствует об усилении конкуренции, но различие сум-

марных выпусков с ростом γ сокращается — значит, рефлексия агентов не

способна бесконечно развивать конкуренцию.

Во-вторых, рис. 5 показывает, что при одном и том же значении парамет-

ра опережения рефлексии (γ = const) имеет место следующее соотношение

148

между суммарными действиями агентов:

Q^∗ (t = 2) > Q^∗ (t = 3,4) > Q^∗ (t = 1) ,

которое позволяет классифицировать влияние типа рефлексивных представ-

лений агентов на интенсивность их конкуренции следующим образом. Слу-

чай t = 2 приводит к наиболее сильной конкуренции, поскольку при этом

достигается наибольшая сумма действий агентов, что ведет к наименьшей

равновесной рыночной цене по (2). Случай t = 1 дает наименьшее суммарное

действие, что ведет к наибольшей равновесной цене, т.е. наиболее слабому

влиянию рефлексии агентов на интенсивность конкуренции. Следовательно,

полученные выводы о влияние типа рефлексивных представлений агентов на

динамику суммарного действия согласуются с классическими результатами,

полученными при отсутствии рефлексии [39].

Из анализа рис. 6, во-первых, следует, что неравномерность равновес-

ных действий снижается с ростом ранга рефлексии r_i, подтверждая свой-

ство (15а), что согласуется с известным для случая совпадения рангов ре-

флексии положением о неэффективности рефлексии [54]. Во-вторых, при

γ = const имеет место следующее соотношение между показателями струк-

туры равновесных действий:

ψ^∗ (t = 4) > ψ^∗ (t = 1) > ψ^∗ (t = 2) > ψ^∗ (t = 3) ,

которое позволяет оценить влияние типа рефлексивных представлений аген-

тов на эффективность опережающего представления для рефлексивного ли-

дера.

Суммарное действие агентов (рис. 7) возрастает с увеличением параметра

опережения рефлексии γ, т.е. конкуренция усиливается, поскольку при этом

фактически возрастает ранг рефлексивного лидера. Также из рис. 7 следует,

что характер зависимости Q^∗ (γ) в различных игровых случаях имеет зако-

номерность

Q^∗ (γ,t = 2) = Q^∗ (γ,t = 3) > Q^∗ (γ,t = 1) = Q^∗ (γ,t = 4) ,

позволяющую оценить влияние опережения рефлексии на интенсивность кон-

куренции.

Из анализа рис. 8 следует, что неравномерность равновесных действий

возрастает с ростом параметра опережения рефлексии, подтверждая свой-

ство (15а). Характер зависимости ψ^∗ (γ) имеет следующую закономерность в

случае γ > 0:

ψ^∗ (γ,t = 2) = ψ^∗ (γ,t = 3) < ψ^∗ (γ,t = 1) = ψ^∗ (γ,t = 4) ,

а в случае запаздывания рефлексии (γ < 0) имеет место обратное соотноше-

ние, т.е. вид функции влияния опережения рефлексии на неравномерность

равновесных действий зависит только от представления рефлексивного по-

следователя. Неравномерность равновесных действий в случаях t = 2, 3 оди-

накова и не превышает этого показателя в случаях t = 1, 4 при любом γ > 0.

149

5. Заключение

Исследована проблема поиска равновесий на рынке олигополии при на-

личии лидера (лидеров) по Штакельбергу с учетом рефлексивного поведе-

ния агентов рынка в случае несовпадения рангов рефлексии. Сформирова-

ны модели рефлексивных игр для рынка дуополии в случаях идентичности

представлений агентов друг о друге как о ведомых агентах, идентичности

представлений агентов друг о друге как о лидерах по Штакельбергу, проти-

воположности представлений агентов, один из которых представляет контр-

агента ведомым, а другой — лидером. Разработаны механизмы установления

равновесия рынка дуополии при данном многообразии рефлексивных пред-

ставлений агентов на одинаковых рангах рефлексии. Моделирование игры в

зависимости от ранга рефлексии показало влияние опережения (запаздыва-

ния) рефлексии одного агента по сравнению с контрагентом, во-первых, на

интенсивность конкуренции, во-вторых, на неравномерность распределения

выигрыша между агентами в пользу рефлексивного лидера.

ПРИЛОЖЕНИЕ

Доказательство утверждения 1. Представления агентов на про-

извольном ранге рефлексии i-го агента r_i = η при произвольном значении

параметра опережения γ = θ записаны в табл. 2. Представления агентов на

первом ранге рефлексии рассчитаны в табл. 2 по формуле [51]

G1ij = (Mm+r-1) ∀ G^rij = (M_m), j ∈ N\i, r ∈ Z, i ∈ N.

Рефлексивная игра в каждом случае получена по наилучшему ответу [51]₍

)

BR_i G¹

∈ Mm+1 ∀G1ij = (M_m) на представления агентов, приведенные к

первому рангу рефлексии. Аналогичные результаты можно получить при

r_i = η + 1, γ = θ + 1, поэтому по индукции формулы (11) доказаны.

Доказательство утверждения 2. Уравнение (6) j-го агента для₍

)

задачи (5) имеет вид a - bQ - bQ_i

1+ρ^r

- c_i = 0, i,j ∈ N, откуда следует

, i, j ∈ N. Предположительные ва-

+ρ^r

риации для уравнения реакции i-го агента получены дифференцированием

Таблица 2. Структуры игры двух агентов в различных случаях рефлексивных

представлений при r_i = η, γ = θ, r_j = η + θ

Случай

G^rij

M₀

M₁

M₀

G1ij

Mη-1

M_η

Mη-1

G^rji

M₀

M₁

M₀

M₁

G1ji

Mη+θ-1

Mη+θ

Mη+θ-1

Mη+θ

G^r

(M_η, Mη+θ) (Mη+1, Mη+θ+1) (Mη+1, Mη+θ)

(M_η, Mη+θ+1)

150

этого уравнения по Q_i для r = 0, 1, 2, . . . , θ:

r_i = 1 ⇒ ρ0ji = 0 ⇒ ρ1ij = -

r_i = 2 ⇒ ρ1ji = -

⇒ρ2ij =-

r_i = 3 ⇒ ρ2ji = -

⇒ρ3ij =-

θ-1

r_i = θ ⇒ ρθ-1ji = -

⇒ρ^θij =-

θ-1

поскольку для r = θ + 1 выражение аналогично, то по индукции формула (12)

доказана.

Доказательство утверждения 3. Система уравнений реакций (6)

в задачах выбора (5) на произвольном ранге рефлексии для двух агентов с

различными предельными издержками

(2 + ρ^rij)Q_i + Q_j = α_i, Q_i + (2 + ρ^rji)Q_j = α_j ,

имеет решение

α_i(2 + ρ^rji) - α_j

α_j(2 + ρ^rij) - α_i

Q^∗i =

Q^∗j =

i, j ∈ N,

(2 + ρ^rij )(2 + ρ^rji) - 1

(2 + ρ^rij)(2 + ρ^rji) - 1

подстановка в которое формулы (12) дает (13). Нахождение суммы и отно-

шения (13) дает (14).

Доказательство утверждения 4. Из (14) следует, что ψ∗ >1, если

(

)

(

)

(

)

(

)

α_j

2-ri

-α_i>α_i

2-ri+^γ

- α_j; далее, α_j

3-ri

>α_i

3-ri+^γ

;

r_i+1

r_i+γ+1

r_i+1

r_i+γ+1

поскольку α_i, α_j > 0, то это неравенство даетαjα_i >ω(ri^{).Дифференцирование}

ψ^∗ (r_i,γ) по γ дает

(

)

α_j

2-ri

-1

∂ψ^∗

α_i

r_i+1

(

)₂

;

∂γ

(r_i + γ + 1)²

2-ri+^γr

-α^j

i+γ+1

α_i

(

)

∂ψ^∗

неравенство

2-ri

- 1 > 0, что дает

∂γ

> 0 выполняется, еслиαjα_i

r_i+1

α_j

> ζ (r_i). Дифференцирование функции ψ∗ (r_i,γ) по r_i дает

α_i

(

)

(

))

α_j

2-ri+^γr

2-ri

∂ψ^∗

i+γ+1

- α^jα_i

(r_i+γ+1)2

1 - αjα_i

r_i+1

=-αi(ri+1)2

(

)₂

∂r_i

2-ri+^γr

-α^j

i+γ+1

α_i

δ₁ + δ₂

=-(

)₂ .

2-ri+^γr

-α^j

i+γ+1

α_i

Отсюда следует, что неравенство∂ψ∗ < 0 выполняется в следующих случаях:_∂r

151

i) если

α_j

r_i + γ

(Π.1)

<2-

ζ (r_i),

α_i

r_i + γ + 1

α_j

(Π.2)

= ζ (r_i

α_i

2-ri

r_i+1

β=ri+^γr

, β

β <1∀r_i ≥1,|γ|<r_i.Поскольку 2

β-

i+γ+1

β)(2-β)-1

−12-β =(2

> 0, т

ζ (r_i) > ζ (r_i), значит неравенство (П.2) является

2-β

необходимым условием для неравенства (П.1), а неравенство (П.2) соответ-

ствует (15).

ii) еслиαjα_i

ζ (r_i) ∧ αjα_i > ζ (ri⁾∧ δ1 > |δ2|, что соответствует (15).

ζ (r_i) > ζ (r_i).

iii) еслиαjα_i

ζ (r_i) ∧αjα_i <ζ(ri)∧δ2^>|δ1|,чтопротиворечи

Неравенство∂ψ∗ > 0 выполняется, если_∂r

α_j

(Π.3)

ζ (r_i)

α_i

α_j

(Π.4)

> ζ (r_i

α_i

В случаях γ ≥ 1 и γ ≤ -1, |γ| < r_i неравенство (П.3) является необходимым

условием для неравенства (П.4), а неравенство (П.3) соответствует (15).

Доказательство утверждения

Покажем, что ψ^∗ > 1: при

< rⁱ+^γr

< 1 ∀r_i ≥ 1, значит 3 -ri+^γr

i+γ+1

поэтому ω (r_i) < 1 ∀i ∈ N. Из (14) следует, что при ψ^∗ > 1 выполняется

; поскольку b > 0, это равносильно

α_j > ω (r_i) α_i, откудаa-cjb>ω(ri)a

a - c_j > ω (r_i)(a - c_i), или

(Π.5)

a (1 - ω (r_i)) > c_j - ω (r_i) c_i.

Если c_j - ω (r_i) c_i < 0, то (П.5) верно для всех c_i, c_j > 0; если c_j - ω (r_i) c_i > 0,

то пусть ∃c > 0: c > cj - ω (ri) ci, c > max {ci,cj}, тогда (П.5) верно при

[₄

)

a (1 - ω (r_i)) > c ⇒^ac >

⇒ a ≫ c, поскольку ω (r_i) ∈

; так как

1-ω(r_i)

c > max{c_i,c_j}, то при условии a ≫ max{c_i,c_j} верно ψ^∗ > 1. Случай ψ^∗ < 1

доказывается аналогично.

> 0, которое верно при

(Π.6)

a(1 - ζ (r_i)) > c_j - ζ (r_i)c_i.

Поскольку ζ (r_i) < 1

∀r_i ≥ 1, то если c_j - ζ (r_i) c_i < 0, то (П.6) верно

для всех c_i, c_j > 0; если c_j - ζ (r_i) c_i > 0, то пусть ∃c > 0: c > c_j - ζ (r_i) c_i,

c > max{c_i,c_j}, тогда (П.6) верно при a(1 - ζ (r_i)) > c ⇒ ^ac >

⇒ a ≫ c,

1-ζ(r_i)

[₂

)

поскольку ζ (r_i) ∈

; так как c > c_i, c_j , то при условии a ≫ max {c_i, c_j } вер-

< 0 доказывается аналогично.

152

> 0. При γ ≥ 1, γ ≤ -1, |γ| < r_i верн

ζ (r_i) > 1

ζ (r_i) ∈

r_i

∈ (1;1,5]. Из (15) следует

)

(Π.7)

ζ (r_i) - 1

ζ (r_i)c_i - c_j.

Есл

ζ(r_i)c_i - c_j < 0, то (П.7) не верно для всех c_i, c_j > 0; есл

ζ(r_i)c_i -c_j > 0,

то пусть

∃c > 0: c

ζ (r_i)c_i - c_j, c < max{c_i,c_j}, тогда (П.7) верно при

ζ(r_i) - 1) < c ⇒^ac <

, что противоречит условию a ≫ max{c_i, c_j } > c.

^ζ(r_i)-1

∂ψ^∗

Значит случай

ζ(r_i) исключен. Поскольку ζ(r_i) < 1, то

∂r_i

>0 приαjα_i

из (15) приαjα_i <ζ(ri^{)следует,что}

(Π.8)

a(1 - ζ (r_i)) < c_j - ζ (r_i)c_i.

По аналогии с (П.7) это исключено. Из (П.7), (П.8) следует, что возможен

ζ (r_i), при котором по (15) ∂ψ∗ < 0._∂r

только случай ζ (r_i) <αjα_i

Доказательство утверждения 6. Из формулы показателя струк-

туры равновесных действий ψ^∗ =Q∗Q_i следует, что ψ^∗ =^Q

Q^∗i

ψ^∗

. Подстановка этих выражений в формулу прибыли (1), а затем в

+ψ^∗

)Q^∗-(1+ψ^∗)d_i

=ψ^∗.

−bQ^∗)Q^∗

СПИСОК ЛИТЕРАТУРЫ

1. Mas-Collel A., Whinston M., Green J. Microeconom. Theory. N.Y.: Oxford Univer.

Press, 1995.

2. Shapiro C. Theories of Oligopoly Behavior // Discussion paper 126. Woodrow Wilson

School. Princeton Univer. Press, 1987.

3. Nash J. Non-cooperative Games // Ann. Math. 1951. No. 54. P. 286-295.

4. Cournot A.A. Researches into the Mathematical Principles of the Theory of Wealth.

London: Hafner, 1960. (Original 1838.)

5. Bowley A.L. The Mathematical Groundwork of Economics. Oxford: Oxford Univers.

Press, 1924.

6. Stackelberg H. Market Structure and Equilibrium: 1st Edition. Translation into

English, Bazin, Urch & Hill, Springer, 2011. (Original 1934.)

7. Karmarkar U.S., Rajaram K. Aggregate Production Planning for Process Industries

under Oligopolistic Competition // Eur. J. Oper. Res. 2012. No. 223 (3). P. 680-689.

8. Ledvina A., Sigar R. Oligopoly Games under Asymmetric Costs and an Application

to Energy Production // Math. Financ. Econom. 2012. No. 6(4). P. 261-293.

9. Currarini S., Marini M.A. Sequential Play and Cartel Stability in Сournot

Oligopoly // Appl. Math. Scie. 2013. No. 7 (1-4). Р. 197-200.

10. Vasin A. Game-theoretic Study of Electricity Market Mechanisms // Procedia

Comput. Sci. 2014. No. 31. Р. 124-132.

11. Sun F., Liu B., Hou F., Gui L., Chen J. Cournot Equilibrium in the Mobile Virtual

Network Operator Oriented Oligopoly Offloading Market // 2016 IEEE Int. Conf.

Commun., ICC 2016. No. 7511340.

153

12.

Lorenczik S., Panke T. Assessing Market Structures in Resource Markets — An

Empirical Analysis of the Market for Metallurgical Coal Using Various Equilibrium

Models // Energy Econom. 2016. No. 59. Р. 179-187.

13.

Li X., Xu X., Sun Y. Advance Selling Strategies for Oligopolists by Considering

Product Diffusion Effect // Kybernet. 2016. No. 45(5). Р. 744-759.

14.

Naimzada A.K., Sbragia L. Oligopoly Games with Nonlinear Demand and Cost

Functions: Two Boundedly Rational Adjustment Processes //Chaos, Solit. Fractal.

2006. No. 29 (3). P. 707-722.

15.

Askar S., Alnowibet K. Nonlinear Oligopolistic Game with Isoelastic Demand

Function: Rationality and Local Monopolistic Approximation // Chaos, Solit.

Fractal. 2016. No. 84. P. 15-22.

16.

Naimzada A., Tramontana F. Two Different Routes to Complex Dynamics in an

Heterogeneous Triopoly Game // J. Difference Equat. Appl. 2015. No. 21 (7).

P. 553-563.

17.

Cavalli F., Naimzada A., Tramontana F. Nonlinear Dynamics and Global Analysis

of a Geterogeneous Cournot Duopoly with a Local Monopolistic Approach Versus

a Gradient Rule with Endogenous Reactivity // Commun. Nonlinear Sci. Numer.

Simulat. 2015 No. 23 (1-3). P. 245-262.

18.

Kalashnikov V.V., Bulavsky V.A., Kalashnykova N.I. Existence of the Nash-Optimal

Strategies in the Meta-Game / Ceberio M., Kreinovich V. (eds.). Constraint

Programming and Decision Making: Theory and Applications. Studies in Systems,

Decision and Control, vol. 100. Springer, Cham, 2018. Р. 95-100.

19.

Colacicco R. Ten Years of General Oligopolistic Equilibrium: A survey // J. Econom.

Surveys. 2015. No. 29 (5). P. 965-992.

20.

Jørgensen S., Zaccour G. A Survey of Dame-theoretic Models of Cooperative

Advertising // Eur. J. Oper. Res. 2014. V. 237. No. 1. P. 1-14.

21.

Ino H., Matsumura T. Welfare-Improving Effect of a Small Number of Followers in

a Stackelberg Model // B.E. J. Theoret. Econom. 2016. No. 16 (1). P. 243-265.

22.

Peng Y., Lu Q., Xiao Y. A Dynamic Stackelberg Duopoly Model with Different

Strategies // Chaos, Solitons Fractals. 2016. Vol. 85. P. 128-134.

23.

Hayakawa H. The Tragedy of the Commons: the Logic of Entry and the Dynamic

Process under Ttwo Scenarios // Eurasian Econom. Rev. 2017. No. 7 (3). Р. 311-328.

24.

Yoo T.-H., Ko W., Rhee C.-H., Park, J.-K. The Incentive Announcement Effect

of Demand Response on Market Power Mitigation in the Electricity Market //

Renewable Sustainable Energy Rev. 2017. No. 76. Р. 545-554.

25.

Sherali H.D. Multiple Leader Stackelberg Model and Analysis // Oper. Res. 1984.

No. 32 (2). P. 390-404.

26.

Boyer M., Moreaux M. Being a Leader or a Follower. Reflections on the Distribution

of Roles in Duopoly // Int. J. Industr. Organ. 1987. No. 5(2). P. 175-192.

27.

DeMiguel V., Xu H. A Stochastic Multiple-leader Stackelberg Model: Analysis,

Computation, and Application // Oper. Res. 2009. No. 57 (5). P. 1220-1235.

28.

Julien L.A. On Noncooperative Oligopoly Equilibrium in the Multiple Leader —

follower Game // Eur. J. Oper. Res. 2017. No. 256 (2). P. 650-662.

29.

Solis C.U., Clempner J.B., Poznyak A.S. Modeling Multileader

— Follower

Noncooperative Stackelberg Games // Cybernet. Syst. 2017. No. 47 (8). P. 650-673.

30.

Лефевр В.А. О самоорганизующихся и саморефлексивных системах и их иссле-

довании. Проблемы исследования систем и структур // Матер. конф. М.: Изд-во

АН СССР, 1965. C. 61-68.

154

31.

Lefebvre V. Reflexive Analysis of Groups (Book Chapter) / Comput. Methods

Counterterr. 2009. P. 173-210.

32.

Lefebvre V. Lectures on the Reflexive Games Theory. N.Y.: Leaf & Oaks Publish.,

2010.

33.

Rgo L., Halpern J. Generalized Solution Concepts in Games with Possibly Unaware

Players // Int. J. Game Theory. 2012. No. 41. P. 131-155.

34.

Heifetz A., Meier M., Schipper B.C. Unawareness, Beliefs, and Speculative Trade //

Games Econom. Behavior. 2013. No. 77 (1). P. 100-121.

35.

Alaoui L., Penta A. Endogenous Depth of Reasoning // Rev. Econom. Studies. 2016.

No. 83(4). P. 1297-1333.

36.

Kneeland T. Coordination under Lmited Depth of Reasoning // Games Econom.

Behavior. 2016. No. 96. P. 49-64.

37.

Brocas I., Carrillo J.D., Wang W., Camerer C.F. Imperfect Choice or Imperfect

Attention? Understanding Strategic Thinking in Private Information Games // Rev.

Econom. Studies. 2014. No. 81 (3). P. 944-970.

38.

Crawford V.P., Costa-Gomes M.A., Iriberri N. Structural Models of Nonequilibrium

Strategic Thinking: Theory, Evidence, and Applications // J. Econom. Literat. 2013.

No. 51 (1). P. 5-62.

39.

Fellner W. Competition among the Few. N.Y.: Knopf A. 1949.

40.

Korepanov V.O., Novikov D.A. The Reflexive Partitions Method in Models of

Collective Behavior and Control // Autom. Remote Control. 2012. Vol. 73. No. 8.

P. 1424-1441.

41.

Chkhartishvili A.G. Reflexive games: Transformation of Awareness Structure //

Autom. Remote Control. 2010. Vol. 71. No. 6. P. 1208-1216.

42.

Novikov D.A., Chkhartishvili A.G. Mathematical Models of Informational and

Strategic Reflexion: a Survey // Advances Syst. Sci. Appl. 2014. No. 3. P. 254-277.

43.

Chkhartishvili A.G., Korepanov V.O. Adding Informational Beliefs to the Players

Strategic Thinking Model // IFAC-PapersOnLine. 2016. No. 49 (32). P. 19-23.

44.

Алгазин Г.И., Алгазина Д.Г. Информационное равновесие в модели динамики

коллективного поведения на конкурентном рынке// УБС. 2016. № 64. С. 112-

136.

45.

Liu Y., Gao L., Guan J. Marketing Strategy of Price Competition and Product

Differentiation in Duopoly Enterprises with Asymmetric Information // Int. Conf.

Servic. Syst. Servic. Management, Proc. of ICSSSM’05. 2005. No. 1. (1499557).

Р. 665-668.

46.

Gilpatric S.M., Li Y. Information Value under Demand Uncertainty and Endogenous

Market Leadership // Econom. Inquiry. 2015. No. 53 (1). Р. 589-603.

47.

Филатов А.Ю. Неоднородность поведения фирм на олигопольном рынке: стра-

тегические фирмы и ценополучатели // Изв. Иркут. гос. ун-та. 2015. Т. 13.

С. 72—83.

48.

Geraskin M.I., Chkhartishvili A.G. Structural Modeling of Oligopoly Market under

the Nonlinear Functions of Demand and Agents’ Costs // Autom. Remote Control.

2017. Vol. 78. No. 2. P. 332-348.

49.

Geraskin M.I., Chkhartishvili A.G. Game-Theoretic Models of an Oligopoly Market

with Nonlinear Agent Cost Functions // Autom. Remote Control. 2017. Vol. 78.

No. 9. P. 1631-1650.

50.

Geraskin M.I. Modeling Reflexion in the Non-Linear Model of the Stakelberg Three-

Agent Oligopoly for the Russian Telecommunication Market// Autom. Remote

Control. 2018. Vol. 79. No. 5. P. 841-859.

155

51. Geraskin M.I. Game-theoretic analysis of Stackelberg oligopoly with arbitrary rank

reflexive behavior of agents // Kybernet. 2017. No. 46(6). P. 1052-1067.

52. Bresnahan T. Duopoly Models with Consistent Conjectures // Amer. Econom. Rev.

1981. 7 No. 1. P. 934-945.

53. Гераськин М.И., Бирюкова И.А. Анализ рефлексивной игры агентов на теле-

коммуникационном рынке для случая двух рефлексирующих агентов // Акту-

альные проблемы экономики и права. 2018. Т. 12 (3). С. 468-480.

54. Novikov D.A., Chkhartishvili A.G. Reflexion and Control: Mathematical Models.

London: CRC Press, 2014.

55. Intriligator M.D. Mathematical Optimization and Economic Theory. New Jersey.

Prentice-Hall. Englewood Cliffs. 1971.

56. Balash V., Sidorov S., Faizliev A. Analysis of news flow dynamics based on the

company co-mention network characteristics // Studies in Comput. Intelligence.

2019. No. 813. Р. 521-533.

57. Sidorov S.P., Faizliev A.R., Balash V.A. A long memory property of economic and

financial news flows // Int. J. Data Analysis Techniques Strategies. 2018. No. 10(4).

Р. 406-420.

Статья представлена к публикации членом редколлегии Д.А. Новиковым.

Поступила в редакцию 02.02.2018

После доработки 28.03.2019

Принята к публикации 18.07.2019

156