Автоматика и телемеханика, № 2, 2020

(Институт проблем управления им. В.А. Трапезникова РАН, Москва;

Математический институт им. В.А. Стеклова, РАН, Москва),

А.Н. СОЗОНТОВ, канд. биол. наук (a.n.sozontov@gmail.com)

(Институт экологии растений и животных УрО РАН, Екатеринбург)

О ДОВЕРИТЕЛЬНОМ ОЦЕНИВАНИИ НА ОСНОВЕ

КОЛИЧЕСТВЕННЫХ КОЭФФИЦИЕНТОВ СХОДСТВА¹

Рассматривается задача оценивания точности количественных коэф-

фициентов сходства. Для этого вводится новое понятие меры сходства

соответствующего коэффициента. Показано, что состоятельными оценка-

ми своих мер сходства являются только частотные формы количествен-

ных коэффициентов сходства. Получены асимптотические доверительные

интервалы для мер сходства Ружички и Брея-Кертиса на основе одно-

именных коэффициентов. Также предложен критерий однородности двух

совокупностей на основе упомянутых коэффициентов.

Ключевые слова: коэффициент сходства, доверительное оценивание, кри-

терий однородности, индекс Брея-Кертиса, индекс Жаккара.

DOI: 10.31857/S0005231020020105

1. Введение

Коэффициенты сходства (КС), изначально предложенные биологами, на-

шли широкое применение в химии, социологии, лингвистике, юриспруденции

и т.д., а также в методах работы с многомерными данными, в частности они

легли в основу некоторых форм кластерного анализа. В настоящее время

насчитывается от нескольких десятков до нескольких сотен КС (см., напри-

мер, [1]), однако статистическая теория, описывающая КС, практически не

развита. Так, при разных соотношениях между объемами выборок большин-

ство используемых количественных КС (определения см. далее), по сути, оце-

нивают различные величины, тогда как данные, используемые для построе-

ния качественных КС, часто бывают достаточно бедны, чтобы делать надеж-

ные статистические выводы. Существующие методы оценивания точности КС

либо основаны на чрезвычайно узких предположениях типа равномерной рас-

пределенности видов в совокупности (наиболее часто — для качественных

КС), либо вообще не носят строгого математического характера. Предприня-

то также несколько попыток построить бутстрепные доверительные интер-

валы для некоторых КС. В настоящей статье получены точные асимптоти-

ческие доверительные интервалы для наиболее популярных количественных

коэффициентов сходства Брея-Кертиса и Ружички и предложен критерий

проверки гипотезы однородности двух совокупностей на основе предыдуще-

го результата.

¹ Разделы 1 и 2 статьи выполнены И.В. Радионовым за счет гранта Российского науч-

ного фонда (проект № 19-11-00290) в Математическом институте им. В.А. Стеклова Рос-

сийской академии наук.

157

Пусть X и Y — два дескриптивных множества [2, 3], описывающие две

сравниваемые выборки, т.е. конечные множества видов (типов объектов) та-

кие, что каждому виду сопоставлено количество его попаданий в соответст-

вующую выборку. Иными словами, занумеруем виды, встретившиеся в двух

исследуемых выборках, числами от 1 до S и обозначим через X_i и Y_i коли-

чество объектов i-го вида в первой и второй выборках соответственно. Обо-

значим через a количество общих видов для двух сравниваемых множеств, а

через b и c — количество уникальных видов для первого и второго множества

соответственно:

∑

a= I(Xi =0,Yi =0), b= I(Xi =0,Yi =0), c= I(Xi =0,Yi =0).

i=1

Легко видеть, что S = a + b + c.

Коэффициентом, или индексом, сходства двух совокупностей C(X, Y ) бу-

дем называть безразмерный показатель, отражающий меру близости (сход-

ства) указанных совокупностей X и Y. Как правило, индексы сходства рас-

сматриваются для сравнения двух совокупностей, однако существуют методы

поиска сходства между тремя и более множествами одновременно [4, 5]. В на-

стоящей статье такие варианты сравнения и соответствующие им КС не рас-

сматриваются. Назовем КС качественным, если он зависит только от a, b и c,

т.е. на значения таких КС влияет только наличие/отсутствие вида в сравни-

ваемых совокупностях. Коэффициент сходства называется количественным,

если для его построения используются величины {X_i}Si=1 и {Y_i}Si=1. Количе-

ственные КС, зависящие только от частот X_i/n и Y_i/m, 1 ≤ i ≤ S, появлений

вида i в совокупностях X и Y соответственно, будем называть частотны-

∑_S

ми. Здесь n =

X_i и m =

Y_i. Для любого качественного КС мож-

i=1

но предложить его количественный аналог, заменив индикаторы I(X_i = 0),

I(Y_i = 0), i = 1, . . . , S, присутствия видов в совокупности на частоты X_i/n

и Y_i/m, 1 ≤ i ≤ S. Как будет показано далее, введение других количествен-

ных аналогов для качественных КС не оправдано со статистической точки

зрения.

Обсудим общие требования, которые, как правило, налагаются на индексы

сходства [6, 7]:

A1. Симметричность: C(X, Y ) = C(X, Y );

A2. Равенство нулю для непересекающихся совокупностей: C(X, Y ) = 0,

если a = 0;

A3. Равенство единице для совпадающих совокупностей: C(X, Y ) = 1, ес-

ли a = b = c для качественных КС и X_i/n = Y_i/m ∀i, 1 ≤ i ≤ S, для

частотных КС;

A4. “Монотонность” по величине сходства.

Для качественных индексов сходства, в частности, последнее свойство

означает следующее: если зафиксировать S и множество видов, то значе-

ние КС должно быть тем больше, чем больше значение a. Впрочем, далеко

не все индексы сходства удовлетворяют условиям A1-A4, см. [1]. Далее, опре-

делим также меру сходства μ качественного КС как величину, равную этому

158

КС в случае, если бы вместо выборок КС вычислялся по генеральным сово-

купностям, из которых взяты данные выборки. Ясно, что при росте разме-

ра выборок к бесконечности качественный КС будет сходиться к своей мере

сходства. Определим также меру сходства количественного КС как величи-

ну, получающуюся при замене X_i и Y_i в записи данного КС на вероятности

p_i и q_i появления i-го вида из первой и второй генеральной совокупности

соответственно. В разделе 2 будет показано, что количественные КС будут

состоятельными оценками своих мер сходства тогда и только тогда, когда они

являются частотными.

Необходимость сравнения множеств стояла перед биологами еще в XIX в.,

однако способы давать степени их (не)сходства количественную оценку по-

явились лишь в начале XX в. По-видимому, самый первый КС, I_J , который

до сих пор наиболее популярен среди индексов сходства, предложил швейцар-

ский ботаник Поль Жаккар [8]. По своей сути I_J есть отношение мощности

пересечения множеств видов в двух совокупностях к мощности их объедине-

ния,

I_J =

a+b+c

и является качественным коэффициентом сходства. Его количественный ана-

лог носит название коэффициента Ружички [9]

^S min(X_i, Y_i)

(1)

C_R =i=1

∑

max(X_i, Y_i)

i=1

Другой популярный КС был предложен практически одновременно

Л.Р. Дайсом в [10] и Т. Сёренсеном в [11]

I_DS =

2a + b + c

количественная форма которого была предложена задолго до них Чеканов-

ским в [12], она также известна под названием индекса Брея-Кертиса [13]

^S 2min(X_i,Y_i)

(2)

C_BC =i=1

∑

X_i + Y_i

i=1

Легко видеть, что индекс Жаккара выражается через индекс Сёренсена-

Дайса как I_J = I_DS /(2 - I_DS ). К настоящему времени предложены десятки

качественных КС. Наряду с индексами Жаккара и Сёренсена-Дайса наибо-

лее используемы индексы Охиаи I_O, Кульчинского I_K и Мориситы I_M , см. [7].

Все они монотонно возрастают от нуля до единицы в зависимости от количе-

ства общих видов и, по сути, отличаются лишь разной чувствительностью к

малым и большим значениям a по сравнению с S.

159

Впервые попытка оценить точность индексов сходства была предпринята

Сёренсеном в [11], однако его метод требует наличия не двух, а достаточ-

но большого количества выборок, что не всегда осуществимо. Немалое ко-

личество публикаций посвящено доверительному оцениванию качественной

меры сходства в предположении, что все виды в генеральной совокупности

распределены одинаково, см. [14-17], что, очевидно, никогда не выполняет-

ся на практике. Однако стоит отметить, что если имеются лишь данные о

наличии/отсутствии вида в выборках и отсутствуют сведения о количестве

объектов каждого из видов в совокупности, то выбор любого другого рас-

пределения не является обоснованным. Кроме того, величины a, b и c сильно

зависят от наличия редко встречающихся видов в выборке. При росте количе-

ства наблюдений соотношения между a, b и c могут существенно измениться,

что препятствует точности статистического анализа качественных КС при

малом и среднем количестве наблюдений. В связи с доверительным оценива-

нием качественной меры сходства отметим также публикацию [18], где пред-

полагается, что распределение видов в генеральной совокупности является

дискретным логнормальным, и публикацию [19], где принято предположе-

ние, что один доминантный вид встречается чаще остальных, которые уже

имеют равную вероятность попадания в выборку.

Для построения доверительных интервалов для качественных мер сход-

ства может быть полезен основанный на бутстрепе метод оценивания коли-

чества видов в генеральной совокупности по выборке из нее, развитый Чао в

[20-22]. Так, в [22] в предположении, что индекс Жаккара меньше своей меры

сходства, предложен доверительный интервал для меры сходства I_J , впрочем,

без какого-либо математического обоснования. Несмотря на перспективность

метода, Чао не удалось построить доверительный интервал для какого-либо

качественного КС в общих предположениях. Авторам данной статьи неиз-

вестны работы, где была бы рассмотрена задача построения доверительных

интервалов для мер сходства на основе количественных КС.

2. Основные результаты

2.1. Статистическая корректность количественных КС

Прежде всего покажем на основе индекса сходства Ружички (1), что коли-

чественные КС являются состоятельными оценками своих мер сходства толь-

ко в случае n/m → 1 при n, m → ∞, где n и m, напомним, — размеры первой

и второй совокупности соответственно. Рассмотрим в рамках исследуемой

задачи две полиномиальных модели: в j-м испытании независимо от других

испытаний появляется по одному объекту из каждой генеральной совокупно-

сти согласно распределениям вероятностей {p_i}i≥1 и {q_i}i≥1 соответственно,

т.е. в j-м испытании i-й объект выпадает с вероятностями p_i и q_i для первой

и второй группы соответственно. Обозначим случайные величины, соответ-

ствующие выпадению объекта определенного вида в первой и второй группе

в j-м испытании как ξ_j и η_j. Таким образом, имеем

∑

X_i = I(ξ_j = i), Y_i =

I(η_j = i).

j=1

160

Тогда поскольку {I(ξ_j = i)}j≥1 и {I(η_j = i)}j≥1 — последовательности неза-

висимых одинаково распределенных случайных величин, то по усиленному

закону больших чисел

X_i

п.н.

--→ EI(ξ_j = i) = P (ξ_j = i) = p_i,

(3)

Y_i

п.н.

--→ q_i (п.н. — почти наверное)

при n, m → ∞.

Вернемся к обсуждению индекса Ружички. Его мера сходства, очевидно,

равна

^S min(p_i,q_i)

μ_R =i=1

∑

max(p_i, q_i)

i=1

Тогда при использовании теоремы о наследовании сходимостей, свойств схо-

димости почти наверное и соотношений (3) в случае n/m → 1 при n, m → ∞

элементарно показывается, что

(

)

X_i

min

m n

п.н.

C_R

= i⁼¹

--→ μ_R.

^∑ max⁽Xi_n , Yi m⁾

m n

i=1

С другой стороны, при n/m = d, n, m → ∞ индекс Ружички почти навер-

ное сходится к величине

^S min(dp_i, q_i)

μ_R(d) =i=1

∑

max(dp_i, q_i)

i=1

отличной при d = 1 от μ_R, тогда как частотный аналог данного индекса

(

)

X_i

min

(4)

C^′R

= i⁼¹

^∑ max ⁽Xi_n , Yi)m

i=1

сходится почти наверное к μ_R в независимости от соотношения между m и n.

Аналогичные рассуждения справедливы и для индекса Брея-Кертиса (2),

и для других количественных индексов сходства, которые не являются ча-

стотными. Тем самым выводы о генеральной совокупности, полученные на

основе количественных КС, не являющихся частотными, не могут считаться

достоверными и статистически корректными.

161

2.2. Асимптотическая нормальность количественных КС

Рассмотрим индекс сходства Ружички и построим доверительный интер-

вал для его меры сходства. Преобразуем данный индекс следующим образом:

∑

min(X_i,Y_i)

n+m-

max(X_i, Y_i)

i=1

n+m

(5)

C_R =i=1

− 1,

∑

max(X_i, Y_i)

i=1

∑_S

т.е. фактически индекс Ружички зависит только от

max(X_i, Y_i).

i=1

Предположим сначала, что n = m. Пусть p_i > q_i, тогда при n → ∞ вы-

полнено, что P (X_i > Y_i) → 1 и P (max(X_i, Y_i) = X_i) → 1, т.е. при больших n

выпадение i-го объекта для второй совокупности не будет влиять на значе-

ние индекса Ружички с вероятностью, близкой к единице. Определим A как

множество номеров i, таких что p_i > q_i, A = {i : p_i ≥ q_i}, и B = {i : q_i > p_i}.

Определим также

∑

P = p_i, Q= q_i.

i∈A

i∈B

Тогда мера сходства индекса Ружички переписывается в виде

∑

max(p_i, q_i)

μ_R

= i⁼¹

- 1.

∑

P +Q

max(p_i, q_i)

i=1

Теорема. Пусть n = m. Тогда при n → ∞

→N (0,V_R),

где

4(P (1 - P ) + Q(1 - Q))

V_R =

(P + Q)⁴

Доказательство теоремы. Определим

ζ_j = I(ξ_j = i,i ∈ A) + I(η_j = i,i ∈ B),j ≥ 1.

Эти случайные величины, очевидно, могут принимать значения 0, 1 и 2. За-

метим, что поскольку по условию количество видов S конечно, то

(

)

∑

(6)

max(X_i, Y_i) =

X_i + Y_i

→1

i=1

i∈A

i∈B

162

при n → ∞. С другой стороны,

∑

∑∑

X_i + Y_i =

I(ξ_j = i) +

I(η_j = i) =

i∈A

i∈B

i∈A j=1

i∈B j=1

∑

(7)

= (I(ξ_j = i, i ∈ A) + I(η_j = i, i ∈ B)) = ζ_j =: T_n.

j=1

Тем самым для доказательства теоремы достаточно показать, что при n → ∞

)

(

)

⁽⁽2n

4(P (1 - P ) + Q(1 - Q))

(8)

√n

-1

-μ_R

→N

T_n

(P + Q)⁴

(

))

√

(9)

n C_R -

-1

→ 0,

T_n

где статистика 2n/T_n - 1 получена подстановкой суммы T_n в выражение (5)

∑_S

вместо

max(X_i, Y_i), и воспользоваться леммой Слуцкого.

i=1

Докажем сначала соотношение (8). Заметим, что {ζ_j}nj=1 — независимые

одинаково распределенные случайные величины, и найдем Eζ₁ и V arζ₁. Име-

ем, что

Eζ₁ = EI(ξ₁ = i,i ∈ A) + EI(η₁ = i,i ∈ B) =

∑

= P(ξ₁ = i) + P(η₁ = i) = p_i + q_i = P + Q,

i∈A

i∈B

i∈A

i∈B

V arζ₁ = V arI(ξ₁ = i, i ∈ A) + V arI(η₁ = i, i ∈ B) = P (1 - P ) + Q(1 - Q).

Из центральной предельной теоремы получаем, что

⎛

⎞

∑

→ N (0,P(1 - P) + Q(1 - Q)), n → ∞.

j=1

Применяя дельта-метод для функции g(x) = 2/x, находим, что

⎛

⎞

(

)

⎟

4(P (1 - P ) + Q(1 - Q))

√n⎜2n

⎟

→N

, n → ∞,

∑

P +Q⎠

(P + Q)⁴

ζ_j

j=1

откуда и следует соотношение (8).

Докажем теперь соотношение (9). Используя (6) и (7), получаем при

n → ∞, что

⎞

⎛∑

^S max(X_i,Y_i)

⎟

i=1

T_n⎟

(10)

√n^⎜

⎟

→ 0.

⎝

⎠

163

Поскольку по закону больших чисел T_n/n → P + Q по вероятности при

∑_S

n → ∞, то из соотношения

(10) следует, что

max(X_i, Y_i)/n так-

i=1

же стремится по вероятности к P + Q. Разделив левую часть (10) на

∑_S

Tni=1 max(X_i,Y_i)/(2n²), имеем по лемме Слуцкого, что

⎛

⎞

⎟

√n⎜2n

⎟

→ 0,

⎝T_n

∑

⎠

max(X_i, Y_i)

i=1

откуда и следует (9). Тем самым, доказательство теоремы закончено.

Обратимся теперь к изучению частотного аналога индекса Ружич-

ки C^′R (4). Следующее утверждение говорит, что асимптотическое поведе-

ние C^′R несколько отличается от асимптотического поведения индекса Ру-

жички при n = m → ∞.

Предложение 1. При n,m → ∞ и n/m → d > 0 выполнено, что

→N (0,V_R(d)),

где

4(P (1 - P ) + dQ(1 - Q))

V_R(d) =

(P + Q)⁴

∑

Доказательство предложения 1. Пользуясь тем, чтоi∈A X_i и

∑

Y_i представимы как суммы независимых одинаково распределенных

i∈B

случайных величин и независимы, из центральной предельной теоремы по-

лучаем, что

(

)

1^∑

√n

→ N(0,P(1 - P))

i∈A

(

)

1^∑

√m

→N(0,Q(1 - Q))

i∈B

при n → ∞ и m → ∞ соответственно, откуда в условиях предложения с по-

мощью леммы Слуцкого имеем, что

(

)

1^∑

(11)

√n

X_i +

→ N(0,(P(1 - P) + dQ(1 - Q))).

i∈A

i∈B

Дальнейшее доказательство повторяет с легкими изменениями соответствую-

щие шаги доказательства теоремы.

164

Рассмотрим теперь частотную форму индекса Брея-Кертиса (2),

∑

C^′BC = min(X_i/n,Y_i/m) = 2 - max(X_i/n,Y_i/m),

i=1

и исследуем ее асимптотическое поведение. Стоит за √тить, что частотная

форма широко используемого индекса Охиаи I_O = a/

(a + b)(a + c) также

равна C^′BC . Из соотношения (11) и из модификации формулы (10) для n = m

вытекает следующее утверждение.

Предложение 2. В условиях предложения 1 выполнено, что

→N (0,V_BC(d)),

где μ_BC = (2 - P - Q) — мера сходства Брея-Кертиса и V_BC (d) = P (1 - P )+

+dQ(1 - Q).

2.3. Доверительное оценивание количественных мер сходства

Чтобы построить доверительные интервалы для мер сходства Ружич-

ки и Брея-Кертиса, необходимо оценить асимптотическую дисперсию од-

ноименных частотных КС. Рассмотрим случайное множество номеров

A^′ = {i : X_i/n > Y_i/m}. Покажем, что

1^∑

P :=

−→ P,

^Q :=1∑

→ Q, n,m → ∞.

i∈A^′

Действительно,

)

(∑

∑

X_i = X_i

≤ P(X_i/n < Y_i/m) + P(X_i/n ≥ Y_i/m) → 0

i∈A^′

i∈A

i∈B

по закону больших чисел. Снова пользуясь законом больших чисел и свой-

ствами сходимости по вероятности, имеем, что

(

)

1^∑

P =

X_i -

X_i

−→ P, n, m → ∞,

i∈A^′

i∈A

а сходимость^Q к Q по вероятности доказывается аналогично.

Используя теорему о наследовании сходимостей и свойства сходимости по

вероятности, легко показать, что при n, m → ∞ и n/m → d выполнено, что

P (1

P) + n Q(1 - Q)/m)

R(d) :=

→V_R(d),

P +^Q)⁴

BC(d) :

P (1

→V_BC(d).

165

Тем самым из леммы Слуцкого в тех же условиях получаем, что

√n(

→N(0,1) и

(12)

√n(V

→ N(0,1),

что позволяет выписать асимптотические доверительные интервалы для мер

сходства Ружички и Брея-Кертиса: с вероятностью, стремящейся к 1 - α,

мера сходства Ружички принадлежит интервалу

(

)

C^′R - u1-α/2(

R(d))1/2n-1/2; C^R + u1-α/2(

(d))1/2n-1/2 ,

где u1-α/2 — квантиль уровня 1 - α/2 стандартного нормального распреде-

ления; доверительный интервал для меры сходства Брея-Кертиса выписыва-

ется аналогично.

2.4. Проверка гипотезы однородности с помощью КС

Наконец, рассмотрим задачу проверки гипотезы об однородности срав-

ниваемых совокупностей. На первый взгляд, применение двухвыборочного

критерия хи-квадрат Пирсона решает данную задачу, однако критерий име-

ет определенные условия применимости, которым получаемые на практике

совокупности не всегда удовлетворяют. Так, часто в сравниваемых группах

видов бывает несколько доминирующих видов, а все остальные виды встреча-

ются в количестве 1-2 экземпляров, что препятствует прямому применению

критерия хи-квадрат. С другой стороны, проверить гипотезу однородности

двух совокупностей при помощи коэффициентов сходства можно всегда.

Итак, будем проверять гипотезу H₀ : μ_R = 1. В случае совпадающих ге-

неральных совокупностей мера сходства двух этих совокупностей равняется

единице, если для соответствующего КС выполнено свойство A3, поэтому

вместо μ_R в определение гипотезы можно подставить любую другую меру

сходства, количественную или качественную, для которой выполняется дан-

ное свойство. Построим критерий проверки H₀ с помощью частотного ин-

декса Ружички C^′R. Поскольку данный индекс всегда меньше либо равен 1,

предложим такой критерий:

если C^′R + u1-α(

R(d))1/2n-1/2 < 1, то отвергаем H0,

где u1-α — (1 - α)-квантиль N(0, 1). Из (12) следует, что данный критерий

будет иметь асимптотический уровень значимости α. С помощью частотного

индекса Брея-Кертиса C^′BC аналогичным образом можно предложить еще

один критерий проверки H₀ :

(13)

если C^′BC + u1-α(V

BC(d))1/2n-1/2 < 1, то отвергаем H0,

он также имеет асимптотический уровень значимости α.

166

3. Моделирование

Цель данного раздела — демонстрация асимптотических свойств предло-

женных доверительных интервалов и критериев однородности, основанных

на КС. Рассмотрим сначала задачу доверительного оценивания меры сход-

ства Брея-Кертиса двух генеральных совокупностей c 10 видами в каждой,

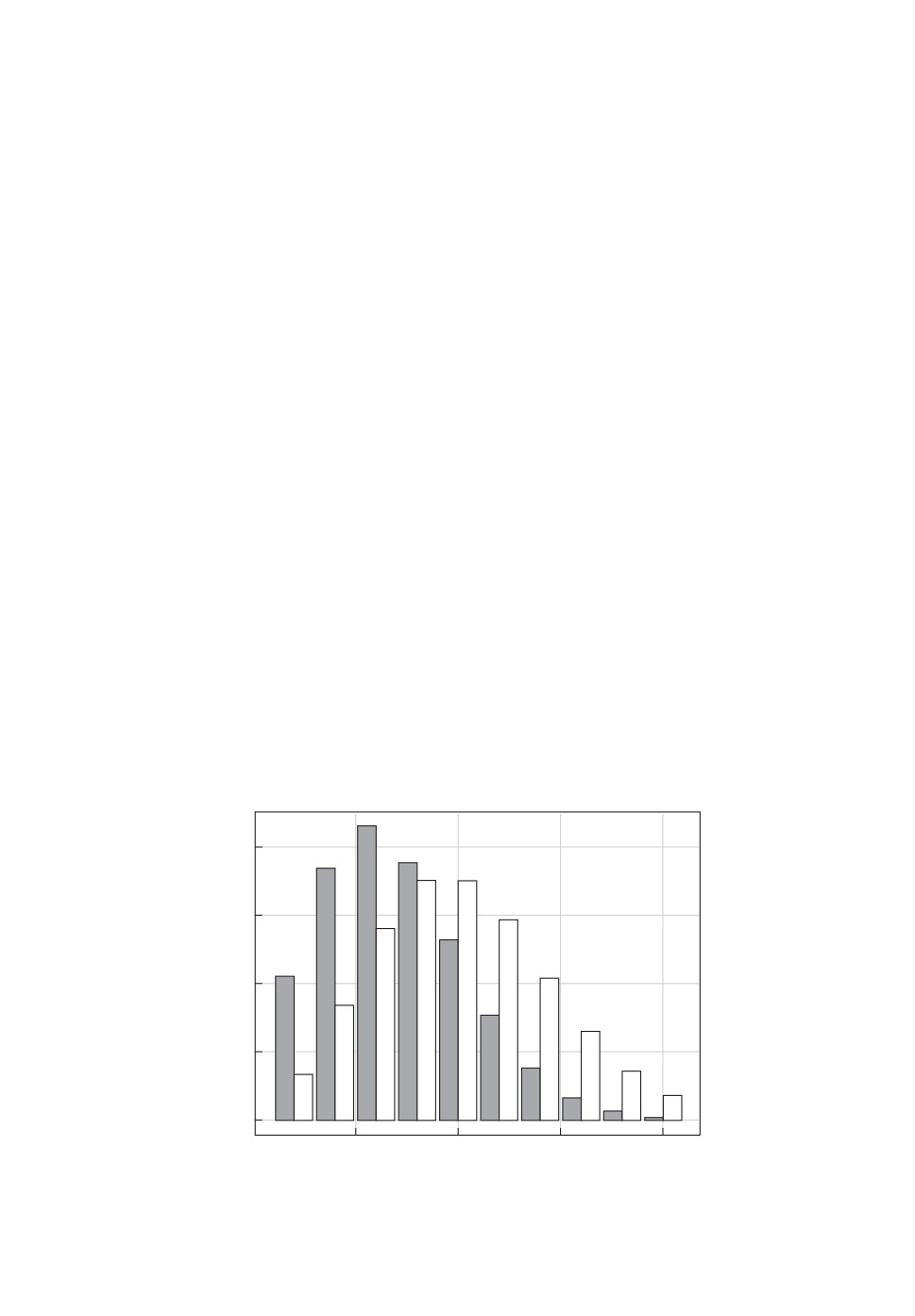
подчиняющихся распределениям {p_i}10i=1 и {q_i}10i=1 соответственно. Для моде-

лирования были выбраны усеченные распределения Пуассона с параметра-

ми 3,5 (темные столбцы) и 5 (светлые столбцы) соответственно, гистограммы

соответствующих распределений P = {p_i}10i=1 и Q = {q_i}10i=1 представлены на

рис. 1.

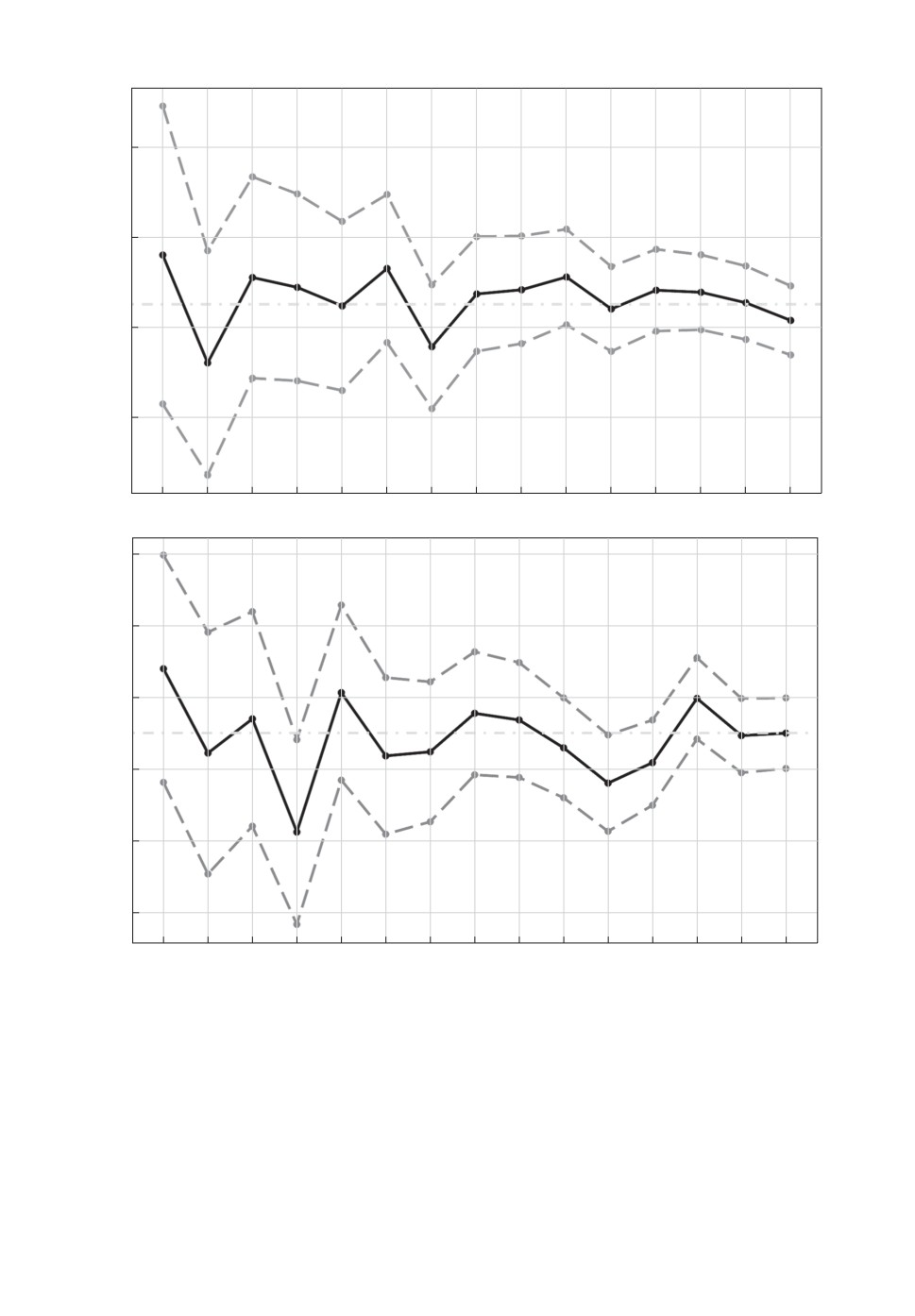
На рис. 2 выведены графики верхней и нижней границ доверительных

интервалов (штриховые линии) уровня доверия α = 0,95 для меры сходства

Брея-Кертиса распределений P и Q и график значений частотного индекса

сходства Брея-Кертиса C^′BC (сплошная линия) в зависимости от n. На ри-

сунке слева n = 2m, на рисунке справа n = m/3. Истинное значение меры

Брея-Кертиса для данных распределений равно μ_BC = 0,76 с точностью до

третьего знака после запятой (штрихпунктирная линия).

Легко видеть, что построенные доверительные интервалы по своему по-

ведению мало отличаются от асимптотических доверительных интервалов,

построенных на основе стандартного условия асимптотической нормальности

оценки. В частности, при возрастании размеров выборок ширина доверитель-

ных интервалов уменьшается, а истинное значение меры сходства практиче-

ски всегда попадает в доверительный интервал.

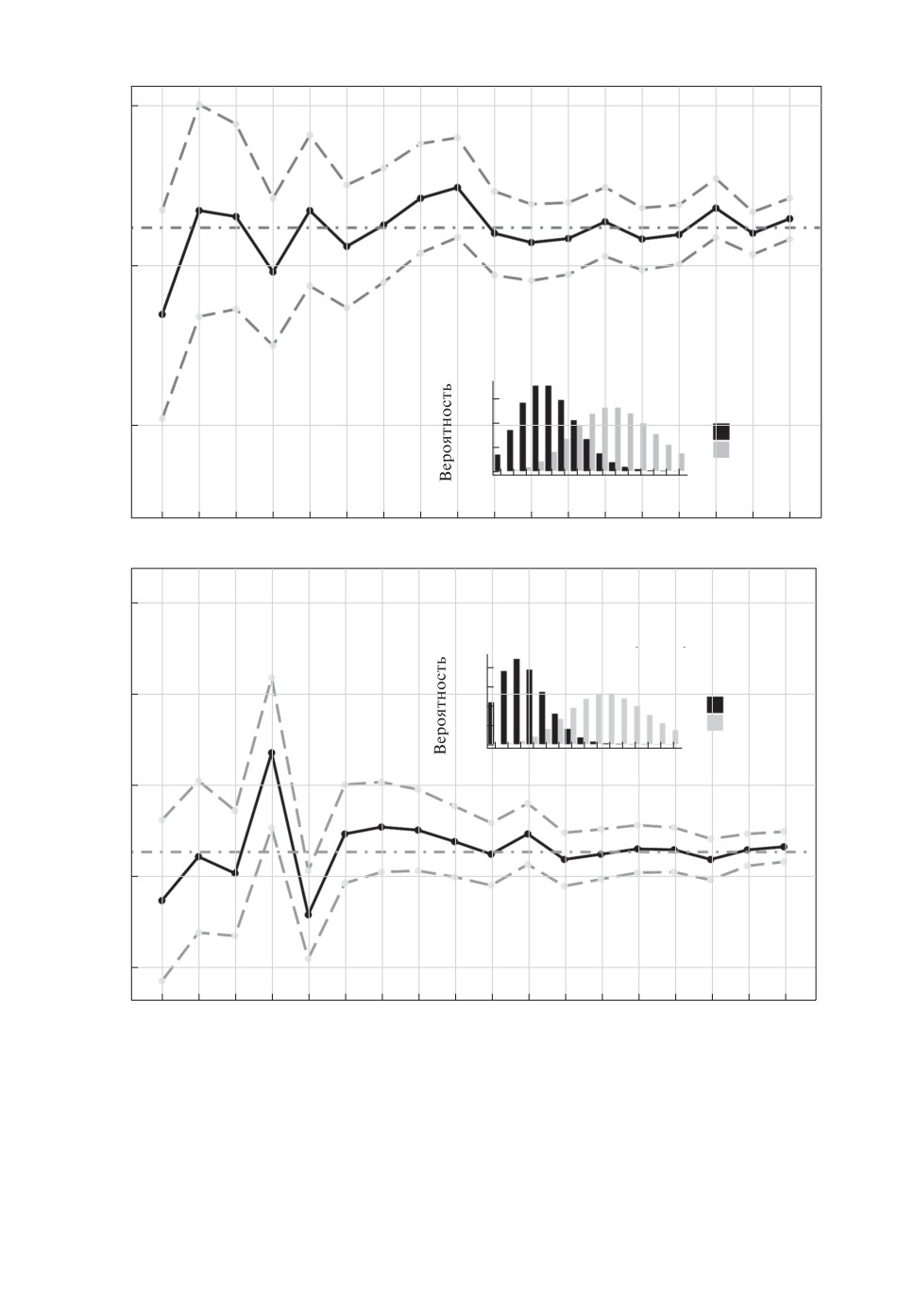
Приведенные на рис. 3 графики доверительных границ для меры сходства

Ружички обладают теми же свойствами, что и доверительные границы для

меры сходства Брея-Кертиса. Здесь доверительные границы и сами значе-

ния частотного коэффициента Ружички C^′R построены для двух разных пар

0,20

0,15

0,10

0,05

Рис. 1. Гистограмма распределений {p_i}10i=1 (темные столбцы для λ = 3,5)

и {q_i}10i=1 (светлые столбцы для λ = 5).

167

0,9

0,8

0,7

0,6

100

150

200

250

300

400

500

600

750

900

1050 1200 1400 1600 1800

0,85

0,80

0,75

0,70

0,65

0,60

100

150

200

250

300

400

500

600

750

900

1050 1200 1400 1600 1800

Рис. 2. Доверительные границы для меры сходства Брея-Кертиса

и значение частотного индекса Брея-Кертиса в зависимости от n

(а — n = 2m, б — n = m/3).

дискретных распределений, гистограммы которых выведены на соответст-

вующих графиках, в зависимости от n при n = m.

Наконец, обратимся к задаче проверки однородности двух совокупностей с

помощью коэффициентов сходства. На рис. 4 представлена верхняя граница

из критерия (13) при α = 0,025 (штриховая линия) для меры сходства Брея-

168

0,3

0,2

Гистограмма

аспр

еделений {pi} и {qi}

0,15

0,1

0,10

= 5)

0,05

= 10)

100 150 200 250 300 400 500 600 750 900 1050 1200 1400 1600

1800

200035004000

0,25

Гистограмма

аспределений

{p_i} и {qi}

,20

,15

0,20

,10

= 3

.5)

,05

= 1

0,15

0,10

0,05

100 150 200 250 300 400 500 600 750 900 1050120014001600

1800

200035004000

Рис. 3. Доверительные границы для меры сходства Ружички и значения ча-

стотного индекса Ружички для выборок X и Y из усеченных распределений

Пуассона с параметрами а - (5, 10) и б - (3,5, 10) в зависимости от n, m = n.

Кертиса (равной в данном случае единице) для выборок из одной генеральной

совокупности из 10 видов в зависимости от n при n = m, гистограмму распре-

деления тоже см. на рисунке. Также на графике выведена нижняя граница

169

1,0

0,9

Гистог

рамма рас

пределения

0,2

0,1

0,8

0,1

0,0

100

200

500

1000

2000

5000

10 000

50 000

Рис. 4. Доверительные границы для меры сходства Брея-Кертиса в зависи-

мости от n в случае выборок из одной генеральной совокупности.

симметричного доверительного интервала (т.е. уровень доверия данного ин-

тервала равен 0,95) и значения частотного индекса Брея-Кертиса (сплошная

линия), с помощью которого и построены данные доверительные интервалы.

Заметим, что доверительные интервалы для разных значений n не всегда

содержат единицу, т.е. при малых n теоретический уровень значимости кри-

терия (13), по-видимому, является заниженным. Это связано с тем, что в

данном случае коэффициент сходства Брея-Кертиса всегда ниже своей меры

сходства из-за особенностей определения КС.

4. Заключение

В статье рассмотрена проблема оценивания точности количественных ко-

эффициентов сходства. Исчерпывающий обзор публикаций, касающихся этой

темы, показал, что до сих пор не было предложено удовлетворительного ал-

горитма, имеющего строгое обоснование, позволяющего найти границы до-

верительного интервала для меры сходства какого-либо КС и/или оценить

его дисперсию. В настоящей статье авторы предлагают способ построения

асимптотических доверительных интервалов для мер сходства двух наиболее

часто применяемых КС — Брея-Кертиса и Ружички. Используя приведенный

метод, можно получить доверительные интервалы для мер сходства любых

других частотных КС. Остаются открытыми вопросы о степени чувствитель-

ности различных КС и о взаимоотношении асимптотических и бутстрепных

доверительных интервалов, которые будут рассмотрены авторами в дальней-

шем.

170

СПИСОК ЛИТЕРАТУРЫ

Cha S.-H. Comprehensive Survey on Distance/Similarity Measures between

Probability Density Functions // Int. J. Math. Model. Meth. Appl. Sci. 2007. V. 1.

No. 4. P. 300-307.

Семкин Б.И. Дескриптивные множества и их приложения // Исследования си-

стем. 1. Сложные системы. Владивосток: 1973. С. 83-94.

Semkin B.I. The Axiomatic Approach to Introducing Measures for Ordering and

Classification of Descriptive Sets // Patt. Recogn. Image Anal. 2011. V. 21. No. 2.

P. 164-166.

Diserud O.H., Ødegaard F. A Multiple-Site Similarity Measures // Biol. Lett. 2007.

V. 3. No. 1. P. 20-22.

Baselga A., Jimenez-Valverde A., Niccolini G. A Multiple-Site Similarity Measure

Independent of Richness // Biol. Lett. 2007. V. 3. No. 6. P. 642-645.

Cheetham A.H., Hazel J.E. Binary (Presence-Absence) Similarity Coefficients //

J. Paleontol. 1969. V. 43. No. 5. P. 1130-1136.

Песенко Ю.А. Принципы и методы количественного анализа в фаунистических

исследованиях. М.: Наука, 1982.

Jaccard P. Distribution de la flore alpine dans le bassin des Dranses et dans quelques

régions voisines // Bulletin de la Société Vaudoise des Sciences Naturelles. 1901.

V. 37. P. 241-272.

Ružička M. Anwendung mathematisch-statistischer Methoden in der Geobotanik

(Synthetische Bearbeitung von Aufnahmen) // Biológia, Bratisl. 1958. V.

13.

P. 647-661.

10.

Dice L.R. Measures of the Amount of Ecologic Association between Species //

Ecology. 1945. V. 26. No. 3. P. 297-302.

11.

Sörensen T. A method of establishing groups of equal amplitude in plant sociology

based on similarity of species content // Kongelige Danske Videnskabernes Selskab.

Biol. krifter. 1948. Bd V. No. 4. P. 1-34.

12.

Czekanowski J. Zur differential Diagnose der Neandertalgruppe // Korrespbl. Dtsch.

Ges. Anthropol. 1909. Bd 40. S. 44-47.

13.

Bray J.R., Curtis J.T. An Ordination of Upland Forest Communities of Southern

Wisconsin // Ecol. Monogr. 1957. V. 27. P. 325-349.

14.

Glime J.M., Clemons R.M. Species Diversity of Stream Insects on Fontinalis Spp.

Compared to Diversity on Artificial Substrates // Ecology. 1972. V. 53. No. 3.

P. 458-464.

15.

Li X., Dubes R.C. A Probabilistic Measure of Similarity for Binary Data in Pattern

Recognition // Patt. Recogn. 1989. V. 22. No. 4. P. 397-409.

16.

Bolton H.C. On the Mathematical Significance of the Similarity Index of Ochiai as

a Measure for Biogeographical Habitats // Aust. J. Zool. 1991. V. 39. P. 143-156.

17.

Baroni-Urbani C., Buser M.W. Similarity of Binary Data // Syst. Zool. 1976. V. 25.

No. 3. P. 251-259.

18.

Engen S., Grøtan V., Sæther B.-E. Estimating Similarity of Communities:

a Parametric Approach to Spatio-Temporal Analysis of Species Diversity //

Ecography. 2011. V. 34. No. 2. P. 220-231.

19.

McCormick W.P., Lyons N.I., Hutcheson K. Distributional Properties of Jaccard’s

Index of Similarity // Commun. Statist. Theor. Meth. 1992. V. 21. No.

P. 51-68.

171