Автоматика и телемеханика, № 4, 2020

Управление в технических системах

(Ереванский государственный университет)

УПРАВЛЯЕМЫЙ ДИНАМИЧЕСКИЙ ПОИСК ПОДВИЖНОГО

ОБЪЕКТА ПРИ МИНИМАЛЬНЫХ ЗАТРАТАХ СВЕТОВОЙ ЭНЕРГИИ¹

Рассматривается задача оптимального управления пространственным

движением динамического объекта с целью поиска подвижного объек-

та, совершающего простое движение в прямоугольной области на плоско-

сти. В качестве критерия оптимальности рассматривается функционал,

учитывающий энергозатрату источника света, расположенного на ищу-

щем объекте. Искомый объект считается обнаруженным при попадании в

световой квадрат заданной освещенности. Предложен способ управления

движением ищущего объекта, а также соответствующий закон изменения

электрического тока в цепи источника света, обеспечивающие обнаруже-

ние искомого объекта за гарантированное время поиска при минимальной

световой энергозатрате.

Ключевые слова: динамический поиск, подвижной объект, оптимальное

управление, световая энергозатрата.

DOI: 10.31857/S000523102004008X

1. Введение

Во многих задачах поиска целевого объекта обнаружение осуществляется

с помощью информационной области чувствительности [1]. В качестве тако-

вой можно рассматривать освещенную источником света область, которую

можно перемещать в пространстве с целью обнаружения искомого объекта

при его попадании в эту область [2]. В случае подвижного искомого объекта

в ограниченной области для решения задачи поиска применяется подход [3],

состоящий в построении управлений, при которых, двигаясь по соответствую-

щим траекториям, ищущий объект осуществляет просмотр, заметая полосы,

покрывающие всю область поиска. При определенных условиях на параметры

поисковой системы такой подход выделяет множество управлений, гаранти-

рующих успешное завершение поиска целевого объекта как подвижного [4, 5],

так и неподвижного [6, 7]. В связи с этим целесообразно рассматривать зада-

чу об оптимальном выборе гарантирующего управления. В качестве критерия

оптимальности рассматривается функционал, учитывающий энергозатрату

электрического точечного источника света, расположенного на ищущем объ-

екте [2]. В отличие от [1-7] в настоящей работе ищущий объект управляется

¹ Работа выполнена при финансовой поддержке Госкомитета по науке МОН РА, грант

№ 18Т-2С127.

110

по ускорению, а областью освещения является квадрат. Предложен способ

управления движением ищущего объекта и закон изменения электрического

тока в цепи источника света, при которых искомый объект обнаруживает-

ся за гарантированное время поиска с минимальным потреблением световой

энергии.

2. Постановка задачи

Рассматривается система из двух управляемых точечных объектов X

(ищущего) и Y (искомого), движение которых описывается следующими

уравнениями, начальными условиями и ограничениями:

X: x₁ =w₁,

x₂ = w₂,

x₃ = w₃ - g, x_i(0) = x0i,

x_i(0) = 0, i = 1,2,3,

(2.1)

|w₁(t)| ≤ W,

|w₂(t)| ≤ W,

|w₃(t)| ≤ W₃, W₃

> g,

x(t) ∈ D⁽³⁾ = {(x₁, x₂, x₃) :

0 ≤ x_i ≤ a_i, i = 1,2,3}, t ≥ 0,

√

Y :

y_i = v_i, y_i(0) = y0i,

v²¹ + v²² ≤ V, i = 1,2,

(2.2)

y(t) ∈ D⁽²⁾ = {(x₁, x₂) : 0 ≤ x_i ≤ a_i, i = 1, 2}, t ≥ 0,

где x_i, yi - координаты положения объектов X, Y ; wi и vi - компоненты

векторов управляющего ускорения w и управляющей скорости v объектов X

и Y соответственно, которые являются кусочно-непрерывными функциями

от времени; W , W₃, V , a_i - заданные постоянные, g - ускорение свободного

падения.

Наличие ограничений на компоненты управляющего ускорения в (2.1) вы-

звано тем, что на практике, в робототехнике, многие управляемые манипуля-

ционные системы [8] работают в трех взаимно перпендикулярных направле-

ниях и управление движением по отдельным направлениям осуществляется

тремя независимыми двигателями. Каждый двигатель создает ограниченное

силовое воздействие, порождающее ограниченное по абсолютной величине

ускорение, которое управляет движением по соответствующей координате.

Пусть объекту X в процессе движения доступна полная информация о со-

отношениях и параметрах (2.1), (2.2) за исключением начальных координат

y_i(0) = y0i и текущeй скорости v(t) объекта Y . Предположим, что для опреде-

ления точных координат Y у объекта X имеется специальное устройство в ви-

де четырехугольной правильной пирамиды, на вершине которой расположен

изотропный точечный источник света. Излучаемые из источника световые

лучи ограничиваются внутри пирамиды, вследствие чего на горизонтальной

плоскости поиска образуется подвижная и изменяющийся по размеру область

освещенности следующего вида:

{

√ }

K(x(t)) = (ζ₁, ζ₂) ∈ D⁽²⁾ : |ζ1,2 - x1,2(t)| ≤ l = Cx3(t), C = tg γ/

(2.3)

x(t) ∈ D⁽³⁾.

Область(2.3) - квадрат с центром в точке O(x₁(t), x₂(t)) ∈ D⁽²⁾ и сo сто-

роной длины 2l; γ, 0 < γ < π/2 - половина угла раствора световых лучей,

111

x₃

O l

Рис. 1. Пирамида с квадратным основанием освещенности.

исходящих из точечного источника и образующих противоположные ребра

лучевой пирамиды (рис. 1).

Скажем, что положение искомого объекта Y становится точно известным

в момент времени t > 0, когда впервые выполняется условие обнаружения,

т.е. условие его попадания в квадрат освещенности

(2.4)

y(t) ∈ K(x(t)).

Искомый объект при попадании его в световой квадрат (2.3) может быть

обнаружен или распознан только при достаточной постоянной освещенно-

сти E, xарактеризующей пороговое значение видимости искомого объекта.

В случае (2.3) минимальная достаточная освещенность определяется сле-

дующим образом. Согласно [9] освещенность в определенной точке на плос-

кости вычисляется по формуле

(2.5)

E_P = I cos γ/(SP)²,

где I - сила света источника S в направлении точки измерения P на плоско-

сти, SP - расстояние между источником света и этой точкой, γ - угол между

направлением падения света и перпендикуляром к этой плоскости.

Из (2.5) следует, что для квадратной области (2.3) при заданных x₃ и γ

освещенность максимальна в наиболее близкой к источнику точке, в центре

квадрата: E_O = E_max = I/x²³ и минимальна в наиболее удаленных, в угловых

точках квадрата:

(2.6)

E = E_min = ξI/x²³, ξ = cos³

γ.

Величину E = E_min (2.6) будем считать постоянной и заданной.

Используя соотношение Q = ηI [9], где η - коэффициент пропорциональ-

ности (коэффициент удельной мощности) между мощностью световой энер-

гии Q, которую можно считать равной электрической мощности потребляе-

мой источником света, и силой света I, величину минимальной освещенно-

сти E (2.6) можно вычислять как мощность энергии светового излучения,

112

падающего на плоскость:

(2.7)

E = ξI/x²³ = ξQ/ηx²³.

Из (2.7) имеем

(2.8)

Q=Eηx²³

/ξ.

Интеграл от этой функции при постоянных E, η, ξ

∫T

∫

(2.9)

J = Qdt = Eηξ-1 x²³

дает величину потребляемой энергии источником света в течение промежут-

ка времени освещения [0, T ]. Функционал (2.9) характеризует энергозатраты

в процессе поиска световым устройством и в соответствии с (2.1) является

функцией от w₃.

Согласно закону Джоуля - Ленца величину электрической энергии, по-

требляемой источником света в течение времени [0, T ] освещения, можно вы-

разить следующим образом:

∫T

∫

(2.10)

J = Qdt = j²Rdt, Q = j²R,

0 ≤ j(t) ≤ j₀

t ∈ [0, T],

где j - действующее значение тока, проходящего через источник света, j₀ -

максимально допустимое действующее значение тока, а R - активное сопро-

тивление в цепи источника света.

Из (2.8), (2.10) получаем зависимость действующего значения электриче-

ского тока j от расстояния x₃ точечного источника света до центра светового

квадрата:

√

j(t) =

Eηξ-1R-1x₃(t), x₃(t) > 0,

(

)

√

(2.11)

0 ≤ j(t) ≤ min j₀,

Eηξ-1R-1a₃

t ∈ [0, T].

Соотношение (2.11) с учетом третьего уравнения (2.1) определяет связь

между управляющей функцией w₃ = w₃(t) и j = j(t).

Замечание. Так как область поиска в (2.2) имеет форму прямоуголь-

ника D⁽²⁾, то рассмотрение квадрата (2.3) в качестве области обнаружения

(освещенности) с практической точки зрения представляется естественным.

Такой выбор в отличие от кругa обнаружения, рассмотренного например

в [2-5], оправдан тем, что перемещение квадрата освещенности внутри обла-

сти поиска - прямоугольника по прямолинейным траекториям, параллель-

ным сторонам прямоугольника, позволяет ищущему объекту осуществить

просмотр, заметая при этом полосы, покрывающие всю область поиска без

зазоров.

113

В связи с вышесказанным в качестве допустимых управлений для ищуще-

го объекта будем рассматривать класс таких управляющих ускорений w(t) с

кусочно-постоянными компонентами, удовлетворяющих наложенным ограни-

чениям (2.1), которым отвечают ломаные траектории, состоящие из отрезков,

параллельных сторонам прямоугольника.

Задача 1. Найти начальное положение x⁰ = (x⁰¹,x⁰²,x⁰³) ∈ D⁽³⁾, число

T > 0, допустимое управление w(t), 0 ≤ t ≤ T объекта X и соответствую-

щий закон изменения электрического тока в цепи источника света j = j(t),

0 ≤ t ≤ T, для которых при любом начальном положении y⁰ = (y⁰¹,y⁰²) ∈ D⁽²⁾

и любом кусочно-непрерывном управлении v(t), 0 ≤ t ≤ T объекта Y гаран-

тируется выполнение условия (2.4) в некоторый момент t ∈ [0, T ] при мини-

мальной световой энергозатрате (2.9).

3. Описание способа поиска

Опишем сначала предлагаемый способ управления, а затем укажем усло-

вия на входящие в него параметры, при которых решается задача 1. Пусть в

начальный момент t₀ = 0 объект X находится в точке

x⁰ = (x⁰¹,x⁰²,x⁰³), x⁰¹ = x⁰² = l₀, x⁰³ = C-1l₀,

(3.1)

0 < x⁰³ ≤ a₃, l₀ ≤ Ca₃ < min(a₁, a₂)/2 = a₂/2.

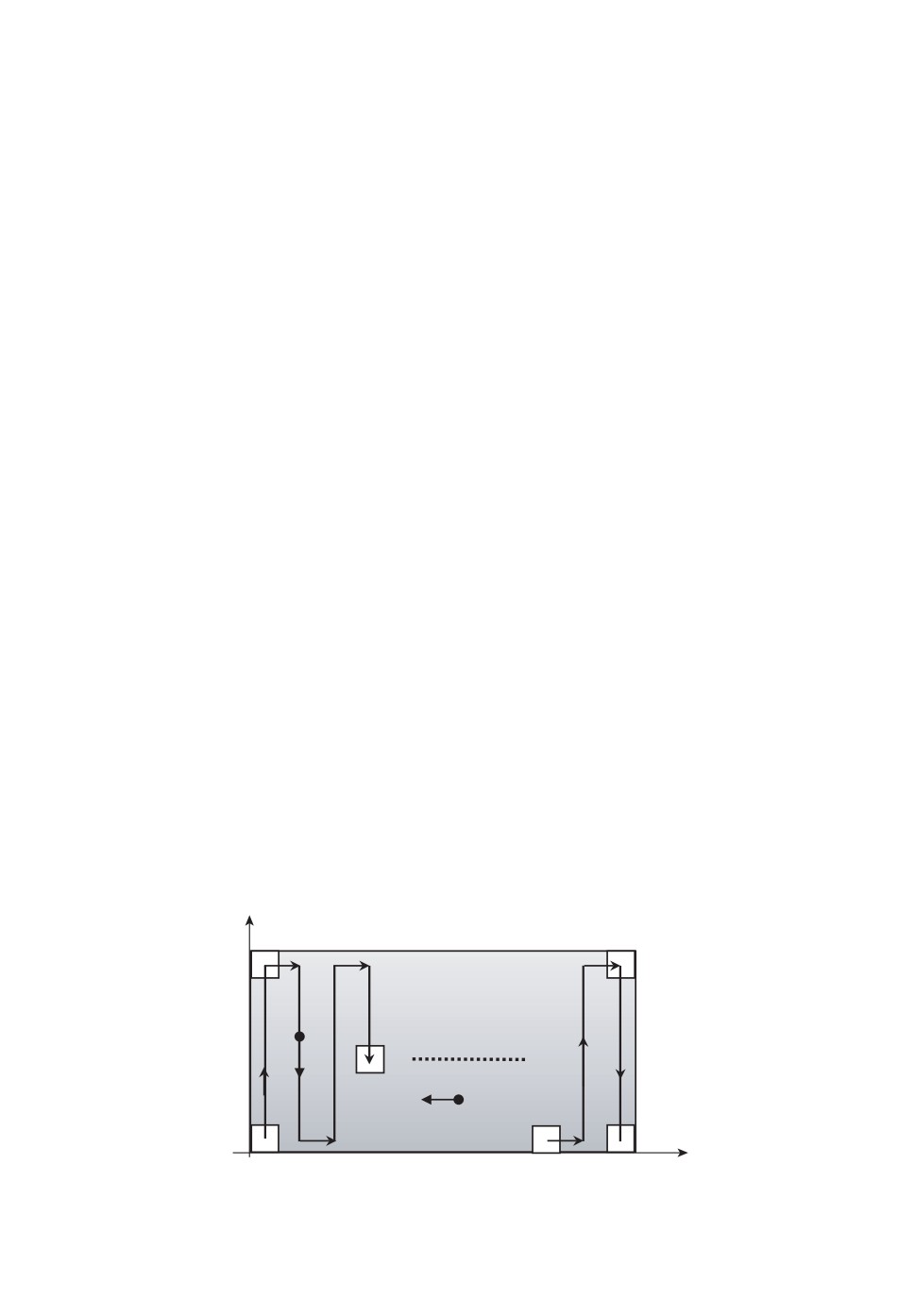
Рассмотрим исходящую из этой точки пространственную ломаную, проек-

ция L0,N = L₀L₁ . . . L_N которой на прямоугольное основание D⁽²⁾ изображена

на рис. 2.

Двигаясь по ломаной L0,N в направлении, показанном на рис. 2, центр

квадрата K сo стороной постоянной длины 2l₀ осуществляет сканирование

прямоугольника с шагом h, 0 < h < 2l₀ по оси x₁, оставляя с каждой стороны

(верхней и нижней) прямоугольника полосы с шириной l₀. Зададим управ-

ление плоским движением X (1.1) (w₃(t) ≡ g, t ≥ 0) так, чтобы перемещение

центра квадрата освещенности по отрезку Lk-1L_k происходило оптимальным

x₂

a₂

LN1

L₁

D⁽²⁾

2l₀

L₀

L_N

a₁

x₁

Рис. 2. Способ перемещения центра квадрата освещенности.

114

по быстродействию образом. Управления w₁, w₂, обеспечивающие перемеще-

ния центра квадрата из одной вершины Lk-1(x(k-1)1, x(k-1)2) с нулевой ско-

ростью x(k-1)1 = x(k-1)2 = 0 в последующую вершину L_k(x(k)1, x(k)2) с нулевой

скоростью x(k)1 = x(k)2 = 0 по прямолинейным отрезкам Lk-1L_k, определяют-

ся из решения двухточечной задачи оптимального быстродействия [10]:

по вертикальным участкам Lk-1L_k

{

}

w∗1(t) = 0, w∗2(t) = Wsign

(t^′/2 - t)Δx₂

tk-1 ≤ t ≤ t_k,

(

)1/2

t_k = tk-1+t^′, t^′= 2

|Δx₂|W-1

, k =2n+1, n=0,1,...,(N -1)/2,

Δx₂ = x(k)2 - x(k-1)2 > 0, x(k)2 = a₂ - l₀, x(k-1)2 = l₀;

(3.2)

k = 4p + 1, p = 0,1,...,P ≤ (N - 1)/2,

Δx₂ = x(k)2 - x(k-1)2 < 0, x(k)2 = l₀, x(k-1)2 = a₂ - l₀;

k = 4q + 3, q = 0,1,...,Q ≤ (N - 1)/2,

t₀ = 0, P,Q - целые числа, N - нечетное целое число,

по горизонтальным участкам Lk-1L_k

{

}

w∗1(t) = Wsign

(t^′′/2 - t)Δx₁

w∗2(t) = 0, tk-1 ≤ t ≤ t_k,

(

)1/2

t_k = tk-1 + t^′′, t^′′ = 2

Δx₁W-1

k = 2n, n = 1,...,(N - 1)/2,

(3.3)

Δx₁ = x(k)1 - x(k-1)1 = h, k = 2n, n = 1,... ,(N - 3)/2,

Δx₁ = x(k)1 - x(k-1)1 ≤ h, k = N - 1, N - нечетное целое число.

Согласно (3.2) перемещение центра квадрата освещенности по верти-

кальным участкам Lk-1L_k (рис. 2) в сторону возрастания координаты x₂:

Δx₂ = x(k)2 - x(k-1)2 > 0 происходит на интервалах времени tk-1 ≤ t ≤ t_k, k =

= 4p + 1, p = 0, 1, . . . , P ≤ (N - 1)/2, а в сторону уменьшения x₂: Δx₂ = x(k)2-

-x(k-1)2 < 0 - на интервалах времени tk-1 ≤ t ≤ t_k, k = 4q + 3, q = 0,1,

...,Q ≤ (N - 1)/2. Поэтому на интервалах tk-1 ≤ t ≤ t_k, когда Δx₂ > 0, име-

ем w∗2(t) = W при tk-1 ≤ t < t^′/2 и w^∗(t) = -W при t^′/2 ≤ t ≤ t_k, а когда

Δx₂ < 0, имеем w∗2(t) = -W при tk-1 ≤ t < t^′/2 и w^∗(t) = W при t^′/2 ≤ t ≤ t_k.

Здесь t^′/2 = (t_k - tk-1)/2 - момент переключения управляющего ускорения

w^∗(t) от значения W к значению -W или наоборот.

Формулу (3.3) можно пояснить аналогичным образом с той разницей, что

в ней учитывается, что перемещение центра квадрата освещенности по го-

ризонтальным участкам Lk-1L_k происходит только в сторону возрастания

координаты x₁ (рис. 2): Δx₁ = x(k)1 - x(k-1)1 > 0.

Соответствующий закон изменения электрического тока в цепи источника

света j = j(t) определяется согласно соотношению (2.11):

√

(3.4)

j(t) ≡

Eηξ-1R-1x⁰³

t ∈ [0,T].

115

Как следует из (3.2), (3.3), оптимальные времена перемещения одинаковы

по каждому вертикальному участку и по каждому горизонтальному участку

длины h и вычисляются соответственно следующим образом:

√

(3.5)

t^′ = 2

(a₂ - 2l₀)W-1, t^′′ = 2

hW-1.

4. Гарантированный поиск при минимальной затрате световой энергии

Перейдем к определению параметров l₀, h. Сначала положим h = 0 и неза-

висимо от траекторий рис. 2 рассмотрим прямолинейное вертикальное пере-

мещение центра квадрата из положения (2l₀, l₀) покоя в конечное положение

(2l₀, a₂ - l₀) покоя, а затем обратное перемещение в исходное положение по-

коя при управляющих ускорениях (3.2). Выясним, при каких условиях объ-

ект Y может пересечь ось x₁ = l₀, избежав обнаружения.

Пусть перед рассматриваемым перемещением центра квадрата освещенно-

сти объект Y занимает положение y₁ ≥ 3l₀ + ε, y₂ = 0 (ε > 0 - сколь угодно

малое число) на нижней стороне прямоугольника, вне квадрата освещенно-

сти. Тогда объекту Y легче всего пересечь ось x₁ = l₀ незамеченным, если

он будет двигаться по нижней стороне прямоугольника с максимальной по

модулю скоростью (v₁ = -V , v₂ = 0) в направлении оси x₁ = l₀. При этом он

√

будет располагать наибольшим временем, равным 2t^′ = 4

(a₂ - 2l₀)W-1, до

очередного возвращения центра квадрата на положение (2l₀, l₀).

√

Объект Y может избежать обнаружения при условии 4

(a₂ - 2l₀)W-1 >

> (2l₀ + ε)V -1, где (2l₀ + ε)V -1 - время перемещения Y по оси x₂ = 0 на

расстояние 2l₀ + ε.

При противоположном строгом неравенстве

√

(4.1)

(a₂ - 2l₀)W-1 < (2l₀ + ε)V-1

X осуществит обнаружение Y , если последний пересечет ось x₁ = l₀.

Неравенство (4.1) заведомо выполнено, если выполнено более простое

условие

√

(4.2)

2t^′ = 4

(a₂ - 2l₀)W-1 < 2l₀V-1.

Разрешая (4.2) относительно l₀ и учитывая условие (3.1), определим диа-

пазон изменения параметра l₀, при котором неравенство (4.2) выполняется:

√

(4.3)

l_min = -4V²W-1 +

16V⁴W-2 + 4V²W-1a₂ < l₀ ≤ Ca₃.

Пусть поиск проводится так, как описано в разделе 3, и выполняется нера-

венство (4.2), т.е. l₀ удовлетворяет условию (4.3). Перейдем к определению

условия на h, h < 2l₀, при котором описанный способ поиска решает задачу 1.

Рассмотрим перемещение центра квадрата освещенности по ломаной

L0,3 = L₀L₁L₂L₃ с вершинами

(4.4)

L₀ = (l₀,l₀), L₁ = (l₀,a₂ -l₀), L₂ = (l₀ +h,a₂ -l₀), L₃ = (l₀ +h,l₀)

116

при управлениях (3.2), (3.3):

⎧

⎨w1(t) ≡ 0,

w₂(t) = w∗2(t), t ∈ [0,t₁),

w(t) =

w₁(t) = w∗1(t), w₁(t) ≡ 0,

t ∈ [t₁,t₂),

⎩

w₁(t) ≡ 0,

w₂(t) = -w∗2(t), t ∈ [t₂,t₃),

где t₁, t₂, t₃ определяются с помощью (3.5): t₁ = t^′, t₂ = t^′ + t^′′, t₃ = 2t^′ + t^′′.

По аналогии со случаем h = 0, чтобы избежать обнаружения, объ-

ект Y должен достичь оси x₁ = 0 так, чтобы все время было выполнено

y(t) ∈ K(x(t)), t ∈ [0, t₃]. Oбъекту Y легче быть необнаруженным, если в на-

чальный момент времени он находится в положении (2l₀ + ε, 0) (ε > 0 - сколь

угодное малое число), вне квадрата обнаружения и движется по нижней сто-

роне прямоугольника D⁽²⁾ в сторону оси x₁ = 0 с максимальной по модулю

скоростью (v₁ = -V , v₂ = 0). При этом Y имеет наибольшее время, равное

t₃ = 2t^′ + t^′′, между перемещениями центра квадрата вверх и вниз при ска-

нировании шагом h.

Следовательно, чтобы осуществить обнаружение искомого объекта, ищу-

щий объект при движении по верхней горизонтальной стороне прямоуголь-

ника должен выбрать величину шага перемещения h, так чтобы имело место

неравенство

√

(a₂ - 2l₀ - ε)W-1 + 2

hW-1 ≤ (2l₀ + ε - h)V-1,

которое заведомо выполняется, если выполняется более сильное неравенство

√

(4.5)

(a₂ - 2l₀)W-1 + 2

hW-1 ≤ (2l₀ - h)V-1, h < 2l₀.

При условии (4.5) искомый объект не может с максимальной по модулю

скоростью V пройти расстояние длиной 2l₀ - h на оси x₂ = 0 будучи не об-

наруженным за время перемещения центра квадрата по ломаной L0,3.

Разрешая (4.5) относительно h, получим диапазон изменения величины

шага, при котором описанный способ поиска гарантирует обнаружение по-

движного объекта Y :

0<h≤h_max,

(4.6)

(

)₂

h_max = -V W-1/2 +(V2W-1 +2l0 -4V (a2 -2l0)1/2W-1/2)1/2

< 2l₀.

Рассмотрим следующую положительную функцию N₁ от l₀ и h:

(4.7)

N₁(l₀, h) = (a₁ - 2l₀)h-1, l_min < l₀ ≤ Ca₃,

0 < h ≤ h_max < 2l₀.

Функция (4.7) по h монотонно убывающая. Следовательно,

(4.8)

min N₁(l₀, h) = (a₁ - 2l₀)h-1max = N₁(l₀

0<h≤hmax

Обозначим:

(4.9)

R₀ = {l₀ ∈ (l_min, Ca₃] : N₁(l₀) = [N₁(l₀

)] } ,

117

где символ [·] означает целую часть действительного числа. Для значе-

ний l₀ ∈ R₀ целое число 1 + N₁(l₀) определяет то количество вертикаль-

ных перемещений с шагом сканирования h_max (4.6), при котором движениe

центра квадрата по ломаной L0,N , N = 2N₁(l₀) + 1 заканчивается в точке

(a₁ - l₀, l₀), если N₁(l₀) - нечетное целое число, и в точке (a₁ - l₀, a₂ - l₀),

если N₁(l₀) - четное целое число.

С учетом этого, используя (3.5), (4.8), функционал (2.9) на множестве (4.9)

можно представить в виде

J (l₀) = (Eηξ-1C-2)L(l₀)T (l₀), l₀ ∈ R₀,

(4.10)

L(l₀) = l²⁰, T (l₀) = t′1(l₀) + (t′1(l₀) + t′2(l₀))N₁(l₀),

где T (l₀) определяет гарантированное время поиска.

Таким образом, задача 1 сводится к нахождению параметра l∗0 ∈ R₀, до-

ставляющего минимум в задаче

(4.11)

J^∗

J (l∗0) = min L(l₀)T (l₀

l₀∈R₀

Функции L(l₀) и T (l₀) на множестве R₀ принимают соответственно моно-

тонно возрастающие и монотонно убывающие дискретные значения. Мини-

мум в (4.11) в зависимости от соотношений между параметрами может дости-

гаться как во внутренней, так и в крайних точках множества (4.9). С учетом

этого проведены численные расчеты определения l∗0 при различных значе-

ниях параметров задачи. В частности, при a₁ = 200 м, a₂ = 100 м, a₃ = 20 м,

C =1,W =1м/c²,V =0,25м/cминимальное значени

J^∗ = 47271,4 м²c до-

стигается во внутренней точке R₀: l∗0 = 4,35 м. Соответствующее количе-

ство полных перемещений с шагом сканирования h_max = 8,24 м (4.6) равно

N₁ = 22 (4.8), a гарантированное время поиска - T = 541,07 c (4.10). Элек-

трический ток в цепи источника света и минимальная величина энергии, по-

требляемой источником света, определяются из (3.4), (4.10) при конкретных

значениях параметров R, E, η, ξ.

5. Заключение

Предложен простой способ управления движением динамического объек-

та в задаче поиска подвижного объекта в прямоугольной области с помощью

квадратной области постоянного размера и заданной освещенности. Получе-

но условие, гарантирующее успешное завершение поиска. Предложен алго-

ритм нахождения оптимального размера квадрата освещенности, при кото-

ром искомый объект обнаруживается за гарантированное время поиска при

минимальной световой энергозатрате.

СПИСОК ЛИТЕРАТУРЫ

1. Хорн Б.К.П. Зрение роботов. М.: Мир, 1989.

2. Аветисян В.В., Мартиросян С.Р. Гарантированный поиск целевого объекта

электромеханической системой при минимальных световых энергозатратах //

Изв. РАН. ТСУ. 2009. № 5. С. 151-164.

118

3. Черноусько Ф.Л. Управляемый поиск подвижного объекта // ПММ. 1980. Т. 44.

Вып. 1. С. 3-12.

4. Чхартишвили А.Г., Шикин Е.В. Динамический поиск объектов. Геометриче-

ский взгляд на проблему // ФПМ. 1995. Т. 1. Вып. 4. С. 827-862.

5. Аветисян В.В., Меликян Т.Т. О задаче гарантированного поиска подвижного

объекта в прямоугольной области // Изв. РАН. ТСУ. 1999. № 2. С. 31-39.

6. Аветисян В.В. Оптимальный по минимальному гарантированному времени по-

иск неподвижного объекта в прямоугольной области // Изв. РАН. ТСУ. 2002.

№ 1. С. 62-69.

7. Аветисян В.В. Управление поиском неподвижного объекта с целью захвата //

Изв. РАН. ТСУ. 2006. № 6. С. 160-168.

8. Черноусько Ф.Л., Болотник Н.Н., Градецкий В.Г. Манипуляционные роботы.

М: Наука, 1989.

9. Савельев И.В. Курс общей физики. Т. 3. М.: Наука, 1970.

10. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Матема-

тическая теория оптимальных процессов. М: Наука, 1983.

Статья представлена к публикации членом редколлегии Б.М. Миллером.

Поступила в редакцию 07.04.2019

После доработки 13.11.2019

Принята к публикации 28.11.2019

119