Автоматика и телемеханика, № 5, 2020

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ОЦЕНКА И ОПТИМИЗАЦИЯ ПРОИЗВОДИТЕЛЬНОСТИ

РЕКУРСИВНОГО КОНВЕЙЕРА

Cформулировано понятие производительности рекурсивного конвейе-

ра, и задача оптимизации распределения возобновляемых ресурсов реше-

на как задача максимизации производительности путем сведения к задаче

целочисленного линейного программирования. Дано определение рекур-

сивных функций вычисления расписания процесса для некоторого произ-

вольного распределения ресурсов. Результаты могут быть использованы

при проектировании конвейера или для вычисления граничных оценок

при использовании комбинаторных алгоритмов построения расписания.

Ключевые слова: теория расписаний, рекурсивные конвейеры, производи-

тельность конвейера, балансировка конвейера.

DOI: 10.31857/S0005231020050025

1. Введение

В массовом производстве [1] или при проектировании производственных

линий распределение ресурсов (станков, инструментов, людей) осуществля-

ется до начала производственного процесса. Так, проектирование сборочно-

го конвейера является долгосрочным решением и обычно требует крупных

капиталовложений. Задача расчета необходимого количества ресурсов и их

распределения возникает и в тех случаях, когда необходимо выполнение неко-

торого объема заказа к заданному сроку. Вычисление оптимального распре-

деления ресурсов (если это возможно) до построения расписания процесса

позволяет существенно упростить задачу построения расписания процесса.

В публикациях по теории расписаний большое количество работ посвящено

данному вопросу. Существуют работы, которые фокусируются на методах

оптимизации балансировки линии и планирования ресурсов на этапе про-

ектирования сборочной линии [2]. Ghosh и Gagnon [3] делают комплексный

обзор и анализ различных методов проектирования и планирования монтажа

систем. Большая часть работ сконцентрирована на балансировке сборочного

конвейера (ALB). Для ALB модели Хельгесоном (Helgeson) и соавторами бы-

ло предложено использование методов поиска оптимальных решений, таких

как линейное программирование [4, 5] и целочисленное программирование [6].

В [7] рассматривается задача распределения ресурсов как задача оптималь-

ного быстродействия. В настоящее время существует большое количество ра-

бот по оптимизации планирования ресурсов для традиционных задач теории

расписаний, например [8-11].

В статье рассматриваются конвейеры, описываемые ациклическим ориен-

тированным графом и набором рекурсивных функций [12]. Примеры при-

ложений таких конвейеров приводятся в [13]. Вводится понятие производи-

тельности конвейера и решается задача максимизации производительности

на множестве распределений дискретных возобновляемых ресурсов. Конеч-

ный этап решения сводится к задаче целочисленного линейного программи-

рования.

Статья имеет следующее содержание. Во второй главе дано формальное

определение рекурсивного конвейера, приведен пример конвейера и времен-

ной диаграммы, описаны основные свойства конвейера. В третьей главе вво-

дится определение производительности рекурсивного конвейера и формули-

руется задача оптимального распределения ресурсов как задача целочислен-

ного программирования. Далее рассматривается пять этапов решения зада-

чи. Приведены модифицированные рекурсивные функции. Каждый этап со-

провождается примером. В четвертой главе рассматривается пять примеров

решения задачи.

2. Определения

Модель конвейера, отношения временного предшествования которого

определяются рекурсивными функциями (далее для краткости просто кон-

вейера), представляет собой связный ациклический ориентированный граф

G = (V,A) с единственной конечной вершиной. V - множество вершин графа

и n - количество вершин. A - множество дуг графа, упорядоченных пар ви-

да (v, w), где v, w ∈ V . Вершины графа помечены номерами от 1 до n таким

образом, что первые n₀ (1 ≤ n₀ < n) вершин являются начальными, а вер-

шина n конечной. Каждая вершина графа обозначает либо производствен-

ную операцию, обрабатывающую заказ с помощью возобновляемого ресур-

са, либо спусковую функцию, определяющую отношения временного пред-

шествования операций и не потребляющей ресурсы. Под операциями будем

подразумевать как производственные операции, так и спусковые функции.

Для идентификации типа вершины помечены с помощью отображения type:

V → E, где E = {bop,op,and,mul,red,get1,get2,put} - конечное перечис-

лимое множество. Каждая константа множества E обозначает тип вершины

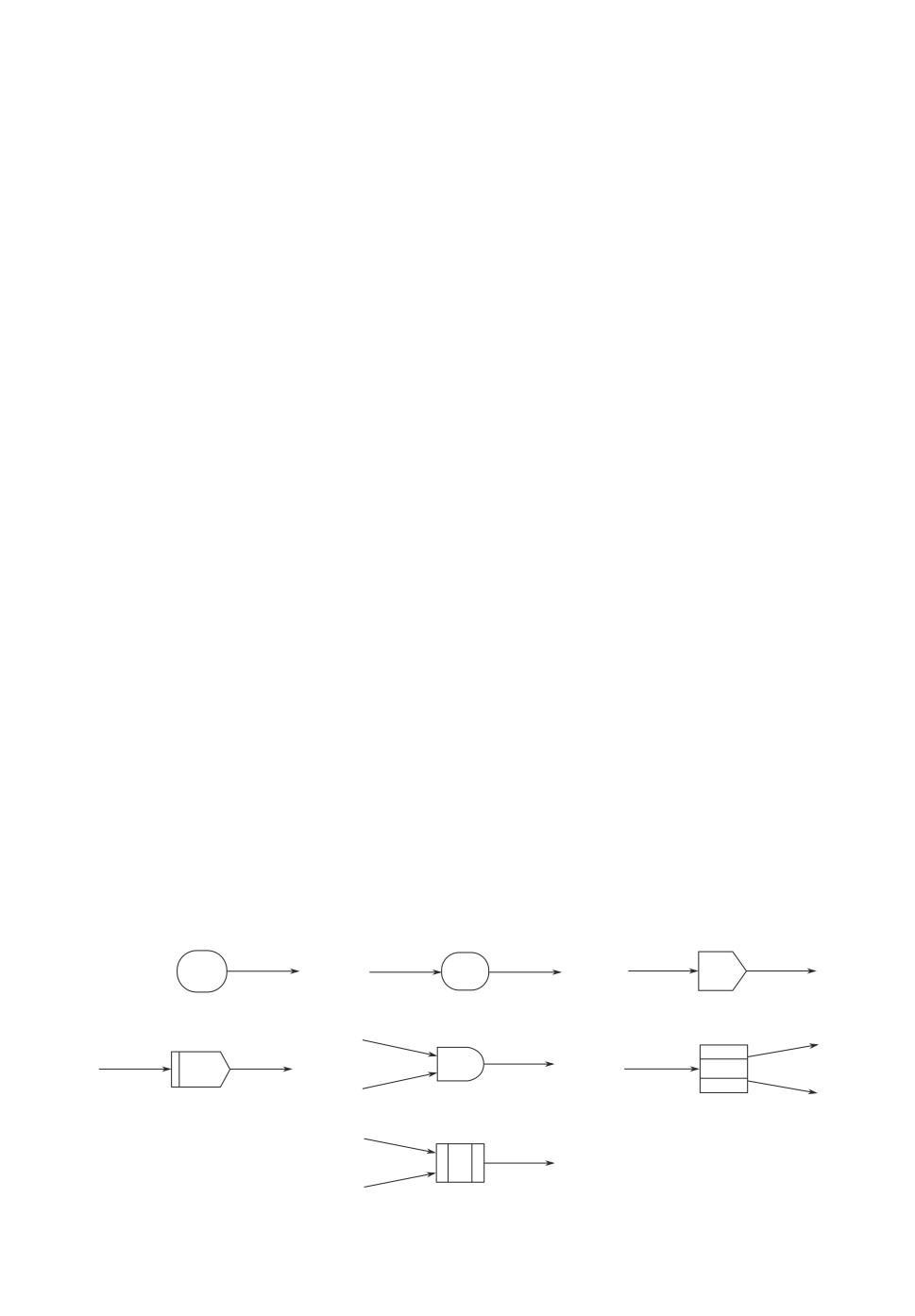
графа, а сама вершина имеет соответствующую графическую нотацию (см.

рис. 1,а-ж).

t(i, k)

t(j, k)

t(i, k)

t(j, k)

t(i, k)

i(p_i)

t(p, j)

t(i, k)

t(j, k)

t(i, k)

t(p, k)

i(q_i)

t(q, l)

t(j, k)

t(p, l)

t(i, k)

t(q, c)

Рис. 1.

Из практики определено пять видов спусковых функций, имеющих приме-

нение для широкого круга конвейерных процессов. Однако можно определять

новые исходя из конкретных потребностей. Для производственной операции

и спусковых функций отношения предшествования описываются с помощью

рекурсивных функций. Расписание выполнения операций строится с помо-

щью суперпозиции рекурсивных функций, вычисляющих значение времени

завершения обработки i-й операцией k-го заказа (k ≥ 0). Для каждого эле-

мента множества E своя функция, т.е. восемь функций и каждая вершина i

графа в соответствии с ее типом ассоциируется с одной из этих функций.

Рекурсивная функция t(i, k) обеспечивает суперпозицию и является обраще-

нием к одной из них в соответствии с типом вершины.



bop(i, k), if type(i) = bop;



op(i, k), if type(i) = op;



and(i, k), if type(i) = and;





mul(i, k), if type(i) = mul;

(1)

t(i, k) =



red(i, k), if type(i) = red;



get1(i, k), if type(i) = get1;



get2(i, k), if type(i) = get2;



put(i, k), if type(i) = put.

Здесь имена рекурсивных функций для взаимно однозначного соответствия

обозначаются теми же именами, что и типы вершин, но не жирным шрифтом.

Каждая вершина графа может иметь одну или две входных дуги в за-

висимости от типа вершины. Переход в процессе вычисления рекурсивной

функции от вершины к вершине графа осуществляется с помощью следую-

щих функций:

pred(i) - определена для вершины, имеющей одну предшествующую вер-

шину, и вычисляет номер j вершины графа такой, что существует единствен-

ная дуга (v_j , v_i) ∈ A;

(Следующие две функции определены для вершин, имеющих две предше-

ствующие вершины. Условно будем считать: вершина 1 и вершина 2. Способ

определения порядка в данном случае не имеет значения. Важно только, что

он существует.)

pred1(i) - вычисляет номер p 1-й вершины графа такой, что существует

дуга (v_p, v_i) ∈ A;

pred2(i) - вычисляет номер q 2-й вершины графа такой, что существует

дуга (v_q, v_i) ∈ A.

Далее описываются все типы вершин: их назначение, тип и соответст-

вующая типу рекурсивная функция. Все рекурсивные функции имеют два

параметра: i - номер вершины графа и k - номер заказа. В каждый мо-

мент времени производственная операция может выполнять только один за-

каз и каждый ресурс может выполнять только одну операцию. Рекурсивные

функции здесь сформулированы при условии, что каждой операции выделен

один ресурс. Задача распределения ограниченного множества ресурсов и со-

ответствующие рекурсивные функции рассматриваются далее. Время начала

функционирования конвейера полагается равным 0.

1. Начальная производственная операция (см. рис. 1,а) с номером 1 ≤ i ≤

≤ n₀ характеризуется временем выполнения p_i, которое является констан-

той. Прерывание выполнения операции запрещено. Время завершения вы-

полнения данной операцией k-го заказа определяется как время завершения

выполнения (k - 1)-го заказа плюс время выполнения операции p_i. Время

выполнения нулевого заказа равно p_i.

bop(i, k) :

{ bop(i, k - 1) + pi, if k > 0,

bop =

p_i, if k = 0.

2. Не начальная производственная операция (см. рис. 1,б) с номером n₀ < i

характеризуется временем выполнения p_i, которое является константой. Вре-

мя завершения выполнения данной операцией k-го заказа определяется как

максимум времен: завершения выполнения данной операцией (k - 1)-го зака-

за и времени завершения выполнения предшествующей ей операцией k-го за-

каза, плюс время выполнения операции p_i. Время выполнения нулевого за-

каза равно времени выполнения нулевого заказа предшествующей операцией

плюс p_i.

op(i, k) :

j = pred(i),

{

max(t(j, k), op(i, k - 1)) + pi, if k > 0,

op =

t(j, k) + p_i, if k = 0.

3. Спусковая функция and (см. рис. 1,д) вычисляет время завершения вы-

полнения k-го заказа для двух предшествующих операций p и q.

and(i, k) :

p = pred1(i), q = pred2(i),

and = max(t(p, k), t(q, k)).

4. Спусковая функция мультиплицирования (см. рис. 1,в) для каждого

времени завершения предшествующей ей операции j вычисляет q_i времен

завершения функции i. Это означает, что на одно выполнение операции j

осуществляется q_i выполнений операции, для которой функция i является

предшествующей.

mul(i, k) :

j = pred(i), l = ⌊k/q_i⌋,

mul = t(j, l),

где ⌊x⌋ обозначает целую часть x.

5. Спусковая функция редуцирования (см. рис. 1,г) является обратной по

отношению к функции мультиплицирования, т.е. она вычисляет время завер-

шения выполнения партии из q_i заказов.

red(i, k) :

j = pred(i), l = (k + 1)q_i - 1,

red = t(j, l).

6. Спусковая функция раздачи (см. рис. 1,е) имитирует разделение кон-

вейерных операций на два потока. Для пользователя она выступает как одна

функция, а в реализации она разбивается на две (условно верхнюю и ниж-

нюю). Для верхнего варианта спусковая функция вычисляет времена завер-

шений четных заказов, т.е. t(i, 0) = t(p, 0), t(i, 1) = t(p, 2), t(i, 2) = t(p, 4),

get1(i, k) :

p = pred(i), l = 2k,

get1 = t(p, l).

Для нижнего вычисляет времена завершения выполнения нечетных заказов,

т.е. t(j, 0) = t(p, 1), t(j, 1) = t(p, 3), t(j, 2) = t(p, 5),

get2(i, k) :

p = pred(i), l = 2k + 1,

get2 = t(p, l).

7. Спусковая функция приема (см. рис. 1,ж) является обратной по отно-

шению к функции раздачи и имитирует слияние двух конвейеров в один.

Проще всего это пояснить последовательностью значений t(i, k):

t(i, 0) = t(p, 0), t(i, 1) = t(q, 0), t(i, 2) = t(p, 1), t(i, 3) = t(q, 1), t(i, 4) = t(p, 2),

t(i, 5) = t(q, 2),

put(i, k) :

p = pred1(i), l = k/2,

q = pred2(i), c = (k - 1)/2,



 t(p,l), if k = 0,

put =

max(put(i, k - 1), t(q, c)), if k mod 2 = 1,



max(put(i, k - 1), t(p, l)), if k mod 2 = 0,

где x mod y - остаток от деления x на y.

Вычисление времени завершения выполнения k-го заказа конвейером осу-

ществляется с помощью обращения к рекурсивной функции t(n, k) по форму-

ле (1). Эта же формула вычисляет время завершения выполнения k-го заказа

любой i-й операцией конвейера обращением t(i, k). Рекурсивность в данном

случае выступает в двух видах:

значение функции для некоторого k зависит от значения этой функции

для (k - 1) или другого меньшего значения;

в случае суперпозиций функции она может обращаться к самой себе с

другим значением аргумента (см. в разделе 4 пример 1).

Важно понимать, что рекурсивные функции определяют отношение вре-

менного предшествования и используются в дальнейшем только для вычис-

ления расписания выполнения операций. Никакого отношения к управлению

конвейером они не имеют. Управление конвейером аналогично классическим

конвейерам, может осуществляться множеством способов и зависит от тех-

нологического решения. В разделе 4 в примере 1 показана модель конвейера,

соответствующая ему суперпозиция рекурсивных функций и вычисление та-

кой функции для некоторых значений аргументов.

Временная сложность вычисления расписания с помощью таких функ-

ций - O(nk), где n - количество вершин графа, k - количество обработанных

заказов.

Интервалом обработки k-го заказа i-й операцией конвейера d(i, k) 1 ≤ n,

k ≥ 1 назовем продолжительность времени между моментами завершений

i-й операции при обработке k и (k - 1) заказов:

d(i, k) = t(i, k) - t(i, k - 1).

Очевидно, что d(i, k) ≥ p_i. Величины d(n, k) для последовательности зна-

чений k определяют промежутки времени, через которые с конвейера сходит

продукция. В общем случае интервал операции зависит от номера заказа k.

Для описанных выше функций предшествования в [14] показано, что в об-

щем случае интервал операции i конвейера для первых ks_i заказов меняется

по некоторому закону переходного процесса, далее процесс переходит в ста-

ционарный режим и интервал меняется по закону периодической функции.

Каждую операцию i конвейера можно характеризовать следующим корте-

жем:

(t0_i, ks_i, ts_i, D_i, T_i),

где i - номер операции;

t0_i - время завершения операции i при обработке нулевого заказа (при i,

равном n, это будет время выхода первого изделия с конвейера);

ks_i - номер заказа, начиная с которого операция i переходит в стационар-

ный режим выполнения;

ts_i - время, начиная с которого операция i переходит в стационарный ре-

жим выполнения;

D_i - определяется как сумма интервалов операции i за период;

T_i - период колебания интервала операции i, измеряется в количествах

заказов и является безразмерной величиной.

Для стационарного режима можно ввести понятие направляющей времени

завершения выполнения заказа t(i, k) операции i - луча, выходящего из точки

(ks_i, ts_i) на котором лежат точки

t(i, k) = ts_i + kD_i, k = 0, T_i, 2T_i,

Параметры t0_i, ks_i, ts_i, D_i, T_i являются константами, и в случае рассмотре-

ния конвейера (i = n) для удобства будем обозначать их как t₀, k_s, t_s, D, T .

В определении не уточняется, относится ли определение стационарного ре-

жима работы конвейера ко всем операциям или только к завершающей опе-

рации конвейера. В данной статье будем считать, что это относится ко всем

операциям конвейера, т.е. после обработки заказа k_s все операции конвейера

перешли в стационарный режим выполнения.

3. Решение задачи оптимизации

В данном разделе рассматривается решение задачи оптимизации распре-

деления ресурсов для стационарного режима работы конвейера как задачи

целочисленного линейного программирования.

Введем ряд обозначений для ресурсов:

J - количество множеств ресурсов (1 ≤ j ≤ J). Каждое множество содер-

жит ресурсы одного типа;

r_j - количество ресурсов в j-м множестве. Ресурс может иметь составную

структуру, например, для выполнения операции нужен один станок и два

человека. Набор ресурсов, обслуживающий одну операцию, будем называть

комплектом и с каждой операцией связывать некоторое целое число комплек-

тов;

aij - коэффициент комплектации i-й операции j-м ресурсом, например,

если выполнение i-й операции требует наличия одного станка и трех рабочих,

то a_i1 = 1, a_i2 = 3;

x_i - количество комплектов ресурсов, используемых i-й операцией, явля-

ется целым числом без размерности. Если i-й операции поставлено в соответ-

ствие x_i комплектов, то операция может x_i раз выполняться с совмещением

во времени;

W_i - производительность i-й операции конвейера, которая измеряется ко-

личеством выполнений операции в составе конвейера в единицу времени и

является вещественным числом.

Интервал конвейера d(n, k) определяет его производительность. Чем боль-

ше интервал конвейера, тем меньше его производительность. Каждая опе-

рация i конвейера [15] может быть охарактеризована кратностью выполне-

ния ω_i. Данная величина показывает, сколько раз операция i выполняется в

пересчете на одно выполнение конечной операции конвейера. Иначе, сколь-

ко раз выполняется операция i при производстве одного изделия конвейера.

Кратность операции увеличивает время выполнения операции в ω_i раз и соот-

ветственно уменьшает производительность операции в ω_i раз. В общем случае

производительность является величиной переменной и может вычисляться по

формуле

x_i

W_i(k) = g_i

d(i, k)ω_i

т.е. прямо пропорционально зависит от количества комплектов ресурсов x_i

и обратно пропорционально зависит от произведения интервала опера-

ции d(i, k) на ее кратность ω_i, g_i является коэффициентом пропорционально-

сти. В случае стационарного процесса можно рассматривать среднюю произ-

водительность (не зависящую от k) за период колебания интервала

T_ix_i

W_i = g_i

D_iω_i

где D_i - приращение интервала за период, T_i - величина периода иDi - сред-_T

ний интервал i-й операции за период, для которого справедливо неравенство

D_i

≥ p_i. Далее в статье рассматривается только средняя производительность

T_i

в стационарном режиме, которую для краткости будем называть произво-

дительностью. В связи с последним неравенством введем неравенство для

производительности

x_i

W_i ≤ g_i

p_iω_i

Поскольку p_i, g_i и ω_i являются константами, для упрощения введем новую

константу c_i, которая вычисляется по формуле

g_i

c_i =

p_iω_i

и является вещественным числом. В этом случае для производительности

справедливо неравенство

W_i ≤ c_ix_i.

В терминах введенных определений задача формулируется следующим об-

разом. Пусть имеется конвейер, выполняющий n операций, каждая продол-

жительностью p_i ≥ 0, 1 ≤ i ≤ n. Имеется некоторое множество ресурсов, раз-

битое на J групп по r_j, 1 ≤ j ≤ J в каждой группе. В этом случае задача

оптимального распределения ресурсов является задачей целочисленного ли-

нейного программирования с целевой функцией

W -→ max

x_i

и системой ограничений

∑

a_ijx_i ≤ r_j,

1 ≤ i ≤ n,

1 ≤ j ≤ J,

i=1

W_i ≤ c_ix_i,

1 ≤ i ≤ n,

W ≤W_i,

1 ≤ i ≤ n,

1≤x_i,

1 ≤ i ≤ n.

Здесь W - производительность конвейера. Ограничение x_i ≥ 1 обусловлено

тем, что при x_i = 0 конвейер не может функционировать. Решение задачи

разбивается на 5 этапов, от модели в виде цепочки операций, далее путем

последовательного рассмотрения спусковых функций к решению модели об-

щего вида.

Этап 1. Рассмотрим конвейер как цепочку из n производственных опера-

ций. Известно, что производительность такого конвейера определяется его уз-

ким местом, т.е. операцией с самым большим временем выполнения. С учетом

данного свойства максимум производительности достигается максимизацией

минимальной производительности операций конвейера. Решим эту задачу ме-

тодом линейного программирования. Целевая функция W - производитель-

ность конвейера, которая равна минимальной производительности операций

конвейера, т.е.

W = min

W_i.

1≤i≤n

Для каждого ресурса можно составить неравенство ограничения на ресурс

∑

a_ijx_i ≤ r_j,

1 ≤ i ≤ n,

1 ≤ j ≤ J.

i=1

Для производительности W_i i-й операции конвейера выполняется неравен-

ство

W_i ≤ c_ix_i,

1 ≤ i ≤ n.

Запишем эту постановку задачи формально в виде задачи линейного про-

граммирования

W -→ max,

x_i

W ≤W_i,

∑

a_ijx_i ≤ r_j,

1 ≤ i ≤ n,

1 ≤ j ≤ J,

i=1

W_i ≤ c_ix_i,

1 ≤ i ≤ n,

1≤x_i,

1 ≤ i ≤ n.

Все переменные x_i принимают целочисленные значения, W может быть ве-

щественным. Таким образом, задача является разновидностью задачи цело-

численного линейного программирования. Описанный метод рассмотрен в

примере 3 раздела 4.

Модифицируем рекурсивные функции для случая, когда i-я операция рас-

полагает x_i комплектами ресурсов. Основу нового вида рекурсивных функ-

ций определяет тот факт, что если i-я операция обеспечена x_i количеством

комплектов, то x_i выполнений этой операции могут пересекаться во времени.

Для начальной операции (см. рис. 1,а) новые рекурсивные функции опреде-

ляются следующим образом:

t(i, k) = p_i, если

1≤i≤n₀

0≤k<x_i;

t(i, k) = t(i, k - x_i) + p_i, если

1≤i≤n₀

и k≥x_i.

and

Рис. 2.

Если операция не начальная (см. рис. 1,б), то рекурсивные функции имеют

вид

t(i, k) = t(j, k) + p_i, если i > n₀ и

0≤k<x_i;

t(i, k) = max(t(j, k), t(i, k - x_i)) + p_i, если i > n₀ и k ≥ x_i.

Изменение расписания при использовании модифицированных рекурсивных

функций хорошо видно на временных диаграммах в системе координат. По

оси абсцисс отложим номер заказа, а по оси ординат - время. Время выпол-

нения i-й операции при обработке k-го заказа будет задаваться отрезком с

координатами (t(i, k) - p_i, t(i, k)) и отмечаться номером операции. В приме-

ре 2 на рис. 5,б,в приведены временные диаграммы для рассматриваемого

конвейера.

Этап 2. В том случае, когда в модели конвейера используется спуско-

вая функция mul, она изменяет кратность ω_i выполнения следующих за ней

операций. В этом случае кратности выполнения некоторых операций будут

отличны от единицы. Это влечет за собой изменение коэффициентов c_i в

соответствии с формулой (2). В остальном задача остается без изменений.

В примере 5 рассматривается конвейер со спусковой функцией mul, решение

задачи и соответствующие временные диаграммы.

Этап 3. Из [15] известно, что спусковые функции: редукции, раздачи и

приема, по сути как и операция мультиплицирования, осуществляют либо

увеличение кратности операции в два раза (get), либо уменьшение (red, put).

Поэтому для данных спусковых функций метод решения будет аналогичным.

Так, для моделей на рис. 2,б,в,г выполняются соотношения

ω₁ = qω₂, ω₃ = 2ω₄ = 2ω₅, ω₈ = 2ω₆ = 2ω₇.

Для данных соотношений и существующих ресурсных ограничений решается

задача максимизации для моделей, содержащих данные спусковые функции.

Ограничения по ресурсам специфики не имеют, а ограничения по производи-

тельности имеют следующий вид:

для варианта а)

W ≤c₁x₁;

W ≤c₂x₂,

для варианта б)

W ≤c₃x₃;

W ≤c₄x₄;

W ≤c₅x₅,

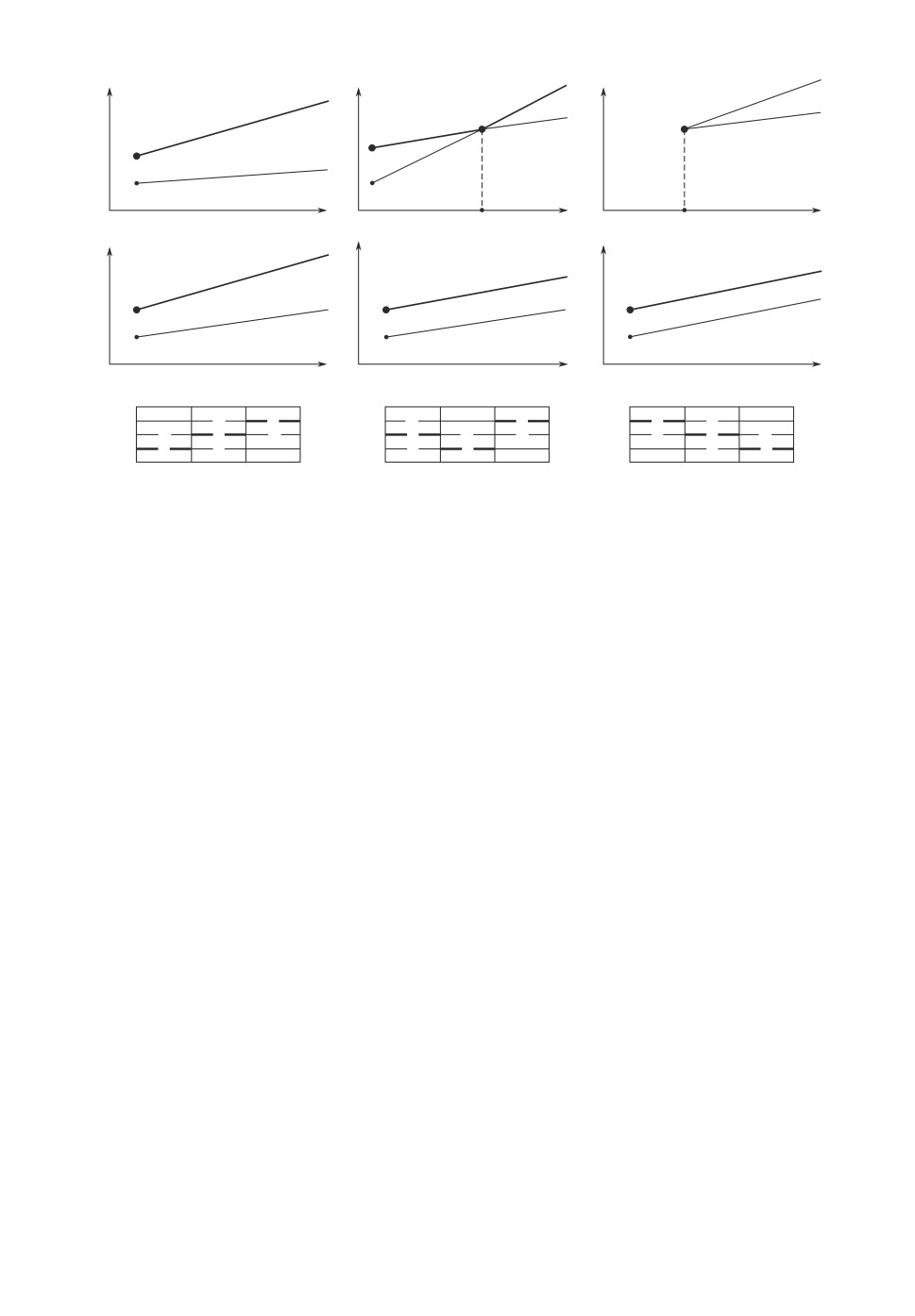
Рис. 3.

для варианта в)

W ≤c₆x₆;

W ≤c₇x₇;

W ≤c₈x₈.

В примере 7 используются все спусковые функции, в том числе и данные.

Этап 4. Рассмотрим спусковую функцию and. На рис. 2,а представлена

конструкция конвейера, в которой 1, 2 и 3 будем интерпретировать как неко-

торые конвейеры. Поскольку рассматривается стационарный конвейерный

процесс и определены соответствующие направляющие функции t(i, k), то

на рис. 3,а,б,в отобразим направляющие для двух конвейеров 1-2 и функ-

ции and. График изменения направляющей спусковой функции and выделен

жирной линией и в данном случае совпадает с графиком 1 (в соответствии с

определением рекурсивной функции для and). Направляющие конвейеров 1

и 2 могут выходить из одной точки, быть параллельны или направляющая 2

может быть выше направляющей 1, но они не могут пересекаться. Пересе-

чение направляющих 1 и 2, как показано на рис. 3,б, означает, что переход-

ный процесс завершился в точке с абсциссой k = k_s. Следовательно ситуа-

ция сводится к случаю, когда обе направляющие выходят из одной точки

рис. 3,в. Таким образом ситуация, показанная на рис. 3,а, является основ-

ной, а остальные сводятся к ней. Проанализируем данную ситуацию. Так как

t(i, k) функции and определяется t(j, k) конвейера, который имеет меньшую

производительность (в данном случае конвейер 1), то существующие ресурсы,

если они есть, необходимо выделить конвейеру 1. На рис. 3,г показаны исход-

ные графики, после выделения ресурсов конвейеру 1 его производительность

вырастет и направляющая станет более пологой, как показано на рис. 3,д.

Если ресурсы заимствованы не из свободного резерва, а у конвейера 2, то

производительность конвейера 2 упадет и его направляющая станет более

крутой (см. рис. 3,д). Данные примеры и рассуждения показывают, что рас-

пределение ресурсов между конвейерами 1 и 2 должны быть такими, чтобы

их производительности были равны и, как следствие, направляющие были

параллельны (см. рис. 3,е).

Если после данного предела в какой-либо конвейер добавить ресурс, то

направляющие пересекутся и ситуация вернется к исходной. Более того, если

рассматривать соотношения производительностей трех конвейеров, то воз-

можны три существенных варианта, представленные на рис. 3,ж,з,и. В ва-

рианте ж производительность конвейера определяется конвейером 1, соот-

ношение двух других не имеет значения. В варианте з аналогичным образом

производительность определяется конвейером 2, а в варианте и - конвейе-

ром 3.

Окончательным итогом данных рассуждений является равенство трех

производительностей W₁ = W₂ = W₃ как условие оптимальности, а система

ограничений на производительности выглядит следующим образом:

W -→ max;

W ≤W₁;

W ≤W₂;

W ≤W₃.

Этап 5. Прежде чем рассмотреть заключительный этап, сформулируем

теорему.

Теорема 1. Если рекурсивный конвейер, состоит из n описанных выше

операций и спусковых функций и W - производительность конвейера, то

для любых двух операций i = j (1 ≤ i, j ≤ n) условие W -→ max означает,

что



 x_i

x_j



→ min .

-

p_iω_i -

p_jω_j

Доказательство теоремы фактически было рассмотрено выше для всех ви-

дов спусковых функций и операции. Данная теорема играет важную роль

при формулировании на основании графической модели конвейера системы

неравенств соответствующей задачи линейного программирования. Описание

системы неравенств, относящейся к ограничениям на ресурсы, не представ-

ляет проблемы. На основании данной теоремы система неравенств для про-

изводительности будет выглядеть следующим образом:

x_i

W ≤

p_iω_i

где i (1 ≤ i ≤ n) является номером производственной операции (не спусковой

функции). Поставленная задача полностью решена. Для иллюстрации метода

в примере 5 рассматривается оптимизация распределения ресурсов для кон-

вейера, содержащего производственные операции и все описанные спусковые

функции.

4. Примеры решения задач

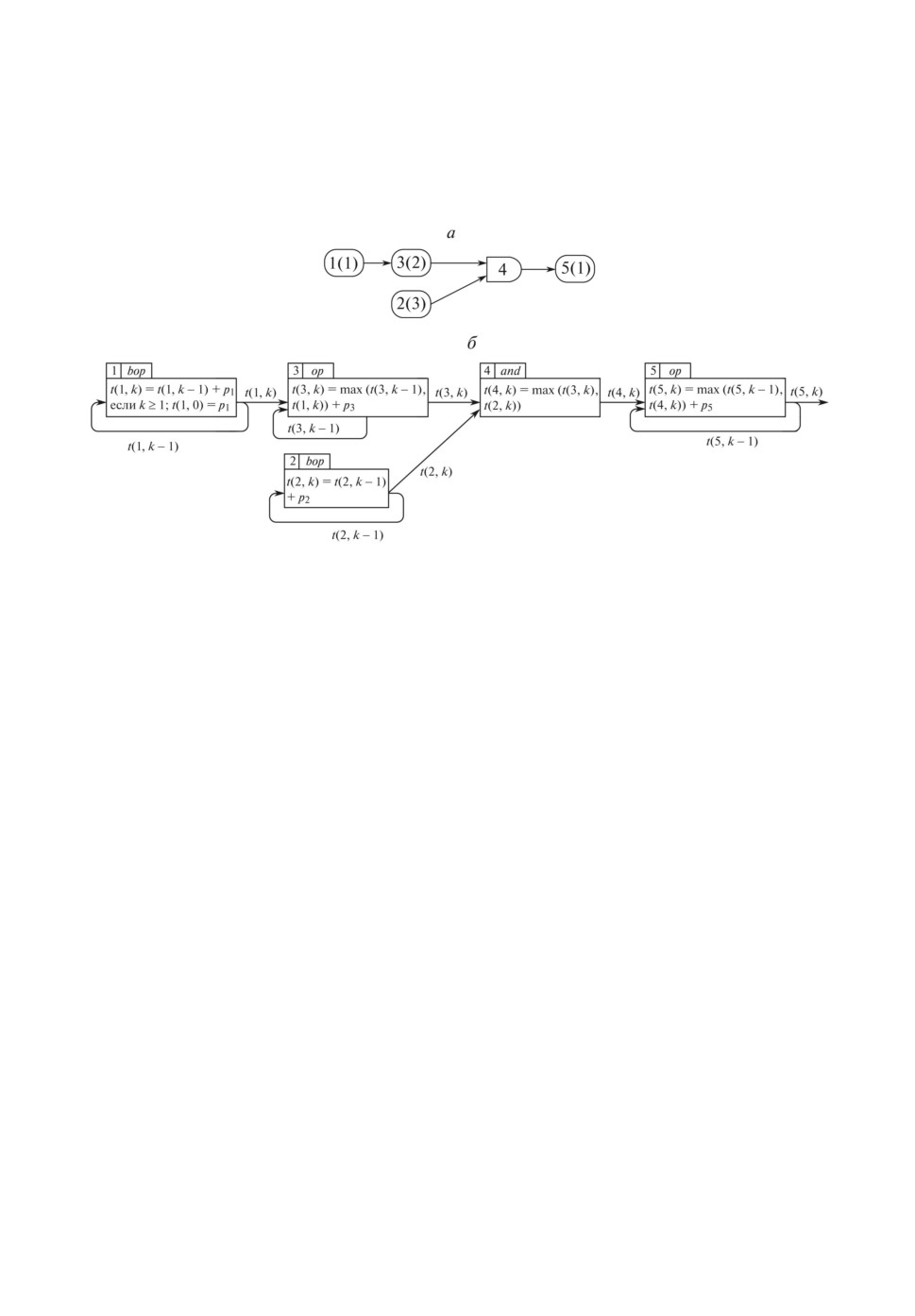
Пример 1. Рассмотрим пример конвейера, представленный на рис. 4,а,

на рис. 4,б представлена соответствующая конвейеру суперпозиция рекур-

сивных функций, вычисляющая время завершения конвейером выполнения

k-го заказа.

Рис. 4.

Ниже приведен пример вычисления времени завершения выполнения

5-й операцией 2-го заказа t(5, 2) для представленной модели. Для каждой

операции - одна исполнительная машина. Другие параметры: n = 5, n₀ = 2.

Приведем последовательность вычисления рекурсивных функций:

t(5, 2) = max(t(4, 2), t(5, 1)) + 1;

t(5, 1) = max(t(4, 1) + t(5, 0)) + 1;

t(5, 0) = t(4, 0) + 1;

t(4, 2) = max(t(2, 2), t(3, 2));

t(4, 1) = max(t(2, 1), t(3, 1));

t(4, 0) = max(t(2, 0), t(3, 0));

t(3, 2) = max(t(1, 2), t(3, 1)) + 2;

t(3, 1) = max(t(1, 1), t(3, 0)) + 2;

t(3, 0) = t(1, 0) + 2;

t(2, 2) = t(2, 1) + 4;

t(2, 1) = t(2, 0) + 4;

t(2, 0) = 4;

t(1, 2) = t(1, 1) + 1;

t(1, 1) = t(1, 0) + 1;

t(1, 0) = 1.

Рис. 5.

Пример 2. Пусть у нас имеется конвейер в виде цепочки из пяти опера-

ций (см. рис. 5). Времена выполнения операций указаны в скобках. Имеется

два комплекта ресурсов. Первый - 6 единиц, второй - 3. Использование ре-

сурсов операциями указаны на рисунке пунктирными линиями. В комплекты

операций входит не больше чем по одному ресурсу (т.е. все 0 ≤ a_ij ≤ 1). Целе-

вая функция W -→ max. Система ограничений будет выглядеть следующим

образом:

{

x₁ + x₃ + x₅ ≤ 6;

а) ограничения на ресурсы

x₂ + x₄ ≤ 3;

б) поскольку для решения задачи оптимизации представляют интерес не

абсолютные значения производительностей, а относительные, коэффициенты

производительности c_i для удобства преобразуем в целые числа по формуле

lcm(c₁, c₂, . . . c₅)

c_i =

c_i

где lcm - наименьшее общее кратное. Осуществляя данное преобразование c_i,

сохраняем пропорции между коэффициентами, но преобразуем их в целые

числа. Вычисленные таким образом коэффициенты представлены в табл. 1.

Рис. 6.

Ограничения на производительность будут выглядеть следующим образом:

W ≤ 2x₁;

W ≤ 6x₂;

W ≤ 6x₃;

W ≤ 3x₄;

W ≤ 3x₅.

Решение данной системы дает следующий результат:

x₁ = 3, x₂ = 1, x₃ = 1, x₄ = 2, x₅ = 2, W = 6.

Построенная на основании вычисленного распределения ресурсов и новых

рекурсивных функций временная диаграмма обработки двенадцати заказов

будет иметь вид, представленный на рис. 5,в. На рис. 5,б представлена диа-

грамма для случая, когда каждая операция использует по одному комплекту

ресурсов.

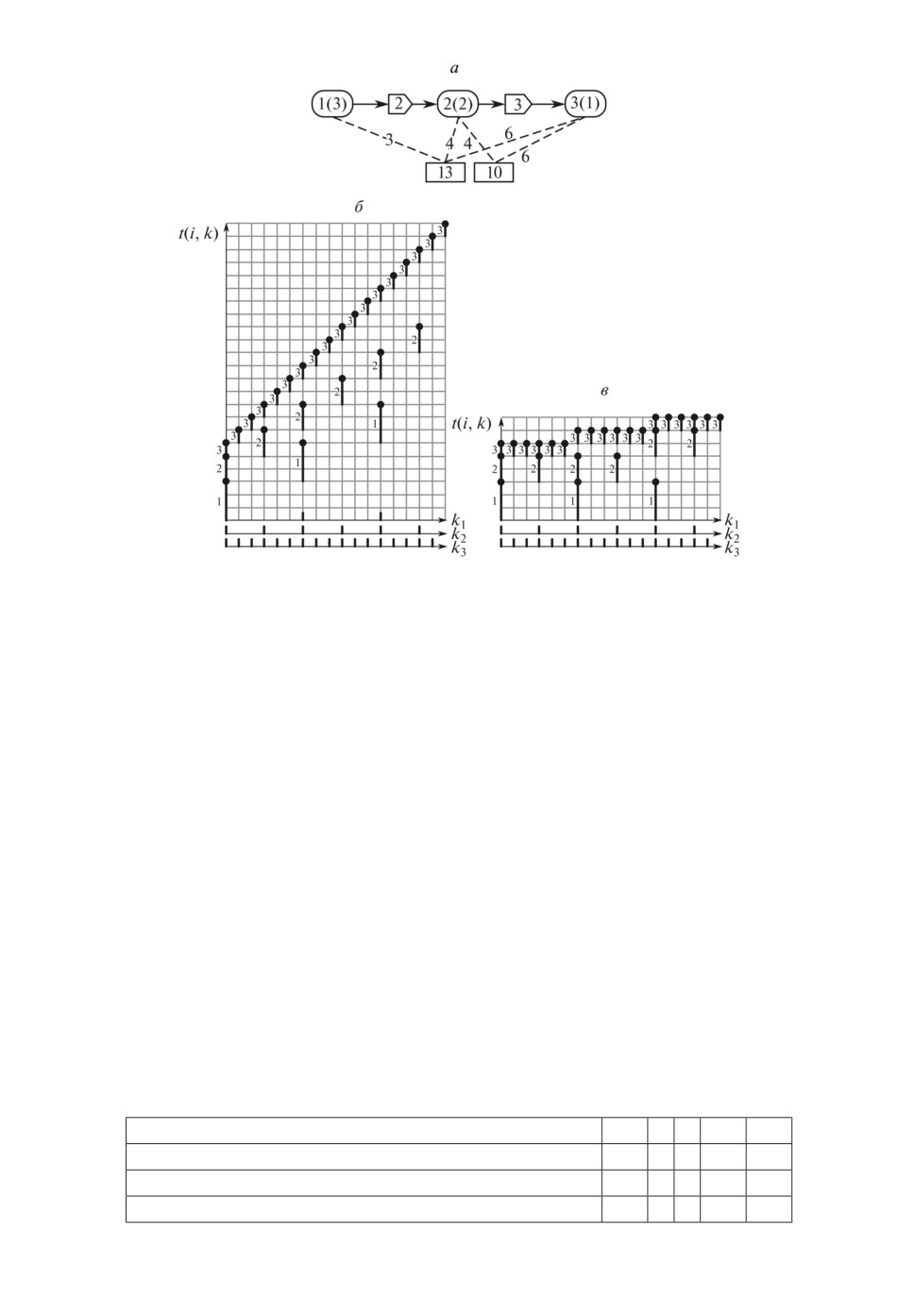
Пример 3. Рассмотрим пример конвейера рис. 6,а. В данном случае при-

сутствуют спусковые функции mul и кратности выполнения операций будут

отличны от единицы.

Таблица 1. Параметры линейного конвейера

Номер операции i

Время выполнения операции t_i

Коэффициент производительности c_i

1/3

1/2

Приведенный коэффициент производительности c_i

Таблица 2. Параметры конвейера с функцией мультиплицирования

Номер операции i

Время выполнения операции t_i

Кратность операции ω_i

1/6

1/3

Приведенная кратность ω_i

Коэффициент производительности c_i

1/9

1/8

1/6

Приведенный коэффициент производительности c_i

В табл. 2 представлены параметры модели. В общем случае кратности

являются дробными величинами, и перейти к целым приведенным значениям

можно по формуле

lcm(ω₁, ω₂, . . . , ω₅)

ω_i =

ω^′

где ω^′i - исходная кратность операции. Задача линейного программирования

будет иметь следующий вид:

W -→ max;

{

x₁ + x₂ + x₃ ≤ 13;

x₂ + x₃ ≤ 10;

W ≤ 4x₁;

W ≤ 3x₂;

W ≤ 2x₃.

Решение данной системы дает следующий результат:

x₁ = 3, x₂ = 4, x₃ = 6, W = 12.

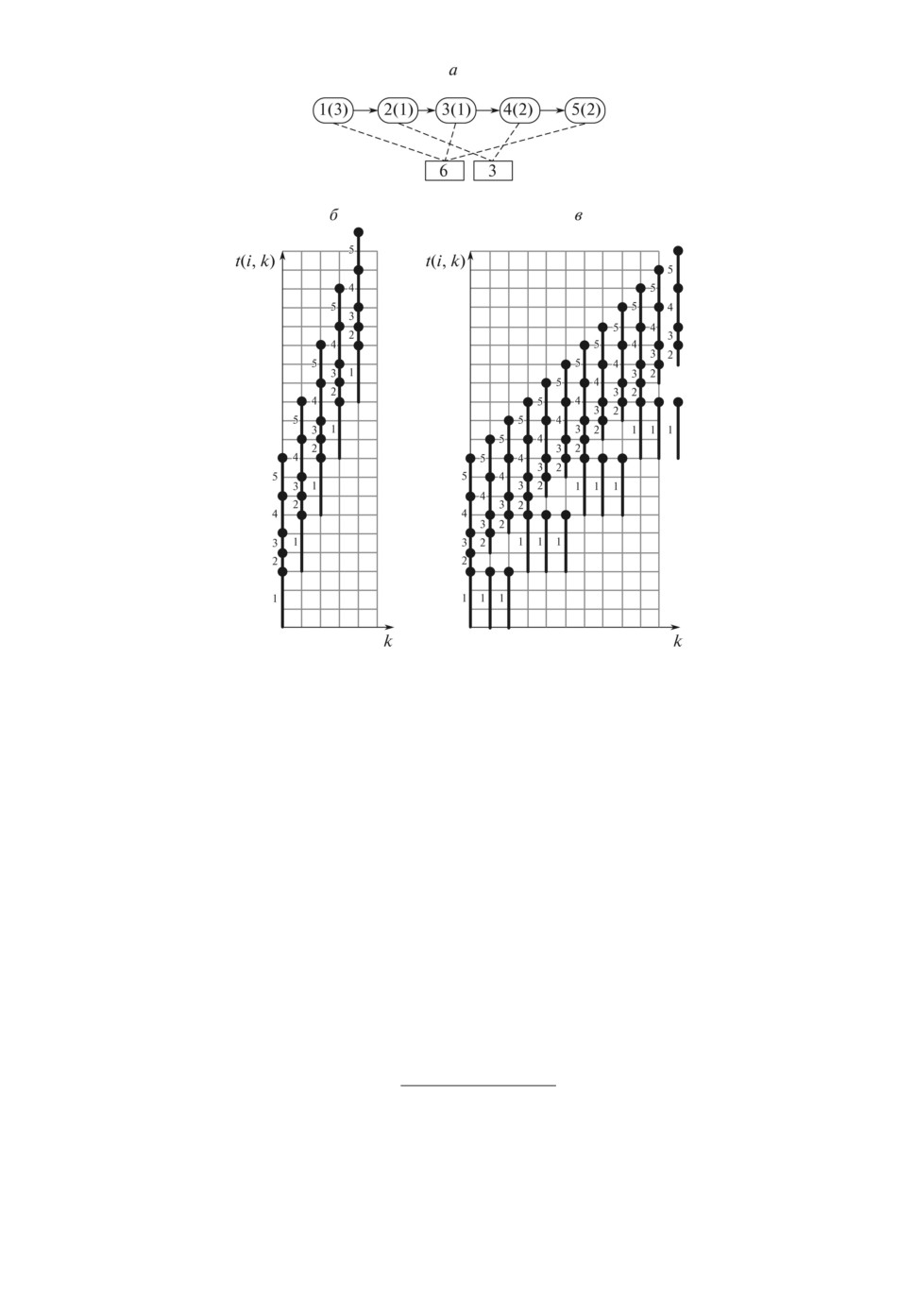
Рекурсивные функции вычисления t(i, k) остаются прежними. На рис. 6,б,в

показаны две диаграммы: вариант диаграммы б, когда каждая операция име-

ет один комплект ресурсов, и вариант в, когда ресурсы распределены в соот-

ветствии с найденным решением. В общем случае каждая операция должна

отображаться на отдельной временной диаграмме, однако для наглядности

их имеет смысл совмещать, при этом для каждой операции рисовать свою

ось абсцисс.

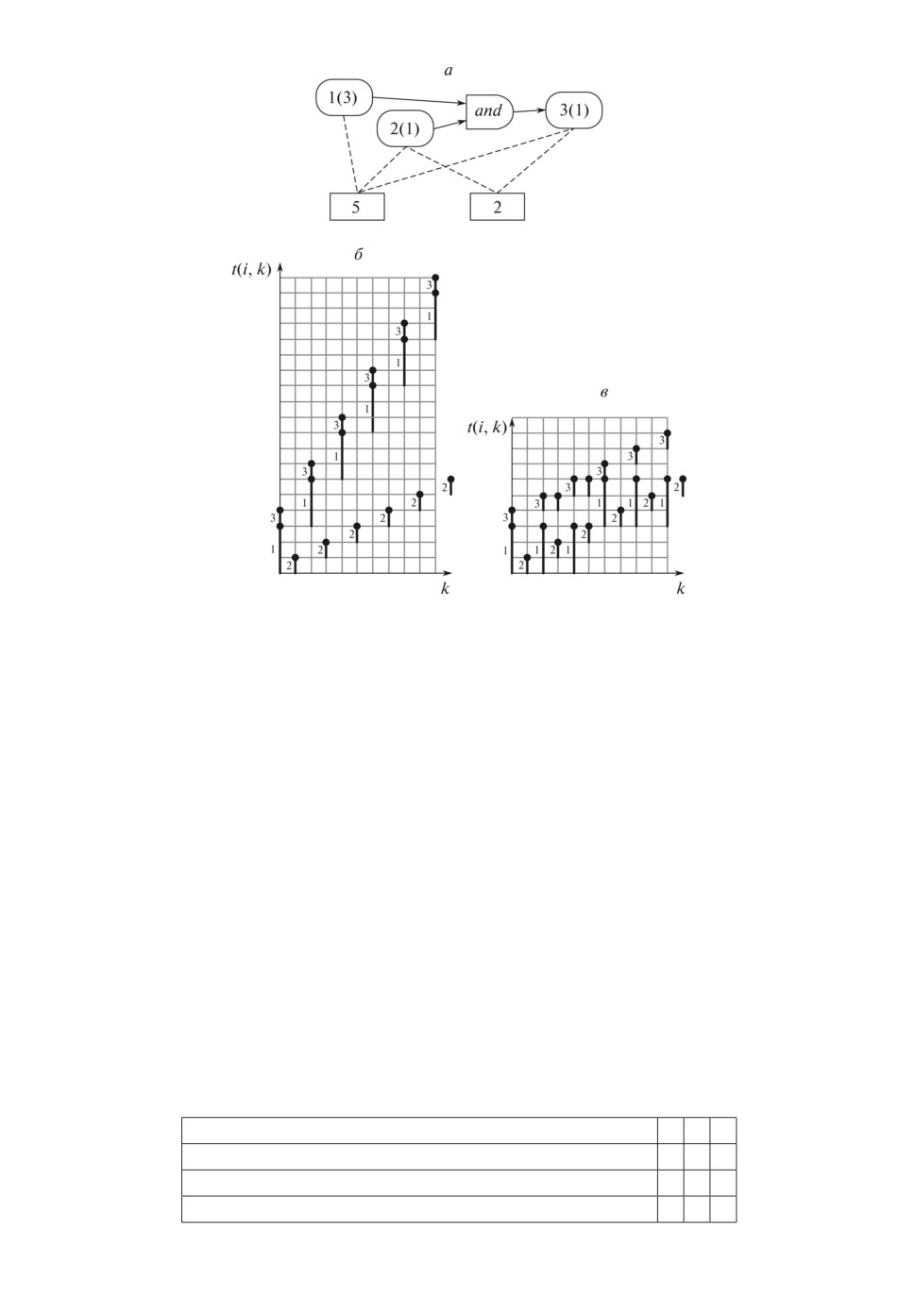
Пример 4. Рассмотрим пример модели, представленной на рис. 7,а. Из

предыдущих рассуждений следует, что операции 1, 2 должны иметь равную

производительность, а так как функция and включена последовательно с

операцией 3, то они все должны быть равны между собой для выполнения

условия оптимальности. Производительность конвейера должна быть мак-

симизирована. Параметры модели представлены в табл. 3. Целевая функция

W -→ max. Система ограничений будет выглядеть следующим образом:

{

x₁ + x₂ + x₃ ≤ 5;

а) ограничения на ресурсы

x₂ + x₃ ≤ 2;

Рис. 7.

б) ограничения на производительность

W ≤x₁;

W ≤ 3x₂;

W ≤ 3x₃.

Решение данной системы дает следующий результат:

x₁ = 3, x₂ = 1, x₃ = 1, W = 3.

На рис. 7,б,в показаны диаграммы выполнения конвейера а - с одним ком-

плектом на каждую операцию, а б - в соответствии с вычисленным распре-

делением ресурсов.

Ось абсцисс у всех операций общая. Отрезки, соответствующие опера-

ции 2, смещены вправо от своих делений. Это сделано для того, чтобы не

сливались диаграммы разных операций.

Таблица 3. Параметры конвейера с функцией and

Номер операции i

Время выполнения операции p_i

Кратность операции ω_i

Приведенный коэффициент производительности c_i

3(1)

1(3)

2(1)

get

3/2

put

6(1)

4(2)

5(1)

3/2

8(1)

7(2)

Рис. 8.

Пример 5. На рис. 8 представлен пример конвейера, использующий все

рассмотренные спусковые функции. Справа снизу у каждой операции пред-

ставлена неприведенная кратность ее выполнения. Целевая функция опре-

деляется как W -→ max. Используется три множества ресурсов. В первом

44 единицы, во втором 26 и в третьем 12. Каждый комплект может содер-

жать только по одному ресурсу. В табл. 4 представлены характеристики кон-

вейера и матрица использования ресурсов операциями конвейера. Система

ограничений на ресурсы выглядит следующим образом





x₁ + x₂ + x₃ + x₄ + x₅ + x₆ + x₇ + x₈ ≤ 44;

x₁ + x₂ + x₇ + x₈ ≤ 26;



x₃ + x₄ + x₅ ≤ 12.

Ограничения на производительность в соответствии с теоремой следую-

щие:

W ≤c₁x₁;

W ≤c₂x₂;

W ≤c₃x₃;

W ≤c₄x₄;

W ≤c₅x₅;

W ≤c₆x₆;

W ≤c₇x₇;

W ≤c₈x₈.

Решение задачи имеет следующий вид:

x₁ = 6, x₂ = 6, x₃ = 3, x₄ = 6, x₅ = 3, x₆ = 6, x₇ = 12, x₈ = 2, W = 12.

Таблица 4. Характеристики конвейера и матрица использования ресурсов

Номер операции i

Время выполнения операции p_i

Приведенная кратность операции ω_i

Приведенный коэффициент производительности c_i

Использование 1-го ресурса

Использование 2-го ресурса

Использование 3-го ресурса

5. Заключение

Разработанная в статье методика решения задачи распределения ресурсов

позволяет в автоматическом режиме на основе графической модели конвейе-

ра и матрицы использования операциями ресурсов формировать исходные

данные для задачи целочисленного линейного программирования. Решение

данной задачи позволяет вычислить верхнюю оценку времени изготовления

k изделий как частное от деления числа изделий на производительность кон-

вейера при условии вычисления параметров в реальных величинах. Получен-

ные результаты могут быть использованы не только при непосредственном

проектировании конвейера, но и осуществлять перераспределение ресурсов

при настройке конвейера на новый заказ. Еще одно возможное применение

метода - получение граничных оценок для других, более сложных и эффек-

тивных методов оптимизации в теории расписаний. Решение задачи в данной

постановке открывает перспективу для решения соответствующей двойствен-

ной задачи линейного программирования. Следует отметить, что полный спи-

сок спусковых функций, приведенный в [12, 14], включает дизъюнкцию or.

Однако для данной функции отсутствует общее решение задачи оптимизации

распределения ресурсов. Поэтому она в данной статье не рассматривается.

СПИСОК ЛИТЕРАТУРЫ

Сачко Н.С. Организация и оперативное управление машиностроительным про-

изводством. Минск: ООО ¾Новое знание¿, 2005.

Rekiek B., Dolgui A., Delchambre A., Bratcu A. State of art of optimization methods

for assembly line design // Ann. Rev. Control. 2002. No. 26. С. 163-174.

Ghosh S., Gagnon R.J. A comprehensive literature review and analysis of the design,

balancing and scheduling of assembly systems // Int. J. Product. Res. 1989. V. C-27.

P. 637-670.

Helgeson W.B., Salveson M.E., Smith W.W. How to balance an assembly line //

Techni. Report, Carr Press. 1954. New Caraan, Conn.

Bowman E.H. Assembly line balancing by linear programming // Oper. Res. 1960.

No. 8(3). P. 385-389.

Salveson M.E. The assembly line balancing problem // J. Indust. Engineer. 1955.

No. 6. P. 18-25.

Бурков В.Н. Распределение ресурсов как задача оптимального быстродей-

ствия // АиТ 1966. Т. 27. Вып. 7. С. 119-129.

Ranjbar M., Kianfar F., Shadrokh S. Solving the resource availability cost problem in

project scheduling by path relinking and genetic algorithm // Appl. Math. Comput.

2008. Т. 196. Вып. 2. С. 879-888.

Kaabi J., Harrath Y. A survey of parallel machine scheduling under availability

constraints // Int. J. Comput. Inform. Technol. 2014. Т. 3. Is. 2. P. 238-245.

10.

Боброва Е.А., Сервах В.В. Построение циклических расписаний при наличии

параллельных машин // Дискретный анализ и исследование операций. 2017.

№ 1. Т. 24. С. 5-20.

11.

Мезенцев Ю.А., Эстрайх И.В. Эффективный параметрический алгоритм оп-

тимизации расписаний параллельных систем с заданным расписанием начала

обслуживания // Научн. вест. НГТУ. 2018. Т. 72. № 3. С. 87-106.

12. Куприянов Б.В. Рекурсивные конвейерные процессы - основные свойства и ха-

рактеристики // Экономика, статистика и информатика. Вестн. УМО. 2015. № 1.

С. 163-170.

13. Куприянов Б.В. Применение модели конвейерных процессов рекурсивного ти-

па для решения прикладных задач // Экономика, статистика и информатика.

Вестн. УМО. 2014. № 5. С. 170-179.

14. Куприянов Б.В. Метод эффективного анализа модели рекурсивного конвейер-

ного процесса // АиТ. 2017. № 3. С. 63-79.

Kupriyanov B.V. Method of Efficient Analysis of the Recursive Conveyor Process

Models // Autom. Remote Control. 2017. V. 78. No. 3. С. 435-449.

15. Куприянов Б.В. Вычисление некоторых производственных характеристик ре-

курсивного конвейера // Открытое образование. 2016. № 1. Т. 20. С. 11-16.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 17.07.2019

После доработки 23.10.2019

Принята к публикации 28.11.2019