Автоматика и телемеханика, № 5, 2020
© 2020 г. Ю.Н. СОТСКОВ, д-р физ.-мат. наук (sotskov48@mail.ru)
(Объединенный институт проблем информатики НАН Беларуси, Минск)
ОБЛАСТЬ ОПТИМАЛЬНОСТИ ПЕРЕСТАНОВКИ
ОБСЛУЖИВАНИЯ НА ОДНОМ ПРИБОРЕ ТРЕБОВАНИЙ
С НЕОПРЕДЕЛЕННЫМИ ДЛИТЕЛЬНОСТЯМИ
Исследуется задача оптимизации расписания обслуживания заданно-
го множества требований на одном приборе. При составлении расписа-
ния для каждого требования известны нижняя граница и верхняя гра-
ница допустимой длительности его обслуживания. В качестве крите-
рия оптимальности расписания рассматривается минимизация суммарно-
го времени обслуживания заданного множества требований. Исследова-
ны свойства области оптимальности перестановки обслуживания требова-
ний. Разработаны полиномиальные алгоритмы построения области опти-
мальности перестановки обслуживания требований и вычисления объема
области оптимальности. Определены условия существования пустой об-
ласти оптимальности для перестановки обслуживания требований. Уста-
новлен критерий существования перестановки обслуживания требований
с максимально возможным объемом области оптимальности.
Ключевые слова: теория расписаний, неопределенные длительности об-
служивания требований, минимизация суммарного времени, область оп-
тимальности.
DOI: 10.31857/S0005231020050050
1. Введение
Оперативно-календарное планирование производства включает этап со-
ставления календарных планов выполнения поступивших заказов (составле-
ние расписаний обслуживания заданного множества требований) на имею-
щемся оборудовании (на множестве обслуживающих приборов). Оптималь-
ное расписание производственного процесса является важным фактором его
эффективности, поскольку позволяет сократить производственные расходы
предприятия, уменьшить время реализации заявок заказчиков на продукцию
предприятия, своевременно снабжать прозводственный процесс сырьем, ма-
териалами и комплектующими деталями, необходимыми для изготовления
конечной продукции предприятия. Оптимальное расписание производствен-
ного процесса позволяет уменьшить расходы на хранение сырья, комплектую-
щих деталей и материалов и в итоге повысить эффективность использования
имеющихся ресурсов (обслуживающих приборов) и капитала.
Для практических задач оперативно-календарного планирования, как
правило, не удается заранее определить точные значения длительностей об-
служивания заданных требований, однако имеется возможность оценить сни-
зу и сверху длительности их обслуживания. Для решения таких задач требу-
60
ются алгоритмы построения расписаний, близких к оптимальным, в условиях
неопределенности числовых параметров [1-9].
В разделе 2 данной статьи рассматривается задача построения близко-
го к оптимальному расписания обслуживания требований множества J =
= {J1, . . . , Jn} на одном приборе с критерием
∑Ci минимизации суммы мо-
ментов Ci завершения обслуживания всех требований Ji ∈ J при условии,
что при построении расписания известны только нижняя граница pLi > 0 и
верхняя граница pUi ≥ pLi возможной длительности pi ∈ [pLi, pUi ] обслужива-
ния требования Ji. В разделе 3 определяется область оптимальности для пе-
рестановки πk = (Jk1 , . . . , Jkn ) обслуживания требований множества J , кото-
рая содержит параллелепипед оптимальности для той же перестановки. Па-
раллелепипед оптимальности для перестановки πk был исследован в [10-17].
В разделе 4 разработаны полиномиальные алгоритмы для определения обла-
сти оптимальности для перестановки πk и для определения объема области
оптимальности. Доказаны необходимые и достаточные условия, при выпол-
нении которых область оптимальности для перестановки обслуживания за-
данных требований является пустым множеством. В разделе 5 исследованы
свойства перестановки πk обслуживания требований множества J , которая
имеет максимальный объем области оптимальности.
2. Постановка задачи и обзор известных результатов
Множество требований J = {J1, . . . , Jn} необходимо обслужить на одном
приборе. Точное значение длительности pi обслуживания требования Ji ∈
∈ J не известно на момент построения расписания обслуживания требо-
ваний J . Прерывания обслуживания требования запрещены. При реализа-
ции расписания обслуживания требований J длительность pi обслужива-
ния требования Ji [ J мо]жет принимать любое действительное значение из
заданного отрезка
pLi,pUi
, где pUi ≥ pLi > 0. Точное значение длительности
[
]
pi ∈
pLi,pUi
становится известным лишь в момент Ci завершения обслужи-
вания требования Ji. Пусть Rn обозначает пространство n-мерных действи-
тельных векторов, а Rn+ - подмножество Rn всех неотрицательных n-мерных
действительных векторов, Rn+ ⊂ Rn. В пространстве Rn множество всех век-
торов (p1, . . . , pn) допустимых длительностей обслуживания требований мно-
жества J представляет собой n-мерный параллелепипед, т.е. множество всех
векторов p = (p1, . . . , pn) ∈ Rn+, удовлетворяющих следующей системе нера-
венств:
pL1 ≤ p1 ≤ pU1; ... ; pLn ≤ pn ≤ pUn .
Множество допустимых длительностей (p1, . . . , pn) = p ∈ Rn+ обслуживания
требований множества J представим как декартово {роизведение отрезков
[pLi, pUi ]:
×ni=1[pLi,pUi ] := [pL1,pU1 ] × ... × [pLn,pUn ] = T =
p∈Rn+:pLi ≤pi ≤pUi,
}
i ∈ {1,...,n}
. Вектор p ∈ T будем называть сценарием. Пусть множе-
ство Π = {π1, . . . , πn!} содержит все перестановки πk = (Jk1 , . . . , Jkn ) тре-
бований J . Для фиксированных сценария p ∈ T и перестановки πk ∈ Π
пусть Ci = Ci(πk, p) обозначает момент завершения обслуживания требова-
61
ния Ji ∈ J в активном расписании [5, 18], однозначно определенном переста-
новкой πk. Критерий
∑Ci обозначает минимизацию суммы моментов завер-
шения обслуживания требований J :
∑
∑
(1)
Ci(πt,p) = min
Ci(πk,p)
πk∈Π
Ji∈J
Ji∈J
Указанная в (1) перестановка πt = (Jt1 , . . . , Jtn ) ∈ Π является оптимальной
перестановкой обслуживания требований J для фиксированного сценария
p∈T.
Поскольку число требований n = |J | известно на момент составления рас-
писания πt обслуживания требований J , то критерий
∑Ci означает также
∑
Ci(πk,p)
минимизацию среднего времениJi∈J
обслуживания требований мно-
n
жества J .
Сформулированная неопределенная задача обозначается как 1|pLi ≤ pi ≤
≤pUi|
∑Ci, если использовать введенную в [19] трехпозиционную фор-
му α|β|γ обозначения задач теории расписаний. Здесь и далее α обозначает
тип обслуживающей системы, β - условия обслуживания требований, а γ -
целевую функцию.
Если сценарий p ∈ T известен к моменту построения расписан [я, ины]ми
словами, для каждого требования Ji ∈ J выполняется равенство
pLi,pUi
=
= [pi, pi], то неопределенная задача 1|pLi ≤ pi ≤ pUi |
∑Ci превращается в де-
терминированную задачу 1||
∑Ci. Обозначение 1|p|∑ Ci будем использовать
для детерминированной задачи 1||
∑Ci, в которой зафиксирован сценарий
p ∈ T к моменту построения оптимального расписания. Как показано в [20],
задачу 1|p|
∑Ci можно решить за время O(nlogn) в силу следующего кри-
терия оптимальности перестановки πk ∈ Π.
Теорема 1. Перестановка πk = (Jk1,...,Jkn) ∈ Π обслуживания требо-
ваний множества J является оптимальной для задачи 1|p|
∑Ci тогда и
только тогда, когда выполняются следующие неравенства:
(2)
pk1 ≤ ... ≤ pkn.
Если pku < pkv , то требование Jku предшествует требованию Jkv в любой
перестановке πk ∈ Π, которая является оптимальной для задачи 1|p|
∑Ci.
Поскольку в неопределенной задаче 1|pLi ≤ pi ≤ pUi |
∑Ci сценарий p ∈ T
не фиксирован на момент построения перестановки πk ∈ Π обслуживания
требований J , то точное время Ci завершения обслуживания требования
Ji ∈ J определить невозможно до момента завершения обслуживания тре-
бования Ji. Следовательно, значение целевой функции
∑Ci для перестанов-
ки πk обслуживания требований J остается неизвестным вплоть до момента
завершения обслуживания всех требований множества J , если для требова-
ний Ji ∈ J выполняются строгие неравенства pLi < pUi .
Для неопределенной задачи α|pLi ≤ pi ≤ pUi |γ, как правило, не существу-
ет расписания, которое оставалось бы оптимальным для всех сценариев из
62
множества T мощности, большей единицы. Поэтому в литературе по ис-
следованию таких некорректных задач теории расписаний вводят дополни-
тельные целевые функции и (или) используют те или иные предположе-
ния. В частности, использование стохастического метода для решения зада-
чи α|pLi ≤ pi ≤ pUi |γ основано на предположении о том, что все длительности
обслуживания требований являются случайными величинами с известными
законами распределения вероятностей [7, 18].
Если нет достаточной информации о распределении вероятностей случай-
ных длительностей, то используют другие методы [5, 21]. Так, при использо-
вании робастного метода [2, 22-24] лицо, принимающее решение, предпочи-
тает исключить наихудший из возможных сценариев для искомого расписа-
ния, которое предлагается для реализации [4, 9, 23]. Для любой перестановки
πk ∈ Π и любого сценария p ∈ T разность γkp - γtp = r(πk,p) принято называть
сожалением (regret) для перестановки πk со значением целевой функции γ,
равным γkp для сценария p. Значение Z(πk) = max{r(πk, p) : p ∈ T } называет-
ся абсолютным сожалением в наихудшем случае (worst-case absolute regret), а
{
}
значение Z∗(πk) = max
r(πk,p) : p ∈ T
- относительным сожалением в наи-
γtp
худшем случае (worst-case relative regret).
Несмотря на то, что задача 1|p|
∑wiCi полиномиально разрешима [20]
при любых весах wi > 0, заданных для множества требований Ji ∈ J , по-
строение перестановки πt ∈ S с наименьшим значением Z(πt) (или переста-
новки с наименьшим значением Z∗(πt)) для задачи 1|pLi ≤ pi ≤ pUi |
∑Ci явля-
ется NP-трудной задачей даже для двух допустимых сценариев
[21, 24, 25].
В [3] разработан метод ветвей и границ для построения перестанов-
ки πt с минимальным значением абсолютного сожаления Z(πt) для задачи
1|pLi ≤ pi ≤ pUi |
∑wiCi. Вычислительные эксперименты на компьютере пока-
зали, что предложенный метод позволяет строить такую перестановку πt для
задачи 1|pLi ≤ pi ≤ pUi |
∑wiCi при условии, что число n заданных требований
не превосходит 40.
Использование метода, основанного на нечетких множествах, позволяет
строить расписания, которые являются оптимальными при нечетких дли-
тельностях обслуживания требований множества J на приборах заданного
множества M [8, 9, 26]. Этот метод позволяет решать неопределенные задачи
теории расписаний только при малых значениях числа n заданных требова-
ний.
В [1] было протестировано несколько эвристик для решения задачи
1|pLi ≤ pi ≤ pUi |
∑wiCi. В проведенных вычислительных экспериментах для
n ∈ {100,300,400,600,800,1000} использовались различные законы распреде-
ления вероятностей для выбора фактических длительностей обслуживания
требований. Вычислительные эксперименты позволили выделить наилучшую
эвристику U2, которая по всем решенным тестовым примерам давала сред-
нюю погрешность целевой функции
∑wiCi, равную 1,1% от значения целе-
вой функции, полученного для фактических длительностей обслуживания
требований.
Метод, основанный на устойчивости расписаний [6, 10-17] включает ана-
лиз устойчивости оптимальных расписаний к возможным вариациям дли-
63
тельностей обслуживания требований множества J и построение на основе
такого анализа минимального доминирующего множества расписаний. Для
любого сценария p ∈ T минимальное доминирующее множество содержит хо-
тя бы одно оптимальное расписание. В отличие от стохастического метода, ро-
бастного метода и метода, основанного на нечетких множествах, цель метода,
основанного на устойчивости расписаний, заключается в поиске расписания,
которое является оптимальным для максимально возможного числа допу-
стимых сценариев из заданного множества T . В частности, если существует
одноэлементное доминирующее множество {πt} для задачи α|pLi ≤ pi ≤ pUi |γ,
то расписание πt является оптимальным для задачи α|p|γ при всех сценариях
p ∈ T, несмотря на неопределенность длительностей обслуживания требова-
ний множества J .
В [10-12, 14, 15] метод, основанный на устойчивости расписаний, исполь-
зовался для решения задачи 1|pLi ≤ pi ≤ pUi |
∑wiCi. В [15] доказан кри-
терий существования одноэлементного доминирующего множества для за-
дачи 1|pLi ≤ pi ≤ pUi |
∑wiCi. В [12] для n ∈ {50,100,500,1000, 5000, 10000}
были случайным образом сгенерированы сложные примеры задачи
1|pLi ≤ pi ≤ pUi |
∑wiCi, которые были решены приближенно разработанным
алгоритмом MAX-OPTBOX со средней погрешностью, равной 1,5%. В [10]
примеры задачи 1|pLi ≤ pi ≤ pUi |
∑Ci были случайным образом сгенерирова-
ны для n ∈ {10, 20, . . . , 100, 200, . . . , 1000, 2000, . . . , 10000} и решены прибли-
женно разработанным алгоритмом 3 со средней погрешностью, равной 0,74%.
Алгоритм MAX-OPTBOX (алгоритм 3) строит перестановку πk ∈ Π, для
которой параллелепипед оптимальности имеет наибольший полупериметр
(наибольший относительный полупериметр соответственно). Алгоритм 3 учи-
тывает следующую особенность целевой функции
∑Ci: увеличение δ значе-
ния целевой функции в результате нарушения неравенства (2) из-за факти-
ческой длительности pki требования Jki влечет увеличение значения целевой
функции на величину δ(n - i + 1). Поэтому ошибка при выборе порядка об-
служивания требования Jki важнее такой же по величине ошибки при выборе
порядка обслуживания требования Jkj , если i < j.
Определение параллелепипеда оптимальности приведено в [10, 12]. Пусть
M = (ki1,...,ki|M|) представляет собой упорядоченное подмножество мно-
жества
{1, . . . , n}, для которого выполняются следующие соотношения:
{k1, . . . , k|M|} ⊆ {1, . . . , n}, |M| ≤ n и ki1 < . . . < ki|M| .
Определение 1. Максимальный по включению параллелепипед
[
]
[
]
[
]
OB(πk,T) = loptk
,uoptk
×...× loptk
,uoptk
=: ×kir ∈M loptk
,uopt
⊆T
i1
i1
i|M|
i|M|
ir
kir
называется параллелепипедом оптимальности для перестановки πk =
= (Jki1 , . . . , Jkin ) ∈ Π, если перестановка πk, будучи оптимальной для
задачи 1|p|
∑Ci со сценарием p = (p1,...,pn) ∈ T, остается оптимальной
и для задачи 1|p′|
∑Ci с любым сценарием p′ = (p′1,...,p′n) ∈ [p1,p1] × ...
[
]
[
]
[
]
...×
pkir -1, pkir -1
× loptk,uoptk
×
pkir +1, pkir +1
× ... × [pn,pn] ∈ T.
Если
ir
ir
нет сценария p ∈ T, для которого перестановка πk является оптимальной
для задачи 1|p|
∑Ci, то полагаем OB(πk,T) = ∅.
64
Любая вариация p′ki
длительности pkir обслуживания требования J
kir
∈
r
[
]
∈ J, принадлежащая максимальному (по включению) отрезку loptk,uopt
,
ir
kir
указанному в определении 1, гарантирует оптимальность перестановки πk ∈
∈ Π для любого сценария p′ = (p′1,...,p′n), если для него выполняется вклю-
[
]
[
]
чение p′ki
∈ loptk,uoptk
. Максимальный отрезок loptk,uoptk
длины uoptk
-lopt ≥0,k
r
ir
ir
ir
ir
ir
ir
loptk
≤ uopt, указанный в определении 1, будем называть отрезком оптималь-k
ir
ir
ности для требования Jkir ∈J в перестановке πk. Если не существует такого[
]
отрезка оптимальности loptk,uoptk
, loptk
≤uoptk, для требования J
kir
∈J , то бу-
ir
ir
ir
ir
дем говорить, что требование J
kir
не имеет отрезка оптимальности в пере-
становке πk.
3. Область оптимальности перестановки требований πk ∈ Π
Определим область оптимальности OR(πk, T ) для перестановки πk ∈
∈ Π, которая содержит параллелепипед оптимальности перестановки πk:
OB(πk,T) ⊆ OR(πk,T).
Определение 2. Максимальное по включению замкнутое подмноже-
ство OR(πk,T) ⊆ T множества Rn+ называется областью оптимально-
сти для перестановки πk = (Jk1 ,... ,Jkn ) ∈ Π относительно T, если пере-
становка πk является оптимальной для задачи 1|p|
∑Ci при любом сцена-
рии p = (p1,... ,pn) ∈ OR(πk,T). Если не существует сценария p ∈ T, для
которого перестановка πk является оптимальной для задачи 1|p|
∑Ci, то
полагаем OR(πk, T ) = ∅.
В силу теоремы 1 будем различать три типа отрезков для каждого требова-
ния Jkr ∈ J в фиксированной перестановке πk = (Jk1 , . . . , Jkn ) ∈ Π, а именно:
[
]
[
]
отрезок оптимальности loptk,uoptk
⊆
pLkr ,pU
;
r
r
kr
[
]
[
]
отрезок условной оптимальности lcoptk,ucoptk
⊆
pLkr ,pU
и
r
r
kr
[
]
[
]
отрезок неоптимальности
lnonk,unonk
⊆
pLkr ,pU
r
kr
[
]
Отрезок оптимальности loptk
,uoptk
для требования Jkr в перестановке πk
r
r
указан в определении 1 параллелепипеда оптимальности.
Отрезком неоптимальности для требования Jkr в перестановке πk =
[ (Jk1 , . . .]Jk[) ∈ Π б]удем называть максимальный по включению отрезок
lnonk,unonk
⊆
pLkr ,pUkr
, для которого перестановка πk = (Jk1 , . . . , Jkn ) не мо-
r
r
жет быть оптимальной для задачи 1|p′|
∑Ci ни при каком сценарии p′ =
= (p′1, . . . , p′n) ∈ T таком, что
{
[
]}
[
]
{
[
]}
(p′1, . . . , p′n) ∈
×r-1i=1
pLk
,pUk
×
lnonk,unonk
×
×ni=r+1
pLk
,pU
i
i
r
r
i
ki
В силу необходимых и достаточных условий (2) оптимальности переста-
новки πk ∈ Π для задачи 1|p|
∑Ci для каждого отрезка неоптимальности
[lnonk,unonk] либо существует требование Jkv ∈ J такое, что r < v и выполняют-
r
r
65
ся соотношения
(3)
pUk
=lnonk
<unonk
=pUk
,
v
r
r
r
либо существует требование Jkw ∈ J такое, что w < r и выполняются соотно-
шения
(4)
pLk
=lnonk
<unonk
=pLk
r
r
r
w
Из определения 1 также следует, что открытый интервал неоптимально-
сти (lnonk,unonk) для требования Jkr в перестановке πk = (Jk1 , . . . , Jkn ) ∈ Π не
r
r
[
]
может иметь общих точек с отрезком оптимальности loptk,uopt
, т.е.
r
kr
⋂[
]
(5)
(lnonk,unonk)
loptk,uopt
= ∅.
r
r
r
kr
Для демонстрации приведенных определений будем использовать при-
мер
1
задачи
1|pLi ≤ pi ≤ pUi |
∑Ci с 18 требованиями, n = 18. Отрезки
[
]
pLi,pUi
, определяющие допустимые длительности обслуживания требова-
[
]
ний Ji ∈ J = {J1, . . . , J18}, заданы в таблице. Отрезки
pLi,pUi
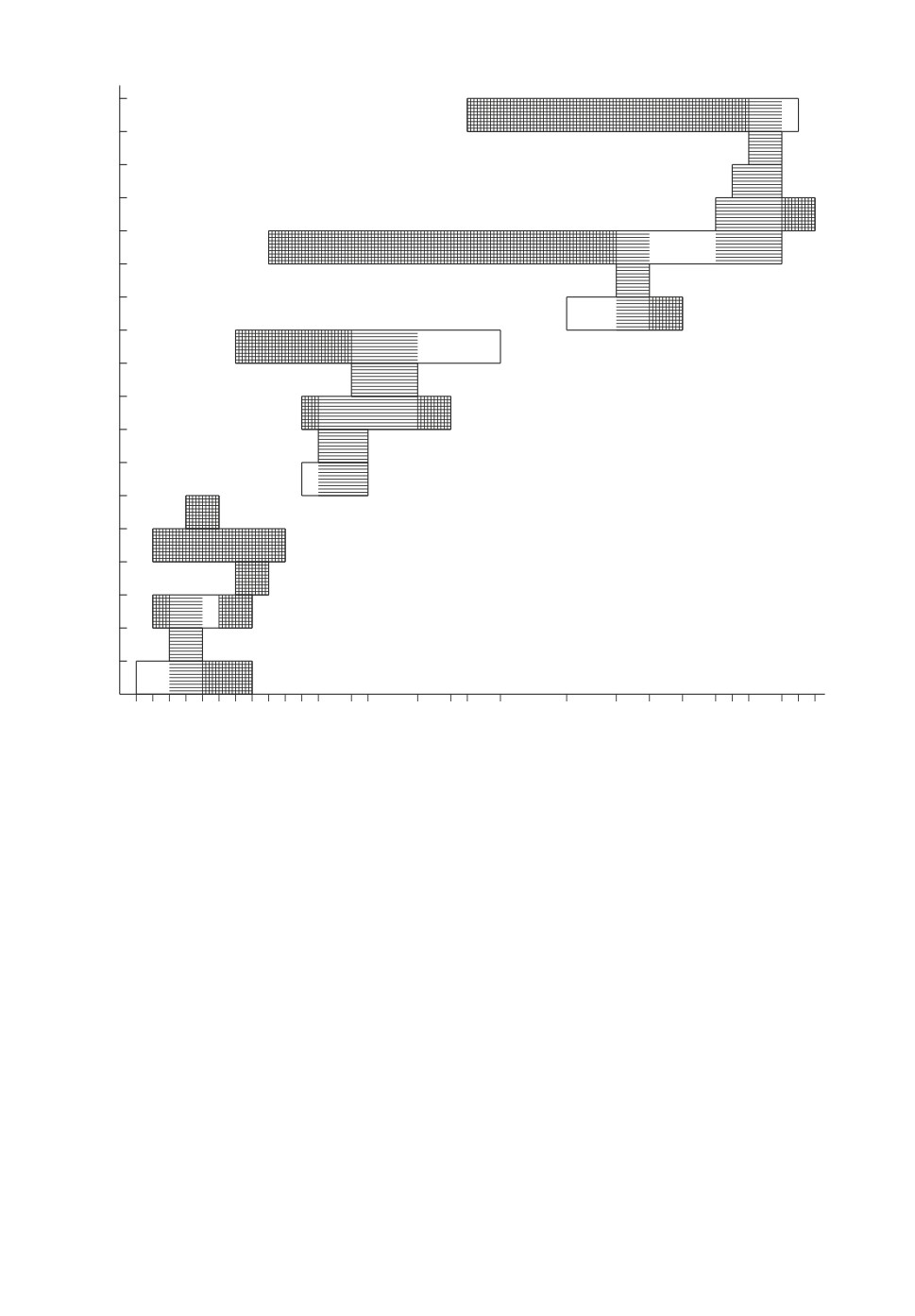
представле-
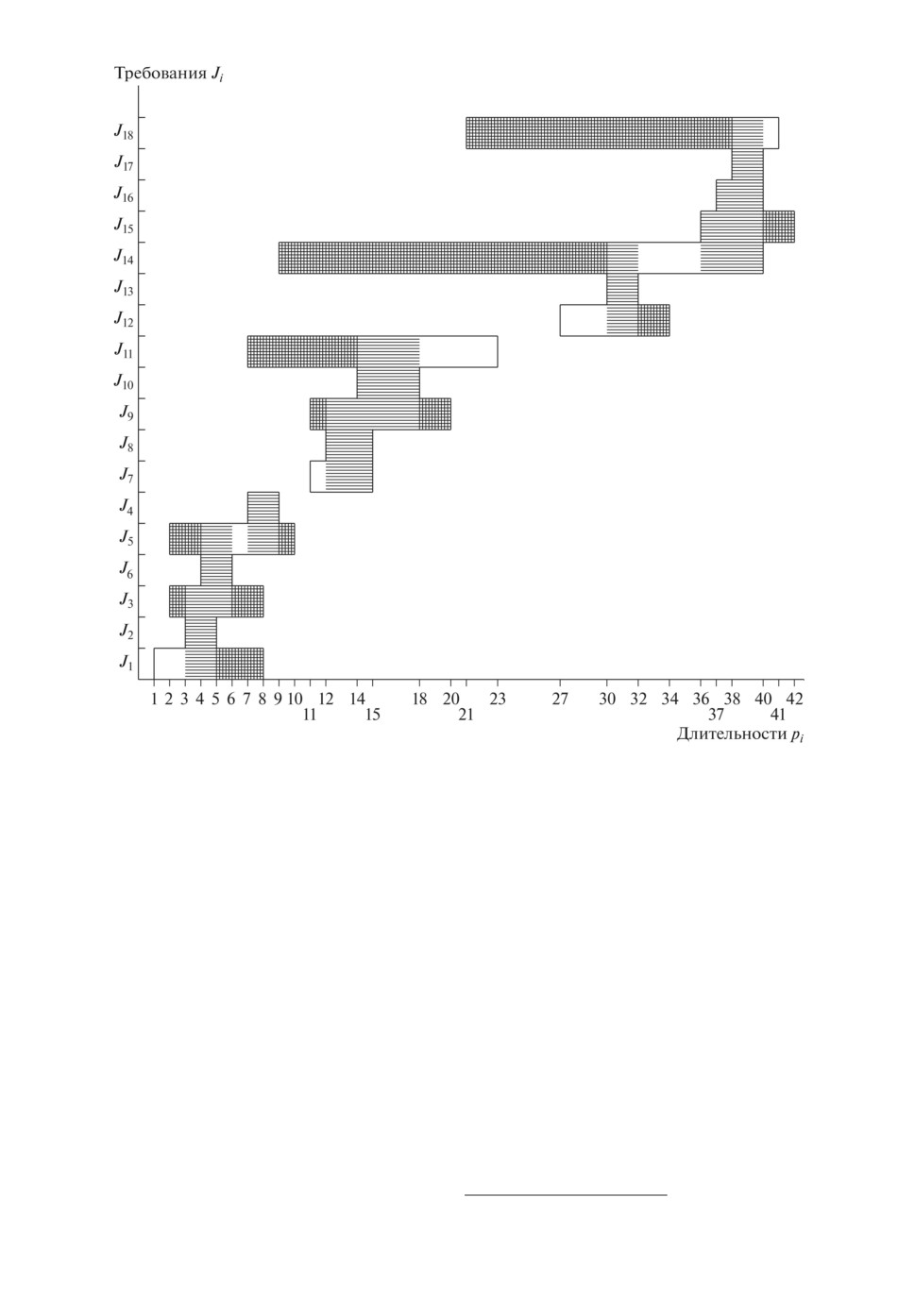
ны также на рис. 1 в системе прямоугольных координат для перестановки
π1 = (J1,... ,J18) ∈ Π. На рис. 1 ось абсцисс определяет отрезки [pLi,pUi ] до-
пустимых длительностей обслуживания требований Ji ∈ J . На оси ординат
указаны требования Ji из множества J .
Отрезком условной оптимальности для требования Jkr в перестанов-
ке πk = (Jk1 , . . . , Jkn ) ∈ Π называется максимальный по включению отрезок
[
]
[
]
[
]
lcoptk,ucoptk
⊆
pLkr ,pUkr
такой, что любая точка p∗kr
∈ lcoptk,ucopt
не принад-
r
r
r
kr
лежит открытому интервалу неоптимальности, p∗kr ∈ (lnonk,unon), и при этомk
r
r
существует хотя бы одно требование Jkd ∈ J , d = r, для которого выполня-
[
]
ется включение p∗kr
∈ pLkd,pU
kd
Из определен[я отрезк] условной оптимальности следует, что существу-
ют точки p∗kr
∈ lcoptk,ucoptk
такие, что перестановка πk ∈ Π является опти-
r
r
мальной для задачи 1|p′|
∑Ci со сценарием p′ = (p′1,...,p′n) ∈ [pk1,pk1] × ...
... × [pkr-1,pkr-1] × [pkr,pkr] ×[[pkr+1,pkr]1] × ... × [pkn,pkn], и при этом су-
ществуют другие точки p∗∗k
∈ lcoptk,ucoptk
такие, что перестановка πk ∈ Π не
r
r
r
является оптимальной для задачи 1|p′′|
∑Ci со сценарием p′′ = (p′′1,...,p′′n) ∈
∈ [pk1 , pk1 ] × . . . × [pkr-1, pkr-1] × [pk∗r, pk∗r] × [pkr+1, pkr +1] × . . . × [pkn , pkn ]. На
рис. 1 отрезки условной оптимальности для требований Ji ∈ J в перестанов-
ке π1 = (J1, . . . , J18) заштрихованы горизонтальными отрезками.
Исходные данные для примера 1 задачи 1|pLi ≤ pi ≤ pUi |
∑Ci
i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
pLi
1
3
2
7
2
4
11
12
11
14
7
27
30
9
36
37
38
21
pUi
8
5
8
9
10
6
15
15
20
18
23
34
32
40
42
40
40
41
66
Требования Ji
J18
J17
J16
J15
J14
J13
J12
J11
J10
J9
J8
J7
J6
J5
J4
J3
J2
J1
1 2 3 4 5 6 7 8 9 10
12
14
18
20
23
27
30
32
34
36
38
40
42
11
15
21
37
41
Длительности pi
Рис. 1. Отрезки оптимальности, отрезки условной оптимальности (заштрихо-
ваны горизонтальными отрезками) и отрезки неоптимальности (заштрихова-
ны горизонтальными и вертикальными отрезками) для требований Ji ∈ J в
перестановке π1 = (J1, . . . , J18) для примера 1 задачи 1|pLi ≤ pi ≤ pUi |
∑Ci.
Отметим также, что в любой фиксированной перестановке πk = (Jk1 , . . .[
]
...,Jkn) ∈ Π отрезок lcoptk,ucoptk
условной оптимальности для требования Jkr
r
r
не имеет общих точек с открытым интервалом оптимальности (loptk,uopt) и сk
r
r
открытым интервалом неоптимальности (lnonk,unon). Иными словами, выпол-k
r
r
няются следующие равенства:
[
]⋂(
)
(6)
lcoptk,ucoptk
loptk,uopt
= ∅,
r
r
r
kr
[
]⋂(
)
(7)
lcoptk,ucoptk
lnonk,unonk
= ∅.
r
r
r
r
Если не существует отрезка [lcoptk,ucoptk], lcoptk
< ucopt, условной оптималь-k
r
r
r
r
ности для требования Jkr ∈ J в перестановке πk, то будем говорить, что тре-
бование Jkr не имеет условной оптимальности в перестановке πk.
67
На рис. 1 для всех требований Ji ∈ J в перестановке π1 = (J1, . . . , J18)
представлены отрезки оптимальности, отрезки условной оптимальности и от-
резки неоптимальности. Отрезки неоптимальности для требований Ji ∈ J в
перестановке π1 зашрихованы дважды (горизонтальными и вертикальными
отрезками).
Замечание 1. В силу теоремы 1 для каждого требования Ji ∈ J в пе-
рестановке πk ∈ Π может существовать не более одного отрезка оптимально-
сти, не более двух отрезков условной оптимальности и не более двух отрезков
неоптимальности.
Как показано на рис. 1, для требования J3 в перестановке π1 ∈ Π имеет-
ся два отрезка неоптимальности [2, 3] и [6, 8], один отрезок [3, 5] условной
оптимальности и один отрезок [5, 6] оптимальности. Для требования J5 в пе-
рестановке π1 имеется два отрезка неоптимальности [2, 7] и [6, 10] с непустым
пересечением [6, 7] = [2, 7]
⋂[6, 10].
Из определений отрезков оптимальности, неоптимальности и условной оп-
тимальности для требования Jkr , r ∈ {1, . . . , n}, в перестановке πk ∈ Π следует
Лемма 1. Отрезок [pLkr,pU ] длительностей обслуживания требованияk
r
Jkr ∈ J можно представить в виде объединения всех отрезков оптималь-
ности, неоптимальности и условной оптимальности для требования Jkr ,
r ∈ {1,... ,n}, в перестановке πk = (Jk1,...Jkn) ∈ Π. Для любого отрез-
ка неоптимальности [lnonk,unon] выполняется хотя бы одно из равенствk
r
r
lnonk
= pLkr или unonk
=pU .k
r
r
r
Построение области оптимальности OR(πk, T ) перестановки πk = (Jk1 ,
...,Jkn) ∈ Π можно свести к построению области оптимальности перестанов-
ки πk для соответствующей задачи 1|pLi ≤ pi ≤ pUi |
∑Ci с сокращенными от-
[
]
[
]
резками допустимых длительностей
pLi, pUi
⊆
pLi,pUi
. Сокращенные отрез-
[
]
ки
pLkr , pUk
, Jkr ∈ J, для перестановки πk = (Jk1,...,Jkn) определяются по
r
формулам
(8)
pLk
= max
pLk
,
pUk
= min
pU
r
j
r
kj
1≤j≤r≤n
1≤r≤j≤n
для каждого требования Jkr ∈ {Jk1 , . . . , Jkn } = J . Множество сокращенных
[
]
сценариев, определенных по формулам (8), обозначим ка
T =
pL1, pU1
×...
[
]
...×
pLn, pUn
Теорема 2. Область оптимальности OR(πk,T) для перестановки
πk = (Jk1 ,... ,Jkn ) ∈ Π для задачи 1|pLi ≤ pi ≤ pUi |
∑Ci совпадает с обла-
стью оптимальности OR(πk
T) для той же перестановки для задачи
1|pLi ≤ pi ≤ pUi |
∑Ci с множеством
T допустимых сценариев.
Доказательство. Из необходимых и достаточных условий (2) опти-
мальности перестановки πk для задачи 1|p|
∑Ci получаем, что из выполне-
ния соотношений
pLk
≤pkr <pLk
= max
pLk
r
r
j
1≤j≤r≤n
68
хотя бы для одной длительности pkr следует, что перестановка πk = (Jk1 ,
...,Jkr,...,Jkn) не может быть оптимальной для задачи
1|p|
∑Ci
{
[
]}
[
]
с каким-либо сценарием p = (p1, . . . , pn) ∈
×r-1i=1
pLki,pUki
×
lnonk,unon
×
{
}
r
kr
×
×ni=r+1[pLki,pU ]
ki
Аналогично, из выполнения соотношений
min
pUk
= pUk
<pkr ≤pUk
j
r
r
1≤r≤j≤n
хотя бы для одной длительности pkr следует, что перестановка πk =
= (Jk1 , . . . , Jkr , . . . , Jkn ) не может быть оптимальной для задачи 1|p|
∑Ci
{
[
]}
[
]
с каким-либо сценарием p = (p1, . . . , pn) ∈
×r-1i=1
pLki,pUki
×
lnonk,unon
×
{
[
]}
r
kr
×
×ni=r+1
pLki,pU
ki
Таким образом, справедливо следующее утверждение: множество всех
сценариев p ∈ T , для которых перестановка πk является оптимальной
для задачи 1|pLi ≤ pi ≤ pUi |
∑Ci, содержится во множестве всех сценари-
ев p ∈ T, для которых перестановка πk является оптимальной для задачи
1|pLi ≤ pi ≤ pUi |
∑Ci с множеством
T допустимых сценариев.
Из включени
T ⊆ T следует обратное утверждение:
Утверждение. Множество всех сценариев p ∈ T, для которых пере-
становка πk является оптимальной для задачи 1|pLi ≤ pi ≤ pUi|
∑Ci, содер-
жится во множестве всех сценариев p ∈ T , для которых перестановка πk
является оптимальной для задачи 1|pLi ≤ pi ≤ pUi |
∑Ci.
Из доказанных утверждений следует, что для исходной задачи 1|pLi ≤
≤pi ≤pUi|
∑Ci и для задачи 1|pLi ≤ pi ≤ pUi|∑Ci с множеством сценариев
[
]
[
]
T =
pL1, pU1 ×
×...×
pLn, pUn ×
области оптимальности совпадают для лю-
бой фиксированной перестановки πk ∈ Π: OR(πk, T ) = OR(πk
T). Tеорема 2
доказана.
Из определения 2 и теоремы 2 нетрудно получить следующее утверждение.
∑Ci с множеством сценариев
T
Лемма 2. Для задачи 1|pLi ≤ pi ≤ pU(i|
)
открытый интервал оптимальности loptk,uoptk
для требования Jkr в пере-
r
r
[
]
становке πk ∈ Π не имеет общих точек с отрезком pLkd,pU
допустимых
kd
длительностей любого другого требования Jkd ∈ J , d = r, т.е. выполняется
следующее равенство:
⋂
(9)
(loptk,uoptk)
[pLk
,pU
] = ∅.
r
r
d
kd
Докажем небходимые и достаточные условия, при выполнении которых об-
ласть оптимальности для перестановки πk ∈ Π является пустым множеством.
Теорема 3. Область оптимальности OR(πk,T) для перестановки
πk = (Jk1 ,... ,Jkn ) ∈ Π является пустым множеством, OR(πk,T) = ∅, то-
гда и только тогда, когда существует хотя бы одно требование Jkr ∈ J ,
r ∈ {1,... ,n}, в перестановке πk = (Jk1,...,Jkn) ∈ Π, которое не имеет
условной оптимальности и одновременно не имеет отрезка оптимально-
сти.
69
Доказательство.
Достаточность. Пусть существует требование Jkr ∈ J в перестановке
πk = (Jk1 ,... ,Jkn ) ∈ Π, которое не имеет условно[ оптимал]но[ти и не]име-
ет отрезка оптимальности. По лемме 1 получаем
lnonk,unonk
=
pLkr ,pU
= ∅.
r
r
kr
Следовательно, либо существует требование Jkv ∈ J такое, что r < v и вы-
полняются соотношения (3), либо существует требование Jkw ∈ J такое, что
w < r и выполняются соотношения (4). В первом случае не[равенст]о pkv<pkr
выполняется для каждой допустимой длительности pkr ∈
pLkr ,pU
обслужи-
kr
[
]
вания требования Jkr и для каждой допустимой длительности pkv ∈
pLkv ,pU
kv
обслуживания требования Jkv . Во втором случае нера[енство]pkw > pkr вы-
полняется для каждой допустимой длительности pkr ∈
pLkr ,pU
обслужива-
kr
[
]
ния требования Jkr и для каждой допустимой длительности pkw ∈
pLkw ,pU
kw
обслуживания требования Jkw .
В силу теоремы 1 в обоих случаях перестановка πk не может быть оп-
тимальной для задачи 1|p|
∑Ci при каком-либо сценарии p ∈ T. Следова-
тельно, согласно определению 2 область оптимальности для перестановки
πk = (Jk1 ,... ,Jkn ) ∈ Π является пустым множеством, OR(πk,T) = ∅. Доста-
точность доказана.
Необходимость. Докажем необходимость методом от противного. Пусть
равенство OR(πk, T ) = ∅ выполняется. Однако предположим, что не суще-
ствует ни одного требования Jkr ∈ J , r ∈ {1, . . . , n}, в перестановке πk =
= (Jk1 , . . . , Jkn ) ∈ Π, которое не имеет условной оптимальности и не имеет
отрезка оптимальности.
Согласно определению 2 pавенство OR(πk, T ) = ∅ означает, что не суще-
ствует ни одного сценария p ∈ T такого, что перестановка πk является оп-
тимальной для задачи 1|p|
∑Ci со сценарием p ∈ T. Тем не менее покажем,
как построить сценарий p∗∈ T , который содержится в области оптимальности
для перестановки πk.
Если для требования Jki существует отрезок оптимальности [loptk,uopt],k
[
i
i
]
loptk≤uoptk, в перестановке πk, то существует хотя бы одна точка p∗ki∈ loptk,uopt
i
i
i
ki
Выберем такое значение p∗ в качестве длительности обслуживания требова-k
i
ния Jki .
Если же не существует отрезка оптимальности для требования Jkj в пере-
[
]
мальности lcoptk,ucoptk
для требования Jkj . Выберем значение lcopt в качествеk
j
j
j
длительности обслуживания требования Jkj : p∗kj = lcopt.k
j
При таком выборе длительностей p∗kj обслуживания всех требований Jkj ∈
∈ {Jk1 , . . . , Jkn } = J получаем сценарий p∗ = (p∗k1 , . . . , p∗ ) ∈ T . Из равенствk
n
(6), (7) и леммы 2 с равенством (9) следует, что перестановка πk являет-
ся оптимальной для задачи 1|p∗|
∑Ci. Следовательно, имеет место вклю-
чение p∗ ∈ OR(πk, T ), которое противоречит предполагаемому равенству
OR(πk, T ) = ∅. Полученное противоречие завершает доказательство теоре-
мы 3.
70
Из теоремы 3 следует, что если OR(πk, T ) = ∅, то в перестановке πk =
= (Jk1 , . . . , Jkn ) ∈ Π для каждого требования Jkr ∈ J , r ∈ {1, . . . , n}, существу-
ет хотя бы один отрезок оптимальности или отрезок условной оптимально-
сти. Поэтому размерность непустой области оптимальности OR(πk, T ) равна
n = |J|. Поскольку из теоремы 3 следует и обратное утверждение, то полу-
чаем
Следствие 1. Размерность области оптимальности OR(πk,T) равна
n = |J| тогда и только тогда, когда OR(πk,T) = ∅.
На рис. 1 для отрезка неоптимальности [lnon4, unon4] = [7, 9] требования J4
в перестановке π1 = (J1, . . . , J18) выполняются равенства [lnon4, unon4] = [7, 9] =
= [pL4, pU4 ], т.е. требование J4 не имеет условной оптимальности и одновремен-
но не имеет отрезка оптимальности в перестановке π1. Из теоремы 3 следует,
что область оптимальности для перестановки π1 является пустым множе-
ством, OR(π1, T ) = ∅.
4. Построение области оптимальности и вычисление ее объема
В результате использования теоремы 3 разработан алгоритм 1 сложности
O(n) для проверки выполнения равенства OR(πk, T ) = ∅ для фиксированной
перестановки πk ∈ Π.
Если алгоритм 1 устанавливает, что для перестановки πk справедливо со-
отношение OR(πk, T ) = ∅, то в соответст[вии с т]оремой 2 алгоритм 1 строит
по формулам (8) сокращенные отрезки
pLi, pUi
допустимых длительностей
обслуживания требований Ji ∈ J . Тем самым определяются исходные данные
для задачи 1|pLi ≤ pi ≤ pUi |
∑Ci смножеством
T допустимых сценариев.
Алгоритм 1.
ВХОД: Отрезки [pLi, pUi ] длительностей обслуживания требований Ji ∈ J ;
перестановка πk = (Jk1 , . . . , Jkn ) ∈ Π обслуживания требований J .
ВЫХОД: Отрезки [pLi, pUi ] для требований Ji ∈ J , если установлено, что
OR(πk, T ) = ∅.
Шаг 1:
pLk
= pLk1, tL = pL , r = 2;k
1
1
Шаг 2: IF pUkr ≥ tL THEN GOTO шаг 3 ELSE GOTO шаг 5;
Шаг 3: IF pLkr > tL THEN tL = pLkr , pLk
= tL, r := r + 1;
r
ELSE pLk
= tL, r := r + 1;
r
IF r ≤ n THEN GOTO шаг 2 ELSE pUk
=pUkn, tU =pU ;k
n
n
Шаг 4: FOR r = n - 1 to 1 STEP -1 DO
IF pUkr < tU THEN tU = pUkr , pUk
= tU ELSE pUk
=tU;
r
r
END FOR STOP.
Шаг 5: OR(πk, T ) = ∅ STOP.
На шагах 1, 2 и 5 алгоритма 1 проверяется равенство OR(πk, T ) = ∅. На
шагах 2-4 строятся сокращенные отрезки допустимых длительностей обслу-
71
живания требований множества J для задачи 1|pLi ≤ pi ≤ pUi |
∑Ci. Соглас-
но теореме 2 область оптимальности для перестановки πk ∈ Π обслужива-
ния требований для задачи 1|pLi ≤ pi ≤ pUi |
∑Ci совпадает с областью опти-
мальности для той же перестановки πk обслуживания требований для зада-
чи 1|pLi ≤ pi ≤ pUi |
∑Ci с множеством
T сокращенных сценариев. Нетрудно
убедиться в том, что для реализации алгоритма 1 требуется выполнить O(n)
элементарных операций.
4.1. Область оптимальности для перестановки πk ∈ Π
в частных случаях
Построим область оптимальности OR(πk, T ) для двух частных случаев пе-
рестановки πk = (Jk1 , . . . , Jkn ) ∈ Π и вычислим объем Vol (πk, T ) области оп-
тимальности OR(πk, T ). В первом случае область оптимальности OR(πk, T )
определяется только отрезками оптимальности всех требований Jkr ∈ J (лем-
ма 3). Во втором случае область оптимальности определяется только отрез-
ками условной оптимальности всех требований Jkr ∈ J (лемма 4).
Лемма 3. Если OR(πk,T) = ∅ и каждое требование Jkr∈J не име-
ет условной оптимальности в перестановке πk = (Jk1 ,... ,Jkn ) ∈ Π, то об-
ласть оптимальности для перестановки πk совпадает с параллелепипедом
оптимальности для той же перестановки:
[
]
(10)
OR(πk, T ) = ×nr=1 loptk,uoptk
= OB(πk
,T).
r
r
Объем такой области оптимальности OR(πk, T ) равен
∏
(11)
Vol (πk, T ) =
(uoptk
-lopt
).
r
kr
Jkr ∈{J : loptk<uoptk
}
r
r
Доказательство. В силу теоремы 2 вместо задачи 1|pLi ≤pi ≤pUi |
∑Ci
будем рассматривать задачу 1|pLi ≤ pi ≤ pUi |
∑Ci. Поскольку OR(πk,T) = ∅,
то по теореме 3 не существует ни одного требования Jkr ∈ J , которое не имеет
условной оптимальности и одновременно не имеет отрезка оптимальности в
перестановке πk.
Поскольку каждое требование Jkr ∈ J не имеет условной оптимальности в
перестановке πk и для него существует не более одного отрезка оптимально-
сти (замечание 1), то для каждого требования Jkr ∈ J выполняется равенство
[
]
[
]
pLk,pUk
= loptk,uopt
. Следовательно, в соответствии с определениями 1 и 2
r
r
r
kr
область оптимальности OR(πk, T ) для перестановки πk совпадает с паралле-
лепипедом оптимальности для т[ой же пе]естановки πk и представляет собой
opt
n-мерный параллелепипед ×n
r=1
lk
,uoptk
= OB(πk,T), объем которого равен
r
r
∏
(uoptk
- lopt). Лемма 3 доказана.k
Jkr ∈{J : loptk<uoptk}
r
r
r
r
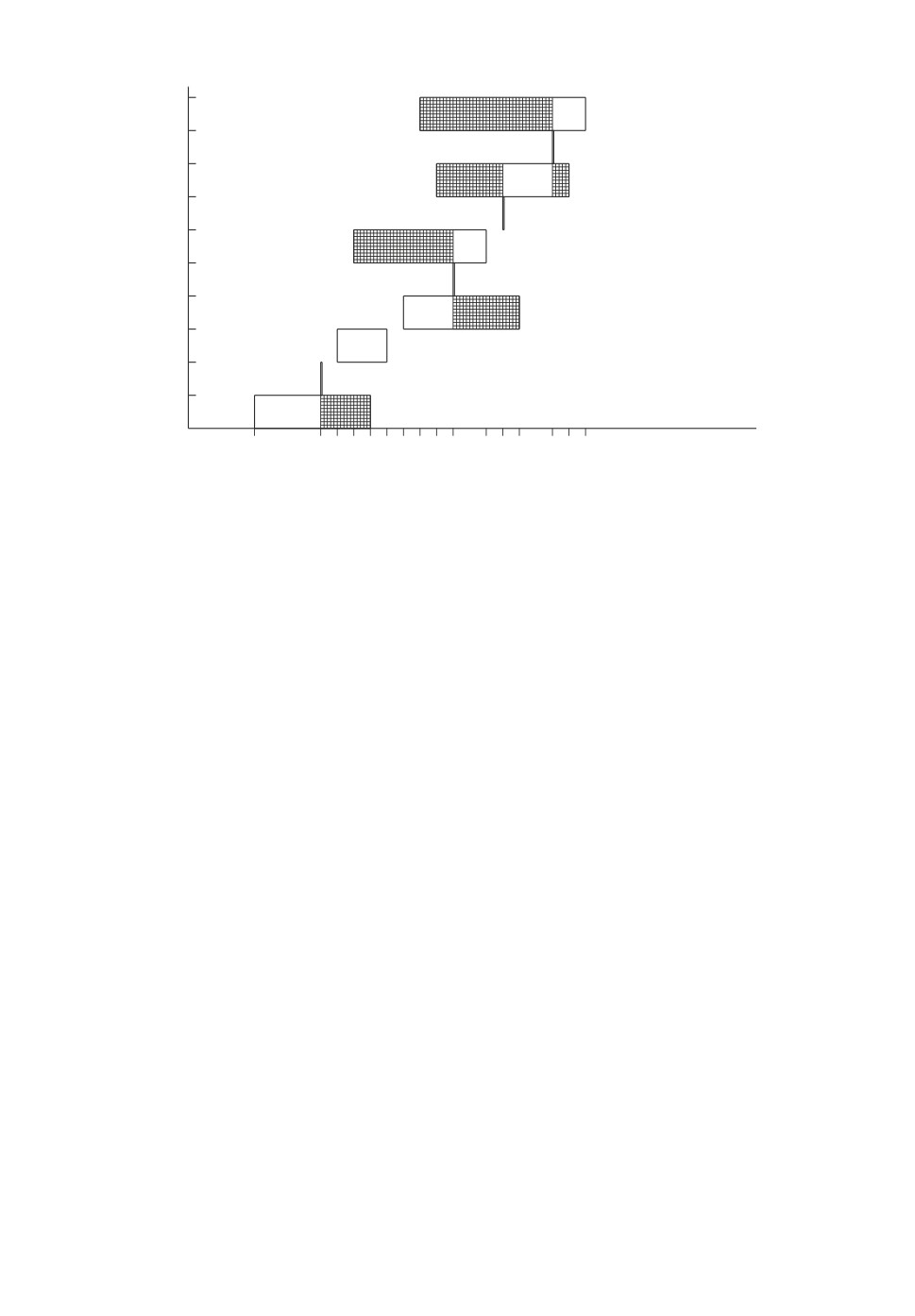
На рис. 2 представлена перестановка π2 = (J1, . . . , J10) требований множе-
ства J = {J1, . . . , J10} для примера 2 задачи 1|pLi ≤ pi ≤ pUi |
∑Ci. Поскольку
72
Требования Ji
J10
J9
J8
J7
J6
J5
J4
J3
J2
J1
4
8 9 10
12
14
16
18
20
22
24
Длительности pi
11
13
15
19
23
Рис. 2. Отрезки оптимальности и неоптимальности (заштрихованы) для тре-
бований Ji ∈ J в перестановке π2 = (J1, . . . , J10) для примера 2 задачи 1|pLi ≤
≤pi ≤pUi|
∑Ci.
перестановка π2 удовлетворяет условию леммы 3, то область оптимальности
OR(π2, T ) представляет собой следующий 10-мерный параллелепипед:
[
]
[
]
OR(π2, T ) = OB(π2, T ) = lopt1, uopt
×...× lopt10,uopt
=
1
10
= [4, 8] × [8, 8] × [9, 12] × [13, 16] × [16, 16] × [16, 18] ×
× [19, 19] × [19, 22] × [22, 22] × [22, 24],
объем которого вычисляется по формуле (11), а именно:
∏
Vol (π2, T ) =
(uoptr - loptr) =
Jr∈{J : lrpt<urpt}
= (8 - 4)(12 - 9)(16 - 13)(18 - 16)(22 - 19)(24 - 22) = 432.
В соответствии с теоремой 2 вместо задачи 1|pLi ≤ pi ≤ pUi |
∑Ci будем рас-
сматривать задачу 1|pLi ≤ pi ≤ pUi |
∑Ci с множеством
T сокращенных сце-
нариев.
Определение 3. Секцией перестановки πk ∈ Π называется макси-
),
1≤v≤v+
мальная по включению перестановка sπkv ( (Jkv , . . . , J
)v+mv
+mv ≤ n, такая что для любого числа d ∈
pLk, pU
существует тре-
v
kv+mv(
)
бование Jkv+i, i ∈ {0,... ,mv}, для которого d ∈
pLk
,
pUk
. Отрезок
v+i
v+i
[
]
pLk,
pUk
v
v+mv
называется охватом секции sπkv .
Отметим, что множество S(πk) = {sπkv , . . . , swk }, 1 ≤ v < . . . < w ≤ n, всех
секций каждой перестановки πk ∈ Π определено однозначно.
73
Замечание 2. Из определения 3 следует, что каждое требование Jki ∈ J
либо содержится в единственной секции перестановки πk, либо не содержится
ни в одной секции перестановки πk. Если существует хотя бы одно требование
Jki ∈ J , которое не содержится ни в одной секции перестановки πk, то по
теореме 3 получаем равенство OR(πk, T ) = ∅.
Из замечания 2 и доказательства теоремы 3 получаем следующее утвер-
ждение.
Следствие 2. Для того чтобы область оптимальности перестановки
πk = (Jk1 ,... ,Jkn ) ∈ Π не была пустым множеством, OR(πk,T) = ∅, необ-
ходимо и достаточно, чтобы выполнялось равенство πk = (sπk1 , . . . , swk ).
Для перестановки π2 = (J1, . . . , J10) в примере 2, представленном на
рис. 2, каждая секция состоит из единственного требования sπ21 = (J1), . . . ,
). Секцию, состоящую
0
0
из единственного требования, будем называть тривиальной.
[
]
Для доказательства леммы 4 разобьем охват
pLk, pU
каждой секции
j
kj+mj
sπkj ∈ S(πk) на максимальныe (по включению) подынтервалы условной опти-
мальности
[
]
[
(
)
(
))⋃
⋃[
(
)
(
))⋃
pLk,
pUk
= lj
sπk
,uj
lj
sπk
,uj
j
j+mj
1
j
1
sπkj
i
j
i
sπkj
(12)
⋃[
(
)
(
)]
πk
j
πk
lj
s
,u
s
,
n(j)
j
n(j)
j
которые отличаются один от другого тем, что для разных подмножеств Jj }{i=
{
}
= Jki,...,Jk
множества Jkj , . . . , Jkj+mj
, j ≤ i ≤ j + mj, выполняют-
j
|J
|
i
(
)
(
)]
[
]
ся включения lji sπk
,uj
sπk
⊆
pLk,pUk
для всех требований Jkr ∈ Jji.
j
i
j
r
r
(
)
Пуст
Jji = Jk
,...,Jk
обозначает перестановку требований множества
i
j
|J
|
i
{
}
Jji = Jk
,...,Jk
i
j
|J
|
i
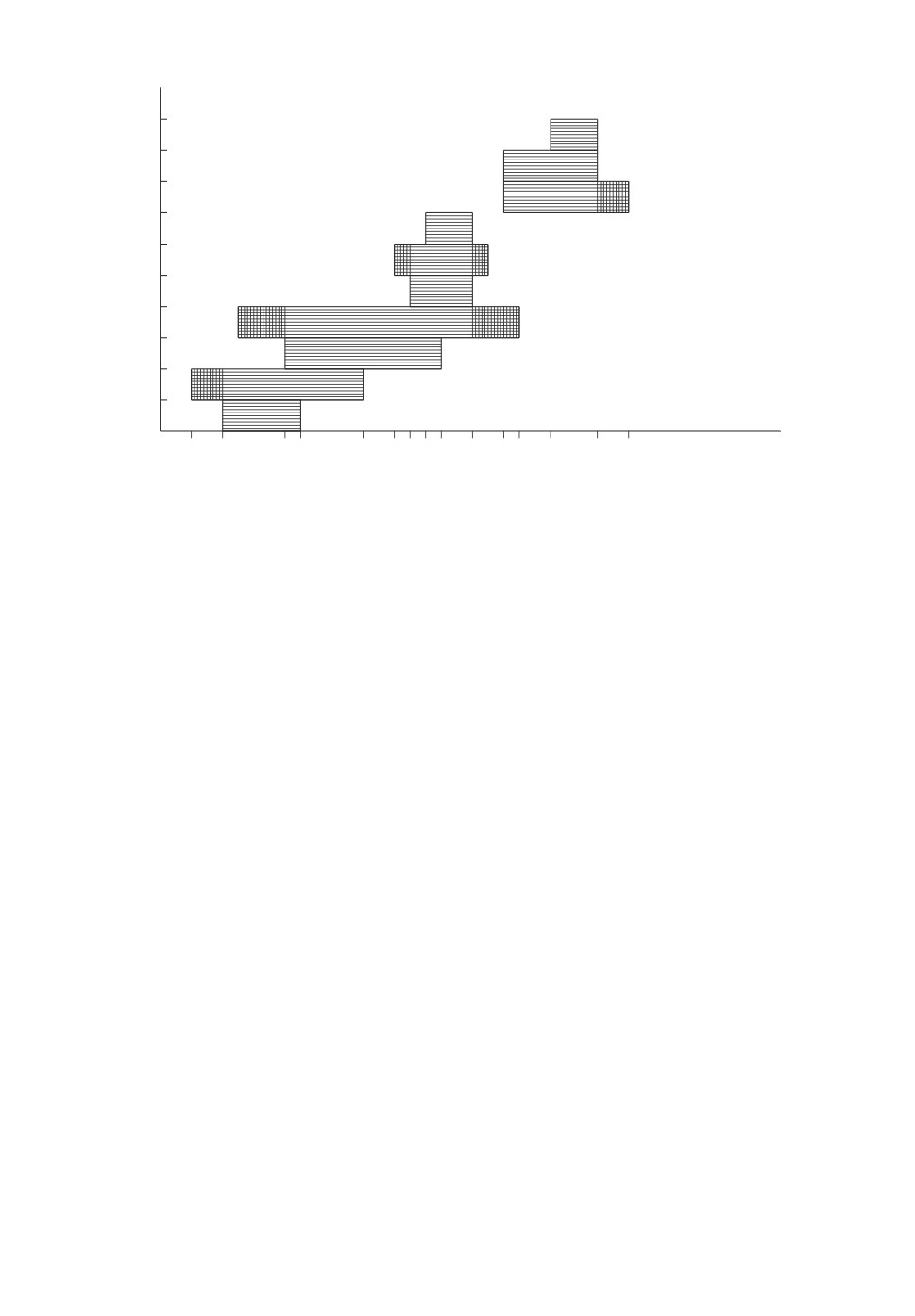
Для иллюстрации введенных обозначений рассмотрим разбиения охва-
тов секций sπ21 и s82 перестановки π2 = (J1, . . . , J10) в примере 3, представ-
ленном на рис. 3. Секция sπ21 состоит из семи упорядоченных требований
, pU7 ] = [4,20]. Получаем следующее раз-
sπ21 =(J1,... ,J7) и имеет охват [
1
биение (12): [4, 20] = [4, 8) ∪ [8, 9) ∪ [9, 13) ∪ [13, 16) ∪ [16, 17) ∪ [17, 18) ∪ [18, 20]
охвата [pL1, pU7 ] на подынтервалы условной оптимальности. Здесь
[
)
[
)
l11 (J1,J2) ,u11 (J1,J2)
= [4, 8);
l12 (J1,... ,J4),u12 (J1,... ,J4)
= [8, 9);
[
)
[
)
l13 (J2,J3,J4),u13 (J2,J3,J4)
= [9, 13);
l14 (J3,J4) ,u14 (J3,J4)
= [13,16);
[
)
l15 (J3,... ,J6) ,u15 (J3,... ,J6)
= [16, 17);
[
)
l16 (J3,... ,J7) ,u16 (J3,... ,J7)
= [17, 18];
[
]
l17 (J4,... ,J7) ,u17 (J4,... ,J7)
= [18,20] .
74
Требования Ji
J10
J9
J8
J7
J6
J5
J4
J3
J2
J1
2
4
89
13
20
25
28
30
Длительности pi
15161718
2223
Рис. 3. Отрезки условной оптимальности (заштрихованы) и отрезки неопти-
мальности (заштрихованы дважды) для требований Ji ∈ J в перестановке
π2 = (J1, . . ., J10) для примера 3 задачи 1|pLi ≤ pi ≤ pUi |
∑Ci.
Отметим равенства
J11 = (J1,J2),
J12 = (J1,... ,J4),
J13 = (J2,J3,J4),
J14 =
= (J3, J4),
J15 = (J3,... ,J6),
J16 = (J3,... ,J7),
J17 = (J4,... ,J7). Секция sπ28
, pU10]= [22,28].
состоит из трех требований sπ28 = (J8, J9, J10) и имеет охват [
8
Получаем разбиение [22,28] = [22,25)∪[25,28] охвата [22,28] на подынтервалы
условной оптимальности [l21(J8, J9), u21(J8, J9)) и [l22(J8, J9, J10), u22(J8, J9, J10)].
Отметим равенств
J21 = (J8,J9)
J22 = (J8,J9,J10).
Поскольку любая секция sπkj ∈ S(πk) перестановки πk и любое упорядочен-
ное множеств
J ji требований множества Jji ⊆ J сами являются перестанов-
ками соответствующего подмножества требований множества J , то для них
можно рассматривать области оптимальности для всех тех требований, из
которых состоят эти перестановки. Для обозначения таких областей опти-
J ji ,T),
мальности будем использовать те же обозначения OR(sπkj , T ) и OR
что и для области оптимальности OR(πk, T ) для перестановки πk ∈ Π всего
множества требований J . Для обозначения объемов областей оптимально-
сти OR(sπkj , T ) и OR
J ji ,T) будем использовать обозначения Vol(sπkj,T) и
Vol
J ji ,T) соответственно.
Доказательство следующей леммы 4 приведено в Приложении. Там же
дано определение d-мерной пирамиды оптимальности P iroptĴji , представляю-
щей собой область оптимальности для перестановки требований Jji ⊆ J , т.е.
показано, что выполняются равенства d = |Jji| и OR
J ji ,T) = PiroptĴji .
Лемма 4. Если OR(πk,T) = ∅ и каждое требование Jkr∈J не имеет
отрезка оптимальности в перестановке πk = (Jk1 ,... ,Jkn ) ∈ Π, то область
оптимальности OR(πk,T) для перестановки πk представляет собой декар-
75
б
J4
(9, 9, 13)
(13, 9, 13)
(9, 13, 13)
(13, 13, 13)
a
J1
J2
(9, 9, 9)
(4, 4)
(8, 4)
(13, 9, 9)
(4, 8)
(8, 8) = (J1, J2)
(9, 13, 9)
(13, 13, 9) = (J2, J3, J4)
J2
J3
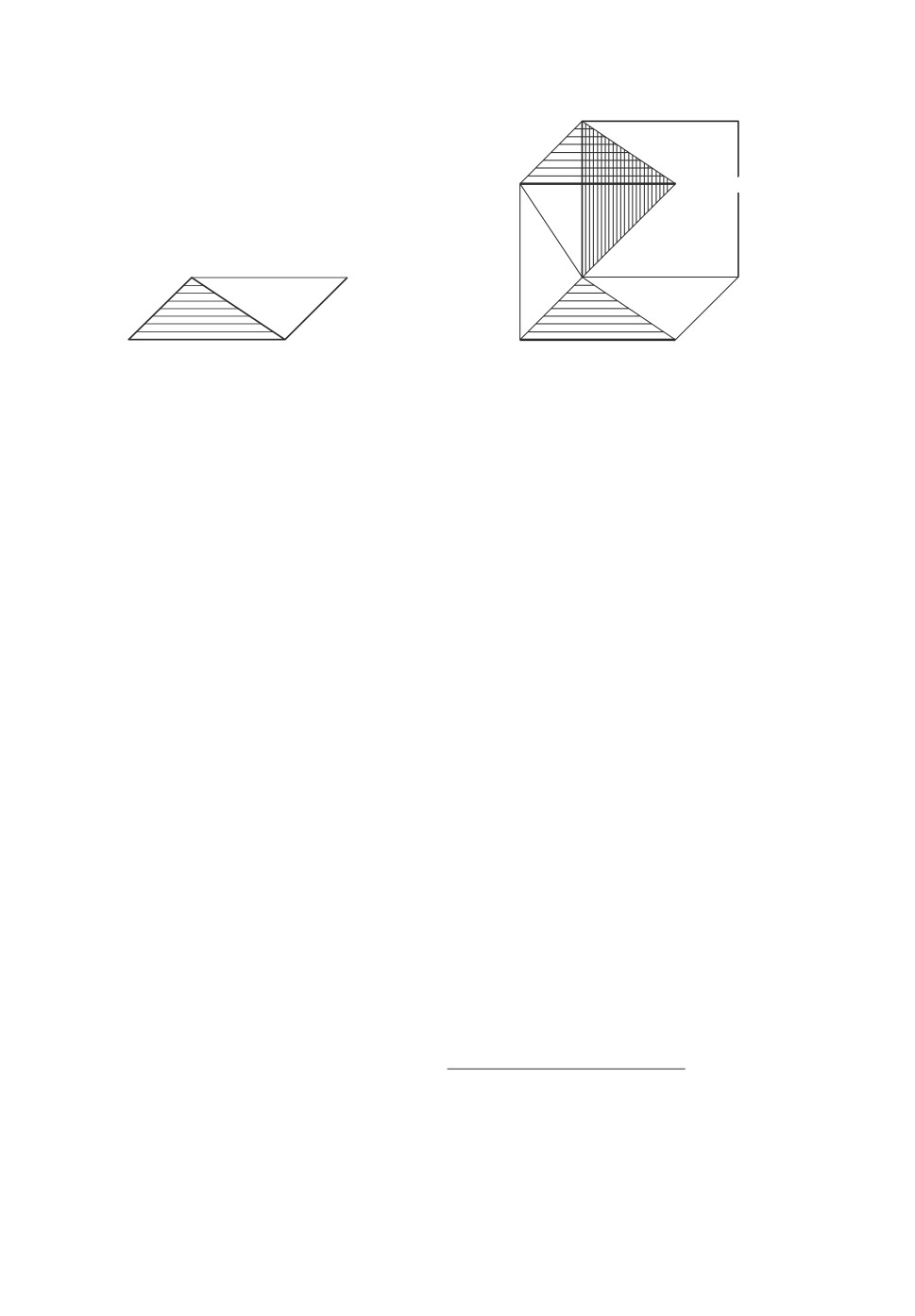
Рис. 4. (a) - Треугольник оптимальности Piropt(J1, J2) с основани-
ем [(4, 8), (8, 8)] и высотой [(4, 8), (4, 4)] для подынтервала условной
оптимальности [4, 8) для перестановки π2
= (J1, . . . , J10) в приме-
ре 3. (b) - Пирамида оптимальности Piropt(J2, J3, J4) с основанием
[(9, 9, 13), (9, 13, 13), (13, 13, 13)] и высотой [(9, 9, 13), (9, 9, 9)] для подын-
тервала условной оптимальности [9, 13) для перестановки π2 в приме-
ре 3.
тово произведение |S(πk)| областей оптимальности OR(sπkj,T) всех секций
S(πk):
(
)
(
)
,T
,
(13) OR (πk, T ) = OR (sπk1 , T ) × . . . × OR sjk , T
×...×OR s
S(πk)|
где OR(sπkj , T ) определяется как следующее объединение d-мерных пирамид{}
оптимальности PiroptĴji в пространстве Rn, d ∈
|Jji|, . . . , |Jjn(j)|
:
n(j)⋃
n(j)⋃
(14)
OR
Jji,T)=
P iroptĴji.
OR(sπkj , T ) =
i=1
i=1
Объем области оптимальности для перестановки πk определяется равен-
ством
(
(
)
(
))|J j
|
i
n(j)
|S(πk)|∏
∑
uj
sπk
-lj
sπk
i
j
i
j
(15)
Vol (πk, T ) =
j
|Ji
|!
j=1
i=1
На рис. 3 представлена перестановка π2 = (J1, . . . , J10) требований множе-
ства J = {J1, . . . , J10} для примера 3 задачи 1|pLi ≤ pi ≤ pUi |
∑Ci. По теоре-
ме 3 область оптимальности для перестановки π2 не является пустым множе-
ством, и поскольку перестановка π2 удовлетворяет условию леммы 4, то объем
76
области оптимальности OR(π2, T ) вычисляется по формуле (15), а именно:
(
(
)
(
))|J j
|
i
n(j)
∏∑
uj
sπk
-lj
sπk
i
j
i
j
Vol (π2, T ) =
=
j
|Ji
|!
j=1 i=1
2
[ (8 - 4)
(9 - 8)4
(13 - 9)3
(16 - 13)2
(17 - 16)4
=
+
+
+
+
+
2!
4!
3!
2!
4!
]
5
(18 - 17)
(20 - 18)4
][(25 - 22)2
(28 - 25)3
+
+
+
=
5!
4!
2!
3!
]
[ 16
1
64
9
1
1
16
][9
27
33
=
+
+
+
+
+
+
+
= 210
2
24
6
2
24
120
24
2
6
40
На рис. 4,a представлен указанный в равенстве
(14) треугольник
P iroptĴ11 = P iropt(J1, J2) для подынтервала условной оптимальности [4, 8),
принадлежащий области оптимальности OR(π2, T ) для перестановки π2 =
= (J1, . . . , J10) в примере 3, а на рис. 4,b представлена указанная в (14)
3-мерная пирамида P iroptĴ13 = P iropt(J2, J3, J4) для подынтервала услов-
ной оптимальности [9, 13), принадлежащая той же области оптимальности
OR(π2, T ).
4.2. Объем области оптимальности для перестановки πk ∈ Π
в общем случае
Пусть S∗(πk) обозначает подмножество тривиальных секций множества
S(πk).
Отметим, что перестановка π2 = (J1, . . . , J10) в примере 2 удовлетворяет
условию леммы 3 и все секции множества S(π2) являются тривиальными:
S(π2) = S∗(π2).
Перестановка π2 = (J1, . . . , J10) в примере 3 удовлетворяет условию лем-
мы 4, и множество S∗(π2) ее тривиальных секций - пустое множество:
S∗(π2) = ∅.
Теорема 4. Если OR(πk,T) = ∅, то область оптимальности
OR(πk, T ) представляет собой декартово произведение
(13) областей
оптимальности секций S(πk) такое, что
(
)
(
)
[
]
= loptk,uopt
OR sπkj,T
= OB sπkj,T
r
kr
для каждой тривиальной секции sπkj=(Jkr)и
n(j)⋃
n(j)⋃
OR
Jji,T)=
P iroptĴji
OR(sπkj , T ) =
i=1
i=1
для каждой нетривиальной секции sπkj ∈ S(πk) \ S∗(πk). Объем области оп-
тимальности равен
(16)
Vol (πk
,T)=
77
(
(
)
(
))|J j
i
|
∏
(
)
∏
∑
uj
sπk
-lj
sπk
i
j
i
j
=
uoptk-lopt
r
kr
j
|Ji
|!
i=1
(Jkr )∈{S∗(πk) : loptkr<uoptkr}
sπkj∈S(πk)\S∗(πk)
Доказательство. В силу теоремы 2 вместо задачи 1|pLi ≤pi ≤pUi |
∑Ci
будем рассматривать задачу 1|pLi ≤ pi ≤ pUi |
∑Ci. Поскольку OR(πk,T) = ∅,
то размерность области оптимальности OR(πk, T ) равна n (следствие 1). Из
теоремы 3 следует, что не существует ни одного требования Jkr ∈ J , которое
не имеет условной оптимальности и одновременно не имеет отрезка опти-
мальности в перестановке πk.
Поскольку OR(πk, T ) = ∅, то из замечания 2 следует, что каждое требо-
вание Jki ∈ J содержится в единственной секции перестановки πk. При этом
согласно следствию 2 справедливо равенство πk = (sπk1 , . . . , swk ).
На основе перечисленных свойств перестановки πk покажем, как доказать
равенство (13) и равенство (16) в результате последовательного применения
леммы 3 или леммы 4 в частных случаях, когда очередная рассматриваемая
перестановка состоит из единственной секции sπkv ∈ S(πk) перестановки πk.
Вначале рассмотрим первую секцию sπk1 = (Jk1 , . . . , J
) перестанов-
k1+m1
ки πk. Если секция sπk1 является тривиальной, т.е. s1k = (Jk1 ), то по лемме 3
получаем первый сомножитель [loptk,uoptk
1
1
] = OR(sπk1,T) в искомом декартовом
произведении (13) и первый сомножитель (uoptk
- lopt) в первом произведенииk
1
1
равенства (16) при условии, что имеет место строгое неравенство loptk
<uoptk
1
1
(если loptk
=uoptk, то сомножитель (uoptk
- lopt) = 0 в равенство (16) не добав-k
1
1
1
1
ляется в соответствии с леммой 3).
Если же секция sπk1 не является тривиальной, т.е.
sπk1 ∈ S(πk)\S∗(πk),
то по лемме 4 получаем первый сомножитель
n(1)⋃
n(1)⋃
OR
J1i,T) =
P iroptĴ1i
OR(sπk1 , T ) =
i=1
i=1
в декартовом произведении (13) и первый сомножитель
n(1)
i
|
∑ (u1i(sπk1 ) - li(s1k ))|
|J1i|!
i=1
во втором произведении равенства (16). Здесь необходимо отметить, что в
разбиение (12) секции sπk1 на подынтервалы условной оптимальности могут
входить и подынтервалы [l1i(sπk1 ), ui(s1k )), для которых выполняется равен-
ство |J1i| = 1 (такая возможность в условии леммы 4 не предусмотрена). По-
кажем, однако, что равенство
j
|
(u
i
i
(sπkj ) - li (sjk ))|
OR
Jji,T)=
,
|Jji|!
78
содержащееся в (16), справедливо и для случая |Jji | = 1. Действительно, если
|Jji | = 1, то
(
(
)
(
))|J j
(
(
)
(
))1
i
|
πk
j
πk
uj
s
-li
s
uj
sπk
-lj
sπk
(
(
)
(
))
i
j
j
i
j
i
j
=
= uj
sπk
-lj
sπk
,
i
j
i
j
|Jji |!
1!
что и требуется для выполнения равенства (16).
Аналогично рассмотрим вторую секцию sπk2 = (Jkm1+1 , . . . , J
) пе-
km1+1+m2
рестановки πk. Применяя лемму 3, если секция sπk2 тривиальная, или лемму 4,
если секция sπk2 не является тривиальной, дополним уже построенную часть
декартова произведения (13) вторым сомножителем и дополним вторым со-
множителем одно (соответствующее) произведение из двух произведений ра-
венства (16).
Продолжив описанный процесс вплоть до рассмотрения последней сек-
ции sπkw перестановки πk и добавления соответствующих сомножителей, по-
лучим оба равенства (13) и (16). Теорема 4 доказана.
Следующий алгоритм вычисления объема Vol (πk, T ) области оптимально-
сти OR(πk, T ) = ∅ для перестановки πk ∈ Π основан на теоремах 2, 3 и 4.
Алгоритм 2.
ВХОД:
Перестановка πk = (Jk1 , . . . , Jkn ) ∈ Π, для которой OR(πk, T ) = ∅;
отрезки [pLi, pUi ] длительностей обслуживания требований Ji ∈ J .
ВЫХОД: Объем области оптимальности OR(πk, T ) для перестановки πk.
Шаг 1:
Определить множество секций{
}
k
,...,sπ
;
+m1
+mj
w
Шаг 2:
j = 1, Vol = 1, Vol∗ = 1, Sum = 0;
Шаг 3:
IF секция sπkj = (Jkj , . . . , Jkj+mj ) тривиальная sjk = (Jkj ) THEN
GOTO шаг 7;
Шаг 4:
kj+mj
) построить разбиение (12)
ELSE для секции sπkj = (Jkj , . . . , J
[
]
охвата
pLk,pU
на подынтервалы условной оптимальности:
j
kj+mj
[
(
)
(
(
)
(
)) ⋃
⋃[
)) ⋃
πk
j
πk
lj
s
,u
s
lj
sπk
,uj
1
j
1
j
i
j
i
sπkj
[
(
)
(
)]
⋃
πk
j
πk
lj
s
,u
s
;
n(j)
j
n(j)
j
j
j
(u
i
(sπkj )-lji (sπkj ))|Ji|
Шаг 5:
FOR i = 1 to n(j) DO вычислить OS =
;
|Jji|!
Sum := Sum + OS END FOR
Шаг 6:
Vol := Vol · Sum, j := j + mj IF j ≤ w THEN GOTO шаг 3;
ELSE GOTO шаг 10;
Шаг 7:
j := j + mj, OS∗ = uoptk
-loptk
IF uoptk
> lopt THEN GOTO шаг 9;k
j
j
j
j
ELSE IF j ≤ w THEN GOTO шаг 3;
Шаг 8:
ELSE GOTO шаг 10;
Шаг 9:
Vol∗ := Vol∗ · OS∗ IF j ≤ w THEN GOTO шаг 3 ELSE
Шаг 10:
Vol (πk, T ) = Vol · Vol∗ STOP.
79
Рис. 5. Отрезки оптимальности, условной оптимальности (заштрихованы) и
отрезки неоптимальности (заштрихованы дважды) для требований Ji ∈ J =
= {J1, . . . , J18} в перестановке π3 = (J1, . . . , J3, J6, J5, J4, J7, . . . , J18) для при-
мера 1.
Для реализации шага 1 требуется O(n) операций. Выполнение шагов 3-6
требует O(n2) операций. Выполнение шагов 7-9 требует O(n) операций. Все-
му алгоритму 2 требуется выполнить O(n2) операций для вычисления объема
Vol (πk, T ) области оптимальности OR(πk, T ) для фиксированной перестанов-
ки πk ∈ Π.
На рис. 5 представлена перестановка π3 = (J1, . . . , J3, J6, J5, J4, J7, . . . , J18)
требований множества J = {J1, . . . , J18} для примера 3 задачи 1|pLi ≤ pi ≤
≤pUi|
∑Ci. По теореме 3 область оптимальности для перестановки π3 не пу-
стая, поэтому вычислим ее объем по формуле (16) из теоремы 4, учитывая
равенство S∗(π3) = ∅.
∏
∑
i
|
(uji (sπ3j) - li(sj3 ))|
Vol (π3, T ) =
=
j
|Ji
|!
sπ3j∈S(π3)
i=1
80
]
[ (3 - 1)1
(4 - 3)3
(5 - 4)5
(6 - 5)3
(7 - 6)1
(9 - 7)2
=
+
+
+
+
+
×
1!
3!
5!
3!
1!
2!
]
1
[ (12 - 11)
(14 - 12)3
(15 - 14)5
(18 - 15)3
(23 - 18)1
×
+
+
+
+
×
1!
3!
5!
3!
1!
1
[ (30 - 27)
(32 - 30)3
(36 - 32)1
(37 - 36)2
(38 - 37)3
×
+
+
+
+
+
1!
3!
1!
2!
3!
]
]
5
(40 - 38)
(41 - 40)1
[2
1
1
1
1
4
+
+
=
+
+
+
+
+
×
5!
1!
1
6
120
6
1
2
]
]
[1
8
1
27
5
[3
8
4
1
1
32
1
×
+
+
+
+
×
+
+
+
+
+
+
= 657,85.
1
6
120
6
1
1
6
1
2
6
120
1
5. Перестановка πk с максимальной областью оптимальности
Если существует одноэлементное доминирующее множество {πk} для за-
дачи 1|pLi ≤ pi ≤ pUi |
∑Ci, то перестановка πk обслуживания требований мно-
жества J является оптимальной для задачи 1|p|
∑Ci при любом сценарии
p ∈ T. В соответствии с определением 2 для такой перестановки πk должно
выполняться равенство OR(πk, T ) = T .
5.1. Максимально возможная область оптимальности
для заданных сценариев
Докажем необходимые и достаточные условия для существования пере-
становки πk ∈ Π с максимально возможной областью оптимальности для за-
данного множества сценариев T , т.е. докажем критерий существования пере-
становки πk, для которой справедливо равенство OR(πk, T ) = T .
Теорема 5. Область оптимальности для перестановки πk = (Jk1,
...,Jkn) ∈ Π является максимально возможной для заданного множества
сценариев T , т.е. OR(πk, T ) = T , тогда и только тогда, когда в перестанов-
ке πk для каждого требования Jkr ∈ J выполняется следующее равенство:
[
]
[
]
(17)
loptk,uoptk
=
pLk
,pUk
s
s
s
s
Доказательство.
Достаточность. Пусть равенство (17) выполняется для каждого тре-
бования Jks ∈ J в перестановке πk = (Jk1 , . . . , Jkn ). Тогда по определе-[
]
нию 1 должны выполняться и равенства OB(πk, T ) = ×kir ∈M lkpti,uopt
=
r
kir
[
]
= ×kir∈M pki
,pUki
= T, такие что множество M = (ki1,...,ki|M|), ki1 < ...
r
r
... < ki|M|, представляет собой упорядоченное множество
{k1, . . . , kn} =
= {1, . . . , n}, для которого n = |M|. Из определения 1 следует, что пере-
становка πk является оптимальной для задачи 1|p′|
∑Ci при любом сце-
нарии p′ ∈ OB(πk, T ) = T . Согласно определению
2
получаем равенство
OR(πk, T ) = T . Достаточность доказана.
81
Необходимость. Пусть справедливо равенство OR(πk, T ) = T . Однако
предположим (от противного), что существует требование Jkr ∈ J в пере-
становке πk = (Jk1 , . . . , Jkn ) ∈ Π такое, что равенство (17) не выполняется.
Тогда в силу леммы 1 существует непустой отрезок неоптимальности
[lnonk,unon] или (и) существует непустой отрезок условной оптимальностиk
r
r
[lcoptk,ucoptk] для требования Jkr ∈ J в перестановке πk = (Jk1 , . . . , Jkn ).
r
r
Если существует отрезок неоптимальности
[lnonk,unon], то выполняет-k
r
r
ся равенство (5). Если же существует отрезок условной оптимальности
[lcoptk,ucopt], то выполняется равенство (7). В обоих случаях существует сцена-k
r
r
рий p∗ ∈ (lnonk,unonk)
⋃(lcoptk
,ucoptk) ⊆ T такой, что перестановка πk не является
r
r
r
r
оптимальной для задачи 1|p∗|
∑Ci со сценарием p∗ ∈ T. Следовательно, в
соответствии с определением 2 получаем соотношение OR(πk, T ) = T , проти-
воречащее предположению о том, что равенство OR(πk, T ) = T выполняется.
Это противоречие завершает доказательство теоремы.
Из теоремы 5 и следствия 1 получаем следующее утверждение.
Следствие 3. Если для каждого требования Jkr∈J в перестановке
πk = (Jk1 ,... ,Jkn ) выполняется равенство (17), то область оптимально-
сти OR(πk,T) является n-мерным параллелепипедом T ⊂ Rn+ c объемом
∏
Vol (πk, T ) =Ji∈{J : pLi<pUi }(pi -pi).
Перестановка πk = (Jk1 , . . . , Jkn ), для которой равенства (17) выполняются
для всех требований Jkr ∈ J , является оптимальной для задачи 1|p|
∑Ci с лю-
бым допустимым сценарием p ∈ T . Следовательно, множество {πk} является
минимальным доминирующим множеством для задачи 1|pLi ≤ pi ≤ pUi |
∑Ci.
5.2. Как использовать перестановку
с максимальной областью оптимальности
Оптимальная для задачи
1|pLi ≤ pi ≤ pUi |
∑Ci перестановка πk, кри-
терий существования которой представлен в теореме
5
и следствии 3,
встречается на практике довольно редко. Однако для конкретной задачи
1|pLi ≤ pi ≤ pUi |
∑Ci, возникающей на практике, как правило, одна переста-
новка должна быть выбрана из множества Π и затем реализована при обслу-
живании требований множества J .
На основе доказанных в разделах 3-5.1 результатов можно рекомендо-
вать выбирать для реализации такую перестановку πt обслуживания требо-
ваний множества J , для которой объем области оптимальности OR(πt, T )
является максимальным среди всех перестановок множества Π. Если ока-
жется, что фактический сценарий p ∈ T обслуживания требований J бу-
дет принадлежать области оптимальности OR(πt, T ), то реализованная пе-
рестановка πt будет оптимальной для фактического сценария обслужива-
ния требований J . Вообще говоря, чем больше объем области оптималь-
ности OR(πk, T ), тем больше вероятность того, что перестановка πk бу-
дет оптимальной для фактического сценария обслуживания требований J .
Поэтому важными задачами для дальнейших исследований представля-
ются разработка эффективных алгоритмов построения перестановки πt с
82
максимальным объемом Volmax(πt, T ) = max{Volmax(πk, T ) : πk ∈ Π} обла-
сти оптимальности OR(πt, T ) и тестирование таких алгоритмов на задачах
1|pLi ≤ pi ≤ pUi |
∑Ci практической размерности.
В общем случае задачи 1|pLi ≤ pi ≤ pUi |
∑Ci разность
Volmax(πk, T )
1-
∏
=: µ
Ji∈{J : lopti<uopti}(pi -pi)
можно рассматривать как меру неопределенности (или меру сложности) за-
дачи. В частности, если µ = 0, то имеется гарантия того, что перестановка πt
с максимальным объемом Volmax(πt, T ) области оптимальности OR(πt, T ) бу-
дет оптимальной для фактического сценария обслуживания требований мно-
жества J , несмотря на неопределенность заданных сценариев T . Наоборот,
если значение µ равно единице (или близко к единице), то вероятность того,
что перестановка πt будет оптимальной для фактического сценария обслужи-
вания требований множества J , равна нулю (близка к нулю). В таких случа-
ях для решения неопределенной задачи 1|pLi ≤ pi ≤ pUi |
∑Ci можно рекомен-
довать использование приближенных алгоритмов таких, как алгоритм U2,
описанный в [1], или описанный в [10] алгоритм 3, который ориентирован на
достижение наименьшей погрешности полученного решения.
6. Заключение
Задачи составления расписаний обслуживания требований с неопределен-
ными числовыми данными на одном приборе возникают, например, при пла-
нировании рабочего времени работника на определенный период времени (ра-
бочий день, неделю или месяц). Как правило, можно заранее оценить диапа-
зоны возможных длительностей планируемых работ. Можно предполагать,
что множество планируемых работ существенно не меняется в ходе реализа-
ции расписания. Критерий минимизации суммы моментов завершения обслу-
живания требований (среднего времени обслуживания требований) можно
рассматривать как суммарный показатель эффективности выполнения ра-
ботником заданного множества работ.
В [27] описан другой пример задачи 1|pLi ≤ pi ≤ pUi |
∑Ci, возникающей
при поиске оптимального расписания доставки продукции от изготовителя
в торговую сеть города при использовании одного транспортного средства.
Время доставки продукции в магазин зависит от множества факторов та-
ких, как автомобильные пробки, погодные условия, состояние транспортного
средства и дорожного покрытия.
Задачи 1|pLi ≤ pi ≤ pUi |
∑Ci могут возникать и в некоторых многостадий-
ных обслуживающих системах, если один обслуживающий прибор является
“узким местом” производственного процесса и для длительностей обслужи-
вания требований на этом приборе известны только границы возможных зна-
чений.
Полученные в разделах 3-5 результаты и алгоритмы 1 и 2 можно исполь-
зовать при построении перестановки πt ∈ Π обслуживания заданных требова-
ний с наибольшим объемом Volmax(πt, T ) области оптимальности OR(πt, T ).
83
Использование перестановки πt для обслуживания заданных требований поз-
воляет повысить вероятность получения фактически оптимального распи-
сания, несмотря на то, что законы распределения вероятностей случайных
длительностей обслуживания требований не известны при построении рас-
писания для задачи 1|pLi ≤ pi ≤ pUi |
∑Ci.
ПРИЛОЖЕНИЕ
При доказательстве леммы 4 будем рассматривать задачу
∑
1|pLi ≤ pi ≤ pUi |
Ci
вместо задачи 1|pLi ≤ pi ≤ pUi |
∑Ci (теорема 2). Поскольку OR(πk,T) = ∅, то
согласно теореме 3 не существует ни одного требования Jkr ∈ J , которое не
имеет условной оптимальности и одновременно не имеет отрезка оптималь-
ности в перестановке πk. По условию леммы 4 каждое требование Jkr ∈ J не
имеет отрезка оптимальности в перестановке πk.
Учитывая замечание 1 и лемму 1, получаем равенство
[
]
pLk,
pUk
= [lcoptk,ucopt],k
r
r
r
r
которое выполняется для каждого требования Jkr ∈ J . Из полученного ра-
венства следует, что множество S(πk) секций перестановки πk не содержит[
]
ни одной тривиальной секции. Построим разбиение (12) охватов
pLk,
pU
j
kj+mj
всех секций sπkj ∈ S(πk) на следующие подынтервалы условной оптимально-
сти:
[
(
)
(
))⋃
⋃[
(
)
(
))⋃
πk
j
πk
lj
s
,u
s
lj
sπk
,uj
1
j
1
j
i
j
i
sπkj
⋃[
(
)
(
)]
[
]
πk
j
πk
lj
s
,u
s
= pLk, pU
n(j)
j
n(j)
j
j
kj+mj
Далее методом математической индукции по мощности |Jj ( )[( ))|множества
i
πk
j
πk
докажем, что для каждого подынтервала lj
s
,u
s
условной опти-
i
j
i
j
мальности в построенном разбиении (12) выполняются следующие равенства:
(
(
)
(
))|J j
|
j
i
(
)
u
sπk
-lj
sπk
i
j
i
j
(Π.1)
Vol
Jji
,T
=
,
|Jji |!
(
)
(
)
(Π.2)
OR
Jji,T
= PiroptĴji = Piropt Jk
,...,Jk
,
i
j
|J
|
i
(
)
где основанием |Jji|-мерной пирамиды P iroptĴji = P iropt Jk
,...,Jk
яв-
i
j
|J
|
i
(яется (|Jj() i| (1)-)) наяпирамида,адлинавысотывсехпирамидравна
uji sπk
-lj
sπk
j
i
j
84
Покажем вначале, что при |Jji | = 2 пирамида P iroptĴji = P iropt(Jk
,Jki+1)
i
превращается в треугольник (как вырожденный случай пирамиды) с основа-[
(
)
(
)]
(
(
)
(
))
πk
j
πk
j
πk
j
πk
нием lj
s
,u
s
и высотой той же длины u
s
-li
s
, что и
i
j
i
j
i
j
j
длина основания треугольника. Такой треугольник P iroptĴ11 = P iropt(J1, J2)
представлен на рис. 4,a для подынтервала
[
)
[4, 8) = l11(J1, J2), u11(J1, J2)
условной оптимальности для перестановки π2 = (J1, . . . , J10) ∈ Π для приме-
ра 3. Из теоремы 1 следует, что для того, чтобы порядок (Jki , Jki+1 )
J ji двух
требований был оптимальным в перестановке πk ∈ Π, необходимо и доста-
точно, чтобы длительности pki и pki+1 требований Jki и Jki+1 удовлетворяли
неравенству pki ≤ pki+1 , а с учетом принадлежности допустимого сценария
(pk1 , . . . , pkn ) заданному множеству T допустимые длительности pki и pki+1
должны удовлетворять следующей системе неравенств:
pki ≤ pki+1,
(Π.3)
pLki ≤ pki ≤ pU ,k
i
pLki+1 ≤ pki+1 ≤ pU
ki+1
Система (Π.3) определяет треугольник P iroptĴji = P iropt(Jk
,Jki+1). Ины-
i
ми словами, системе (Π.3) удовлетворяют все точки, принадлежащие тре-
угольнику P iroptĴji, и только они. Таким образом, равенство (Π.2) доказано
для случая |Jji | = 2. Поскольку площадь треугольника P iroptĴji равна про-
j
(u
i
(sπkj )-lji (sπkj ))2
изведению основания на половину высоты:
, то и равенство
2
(Π.1) доказано для случая |Jji| = 2.
Рассмотрим следующее по мощности множество Jji , т.е. |Jji | = 3, и пока-
жем, что в этом случае область оптимальности
OR
J ji ,T) = OR((Jk
,Jki+1,Jki+2),T)
i
представляет собой 3-мерную пирамиду P iroptĴj ( ) ( ))(i,длинавысотыкоторойрав-
πk
j
πk
на uj
s
-li
s
и основанием которой является треугольник с высо-
i
j
j
(
(
)
(
))
[
(
)
(
)]
πk
j
πk
j
πk
j
πk
той той же длины uj
s
-li
s
и с основанием li
s
,u
s
i
j
j
j
i
j
Отметим, что такая пирамида оптимальности P iroptĴ11 = P iropt(J2, J3, J4)
представлена на рис. 4,b для подынтервала
[
)
[9, 13) = l13(J2, J3, J4), u13(J2, J3, J4)
условной оптимальности для перестановки π2 = (J1, . . . , J10) для примера 3.
Из теоремы 1 следует, что для того, чтобы порядок (Jki , Jki+1 , Jki+2 )
Jji
трех требований был оптимальным в перестановке πk ∈ Π, необходимо и до-
статочно, чтобы длительности pki , pki+1 и pki+2 требований Jki , Jki+1 и Jki+2
85
удовлетворяли неравенствам pki ≤ pki+1 ≤ pki+2 , а с учетом принадлежности
допустимого сценария (pk1 , . . . , pkn ) заданному множеству T длительности
pki, pki+1 и pki+2 должны удовлетворять следующей системе неравенств:
pki ≤ pki+1 ≤ pki+2,
pLki ≤ pki ≤ pU,
ki
(Π.4)
pLki+1 ≤ pki+1 ≤ pU
,
ki+1
pLki+2
≤pki+2 ≤pU
ki+2
Система (Π.4) определяет 3-мерную пирамиду
P iroptĴji = P iropt(Jk
, Jki+1, Jki+2),
i
основанием которой является треугольник
[(
)
(
)
(
)]
pLk
, pLk
, pUk
,
pLk
, pUk
, pUk
,
pUk
, pUk
, pU
,
i
i+1
i+2
i
i+1
i+2
i
i+1
ki+2
а высотой - отрезок
[(
)
(
)]
pLk
, pLk
, pUk
,
pLk
, pLk
, pL
ki+2
i
i+1
i+2
i
i+1
Следовательно, системе (Π.4) удовлетворяют все точки пирамиды P iroptĴji =
= Piropt(Jki,Jki+1,Jki+2) и только они. Таким образом, равенство (Π.2) дока-
зано и для случая |Jji| = 3. Поскольку объем 3-мерной пирамиды P iroptĴji
равен произведению площади основания, т.е. площади треугольника
[(
) (
) (
)]
pLk
,pLk
,pUk
, pLk
,pUk
,pUk
, pUk
,pUk
,pU
ki+2
i
i+1
i+2
i
i+1
i+2
i
i+1
на треть высоты:
(
(
)
(
))2
(
(
)
(
))
πk
j
πk
uj
s
-li
s
uj
sπk
-lj
sπk
i
j
j
i
j
i
j
=
2
3
(
(
)
(
))3
j
πk
j
πk
u
s
-li
s
(
)
i
j
j
=
= Vol
Jji,T
,
3!
то равенство (Π.1) доказано и для случая |Jji | = 3.
Сделаем индуктивное предположение, т.е. предположим, что оба ра-
венства (Π.1) и (Π.2) выполняются в случае |Jji | = d, т.е. область опти-
мальности OR
J ji ,T) представляет собой d-мерную пирамиду PiroptĴji =
= Piropt(Jki,...,Jkt), основанием которой является (d - 1)-мерная пирамида,
a (uji (sπkj ) - li (sjk )) - это длина высоты каждой из этих пирамид. Покажем,
что на основе индуктивного предположения можно получить равенства (Π.1)
и (Π.2) для случая |Jji | = d + 1.
86
[
(
)
(
))
πk
j
πk
Рассмотрим подынтервал
lj
s
,u
s
условной оптимальности,
i
j
i
j
для которого
(
)
Jji = Jk
,...,Jk
,Jk
и
|Jji | = d + 1.
i
j
j
|J
|-1
|J
|
i
i
Из и{дукти}ного предположения следует, что для множества требований
Jji \ Jk
оба равенства (Π.1) и (Π.2) выполняются, и область оптималь-
j
|J
|
i
((
)
)
ности OR Jki , . . . , Jk
,T представляет собой d-мерную пирамиду
j
|J
|-1
i
((
)
)
P iropt (Jk
,...,Jkt)=OR
Jki ,... ,Jk
,T
i
j
|J
|-1
i
Сле
(
)
ний Jki , . . . , Jk
был оптимальным в перестановке πk ∈ Π, необходимо
j
|J
|-1
i
и достаточно, чтобы длительности pki , . . . , pk
требований Jki , . . . , Jk
j
j
|J
|-1
|J
|-1
i
i
удовлетворяли следующей системе неравенств:
pki ≤ ... ≤ pk
,
j
|J
|-1
i
pLki ≤ pki ≤ pU ,k
(Π.5)
i
pLk
≤pk
≤pUk
j
|J
j|-1
j
|J
|-1
i
|J
|-1
i
i
Добавив к системе (Π.5) неравенства
pk
≤pk
и pLk
≤pk
≤pUk
,
j
j
j
j
j
|J
|-1
|J
|
|J
|
|J
|
|J
|
i
i
i
i
i
получим следующую систему неравенств:
pki ≤ ... ≤ pk
,
j
|J
|-1
i
pk
≤pk
,
j
j
|J
|-1
|J
|
i
i
pLki ≤ pki ≤ pU ,k
i
(Π.6)
pLk
≤pk
≤pUk
,
j
j
j
|J
|-1
|J
|-1
|J
|-1
i
i
i
pLk
≤pk
≤pUk
,
j
j
j
|J
|
|J
|
|J
|
i
i
i
которая определяет (d + 1)-мерную пирамиду
(
)
P iroptĴji = P iropt Jk
,...,Jk
,
i
j
|J
|
i
87
(
)
основанием которой является d-мерная пирамида P iropt
Jki ,... ,Jk
,а
j
|J
|-1
(
(
)
(
))
i
πk
j
πk
разность uj
s
-li
s
равна длине высоты каждой из двух пирамид.
i
j
j
Из сдел((ного предпол)же)я и теоремы 1 следует, что область оптималь-
ности OR Jki , . . . , Jk
,T представляет собой (d+1)-мерную пирамиду
j
|J
|
i
(
)
((
)
)
P iropt Jki , . . . , Jk
= OR Jki,... ,Jk
,T
. Следовательно, равенство
j
j
|J
|
|J
|
i
i
(Π.2) установлено и для случая |Jji| = d + 1. Поскольку объем (d + 1)-мерной
пирамиды P iroptĴji равен произведению объема основания, т.е. объема d-мер-(
)
((
)
)
ной пирамиды P iropt Jki , . . . , Jk
= OR Jki,... ,Jk
,T на вы-
j
j
|J
|-1
|J
|-1
i
i
соту, деленную на (d + 1):
(
(
)
(
))d
(
(
)
(
))
πk
j
πk
uj
s
-li
s
uj
sπk
-lj
sπk
i
j
j
i
j
i
j
=
d!
d+1
j
(u
i
(sπkj ) - li(sjk ))d+1
j
=
= Vol
Ji
,T),
(d + 1)!
то равенство (Π.1) установлено и для случая |Jji | = d + 1. Таким образом,
равенства (Π.1) и (Π.2) доказаны методом математической индукции.
Равенство (14) следует из равенства (Π.2) и того, что при любом сцена-
рии p ∈ T длительность каждого требования Ji ∈ J принимает единственное
значение pi. Равенство (13) следует из замечания 2 и равенства (14). Равен-
ство (15) следует из равенств (13), (14) и (Π.1). Лемма 4 доказана.
СПИСОК ЛИТЕРАТУРЫ
1. Allahverdi A., Aydilek H., Aydilek A. Single machine scheduling problem with inter-
val processing times to minimize mean weighted completion times // Comput. Oper.
Res. 2014. V. 51. P. 200-207.
2. Goren S., Sabuncuoglu I. Robustness and stability measures for scheduling: single-
machine environment // IIE Transact. 2008. V. 40. P. 66-83.
3. Pereira J. The robust (minmax regret) single machine scheduling with interval pro-
cessing times and total weighted completion time objective // Comput. Oper. Res.
2016. V. 66. P. 141-152.
4. Lu C.-C., Lin S.-W., Ying K.-C. Robust scheduling on a single machine total flow
time // Comput. Oper. Res. 2012. V. 39. P. 1682-1691.
5. Sotskov Y.N., Werner F. Sequencing and Scheduling with Inaccurate Data. N.Y.,
USA: Nova Science Publishers, Hauppauge, 2014.
6. Braun O., Lai T.C., Schmidt G., Sotskov Y.N. Stability of Johnson’s schedule with
respect to limited machine availability // Int. J. Product. Res. 2002. V. 40. No. 17.
P. 4381-4400.
7. Davis W., Jones A. A real-time production scheduler for a stochastic manufacturing
environment // Int. J. Product. Res. 1988. V. 1. No. 2. P. 101-112.
88
8.
Grabot B., Geneste L. Dispatching rules in scheduling: a fuzzy approach // Int. J.
Product. Res. 1994. V. 32. No. 4. P. 903-915.
9.
Kasperski A., Zielinski P. Possibilistic minmax regret sequencing problems with
fuzzy parameters // IEEE Transact. Fuzzy Syst. 2011. V. 19. P. 1072-1082.
10.
Sotskov Y.N., Egorova N.G. Single machine scheduling problem with interval pro-
cessing times and total completion time objective // Algorithms. 2018. V. 11. No. 66.
P. 21-40.
11.
Sotskov Y.N., Lai T.-C. Minimizing total weighted flow time under uncertainty
using dominance and a stability box // Comput. Oper. Res. 2012. V. 39. No. 6.
P. 1271-1289.
12.
Lai T.-C., Sotskov Y.N., Egorova N.G., Werner F. The optimality box in uncertain
data for minimising the sum of the weighted job completion times // Int. J. Product.
Res. 2018. V. 56. No. 19. P. 6336-6362.
13.
Сотсков Ю.Н., Егорова Н.Г. Многогранники устойчивости оптимальной пере-
становки обслуживания требований // АиТ. 2014. № 7. С. 136-154.
Sotskov Y.N., Egorova N.G. Stability polyhedra of optimal permutation of jobs ser-
vicing // Autom. Remote Control. 2014. V. 75. No. 7. P. 1267-1282.
14.
Sotskov Y.N., Lai T.-C., Werner, F. Measures of problem uncertainty for scheduling
with interval processing times // OR Spectrum. 2013. V. 35. P. 659-689.
15.
Sotskov Y.N., Egorova N.G., Lai T.-C. Minimizing total weighted flow time of a
set of jobs with interval processing times // Math. Comput. Modell. 2009. V. 50.
P. 556-573.
16.
Lai T.-C., Sotskov Y.N., Sotskova N., Werner F. Optimal makespan scheduling with
given bounds of processing times // Math. Comput. Modell. 1997. V. 26. No. 3.
P. 67-86.
17.
Сотсков Ю.Н., Егорова Н.Г., Вернер Ф. Минимизация суммарного взвешен-
ного времени обслуживания требований с неопределенными данными: метод,
основанный на устойчивости // АиТ. 2010. № 10. С. 26-49.
Sotskov Y.N., Egorova N.G., Werner F. Minimizing total weighted completion time
with uncertain data: a stability approach // Automat. Remote Control. 2010. V. 71.
No. 10. P. 2038-2057.
18.
Pinedo M. Scheduling: Theory, Algorithms and Systems. N.J., USA: Prentice-Hall,
Englewood Cliffs, 2002.
19.
Graham R.E., Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Optimization and
approximation in deterministic sequencing and scheduling: a survey // Ann. Discret.
Math. 1979. V. 5. P. 287-326.
20.
Smith W. Various optimizers for single-stage production // Naval Res. Logist. Quar-
terly. 1956. V. 3. No. 1. P. 59-66.
21.
Kouvelis P., Yu G. Robust Discrete Optimization and its Application. Boston, USA:
Kluwer Academ. Publish., 1997.
22.
Burdett R.L., Kozan E. Techniques to effectively buffer schedules in the face of
uncertainties // Comput. Industr. Engineer. 2015. V. 87. P. 16-29.
23.
Kasperski A., Zielinski P. A 2-approximation algorithm for interval data minmax
regret sequencing problems with total flow time criterion // Oper. Res. Lett. 2008.
V. 36. P. 343-344.
24.
Daniels R.L., Kouvelis P. Robust scheduling to hedge against processing time
uncertainty in single stage production // Management Sci. 1995. V. 41. No. 2.
P. 363-376.
89
25. Yang J., Yu G. On the robust single machine scheduling problem // J. Combinat.
Optim. 2002. V. 6. P. 17-33.
26. Harikrishnan K.K., Ishii H. Single machine batch scheduling problem with resource
dependent setup and processing time in the presence of fuzzy due date // Fuzzy
Optim. Decision Making. 2005. V. 4. P. 141-147.
27. Sotskov Y.N., Egorova N.G. Single-machine scheduling with uncertain durations
for optimizing service logistics with one truck // EURO Mini-conf. Logist. Anal.,
June 18-19, 2018, Minsk, Belarus. 29 р.
Статья представлена к публикации членом редколлегии А.А. Лазаревым.
Поступила в редакцию 03.07.2019
После доработки 14.10.2019
Принята к публикации 28.11.2019
90