Автоматика и телемеханика, № 5, 2020

В.В. СЕРВАХ, д-р физ.-мат. наук (svv_usa@rambler.ru)

(Институт математики им. С.Л. Соболева СО РАН, Омск)

МАКСИМИЗАЦИЯ УДЕЛЬНОЙ ПРИВЕДЕННОЙ ПРИБЫЛИ

В СИСТЕМАХ УПРАВЛЕНИЯ ЗАПАСАМИ¹

Исследуется модель максимизации прибыли коммерческой компании

с учетом интенсивности продажи товаров, стоимости закупки, доставки,

хранения и реализации, а также возможности альтернативного размеще-

ния свободного капитала. Показано, что функция прибыли в зависимости

от периода завоза товаров имеет единственную точку максимума. По-

строена модель и разработаны алгоритмы решения задачи максимизации

прибыли в многономенклатурных системах при ограниченном оборотном

капитале.

Ключевые слова: исследование операций, управление запасами, максими-

зация прибыли, динамическое программирование.

DOI: 10.31857/S0005231020050074

1. Введение

Рассматривается задача оптимизации деятельности торговой компании,

которая закупает товары на бирже и реализует их на розничном рынке.

На предприятии построен специализированный склад, внедрены современ-

ные логистические технологии с соответствующими базами данных, постоян-

ным мониторингом движения товаров, автоматизацией склада и погрузочно-

разгрузочных работ. Новейшие технологии, эффективная организация соб-

ственного склада позволили существенно сократить издержки. Сложилась

ситуация, когда классические модели, например [1-5], основанные на мини-

мизации затрат, не всегда адекватно отражают ситуацию. В настоящее время

с учетом высокой мобильности экономики, острой конкуренции и внедрения

современных систем логистики возникла необходимость использования но-

вых моделей, направленных, в первую очередь, на эффективное использова-

ние капитала и получение максимальной прибыли. Одной из первых в этом

направлении была статья [6]. Из российских публикаций отметим [7-11] и

недавно изданную монографию [12]. Такой подход особенно важен при оп-

тимизации закупок товаров, для которых отношение объем/цена является

малой величиной, например радиодеталей, медикаментов и др. [13, 14]. Затра-

ты на доставку и хранение становятся незначительными, и большее значение

приобретает скорость оборота денег.

¹ Работа выполнена при поддержке программы фундаментальных научных исследо-

ваний государственных академий наук на 2013-2020 гг., п. I.5, проект № 0314-2019-0019

¾Анализ и решение задач проектирования сложных систем методами дискретной оптими-

зации¿.

106

Другой проблемой является разработка алгоритма автоматической кор-

ректировки заявок при ограничении оборотного капитала. Автоматизирован-

ная система при формировании очередной заявки определяет оптимальные

объемы закупки товаров. В некоторые моменты времени общая стоимость

заказываемых товаров может оказаться больше имеющихся в наличии сво-

бодных денег. В такой ситуации приходится либо сокращать заказ, либо брать

кредит. Кредит меняет стоимость денег, и тем самым меняются и оптималь-

ные объемы закупок. Сокращение заказа также приводит к отклонению от

оптимума. Возникает задача корректировки многономенклатурного заказа с

учетом ограничений на размер оборотного капитала.

Большое влияние на представляемую работу оказали успехи ученых бело-

русской школы по комбинаторной оптимизации, созданной В.С. Танаевым.

Работы [15, 16] и многие другие стали источником получения качественной

систематизированной информации, базой для дальнейших исследований. Ра-

боты по логистике поставок [19, 20] выполнялись в рамках проектов INTAS в

тесном сотрудничестве с белорусскими учеными. Настоящая публикация опи-

рается на современные разработки, проводимые в объединенном институте

проблем информатики Национальной академии наук Беларуси. В частности,

отметим статьи, связанные с задачами максимизации прибыли [17, 18].

Структура статьи. В разделе 2 рассматривается модель управления запа-

сами при наличии альтернативных возможностей использования капитала.

Раздел 3 посвящен построению модели и разработке алгоритмов решения за-

дачи оптимизации текущих закупок в многономенклатурных системах при

ограниченном оборотном капитале, в том числе и при возможности исполь-

зования кредитов. В раздел 4 рассматривается более общая модель с учетом

особенностей ее реализации на практике.

2. Задача максимизации чистой приведенной прибыли

Рассматривается классическая модель управления запасами и ее развитие

с учетом факторов современной экономики. Основное внимание уделяется

эффективному использованию капитала при наличии альтернативных воз-

можностей его использования.

Модель будем рассматривать в предположении, что имеется гарантиро-

ванная возможность альтернативного безрискового размещения капитала под

ставку r₀. Тогда деньги в разные моменты времени будут иметь различную

ценность. Чтобы сравнивать поступления, полученные в разное время, ис-

пользуется следующий подход. Если в момент t₁ имеется некоторый капи-

тал K₁, то его всегда можно разместить на рынке под текущую рыночную

процентную ставку r₀. При таком размещении к моменту t₂ капитал увели-

чится до значения K₁(1 + r₀)t2-t1 . И наоборот, если в момент t₂ необходим ка-

питал K₂, то в момент t₁ достаточно иметь его в количестве K₂/(1 + r₀)t2-t1 .

Поэтому чтобы сравнить капитал K₁ в момент времени t₁ и K₂ в момент вре-

мени t₂, необходимо сравнить величины K₁ и K₂/(1 + r₀)t2-t1 . Эта операция

называется операцией приведения к моменту времени t₁ или дисконтирова-

нием.

107

0,15

0,10

0,05

40 T

-0,05

-0,10

-0,15

-0,20

-0,25

-0,30

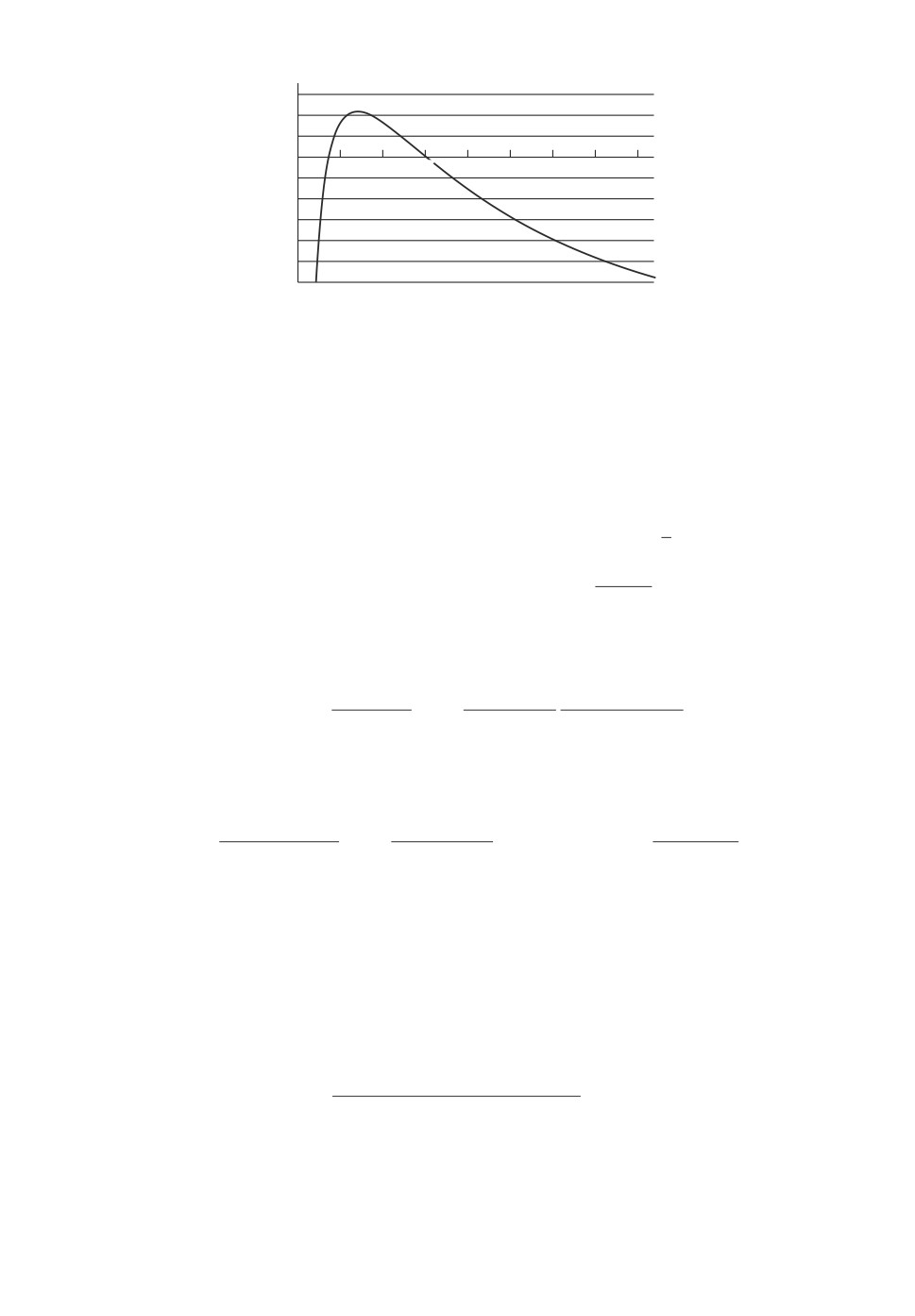
Рис. 1. Зависимость удельной прибыли от T .

Процесс закупки и реализации товара будем рассматривать, как в класси-

ческой модели: закупаем товар в объеме v по цене β и продаем его с интен-

сивностью λ по цене c. Затраты на доставку задаются функцией α + βv, где

α постоянные издержки, включающие стоимость заявки и доставки про-

дукции. Стоимость хранения единицы товара в единицу времени обозначим

через c_xp.

Время реализации закупленного товара составит T =^vλ . Интенсивность

поступления денег от продажи равна cλ. С учетом дисконтирования интен-

сивность поступления денег выражается функцией^cλ(1+r

. За период реали-

0)^t

зации товара [0, T ] суммарные поступления, дисконтированные к начальному

моменту времени, будут равны

∫T

cλ

(1 + r₀)^T - 1

Q(T ) =

dt =

(1 + r₀)^t

ln(1 + r₀)

(1 + r₀)^T

а затраты на хранение товара с учетом дисконтирования составят

∫T

(

)

(T λ - tλ)c_xp

c_xpλ

Z(T ) =

dt =

T ln(1 + r₀) +

-1

(1 + r₀)^t

ln²(1 + r₀)

(1 + r₀)T

Таким образом, за указанный период [0, T ] чистая приведенная прибыль бу-

дет получена в размере

Q(T ) - (α + βv) - Z(T ).

В задаче требуется максимизировать удельную прибыль, которая выражает-

ся следующей функцией:

Q(T ) - (α + βT λ) - Z(T )

U (T ) =

→ max .

На графике (рис. 1) приведен пример функции U(T ) в зависимости от

периода завоза товара при входных данных λ = 1, α = 2, β = 0,25, c = 1,

r₀ = 0,1, c_xp = 0,03. Оптимальное значение удельной чистой привиденной

прибыли равно 0,109 и достигается при T = 7,02.

108

1 - a/g

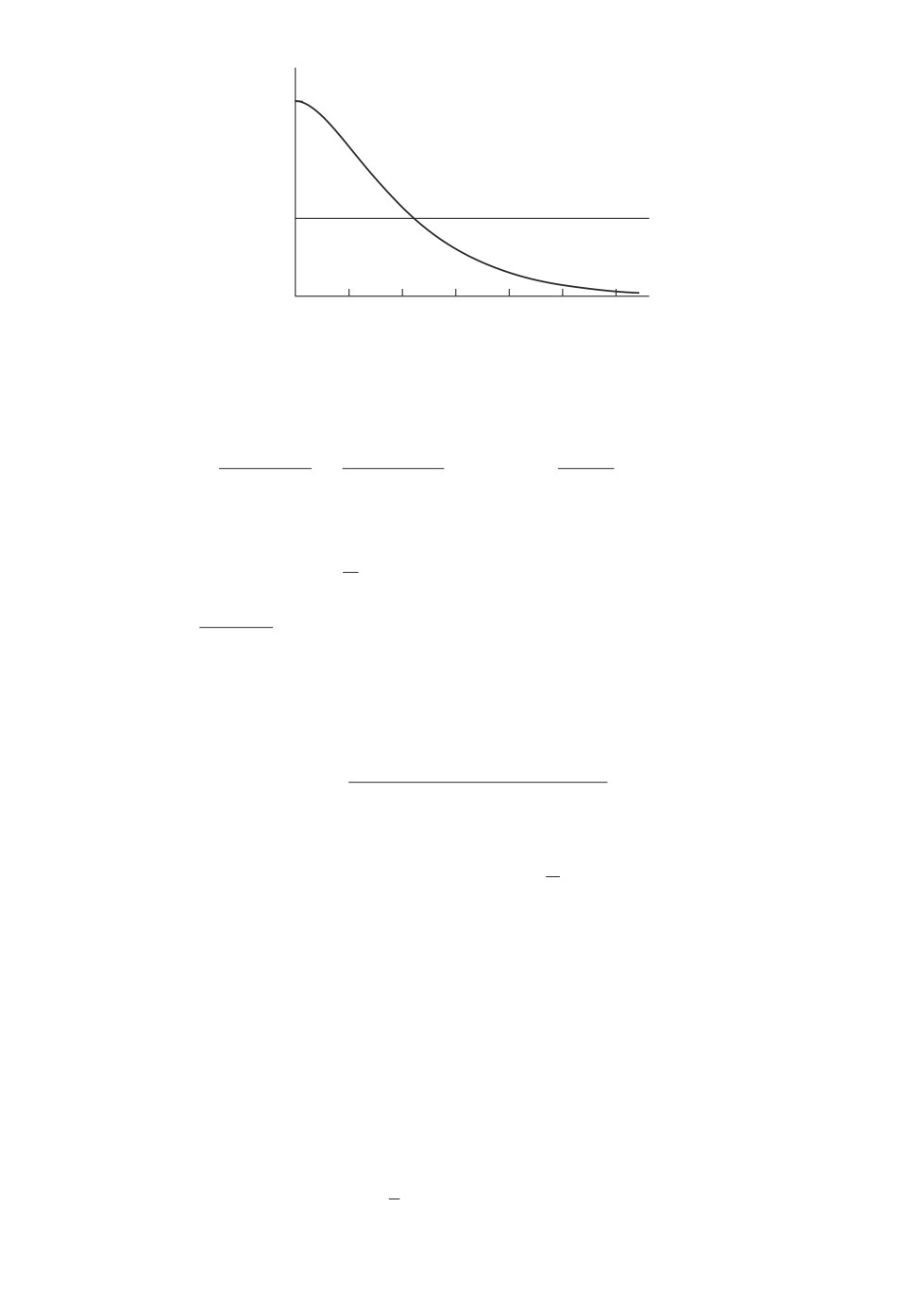
Рис. 2. Изменение функции W (T ) в зависимости от T .

Исследуем экстремальные значения функции U(T ). Обозначим

cλ

c_xpλ

γ=

> 0, δ =

0 < δ < 1.

ln(1 + r₀)

ln²(1 + r₀)

1+r₀

Тогда

U (T ) =

(γ(1 - δ^T) - α - βT λ) - const,

где const =cxpλ

ln²(1+r₀)

lim

U (T ) = -∞, lim U(T ) = -βλ.

T→+0

T→+∞

Исследуем нули производной

-γδ^T ln δT - γ(1 - δ^T) + α

U^′(T) =

= 0.

T²

Получаем следующее уравнение:

δ^T(1 - T ln δ) = 1 -

Решим его графически. Обозначим W (T ) = δ^T(1 - T ln δ).

W (0) = δ⁰ = 1;

W^′(T) = δ^T ln δ - δ^TT ln² δ - δ^T ln δ = -δ^TT ln² δ < 0;

lim W (T ) = 0.

T→∞

Следовательно, функция W (T ) всегда положительна и монотонно убывает.

График ее изображен на рис. 2. Графиком правой части уравнения является

прямая, параллельная оси Ox.

При α < γ графики пересекаются и существует единственное

решение

уравнения δ^T(1 - T ln δ) = 1 -^αγ . Очевидно, что это точка максимума. Тем

самым доказана следующая

109

cxpλ

Теорема 1. При α <^cλ

функция прибыли имеет един-

ln(1+r₀)

+ ln2

(1+r₀)

ственную точку максимума. При α ≥^cλln(1+r

функция прибыли

1+r₀)

монотонно возрастает на всем промежутке (0,∞) и при этом значение

прибыли всегда отрицательно и меньше величины -βλ -cхрλln(1+r

Таким образом, при определенных условиях существует такой период за-

воза продукции, при котором вложенные деньги используются максимально

эффективно, принося наибольшую прибыль. Точка максимума находится как

единственное решение уравнения δ^T(1 + T ln δ) = 1 -^αγ .

3. Задача с ограничением на оборотный капитал

Описанный выше подход является математической основой моделей, реа-

лизованных на практике в сетевых торговых структурах. В многономенкла-

турных системах определяется, какие товары завозить и в каком объеме с

учетом текущего спроса, цен закупки и продажи, стоимости доставки и хра-

нения. Критерием является максимизация удельной приведенной прибыли.

Используемая модель позволяет учитывать различные дополнительные огра-

ничения по страховым запасам товаров, временным лагам и т.д. Сроки и объе-

мы заказов рассчитываются автоматически программой-роботом без участия

работников фирмы.

Сложности возникают, когда при формировании заявки общая стоимость

заказываемых товаров может оказаться больше имеющихся в наличии сво-

бодных денег. Во-первых, стоимость заявки колеблется, так как в разные мо-

менты времени завозятся разные виды и объемы товаров. Во-вторых, размер

оборотного капитала может сократиться, например в период уплаты налогов

или при внешнем отвлечении оборотных средств. В такой ситуации приходит-

ся либо сокращать заказ, либо брать кредит. Сокращение заказа приводит

к дополнительным издержкам. Кредит уменьшает прибыль из-за выплаты

процентов. Ниже построена модель и разработан алгоритм решения задачи

минимизации издержек в случае ограничения на объем оборотного капитала.

Опишем параметры задачи:

N количество видов товара;

α_i стоимость доставки одной партии товара i;

β_i

цена закупки единицы продукции товара i;

α_i + β_iv_i стоимость заказа и доставки партии товара i объемом v_i;

λ_i

интенсивность продажи товара i;

c_i

цена продажи единицы товара i;

c^xpi

стоимость хранения единицы товара i в единицу времени;

r₀

ставка альтернативного безрискового ликвидного размещения капи-

тала.

В текущий момент времени для каждого товара i с нулевым остатком на

складе требуется найти период завоза T_i, при котором удельная приведенная

прибыль U_i(T_i), равная

110

1( c_iλ_i

(1 + r₀)Ti - 1

-β_iT_iλ_i -

T_i ln(1 + r₀)

(1 + r₀)^Ti

(

))

λ_i

T_i ln(1 + r₀) +

-1

ln²(1 + r₀)

(1 + r₀)^Ti

будет максимальна.

Отметим, что параметры задачи постоянны только на определенном вре-

менном промежутке. При следующем заказе товаров используются новые,

актуальные на момент расчета значения параметров. Сделаем еще некото-

рые естественные допущения, которые не влияют на общность рассматривае-

мой модели. Заказы невозможно делать в любой момент времени. Дискрет-

ность планирования во времени естественна для экономических задач. Если

выбрать подходящую единицу измерения, то можно рассматривать только

целочисленные моменты времени. Временные лаги при отгрузке и доставке

товара учитывать не будем, так как это не влияет на суть задачи.

При этих условиях достаточно рассматривать только такие объемы завоза,

чтобы товар заканчивался в целочисленные моменты времени, и новый завоз

делать, когда остаток товара будет равен нулю. Тогда и значения T_i долж-

ны быть целыми. Действительно, если T_i не является целым, то в момент

времени ⌊T_i⌋ все равно придется делать очередной завоз, так как остатка

(T_i - ⌊T_i⌋)λ_i до следующего завоза не хватит. Целочисленный оптимум U_i(T_i)

обозначим через T^∗i. Соответствующее значение объема завозимого товара

равно v^∗i = T^∗iλ_i.

Очередная заявка формируется в текущий момент t ∈ Z⁺. Закупаем толь-

ко те товары, которые к этому моменту заканчиваются. Без ограничения общ-

ности для удобства изложения перенумеруем их числами от 1 до n. Считыва-

ем из базы данных текущие параметры по этим позициям, далее по каждому

товару i = 1, . . . , n находим целочисленные оптимумы T^∗i и cоответствующие

значения завозимых объемов v^∗i = T^∗iλ_i. Для их покупки потребуется

∑

(α_i + β_iv^∗i)

i=1

единиц капитала. При наличии необходимой суммы заявка оплачивается и

товар поставляется.

3.1. Задача сокращения заявки

Проблемы возникают, когда текущего капитала K не хватает для опла-

ты заявки целиком. На практике рассматриваются три варианта: сокраще-

ние заявки, банковский краткосрочный кредит, товарный кредит. Последние

два варианта отличаются организационно, однако с позиций максимизации

чистой приведенной прибыли между ними различий нет, часть дохода при-

ходится отдавать. Рассмотрим сначала задачу сокращения заявки, а потом

обобщим ее на случай возможности использования кредитов.

Введем переменную x_i ≤ v^∗i объем заказа товара i = 1, . . . , n. Как было

упомянуто выше, T_i является целым числом, и, значит, x_i ∈ {λ_i, 2λ_i, 3λ_i, . . .

111

...,v∗i }. Здесь x_i ≥ λ_i, так как спрос должен быть удовлетворен. Сокращение

(

)

v^∗i

заказа до уровня x_i приводит к потере прибыли в размере H_i(x_i) = U_i

λ_i

(

)

x_i

-U_i

. Отметим, что на множестве {λ_i, 2λ_i, 3λ_i, . . . , v^∗i} функция H_i(x_i)

λ_i

монотонно убывает.

∑

Таким образам, если K < (α_i + β_iv^∗i), то денег на оплату текущей заяв-

i=1

ки не хватает и закупки необходимо сократить. При этом желательно, чтобы

потери прибыли были минимальны. Получаем следующую модель:

∑

H_i(x_i) → min,

i=1

∑

(α_i + β_ix_i) ≤ K,

i=1

x_i ∈ {λ_i,2λ_i,3λ_i,... ,v^∗i}, i = 1,... ,n.

∑

Заметим, что в данной постановке K ≥ (α_i + β_iλ_i), так как до следующего

i=1

∑

завоза спрос должен быть удовлетворен. Величину (α_i + β_iλ_i) обозначим

i=1

через K_min.

Для решения данной задачи используем схему динамического программи-

рования [21]. Обозначим через ϕ(m, k) оптимальное значение целевой функ-

ции при текущем капитале k и подмножестве товаров {1, . . . , m}, где m =

= 1, . . . , n, k = 1, . . . , K. Закупка товара m в количестве x_m допустима, если

∑

x_m ∈ {λ_m,2λ_m,3λ_m,... ,v^∗m} и

(α_i + β_iλ_i) + α_m + β_mx_m ≤ k. Множество

i=1

допустимых значений x_m обозначим через P (m, k).

Для вычисления ϕ(m, k) перебираем все значения x_m ∈ P (m, k). Если то-

вар m закупаем в объеме x_m, то получаем подзадачу

∑

H_i(x_i) + H_m(x_m) → min,

i=1

∑

(α_i + β_ix_i) ≤ k - (α_m + β_mx_m),

i=1

x_i ∈ {λ_i,2λ_i,3λ_i,... ,v^∗i},i = 1,... ,m - 1,

оптимум для которой равен ϕ(m - 1, k - α_m - β_mx_m). Таким образом имеем

рекуррентное соотношение

ϕ(m, k) = min

{H_m(x_m) + ϕ(m - 1, k - α_m - β_mx_m)}.

xm∈P(m,k)

Для нахождения ϕ(n, k) данное рекуррентное соотношение необходи-

мо реализовать в двойном цикле m = 2, . . . , n, k = 1, . . . , K при начальных

112

условиях ϕ(1, k) = H₁(x₁), где x₁ = min{⌊k-λ1β₁₁ ⌋λ1,v1}.Восстановлениеоп-

тимального решения осуществляется обратным ходом по стандартной схе-

ме. Заметим, что реализация алгоритма требует целочисленности вели-

чин α_m + β_mx_m, что может быть обеспечено подбором единиц измерения

капитала.

Трудоемкость алгоритма псе

(

)

∑

входных данных и составляет O K

T^∗

операций, где K имеющийся

m=1

капитал в выбранных единицах измерения, T^∗m оптимальный период завоза

товара m.

3.2. Формирование заявки при возможности использования кредитов

Обобщим выписанную модель на случай возможности использования кре-

дитов. Ставка по кредиту r известна. Переменной D будем обозначать размер

∑

кредита. Как и ранее, K_min = (α_i + β_iλ_i) это минимально необходимый

i=1

∑

объем оборотных средств. Введем также величину K_max = (α_i + β_iλ_iT^∗i)

i=1

размер средств, достаточный для полного обеспечения заявки.

В случае, если минимально необходимый размер оборотных средств K_min

больше наличного капитала K, размер кредита не может быть меньше

величины K_min - K. Максимальное значение кредита D не превосходит

K_max - K.

Приведенные издержки на использование кредита составят^D(1+r) - D._1+r

Размер доступного капитала будет равен K + D. Получаем следующую мо-

дель:

∑

D(1 + r)

H_i(x_i) +

- D → min,

1+r

i=1

∑

(α_i + β_ix_i) ≤ K + D,

i=1

max{0, K_min - K} ≤ D ≤ K_max - K,

x_i ∈ {λ_i,2λ_i,3λ_i,... ,v^∗i}.

Если переменную D зафиксировать, то величина^D(1+r) - D будет кон-_1+r

стантой и получим задачу, описанную в предыдущем параграфе, с начальным

капиталом K + D. Ее решаем описанным там же алгоритмом и находим все

ϕ(m, k) для m = 1, . . . , n и k = 1, . . . , K_max. После этого остается перебрать

все целые значения D ∈ [max{0, K_min - K}, K_max - K] и найти минимум

{

}

D(1 + r)

min

ϕ(n, K + D) - D +

D∈[max{0,K_min-K},Kmax-K]

1+r₀

113

(

)

∑

Трудоемкость алгоритма составит O

K_max T^∗

операций.

i=1

Расчеты на реальных данных показали актуальность модели с кредитами.

Часто оптимум по D достигается внутри интервала

[

]

max{0, K_min - K}, K_max - K

т.е. заявка все-таки сокращается, но ее часть оплачивается за счет кредита.

Аналогичный результат был получен для задачи календарного планирования

инвестиционных проектов, когда за счет кредитов выполнялась только часть

работ проекта [22].

4. Формирование заявки с учетом неравномерности потребления

В рассмотренных моделях в момент формирования заявки предполага-

лось, что интенсивность потребления каждого товара не меняется в течение

всего периода его реализации. При следующем формировании заявки будет

использоваться другое актуальное значение λ_i и остатков на складе. При

этом значение λ_i могло измениться. Таким образом, функция интенсивности

потребления хоть и являлась кусочно-постоянной по времени, но в рассмат-

риваемый период была константой. В реальности процесс реализации това-

ра может оказаться неравномерным. Поэтому наиболее эффективно вместо

константы λ_i использовать функцию λ_i(t), t = 1, . . . , T , где за t = 0 берем те-

кущий момент времени очередного заказа. Отметим, что в рассматриваемой

практической задаче величины λ_i(t) на период планирования T достаточно

хорошо прогнозируются. Это обусловлено и спецификой задачи, и небольшим

горизонтом планирования. Несмотря на это, в модели необходимо учесть, что

реальный спрос может отклониться от заданного. Поэтому необходим неко-

торый механизм, который устраняет данную проблему. Как вариант можно

формировать страховой запас, но это приводит к снижению прибыли и допол-

нительной оптимизации. Получаем две противоположные тенденции. С одной

стороны, нежелательно возникновения дефицита товара на складе, так как

это приводит к недополученной прибыли. С другой стороны, лишние запасы

на складе уменьшают прибыль. Задачи такого типа исследуются в многочис-

ленных публикациях, например [23]. В данной задаче ситуация проще. Так

как в каждый целочисленный момент ситуация на складе отслеживается, то

в момент T_i - 1 можно сравнить остаток на складе и значение λ_i(T_i). Если

остаток меньше, то очередной заказ товара делаем в момент T_i - 1. Пусть

в момент очередного заказа на складе имеется остаток R_i ≥ 0, которого не

хватает для покрытия спроса на ближайший единичный период времени.

∑

При этих условиях объем заказа товара i на период T_i составит λ_i(t)-

t=1

∑

-R_i, а начальный объем на складе λ_i(t). Приведенный доход будет равен

t=1

∑

c_iλ_i(t)

Q(T_i) =

. Здесь можно учесть и изменения цен продажи, используя

(1+r₀)^t

t=1

114

вместо c_i заданные значения c_i(t):

∑

c_i(t)λ_i(t)

Q_i(T_i) =

(1 + r₀)^t

t=1

Величины α_i и β_i учитываются только в момент t = 0. Поэтому нет смысла

их варьировать.

Выпишем затраты на хранение Z_i(T_i). Остаток товара i на складе на мо-

∑

мент t = 1, . . . , T_i составит

λ_i(τ) -

λ_i(τ) =

λ_i(τ). Средний остаток

τ=1

τ=t+1

∑

на интервале [t - 1, t], за который приходится платить, равен

λ_i(τ)+

τ=t+1

+λi(t)2. Можно также учесть изменение удельной стоимости хранения това-

ров во времени. В результате получаем следующую формулу:

(

)

∑

λ_i(τ) +λi(t)

c^xpi(t)

∑

τ=t+1

Z_i(T_i) =

(1 + r₀)^t

t=1

Функция удельной приведенной прибыли будет равна

(

)

∑

U_i(T_i) =

Q_i(T_i) - α_i - β_i

λ_i(t) - Z_i(T_i)

t=1

Оптимум T^∗i находим простым перебором для T_i = 1, 2, . . . , до тех пор пока

функция U_i(T_i) не начнет убывать.

Уточним математическую модель задачи. Пусть, как и ранее, {1, . . . , n}

это множество номеров товаров, заказываемых в момент t = 0. Оптимальный

∑

объем товара i в заявке равен

λ_i(t) - R_i. Тогда стоимость оптимальной

t=1

заявки составит





T^∗i

∑

K_max =

α_i + β_i  λ_i(t) - R_i.

i=1

t=1

Средства, необходимые для удовлетворения минимального спроса, будут рав-

ны

∑

K_min = (α_i + β_i(λ_i(1) - R_i)).

i=1

∑

Переменная x_i может принимать значения

λ_i(t) - R_i, T_i = 1,... ,T^∗i.

t=1

Функция потерь H_i(x_i) определяется как отклонение от оптимального значе-

ния прибыли U_i(T^∗i) - U_i(T_i). Таким образом, итоговая модель сокращения

115

заявки и оптимизации кредитных заимствований принимает вид:

∑

D(1 + r)

H_i(x_i) +

- D → min,

1+r

i=1

∑

(α_i + β_ix_i) ≤ K + D,

i=1

max{0, K_min - K} ≤ D ≤ K_max - K,

{

}

∑

x_i ∈

λ_i(t) - R_i | T_i = 1,... ,T^∗

t=1

Для решения сформулированной задачи используем описанный выше ал-

горитм динамического программирования. Алгоритм реализован и внед-

рен в логистической системе управления закупками одного из дистрибью-

теров фармацевтического рынка. Общее число позиций в номенклатуре то-

варов составляет более 40 тысяч. Ежедневный заказ включает несколько ты-

сяч наименований товаров. Оптовая отгрузка осуществляется через кросс-

докинговый склад. База данных о ценах, спросе и других параметрах обнов-

ляется ежедневно. Информация об остатках на складе компании отслежива-

ется в реальном режиме времени. Расчет заявки происходит в конце каждого

дня с учетом текущих параметров системы.

5. Заключение

В работе исследована задача максимизации прибыли с учетом альтерна-

тивного использования капитала. Доказана теорема о единственности точки

максимума функции прибыли. Построена модель задачи формирования за-

явки максимизации прибыли с учетом ограничения оборотного капитала, вы-

явлены и обоснованы ее свойства, предложен и реализован алгоритм решения

задачи, основанный на схеме динамического программирования. Предложен

и реализован алгоритм решения задачи формирования заявки при возмож-

ности использования кредитов. Рассмотрен случай формирования заявки с

учетом неравномерности потребления. Разработанный подход используется

при оперативном управлении поставками в компании, торгующей медика-

ментами.

СПИСОК ЛИТЕРАТУРЫ

1. Wilson R.H. A Scientific Routine for Stock Control // Harvard Business Rev. 1934.

No. 13. P. 116-128.

2. Букан Дж., Кенигсберг Э. Научное управление запасами. М.: Наука, 1967.

3. Первозванский А.А. Математические модели в управлении производством. М.:

Наука. Главная редакция физ.-мат. лит. 1975.

4. Рыжиков Ю.И. Теория очередей и управление запасами. СПб.: Питер, 2001.

5. Хедли Дж., Уайтин Т. Анализ систем управления запасами. М.: Наука, 1969.

116

Chandra M.J., Bahner M.L. The effects of inflation and the time value of money on

some inventory systems // Int. J. Product. Res. 1985. V. 23. No. 4. P.723-729.

Бродецкий Г.Л. Модели оптимизации систем управления запасами с учетом вре-

менной стоимости денег при ограничениях на размер капитала // Логистика и

управление цепями поставок. 2007. № 2. С. 70-88.

Бродецкий Г.Л. Многономенклатурное управление запасами: новый подход к

оптимизации решений // Логистика сегодня. 2014. № 1. С. 34-45.

Brodetskiy G.L. The new approach to inventory optimization // Int. J. Logist. Syst.

Management (IJLSM). 2015. V. 22. No. 3. P. 251-266.

10.

Лукинский В.В. Актуальные проблемы формирования теории управления запа-

сами. СПб.: СПбГИЭУ, 2008.

11.

Лукинский В.В. Управление запасами в цепях поставок: в 2 ч. Ч. 2: учебник и

практикум для бакалавриата и магистратуры. М.: Изд-во Юрайт, 2017.

12.

Бродецкий Г.Л., Герами В.Д., Колик А.В., Шидловский И.Г. Управление за-

пасами: многофакторная оптимизация процесса поставок. М.: Изд-во Юрайт,

2019.

13.

Бурлакова Н.И., Сервах В.В. Максимизация чистой приведенной прибыли

в задаче управления запасами // Сб. научных тр. VIII Междунар. школы-

симпозиума “Анализ, управление, моделирование, развитие”. Симферополь:

ТНУ им. В.И. Вернадского, 2014. С. 61-62.

14.

Бурлакова Н.И., Полянцева И.А., Сервах В.В. Оптимизация закупок с учетом

альтернативного использования капитала // Тез. докл. XVI Байкал. междунар.

школы-семинара “Методы оптимизации и их приложения”, Иркутск, ИСЭМ СО

РАН, 2014. 32 с.

15.

Танаев В.С., Гордон В.С., Шафранский Я.М. Теория расписаний. Одностадий-

ные системы. М.: Наука, 1984.

16.

Танаев В.С., Сотсков Ю.Н., Струсевич В.А. Теория расписаний. Многостадий-

ные системы. М.: Наука, 1989.

17.

Braun, O., Sotskov, Yu.N. Scheduling personal finances via integer programming //

J. Math. Modell. Algorithm., 2013. V. 12. No. 2. Р. 179-199.

18.

Голами О., Сотсков Ю.Н, Вернер Ф. Затюпо О.С. Эвристические алгоритмы

для максимизации дохода и количества требований, обслуживаемых на парал-

лельных приборах // АиT. 2019. № 2. С. 125-151.

Gholami O., Sotskov Y.N., Werner F., Zatsiupo A.S. Heuristic Algorithms to Max-

imize Revenue and the Number of Jobs Processed on Parallel Machines // Autom.

Remote Control. 2019. Vo. 80. No. 2. P. 297-316.

19.

Chauhan S.S., Eremeev A.V., Romanova A.A., Servakh V.V., Woeginger G.J. Ap-

proximation of the supply scheduling problem // Oper. Res. Lett. 2005. V. 33. No. 3.

P. 249-254.

20.

Eremeev A.V., Romanova A.A., Chauhan S.S., Servakh V.V. Approximate Solution

of the Supply Management Problem // J. Appl Industr. Math. 2007. V. 1. No. 4.

С. 1-9.

21.

Гимади Э.Х., Глебов Н.И. Математические модели и методы принятия решений.

Уч. пос. / Новосибирск: Изд-во Новосиб. гос. ун-тa. 162c.

22.

Мартынова Е.А., Сервах В.В. О задаче календарного планирования проектов

с использованием кредитов // АиТ. 2012. № 3. С. 107-116.

Martynova E.A., Servakh V.V. On Scheduling Credited Projects // Autom. Remote

Control. 2012. V. 73. No. 3. P. 508-516.

117