Автоматика и телемеханика, № 5, 2020

(Институт проблем управления им. В.А. Трапезникова РАН, Москва),

А.А. ЛАЗАРЕВ, д-р физ.-мат. наук (jobmath@mail.ru )

(Институт проблем управления им. В.А. Трапезникова РАН, Москва),

Ф. ВЕРНЕР, профессор (frank.werner@mathematik.uni-magdeburg.de)

(Университет Отто-фон-Герике, Магдебург, Германия)

МИНИМИЗАЦИЯ СУММАРНОГО ВЗВЕШЕННОГО ЗАПАЗДЫВАНИЯ

НА ОДНОМ ПРИБОРЕ С РАВНЫМИ ПРОДОЛЖИТЕЛЬНОСТЯМИ

ОБСЛУЖИВАНИЯ ТРЕБОВАНИЙ¹

Рассматривается задача теории расписаний, в которой необходимо

минимизировать суммарное взвешенное запаздывание на одном приборе

с равными продолжительностями обслуживания требований и неодно-

временным поступлением требований на обслуживание. Эта задача упо-

мянута как минимальная, статус вычислительной сложности которой не-

известен: http://www2.informatik.uni-osnabrueck.de/knust/class/dateien/

classes/ein_ma/ein_ma. Последние результаты по данной задаче опубли-

кованы в 2000 и 2005 гг., а именно, алгоритмы решения частных случаев

задачи. В данной статье представлены некоторые свойства задачи и пути

дальнейших исследований.

Ключевые слова: теория расписаний, один прибор, суммарное взвешенное

запаздывание.

DOI: 10.31857/S0005231020050086

1. Введение

Формулировка задачи: дано множество N = {1, . . . , n} из n требований,

которые должны быть обслужены на одном приборе. Прерывание обслужива-

ния требований не допускается. Одновременно прибор может обслуживать не

более одного требования. Прибор готов к обслуживанию требований с момен-

та времени 0. Для каждого требования j ∈ N заданы фиксированное время

обслуживания p_j = p ∈ Z⁺, директивный срок d_j ∈ Z⁺, время поступления

r_j ∈ Z⁺ (т.е. наиболее раннее время начала обслуживания) и вес w_j ∈ Z⁺.

Будем называть активным такое расписание, при котором ни одно требо-

вание не может быть перемещено на более ранний срок обслуживания без

нарушения ограничений задачи. В данной статье рассматриваются только

активные расписания.

Расписание π однозначно определяется перестановкой требований из мно-

жества N. Пусть C_j (π) - время завершения обслуживания требования j при

расписании π. Если C_j (π) > d_j , тогда требование j запаздывает и принимает-

ся U_j = 1, иначе U_j = 0. Если C_j (π) ≤ d_j , тогда требование j не запаздывает.

¹ Исследование выполнено при частичной поддержке гранта Российского научного фон-

да (проект № 17-19-01665).

119

Пусть T_j (π) = max{0, C_j (π) - d_j } запаздывание требования j при расписа-

нии π. Определим S_j = C_j - p как время начала обслуживания требования j

при расписании π.

В задаче минимизации суммарного взвешенного запаздывания на одном

приборе с равными продолжительностями обслуживания требований и неод-

новременным поступлением требований на обслуживание необходимо постро-

ить оптимальное расписание π^∗, при котором достигается минимум функции

∑

f_j(C_j) =

w_jT_j.

j=1

Обозначим данную задачу как 1|r_j , p_j = p|

∑w_jT_j в соответствии с обозначе-

нием α|β|γ задач теории расписаний, представленным в работе [1], где α опи-

сывает характеристики приборов, β описывает характеристики требований и

ограничения, а γ целевую функцию. Если w_j = 1, j ∈ N, то этот частный

случай обозначим как 1|r_j , p_j = p|

∑T_j. В задаче минимизации взвешенно-

го числа запаздывающих требований необходимо минимизировать значение

функции

∑

f_j(C_j) =

w_jU_j.

j=1

Обозначим эту задачу как 1|r_j , p_j = p|

∑w_jU_j.

[2, 3] предложены полиномиальные алгоритмы решения задач

1|r_j , p_j = p|

∑T_j и 1|r_j,p_j = p|∑w_jU_j. Оба алгоритма основаны на следу-

юших свойствах:

• известно множество времен начала обслуживания требований

Θ = {t : t = r_j + kp,j ∈ N,k = 0,1,...,n - 1}.

Мощность множества |Θ| ≤ n²;

• известны отношения доминирования между требованиями. Существует

оптимальное расписание, при котором требование j обслуживается после

всех требований i, где r_i ≤ S_j и d_i ≤ d_j .

Частный случай, задача 1|r_j , p_j = p|

∑w_jT_j, с общим директивным сроком

может быть решен с помощью алгоритмов [3]. Для данной задачи существует

оптимальное расписание, при котором требование j обслуживается после всех

требований i, где r_i ≤ S_j и w_i ≥ w_j .

Частный случай задачи 1|r_j , p_j = p|

∑w_jT_j, при котором все значения r_j

кратны p, может быть сведен к задаче о назначениях и решен за полиноми-

альное время.

В [4] авторы рассматривают одноприборную задачу теории расписаний

минимизацию суммарного взвешенного штрафа за отклонение от директив-

ного срока 1|p_j = p|

∑(α_j E_j + β_j T_j), где E_j(π) = max{0, d_j - C_j(π)}. Авторы

представили постановку задачи как задачи целочисленного линейного про-

граммирования (ЦЛП), предложили схему ее релаксации, для которой по-

строен полиномиальный алгоритм решения. В задаче ЦЛП определены пе-

ременные x_j,t для каждого требования j и возможного времени завершения

120

обслуживания требования t, где x_j,t = 1, если обслуживание требования j за-

канчивается в момент времени t, и x_j,t = 0 иначе. В релаксированной задаче

x_j,t ∈ [0,1]. Авторы представили полиномиальный алгоритм преобразования

решения релаксированной задачи в целочисленное решение исходной задачи

с тем же значением целевой функции.

В [5] авторы представили аналогичную модель ЦЛП и аналогичную релак-

сацию для задачи 1|r_j , p_j = p|

∑w_jT_j. Авторы утверждают, что если в задаче

нет двух требований i и j, для которых d_i < d_j и w_i < w_j , то построенный по-

линомиальный алгоритм преобразует решение релаксированной задачи в оп-

тимальное целочисленное решение исходной задачи. К сожалению, в работе

не представлен подобный алгоритм, а дана ссылка на алгоритм из [4], хо-

тя в отличие от задачи 1|r_j , p_j = p|

∑w_jT_j в задаче 1|p_j = p|∑(α_jE_j + β_jT_j)

требования поступают на обслуживание одновременно, а множество времен

окончания обслуживания требований относятся к другому интервалу.

Обзор результатов по задачам для параллельных машин с одинаковыми

продолжительностями обслуживания требований представлен в [6].

В разделе 2 представлены найденные свойства задачи. В разделе 3 рас-

смотрены подходы к ее решению. В разделе 4 представлены алгоритмы реше-

ния частных случаев, а в разделе 5 результаты исследования вычислитель-

ной сложности. Некоторые задачи максимизации рассмотрены в разделе 6.

2. Свойства задачи 1|r_j , p_j = p|

∑w_jT_j

Рассмотрим отношения предшествования между двумя требованиями i и j

в оптимальном расписании.

Свойство 1. Пусть t₁ наиболее ранний момент времени из момен-

тов начала обслуживания требований {i,j} и t₂ поздний момент време-

ни, где t₂ ≥ t₁ + p. Тогда выполняются следующие отношения предшество-

вания.

1. Если w_i ≥ w_j , d_i ≤ d_j и t₁ ≥ r_i, тогда требование i обслуживается раньше

требования j.

2. Если w_i < w_j , d_i ≤ d_j и t₁ ≥ max{r_i, r_j }, то

(a) если t₂ + p ≤ d_j (требование j не запаздывает, если оно обслуживает-

ся начиная со времени t₂), тогда требование i обслуживается раньше

требования j;

(б) если t₁ > d_j - p (оба требования запаздывают), тогда требование j

обслуживается раньше требования i;

(в) пусть d_i - p < t₁ ≤ d_j - p и пусть при расписании π = (π₁, i, π₂, j, π₃)

имеем S_i(π) = t₁ и S_j(π) = t₂, а при расписании π^′ = (π₁,j,π₂,i,π₃)

имеем S_i(π^′) = t₂ и S_j(π^′) = t₁. Тогда требование i обслуживается

раньше требования j, если выполняется

∑

w_jT_j(π) <

w_jT_j(π^′) ⇐⇒ w_i(t₂ - t₁) - w_j(t₂ + p - d_j) > 0

w_j(d_j - p) - w_it₁

⇐⇒ t₂ <

;

w_j - w_i

121

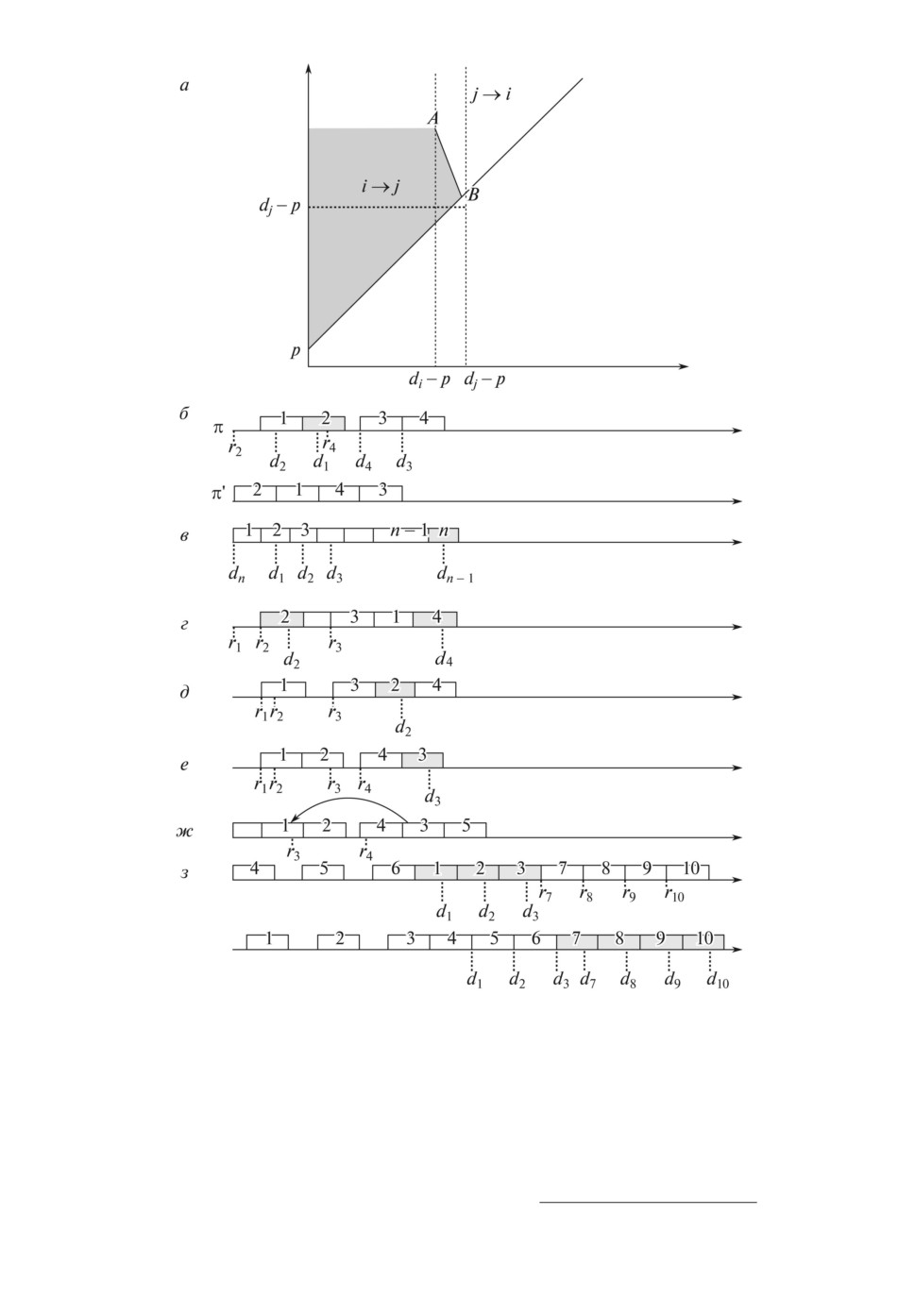
Эти отношения предшествования изображены на рисунке,a, где начало

координат точка (r_max, r_max), r_max = max{r_i, r_j }, точка A есть

(

)

w_j(d_j - p) - w_i(d_i - p)

A = d_i - p;

w_j - w_i

и точка B есть точка пересечения двух линий

w_j(d_j - p) - w_it₁

t₂ = t₁ + p

t₂ =

w_j - w_i

Точки ниже линии t₂ = t₁ + p не рассматриваются.

Отметим, что если t₁ < r_j , то сложно установить подобные отношения

предшествования, так как при расписании π^′ требования, которые обслужи-

ваются в интервале времени [t₁ + p, t₂), могут быть смещены в обслуживании

на более поздний срок.

В алгоритме динамического программирования, представленного в [3],

рассматриваются интервалы [s, e], s, e ∈ Θ, в которых обслуживаются тре-

бования подмножества N^′ = {1, . . . , k}, k ≤ n, т.е. не более k требований в

каждом из интервалов. Трудоемкость алгоритма динамического программи-

рования полиномиально зависит от количества таких интервалов и равна

O(n⁴) операций, так как |Θ| = O(n²). Возникает вопрос, как много точек e

необходимо рассмотреть для фиксированного значения s, т.е. существует ли

пример, в котором нужно рассмотреть порядка O(n²) точек e?

Свойство 2. Для фиксированных s и k существует порядка O(k²) то-

чек e ∈ Θ.

Доказательство. Существует пример, в котором

⌈k⌉

p≫k.

Для первых^k4 требований пусть

r₁ = s, r₂ = r₁ + 2p, r₃ = r₂ + 2p, ... ,

т.е.

r_i = s + 2p(i - 1), i = 1,... ,

Для следующих^k4 требований пусть

r_i = r_i-k

+ 1, i =

+ 1, . . . ,

Для следующих^k2 требований пусть

(

)

r_i =

p+1+ i-

+ 1, . . . , k.

123

до₂ активных требований обслуживаются

в начале расписания перед временем rk

, а от ^k2 до ^3k4 требований обслужи-

ваются начиная с момента времени r_i, i ∈ [^k2 + 1, k], без простоя прибора.

Тогда для данного примера существует O(k²) активных расписаний и

O(k²) возможных моментов времени окончания обслуживания e.

Свойство 3. Пусть

{

⋂

}

T = t:t∈Θ

[t₁, t₁ + p]

т.е. T есть подмножество точек, входящих в интервал длины p. Тогда

|T | = O(n).

3. Алгоритмы решения задачи

Рассматриваемая задача может быть решена с помощью алгоритма дина-

мического программирования и функциональных равенств, представленных

в [7].

Пусть дано расписание, при котором первые k обслуживаемых требований

составляют подмножество N \ J, а оставшиеся n - k требований составляют

подмножество J. Пусть функция F (J, t) задает минимальное суммарное взве-

шенное запаздывание требований из подмножества J при условии, что обслу-

живание этих требований начинается не ранее момента времени t ∈ Θ. В ал-

горитме динамического программирования необходимо вычислить значение

F (N, 0) и найти соответствующее расписание. Функциональные равенства,

предложенные в [7], имеют следующий вид:

{

}

F (J, t) = min

w_i max{0,t + p - d_i} + F(J \ {i},t + p)

i∈J

и F(∅,t) = 0,∀t ∈ Θ.

В алгоритме динамического программирования вычисления производятся

согласно данным функциональным равенствам. Трудоемкость алгоритма

O(n³2ⁿ) операций.

Альтернативный алгоритм решения имеет такую же вычислительную

сложность. В этом алгоритме рассматриваются 2ⁿ подмножеств N^′ ⊆ N, где

|rj1 - rj2 | ≥ p, j₁, j₂ ∈ N^′.

Для каждого подмножества N^′ примем S_j = r_j , j ∈ N^′, и для каждого требо-

вания i ∈ N \ N^′ возможные моменты времени начала обслуживания требо-

ваний принадлежат множеству Θ^′, являющемуся подмножеством из n - |N^′|

наименьших значений множества

{

}

t : t = r_j + kp,j ∈ N^′,k = 1,...,n - |N^′|

Тогда данная задача может быть сведена к задаче о назначениях, которая

может быть решена за время O((n - |N^′|)³).

124

Алгоритм, представленный в [3] для частного случая с равными весами

требований, может быть использован как эвристика для решения исходной

задачи. Несложно представить пример исходной задачи, для которого ал-

горитм из [3] не вернет оптимальное решение. Пусть в данном алгоритме

зафиксировано отношение предшествования, где обслуживание требования j

предшествует обслуживанию всех требований i, таких, что r_i ≤ S_j и w_i ≥ w_j.

Тогда несложно представить пример, где при оптимальном расписании тре-

бование j предшествует требованию i и

C_j - d_j = 1,

C_i - d_i = 1,

C_j < C_i.

3.1. Алгоритмы локального поиска

Локальный поиск это эвристический метод решения задач комбинатор-

ной оптимизации. В этом методе из исходного решения с помощью локальных

модификаций строится альтернативное допустимое решение. Эта модифика-

ция повторяется до тех пор, пока не найден локальный оптимум или достиг-

нут лимит выполненных операций.

В данной работе рассмотрим следующие модификации расписания. Обо-

значим активное расписание следующей последовательностью обслуживания

требований π = (π₁, i, π₂, j, π₃):

• левый сдвиг. Обслужить требование j сразу после частичного выполнения

частичного расписания π₁, т.е. имеем модифицированное расписание π^′ =

= (π₁, j, i, π₂, π₃);

• правый сдвиг. Обслужить требование i сразу после частичного выполне-

ния частичного расписания π₂, т.е. имеем модифицированное расписание

π^′ = (π₁,π₂,i,j,π₃);

• парная перестановка. Поменять местами требования i и j в последователь-

ности обслуживания требований, т.е. π^′ = (π₁, j, π₂, i, π₃).

Возникает вопрос: “Можно ли с помощью данных модификаций найти оп-

тимальное расписание, причем при каждой модификации значение целевой

функции не должно увеличиваться.”

Свойство 4. Существуют пример задачи и расписание, при котором

каждый левый сдвиг увеличивает значение целевой функции, но применение

нескольких левых сдвигов уменьшает значение целевой функции.

Доказательство. Рассмотрим пример, где

r₁ = 2, r₂ = 0, r₃ = 9, r₄ = 6, p = 3, d₁ = 6, d₂ = 3, d₃ = 12, d₄ = 9,

w₁ = w₃ = 100, w₂ = w₄ = 1

(см. рисунок,b). Пусть исходное расписание π = (1, 2, 3, 4). При левом сдви-

ге требования 2 на позицию перед требованием 1 значение целевой функции

увеличивается. Аналогично при левом сдвиге требования 4 на позицию пе-

ред требованием 3 значение целевой функции увеличивается. Но при при-

менении обоих левых сдвигов будет получено расписание π^′ = (2, 1, 4, 3), при

котором значение целевой функции уменьшается. При расписании π^′ суммар-

ное взвешенное запаздывание равно 0, а при расписании π имеем суммарное

взвешенное запаздывание, равное 11.

125

Следствие 1. Пусть π расписание, при котором каждый левый сдвиг

увеличивает значение целевой функции. Тогда относительная погрешность

расписания π может быть сколь угодно большой.

Аналогичное доказательство можно представить для следующего свой-

ства.

Свойство 5. Существуют пример задачи и расписание, при котором

каждый правый сдвиг увеличивает значение целевой функции, но примене-

ние нескольких правых сдвигов уменьшает значение целевой функции.

Свойство 6. Пусть π

некоторое расписание и N^′ = {j₁,... ,j_k}

подмножество требований, которые должны быть сдвинуты влево, и

пусть порядок обслуживания требований из N^′ фиксирован, т.е. обслужи-

вание требования j₁ предшествует обслуживанию требования j₂, требо-

вание j₂ предшествует требованию j₃ и т.д. Тогда оптимальная модифи-

кация расписания путем левого сдвига каждого требования из N^′ может

быть найдена за O(n⁸) операций.

Доказательство. Оптимальная модификация может быть найдена с

помощью следующего алгоритма динамического программирования. На каж-

дой стадии l = k, k - 1, . . . , 1 для каждого требования j_l ∈ N^′ необходимо

рассмотреть x_l позиций в перестановке, в которой порядок обслуживания

требований из N \ N^′ остается неизменным и все возможные моменты на-

чала обслуживания t_l ∈ Θ. Таким образом, состояние системы в алгоритме

динамического программирования определяется вектором (x_l, t_l). На каждой

стадии необходимо вычислить функцию F_l(x_l, t_l), являющуюся суммарным

взвешенным запаздыванием требований, обслуживаемых при активном рас-

писании с момента t_l согласно последовательности, начинающейся с требова-

ния j_l. Эта функция используется на следующей стадии для требования j_l-1.

На каждой стадии необходимо рассмотреть O(n¹⁺²) состояний системы. Для

каждого состояния системы (x_l, t_l) необходимо рассмотреть состояния систе-

мы, полученные на предыдущей стадии, чтобы за O(n) операций вычислить

значение функции F_l(x_l, t_l). Таким образом, трудоемкость алгоритма дина-

мического программирования составляет O(n⁸) операций.

Свойство 7. Пусть для расписания (1,2,3) две попарные перестановки

1 ⇐⇒ 2 и 2 ⇐⇒ 3 приводят к увеличению значения целевой функции. Тогда

существует пример, для которого попарная перестановка 1 ⇐⇒ 3 приводит

к уменьшению значения целевой функции.

Параметры данного примера:

r₁ = r₂ = r₃ = 0, p = 3, d₁ = 5, d₂ = 7, d₃ = 8, w₁ = 1, w₂ = w₃ = 5.

При расписании (1, 2, 3) имеем

∑w_jT_j = 5, а при расписании (3,2,1) имеем

∑

w_jT_j = 4.

Следствие 2. При локальном поиске с помощью попарной перестанов-

ки необходимо рассмотреть O(n²) пар требований.

Свойство 8. Пусть для расписания (1, . . . , n - 1, n) любая попарная

перестановка приводит к увеличению значения целевой функции. То-

126

гда существует пример, в котором левый сдвиг приводит к расписанию

(n, 1, . . . , n - 1) с меньшим значением целевой функции.

Доказательство. См. рисунок,в. Рассмотрим следующий пример:





n > 3,



r_i = 0,

i = 1...,n,



p = 2,

(1)

w_i = pw_n - 1,

i = 1...,n - 2,



w_n-1 = pw_n + 1,

i = 1...,n - 2,





d_n = 0,

d_i = (i + 1)p - 1, i = 1... ,n - 1.

При расписании π = (1, . . . , n - 1, n) любая попарная перестановка приводит

к увеличению значения целевой функции. Но при расписании π^′ = (n,1,

...,n - 1) имеем

∑

F (π^′) = F (π) +

w_n - p(n - 1)w_n =

i=1

= F(π) + p(n - 1)w_n - (n - 2) + 1 - p(n - 1)w_n < F(π).

Свойство 9. Существуют пример и расписание, при котором любой ле-

вый сдвиг приводит к увеличению значения целевой функции, но возможен

правый сдвиг, который приводит к уменьшению значения целевой функции.

3.2. Релаксация задачи

Рассмотрим релаксацию задачи, при которой все значения r_i округлены

таким образом, что расстояние между ними кратно p. Например,

⌋

⌊r_j

r^′j =

d^′j = d_j - (r_j - r^′j).

Такой модифицированный пример I^′ может быть сведен к задаче о назна-

чениях и решен за полиномиальное время. Пусть π оптимальное расписание

для исходного примера I и π^′ оптимальное расписание для модифициро-

ванного примера I^′ с округленными параметрами.

Рассмотрим вопросы:

• какова относительная погрешность

F (π) - F (π^′)

F (π)

для примера I?

• какова разница значений F (π) для примера I и F^′(π^′) для примера I^′, где

F^′ значение целевой функции для примера с округленными параметра-

ми?

127

Свойство 10. Существует пример, для которого значение

F (π)

F^′(π^′)

может быть сколь угодно большим.

Рассмотрим следующий пример, где n = 2, p = 3, r₁ = 1, r₂ = 3, d₁ = 4,

d₂ = 6, w₁ = w₂ = 1. При расписании π = π^′ = (1,2) имеем F(π) = 1, а также

F^′(π^′) = 0, где r^′1 = 0, d^′1 = 3, r^′2 = r₂, d^′2 = d₂.

Свойство 11. Существует пример, для которого

F (π) - F (π^′)

F (π)

может быть сколь угодно большим.

Рассмотрим следующий пример:





p = 4,



r_n = 0,





r_i =

i = 1...,n - 1,

(2)

d_i = r_i + 2p - 1, i = 1... ,n - 1,



d_n = p,



w_n = 1,



w_i = np,

i = 1...,n - 1.

Расписание π^′ = (1, . . . , n - 1, n) является оптимальным для примера I^′,

при котором запаздывает только требование n. Для примера I при этом

расписании также запаздывает только требование n. При расписании

π = (n,1,...,n - 1), оптимальном для примера I, ни одно из требований не

запаздывает.

Можно рассмотреть другую релаксацию, при которой значения r^′i вычис-

∑_n

ляются таким образом, чтобы минимизировать значение

|r_j - r^′j|. Для

j=1

такой релаксации свойства 10 и 11 также верны. Чтобы доказать это, необ-

ходимо рассмотреть n дополнительных требований, для которых r_j = np,

j = n + 1,...,2n.

4. Частные случаи задачи 1|r_j , p_j = p|

∑w_jT_j

Представим алгоритмы решения двух частных случаев задачи. Как было

сказано выше, частный случай задачи с общим директивным сроком может

быть решен за полиномиальное время.

Рассмотрим частный случай, в котором разница максимального и мини-

мального директивных сроков составляет d_max - d_min ≤ p. Этот частный слу-

чай может быть решен с помощью следующего алгоритма.

Выберем два пограничных требования j₁ и j₂, которые будут обслужены

при активном расписании одно за другим начиная с момента времени Sj1

128

так, что никакое другое требование не может быть обслужено в интервале

[d_min, d_max], т.е.

Sj1 ≤ d_min, Cj2 ≥ d_max.

Тогда подзадача со множеством требований N \ {j₁, j₂} может быть решена

модификацией алгоритма, представленного в [3], за O(n⁷) операций, где тре-

бование j обслуживается после обслуживания всех требований i, для которых

r_i ≤ S_j и w_i ≥ w_j. В модифицированном алгоритме рассматриваются только

интервалы [s, e], которые не пересекаются с интервалом [Sj1 , Cj2 ].

Имеется O(n²) пар пограничных требований j₁ и j₂, O(n) возможных мо-

ментов начала обслуживания Sj1 ∈ Θ согласно свойству 3 и единственное зна-

чение Sj2 для выбранного Sj1 , так как рассматриваются только активные

расписания. Тогда данный частный случай может быть решен за O(n²⁺¹⁺⁷)

операций.

Далее рассмотрим частный случай с n требованиями, где

{

w₁ ≤ w₂ ≤ ... ≤ w_n-1,

(3)

d₁ ≥ d₂ ≥ ... ≥ d_n-1.

Для решения данного частного случая необходимо выбрать время начала

обслуживания S_n ∈ Θ и затем решить оставшуюся подзадачу с помощью мо-

дифицированного алгоритма из [3]. То есть данный частный случай может

быть решен за O(n²⁺⁷) операций.

5. Результаты численных экспериментов

В разделе представлены результаты численных экспериментов, проведен-

ных с целью выяснить количество возможных точек в Θ, если для k требо-

ваний время начала обслуживания фиксировано.

При этом был рассмотрен следующий частный случай задачи:

{

w₁ ≤ w₂ ≤ ... ≤ w_n,

(4)

d₁ ≤ d₂ ≤ ... ≤ d_n

с n = 10.

Числовые параметры примеров были сгенерированы следующим образом.

Для каждого значения p ∈ {5, 10, 15, 20, 25, 30} были рассмотрены 10 приме-

ров, для которых значения r_j ∈ [0, (n - 2)p], d ∈ [0, (n - 1)p], w ∈ [1, 120] были

определены случайным образом согласно равномерному распределению. Для

каждого примера был использован алгоритм ветвей и границ с подпрограм-

мой ветвления (j, Π), где j требование, для которого в подпрограмме необ-

ходимо определить время начала обслуживания, и Π частично построенное

расписание, при котором моменты начала обслуживания S_i, i = 1, . . . , j - 1,

уже определены. В данной подпрограмме вычисляется множество Θ_j соглас-

но Π и значению r_j. Пусть S_j′ < S_j′′ , j^′, j^′′ ≤ j - 1, и нет других требований

129

j′′′ ≤ j - 1, для которых Sj′ < Sj′′′ < Sj′′. Тогда определим множества:

Ω₁ = {S_j′ + kp,k = 1,... ,n - j : S_j′ + kp + p ≤ S_j′′,S_j′ + kp ≥ r_j},

Ω₂ = {r_i + kp,k = 1,... ,n - j,i ≥ j,r_j ≤ r_i + kp ≤ S_j′′ - p,r_i > S_j′ + p} и

Ω₃ = {S_j′′ - kp,k = 1,... ,n - j : S_j′′ - kp - p ≥ S_j′,S_j′′ - kp ≥ r_j}.

Пусть t максимальное значение из множества Ω₂, где (S_j′′ -t) кратно значе-

нию p. Если такое t существует, тогда из множества Ω₂ удаляются все значе-

ния, которые больше t, и из множества Ω₃ удаляются все значения, которые

меньше t. Тогда множество Θ_j состоит из элементов множеств Ω₁, Ω₂, Ω₃ и

значения r_j, если S_j′ + p < r_j < S_j′′ - p.

В подпрограмме ветвления рассматриваются все возможные моменты вре-

мени t ∈ Θ_j. Пусть T W T (Π) суммарное взвешенное запаздывание требо-

ваний, обслуживаемых при частичном расписании Π. Если

TWT(Π) + w_j max{t + p - d_j,0} ≥ UB,

тогда t исключается из рассмотрения, где верхняя оценка UB лучшее (ми-

нимальное) найденное на данный момент значение целевой функции.

Представим результат численного эксперимента для одного примера.

p = 10,r_j ∈ {72,58,29,56,49,58,55,70,57,72},

d_j ∈ {66,71,73,75,76,76, 82,85,88, 88},

w_j = {22,30,42,56,68,75,75, 94,103, 111}.

Для данного примера в алгоритме ветвей и границ общее количество ветвей к

рассмотрению 33 346 541, на каждом шаге (уровне дерева поиска) j = 1, . . . , n

рассмотрено

{58; 1 926; 43 059; 588 149; 3 820 730; 9 432 283; 14 004 668; 4 636 929; 818 539; 200}

точек. При использовании свойства 1 количество ветвей можно сократить до

5 303 348, и на каждом шаге j = 1, . . . , n рассмотрено

{58; 1 666; 26 343; 233 762; 962 857; 1 457 811; 1 979 532; 531 006; 110 311; 2}

точек.

В соответствии с результатами численных экспериментов свойство 1 поз-

воляет сократить количество точек в Θ_j на 47%. В таблице представлены ре-

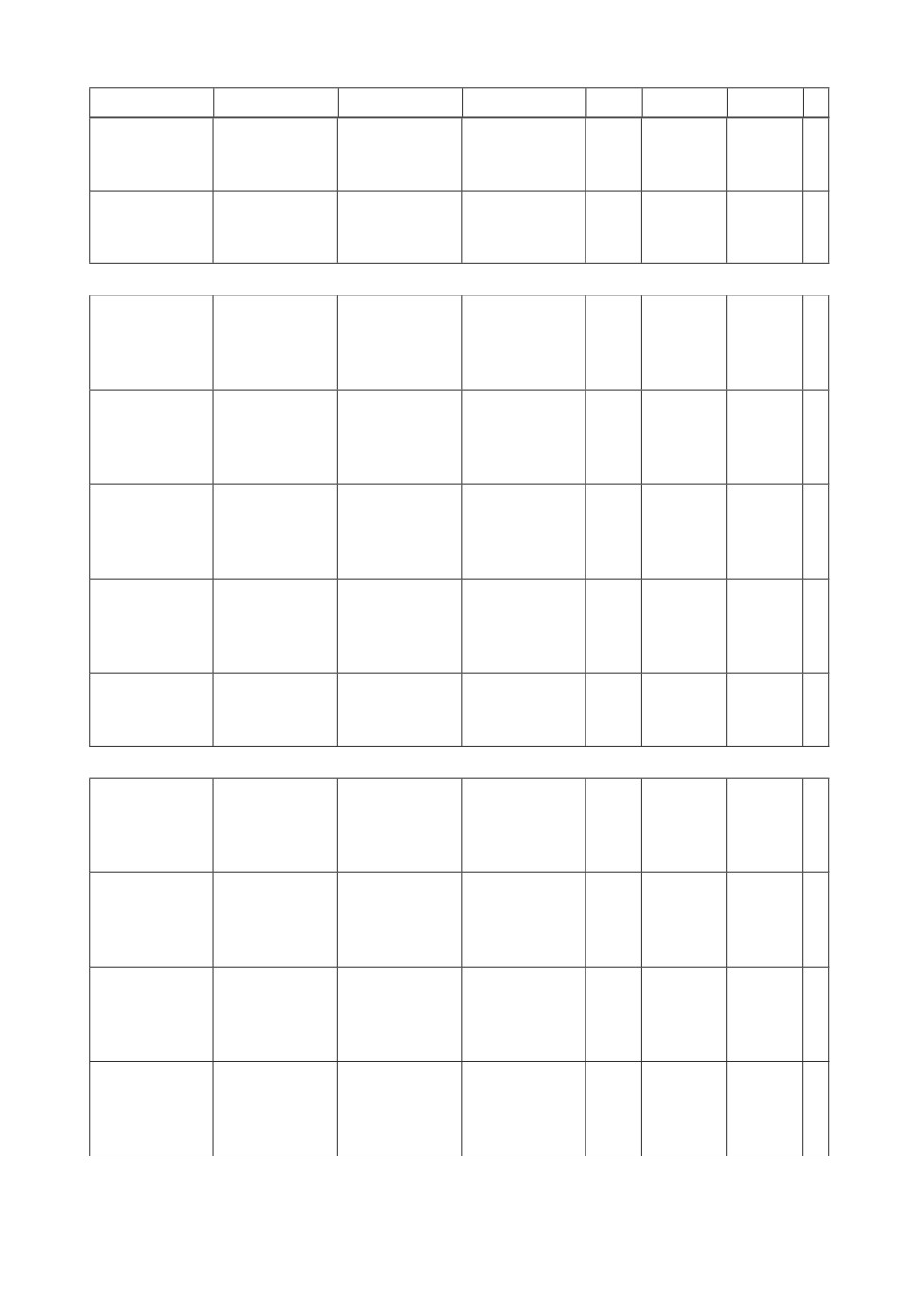
зультаты численного эксперимента для примеров, где p ∈ {5, 10, 15, 20, 25, 30}.

В колонках 1-3, представлены времена поступления, директивные сроки и ве-

са для 10 требований. В колонке 4 представлено расписание (время начала

обслуживания требований). В колонке 5 дано оптимальное значение целевой

функции T W T для примера. В колонках 7 и 8 представлено количество вет-

вей в алгоритме ветвей и границ без использования свойства 1 T NN1

и с использованием свойства 1 TNN2. В колонке 8 представлен процент

рассмотренных ветвей при использовании свойства 1.

Заметим, что трудоемкость алгоритма ветвей и границ экспоненциальна,

что не позволяет решать примеры размерности n = 20 за 60 минут на ПЭВМ

Intel Core 2 Duo CPU P8600 2,4 GHz, 4 GB RAM.

130

Таблица. Результаты для p ∈ {5, 10, 15, 20, 25, 30}

d_j

w_j

Расписание

TWT

TNN1

TNN2

p=5

21,0,35,31,

8,26,35,35,

6,13,20,20,

50,0,40,45,

782

199344

107496

26,11,10,

38,40,42,

58,59,84,

30,15,10,

25,11,14

43,44,44

90,110,116

25,20,35

17,36,8,34,

19,19,28,32,

14,21,23,46,

51,46,11,36,

2227

620833

298294

20,25,16,

32,37,38,39,

50,60,67,89,

21,26,16,41,

39,6,23

43,44

103,107

6,31

16,26,10,5,

30,31,33,34,

9,15,44,50,

50,45,10,5,

601

196973

112646

25,29,11,19,

36,39,39,43,

52,64,77,89,

25,30,15,20,

31,14

44,44

91,113

40,35

35,35,37,2,

16,22,23,31,

22,27,31,54,

50,45,40,2,

2296

205273

80800

22,9,16,8,

35,35,40,41,

65,77,84,

23,13,18,8,

35,21

42,44

105,105,108

35,28

7,18,10,31,

11,20,30,30,

9,9,45,48,

41,46,10,31,

882

264585

207667

4,7,4,20,

33,34,35,37,

50,62,64,85,

5,15,20,25,

19,0

41,44

87,117

36,0

p = 10

7,65,56,9,

35,50,56,70,

39,46,54,55,

7,97,57,17,

4132

100035

54247

17,39,77,16,

74,81,86,87,

64,71,84,97,

27,47,77,37,

64,79

87,89

104,104

67,87

53,63,4,23,

36,36,42,55,

1,24,26,27,

94,84,4,24,

1460

592976

416717

26,27,18,10,

55,68,75,81,

27,46,58,79,

34,44,54,14,

49,28

85,88

95,107

64,74

32,56,10,4,

41,51,67,72,

11,28,29,34,

34,56,14,4,

1972

414289

316671

49,78,57,42,

83,84,84,85,

41,48,56,61,

96,86,66,44,

40,23

87,89

77,85

76,24

24,76,5,36,

27,35,48,69,

9,23,26,34,

107,97,5,36,

4608

6476173

3329563

21,57,70,36,

71,73,76,79,

71,72,102,

21,57,87,46,

59,52

83,88

105,113,114

67,77

65,2,8,3,

16,46,47,62,

25,31,32,49,

92,2,12,22,

2690

849744

367675

29,34,37,33,

64,79,79,83,

79,90,94,

32,42,52,62,

47,57

83,87

100,101,108

72,82

p = 15

97,105,22,

67,89,103,

5,36,36,47,

158,143,22,

4386

1709603

1166960

98,42,32,114,

112,114,116,

47,48,53,103,

98,52,37,128,

47,79,86

118,130,131,

112,116

67,82,113

134

93,31,60,55,

50,68,68,76,

12,13,17,27,

166,151,136,

5719

4417446

1328448

28,90,51,29,

86,89,105,

50,52,60,63,

58,28,90,73,

106,85

119,122,129

63,90

43,106,121

54,37,9,104,

41,109,118,

6,11,20,35,

144,129,9,

1303

386234

318040

93,64,35,26,

123,126,127,

45,56,59,63,

114,99,69,

20,61

128,129,130,

91,109

39,54,24,84

133

131

Таблица. (продолжение)

19,58,44,22,

65,70,79,80,

2,18,29,43,

157,142,52,

4610

1950750

843607

101,44,61,

88,90,102,

50,56,67,81,

22,112,67,82,

27,81,119

112,122,134

95,110

37,97,127

18,51,73,14,

54,73,86,89,

1,13,20,35,

18,155,140,

3307

3689263

1928262

57,50,72,57,

95,105,110,

44,68,85,95,

33,65,50,80,

56119

116,132,134

96,111

95,110,125

p = 20

71,25,58,69,

102,116,125,

3,6,8,10,43,

218,25,58,

3924

29709961

6809732

93,122,72,

140,142,151,

51,67,87,93,

198,98,178,

123,95,70

164,166,166,

113

78,138,118,

175

158

83,67,52,154,73,103,103,

18,18,47,58,

198,218,58,

10092

1849948

1203732

92,60,38,49,

117,146,156,

67,69,77,81,

178,98,78,38,

65,80

166,171,172,

105,118

118,138,158

175

101,41,18,

86,111,117,

2,19,23,24,

201,41,18,

2692

2074218

884291

116,101,42,

123,137,158,

25,27,52,59,

181,101,61,

59,138,104,

166,169,170,

110,110

81,141,121,

140

176

161

55,84,135,

83,98,106,

2,22,34,37,

188,128,168,

5002

758835

471049

56,36,98,60,

106,111,112,

52,54,63,72,

68,48,108,88,

5,28,43

130,149,165,

82,113

5,28,148

170

145,95,25,

87,87,93,122,18,29,36,38,

205,105,25,

7412

1288063

579338

148,40,28,84,153,155,160,

42,54,75,84,

185,45,65,85,

135,46,52

166,171,178

90,96

145,125,165

p = 25

5,93,118,175,121,129,146,

26,31,32,51,

5,105,230,

8275

46808

29428

140,129,22,

150,167,168,

52,56,84,89,

205,155,130,

63,20,74

169,173,178,

96,106

30,80,55,180

211

193,142,193,

152,197,200,

25,33,44,46,

317,142,292,

17845

2103722

444158

194,168,175,

200,218,219,

50,55,64,71,

267,242,217,

107,186,164,

220,222,222,

84,97

107,192,167,

224

176,177,167,

100,120,136,

5,17,26,28,

250,225,175,

5221

973995

807576

25,48,113,65,142,152,186,

58,81,100,

25,50,125,75,

80,66,170

201,202,205,

106,109,118

100,150,200

221

137,41,14,

83,

92,

127,

5, 11, 31, 50,

246,41,14,

9240

513204

278014

164,146,186,

132, 167, 174,

58, 66, 80, 83,

171,146,221,

74,36,119,74 196, 208, 217,

114, 116

91,66,119,

220

196

132

Таблица. (окончание)

138,79,40,50,72,105,110,

4,48,53,57,

240,90,40,65,

3652

217856

173628

109,2,163,

151,153,169,

59,60,60,74,

115,2,215,

156,132,190

200,204,208,

80,118

165,140,190

221

p = 30

55,1,219,107,119,129,143,

7,9,36,40,

280,1,250,

9333

641049

342412

32,190,92,17,150,180,184,

53,84,87,102,121,61,190,

80,130

198,253,255,

112,112

151,31,91,

263

220

46,239,103,

117,129,163,

19,28,52,53,

46,316,106,

19060

494327

325578

164,226,50,

166,208,210,

79,81,84,106,166,286,76,

209,83,117,

245,264,268,

110,114

226,136,196,

269

256

139,13,155,

173,191,192,

15,16,17,31,

139,13,289,

6502

620830

377214

191,31,182,

208,214,221,

44,45,61,80,

259,43,229,

175,158,53,

227,241,246,

84,101

199,169,73,

101

257

103

191,75,230,

112,119,154,

9,13,26,26,

298,86,268,

6376

536269

269281

187,26,51,77,220,222,230,

58,68,88,99,

208,26,56,

152,148,45

232,242,246,

106,110

116,178,148,

266

238

79,132,172,

166,178,205,

2,13,20,27,

358,328,298,

9216

22248262

7730427

203,126,81,

210,219,241,

66,83,95,98,

268,143,81,

179,178,183,

242,247,254,

114,119

208,178,238,

113

255

113

6. Вычислительная сложность задачи 1|r_j , p_j = p|

∑w_jT_j

Насколько известно, при доказательстве NP-трудности задачи теории

расписаний с классическими ограничениями p_j, w_j , d_j , r_j, D_j и целевыми

функциями C_max, L_max,

∑w_jC_j,∑w_jT_j,∑w_jU_j используются следующие

два подхода:

• сведение к исходной задаче задачи типа “Разбиения” (Одномерный ранец,

3-Разбиение), если принять, что p_j зависят от чисел b_j из задачи о Раз-

биении. При таком сведении количество моментов времени возможного

окончания обслуживания требований не ограничено значением O(n²);

• сведение к исходной задаче задачи теории графов (например, задачи о

клике), если заданы отношения предшествования между требованиями.

Однако оба эти подхода не приводят к доказательству NP-трудности за-

дачи 1|r_j , p_j = p|

∑w_jT_j.

В упомянутых выше подходах к доказательству NP-трудности рассматри-

ваются частные случаи исходных задач, где структура оптимального распи-

сания известна, см., например, [8]. Однако для задач с равными продолжи-

тельностями обслуживания требований при известной структуре оптималь-

133

ного расписания просто построить полиномиальной алгоритм решения и ис-

пользованием динамического программирования.

Таким образом,

• с одной стороны, задача 1|r_j,p_j = p|

∑w_jT_j не содержит сложностей типа

экспоненциального количества моментов времени завершения обслужива-

ния требований или отношений предшествования,

• с другой стороны, для данного примера неизвестны правила предшество-

вания, позволяющие построить полиномиальный алгоритм решения.

Предполагаем, что задача 1|r_j , p_j = p|

∑w_jT_j является NP-трудной, но

чтобы доказать это, необходим новый подход к доказательству NP-трудности.

7. Задачи с обратными критериями оптимизации

Обычно в теории расписаний рассматриваются задачи, где необходимо

найти минимум некоторой целевой функции. Например, минимизация вре-

мени завершения обслуживания всех требований является популярным кри-

терием оптимизации. Также в классических задачах рассматриваются кри-

терии минимизации суммарного запаздывания, минимизации количества за-

паздывающих требований. В этом разделе рассмотрим задачи с обратными

критериями оптимизации, а именно: максимизация времени завершения об-

служивания всех требований, максимизация суммы моментов времен завер-

шения обслуживания требований, максимизация количества запаздывающих

требований. В этих задачах допустимыми являются только активные распи-

сания, иначе задачи были бы тривиальны.

Исследование задач с обратными критериями оптимизации имеет теорети-

ческую значимость, сами задачи имеют практическую интерпретацию [9-11].

Максимальное значение времени завершения обслуживания всех требований

может быть использовано, чтобы сократить множество Θ в задаче миними-

зации.

В задаче максимизации времени завершения обслуживания всех требо-

ваний необходимо найти активное расписание π^∗, при котором максими-

зировано значение C_max(π) = max^nj=1{C_j }. Обозначим данную задачу как

1|r_j , p_j = p| max C_max. Аналогично обозначим другие две рассматриваемые за-

дачи как 1|r_j , p_j = p| max

∑C_j и 1|r_j,p_j = p|max∑U_j задачи максимиза-

ции суммы моментов времен завершения обслуживания требований и макси-

мизации количества запаздывающих требований.

Представим полиномиальный алгоритм решения задач

1|r_j , p_j = p| max C_max и 1|r_j , p_j = p| max

∑C_j и некоторые свойства задачи

1|r_j , p_j = p| max

∑U_j.

7.1. Алгоритм решения задач

1|r_j , p_j = p| max C_max и 1|r_j , p_j = p| max

∑C_j

Обозначим работы согласно порядку r₁ ≤ r₂ ≤ . . . ≤ r_n. Без потери общ-

ности примем r₁ = 0.

134

Идея алгоритма заключается в следующем. В перестановке, однозначно

определяющей расписание обслуживания требований, одна за одной рассмат-

риваются позиции. Для каждой позиции выбирается одно требование j в со-

ответствии с r_j так, чтобы сделать промежуток (простой) между временем

завершения обслуживания предыдущего требования и r_j как можно больше,

но меньше, чем p. Таким образом, ни одно другое требование не может быть

обслужено раньше момента времени r_j .

Алгоритм 1.

1. Пусть t := 0 время завершения обслуживания последнего требования,

поставленного в перестановку (в расписание), т.е. требования, время обслу-

живания которого определено, и N_u := N множество требований, время

обслуживания которых не определено. Примем также π := () найденная

частичная перестановка.

2. Для l := 1 до n выполнить

2.1. Выбрать требование j := argmax{r_i, t ≤ r_i < t + p}.

i∈Nu

2.2. Если такого требования j нет, тогда

Выбрать требование j из множества N_u, где r_i ≤ t.

Если такого требования j нет, тогда

t := min{r_i, t < r_i}. Перейти к шагу 2.1.

i∈Nu

2.2. π := (π, j). N_u := N_u \ {j}. t := C_j (π).

3. π

оптимальное расписание.

Трудоемкость алгоритма 1 O(n) операций, и O(n log n) необходимо для

упорядочивания работ согласно правилу r₁ ≤ r₂ ≤ . . . ≤ r_n.

Лемма 1. Алгоритм

строит оптимальное расписание для задач

1|r_j , p_j = p| max C_max и 1|r_j , p_j = p| max

∑C_j.

Доказательство. Предположим, что существует оптимальное распи-

сание π^∗ = (l, π₁, j, π₂), при котором первым обслуживается требование l, хо-

тя в алгоритме 1 строится расписание, в котором первое обслуживаемое

требование

l. Если r_l ≤ r_j, тогда при расписании π = (j,π₁,l,π₂) имеем

C_i(π) ≥ C_i(π^∗) для кажого требования i ∈ N \ {j} и C_max(π) ≥ C_max(π^∗).

Если r_j < r_l, тогда расписание π^∗ не является активным, так как требова-

ние 1 может быть обслужено первым, начиная с момента времени S₁ = 0.

Дальнейшее доказательство может быть выполнено по индукции.

7.2. Свойства задачи 1|r_j , p_j = p| max

∑U_j

Известно, что задача 1|r_j | max

∑U_j является NP-трудной [11], но ее част-

ный случай 1|r_j = 0| max

∑U_j может быть решен за O(n²) операций [9]. Для

данного частного случая существует оптимальная последовательность обслу-

живания требований (G, W ), при которой все требования из G обслуживают-

ся вовремя, а все требования из W запаздывают и обслуживаются в порядке

неуменьшения директивных сроков.

Представим найденные свойства для задачи 1|r_j , p_j = p| max

∑U_j.

135

Свойство 12. Существует оптимальное расписание, при котором об-

служивание запаздывающего требования i предшествует обслуживанию не

запаздывающего требования j и r_j < r_i.

Подобный пример представлен на рисунке, г, где требования i равные 2 и 4

запаздывают, а требования j равные 1 и 3 не запаздывают.

Свойство 13. Существует оптимальное расписание, при котором об-

служивание запаздывающего требования i предшествует обслуживанию за-

паздывающего требования j и d_i < d_j .

Подобный пример представлен на рисунке, г, где i = 2, d₂ = r₂ + p - 1 и j = 1,

d₁ = r₂ + p.

Свойство 14. Существует пример, для которого алгоритм 1 строит

неоптимальное расписание.

Подобный пример представлен на рисунке, д, при котором только требова-

ние 2 запаздывает. А на рисунке, е показано, что максимальное время простоя

не приводит к оптимальному расписанию, где требование 3 единственное

запаздывающее требование.

Для решения задачи предлагается следующая эвристика: если при распи-

сании π требование j обслуживается вовремя и S_j(π) > r_j, тогда необходимо

переставить это требование на более раннее время обслуживания.

Свойство 15. Если при расписании π требование j обслуживается во-

время, а требование i запаздывает и оба требования обслуживаются не

ранее чем с момента времени t ≥ max{r_i, r_j }, тогда существует расписа-

ние π^′, где обслуживание требования j предшествует обслуживанию i и

∑U_j(π^′) ≥ ∑U_j(π).

Другими словами, если два требования обслуживаются не ранее чем с мо-

мента времени t ≥ max{r_i, r_j }, то при оптимальном расписании обслуживание

незапаздывающего требования предшествует обслуживанию запаздываю-

щего.

Свойство 16. Если при расписании π оба требования j и i запаздывают,

d_j ≤ d_i и оба требования обслуживаются не ранее чем с момента времени

t ≥ max{r_i,r_j}, тогда существует расписание π^′, где обслуживание требо-

вания j предшествует обслуживанию i и

∑U_j(π^′) ≥ ∑U_j(π).

Другими слова, если два запаздывающих требования обслуживаются не

ранее чем с момента времени t ≥ max{r_i, r_j}, то при оптимальном расписании

они могут быть обслужены в порядке неубывания директивных сроков.

Свойство 17. Если необходимо из двух требований j и i выбрать то,

что будет обслуживаться с момента времени

max{r_i, r_j } ≤ t ≤ min{d_j - p, d_i - p},

а второе будет обслужено позже, то необходимо выбрать требование с

наибольшим директивным сроком.

136

Свойство 18. Пусть при расписании π = (π₁,j₁,j₂,j₃,j₄,π₂,j₅,π₃) вы-

полняется:

Sj2(π) < rj5 < Cj2(π), Cj1 > rj5 - p, Sj4 = rj4 < rj5 + 2p и Cj5(π) < dj5 .

Тогда при расписании π^′ = (π₁, j₅, j₃, j₄, π₂, j₁, j₂, π₃) имеем F (π) ≤ F (π^′).

См. рисунок, ж. Согласно этому свойству необходимо исключить пред-

ставленную ситуацию перестановкой требования j₅ и требований j₂, j₃.

Свойство 19. Существует расписание, при котором любая попарная

перестановка уменьшает значение целевой функции, но одновременное при-

менение нескольких перестановок увеличивает значение целевой функции.

См. рисунок, з. При расписании π = (4, 5, 6, 1, 2, 3, 7, 8, 9, 10) любая по-

парная перестановка,например, перестановки 4 ↔ 1, 5 ↔ 2, сокращает ко-

личество запаздывающих требований, но их одновременное применение

π = (1,2,3,4,5,6,7,8,9,10) увеличивает количество запаздывающих требова-

ний.

8. Заключение

Представлены свойства задачи и алгоритм решения задачи

1|r_j , p_j = p|

∑w_jT_j. Вопрос о статусе вычислительной сложности задачи

остается открытым. В том числе авторам не известны псевдополиномиаль-

ные алгоритмы решения или схемы приближенного решения с заданной от-

носительной погрешностью.

Предполагаем, что задача 1|r_j , p_j = p|

∑w_jT_j является NP-трудной, но

чтобы доказать это, необходим новый подход к доказательству NP-трудности.

Также в статье представлены новые задачи теории расписаний с обратны-

ми критериями оптимизации и их свойства.

СПИСОК ЛИТЕРАТУРЫ

1. Graham R.L., Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Optimization and

Approximation in Deterministic Machine Scheduling: a Survey // Ann. Discret.

Math. 1979. No. 5. P. 287-326.

2. Leung J.Y.-T. Handbook of Scheduling. N.Y.: Chapmann and Hall/CRC, 2004.

3. Baptiste P. Scheduling Equal-Length Jobs on Identical Parallel Machines // Discret.

Appl. Math. 2000. No. 103(1-3). P. 21-32.

4. Verma S., Dessouky M. Single-Machine Scheduling of Unit-Time Jobs with Earliness

and Tardiness Penalties // Math. Oper. Res. 1998. No. 23(4). P. 930-943.

5. Van den Akker J.M., Diepen G., Hoogeveen J.A. Minimizing Total Weighted Tardi-

ness on a Single Machine with Release Dates and Equal-Length Jobs // J. Scheduling.

2010. No. 13. P. 561-576.

6. Kravchenko S.A., Werner F. Parallel Machine Problems with Equal Processing

Times: a Survey // J. Scheduling. 2011. No. 14. P. 435-444.

7. Held M., Karp R.M. A Dynamic Programming Approach to Sequencing Problems //

J. Soc. Indust. Appl. Math. 1962. No. 10. P. 196-210.

137

8. Du J., Leung J.Y.-T. Minimizing Total Tardiness on One Processor is NP-hard //

Math. Oper. Res. 1990. No. 15. P. 483-495.

9. Aloulou M.A., Kovalyov M.Y., Portmann M.-C. Evaluation Flexible Solutions in

Single Machine Scheduling via Objective Function Maximization: the Study of Com-

putational Complexity // RAIRO Oper. Res. 2007. No. 41. P. 1-18.

10. Gafarov E.R., Lazarev A.A., Werner F. Transforming a Pseudo-Polynomial Algo-

rithm for the Single Machine Total Tardiness Maximization // Probl. Polynom. One.

Annal. Oper. Res. 2012. No. 196(1). P. 247-261.

11. Gafarov E.R., Lazarev A.A., Werner F. Single Machine Total Tardiness Maximiza-

tion Problems: Complexity and Algorithms // Ann. Oper. Res. 2013. No. 207.

P. 121-136.

Статья представлена к публикации членом редколлегии Ф.Т. Алескеровым.

Поступила в редакцию 07.07.2019

После доработки 03.11.2019

Принята к публикации 28.11.2019

138