Автоматика и телемеханика, № 5, 2020

(Белорусский государственный университет

информатики и радиоэлектроники, Минск)

ГЕОМЕТРИЧЕСКИЕ АЛГОРИТМЫ ОПРЕДЕЛЕНИЯ

ТОЧКИ В ПЕРЕСЕЧЕНИИ ШАРОВ

Рассматривается задача определения точки в пересечении n шаров в

евклидовом пространстве E^m. Для случая m = 2 предлагаются два алго-

ритма сложности O(n² log n) и O(n³) операций. Для общего случая пред-

лагается точный полиномиальный рекурсивный алгоритм, использующий

ортогональное преобразование пространства E^m.

Ключевые слова: пересечение шаров, аппроксимация эллипсоидами вы-

пуклого множества, полиномиальный алгоритм, доставка с помощью дро-

нов, конфигурация роя дронов.

DOI: 10.31857/S0005231020050098

1. Введение

В [1] была сформулирована следующая задача. В m-мерном евклидовом

пространстве E^m рассматривается множество n шаров. Каждый шар B_i,

1 ≤ i ≤ n, задается указанием его центра O_i и радиуса R_i. Необходимо опре-

делить, является ли пересечение n шаров непустым множеством, и в случае

положительного ответа найти точку из этого пересечения.

В [1] отмечается, что при m = 2 данная задача является математической

моделью для следующей практической задачи. На плоскости располагаются

n передающих станций различной мощности. Сигнал от станции i, располо-

женной в точке O_i, может быть получен на расстоянии, не превышающем R_i

единиц измерения. Необходимо определить, можно ли найти место для строи-

тельства принимающей станции (принимая во внимание только характери-

стики дальности распространения сигналов от передающих станций) таким

образом, чтобы принимающая станция могла получать сигналы от всех пе-

редающих станций. Такая техническая интерпретация может быть обобщена

и на случай трехмерного пространства (m = 3), когда в модели учитывается

высота расположения передающих и принимающей станций. Кроме того, в

трехмерном случае рассматриваемой задаче можно придать различные ин-

терпретации в контексте актуального направления, связанного с использова-

нием непилотируемых летательных аппаратов (дронов) [2]. Например, жите-

ли небольших поселений, расположенных в труднодоступной гористой мест-

ности, могут использовать дроны для доставки лекарств, различных мелких

товаров и почтовых пакетов. Стартовая площадка для дрона в населенном

пункте i находится в точке O_i. С учетом технических характеристик дрон,

которым владеют жители поселка i, может без дозарядки преодолеть расстоя-

ние, не превышающее 2R_i единиц измерения (туда и обратно). Необходимо

139

определить координаты точки зависания воздушного транспортного средства

(вертолета, дирижабля), используемого в качестве склада товаров, таким об-

разом, чтобы этот склад был достижим для дронов каждого поселка. Ана-

логичная постановка может быть рассмотрена и при планировании доставки

с помощью дронов лекарств, медицинских приборов, расходных материалов

и т.д. различным бригадам спасателей в районах стихийных бедствий или

широкомасштабных катастроф. При этом постоянно меняющаяся обстановка

может потребовать многократного эффективного решения задачи определе-

ния координат точки зависания воздушного транспортного средства-склада,

достижимого для дронов всех бригад спасателей.

В [1] предлагаются два подхода к решению рассматриваемой задачи в об-

щем m-мерном случае. Первый подход связан с задачей минимизации линей-

ной функции с квадратичными ограничениями. Второй подход основан на

известном методе эллипсоидов (см., например, [3]). Следует отметить, что

рассматриваемую задачу можно отнести к широкому классу задач аппрок-

симации эллипсоидами выпуклого множества в пространстве E^m [4]. Этот

класс задач подразделяется на задачи внутренней и внешней аппроксима-

ции. Решение рассматриваемой задачи может быть получено из решения

следующей задачи внутренней аппроксимации: найти эллипсоид наибольше-

го объема, содержащийся в пересечении n заданных эллипсоидов, если это

пересечение непусто (естественно, для решения интересующей задачи надо

рассматривать частный случай, в формулировке которого эллипсоиды заме-

няются на шары). В [4] демонстрируется, что последняя задача может быть

сведена к задаче выпуклого программирования. Аналогичная задача внеш-

ней аппроксимации может быть сформулирована следующим образом: найти

эллипсоид наименьшего объема, содержащий пересечение заданных эллип-

соидов, если это пересечение непусто. Однако (в отличие от указанной выше

задачи внутренней аппроксимации) данная задача внешней аппроксимации

является NP-трудной [4]. В [5] рассматривается ее частный случай: найти

шар наименьшего радиуса, содержащий пересечение заданных n шаров. В [5]

показано, что если пересечение заданных шаров непусто и n ≤ m - 1, то за-

дача нахождения шара наименьшего радиуса может быть решена с помощью

задачи минимизации выпуклой квадратичной функции.

Следует отметить, что все ранее предложенные подходы к рассмотренным

задачам с теоретической точки зрения являются полиномиальными. Однако

их реализация на практике либо может оказаться не очень эффективной,

особенно при больших значениях n (см., например, комментарий в [6], ка-

сающийся алгоритма эллипсоидов), либо затруднена в связи с достаточно аб-

страктным характером используемых конструкций (см., например, в [4] све-

дение задачи нахождения эллипсоида наибольшего объема, содержащегося

в пересечении заданных эллипсоидов, к задаче выпуклого программирова-

ния). В данной статье представлен альтернативный геометрический подход

к задаче нахождения точки в пересечении n шаров из пространства E^m, ре-

зультатом которого явилась разработка точных полиномиальных алгоритмов

ее решения. Предлагаемый подход использует известный аппарат линейной

алгебры и аналитической геометрии.

140

Статья организована следующим образом. В разделе 2 описаны два ал-

горитма решения задачи для случая m = 2. Более специфический алго-

ритм BALLS1 имеет вычислительную сложность O(n² log n) операций. Ал-

горитм BALLS2 проще по своей структуре, но имеет более высокую слож-

ность O(n³) операций. В разделе 3 рассматривается общий m-мерный слу-

чай, для которого разработан рекурсивный алгоритм BALLS3(m, n). В про-

цессе работы алгоритм BALLS3(m, n) использует либо алгоритм BALLS1,

либо алгоритм BALLS2, отчего зависит его вычислительная сложность

O(n^2m-4(nm² + m³ + n² log n)) или O(n^2m-4(nm² + m³ + n³)) операций. За-

ключительные замечания представлены в разделе 4.

2. Алгоритмы определения точки в пересечении кругов

Несмотря на то, что в данном разделе будут описаны алгоритмы опреде-

ления точки в пересечении кругов на плоскости, для построения первого ал-

горитма необходимо точки на плоскости трактовать как точки в трехмерном

пространстве с нулевой третьей координатой. Поэтому введем в рассмотрение

декартову прямоугольную систему координат (O;i,j,k).

Пусть на плоскости Oxy имеется n кругов. Каждый круг B_i, 1 ≤ i ≤ n,

задается указанием его центра O_i(x_i, y_i, 0) и радиуса r_i. Границей круга B_i

является окружность C_i, определяемая уравнением (x - x_i)² + (y - y_i)² = r²ⁱ.

Занумеруем круги B_i, 1 ≤ i ≤ n, в порядке невозрастания их радиусов: r₁ ≥

≥r₂ ≥...≥r_n.

2.1. Предварительная обработка

Вначале проверим, пересекаются ли заданные круги попарно. Для каждой

пары кругов B_i и B_j, 1 ≤ i ≤ n - 1, i < j ≤ n, вычислим расстояние d_ij между

их центрами.

Если d_ij > r_i + r_j, то круги B_i и B_j не пересекаются, следовательно, задача

не имеет решения.

Если d_ij ≤ r_i - r_j, то круг B_j находится внутри круга B_i. Поэтому можно

удалить из дальнейшего рассмотрения круг B_i и решать задачу для n - 1

круга.

Если d_ij = r_i + r_j , то круги B_i и B_j имеют единственную общую точку M -

---→

точку касания их границ C_i и C_j . Найдем вектор

O_iO_j и нормируем его.

−-→

Пустьeij - это орт вектораOiOj. От точки Oi отложим вектор rie

ij, получим

точку M - точку касания кругов B_i и B_j. Остается проверить, принадлежит

ли точка M всем остальным кругам. Если да, то найденная точка M является

решением задачи. В противном случае задача не имеет решения.

2.2. Основная часть алгоритма BALLS1

В дальнейшем изложении будем без ограничения общности считать, что

для любой пары кругов B_i и B_j, 1 ≤ i ≤ n - 1, i < j ≤ n, выполняется нера-

венство r_i - r_j < d_ij < r_i + r_j . Это означает, что окружности C_i и C_j пересе-

каются в двух точках.

141

(1)

B_i

B_j

(2)

M_ĳ

Рис. 1. Пересечение кругов B_i и B_j .

Зафиксируем одну из окружностей, например окружность C_i, и найдем

точки пересечения ее с какой-либо другой окружностью C_j, i = j. Для этого

решим систему уравнений:

{

(x - x_i)² + (y - y_i)² = r²ⁱ,

(1)

(x - x_j)² + (y - y_j )² = r^2j.

Вычитая первое уравнение системы (1) из второго, получим уравнение ви-

да fx + gy + h = 0, задающее прямую, проходящую через точки пересечения

окружностей C_i и C_j. Выражая y из уравнения fx + gy + h = 0 и подстав-

ляя его в первое уравнение системы (1), получим квадратное уравнение вида

ax² + bx + c = 0, которое имеет два различных действительных корня x^(1)ij

и x(2)ij . Из уравнения fx + gy + h = 0 получим соответствующие значения y^(1)ij

и y^(2)ij и тем самым определим точки M^(1)ij(x^(1)ij,y^(1)ij,0) и M^(2)ij(x^(2)ij,y^(2)ij,0) пе-

ресечения окружностей C_i и C_j. Отметим, что круги B_i и B_j гарантированно

будут иметь общий отрезок [M^(1)ij, M^(2)ij] (см. рис. 1).

Точки M^(1)ij и M^(2)ij разбивают окружность C_i на две дуги. В дальнейшем

представляет интерес только та дуга, которая находится внутри круга B_j . До-

говоримся, что движение вдоль выбранной дуги будет осуществляться против

часовой стрелки. Тем самым одна из точек M^(1)ij , M^(2)ij будет выбрана в ка-

честве начальной точки пути, а другая в качестве конечной. Рассмотрим

------→

---→

тройку некомпланарных векторов

O_iO_j, M^(1)ijM^(2)ij,k и найдем их смешан-

------→

---→

−-→

ное произведение. Если (OiOj,M(1)ijM(2)ij,k) > 0, т.е. тройка векторовOiOj,

−-----→

M^(1)ijM^(2)ij,k

правая, то точка M^(1)ij будет начальной точкой пути (покра-

сим ее белым цветом), а точка M^(2)ij будет конечной точкой пути (покрасим ее

------→

---→

−-→

черным цветом). Если же (OiOj,M(1)ijM(2)ij,k) < 0, т.е. тройка векторовOiOj,

−-----→

M^(1)ijM^(2)ij,k

левая, то точка M^(2)ij будет начальной точкой пути (покрасим

ее белым цветом), а точка M^(1)ij будет конечной точкой пути (покрасим ее чер-

ным цветом). Указание начальной (белой) и конечной (черной) точек пути

142

Рис. 2. Ситуации взаимного расположения трех кругов.

при договоренности о направлении обхода против часовой стрелки полностью

определяет дугу окружности C_i, находящуюся внутри круга B_j. Обозначим

такую дугу через L_ij и назовем ее подходящей дугой окружности C_i для

круга B_j.

Рассмотрим последовательно все круги B_j, 1 ≤ j ≤ n, j = i, и найдем мно-

жество всех подходящих дуг L_ij окружности C_i. Если пересечение L_i всех⋂

подходящих дуг непусто, т.е. L_i =

L_ij = ∅, то дуга L_i окружно-

1≤j≤n,j=i

сти C_i будет находиться внутри каждого круга B_j , 1 ≤ j ≤ n, j = i. Кроме

того, хорда, соединяющая концы дуги L_i, будет находиться внутри пересече-

ния всех кругов B_j , 1 ≤ j ≤ n. Отметим, что дуга L_i является частью границы

области пересечения всех кругов. Если же пересечение всех подходящих дуг⋂

пусто, т.е. L_i =

L_ij = ∅, то либо никакая часть границы области

1≤j≤n,j=i

пересечения всех кругов не принадлежит окружности C_i (т.е. пересечение

всех кругов находится внутри открытого круга B_i \ C_i), либо пересечение

всех кругов пусто. Если пересечение всех кругов находится внутри откры-

того круга B_i \ C_i, то найдется другой круг, например круг B_k, k = i, такой

что часть границы области пересечения всех кругов является некоторой ду-

гой L_k окружности C_k. Перебирая последовательно все круги B_i, 1 ≤ i ≤ n,

либо найдем такой круг B_k, либо придем к выводу, что пересечение всех

кругов пусто.

Рассмотрим все возможные типичные ситуации взаимного расположения

кругов на примере трех кругов (см. рис. 2).

1. Дуга L₁ окружности C₁ является пересечением подходящих дуг L₁₂ и

L₁₃, при этом дуга L₁ является частью границы области пересечения кругов

B₁, B₂ и B₃.

2. Граница области пересечения кругов B₁, B₂ и B₃ не содержит какой-

либо дуги окружности C₁. При этом граница области пересечения всех кругов

состоит из дуг L₂ и L₃ окружностей C₂ и C₃.

3. Пересечение попарно пересекающихся кругов B₁, B₂ и B₃ пусто.

Рассмотрим вопрос об эффективном определении пересечения L_i =

⋂

L_ij всех подходящих дуг окружности C_i, 1 ≤ i ≤ n.

1≤j≤n,j=i

Каждая подходящая дуга L_ij определяется заданием точек M^(1)ij(x^(1)ij, y^(1)ij, 0)

и M^(2)ij(x^(2)ij,y^(2)ij,0) пересечения окружностей C_i и C_j и указанием, какая

143

из этих точек является начальной, а какая

конечной точкой пути. По-

ставим в соответствие каждой точке M^(l)ij(x^(l)ij, y^(l)ij, 0), 1 ≤ l ≤ 2, элемент

φ^(l)ij(x^(l)ij,y^(l)ij,α^(l)ij). Индикатор α^(l)ij указывает, в какой цвет покрашена точ-

ка M^(l)ij. Если M^(l)ij покрашена в черный цвет, то полагаем α^(l)ij = 1, в против-

ном случае α^(l)ij = 0. Таким образом, каждая подходящая дуга определяется

заданием двух элементов φ^(1)ij и φ^(2)ij.

Пусть для окружности C_i найдено множество всех элементов φ^(l)ij, 1 ≤ l ≤ 2,

1 ≤ j ≤ n, j = i. Разобьем множество элементов φ^(l)ij на два подмножества.

Если y^(l)ij < 0, то отнесем элемент φ^(l)ij(x^(l)ij, y^(l)ij, α^(l)ij) ко множеству N₁, а ес-

ли y^(l)ij ≥ 0, то отнесем φ^(l)ij ко множеству N₂. Таким образом, множество N₁

(множество N₂) элементов φ^(l)ij задает множество точек M^(l)ij окружности C_i,

которым можно поставить во взаимно однозначное соответствие их проекции

на ось Ox (естественно, совпадающие точки M^(l)ij проектируются в одинако-

вые точки на оси Ox).

Упорядочим множество N₁ элементов φ^(l)ij по неубыванию x^(l)ij, а множе-

ство N₂

по невозрастанию x^(l)ij. Полученные последовательности элемен-

тов φ^(l)ij обозначим соответственно как π₁ и π₂. Составим последовательность

π = (π₁,π₂), которая представляет собой перечисление начальных и конечных

точек подходящих дуг L_ij в процессе обхода окружности C_i против часовой

стрелки. Занумеруем элементы последовательности π, обозначив их через

ψ_k(x_k,y_k,α_k), т.е. π = (ψ₁,ψ₂,... ,ψ_2n-2).

Просматривая последовательность π слева направо, выделим в ней подпо-

следовательности элементов, соответствующих совпадающим точкам окруж-

ности C_i, если такие существуют. Пусть π = (ψ_k, ψ_k+1, . . . , ψ_k+t) одна из

таких подпоследовательностей. У всех элементов ψ_p(x_p, y_p, α_p) подпоследо-

вательности π одинаковые значения x_p и одинаковые значения y_p, а вот ин-

дикаторы α_p у них могут быть разные. Разобьем элементы π на две подпо-

следовательности: к подпоследовательности π^′ отнесем все элементы, у кото-

рых α_p = 0, остальные элементы отнесем к подпоследовательности π^′′ (у них

α_p = 1). Если у элемента ψ_k-1, предшествующего подпоследовательности π

в последовательности π, индикатор α_k-1 = 0, то в последовательности π за-

меним подпоследовательность π подпоследовательностью (π^′, π^′′). Если же

α_k-1 = 1, то заменим в π подпоследовательность π подпоследовательностью

(π^′′, π^′). Аналогичные действия проделаем со всеми подпоследовательностя-

ми элементов, соответствующих совпадающим точкам окружности C_i. Такие

построения выполняются с целью минимизации количества переключений

индикатора α_k в процессе перечисления начальных и конечных точек подхо-

дящих дуг L_ij при обходе окружности C_i.

Перенумеруем элементы преобразованной последовательности π в соот-

ветствии с их расположением. Если у соседних элементов ψ_k(x_k, y_k, α_k)

и ψ_k+1(x_k+1,y_k+1,α_k+1), 1 ≤ k ≤ 2n - 3, последовательности π имеем α_k =

144

(1)

M₁

B₃

(2)

B₂

B₁

(2)

M₁

(1)

M₁

Рис. 3. Граница области пересечения кругов содержит две дуги окружности C₁.

= α_k+1, то назовем эту ситуацию переключением индикатора. Просматривая

слева направо последовательность π, подсчитаем у нее количество ρ пере-

ключений индикатора.

Лемма 1. Пусть последовательность π элементов ψ_k(x_k,y_k,α_k), 1 ≤

≤ k ≤ 2n - 2, соответствующих начальным и конечным точкам подходя-

щих дуг окружности C_i, построена по правилам, описанным выше. Тогда

если 1 ≤ ρ ≤ 2, то пересечение L_i всех подходящих дуг окружности C_i непу-⋂

сто, т.е. L_i =

L_ij = ∅.

1≤j≤n,j=i

В Приложении приводится конструктивное доказательство леммы 1, в⋂

процессе которого показано, как найти дугу L_i =

L_ij = ∅, а зна-

1≤j≤n,j=i

чит, решить задачу, поскольку любая точка на дуге L_i, а также любая точка,

принадлежащая хорде, соединяющей концы L_i, принадлежит пересечению

всех кругов.

Отметим, что если ρ ≥ 3, то, как показывает следующий пример, никакого⋂

вывода о существовании непустого пересечения L_i =

L_ij подходя-

1≤j≤n,j=i

щих дуг окружности C_i сделать нельзя.

Пример 1. Пусть задана последовательность индикаторов

(0, 1, 0, 1).

Для этой последовательности количество переключений индикатора ρ = 3.

На рис. 2,б и рис. 2,в изображены две возможные ситуации. Для каждой из

этих ситуаций пересечение подходящих дуг окружности C₁ пусто. На рис. 3

изображена третья возможная ситуация, когда пересечение подходящих дуг

окружности C₁ состоит из двух дуг ⌣ M⁽¹⁾¹²M⁽²⁾¹³ и ⌣ M⁽¹⁾¹³M⁽²⁾¹². Заметим, что

при этом градусная мера по крайней мере одной из дуг L₁₂ и L₁₃ больше 180^◦.

Лемма 2. Градусная мера подходящей дуги L_ij окружности C_i больше

180^◦ только в том случае, если ее радиус r_i меньше радиуса r_j окружно-

сти C_j, j = i.

Следствие 1. Если радиус r_i окружности C_i больше радиусов всех⋂

остальных окружностей C_j, j = i, и ρ ≥ 3, то L_i =

L_ij = ∅.

1≤j≤n,j=i

Напомним, что все круги B_i, 1 ≤ i ≤ n, занумерованы в порядке невоз-

растания их радиусов: r₁ ≥ r₂ ≥ . . . ≥ r_n. Рассмотрим круг B₁ и определим

для окружности C₁ количество ρ переключений индикатора. В соответствии

с леммой 1 и следствием 1 для окружности C₁, имеющей наибольший радиус,

в зависимости от значения ρ можно сделать вывод, имеет ли место ситуация

L₁ = ∅.

145

Предположим, исследовали окружность C₁ и пришли к выводу, что L₁ = ∅.

Если при этом пересечение всех кругов непустое множество, то оно нахо-

дится внутри открытого круга B₁ \ C₁. Временно удаляем круг B₁ и перехо-

дим к рассмотрению круга B₂, т.е. круга со следующим по величине радиу-

сом. Процесс продолжаем до тех пор, пока не найдем круг B_k такой, что для⋂

окружности C_k имеем L_k =_k<j≤n L_kj = ∅. Пусть M_kp и M_kq начальная и

конечная точки дуги L_k окружности C_k. По построению точка M_kp (и вообще

любая точка дуги L_k и любая точка хорды, соединяющей ее концы) принад-

лежит всем кругам B_k, B_k+1, . . . , B_n. Остается проверить, принадлежит ли

точка M_kp (либо какая-то из указанных точек) кругам B₁, . . . , B_k-1. Если

да, то проверяемая точка искомая. В противном случае задача не имеет

решения.

Ниже приводится формальное описание алгоритма.

Алгоритм 1. BALLS1

Вход: Круги B₁, . . . , B_n, заданные указанием их центров O_i(x_i, y_i, 0) и ра-

диусов r_i, i = 1, n.

Выход: Общая точка для всех кругов B₁, . . . , B_n либо ответ, что задача не

имеет решения.

1. Занумеровать круги B₁, . . . , B_n таким образом, что r₁ ≥ r₂ ≥ . . . ≥ r_n.

2. FOR i = 1 to n DO

3. N₁ = ∅, N₂ = ∅.

FOR j = i + 1 to n DO

Для окружностей C_i и C_j найти их точки пересечения

M^(1)ij(x^(1)ij,y^(1)ij,0) и M^(2)ij(x^(2)ij,y^(2)ij,0), решив систему (1).

------→

---→

IF (

O_iO_j,M^(1)ijM^(2)ij,k) > 0 THEN полагаем α^(l)ij = 0, α^(2)ij = 1

(для дуги L_ij точка M^(1)ij начальная, а M^(2)ij конечная)

ELSE полагаем α^(l)ij = 1, α^(2)ij = 0 (для дуги L_ij точка M^(2)ij

начальная, а M^(1)ij конечная).

FOR l = 1 to 2 DO

Создать элемент φ^(l)ij(x^(l)ij, y^(l)ij, α^(l)ij).

IF y^(l)ij < 0 THEN N₁ = N₁ ∪ {φ^(l)ij} ELSE N₂ = N₂ ∪ {φ^(l)ij}.

END FOR l

END FOR j

10. Упорядочить множество N₁ элементов φ^(l)ij(x^(l)ij, y^(l)ij, α^(l)ij) по неубыва-

нию x^(l)ij, а множество N₂ по невозрастанию x^(l)ij. Обозначить полу-

ченные последовательности π₁ и π₂ соответственно.

11. Составить последовательность π = (π₁, π₂). Найти в последователь-

ности π подпоследовательности элементов, соответствующих совпа-

дающим точкам, и переупорядочить их (см. выше описание процесса

переупорядочивания).

12. Просматривая слева направо последовательность π, определить ко-

личество ρ переключений индикатора.

146

⋂

13. IF 1 ≤ ρ ≤ 2, THEN определить дугу L_i =

L_ij = ∅ (см.

1≤j≤n,j=i

доказательство леммы 1), положить k = i и перейти на шаг 15.

END FOR i

14. Перейти на шаг 19.

15. Определить M_kp и M_kq-начальную и конечную точки дуги L_k окруж-

ности C_k.

16. FOR i = 1 to k - 1 DO

17. IF M_kp ∈ B_i, THEN перейти на шаг 19.

END FOR i

18. Точка M_kp решение задачи. Стоп.

19. Задача не имеет решения. Стоп.

Упорядочение множеств N₁ и N₂ (шаг 10) представляет собой наиболее

трудоемкую операцию, входящую в цикл по i (шаги 2-13). Общая вычисли-

тельная сложность алгоритма составляет O(n² log n) операций.

2.3. Основная часть алгоритма BALLS2

Каждый круг B_i, 1 ≤ i ≤ n, представляет собой выпуклое множество то-

чек. Известно, что пересечение конечного числа выпуклых множеств есть вы-

пуклое множество (см., например, [6]). Граница области пересечения n кругов

состоит из дуг некоторых из окружностей C_i, 1 ≤ i ≤ n. Пересечение кругов

фактически является выпуклой комбинацией (см. [6]) точек своей границы.

Среди всех граничных точек области пересечения кругов в первую очередь

представляют интерес точки стыковки дуг окружностей. Используя выпук-

лые комбинации этих точек, при необходимости можно будет найти и другие

точки пересечения кругов.

Алгоритм просматривает все пары окружностей C_i и C_j , 1 ≤ i, j ≤ n, i = j,

определяет их точки пересечения M^(1)ij и M^(2)ij и проверяет, принадлежит ли

хотя бы одна из них всем остальным кругам B_k, 1 ≤ k ≤ n, k = i, j. В случае

положительного ответа найденная точка (например, M^(1)ij) решение задачи.

Если пересечение кругов не является пустым множеством, то граница об-

ласти пересечения содержит не менее двух дуг (с учетом предварительной

обработки), а значит, и не менее двух точек стыковки дуг. Поэтому перебрав

точки пересечения всех пар окружностей C_i и C_j , 1 ≤ i, j ≤ n, i = j, алгоритм

определит искомую точку.

Ниже приводится формальное описание алгоритма.

Алгоритм 2. BALLS2

Вход: Круги B₁, . . . , B_n, заданные указанием их центров O_i(x_i, y_i, 0) и ра-

диусов r_i, i = 1, n.

Выход: Общая точка для всех кругов B₁, . . . , B_n либо ответ, что задача не

имеет решения.

1. FOR i = 1 to n - 1 DO

FOR j = i + 1 to n DO

Для окружностей C_i и C_j найти их точки пересечения M^(1)ij и M^(2)ij.

147

l=1

FOR k = 1 to n, k = i, k = j DO

IF M^(l)ij ∈ B_k, THEN перейти на шаг 8.

END FOR k

Точка M^(l)ij решение задачи. Стоп.

l=l+1

IF l ≤ 2, THEN перейти на шаг 5.

END FOR j

END FOR i

10. Задача не имеет решения. Стоп.

Цикл по переменной i содержит вложенный цикл по переменной j, кото-

рый в свою очередь содержит цикл по переменной k. Следовательно, общая

вычислительная сложность алгоритма составляет O(n³) операций.

3. Определение точки в пересечении шаров в пространстве E^m

Пусть в m-мерном аффинном евклидовом пространстве E^m задана декар-

това прямоугольная система координат (O,

m), где

m орто-

нормированный базис. Имеется n шаров. Каждый m-мерный шар B_i, i = 1, n,

задается указанием его центра O_i(x⁽ⁱ⁾¹, . . . , x^mi)) и радиуса R_i. Границей ша-

ра B_i является m-мерная сфера S_i, определяемая уравнением (x₁ - x⁽ⁱ⁾¹)²+

... + (x_m - x^mi))² = R²ⁱ. Предварительная обработка, т.е. проверка, пересека-

ются ли заданные шары попарно, проводится аналогично тому, как это было

проделано для случая m = 2 (см. раздел 2.1) с учетом, что в аффинном евкли-

довом пространстве E^m расстояние между двумя точками O_i(x⁽ⁱ⁾¹, . . . , x^mi)) и

O_j(x^(j)1,... ,x^mj)) определяется по формуле

√

d_ij = (x⁽ⁱ⁾¹ - x^(j)1)² + ... + (x^mi) - x^mj))².

В дальнейшем будем без ограничения общности считать, что для любой пары

шаров B_i и B_j такой, что R_i ≥ R_j, выполняется неравенство R_i - R_j < d_ij <

< R_i + R_j, где d_ij расстояние между их центрами O_i и O_j. Это означает, что

m-мерные сферы S_i и S_j пересекаются по “окружности” (т.е. по (m - 1)-мер-

ной сфере) C_ij.

Зафиксируем две сферы S_i и S_j с центрами в точках O_i(x⁽ⁱ⁾¹, . . . , x^mi)) и

O_j(x^(j)1,... ,x^mj)) соответственно и рассмотрим систему уравнений



(x1 - x⁽ⁱ⁾¹)² + ... + (x_m - x^mi))² = R²ⁱ,

(2)

(x₁ - x^(j)1)² + . . . + (x_m - x^mj))² = R^2j.

С геометрической точки зрения ее решение представляет собой (m - 1)-мер-

ную сферу (окружность при m - 1 = 2) C_ij , по которой пересекаются m-мер-

148

ные сферы S_i и S_j. Вычитая первое уравнение системы (2) из второго, полу-

чим уравнение вида

(3)

α₁x₁ + ... + α_mx_m

+ β = 0,

которое представляет собой уравнение гиперплоскости в аффинном про-

странстве E^m. Гиперплоскость (3) как бы отрезает от шаров B_i и B_j части, из

которых состоит их область пересечения, причем (m - 1)-мерная сфера C_ij

лежит в этой гиперплоскости и является границей “срезов” шаров B_i и B_j.

“Срезы” шаров B_i и B_j, т.е. (m - 1)-мерные шары (круги при m - 1 = 2) с гра-

ницей C_ij , склеены по гиперплоскости (3). В пространстве E^m (m - 1)-мер-

ный шар с границей C_ij является аналогом хорды, соединяющей точки пере-

сечения двух окружностей (в случае m = 2).

С помощью некоторого ортогонального преобразования декартовой систе-

мы координат (некоторого поворота системы координат вокруг ее начала

в случае m = 3) уравнение (3) можно привести к виду x_m = x^∗, где x^∗

константа. Подставляя x_m = x^∗ в уравнение (x₁ - x⁽ⁱ⁾¹)² + . . . + (x_m - x^mi))² =

= R²ⁱ (первое уравнение системы (2)), получаем каноническое уравнение

(m - 1)-мерной сферы C_ij . Покажем, как построить матрицу T такого ор-

тогонального преобразования (оператора).

Просматривая коэффициенты α₁, . . . , α_m уравнения (3), найдем коэффи-

циент α_l = 0. Зададим координаты x_i, i = 1, m, i = l точек P₀, P₁, . . . , P_m-1,

принадлежащих гиперплоскости (3), в соответствии со следующей таблицей:

x₁

x₂

x_l

... x_m

P₀

x^(0)l

P₁

x^(1)l

P₂

x^(2)l

P_m-1

x^(m-1)l ...

Координата x_l каждой из этих точек находится из уравнения (3).

---→

-----→

Система векторо

f₁ =

P₀P₁, ...

f_m-1 =

P₀P_m-1 линейно независима, при-

чем каждый из этих векторов ортогонален вектор

f_m = (α₁,... ,α_m). Таким

образом, система векторов

f₁,...

f_m может служить базисом в простран-

стве E^m. Для системы векторо

f₁,..

f_m выполним процесс ортогонализа-

ции:

f₁

h₁ =

;

f₁ |

g_i

f_i -

f_i,h1)h1 - ... -

f_i,hi-1)hi-1,hi =

i = 2,...,m - 1;

|g_i |

f_m

h_m =

f_m |

149

В итоге получили ортонормированный базис h1, . . . ,hm. Составим матри-

цу T перехода от исходного ортонормированного базиса e₁, . . . , e_m к базису

h₁,... ,hm, записав в столбцы матрицы T координаты векторовh1,... ,hm в

базисе e₁, . . . , e_m. Матрица T также является матрицей ортогонального опе-

ратора, переводящего гиперплоскость (3) в гиперплоскость вида x_m = x^∗.

Пересчитаем координаты центров O_k шаров B_k, k = 1, n, по формуле

X (k)_=T -1_X(k)_,

(4)

где X^(k) = (x^(k)1, . . . , x^mk))^T

вектор-столбец координат точки O_k в базисе

X (k)=(x(k)

e₁,... ,e_m, а

,...,x^mk))^T

вектор-столбец ее координат в базисе

h₁,... ,hm.

Для сфер S_i и S_j рассмотрим систему уравнений (2) с новыми координа-

тами их центров O_i и O_j . Вычитая первое уравнение системы (2) из второго,

получим уравнение x_m = x^∗.

Далее, для каждой сферы S_k, k = 1, n, k = j, рассмотрим ее уравнение

(5)

(x₁ - x^(k)1)² + . . . + (x_m - x^(k)m)² = R^2k

и подставим в него x_m = x^∗. Если R^2k - (x^∗ - x^mk))² ≥ 0, то полагаем

(6)

r^2k = R^2k - (x^∗ - x^(k)m)².

Это будет означать, что m-мерная сфера S_k пересекается с плоскостью

x_m = x^∗ и в результате получается (m - 1)-мерная сфера (окружность при

m - 1 = 2), задаваемая уравнением

(x₁ - x^(k)1)² + . . . + (x_m-1 - x^(k)m-1)² = r^2k.

Если все сферы S_k (а значит, и все шары B_k), k = 1, n, k = j, пересекаются

с гиперплоскостью x_m = x^∗, то на данном этапе задача сводится к определе-

нию точки в пересечении множества n - 1 шаров в пространстве E^m-1. Если

такая точка M₀(x⁰¹, . . . , x^0m-1, x^∗) будет найдена, то остается только пересчи-

тать ее координаты в соответствии со следующей формулой:

(7)

X⁰ = TX0,

где

X⁰ =(x⁰¹,...,x^0m-1,x^∗)^T

координаты точки M₀ в базисеh1, . . . ,hm, а

X⁰ = (x⁰¹,... ,x^0m)^T

ее координаты в исходном базисе e₁, . . . , e_m. Форму-

ла (7) задает преобразование координат, обратное преобразованию, опреде-

ляемому формулой (4).

Если же полученное на данном этапе множество n - 1 шаров из простран-

ства E^m-1, определяемого гиперплоскостью x_m = x^∗, не пересекается, то пе-

реходим к следующему этапу алгоритма, т.е. к рассмотрению следующей

фиксированной пары сфер S_i и S_j . Переход к следующему этапу алгоритма

150

осуществляется и в случае, когда не все сферы S_k, k = 1, n, k = j, пересека-

ются с гиперплоскостью x_m = x^∗, т.е. если для некоторой сферы S_k имеем

R^2k - (x^∗ - x^mk))² < 0.

Вообще, если пересечение шаров не является пустым множеством, то гра-

ница области пересечения состоит из частей некоторых ограничивающих их

сфер (с учетом предварительной обработки таких сфер будет не менее двух).

Гиперплоскости, по которым стыкуются части сфер, ограничивающих об-

ласть пересечения шаров, проходят через область пересечения шаров. Пе-

ребирая все такие гиперплоскости (т.е. все пары m-мерных сфер S_i и S_j,

1 ≤ i,j ≤ n, i = j) найдем гиперплоскость, содержащую искомую точку.

Ниже приводится краткое формальное описание рассмотренных выше ос-

новных этапов рекурсивного алгоритма BALLS3(m, n), решающего задачу в

пространстве E^m, где m ≥ 3.

Алгоритм 3. BALLS3(m,n)

Вход: m-мерные шары B^(m)1, . . . , B^nm), заданные указанием их центров

O^(m)i(x⁽ⁱ⁾¹,... ,x^mi)) и радиусов R^(m)i,i = 1,n.

Выход: Общая точка для всех шаров B^(m)1, . . . , B^nm) либо ответ, что задача

не имеет решения.

1. Выполнить предварительную обработку.

2. FOR i = 1 to n - 1 DO

3. j = 2.

FOR j ≤ n DO

Из системы (2) определить гиперплоскость α₁x₁ +. . .+α_mx_m +β = 0,

содержащую пересечение сфер S^(m)i и S^(m)j.

Построить матрицу T ортогонального преобразования, переводящего

гиперплоскость α₁x₁ + . . . + α_mx_m + β = 0 в гиперплоскость x_m = x^∗.

Найти матрицу T^-1.

Ортогональное преобразование: для всех шаров B^(m)k, k = 1, n, k = i,

пересчитать координаты их центров O^(m)k по формуле (4).

Из системы (2) уравнений сфер с новыми координатами их центров

определить плоскость x_m = x^∗, содержащую пересечение сфер S^(m)i

и S^(m)j.

10.

FOR k = 1 to n, k = j DO

11.

IF гиперплоскость x_m = x^∗ не пересекает сферу S^(m)k

THEN перейти на шаг 14

ELSE для (m - 1)-мерного шара B^(m-1)k определить его радиус

R^(m-1)k = r_k по формуле (6) и центр O^(m-1)k (отбрасывая

последнюю координату у точки O^(m)k).

END FOR k

12.

IF m > 3 THEN для множества шаров B^(m-1)k, 1 ≤ k ≤ n, k = j,

выполнить BALLS3(m - 1, n - 1)

ELSE выполнить для этого множества шаров BALLS1 или BALLS2.

13.

IF найдена точка M₀(x⁰¹, . . . , x^0m-1, x^∗) в пересечении (m-1)-мерных

151

шаров B^(m-1)k, 1 ≤ k ≤ n, k = j THEN обратное ортогональное

преобразование: пересчитать координаты точки M₀ по формуле (7)

и стоп.

14.

Положить j = j + 1 и перейти на шаг 4.

END FOR j

END FOR i

15. Задача не имеет решения. Стоп.

Оценим вычислительную сложность алгоритма BALLS3(m, n). В про-

странстве E^m расстояние d_ij между двумя точками O_i и O_j может быть

вычислено за O(m) операций. Поэтому предварительная обработка (шаг 1)

требует O(n²m) операций. Шаги 5 и 9 выполняются за O(m) операций.

Построение системы векторо

f₁,...

f_m может быть выполнено за O(m²)

операций (см. таблицу), а процесс ортогонализации системы векторов за

O(m³) операций (с учетом того, что скалярное произведение двух векторов

вычисляется за O(m) операций). Следовательно, матрица T , столбцами кото-

рой являются координаты ортонормированной системы векторовh1, . . .hm,

может быть построена за O(m³) операций (шаг 6). Обратная матрица T^-1

может быть построена за O(m²) операций (шаг 7) с помощью следующе-

го известного метода, основанного на методе Гаусса. К расширенной матри-

це [T |I_m], где I_m единичная матрица порядка m, применяются элементар-

ные преобразования над строками, приводящие эту матрицу к виду [I_m|C].

В итоге получается матрица T^-1 = C.

Вычисление координат точки в новом базисе по формуле (4) может быть

выполнено за O(m²) операций. Следовательно, шаг 8 выполняется за O(nm²)

операций. Цикл по k (шаги 10-11) выполняется за O(n) операций. Пересчет

координат точки M₀ по формуле (7) (шаг 13) выполняется за O(m²) операций.

С учетом двух основных циклов по i (шаги 2-14) и по j (шаги 4-14)

общая вычислительная сложность T (m, n) алгоритма BALLS3(m, n) может

быть выражена следующим рекуррентным уравнением:

(8)

T (m, n) = O(n³m² + n²m³) + n²

T (m - 1, n - 1), m ≥ 3,

где T (2, n) = O(n² log n), если используется алгоритм BALLS1, и T (2, n) =

= O(n³), если используется алгоритм BALLS2. Решение T (m,n) рекуррент-

ного уравнения (8) при m ≥ 3 не превосходит O(n^2m-4(nm² + m³ + T (2, n))).

Следовательно, в пространстве E^m исходная задача может быть решена

за O(n^2m-4(nm² + m³ + n² log n)) или O(n^2m-4(nm² + m³ + n³)) операций.

В частности, для трехмерного пространства сложность алгоритма составит

O(n⁴ log n) либо O(n⁵) операций.

4. Заключение

В статье предлагаются точные полиномиальные алгоритмы для опреде-

ления некоторой точки, принадлежащей пересечению n шаров в m-мерном

евклидовом пространстве. В практически значимых случаях m = 2 и m = 3

представленные алгоритмы могут быть использованы при разработке про-

граммного обеспечения в задачах управления различными динамическими

152

системами, включающими в себя множество дронов. Например, для заданной

конфигурации роя дронов необходимо определить местоположение управ-

ляющего дрона либо определить, возможно ли желаемое изменение конфигу-

рации без потери управления всеми дронами управляющим дроном. Другие

практические интерпретации рассматривались в разделе 1.

Отметим также, что можно выполнить небольшую модификацию пред-

ставленных алгоритмов таким образом, что будет найдена не одна точка,

принадлежащая пересечению шаров, а несколько таких точек (если это пе-

ресечение непусто и не состоит из единственной точки). Значит, возможно

определить и линейную комбинацию этих точек, целиком принадлежащую

области пересечения шаров. Заметим, что такая линейная комбинация угло-

вых точек границы области пересечения шаров не совпадает с множеством

точек шара наибольшего объема, содержащегося в области пересечения ша-

ров, который необходимо найти в задаче внутренней аппроксимации [4]. По-

этому предложенный в данной статье подход является альтернативным не

только по методу, но и по множеству получаемых решений, что предоставля-

ет дополнительные возможности при принятии решений.

ПРИЛОЖЕНИЕ

Доказательство леммы 1. 1. Пусть ρ = 1, т.е. последовательность

π имеет единственное переключение индикатора. Заметим, что в этом слу-

чае переключение индикатора произошло на элементе с номером n - 1, т.е.

α_n-1 = α_n. Возможны две ситуации.

а) α_n-1 = 0, α_n = 1. В этом случае последовательность π может быть

разбита на две подпоследовательности: π = (π⁽¹⁾, π⁽²⁾), где π⁽¹⁾ = (ψ₁, ψ₂,

...,ψ_n-1), π⁽²⁾ = (ψ_n,ψ_n+1,...,ψ_2n-2). Все элементы подпоследовательно-

сти π⁽¹⁾ имеют нулевой индикатор, т.е. они соответствуют белым точкам на

окружности C_i (начальным точкам подходящих дуг). Все элементы подпо-

следовательности π⁽²⁾ имеют индикатор 1, т.е. они соответствуют черным

точкам на окружности C_i (конечным точкам подходящих дуг). Любая под-

ходящая дуга L_ij окружности C_i начинается в белой точке и заканчивается

в черной точке при договоренности, что движение вдоль дуги происходит

против часовой стрелки. Последовательность π соответствует перечислению

точек на окружности C_i в процессе обхода ее против часовой стрелки. По-

этому обходу любой дуги L_ij от начальной до конечной точки соответствует

некоторая подпоследовательность (ψ_p, ψ_p+1, . . . , ψ_n-1, ψ_n, ψ_n+1, . . . , ψ_q) после-

довательности π, где (ψ_p, ψ_p+1, . . . , ψ_n-1) последовательность элементов с

индикатором 0, а (ψ_n, ψ_n+1, . . . , ψ_q)

последовательность элементов с ин-

дикатором 1. Заметим, что каковы бы ни были номера p и q, 1 ≤ p ≤ n - 1,

n ≤ q ≤ 2n - 2, в любую такую подпоследовательность обязательно войдут

элементы ψ_n-1 и ψ_n. Поэтому дуга L_i, соединяющая точки окружности C_i,

соответствующие элементам ψ_n-1 (начальная точка) и ψ_n (конечная точка),⋂

будет содержаться в любой подходящей дуге L_ij , т.е. L_i =

L_ij = ∅.

1≤j≤n,j=i

б) α_n-1 = 1, α_n = 0. В этом случае все элементы подпоследовательно-

сти π⁽¹⁾ имеют индикатор 1, а все элементы подпоследовательности π⁽²⁾

имеют индикатор 0. Обход окружности C_i против часовой стрелки может

быть осуществлен в порядке π^∗ = (π⁽²⁾, π⁽¹⁾) = (ψ_n, ψ_n+1, . . . , ψ_2n-2, ψ₁, ψ₂, . . .

153

...,ψ_n-1). Тогда обходу любой подходящей дуги L_ij от начальной до ко-

нечной точки соответствует некоторая подпоследовательность (ψ_p, ψ_p+1,

...,ψ_2n-2,ψ₁,ψ₂,...,ψ_q) последовательности π^∗, где (ψ_p,ψ_p+1,...,ψ_2n-2)

подпоследовательность элементов с индикатором 0, а (ψ₁, ψ₂, . . . , ψ_q) под-

последовательность элементов с индикатором 1. Каковы бы ни были номе-

ра p и q, n ≤ p ≤ 2n - 2, 1 ≤ q ≤ n - 1, в любую такую подпоследователь-

ность (ψ_p, ψ_p+1, . . . , ψ_2n-2, ψ₁, ψ₂, . . . , ψ_q) обязательно войдут элементы ψ_2n-2

и ψ₁. Поэтому дуга L_i, соединяющая точки окружности C_i, соответствую-

щие элементам ψ_2n-2 и ψ₁, будет содержаться в любой подходящей дуге, т.е.⋂

L_i =

L_ij = ∅.

1≤j≤n,j=i

2. Пусть ρ = 2, т.е. переключение индикатора происходит дважды: один

раз с 0 на 1, а другой раз с 1 на 0, причем порядок этих переключений может

быть произвольным. Следовательно, возможны две ситуации.

а) Пусть первое переключение индикатора присходит с 0 на 1 на элементе

с номером k, т.е. α_k = 0, α_k+1 = 1. В этом случае последовательность π может

быть разбита на три подпоследовательности: π = (π⁽¹⁾, π⁽²⁾, π⁽³⁾), где π⁽¹⁾ =

= (ψ₁, ψ₂, . . . , ψ_k), π⁽²⁾ = (ψ_k+1, ψ_k+2, . . . , ψ_k+n-1), π⁽³⁾ = (ψ_k+n, ψ_k+n+1,

...,ψ_2n-2), 1 ≤ k ≤ n - 2. Все элементы подпоследовательностей π⁽¹⁾ и π⁽³⁾

имеют индикатор 0, а все элементы подпоследовательности π⁽²⁾ имеют ин-

дикатор 1. Обход окружности C_i против часовой стрелки может быть осу-

ществлен в порядке π = (π⁽³⁾, π⁽¹⁾, π⁽²⁾). Тогда обходу любой подходящей

дуги L_ij от начальной до конечной точек соответствует некоторая под-

последовательность (ψ_p,

,ψ_k,ψ_k+1,...,ψ_q), где (ψ_p,,...,ψ_k)

подпосле-

довательность элементов с индикатором 0, а (ψk+1, . . . , ψq)

подпосле-

довательность элементов с индикатором 1, k + n ≤ p ≤ 2n - 2, 1 ≤ p ≤ k,

k + 1 ≤ q ≤ k + n - 1, 1 ≤ k ≤ n - 2. В любую такую подпоследовательность

(ψ_p, . . . , ψ_k, ψ_k+1, . . . , ψ_q) обязательно войдут элементы ψ_k и ψ_k+1. Поэтому

дуга L_i, соединяющая точки, соответствующие элементам ψ_k и ψ_k+1, будет⋂

содержаться в любой подходящей дуге, т.е. L_i =

L_ij = ∅.

1≤j≤n,j=i

б) Пусть первое переключение индикатора происходит с 1 на 0 на элементе

с номером k, т.е. α_k = 1, α_k+1 = 0. Как и в случае 2а, последовательность π

может быть разбита на те же три подпоследовательности π = (π⁽¹⁾, π⁽²⁾, π⁽³⁾).

Однако в данном случае все элементы подпоследовательностей π⁽¹⁾ и π⁽³⁾

имеют индикатор 1, а все элементы подпоследовательности π⁽²⁾ имеют ин-

дикатор 0. Обход окружности C_i против часовой стрелки может быть осу-

ществлен в порядке π = (π⁽²⁾, π⁽³⁾, π⁽¹⁾). Обходу любой подходящей дуги L_ij

от начальной до конечной точек соответствует некоторая подпоследователь-

ность (ψ_p,

,ψ_k+n-1,ψ_k+n,... ,ψ_q), где (ψ_p,,... ,ψ_k+n-1)

подпоследова-

тельность элементов с индикатором 0, а (ψ_k+n, . . . , ψ_q)

подпоследова-

тельность элементов с индикатором 1, k + 1 ≤ p ≤ k + n - 1, k + n ≤ q ≤ 2n - 2,

1 ≤ q ≤ k, 1 ≤ k ≤ 2n - 2. В любую такую подпоследовательность (ψ_p,

...,ψ_k+n-1,ψ_k+n,...,ψ_q) обязательно войдут элементы ψ_k+n-1 и ψ_k+n. По-

этому дуга L_i, соединяющая точки, соответствующие элементам ψ_k+n-1 и⋂

ψ_k+n, будет содержаться в любой подходящей дуге, т.е. L_i =

L_ij =

1≤j≤n,j=i

= ∅.

Лемма 1 доказана.

154

Рис. 4.

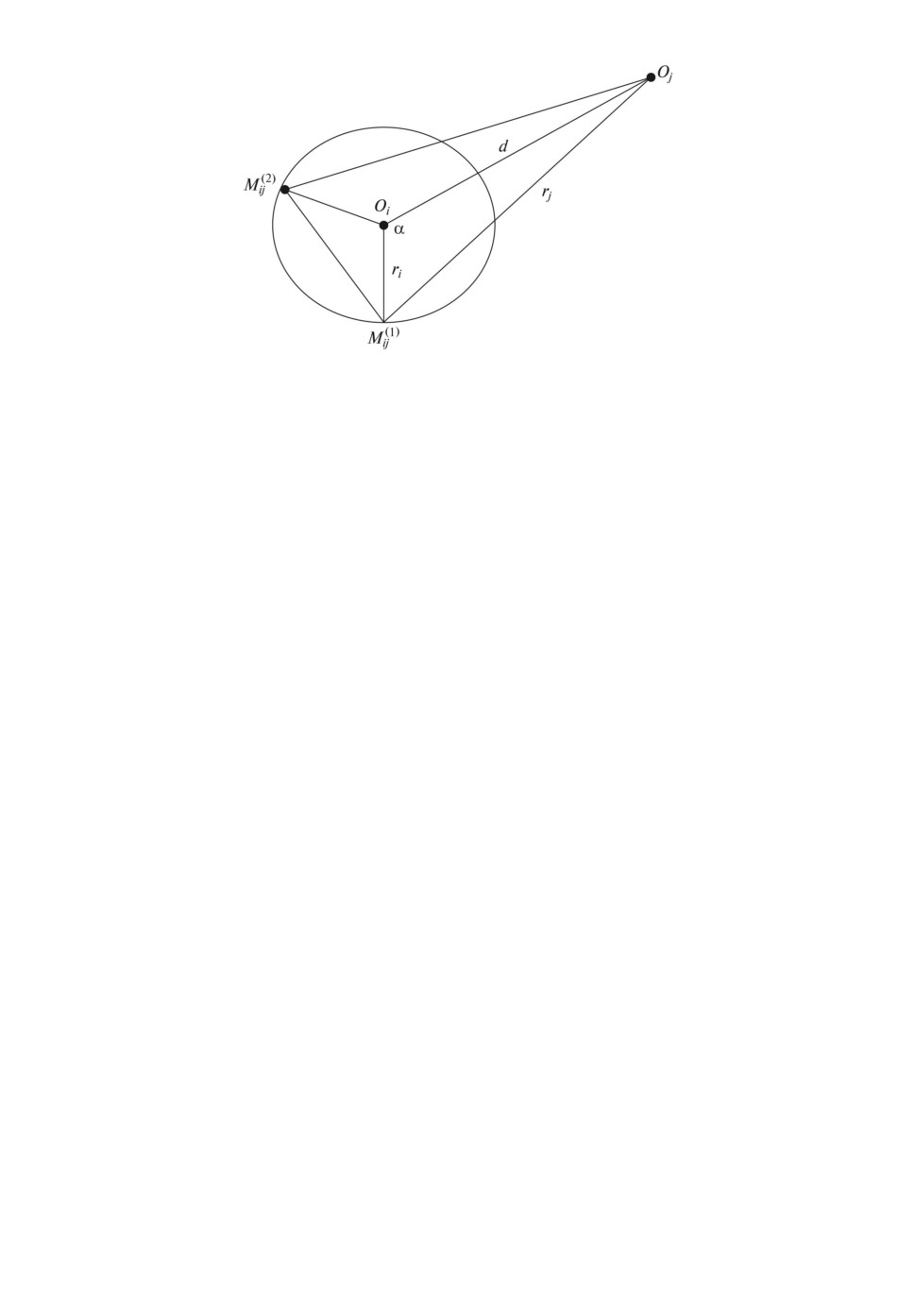
Доказательство леммы 2. Пусть градусная мера подходящей ду-

ги L_ij равна 2α > 180^◦. Для определенности будем считать точку M^(1)ij на-

чалом дуги L_ij, а точку M^(2)ij

ее концом. Градусная мера подходящей

дуги L_ij равна сумме двух одинаковых тупых углов M^(1)ijO_iO_j и M^(2)ijO_iO_j

(см. рис. 4). Пусть d

это расстояние между центрами O_i и O_j окружно-

стей C_i и C_j . Тогда из треугольника M^(1)ijO_iO_j по теореме косинусов имеем

r^2j = r²ⁱ + d² - 2r_idcos α. Поскольку α тупой угол, то cos α < 0, следователь-

но, r_j > r_i, что и требовалось доказать.

СПИСОК ЛИТЕРАТУРЫ

1. Баркетов М.С. Полиномиальные методы определения точки в пересечении неко-

торого числа шаров // Танаевские чтения. Докл. Восьмой междунар. научн.

конф. 27-30 марта 2018 г. ОИПИ, Минск. 2018. С. 18-22.

2. Otto A., Agatz N., Campbell J., Golden B., Pesch E. Optimization approaches for

civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey /

Networks, Wiley Periodicals. 2018. V.72. P. 411-458.

3. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация: алгоритмы и

сложность. М.: Мир, 1985.

4. Boyd S.S., El Ghaoui L., Feron E., Balakrishnan V. Linear matrix inequalities in

system and control theory // SIAM Studies Appl. Math. 1994. V. 15. Philadelphia:

PA.

5. Beck A. On the convexity of a class of quadratic mappings and its application to

the problem of finding the smallest ball enclosing a given intersection of balls //

J. Global Optim., Elsevier Publ. 2007. V. 39. No. 1. P. 113-126.

6. Мину М. Математическое программирование. Теория и алгоритмы. М.: Наука,

1990.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 18.07.2019

После доработки 15.09.2019

Принята к публикации 28.11.2019

155