Автоматика и телемеханика, № 6, 2020

Тематический выпуск (окончание)¹

А.Н. ИГНАТОВ, канд. физ.-мат. наук (alexei.ignatov1@gmail.com),

А.В. НАУМОВ, д-р физ.-мат. наук (naumovav@mail.ru),

В.А. РАССКАЗОВА, канд. физ.-мат. наук (varvara.rasskazova@mail.ru)

(Московский авиационный институт)

О ЗАДАЧЕ НАЗНАЧЕНИЯ “ТЕХНОЛОГИЧЕСКОГО ОКНА”

НА УЧАСТКАХ ЖЕЛЕЗНОДОРОЖНОЙ СЕТИ²

Исследуется задача назначения “технологического окна”

времени,

в течение которого на некоторых участках железнодорожной сети пре-

кращается движение поездов для производства ремонтно-строительных

работ. Железнодорожная сеть представляется в виде неориентированно-

го мультиграфа. Движение по мультиграфу осуществляется при помощи

множества бесконфликтных “подниток”, каждый элемент которого пред-

ставляет пятерку из индекса вершины начала движения, индекса верши-

ны конца движения, номера пути, по которому осуществляется движение,

времени начала движения и времени конца движения. В статье строит-

ся математическая модель осуществления перевозок по железнодорожной

сети с учетом времени готовности состава к отправлению и ограничению

на время движения состава в пункт назначения. Производится оптимиза-

ция времени назначения “технологического окна” и расписания движения

составов по мультиграфу на основе решения задач смешанного целочис-

ленного линейного программирования путем минимизации суммарного

времени нахождения поездов на железнодорожной сети. Практическая

реализация предлагаемого метода решения выполнена с использованием

математического пакета ILOG CPLEX. Приводятся результаты числен-

ного эксперимента.

Ключевые слова: “технологическое окно”, железнодорожная сеть, мульти-

граф, “поднитка”, смешанное целочисленное линейное программирование.

DOI: 10.31857/S0005231020060013

1. Введение

Задача составления расписаний движения грузовых/пассажирских поез-

дов одна из наиболее важных задач в области оптимизации функциони-

рования движения железнодорожной сети. Исследования этой задачи можно

¹ Первые две статьи являются окончанием тематического выпуска, посвященного

В.С. Танаеву (№ 5, 2020).

² Работа выполнена при поддержке Российского фонда фундаментальных исследований

(проект № 20-07-00046 А).

разделить на несколько направлений: задача формирования бесконфликт-

ного набора ниток (по сути, последовательностей из вершины начала дви-

жения, конца движения и соответствующих времен) для последующего со-

ставления из этих ниток маршрутов движения поездов [1]; задача поиска

маршрутов движения поездов по железнодорожной сети [2-6]; задача на-

значения локомотивов составам [7-11]. В [2] приведен подробный обзор пуб-

ликаций, посвященных задаче составления расписаний и поиска маршрутов

поездов по железнодорожной сети, на начало XXI в. В [3] решалась зада-

ча составления циклического расписания с учетом задержек в исполнении

расписания. В [4] рассмотрена задача формирования составов, расписания

и маршрутов их движения до станций назначения, чтобы минимизировать

суммарное взвешенное время выполнения заказов. Задача в [4] была сфор-

мулирована в виде задачи целочисленного линейного программирования.

В [5] рассмотрена задача построения расписания двухстороннего движения

поездов между двумя станциями, соединенными однопутной железной доро-

гой с разъездом. Оптимальное расписание строится методом динамического

программирования. В [6] решалась задача по оптимизации движения манев-

ровых составов по железнодорожной станции с целью исполнения всех ма-

невровых работ. В [7] задача назначения локомотивов с критерием в фор-

ме минимизации затрат была сведена к задаче смешанного целочисленного

нелинейного программирования, решение которой найдено приближенно при

помощи метода декомпозиции Данцига-Вульфа. В [8] задача подвязки ло-

комотивов была сформулирована в виде задачи целочисленного линейного

программирования с критерием в форме минимизации затрат, которая ре-

шалась эвристическими методами. В [9] задача назначения локомотивов ре-

шалась с учетом случайных задержек в готовности составов и с критерием

в форме минимума числа задействованных локомотивов. В [10] рассматри-

вался аналогичный критерий, что и в [9], а поиск решения задачи назначе-

ния локомотивов решался приближенно с использованием функции полез-

ности. В [11] ставилась задача о назначении локомотивов составам в самой

общей динамической постановке в дискретном времени. Для решения задачи

в [11] с использованием соотношений метода динамического программирова-

ния предложено решение, приближенное к оптимальному.

В силу того что некоторые участки пути железнодорожной сети должны

подлежать срочному/плановому ремонту, конструируемое расписание долж-

но включать в себя “технологические окна”

время, в течение которого

прекращается движение поездов по отдельным железнодорожным путям для

производства ремонтно-строительных работ [12]. Как правило, технологиче-

ское окно имеет 2 основных параметра: перегон, на котором должны вы-

полняться работы, и продолжительность окна. Обычно запрашивают окна

определенной продолжительности для конкретного перегона, и при этом тре-

буется, чтобы окно располагалось в заданном временном промежутке или

интервале предоставления окна. Например, требуется предоставить техно-

логическое окно на перегон между станциями A и B продолжительностью

4 часа в светлое время суток (с 9 часов утра до 18 часов вечера). При этом

на каждые сутки имеется план перевозок, в котором задано, какие перевозки

необходимо осуществить в эти сутки. Проблема назначения “технологических

окон” ранее исследовалась в [13-16]. В [13] рассматривалась задача назначе-

ния “технологического окна” для однопутной железной дороги с разъездами,

для которой все исходное расписание грузовых поездов перестраивается с

учетом необходимости проведения “технологических окон” при помощи ме-

таэвристик. В [14, 15] рассматривалась задача назначения “технологического

окна” для железнодорожной сети общего вида, в которой поезда могут быть

отменены, задержаны или отправлены по другому маршруту с критерием

в форме минимизации расходов на осуществление движения. Подходы для

назначения “технологического окна”, предложенные в [13-15], близки к ма-

териалу настоящей статьи, однако в полной мере неприменимы. В отличие

от австралийских железных дорог, которым посвящена [13], в сети железных

дорог России имеются и двухпутные, и трехпутные участки пути. Помимо

этого, в [13] отсутствует формализованная постановка задачи. В [14] “техно-

логическое окно” выбирается из некоторого наперед заданного набора. Время

в [15] полагалось дискретным, однако время поиска существенно растет, если

временные периоды очень малы, а если периоды времени очень крупны, то

можно не осуществить план перевозок. В [16] рассматривалась задача назна-

чения “технологического окна” на станции на основе различных критериев,

например поиска промежутка времени длительности не меньше заданной, в

который нужно будет перенести минимальное количество пассажирских по-

ездов. Однако в [16] не рассматривался вопрос о том, на какие пути и когда

переносить движение пассажирских поездов/маневровых локомотивов. Для

станции такой подход оправдан, поскольку сортировочная станция характе-

ризуется большим количеством приемоотправочных путей, а объезд закры-

тых путей не является длительным. Для перегонов подобный в [16] подход

неприменим, поскольку объезд закрытых путей может быть либо невозмо-

жен, либо очень длителен по времени.

В настоящей статье исследуется задача назначения “технологического ок-

на” на некоторых участках железнодорожной сети, представляемой неориен-

тированным мультиграфом. Движение поездов между смежными вершинами

мультиграфа возможно только в особые промежутки времени, задаваемые

множеством бесконфликтных “подниток”. Временной интервал для “техно-

логического окна” ищется на основе минимизации суммарного времени на-

хождения поездов на железнодорожной сети начиная с момента отправления.

Данная задача формулируется в виде задачи смешанного целочисленного ли-

нейного программирования. В рамках задачи нахождения “технологического

окна” предлагаемая математическая модель позволяет не только находить

указанный временной интервал, но и маршруты с расписанием следования

поездов по железнодорожной сети. Рассматривается пример.

2. Основные обозначения и предположения

Рассмотрим железнодорожную сеть, представляемую неориентированным

мультиграфом G =< V, E >, где V множество узлов (станций, где происхо-

дит ветвление железнодорожной сети, станций, у которых количество входя-

щих путей не равно количеству исходящих путей, сортировочных станций и

конечных станций), а E множество ребер (железнодорожных путей), соеди-

няющих данные вершины. Пусть |V | = m. Перенумеровав вершины графа G

от единицы до m, составим множество индексов V^′ = {1, 2, . . . , m}, каждый

элемент которого однозначно определяет вершину графа G.

Пусть имеется I поездов, для каждого из которых заданы:

• индекс вершины отправления v^{отправi} ∈ V^′;

• индекс вершины назначения v^прибi ∈ V^′;

• время готовности к отправлению t^{отправi}, которое вычисляется как коли-

чество минут от некоторого момента отсчета;

• максимальное количество времени d_i, в течение которого поезду позволя-

ется находиться в пункте отправления с момента готовности;

• время в пути поезда T_i в минутах, т.е. максимальное время, в течение

которого поезду позволяется находиться на железнодорожной сети.

Движение поездов по перегонам (между вершинами) железнодорожной се-

ти может осуществляться только в определенные промежутки времени. Для

описания таких промежутков по аналогии с [9] воспользуемся множеством

бесконфликтных “подниток” Z, каждый элемент z_k которого представляет

собой пятерку

z_k = (v^начk,v^конk,n_k,t^начk,t^конk) ,

где v^начk ∈ V^′ индекс вершины начала движения, v^конk ∈ V^′ индекс вер-

шины конца движения, причем v^начk и v^конk индексы смежных вершин в

графе G, n_k номер пути, соединяющего вершины с индексами v^начk и v^конk,

t^начk

время начала движения, t^конk время конца движения. Пусть

dimZ = K.

Множество Z может быть получено методами из [1]. Пронумеруем элементы

множества Z от единицы до K. Таким образом, число от единицы до K

однозначно определяет параметры “поднитки”. Зададим также минимальную

t^минст и максимальную длительности t^максст стоянки поездов на промежуточных

между вершиной отправления и вершиной назначения станциях.

3. Постановка задачи

Пусть для ремонта длительности не меньше заданного параметра Δ, кото-

рый должен быть осуществлен не ранее t^нач1 и не позднее t^кон2, должны быть

закрыты некоторые перегоны (дуги) графа G. Поставим задачу отыскания

маршрутов и времени следования указанных выше I поездов через железно-

дорожную сеть, задаваемую графом G, на основе множества “подниток” Z

с учетом того, что некоторые дуги графа G должны быть закрыты для ре-

монта длительности не меньше заданного параметра Δ на основе различных

критериев: с целью минимизации суммарного времени в движении и с целью

минимизации суммарного времени нахождения поездов на железнодорожной

сети.

Предварительно отметим, что без учета “подниток” в графе G может ока-

заться бесконечное число способов добраться из одной вершину в другую

из-за наличия циклов. В случае переходов по графу G только по “поднит-

кам” количество способов будет конечным, однако может оказаться довольно

большим. В этой связи ограничим все возможные маршруты следования по-

ездов из пункта отправления в пункт назначения максимум J “поднитками”.

В этом случае движение поезда однозначно задается последовательностью

“подниток”, длины не более J, причем для любых двух соседних “подниток”

должно выполняться условие согласованности как по вершине начала/конца

движения, так и по времени начала/конца движения. В дальнейшем j-ю “под-

нитку” в этой последовательности будем называть j-м этапом маршрута сле-

дования поезда.

Выделим из множества Z номера тех “подниток”, у которых ребро, обра-

зовываемое первыми тремя компонентами пятерки, подлежит ремонту. На

основе этих номеров составим множество Z^′ ⊂ {1, 2, . . . , K}.

Введем вспомогательные переменные δ_i,j,k, характеризующие использова-

ние i-м поездом “поднитки” с номером k на j-м этапе маршрута следования

по железнодорожной сети, i = 1, I, j = 1, J, k = 1, K. Переменная δ_i,j,k равна

нулю, если i-м поездом на j-м этапе маршрута “поднитка” с номером k не

задействована, и равна единице в обратном случае. Также введем перемен-

ныеδi,j,k, характеризующие, что поезд с номером i, используя “поднитку” с

номером k, по окончании j-го этапа маршрута прибыл в пункт назначения,

i = 1,I, j = 1,J, k = 1,K. А именно переменнаяδi,j,k равна единице, если

поезд с номером i, используя “поднитку” с номером k, по окончании j-го эта-

па маршрута прибыл в пункт назначения, и равна нулю во всех остальных

случаях.

Пусть t₁

время начала “технологического окна” и t₂ время окончания.

Используя указанные переменные, составим множество допустимых стра-

тегий. По определению переменных δ_i,j,k иδi,j,k имеем:

(3.1)

δ_i,j,k

∈ {0, 1}, i = 1, I, j = 1, J, k = 1, K,

(3.2)

δi,j,k

∈ {0, 1}, i = 1, I, j = 1, J, k = 1, K.

Для того чтобы движение поездов осуществлялось из мест отправления

поездов, введем ограничения:

∑

(3.3)

δ_i,1,k

= 1, i = 1, I,

k=1

∑

(3.4)

δ_i,1,kv^начk = v^{отправi}

i = 1,I,

k=1

а для того чтобы отправление произошло не раньше времени начала движе-

ния по используемой “поднитке”, используем ограничения

∑

(3.5)

δ_i,1,kt^начk ≥ t^{отправi}

i = 1,I.

k=1

Учитывая ограничение на максимальное количество времени, в течение ко-

торого поезду позволяется находиться в пункте отправления с момента го-

товности, имеем:

∑

(3.6)

δ_i,1,kt^начk ≤ t^{отправi} + d_i

i = 1,I.

k=1

Для того чтобы на каждом этапе (за исключением первого) каждым по-

ездом было занято не более одной “поднитки” введем ограничения

∑

(3.7)

δ_i,j,k

≤ 1, i = 1, I, j = 2, J.

k=1

Обеспечим условие стыковки “подниток” по пути следования поезда с но-

мером i на j-м этапе маршрута с помощью следующих ограничений:

∑

(3.8)

(δ_i,j,k -δi,j,k)v^конk =

δ_i,j+1,kv^начk

i = 1,I, j = 1,J - 1.

k=1

При этом должно быть выполнено ограничение

(3.9)

δ_i,j,k ≥δi,j,k

i = 1,I, j = 1,J, k = 1,K.

Добавим ограничения на минимально возможную и максимально возмож-

ную по длительности остановку поезда на промежуточных между вершиной

отправления и вершиной назначения станциях:

∑

δ_i,j+1,kt^начk -

(δ_i,j,k -δi,j,k)t^конk ≥ t^мин

δ_i,j+1,k,

ст

(3.10)

k=1

i = 1,I, j = 1,J - 1,

∑

(3.11)

δ_i,j+1,kt^начk -

(δ_i,j,k -δi,j,k)t^конk ≤ t^максст

i = 1,I, j = 1,J - 1.

k=1

Прокомментируем ограничения (3.8)-(3.11). Если поезд с номером i при-

был в пункт назначения по окончании j_T -го этапа, j_T ∈ {1, 2, . . . , J}, то ис-

пользование других “подниток” для осуществления движения поезда с но-

мером i не имеет смысла, что учитывается в рамках предлагаемой модели

использованием переменныхδi,j,k. А именно в рассматриваемом случае ока-

жется, что для некоторого k будет выполнено δi,jT ,k =δi,j_T ,k = 1 вследствие

ограничений (3.9). Это приведет к тому, что для рассматриваемого поезда

с номером i для j = j_T левая часть равенства (3.8) обратится в ноль. Так

как величины v^начk по определению положительны, то это приведет к тому,

что δi,jT +1,k = 0 для любого k = 1, K. Это в свою очередь приведет к тому,

что ∀j ∈ {j_T + 2, . . . , J} и ∀k ∈ {1, . . . , K} будет выполнено δ_i,j,k = 0 вслед-

ствие того же ограничения (3.8). Соответственно ∀j ∈ {j_T , . . . , J} ограниче-

ния (3.10)-(3.11) будут выполняться автоматически. Для j < j_T окажется,

чтоδi,j,k = 0 ∀k ∈ {1, . . . , K} и левая часть неравенств (3.10)-(3.11) превра-

тится в разность между временем отправления и временем прибытия на неко-

торую станцию по окончании j-го этапа.

Для определения этапа маршрута, по окончании которого поезд прибывает

в точку назначения, введем ограничения:

∑

(3.12)

δ_i,j,kv^конk ≥

δi,j,kv^iриб

i = 1,I, j = 1,J,

k=1

(

)

∑

(3.13)

δ_i,j,kv^конk ≤

δi,j,kviприб

+m 1-

δi,j,k

i = 1,I, j = 1,J,

k=1

∑ˆδ

(3.14)

i,j,k

= 1, i = 1, I.

j=1 k=1

Ограничение (3.14) гарантирует, что каждый поезд должен прибыть в место

назначения на каком-то этапе следования. Из-за ограничений (3.14) ограниче-

ния (3.12)-(3.13) будут пассивными всегда за исключением случая, когда для

рассматриваемого поезда с номером i и каких-тоj иk выполняетсяδi,ˆj,ˆk= 1.

В этом случае вследствие ограничения (3.8) окажется, что δi,ˆj,ˆk = δ_i,ˆj,ˆk. Вслед-

ствие ограничений (3.12) окажется, что v^конˆ

≥v^прибi, а вследствие ограниче-

ний (3.13) v^конˆ

≤v^прибi, что приведет к тому, что v^конˆ

= v^прибi, а, значит, поезд

с номером i прибудет в пункт назначения, используя “поднитку” с номером k

наj-м этапе.

Для того чтобы каждая “поднитка” была занята не более чем одним поез-

дом, введем ограничения

∑

(3.15)

δ_i,j,k

≤ 1, k = 1, K.

i=1 j=1

Для того чтобы “технологическое окно” было длиной не меньше заданного

параметра Δ, введем ограничение

(3.16)

t₂ - t₁

≥ Δ.

А для того чтобы “технологическое окно” было в заданный временной про-

межуток времени, наложим ограничения

(3.17)

t^нач1 ≤ t₁, t₂ ≤ t^кон2.

Теперь исключим возможность движения по “подниткам”, связанным с ду-

гами графа G, подлежащими ремонту, попадающим в “технологическое окно”.

Для этого движение по “подниткам”, подлежащим ремонту, возможно либо

до начала “технологического окна”, либо по его окончании. С этой целью

введем вспомогательные бинарные переменные γ_k и æ_k, k ∈ Z^′. Если момент

окончания “поднитки” наступает до начала “технологического окна”, то толь-

ко в этом случае γ_k = 1, k ∈ Z^′. Если момент начала “поднитки” наступает

после “технологического окна”, то только в этом случае æ_k = 1, k ∈ Z^′. Соот-

ветственно для того чтобы движение по “поднитке” было разрешено, нужно,

чтобы хотя бы одна из переменных γ_k и æ_k оказалась равной единице, k ∈ Z^′.

С учетом введенных переменных заключаем, что

(3.18)

γ_kt^конk ≤ t₁, k ∈ Z^′,

(3.19)

t₂ ≤ æ_kt^начk + (1 - æ_k)T, k ∈ Z^′,

где T некоторый параметр. Например, если расписание строится на сутки,

то T равно 1440 минутам при

(3.20)

δ_i,j,k ≤ æ_k + γ_k, i = 1,I, j = 1,J, k ∈ Z^′.

Поясним смысл ограничений (3.18)-(3.20). Если хотя бы одна из перемен-

ных æ_k и γ_k будет равна единице, то ограничения (3.20) выродятся в огра-

ничения (3.1) и движение по “поднитке” с номером k вследствие “технологи-

ческого окна” не будет закрыто, k ∈ Z^′. В оcтальных случаях окажется, что

δi,j,k ≤ 0, а значит, δi,j,k = 0, что приведет к невозможности движения по

“поднитке” с номером k, k ∈ Z^′.

Для того чтобы время в пути поезда было ограничено наперед заданной

величиной T_i, введем ограничения

∑

(3.21)

δi,j,kt^kон -

δ_i,1,kt^начk ≤ T_i

i = 1,I.

j=1 k=1

k=1

4. Различные критерии для формирования плана перевозок

и назначения “технологического окна”

Рассмотрим различные критерии для формирования плана перевозок и

назначения “технологического окна”.

Вначале рассмотрим задачу минимизация суммарного времени нахожде-

ния поездов на железнодорожной сети

∑

∑∑

(4.1)

δi,j,kt^kон -

δ_i,1,kt^начk →

i=1 j=1 k=1

i=1 k=1

→

min

t₁,t₂,δ_i,j,k,δi,j,k,γk′,æk′,i=1,I,j=1,J,k=1,K,k^′∈Z^′

с ограничениями (3.1)-(3.21).

Решение задачи (4.1) с ограничениями (3.1)-(3.21), т.е. задачи составления

расписания движения поездов по железнодорожной сети с учетом наличия

“технологического окна”, может не существовать вследствие недостаточно-

сти множества “подниток”. Решение задачи (4.1) с ограничениями (3.1)-(3.21)

также зависит от выбора параметра J. В частности, если выбрать параметр J,

равный единице, то решение задачи (4.1) с ограничениями (3.1)-(3.21) может

существовать, только если пункт отправления и место назначения смеж-

ные вершины графа G. При этом если выбрать J очень большим, то количе-

ство бинарных переменных в задаче (4.1) с ограничениями (3.1)-(3.21) станет

огромным, что приведет к долгому времени поиска решения этой задачи в

любом математическом пакете.

Еще одним путем нахождения “технологического окна” является миними-

зация времени движения поездов

∑

(4.2)

δ_i,j,k(t^конk - t^начk) →

min

t₁,t₂,δ_i,j,k,δi,j,k,γk′,æk′,i=1,I,j=1,J,k=1,K,k^′∈Z^′

i=1 j=1 k=1

с ограничениями (3.1)-(3.21).

Отличие критерия (4.1) от критерия (4.2) в том, что последний, по сути,

минимизирует количество топлива и электроэнергии, которое придется за-

тратить при перевозке грузов, а первый критерий минимизирует суммарное

время, которое локомотивы и вагоны проведут на железнодорожной сети с

момента начала движения, таким образом позволяя им высвободиться рань-

ше для исполнения других перевозок.

Возможно как отдельное, так и совместное применение предложенных

критериев. Пусть решение задачи (4.1) с ограничениями (3.1)-(3.21) суще-

ствует, а оптимальное значение критерия равно T^∗. Далее следует решить

задачу:

∑

(4.3)

δ_i,j,k(t^конk - t^начk) →

min

t₁,t₂,δ_i,j,k,δi,j,k,γk′,æk′,i=1,I,j=1,J,k=1,K,k^′∈Z^′

i=1 j=1 k=1

с ограничениями (3.1)-(3.21) и

∑

∑∑

(4.4)

δi,j,kt^kон -

δ_i,1,kt^начk = T^∗.

i=1 j=1 k=1

i=1 k=1

Пусть решение в задаче (4.3) с ограничениями (3.1)-(3.21) и (4.4) суще-

ствует, а оптимальное значение критерия равно τ^∗. Возможен случай, ко-

гда решение задачи (4.3) с ограничениями (3.1)-(3.21), (4.4) неединственно.

В этой связи выберем наибольшее по длительности “технологическое окно”,

при котором суммарное время движения составит τ^∗, а суммарное время на-

хождения на железнодорожной сети составит T^∗. Для этого нужно решить

задачу

(4.5)

t₂ - t₁ →

max

t₁,t₂,δ_i,j,k,δi,j,k,γk′,æk′,i=1,I,j=1,J,k=1,K,k^′∈Z^′

с ограничениями (3.1)-(3.21), (4.4) и

∑

(4.6)

δ_i,j,k(t^конk - t^начk) = τ^∗.

i=1 j=1 k=1

5. Пример

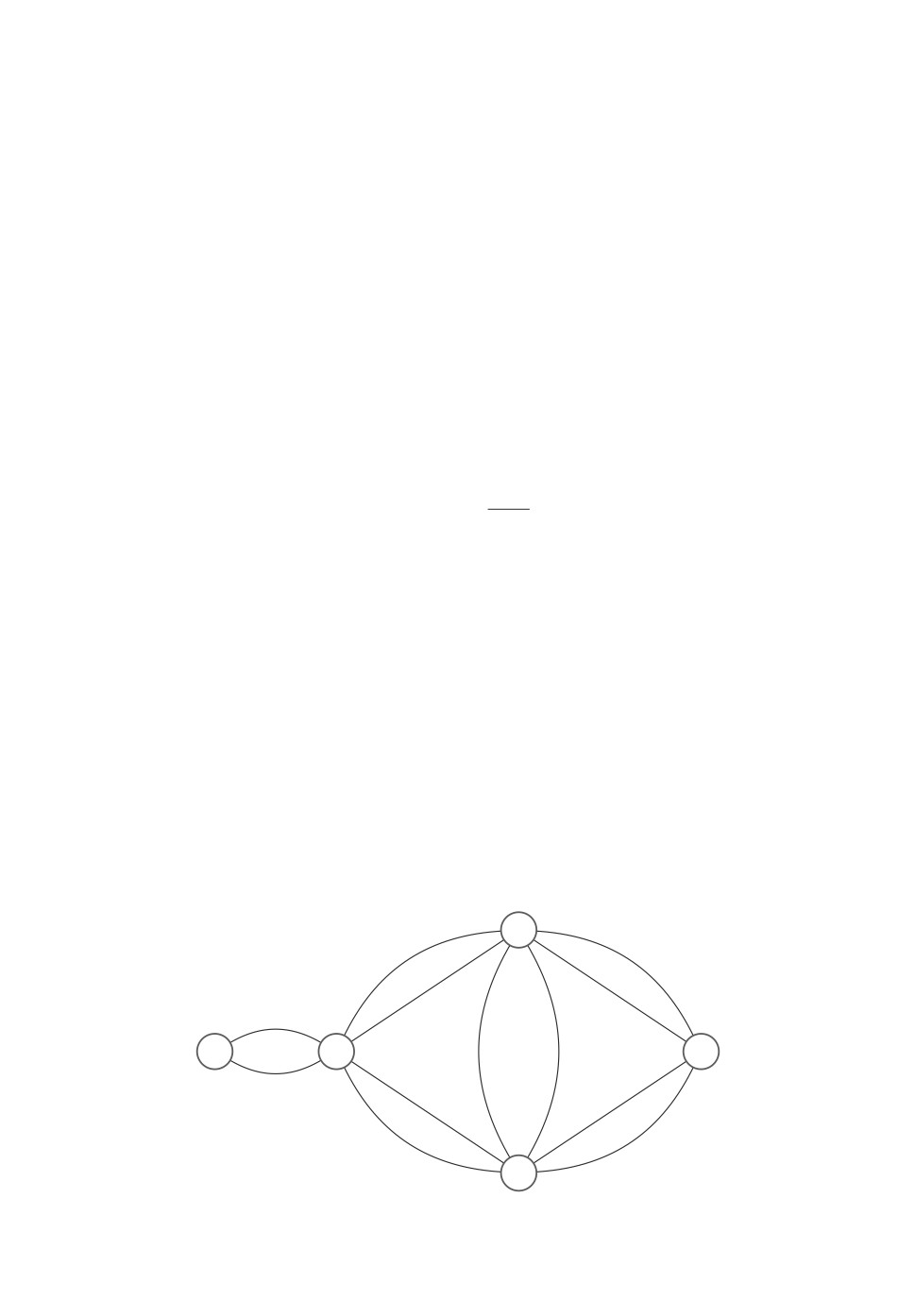
Рассмотрим модельный пример. Пусть мультиграф железнодорожной се-

ти G имеет вид, представленный на рисунке.

Пусть для некоторого дня имеется следующее множество “подниток” Z,

см. табл. 1.

Пусть имеется 12 поездов, которые нужно переместить по железнодорож-

ной сети из пунктов отправления в соответствующие пункты назначения в

рассматриваемые сутки. Данные об этих поездах приведем в табл. 2.

Пусть также t^нач1 = 0, t^кон2 = 1440, t^минст = 0, t^максст = 1440. Такие значения

параметров t^нач1, t^кон2, t^минст, t^максст означают, что “технологическое окно” можно

установить в любое время суток, а остановки на станциях не ограничены по

длительности. Пусть также d_i = 500, i = 1, 12.

Проанализируем маршруты движения в зависимости от различных зна-

чений параметра Δ на основе решения задачи

(4.5) с ограничениями

(3.1)-(3.21),

(4.4),

(4.6) в случае установления

“технологического окна”

на пути № 1 между вершиной с № 4 и вершиной с № 5. Предваритель-

но отметим, что вследствие “технологического окна” могут быть исклю-

чены из маршрутов следования поезда “поднитки” с номерами 37-42, т.е.

Z^′ = {37,38,39,40,41, 42}.

Случай Δ = 0 соответствует задаче составления расписания и маршрутов

движения поездов без учета “технологического окна”, поскольку при Δ = 0

можно положить, к примеру, t₁ = t₂ = 0, и тогда для каждой “поднитки” бу-

дет выполнено æ_k = 1, что приведет к тому, что ограничения (3.20) выро-

дятся в ограничения (3.1). Случай Δ = 1440 соответствует ситуации, когда

рассматриваемый набор ребер/ребро закрывается на сутки. Случаи Δ = 600

и Δ = 1100

промежуточные.

Рисунок.

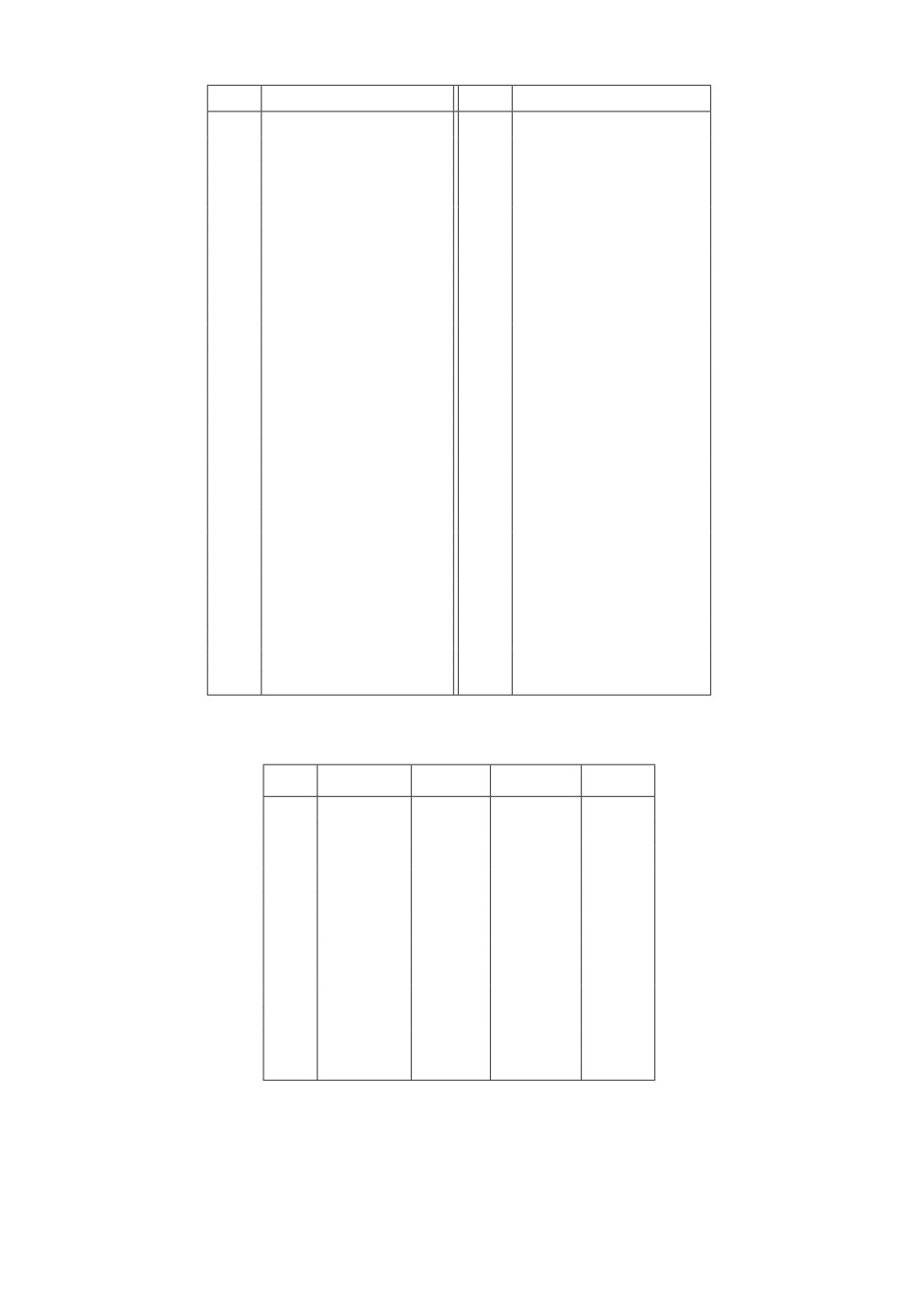
Таблица 1. Множество “подниток” Z

z_k

(1, 2, 1, 480, 500)

(3, 5, 1, 975, 1005)

(1, 2, 1, 730, 750)

(3, 5, 1, 1170, 1200)

(1, 2, 1, 920, 940)

(4, 2, 2, 60, 100)

(1, 2, 1, 1200, 1220)

(4, 2, 2, 340, 380)

(2, 1, 2, 360, 380)

(4, 2, 2, 600, 640)

(2, 1, 2, 690, 710)

(4, 2, 2, 810, 850)

(2, 1, 2, 1035, 1055)

(4, 2, 2, 900, 940)

(2, 3, 1, 300, 340)

(4, 2, 2, 1260, 1300)

(2, 3, 1, 560, 600)

(4, 3, 2, 690, 750)

(2, 3, 1, 1060, 1100)

(4, 3, 2, 930, 990)

(2, 3, 1, 1260, 1300)

(4, 3, 2, 1320, 1380)

(2, 4, 1, 240, 280)

(4, 5, 1, 360, 390)

(2, 4, 1, 670, 710)

(4, 5, 1, 900, 930)

(2, 4, 1, 920, 960)

(4, 5, 1, 1350, 1380)

(2, 4, 1, 1140, 1180)

(4, 5, 1, 1120, 1150)

(2, 4, 1, 1275, 1315

(4, 5, 1, 555, 585)

(3, 2, 2, 120, 160)

(4, 5, 1, 1260, 1290)

(3, 2, 2, 240, 280)

(5, 3, 2, 480, 510)

(3, 2, 2, 720, 760)

(5, 3, 2, 805, 835)

(3, 2, 2, 1320, 1360)

(5, 3, 2, 1030, 1060)

(3, 4, 1, 540, 600)

(5, 3, 2, 1380, 1410)

(3, 4, 1, 1260, 1320)

(5, 4, 2, 360, 390)

(3, 4, 1, 1080, 1140)

(5, 4, 2, 660, 690)

(3, 5, 1, 270, 300)

(5, 4, 2, 860, 890)

(3, 5, 1, 740, 770)

(5, 4, 2, 1200, 1230)

Таблица 2. Информация о поездах

v^{отправi}

v^прибi

t^{отправi}

T_i

720

300

1170

240

910

300

470

480

525

120

180

480

840

650

780

580

840

540

1200

180

1020

120

По результатам численных экспериментов было выяснено, что назначение

“технологического окна” (случай Δ = 600) в сравнении с задачей построения

расписания (случай Δ = 0) приводит к тому, что для поездов №№ 2, 3, 4,

9, 10 меняются используемые “поднитки”. Однако если в случае с поездами

Таблица 3. Оптимальные маршруты (наборы номеров “подниток”) движения поез-

дов для различных значений параметра Δ при J = 5

Δ\i

4,16

1,9,25

12,37

13,38 14,40 24 31,7 43,21,30,6 45,20 49,32 50,33

600

4,16 1,10,27

12,37

9,25

14,40 24 31,7 43,21,30,6 49,32 45,20 50,33

1100 4,16

1,9,26

13,35,27

8,25

14,40 24 31,7 43,21,30,6 49,32 45,20 50,33

1440

Нет решения

Таблица 4. Результаты работы предлагаемого алгоритма

t^∗1

t^∗2

T^∗

390

900

2090

600

390

1120

2470

1100

1120

2915

1440

Нет решения

№№ 9, 10 это связано с тем, что замена используемых “подниток” не влия-

ет на значение критериев (4.1) и (4.3), то в случае поездов №№ 2, 3, 4 это

связано с наличием “технологического окна”, которое, в частности, не позво-

ляет использовать “поднитку” с № 38 (случай Δ = 600) и “поднитки” №№ 37,

38 (случай Δ = 1100). Причем в случае Δ = 1100 поезд № 3 должен допол-

нительно посетить вершину с № 3, что не предполагалось (случай Δ = 0 и

Δ = 600). В случае Δ = 1440 оказывается невозможным найти пути объезда

и исполнить все расписание.

Теперь проанализируем оптимальные значения критерия в задаче (4.5) с

ограничениями (3.1)-(3.21), (4.4), (4.6): время поиска оптимального решения

пакетом CPLEX и оптимальный промежуток времени для назначения “тех-

нологического окна” для различных значений параметра Δ при J = 5.

Как следует из результатов численного эксперимента, ожидаемо с ростом

параметра Δ увеличивается суммарное время нахождения поездов на желез-

нодорожной сети начиная с момента отправления.

Результаты численного эксперимента были получены с помощью матема-

тического пакета ILOG CPLEX на персональном компьютере (Intel Core i5

4690, 3.5 GHz, 8 GB DDR3 RAM).

6. Заключение

В настоящей статье рассмотрена задача назначения “технологического ок-

на” на некоторых участках железнодорожной сети. Железнодорожная сеть

представлялась неориентированным мультиграфом, движение по которому

могло осуществляться только в определенные промежутки времени с ис-

пользованием “подниток”. Оптимизационными переменными являлись время

начала и конца “технологического окна”, а также время и маршруты движе-

ния поездов по железнодорожной сети. Главным критерием являлась мини-

мизация суммарного времени нахождения поездов на железнодорожной сети

с момента начала движения. Задача назначения “технологического окна” бы-

ла сформулирована в виде трех задач смешанного целочисленного линейного

программирования. На примере было показано, что с изменением длительно-

сти “технологического окна” меняются как маршруты движения поездов по

сети, так и оптимальное значение суммарного времени нахождения поездов

на железнодорожной сети с момента начала движения.

СПИСОК ЛИТЕРАТУРЫ

Гайнанов Д.Н., Коныгин А.В., Рассказова В.А. Моделирование грузовых же-

лезнодорожных перевозок методами теории графов и комбинаторной оптимиза-

ции // АиТ. 2016. № 11. С. 60-79.

Gainanov D.N., Konygin A.V., Rasskazova V.A. Modelling Railway Freight Traffic

Using the Methods of Graph Theory and Combinatorial Optimization // Autom.

Remote Control. 2016. V. 77. No. 11. P. 1928-1943.

Cordeau J.-F. Toth P., Vigo D. A Survey of Optimization Models for Train Routing

and Scheduling // Transport. Sci. 1998. V. 32. No. 4. P. 380-404.

Kroon L., Maroti G., et al. Stochastic Improvement of Cyclic Railway Timetables //

Transportation Research Part B: Methodological. 2008. V. 42. No. 6 P. 553-570.

Лазарев А.А., Мусатова Е.Г. Целочисленные постановки задачи формирования

железнодорожных составов и расписания их движения // Управление большими

системами. 2012. № 38. С. 161-169.

Зиндер Я.А., Лазарев А.А. и др. Построение расписаний двухстороннего движе-

ния на однопутной железной дороге с разъездом // АиТ. 2018. № 3. С. 144-166.

Zinder Y., Lazarev A.A., et al. Scheduling the Two-Way Traffic on a Single-Track

Railway with a Siding // Autom. Remote Control. 2018. V. 79. No. 3. P. 506-523.

Босов А.В., Игнатов А.Н., Наумов А.В. Модель передвижения поездов и ма-

невровых локомотивов на железнодорожной станции в приложении к оценке и

анализу вероятности бокового столкновения // Информатика и ее применения.

2018. Т. 12. № 3. C. 107-114.

Ziarati K., Soumis F., et al. Locomotive Assignment with Heterogeneous Consists

at CN North America // Eur. J. Oper. Res. 1997. No. 97. P. 281-292.

Ahuja R. K., Liu J., et al. Solving Real-Life Locomotive-Scheduling Problems //

Transport. Sci. 2005. V. 39. No. 4. P. 503-517.

Буянов М.В., Иванов С.В., Кибзун А.И., Наумов А.В. Развитие математиче-

ской модели управления грузоперевозками на участке железнодорожной сети с

учетом случайных факторов // Информатика и ее применения. 2017. Т. 11. № 4.

С. 85-93.

10.

Буянов М.В., Наумов А.В. Оптимизация функционирования подвижного соста-

ва при организации грузовых перевозок на участке железнодорожной сети //

АиТ. 2018. № 9. С. 143-158.

Buyanov M.V., Naumov A.V. Optimizing the Operation of Rolling Stock in Or-

ganizing Cargo Transportation at a Railway Network Segment // Autom. Remote

Control. 2018. V. 79. No. 9. P. 1661-1672.

11.

Powell W.B., Simao H.P., Bouzaiene-Ayari B. Approximate dynamic programming

in transportation and logistics: a unified framework // EURO J. Transp. Logist.

2012. No. 1. P. 237-284.

12.

Правила технической эксплуатации железных дорог Российской Федерации в

редакции от 09.02.2018.

13.

Albrecht A.R., Panton D.M., Lee D.H. Rescheduling Rail Networks with Mainte-

nance Disruptions Using Problem Space Search // Comput. Oper. Res. 2013. V. 40.

No. 3. P. 703-712.