Автоматика и телемеханика, № 6, 2020
© 2020 г. В.Н. БУРКОВ, д-р техн. наук (vlab17@bk.ru),
И.В. БУРКОВА д-р техн. наук (irbur27@gmail.com)
(Институт проблем управления им. В.А. Трапезникова, Москва),
В.Г. ЗАСКАНОВ, д-р техн. наук (zaskanov@mail.ru)
(Самарский государственный аэрокосмический
университет им. академика С.П. Королева)
МЕТОД СЕТЕВОГО ПРОГРАММИРОВАНИЯ
В ЗАДАЧАХ КАЛЕНДАРНОГО ПЛАНИРОВАНИЯ1
Рассматривается применение метода сетевого программирования к ре-
шению дискретной задачи минимизации стоимости проекта при заданной
продолжительности его реализации. Описаны два базовых алгоритма ре-
шения задачи для случаев независимых и последовательных работ. Более
сложные случаи (сеть типа дерева и агрегируемая сеть) решаются на ос-
нове последовательного применения базовых алгоритмов. Для сети ¾сбор-
ка с комплектующими¿ предлагается метод, который состоит в определе-
нии множества работ, фиксация продолжительности которых приводит к
одному из рассмотренных случаев (либо сеть - дерево, либо - агрегируе-
мая сеть).
Рассматриваются все возможные варианты фиксации продолжитель-
ностей работ выделенного множества и решение задачи для каждого ва-
рианта. Из всех вариантов выбирается лучший. Рассмотрен также случай
произвольного сетевого графика.
Ключевые слова: продолжительность работ, стоимость работ, сетевой гра-
фик дерево, агрегируемая сеть, метод сетевого программирования.
DOI: 10.31857/S0005231020060025
1. Введение
Задачи календарного планирования относятся, как правило, к сложным
(NP-трудным) задачам дискретной оптимизации ([1-8] и др.). В статье рас-
сматривается так называемая задача оптимизации сети по стоимости. Она
заключается в определении стоимости выполнения работ проекта так, что-
бы проект был выполнен за определенное время, а суммарная стоимость
работ была минимальной. При этом для каждой работы имеется конечное
число вариантов ее выполнения, отличающихся величиной стоимости и ве-
личиной продолжительности выполнения. В статье рассматривается случай,
когда для каждой работы имеется два варианта. Однако предложенные ал-
горитмы несложно обобщить и на случаи, когда для каждой работы имеется
более двух вариантов.
1 Работа выполнена при частичной финансовой поддержке Российского фонда фунда-
ментальных исследований (проект № 18-07-01258) и Российского научного фонда (проект
№ 16-19-10609).
17
2. Постановка задачи
Рассмотрим сетевой график, содержащий n работ (работы изображают-
ся вершинами). Обозначим через τi - продолжительность i-й работы. Для
каждой работы i задана величина ∆i возможного сокращения ее продолжи-
тельности и затраты si на это сокращение. Обозначим Tk - продолжитель-
ность проекта (длина критического пути) при продолжительностях работ τi,
T - требуемая продолжительность проекта (Q = Tk - T - требуемое сокра-
щение). Пусть xi = 1, если продолжительность работы i сокращается, xi = 0
в противном случае.
{
}
Задача 1. Определить
xi; i = 1,n
так, чтобы продолжительность про-
екта была не более T , а суммарные затраты на ее уменьшение были мини-
мальными:
∑
(1)
S (x) =
sixi
→ min.
i
Будем рассматривать пять вариантов сетевых графиков.
2.1. Независимые работы
В этом случае задача 1 принимает вид: минимизировать (1) при ограни-
чениях
(2)
xi∆i ≥ τi
− T, i = 1,n.
Задача легко решается. Оптимальное решение имеет вид
{
0, если τi ≤ T,
(3)
xi =
i = 1,n.
1, если τi > T,
Этот алгоритм назовем базовым алгоритмом А. В дальнейшем потребу-
ется его параметрическая реализация, т.е. параметрическая зависимость ми-
нимальных затрат S (Y ) от продолжительности проекта Y , где величина Y
меняется в пределах
(4)
max(τi - ∆i) ≤ Y ≤ maxτi.
i
i
Пример 1. Имеются itcnm работ, данные о которых приведены в табл. 1.
Таблица 1
i
1
2
3
4
5
6
τi
5
9
8
10
6
7
∆i
2
5
4
7
2
3
si
3
7
6
12
4
5
Вычисляем 4 ≤ Y ≤ 10. Таблица вариантов имеет вид табл. 2.
Таблица 2
Вариант
0
1
2
3
4
5
6
Y
10
9
8
7
6
5
4
S (Y )
0
12
19
25
30
34
37
18
2.2. Последовательные работы (сетевой график-путь)
В этом случае ограничение задачи 1 принимает вид
∑
(5)
xi∆i
≥ Q.
i
Этот и последующие случаи решаются методом сетевого программирования,
который будет рассмотрен ниже.
Получение параметрической зависимости S (Y ) для последовательности
работ будем называть базовым алгоритмом В.
2.3. Сетевой график-дерево
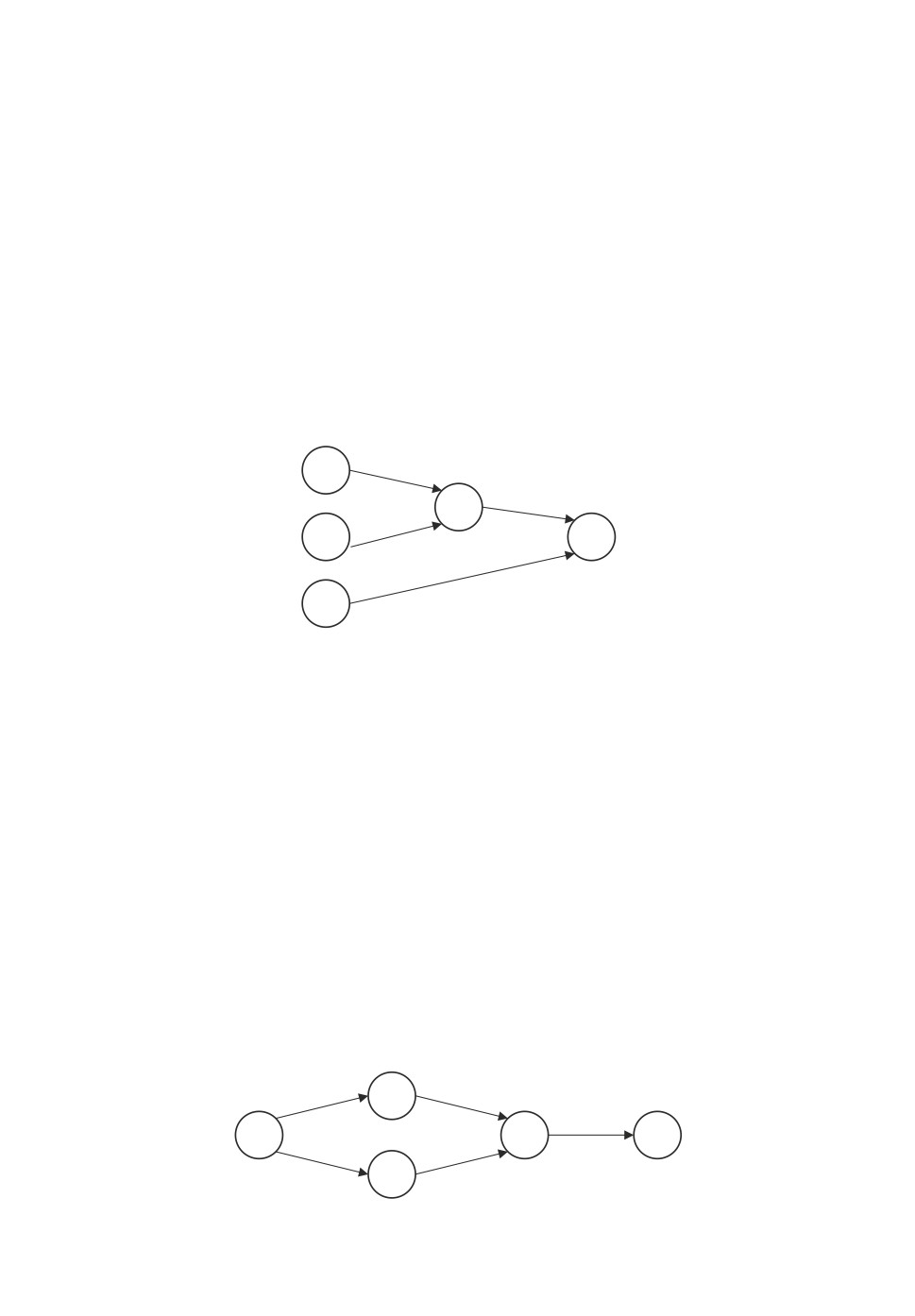
Сетевой график типа дерева, как правило, соответствует процессам сборки
сложных изделий (см. рис. 1), где работы обозначены номерами 1-5.
1
4
2
5
3
Рис. 1.
2.4. Агрегируемый сетевой график
Дадим определения множеств параллельных и последовательных работ.
Определение 1. Параллельными называется множество работ, для
которых множество предшествующих работ одно и то же и множество
последующих работ одно и то же.
Определение 2. Последовательным называется множество работ,
образующих путь такой, что полустепени исхода и захода вершин пути
(за исключением начальной и конечной вершины) равны единице.
Агрегируемым называется сетевой график, который путем замены после-
довательных и (или) параллельных работ одной работой можно свести к од-
ной работе (рис. 2).
2
1
4
5
3
Рис. 2.
19
На рис. 2 две работы 2 и 3 можно заменить одной работой (2, 3) (эти
работы независимые, т.е. параллельные). Затем последовательность работ
1→(2,3)→4→5 можно также заменить одной работой.
2.5. Сетевой график ¾сборка с комплектацией¿
Мы не будем рассматривать общий случай производственного сетевого
графика, а ограничимся сетевым графиком типа ¾сборка с комплектацией¿
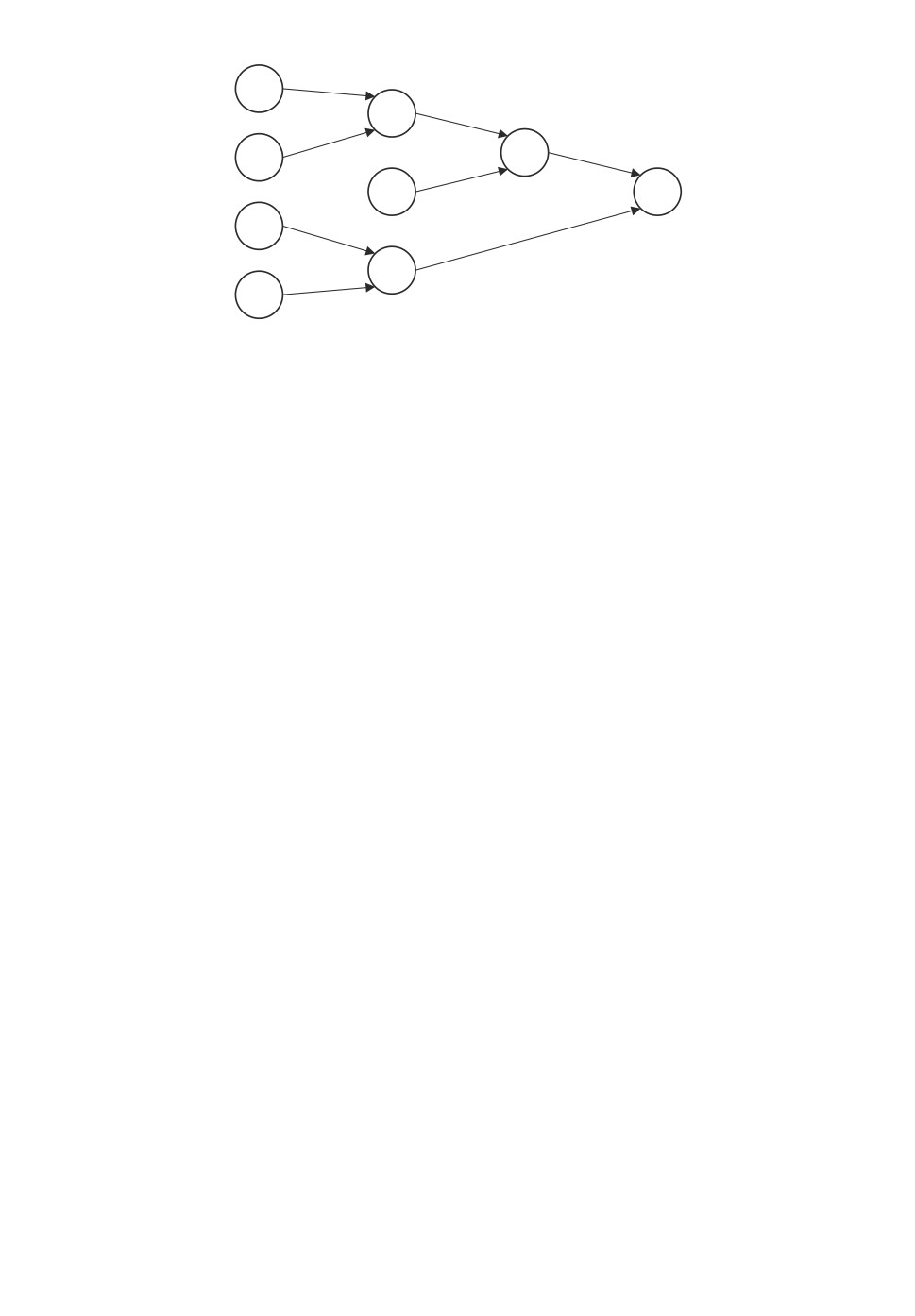
(рис. 3). К дереву сборки добавляются работы 1, 2 и 3, производящие необ-
ходимые комплекты для сборки.
1
4
7
2
5
8
3
6
Рис. 3.
3. Метод сетевого программирования
Суть метода сетевого программирования состоит в том, что целевую функ-
цию и ограничение в задаче календарного планирования можно представить
в виде суперпозиции более простых функций. Такое представление удобно
изображать в виде сети, на нижнем уровне которой находятся вершины, со-
ответствующие переменным (входы сети), промежуточные вершины соответ-
ствуют функциям, входящим в суперпозицию, а конечная вершина (выход)
соответствует исходной функции (сетевое представление).
Метод применим, если и целевая функция, и ограничение имеют одина-
ковые сетевые представления. Если сетевое представление имеет вид дерева,
то метод дает оптимальное решение задачи. В противном случае получаем
верхнюю (нижнюю) оценку, которую можно использовать в методе ветвей и
границ [9]. Метод сетевого программирования подробно изложен в [9]. По-
этому дадим иллюстрацию его работы на примере последовательности работ
(базовый алгоритм B).
Пример 2. Проект состоит из четырех последовательных работ, данные
о которых приведены в табл. 3.
Таблица 3
i
1
2
3
4
τi
5
6
9
8
∆i
2
3
5
4
si
7
8
4
6
20
III
I
II
1
2
3
4
Рис. 4.
Пусть T = 20, Q = 28 - 20 = 8.
Задача имеет вид
7x1 + 8x2 + 4x3 + 6x4 → min
при ограничении
2x1 + 3x2 + 5x3 + 4x4 ≥ 8.
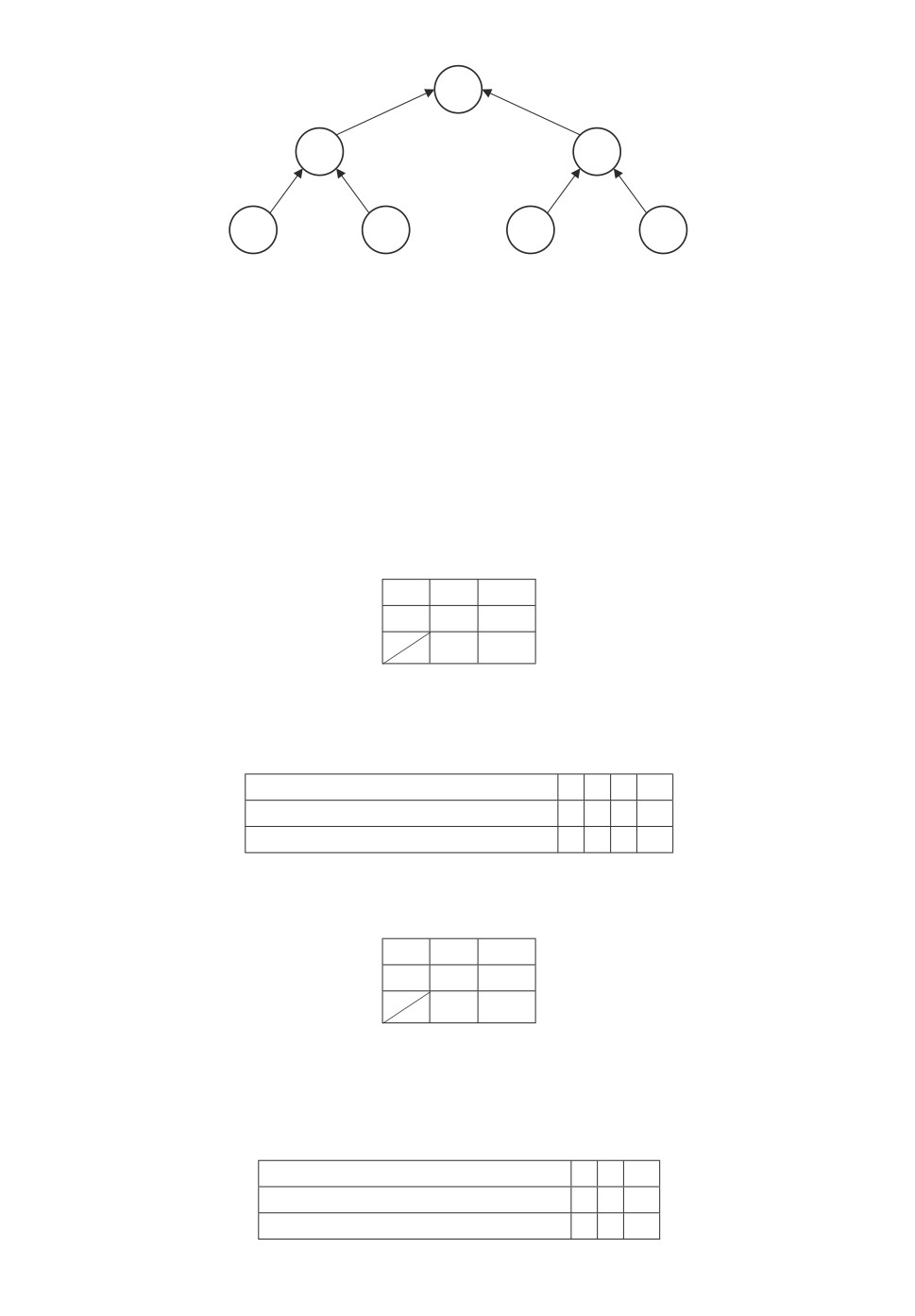
Возьмем структуру сетевого представления, приведенную на рис. 4.
1 шаг. Рассматриваем работы 1 и 2. Решение приведено в табл. 4.
Таблица 4
1
8; 3
15; 5
0
0; 0
7; 2
2
0
1
1
Первое число в клетке - это затраты, а второе - сокращение продолжитель-
ности. Результаты сведены в табл. 5.
Таблица 5. Объединенная работа I
Вариант
0
1
2
3
Затраты
0
7
8
15
Сокращение продолжительности
0
2
3
5
2 шаг. Рассматриваем работы 3 и 4. Решение приведено в табл. 6.
Таблица 6
1
6; 4
10; 9
0
0; 0
4; 5
4
0
1
3
Результат сведены в табл. 7. Вариант 2 (затраты равны 6, сокращение рав-
но 4) исключен, поскольку он доминируется вариантом 1 (затраты равны 4,
сокращение равно 5).
Таблица 7. Объединенная работа II
Вариант
0
1
2
Затраты
0
4
10
Сокращение продолжительности
0
5
9
21
3 шаг. Рассматриваем объединенные работы I и II. Решение приведено в
табл. 8.
Таблица 8
2
10; 9
17; 11
18; 12
25; 14
1
4; 5
11; 7
12; 8
19; 10
0
0; 0
7; 2
8; 3
15; 5
II
0
1
2
3
I
Результаты сведены в табл. 9. В этой таблице варианты упорядочены по
возрастанию затрат. При этом оставлены только Парето-оптимальные вари-
анты (варианты (7; 2), (8 3), (11, 7), (12, 8), (19, 10), (15, 5) исключены).
Таблица 9. Объединенная работа III
Вариант
0
1
2
3
4
5
Затраты
0
4
10
17
18
25
Сокращение продолжительности
0
5
9
11
12
14
В результате получили параметрическую таблицу S (Y ). Для Y ≥ Q = 8
имеем: Y = 9, S (9) = 10, что соответствует сокращению продолжительностей
работ 3 и 4. Фактически рассматривается случай последовательных работ, т.е.
базовый алгоритм B. Далее покажем, как на основе базовых алгоритмов A
и B решать задачу для вариантов ¾сетевой график-дерево¿, ¾агрегируемый
сетевой график¿ и ¾сетевой график ¾сборка с комплектацией¿.
4. Сетевой график-дерево
Если сетевой график является деревом, то сетевое представление также
является деревом. На рис. 5 приведено сетевое представление сетевого гра-
фика, рис. 1. На нижнем уровне расположены вершины, соответствующие
работам. В остальных вершинах указаны базовые алгоритмы A и B, приме-
няемые для решения соответствующих задач.
B
A
B
A
1
2
3
4
5
Рис. 5.
22
Пример 3. Данные о работах приведены в таблице 10.
Таблица 10
i
1
2
3
4
5
τi
6
5
8
6
9
∆i
3
2
4
4
5
si
7
5
6
5
8
Примем T = 13; Q = 21 - 13 = 8.
1 шаг. Рассматриваем работы 1 и 2, применяя базовый алгоритм A. Реше-
ние приведено в табл. 11.
Таблица 11
Вариант
0
1
2
Затраты
0
7
12
Сокращение продолжительности
0
1
3
2 шаг. Рассматриваем объединенную работу (1, 2) и работу 4. Применяем
базовый алгоритм B. Решение приведено в табл. 12.
Таблица 12
Вариант
0
1
2
3
Затраты
0
5
12
7
Сокращение продолжительности
0
4
5
7
3 шаг. Рассматриваем объединенную работу (1, 2, 4) и работу 3. Приме-
няем базовый алгоритм A. Решение приведено в табл. 13.
Таблица 13
Вариант
0
1
2
3
Затраты
0
5
18
23
Сокращение продолжительности
0
4
5
7
4 шаг. Рассматриваем объединенную работу (1, 2, 4, 3) и работу 5. При-
меняем базовый алгоритм B. Решение приведено в табл. 14.
Таблица 14
Вариант
0
1
2
3
Затраты
0
5
8
13
Сокращение продолжительности
0
4
5
9
Множество сокращаемых работ определяется алгоритмом обратного хода
аналогично методу динамического программирования.
Оптимальному решению соответствует вариант 3 с затратами 13. При этом
варианте сокращается продолжительность работ 4 и 5.
23
5. Агрегируемый сетевой график
Агрегируемые сети также имеют сетевое представление в виде дерева.
Пример сетевого представления для агрегируемой сети рис. 2 приведен на
рис. 6. Как и в случае дерева, решение задачи состоит в последовательном
применении базовых алгоритмов AиB согласно структуре сетевого представ-
ления.
B
A
2
3
1
4
5
Рис. 6.
Пример 4. Возьмем данные примера 3 (табл. 10). Примем T = 21; Q =
= 29 - 21 = 8.
1 шаг. Рассматриваем работы 2 и 3, применяя базовый алгоритм A. Реше-
ние приведено в табл. 15.
Таблица 15
Вариант
0
1
2
Затраты
0
5
11
Сокращение продолжительности
0
2
4
2 шаг. Рассматриваем объединенную работу (2, 3) и работы1, 4, 5, приме-
няя базовый алгоритм B.
2.1. Рассматриваем работы (2, 3) и 1. Решение приведено в табл. 16.
Таблица 16
Вариант
0
1
2
3
4
5
Затраты
0
5
7
11
12
18
Сокращение продолжительности
0
2
3
4
5
7
2.2. Рассматриваем объединенную работу (1, 3) и работу 4. Решение при-
ведено в табл. 17.
Таблица 17
Вариант
0
1
2
3
4
Затраты
0
5
10
12
16
Сокращение продолжительности
0
4
6
7
8
24
2.3. Рассматриваем объединенную работу (1, 4) и работу 5. Решение при-
ведено в табл. 18.
Таблица 18
Вариант
0
1
2
3
4
5
Затраты
0
5
8
10
12
13
Сокращение продолжительности
0
4
5
6
7
9
Оптимальное решение определяется вариантом 5 с затратами 13 и сокра-
щением продолжительности на 9. Ему соответствует сокращение продолжи-
тельностей работ 4 и 5.
6. Сетевой график ¾сборка с комплектацией¿
Сетевой график ¾сборка с комплектацией¿ уже не допускает сетевого
представления в виде дерева. Рассмотрим два подхода к решению задачи.
Подход 1
Определим множество вершин G первого слоя таких, что их степени боль-
ше 1 (фиксация продолжительностей соответствующих работ превращает
оставшуюся сеть в сеть типа дерево). Если число вершин множества G рав-
но q, то существует 2q различных вариантов фиксации их продолжительно-
стей. Рассматриваем каждый вариант и решаем задачу для сети типа дере-
во. К затратам полученного решения добавляем затраты работ множества G,
продолжительности которых в рассматриваемом варианте уменьшены.
Пример 5. Рассмотрим сетевой график рис. 3. Заметим, что если зафик-
сировать продолжительность работы 2, то сетевой график превращается в де-
рево с ограничениями на моменты начала работ 4 и 6. Поскольку q = 1, необ-
ходимо рассмотреть два варианта. Данные о работах приведены в табл. 19.
Таблица 19
i
1
2
3
4
5
6
7
8
τi
7
8
4
6
5
9
5
3
si
8
6
3
5
7
7
6
4
∆i
4
3
2
3
2
6
2
1
Вариант 1. Продолжительность работы 2 равна τ2 = 8. В этом случае
работы 4 и 6 не могут начаться раньше 8 единиц времени. Поэтому очевидно,
что x1 = 0 и x3 = 0. Примем Q = 6.
1 шаг. Рассматриваем работы 4 и 5. Применяем базовый алгоритм A. Ре-
шение приведено в табл. 20.
Таблица 20
Вариант
0
1
Затраты
0
5
Сокращение продолжительности
0
3
25
2 шаг. Рассматриваем объединенную работу (4, 5) и работу 7. Применяем
базовый алгоритм B. Решение приведено в табл. 21.
Таблица 21
Вариант
0
1
2
Затраты
0
5
11
Сокращение продолжительности
0
3
5
3 шаг. Рассматриваем объединенную работу (4, 5, 7) и работу 6. Приме-
няем базовый алгоритм A. Решение приведено в табл. 22.
Таблица 22
Вариант
0
1
2
3
Затраты
0
5
12
18
Сокращение продолжительности
0
2
3
5
4 шаг. Рассматриваем объединенную работу (4, 7) и работу 8. Применяем
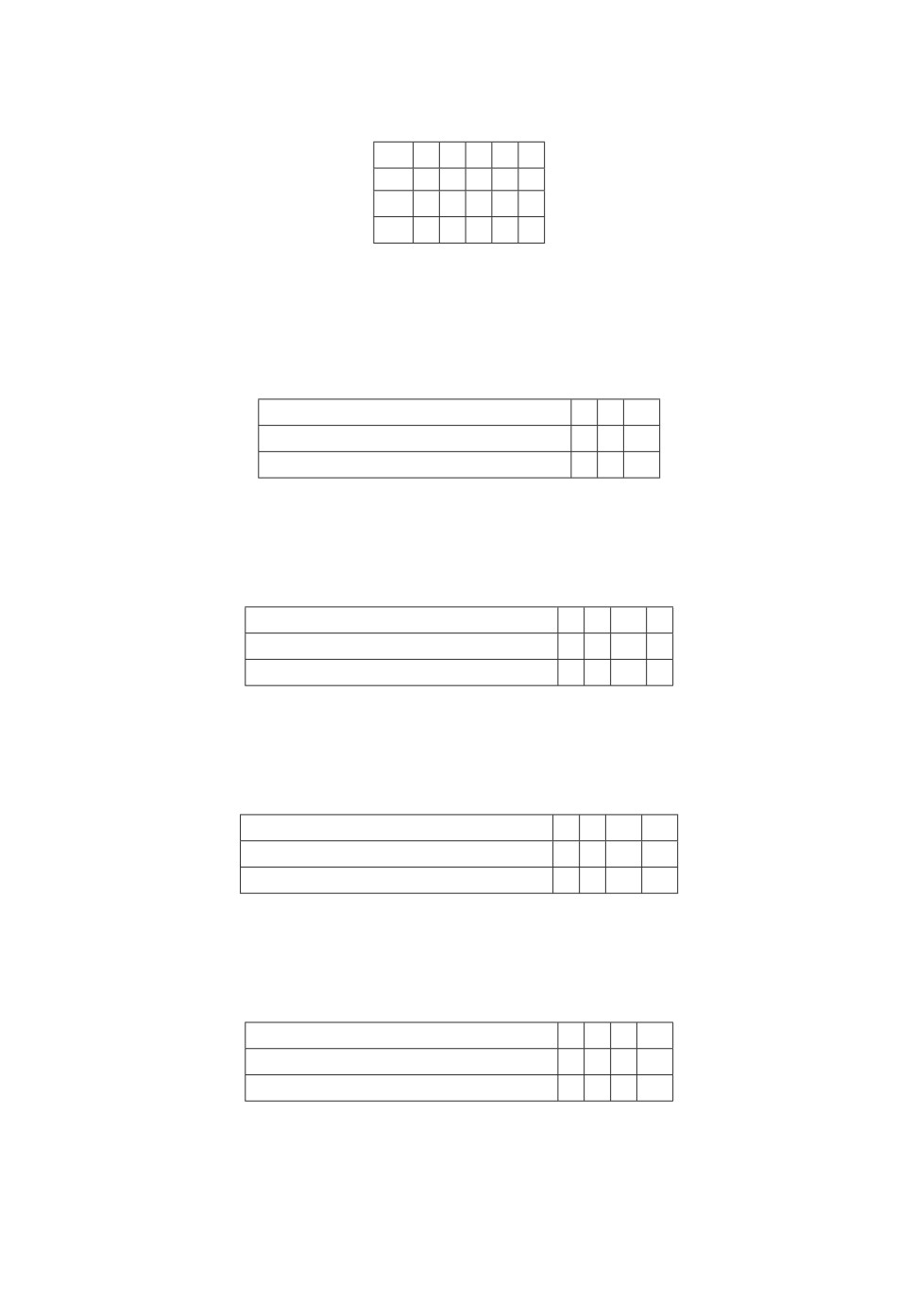
базовый алгоритм B. Решение приведено в табл. 23.
Таблица 23
1
4; 1
9; 3
16; 4
22; 6
0
0; 0
5; 2
12; 3
18; 5
8
0
1
2
3
(4, 7)
Оптимальное решение определяется клеткой (22; 6) с затратами 22. Ему
соответствует уменьшение продолжительности работ 4, 6, 7 и 8.
Вариант 2. Продолжительность работы 2 равна τ2 - ∆2 = 5. В этом слу-
чае работа 6 может начаться не раньше, чем через 5 единиц времени. Поэтому
x3 = 0, так как τ3 = 4. Не будем повторять все шаги последовательного при-
менения базовых алгоритмов, а приведем окончательную табл. 24.
Таблица 24
Вариант
0
1
2
3
4
5
Затраты
0
4
5
9
11
15
Сокращение продолжительности
0
1
3
4
5
6
Оптимальным является вариант 5 с затратами 15. С учетом затрат на
сокращение продолжительности работы 2 получаем 21. Выбираем второй ва-
риант, т.е. сокращаем продолжительности работ 2, 4, 7 и 8.
Подход 2
Разделим затраты si, i ∈ G произвольным образом на столько частей,
сколько работ обеспечивает комплектующими работа i. Без ограничения общ-
ности примем, что число таких работ равно двум для каждой i ∈ G, т.е.
si = vi + ui, i ∈ G.
Фактически как бы произведено разделение вершины i на две вершины, по-
делились соответственно и затраты. При этом сетевой график превратился
в дерево, и можно применить описанный выше алгоритм. Из теории сете-
вого программирования [9] известно, что полученная в результате величина
26
1
4
2
7
5
8
2'
6
3
Рис. 7.
затрат дает нижнюю оценку для исходной задачи. Эту оценку применяем в
методе ветвей и границ.
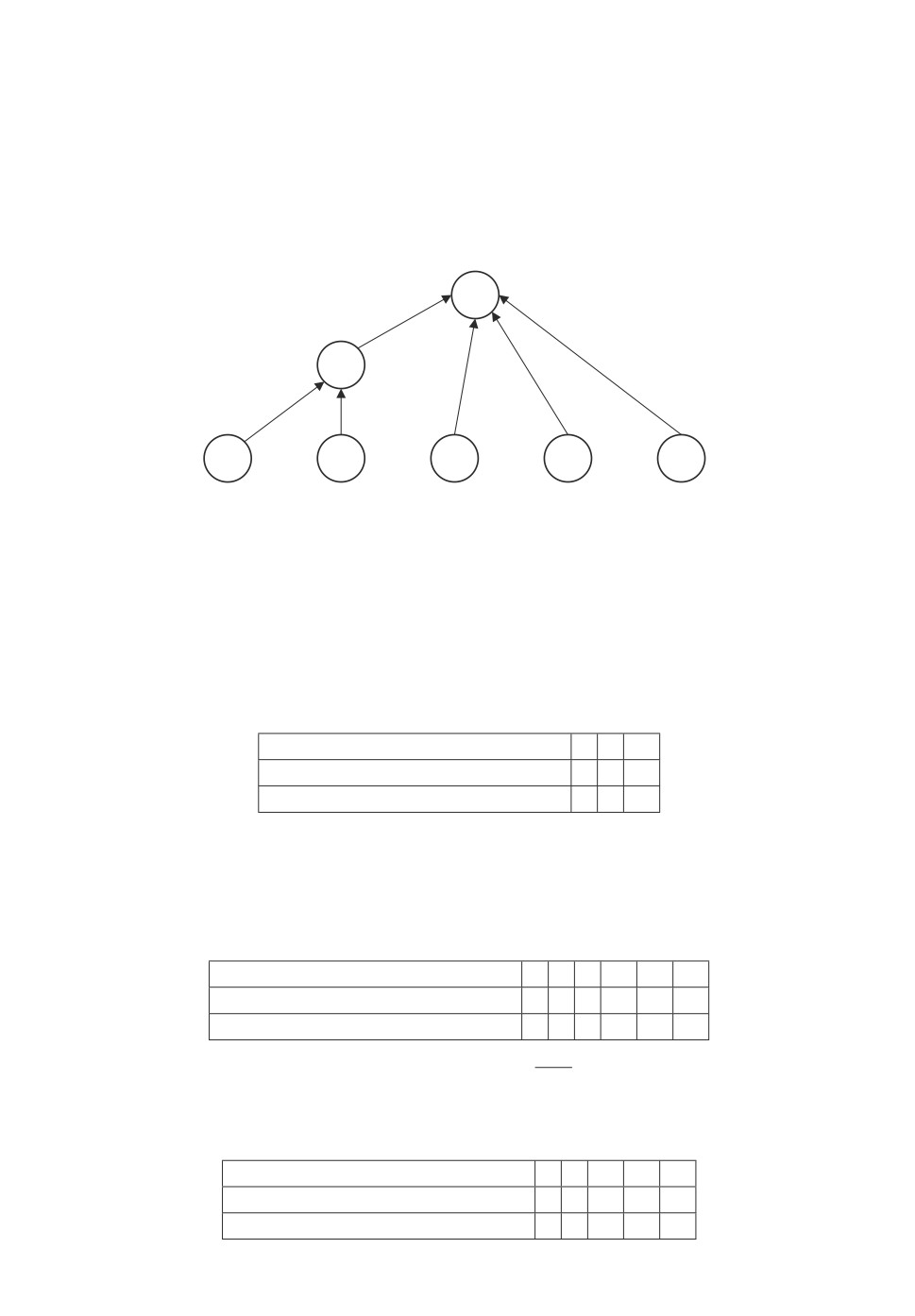
Пример 6. Возьмем данные примера 5 (табл. 19). Пусть u2 = v2 = 3. По-
сле разделения вершины 2 на две вершины получаем дерево, приведенное на
рис. 7.
Теперь можно применить алгоритм для дерева. Получаем оптимальное
решение с затратами 18. Сокращаются работы 2′, 4, 7, 8. Однако работа 2
не сокращается. Поэтому решение является недопустимым для исходной за-
дачи и дает только оценку снизу. Применяем метод ветвей и границ. Делим
множество всех решений на два подмножества. В первом x2 = 1, а во вто-
ром x2 = 0. Выбираем подмножество с лучшей оценкой (в данном случае это
будет оптимальное решение, поскольку всего одна вершина 2 имеет степень
исхода 2). Это решение было получено ранее. Сокращаются работы 2, 4, 7 и 8
с затратами 21.
Нижнюю оценку можно улучшить, изменяя разбиение затрат вершин
множества G. Задача поиска варианта разбиения затрат, максимизирую-
щего нижнюю оценку, называется обобщенной двойственной задачей [9].
Однако решение обобщенной двойственной задачи требует затрат време-
ни. По-видимому, рациональной является смешанная стратегия, когда после
нескольких шагов улучшения нижней оценки производится ветвление, затем
снова несколько шагов улучшения и т.д.
Вычислительная сложность описанных алгоритмов определяется вычис-
лительной сложностью базового алгоритма В, которая равна O(nQ2) при це-
лочисленных значениях временных параметров.
Данная оценка не относится к задаче сборки с комплектацией, для которой
вычислительная сложность равна O(2qnQ2).
Оценка вычислительной сложности метода ветвей и границ требует экс-
периментальных исследований.
7. Заключение
Предложенный способ решения задач календарного планирования, осно-
ванный на методе сетевого программирования, позволяет использовать про-
стые алгоритмы, легко поддающиеся программной реализации. При сетевой
27
структуре типа дерева получается точное решение задачи, а в общем случае -
верхняя или нижняя оценка для использования в методе ветвей и границ.
СПИСОК ЛИТЕРАТУРЫ
1. Бурков В.Н., Ланда Б.Д., Ловецкий С.Е. и др. Сетевые модели и задачи управ-
ления. М.: Сов. радио, 1967.
2. Баркалов С.А., Буркова И.В., Воропаев В.И. и др.; под ред. В.Н. Буркова. Ма-
тематические основы управления проектами. М.: Высш. школа, 2005.
3. Andres C., Hatami S. Evolutionary heuristics and an algorithm for the two-stage as-
sembly scheduling problem to minimize makespan with setup times // Int. J. Prod-
uct. Res.2011. No. 44. P. 4713-4735.
4. Allaoui H., Artiba A. Johnson’s algorithm: a kay to solve optimally or approxi-
mately flow shop scheduling problems with unavailability periods // Int. J. Product.
Econom. 2009. No. 121. P. 81-87.
5. Chenkong V., Haimes Y.Y. The tree stage assembly permutation flowshopscheduling
problem // Proc. 5th Int. Conf. on Industrial Engineer. and Industrial Management,
Cartagena. September 7-9. 2011.
6. Demeulemeester E.L., Herroelen W. Project scheduling: a research handbook.
Kluwer Academ. Publisherr, 1976. 710p.
7. Garey M.R. The complexity of flowshop and jobshopscheduling // Math. Oper. Res.
1976. No. 1(2). P. 117-129.
8. Sun Y., Zhang C.Y., Gao L., Wang X.J. Multy-objactive optimization algorithms
for flow shop scheduling problem: a review and prospects // Int. J. Advanced Man-
ufactur. Technol. 2011. No. 55. P. 723-739.
9. Буркова И.В. Метод сетевого программирования в задачах нелинейной оптими-
зации // АиТ. 2009. № 10. С. 15-21.
Burkov I.V. A Method of Network Programming in Problems of Nonlinear Opti-
mization // Autom. Remote Control. 2009. V. 70. No. 10. P. 1606-1613.
Статья представлена к публикации членом редколлегии А.А. Лазаревым.
Поступила в редакцию 10.07.2019
После доработки 22.10.2019
Принята к публикации 28.11.2019
28