Автоматика и телемеханика, № 6, 2020
Робастное, адаптивное и сетевое
управление
© 2020 г. А.А. ГАЛЯЕВ, чл.-корр. РАН (galaev@ipu.ru),
П.В. ЛЫСЕНКО (pashlys@yandex.ru),
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
СИНХРОНИЗАЦИЯ И КОЛЛЕКТИВНОЕ ДВИЖЕНИЕ ГРУППЫ
СЛАБО СВЯЗАННЫХ ИДЕНТИЧНЫХ ОСЦИЛЛЯТОРОВ1
Изучаются явления синхронизации большого количества слабо связан-
ных осцилляторов при наличии диссипативных связей. Эти связи учиты-
ваются в уравнениях динамики системы в форме диффузионных мат-
риц и обеспечивают ассимптотически устойчивые колебания ансамбля
как единого целого. В качестве примеров рассмотрены три типа взаимо-
действия осцилляторов: “каждый с каждым”, “с ближайшими соседями”
и “кольцевое с ближайшими соседями”.
Ключевые слова: линейные системы, синхронизация, слабо связанные ос-
цилляторы, мультиагентные системы.
DOI: 10.31857/S0005231020060050
1. Введение
Синхронизация процессов приведение двух или нескольких процессов к
такому их протеканию, когда определенные стадии разных процессов совер-
шаются в определенном порядке или одновременно. Синхронизация возни-
кает в тех случаях, когда параллельно протекающим процессам необходимо
взаимодействовать. Синхронизация колебательных систем давно извест-
ный человечеству феномен, широко распространенный в биологии, технике
и обществе. Механические часы и метрономы, лазеры, стрекочущие сверчки,
клетки сердца, аплодирующие зрители лишь некоторые примеры систем,
проявляющих тенденцию к синхронному поведению. Оказалось, что эти и
многие другие случаи могут быть объединены и объяснены в рамках единой
теории.
Христиан Гюйгенс был первым исследователем, описавшим явление син-
хронизации еще в XVII в. Во время морских испытаний механических маят-
никовых часов он заметил, что, будучи подвешенными на общей опоре, часы
рано или поздно начинают двигаться так, что их фазы становятся строго
противоположны друг другу: в тот момент, когда один маятник отклонен
максимально влево, другой отклонен строго вправо. К такому движению ма-
ятники приходили вне зависимости от разницы их начальных фаз. Назвав
1 Работа выполнена при частичной финансовой поддержке Программы Президиума
РАН № 7.
62
открытое явление “симпатией часов”, Гюйгенс дал ему качественное объяс-
нение, правильно указав на причину такого поведения связь двух часов
через общую опору, балку.
С тех пор это явление, получив название синхронизации, было открыто во
всех областях науки и техники от акустики до биологии. Ярким примером
являются колебания свечения светлячков на берегах реки Амазонки. Изна-
чально “переключаясь” хаотически, светлячки каким-то образом чувствуют
друг друга, начиная, подобно хлопающим в унисон аплодирующим зрителям
после концерта, зажигаться и гаснуть синфазно, производя впечатление еди-
ного живого организма. Другие примеры синхронизации в биологических си-
стемах могут быть найдены, например, в [1]. Будем понимать синхронизацию
как подстройку ритмов осциллирующих объектов за счет слабого взаимодей-
ствия между ними [2]. При этом важно, чтобы осцилляции каждого объекта
были самоподдерживающимися, т.е. происходили бы без внешнего источни-
ка. Взаимодействие осцилляторов определяется степенью связи между ними.
Уже приведенный случай взаимодействия механических часов посредством
опоры обусловлен слабой связью. В публикациях синхронизацией в общем
случае называется совпадение частот осцилляторов. Установившиеся фазы
при этом ведут себя двояко, в системе наблюдается либо синфазное, либо про-
тивофазное движение. В первом случае фазы объектов совпадают (или почти
совпадают), а во втором отличаются на π. Первой моделью синхронизации
следует считать модель Артура Уинфри, датируемую 60-ми годами XX в.
Он стремился описать коллективную синхронизацию в больших группах ос-
циллирующих объектов, исходя из того, что все объекты почти идентичны и
связь между ними является слабой. В его модели фаза каждого осциллятора
зависит от суммарного воздействия остальных объектов группы:
∑
˙θi = ωi +
X(θj ) Z(θi), i = 1, . . . , N,
j=1, j=i
где θi
фаза i-го осциллятора, ωi собственная частота i-го осциллятора,
N количество осцилляторов. Чувствительность осциллятора к коллектив-
ному движению характеризуется функцией Z, а его собственный вклад в
общее движение функцией X.
Уинфри исследовал эту модель с помощью компьютерного моделирова-
ния и аналитических приближений. Он сделал ряд качественных выводов
о возможностях синхронизации в зависимости от силы связи между объек-
тами и распределения частот объектов. В дальнейшем Йошики Курамото
заинтересовался результатами Уинфри и начал работать над коллективной
синхронизацией начиная с 1975 г. Исходя из тех же положений, что и его
предшественник, он упростил модель и показал, что поведение систем может
быть описано моделью
∑
θi = ωi +
Гij (θj - θi), i = 1, . . . , N,
j=1
где функция Гij определяет связь между осцилляторами i и j.
63
Впоследствии это выражение приобрело вид
∑
sin(θj - θi), i = 1, . . . , N,
N
j=1
где коэффициент K характеризует силу связи между осцилляторами, став
общеизвестной моделью Курамото, которая заняла доминирующее положе-
ние в области работ по синхронизации. Несмотря на кажущуюся простоту
идеи, стоящей за этой моделью, она представляет большой интерес и ее ис-
следованию и численным экспериментам посвящено множество публикаций
(см. [2, 3]). Как видим, связь осцилляторов в данной модели является нели-
нейной, тогда как линейным моделям в контексте синхронизации в публи-
кациях уделялось меньшее внимание. Они упоминаются, например, в [2, 4].
В [5-7] рассмотрены колебания в системе осцилляторов под действием упру-
гих сил связи и описан известный эффект перекачки энергии между осцил-
ляторами, а также гашение колебаний в случае наличия диссипативной вяз-
коупругой связи между осцилляторами и при взаимодействии с жестко за-
крепленной средой.
В последние годы данное направление науки активно развивается как тео-
рия мультиагентных систем. Синхронизация линейных систем второго поряд-
ка рассматривается в [8, 9] с приложением к механическим системам и энер-
гетическим сетям, в которых также известны явления синхронизации фазы
и уход основной частоты под нагрузкой. Общий критерий устойчивости для
систем такого рода указан в [10]. В рамках сложившейся терминологии син-
хронное движение связанных объектов системы называется консенсусом, а
алгоритмы управления, приводящие систему к такому движению, алгорит-
мами консенсуса. В [8] рассматриваются системы с диффузионно-связанными
объектами. Используя язык матриц Лапласа, лапласовских потоков в графе и
произведение матриц Кронекера, авторы [8] приводят и доказывают теорему
о синхронизации, которая говорит о собственных числах матриц, описываю-
щих динамическую систему. Однако в [8] не приводится качественных оценок
параметров движения объектов, соответствующих разным собственным чис-
лам. Кроме того, основной упор делается на внешнее управление системами
и алгоритмы консенсуса.
В настоящей статье предлагается подход к описанию явления синхрони-
зации в системе линейно связанных идентичных осцилляторов с упругими и
вязкоупругими связями при наличии и отсутствии массивной среды передачи
взаимодействия. Будут рассмотрены взаимодействия осцилляторов “каждый
с каждым”, “с ближайшими соседями” и “кольцевое взаимодействие с бли-
жайшими соседями”. Эти взаимодействия будут описаны при помощи диф-
фузионных матриц, и будет исследована скорость установления консенсуса в
зависимости от устройства этих матриц и, как следствие, их собственных чи-
сел. Для обсуждаемых матриц будут получены результаты, которые расши-
ряют и дополняют результаты, известные для классических матриц Тёплица,
представленных, например, в [11].
64
2. Слабое вязкоупругое взаимодействие осцилляторов друг с другом
2.1. Уравнения движения группы синхронных осцилляторов
при наличии слабого вязкоупругого взаимодействия
Рассмотрим систему синхронных осцилляторов, состоящую из N осцилля-
торов одной основной единичной частоты, связанных между собой слабыми
вязкоупругими связями. Пронумеруем все осцилляторы по порядковому но-
меру i, так что i = 1, . . . , N. Пусть xi является координатой i-го осциллятора,
тогда вязкоупругая сила, действующая со стороны всех осцилляторов на i-й,
равна
∑
∑
Fi = - kij (xi - xj ) - 2 αij ( xi - xj),
j=1
j=1
i, j = 1, . . . , N, а kij , αij ≥ 0.
Движение группы осцилляторов описывается системой линейных диффе-
ренциальных уравнений (ЛДУ) следующего вида
∑
∑
(2.1)
xi = -xi - kij(xi - xj) - 2
αij( xi - xj
), i = 1, . . . , N.
j=1
j=1
∑N
∑N
Слабость связи определяется условиями
kij ≪ 1,
αij ≪ 1 для всех
j=1
j=1
i = 1,...,N, взаимность связи
условиями kij = kji, αij = αji для всех
i, j = 1, . . . , N .
Через H обозначим сумму энергий осцилляторов без учета энергии взаи-
модействия их друг с другом, т.е.
∑(
)
1
(2.2)
H =
x2i + x2i
2
i=1
Потенциальная энергия слабого вязкоупругого взаимодействия определяется
выражением
∑
1
(2.3)
U =
kij (xi - xj)2 .
2
i,j=1, i>j
Полная энергия системы равна H + U.
2.2. Преобразование уравнений движения
В тензорных обозначениях, где ведется суммирование по повторяющимся
индексам, система уравнений движения принимает вид
(2.4)
xi(t) = -Eijxj(t) - Kijxj(t) - 2Φij xj
(t),
65
где E единичная матрица. Матрицы K, Φ являются симметрическими,
причем
Φij = αij, Kij = kij при i = j
и
∑
∑
Φii = -
αij, Kii = -
kij.
j=1, i=j
j=1, i=j
В дальнейшем будем исследовать случай, когда Φ = αA, K = βA, где α,
β константы. Тогда уравнение (2.4) примет вид
(2.5)
xi(t) = -Eijxj(t) - βAijxj(t) - 2αAij xj
(t).
3. Основные положения
3.1. Собственные числа системы (2.5)
Справедлива лемма 1.
Лемма 1. Характеристическое уравнение, порожденное системой (2.5),
(3.1)
det(σ2Eij + 2σαAij + Eij + βAij
) = 0,
имеет решения вида
√
(3.2)
σi = -αλi ± i
1+βλi -α2λ2i
,
i = 1,...,N,
где λi собственные числа матрицы A.
Далее, чтобы определить динамику системы (2.5), нужно найти собствен-
ные числа матрицы A.
Лемма 2. Хотя бы одно из собственных чисел матрицы A равно нулю.
3.2. Динамика систем (2.4)-(2.5)
Лемма 3. Для системы ЛДУ вида (2.4) с любыми отличными от три-
виальных начальными условиями существует решение, соответствующее
коллективному периодическому движению центра масс с периодом 2π.
Лемма 4. Если λi > 0 для ∀ i = 2,...,N, а λ1 = 0, то для любого началь-
ного положения системы (2.5) при t → ∞ остается только синхронизованное
коллективное движение.
Леммы 1-4 известны как теорема о синхронизации [8].
Пусть начальное состояние системы (2.5) задается векторами xi(0) = x0i,
xi(0) = x0i. Тогда начальное состояние для коллективного движения задается
∑N
векторами X(0) =
xi(0) = X0,
X(0) =∑Ni=1 xi(0) =
X0.
i=1
66
Энергия системы осцилляторов в начальный момент времени была равна
∑(
)
1
(3.3)
H(0) =
x2i(0) + x2i(0)
2
i=1
На бесконечном горизонте времени все осцилляторы движутся синхронно и
в системе осцилляторов остается энергия, равная начальной энергии коллек-
тивного движения, а именно
∑(
)
(
)
1
1
(3.4)
H∗ =
X2(0) +X2(0) =
X2(0) +X2(0)
2N2
2N
i=1
Соотношение (3.4) может быть переписано в виде
(
)2
(
)2
∑
∑
1
(3.5)
H∗ =
xi(0)
+
xi(0)
.
2N
i=1
i=1
Следствие 1. Из сравнения (3.3) и (3.5) следует, что
H(0) ≥ H∗,
причем знак равенства возможен, только если xi(0) = xj(0), xi(0) = xj(0)
для любых i, j = 1, . . . , N .
Действительно,
∑
∑
1
H(0) - H∗ =
(xi(0) - xj(0))2 +
(xi(0) - xj(0))2 ≥ 0.
2N
i,j=1, i>j
i,j=1, i>j
4. Примеры матриц взаимодействия
4.1. Идентичное взаимодействие осцилляторов каждый с каждым
Предположим, что каждый из осцилляторов взаимодействует с каждым
одинаково, тогда матрица A имеет вид
N-1
-1
-1
-1 ...
-1
-1
-1
−1
N-1
-1
-1 ...
-1
-1
-1
−1
-1
N - 1 -1 ...
-1
-1
-1
(4.1)
A=
-1
-1
-1
-1 ...
-1 N - 1
-1
−1
-1
-1
-1 ...
-1
-1
N -1
Такая матрица A описана в монографии [12] как матрица простой сим-
метричной системы. В [12] исследованы ее собственные числа и указан ис-
следуемый в данной статье случай a = (n - 1)b, перекрестные связи между
осцилляторами в этом случае называются синхронизирующими.
67
xi
a
1,0
0,5
0
-0,5
-1,0
0
5
10
15
20
t
xi
б
1,0
0,5
0
-0,5
-1,0
0
5
10
15
20
t
x1 - x2
в
0
-0,2
-0,4
-0,6
-0,8
0
5
10
15
20
t
H
г
0,178
0,177
0,176
0,175
0,174
0,173
0,172
6
8
10
12
14
16
18
20
t
Рис. 1. Поведение системы осцилляторов.
68
Лемма 5. Матрица A имеет два собственных значения, а именно:
λA = 0 кратности единица и λA = N кратности N - 1.
Согласно леммам 1 и 5 динамика системы (2.5) обуславливается собствен-
√
ными числами σ1,2 = ±i кратности единица и σ3,4 = -αN ± i
1+βN-α2N2
кратности N - 1.
Результат моделирования динамики системы осцилляторов в случае
N = 32 показан на рис. 1.
4.2. Идентичное взаимодействие осцилляторов
с ближайшими соседями
Пусть матрица A имеет вид
1
-1
0
0
0
0
0
−1
2
-1
0
0
0
0
0
-1
2
-1 ...
0
0
0
(4.2)
A=
.
0
0
0
0
-1
2
-1
0
0
0
0
0
-1
1
Вместо матрицы A подвергнем исследованию матрицу B = 2E - A, кото-
рую выпишем в явном виде
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
0
1
0
0
0
(4.3)
B=
.
0000
1
0
1
0
0
0
0
0
1
1
Собственные значения матрицы B находятся по свойству собственных значе-
ний матриц, приведенному в доказательстве леммы 5, а именно λBi = 2 - λi.
Пусть N размер квадратной матрицы B. Обозначим через
GN (λ) = det(B - λE)
характеристические полиномы матрицы B.
Теорема 1. Функции GN(λ) при различных фиксированных N ≥ 3 удо-
влетворяют рекуррентной формуле
GN+1(λ) = -λGN(λ) - GN-1(λ),
(4.4)
G3(λ) = (1 - λ)(λ - 2)(1 + λ),
G2(λ) = λ(λ - 2).
Лемма 6. Члены последовательности (4.4) имеют формулу общего чле-
на вида
(
√
)N
(
√
)N
2-λ
λ2 - 4
-λ -
λ2 - 4
(4.5)
√
-λ+
-
.
GN (λ) =
λ2 - 4
2
2
69
2
1
0
0
20
40
60
80
100
120
Рис. 2. Распределение собственных чисел матрицы A для N = 8.
Проведем сравнение полученного результата с результатом в [11, с. 219].
Матрица B - λE похожа на матрицу Тёплица A из [11], за исключени-
ем первого и последнего диагональных элементов. В терминах [11] b = -λ,
a = c = 1, а первый и последний диагональные элементы равны
1 - λ.
Нетрудно видеть, что формула (4.5) аналогична формуле из факта 3.20.7
монографии [11] в случае b2 = 4ac за исключением степени, равной N вместо
N + 1 и дополнительного коэффициента 2 - λ.
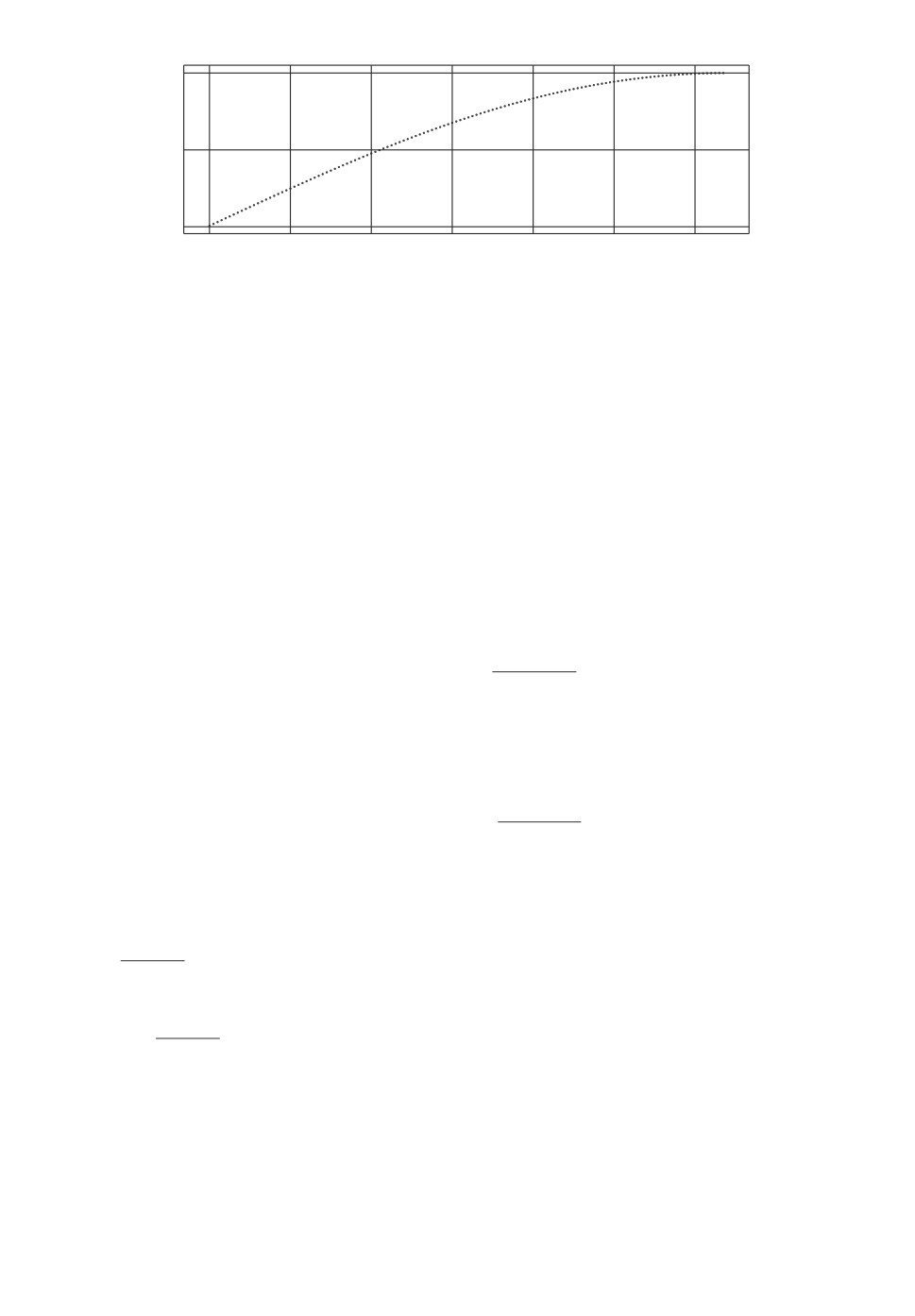
Пример расположения на числовой оси собственных чисел, которые явля-
ются решением уравнения GN (λ) = 0, приведен на рис. 2.
Лемма 7. Пусть матрицы A и B имеют размеры N × N, где N = 2n,
n ≥ 2 и G2n(λ) = det(B - λE). Тогда
)
(G2
(λ)
2n-1
G2n (λ) = G2n-1 (λ) ·
-2
,
(4.6)
G2
(λ)
2n-2
где G21 (λ) = λ(λ - 2), G20 (λ) ≜ λ,
или, что то же самое,
(
)
∏
G2
(λ)
2k-1
G2n (λ) = G21 (λ) ·
-2
,
G2
(λ)
k=2
2k-2
при этом вычисленное по матрице B - λE значение G20 (λ) = 1 - λ и отли-
чается от допущения в формуле (4.6).
Лемма 8. Если λB
собственные числа матрицы B размера 2n-1, то
√
k
±
2 + λBk собственные числа матрицы B размера 2n.
Следствие 2. Если λk√собственныечисламатрицыBразмераN,
то ±
2 + λBk собственные числа матрицы B размера 2N.
Доказательство следствия аналогично доказательству леммы 8.
Рассмотрим свойства собственных чисел матрицы B размера 2n.
Свойство 1. Числа 0 и 2 являются собственными числами матрицы
B размера 2n для всех n ≥ 1.
λB≤2длявсехn≥1иk=1,...,2n.
Свойство 2.
k
70
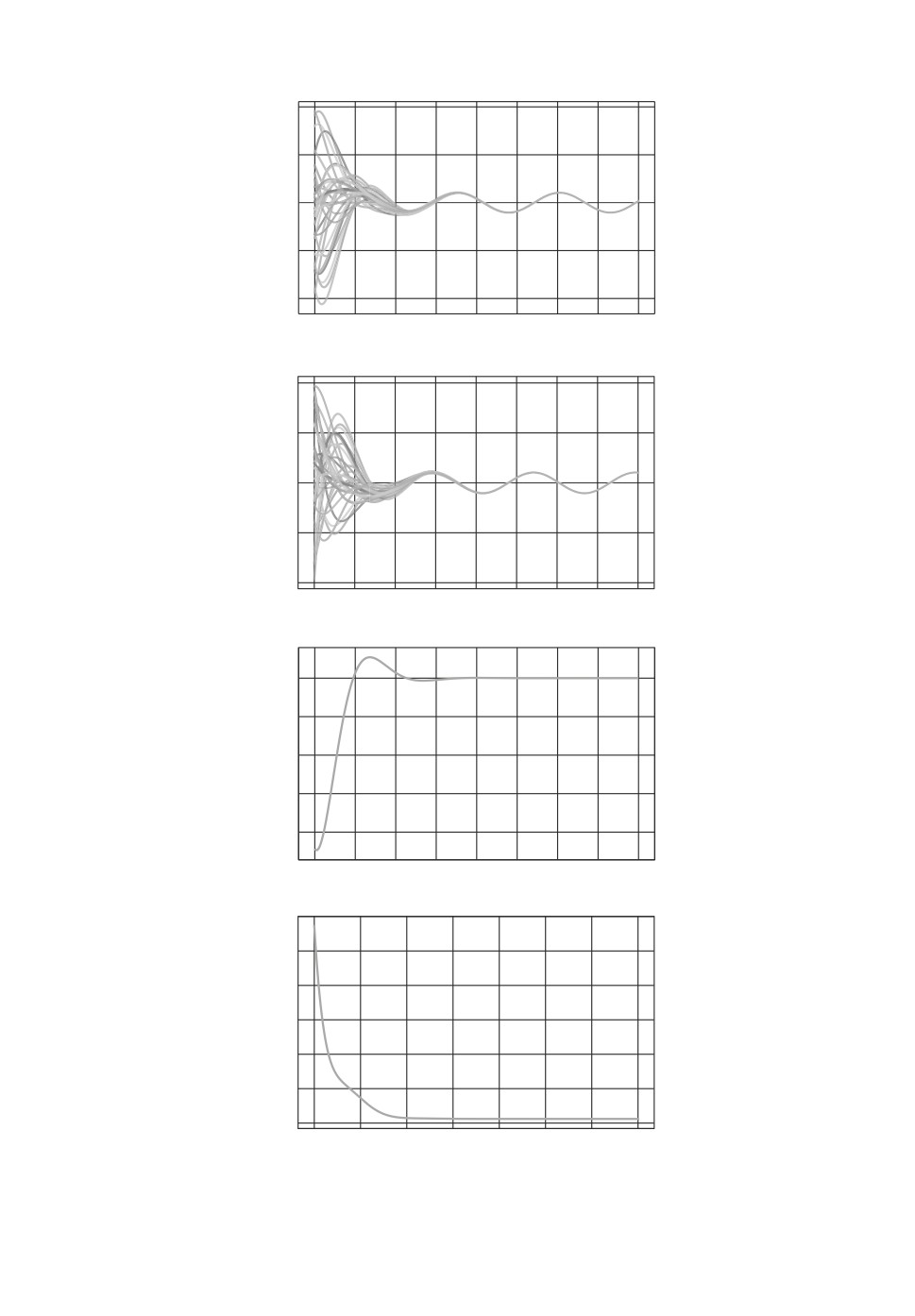
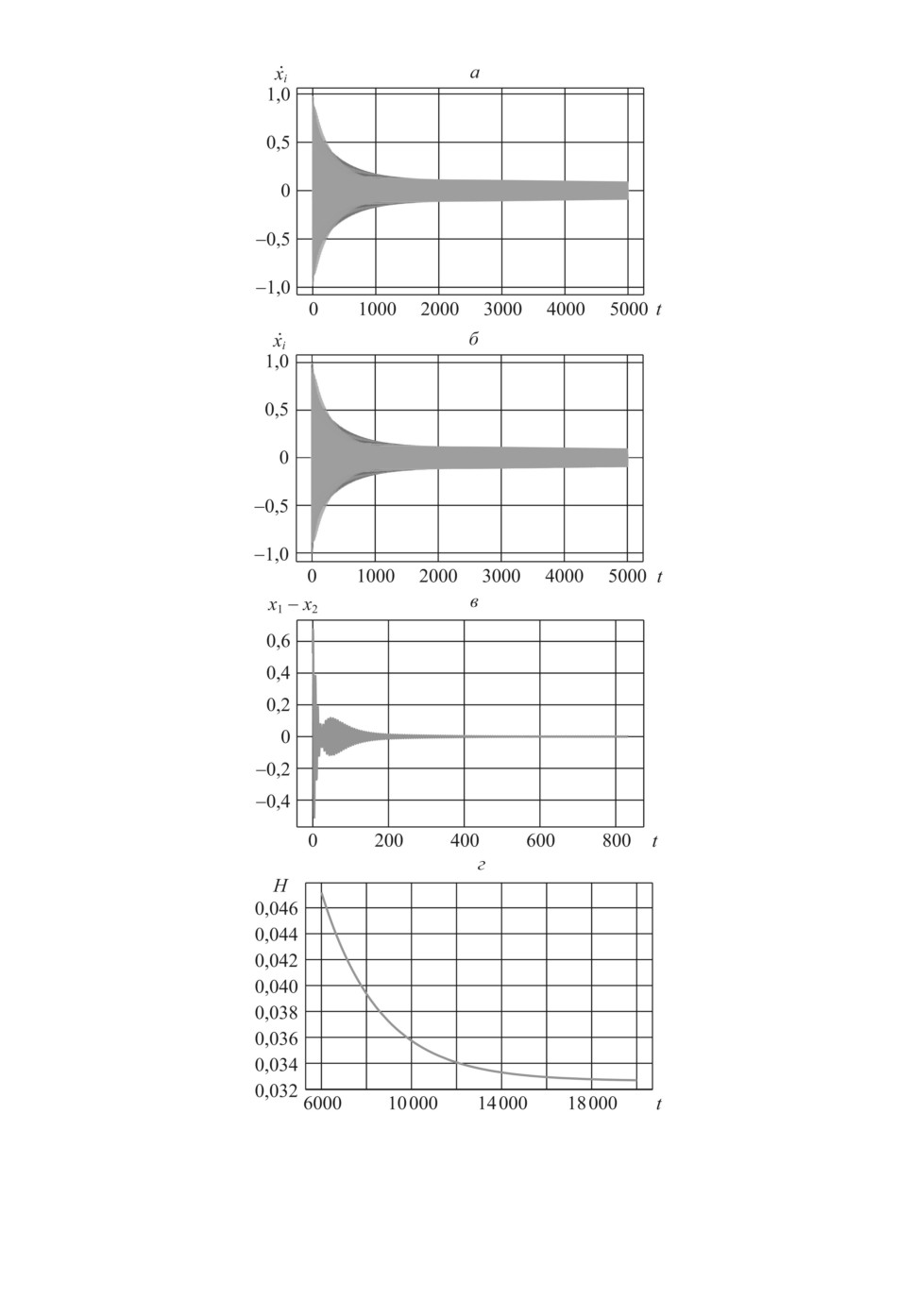
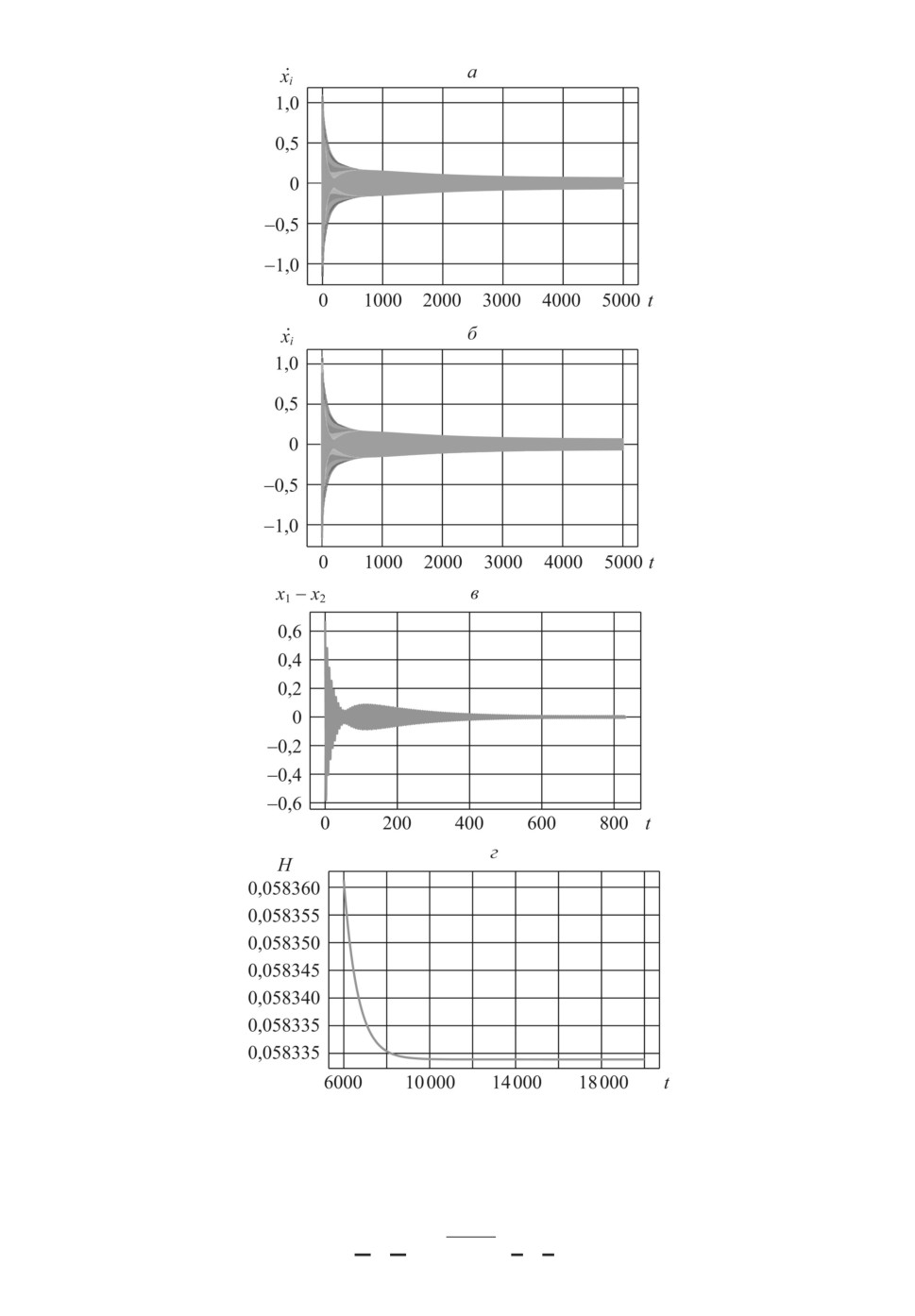
Рис. 3. Поведение системы осцилляторов при взаимодействии с “ближайшими
соседями”.
71
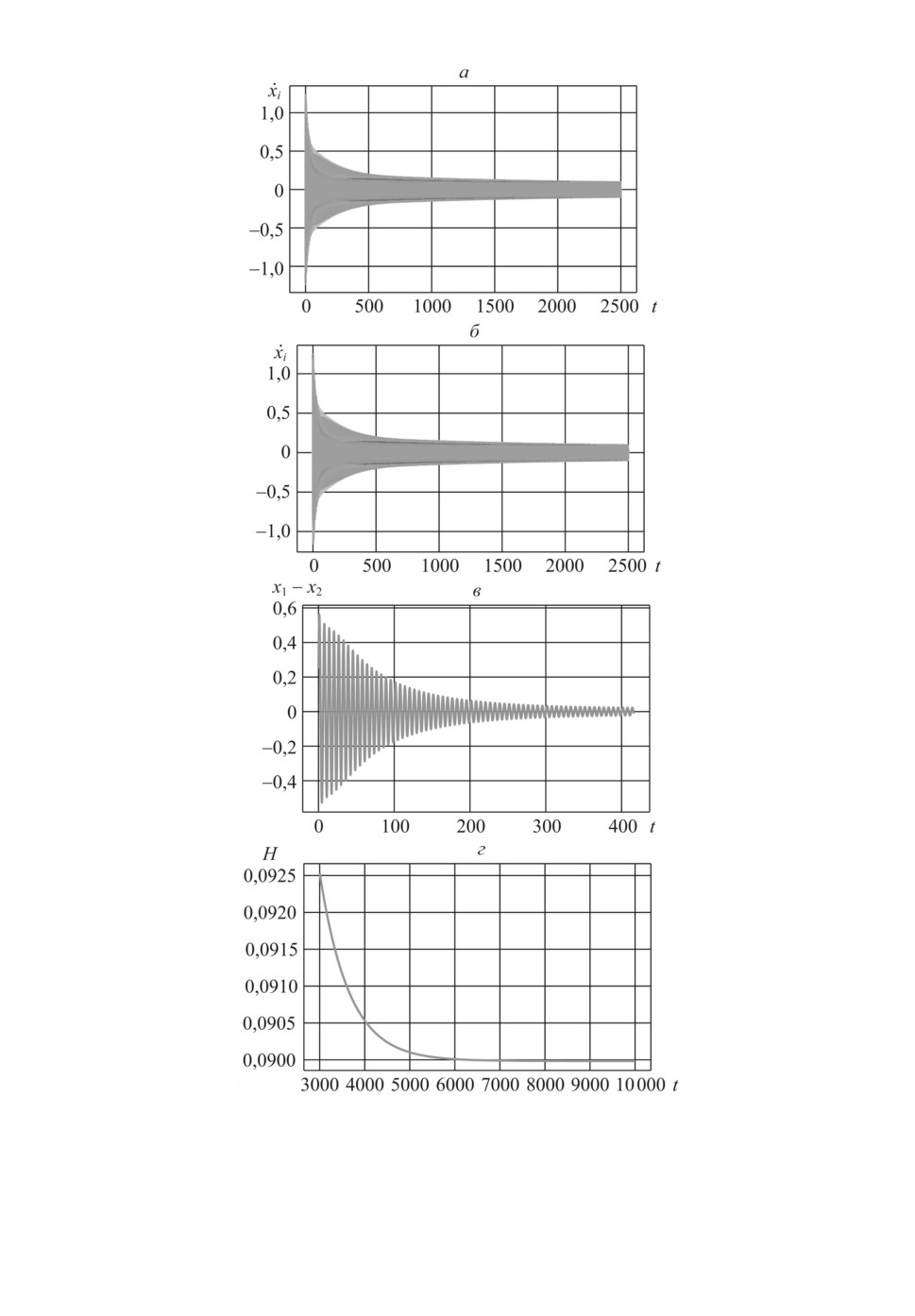
Рис. 4. Поведение системы осцилляторов при взаимодействии с “ближайшими
соседями”.
72
Свойство 3. Среди λBk присутствует собственное значение
√
√
√
(4.7)
λB =
2+
2+...+
2
|
{z
}
n-1
Свойство 1 следует из леммы 7, так как корни уравнения G21 (λ) = 0 яв-
ляются общими для всех многочленов G2n (λ) и всех n ≥ 1.
Свойство 2 следует из вида собственных чисел, представленных в лемме 8,
и свойства функции квадратного корня.
Свойство 3 справедливо, если в лемме 8 выбирать только знак “плюс” при
вычислении собственных чисел начиная с λB1 = 0.
Свойство 2 означает, что у исходной матрицы A все λi > 0 кроме един-
ственного собственного значения, отвечающего за коллективное движение
системы как единого целого. Выбрав собственное число матрицы B из свой-
ства 3, получим, что у матрицы A размера 2n есть собственное число, равное
√
√
√
(4.8)
λA(n) = 2 -
2+
2+...+
2
|
{z
}
n-1
Поскольку λA близко к нулю, то в системе, помимо коллективного движения
с единичной частотой, будет присутствовать слабо затухающее движение с
частотой примерно 1 +βλA2.
Следствие 3. Для λA(n) выполняется предельное соотношение
λA(n)
lim
= 4.
n→∞ λA(n + 1)
Следствие 3 означает, что для больших n скорость затухания осцилляций
моды колебаний, наиболее близкой к основной частоте равной единице, или
скорость установления консенсуса, при увеличении размерности системы в 2
раза уменьшается в 4 раза.
Результат моделирования в случае N = 32 для двух наборов начальных
условий показан на рис. 3 и 4.
4.3. Идентичное кольцевое взаимодействие осцилляторов
с ближайшими соседями
Матрица A имеет вид
2
-1
0
0
0
0
-1
−1
2
-1
0
0
0
0
0
-1
2
-1 ...
0
0
0
(4.9)
A=
.
0
0
0
0
-1
2
-1
−1
0
0
0
0
-1
2
73
Как и в подразделе 4.2, вместо матрицы A будем исследовать матрицу
B = 2E - A, которая имеет вид
0
1
0
0
0
0
1
1
0
1
0
0
0
0
0
1
0
1
0
0
0
(4.10)
B=
.
0000
1
0
1
1
0
0
0
0
1
0
Стоит отметить, что исследуемая матрица A по сути является матрицей
Лапласа в терминах теории мультиагентных систем и теории сетей [8, 11], так
как матрица 2E это степенная матрица D для графа с матрицей смежно-
сти B, соответствующего исследуемой системе.
Собственные значения матрицы B находятся по свойству собственных зна-
чений матриц, приведенному в доказательстве леммы 5, а именно λBi = 2 - λi.
Для характеристических полиномов матрицы B справедлива теорема 2.
Теорема 2. Функции GN(λ) при различных фиксированных N ≥ 5 удо-
влетворяют рекуррентной формуле
GN+1(λ) = -(1 + λ)GN (λ) - (1 + λ)GN-1(λ) - GN-2(λ),
G5(λ) = -λ5 + 5λ3 - 5λ + 2,
(4.11)
G4(λ) = λ4 - 4λ2,
G3(λ) = -λ3 + 3λ + 2.
Выведем формулу общего члена последовательности (4.11).
Лемма 9. Члены последовательности (4.11) имеют формулу общего
члена вида
(
√
)N
(
√
)N
-λ +
λ2 - 4
-λ -
λ2 - 4
(4.12)
GN (λ) =
+
+ 2 · (-1)N+1.
2
2
Лемма 10. Если λB
собственные числа матрицы B размера 2n-1, то
√
k
±
2 + λBk собственные числа матрицы B размера 2n.
Следствие 4. Если λk√собственныечисламатрицыBразмераN,
то ±
2 + λBk собственные числа матрицы B размера 2N.
Доказательство следствия аналогично доказательству леммы 10.
Лемма 11. Если λBk
собственные числа матрицы B размера N ви-
да (4.3) (отсутствие кольцевого взаимодействия между ближайшими со-
седями), являющиеся нулями GN (λ) вида (4.5), то λBk собственные числа
кратности два матрицы B размерности 2N вида (4.10) (наличие кольце-
вого взаимодействия между ближайшими соседями), являющиеся нулями
74
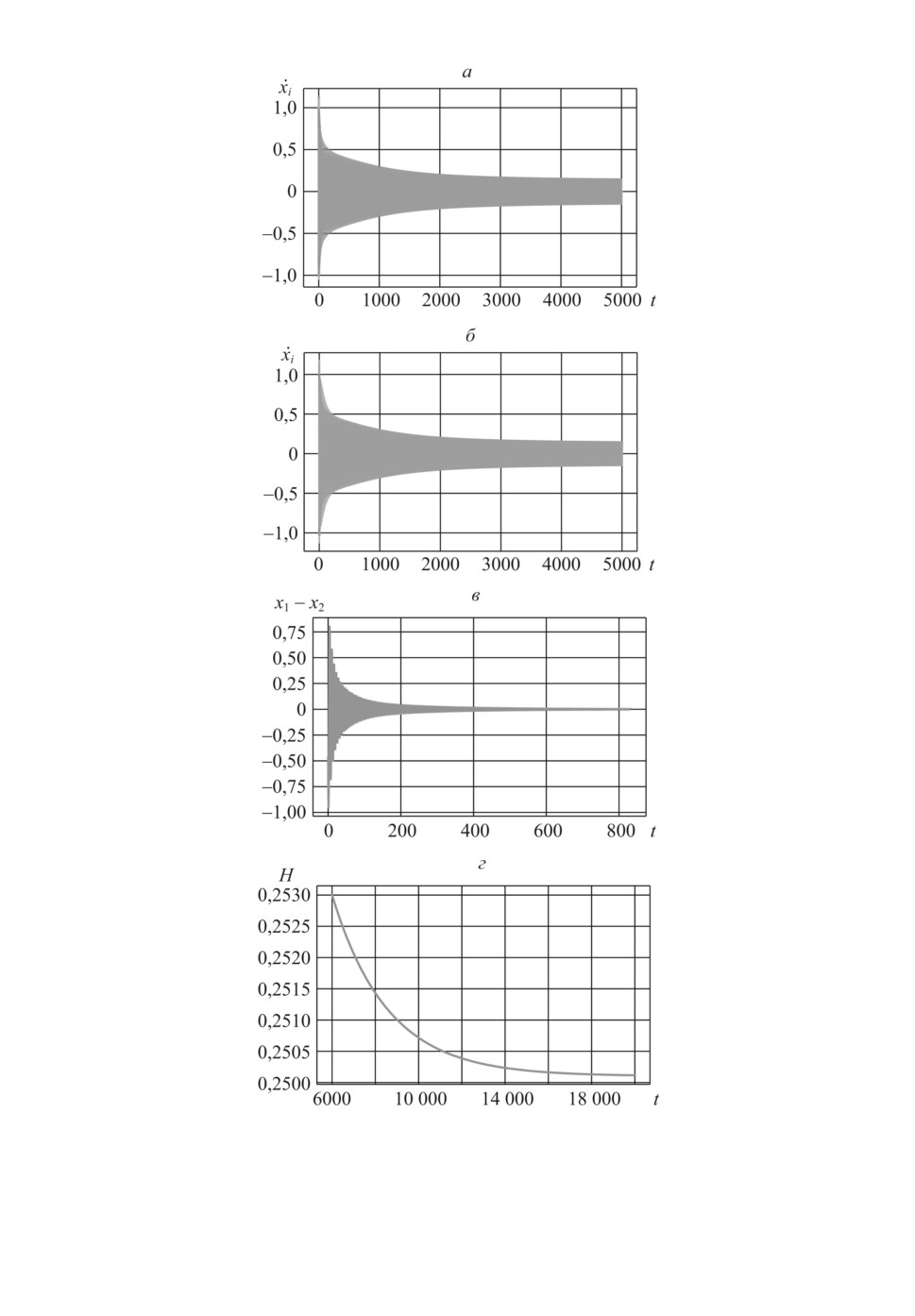
Рис. 5. Поведение системы осцилляторов при кольцевом взаимодействии с
“ближайшими соседями”.
G2N (λ) вида (4.12), кроме λB = ±2 кратности единица, т.е.
λ+2
(4.13)
G2N (λ)
=
G2N (λ)
|
{z
}
2-λ
| {z }
75
(4.12)
(4.5)
Рис. 6. Поведение системы осцилляторов при кольцевом взаимодействии с
“ближайшими соседями”.
Результат моделирования в случае N = 32 для двух наборов начальных
условий показан на рис. 5 и 6.
76
5. Взаимодействие осцилляторов друг с другом и со средой
Добавим в рассматриваемую систему осцилляторов среду и предположим,
что у каждого из осцилляторов есть возможность воздействовать на среду
посредством только упругой связи. Пусть координаты среды имеют индекс 0,
а взаимодействие осуществляется посредством силы Fi0 = -ki0(xi - x0).
Движение группы осцилляторов и среды описывается системой ЛДУ вида:
∑
Mx0 = - k0j(x0 - xj),
j=1
(5.1)
∑
∑
xi = -xi - kij(xi - xj) - 2
αij( xi - xi), i = 1,... ,N.
j=0
j=1
Здесь M безразмерная константа, пропорциональная массе среды. Допол-
нительное условие взаимности связи со средой определяется соотношением
k0j = kj0 = k для всех j = 1,... ,N, остальные условия такие же, как в слу-
чае отсутствия среды.
Лемма 12. В системе
“осцилляторы-среда”, описываемой систе-
мой
(5.1), для любых начальных условий существует периодическое
коллективное движение двух типов с частотами
√
√
1
kM +Nk+M ±
M2k2 +2MNk2 +N2k2 +2M2k-2MNk+M2
(5.2)
ω1,2 =
√
√
2
M
В случае когда k ≪ 1,NkM ≪ 1, эти частоты становятся приблизительно
равными
√
k
Nk
(5.3)
ω1 ≈ 1 +
,
ω2 ≈
2
M
Это означает, что в системе присутствуют колебания осцилляторов как еди-
ного целого с незначительно измененной основной частотой ω1 (ω1-1 =k2 ≪1)
H
2,00
1,75
1,50
1,25
1,00
0,75
0,50
0,25
0
50
100
150
200
250
t
Рис. 7. Энергия системы осцилляторов.
77
и низкочастотные колебания системы с частотой ω2, связанные с массивной
средой. Интересен случай N = M. Оказывается, что при малых k сохраняет-
ся неравенство ω2 ≪ ω1. Пример зависимости H(t) приведен на рис. 7.
6. Обсуждение результатов
На рис. 1, 3, 4, 5 и 6 представлены динамика каждого осциллятора в от-
дельности, динамика разности координат первого и второго осцилляторов,
а также поведение энергии системы (без учета взаимодействия) как функ-
ции времени для трех типов взаимодействия между осцилляторами. Сред-
ствами языка Python моделируется движение каждого из осцилляторов. На-
чальные значения скоростей и координат выбраны произвольным образом в
диапазоне [0, 1], α = 0,02, β = 0,01. На рис. 5 и 6 темпы установления коллек-
тивного движения соответствуют отличному от нулевого минимальному по√
√
√
модулю собственному значению матрицы A, λ = 2 -
2+
2+
2 и равны
2αλ = 0,001536. На рис. 3 и 4 темпы установления коллективного движения
в четыре раза меньше и равны 0,000384, что согласуется со следствием 3. На
рис. 1, 3, 4, 5 и 6 отличаются установившиеся уровни кинетической энергии
системы осцилляторов, которые могут быть найдены по формуле (3.5) по из-
вестным начальным условиям. Из сравнения динамики разности x1 - x2 на
рис. 3 и 4, а также на рис. 5 и 6 видно, что амплитуда этой разности изменяет-
ся во времени по-разному. На рис. 3 и 6 амплитуда уменьшается монотонно,
а на рис. 4 и 5 монотонность отсутствует, имеется во времени ярко выра-
женный максимум, после которого появляется монотонность убывания. Со
временем в системе осцилляторов остается только их коллективное движе-
ние как единого целого, а именно незатухающие колебания на их основной
частоте.
Когда появляется массивная среда, то в системе со временем остаются ко-
лебания двух типов: низкочастотные, соответствующие взаимодействию си-
стемы со средой, и собственные колебания осцилляторов как единого целого.
Как видно из рис. 7, при наличии среды происходит перераспределение энер-
гии между осцилляторами и средой, амплитуда колебаний осцилляторов то
увеличивается, то уменьшается.
7. Заключение
Скорость установления консесуса в динамических и мультиагентных си-
стемах является определяющей для их возможности проявлять на конечном
горизонте времени коллективное поведение. Оказывается, что с возрастанием
размерности системы в два раза эта скорость линейно возрастает с установ-
ленным в статье коэффициентом, равным четырем. С другой стороны, когда
в системе присутствуют различные типы агентов, ее коллективная динамика
становится более разнообразной, зависящей от свойств подсистем. Исполь-
зуемая модель позволяет в любой момент времени изменить количественный
состав осцилляторов добавлением или удалением из нее любого их числа.
Поэтому будущая статья будет посвящена исследованию явления синхрони-
зации в переменной по количественному составу системе идентичных осцил-
ляторов.
78
ПРИЛОЖЕНИЕ
Доказательство леммы 1. Поскольку собственные значения сим-
метрической матрицы A вещественные, то существует ортогональная замена
переменной ξi = Qijxj , где QikQ-1kj = Eij , которая приводит систему уравне-
ний (2.5) к виду (здесь суммирование по индексу i отсутствует)
(Π.1)
ξi(t) + 2α(diagλi
(t) = 0.
Характеристическое уравнение для системы (Π.1) принимает вид
∏
(Π.2)
(σ2 + 2αλiσ + 1 + βλi
) = 0.
i=1
Все решения уравнения (Π.2) задаются выражением (3.2). Лемма 1 доказана.
Доказательство леммы 2. Строки матрицы A являются линейно
∑N
зависимыми. Действительно, из вида матрицы A следует, что
Aij = 0
i=1
для ∀j. Лемма 2 доказана.
Доказательство леммы 3. При доказательстве леммы 3 зависи-
∑N
мость от t опускаем. Обозначим X =
xi. Просуммируем все уравнения
i=1
системы (2.4). Получим цепочку равенств
∑
∑∑
X=
xi =
(-Eijxj - Kijxj - 2Φij xj) =
i=1
i=1 j=1
∑
∑
∑
∑
∑
∑
∑
=- xi - Kiixi -
Kijxj - 2
Φii xi - 2
Φij xj =
i=1
i=1
i=1 j=1, j=i
i=1
i=1 j=1, j=i
∑
∑
∑
∑
= -X +
Kijxj -
Kijxj +
i=1 j=1, j=i
i=1 j=1, j=i
∑
∑
∑
∑
+2
Φij xj - 2
Φij xj = -X.
i=1 j=1, j=i
i=1 j=1, j=i
Получили ЛДУ второго порядка
(Π.3)
X
= -X,
которому соответствует периодическое движение с периодом 2π для любых
отличных от тривиальных начальных условий. Лемма 3 доказана.
Доказательство леммы 4. Утверждение леммы следует из леммы 1,
так как Re σi = -αλi < 0 при λi > 0. Лемма 4 доказана.
Доказательство леммы 5. Воспользуемся свойством для собствен-
ных чисел матриц
A=A-NE. Еслиλi собственное число матриц
A,
79
тоλi = λi - N. Матриц
A имеет вид
-1 -1 -1 -1 ...
-1 -1 -1
−1 -1 -1 -1 ...
-1 -1 -1
−1 -1 -1 -1 ...
-1 -1 -1
A=
.
-1-1-1-1...
-1 -1 -1
−1 -1 -1 -1 ...
-1 -1 -1
Все строки матриц
A одинаковы, поэтомуλ = 0 собственное число этой
матрицы кратности N - 1, т.е.λi = 0 для i = 1, . . . , N - 1. Далее заметим,
что S
A = -N = λN. Такой же вывод последовал бы, если сравнить λN = 0,
полученное в лемме 2, и оставшееся последним ненайденнымλN . Лемма 5
доказана.
Доказательство теоремы 1. Вычислим сначала GN(λ) через Ji(λ),
где Ji(λ) детерминанты матрицы, полученной из матрицы B - λE вычер-
киванием последних N - i строк и столбцов при i = 2, . . . , N - 1. Далее до-
казательство аналогично теореме 1 из [6].
Справедливы следующие рекуррентные формулы, если начать вычислять
детерминант со строки с номером N, в которых опускаем зависимость от λ,
GN = (1 - λ)JN-1 - JN-2,
JN-1 = -λJN-2 - JN-3,
(Π.4)
Jn+1 = -λJn - Jn-1,
J2 = -λ(1 - λ) - 1.
Применим формулы (Π.4) для систем, состоящих из N и N + 1 тел, и соста-
вим разность GN+1 - GN . Она равна
GN+1 - GN = (1 - λ)JN - JN-1 - (1 - λ)JN-1 + JN-2 =
= (1 - λ)JN - (2 - λ)JN-1 + JN-2.
Заменим JN-2 его выражением из (Π.4) на (-λJN-1 - JN ). Тогда эта раз-
ность равна
GN+1 - GN = (1 - λ)JN - (2 - λ)JN-1 - λJN-1 - JN = -λJN - 2JN-1.
(Π.5)
Из первой формулы (Π.4) и (Π.5) получаем еще одно равенство
GN = JN + JN-1.
Из двух последних формул получаем
GN+1 - GN = -λGN + (λ - 2)JN-1.
Справедлива цепочка равенств
GN+1 = -λGN + (λ - 2)JN-1 + GN = -λGN + (λ - 1)JN-1 + JN =
= -λGN - JN-1 - JN-2 = -λGN - GN-1.
80
Получили первое уравнение рекуррентной формулы (4.4). Функции G2(λ),
G3(λ) появляются в результате прямого вычисления детерминантов при
N = 2,3 соответственно. Доказательство теоремы 1 завершено.
Доказательство леммы 6. Запишем характеристическое уравнение
для последовательности (4.4):
γN+1 = -λγN - γN-1.
Получаем квадратное уравнение для γ
γ2 + λγ + 1 = 0,
корни которого равны
√
-λ ±
λ2 - 4
γ1,2 =
2
Таким образом, для общего члена последовательности GN (λ) можно записать
(Π.6)
GN (λ) = C1(λ)γ1 + C2(λ)γ2 .
C1(λ),C2(λ) можно найти, используя первые члены последовательности
GN (λ):
G2(λ) = λ(λ - 2),
G3(λ) = (1 - λ)(λ - 2)(1 + λ).
Подставив функции G2(λ), G3(λ) в (Π.6), получаем систему уравнений
относительно C1(λ), C2(λ):
(
√
)2
(
√
)2
-λ+
λ2 - 4
-λ-
λ2 -4
C1(λ) ·
+C2(λ) ·
= λ(λ - 2),
2
2
(
√
)3
(
√
)3
-λ+
λ2 - 4
-λ-
λ2 -4
C1(λ) ·
+C2(λ) ·
= (1 - λ)(λ - 2)(1 + λ).
2
2
Из этой системы находим функции
2-λ
C1(λ) =
√
,
λ2 - 4
2-λ
C2(λ) = -√
λ2 - 4
Подставляя выражения для C1(λ), C2(λ), γ1 и γ2 в (Π.6), получаем утвержде-
ние леммы 6.
81
Доказательство леммы
7.
Для доказательства воспользуемся
утверждением леммы 6. Введем обозначения:
2-λ
C1 =
√
,
λ2 - 4
√
-λ +
λ2 - 4
a=
,
2
√
-λ -
λ2 - 4
b=
2
Формула общего члена последовательности GN примет вид (зависимость от λ
опускаем)
GN = C1(aN - bN ).
Подставим GN в таком виде в правую часть (4.6) и получим цепочку равенств:
(
)2
(
)
G2n = C1 a2n-1 - b2n-1
a2n-1-b2n-1
-2=
a2n-2 - b2n-2
(
)2
(
)
=C1
a2n-1 - b2n-1
(a2n-2 -b2n-2)(a2n-2 +b2n-2)
-2=
a2n-2 - b2n-2
)
(
)((
)2
=C1
a2n-1 - b2n-1
a2n-2 + b2n-2
-2
=
(
)(
)
(Π.7)
=C1
a2n-1 - b2n-1 a2n-1 + b2n-1 + 2(ab)2n-2 - 2
Нетрудно заметить, что
1
ab =
(λ2 - λ2 + 4) = 1.
4
Поэтому выражение (Π.7) принимает вид
(
)(
)
(Π.8)
G2n = C1
a2n-1 - b2n-1 a2n-1 + b2n-1
,
что является полным квадратом и приводится к виду
(
)
G2n = C1
a2n - b2n
= G2n.
Лемма 7 доказана.
Доказательство леммы 8. Воспользуемся обозначениями леммы 7.√
Предположим, что λ = ±
2 + λBk , где λBk собственные числа матрицы B
(
√
)
размера 2n-1, и вычислим G2n
±
2+λB
. Справедлива цепочка равенств:
k
( √
)
(
)
((
)2n-1
(
)2n-1)
G2n
±
2+λB
=C1
a2n - b2n
=C1
a2
-
b2
=
k
82
√
2n-1
2 + λBk - 2 + λBk - 2 (λBk )2 - 4
=C1
-
4
√
2n-1
2 + λBk - 2 + λBk + 2 (λBk)2 - 4
-
=
4
√
2n-1
√
2n-1
λBk - (λBk)2 - 4
λBk + (λBk)2 - 4
=C1
-
=
2
2
√
2n-1
√
2n-1
-λBk + (λBk)2 - 4
-λBk - (λBk)2 - 4
=C1
-
=
2
2
G2n-1 (λBk) = 0.
Лемма 8 доказана.
Доказательство следствия
2.
Выпишем отношение указанных
собственных значений в явном виде и получим
√
√
√
2-
2+
2+...+
2
√
|
{z
}
√
λA(n)
√
n-1
=
√
=2+
2+
2+...+
2
√
λA(n + 1)
√
|
{z
}
2-
2+
2+...+
2
n
|
{z
}
n
Осуществим предельный переход в последнем выражении при n → ∞. След-
ствие 2 доказано.
Доказательство теоремы
2.
Доказательство теоремы 2 прове-
дем аналогично доказательству теоремы 1. Вычислим сначала GN+1(λ) че-
рез Ji(λ), которые являются детерминантами матрицы
-λ
1
0
0
0
0
0
1
-λ
1
0
0
0
0
0
1
-λ 1 ...
0
0
0
(Π.9)
D=
0
0
0
0
1
-λ
1
0
0
0
0
0
1
-λ
размера i.
Справедливы следующие рекуррентные формулы, если начать вычислять
детерминант матрицы D со строки с номером 1, а затем со столбца с номе-
ром 1, в которых опускаем зависимость от λ,
(Π.10)
GN+1 = -λJN - 2JN-1 + 2(-1)N .
83
Для JN+1 справедлива рекуррентная формула
(Π.11)
JN+1 = -λJN - JN-1.
Покажем справедливость первой формулы в (4.11), вычислив разность ее
левой и правой частей и несколько раз воспользовавшись соотношениями
(Π.10) и (Π.11):
GN+1 + (1 + λ)GN + (1 + λ)GN-1 + GN-2 =
= -λJN - 2JN-1 + 2(-1)N - (1 + λ)(λJN-1 + 2JN-2 + 2(-1)N )-
-(1 + λ)(λJN-2 + 2JN-3 - 2(-1)N ) - λJN-3 - 2JN-4 - 2(-1)N =
= -λJN - 2JN-1 - (1 + λ)(-JN + JN-2) -
- (1 + λ)(-JN-1 + JN-3) - λJN-3 - 2JN-4 =
= JN - JN-1 + λJN-1 - JN-2 - λJN-2 - JN-3 - λJN-3 + JN-2 - JN-4 =
= -JN-2 - λJN-3 - JN-4 = 0.
Значения G3(λ), G4(λ), G5(λ) вычисляются непосредственно. Теорема 2 до-
казана.
Доказательство леммы 9. Запишем характеристическое уравнение
для последовательности (4.11):
γN+1 = -(1 + λ)γN - (1 + λ)γN-1 - γN-2.
Получаем кубическое уравнение для γ:
γ3 + (1 + λ)γ2 + (1 + λ)γ + 1 = 0,
корни которого равны
√
-λ ±
λ2 - 4
γ1,2 =
,
γ3 = -1.
2
Таким образом, для общего члена последовательности GN (λ) справедливо
(Π.12)
GN (λ) = C1(λ)γ1 + C2(λ)γ2 + C3(-1)N .
C1,2,3(λ) можно найти, используя первые члены последовательности GN (λ)
при N = 3, 4, 5:
G3(λ) = -λ3 + 3λ + 2,
G4(λ) = λ4 - 4λ2,
G5(λ) = -λ5 + 5λ3 - 5λ + 2.
84
Подставив функции G3(λ), G4(λ) и G5(λ) в (Π.12), получаем систему урав-
нений относительно C1(λ), C2(λ) и C3(λ):
(
√
)3
(
√
)3
-λ +
λ2 - 4
-λ -
λ2 - 4
C1(λ) ·
+ C2(λ) ·
- C3(λ) =
2
2
= -λ3 + 3λ + 2,
(
√
)4
(
√
)4
-λ +
λ2 - 4
-λ -
λ2 - 4
C1(λ) ·
+ C2(λ) ·
+ C3(λ) =
2
2
= λ4 - 4λ2,
(
√
)5
(
√
)5
-λ +
λ2 - 4
-λ -
λ2 - 4
C1(λ) ·
+ C2(λ) ·
+ C3(λ) =
2
2
= -λ5 + 5λ3 - 5λ + 2.
Из этой системы находим функции
C1(λ) = 1,
C2(λ) = 1,
C3(λ) = -2.
Подставляя выражения для C1,2,3(λ) и γ1,2,3 в (Π.12), получаем утверждение
леммы 9.
Доказательство леммы 10. Воспользуемся обозначениями леммы 7.√
Предположим, что λ = ±
2 + λBk , где λBk собственные числа матрицы B
(
√
)
размера 2n-1, и вычислим G2n
±
2+λB
. Справедлива цепочка равенств:
k
)
( √
)
(
)
((
)2n-1
(
)2n-1
G2n
±
2+λB
=
a2n + b2n - 2
=
a2
+
b2
-2
=
k
√
2n-1
)2 - 4
2 + λBk - 2 + λBk - 2 (λBk
=
+
4
√
2n-1
2 + λBk - 2 + λBk + 2 (λBk)2 - 4
+
-2=
4
√
√
2n-1
2n-1
λBk - (λBk)2 - 4
λBk + (λBk)2 - 4
=
+
-2=
2
2
√
√
2n-1
2n-1
-λBk + (λBk)2 - 4
-λBk - (λBk)2 - 4
=
+
-2=
2
2
= G2n-1 (λBk ) = 0.
85
Лемма 10 доказана.
Доказательство леммы 11. В лемме 7 было получено выражение
√
2-λ
GN (λ)
=
(aN - bN ),
| {z }
λ+2
(4.5)
которое возведем в квадрат. Получим
(√
)2
2-λ
2-λ
(
)
(aN - bN )
=
a2N + b2N - 2(ab)N
=
λ+2
λ+2
2-λ
=
(a2N + b2N - 2).
λ+2
Умножим последнее выражение наλ+22-λ и получим (4.12), а значит, справед-
ливо (4.13).
Поскольку среди нулей GN (λ)
присутствует λB = 2 кратности единица,
| {z }
(4.5)
то после возведения в квадрат и умножения кратность единица у λB = 2
остается, а появляется λB = -2 тоже кратности единица. Лемма 11 доказана.
Доказательство леммы 12. Первое уравнение в системе (5.1) в
обозначениях леммы 3 имеет вид
(Π.13)
Mx0 = -Nkx0
+ kX.
Система уравнений движения осцилляторов в системе (5.1), как и в дока-
зательстве леммы 3, переписывается так:
(Π.14)
X= -X - kX + Nkx0.
В системе уравнений (Π.13) и (Π.14) присутствуют две моды колебаний с
частотами
√
√
1
kM + Nk + M ±
M2k2 + 2MNk2 + N2k2 + 2M2k - 2MNk + M2
ω1,2 =
√
√
2
M
Лемма 12 доказана.
СПИСОК ЛИТЕРАТУРЫ
1. Strogatz Steven H. From Kuramoto to Crawford: Exploring the Onset of Synchro-
nization in Populations of Coupled Oscillators // Physica D. 2000. No. 143. P. 1-20.
2. Пиковский А., Розенблюм М., Куртс Ю. Синхронизация. Фундаментальное
нелинейное явление. М.: Мир физики и техники, 2003.
3. Strogatz Steven H., Stewart Ian. Coupled Oscillators and Biological Syncronization //
Sci. Amer. 1993. No. 12. P. 68-75.
86
4. Shyam Krishan Joshi, Shaunak Sen, Indra Narayan Kar. Synchronization of Coupled
Oscillator Dynamics // IFAC-PapersOnLine. 2016. V. 49. No. 1. P. 320-325.
5. Трубецков Д.И., Рожнёв А.Г. Линейные колебания и волны. М.: Физматлит,
2001.
6. Галяев А.А. О математической модели импульсного воздействия, вызванного
ударом системы материальных точек об абсолютно жесткое препятствие // АиТ.
2006. № 6. C. 27-40.
Galyaev A.A. Impact of a System of Material Points Against an Absolutely Rigid
Obstacle: a Model for its Impulsive Action // Autom. Remote Control. 2006. V. 67.
No. 6. P. 856-867.
7. Галяев А.А. О математической модели одномерного удара цепочки тел, обла-
дающей вязкоупругими свойствами // АиТ. 2015. № 10. С. 40-49.
Galyaev A.A. On the Mathematical Model of One-Dimensional Impact of a Chain of
Viscoelastic Bodies // Autom. Remote Control. 2015. V. 76. No. 10. P. 1743-1750.
8. Bullo F. Lectures on Network Systems. Ed. 1.3. Kindle Direct Publishing, 2019.
9. Ren Wei Wu, Yongcan Cao. Distributed Coordination of Multi-agent Networks:
Emergent Problems, Models, and Issues. London: Springer-Verlag, 2010.
10. Поляк Б.Т., Цыпкин Я.З. Устойчивость и робастная устойчивость однотипных
систем // АиТ. 1996. № 11. С. 91-104.
Polyak B.T., Tsypkin Y.Z. Stability and Robust Stability of Uniform System //
Autom. Remote Control. 1996. V. 57. No. 11. P. 1606-1617.
11. Bernstein, Dennis S. Matrix Mathematics: Theory, Facts, and Formulas. Princeton
University Press, 2011.
12. Соболев О. Однотипные связанные системы регулирования. М.: Энергия, 1973.
Статья представлена к публикации членом редколлегии М.В. Хлебниковым.
Поступила в редакцию 12.08.2019
После доработки 18.09.2019
Принята к публикации 28.11.2019
87