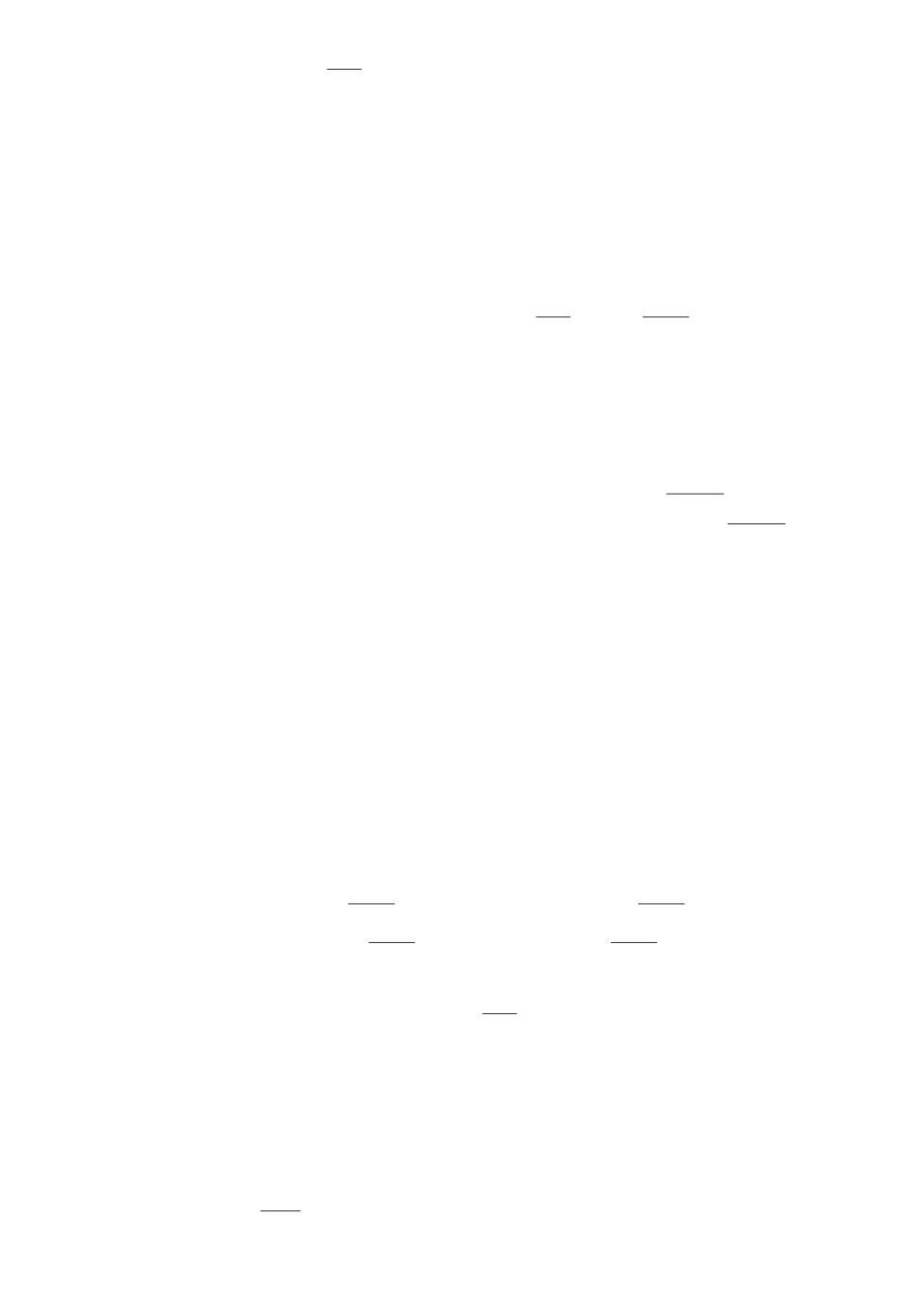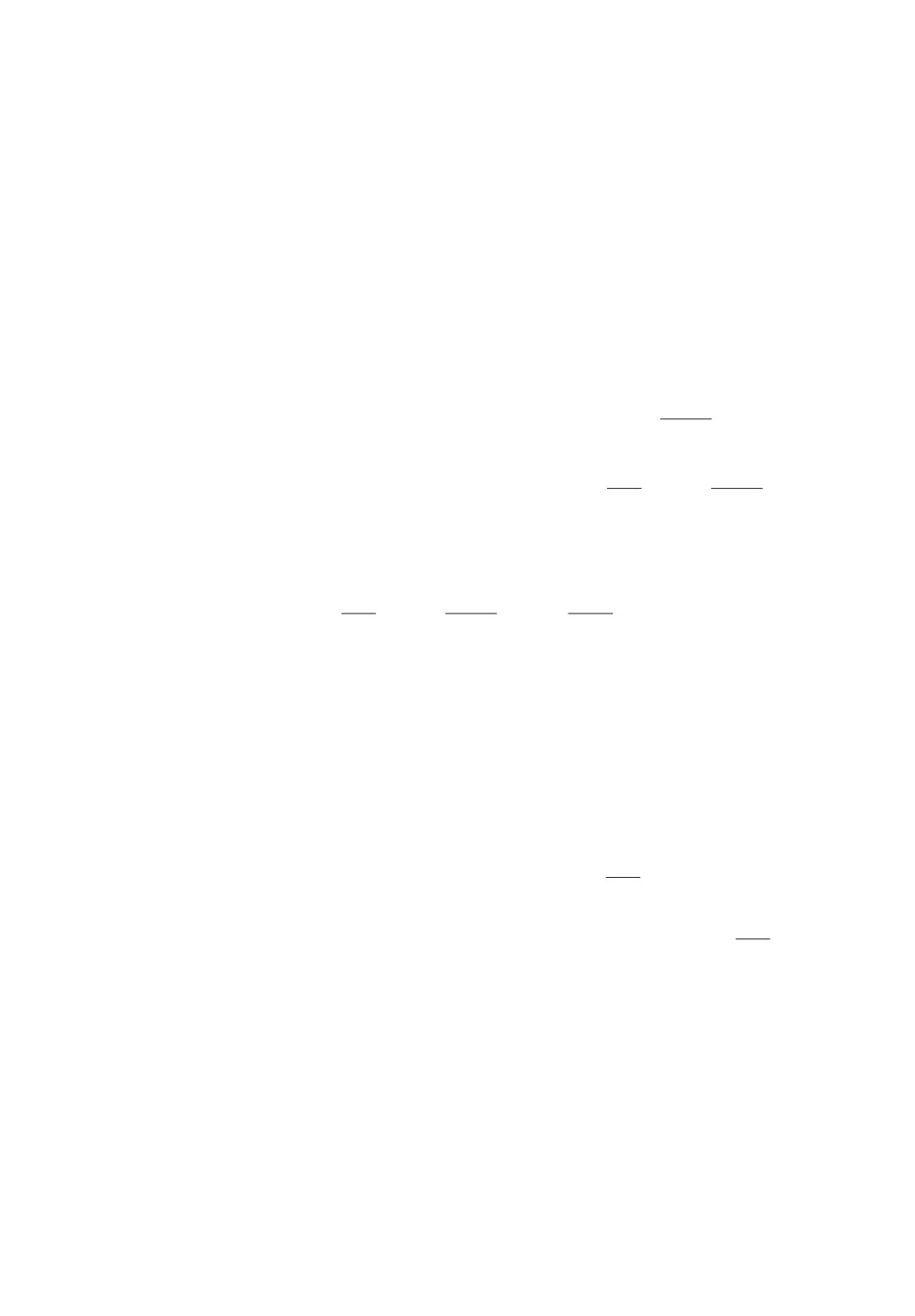Автоматика и телемеханика, № 6, 2020

(АО “ВНИИ “Градиент”, Ростов-на-Дону)

НЕКОТОРЫЕ АСПЕКТЫ ИДЕНТИФИКАЦИИ ДИНАМИЧЕСКИХ

ОБЪЕКТОВ ПРИ НЕКОРРЕКТНЫХ УСЛОВИЯХ НАБЛЮДЕНИЯ

Решаются задачи численно-аналитического представления решения

уравнения, описывающего динамический объект и его измеряемого выхо-

да, а также оптимального вычисления значений непрерывных линейных

функционалов (числовых характеристик) от измеряемых функций на ос-

нове некорректных данных, содержащих не только флуктуационную по-

грешность, но и сингулярную помеху. Метод обеспечивает максимально

возможную декомпозицию вычислительных процедур, не требует выпол-

нения традиционных операций линеаризации и выбора начальных при-

ближений, а также не связан с расчетом спектральных коэффициентов в

конечных линейных комбинациях (с заданными базисными функциями),

описывающих интегральные кривые, измеряемые функции и сингуляр-

ную помеху.

Ключевые слова: идентификация, динамический объект, измеряемый вы-

ход, непрерывный линейный функционал, числовая характеристика, син-

гулярная помеха, некорректные наблюдения, автокомпенсационное оце-

нивание.

DOI: 10.31857/S0005231020060086

1. Введение

В различных областях, связанных с решением задач оптимального управ-

ления, оценивания, фильтрации, прогнозирования и распознавания образов

[1-12], возникает необходимость решения векторного обыкновенного диффе-

ренциального уравнения (например, уравнения свободного движения), соот-

ветствующего некоторому многомерному динамическому объекту (ДО). При

этом необходимо заранее строить приближенное аналитическое решение (тре-

буемого качества) для данного уравнения, которое должно зависеть от на-

чального условия и других характерных параметров, принимающих значе-

ния из заданного множества допустимости. Если ДО снабжен измеряемым

выходом, то также целесообразно иметь приближенное аналитическое описа-

ние (требуемого качества) данного выхода для указанного множества допу-

стимости. Кроме того, часто возникает необходимость оптимального оцени-

вания некоторых числовых характеристик (ЧХ) от измеряемых функций, к

которым можно отнести начальное условие, производные различного поряд-

ка, определенные интегралы, спектральные коэффициенты соответствующих

разложений и др., т.е. речь идет об оценке значений непрерывных линейных

функционалов [13-16]. Так, для триангуляционных комплексов пассивной ло-

кации движущихся излучающих целей весьма важной является задача на-

хождения производных от измеряемых пеленгов (азимута и угла места) для

131

каждой приемной позиции комплекса [5, 6]. Использование указанных ЧХ

позволяет решать актуальные задачи прогнозирования угловых траекторий

(например, при срыве и пропуске наблюдений) и отождествления пеленгов

группы движущихся излучающих целей для многопозиционного триангуля-

ционного комплекса [5].

В [13-16] развит эффективный в вычислительном плане метод оптималь-

ного автокомпенсационного оценивания ЧХ от информационного сообщения,

реализация которого наблюдается в аддитивной смеси с флуктуационным

шумом и сингулярной помехой (не исключается также наличие маскирующе-

го сигнала). Помеха на интервале наблюдения может многократно превосхо-

дить (по абсолютной величине) сумму реализаций информационного сообще-

ния и шума, т.е. речь идет о так называемых некорректных наблюдениях, с

которыми часто приходится сталкиваться на практике [5, 6, 13-16]. Достоин-

ство метода автокомпенсационного оценивания (инвариантного к сингуляр-

ной помехе) состоит в том, что он позволяет решать задачу вычисления ЧХ

без традиционного расширения пространства состояний и ориентирован не

только на гладкие, но и на кусочно-непрерывные помехи с известными и неиз-

вестными точками разрыва первого рода, когда на участке непрерывности

помеха описывается одним из базисов (априорно неизвестным), принадлежа-

щим конечному семейству возможных (для данной помехи) функциональных

базисов.

В [13] на основе идей автокомпенсационного оценивания [14-16] и опорных

интегральных кривых ([17] скалярный случай, [18] векторный случай)

развит метод численно-аналитического описания ДО (для заданной области

допустимости) и оценивания ЧХ его интегральной кривой по выборкам этой

кривой, содержащей флуктуационный шум и сингулярную помеху. К недо-

статкам такого метода можно отнести то, что рассматривается лишь ска-

лярный ДО, в качестве измеряемого параметра выступает непосредственно

интегральная кривая ДО, а это, как правило, не вполне соответствует по-

требностям практики. Для большинства прикладных задач более актуаль-

ным является оценивание ЧХ для векторного измеряемого выхода ДО.

Цель статьи разработать метод численно-аналитического описания ре-

шения дифференциального уравнения и измеряемого выхода многомерно-

го ДО для заданной области допустимости, а также оптимального оценива-

ния ЧХ измеряемых функций (сохраняя достоинства метода [13]) по резуль-

татам некорректных наблюдений. Очевидно, что возможная нелинейность,

отсутствие (как правило) общего решения соответствующего дифференци-

ального уравнения, его зависимость не только от времени, но и от других

характерных параметров (начального условия и коэффициентов правой ча-

сти уравнения) делают эту задачу нетривиальной.

2. Постановка задачи

Рассмотрим многомерный ДО, описываемый моделью

∕

f (t, z, η), z ∈ G_z ⊂ RI1 , η ∈ G_η ⊂ RI2 , t ∈ G_t = [t₀, t₀ + T ] ⊂ R¹,

132

[

]_T

где η =

η_i,i = 1,I₂

вектор постоянных параметров неопределенности,

которые могут принимать значения из заданной области допустимости G_η =

= {[r₁, p₁] , [r₂, p₂] , . . . , [rI2 , pI2 ]},

[r_i, d_i] ⊂ R¹, i = 1, I₂, z₀ = z (t₀) ∈ G_z0 =

= {[c₁, d₁] , [c₂, d₂] , . . . , [cI1 , dI1 ]}, G_z0 ⊆ G_z, [c_i, d_i] ⊂ R¹, i = 1, I₁. Данная мо-

дель может рассматриваться как самостоятельно, так и в качестве уравнения

свободного движения для некоторого управляемого детерминированного или

[

]_T

стохастического ДО. Вводя расширенный вектор x =

z^T,η^T

∈RI1+I2 = R^I и

учитывая, что dη/dt ≡ 0, приходим к другому описанию ДО в виде диффе-

ренциального уравнения

(2.1)

dx/dt = f(t, x), t ∈ G_t = [t₀, t₀ + T ] ⊂ R¹, x ∈ R^I ,

где x = x(t, x₀) = [x_i(t, x₀), i = 1, I]^T - решение уравнения с начальным услови-

ем x₀ = x(t₀, x₀) = [x_i0, i = 1, I]^T ∈ G_x0, G_x0 = {x₀ ∈ R^I : c_i ≤ x_i0 ≤ d_i, i = 1, I} -

гиперпараллелепипед возможных начальных условий, f(t, x) - функция,

имеющая ту гладкость (по аргументам t и x), которая соответствует рассмат-

риваемому ДО и требуется по смыслу проводимых в дальнейшем выкладок.

Для уравнения (2.1) справедливо

[

]_T

[

]_T

f (t, x) =

f_i(t,x),i = 1,I

f_i (t,z,η) ,i = 1,I₁

f_j (t,z,η) ,j = I₁ + 1,I

где

f_j (t,z,η) ≡ 0, j = I₁ + 1,I. При гладкой правой части f(t,x) (с учетом

существования всевозможных производных определенного порядка по t и x)

решение x (t, x₀) уравнения (2.1) и его соответствующие частные производные

существуют и непрерывны в области G_xt = {G_x0, G_t} (см. [19, с. 124, 125]).

Будем полагать, что гладкие частные решения x_i (t, x₀) принадлежат про-

странству непрерывных функций C [G_xt] с равномерной сходимостью, при

этом норме этого пространства соответствует обозначение ∥·∥C[Gxt]^(см.[20,

с. 51, 52]).

Уравнению (2.1) можно поставить в соответствие приближенное анали-

тическое решение x = x (t, x₀), где x₀ = x (t₀, x₀), при этом в общем случае

[

max|xi0 - xi0| = 0, i = 1,I. Считаем, что x = x(t,x0) =

x_i (t,x₀) ,i = 1,I

является ε₀-приближенным по невязке решением [21]: max|xi0 -xi0|≤ε0,

dx_i/dt = f_i(t, x) + ϑi (t), max|ϑi (t)| ≤ ε0, t ∈ Gt. В дальнейшем близость

i,t

точной x_i = x_i (t, x₀) и приближенной

x_i = x_i (t,x₀) фазовых координат

ДО для фиксированного x₀ будем характеризовать невязкой ε_xi (x₀) =

= max|x_i (t,x₀) - x_i (t,x₀)|, соответственно для оценки близости их про-

t∈Gt

изводных первого порядка (по аргументу t) вводится невязка ε^(1)xi (x₀) =

= max|x⁽¹⁾ⁱ (t,x₀) - x⁽¹⁾ⁱ (t,x₀) |. Для оценки близости векторных решений

t∈Gt

x (t, x₀), x (t, x₀) и их производных x⁽¹⁾ (t, x₀), x⁽¹⁾ (t, x₀) используются невяз-

ки ε_x (x₀) = maxεxi (x0) и εx1) (x0) = maxε(1)xi (x0) соответственно.

Зададимся также векторным уравнением измеряемого выхода ДО

(2.2)

y (t) = ϕ(t, x (t, x₀)) ∈ R^J , t ∈ G_t,

133

[

]_T

где y (t) =

y_j (t,x₀) ,j = 1,J

- вектор измеряемых функций с координата-

ми y_j (t, x₀), которые также принадлежат C [G_xt], ϕ(t, x) гладкая функция

своих аргументов (степень гладкости также определяется типом измеряемого

выхода рассматриваемого ДО).

На траекториях y_j (t, x₀) ∈ C^r [G_xt] вводится семейство Ω ЧХ (ω ∈ Ω), ко-

торые необходимы при решении тех или иных целевых задач, связанных с

наблюдением за конкретным ДО, при этом будем использовать представле-

ние ω {y_j(t, x₀)} = ω_j {x₀} ∈ R¹.

Воспользуемся дискретными уравнениями наблюдения за ДО

(

)

(2.3)

h_jn = y_jn

x^′0

+ s_jn + ξ_jn, j = 1,J, n = 0,N_j,

где h_jn = h_j (t_jn), y_jn (x₀) = y_j (t_jn, x₀), s_jn = s_j (t_jn), ξ_jn = ξ_j (t_jn), t_jn ∈ G_t.

В этом уравнении: x^′0 ∈ G_x0 неизвестное начальное условие, s_j (t) сингу-

лярная помеха, ξ_j (t) флуктуационная погрешность. Введение индекса j во

позволяет рассмотреть случай асинхронных изме-

рений различных функций выхода ДО.

Помеху опишем в виде s_j(t) = C^TjΘ_j (t), где C_j = [c_jp, p = 1, M_sj ]^T вектор

неизвестных спектральных коэффициентов, Θ_j (t) = [θ_jp(t), p = 1, M_sj ]^T

вектор заданных базисных функций, M_sj заданное число степеней свобо-

ды (на практике часто прибегают к упрощениям M_sj = M_s и Θ_j (t) = Θ (t)).

Вектор Θ_j (t), соответствующий y_j (t, x₀), может формироваться из семейства

базисных функций, которые в наибольшей степени соответствуют основным

факторам неопределенности, отвечающим различным наиболее вероятным

условиям наблюдения за ДО. Такое семейство должно предусматривать воз-

можность появления сингулярных помех самого разного типа, с которыми

можно столкнуться на практике при исследовании конкретного ДО в тех

или иных условиях наблюдения.

характеризуется нулевым ма-

тематическим ожиданием и соответствующей невырожденной корреляцион-

ной матрицей K_Ξj .

Введем векторные обозначения:

[

]_T

[

(

)

H_j =

h_jn,n = 0,N_j

Y_j =

y_jn

x^′0

,n = 0,N_j

]^T ,

[

]_T

[

]_T

S_j =

s_jn,n = 0,N_j

Ξ_j =

ξ_jn,n = 0,N_j

Это позволяет перейти от (2.3) к векторному уравнению наблюдения H_j =

= Y_j + S_j + Ξ_j. Для фиксированного j ∈ 1,J из Ω выберем произвольную ЧХ

ω: y_j (t,x₀) → R¹, в другой записи ω {y_j (t,x₀)} = ω_j ∈ R¹. На основе наблю-

дения H_j нужно дать оценку значения ω_j, т.е. вычислить ЧХ измеряемой

функции y_j (t, x₀). Данную оценку будем искать в классе линейных оценок

(здесь и далее индекс^∗ соответствует некоторой оценке)

ω^∗j = P^TjH_j = P^Tj(Y_j +S_j +Ξ_j) = P^TjY_j +P^TjS_j +P^TjΞ_j = ω^∗Yj +ω^∗Sj +ω^∗Ξj,

(2.4)

[

]_T

где P_j =

p_jn,n = 0,N

вектор искомых весовых коэффициентов.

134

В силу линейности процедуры оценивания (2.4) при фиксированном P_j

дисперсия ошибки вычисления характеристики ω_j находится как

σ^2j = P^TjK_jΞP_j.

Выбор оптимального значения P^∗j для вектора P_j соответствует критерию

P^∗j = minσ^2j,

P_j

при этом должны выполняться условия несмещенности оценки

P^TjY_j = ω {y_j (t,x₀)} = ω_j

и ее инвариантности к помехе

P^TjS_j = 0.

Требуется с учетом (2.1)-(2.4): сформировать алгоритм построения чис-

ленно-аналитического решения x (t, x₀); обсудить вопросы точности и опти-

мизации выбора параметров данного алгоритма; сформировать алгоритм по-

строения численно-аналитического выражения для измеряемого многомер-

ного выхода ДО; сформировать алгоритм нахождения оптимального векто-

ра P^∗j и оценки ω^∗j и рассмотреть возможность оценивания различных ЧХ на

основе наблюдений H_j ; исследовать методическую погрешность данного ал-

горитма; определить условия и границы применимости развиваемого метода,

дать комментарии к достигаемому вычислительному эффекту.

3. Численно-аналитическое решение дифференциального уравнения

динамического объекта (этап 1)

Для формирования решения уравнения (2.1) в области G_xt можно исполь-

зовать широко применяющуюся в общей теории приближенных методов [22]

математическую конструкцию

∑

(3.1)

x_i (t,x₀) =

β^xikς^xik (t,x₀

i = 1,I,

∑

где

одномерная сумма по индексу k с заданным числом неизвестных

коэффициентов β^xik и известных базисных ς^xik (t, x₀). Очевидно, что с учетом

гладкости решения x_i (t, x₀) число слагаемых в сумме можно подобрать так,

чтобы для любого сколь угодно малого δ_xi ≥ 0 обеспечивалось выполнение

условия ε_xi (x₀) < δ_xi независимо от конкретного значения x₀ ∈ G_x0. В част-

ном случае можно перейти от (3.1) к приближению на основе многомерного

многочлена (см. [23, с. 152])

∑

(3.2)

x_i (t,x₀) =

α^ximz^m

i = 1,I,

∑

z = (t,x₁₀,...,x_I0),

многомерная сумма по мультиндексу m с заданным

числом неизвестных коэффициентов α^xim. Представление (3.2) используется в

135

теореме Вейерштрасса [23], подтверждающей возможность наилучшего при-

ближения к x_i (t, x₀) в равномерной метрике для области G_xt. Для гладких

решений хорошее приближение можно получить на основе конструкции

(3.3)

x_i (t,x₀) = [Ψ^xi (t)]^T B^xiΛ^xi (x₀

), i = 1,I,

где Ψ^xi (t) и Λ^xi (x₀)

векторы заданных гладких базисных функций соот-

ветствующей размерности, B^xi матрица неизвестных коэффициентов. Ес-

ли в качестве координат векторов Ψ^xi (t) и Λ^xi (x₀) использовать многомерные

многочлены с соответствующими мультиндексами (по аналогии с [23, с. 152]),

то представление (3.3) несложно получить из (3.1). На практике конструк-

ция (3.3) широко распространена для описания большого класса ДО.

Для расчета коэффициентов, фигурирующих в математических конструк-

циях (3.1)-(3.3), воспользуемся методом опорных интегральных кривых

(ОИК) решения дифференциальных уравнений [17, 18]. Обобщим метод ОИК

на векторное уравнение (2.1). Для этого в области G_x0 рассмотрим сетку, со-

стоящую из многомерных узлов x_0(r) ∈ G_x0, r ∈ 1, M_x. Этим узлам поставим

(

)

в соответствие семейство ОИК x_i(r) = x_i

t,x_0(r)

, i = 1,I, r = 1,M_x, которое

формируется на основе одного из известных высокоточных численных мето-

дов интегрирования. Погрешностями построения ОИК в дальнейшем будем

пренебрегать (по аналогии с [17, 18]). На практике данное семейство задается

таблично.

{

}

Теперь в области G_t задается временная сетка

t_(ik)

, k = 1,M_ti, объема

(

)

которой достаточно для представления фазовых координат x_i

t,x_0(r)

в об-

ласти G_xt с требуемой точностью. Далее с использованием семейства ОИК

формируется массив чисел

(

)

(3.4)

x_i(rk) = x_i

t_(ik),x_0(r)

i = 1,I, r = 1,M_x, k = 1,M_ti.

Для нахождения неизвестных коэффициентов в формулах (3.1)-(3.3) можно

применять известные операторы E^x1, E^x2 и E^x3 (интерполяции или аппроксима-

ции [23-25]), при этом с учетом (3.4), используя эти операторы, вычисляются

указанные коэффициенты

{

}

{

}

{

}

(3.5)

E^x1 :

x_i(rk)

→ {β^xik} , E^x2 :

x_i(rk)

→ {α^xim} , E^x3 :

x_i(rk)

→ {B^xi}.

При построении численно-аналитического решения x(t, x₀) уравн{ния}2.1)

на базе (3.5) в общем случае применяется неравномерная сетка

t_(ik)

по

аргументу t. Кроме того, для многих ДО зависимость фазовой координаты

x_i (t,x₀) от x₀ является слабо выраженной, что существенно снижает объ-

ем M_x вычислительной сетки по начальному условию x₀ и упрощает рассмот-

ренную процедуру (интерполяционную или аппроксимационную) построения

численно-аналитического решения x (t, x₀) уравнения (2.1).

Таким образом, априорно на первом этапе (до получения измеритель-

ных данных) строится приближенное аналитическое решение x (t, x₀) урав-

нения (2.1), обеспечивающее в области G_xt требуемую для практики точ-

ность анализа ДО. В число параметров, позволяющих достичь такой точ-

ности, можно отнести объемы используемых сеток (M_ti и M_x), кроме того,

136

важен выбор систем базисных функций в приближениях (3.1)-(3.3) с учетом

вида правой части уравнения (2.1).

Конкретизируем описанную процедуру на случай, когда при построении

решения на базе (3.3) используются фундаментальные многочлены интер-

поляции (как тензорное произведение одномерных фундаментальных мно-

гочленов [23]). С {той }ль{ в области}Gx0 зададим многомерную вычис-

лительную сетку

x_0(m)

x0(m1,...,m_I )

(где m = (m₁, . . . , m_I ) мультин-

декс, m_i = 1, M_xi, i = 1, I,

∏M_xi = M_x,∏ знак умножения по индексу

i = 1,I) и для всех ее узлов построим семейство ОИК x_i(m) = xi(m1,...,m_I) =

(

)

(

)

=x_i

t,x_0(m)

=x_i

t, x0(m1,...,m_I)

, i = 1,I. На отрезке c_i ≤ x_i0 ≤ d_i задаются

узлы x_i0(1), . . . , xi0(Mxi) и принимается, что

∏

(

)

(

)

ψ^xik (t) = L_i(k) (t) =

t-t_i(j)

t_i(k) - t_i(j)

j=1,j=k

В этом случае решение (3.3) имеет вид

∑∑

x_i (t,x₀) =

x_i(mk)L_i(k) (t)L_i(m) (x₀) , i = 1,I,

k=1 m

∑

где_m многомерная сумма по мультиндексу m,

∏

L_i(m) (x₀) =

L(mi) (xi0),

i=1

∑

(

)

(

)

L(mi) (xi0) =

x_i0 - x_i0(q)

xi0(mi) - xi0(q)

q=1,q=m_i

Если x_i (t, x₀) является ε₀-приближенным по невязке решением, то для

погрешности ε_xi (x₀) представления фазовой координаты x_i (t, x₀) с исполь-

зованием x_i (t, x₀) справедлива оценка (по аналогии с [21])

]

[(

)

ε_xi (x₀) ≤ ε₀ L^-10 + 1

exp (L₀ |t - t₀|) - L^-1

где t ∈ G_t, x₀ ∈ G_x0, L₀

константа Липшица для правой части уравне-

ния (2.1). Соответственно для оценки близости точного x (t, x₀) и прибли-

женного x (t, x₀) векторных решений применима оценка

{√

(

)

[

(

)

]}

ε_x (x₀) ≤ ε₀

I exp

L₀I²T

+ (L₀I)^-1

exp

L₀I²T

-1

Опираясь на [23-25], можно также оценить вклад наследственной погреш-

ности и погрешности округлений в результирующую ошибку построения при-

ближенного решения уравнения (2.1). При учете погрешностей интерполяции

и аппроксимации на качество формируемого численно-аналитического реше-

ния достаточно воспользоваться оценками, которые приводятся в [23-25].

137

4. Численно-аналитическое описание измеряемого выхода

динамического объекта (этап 1)

Точный выход ДО можно представить в виде

y (t) = ϕ(t, x (t, x₀)) = γ (t, x₀) ∈ R^J ,

при этом ϕ : G_xt → G_yt гладкая функция по t и x₀. Соответственно для

приближенного выхода ДО имеем

y (t) = ϕ(t, x (t, x₀)) = γ (t, x₀) ∈ R^J .

По аналогии с разделом 3 для численно-аналитического описания изме-

ряемого выхода ДО можно использовать семейство ОИК, при этом также

применяем принцип гладкой зависимости y (t) = γ (t, x₀) от своих аргумен-

(

)

тов. Для этой цели семейству ОИК x_(r) = x

t,x_0(r)

, r = 1,M_x, поставим в

соответствие семейство выходных траекторий

(

))

(

)

y_j(r) (t) = ϕ_j

t,x

t,x_0(r)

=γ_j

t,x_0(r)

j ∈ 1,J, r = 1,M_x,

которые представим массивом чисел

(

))

(

)

y_j(rk) = ϕ_j

t_i(k),x

t_i(k),x_0(r)

=γ_j

t_i(k),x_0(r)

j ∈ 1,J, r = 1,M_x, k = 1,K.

Теперь по аналогии с (3.5) можно получить оценки неизвестных коэффи-

циентов в приближенных выражениях для измеряемого выхода ДО, если в

формулах (3.1)-(3.3) заменить символ x на y, а символ i на j:

{

}

{

}

{

}

{

}

{

}

{

}

E^y1 :

y_j(rk)

→ β^y

E^y2 :

y_j(rk)

→ α^y

E^y3 :

y_j(rk)

→ B^y

По аналогии с (3.3) выход ДО представим так:

[

]_T

(4.1)

yj (t) = Ψ^j (t)

B^yjΛ^yj (x₀

), j = 1,J,

∑∑

(4.2)

yj (t) = γj (t, x0) =

y_j(mk)L_j(k) (t)L_j(m) (x₀

j = 1,J.

k=1 m

Формулы (4.1) и (4.2) являются удобными в численно-аналитических рас-

четах и в максимальной степени ориентированы на оперативные вычисления.

5. Оценивание числовых характеристик измеряемых параметров

динамического объекта (этап 2)

Этап 2 связан непосредственно с обработкой поступающих измерений и

согласно современной концепции должен характеризоваться минимальными

вычислительными затратами, заданной оперативностью и устойчивостью к

138

сингулярной помехе. Выполнить эти требования возможно, если воспользо-

ваться процедурой автокомпенсационного оценивания ЧХ при некорректных

условиях наблюдения. С учетом (4.1) выходную траекторию ДО зададим в

виде

[

(

)

(

(5.1)

yj (t) = γj

t,x^′0

= B^yj

x^′0

)]T Ψ^yj(t) =

Y^TjΨ^yj

(t), j = 1, J,

[

(

)

гд

Y_j =

y_j

t_(k)

,k = 1,M_t

]^T = B^yj (x^′0) вектор временных отсчетов траек-

{

}Mt

тории y_j (t) = γ_j (t, x^′0) на вычислительной сетке

t_(k)

, x^′0 ∈G_x0

неиз-

k=1

вестное начальное условие, фигурирующее в уравнении наблюдения (2.3),

[

]_T

Ψ^yj(t) = ψ^yjk(t),k = 1,M_t

вектор базисных функций. Полагаем, что

(

)

(

)

γj

t_(k),x^′0

Y^TjΨ^yj(t_(k)) ≈ y_j

t_(k)

при этом вектор временных отсчетов координаты y_jn = γ_j (t_jn, x₀) на измери-

(где N_j ≫ M_t) приближенно может быть задан в виде[

]

Y_j

Y^TjΨ^yj, j = 1,J, где Ψ^yj = ψ^y

,k = 1,M_t,n = 0,N_j

матрица отсчетов

jkn

ψ^yjkn = ψ^yjk (t_jn) функций ψ^yjk(t).

Условие несмещенности оценки ЧХ (см. раздел 2) принимает вид

[

{

}]_T

(

)_T

P^TjY_j = ω {γ_j (t,x₀)} = ω Ψ^yj(t)

Y_j = P^T

Ψ^yj

Y_j = ω_j,

{

}

[

{

}

]_T

где ω Ψ^yj(t)

= ω ψyjk (t) ,k = 1,Mt

вектор значений ЧХ ω на базис-

ных функциях ψ^yjk(t). Отсюда следует окончательное условие несмещенности

{

}

(5.2)

Ψ^yjP_j = ω Ψ^yj(t)

Поскольку необходимо, чтобы

{

}

ω {s_j (t)} = ω

C^TjΘ_j (t)

= CTj ω {Θ_j (t)} = PTj S_j = 0,

то условие инвариантности (см. раздел 2) можно преобразовать к виду

(5.3)

Θ_jP_j = [0]Msj×1^,

где [0]Msj ×1^{нулевойвектор-столбецразмерностиM}sj^×1,

[

]

Θ_j =

θ_jsn, s = 1,M_sj, n = 0,N_j

матрица отсчетов θ_jsn = θ_js (t_jn) ба-

зисных функций сингулярной помехи.

Задача нахождения оптимальной оценки P^∗j вектора P_j решается мето-

дом условной оптимизации Лагранжа на базе критерия P^∗j = min σ^2j с учетом

P_j

139

ограничений (5.2) и (5.3). В итоге получаем процедуру автокоменсационного

оценивания ЧХ применительно к измеряемому выходу ДО

[

(

)_T

(

)_T]-1

{

}

(5.4)

P^∗j = Z_j1 Ψ^yj

Ψ^yZj1

Ψ^yj

ω Ψ^yj(t) ,

[

]_T

(5.5)

ω^∗j0 =

P^∗j

H_j = H^TjP^∗j,

(

)_-1

где Z_j1 = Z_j2K^-1jΞ, Z_j2 = E_j - K^-1jΞΘ^Tj Θ_jK^-1jΞΘ^Tj

Θ_j, E_j единичная мат-

рица.

Из (5.4) непосредственно вытекает, что матрицы K_jΞ, Θ_jK^-1jΞΘ^Tj и

(

)_T

Ψ^yjZ_j1

Ψ^yj

должны быть невырожденными и хорошо обусловленными, что

соответствует получению единственного и устойчивого решения P^∗j. Данный

вопрос относится к сфере оптимального планирования измерительного экс-

перимента и в данной статье не рассматривается. При рациональном выборе

основных параметров процедуры (5.4), (5.5) можно избежать необходимости

решения некорректной (с вычислительной точки зрения) задачи оценивания.

Для дисперсии оптимальной оценки ω^∗j числовой характеристики ω_j имеем

выражение

[

]_T

σ^2j =

P^∗j

K_jΞP^∗j =

(5.6)

[

{

}]_T

(

)_T

{

}

= ω Ψ^yj(t)

W_j1Ψ^yjZ^TKjΞZj1

Ψ^yj

W_j2ω Ψ^yj(t) ,

[

(

)_T]-1

(

)_T]-1

где W_j1 = Ψ^yj (Z_j1)T Ψyj

,W_j2 = Ψ^yZj1

Ψ^yj

Выражения (5.4)-(5.6) имеют явный векторно-матричный вид, что суще-

ственно упрощает их применение в любой вычислительной среде. Оценка ЧХ

(5.5) формируется сразу, без промежуточного вычисления спектральных ко-

эффициентов измеряемой функции и сингулярной помехи, т.е. без расшире-

ния пространства состояний. Кроме того, эта оценка является несмещенной,

поскольку достигается инвариантность результата оценивания к сингуляр-

ной помехе. В силу этого алгоритм нахождения оптимального значения ЧХ

на базе выражений (5.4) и (5.5) можно отнести к классу линейных автоком-

пенсационных алгоритмов.

Следует отметить, что задачу оценивания ЧХ можно было бы решать тра-

диционно путем расширения пространства состояний. Но тогда в вектор

оцениваемых параметров надо было бы включить все спектральные коэффи-

циенты, входящие в линейные комбинации измеряемой функции и сингуляр-

ной помехи. Оценив эти коэффициенты, далее можно находить искомую ЧХ

с учетом этих комбинаций. Однако в [13-16] показано (а также это следует

из (5.4) и (5.5)), что можно сразу найти оценку скалярной ЧХ (без вычисле-

ния указанных коэффициентов), оперируя с обратными матрицами гораздо

меньшего размера (что очень полезно с вычислительной точки зрения).

Дадим оценку усредненной методической погрешности δ_j оценивания ЧХ

применительно к представлению (4.1). Поскольку в (4.1) не учитывается

140

“хвост”

[

]_T

Δ_j (t,x₀) = γ_j (t,x₀) - Ψ^yj (t)

B^yjΛ^yj (x₀)

бесконечного ряда, то имеем (используя символ математического ожида-

ния M [·]), что

[

}

{[

]_T

[

]

δ_j = M

ω_j - ω^∗j

= M ω Ψyj (t)

B^yjΛ^yj (x₀)

]

+ ω {Δ_j (t,x₀)} - ω^∗Yj - ω^∗Δj - ω^∗Sj - ω∗Ξj ,

где

(

)_T

(

)_T

[

]_T

ω^∗Yj =

P^∗j

Y_j, ω^∗Δj =

P^∗j

Δ_j, Δ_j =

Δ(t_n,x_j0),n = 0,N

ω^∗Sj = P^TjS_j, ω^∗Ξj = P^TjΞ_j.

}

{[

]_T

Так как ω Ψ^yj (t)

B^yjΛ^yj (x₀)

= ω^∗yj (условие несмещенности), ω^∗Sj =

= PTj S_j = 0 (условие инвариантности) и M[Ξ_j] = 0 (шум является центри-

рованным), то вытекает равенство

[

]

(

)_T

(

)_T

δ_j = M ω {Δ_j (t,x₀)} -

P^∗j

Δ_j -

P^∗j

Ξ_j

(5.7)

(

)

= ω {Δ_j (t,x₀)} -

P^∗j

^TΔ_j.

Таким образом, методическая погрешность оценивания в среднем опре-

деляется значением ЧХ на “хвосте” бесконечного ряда и линейной оценкой

этого значения.

Необходимые и достаточные условия существования и единственности

решения (5.4), (5.5) задачи оценивания ЧХ измеряемого выхода ДО требуют

невырожденности и соблюдения некоторых ограничений на ранги ряда мат-

риц. Выполнение этих условий на практике обеспечивается рациональным

выбором векторов Ψ^yj (t) и Θ_j (t) базисных функций, числа измерительных

и их расположением, числа степеней свободы в моделях при-

ближенного решения дифференциального уравнения и измеряемого выхода

ДО, а также сингулярной помехи. Все эти вопросы относятся к планированию

измерительного эксперимента. Используя результаты из [9, 10], можно полу-

чить оптимальные оценки параметров предлагаемого метода с учетом стати-

стических характеристик флуктуационных погрешностей измерений. В ста-

тье не рассматриваются эти вопросы, чтобы не перегружать объем статьи,

хотя они и важны для практики, но являются второстепенными для теории

результатами.

Теперь рассмотрим вопрос, связанный с параметрической идентификаци-

ей j-го измеряемого выхода ДО (где j ∈ 1, J). Для этого в соответствии с

141

алгоритмом (5.4), (5.5) необходимо оценить вектор коэффициенто

Y_j в мо-

дели (5.1). Согласно данному алгоритму находятся оптимальные оценки y^∗j(k)

отсчетов измеряемой функции y_j (t) = γ_j (t, x^′0) в узлах t_(k), k = 1, M_t, с уче-

том некорректных наблюдений (2.3). Если истинные значения отсчетов y_j(k)

рассматривать как ЧХ измеряемой функции y_j (t) = γ_j (t, x^′0) с фиксирован-

ным (но неизвестным) начальным условием x^′0, т.е. y_j(k) = ω {γ_j (t, x^′0)}, то

можно воспользоваться оценками

[

(

)_T

(

)_T]-1

{

}

(5.8)

ω^∗j = y^∗j(k) = H^TjZ_j1 Ψ^yj

Ψ^yZj1

Ψ^yj

ω Ψ^yj(t)

j = 0,J,

положив ω{Ψ_yj (t)} = [0,0, . . . ,1,0, . . . , 0]^T - нулевой столбец с единицей в k-й

позиции. Зная оценк

Y∗j=[y^∗j(k),k=1,M_t]^T вектор

Y_j =[y_j(t_(k)),k =1,M_t]^T,

формируем оценки выходных траекторий y^∗j(t) = [Ψ^yj(t)]^T

Y ∗j , j = 1,J, для рас-

сматриваемого ДО.

Таким образом, несмотря на то что рассматриваемый ДО и его выход явля-

ются нелинейными, оценивание ЧХ на выходных траекториях ДО осуществ-

ляется без привлечения традиционно используемых процедур линеаризации

нелинейных функций.

6. Некоторые обобщения, вычислительные аспекты,

практические рекомендации

Задачу оценивания, рассмотренную в разделе 5, также можно обоб-

щить на многомерный случай, который связан с оценкой векторной ЧХ ω =

= [ω_d, d = 1, D]^T на выходных траекториях ДО. В этом случае оценка нахо-

дится в векторно-матричном виде ω^∗j = P^∗jH_j , где

P^∗j = [p^∗jdn, d = 1,D, n = 0,N]

оценка матрицы P_j весовых коэффициентов. Данная матрица находит-

ся из условия минимизации следа корреляционной матрицы K_j = P_j K_jΞP^Tj

этой оценки, кроме того, также должны быть выполнены условия несмещен-

ности и инвариантности, рассмотренные в разделе 5, по отношению ко всем

координатам вектора ω^∗j. Несложный анализ показывает, что данная задача

развивается на D подзадач, связанных с оцениванием по каждой координате

[

вектора ω =

ω_d,d = 1,D

]^T, т.е. достигается максимально возможная деком-

позиция вычислительной процедуры.

Для оценки вычислительной эффективности развитого автокомпенсацион-

ного метода оценивания ЧХ измеряемых функций ДО достаточно воспользо-

ваться результатами из [15], которые демонстрируют возможность реализа-

ции процедуры оценивания в некорректных условиях наблюдения на основе

распределенной обработки данных. В качестве показателя вычислительной

эффективности метода можно принять время, затрачиваемое на получение

искомых оценок. Данное время определяется быстродействием распределен-

ной среды, общим числом операций, необходимых при реализации метода, и

142

способом программирования. В [15] показано, что поскольку процедура оце-

нивания не требует расширения пространства состояний, то реализуемые на

ее основе алгоритмы позволяют достичь значительного выигрыша в вычис-

лительной эффективности. В [15] дана количественная оценка достигаемого

выигрыша на конкретном примере, связанном с решением известной задачи

сглаживания результатов измерений, когда в качестве ЧХ выступает зна-

чение измеряемой функции в фиксированной точке интервала наблюдения.

Показано, что для принятых исходных данных выигрыш по сравнению с из-

вестным расширенным методом наименьших квадратов составил 1,47 раза.

В качестве ЧХ могут рассматриваться выборочное значение j-й изме-

ряемой функции в произвольной точке t^′ ∈ G_t (в этом случае ω {Ψ_y (t)} =

[

]_T

ψ_yk (t^′) ,k = 1,M_t

), значение производной r-го порядка в точке t^′ (в этом

случае ω {Ψ_y (t)} = [ψ^(r)yk (t^′) , k = 1, M_t]^T), значение определенного интеграла

∫ t₀+T

на отрезке [t₀, t₀ + T ] (в этом случае ω {Ψ_y (t)} = [

ψ_yk (τ)dτ,k = 1,M_t]^T)

t₀

и др.

Предложенный алгоритм оценивания можно выполнять на подвижной сет-

ке (“скользящем окне”) {t_j,r+l-1}nj /2l=-¯n

∈ G_t, где (n_j+1 + 1) объем “сколь-

j /2

зящего окна”, r характеризует положение его центрального узла в момент

времени t_jr ∈ G_t, а символ j позволяет занумеровать узлы “скользящего ок-

на” при фиксированном r. Очевидно, что для формирования полномерно-

го “скользящего окна” объемом n_j+1 + 1 должны выполняться ограничения

1 + n_j/2 ≤ r ≤ 1 + N_j - n_j/2 и -n_j/2 ≤ l ≤ n_j/2, в противном случае алго-

ритм оценивания реализуется на неполномерном “скользящем окне” нарас-

тающего объема (это относится к краям временного отрезка [t₀, T ]). Но и в

этом случае имеется ограничение этого объема должно быть достаточно

для обеспечения невырожденности задачи оценивания.

Известно, что точность оценивания сглаженного значения измеряемой

функции наибольшая в середине “скользящего окна”, что также в полной

мере относится к нахождению различных ЧХ (например, производных), ко-

торые соответствуют некоторой произвольной точке t^′ ∈ G_t, являющейся од-

ним из узлов подвижной сетки. Алгоритм оценивания несложно реализовать

и на адаптивном “скользящем окне”, объем которого меняется оптимальным

образом с учетом условий наблюдения за ДО.

7. Иллюстративный пример

Оценим эффективность предлагаемого метода применительно к ракете,

движущейся в однородном поле силы тяжести, при линейном законе расхода

массы и отсутствии сопротивления среды (см. [12, с. 31-34]). Криволинейное

движение ракеты описывается системой дифференциальных уравнений

dz₁/dt = -g₀z^-12, dz₂/dt = c_vη (1 - ηt)^-1 - g₀th (z₁) ,

где время измеряется в секундах, z₁ = x₁

фазовая координата (безраз-

мерная), соответствующая углу β (рад) наклона вектора скорости к гори-

зонту, z₁ = ln [tg (π/4 + β/2)] , z₂ = x₂

величина скорости ракеты (м/с),

143

g₀

ускорение силы тяжести (м/с2), η = x₃ удельный расход массы раке-

ты (с^-1), c_v

относительная скорость отбрасываемых частиц (м/с). Далее

полагаем, что g₀ = 9,80665 (взято из справочника), c_v = 2290, t₀ = 0, T = 70,

x_i0 = x_i (0) ∈ G_xi = [c_i,d_i], i = 1,3, c₁ = 1,0107, d₁ = 2,4362, c₂ = 100, d₂ = 200,

c₃ = r = 0,0060, d₃ = p = 0,0100, в качестве измеряемой функции y использу-

ем угол β, т.е. J = 1, y = β (с учетом скалярного выхода ДО в используемых

далее формулах индекс j опускается).

Для построения численно-аналитического решения принято I₁ = 2 и

I₂ = 1, следовательно, I = I₁ + I₂ = 3, при этом: f₁(t,x) = -g₀x^-12, f₂(t,x) =

= c_vx₃(1 - x₃t)^-1 - g₀th(x₁), f₃(t,x) ≡ 0, m = (m₁,m₂,m₃), M_x1 = 4, M_x2 = 6,

M_x3 = 5, M_x = M_x1M_x2M_x3 = 120, M_t = 11, M_s = 2, ψ_xk(t) = L_(k)(t), L_(m)(x₀) =

= L(m1,m₂,m₃)(x01,x02,x03) = L(m₁)(x10)L(m₂)(x20)L(m₃)(x30), t(k) = 7(k - 1),

k = 1,11.

При расчетах погрешность операций над числами составляла 2,2 · 10^-16, а

результаты вычислений представлены с точностью до четвертого знака после

запятой. Вычисления выполнялись на компьютере средней мощности, аппа-

ратная часть которого построена на базе процессора Intel Core i7 с оператив-

ной памятью объемом 8 Гб и твердотельным диском Samsung 850 Pro. В ка-

честве операционной системы использовалась Windows 10 Pro, а среды чис-

ленного моделирования MATLAB R2018b. Средняя загрузка ресурсов про-

цессора составила 45 %, а оперативной памяти

80 %. При построении при-

ближенного аналитического решения на базе полиномов Лагранжа исполь-

зовалась откомпилированная функция [26], написанная на языке MATLAB,

что позволило увеличить оперативность вычислений в 40 раз за счет опти-

мизации работы с циклическими операциями [27].

Этап 1. Для построения семейства ОИК применялся метод Рунге-Кутты

4-го порядка с контролируемой точностью 10^-5. Время вычислений в части

формирования семейства ОИК составило 17,3 секунд, в части приближенного

аналитического решения на основе построенного семейства ОИК

195,7 се-

кунд. В итоге общее время расчета составило 222,5 секунд (с учетом подго-

товки исходных данных и представления результатов расчета).

С целью наглядности результатов моделирования для оценки точности ис-

пользовалась частная невязка ε_xi = |x_i (t, x₀) - x_i (t, x₀)|, i ∈ {1, 2}, как функ-

ция от времени t и начального условия x₀. Так, на рис. 1 представлена зависи-

мость частной невязки ε_x1 от t и x₁₀ для фиксированных значений x₂₀ = 104

и x₃₀ = 0,0063. При этом на исходной области {Gx0,Gt} имеем общую

невязку ε_x1 = maxεx1 (x0) = 0,0020 (где εx1 (x0) = max|x1 (t,x0) - x1 (t,x0)|),

x₀

что составляет

0,3237 %. Данный максимум соответствует{узлу (}= 27,

x₁₀ = 2,1466, x₂₀ = 104, x₃₀ = 0,0063). На усеченной области

Gx0,Gt

(где

Gx0 = {[1,3170; 1,7454] , [120; 180] , [0, 0070; 0,0090]} и Gt = [7,63]) получили об-

щую невязку ε_x1 = 0,0004, что составляет 0,1853 %. Данный максимум соот-

ветствует узлу (t = 36, x₁₀ = 1,5065, x₂₀ = 128, x₃₀ = 0,0070).

На рис. 2 представлена зависимость частной невязки ε_x2 от t и x₃₀ для

фиксированных значений x₁₀ = 2,1466 и x₂₀ = 124. При этом на исходной обла-

сти {G_x0, G_t} имеем общую невязку ε_x2 = max ε_x2(x₀) = 4,0542 (где ε_x2(x₀) =

x₀

144

0,10

0,08

0,06

0,04

0,02

x₁₀

50 0

Рис. 3. Зависимость частной невязки ε_β от t и x₁₀ для фиксированных значе-

ний x₂₀ и x₃₀.

Учитывая, что выход ДО может быть представлен в виде

y = β = 2{arctg[exp(z₁)] - π/4},

на рис. 3 представлен трехмерный график частной невязки

εβ = |γ (t, x0) - γ^∗ (t, x0)|

как функции от t и x₁₀ для фиксированных значений x₂₀ = 108 и x₃₀ = 0,0063.

Соответственно на рис. 4 рассмотрен случай зависимости ε_β от t и x₃₀ для

фиксированных значений x₁₀ = 2,1466 и x₂₀ = 108. При этом на исходной об-

ласти {G_x0, G_t} имеем общую невязку ε_β = max ε_β(x₀) = 0,0988 (где ε_β (x₀) =

x₀

= max

β (t, x₀) - β (t, x₀) |), что составляет 0,3303 %. Данный максимум со-

ответствует у{лу (t =}31, x10 = 2,1466, x20 = 108, x30 = 0,0063). На усечен-

ной области

Gx0,Gt

получили общую невязку ε_β = 0,0199, что состав-

ляет 0,2197 %. Данный максимум соответствует узлу (t = 38, x₁₀ = 1,5065,

x₂₀ = 128, x₃₀ = 0,0070).

Соответственно для производной y⁽¹⁾ = β⁽¹⁾ на исходной области {G_x0, G_t}

имеем общую невязку

ε^(1)β = maxε(1)β(x0) = 5,4919

x₀

(где ε^(1)β(x₀) = max

β⁽¹⁾ (t,x₀) - β⁽¹⁾ (t,x₀) |), что составляет 6,9520 %. Дан-

ный максимум соответствует узлу (t = 1, x₁₀ = 2,4362, x₂₀ = 100, x₃₀ = 0,0060).

}

{G_x

На усеченной области

0,Gt

получили общую невязку ε^(1)β = 3,1612,

146

0,10

0,08

0,06

0,04

0,02

Рис. 4. Зависимость частной невязки ε_β от t и x₃₀ для фиксированных значе-

ний x₁₀ и x₂₀.

что составляет

5,5860 %. Данный максимум соответствует узлу (t = 8,

x₁₀ = 1,7354, x₂₀ = 120, x₃₀ = 0,0070).

Результаты численного эксперимента наглядно показывают возможность

качественного описания как входных, так и выходных параметров ДО с помо-

щью разработанного численно-аналитического метода. Для уменьшения нега-

тивных краевых эффектов необходимо сужать области задания параметров

tиx₀.

Этап 2. При реализации данного этапа использовались также следую-

щие данные: x^′10 = 1,7354, x^′20 = 112, x^′30 = 0,0800, s (t) = c₁θ₁ (t) + c₂θ₂ (t),

c₁ = 5, θ₁ (t) = sin (0,64t), c₂ = 15, θ₂ (t) = exp (-0,07t), K_Ξ = diag (σ,... ,σ),

σ = π/360, {t_n}^Nn=0, N = 70, t_n - t_n-1 = 1, n = 20, 11 ≤ r ≤ 61. Алгоритм оце-

нивания реализовывался на полномерном “скользящем окне” с 21 узлом, при

этом первая оценка измеряемого параметра и его производной относятся к

текущему моменту времени t₂₀ = 20, а последняя к моменту t₇₀ = 70. Имен-

но при t₂₀ = 20 было сформировано первое полномерное “скользящее окно”,

а при t₇₀ = 70 последнее. Поскольку все оценки привязываются к середине

“скользящего окна”, то первая полученная оценка соответствовала моменту

t₁₀ = 10, а последняя

моменту t₆₀ = 60. Следовательно, приводимые да-

лее характеристики точности относятся к усеченному отрезку времениGt =

= [10, 60].

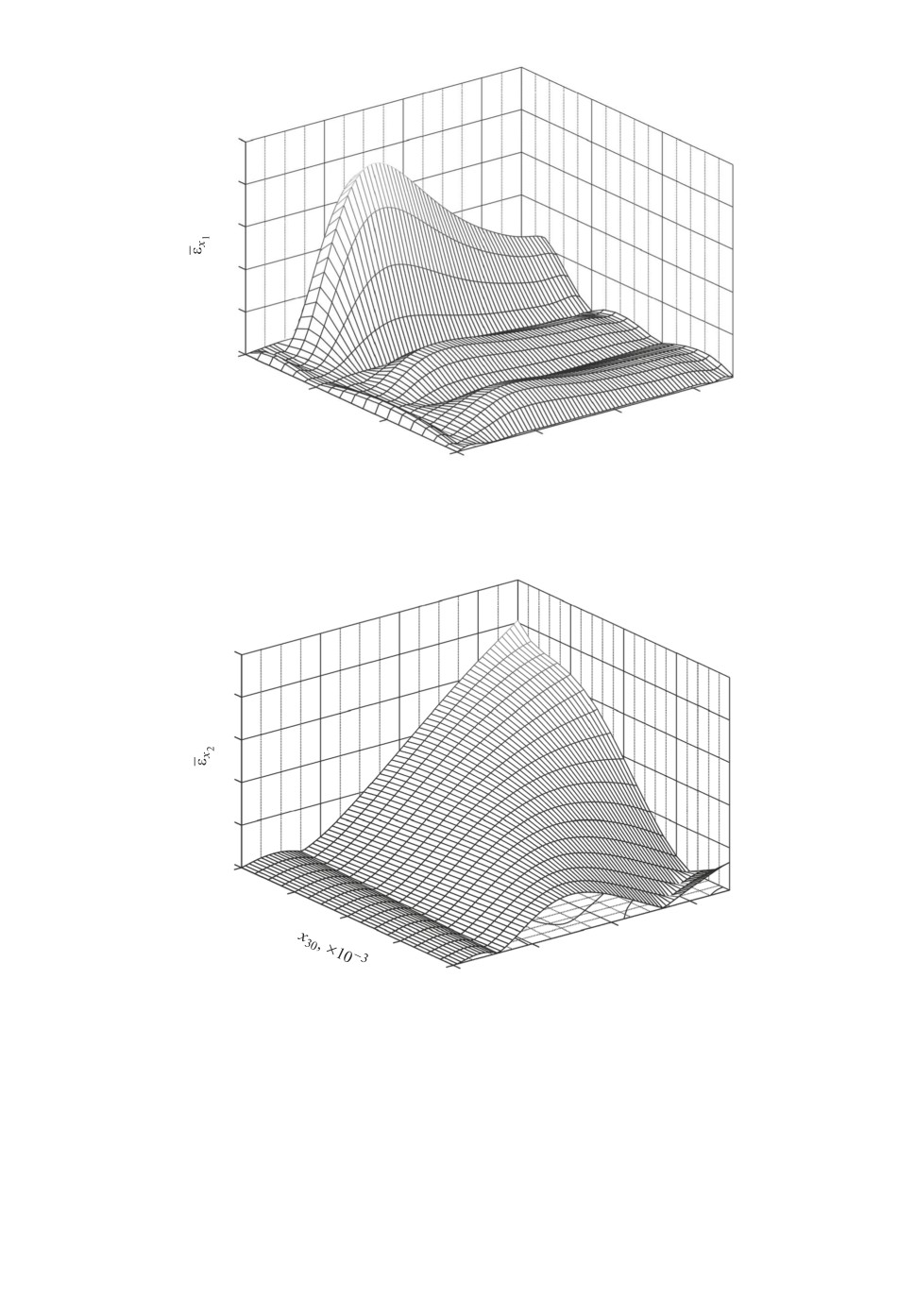
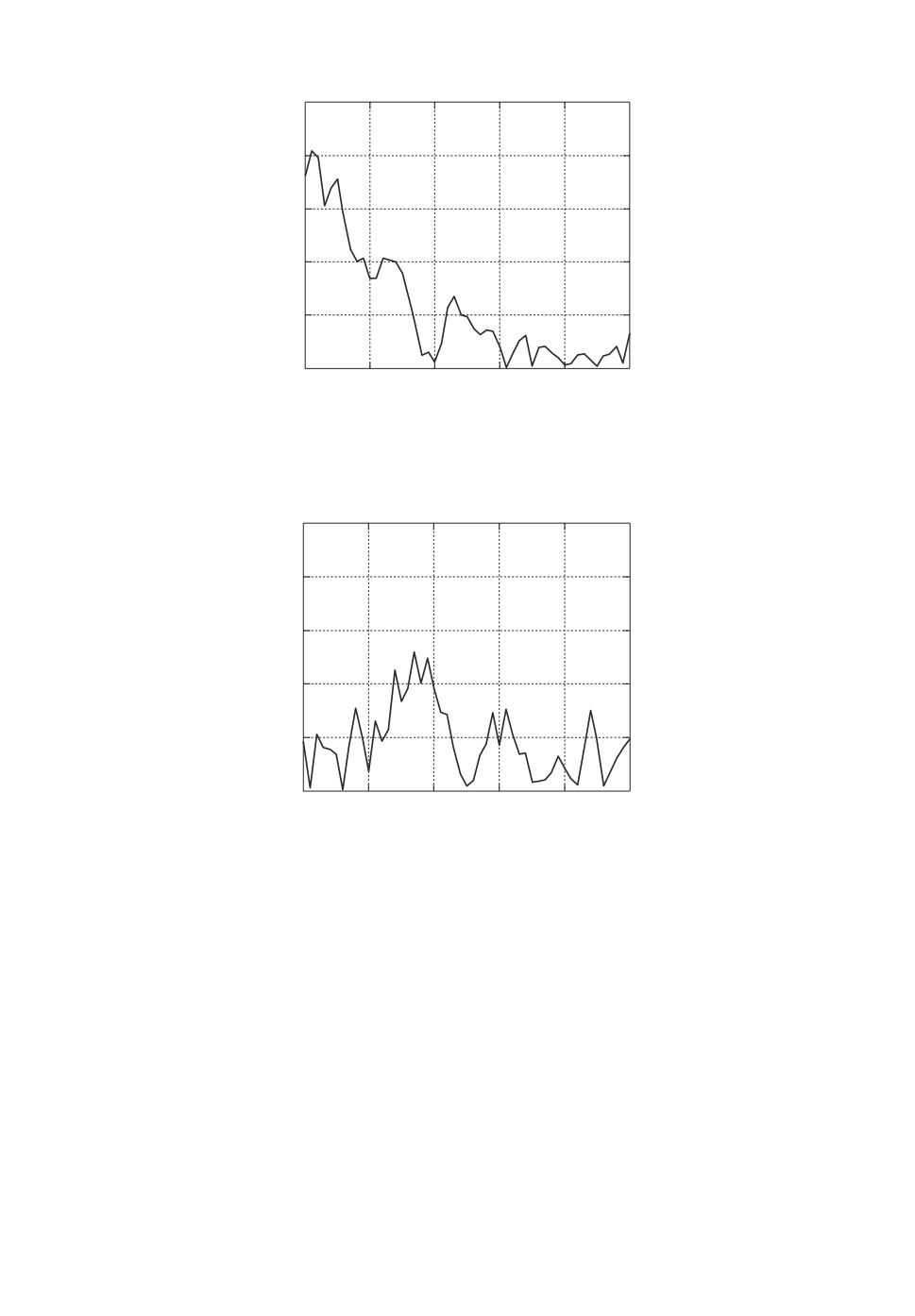
На рис. 5 приведены графики зависимости, характеризующие сингуляр-

ную помеху s (t). С использованием датчика случайных чисел и принятых

исходных данных было сформировано уравнение наблюдения, при этом на

рис. 6 представлены графики истинного значения измеряемой функции y = β

и наблюдения h = y + s + ξ. Начиная с момента времени t_n = 20 для каж-

дого положения “скользящего окна” (всего 51 положение, т.е. 11 ≤ r ≤ 61)

147

q₁, q₂

-5

Рис. 5. Зависимости, характеризующие сингулярную помеху: а семейство

базисных функций, б сингулярная помеха.

b, h

100

Рис. 6. Графики измеряемой функции и наблюдения: сплошная линия из-

меряемая функция; точечная линия наблюдение.

формировались текущие оценки β^∗n и β^n1)∗, соответствующие центральному

узлу. Для описания выходной координаты y (t) = β (t) в пределах “скользя-

щего окна” использовалась линейная комбинация из трех первых полиномов

Лежандра, т.е. в формуле (4.1) принималось: M_t = 3,

[(

)_k-1]

d^k-1

τ² - 1

ψ_yk(t) = P_k-1 (τ) =

2k-1 (k - 1)!

dτ^k-1

k = 1,3, τ = τ (t), τ ∈ [-1,1].

Для перехода от параметра τ ∈ [-1, 1] к временной координате

[

]

t ∈ tj,r-nj/2-1, tj,r+n_j/2-1

∈G_t

148

e_b

1,0

0,8

0,6

0,4

0,2

Рис. 7. Невязка оценивания выходной координаты.

(1)*

-2

eb , ´10

Рис. 8. Невязка оценивания производной выходной координаты.

применялось линейное преобразование:

[

(

)]

t=2^-1

tj,r-nj/2-1 + tj,r+n_j/2-1 - τ tj,r-n_j/2-1 - tj,r+n_j/2-1

Далее представлены графики зависимости частной невязки ε^∗β оценивания

выходной координаты (рис. 7) и ее производной ε^(1)∗β (рис. 8) в от времени при

фиксированном начальном условии x^′0 = [1,7354; 112; 0,0800]^T, при этом об-

щая невязка для выходной координаты составляет ε^∗β = max

ε∗β = 0,8162 (со-

ответственно 1,5717 %), а для производной ε^(1)∗β = max

ε(1)∗β = 0,0518 (соответ-

ственно 5,0601 %).

149

Проводился сравнительный анализ по оперативности (т.е. по времени фор-

мирования оценок, выраженном в секундах) разработанного автокомпенса-

ционного метода (АМ) и известного расширенного метода наименьших квад-

ратов (РМНК). Для одного фиксированного положения “скользящего окна”

фиксировалось частное время (T_РМНК и T_АМ) построения оценки производ-

ной β⁽¹⁾ в середине этого окна (один эксперимент). Проводилась тысяча та-

ких экспериментов с последующим усреднением п{ученных результатов,}ри

этом для частных результатов имеем T_РМНК ∈

71 · 10^-6, . . . , 123 · 10^-6

{

}

T_АМ ∈

31 · 10^-6, . . . , 54 · 10^-6

, а общий усредненный выигрыш по оператив-

ности состави

T_РМНК

T_АМ = 2,32 раза (здесь черта означает усреднение).

Также обнаружено, что при наличии в уравнении наблюдения одновре-

менно гармонической и экспоненциальной составляющих сингулярной помехи

РМНК приводит к некорректным оценкам производной для всех положений

“скользящего окна”, что объясняется известным эффектом “размазывания

точности” при расширении пространства состояний. Удовлетворительный по

точности результат оказался возможным только при наличии одной (гармо-

нической) составляющей, в этом случае частная невязка составила 0,0025 для

последнего положения “скользящего окна”.

Результаты моделирования подтверждают возможность эффективного ре-

шения задачи оценивания ЧХ на выходных траекториях ДО даже при некор-

ректных наблюдениях, содержащих сингулярную помеху.

8. Заключение

Развитый численно-аналитический метод исследования ДО ориентирован,

в первую очередь, на случаи, связанные с решением широкого круга при-

кладных задач, требующих вычислений в реальном времени. Данный метод

предполагает вынесение основного объема вычислений на первый (предва-

рительный) этап, не связанный непосредственно с наблюдением ДО. К кон-

цу этого этапа на базе семейства ОИК необходимо сформировать аналити-

ческое решение дифференциального уравнения и аналитическое выражение

для измеряемого выхода ДО, справедливые для заданной области изменения

временной координаты, начальных условий и других характерных парамет-

ров. К первому этапу также относятся операции, связанные с формировани-

ем вектор-столбца или матрицы весовых коэффициентов оптимального оце-

нивания, учитывающих спектральный состав измеряемых параметров, син-

гулярной помехи и статистические характеристики флуктуационного шума.

На втором (основном) этапе реализуются операции, связанные с оператив-

ным оцениванием значений ЧХ измеряемых функций по результатам некор-

ректных наблюдений, а также решением других целевых задач, требующих

использования полученных численно-аналитических описаний входных и вы-

ходных переменных ДО. Любые ЧХ поведения ДО находятся в виде скаляр-

ного произведения вектора наблюдений и соответствующего вектора весовых

коэффициентов.

Выражаю свою благодарность моим аспирантам Раду П.Ю. и Кондра-

шову А.Г. за помощь в проведении вычислительного эксперимента.

150

СПИСОК ЛИТЕРАТУРЫ

Александров А.Г. Оптимальные и адаптивные системы. М.: Высш. шк., 1989.

Пантелеев А.В., Бортаковский А.С. Теория управления в примерах и задачах.

М.: Высш. шк., 2003.

Красовский А.А. Науковедение и состояние теории процессов управления. Об-

зор // АиТ. 2000. № 4. С. 3-19.

Krasovskii A.A. Theory of Science and Status of the Control Teory // Autom. Re-

mote Control. 2000. V. 61. No. 4. Part 1. P. 537-553.

Жданюк Б.Ф. Основы статистической обработки траекторных измерений. М.:

Сов. радио, 1978.

Булычев Ю.Г., Манин А.П. Математические аспекты определения движения

летательных аппаратов. М.: Машиностроение, 2000.

Булычев Ю.Г., Васильев В.В., Джуган Р.В. и др. Информационно-измеритель-

ное обеспечение натурных испытаний сложных технических комплексов / Под

ред. А.П. Манина и В.В. Васильева. М.: Машиностроение - Полет, 2016.

Булычев Ю.Г., Бурлай И.В., Манин А.А. Аналитическое конструирование си-

стем управления на основе метода опорных интегральных кривых // АиТ. 1994.

№ 7. С. 37-48.

Bulychev Yu.G., Burlai I.V., Manin A.A. Analytic Construction of Control Systems

by the Method of Supporting Integral // Autom. Remote Control. 1994. V. 55. No. 7.

Part 1. P. 954-963.

Булычев Ю.Г., Манин А.А. Синтез адаптивных систем оптимального управ-

ления стохастическими объектами на основе прогнозирующей модели // АиТ.

1995. № 9. С. 81-92.

Bulychev Yu.G., Manin A.A. Synthesis of Adaptive Optimal Control Systems for

Stochastic Objects from a Forecast Model // Autom. Remote Control. 1995. V. 56.

No. 9. Part 2. P. 1268-1277.

Брандин В.Н., Васильев А.А., Худяков С.Т. Основы экспериментальной косми-

ческой баллистики. М.: Машиностроение, 1974.

10.

Брандин В.Н., Разоренов Г.Н. Определение траекторий космических аппаратов.

М.: Машиностроение, 1978.

11.

Льюнг Л. О точности модели в идентификации систем // Изв. АН. Техн. кибер-

нетика. 1992. № 6. С. 55-64.

12.

Воробьев Л.М. К теории полета ракет. М.: Машиностроение, 1970.

13.

Булычев Ю.Г., Мельников А.В. Численно-аналитический метод исследования

поведения динамической системы по результатам некорректных наблюдений без

расширения пространства состояний // Журн. вычисл. матем. и мат. физ. 2019.

Т. 59. № 6. С. 937-950.

14.

Леонов В.А., Поплавский Б.К. Фильтрация ошибок измерений при оценивании

линейного преобразования полезного сигнала // Изв. АН. Техн. кибернетика.

1992. № 1. С. 163-170.

15.

Булычев Ю.Г., Елисеев А.В. Вычислительная схема инвариантно-несмещенного

оценивания значений линейных операторов заданного класса // Журн. вычисл.

матем. и мат. физ. 2008. Т. 48. № 4. С. 580-592.

16.

Булычев Ю.Г., Елисеев А.В., Бородин Л.И. и др. Обобщенное инвариантно-

несмещенное маскирование и оценивание информационных процессов в усло-

виях мультиструктурных помех // АиТ. 2010. № 4. С. 140-149.

151

Bulychev Yu.G., Eliseev A.V., Borodin L.I., et al. Generalized Invariant-Unbiased

Masking and Estimation of Informational Processes with Multistructural Noise //

Autom. Remote Control. 2010. V. 71. No. 4. P. 672-680.

17. Булычев Ю.Г. Метод опорных интегральных кривых решения задачи Коши для

обыкновенных дифференциальных уравнений // Журн. вычисл. матем. и мат.

физ. 1988. Т. 28. № 10. С. 1482-1490.

18. Булычев Ю.Г. Методы численно-аналитического интегрирования дифференци-

альных уравнений // Журн. вычисл. матем. и мат. физ. 1991. Т. 31. № 9.

С. 1305-1319.

19. Бибиков Ю.Н. Общий курс обыкновенных дифференциальных уравнений. Л.:

Изд-во Ленингр. ун-та, 1981.

20. Треногин В.А. Функциональный анализ. М.: Наука, 1980.

21. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения.

М.: Наука, 1985.

22. Канторович Л.В., Акилов Г.П. Функциональный анализ. М.: Наука, 1977.

23. Бабенко К.И. Основы численного анализа. М.: Наука, 1986.

24. Иванов В.В. Методы вычислений на ЭВМ. Киев.: Наук. думка, 1986.

25. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: БИНОМ.

Лаборатория знаний, 2008.

26. Mex-Files // GNU Octave [Электронный ресурс]

URL: https://octave.org/doc/interpreter/Mex_002dFiles.html.

27. Techniques to Improve Performance // MATLAB Documentation [Электронный

ресурс] URL: https://www.mathworks.com/help/matlab/matlab_prog/techniques-

for-improving-performance.html.

Статья представлена к публикации членом редколлегии М.М. Хрусталевым.

Поступила в редакцию 18.09.2019

После доработки 14.11.2019

Принята к публикации 28.11.2019

152