Автоматика и телемеханика, № 7, 2020
Стохастические системы
© 2020 г. А.С. АРХИПОВ (ege3145@yandex.ru),
К.В. СЕМЕНИХИН, д-р физ.-мат. наук (siemenkv@rambler.ru)
(Московский авиационный институт)
МИНИМАКСНОЕ ЛИНЕЙНОЕ ОЦЕНИВАНИЕ
ПО ВЕРОЯТНОСТНОМУ КРИТЕРИЮ
ПРИ НАЛИЧИИ УНИМОДАЛЬНЫХ ПОМЕХ
И ОГРАНИЧЕННЫХ ПАРАМЕТРОВ1
Рассмотрена модель линейной регрессии с вектором ограниченных па-
раметров и центрированным вектором помех, имеющим неопределенное
унимодальное распределение, но известную ковариационную матрицу.
Сформулирована задача минимаксного оценивания линейной комбинации
неизвестных параметров с использованием вероятностного критерия. Ми-
нимаксная оценка определяется в результате минимизации вероятностной
границы на области возможных значений дисперсии и квадрата смещения
всевозможных линейных оценок. Установлена меньшая консервативность
полученного робастного решения в сравнении с более широкими классами
распределений.
Ключевые слова: минимаксная оценка, вероятностный критерий, ограни-
ченные параметры, унимодальные помехи, наихудшее распределение.
DOI: 10.31857/S0005231020070028
1. Введение
Минимаксные постановки задач оценивания возникают при необходимости
построить оценку, имеющую наилучшие показатели погрешности из расчета
на наихудший случай сочетания неопределенных характеристик модели на-
блюдения. При такой трактовке проблема оценивания формулируется в виде
задачи оптимизации, целью которой является выбор оценки, доставляющей
минимум максимальному значению погрешности. При выборе оптимизаци-
онной формулировки необходимо учитывать, что широкие классы неопреде-
ленности приводят к сильно перестраховочным и потому малоэффективным
статистическим решениям. Поэтому поиск минимаксных постановок, кото-
рые приводят к оценкам, сочетающим в себе свойства робастности и эффек-
тивности, остается актуальной проблемой. Одним из вариантов решения этой
проблемы является сравнительный анализ решений минимаксных задач, со-
ответствующих различным классам распределений.
В данной статье основным показателем качества оценивания выступает ве-
роятность ошибки, т.е. вероятность превышения ошибкой оценки заданного
1 Результаты работы получены в рамках выполнения госзадания № 9.7555.2017/БЧ.
14
порога. Этот вероятностный критерий был использован Бахадуром для опре-
деления специального понятия асимптотической эффективности [1]. В от-
личие от классического подхода, предложенного Фишером и развитого Рао
и Крамером, это понятие основано на сравнении вероятности ошибки, а не
среднеквадратической погрешности [2]. Неасимптотические границы для ве-
роятности ошибки были получены при решении статистических задач рас-
познавания и обучения [3]. При построении минимаксных линейных оценок
скалярных параметрических функций по вероятностному критерию в [4] ис-
пользовалось обобщенное неравенство Чебышёва. Для оценивания многомер-
ных параметров, близких к минимизации вероятности ошибки является метод
доверительного оценивания, при котором требуется построить доверительное
множество наименьшего размера. Для моделей, содержащих одновременно
гауссовские помехи и неопределенные параметры, метод нелинейного довери-
тельного оценивания разработан в [5, 6]. Для стохастических многошаговых
систем метод мультиоценок разработан в [7]. Задача минимаксного оцени-
вания по вероятностному критерию при наличии неограниченных неизвест-
ных параметров и случайных ошибок с неопределенным распределением и
частично заданной ковариационной матрицей рассматривалась в [8]. В срав-
нении с этой работой специфика данной статьи определяется тем, что на
неизвестные параметры накладываются априорные ограничения, а совмест-
ное распределение помех принадлежит классу унимодальных распределений.
Для построения минимаксных статистических решений в условиях неопре-
деленности, описываемой с помощью ограничений на математические ожи-
дания и ковариационные матрицы, применяется методология полуопределен-
ного программирования и техника линейных матричных неравенств [9, 10].
Однако наихудшие значения вероятностных показателей качества на клас-
се распределений, определяемых лишь условиями на моментные характе-
ристики второго порядка, оказываются достаточно пессимистичными. Это
легко видно из сравнения неравенств Чебышёва и Гаусса: сужение класса
до унимодальных распределений позволяет снизить вероятностную границу
в 9/4 раз [11].
Важные факты об унимодальных распределениях собраны в [12]. Утверж-
дение о том, что равномерное распределение доставляет минимум вероятно-
сти попадания в выпуклое множество на классе унимодальных распределе-
ний, обосновано в [13-15]. Если дополнительно наложены моментные огра-
ничения, то эту оптимизационную постановку для некоторых специальных
классов унимодальных распределений можно свести к задаче полуопреде-
ленного программирования [16].
В настоящей статье рассматривается задача минимаксного оценивания ли-
нейной комбинации ограниченных параметров в модели линейной регрессии
при наличии центрированных помех с неопределенным распределением, но
фиксированными дисперсиями и ковариациями. Основное внимание уделя-
ется случаю симметричного унимодального распределения. Для этого клас-
са помех разработан метод построения неасимптотических доверительных
множеств [17, 18]. Благодаря [19], радиус доверительного интервала можно
выбирать оптимальным образом на основе неулучшаемой границы для веро-
ятности превышения симметричной унимодальной величиной заданного по-
15
рога. Таким образом, решение задачи минимаксного оценивания для разных
классов распределений получается за счет использования известных вероят-
ностных границ, следующих из неравенств Селберга, Гаусса, Высочанского-
Петунина и др.
2. Постановка задачи
Рассмотрим линейную регрессионную модель
(1)
X = 〈a,θ〉, Y = Bθ + η,
в которой скалярная величина X подлежит оцениванию по фиксированному
набору наблюдений, представленному в виде вектора Y ∈ Rn (скобки 〈·, ·〉
обозначают скалярное произведение).
Допустим, что вектор неизвестных параметров θ принадлежит заданно-
му компактному множеству Θ ⊂ Rp, а вектор случайных помех η ∈ Rn имеет
нулевое математическое ожидание и известную положительно определенную
матрицу ковариаций K:
(2)
Mη = 0, cov{η,η} = K ≻ O.
Матрица регрессии B ∈ Rn×p и вектор коэффициентов a ∈ Rp предполага-
ются заданными, а информационная матрица D = B∗K-1B - невырожден-
ной (символ∗ обозначает транспонирование).
Распределение вектора помех Pη будем считать неопределенным с точно-
стью до принадлежности некоторому классу H(K), который содержит n-мер-
ные распределения с учетом ограничений на моментные характеристики (2).
Это условие будем записывать кратко в виде η ∼ H(K).
В качестве H(K) будут рассматриваться:
1) класс U(K) симметричных унимодальных распределений;
2) класс V(K) унимодальных распределений;
3) класс P(K) всевозможных распределений.
Условие унимодальности случайного вектора η ∈ Rn означает, что при
любом выборе вектора коэффициентов g ∈ Rn унимодальной будет величи-
на 〈η, g〉. В [12] это свойство многомерного распределения именуется линейной
унимодальностью. Выбор этого понятия связан с двумя причинами. Во-пер-
вых, его проверка требует лишь анализа линейных форм случайного вектора
вместо изучения многомерного распределения. Во-вторых, понятие линейной
унимодальности в сравнении с другими видами многомерной унимодальности
определяет наиболее широкий класс распределений, в котором соблюдается
инвариантность относительно линейных преобразований случайного вектора.
По определению
(3)
η ∼ U(K)
⇐⇒
〈η, b〉 ∼ U(d)
∀b∈Rn, d ≥ 0: d = 〈Kb,b〉,
где U(d) обозначает класс симметричных унимодальных распределений на
прямой с нулевым средним и дисперсией d. Для скалярной величины усло-
вие ξ ∼ U(d), помимо равенства Dξ = d, означает, что вероятность попадания
16
в любое борелевское множество B можно записать в виде
∫
(4)
P{ξ ∈ B} = (1 - q)δm(B) + q
f (x) dx,
B
где q
число из отрезка [0, 1], δm
мера Дирака, сосредоточенная в точ-
ке m = 0, f(x) четная плотность вероятности, невозрастающая на полу-
оси (0, ∞). Таким образом, для величины ξ ∼ U(d) точка m = 0 является од-
новременно центром симметрии, математическим ожиданием и модой.
В случае ξ ∼ V(d) имеет место представление (4), в котором плотность ве-
роятности f(x) монотонно не возрастает при x > m и монотонно не убывает
при x < m, хотя точка m не обязана совпадать с нулем, а плотность веро-
ятности f(x) может быть несимметричной. Поэтому унимодальная величина
ξ ∼ V(d) имеет те же моментные характеристики Mξ = 0, Dξ = d, но произ-
вольную моду m. Теперь формальное определение класса V(K) можно дать
аналогично (3).
Описанные классы распределений связаны включениями
U (K) ⊂ V(K) ⊂ P(K).
При построении оценок условие η ∼ U(K) будет рассматриваться в каче-
стве основного предположения о распределении помех, а классы V(K) и P(K)
будут использоваться для анализа консервативности построенных оценок.
Рассмотрим линейную оценку величины X
(5)
X
= 〈f, Y 〉 + c,
где f ∈ Rn вектор коэффициентов (оцениватель), а c ∈ R - коэффициент
сдвига.
Пусть положительное число h определяет величину порога, превышение
которого модулем ошибки оценивания
X- X является весьма нежелатель-
ным событием. Вероятность этого события
{
}
(6)
P
|X - X| ≥ h ,
называемая далее вероятностью ошибки, характеризует надежность оценки:
чем меньше вероятность (6), тем более надежна оценка
X. Следовательно,
для построения наиболее надежной оценки вероятность ошибки требуется
минимизировать. Однако непосредственно сделать это невозможно, так как
(6) зависит и от неопределенного распределения вектора помех, и от вектора
неизвестных параметров. При этом пополнить или уточнить информацию об
этих характеристиках невозможно в силу ограниченности объема наблюде-
ний. Поэтому для формулировки корректной оптимизационной постановки
задачи оценивания будем использовать минимаксный подход.
Итак, требуется минимизировать гарантированное значение вероятности
ошибки в рамках имеющейся априорной информации за счет выбора коэф-
фициентов оценки:
{
}
(7)
sup sup
P
|X - X| ≥ h
→ min
f ∈Rn,c∈R
θ∈Θ η∼H(K)
17
Если пара
f,ĉ) доставляет минимум в (7), то соответствующую оценку
X=
f,Y〉+ĉбудем называть минимаксной, а векто
f при ĉ = 0 мини-
максным оценивателем.
Таким образом, цель данной работы решение задачи минимаксного оце-
нивания по вероятностному критерию (7) при наличии ограниченных неиз-
вестных параметров и случайных помех с неопределенным унимодальным
распределением.
Помимо построения минимаксной оценкиX, важным представляется на-
хождение наихудшего распределенияPη, на котором достигается максимум
вероятности ошибки на классе H(K):
{
}
{
}
sup P
|X-X|≥h
=P
|X-X|≥h
,
η∼H(K)
гдеP символ вероятности, вычисляемой в предложении η ∼Pη.
Замечание 1. Предположение о том, что ковариационная матрица век-
тора помех фиксирована, не является принципиальным. Условие (2) можно
без ограничения общности заменить на матричное неравенство cov{η, η} ≼ K,
которое позволяет учесть ограниченность дисперсий и неопределенность ко-
вариаций. Однако рассмотрение более общих множеств неопределенности для
матриц cov{η, η} выходит за рамки данной статьи.
3. Вероятностные границы
Определим гарантированное значение вероятности ошибки
{
}
(8)
sup P
|X - X| ≥ h
η∼H(K)
при условии, что задано определенное значение вектора параметров θ. В этом
случае дисперсия и смещение оценки (5) также будут фиксированы:
(9)
d = D X = 〈Kf,f〉,
r = M{ X - X} = c + 〈B∗
f - a,θ〉.
Тогда вероятность ошибки равна P{|ε + r| ≥ h}, где ε
центрированная
ошибка. Она имеет нулевое математическое ожидание, дисперсию d и распре-
деление из соответствующего класса, который будем обозначать как H(d).
Если H(d) совпадает с одним из определенных выше классов U(d), V(d)
или P(d), то условия ε ∼ H(d) и -ε ∼ H(d) равносильны, поэтому знак смеще-
ния r не имеет значения. Благодаря этому факту, определим вероятностную
границу
(10)
πHh(d,r2) = sup
P{|ε + r| ≥ h}
ε∼H(d)
как функцию пары аргументов: дисперсии d и квадрата смещения r2.
18
Для решения задачи минимаксного оценивания по вероятностному кри-
терию принципиальным является следующий вопрос: “Совпадает ли грани-
ца (10) с гарантированным значением вероятности ошибки (8)?”
Как показывает приведенная ниже теорема, ответ на этот вопрос положи-
телен, по крайней мере, для двух классов U(K) или P(K).
Теорема 1. Для любой линейной оценки (5) гарантированное значение
вероятности ошибки при фиксированном значении θ равно соответствую-
щей вероятностной границе:
{
}
(11)
sup P
|X - X| ≥ h
= πHh (d,r2
),
η∼H(K)
где d, r определяются выражениями (9), а H(K) любой из двух классов
распределений U(K) или P(K).
Доказательства этой и последующих теорем вынесены в Приложение.
В доказательстве теоремы 1 используется специальная конструкция векто-
ра помех, имеющего наихудшее распределение. Однако для того чтобы утвер-
ждать, что это распределение действительно принадлежит классу V(K), не
хватает факта об унимодальности свертки унимодального и симметричного
унимодального распределений. Но такое утверждение без дополнительных
предположений неверно. К тому же вид наихудшего распределения центри-
рованной ошибки в задаче (10) в случае H = V не известен. Поэтому для
класса унимодальных распределений V(K) можно утверждать лишь нера-
венство
{
}
sup P
|X - X| ≥ h
≤ πVh(d,r2).
η∼V(K)
О вероятностных границах известно следующее:
√
4d/(9h2),
d ≤ 3h2/4,
|r| ≤ (1 - 1/
2)h,
√
√
(12)
πUh(d,r2) =
1 - h/
3d, d ≥ 3h2/4,
|r| ≤ (1 - 1/
2)h,
1,
|r| ≥ h,
4(d + r2)/(9h2),
d + r2 ≤ 3h2/8,
(13) πVh (d, r2) ≤ πVh (d, r2) =
4(d + r2)/(3h2) - 1/3,
3h2/8 ≤ d + r2 ≤ h2,
1,
d+r2 ≥h2;
d/(d + (h - |r|)2), d + r2 ≤ |r|h,
(14)
πPh(d,r2) =
(d + r2)/h2,
|r|h ≤ d + r2 ≤ h2,
1,
d+r2 ≥h2.
19
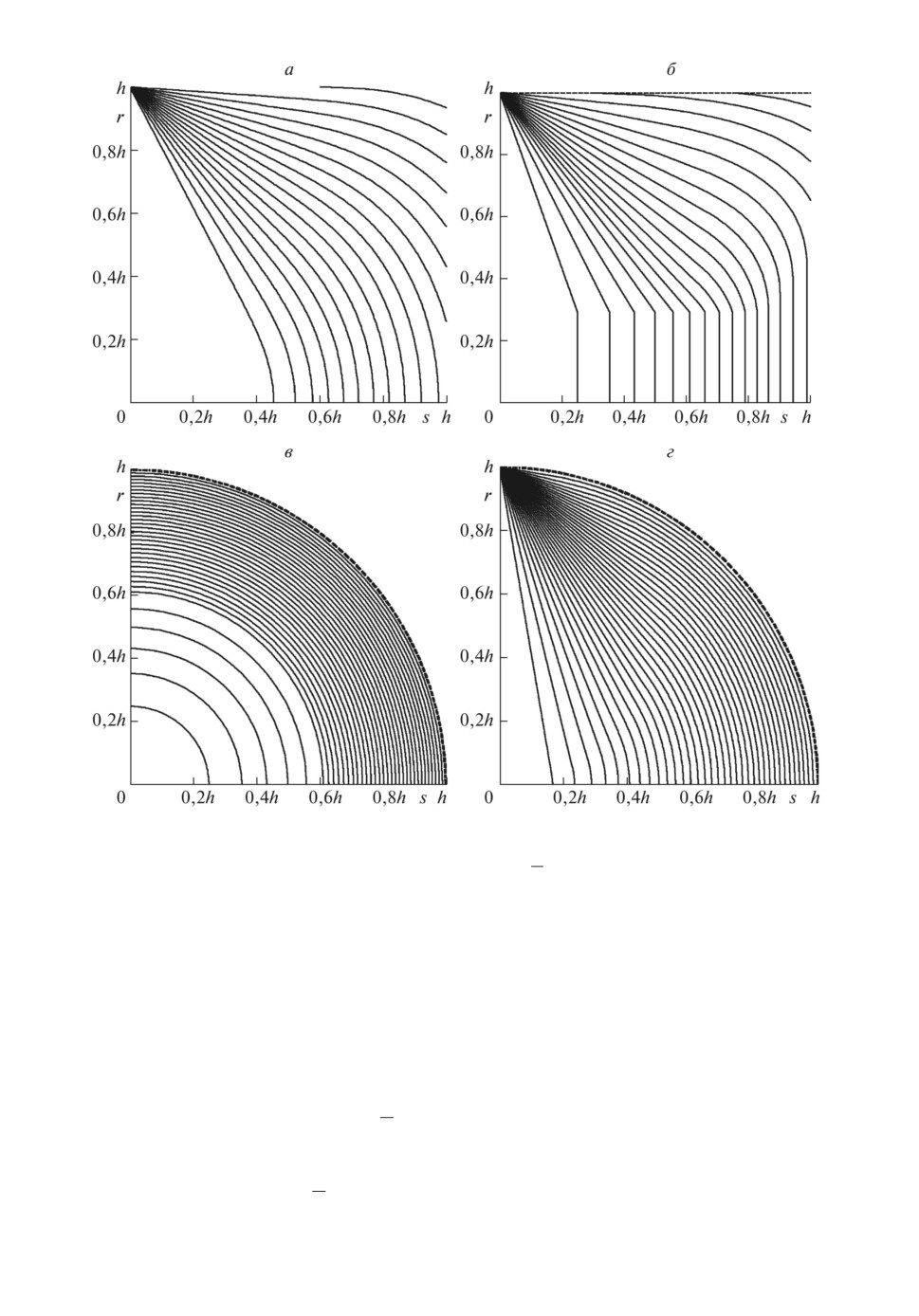
Рис. 1. Линии уровня а вероятности нормальной ошибки πNh (s2, r2) = α и
вероятностных границ б πUh (s2, r2) = α, в πVh(s2, r2) = α, г πPh(s2, r2) =
= α для α = k/36, k = 1,...,35.
Полное выражение для границы πUh на классе симметричных унимодаль-
ных распределений показано в [19]. Первые два случая в (12) соответствуют
ситуации, при которой смещение оценки составляет меньше 29 % от порога
ошибки h. При этом πUh совпадает с правой частью неравенства Гаусса, кото-
рое описывает неулучшаемую границу в ситуации нулевого смещения [11].
К сожалению, замкнутое выражение для границы πVh на классе унимо-
дальных распределений не известно. Тем не менее вместо πVh можно ис-
пользовать ее оценку сверху πVh , известную из неравенства Высочанского-
Петунина [20, 21]. Выражение (13) полностью определяется вторым моментом
M(ε + r)2 = d + r2, в то время как мода является неопределенной. В первом
случае из (13) граница πVh по форме совпадает с тем, что давало бы неравен-
ство Гаусса для величины с нулевой модой.
20
Наконец, πPh представляет собой правую часть неравенства Селберга, опи-
сывающую вероятностную границу для величины с произвольным распреде-
лением, но фиксированными средним и дисперсией [11]. Во втором случае
из (14) соответствующая граница определяется неравенством Маркова, в ко-
тором используется только второй момент.
В дополнение к указанным выше вероятностным границам приведем выра-
жение для вероятности ошибки πNh (d, r2) = P{|ε + r| ≥ h} в случае нормаль-
ной случайной величины ε ∼ N (0, d):
)
)
∫
∞
(h-r
(h+r
e-t2/2
(15)
πNh (d,r2) = Ψ
√
+Ψ
√
,
где Ψ(x) =
√
dt.
d
d
2π
x
На рис. 1 изображены линии уровня вероятности ошибки в четырех случа-
ях на плоскости переменных (s, r), где s среднеквадратичное отклонение
(с.к.о.), а r
смещение. Случай a соответствует нормальному распределе-
нию, а случаи б, в и г описывают границы вероятности ошибки на клас-
сах распределений U, V и P соответственно. Сплошные линии соответствуют
уровням α = 1/36 ≈ 0,028, 1/18 ≈ 0,056, 1/12 ≈ 0,083, 1/9 ≈ 0,111 и далее с ша-
гом 1/36. На графиках они идут слева направо. Штриховая линия определяет
границу области, вне которой вероятностная граница равна единице.
Отметим, что граница πVh из неравенства Высочанского-Петунина явля-
ется перестраховочной. Поэтому, несмотря на включение V ⊂ P, неравенство
πVh ≤ πPh нарушается при достаточно большом смещении r < h.
4. Геометрический метод решения задачи минимаксного оценивания
Теорема 1 позволяет высказать предположение о том, что исходная мини-
максная задача (7) может быть сведена к минимизации вероятностной гра-
ницы
(16)
min
πHh
(d, ρ)
(d,ρ)∈Q
по области возможных значений характеристик ошибки:
{
(17) Q = (d, ρ):
∃ (f, c) ∈ Rn × R:
}
d ≥ 〈Kf,f〉, ρ ≥ (c + 〈B∗f - a,θ〉)2 ∀θ ∈ Θ
Согласно определению область Q образована парами (d, ρ), где d - диспер-
сия, а ρ = r2 - квадрат смещения произвольной линейной оценки. Свойства
области (17) описаны ниже.
Теорема 2. На плоскости переменных (d,ρ) область Q представляет
собой надграфик выпуклой непрерывной функции
{
}
(18)
ρ(d) = min
max (c + 〈B∗f - a, θ〉)2 : 〈Kf, f〉 ≤ d
,
d ≥ 0.
(f,c)∈Rn×R
θ∈Θ
21
Для λ ≥ 0 прямая ρ + λd = γλ будет опорной к Q тогда и только тогда,
когда
{
}
(19)
γλ = min
λ〈Kf, f〉 + max (c + 〈B∗f - a, θ〉)2
(f,c)∈Rn×R
θ∈Θ
Если (fλ, cλ) решение задачи (19), то точка
(20)
dλ = 〈Kfλ,fλ〉, ρλ = max(cλ + 〈B∗fλ - a, θ〉)2
θ∈Θ
лежит на кривой (18).
Таким образом, построение нижней огибающей множества Q связано с ре-
шением семейства минимаксных задач (18), каждая из которых состоит в ми-
нимизации максимального смещения при ограниченной дисперсии ошибки.
Благодаря выпуклости и замкнутости, множество Q можно описать набором
опорных прямых ρ + λd = γλ. При этом величина γλ равна минимаксному
значению среднеквадратичной (с.к.) ошибки в исходной модели (1) при усло-
вии, что коэффициент λ задает уровень помех: cov{η, η} = λK.
Отметим, что при λ = 0 соответствующее γ0 равно минимально возмож-
ному значению максимума квадрата смещения. Но в силу невырожденности
информационной матрицы D существуют несмещенные оценки, поэтому ука-
занное значение равно нулю: γ0 = ρ(d) = 0 при d ≥ d0, где d0 = 〈D-1a, a〉
дисперсия наилучшей линейной несмещенной оценки
X0 = 〈f0,Y 〉, f0 = K-1BD-1a.
Если же λ > 0 достаточно велико, то γλ = R2, где R радиус интервала
возможных значений оцениваемой величины X, т.е.
(
)
1
R=
max〈a, θ〉 - min 〈a, θ〉
2
θ∈Θ
θ∈Θ
Для решения минимаксной задачи (19) можно использовать методы двой-
ственной оптимизации (см., например, теорему 3.4.1 из [22]).
Если H(K) один из классов N (0, K), U(K) или P(K), то связь между
задачей минимаксного оценивания по вероятностному критерию (7) и дву-
мерной оптимизацией вероятностной границы (16) раскрыта в следующей
теореме.
Теорема 3. Если точка
d, ρ) доставляет минимум вероятностной
границе в (16), а пара
f,ĉ) образует решение минимаксной задачи (19) c па-
раметром λ ≥ 0, равным коэффициенту опорной прямой к области Q в точ-
ке
d, ρ), то оценка
X=
f,Y 〉 + ĉ является минимаксной по вероятност-
ному критерию, причем
{
}
(21)
πHh
d, ρ) = sup sup P
|X-X|≥h
θ∈Θ η∼H(K)
22
Замечание 2. Утверждение теоремы 3 для случая H = P фактически
содержится в теореме 7.13.1 из [4].
Замечание 3. Если вместо πVh взять границу Высочанского-Петуни-
на πVh , то все утверждения теоремы 3 остаются в силе для класса унимодаль-
ных распределений V(K), кроме равенства (21).
Замечание 4. Теоремы 1-3 допускают обобщение на бесконечномерный
случай, когда Θ образует ограниченное подмножество некоторого нормиро-
ванного пространства T, 〈a, ·〉 определяет ограниченный линейный функцио-
нал на T, а B является ограниченным линейным оператором из T в Rn. В этом
случае в формулировках теорем все максимумы по множеству Θ необходимо
заменить на супремумы.
Геометрическая иллюстрация способа решения, представленного в теоре-
ме 3, описана в следующем примере.
Пример 1. Рассмотрим случай, когда множество неизвестных парамет-
ров представляет собой эллипсоид
{
}
(22)
Θ = θ ∈ Rp: 〈Σθ,θ〉 ≤ 1 ,
где Σ - положительно определенная матрица размера p × p.
В этом случае минимаксная задача (19) может быть решена непосред-
ственно. Для этого заметим, что имеет место равенство
(23)
max〈u, θ〉2 = 〈Σ-1
u, u〉.
θ∈Θ
Отсюда следует, что задача (19) принимает вид
{
}
γλ = min λ〈Kf,f〉 + Σ-1(B∗f - a),B∗f - a
f ∈Rn
Тогда ее решением будет
(24)
fλ = K-1B(D + λΣ)-1a,
γλ = λ (D + λΣ)-1
a, a ,
где вектор fλ известен как оцениватель Кукса-Ольмана.
Укажем выражения для дисперсии и квадрата смещения с помощью (20)
и (23):
dλ = (D + λΣ)-1D(D + λΣ)-1a,a ,
ρλ = λ2
(D + λΣ)-1Σ(D + λΣ)-1a, a .
В специальном случае, когда a является собственным вектором матрицы
DΣ-1, данные выражения можно упростить:
(
dλ = d0
1 + λd0/R2
)-2, ρλ = R2(1 + R2/(λd0))-2.
23
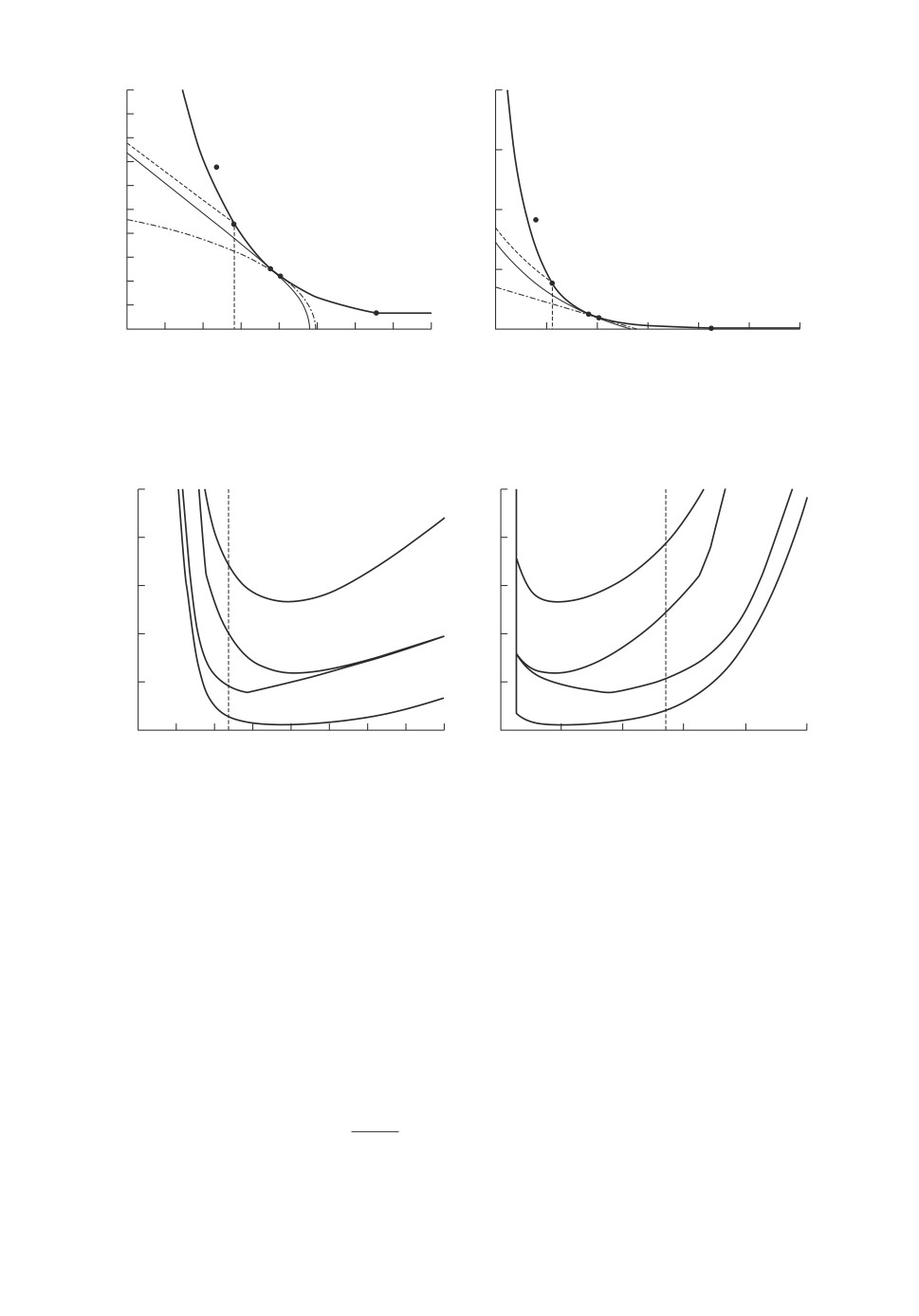
Рис. 2. Граница области Q с линиями уровня двух вероятностных границ:
πUh (d, ρ) (слева) и πVh(d, ρ) (справа).
Отсюда получаем явное уравнение кривой, определяющей левую нижнюю
часть границы области Q:
(
√
)2
ρ=R2
1-
d/d0
,
0≤d≤d0.
Данная кривая выходит при λ = 0 из нижней точки (d0, 0), соответ-
ствующей несмещенной оценке с наименьшей дисперсией d0 = 〈D-1a, a〉,
и заканчивается при λ → ∞ в верхней точке c координатами (0, R2), где
R = 〈Σ-1a,a〉1/2 радиус интервала возможных значений оцениваемой ве-
личины X = 〈a, θ〉. При этом касательная к границе в точке (d0, 0) будет го-
ризонтальна, а в точке (0, R2) вертикальна.
Геометрическая иллюстрация этих фактов приведена на рис. 2. На обоих
графиках сплошной жирной кривой показана граница области Q в перемен-
ных d, ρ, а тонкими сплошными линии уровня двух вероятностных гра-
ниц. Кроме того, на каждом графике отмечены три точки, две из которых
(d0, 0) и (0, R2) лежат на координатных осях, а третья представляет собой
точку минимума
d, ρ) соответствующей вероятностной границы πUh или πVh .
Касательная к границе области Q в точке минимума πUh изображена штрих-
пунктиром, а для вероятностной границы πVh касательная совпадает с линией
уровня.
Важно отметить, что для оценки, минимаксной по вероятностному крите-
рию на классе симметричных унимодальных распределений U, максимальное
смещение не может быть меньше 29% порога ошибки h. Это следует из того,
24
√
что ниже прямой ρ = β2h2, где β = 1 - 1/
2 ≈ 0,29, линии уровня вероят-
ностной границы πUh представляют собой вертикальные отрезки (см. левый
график рис. 2).
Для оценки, которая определяется из условия минимума границы на клас-
се V, оптимальные значения дисперси
d и квадрата смещения ρ лежат на
прямой ρ + d = const, поэтому касательная в точке
d, ρ) будет иметь коэф-
фициент наклона λ = 1. В силу теоремы 2 это означает, что искомая оценка
будет идентична с.к. минимаксной оценке.
Для визуального сравнения вероятностных границ были взяты несколь-
ко уровней вероятности ошибки, составляющих арифметическую прогрессию
α1 < ... < α7, где πUh = α3 и πVh = α5 - оптимальные значения (на рис. 2 этим
уровням соответствуют третья и пятая линии, если считать слева направо).
5. Оценивание терминального положения маневрирующей цели
Данный раздел посвящен нахождению характеристик оценок, минимакс-
ных по вероятностному критерию в задаче определения движения маневри-
рующей цели.
Движение цели описывается дважды непрерывно дифференцируемой
функцией x(t) ∈ R, которая определяет положение цели в момент t ∈ [0, T ].
Для начального положения x(0) и начальной скорости x(0) известны диапа-
зоны
|x(0) - x0| ≤ δx,
|x(0) - v0| ≤ δv,
а ускорение цели подчинено ограничению
(25)
|x(t)| ≤ δw.
Предположим, что имеются измерения Y1, . . . , Yn, проведенные в заданные
моменты времени 0 < t1 < . . . < tn < T :
Yk = x(tk) + ηk, k = 1,... ,n,
с центрированными некоррелированными ошибками одинаковой диспер-
сии σ2.
Допустим, что оцениванию подлежит терминальное положение цели
X = x(T), а критерием качества является минимум вероятности ошибки
P{|X - X| ≥ h} с учетом того, что помехи имеют неопределенное совместное
распределение (здесь h заданный порог ошибки, аX искомая оценка).
Подобная задача со с.к. критерием качества и непрерывным процессом
наблюдений рассматривалась в [23].
С учетом замечания 4 описанную модель можно записать в виде (1), если:
обозначить вектор наблюдения, вектор помех и оцениваемую величину
как
Y = col[Y1,...,Yn], η = col[η1,...,ηn] ∈ Rn, X = x(T) ∈ R;
25
определить вектор параметров
θ = (θ0,θ1,θ2), θ0 = x(0), θ1 = x(0), θ2(t) = x(t)
как элемент пространства T = R × R × C[0, T ];
задать множество неопределенности
Θ = [x0 - δx,x0 + δx] × [v0 - δv,v0 + δv] × B,
где B шар радиуса δw в пространстве непрерывных функций C[0, T ];
ввести оператор B : T → Rn и функционал 〈a, ·〉 на T
∫T
(Bθ)k = θ0 + θ1tk + (tk - τ)+θ2(τ) dτ, k = 1, . . . , n,
0
∫T
〈a, θ〉 = θ0 + θ1T + (T - τ)θ2(τ) dτ,
0
где (·)+ = max{·, 0}.
В силу симметричности множества Θ относительно точки θo = (x0, v0, 0)
оценку можно искать в виде
∑
(26)
X= x0 + v0T + fk(Yk - (x0 + v0tk)), f = col[f1,... ,fn
].
k=1
Запишем выражение для смещения, используя сопряженный оператор B∗:
M{X - X} = 〈B∗f - a,θ - θo〉 =
{
}
{
}
∑
∑
=
fk - 1
(θ0 - x0) +
fktk - T (θ1 - v0) +
k=1
k=1
{
}
∫T
∑
+
fk(tk - τ)+ - (T - τ) θ2(τ)dτ.
k=1
0
Если к данному выражению применить равенство
∫
T
∫
T
sup
φ(τ)ψ(τ) dτ = δw
|ψ(τ)| dτ,
φ∈B
0
0
то получим точную верхнюю грань смещения
(27) r(f) = sup M{X - X} =
θ∈Θ
T
∫
∑
∑
∑
=δx
fk - 1
+δv
fktk - T
+δw
fk(tk - τ)+ - (T - τ)
dτ.
k=1
k=1
k=1
0
26
Теперь задача минимизации гарантированного значения смещения при
ограничении на дисперсию (18) принимает вид
{
}
(28)
ρ(s2) = min
r2(f): σ2〈f,f〉 ≤ s2
f ∈Rn
Если разбить [0, T ] на интервалы между наблюдениями, включая точки
t0 = 0 и tn+1 = T, то получится представление
tl
∫
∑
(T - tn)2
r(f) = δx|g1| + δv|u1| + δw
|ul - glτ| dτ + δw
,
2
l=1
tl-1
∑
∑
gl =
fk - 1,
ul =
fktk - T.
k=l
k=l
Можно проверить, что имеет место равенство
tl
∫
tl - tl-1
|ul - glτ| dτ =
µ(pl, ql), pl = ul - gltl, ql = ul - gltl-1,
2
tl-1
{
∫1
|p + q|,
pq ≥ 0,
µ(p, q) = 2
|(1 - t)p + tq| dt =
(p2 + q2)/|p - q|,
pq ≤ 0.
0
Для аппроксимации r(f) кусочно-линейными функциями можно исполь-
зовать приближение, основанное на формуле трапеций:
∑
r(f) ≈ δx
fk - 1
+
k=1
(
)
∑
∑
∑
δwΔ
+ δv +
fktk - T
+δwΔ
fk(tk - τm)+ - (T - τm),
2
k=1
m=1
k=1
где 0 = τ0 < τ1 < . . . < τM = T равномерная сетка на [0, T ] с шагом Δ < t1.
После этого преобразования задача (28) приспособлена для решения в пакете
cvx, реализованном на платформе MATLAB [24].
Необходимо отметить, что применение пакета cvx было связано с некото-
рыми ограничениями: при количестве наблюдений n ≥ 10 решатель не мог
определить значимого направления минимизации. Частично это объясняет-
ся структурой решения задачи гарантирующего оценивания с непрерывным
процессом наблюдений и равномерно ограниченными возмущениями. В та-
ких задачах, зачастую, хватает небольшого числа измерений для достаточно
точной аппроксимации минимаксной оценки [23]. Кроме того, для решения
задачи (28) более приспособлены специальные методы ℓ1-оптимизации [25].
27
r
r
200
40 000
180
160
LS
30 000
140
120
100
б
20 000
LS
80
60
а
в
10 000
б
40
МВ
20
ав
МВ
0
0
60
70
80
90
100
110
120
130
140
5000
7500
10 000 12 500
15 000
17 500
20 000
s
d
Рис. 3. Граница области Q в переменных (s, r) (слева) и в переменных (d, ρ)
(справа), где s - с.к.о., r - смещение (м) и d = s2, ρ = r2 (м2).
p
p
0,25
0,25
0,20
0,20
0,15
г
0,15
г
0,10
0,10
в
в
0,05
б
0,05
б
а
а
0
60
70
80
90
100
110
120
130
140
0
50
100
150
200
250
s
s
Рис. 4. Зависимость вероятности ошибки p от с.к.о. s (м) (слева) и смеще-
ния r (м) (справа) на границе области Q для четырех гипотез а-г.
Для расчетов были взяты следующие значения параметров:
n = 5, δx = 50м, δv = 10м/с, δw = 5м/с2,
σ = 100м, h = 300м, t1 = 2с, t2 = 6,25с,
t3 = 10,5с, t4 = 14,75с, t5 = 19с, T = 20с.
Относительно распределения вектора помех η = col [η1, . . . , ηn] введены че-
тыре гипотезы:
a) η ∼ N (0, K), б) η ∼ U(K), в) η ∼ V(K), г) η ∼ P(K), где K = σ2In.
На рис. 3 изображена √аница области Q, точки которой представляют со-
бой пары (s2, r2), где r =
ρ(s2) минимум гарантированного значения сме-
щения (28) при ограничении на дисперсию оценок s2. Точка LS соответствует
оценкеXLS, полученной по методу наименьших квадратов (МНК) в упрощен-
ной модели без учета ускорения цели: x(t) = θ0 + θ1t. Как видно из рисунка,
28
Значения вероятности ошибки на нескольких оценках
Гипотеза H
ŝ (м)
r (м)
πHh(ŝ2, r2)
πHh(s2LS, r2LS)
πHh(s2MB, r2MB)
а) N(0, K)
97,87
50,20
0,005520
0,013810
0,021324
б) U(K)
88,66
85,63
0,038821
0,045803
0,083008
в) V(K)
100,37
43,95
0,059290
0,100724
0,083859
г) P(K)
98,70
47,99
0,132998
0,170892
0,188684
МНК-оценка является сильно смещенной: ее смещение в наихудшем случае
будет rLS ≈ 135 м. Это объясняется тем, что в исходной модели оценивае-
мая траектория x(t) зависит от элемента бесконечномерного пространства
θ2 = x(t), поэтому несмещенных оценок по конечному числу наблюдений не
существует. Тем не менее в силу условия (25) смещения оценок будут ограни-
чены. Можно выбрать оценкуXMB c минимально возможной верхней гранью
смещения rMB ≈ 13 м. Это значительно меньше, чем в случае МНК-оценки,
хотя с.к.о. оказывается больше: sMB ≈ 125 м и sLS ≈ 84 м.
На рис. 4 изображены графики гарантированных значений вероятности
ошибки P{|X - X| ≥ h} на оценках (26), (28) при различном выборе диспер-
сии s2. Штриховая линия соответствует характеристикам МНК-оценки.
В таблице приведены значения вероятности ошибки на трех оценках: ми-
нимаксной, МНК и оценке с минимальным смещением. Согласно теореме 1
характеристики минимаксной оценки ŝ2, r2 образуют точку минимума веро-
ятностной границы πHh на границе области Q. В зависимости от выбора клас-
са H эти характеристики будут разными, что видно из рис. 4 и таблицы.
6. Заключение
В работе описан геометрический способ решения задачи минимаксно-
го оценивания по вероятностному критерию в модели линейной регрессии
с ограниченными параметрами и симметричными унимодальными помеха-
ми. Проведено сравнение минимаксных оценок линейной комбинации неиз-
вестных параметров для нескольких классов совместных распределений по-
мех. Способ описания априорной информации о неопределенном многомер-
ном распределении в виде набора условий на симметричность, унимодаль-
ность, математическое ожидание и ковариационную матрицу приводит к ро-
бастным статистическим решениям, которые оказываются менее консерва-
тивными, чем известные ранее.
ПРИЛОЖЕНИЕ
Доказательство теоремы 1. Рассмотрим линейную оценкуX, опре-
деляемую вектором коэффициентов f ∈ Rn и сдвигом c ∈ R согласно (5).
Если оцениваемая величина X и вектор наблюдений Y удовлетворяют
уравнениям модели регрессии (1) с вектором параметров θ ∈ Θ и вектором по-
мех η ∼ H(K), то ошибкаX - X допускает представление ε + r, где ε ∼ H(d),
а d, r удовлетворяют соотношениям (9). Следовательно, в (11) имеет место
знак неравенства ¾≤¿.
29
Чтобы доказать обратное неравенство, достаточно для заданного век-
тора параметров θ ∈ Θ и случайной величины ε ∼ H(d), где d и r имеют
вид (9), подобрать случайный вектор η ∼ H(K), удовлетворяющий равенству
ε + r =X - X с вероятностью 1. В силу (1) и (9) требуемое равенство равно-
сильно следующему:
ε = 〈f,η〉.
Действуя так же, как в [26], определим искомый вектор по правилу
{
}
η=K1/2 ε|g|-2g + P ζ ,
где P = In - |g|-2gg∗, g = K1/2f, In единичная матрица размера n × n, а
ζ
стандартный n-мерный гауссовский вектор, не зависящий от случайной
величины ε. Проверка условий ε = 〈f, η〉, Mη = 0 и cov{η, η} = K идентична
выкладкам из [26].
В случае H = P доказательство заканчивается.
При H = U остается проверить, что распределение вектора η симметрично
и линейно унимодально. Согласно [12] это условие означает, что при любом
выборе вектора коэффициентов b ∈ Rn распределение линейной комбинации
〈b, η〉 = ε|g|-2〈b, T g〉 + 〈b, T P ζ〉
является симметричным унимодальным. А этот факт следует из унимодаль-
ности свертки двух симметричных унимодальных одномерных распределе-
ний, каковыми являются распределения обоих слагаемых в силу ε ∼ U(d) и
ζ ∼ N(0,In) (см. теорему 1.6 из того же источника).
Доказательство теоремы 2. Выпуклость области Q непосредствен-
но следует из выпуклости по (f, c) ∈ Rn × R двух функций
〈Kf, f〉 и
max(c + 〈B∗f - a, θ〉)2.
θ∈Θ
Поэтому функция ρ(d) как нижняя огибающая выпуклого множества Q тоже
будет выпуклой (см. теорему I.5.3 из [27]). А в силу того, что она всюду
конечна, она будет непрерывной.
Второе утверждение следует из определения опорной прямой для вы-
пуклого множества. При фиксированном λ ≥ 0 прямая ρ + λd = γλ является
опорной к области Q в точке (dλ, ρλ), если линейная форма ρ + λd достига-
ет на Q минимума (или максимума) в указанной точке. Случай максимума
можно отбросить, поскольку указанная линейная форма на области Q не
ограничена сверху. Таким образом, получаем требуемые факты (19) и (20).
Доказательство теоремы 3. Из теоремы 1 в силу монотонной зави-
симости πHh(d, ρ) по ρ следует равенство
{
}
(1)
sup sup P
|X - X| ≥ h
=πHh
(d, ρ),
θ∈Θ η∼H(K)
(
)2
где d = 〈Kf, f〉 и ρ = supθ∈Θ
c + 〈B∗f - a,θ〉
30
Пусть
d, ρ)
точка минимума πHh(d, ρ) по (d, ρ) ∈ Q, а
f,ĉ)
решение
минимаксной задачи (19) c параметром λ, равным коэффициенту опорной
прямой к области Q в точке
d, ρ). Тогда согласно теореме 2 будут иметь
место равенства
(
)2
d=〈
f
f 〉,
ρ = max ĉ+ 〈B∗fˆ- a,θ〉
θ∈Θ
Поэтому на оценкеX =
f,Y 〉 + ĉ реализуется равенство
{
}
(2)
sup sup P
|X-X|≥h
=πHh(d, ρ).
θ∈Θ η∼H(K)
Теперь в силу πHh
d, ρ) ≤ πHh(d,ρ) получаем, что левая часть (2) не превос-
ходит левую часть (1). Следовательно,
X минимаксная оценка по вероят-
ностному критерию на классе H(K), что и требовалось доказать.
СПИСОК ЛИТЕРАТУРЫ
1.
Bahadur R.R. On the Asymptotic Efficiency of Tests and Estimates // Sankhya:
Indian J. Statist. 1960. V. 22. No. 3-4. P. 229-252.
2.
Ибрагимов И.А., Хасьминский Р.З. Асимптотическая теория оценивания. М.:
Наука, 1977.
3.
Вапник В.Н., Червоненкис А.Я. Теория распознавания образов (статистические
проблемы обучения). М.: Наука, 1974.
4.
Бахшиян Б.Ц., Назиров Р.Р., Эльясберг П.Е. Определение и коррекция движе-
ния. М.: Наука, 1980.
5.
Тимофеева Г.А. Нелинейные доверительные множества для статистически
неопределенных систем // АиТ. 2003. № 11. С. 84-95.
Timofeeva G.A. Nonlinear Confidence Estimates for Statistically Uncertain Sys-
tems // Autom. Remote Control. 2003. V. 64. No. 11. P. 1724-1733.
6.
Медведева Н.В., Тимофеева Г.А. Сравнение линейных и нелинейных методов
доверительного оценивания для статистически неопределенных систем // АиТ.
2007. № 4. С. 51-60.
Medvedeva N.V., Timofeeva G.A. Comparison of Linear and Nonlinear Methods
of Confidence Estimation for Statistically Uncertain Systems // Autom. Remote
Control. 2007. V. 68. No. 4. P. 619-627.
7.
Ананьев Б.И. Многошаговые стохастические включения специального вида и их
мультиоценки // АиТ. 2007. № 11. С. 3-11.
Anan’ev B.I. Multistep Specific Stochastic Inclusions and Their Multiestimates //
Autom. Remote Control. 2007. V. 68. No. 11. P. 1891-1899.
8.
Панков А.Р., Семенихин К.В. О минимаксном оценивании по вероятностному
критерию // АиТ. 2007. № 3. С. 66-82.
Pankov A.R., Semenikhin K.V. Minimax Estimation by Probabilistic Criterion //
Autom. Remote Control. 2007. V. 68. No. 3. P. 430-445.
9.
Delage E., Ye Y. Distributionally Robust Optimization under Moment Uncertainty
with Application to Data-Driven Problems // Oper. Res. 2010. V. 58. P. 595-612.
31
10.
Коган М.М. Робастное оценивание и фильтрация в неопределенных линейных
системах при неизвестных ковариациях // АиТ. 2015. № 10. С. 50-66.
Kogan M.M. Robust Estimation and Filtering in Uncertain Linear Systems under
Unknown Covariations // Autom. Remote Control. 2015. V. 76. No. 10. P. 1751-1764.
11.
Карлин С., Стадден В. Чебышевские системы и их применение в анализе и
статистике. М.: Наука, 1976.
12.
Dharmadhikari S., Joag-dev K. Unimodality, Convexity, and Applications. San
Diego: Academic, 1988.
13.
Barmish B.R., Lagoa C.M. The Uniform Distribution: A Rigorous Justification for
Its Use in Robustness Analysis // Math. Control Signal. Syst. 1997. V. 10. P. 203-222.
14.
Кибзун А.И. О наихудшем распределении в задачах стохастической оптимиза-
ции с функцией вероятности // АиТ. 1998. № 11. С. 104-116.
Kibzun A.I. On the Worst-Case Distribution in Stochastic Optimization Prob-
lems with Probability Function // Autom. Remote Control. 1998. V. 59. No. 11.
P. 1587-1597.
15.
Кан Ю.С. Об обосновании принципа равномерности в задаче оптимизации ве-
роятностного показателя качества // АиТ. 2000. № 1. С. 54-70.
Kan Yu.S. On the Justification of the Uniformity Principle in the Optimization of
a Probability Performance Index // Autom. Remote Control. 2000. V. 61. No. 1.
P. 50-64.
16.
Van Parys B.P.G., Goulart P.J., Kuhn D. Generalized Gauss Inequalities via
Semidefinite Programming // Math. Program. 2016. V. 156. P. 271-302.
17.
Граничин О.Н. Неасимптотическое доверительное множество для параметров
линейного объекта управления при произвольном внешнем возмущении // АиТ.
2012. № 1. С. 24-35.
Granichin O.N. The Nonasymptotic Confidence Set for Parameters of a Linear Con-
trol Object under an Arbitrary External Disturbance // Autom. Remote Control.
2012. V. 73. No. 1. P. 20-30.
18.
Weyer E., Campi M.C., Csaji B.C. Asymptotic Properties of SPS Confidence Re-
gions // Automatica. 2017. V. 82. P. 287-294.
19.
Семенихин К.В. Двусторонняя вероятностная граница для симметричной уни-
модальной случайной величины // АиТ. 2019. № 3. С. 103-122.
Semenikhin K.V. Two-Sided Probability Bound for a Symmetric Unimodal Random
Variable // Autom. Remote Control. 2019. V. 80. No. 3. P. 474-489.
20.
Высочанский Д.Ф., Петунин Ю.И. Об одном неравенстве Гаусса для одно-
вершинных распределений // Теория вероятн. и ее примен. 1982. Т. 27. № 2.
С. 339-341.
Vysochanskii D.F., Petunin Yu.I. On a Gauss Inequality for Unimodal Distribu-
tions // Theory Probab. Appl. 1983. V. 27. No. 2. P. 359-361.
21.
Pukelsheim F. The Three Sigma Rule // Amer. Statist. 1994. V. 48. P. 88-91.
22.
Соловьёв В.Н. Двойственные экстремальные задачи и их применение к задачам
минимаксного оценивания // Успехи матем. наук. 1997. Т. 52. № 4. С. 49-86.
Solov’ev V.N. Dual Extremal Problems and Their Applications to Minimax Estima-
tion Problems // Russian Math. Surveys. 1997. V. 52. No. 4. P. 685-720.
23.
Matasov A.I. Estimators for Uncertain Dynamic Systems. Dordrecht: Kluwer Acad.
Publ., 1998.
24.
Grant M.C., Boyd S.P. The CVX Users’ Guide. Release 2.1. CVX Research, Inc.
32
25. Акимов П.А., Матасов А.И. Итерационный алгоритм для ℓ1-аппроксимации
в динамических задачах оценивания // АиТ. 2015. № 5. С. 7-26.
Akimov P.A., Matasov A.I. An Iterative Algorithm for ℓ1-Norm Approximation
in Dynamic Estimation Problems // Autom. Remote Control. 2015. V. 76. No. 5.
P. 733-748.
26. Архипов А.С., Семенихин К.В. Анализ надежности линейных несмещенных
оценок при наличии помех с неизвестным унимодальным распределением //
Изв. РАН. Теория и сист. управления. 2019. № 5. С. 8-17.
Arkhipov A.S., Semenikhin K.V. Confidence Analysis of Linear Unbiased Estimates
under Uncertain Unimodal Noise Distributions // J. Comput. Syst. Sci. Int. 2019.
V. 58. No. 5. P. 674-683.
27. Рокафеллар Р. Выпуклый анализ. М.: Мир, 1973.
Статья представлена к публикации членом редколлегии Л.Б. Рапопортом.
Поступила в редакцию 02.12.2019
После доработки 23.01.2020
Принята к публикации 30.01.2020
33