Автоматика и телемеханика, № 7, 2020

(Арзамасский политехнический институт (филиал)

Нижегородского государственного технического

университета им. Р.Е. Алексеева)

УПРАВЛЕНИЕ С ИТЕРАТИВНЫМ ОБУЧЕНИЕМ

НЕОПРЕДЕЛЕННОЙ СИСТЕМОЙ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ

НА ОСНОВЕ НАБЛЮДАТЕЛЯ СОСТОЯНИЯ¹

Рассматриваются линейные системы с аффинной моделью параметри-

ческой неопределенности, функционирующие в повторяющемся режиме.

Для таких систем предлагается новый метод синтеза управления с итера-

тивным обучением. Этот метод основан на использовании наблюдателя

состояния полного порядка и вспомогательной 2D-модели в форме диф-

ференциального повторяющегося процесса, устойчивость которой гаран-

тирует сходимость процесса обучения. Для получения условий устойчи-

вости используется дивергентный метод векторных функций Ляпунова.

Приведен пример, демонстрирующий особенности и преимущества нового

метода.

Ключевые слова: управление с итеративным обучением, наблюдатель,

2D-системы, устойчивость, векторная функция Ляпунова, дифференци-

альные повторяющиеся процессы.

DOI: 10.31857/S0005231020070053

1. Введение

Управление с обратной связью является наиболее эффективным спосо-

бом достижения таких свойств системы, как устойчивость, робастность, оп-

тимальность в смысле заданного критерия и т.п. На практике существует

много систем, которые функционируют в повторяющемся режиме с одной

и той же продолжительностью каждого повторения, в течение которого си-

стемы должны отслеживать заданный сигнал с требуемой точностью. При

использовании обратной связи ошибка слежения будет одинаковой независи-

мо от количества повторений (итераций). Это обстоятельство заставило ис-

кать новые решения, которые обеспечили бы уменьшение ошибки слежения

с увеличением числа повторений.

Таким решением является управление с итеративным обучением, которое

организовано таким образом, чтобы последовательно уменьшать ошибку сле-

жения (обучения) в повторяющихся операциях. Задача управления с итера-

тивным обучением состоит в том, чтобы найти соответствующий управляю-

щий сигнал, который заставляет выходную переменную следить за желаемой

¹ Работа выполнена при поддержке Российского научного фонда (грант № 18-79-00088).

траекторией, определенной на конечном интервале времени, за счет итератив-

ного уточнения этого сигнала. Такой тип управления использует информа-

цию об ошибке, информацию с предыдущих повторений, а также некоторую

предварительную информацию о системе, чтобы получить такой входной сиг-

нал, который обеспечит сходимость ошибки обучения к нулю по мере увели-

чения числа повторений. В отличие от адаптивного управления параметры

системы здесь остаются неизменными.

Обзорные публикации [1, 2] могут служить отправной точкой. Управление

с итеративным обучением успешно используется в огромном числе приложе-

ний от медицинских роботов для реабилитации после инсульта [3, 4] и для

поддержки желудочка сердца [5] до лазерного напыления металла [6], мор-

ских систем [7] и производственных систем [8].

Начиная с пионерской публикации [9] отмечено, что управление с итера-

тивным обучением адекватно моделируется двумерной (2D) системой. Дей-

ствительно, с одной стороны, управление с итеративным обучением застав-

ляет систему многократно выполнять одну и ту же команду на конечном

интервале времени. С другой стороны, управление с итеративным обучением

исправляет команду от повторения к повторению, чтобы уменьшить ошибку

обучения. Таким образом, в качестве двух независимых переменных высту-

пают шаг по оси времени и номер повторения по оси итераций.

Наиболее распространенными двумерными (2D) моделями управления с

итеративным обучением являются повторяющиеся процессы. Сведения об

этих процессах, включая теорию устойчивости в рамках линейной динамики

с использованием моделей в банаховом пространстве, можно найти в [10] и в

источниках из приведенной там библиографии. Теории устойчивости и дис-

сипативности повторяющихся процессов, основанные на векторных функци-

ях Ляпунова и векторных функциях накопления, были разработаны в [11] и

в предшествующих публикациях тех же авторов, приведенных в списке ли-

тературы. Основная особенность этих результатов заключается в том, что

для получения условий устойчивости вместо полной производной или пол-

ного приращения скалярной функции Ляпунова используется дивергенция

векторной функции или ее дискретный аналог.

Как правило, в алгоритмах управления с итеративным обучением не ис-

пользуются ни переменные состояния системы, ни их оценки. В то же время

ясно, что использование этих переменных может гарантировать более высо-

кое качество управления в смысле увеличения скорости сходимости процесса

обучения и в смысле достижения более высокой точности. В частности, это

демонстрирует публикация [12], в которой результаты были подтверждены

экспериментом. Алгоритмы управления с итеративным обучением с оценками

состояния, полученными наблюдателем полного порядка, были предложены

в [13-15], где рассматривались детерминированные системы с измеряемым

выходом.

В недавней работе автора [14] получен алгоритм управления с итератив-

ным обучением, использующий информацию о выходной переменной и оцен-

ках состояния на текущем и предыдущем повторениях для случая, когда па-

раметры системы точно известны. Данная статья развивает эти результаты

на случай систем с неопределенными параметрами.

В [14] были отмечены трудности подхода в рамках дифференциальных

моделей - конечные результаты выражаются через решение модифицирован-

ного неравенства Риккати, которое в известных публикациях не изучалось,

и для нахождения его решения пока можно предложить лишь эвристиче-

ские итерационные методы. В то же время для систем с неопределенными

параметрами использование дифференциальных моделей предпочтительно,

поскольку в этом случае неопределенности учитываются проще и нагляднее.

Попытки преодолеть эти трудности привели к разработке нового подхода,

позволяющего в случае систем с постоянными параметрами свести задачу к

решению линейного матричного неравенства вместо упомянутого сложного

неравенства типа Риккати. В случае систем с неопределенными параметра-

ми задача сводится к решению системы линейных матричных неравенств.

Таким образом, указанное затруднение удается обойти не только для случая,

изучаемого в [14], но и для более общего случая.

В данной статье рассматриваются линейные системы с непрерывным вре-

менем с аффинной моделью параметрической неопределенности. На основе

предложенного нового подхода решается задача синтеза управления с ите-

ративным обучением в предположении, что непосредственному измерению

доступен только вектор выхода. Закон управления формируется на основе

этого вектора и оценок вектора состояния номинальной модели. Выбор пара-

метров закона управления, обеспечивающих сходимость процесса обучения,

осуществляется на основе условий устойчивости вспомогательной 2D-модели

в форме дифференциального повторяющегося процесса, которые выводятся

на основе дивергентного метода векторных функций Ляпунова [11] и выра-

жаются в виде системы линейных матричных неравенств. Приведен пример,

демонстрирующий эффективность и преимущества нового метода.

2. Синтез управления с итеративным обучением

дифференциальными повторяющимися процессами

2.1. Постановка задачи

Рассмотрим линейную систему с неопределенными параметрами, которая

функционирует в повторяющемся режиме и описывается на k-м повторении

моделью в пространстве состояний

x_k(t) = A(δ(t))x_k(t) + B(δ(t))u_k(t),

(1)

y_k(t) = Cx_k

(t), t ∈ [0, T ], k = 0, 1, . . . ,

где x_k(t) ∈ Rnx

вектор состояния, u_k(t) ∈ Rnu

вектор управления и

y_k(t) ∈ Rny

вектор выходных переменных, называемый профилем повто-

рения, k номер повторения, T продолжительность повторения. Модель

неопределенности задается в форме

∑

(2)

A(δ(t)) = A + δ_j (t)A_j , B(δ(t)) = B +

δ_j(t)B_j,

j=1

где A и B - матрицы номинальной модели, A_j и B_j (j = 1, 2, . . . , l) посто-

янные матрицы соответствующих размеров и δ_j (t) ∈ [δ_j, δ_j]. Далее повсюду

для компактности записи зависимость δ от t не указывается.

Обозначим

{

}

D = δ = [δ1 ...δ_l]^T, δ_j ∈ [δ_j, δ_j] ,

{

}

D_v = δ = [δ₁ ... δ_l]^T, δ_j ∈ {δ_j, δ_j} ,

где D_v конечное множество из 2^l элементов.

Пусть y_ref (t), 0 ≤ t ≤ T , заданная желаемая траектория. Тогда

(3)

e_k(t) = y_ref(t) - y_k

(t)

является ошибкой обучения на повторении k. Задача состоит в нахождении

такой последовательности управлений u_k(t), k = 0, 1, . . . , которая обеспечи-

вает достижение заданной точности воспроизведения профиля за конечное

число повторений k_fin и сохранение этой точности при дальнейших повторе-

ниях, т.е.

(4)

||e_k(t)|| ≤ e^∗, k ≥ k_fin

0≤t≤T.

Величина k_fin определяется требуемой точностью, и всегда желательно,

чтобы эта величина была как можно меньше. Прямой метод выбора этой ве-

личины неизвестен, и здесь прослеживается полная аналогия с достижением

требуемого времени переходного процесса в классических задачах управле-

ния.

Поставленная задача будет решена, если указанная последовательность

u_k(t) удовлетворяет условиям

(5)

lim

||e_k(t)|| = 0,

lim

||u_k(t) - u_∞

(t)|| = 0,

k→∞

где u_∞(p) ограниченная переменная, обычно называемая обученным управ-

лением.

Закон управления с итеративным обучением на текущем повторении фор-

мируется в виде

(6)

u_k+1(t) = u_k(t) + Δu_k+1

(t),

где Δu_k+1(t) корректирующая поправка, которая должна быть синтезиро-

вана так, чтобы обеспечить условия сходимости (5).

Выбор закона управления с обратной связью по текущему повторению

дает одинаковую ошибку на каждом повторении. Закон управления с ите-

ративным обучением должен изменять входной сигнал на основе состояния

на текущем повторении (x_k+1(t)) и упреждающих значений выходной пере-

менной на предыдущем повторении (y_k(t)). В данной статье предполагается,

что вектор состояния недоступен для измерения и вместо него используется

оценка.

Для построения оценки вектора состояния очевидным подходом являет-

ся использование наблюдателя полного порядка; некоторые результаты по

оценке вектора состояния при управлении с итеративным обучением для си-

стем с известными параметрами были опубликованы в [13-15] для систем с

известными параметрами. В [14] наблюдатель состояния используется в со-

четании с подходом на основе диссипативности 2D-моделей и дивергентного

метода векторных функций Ляпунова. Конечные результаты представлены

в виде линейных матричных неравенств. В [13], наблюдатель состояния ис-

пользовался в сочетании с синтезом управления с итеративным обучением

на основе линейных матричных неравенств в конечных частотных областях.

В [15] коэффициент усиления хорошо известного закона управления с итера-

тивным обучением P -типа обновлялся на каждом повторении путем решения

соответствующего дискретного уравнения Риккати. Данная статья развивает

результаты [14] на случай систем с неопределенными параметрами.

Зададим наблюдатель состояния для системы (1) в виде модели в про-

странстве состояний с номинальными параметрами

dx_k(t)

(7)

= Ax_k(t) + Bu_k(t) + F[y_k(t) - Cx_k

(t)],

где x_k(t)

оценка вектора состояния на повторении k; F

матрица уси-

ления наблюдателя; и, как обычно, x_k(t) = x_k(t) - x_k(t) обозначает ошибку

оценивания.

Потребуем, чтобы для начального состояния наблюдателя выполнялось

соотношение

(8)

ŷk(0) = C xk(0) = yref(0).

2.2. Дифференциальная 2D-модель

Для управления с итеративным обучением синтезу подлежит корректи-

рующая поправка Δu_k+1(p), которая синтезируется как обычное управление с

обратной связью для вводимой далее в рассмотрение вспомогательной систе-

мы относительно приращений переменных приращения оценки и ошибки

оценивания:

ξ_k+1(t) = x_k+1(t) - x_k(t),

ξ_k+1(t) = x_k+1(t) - x_k(t).

В терминах этих переменных динамика системы (1) с наблюдателем (7)

может быть описана уравнениями

ξ_k+1(t)

ξ_k+1(t) + F

ξ_k+1(t) + Bv_k+1(t),

(9)

dξ

k+1(t)

=A_a(δ

ξ_k+1(t) + (A(δ) - FC

ξ_k+1(t) + B_a(δ)v_k+1(t),

где

∑

A_a(δ) =

δ_jA_j, B_a(δ) =

δ_jB_j, v_k+1(t) = Δu_k+1(t).

j=1

Динамику процесса изменения ошибки относительно переменной k можно

описать только с использованием производной от ошибки, которая в рассмат-

риваемом случае недоступна измерению. В связи с этим будем использовать

оценку производной ошибки

ė_k(t) = y_ref(t) - Cˆxk(t).

Обозначим ε_k(t) =ˆė(t). С учетом (9) изменение оценки ошибки обуче-

ния (3) в зависимости от числа повторений k опишется уравнением

(10)

ε_k+1(t) = ε_k(t) - CA(δ

ξ_k+1(t) - CFC(δ

ξ_k+1(t) - CB(δ)v_k+1

(t).

[

]_T

Обозначим η_k+1(t) =

ξ_k+1(t)^T

ξ_k+1(t)^T и запишем (9), (10) в стандарт-

ной форме дифференциального повторяющегося процесса

η_k+1(t) = A₁₁(δ)η_k+1(t) + A₁₂ε_k(t) + B₁(δ)v_k+1(t),

(11)

ε_k+1(t) = A₂₁η_k+1(t) + A₂₂ε_k(t) + B₂v_k+1(t),

где

[

]

A₁₁(δ) =

A₁₂ = 0,

A_a(δ) A(δ) - FC

[

]

A₂₁ =

-CA -CFC

A₂₂ = I,

[

]

B₁(δ) =

B₂ = -CB.

B_a(δ)

Выберем корректирующую поправку в виде

(12)

Δu_k+1(t) = K₁

ξ_k+1(t) + K₂ε_k(t),

и тогда (9), (10) с учетом (12) запишется уравнениями

ξ_k+1(t)

= (A + BK₁

ξ_k+1(t) + F

ξ_k+1(t) + BK₂ε_k(t),

ξ_k+1(t)

(13)

= (A_a(δ) + B_a(δ)K₁

ξ_k+1(t) + (A(δ) - FC

ξ_k+1(t) +

+ B_a(δ)K₂ε_k(t),

ε_k+1(t) = -C(A + BK₁

ξ_k+1(t) - CF

ξ_k+1(t) + (I - CBK₂)ε_k(t),

которые в более компактной форме имеют вид

η_k+1(t) = A_c11(δ)η_k+1(t) + A_c12ε_k(t),

(14)

ε_k+1(t) = A_c21η_k+1(t) + A_c22ε_k(t),

где

[

]

[

]

A+BK₁

BK₂

A_c11(δ) =

A_c12 =

(A_a(δ) + B_a(δ)K₁) A(δ) - F C

B_a(δ)K₂

[

]

A_c21 =

-C(A + BK₁) -CFC

A_c22 = I - CBK₂.

2.3. Решение на основе дивергентного метода

векторных функций Ляпунова

Закон управления с итеративным обучением (12) должен обеспечивать

условия сходимости (5). Чтобы найти матрицы K₁ и K₂, гарантирующие это

свойство, воспользуемся методом векторных функций Ляпунова для диффе-

ренциальных повторяющихся процессов [11].

Определение. Дифференциальный повторяющийся процесс (14) назы-

вается экспоненциально устойчивым, если существуют действительные

числа κ > 0, λ > 0 и 0 < ζ < 1 такие, что

(15)

∥η_k(t)∥² + ∥ε_k(t)∥² ≤ κe^-λtζ^k,

где κ, ζ и λ не зависят от продолжительности повторения T .

Рассмотрим векторную функцию Ляпунова вида

[

]

V1(ηk(t))

(16)

V (η_k(t), e_k(t)) =

V₂(ε_k(t))

где

V₁(η) > 0, η = 0, V₂(ε) > 0, e = 0, V₁(0) = 0, V₂(0) = 0.

Аналог оператора дивергенции, который будем называть далее дивергенцией,

для этой функции вдоль траекторий системы (13) задается в виде

dV₁(η_k(t))

(17)

D_cV (η_k(t),ε_k(t)) =

+ Δ_kV₂(ε_k

(t)),

где

Δ_kV₂(ε_k(t)) = V₂(ε_k+1(t)) - V₂(ε_k(t)).

Следующая теорема дает достаточные условия экспоненциальной устойчиво-

сти.

Теорема

[11]. Дифференциальный повторяющийся процесс (14) экспо-

ненциально устойчив, если существуют векторная функция Ляпунова (16)

и положительные скаляры c₁,c₂ и c₃, такие что

c₁∥η_k(t)∥² ≤ V₁(η_k(t)) ≤ c₂∥η_k(t)∥²,

c₁∥ε_k(t)∥² ≤ V₂(ε_k(t)) ≤ c₂∥ε_k(t)∥²,

D_cV (η_k(t),ε_k(t)) ≤ -c₃(∥η_k(t)∥|² + ∥ε_k(t)∥²),



∂V1(η_k(t))



−c₄∥η_k(t)∥.



≤

∂η

Если система (14) экспоненциально устойчива, то ε_k(t) → 0 при k → ∞.

Тогда поскольку выполняется (8), то ê_k(t) → 0 при k → ∞, и если при этом

e_k = ê_k + e_k будет удовлетворять заданным требованиям точности, то постав-

ленная задача будет решена.

Для дальнейшего анализа введем обозначения:

[

]

[

]

A₁₁(δ) A₁₂

A_c11(δ) A_c12

A(δ) =

A_c(δ) =

A₂₁

A₂₂

A_c21

A_c22

A_cij(δ) = A_ij(δ) + B_i(δ)K_j, i,j = 1,2,

[

]

[

]

[

]

B₁(δ)

I^(1,0) =

I^(0,1) =

B(δ) =

B₂

Пусть матрицы P = diag[P₁ P₂] и K = [K₁ K₂] удовлетворяют билинейно-

му матричному неравенству

A^Tc(δ)I^(1,0)P + PI^(1,0)A¯_c(δ)

A^Tc(δ)I^(0,1)

A_c(δ) - I^(0,1)P +

(18)

+ Q + K^TRK ≼ 0, δ ∈ D,

где Q = diag[Q₁ Q₂] ≻ 0 и R ≻ 0 весовые матрицы, которыеподлежат вы-

бору. Они аналогичны весовым матрицам в теории линейно-квадратичного

регулятора, и их выбор осуществляется на основе результатов этой теории.

Поскольку

ξ недоступна, то для дальнейшего анализа матрицы

A_c11(δ),A_c21 необходимо представить в виде

A_c11(δ) = A₁₁ + B₁(δ)K₁C₀,

(19)

A_c21 = A₂₁ + B₂K₁C₀,

где

C₀ = [I 0] .

Выберем компоненты векторной функции Ляпунова (16) в виде квадра-

тичных форм V₁(η_k(t)) = η^Tk(t)P₁η_k(t), V₂(ε_k(t)) = ε^Tk(t)P₂ε_k(t), где P₁ ≻ 0 и

P₂ ≻ 0. Тогда, вычисляя D_cV , получим, что при выполнении неравенства (18)

D_cV ≤ -Q - K^TRK и все условия теоремы оказываются выполненными, что

гарантирует экспоненциальную устойчивость (11). Используя формулу до-

полнения Шура, учитывая (19) и вводя вспомогательную переменную Z₁

как решение уравнения C₀X₁ = Z₁C₀, сведем (18) к линейному матрично-

му неравенству относительно X = diag[X₁ X₂], где X₁ = P^-11 и X₂ = P^-12 и

Y₁ = K₁Z₁, Y₂ = K₂X₂:



(A₁₁(δ)X₁ + B₁(δ)(Y₁C₀)) + (A₁₁(δ)X₁ + B₁(δ)(Y₁C₀))^T (A₁₂X₂ + B₁(δ)Y₂)



(A₁₂X₂ + B₁(δ)Y₂)^T

-X₂



(A₂₁X₁ + B₂(Y₁C₀))

(A₂₂X₂ + B₂Y₂)



X₁





X₂

(Y₁C₀)

Y₂



(A₂₁X₁ + B₂(Y₁C₀))^T X₁

(Y₁C₀)^T



(A₂₂X₂ + B₂Y₂)^T

X₂

Y^T2



−X₁



(20)

-X₂



≼ 0, δ ∈ D,



-Q^-11



-Q^-12



-R^-1

C₀X₁ = Z₁C₀, X₁ ≻ 0, X₂ ≻ 0.

Поскольку (20) линейное неравенство и зависимость от δ аффинная,

то (20) будет выполняться для всех δ ∈ D тогда и только тогда, когда оно

выполняется для δ ∈ D_v.

Таким образом, если неравенство (20) разрешимо для δ ∈ D_v, то K =

= [K₁C₀ K₂], K₂ = Y₂X^-12 и поскольку матрица C₀ имеет ранг, совпадаю-

щий с рангом единичной матрицы ее первого блока, то матрица Z₁ будет

невырожденной и K₁ = Y₁Z^-11.

Замечание. При практическом нахождении матрицы K целесообразно

вместо линейного матричного неравенства (20) решать задачу максимиза-

ции следа матрицы X при ограничениях в виде этого линейного матричного

неравенства. Это позволит ускорить процесс нахождения решения.

3. Пример

Рассмотрим модель однозвенного гибкого манипулятора [16], функциони-

рующего в повторяющемся режиме с постоянным периодом повторения. Ди-

намика движения манипулятора в пространстве состояний описывается урав-

[

]_T

нениями (1), где x =

θ α

, θ

угол поворота сервопривода, α

угол отклонения гибкого звена,



















K_s

B_eq





,



J_eq









K_s(J_l + J_eq) B_eq



J_lJ_eq

J_eq























,

C = [1

0] ,



J_eq











J_eq

B_eq коэффициент вязкого трения сервопривода, K_s жесткость гибкого

звена, J_l

момент инерции гибкого звена относительно центра масс, J_eq

момент инерции сервопривода. Движение гибкого звена происходит в гори-

зонтальной плоскости.

Задача состоит в том, чтобы найти алгоритм управления с итеративным

обучением, при котором выходная переменная y(t) воспроизводила бы же-

лаемую траекторию y_ref (t) с заданной точностью e^∗. Непосредственному из-

мерению доступен только угол θ.

Для расчетов и моделирования были приняты следующие значения пара-

метров из [16]: B_eq = 0,004 Н·м/(рад/с), K_s = 1,3 Н·м/рад, J_l = 0,038 кг·м²,

J_eq = 2,08 · 10^-3 кг·м². Продолжительность цикла повторения 3 c, требуемая

точность e^∗ = 0,005 рад. При вычислениях использовался метод Эйлера с ша-

гом T_s = 0,001 c.

Желаемая траектория движения звена представлена на рис. 1 и описыва-

ется уравнением

πt

πt³

y_ref(t) =

t ∈ [0,T].

В данном примере CB = 0, а разработанная теория предполагает, чтобы

CB = 0. С целью обойти это затруднение воспользуемся тем, что для данной

системы

y_k = C x_k = C₁x_k,

где C₁ = [0

0] .

Поскольку непосредственно измеряется только угол, то вместо производ-

ной можно использовать лишь ее оценкуˆyk = C1xk, где xk определяется на-

блюдателем (7). В этом случае динамику процесса изменения ошибки относи-

тельно переменной k можно описать только с использованием оценки второй

Желаемый угол поворота сервопривода (q_ref)

1,6

1,4

1,2

1,0

0,8

0,6

0,4

0,2

500

1000

1500

2000

2500

3000

Время t, мс

Рис. 1. Желаемая траектория.

производной

ëk = ÿref - C1

x_k.

Обозначим ǫ_k =ëk, и тогда ошибка обучения опишется уравнением

(21)

ǫ_k+1 = ǫ_k - C₁

ξ_k+1 - C₁F

ξ_k+1 - C₁BΔu_k+1.

Динамика системы с учетом наблюдателя теперь будет описываться урав-

нениями

η_k+1(t) = A₁₁(δ)η_k+1(t) + A₁₂ǫ_k(t) + B₁v_k+1(t),

(22)

ǫ_k+1(t) = A₂₁η_k+1(t) + A₂₂ǫ_k(t) + B₂v_k+1(t),

где

[

]

[

]

A₁₁(δ) =

A₁₂ = 0, A₂₁ =

-C₁A -C₁FC

A_a(δ) A(δ) - FC

[

]

A₂₂ = I, B₁ =

B₂ = -C₁B.

Начальные условия для наблюдателя в дополнение к (8) должны удовле-

творять условию

y_k(0) = Cˆxk(0) = yref(0).

Выберем корректирующую поправку в виде

Δu_k+1 = K₁

ξ_k+1 + K₂ǫ_k.

1,0

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

Рис. 2. Cреднеквадратическая ошибка обучения при различных разбросах

неопределенных параметров J_l и K_s.

Тогда закон управления с итеративным обучением будет иметь вид

u_k+1 = u_k + Δu_k+1 = u_k + K₁(x_k+1 - x_k) + K₂(ÿ_ref - C₁xk) =

(23)

= u_k + K₁(x_k+1 - x_k) + K₂(ÿ_ref - C₁Ax_k - C₁Bu_k - C₁F(y_k - Cx_k)).

Чтобы оценить эффективность этого закона управления с итеративным

обучением, для каждого повторения k введем среднеквадратическое откло-

нение ошибки обучения

∫

(24)

E(k) =

√

|e_k(t)|²

dt.

Предположим, что момент инерции гибкого звена может принимать значе-

ния от J_l + ΔJ_l до J_l + ΔJ_l, что с физической точки зрения может означать

наличие или отсутствие груза на гибком звене или наличие различных гру-

зов. Также добавим неопределенность по жесткости K_s, полагая, что жест-

кость может принимать значения от K_s + ΔK_s до K_s + ΔK_s. В этом случае

матрица параметров A(δ) будет иметь вид

A(δ) = A + A_a(δ), A_a(δ) = δA, δ = {δ₁; δ₂} ,

δ₁ = [J_l;J_l], δ₂ = [K_s;K_s].

Параметры фильтра выберем с помощью стандартной функции lqr

пакета MATLAB из условия, что вещественные части собственных значений

матрицы (A - F C) меньше -0,15. Этому условию удовлетворяет матрица

F = [0,1881

- 0,0026 0,0127

- 0,0055]. Решая задачу максимизации tr[X]

при ограничениях в виде неравенства (20), с учетом очевидных изменений

Ошибка по углу q

2,0

1,5

1,0

0,5

3000

2000

1000

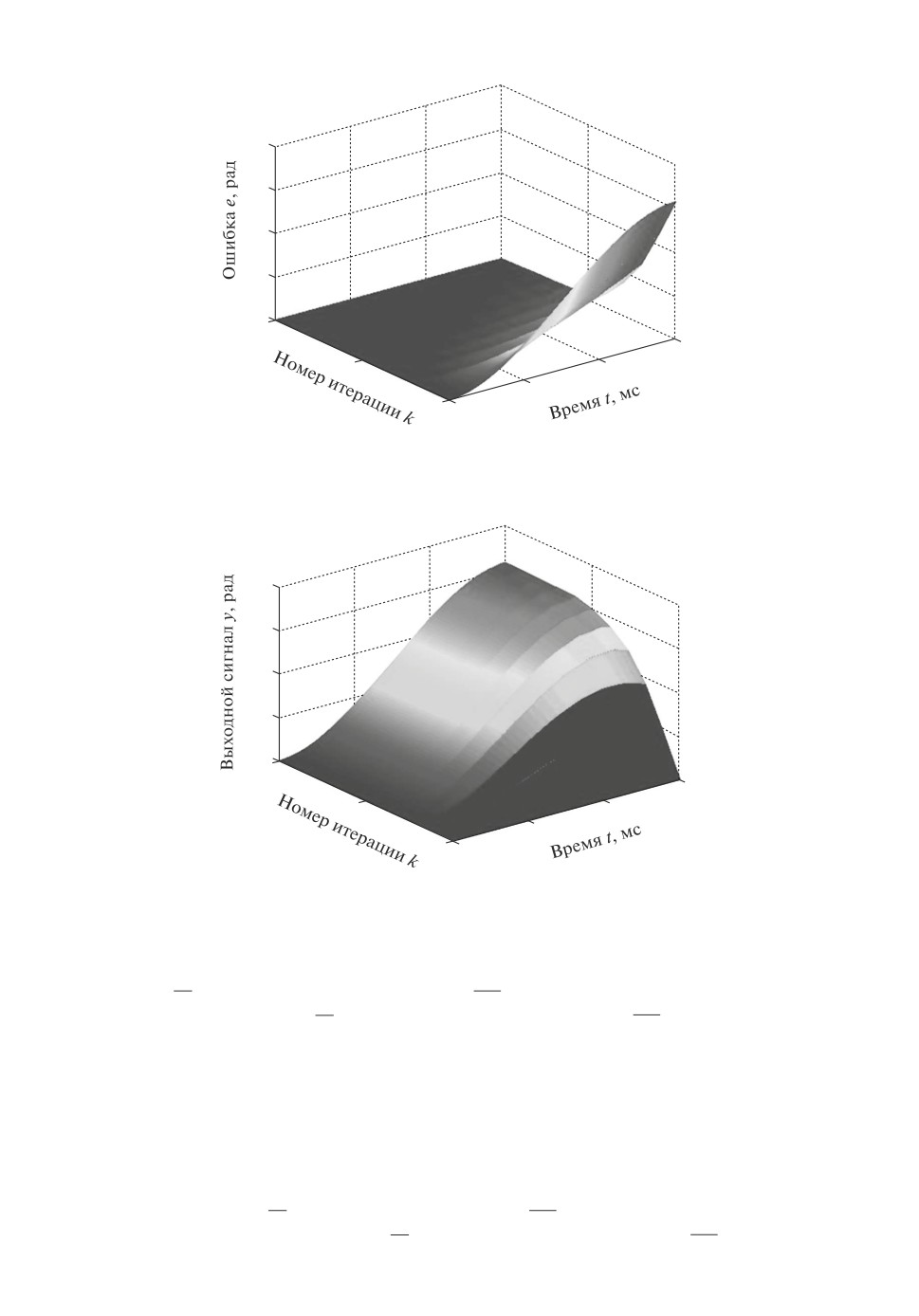
Рис. 3. Изменение ошибки обучения в зависимости от числа повторений.

Угол поворота сервопривода q

2,0

1,5

1,0

0,5

3000

2000

1000

Рис. 4. Изменение выходной переменной в зависимости от числа повторений.

матриц A₁₁(δ), A₁₂, A₂₁, A₂₂, B₁(δ), B₂, и задавая

ΔJ_l = 0,3J_l, ΔJ_l = -0,3J_l, ΔK_s = 0,1K_s, ΔK_s = -0,1K_s,

Q = diag[Q₁ Q₂], Q₁ = 10^-2I, Q₂ = 10^-3I,R = 1,

получим

K₁ = [-0,0000

- 1,2385

0,0019

- 0,0004], K₂ = 0,0020.

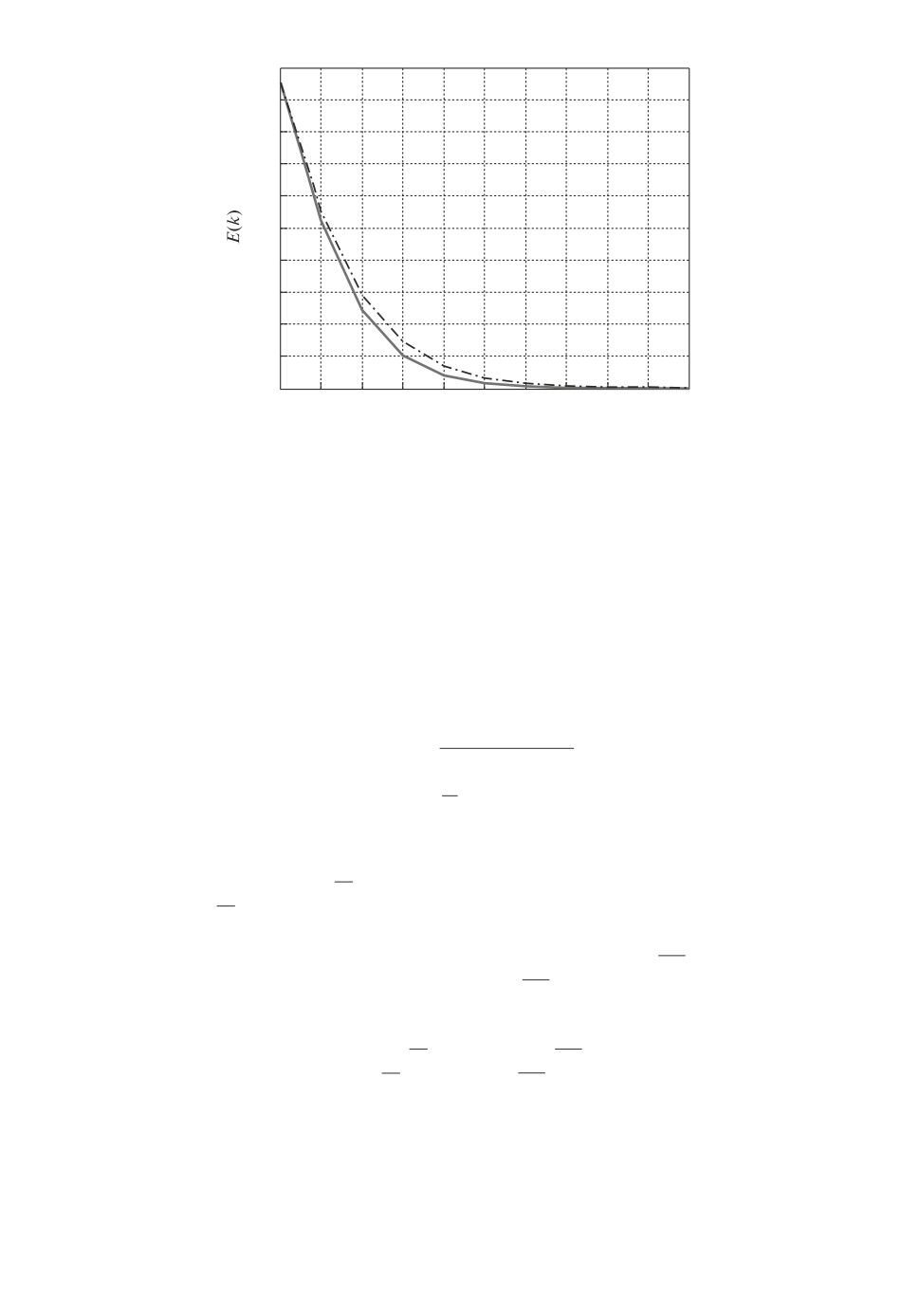
На рис. 2 представлен график изменения среднеквадратической ошибки

обучения (24) в зависимости от числа повторений k при указанном разбро-

се параметров J_l и K_s (штрихпунктирная линия). При меньшем разбросе

этих параметров ΔJ_l = 0,1J_l, ΔJ_l = -0,1J_l, ΔK_s = 0,005K_s, ΔK_s = -0,005K_s

Управление и

0,10

0,05

-0,05

-0,10

3000

2000

1000

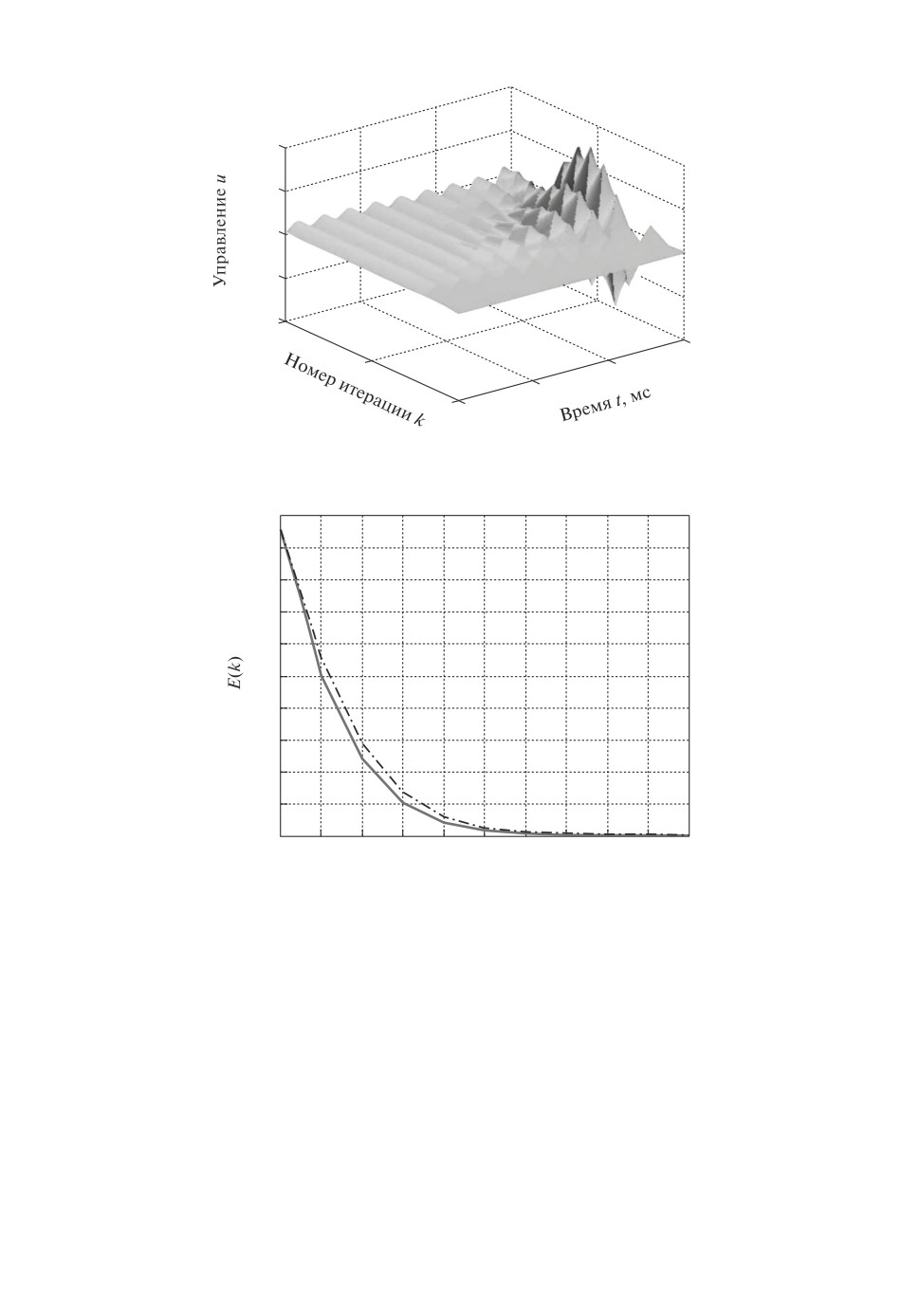
Рис. 5. Изменение управления в зависимости от числа повторений.

1,0

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

Рис. 6. Cреднеквадратическая ошибка обучения в случае сочетания неопреде-

ленных параметров J_l и K_s на верхней границе (штрихпунктирная линия) и

на нижней границе.

ошибка сходится к нулю быстрее (сплошная линия). Требуемая точность

e^∗ = 0,005 рад достигается за 8 повторений (k_fin = 8, E(8) = 0,003454 рад ≈

≈ 0,2^◦). При большем разбросе неопределенных параметров система может не

только не достичь требуемой точности, но и не стабилизироваться, это вполне

объяснимо энергии управления не хватает для компенсации неопределен-

ности.

На рис. 3-5 представлены изменения ошибки, выходной переменной и

управления в зависимости от времени на текущем повторении и числа по-

вторений.

На рис. 6 представлен случай, когда оба неопределенных параметра J_l и K_s

находятся на верхней границе, а именно ΔJ_l = 0,3J_l, ΔK_s = 0,1K_s (штрих-

пунктирная линия), или на нижней границе ΔJ_l = -0,3J_l, ΔK_s = -0,1K_s

(сплошная линия).

4. Заключение

В данной статье разработан метод синтеза управления с итеративным обу-

чением с использованием наблюдателя состояния для случая дифференци-

альных повторяющихся процессов, когда модель объекта управления содер-

жит аффинные неопределенности. Результаты решения данной задачи поз-

воляют повысить скорость сходимости процессов управления с итеративным

обучением и обеспечить робастность этих процессов по отношению к различ-

ным неопределенностям, неизбежно возникающим при функционировании

реальных систем. Значительный интерес представляет исследование влия-

ния динамики наблюдателя на ошибку обучения. Эта задача пока остается

открытой. Сочетание управления с итеративным обучением и управления с

обратной связью также представляет интересную задачу для дальнейших ис-

следований.

СПИСОК ЛИТЕРАТУРЫ

Bristow D.A., Tharayil M., Alleyne A.G. A Survey of Iterative Learning Control:

A Learning-Based Method for High-Performance Tracking Control // IEEE Control

Syst. Magaz. 2006. V. 26. No. 3. P. 96-114.

Ahn H-S., Chen Y.Q., Moore K.L. Iterative Learning Control: Survey and Catego-

rization // IEEE Trans. Syst. Man Cybern. Part C: Appl. Rev. 2007. V. 37. No. 6.

P. 1099-1121.

Freeman C.T., Rogers E., Hughes A.-M., Burridge J.H., Meadmore K.L. Iterative

Learning Control in Health Care: Electrical Stimulation and Robotic-Assisted Upper-

Limb Stroke Rehabilitation // IEEE Control Syst. Magaz. 2012. V. 47. P. 70-80.

Meadmore K.L., Exell T.A., Hallewell E., Hughes A.-M., Freeman C.T., Kutlu M.,

Benson V., Rogers E., Burridge J.H. The Application of Precisely Controlled Func-

tional Electrical Stimulation to the Shoulder, Elbow and Wrist for Upper Limb

Stroke Rehabilitation: a Feasibility Study // J. NeuroEngineer. Rehabilitation. 2014.

P. 11-105.

Ketelhut M., Stemmler S., Gesenhues J., Hein M., Abel D. Iterative Learning Control

of Ventricular Assist Devices with Variable Cycle Durations // Control Engin. Pract.

2019. V. 83. P. 33-44.

Sammons P.M., Gegel M.L., Bristow D.A., Landers R.G. Repetitive Process Control

of Additive Manufacturing with Application to Laser Metal Deposition // IEEE

Trans. Control Syst. Technol. 2019. V. 27. No. 2. P. 566-575.

Sornmo O., Bernhardsson B., Kroling O., Gunnarsson P., Tenghamn R. Frequency-

Domain Iterative Learning Control of a Marine Vibrator // Control Engin. Pract.

2016. V. 47. P. 70-80.

Lim I., Hoelzle D.J., Barton K.L. A Multi-Objective Iterative Learning Control

Approach for Additive Manufacturing Applications // Control Eng. Pract. 2017.

V. 64. P. 74-87.

9. Arimoto S., Kawamura S., Miyazaki F. Bettering Operation of Robots by Learn-

ing // J. Robot. Syst. 1984. V. 1. P. 123-140.

10. Rogers E., Galkowski K., Owens D.H. Control Systems Theory and Applications

for Linear Repetitive Processes / Lect. Notes Control Inform. Sci. Berlin: Springer-

Verlag, 2007. V. 349.

11. Pakshin P., Emelianova J., Emelianov M., Galkowski K., Rogers E. Dissipivity and

Stabilization of Nonlinear Repetitive Processes // Syst. Control Lett. 2016. V. 91.

P. 14-20.

12. Hladowski L., Galkowski K., Cai Z., Rogers E., Freeman C., Lewin P. Experimen-

tally Supported 2D Systems Based Iterative Learning Control Law Design for Error

Convergence and Performance // Control Engin. Pract. 2010. V. 18. P. 339-348.

13. Paszke W., Rogers E., Patan K. Observer-Based Iterative Learning Control Design in

the Repetitive Process Setting // IFAC-PapersOnline. 2017. V. 50. No. 1. P. 13390-

13395.

14. Емельянова Ю.П., Пакшин П.В. Синтез управления с итеративным обучением

на основе наблюдателя состояния // АиТ. 2019. № 9. С. 9-24.

Emelianova J.P., Pakshin P.V. Iterative Learning Control Design Based on State

Observer // Autom. Remote Control. 2019. V. 80. No. 9. P. 1561-1573.

15. Jayawardhana R.N., Ghosh B.K. Kalman Filter Based Iterative Learning Control

for Discrete Time MIMO Systems // Proc. 30th Chinese Control and Decision Conf.

(2018 CCDC). 2018. P. 2257-2264.

16. Apkarian J., Karam P., Levis M. Workbook on Flexible Link Experiment for Mat-

lab/Simulink Users. Quanser, 2011.

Статья представлена к публикации членом редколлегии С.А. Красновой.

Поступила в редакцию 27.11.2019

После доработки 11.02.2020

Принята к публикации 04.03.2020