Автоматика и телемеханика, № 7, 2020

Управление в технических системах

(Севастопольский государственный университет)

СТАЦИОНАРНЫЕ ХАРАКТЕРИСТИКИ НЕНАДЕЖНОЙ

ОДНОЛИНЕЙНОЙ СИСТЕМЫ ОБСЛУЖИВАНИЯ

С ПОТЕРЯМИ И УЧЕТОМ ТЕХНИЧЕСКОГО

ОБСЛУЖИВАНИЯ ПО НАРАБОТКЕ¹

Рассматривается ненадежная восстанавливаемая одноканальная систе-

ма обслуживания с потерями, в которой во время обслуживания требо-

ваний могут происходить отказы прибора. Случайные величины, описы-

вающие систему, имеют распределения общего вида. Для повышения эф-

фективности системы предлагается проводить профилактическое техни-

ческое обслуживание прибора в тот момент, когда накопленное время об-

служивания требований превышает заранее заданный уровень. Построена

полумарковская модель эволюции системы во времени. С помощью най-

денного стационарного распределения вложенной цепи Маркова устанав-

ливаются выражения для определения финальных вероятностей и сред-

них времен пребывания системы в различных физических состояниях.

Решается задача оптимизации периодичности проведения технического

обслуживания прибора с целью максимизации средней удельной прибы-

ли и минимизации средних удельных затрат системы.

Ключевые слова: одноканальная система обслуживания с отказами, тех-

ническое обслуживание, стационарное распределение вложенной цепи

Маркова, финальные вероятности состояний, стационарные показатели

эффективности.

DOI: 10.31857/S0005231020070065

1. Введение

Интерес к системам с отказами каналов обслуживания связан с практиче-

ской важностью адекватного описания функционирования современных тех-

нических и информационных систем. Обзор по ненадежным системам обслу-

живания можно найти, например, в [1, 2]. Отметим некоторые результаты

исследований в этом направлении. Так, в [3] исследована многоканальная

система обслуживания с каналами конечной надежности при частном виде

функций распределения случайных величин, описывающих процессы в си-

стеме. В [4] описана система M/G/1/1 с двумя типами заявок, в которой

¹ Работа выполнена в рамках Государственного задания Министерства образования и

науки РФ (№ 1.10513.2018/11.12) и при финансовой поддержке Российского фонда фунда-

ментальных исследований (проект № 19-01-00704).

функции распределения времени восстановления и времени между отказа-

ми имеют общий вид. В [5] решена задача оптимизации групповой полити-

ки восстановления отказавших обслуживающих приборов. В [6] исследована

дисциплина обслуживания в двухканальной неоднородной системе обслужи-

вания с различными надежностными характеристиками и интенсивностями

обслуживания заявок. Следует отметить, что наиболее полные результаты

получены при условии, что случайные факторы, описывающие ненадежные

системы, имеют показательные распределения. Модели ненадежных однока-

нальных систем обслуживания в случае общего вида распределений построе-

ны в [7, 8]. Упомянутые публикации далеко не полный список исследований

по определению характеристик систем обслуживания с каналами, которые

могут отказывать.

Системы с ненадежными приборами часто являются предметом современ-

ных исследований, поскольку развитие технологий приводит к появлению

новых содержательных математических задач. Наряду с определением ха-

рактеристик систем с отказами каналов важно оказывать воздействия на

эти показатели. В ряде случаев повысить эффективность системы можно за

счет проведения предупредительного технического обслуживания (ТО) кана-

ла. Так, в [9] исследована стратегия, при которой решение о проведении ТО

зависит от длительности обслуживания требования. В [10] построена модель

системы с учетом наработки прибора на отказ и отложенным ТО, в [11]

с учетом ТО системы в случае скрытых отказов прибора, в [12] с учетом

ТО в зависимости от суммарной наработки прибора на отказ, в [13] с уче-

том различных типов восстановления прибора. В данной статье исследуется

еще одна стратегия ТО ненадежной одноканальной системы обслуживания

с потерями: ТО прибора начинается в тот момент, когда накопленное время

обслуживания требований после завершения восстановительных работ пре-

высит заранее заданный уровень.

2. Постановка задачи

В ненадежную систему обслуживания GI/G/1/0 поступает рекуррентный

поток требований, порожденный случайной величиной (СВ) β с функцией

распределения (ФР) G(t) = P { β ≤ t}. Длительность обслуживания требова-

ния СВ α с ФР F (t) = P { α ≤ t}. В начальный момент времени начинается

обслуживание поступившего требования и отсчет наработки прибора до от-

каза. Под наработкой понимается накопленное время, затраченное прибором

на обслуживание требований. Во время обслуживания требования возможен

отказ прибора, который происходит в момент достижения прибором нара-

ботки, реализуемой как СВ γ с ФР Φ(t) = P {γ ≤ t}. Отказ обнаруживается

мгновенно, и сразу же начинается аварийное восстановление (АВ) прибора,

которое длится случайное время σ_a с ФР Ψ_a(t) = P {σ_a ≤ t}.

Перед началом эксплуатации назначается предельно допустимый детер-

минированный уровень наработки τ, при достижении которого незамедли-

тельно начинается ТО прибора. Длительность проведения ТО СВ σ_p с

ФР Ψ_p(t) = P {σ_p ≤ t}. Обслуживание требования, находящегося на приборе

в момент начала АВ или ТО, прерывается и на дообслуживание требование

не возвращается. В результате любого вида восстановления надежностные

характеристики прибора полностью обновляются, и в момент поступления

первого требования в обновленную систему весь процесс ее функционирова-

ния повторяется.

Предполагается, что 0 < P {α < β} < 1 и 0 < P {α < γ} < 1; СВ α, β, γ, σ_a, σ_p

независимы, имеют соответственно плотности распределения вероятностей

f (t), g(t), ϕ(t), ψ_a(t), ψ_p(t), конечные математические ожидания Mα, Mβ,

Mγ, Mσ_a, Mσ_p и дисперсии.

Требуется построить полумарковскую модель функционирования описан-

ной выше системы обслуживания, найти ее стационарные вероятностные и

экономические характеристики, решить задачу оптимизации периодичности

проведения ТО прибора с целью повышения средней удельной прибыли в еди-

ницу календарного времени и снижения средних удельных затрат в единицу

времени обслуживания требований.

3. Построение полумарковской модели системы

Для описания функционирования системы используем аппарат теории по-

лумарковских процессов с дискретно-непрерывным фазовым пространством

состояний. Приведем краткие сведения из теории этих процессов. Пусть

(E, ξ)

измеримое пространство, E интерпретируется как фазовое про-

странство состояний стохастической системы, ξ булева алгебра выделен-

ных подмножеств из E, интерпретируемых как совокупность наблюдаемых

подмножеств состояний системы. Полумарковский процесс с общим фазо-

вым пространством состояний определяется с помощью процесса марковско-

го восстановления, который, в свою очередь, задается полумарковским ядром

Q(t, x, B), x ∈ E, B ∈ ξ, t ≥ 0 [14, 15].

Процесс марковского восстановления есть двухмерная цепь Маркова

{S_n, θ_n; n ≥ 0} со значениями в E × [0, ∞), вероятности перехода которой

определяются равенством

P {S_n+1 ∈ B, θ_n+1 ≤ t / S_n = x} = Q(t, x, B).

Первая компонента

{S_n; n ≥ 0} процесса марковского восстановления

{S_n, θ_n; n ≥ 0} является однородной цепью Маркова с переходными вероят-

ностями

P (x, B) = P {S_n+1 ∈ B / S_n = x} = Q(+∞, x, B),

и называется вложенной цепью Маркова (ВЦМ). Случайные величины

{θ_n+1, n ≥ 0}, составляющие вторую компоненту процесса марковского вос-

становления, можно интерпретировать как времена пребывания системы в

состояниях {S_n; n ≥ 0}, они определяют интервалы между моментами мар-

ковского восстановления τ_n :

∑

τ_n =

θ_k, n ≥ 1, τ₀ = θ₀ = 0.

k=1

Полумарковский процесс S(t), t ≥ 0, в измеримом фазовом про-

странстве (E, ξ), соответствующий процессу марковского восстановления

{S_n, θ_n; n ≥ 0}, задается соотношением

S(t) = S_ν(t), t ≥ 0,

где ν(t) число моментов марковского восстановления на отрезке [0, t].

Полумарковское ядро Q(t, x, B) процесса марковского восстановления

{S_n, θ_n; n ≥ 0} с условно независимыми компонентами представимо в виде

Q(t, x, B) = P (x, B)G_x(t), x ∈ E, B ∈ ξ, t ≥ 0,

где

Gx(t) = P {θn+1 ≤ t / Sn = x} = Q(t, x, E)

функции распределения СВ θ_n+1, зависящие от первой компоненты. Таким

образом, для задания процесса марковского восстановления достаточно опи-

сать фазовое пространство состояний E, определить переходные вероятности

ВЦМ {S_n; n ≥ 0} и функции распределения случайных величин θ_n.

Начнем с описания фазового пространства состояний. Рассматриваемая

система может находиться в следующих физических состояниях: 0 прибор

в работоспособном состоянии ожидает требование; 1 прибор занят обслу-

живанием; 2 проводится АВ прибора; 3 проводится ТО прибора. Расши-

рим пространство физических состояний за счет введения непрерывных ком-

понент, в результате фазовое пространство состояний системы будет иметь

вид

E = {1, 1uv, 2x, 3x, 0x, 0xuv; x > 0, u > 0, 0<v<τ}.

Поясним коды состояний: 1 начинается обслуживание первого требова-

ния, поступившего после завершения ТО или АВ прибора; 1uv начинается

обслуживание поступившего требования, наработка прибора в этот момент

равна v, величина оставшейся наработки до отказа равна u; 2x произошел

отказ и начинается АВ прибора, до поступления следующего требования в

систему остается время x ; 3x величина наработки достигла предельного

уровня и начинается ТО прибора, до поступления следующего требования

в систему остается время x ; 0x завершилось ТО или АВ прибора, до по-

ступления следующего требования остается время x; 0xuv

закончилось

обслуживание требования, наработка прибора в этот момент равна v, вели-

чина оставшейся наработки до отказа равна u, до поступления следующего

требования в систему остается время x.

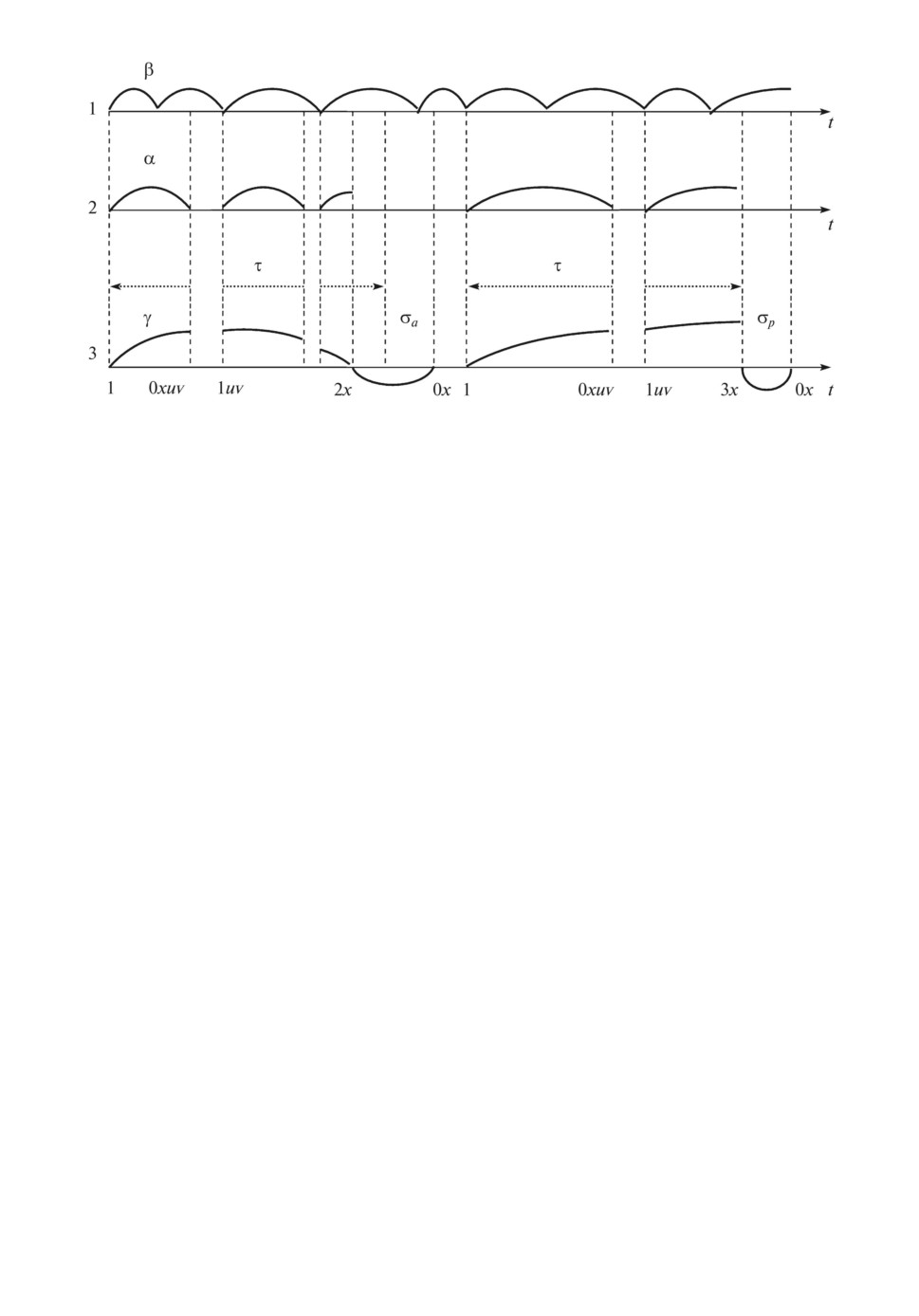
Временная диаграмма функционирования системы представлена на рис. 1.

Времена пребывания системы в соответствующих состояниях определяются

формулами

θ₁ = α ∧ γ ∧ τ, θ_1uv = α ∧ u ∧ (τ - v);

θ_2x = σ_a; θ_3x = σ_p; θ_0xuv = θ_0x = x,

Рис. 1. Временная диаграмма функционирования системы: 1 входящий по-

ток (β время между требованиями); 2 процесс обслуживания требований

(α время обслуживания); 3 процесс функционирования прибора (γ

наработка до отказа, σ_a аварийное восстановление, σ_p техническое об-

служивание; τ предельно допустимый уровень наработки).

где ∧

знак минимума, исходя из которых нетрудно выписать функции

распределения времен пребывания в состояниях.

Опишем случайные события и вероятности переходов из состояний ВЦМ

{S_n; n ≥ 0} с учетом их содержательного смысла. Например, переходы из со-

стояния 1uv, в котором система пребывает время α ∧ u ∧ (τ - v), зависят

от реализации минимума случайного времени α обслуживания требования

и детерминированных величин в момент начала обслуживания требования:

оставшейся наработки прибора u до отказа и оставшейся наработки τ - v

до проведения ТО прибора. Если время обслуживания требования меньше

указанных наработок, причем u < (τ - v), тогда в момент окончания обслу-

живания требования система переходит в состояние (0xu^′, v + u - u^′), где u^′

величина оставшейся наработки прибора до отказа в этот момент, v + u - u^′

наработка прибора, x время до поступления ближайшего требования в си-

стему (время обслуживания реализуется как u - u^′).

Аналогично рассматриваются и другие случаи реализации времени пре-

бывания системы в состоянии 1uv. В результате получаем:

{

}

1uv → (0xu^′, v + u - u^′)

{

}

α < u < (τ - v),α ∈ u - du^′,β_u-u′ ∈ dx,u^′ < u,x > 0

{

}

1uv → (0x, u + v - v^′, v^′)

{

}

α < (τ - v) < u,α ∈ dv^′ - v,β_v′_-v ∈ dx,v < v^′ < τ,x > 0

{1uv → 2x} = {u < α ∧ (τ - v), β_u ∈ dx, x > 0} ,

{1uv → 3x} = {τ - v < α ∧ u, β_τ-v ∈ dx, x > 0} .

Здесь β_t

прямое остаточное время для процесса восстановления, порож-

денного СВ β, с плотностью распределения

∫t

v_g(t,x) = g(t + x) + h_g(t - s)g(s + x)ds,

∑_∞

h_g(t) плотность функции восстановления H_g(t) =

G∗(n)(t) этого про-

n=1

цесса [16]. Величина β_t фиксирует время в момент t до ближайшего момента

поступления требования в систему. Запись, например, α ∈ u - du^′ означает,

что u - u^′ < α ≤ u - u^′ + du^′.

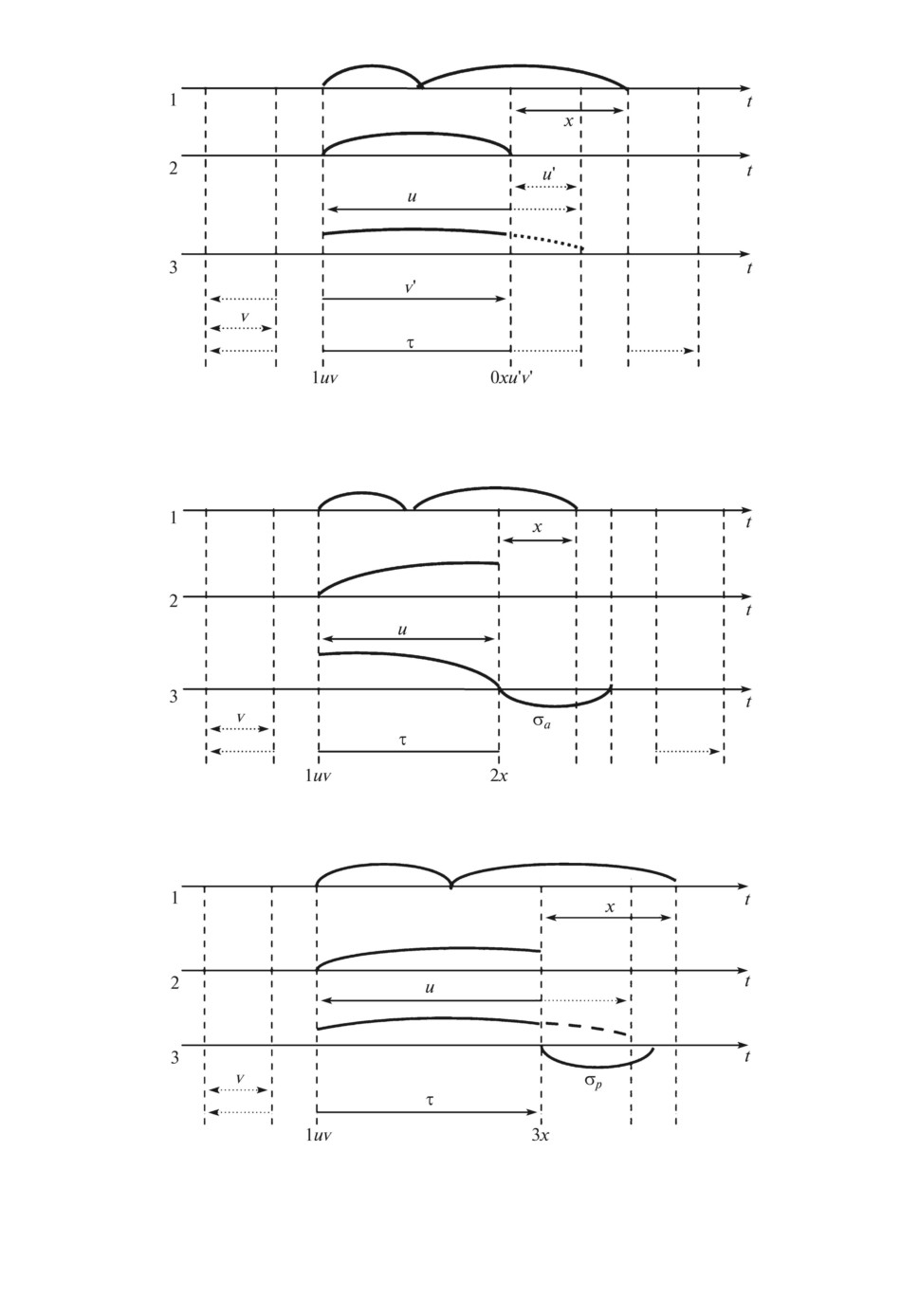
Иллюстрации переходов приведены на рис. 2-4, где использованы обозна-

чения: 1

входящий поток требований; 2 процесс обслуживания требо-

ваний; 3

процесс функционирования прибора (v, v^′ наработка, u, u^′

оставшаяся наработка до отказа; τ предельно допустимый уровень нара-

ботки; σ_a длительность АВ; σ_p длительность ТО прибора).

Вероятности переходов из состояния 1uv определяются формулами:

p(0dx,du′,v+u-du′)1uv = f(u - u^′)v_g(u - u^′,x)dxdu^′, u^′ < u, x > 0, u < τ - v;

p(0dx,v+u-dv′,dv′)1uv = f(v^′ -v)v_g(v^′ -v,x)dxdv^′, v < v^′ < τ, x > 0, u > τ -v;

p^2dx1uv = F(u)v_g(u,x)dx, x > 0, u < τ - v, F(u) = 1 - F(u);

p^3dx1uv = F(τ - v)v_g(τ - v,x)dx, x > 0, u > τ - v.

Аналогично определяются вероятности перехода из других состояний:

p^0dxdudv1 = f(v)ϕ(v + u)v_g(v,x)dudvdx, u > 0, x > 0,

0<v<τ;

∫τ

p^2dx1 = ϕ(t)F(t)v_g(t,x)dtdx, x > 0;

p^3dx1 = F(τ)Φ(τ)v_g(τ,x), x > 0,

Φ(τ) = 1 - Φ(τ); P^1uv0xuv = P^10x = 1;

∫∞

p^0dy3x = ψ_p(x - y) + ψ_p(t)v_g(t - x,y)dtdy,

0 < y < x;

∫∞

p^0dy3x = ψ_p(t)v_g(t - x,y)dtdy, y > x;

∫∞

p^0dy2x = ψ_a(x - y) + ψ_a(t)v_g(t - x,y)dtdy,

0 < y < x;

∫∞

p^0dy2x = ψ_a(t)v_g(t - x,y)dtdy, y > x.

100

Отметим, что построенный процесс S(t), t ≥ 0, является регенерирующим.

Точкой регенерации является момент попадания системы в состояние 1, т.е.

начало обслуживания первого требования после завершения любой из вос-

становительных работ.

4. Стационарные характеристики системы

Для нахождения стационарных характеристик системы потребуется опре-

делить стационарное распределение ВЦМ {S_n; n ≥ 0} полумарковского про-

цесса S(t), t ≥ 0, описывающего ее функционирование. Введем следующие

обозначения: ρ₁

стационарная вероятность пребывания в состоянии 1, а

ρ(1uv), ρ(0xuv), ρ(0x), ρ(2x) и ρ(3x) плотности стационарного распределе-

ния ВЦМ для соответствующих состояний.

Теорема 1. Стационарное распределение вложенной цепи Маркова

{S_n; n ≥ 0} полумарковского процесса S(t), t ≥ 0, определяется формулами:

ρ(1uv) = ρ₁h_f (v)ϕ(u + v),





∫

ρ(0xuv) = ρ₁ϕ(u + v)f(v)v_g(v, x) + h_f (v - s)f(s)v_g(s, x)ds ,





∫

ρ(3x) = ρ₁Φ(τ)F (τ)v_g(τ, x) + h_f (τ - s)F (s)v_g(s, x)ds ,





∫τ

∫

(1)

ρ(2x) = ρ₁ ϕ(t)F (t)v_g(t, x) + h_f (t - s)F (s)v_g(s, x)ds

dt,





∫∞

∫

ρ(0x) = ρ₁Φ(τ) ψ_p(t)F (τ)v_g(τ + t, x) + h_f (τ - s)F (s)v_g(s + t, x)dsdt +





∫∞

∫

+ρ₁

ψ_a(t)dt ϕ(y)F(y)v_g(y + t,x) + h_f (y - s)F(s)v_g(s + t,x)ds dy,



_-1

∫

ρ₁ =3 + 2 h_f (s)Φ(s)ds

где h_f (v)

плотность функции восстановления H_f (v), порожденной слу-

чайным временем α обслуживания требования.

Доказательства теоремы 1 и последующих теорем 2 и 3 приводятся в При-

ложении.

Отметим вероятностный смысл выражений, входящих в формулы

для плотностей стационарного распределения. По переменной x функ-

102

∫v

ция f(v)v_g(v, x) +

h_f (v - s)f(s)v_g(s,x)ds является плотностью распреде-

ления интервала времени от момента окончания обслуживания требова-

ния до момента поступления следующего требования при условии, что

наработка прибора в момент завершения обслуживания равна v. По пе-

∫t

ременной x функция F (t)v_g(t, x) +

h_f(t - s)F(s)v_g(s,x)ds

плотность

распределения интервала времени между моментом отказа прибора и

моментом поступления следующего требования в систему при условии,

что наработка п∫ибора в момент отказа достигла уровня t. Функция

F (τ)v_g(τ + t, x) +

h_f(τ - s)F(s)v_g(s + t,x)ds по переменной x плотность

распределения интервала времени между моментом завершения ТО прибо-

ра и первым после этого моментом поступления требования в систему при

условии, что ТО прибора длилось время t.

Найдем финальные вероятности и средние стационарные времена пребы-

вания системы в различных физических состояниях. Для этого разобьем фа-

зовое пространство состояний E на непересекающиеся подмножества, соот-

ветствующие различным физическим состояниям прибора: E₀ = {0x, 0xuv}

работоспособный прибор находится в состоянии ожидания требования;

E₁ = {1,1uv} прибор обслуживает требование; E₂ = {2x} проводится

АВ прибора; E₃ = {3x} проводится ТО прибора.

В следующей теореме 2 устанавливаются выражения для предельных зна-

чений p^∗i переходных вероятностей

Φ(t, x, E_i) = P {S(t) ∈ E_i / S(0) = x}, x ∈ E, i = 0, 3,

полумарковского процесса S(t), t ≥ 0, а в теореме 3 выражения для средних

стационарных времен пребывания в этих состояниях. Утверждения этих тео-

рем содержат следующие характеристики S(t), t ≥ 0, как регенерирующего

процесса:

∫τ

N_обс(τ) = Φ(v)h_f (v)dv

среднее число полностью обслуженных требований в интервале между вос-

становительными работами;

∫τ

∫

N^обспот(τ) = Φ(v)f(v)H_g(v)dv + Φ(v)dv h_f (v - s)f(s)H_g(s)ds

среднее число требований, потерянных по причине занятости прибора об-

служиванием этих требований;





∫∞

∫

N^pпот(τ) = Φ(τ) ψ_p(t)F(τ) H_g(τ + t) + h_f (τ - s)F(s) H_g(s + t)ds dt

среднее число потерянных требований на периоде регенерации по причине

ТО прибора и за время обслуживания требования, на котором достигается

103

предельно допустимая наработка на отказ;

N^aпот(τ) =





∫∞

∫

= ψ_a(t)dt ϕ(y)F(y)Hg(y + t) + h_f(y - s)F(s)Hg(s + t)ds dy

среднее число потерянных требований на периоде регенерации по причине

АВ прибора и за время обслуживания требования, находящегося на приборе

в момент его отказа. Здесь

Ĥ_g(t) = 1 + H_g(t).

Теорема 2. Финальные вероятности p^∗i(τ) пребывания системы в со-

стояниях E_i, i = 0,3, определяются формулами:

M(γ ∧ τ) + Mσ_aP (γ < τ) + Mσ_pP (γ > τ)

p^∗0(τ) = 1 -

MβN (τ)

(2)

M(γ ∧ τ)

Mσ_aP (γ < τ)

Mσ_pP (γ > τ)

p^∗1(τ) =

p^∗2(τ) =

p^∗3(τ) =

MβN (τ)

MβN(τ)

где

N (τ) = N_обс(τ) + N^обспот(τ) + N^pпот(τ) + N^aпот(τ)

среднее число требований, поступающих в систему на периоде регенера-

ции.

Теорема 3. Средние стационарные времена пребывания системы в со-

стояниях E_i, i = 0,3, определяются выражениями:

M(γ ∧ τ)

T (E₁) =

T (E₂) = Mσ_a, T (E₃) = Mσ_p,

1 + N_обс(τ)

MβN (τ) - M(γ ∧ τ) - Mσ_aP (γ < τ) - Mσ_pP (γ > τ)

T (E₀) =

1 + N_обс(τ)

Перейдем к нахождению стационарных экономических показателей эф-

фективности функционирования системы [17]. Для этого воспользуемся тем,

что случайный процесс, описывающий эволюцию технической системы во

времени, является регенерирующим. Пусть c₁ доход, получаемый за об-

служивание одного требования; c_a затраты в единицу времени АВ; c_p

затраты в единицу времени на проведение ТО прибора. Тогда средняя удель-

ная прибыль S(τ) в единицу календарного времени и средние удельные за-

траты C(τ) в единицу времени обслуживания требований определяются со-

отношениями:

c₁N_ser(τ) - c_pMσ_pΦ(τ) - c_aMσ_aΦ(τ)

S(τ) =

Mβ N(τ)

(3)

c_aMσ_aΦ(τ) + c_pMσ_pΦ(τ)

C(τ) =

M(γ ∧ τ)

104

Для частных видов входящих потоков и времени обслуживания требова-

ний выражения для вычисления характеристик системы упрощаются. Так,

в случае простейшего входящего потока требований с интенсивностью λ при

вычислении стационарных характеристик ненадежной системы M/G/1/0 в

соответствующих формулах следует полагать, что

∫τ

∫

N (τ) = 1 + h_f (t)Φ(t)dt + λ Φ(t)dt + λMσ_aΦ(τ) + λMσ_pΦ(τ).

Для системы GI/M/1/0, в которой длительность обслуживания требова-

ния имеет показательное распределение с параметром µ, в формулах для

вычисления стационарных характеристик следует подставить:

∫τ

N_обс(τ) = µ Φ(x)dx,

∫τ

∫

N (τ) = µ Φ(t)dt + µ Φ(t)dt e^-µsh_g(s)ds +

∞

∫∞

∫

+ Φ(τ) ψ_p(t) Ĥg(t)dt + Φ(τ) ψ_p(t)dt e^-µsh_g(s + t)ds +

∞

∫∞

∫

+ Φ(τ) ψ_a(t) Ĥg(t)dt + ψ_a(t)dt ϕ(y)dy e^-µsh_g(s + t)ds.

Для системы M/M/1/0, в которой входящий поток требования является

простейшим с параметром λ, а длительность обслуживания требования имеет

показательное распределение с параметром µ, в формулах для определения

стационарных характеристик имеем:

∫τ

N_обс(τ) = µ Φ(x)dx,

∫τ

N (τ) = 1 + (λ + µ) Φ(t)dt + λMσ_aΦ(τ) + λMσ_pΦ(τ).

В частности, когда СВ γ, σ_a и σ_p, описывающие процессы отказа и

восстановления, имеют экспоненциальные распределения, т.е. ϕ(t) = ηe^-ηt,

ψ_a(t) = ν_ae-νat и ψ_p(t) = ν_pe-νpt, тогда финальные вероятности пребывания

системы в состояниях вычисляются по формулам:

η + µ(1 - e^-ητ)

p^∗0(τ) =

(

) (

)

1+^λν

e^-ητ

+ λ+µ+^ηλ

(1 - e^-ητ )

νa

105

λ(1 - e^-ητ )

p^∗(τ) = (

) (

)

1+^λν

e^-ητ

+ λ+µ+^ηλ

(1 - e^-ητ )

νa

λη

(1 - e^-ητ )

νa

p^∗2(τ) =

(

)

(

)

1+^λν

e^-ητ

+ λ+µ+^ηλ

(1 - e^-ητ )

νa

λη

e^-ητ

νp

p^∗3(τ) =

(

)

(

)

1+^λν

e^-ητ

+ λ+µ+^ηλ

(1 - e^-ητ )

νa

5. Оптимизация периодичности проведения ТО прибора

Рассмотрим задачу оптимизации допустимого уровня наработки для про-

ведения ТО прибора. Вначале выберем в качестве критерия оптимизации

средние удельные затраты C(τ) в единицу времени обслуживания требова-

ний. Достаточные условия существования конечной точки минимума τ_c функ-

ции C(τ) приводятся в [16]. Заметим, что в случае τ_c = ∞ оптимальной яв-

ляется пассивная стратегия обслуживания прибора, т.е. проведение его ТО

нецелесообразно.

Если в качестве критерия оптимальности взять среднюю удельную при-

быль S(τ) в единицу времени, то точка максимума этой функции удовлетво-

ряет уравнению S^′(τ) = 0 или ему эквивалентному:

′

N_пот(τ)

c₁h_f (τ)N_пот(τ) - λ_ϕ(τ)(c_aMσ_a - c_pMσ_p)N(τ) - c₁N_обс(τ)

Φ(τ)

(4)

(

)

′

(

)

N_пот(τ)

c_aMσ_aΦ(τ) + c_pMσ_pΦ(τ)

h_f(τ) +

= 0,

Φ(τ)

где N_пот(τ) = N^обспот(τ) + N^pпот(τ) + N^aпот(τ) среднее число потерянных тре-

бований на периоде регенерации, λ_ϕ(τ) = ϕ(τ)/Φ(τ) интенсивность отказа

прибора.

Обозначим функцию в левой части (4) через Z(τ), и предположим,

что она является непрерывной. Тогда достаточным условием существова-

ния конечного решения этого уравнения является выполнение неравенства

Z(0)Z(∞) < 0. В частности, неравенство выполняется, если интенсивность

отказов в ненадежной системе обслуживания неограниченно возрастает, т.е.

λ_ϕ(∞) = ∞; средние затраты за период регенерации на АВ больше, чем на

ТО и меньше прибыли от обслуженных требований, т.е. c_aMσ_a > c_pMσ_p и

c_aMσ_a < c₁N_обс(∞); среднее число потерянных заявок по причине АВ боль-

ше, чем по причине ТО, т.е.

∞

∫

F (y)dy (ψ_a(t) - ψ_p(t))Ĥg(y + t)dt > 0;

а также

c₁h_f (0) - λ_ϕ(0)c_aMσ_a ≥ 0.

106

При решении двухкритериальной задачи оптимизации в качестве целе-

вой функции можно использовать линейную свертку K(τ) = a_sS(τ) - a_cC(τ)

частных критериев S(τ) и C(τ) при весовых коэффициентах a_s > 0 и a_c > 0,

a_s + a_c = 1.

6. Численный пример

Интервал времени между поступающими в систему требованиями име-

ет распределение Эрланга

4-го порядка с плотностью распределения

g(t) = 20(20t)³e^-20t/3!, длительность времени обслуживания требования

распределение Эрланга 3-го порядка с плотностью f(t) = 12(12t)²e^-12t/2!.

Наработка прибора до отказа и длительность времени его АВ распределе-

ны по закону Вейбулла-Гнеденко с плотностями ϕ(t) = 0,3(0,1t)²e-(0,1t)3 и

ψ_a(t) = 5(10t)^-0,5e-(10t)0,5 соответственно. Длительность ТО прибора имеет

гамма-распределение с плотностью ψ_p(t) = 5(5t)^-0,5e^-5t / Γ(0,5). Средние зна-

чения перечисленных случайных величин (в часах), доход от обслуживания

требования и затраты в единицу времени на восстановительные работы (в де-

нежных единицах) помещены в табл. 1.

Вычисленные в пакете MathCAD по формулам (2) и (3) значения ста-

ционарных характеристик системы в зависимости от предельного уровня τ

наработки прибора на ТО помещены в табл. 2. В ней использованы следую-

щие обозначения: τ_s точка максимума функции удельной прибыли S(τ);

τ_c

точка минимума функции удельных затрат C(τ); τ_k точка максимума

линейной свертки K(τ) = 0,2S(τ) - 0,8C(τ); p^∗0(τ) вероятность пребыва-

ния системы в свободном работоспособном состоянии; N_обс(τ) и N_пот(τ)

среднее число обслуженных и потерянных требований на периоде регенера-

ции соответственно; Mβ N(τ) средняя длина периода регенерации. Случай

τ = ∞ соответствует характеристикам системы для пассивной стратегии об-

служивания (ТО не проводится).

Таблица 1. Исходные параметры системы

c₁,

c_a,

c_p,

Mβ, ч Mα, ч Mγ, ч Mσ_a, ч Mσ_p, ч денежных

денежных

единиц

0,2

0,25

8,930

0,2

0,1

Таблица 2. Стационарные характеристики системы в зависимости от периодично-

сти технического обслуживания прибора

Уровень

S(τ),

C(τ),

p^∗0(τ) N_обс(τ) N_пот(τ)

Mβ N(τ)

наработки

денежных

на ТО, ч

единиц

τ =∞

10,006

0,448

0,336

35,386

33,343

13,746

τ_c = 4,162

9,964

0,182

0,340

16,019

15,763

6,356

τ_s = 7,589

10,101

0,254

0,338

27,081

25,681

10,552

τ_k = 5,099

10,041

0,189

0,339

19,410

18,787

7,639

107

0,6

10,5

0,5

10,0

0,4

9,5

C(t)

S(t)

0,3

9,0

0,2

8,5

0,1

8,0

2,0

1,8

1,6

K(t)

1,4

1,2

Рис. 5. Графики зависимостей экономических показателей системы и их ли-

нейной сверки от периодичности проведения ТО прибора.

При минимизации удельных затрат оптимально допустимый уровень на-

работки на ТО равен τ_c = 4,162 ч, а при максимизации удельной прибыли

τ_s = 7,589 ч. При этом по сравнению с пассивной стратегией обслуживания

прибора затраты снижаются на 59,405 %, а прибыль увеличивается на 0,942 %

соответственно. В случае двухкритериальной оптимизации оптимальный до-

пустимый уровень наработки на ТО составляет τ_k = 5,099 ч, по сравнению

с пассивной стратегией обслуживания удельная прибыль увеличивается на

0,345 %, а удельные затраты снижаются на 57,735 %.

Графики зависимостей частных критериев и их линейной свертки от пе-

риодичности проведения ТО прибора представлены на рис. 5.

7. Заключение

С помощью аппарата теории полумарковских процессов с дискретно-

непрерывным множеством состояний построена модель функционирования

системы обслуживания GI/G/1/0, в которой во время обслуживания требо-

вания может произойти отказ прибора. С помощью найденного стационар-

ного распределения вложенной цепи Маркова и предельных теорем найдены

выражения для нахождения стационарных вероятностных и экономических

показателей системы с учетом проведения профилактического обслужива-

ния прибора. Приводятся достаточные условия, при которых целесообразно

проведение технического обслуживания в зависимости от уровня наработки

прибора. В приведенном численном примере найдены стационарные харак-

108

теристики системы и количественно оценено влияние периодичности прове-

дения профилактического обслуживания на среднюю удельную прибыль в

единицу календарного времени и средние удельные затраты в единицу вре-

мени обслуживания требований.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Система уравнений

∫

ρ(B) = ρ(dx)P (x, B)

для стационарного распределения ρ(·) ВЦМ { S_n, n ≥ 0} с учетом вероятно-

стей переходов P (x, B) из состояний имеет вид:

∫v

ρ(0xuv) = f(t)v_g(t, x)ρ(1, t + u, v - t)dt + ρ₁f(v)v_g(v, x)ϕ(v + u),

∫∞

ρ(1uv) = ρ(0xuv)dx,

∞

∫τ

∫

ρ(3x) = v_g(t, x)F (t)dt ρ(1u, τ - t)du + ρ₁F (τ)v_g(τ, x)Φ(τ),

∫τ

∫

ρ(2x) = v_g(t, x)F (t)dt ρ(1t, v - t)dv + ρ₁ F (t)v_g(t, x)ϕ(t)dt,

∫∞

∫

∞

∫

ρ(0x) = ψ_p(t)ρ(3, t + x)dt + ψ_p(t)dt v_g(t - s, x)ρ(3s)ds +

∞

∫∞

∫

+ ψ_a(t)ρ(2,t + x)dt + ψ_a(t)dt v_g(t - s,x)ρ(2s)ds,

∫∞

ρ₁ = ρ(0x)dx.

В результате исключения из первых двух уравнений системы функции

ρ(0xuv) получаем уравнение восстановления для плотности ρ(1uv) по пере-

менной v:

∫v

ρ(1uv) = ρ₁f(v)ϕ(u + v) + f(t)ρ(1, t + u, v - t)dt,

109

решением которого является функция ρ(1uv) = ρ₁h_f (v)ϕ(u + v). Выражения

для остальных плотностей находятся с помощью свойств плотностей функ-

ции восстановления и прямого остаточного времени восстановления. Значе-

ние стационарной вероятности ρ₁ определяется из условия нормировки. Тео-

рема 1 доказана.

Доказательство теоремы 2. Предельные значения p^∗i переходных

вероятностей полумарковского процесса S(t), t ≥ 0, определяются с помощью

соотношений [14, 15]

_-1

∫

∫

p^∗i = lim

Φ(t, x, E_i) = m(x)ρ(dx) m(x)ρ(dx)

i = 0,3.

t→∞

E_i

С учетом найденного стационарного распределения ВЦМ (1), средних вре-

мен пребывания в состояниях:

∫τ

∫

Mθ₁ = F (t)Φ(t)dt, Mθ_1uv =

F (t)dt,

Mθ_2x = Mσ_a; Mθ_3x = Mσ_p; Mθ_oxuv = Mθ_0x = x

и тождества Mβ_t = Mβ(1 + H_g(t)) - t получаем, что

∫

∞

∫

m(x)ρ(dx) = ρ₁ F (t)Φ(t)dt + ρ₁ h_f (v)dv ϕ(u + v)du

F (t)dt =

E₁

∫τ

∫

=ρ₁

F (t)Φ(t)dt + ρ₁ Φ(s)ds h_f (t)F (s - t)dt = ρ₁ Φ(t)dt = ρ₁M(γ ∧ τ);

∫

∞

m(x)ρ(dx) = Mσ_a ρ(2x)dx = ρ₁Mσ_aΦ(τ) = ρ₁Mσ_aP (γ < τ);

E₂

∫

∞

m(x)ρ(dx) = Mσ_p ρ(3x)dx = ρ₁Mσ_pΦ(τ) = ρ₁Mσ_pP (γ > τ);

E₃

∫

[

]

m(x)ρ(dx) = ρ₁Mβ N_обс(τ) + N^обспот(τ) + N^pпот(τ) + N^aпот(τ)

E₀

∫τ

-ρ₁

Φ(t)dt - ρ₁Φ(τ)Mσ_p - ρ₁Φ(τ)Mσ_a;

∫

[

]

m(x)ρ(dx) = ρ₁Mβ N_обс(τ) + N^обспот(τ) + N^pпот(τ) + N^aпот(τ)

110

Теорема 2 доказана.

Доказательство теоремы 3. Средние времена T(E_i) пребывания

системы в подмножествах состояний E_i определяются с помощью соотноше-

ний [14, 15]



_-1

∫





(Π.1)

T (E_i) = m(x)ρ(dx) ρ(dx)P (x, Ei)

i = 0,3.

E_i

E \E_i

Учитывая вероятности переходов и вид стационарного распределения

ВЦМ (1), интегралы в знаменателях дробей выражений (П.1) преобразуются

к виду:

∫

∞

∫

∞

∫

∞

ρ(dx)P (x, E₁) = ρ(0x)dx + dv du ρ(0xuv)dx =

E \E₁

∫τ

[

]

=ρ₁ +ρ₁

h_f (x)Φ(x)dx = ρ₁

1 + N_обс(τ)

;

∫

∞

ρ(dx)P (x, E₂) = ρ(dx)P (x, E \E₂) = ρ(2x)dx = ρ₁Φ(τ);

E \E₂

E₂

∞

∫

ρ(dx)P (x, E₃) = ρ(dx)P (x, E \E₃) = ρ(3x)dx = ρ₁Φ(τ);

E \E₃

E₃

∫

ρ(dx)P (x, E₀) = ρ(dx)P (x, E \E₀) =

E \E₀

E₀

∞

∫∞

∫

[

]

= ρ(0x)dx + dv du ρ(0xuv)dx = ρ₁

1 + N_обс(τ)

Теорема 3 доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. М.:

Наука, 1987.

2. Бочаров П.П., Печинкин А.В. Теория массового обслуживания. М.: Изд-во

РУДН, 1995.

3. Печинкин А.В., Чаплыгин В.В. Стационарные характеристики системы массо-

вого обслуживания SM/MSP/n/r // АиТ. 2004. № 9. С. 85-100.

Pechinknin A.V., Chaplygin V.V. Stationary Characteristics of the SM/MSP/n/r

Queuing System // Autom. Remote Control. 2004. V. 65. No. 9. P. 1429-1443.

111

Krishna Kumar B., Arivudainambi D., Vijayakumar A. An M/G/1/1 Queue with

Unreliable Server and no Waiting Capacity // Inf. Manage. Sci. 2002. V. 13. P. 35-50.

Wu C.-H., Lee W.-C., Ke J.-C., Liu T.-H. Optimization Analysis of an Unreliable

Multi-server Queue with a Controllable Repair Policy // Comput. Oper. Res. 2014.

No. 49. P. 83-96.

Özkan E., Kharoufeh J.P. Optimal Control of a Two-server Queuing System with

Failures // Prob. Eng. Inform. Sci. 2014. No. 28 (4). P. 489-527.

Песчанский А.И. Полумарковская модель однолинейной системы обслуживания

с потерями и ненадежным восстанавливаемым каналом // Динамические систе-

мы. 2017. Т. 7 (35). № 1. С. 53-61.

Peschansky A.I. Semi-Markov Models of One-Server Loss Queues with Recurrent

Input. Germany. LAP LAMPERT Acad. Publish., 2013.

Песчанский А.И., Коваленко А.И. Полумарковская модель однолинейной систе-

мы обслуживания с учетом технического обслуживания ненадежного канала //

Сб. науч. тр. Оптимизация производственных процессов. 2014. Вып. 15. С. 63-70.

10.

Peschansky A.I., Kovalenko A.I. On a Strategy for the Maintenance of an Unreliable

Channel of a One-Server Loss Queue // Automat. Contr. Comput. Sci. 2016. V. 50.

No. 6. P. 397-407.

11.

Песчанский А.И., Коваленко А.И. Полумарковская модель технического обслу-

живания ненадежной однолинейной системы обслуживания с потерями и скры-

тым отказом // Сб. науч. тр. Вестн. СевНТУ. Автоматизация процессов и управ-

ление. 2014. Вып. 147. С. 64-72.

12.

Peschansky A.I., Kovalenko A.I. Semi-Markov Model of a Single-Server Queue with

Losses and Maintenance of an Unreliable Server // Cybern. Syst. Anal. 2015. V. 51.

No. 4. P. 632-643.

13.

Песчанский А.И., Коваленко А.И. Полумарковская модель ненадежной одноли-

нейной системы обслуживания с потерями и различными типами восстановле-

ния // АиТ. 2016. № 11. С. 112-126.

Peschansky A.I., Kovalenko A.I. A Semi-Markov Model for an Unreliable Single-Line

Queueing System with Losses and Different Restoration Types // Autom. Remote

Control. 2016. V. 77. No. 12. P. 2192-2204.

14.

Королюк В.С., Турбин А.Ф. Процессы марковского восстановления в задачах

надежности систем. Киев: Наук. думка, 1982.

15.

Корлат А.Н., Кузнецов В.Н., Новиков М.И. и др. Полумарковские модели вос-

станавливаемых систем и систем массового обслуживания. Кишинев: Штиинца,

1991.

16.

Beichelt F., Franken P. Zuverlässigkeit und Instanphaltung, Mathematische Metho-

den. StateplaceBerlin: VEB Verlag Technik, 1983.

17.

Каштанов В.А., Медведев А.И. Теория надежности сложных систем (теория и

практика). М.: Европейский центр по качеству, 2002.

Статья представлена к публикации членом редколлегии В.М. Вишневским.

Поступила в редакцию 30.09.2019

После доработки 22.01.2020

Принята к публикации 30.01.2020

112