Автоматика и телемеханика, № 7, 2020
Интеллектуальные системы управления,
анализ данных
© 2020 г. Ю.С. ПОПКОВ, д-р техн. наук (popkov@isa.ru)
(Федеральный исследовательский центр
“Информатика и управление” РАН, Москва;
Институт проблем управления, Москва),
А.Ю. ПОПКОВ, канд. техн. наук (apopkov@isa.ru)
(Федеральный исследовательский центр
“Информатика и управление” РАН, Москва),
Ю.А. ДУБНОВ (yury.dubnov@phystech.edu)
(Федеральный исследовательский центр
“Информатика и управление” РАН, Москва;
Национальный исследовательский университет
“Высшая школа экономики”, Москва)
ЭЛЕМЕНТЫ РАНДОМИЗИРОВАННОГО ПРОГНОЗИРОВАНИЯ
И ЕГО ПРИМЕНЕНИЕ ДЛЯ ПРЕДСКАЗАНИЯ СУТОЧНОЙ
ЭЛЕКТРИЧЕСКОЙ НАГРУЗКИ ЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ1
Развит метод рандомизированного прогнозирования, основанный на
генерации ансамблей энтропийно-оптимальных прогнозных траекторий.
Последние генерируются рандомизированными моделями динамической
регрессии, содержащими случайные параметры, измерительные шумы и
случайный вход. Функции плотности распределения вероятностей слу-
чайных параметров и измерительных шумов оцениваются с использова-
нием реальных данных в рамках процедуры рандомизированного машин-
ного обучения. Генерация ансамблей прогнозных траекторий осуществля-
ется путем сэмплирования энтропийно-оптимальных распределений веро-
ятностей. Предлагаемая процедура применяется для рандомизированного
прогнозирования суточной нагрузки региональной энергетической систе-
мы. Синтезирована стохастическая модель колебательной динамической
регрессии. Построены одно- двух- и трехсуточные прогнозы и исследова-
ны их погрешности.
Ключевые слова: прогнозирование, иерархическая рандомизация, колеба-
тельная динамическая регрессия, энтропийный функционал, эмпириче-
ский баланс, суточная нагрузка энергетической системы, сэмплирование
функций ПРВ.
DOI: 10.31857/S0005231020070107
1. Введение
Традиционный путь решения задач прогнозирования состоит в моделиро-
вании исследуемого процесса, “обучении” его параметризованной модели на
1 Работа выполнена при поддержке Российского фонда фундаментальных исследований
(проекты №№ 19-07-00282, 20-07-00223).
148
ретроспективной информации и затем использовании “обученной” модели как
предсказывающей. Отсюда следуют два этапа в прогнозировании развиваю-
щихся процессов: этап машинного обучения модели процесса и собственно
этап прогнозирования.
Современная концепция машинного обучения базируется на детерминиро-
ванной параметризации моделей и оценках параметров, использующих па-
кеты данных с постулируемыми свойствами. Качество оценивания характе-
ризуется функциями эмпирическго риска, минимизация которого дает опти-
мальные оценки [1, 2].
Наиболее распространенными являются параметрические модели дина-
мической регрессии (ПМДР), в которых текущее состояние модели опреде-
ляется ее состояниями на некотором временном отрезке в прошлом [3, 4].
Формальный образ ПМДР это разностные уравнения, в общем случае
p-го порядка [5]. Наиболее распространены в прикладных задачах линейные
ПМДР. В частности, они являются базовыми во многих проблемах макро-
экономического моделирования и прогнозирования, таких как моделирование
временных рядов экономических индикаторов [6], определении адекватности
ПМДР [7], прогнозирование обменных курсов [8]. Линейные ПМДР оказы-
ваются достаточно эффективными для краткосрочного прогнозирования. Но
для больших горизонтов прогноза они приводят к значительным погрешно-
стям. Поэтому естественными являются попытки улучшения прогнозов путем
введения в ПМДР различных нелинейностей. Общему подходу к формирова-
нию и использованию нелинейных ПМДР посвящена монография [9]. Однако
прикладные задачи требуют более адекватного подхода к выбору наиболее
полезной и эффективной нелинейности. На этом пути кажется полезным, на-
пример, для прогнозирования обменных курсов применение логистической
и экспоненциальной нелинейностей [10], периодических авторегрессионных
моделей [11] или многомерных временных рядов [12] для прогнозирования
суточной электрической нагрузки энергетической системы.
При переходе к этапу прогнозирования необходимо быть уверенным, что
состояние и свойства исследуемого процесса сохраняются на интервале про-
гноза, что надежно утверждать сложно. Поэтому возникают погрешности
прогноза как следствие воздействия каких-то неучтенных факторов. Одним
из подходов к уменьшению таких погрешностей является придание прогно-
зу некоторых вероятностных характеристик [13, 14]. Наиболее распростра-
ненным на этом пути является использование формулы Байеса об апосте-
риорной вероятности. Если задать некоторую структуру параметризованной
условной плотности распределения вероятностей (ПРВ) данных и априор-
ную плотность распределения параметров, то их произведение после нор-
мировки определяет апостериорную плотность параметров при фиксирован-
ных данных. Принципиальные проблемы в этом подходе связаны с выбором
структуры условной ПРВ и априорной ПРВ. Обычно выбираются нормаль-
ные ПРВ или их смесь, причем веса смеси оцениваются по ретроспективным
данным [15-17]. Аналогичный подход используется в прикладных исследо-
ваниях: в популяционной генетике [18], где развивается метод численной ап-
проксимации апостериорных ПРВ, во взаимодействии финансового сектора
экономики и трудового ранка [19], где для оценивания параметров указанных
149
выше ПРВ используется алгоритм Метрополиса-Гастингса, в прогнозирова-
нии динамики населения [20], где использовалась иерархия байесовских мо-
делей для факторов рождаемости, смертности и миграционной активности.
Вероятностные прогнозы формируются и другими методами с учетом спе-
цифики прикладных задач. В частности, в метеорологии путем накопления
ретроспективных прогнозов погоды определяются оценки функций ПРВ, ко-
торые затем используются для кратковременного прогнозирования [21-24].
Довольно любопытным является формирование вероятностного прогноза пу-
тем смешивания прогнозов, полученных разными методами [25].
Из далеко не полного обзора и анализа указанных работ можно сделать
вывод, что основная проблема прикладного прогнозирования это неопре-
деленность, заложенная в исследуемом процессе. Флуктуация наших знаний
о природе процессов и, следовательно, неадекватность их математических
моделей; достаточность, достоверность и точность ретроспективных данных
о процессе; и, главное, сохранение основных свойств процессов в будущем,
чтобы накопленные знания и модели сохраняли свою полезность при прогно-
зировании все эти факторы являются следствием неопределенности.
Как повысить надежность прогноза? Один из рецептов связан с концеп-
цией рандомизации, т.е. искусственной генерации искусственной случайности.
Этот подход использовался в самых разных задачах, не связанных с прогно-
зированием. Существует много примеров в самых разных областях науки,
управлении, экономики, таких как, например, рандомизированные числен-
ные методы оптимизации [26-28], смешаные (случайные) стратегии в бир-
жевой торговле [29], рандомизированное прогнозирование динамики населе-
ния [30], вибрационное управление технологическими процессами [31]. При
этом рандомизация предполагает придание неслучайным объектам искус-
ственных стохастических свойств с оптимальными, в выбранном смысле, ве-
роятностными характеристиками.
В большинстве работ, которые можно было бы отнести к использованию
в той или иной форме рандомизации, искусcтвенная случайность вводилась
произвольно, в том смысле, что ее вероятностные характеристики функции
ПРВ выбирались из известных: равномерных, нормальных, экспоненциаль-
ных и др.
Хотелось бы эти характеристики формировать с точки зрения предсказуе-
мого качества рандомизации и ее ожидаемых свойств. Поскольку причиной
для привлечения этого подхода является неопределенность, то полезность
рандомизации целесообразно характеризовать информационной энтропией,
которая является мерой неопределенности [32-34]. Максимизация информа-
ционной энтропии соответствует максимальной неопределенности.
В данной статье предлагается принципиально иной метод формирования
прогнозов, названный энтропийно-рандомизированным прогнозированием
(ЭРП). Он основан на генерации ансамбля случайных прогнозов моделью ди-
намической регрессии со случайными оптимизированным входом и парамет-
рами. Соответствующие вероятностные характеристики, а именно функции
ПРВ, определяются с помощью процедуры энтропийно-рандомизированного
150
машинного обучения [35]. Ансамбли прогнозных траекторий строятся путем
сэмплирования энтропийно-оптимальных ПРВ.
Предлагаемый метод применяется для рандомизированного прогнозиро-
вания суточной электрической нагрузки энергетической системы. Построена
иерархическая рандомизированная модель динамической регрессии, описы-
вающая зависимость нагрузки от температуры окружающего воздуха. Вре-
менная эволюция температуры моделируется колебательной моделью дина-
мической регрессии второго порядка со случайным параметром и случайным
входом. Приводятся результаты рандомизированного обучения указанной мо-
дели на реальных данных GEFCom2014 [36]. Предлагается технология рандо-
мизированного прогнозирования и исследуется ее адекватность в зависимости
от длины горизонта прогноза.
2. Рандомизированные модели динамической регрессии
со случайным входом и параметрами
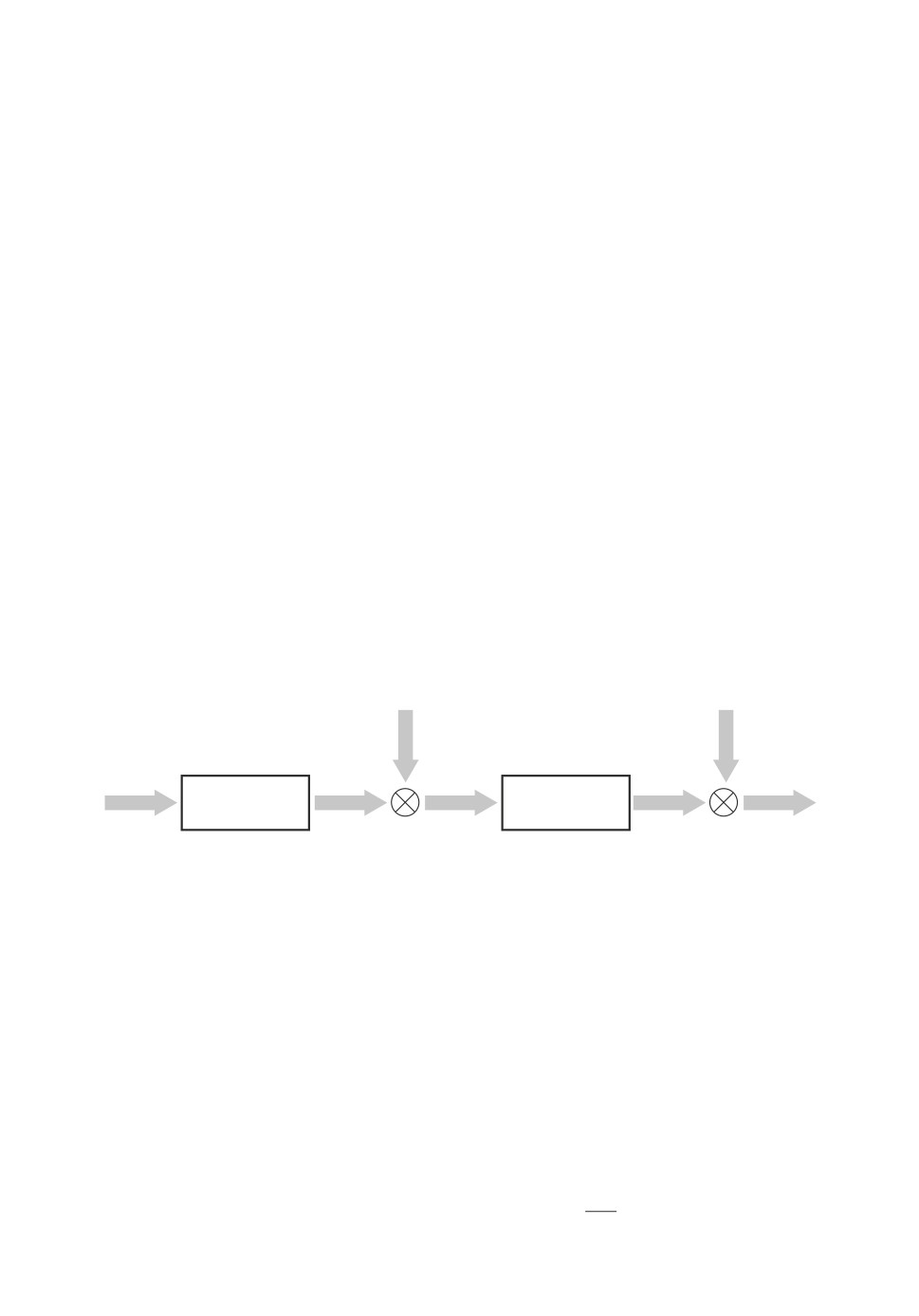
Структура, предлагаемой рандомизированной модели динамической ре-
грессии (РМДР) изображена на рис. 1. Она состоит из модели основного
объекта РМДР-О со случайными параметрами a ∈ Rp и модели внешних
факторов РМДР-Ф со случайными параметрами b ∈ Rs и случайным входом
ζ ∈ Rq. Состояния объекта и его модели принадлежат векторному простран-
ству Rm, в котором x[n] векторы состояний объекта, x[n] ∈ Rm векторы
состояний РМДР-О. Внешние факторы характеризуются вектором ŷ[n] ∈ Rq,
а изменение во времени состояния РМДР-Ф вектором y[n] ∈ Rq. Перемен-
ная n целочисленная, обозначает дискретное время в интервале L = [n-, n+].
x[n]
m[n]
РМДР-Ф
РМДР-О
z[n]
y[n]
z[n]
x[n]
v[n]
Рис. 1.
Рассмотрим линейную версию РМДР-О. Состояние модели x[n] в момент
времени n меняется под влиянием p ретроспективных состояний x[n - 1],
...,x[n - p] и измеряемых в каждый момент времени внешних факторов
z[n] ∈ Rq. Соответствующее уравнение имеет вид
(2.1)
x[n] = X(n,p)A(p) + A(p+1)
z[n],
где:
• блочный вектор-столбец параметров
(2.2)
A(p) = ⌊A1,... ,Ap⌋⊺,
Ai (m × m)-матрица со случайными элементами интервального типа
(2.3)
Ai ∈ Ai = [A-i,A+i
],
i = 1,p;
151
• A(p+1) (m×q)-матрица со случайными элементами интервального типа
(2.4)
A(p+1) ∈ A(p+1) = [A-(p+1),A+(p+1)
];
• блочный вектор-строка p ретроспективных состояний
(2.5)
X(n,p)
= ⌊x[n - 1], . . . , x[n - p]⌋.
Здесь ⌊•⌋ обозначает блочный вектор-строку.
Вероятностные свойства блочного вектора A(p) характеризуются функци-
ей совместной ПРВ P (A(p)), а матрицы A(p+1) функцией ПРВ F (A(p+1)).
Предполагается, что измеряемое в каждый момент времени n состояние
РМДР-О содержит аддитивный шум µ[n]:
(2.6)
v[n] = x[n] + µ[n].
Случайные векторы µ[n] интервального типа:
(2.7)
µ[n] ∈ Mn = [µ-n, µ+n]
с функцией ПРВ Mn(µ[n]). Случайные векторы, измеряемые в разные мо-
менты времени, предполагаются статистически независимыми.
Рассмотрим линейную версию РМДР-Ф, которая имеет аналогичную
РМДР-О структуру. Будем иметь:
(2.8)
y[n] = Y(n,s)B(s)
+ ζ[n],
где
• блочный вектор-столбец
(2.9)
B(s) = ⌊B1,... ,Bs⌋⊺,
• Bi (q × q)-матрица со случайными элементами интервального типа
(2.10)
Bi ∈ Bi = [B-i,B+i
],
i = 1,s,
• блочная вектор-строка
(2.11)
Y(n,p)
= ⌊y[n - 1], . . . , y[n - s]⌋.
Вероятностные свойства параметров характеризуются непрерывно-диффе-
ренцируемой функцией ПРВ W (B(s)).
Случайный вектор ζ[n] интервального типа:
(2.12)
ζ[n] ∈ En = [ζ-n, ζ+n]
с функцией ПРВ Qn(ζ[n]), также непрерывно-дифференцируемой. Векто-
ры ζ[n] для разных моментов времени статистически независимые.
152
По аналогии с РМДР-О измеряемое в каждый момент времени n состояние
РМДР-Ф z[n] содержит аддитивный шум ξ[n]:
(2.13)
z[n] = y[n] + ξ[n].
Случайный вектор ξ[n] интервального типа:
(2.14)
ξ[n] ∈ Ξn = [ξ-n, ξ+n
],
с непрерывно-дифференцируемой функцией ПРВ Gn(ξ[n]). Случайные векто-
ры, измеряемые в разные моменты времени, предполагаются статистически
независимыми.
Итак, в общей РМДР (РМДР-О и РМДР-Ф) неизвестными являются
функции ПРВ параметров P (A(p)), F (A(p+1)), W (B(s)) и шумов Mn(µ[n]),
Qn(ζ[n]), Gn(ξ[n]), n ∈ L.
3. Модели данных из обучающей коллекции
Оценивание указанных в предыдущем параграфе ПРВ производится с ис-
пользованием обучающих коллекций данных, полученных на интервале обу-
чения n ∈ L = [n-, n+] и согласованных с РМДР.
Рассмотрим РМДР-О. На интервале обучения будем иметь:
x[n-] = X(n-,p)A(p) + A(p+1)z[n-],
x[n- + 1] = X(n-+1,p)A(p) + A(p+1)z[n- + 1],
····································
(3.1)
x[n+] = X(n+,p)A(p) + A(p+1)z[n+
].
Тогда наблюдаемые состояния РМДР-О на интервале обучения L пред-
ставляют собой набор векторов
(3.2)
v[n] = x[n] + µ[n],
n=n-,n+.
Отсюда следует, что коллекция обучающих данных состоит из данных о ре-
троспективных состояниях объекта
(3.3)
X(n-,p), X(n-+1,p),... , X(n+,p)
и д анных о наблюдаемых текущих состояниях
(3.4)
v[n-], . . . , v[n+],
z[n-], . . . , z[n+
].
Рассмотрим РМДР-Ф. На интервале обучения будем иметь:
y[n-] = Y(n-,s)B(s) + ζ[n-],
y[n- + 1] = Y(n-+1,s)B(s) + ζ[n- + 1],
······························
(3.5)
y[n+] = Y(n+,p)B(s) + ζ[n+
].
153
Наблюдаемые состояния РМДР-Ф на интервале обучения L представляют
собой набор векторов
(3.6)
z[n] = y[n] + ξ[n],
n=n-,n+.
Отсюда следует, что коллекция обучающих данных состоит из данных о ре-
троспективных состояниях объекта
(3.7)
Ŷ(n-,s), Ŷ(n-+1,s),... , Ŷ(n+,s)
и д анных о наблюдаемых текущих состояниях
(3.8)
z[n-], . . . , z[n+].
Итак, в процедуре обучения РМДР участвуют коллекции данных (3.4), (3.7),
(3.8).
4. Алгоритм рандомизированного машинного обучения (РМО)
Энтропийная версия [35] алгоритмов РМО используется для оценивания
функций ПРВ параметров и шумов для РМДР-О и РМДР-Ф. Применительно
к РМДР-О соответствующий алгоритм имеет вид
∫
∫
HO = - P(A(p))ln P(A(p))dA(p) -
F (A(p+1)) ln F (A(p+1))dA(p+1) -
A
A(p+1)
∫
∑
(4.1)
-
Mn(µ[n])ln Mn(µ[n])dMn(µ[n]) ⇒ max
P,F,M
Mn
n=n-
при ограничениях:
нормировки ПРВ
∫
∫
P (A(p))dA(p) = 1,
F (A(p+1))dA(p+1) = 1,
A
A(p+1)
∫
Mn(µ[n])dMn(µ[n]) = 1, n = n-,n+,
Mn
эмпирических балансов
∫
∫
P (A(p))X(n,p)A(p)dA(p) +
F (A(p+1))A(p+1)z[n]dA(p+1) +
A
A(p+1)
∫
(4.2)
+ Mn(µ[n])µ[n]dµ[n] = v[n], n = n-,n+.
Mn
154
Заметим, что эмпирические балансы представляют собой систему
(n+ - n-) блоков из m уравнений. Каждому такому блоку соответствует век-
тор множителей Лагранжа θ(n) размерности m. Эта задача относится к клас-
су функциональных задач энтропийно-линейного программирования ляпу-
новского типа, см. [37, 38], c. 354, теорема (принцип Лагранжа для ляпунов-
ской задачи). Она имеет аналитическое решение, параметризованное множи-
телями Лагранжа:
(
)
∑
exp
-
〈θ(n),X(n,p)A(p)〉
n=n
-
P∗(A(p)) =
,
P(θ)
(
)
∑
exp
-
〈θ(n), A(p+1)z[n]〉
-
n=n
F∗(A(p+1)) =
,
F (θ)
(
)
exp
-〈θ(n), µ[n]〉
(4.3)
M∗n(µ[n]) =
,
n=n-,n+.
Mn(θ(n))
В этих равенствах
∫
∑
P(θ) = exp-
〈θ(n),X(n,p)A(p)〉 dA(p),
A
n=n-
∫
∑
F (θ) =
exp-
〈θ(n), A(p+1)z[n]〉 dA(p+1),
A(p+1)
n=n-
∫
(
)
(4.4)
Mn(θ(n)) = exp
-〈θ(n), µ[n]〉 dµ[n], n = n-, n+.
Mn
Матрица множителей Лагранжа θ = [θ(n-), . . . , θ(n+)] определяется реше-
нием следующих балансовых уравнений:
∫
∑
1
exp-
〈θ(n),X(n,p)A(p)〉 X(n,p)A(p)dA(p)+
P(θ)
A
n=n-
∫
∑
1
+
exp-
〈θ(n), A(p+1)z[n]〉 A(p+1)z[n]dA(p+1)+
F (θ)
n=n-
A(p+1)
∫
(
)
1
(4.5)
+
exp
-〈θ(n), µ[n]〉 µ[n]dµ[n] = x[n],
n=n-,n
+.
Mn(θ(n))
Mn
Из выражений (4.3)-(4.5) следует, что функции ПРВ P∗(A(p)), F∗(A(p+1))
параметров РМДР-О и измерительных шумов M∗n(µ[n]), n = n-, n+ опре-
деляются по обучающим коллекциям ретроспективных данных
X(n-, p),
155
X(n- + 1, p), . . . ,
X(n+, p), данных о текущих состояниях x[n-], . . . , x[n+] и
данных z[n-], . . . , z[n+], которые генерируются РМДР-Ф.
Для получения последних применим алгоритм РМО к оцениванию функ-
ций ПРВ параметров и шумов для РМДР-Ф. Согласно [35] будем иметь:
∫
HF = - W(B)ln W(B)dB -
B
∫
∑
-
Qn(ζ[n])ln Qn(ζ[n])dQn(ζ[n]) -
n=n-En
∫
∑
(4.6)
-
Gn(ξ[n]) ln Gn(ξ[n])dGn(ξ[n]) ⇒ max
W,Q,G
n=n-Ξn
при ограничениях:
нормировки ПРВ
∫
W (B)dB = 1,
B
∫
∫
Qn(ζ[n])dQn(ζ[n]) = 1,
Gn(ξ[n])dGn(ξ[n]) = 1, n = n-, n+;
En
Ξn
эмпирических балансов
∫
∫
W (B(s))Ŷ(n,s)B(s)dB(s) + Qn(ζ[n])ζ[n]dζ[n] +
B
En
∫
(4.7)
+ Gn(ξ[n])ξ[n]dξ[n] = z[n], n = n-,n+.
Ξn
Эта задача того же класса, что и (4.3)-(4.5). Она имеет аналитическое
решение в терминах множителей Лагранжа:
(
)
∑
exp
-
〈η(n),Ŷ(n,s)B(s)〉
n=n
-
(4.8)
W∗(B(s)) =
,
W(η)
(
)
exp
-〈ζ[n], η(n)〉
Q∗n(ζ[n]) =
,
Qn(η(n))
(
)
exp
-〈ξ[n], η(n)〉
G∗n(ξ[n]) =
, n=n-,n+,
Gn(η(n))
η = [η(n-),... ,η(n+)].
156
В этих равенствах
∫
∑
(4.9)
W(η) = exp-
〈η(n),Ŷ(n,s)B(s) dB(s),
n=n-
B
∫
(
)
Qn(η(n)) = exp
-〈ζ[n], η(n)〉 dζ[n],
En
∫
(
)
Gn(η(n)) = exp
-〈ξ[n], η(n)〉 dξ[n],
Ξn
n=n-,n+.
Матрица множителей Лагранжа η определяется решением следующих ба-
лансовых уравнений:
∫
∑
1
exp-
〈η(n),Ŷ(n,s)B(s) Ŷ(n,s)B(s)dB(s) +
W(η)
n=n-
B
∫
(
)
1
+
exp
-〈ζ[n], η(n)〉 ζ[n]dζ[n] +
Qn(η(n))
En
∫
(
)
1
(4.10)
+
exp
-〈ξ[n], η(n)〉
ξ[n]dξ[n] = z[n],
Gn(η(n))
Ξn
n=n-,n+.
5. Рандомизированное прогнозирование суточной
электрической нагрузки энергетической системы
5.1. Модель динамической регрессии
Суточная электрическая нагрузка L энергосистемы зависит от многих и
разнообразных факторов. Здесь ограничимся одним наиболее существенным
внешним фактором, а именно температурой T окружающего воздуха. Су-
точное изменение температуры носит колебательный характер. Эти колеба-
ния отражаются на нагрузке, но с некоторым временным сдвигом. Причиной
этого сдвига является инерция электрической сети, по которой передается
электрическая энергия от генератора к потребителям.
Следуя общей структуре РМДР, изложенной в разделе 2, модель нагрузки
(LT -модель) описывает динамическую связь нагрузки и температуры окру-
жающего воздуха, а модель температуры (T ξ-модель) описывает динамику
суточной температуры. Что касается LT -модели, то существует довольно
много ее версий, но все они статические, т.е. описывающие связь нагрузки
и температуры в текущие моменты времени [39]. Температурная суточная
157
динамика имеет колебательный характер, который, в частности, описывает-
ся периодической авторегрессионной моделью [40].
Следует отметить, что влияние температуры на нагрузку динамическое,
т.е. изменение нагрузки под влиянием температуры в данный момент вре-
мени зависит от ее значения в предыдущий момент времени. Аналогичным
свойством обладает температурная колебательная динамика.
Поэтому в рамках общего рандомизированного подхода предлагается LT -
модель описывать моделью динамической регрессии первого порядка со слу-
чайными параметрами, T ξ-модель формировать в виде динамической регрес-
сии второго порядка со случайным параметром и случайным входом ξ. Тогда
LTξ-модель будет композицией двух предыдущих.
Ограничиваясь линейным классом моделей, рандомизированную динами-
ческую регрессионную модель “нагрузка-температура” (LT -модель) первого
порядка можно представить в следующем виде:
L[n] = aL[n - 1] + bT [n],
(5.1)
v[n] = L[n] + µ[n], n = 1, 24,
где случайные независимые параметры a, b принимают значения в интерва-
лах:
(5.2)
a ∈ A = [a-,a+], b ∈ B = [b-,b+
].
Их вероятностные свойства характеризуются функциями ПРВ P (a), F (b),
определенными на множествах A и B соответственно. Случайный шум µ[n],
имитирующий ошибки в измерениях нагрузки, также интервального типа.
В общем случае для каждого момента времени размеры интервалов могут
быть различными, т.е.
(5.3)
µ[n] ∈ Mn = [µ-[n], µ+
[n]],
с функциями ПРВ Mn(µ[n]), n = 1, 24.
Рассмотрим T ξ-модель. Для имитации колебательного характера суточно-
го изменения температуры воспользуемся рандомизированной моделью дина-
мической регрессиии второго порядка
1
τ [n] = c (2, 1τ[n - 1] - 1, 1τ[n - 2]) , c =
,
1+ω2
(5.4)
T [n] = t + τ[n] + ξ[n],
где ω частота колебаний температуры, t среднесуточная температура.
Эти параметры случайные, интервального типа, т.е.
ω ∈ Ω = [ω-,ω+],
c ∈ C = [c-,c+],
1
1
(5.5)
c- =
> 0, c+ =
>c-
> 0.
1 + (ω+)2
1 + (ω-)2
Вероятностные свойства параметров характеризуются функциями ПРВ
W (c), определенными на соответствующих интервалах.
158
В уравнение (5.4) входит случайный шум, имитируемый независимыми
случайными величинами ξ[n], значения которых в каждом измерении n могут
принадлежать различным интервалам, т.е.
(5.6)
ξ[n] ∈ Ξn = [ξ-n, ξ+n
].
Вероятностные свойства случайной величины ξ[n] характеризуются функци-
ей ПРВ Qn(ξ[n]), n = 1, 24.
Таким образом, уравнения (5.1), (5.4), моделирующие динамику нагрузки
в энергосистеме, характеризуются следующими функциями ПРВ:
• LT-модель: параметры P(a),F(b), шум Mn(µ[n]), n = n-,n+;
• Tξ-модель: параметры W(c), шум Qn(ξ[n]), n = n-,n+.
5.2. Обучающая коллекция данных
Для оценивания функций ПРВ будут использоваться приведенные к еди-
ничному интервалу реальные данные из датасета GEFCom2014 (см. [36]) по
изменению суточной нагрузки 0 ≤ Lri)[n] ≤ 1, среднесуточной температуры
0≤tri) ≤1иотклонениятемпературы0≤
r
[n] ≤ 1 от среднесуточного зна-
чения.
Нормировка осуществлялась следующим образом:
(i)
L(i)[n] -L
r
min
L(i)r[n] =
,
L(i)
max -L(i)
min
(i)
r
[n] - τm
in
τ(i)r[n] =
,
τmiax - τ(i)
min
∑
1
(5.7)
t(i)r =
τ(i)r
[n],
n+ - n-
n=n-
где
L(i)
L(i)
= min
L(i)[n],
= max L(i)[n],
min
max
n
n
τ(i)min = min
τ(i)[n],
τ(i)max = max τ(i)[n].
n
n
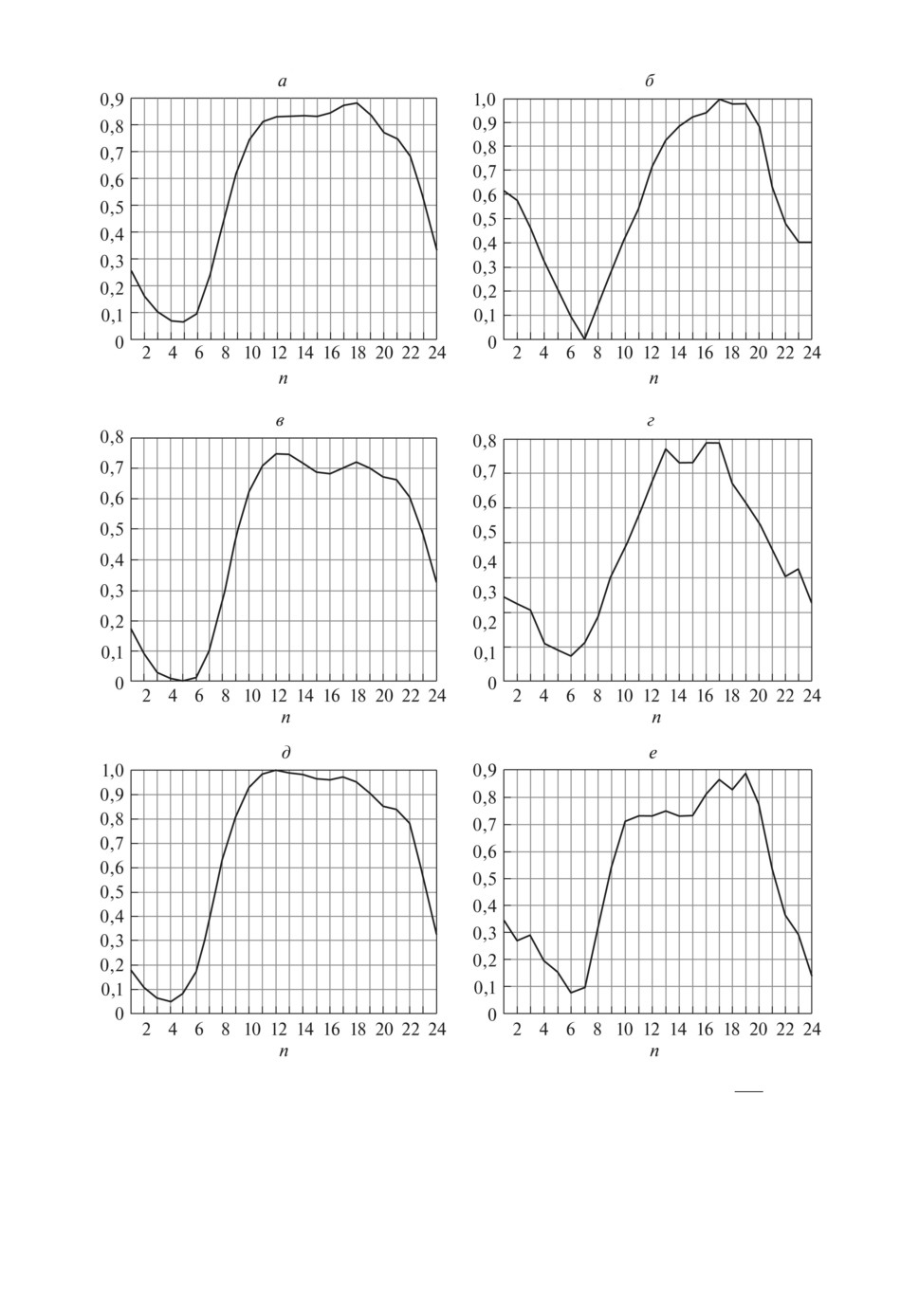
На рис. 2 показаны графики нагрузки Lri)[n], отклонения температуры
r
[n] и данные по среднесуточной температуре tri) для 03.07.2016 (i = 1),
04.07.2016 (i = 2), 05.07.2016 (i = 3) в качестве обучающей коллекции. Обо-
значим интервал обучения как Tl = [n-, n+] = [1, 24], т.е. обучение будет про-
изводиться по данным за 24 ч.
Согласно (5.1), (5.4) сформируем векторы переменных модели на интер-
вале обучения n ∈ Tl и соответствующих им реальных данных:
{
}
{
}
L(i)(Tl) = L(i)[1],... ,L(i)[24]
,
L(i)r(Tl) = L(i)r[1],... ,L(i)r[24]
,
{
}
{
}
L(i)(Tl - 1) = L(i)[0],... ,L(i)[23]
,
L(i)r(Tl - 1) = L(i)r[0],... ,L(i)r[23]
,
159
Рис. 2. Нагрузка Lri)[n] и отклонение температуры
r
[n] для i = 1, 3. а
Lr1)[n], б
r
[n], tr1)
= 0,5721, в Lr2)[n], г
r
[n], tr2) = 0,4784, д
Lr3)[n], е
r
[n], tr3) = 0,5056.
160
{
}
{
}
V(i)(Tl) =
v(i)[1],... ,v(i)[24]
,
V(i)r(Tl) = v(i)r[1],... ,v(i)r[24]
,
{
}
{
}
T(i)(Tl) = τ(i)[1],... ,τ(i)[24]
,
T(i)r(Tl) = τ(i)r[1],... ,τ(i)r[24]
,
{
}
T(i)(Tl - 1,Tl - 2) = 2, 1τ(i)[0] - 1, 1τ(i)[-1], . . . , 2, 1τ(i)[23] - 1, 1τ(i)[22]
,
{
}
T(i)(Tl - 1, Tl - 2) =
2, 1τ(i)r[0] - 1, 1τ(i)r[-1], . . . , 2, 1τ(i)r[23] - 1, 1τ(i)r[22]
,
r
{
}
{
}
µ(i)(Tl) = µ(i)[1],... ,µ(i)[24]
,
ξ(i)(Tl) = ξ(i)[1],... ,ξ(i)[24]
В терминах (5.2) LT - и T ξ-модели на интервале обучения Tl имеют вид
L(i)(Tl) = aL(i)(Tl - 1) + bT(i)(Tl),
V(i)(Tl) = L(i)(Tl) + µ(i)(Tl),
(5.8)
T(i)(Tl) = cT(i)(Tl - 1, Tl - 2),
T(i)(Tl) = t +T(i)(Tl) + ξ(i)(Tl).
Значения случайных параметров лежат в следующих интервалах:
(5.9)
A = [0,05;0,15], B = [0,5;1,0], C = [0,75;0,85].
Шумы принимают значения в следующих интервалах:
(5.10)
Mn = [-0,1;0,1], Ξn
= [-0,1; 0,1].
5.3. Энтропийно-оптимальные функции ПРВ параметров и шумов
Применяя технику из раздела 3, получим следующие выражения для
функций ПРВ, параметризованных множителями Лагранжа θ(i) = {θ(i)1,
...,θ(i)24} для LT-модели (5.1)-(5.3):
(
)
(
)
lri) (θ)exp
-alri) (θ)
P∗i
a, θ(i)
=
(
)
(
),
exp
-a-lri) (θ) - exp
-a+lri) (θ)
(
)
(
)
hri) (θ)exp
-bhri) (θ)
(5.11)
F∗i
b, θ(i)
=
(
)
(
),
exp
-b-hri) (θ) - exp
-b+hri) (θ)
(
)
θni) exp
-θni)µ[n]
M∗i,n (µ[n]) =
(
)
(
), n = 1,24.
exp
-µ-[n]θn)
- exp
-µ+[n]θn)
В этих равенствах
∑
∑
(5.12)
l(i)r(θ) =
θnL(i)r[n - 1], h(i)r(θ) =
θnT(i)r
[n].
n=1
n=1
161
Множители Лагранжа θ(i) определяются решением следующей системы ба-
лансовых уравнений:
(5.13)
L(i)(θ(i)) + T(i)(θ(i)) + M(i)n(θ(i)n) = L(i)r
[n],
n = 1,24,
где
(
)
L(i) θ(i)
=
(
(
(
)) (
(
)
)
(
))(
(
)
)
exp
-a-lri)
θ(i)
a-l(i)
θ(i)
+1
- exp
-a+lri)
θ(i)
a+l(i)
θ(i)
+1
=
(
(
))
(
(
))
,
exp
-a-l(i)
θ(i)
- exp
-a+l(i)
θ(i)
(
)
T(i) θ(i)
=
(
(
(
)) (
(
)
)
(
))(
(
)
)
exp
-b-hri)
θ(i)
b-h(i)
θ(i)
+1
- exp
-b+hri)
θ(i)
b+h(i)
θ(i)
+1
=
(
(
))
(
(
))
,
exp
-b-h(i)
θ(i)
- exp
-b+h(i)
θ(i)
(
)
M(i)n θ(i)
=
n
(
)(
)
(
)(
)
exp
-µ-[n]θn)
µ-[n]θni) + 1 - exp
-µ+[n]θn)
µ+[n]θni) + 1
(5.14)
=
( (
)
(
))
θn)
exp
-µ-[n]θn)
- exp
-µ+[n]θn)
Рассмотрим T ξ-модель. Энтропийно-оптимальные ПРВ, параметризован-
ные множителями Лагранжа, имеют вид
(
)
h(i)
r (η) exp
-chri)(η)
W∗i(c,η(i)) =
(
)
(
),
exp
-a-hri)(η) - exp
-a+hri)(η)
(
)
ηni) exp
-ηni)ξ[n]
Q∗i,n(ξ[n]) =
(
)
(
), n = 1,24.
exp
-ξ-[n]ηn)
- exp
-ξ+[n]ηn)
В этих равенствах
∑
∑
(5.15)
h(i)
(η) =
ηn(2,1T(i)r[n - 1] - 1,1T(i)r[n - 2]), q(i)(η(i)) =
η(i)n.
r
n=1
n=1
Множители Лагранжа η(i) определяются решением следующей системы ба-
лансовых уравнений:
(5.16)
D(i)(η(i)) + N(i)(η(i)) + K(i)n(η(i)n) = T(i)r
[n], n = 1, 24,
где
(
)
D(i) η(i)
=
(
(
)) (
(
)
)
exp
-t-q(i)
η(i)
t-q(i)
η(i)
+1
- exp(-t+q(i)(η(i)))(t+q(i)(η(i)) + 1)
=
,
exp(-t-q(i)(η(i))) - exp(-t+q(i)(η(i)))
162
(
)
N(i)
η(i)
=
(
)
(
))(
(
)
exp
-c-hri)
η(i)
c-h(i)
η(i)
+1
- exp(-c+hri)(η(i)))(c+h(i)(η(i)) + 1)
=
,
exp(-c-h(i)(η(i))) - exp(-c+h(i)(η(i)))
(
)
K(i)n η(i)
=
n
(
)(
)
(
)(
)
exp
-ξ-[n]ηn)
ξ-[n]ηni) + 1 - exp
-ξ+[n]ηn)
ξ+[n]ηni) + 1
(5.17)
=
(
)
ηn)
exp(-ξ-[n]ηni)) - exp(-ξ+[n]ηni))
5.4. Обучение модели
Использованием данных по суточным изменениям нагрузки и температу-
ры (см. рис. 2) для трех указанных выше суток были сформированы балансо-
вые уравнения (5.13), (5.14), (5.16), (5.17). Решение этих уравнений определя-
лось путем минимизации квадратичной невязки между левой и правой частя-
ми этих уравнений. Поскольку уравнения существенно нелинейные, найден-
ные значения множителей Лагранжа, приведенные в табл. 1, соответствуют
Таблица
1. Множители Лагранжа θ, η
Время
θ(1)
θ(2)
θ(3)
η(1)
η(2)
η(3)
1
-29,72
7009,28
1038,07
14,63
21,22
17,34
2
1,58
230,89
35,35
19,52
26,71
28,32
3
-4,09
369,96
26,23
35,91
31,60
26,33
4
-4,68
29,93
11,96
55,83
127,82
52,08
5
-7,21
24,25
1,03
96,85
642,35
110,94
6
-9,26
13,72
-15,76
592,99
7009,28
4729,52
7
-59,09
-5,96
-7009,28
7009,28
183,92
7009,28
8
-7009,28
-33,99
-767,99
48,21
39,94
23,16
9
-766,00
-1409,28
-22,91
66,58
12,28
-1,26
10
-50,90
-4229,90
-4,27
37,38
2,35
-19,78
11
-18,97
-45,22
3,72
22,51
-8,82
-22,73
12
-11,42
-15,07
9,17
7,16
-27,06
-23,06
13
-13,94
2,59
17,38
5,72
-172,25
-27,06
14
-17,62
5,82
14,94
2,83
-65,29
-23,02
15
-18,18
9,33
17,74
-0,30
-57,45
-23,15
16
-27,28
11,35
21,85
-1,24
-482,69
-47,78
17
-49,55
4,50
22,68
-5,49
-889,02
-130,49
18
-25,41
-7,09
29,39
-0,89
-28,12
-60,71
19
-8,20
-4,66
98,03
-4,23
-14,20
-270,17
20
0,95
-4,89
52,27
3,70
-6,41
-31,47
21
1,01
-16,37
8,15
21,16
2,48
-1,23
22
22,00
-8,24
7,45
17,85
12,15
14,86
23
2881,43
17,00
902,73
26,78
9,98
26,39
24
512,14
36,30
355,47
27,32
24,65
121,44
lri)(θ∗)
9,71
6,04
6,09
hri)(θ∗)
0,06
0,58
0,81
h(i)
r (η∗)
0,41
0,05
0,19
163
a
б
10
9
40
8
7
30
6
20
5
4
10
1,5
3
2
1,0
0,15
1
b
0,10
0
m
-0,08
-0,04
0
0,04
0,08
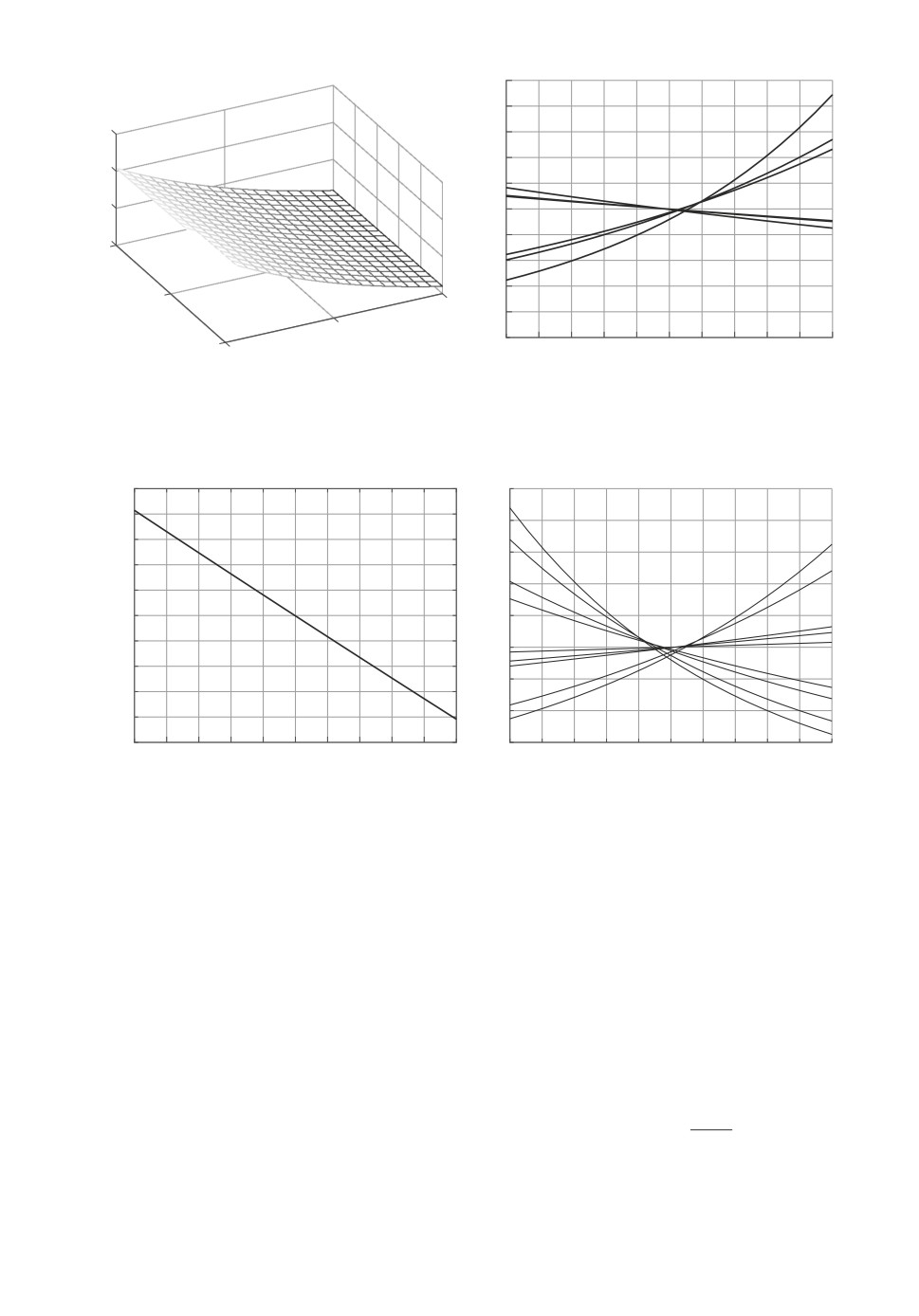
0,5 0,05
m
Рис. 3. а U∗1(a, b), б M∗1,n(µ).
a
б
10,25
10
10,20
9
10,15
8
10,10
10,05
7
10,00
6
9,95
5
9,90
4
9,85
3
9,80
9,75
2
0,76
0,78
0,80
0,82
0,84
-0,08
-0,04
0
0,04
0,08
c
x
Рис. 4. а W∗1(c), б Q∗1,n(ξ).
одному из локальных минимумов невязки. Все вычисления были реализова-
ны в среде MATLAB, оптимизация проводилась с помощью функции fsolve.
Поскольку в LT -модели параметры независимые, функции совместной
ПРВ параметров U∗i(a, b) = P∗i(a)F∗i(b) и шумов имеют вид
U∗1(a,b) = 53,09exp(-9,72a) exp(0,06b),
(5.18)
U∗2
(a, b) = 55,49 exp(-6,04a) exp(0,58b),
U∗3(a,b) = 65,81exp(-6,09a) exp(-0,81b),
⋃
(a, b) ∈ [0,05; 0,15]
[0,5; 1,0], µ ∈ [-0,1, 0,1], i = 1, 24.
Функции ПРВ экспоненциального типа. Графики для i = 1 показаны на
рис. 3.
164
Функции ПРВ параметров и шумов для T ξ-модели имеют вид
W∗1(c) = 13,90exp(-0,41c),
W∗2(c) = 10,43exp(-0,05c),
W∗3(c) = 11,65exp(-0,19c),
c ∈ [0,75;0,85], ξ ∈ [-0,1;0,1], i = 1,24.
Графики для i = 1 показаны на рис. 4.
Таким образом, рандомизированная LT ξ-модель представляет собой гене-
ратор случайных траекторий с энтропийно-оптимальными функциями ПРВ
параметров и шумов,
L[n] = aL[n - 1] + bT [n], (P∗(a), F∗(b)) ,
v[n] = L[n] + µ[n], M∗n(µ[n]),
(5.19)
τ [n] = c (2τ[n - 1] - τ[n - 2]) , W∗
(c), i = 1, 3,
T [n] = t + τ[n] + ξ[n], Q∗n(ξ[n]).
Генерация соответствующих ансамблей происходит путем сэмплирования
найденных ПРВ параметров и шумов методом исключений (Acceptance-
Rejection (AR), Rejection Sampling (RS)) [41]. При реализации расчетов было
использовано 100 сэмплов по каждому параметру и 100 сэмплов по шуму,
таким образом, ансамбль состоял из 104 траекторий.
5.5. Тестирование модели
Исследование адекватности модели осуществляется путем собственного и
перекрестного тестирования LT -модели и T ξ-модели на реальных данных
по нагрузке и температуре соответственно за 03.07.2016 (i = 1), 04.07.2016
(i = 2), 05.07.2016 (i = 3). Под собственным тестированием понимается гене-
рирование ансамбля траекторий с энтропийно-оптимальными параметрами
и шумами для дня i, вычисления средней (mean) и медианной (med) траек-
торий и дисперсионной трубки (std±) ансамбля и сравнения средней траек-
тории с реальными траекториями по нагрузке и температуре для этого же
дня i. Качество приближения характеризуется относительными ошибками по
нагрузке
24
(
)2
(i)
Lmi)ean[n] - L
r
[n]
(5.20)
δ(i)L
= ∑ (=1
,
i = 1,3,
)2
(
)2
∑
Lmi)ean[n]
+
Lri)[n]
n=1
n=1
и по температуре
24
(
)2
(i)
mean[n] - T
r
[n]
(5.21)
δ(i)T
= ∑ (=1
,
i = 1,3.
)2
(
)2
∑
mean[n]
+
r
[n]
n=1
n=1
165
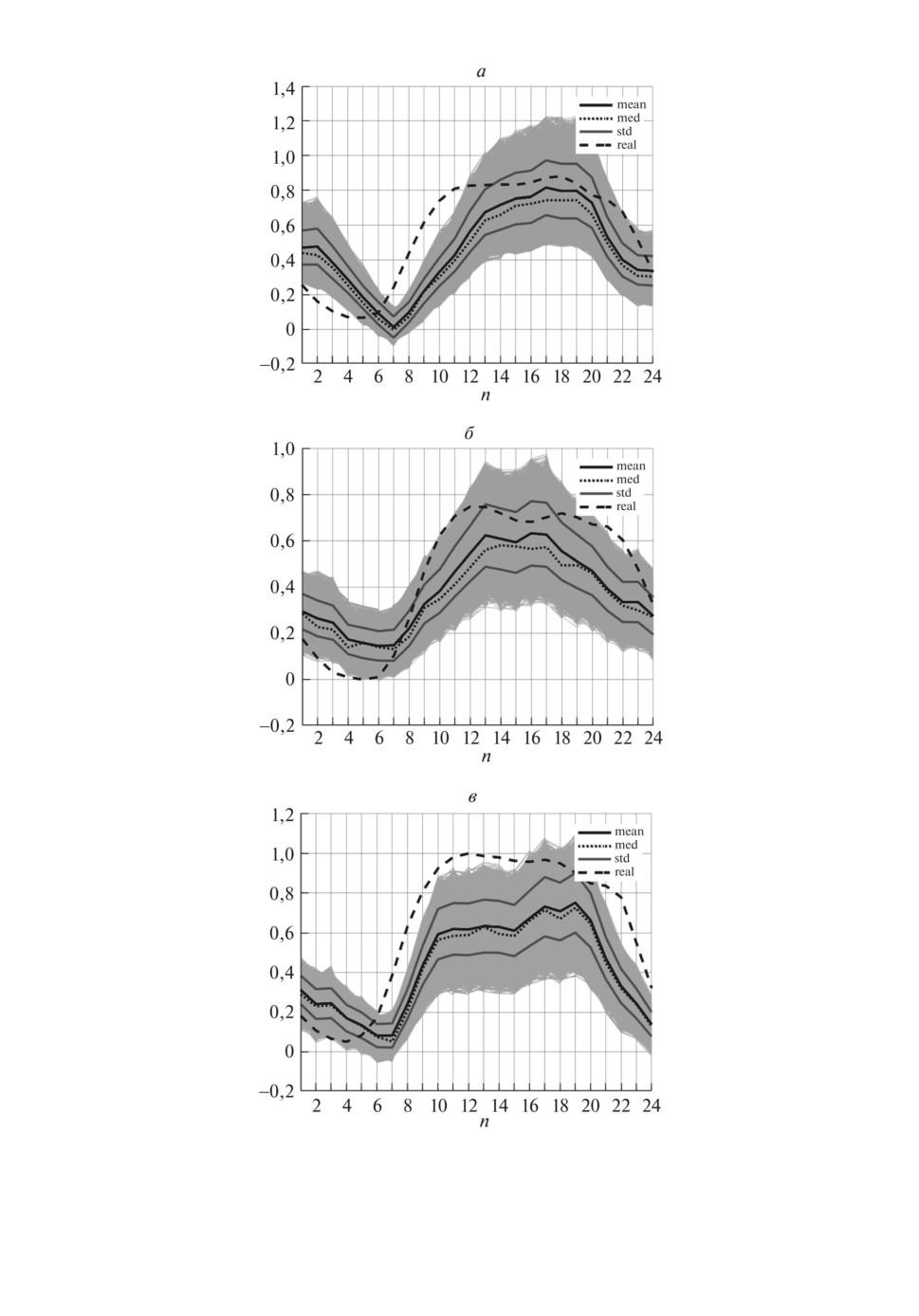
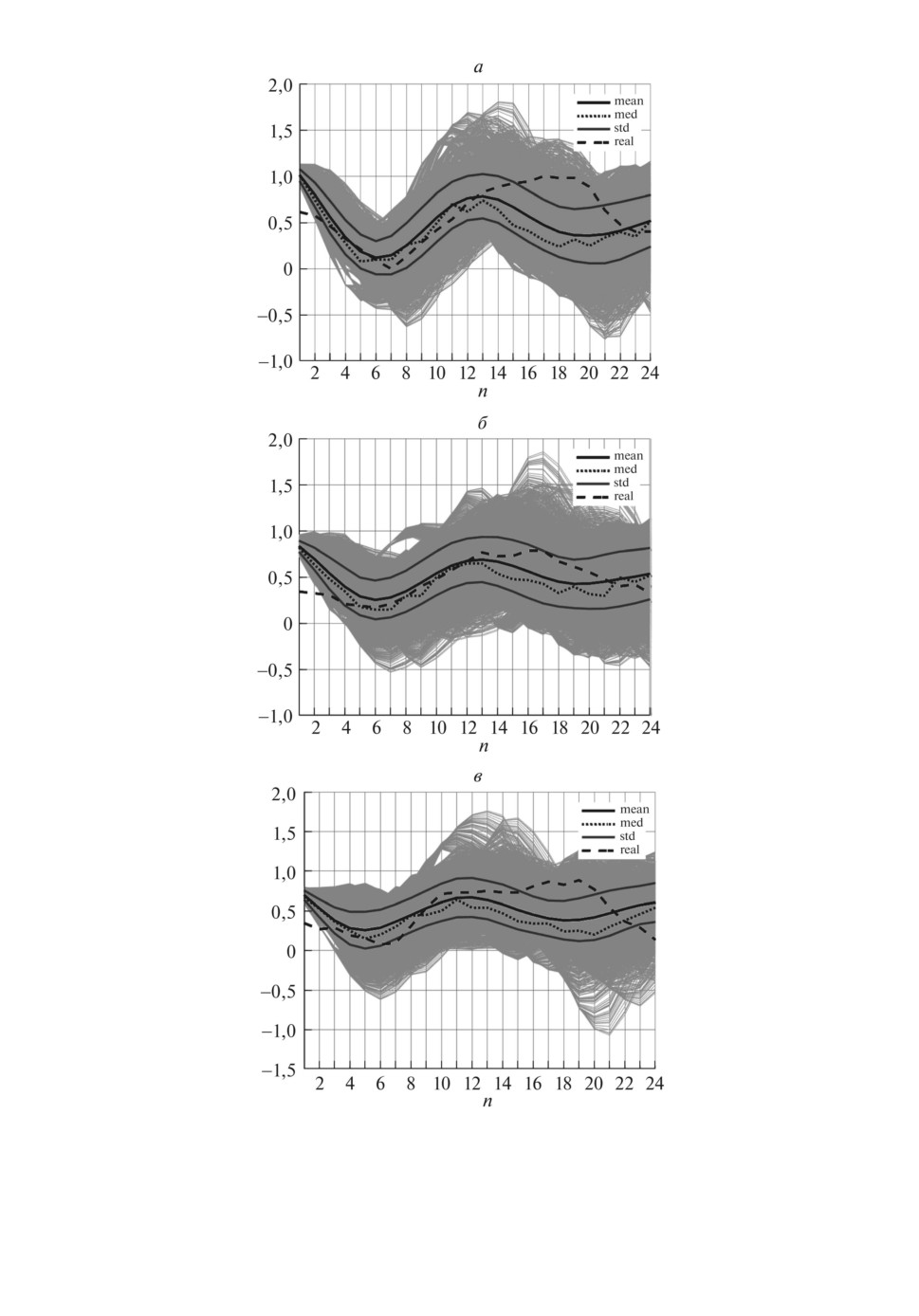
Рис. 5. Ансамбли LT -модели. а δ(1)L = 0,0703, б δ(2)L = 0,0523, в δ(3)L = 0,1038.
166
Рис. 6. а
Ансамбли T ξ-модели, б δ(1)T = 0,1004, в δ(2)T = 0,0582, г
δ(3)T = 0,0942.
167
Таблица 2. Значения δL на перекрестном тестировании LT -модели.
Среднее значение δL = 0,0530
i/j
1
2
3
1
0,0495
0,1052
2
0,0858
0,1428
3
0,0569
0,0364
Таблица 3. Значения δT на перекрестном тестировании T ξ-модели.
Среднее значение δL = 0,0757
i/j
1
2
3
1
0,1051
0,1079
2
0,1506
0,1185
3
0,1315
0,0676
Таблица 4. Значения δT на перекрестном тестировании
LTξ-модели. Среднее значение δL = 0,1478
i/j
1
2
3
1
0,1437
0,2659
2
0,1756
0,2322
3
0,3475
0,1655
Под перекрестным тестированием понимается та же процедура, но сравне-
ния средних траекторий с реальными по нагрузке и температуре производит-
ся для дней j = i. Качество приближения характеризуется относительными
ошибками по нагрузке
24
(
)2
(j)
Lmi)ean[n] - L
r
[n]
(5.22)
δ(i,j)L
= ∑ (=1
,
i = 1,3, i = j,
)2
(
)2
∑
Lmi)ean[n]
+
Lrj)[n]
n=1
n=1
и по температуре
24
(
)2
(j)
mean[n] - T
r
[n]
(5.23)
δ(i,j)T
= ∑ (=1
,
i = 1,3, i = j.
)2
(
)2
∑
mean[n]
+
r
[n]
n=1
n=1
Собственное тестирование. Для LT -модели используются реальные дан-
ные по температуре
r
[n] и энтропийно-оптимальные ПРВ P∗i(a), F∗i(b) па-
раметров (a, b) и M∗1µ[1], . . . , M∗24(µ[24]) шумов µ[n]. Генерируются ансам-
бли L(i) с помощью сэмплирования указанных ПРВ. Вычисляются средняя
траектория Lmi)ean[n], медианная траектория L(i)med[n] и траектории L(i)std±[n], со-
ответствующие границам дисперсионной трубки. Вычисляются ошибки δL(i).
На рис. 5 показаны ансамбли и относительные ошибки δ(i)L для трех указан-
ных дней.
168
2,5
mean
med
std
2,0
real
1,5
1,0
0,5
0
-0,5
-1,0
1
24
48
72
n
Рис. 7. Прогноз на 3 дня с помощью LT ξ-модели.
Тестирование T ξ-модели осуществляется путем генерации ансамбля T(i)
случайных траекторий T(i)[n], n = 1, 24 с энтропийно-оптимальными ПРВ
W(i)(c) и Q∗1(ξ[1]),... ,Q∗24(ξ[24]) путем их сэмплирования. Вычисляются
средняя траектория
mean[n], медианная траектория T(i)med[n] и траектории
T(i)std±[n], соответствующие границам дисперсионной трубки. На рис. 6 пока-
заны ансамбли и относительные ошибки δ(i)T для трех контрольных дней.
Перекрестное тестирование. При перекрестном тестировании используют-
ся модели LT и LT ξ, обученные по данным для дня i, а их средняя траек-
тория сравнивается с данными дней j = i. В табл. 2-4 указаны полученные
значения ошибок.
5.6. Рандомизированное прогнозирование N-суточной нагрузки
При рандомизированном прогнозировании N-суточной нагрузки исполь-
зуется LT ξ-модель, обученная на интервале Tl. Для характеристики качества
прогноза будем использовать LT ξ-модель с энтропийно-оптимальными ПРВ,
полученными по данным первого (i = 1) дня.
Сэмплируя указанные ПРВ, построим односуточный (n ∈ [1, 24]), двухсу-
точный (n ∈ [1, 48]) и трехсуточный (n ∈ [1, 72]) ансамбли. Для этих ансам-
блей определим средние траектории Lmean[n], медианные траектории Lmed[n],
граничные дисперсионные траектории Lstd±[n]. Результаты прогнозов срав-
ниваются с реальными данными с 03.07.2006 по 06.07.2006 (i = 1, 4.). Качество
прогнозирования характеризуется относительными ошибками, вычисляемы-
ми аналогично (5.22)-(5.23).
На рис. 7 показаны результаты 24, 48 и 72 часовых рандомизированных
прогнозов нагрузки, их вероятностные характеристики: средние и медианные
траектории, граничные траектории дисперсионных трубок. Ошибки между
модельным прогнозом и реальными данными показаны в табл. 5.
Таблица 5. Точность трехдневного прогноза с помощью LT ξ-модели
δ(2)L
δ(3)L
δ(4)L
0,1509
0,2515
0,2133
169
6. Заключение
Предлагается новый метод прогнозирования рандомизированное прог-
нозирование, ориентированное на осуществление предсказательных состоя-
ний в условиях неопределенности. Метод базируется на моделях динамиче-
ской регрессии со случайными параметрами. Предложен алгоритм рандо-
мизированного обучения модели. Реализация рандомизированного прогно-
за осуществляется путем сэмплирования энтропийно-оптимальных ПРВ па-
раметров модели и измерительных шумов. Предлагаемый метод применен
для рандомизированного прогнозирования суточной электрической нагрузки
энергетической системы с использованием реальных данных, заимствован-
ных из GEFCom2014.
СПИСОК ЛИТЕРАТУРЫ
1.
Vapnik V.N. Statistical Learning Theory. N.Y.: John Wiley& Sons Inc., 1998.
2.
Bishop C.M. Pattern Recognition and Machine Learning. Springer, Series: Informa-
tion Theory and Statistics, 2006.
3.
Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning. Springer,
4.
Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Исследо-
вание зависимостей. М.: Финансы и статистика, 1985.
5.
Tarasov A. Forecasting US money growth using economic uncertainty measures and
regularization techniques // Int. J. Forecast. 2019. V. 35. P. 443-457.
6.
Marcellino M., Stock J.H., Warson M. A comparison of direct and iterated multi-
steps AR methods for forecasting macroeconomic time series // J. Economet. 2006.
V. 135(1-2). P. 499-526.
7.
Eitrheim O., Terasirta T. Testing the adequacy of smooth transition autoregressive
models // J. Economet. 1996. v.74(1), P. 59-75.
8.
MolodtsovaT., Papell D. Out-of-simple exchange rate predictability with TR funda-
mentals // J. Int. Econom. 2009. V. 77. P. 167-180.
9.
Granger C.W. Terasirta T. Modelling Nonlinear Economic Relationship. Oxford:
Oxford Univer. Press, 1993.
10.
Wang R., Motley B., Stamatogiannis M. Forecasting the exchange rate using non-
linear Taylor rule based model // Int. J. Forecast. 2019. V. 35. P. 429-442.
11.
Bessec M., Fuaguau J. Short-run electricity load forecasting with combinations of
stationary wavelet transforms // EJOR. 2018. V. 264. P. 149-163.
12.
Clements A.E., Hurn A.S., Li Z. Forecasting day-ahead electricity load using a mul-
tiple equation time series approach // EJOR. 2016. V. 251. P. 522-530.
13.
Hong T., Fan S. Probabilistic electric load forecasting: a tutoral review // Int. J.
Forecast. 2016. V. 32. P. 914-938.
14.
Wheatcroft E. Interpreting the skill score from of forecast performance metrics //
Int. J. Forecast. 2019. V. 35. P. 573-579.
15.
Canale A., Ruggiero M. Bayesian nonparametric forecasting of nonmonotonic func-
tional time series // Electron. J. Statist. 2016. V. 10(2). P. 3265-3288.
16.
Дубнов Ю.А., Булычев А.В. Байесовская идентификация парметров смеси нор-
мальных распределений // Информ. технологии и вычислит. системы. 2017. № 1.
C. 101-114.
170
17.
Frazier D.T., Maneesoonthern W., Martin G.M., McCabe B.P.M. Approximate
Bayesian forecasting // Int. J. Forecast. 2019. V. 35. P. 521-539.
18.
Beaumont M.A., Zhang W., Baldung D.J. Approximate Bayesian computation in
population genetics // Genetics. 2001. V. 162(4). P. 2025-2035.
19.
McAdam P., Warne A. Eure-area real time density forecasting with financial or
labour market friction // Int. J. Forecast. 2019. V. 35. P. 580-600.
20.
Alkema L., Gerland P., Raftery A., Wilmoth T. The UN probabilistic population
projection: an introduction to demographic forecasting with uncertainty // Forsight.
2015. V. 37. P. 19-24.
21.
Brier C.W. Verification of forecast expressed in term probability // Monthly Weather
Rev. 1950. V. 78. P. 1-3.
22.
Brocker J., Smith L.A. From ensembles forecasts to predictive distribution func-
tions // Tellus A. 2008. V. 60(4). P. 663-678.
23.
Christensen H.M., Moroz I.M., Palmer T.N. Evaluation of ensemble forecast uncer-
tainty using a new proper score: application to medium-range and seasonial fore-
cast // Quart. J. Royal Meteorog. Sci. 2015. V. 141(687). P. 538-549.
24.
Gneiting T., Katzfuss M. Probabilistic Forecasting // Ann. Rev. Statist. Its Appl.
2014. V. 1. P. 125-151.
25.
Lahiri K., Wang J.C. Evaluating probability forecasts for GDP declines using alter-
native methodological // Int. J. Forecast. 2013. V. 29(1). P. 175-190.
26.
Vidyasagar M. Statistical Learning Theory and Randomized Algorithms for Con-
trol // IEEE Control Syst. Magazin. 1998. V. 1/17. P. 69-88.
27.
Граничин О.Н., Поляк Б.Т. Рандомизированные алгоритмы оценивания и опти-
мизации при почти произвольных помехах. М.: Наука, 2002.
28.
Назин А.В. Алгоритмы инерционного зеркального спуска в выпуклых задачах
стохастической оптимизации // АиТ. 2018. № 1. C. 100-112.
Nazin A. V. Algorithms of inertial mirror descent in convex problems of stochastic
optimization // Autom. Remote Control, 2018. V. 79. No. 1. P. 78-88.
29.
Biondo A.E., Pluchino A., Rapisarda A., Helbing D. Are random traiding strategies
more successful than technical ones? // PLoS ONE. 2013. V. 6(7). P. 68344.
30.
Lutz W., Sandersen S., Scherbov S. The end of world population growth // Nature.
2001. V. 412(6846). P. 543-545.
31.
Цирлин А.М. Методы усредненной оптимизации и их применение. М.: Физмат-
лит, 1997.
32.
Shannon C. Communication Theory of Secrecy Systems // Bell Syst. Technic. J.
1949. V. 28(4). P. 656-715.
33.
Jaynes E.T. Information Theory and Statistical Mechanics // Physics Rev. 1957.
V. 106. P. 620-630.
34.
Jaynes E.T. Papers on probability, statistics and statistical physics. Dordrecht,
Kluwer Academ. Publisher, 1989.
35.
Попков Ю.С., Попков А.Ю., Дубнов Ю.А. Рандомизированное машинное обу-
чение. М.: ЛЕНАНД, 2018.
36.
Hong T., Prinson P., Fan S., Zareipour H., Triccoli A., Hyndman R.J. Probabilistic
energy forecasting: Global Energy Forecasting Competition 2014 and beyond // Int.
J. Forecast. 2016. V. 32. P. 896-913.
37.
Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М.: Наука, 1974.
38.
Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М.: Нау-
ка, 1979.
171
39. Fiedner G. Hierarchical forecasting: issues and use guidelines // Indust. Management
Data Syst. 2001. V. 101(1). P. 5-12.
40. Amaral L.F., Castro S.R., Stevenson M. A smooth transition periodic autoregres-
sive (STAR) model for short-term load forecasting // Int. J. Forecast. 2008. V. 24.
P. 603-615.
41. J. von Neumann. Various techniques in connection with random digits, in Monte
Carlo Methods / A.S. Householder, G.E. Forsythe, H.H. Germond. National Bu-
reau of Standards Applied Mathematics Series (U.S. Government Printing Office,
Washington, DC, 1951). P. 36-38.
Статья представлена к публикации членом редколлегии А.И. Кибзуном.
Поступила в редакцию 14.10.2019
После доработки 11.12.2020
Принята к публикации 30.01.2020
172