Автоматика и телемеханика, № 8, 2020

(Нижегородский государственный университет им. Н.И. Лобачевского),

М.М. КОГАН, д-р физ.-мат. наук (mkogan@nngasu.ru)

(Нижегородский государственный архитектурно-строительный университет)

УПРАВЛЕНИЕ И ОЦЕНИВАНИЕ В ЛИНЕЙНЫХ

НЕСТАЦИОНАРНЫХ СИСТЕМАХ НА ОСНОВЕ

ЭЛЛИПСОИДАЛЬНЫХ МНОЖЕСТВ ДОСТИЖИМОСТИ¹

Показано, что множеством достижимости линейной нестационарной

непрерывной или дискретной системы, в которой сумма квадратичной

формы начального состояния и интеграла или суммы квадратичных

форм возмущения на конечном интервале времени ограничена сверху

заданной величиной, является эволюционирующий эллипсоид. Матри-

ца эллипсоида удовлетворяет линейному матричному дифференциаль-

ному или разностному уравнению соответственно. Синтезированы оп-

тимальные эллипсоидальные наблюдатель и алгоритм идентификации,

обеспечивающие наилучшие эллипсоидальные оценки состояния системы

и неизвестных параметров, а также оптимальные регуляторы, обеспечи-

вающие попадание состояния системы в целевое множество или удержа-

ние траектории системы в эллипсоидальной трубке. Установлено соответ-

ствие между оптимальным эллипсоидальным наблюдателем и фильтром

Калмана. Приведены иллюстрирующие примеры для уравнения Матье,

описывающего параметрические колебания линейного осциллятора.

Ключевые слова: линейная нестационарная система, эллипсоидальное

множество достижимости, оптимальное управление, оптимальное оцени-

вание.

DOI: 10.31857/S0005231020080024

1. Введение

Авторы посвящают эту статью памяти Ю.И. Неймарка, учениками кото-

рого (прямыми или косвенными) они являются. Хочется повторить слова,

которые Юрий Исаакович написал в эпиграфе своей последней монографии

“Математическое моделирование как наука и искусство” [1, 2]: “В науке и ее

приложениях, как и в жизни, самое главное - понимание. Оно всегда просто,

но добывается трудно.”

В монографии [3] Ю.И. Неймарк изложил результаты широкого круга сво-

их исследований, касающихся вопросов устойчивости, управления и опти-

мизации в динамических системах. Одна из важных тем этих исследований

относилась к задачам управления в условиях неопределенности математи-

ческой модели объекта управления и действующих возмущений. Эта тема

развивалась в последующих работах Ю.И. Неймарка (см., например, [4-7]) и

изучается в настоящей работе.

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проекты №№ 18-41-520002, 19-01-00289), проекта № 0729-2020-0055 и научно-

образовательного математического центра “Математика технологий будущего”.

В задачах оценивания и управления в динамических системах при отсут-

ствии полной информации о начальных условиях, возмущениях и помехах

в измерениях важную роль играет множество достижимости системы, пони-

маемое как множество всех состояний, в которых система может оказаться в

данный момент времени при всевозможных допустимых значениях неопреде-

ленных факторов. Характеризация множеств достижимости и их зависимо-

сти от параметров системы позволяет проектировать оптимальные системы

оценивания и управления, при которых множества достижимости синтези-

рованной системы в данный момент времени или в течение некоторого ин-

тервала времени включены в желаемые целевые множества с оптимальными

характеристиками.

Классическая задача Б.В. Булгакова о влиянии ограниченных возмущений

на линейную динамическую систему была поставлена и решена в [8]. Пробле-

ма нахождения или оценивания множеств достижимости активно изучается

с конца 60-х г. прошлого века и до сих пор продолжает привлекать внимание

специалистов в области теории управления и ее приложений [9-19]. В силу

линейности системы состояние в данный момент времени есть сумма двух

векторов: состояния невозмущенной системы с неопределенным начальным

состоянием и состояния возмущенной системы с нулевым начальным состоя-

нием. Если множество начальных состояний выбрать эллипсоидальным и

множество достижимости возмущенной системы аппроксимировать эллип-

соидом, то возникает задача описания геометрической суммы двух эллипсои-

дов, которая является выпуклым множеством, но не эллипсоидом. В задачах

рекуррентного оценивания возникает необходимость в нахождении эллипсои-

да наименьшего размера, включающего пересечение двух эллипсоидов. Для

описания таких множеств обычно стараются получать их верхние и ниж-

ние эллипсоидальные аппроксимации. Все это привело к развитию техники

оперирования с эллипсоидами. Несмотря на значительный прогресс в этом

направлении, связанный с применением линейных матричных неравенств и

соответствующего программного обеспечения, проблема остается открытой

в силу того, что методы, основанные на эллипсоидальных аппроксимациях

множеств достижимости, трудно применить для синтеза оптимальных систем

оценивания и управления за исключением очень простых случаев.

В недавних работах [20-23] было введено понятие максимального укло-

нения выхода линейной нестационарной системы на конечном интерва-

ле времени при неопределенных начальном состоянии и возмущении. По-

существу, это индуцированная норма оператора, порожденного системой и

отображающего пару, состоящую из вектора начального состояния и вектор-

функции возмущения, в целевой выход, где квадрат “величины” пары изме-

ряется суммой квадратичной формы начального состояния и интеграла от

квадратичной формы возмущения, а “величина” выхода измеряется макси-

мальным по времени значением его евклидовой нормы. Для линейной стацио-

нарной системы на бесконечном интервале времени при нулевых начальных

условиях подобная характеристика была введена в [24] и названа обобщенной

H₂-нормой системы. В [20-23] максимальное уклонение выхода характеризу-

ется в терминах решений линейного матричного дифференциального уравне-

ния или неравенств и на основе этого синтезируется оптимальное управление,

минимизирующее максимальное уклонение выхода. Эти результаты навели

авторов на мысль о том, что когда сумма квадратичной формы начального со-

стояния и интеграла от квадратичной формы возмущения ограничена сверху

заданной величиной, состояние системы принадлежит эллипсоиду с матри-

цей, удовлетворяющей указанному линейному дифференциальному уравне-

нию. Подтверждение такого предположения было найдено в работах [11, 13],

в последней из которых методом динамического программирования показа-

но, что при аналогичном ограничении множеством достижимости системы

является эллипсоид, матрица которого является решением дифференциаль-

ного уравнения Риккати. На этой основе в [13] был построен оптимальный

наблюдатель, обеспечивающий эллипсоидальную оценку состояния системы.

Однако указанные результаты получены при достаточно жестких условиях

невырожденности квадратичных форм начального состояния и возмущений,

которые означают, что начальное состояние должно принадлежать невырож-

денному эллипсоиду, а возмущения должны присутствовать в уравнении для

каждой компоненты состояния и в измерении каждой компоненты выхода.

В данной работе эти результаты развиваются в нескольких направлени-

ях одновременно как для непрерывных (см. также [25]), так и для дискрет-

ных линейных нестационарных систем. Во-первых, показано, что в случае

вырожденных квадратичных форм в совместном ограничении на начальное

состояние и возмущение и, в частности, в крайних случаях, когда возмущение

отсутствует или когда начальное состояние нулевое, множествами достижи-

мости системы также являются эллипсоиды, в том числе и вырожденные.

Необходимость в изучении множеств достижимости в случае вырожденной

квадратичной формы начального состояния возникает, например, в зада-

чах управления механическими системами с ударными воздействиями, когда

некоторые переменные состояния известны, а некоторые испытывают мгно-

венные неопределенные изменения. Рассмотрение этого вопроса потребовало

применить иной подход для обоснования результата, который привел к ли-

нейным матричным дифференциальному или разностному уравнениям Ляпу-

нова, описывающим динамику эллипсоидального множества достижимости в

непрерывном и дискретном случаях. Установлено, что величина максималь-

ной на заданном интервале времени полуоси эллипсоидального множества

достижимости для данного выхода системы действительно совпадает с обоб-

щенной H₂-нормой системы при ненулевых начальных условиях. Во-вторых,

получено уравнение оптимального эллипсоидального наблюдателя, обеспе-

чивающего оценку состояния в виде эллипсоида минимального размера в

том числе и в вырожденном случае, когда возмущения в системе и поме-

хи в измерениях могут отсутствовать в некоторых уравнениях. Выявлена

связь оптимального эллипсоидального наблюдателя в задачах фильтрации и

идентификации неизвестных параметров с фильтром Калмана и рекуррент-

ным алгоритмом метода наименьших взвешенных квадратов соответственно.

В-третьих, показано, как синтезировать ограниченное управление, при кото-

ром состояние системы попадает в целевое эллипсоидальное множество или

траектория системы удерживается в заданной эллипсоидальной трубке. Все

результаты иллюстрируются на примере линейного нестационарного осцил-

лятора, описываемого уравнением Матье.

2. Эллипсоидальные множества достижимости

Рассмотрим динамический объект, описываемый нестационарной системой

линейных дифференциальных или разностных уравнений

(2.1)

∂x(t) = A(t)x(t) + B(t)v(t), x(t₀) = x₀, t ∈ [t₀,t_f

где ∂ - оператор дифференцирования в непрерывном случае или опера-

тор сдвига на единицу вперед в дискретном случае при t = t₀, t₀ + 1, . . . , t_f ,

x ∈ Rnx - состояние объекта, v ∈ Rnv - возмущение, действующее на объект.

Введем обозначения, позволяющие в дальнейшем рассматривать параллель-

но непрерывный и дискретный случаи: для вектора a и для непрерывной или

дискретной вектор-функции b(t) на интервале [t₀, t] обозначим:



∫



b^T(σ)M^-1(σ)b(σ)dσ,



|a|^2Q = a^TQ^-1a,

∥b∥^2M[t

t₀

0,t]

=

∑





b^TiM^-1ib_i

i=t₀

для обратимых матриц Q, M(σ) и M_i. Если обозначение матрицы у нормы

отсутствует, это значит матрица единичная.

Предположим, что начальное состояние x(t₀) и возмущение v = v(σ),

σ ∈ [t₀,t] принадлежат множеству допустимых пар начальных состояний и

возмущений, определяемому как

S(t, t₀; R, G) =

{

}

(2.2)

= (x, v(σ)) : x = R^1/2w₁, v(σ) = G^1/2(σ)w₂(σ), |w₁|² + ∥w₂∥^2[t

≤1

,t]

для заданных матрицы R^T = R ≥ 0 и матричной функции G^T(σ) = G(σ) ≥ 0,

σ ∈ [t₀,t]. Если R > 0 и G(σ) > 0, σ ∈ [t₀,t], то, выражая w₁ и w₂(σ) из пер-

вых двух равенств в (2.2) и подставляя в последнее неравенство, получим,

что в невырожденном случае допустимые начальные условия и возмущения

удовлетворяют неравенству

(2.3)

|x(t₀)|^2R + ∥v∥^2G[t

≤ 1.

0,t]

Левую часть этого неравенства можно интерпретировать как квадрат меры

неопределенности в системе для текущего момента времени, а само условие

(2.3)

как то, что мера неопределенности в системе не превышает известной

величины, которую, не умаляя общности, можно принять единицей. Други-

ми словами, начальное состояние находится внутри заданного эллипсоида, а

“энергия” возмущения ограничена величиной, зависящей от начального со-

стояния. Смысл этого совместного ограничения на начальное состояние и

возмущение можно пояснить следующим образом. Состояние линейной си-

стемы в текущий момент времени зависит линейно от начальных условий

и возмущения и их увеличение приводит к соответствующему увеличению

переменных состояния. Для того чтобы характеризовать поведение системы

при неопределенных начальных условиях и возмущениях, имеет смысл нор-

мировать текущее значение евклидовой нормы состояния величиной, равной

указанной сумме, или, что то же самое для линейных систем, ограничить

указанную сумму единицей.

Весовая матрица R при заданной G(σ) отражает относительную важность

учета неопределенностей начальных условий и внешнего возмущения: чем

“больше” R, тем больший вес придается неопределенности в начальных усло-

виях. Из (2.2) следует, что множество начальных состояний системы совпа-

дает с эллипсоидом E(R) = {x = R^1/2w : |w| ≤ 1}. Если R > 0, то приходим

к стандартному представлению эллипсоида E(R) = {x : x^TR^-1x ≤ 1}. Если

R ≥ 0, то E(R) - вырожденный эллипсоид, аффинная размерность которого

совпадает с рангом матрицы R [26, с. 30]. Обозначим через ϕ(t; τ, x, v) ре-

шение уравнения (2.1) с начальным условием ϕ(τ) = x при соответствующей

функции v = v(σ), σ ∈ [τ, t].

Задача состоит в описании множества состояний, в которых система мо-

жет оказаться в определенный момент времени при всевозможных начальных

состояниях и возмущениях, принадлежащих множеству S(t, t₀; R, G).

Определение 1. Множеством достижимости D(t,τ,E(R)) систе-

мы (2.1) в момент времени t ≥ τ называется совокупность концов траек-

торий ϕ(t;τ,x_τ ,v) при всех допустимых начальных состояниях x_τ ∈ E(R) в

момент времени τ и возмущениях v(σ), σ ∈ [τ, t], принадлежащих множе-

ству S(t,τ;R,G).

Теорема 2.1. Множеством достижимости системы (2.1) в момент

времени t ≥ t₀ при всех допустимых начальных состояниях и возмущени-

ях, принадлежащих множеству S(t, t₀; R, G), t ∈ [t₀, t_f ] с R ≥ 0 и G(σ) ≥ 0,

σ ∈ [t₀,t], является эллипсоид

(2.4)

D(t, t₀

,E(R)) = E(P(t)),

матрица P (t) ≥ 0 которого в непрерывном случае

решение линейного

матричного дифференциального уравнения

(2.5)

= A(t)P + P A^T(t) + B(t)G(t)B^T

(t)

и в дискретном случае решение линейного матричного разностного урав-

нения

(2.6)

P (t + 1) = A(t)P (t)A^T(t) + B(t)G(t)B^T

(t)

с начальным условием P(t₀) = R.

Доказательство теоремы 2.1. В непрерывном случае решение урав-

нения (2.5) имеет вид

∫t

(2.7)

P (t) = Φ(t, t₀)P (t₀)Φ^T(t, t₀) + Φ(t, τ)B(τ)G(τ)B^T(τ)Φ^T

(t, τ)dτ ,

t₀

где Φ(t, τ) - решение уравнения

dΦ(t, τ)

= A(t)Φ(t, τ), Φ(τ, τ) = I.

Рассмотрим сначала регулярный случай R > 0 и G(t) > 0, t ∈ [t₀, t_f ]. Так

как Φ(t, τ) - невырожденная матрица, то тогда P (t) > 0, t ∈ [t₀, t_f ]. Рассмот-

рим положительно определенную квадратичную форму V (t, x) = x^TP^-1(t)x

с матрицей P (t), удовлетворяющей уравнению (2.5). Вычислим ее про-

изводную в силу системы (2.1), принимая во внимание, что d(P^-1)/dt =

= -P^-1( P)P^-1:

(2.8)

= v^TG^-1v - (v - v_∗)^TG^-1(v - v_∗

где v_∗(t) = G(t)B^T(t)P^-1(t)x(t), а x(t) - решение уравнения

[

]

(2.9)

A(t) + B(t)G(t)B^T(t)P^-1(t)

Интегрируя (2.8) на интервале [t₀, t], имеем

(2.10)

x^T(t)P^-1(t)x(t) = |x(t₀)|^2R + ∥v∥2G[t0,t]^-∥v-v∗∥G [t₀,t]^.

Так как R > 0 и G(σ) > 0, то для (x₀, v(σ)) ∈ S(t, t₀; R, G) выполняется нера-

венство (2.3). Следовательно,

(2.11)

x^T(t)P^-1

(t)x(t) ≤ 1,

т.е. x(t) ∈ E(P (t)).

Покажем, что для любой точки x ∈ E(P (t)) найдется точка x₀ ∈ E(R) и

возмущение v(σ), σ ∈ [t₀, t], принадлежащие S(t, t₀; R, G), такие что выпол-

няется ϕ(t; t₀, x₀, v) = x. Возьмем v(σ) = v_∗(σ), где x(σ) - решение уравнения

(2.9) с конечным условием x(t) = x. Очевидно, что в качестве искомой точки

следует взять начальную точку x₀ = x(t₀) этой траектории. С учетом (2.10)

получим

|x₀|^2R + ∥v_∗∥^2G[t

= x^TP^-1(t)x ≤ 1.

0,t]

Следовательно, |x₀|^2R ≤ 1, т.е. x₀ ∈ E(R₀).

Рассмотрим теперь вырожденный случай R ≥ 0 и G(t) ≥ 0, t ∈ [t₀, t_f ]. Вве-

дем матрицы

R_ε = R + εI > 0, G_ε(t) = G(t) + εI > 0.

Решение уравнения (2.5), в котором матрица G(t) заменена матрицей G_ε(t)

и начальное условие есть P (t₀) = R_ε, имеет вид P_ε(t) = P (t) + εP₁(t) > 0,

где P₁(t) > 0 - решение уравнения (2.5) при G(σ) ≡ I и R = I. Согласно

доказанному невырожденный эллипсоид E(P_ε(t)) есть множество достижи-

мости системы при начальных состояниях и возмущениях из множества

S(t, t₀; R_ε, G_ε).

Покажем, что множество достижимости системы при начальных со-

стояниях и возмущениях из множества S(t, t₀; R, G) в случае R ≥ 0

и G(t) ≥ 0 также представляется в виде вырожденного эллипсоида{}

E (P (t)) = x = P^1/2(t)w, |w| ≤ 1 . Для этого сначала покажем, что для про-

извольной пары из S(t, t₀; R, G) конец траектории в момент t будет принад-

лежать эллипсоиду E(P (t)). Зафиксируем начальное состояние x₀ ∈ E(R) и

выберем некоторое малое ε > 0. Поскольку S(t, t₀; R, G) ⊂ S(t, t₀; R_ε, G_ε), то

для данного начального состояния и некоторого допустимого возмущения

конец фазовой траектории x(t) = ϕ(t; t₀, x₀, v) в момент t будет принадле-

жать эллипсоиду E(P_ε(t)) для любого сколь угодно малого ε. Это значит, что

x(t) ∈ E(P (t)).

Покажем теперь, что для любого состояния x(t) ∈ E(P (t)) найдется па-

ра (x^∗0, v^∗(σ)) ∈ S(t, t₀; R, G), для которой x(t) = ϕ(t; t₀, x^∗0, v^∗). Так как x(t) ∈

∈ E(P_ε(t)) и E(P_ε(t)) - область достижимости системы в регулярном слу-

чае при R_ε > 0 и G_ε(σ) > 0, то найдется пара (x^ε0, v^ε(σ)) ∈ S(t, t₀; R_ε, G_ε), где

x^ε0 = (R + εI)^1/2w^ε1, v^ε(σ) = (G + εI)^1/2w^ε2(σ), |w^ε1|² + ∥w^ε2(σ)∥² ≤ 1, для кото-

рой x(t) = ϕ(t; t₀, x^ε0, v^ε). Возьмем последовательность ε_n → 0 при n → ∞. Так

как последовательность (wεn1 , w2n (σ)) ограничена в гильбертовом простран-

стве со скалярным произведением

∫

(

) (

)

< w⁽¹⁾¹,w⁽¹⁾²(σ)

, w⁽²⁾¹,w⁽²⁾²(σ)

>= w^(1)T1w⁽²⁾¹ + w^(1)T2(σ)w⁽²⁾²(σ)dσ,

t₀

то она содержит слабо сходящуюся подпоследовательность [27, теорема 1.8.1].

Согласно [27, теорема 1.8.4] из указанной подпоследовательности можно

извлечь такую подпоследовательность (wεnk1 , w2nk (σ)), что последователь-

∑_m

ность ее средних арифметических

k=1

(wεnk1 , w2nk (σ))/m сильно сходится к

(w^∗1, w^∗2(σ)) при m → ∞. Так как множество {(w₁, w₂(σ)): |w₁|² + ∥w₂(σ)∥² ≤ 1}

выпукло и замкнуто, то все члены последней последовательности принад-

лежат этому множеству и |w^∗1|² + ∥w^∗2(σ)∥² ≤ 1. В силу принципа супер-

позиции для линейной системы траектории с начальными состояниями и

возмущениями, соответствующими каждой паре указанной последователь-

ности средних арифметических, в момент времени t попадают в x(t). Так

∑_m

как ε_m =

εnk /m → 0 при m → ∞, то R + ε_mI → R, G(σ) + ε_mI → G(σ),

k=1

P (t) + ε_mP₁(t) → P (t) при m → ∞. Следовательно, (x^∗0, v^∗(σ)) с x^∗0 = R^1/2w^∗1

и v^∗(σ) = G^1/2w^∗2(σ) есть искомая пара.

Замечание 1. Возможно альтернативное доказательство утверждения

теоремы, основанное на понятии опорной функции множества достижимо-

сти [11], вычисление которой сводится к максимизации скалярного произве-

дения на шаре².

Переходим к дискретному случаю. Начнем со вспомогательного утвержде-

ния, доказательство которого приведено в Приложении.

Лемма 2.1. Пусть S (m × n)-матрица, причем m ≤ n. Следующие два

множества совпадают:

S₁ = {x = Sg

∀g ∈ Rⁿ : |g| ≤ 1} =

{

}

= x = (SS^T)^1/2w

∀w ∈ R^m : |w| ≤ 1

=S₂,

где S₂ - эллипсоид, матрица которого SS^T.

² Это доказательство любезно предоставил авторам А.И. Матасов.

Решение уравнения (2.1) имеет вид

∑

(2.12)

x(t) = Ψ(t, t₀)x(t₀) +

Ψ(t, i + 1)B(i)v(i), t ≥ t₀

+ 1,

i=t₀

где переходная матрица

{

A(t - 1)A(t - 2) · · · A(t₀), t ≥ t₀ + 1,

Ψ(t, t₀) =

I, t=t₀,

является решением разностного уравнения

(2.13)

Ψ(t + 1, t₀) = A(t)Ψ(t, t₀), Ψ(t₀, t₀) = I, t ≥ t₀.

С учетом (2.2) запишем (2.12) в виде

(2.14)

x(t) = S_tg_t, g^Ttg_t

≤ 1,

где

(

)

S_t =

Ψ(t, t₀)R^1/2 Ψ(t, t₀ + 1)B(t₀)G^1/2(t₀) · · · Ψ(t, t)B(t - 1)G^1/2(t - 1)

(

)

g_t = col

w₁,w₂(t₀),··· ,w₂(t - 1)

Заметим, что S_tS^Tt = P (t) ≥ 0, где

∑

P (t) = Ψ(t, t₀)RΨ^T(t, t₀) +

Ψ(t, i + 1)B(i)G(i)B^T(i)Ψ^T(t, i + 1),

i=t₀

т.е. матрица P (t) является решением разностного уравнения (2.6). Таким об-

разом, множество достижимости в момент времени t образуют все векто-

ры вида (2.14). В силу леммы 2.1 это множество совпадает с эллипсоидом

E (P (t)). Теорема доказана.

Следствие 2.1. Множество достижимости системы (2.1) при на-

чальных состояниях и возмущениях из множества S(t, t₀; R, G) обладает

эволюционным свойством

D(t, t₀, E(R)) = D(t, τ, D(τ, t₀, E(R))),

так как D(τ, t₀, E(R)) = E(P (τ)) и D(t, τ, E(P (τ))) = D(t, t₀, E(R)) для любого

τ ∈ [t₀,t].

Замечание 2. Заметим, что уравнения (2.5) и (2.6) в теореме 2.1 совпа-

дают с уравнениями для ковариационных матриц Ex(t)x^T(t) состояния си-

стемы (2.1) в непрерывном и дискретном случаях, когда начальное состояние

и возмущения являются случайными независимыми процессами с нулевыми

математическими ожиданиями и заданными ковариационными матрицаами

Ex(t₀)x^T(t₀) = R, Ev(t)v^T(t) = G(t) [28].

Замечание 3. Непосредственно, но достаточно громоздко проверяется,

что в дискретном случае при условии det A(t) = 0, R > 0 и G(t) > 0 для при-

ращения функции V (t) = x^TP^-1(t)x, где P (t) > 0, t ∈ [t₀, t_f ] решение урав-

нения (2.6), в силу системы тождественно выполняется

ΔV (t) = v^T(t)G^-1(t)v(t) -

(2.15)

-(v(t) - v_∗(t))^T[G^-1(t) - B^T(t)P^-1(t + 1)B(t)](v(t) - v_∗(t)),

где v_∗(t) = [G^-1(t) - B^T(t)P^-1(t + 1)B(t)]^-1B^T(t)P^-1(t + 1)A(t)x(t). Нера-

венство G^-1(t) - B^T(t)P^-1(t + 1)B(t) > 0 по лемме Шура эквивалентно нера-

венству P (t + 1) - B(t)G(t)B^T(t) > 0, которое выполняется в силу уравне-

ния (2.6). Следовательно, суммируя тождества (2.15) и учитывая начальное

условие P (t₀) = R, а также (2.3), получим

x^T(t_f)P^-1(t_f)x(t_f ) ≤ 1,

т.е. x(t_f ) ∈ E(P (t_f )) для всех допустимых начальных состояний и возмуще-

ний.

В частном случае, когда возмущения отсутствуют и начальное состояние

принадлежит эллипсоиду E(R), R ≥ 0, т.е. множеством допустимых началь-

ных состояний и возмущений является S(t, t₀; R, 0), множество достижимости

системы (2.1) есть эллипсоид E(P₀(t)), матрица которого P₀(t) ≥ 0 - реше-

ние уравнения (2.5) или (2.6) при G(t) ≡ 0 с начальным условием P₀(t₀) = R.

В другом частном случае при нулевом начальном состоянии, когда множе-

ство допустимых начальных состояний и возмущений составляет S(t, t₀; 0, G),

множеством достижимости является эллипсоид E(P_v(t)), матрица которого

P_v(t) ≥ 0 - решение уравнения (2.5) или (2.6) с нулевым начальным усло-

вием P_v(t₀) = 0. Так как решение неоднородного уравнения представимо в

виде

(2.16)

P (t) = P₀(t) + P_v

(t),

то E(P₀(t)) ⊆ E(P (t)) и E(P_v(t)) ⊆ E(P (t)).

Замечание 4. Обратим внимание на возможность определения множе-

ства достижимости с помощью решения обратной задачи: для заданной мат-

рицы S > 0 найти матрицу R > 0 такую, что множество достижимости систе-

мы (2.1) в момент времени t ≥ t₀ при всех допустимых начальных состояниях

и возмущениях, принадлежащих множеству S(t, t₀; R, G), совпадает с эллип-

соидом E(S). Действительно, запишем уравнения

(2.17)

Q=-AT_{(t)Q-QA(t)-QB(t)G(t)B}T(t)Q

для непрерывного случая и

(2.18)

Q(t) = A^T(t)Q(t + 1)A(t) - A^T(t)Q(t + 1)B(t)M^-1(t)B^T

(t)Q(t + 1)A(t)

с M(t) = G^-1(t) - B^T(t)Q(t + 1)B(t) > 0 для дискретного случая, которые

являются сопряженными к уравнениям (2.5) и (2.6). Задавая Q(t_f ) = S^-1

в уравнениях (2.17) и (2.18) и находя Q(t₀), получим, что заданный эллипсо-

ид E(S) является областью достижимости системы (2.1) при всех начальных

состояниях и возмущениях, принадлежащих множеству S(t, t₀; Q^-1(t₀), G).

Далее, пусть z = C_z(t)x - некоторый выход системы (2.1). Если x(t) ∈

∈ E(P(t)), т.е. x(t) = P^1/2(t)w, где |w| ≤ 1, то z(t) = Cz(t)P1/2(t) w. Со-

гласно лемме 2.1 множество всех таких векторов составляет эллипсоид

{

}

(

)

(

)

C_z(t)P(t)C^Tz(t)

= z:z=

C_z(t)P(t)C^Tz(t)

^1/2 g, |g| ≤ 1 , а максимальное

значение евклидовой нормы выхода совпадает с величиной максимальной по-

луоси этого эллипсоида, т.е.

(

)

(2.19)

max

|z(t)| = λ^1/2max

C_z(t)P(t)C^Tz(t)

(x₀,v)∈S(t,t₀;R,G)

Если R > 0 и G(σ) > 0, σ ∈ [t₀, t], то максимальное значение этой величины

на заданном отрезке времени [t₀, t_f ]

sup

|z(t)|

t∈[t₀,t_f ]

sup

max

|z(t)| =

max

(

)_1/2 =

(x₀,v)∈S(t,t₀;R,G)

x(t₀)=0,v≡0

t∈[t₀,t_f ]

(2.20)

|x(t₀)|^2R + ∥v∥²

G [t₀,t]

= sup λ^1/2max(C_z(t)P(t)C^Tz(t))

t∈[t₀,t_f ]

совпадает с максимальным уклонением выхода, которое при G(σ) ≡ I яв-

ляется обобщенной H₂-нормой системы при ненулевых начальных услови-

ях [20-23].

Полученный в теореме 2.1 результат непосредственным образом перено-

сится на случай, когда область неопределенности начального состояния есть

эллипсоид с центром не в нуле, а в заданной точке x_∗. Действительно, пусть

начальное состояние и возмущение системы (x₀, v(σ)) представимы в виде

x₀ = x_∗ + R^1/2w₁, v(σ) = G^1/2(σ)w₂(σ),

|w₁|² + ∥w₂∥^2[t

≤ 1.

0,t]

Отсюда следует, что начальное состояние принадлежит эллипсоиду E(R, x_∗)

с центром в x_∗ и матрицей R. В силу линейности системы представим ее

решение в виде двух слагаемых: решения возмущенной системы с началь-

ным состоянием, принадлежащим соответствующему эллипсоиду с центром

в начале координат, и решения невозмущенной системы с начальным состоя-

нием x_∗, т.е.

ϕ(t; t₀, x₀, v) = ϕ(t; t₀, x₀ - x_∗, v) + ϕ_∗(t), ϕ_∗(t) = ϕ(t; t₀, x_∗, 0).

Тогда из теоремы 2.1 следует, что в этом случае множество достижимости

системы в момент времени t представляет собою эллипсоид с центром в точ-

ке ϕ_∗(t) и матрицей P (t), т.е.

D(t, t₀, E(R, x_∗)) = E(P (t), ϕ_∗(t)).

Для иллюстрации теоремы 2.1 рассмотрим известное уравнение Матье,

описывающее параметрические колебания линейного осциллятора. Предста-

вим это уравнение в виде системы дифференциальных уравнений

x₁ = x₂,

(2.21)

x₂ = -ω²⁰(1 + εsin ωt)x₁ + v,

x₁(0) = x₁₀, x₂(0) = x₂₀,

где ω₀, ω и ε - заданные параметры, v = v(t) - внешнее возмущение, дейст-

вующее на осциллятор. Известно [1, с. 162], что при определенном соотно-

шении параметров в рассматриваемой системе возможен параметрический

x₂

1,6

2,4

t = 1,0

t = 5,1

0,8

1,2

-0,8

-1,2

-2,4

-1,6

-0,8

0,8

1,6

-1,8

-0,9

0,9

1,8

x₁

x₂

-8

t = 20,7

t = 60,0

-16

-4

-2

-160

-80

160

x₁

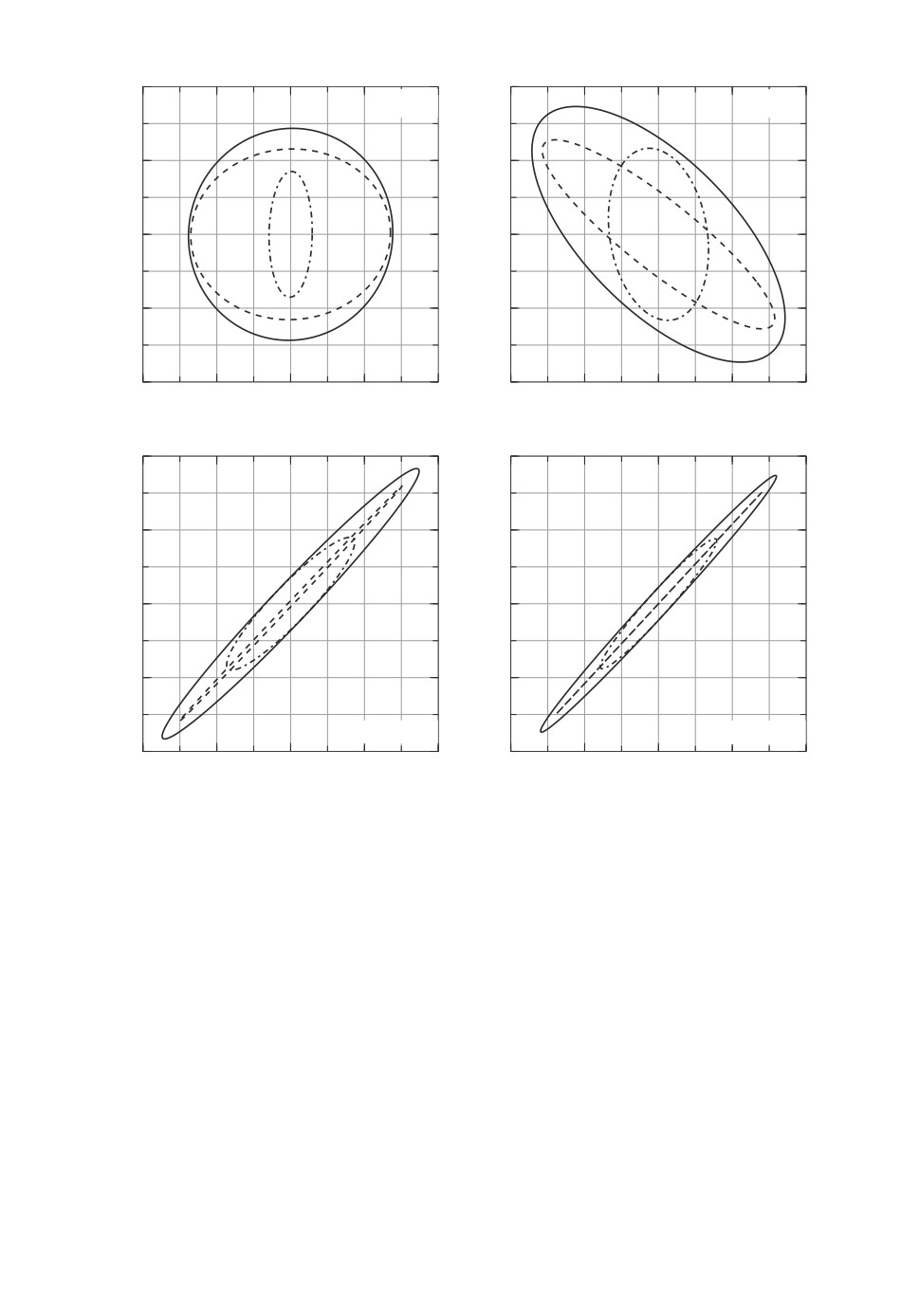
Рис. 1. Динамика множеств достижимости уравнения Матье в регулярном случае.

резонанс. Основной резонанс возникает при соотношении ω₀/ω = 1/2. Далее

при проведении вычислительных экспериментов будем полагать, что ω₀ = π,

ω = 2π, ε = 0,1.

На рис. 1 для моментов времени 1, 5,1, 20,7, 60 показаны множества дости-

жимости для регулярного случая, когда R = diag(1, 1), G(σ) ≡ 1 (сплошная

линия), для вырожденного случая, когда отсутствует внешнее возмущение

G(σ) ≡ 0 (пунктирная линия), и для вырожденного случая, когда началь-

ное состояние нулевое R = 0 (штрих-пунктирная линия). Заметим, что при

t = 60 эллипс, обозначенный пунктирной линией, имеет длины полуосей, рав-

ные 0,0093 и 111,75 соответственно.

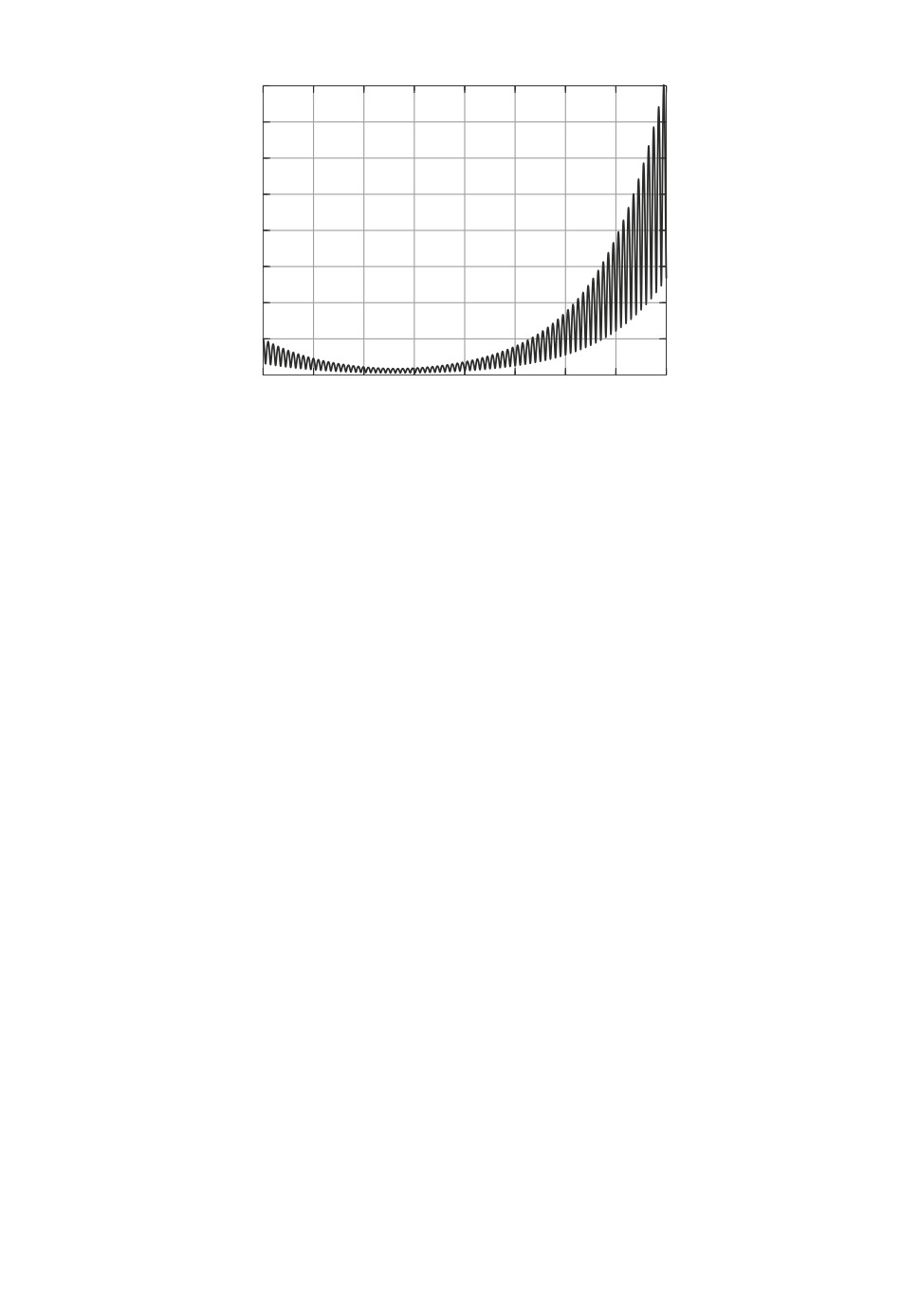
Далее рассмотрим вырожденный случай, когда внешнее возмущение от-

сутствует (G(σ) ≡ 0), а в качестве матрицы R выбрана вырожденная диаго-

нальная матрица R = diag(0, 1). Другими словами, в качестве допустимых

начальных условий полагается x₁₀ = 0, x₂₀ ∈ [-1, 1]. Для этого случая на

рис. 2 показана эволюция во времени величины L, определяющей длину по-

Рис. 2. Динамика “размера” множества достижимости уравнения Матье в вы-

рожденном случае.

ловины отрезка множества достижимости. Заметим, что эта зависимость

носит колебательный характер с частотой, близкой к 2π.

3. Оптимальное эллипсоидальное оценивание состояния и параметров

Рассмотрим задачу оценивания состояния x(t) линейной нестационарной

системы

∂x(t) = A(t)x(t) + B(t)v(t),

(3.1)

y(t) = C(t)x(t) + D(t)v(t)

с неизвестным начальным состоянием x(t₀) по измерениям выхода y(σ),

σ ∈ [t₀,t]. Предположим, что начальное состояние системы и возмущения

представимы в виде

x(t₀) - x_∗ = R^1/2w₁, v(σ) = G^1/2(σ)w₂(σ),

(3.2)

|w₁|² + ∥w₂∥^2[t

≤ 1, t ∈ [t₀, t_f ]

0,t]

для заданных матрицы R^T = R ≥ 0 и матричной функции G^T(σ) = G(σ) ≥ 0,

σ ∈ [t₀,t]. Построим наблюдатель полного порядка

(3.3)

∂ x(t) = A(t)x(t) + L(t)[y(t) - C(t)x(t)],

x(t₀) = x_∗,

где x(t) - оценка состояния x(t), а L(t) - матрица параметров наблюдателя,

подлежащая определению. Обозначим ошибку оценивания: e(t) = x(t) - x(t),

которая удовлетворяет уравнению

(3.4)

∂e(t) = A_c(t)e(t) + B_c(t)v(t), e(t₀) = x(t₀) - x_∗,

где A_c(t) = A(t) - L(t)C(t), B_c(t) = B(t) - L(t)D(t). Тогда множество дости-

жимости системы (3.4) в момент времени t согласно теореме 2.1 есть эллип-

соид E(P (t)), матрица которого в непрерывном случае удовлетворяет урав-

нению

(3.5)

= A_c(t)P + PATc (t) + B_c(t)G(t)B^Tc

(t)

с начальным условием P (t₀) = R, а в дискретном случае - уравнению

(3.6)

P (t + 1) = A_c(t)P (t)A^Tc(t) + B_c(t)G(t)B^Tc

(t)

с начальным условием P (t₀) = R. Это означает, что состояние x(t) систе-

мы (3.1) находится внутри соответствующего эллипсоида E(P (t), x(t)) с цен-

тром в точке x(t), определяемой уравнением наблюдателя (3.3). Это множе-

ство естественно назвать эллипсоидальной оценкой состояния x(t) в момент

времени t, а наблюдатель с матрицей L_∗(t), при которой, например, след мат-

рицы P (t) будет минимальным, назвать оптимальным.

Согласно замечанию 2 динамика матрицы эллипсоидального множества

достижимости уравнения (3.4) описывается тем же уравнением, что и ди-

намика ковариационной матрицы ошибки Ee(t)e^T(t) в стохастическом слу-

чае, когда ковариация начального состояния равна Ex(t₀)x^T(t₀) = R, а ко-

вариация возмущения равна Ev(t)v^T(t) = G(t). Так как след матрицы эл-

липсоидальной оценки равен дисперсии ошибки оценивания, то уравнение

оптимального наблюдателя совпадает с уравнением фильтра Калмана для

оценки состояния системы (3.1), в которой возмущения ξ₁(t) = B(t)v(t) и

ξ₂(t) = D(t)v(t), входящие аддитивно в уравнение состояния и в уравнение

измерения, являются коррелированными

(

)

( ξ

)(

)

B(t)G(t)B^T(t)

∗

1(t)

(3.7)

ξ^T1(t)ξ^T2(t)

ξ₂(t)

D(t)G(t)B^T(t) D(t)G(t)D^T(t)

где ∗ замещает матрицу, транспонированную к симметрично расположенному

блоку. Принимая во внимание стандартное требование в контексте калманов-

ской фильтрации о невырожденности ковариационной матрицы возмущений

в измерениях [28, с. 404], приходим к следующему результату.

Теорема 3.1. Если det[D(σ)G(σ)D^T(σ)] = 0, σ ∈ [t₀,t], то оптималь-

ный наблюдатель (3.3), обеспечивающий наилучшую эллипсоидальную оцен-

ку E(P_∗(t), x(t)) состояния системы (3.1) в момент времени t ≥ t₀ при лю-

бых начальных состояниях и возмущениях, удовлетворяющих условию (3.2)

при R ≥ 0 и G(σ) ≥ 0, σ ∈ [t₀,t], определяется в непрерывном случае матри-

цей L(t), равной

[

]_T [

]_-1

(3.8)

L^(c)(t) =

D(t)G(t)B^T(t) + C(t)P_∗(t)

D(t)G(t)D^T(t)

где матрица P_∗(t) ≥ 0 является решением уравнения (3.5) при L(t) = L^(c)(t),

а в дискретном случае - матрицей L(t), равной

(3.9)

L^(d)

(t) =

[

][

]_-1

A(t)P_∗(t)C^T(t) + B(t)G(t)D^T(t)

C(t)P_∗(t)C^T(t) + D(t)G(t)D^T(t)

где P_∗(t) ≥ 0 - решение уравнения (3.6) при L(t) = L^(d)(t).

Замечание 5. Если z(t) = C_z(t)x(t) ∈ Rnz - некоторый выход системы

(3.1), то оптимальной эллипсоидальной оценкой выхода в момент времени t

является эллипсоид E(C_z(t)P_∗(t)C^Tz(t), z(t)), где z(t) = C_z(t)x(t), а x(t) - оцен-

ка состояния, определяемая оптимальным наблюдателем (3.3).

Замечание 6. Установленное соответствие между оптимальным наблю-

дателем и фильтром Калмана позволяет выявить важное свойство послед-

него. Пусть

x(t) - оценка состояния системы (3.1), определяемая филь-

тром Калмана при заданных ковариационных матрицах начального состоя-

ния K_x(t₀) = R и возмущения K_v(t) ≡ G(t), а P_∗(t) - ковариация ошибки

этой оценки. Тогда при любых детерминированных начальных состояниях

и возмущениях вида (3.2) состояние системы x(t) принадлежит эллипсоиду

E (P_∗(t), x(t)).

Представим теперь задачу оценивания неизвестных параметров линейной

регрессии

(3.10)

χ(t) = Φ(t)ζ₀ + v(t), t = t₀, . . . , t_f ,

где χ(t) - вектор измерений, Φ(t) - матрица регрессоров, ζ₀ - вектор неиз-

вестных параметров, v(t) - вектор помех измерений, как задачу оптимального

эллипсоидального оценивания состояния системы

(3.11)

ζ(t + 1) = ζ(t), ζ(t₀) = ζ₀

по измерениям зашумленного выхода χ(t). Предположим, что неизвестные

параметры и возмущения удовлетворяют ограничению

(3.12)

(ζ₀ - ζ_∗)^TR^-1(ζ₀ - ζ_∗) + ∥v∥^2G[t

≤ 1, t ∈ [t₀, t_f ]

0,t]

при R > 0 и G(t) > 0, где ζ_∗ - заданный вектор. Согласно теореме 3.1 оп-

тимальный наблюдатель описывается уравнениями, которые приводятся к

следующему виду:

ζ(t + 1) =ζ(t) + P (t + 1)Φ^T(t)G^-1(t)[χ(t) - Φ(t)ζ(t)],

ζ(t₀) = ζ_∗,

(3.13)

P (t +1) = P (t)- P (t)Φ^T(t)[Φ(t)P (t)Φ^T(t) + G(t)]^-1Φ(t)P (t), P (t₀) = R.

Нетрудно убедиться в том, что эти уравнения описывают рекуррентный ал-

горитм метода наименьших взвешенных квадратов [29], а также согласно [30,

с. 56], и фильтр Калмана при ковариациях Eζ₀ζ^T0 = R и Ev(t)v^T(t) = G(t), а

оценкаζ(t) минимизирует функционал

∑(

)_T

(

)

J_t(ζ) = (ζ - ζ_∗)^TR^-1(ζ - ζ_∗) +

χ(i) - Φ(i)ζ

G-1(i)

χ(i) - Φ(i)ζ

i=0

Таким образом, в предположениях (3.12) метод наименьших взвешенных

квадратов обеспечивает оптимальную эллипсоидальную оценку неизвестных

параметров, т.е. гарантирует в момент времени t, что неизвестный вектор ζ₀

принадлежит эллипсоиду E(P (t),ζ(t)).

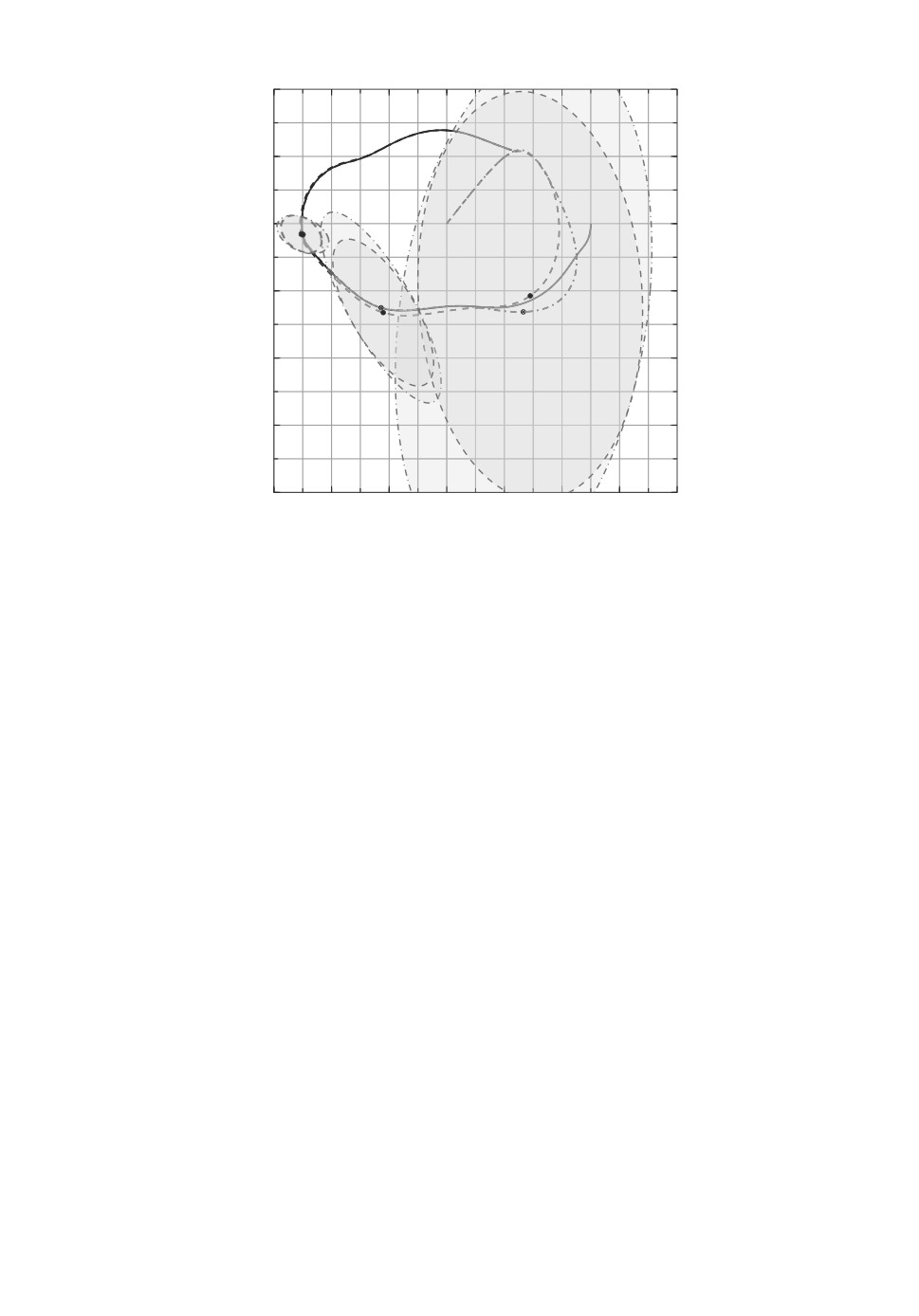
Для иллюстрации утверждения теоремы 3.1 обратимся к уравнению Ма-

тье, представленному в виде системы (2.21). Будем полагать, что измеряемый

x₂

0,4

0,2

-0,2

-0,4

-0,6

-0,8

-0,6

-0,4

-0,2

0,2

0,4

0,6

0,8

0x₁

Рис. 3. Динамика оптимальной эллипсоидальной и обобщенной H_∞-оптималь-

ной оценок состояния для уравнения Матье.

выход этой системы

y=x₁ +x₂ +v.

При проведении вычислительных экспериментов будем считать, что ω₀ =

= π/6, ω = 2π, ε = 0,1, R = 10,5I, G(σ) ≡ 1. На рис. 3 на плоскости (x₁, x₂)

представлены траектория системы (сплошная линия) x(t), отвечающая на-

чальным условиям x₁₀ = 0,5, x₂₀ = 0 и возмущению v(t) = 0,05 sin πt, а также

траектория оптимальной оценки x(t) (пунктирная линия) и соответствующие

эллипсы E(P_∗(t), x(t)) в моменты времени t₁ = 2, t₂ = 4, t₃ = 6. На этом же

рисунке для сравнения приведена траектория обобщенной H_∞-оптимальной

оценки (штрих-пунктирная линия), при которой обобщенная H_∞-норма си-

стемы (3.4) [31] является минимальной, а также соответствующие эллипсои-

дальные оценки состояния. Эксперимент показывает, что “размеры” эллипсов

с течением времени заметно уменьшаются и что эллипсы, получаемые в соот-

ветствии с обобщенной H_∞-нормой ошибки, “больше” эллипсов, отвечающих

оптимальным эллипсоидальным оценкам.

4. Оптимальные эллипсоидальные управления

Выше было установлено, что состояние линейной системы при неопреде-

ленных начальных условиях и возмущениях, связанных общим ограничени-

ем, в каждый момент времени находится внутри эволюционирующего эллип-

соида. Покажем, что это позволяет синтезировать ограниченное управление

вида нестационарной обратной связи по состоянию u = Θ(t)x, обеспечиваю-

щее выполнение одной из следующий целей: (i) попадание состояния или вы-

хода замкнутой системы в заданное эллипсоидальное множество в определен-

ный момент времени, (ii) нахождение в заданной эллипсоидальной трубке в

каждый момент времени. Такие законы управления будем называть эллип-

соидальными.

Уравнение замкнутой системы имеет вид

∂x(t) = [A(t) + B_u(t)Θ(t)]x(t) + B(t)v(t), x(t₀) = x₀, t ∈ [t₀,t_f],

(4.1)

z(t) = [C_z(t) + D(t)Θ(t)]x(t),

где z(t) - управляемый выход системы. Предполагается, что допустимые

начальные состояния и возмущения принадлежат множеству S(t, t₀; R, G),

вектор управления в любой момент времени должен принадлежать эл-

липсоиду u(t) ∈ E(Q_u(t)) с Q_u(t) > 0, а целевое множество есть эллипсоид

E_z(Q(t)) = {z : z^TQ^-1(t)z ≤ 1} с Q(t) > 0.

Далее потребуется вспомогательное утверждение, доказательство которо-

го приведено в Приложении.

Лемма 4.1. Для заданной матрицы Θ(t) имеет место u(t) = Θ(t)x(t) ∈

∈ E(Q_u(t)) с Q_u(t) > 0 при всех x(t) ∈ E(P(t)) с P(t) ≥ 0 тогда и только то-

гда, когда линейное матричное неравенство

(

)

P (t)

∗

(4.2)

≥0

Θ(t)P (t) Q_u(t)

разрешимо относительно P (t).

Согласно теореме 2.1 состояние замкнутой системы (4.1) в непрерывном

случае в каждый момент времени находится внутри эллипсоида E(P (t)), мат-

рица которого удовлетворяет уравнению

(4.3)

= A(t)P + P A^T(t) + B_u(t)Z(t) + Z^T(t)BTu (t) + B(t)G(t)B^T

(t)

с начальным условием P (t₀) = R, в котором Z(t) = Θ(t)P (t). Тогда при

всех допустимых начальных условиях и возмущениях целевой выход за-

мкнутой системы будет находиться внутри эллипсоида E_z(Q_z(t)), где

Q_z(t) = [C(t) + D(t)Θ(t)]P(t)[C(t) + D(t)Θ(t)]^T, и будет содержаться внутри

целевого множества, если E_z(Q_z(t)) ⊆ E(Q(t)), т.е. Q_z(t) ≤ Q(t). Подставляя

в это неравенство выражение для Q_z(t) и применяя лемму Шура, а также

учитывая лемму 4.1, приходим к следующему результату.

Теорема 4.1. Закон управления u = Θ(t)x с параметрами Θ(t) =

= Z(t)P^-1(t) удовлетворяет ограничению u(t) ∈ E(Q_u(t)), Q_u(t) > 0,

∀t ∈ [t₀,t_f] и обеспечивает выполнение z(t_f) ∈ E_z(Q(t_f)) для цели (i)

(z(t) ∈ E_z(Q(t)), ∀ t ∈ [t₀, t_f ] для цели (ii)) при всех начальных состояниях и

возмущениях, принадлежащих множеству S(t, t₀; R, G), если существуют

матричные функции P (t) > 0 и Z(t), удовлетворяющие матричному диф-

ференциальному уравнению (4.3), неравенствам (4.2) и Q_z(t_f ) ≤ Q(t_f ) для

цели (i) (Q_z(t) ≤ Q(t), ∀ t ∈ [t₀, t_f ] для цели (ii)).

Для вычисления искомых параметров обратной связи проведем дискрети-

зацию указанной задачи. Введем на отрезке [t₀, t_f ] равномерную сетку t_k =

= t_k-1 + h, k = 1,...,N, где h = (t_f - t₀)/N, и запишем дискретный аналог

рассматриваемой задачи в виде следующих соотношений при k = 0, . . . , N :

(

)

Y (k + 1) - Y (k) - h

A(k)Y (k) + Y (k)A^T(k)

(

)

−h

B_u(k)Z(k) + Z^T(k)B^Tu (k) + B(k)G(k)B^T(k)

= 0, k = N,

(

)

Y (k)

∗

≥ 0, Y (k) > 0, Y (0) = R,

Z(k) Q_u(k)

(4.4)

(

)

Y (N)

∗

(i) :

≥ 0,

C(N)Y (N) + D(N)Z(N) Q(N)

(

)

Y (k)

∗

(ii) :

≥ 0,

C(k)Y (k) + D(k)Z(k) Q(k)

где аргумент k указывает на значение соответствующей переменной в момент

времени t_k. Решив эту задачу полуопределенного программирования относи-

тельно неизвестных Y (k), Z(k), найдем матрицы Θ(k) = Z(k)Y^-1(k).

В теореме 4.1 и в процедуре (4.4) вычисления параметров регулятора

сделаны дополнительные предположения о положительной определенности

матриц P (t) > 0 и Y (k) > 0, которые обеспечивают возможность вычисления

параметров регулятора. Заметим, что имеются различные возможности для

оптимизации в рассматриваемой задаче. В частности, можно искать опти-

мальное эллипсоидальное управление, обеспечивающее попадание в целевой

эллипсоид, матрица которого имеет минимальный след. В таком случае мат-

рица Q(N) становится переменной и решается задача min tr Q(N) при огра-

ничениях, определенных в (4.4).

В дискретном случае имеет место следующий результат.

Теорема 4.2. Закон управления u(t) = Θ(t)x(t) с параметрами Θ(t) =

= Z(t)Y ^-1(t) удовлетворяет ограничению u(t) ∈ E(Q_u(t)), Q_u(t) > 0,

∀t ∈ [t₀,t_f] и обеспечивает выполнение ztf ∈ E_z(Q(t_f)) для цели (i)

(z_t ∈ E_z(Q(t)), ∀ t ∈ [t₀, t_f ] для цели (ii)) при всех начальных состояниях и

возмущениях, принадлежащих множеству S(t, t₀; R, G), если разрешимы

линейные матричные неравенства при t = t₀, . . . , t_f :





Y (t)

∗

A(t)Y(t)+Bu(t)Z(t) Y (t + 1)

∗

≥0,t=tf,

B^T(t) G^-1(t)

)

( Y (t)

∗

≥ 0, Y (t₀) ≥ R,

Z(t) Q_u(t)

(4.5)

(

)

Y (t_f )

∗

(i) :

≥ 0,

C(t_f )Y (t_f ) + D(t_f )Z(t_f ) Q(t_f )

(

)

Y (t)

∗

(ii) :

≥0

C(t)Y (t) + D(t)Z(t) Q(t)

относительно неизвестных матриц Y (t) > 0, Z(t).

Доказательство теоремы 4.2 приведено в Приложении.

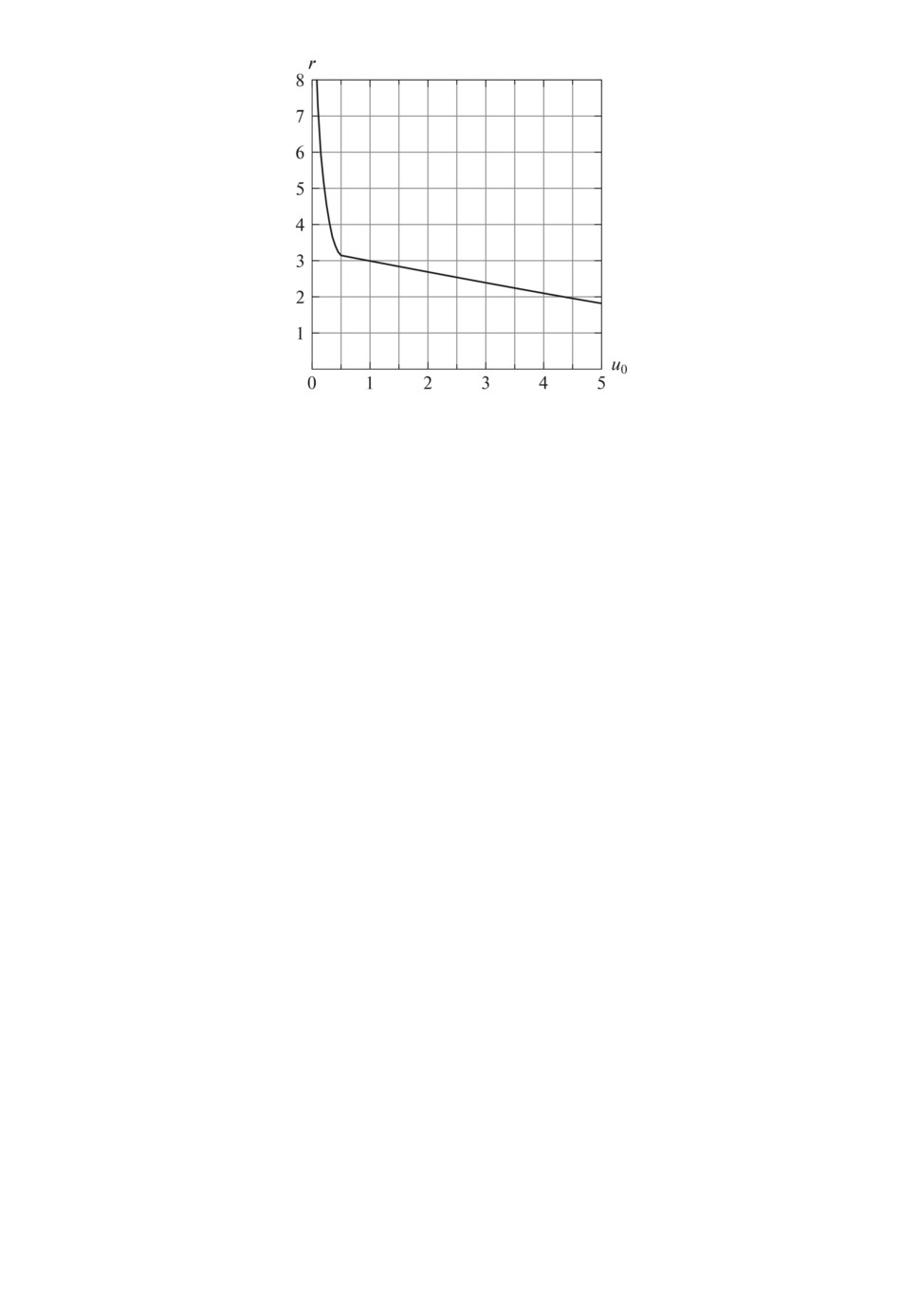
Рис. 4. Зависимость минимального радиуса трубки от максимальной величи-

ны управления.

Для иллюстрации приведенных в данном разделе результатов обратимся

к системе

x₁ = x₂,

(4.6)

x₂ = -ω²⁰(1 + εsin ωt)x₁ + u + v,

x₁(0) = x₁₀, x₂(0) = x₂₀,

описывающей параметрические колебания управляемого линейного осцилля-

тора. Зададим параметры осциллятора точно такие же, как и разделе 2, т.е.

ω₀ = π, ω = 2π, ε = 0,1. Рассмотрим задачу синтеза нестационарного управ-

ления по состоянию в виде u = θ₁(t)x₁ + θ₂(t)x₂ при заданном ограниче-

нии |u| ≤ u₀, обеспечивающего на конечном отрезке времени [0, 60] удержа-

ние траекторий системы (4.6) при неопределенных начальных условиях и

возмущениях, связанных общим ограничением c матрицей R = diag(1, 1) и

G(σ) ≡ 1, в круглой трубке x²¹(t) + x²²(t) ≤ r², t ∈ [0, 60] с минимально воз-

можным радиусом r. На рис. 4 показана зависимость минимального радиуса

трубки от параметра u₀.

5. Заключение

Показано, что при наличии совместного ограничения на неточно задан-

ные начальное состояние и возмущение множествами достижимости линей-

ной нестационарной непрерывной или дискретной системы являются эволю-

ционирующие эллипсоиды, матрицы которых удовлетворяют линейному мат-

ричному дифференциальному или разностному уравнению. Применение это-

го результата позволяет синтезировать оптимальный наблюдатель неизме-

ряемого состояния системы, обеспечивающий эллипсоидальную оценку с ми-

нимальным следом матрицы эллипсоида, а также линейные нестационарные

регуляторы для приведения состояния системы в заданное эллипсоидальное

множество. Доказано, что фильтр Калмана в задаче оценивания состояния и

рекуррентный алгоритм метода наименьших взвешенных квадратов в задаче

идентификации неизвестных параметров обеспечивают оптимальные эллип-

соидальные оценки состояния и параметров при детерминированных началь-

ном состоянии системы и возмущении с заданной мерой неопределенности.

Тем самым устанавливается связь между стохастическим и детерминирован-

ным подходами к задачам фильтрации и идентификации. Иллюстративные

примеры для уравнения Матье демонстрируют эффективность предложен-

ного подхода.

Авторы признательны А.И. Матасову за полезные обсуждения и конструк-

тивные предложения по доказательству теоремы 2.1.

ПРИЛОЖЕНИЕ

Доказательство леммы 2.1. В соответствии с полярным разложе-

нием [32, с. 490] представим матрицу S в виде S = (SS^T)^1/2U, где UU^T = I.

Тогда x = Sg = (SS^T)^1/2Ug = (SS^T)^1/2w, где w = Ug. Так как w^Tw ≤ 1 и для

каждого такого w найдется g = U^Tw такой, что g^Tg = w^Tw ≤ 1, то лемма до-

казана.

Доказательство леммы 4.1. Запишем эквивалентные условия

u ∈ E(Q_u)

∀x ∈ E(P) ⇔ maxx^TΘ^TQ^-1uΘx ≤ 1, x = P^1/2w

∀w : w^Tw ≤ 1.

Вводя функцию Лагранжа

(

)

L = w^TP^1/2Θ^TQ^-1uΘP^1/2w + µ

1-w^Tw

приходим к условию

(

)

(

)

µ=λ_max P^1/2Θ^TQ^-1u

ΘP^1/2

= λ_max Q^-1/2uΘPΘ^TQ^-1/2

≤ 1,

которое эквивалентно неравенству ΘP Θ^T ≤ Q_u. Согласно характеризации

псевдообратной матрицы представим P = P P⁺P и запишем последнее нера-

венство как ΘP P⁺P Θ^T ≤ Q_u. С учетом варианта леммы Шура для вырож-

денных матриц, доказанного в [29, с. 190], приходим к (4.2). Лемма доказана.

Доказательство теоремы

4.2. Замкнутая система описывается

уравнением

x(t + 1) = A_c(t)x(t) + B(t)v(t), A_c(t) = A(t) + B_u(t)Θ(t).

Множества достижимости этой системы - эллипсоиды E(P_c(t)) с матри-

цами P_c(t), определяемыми согласно теореме 2.1. Введем матрицы Y (t) =

= Y ^T(t) > 0, t = t₀,··· ,t_f, удовлетворяющие неравенствам

(Π.1)

Y (t + 1) ≥ A_c(t)Y (t)ATc (t) + B(t)G(t)B^T(t), Y (t₀

)≥R.

Если обозначить Θ(t)Y (t) = Z(t) и применить лемму Шура, то это неравен-

ство превратится в первое неравенство в (4.5). Из (Π.1) следует, что соотно-

шения

Y (t + 1) - P_c(t + 1) = A_c(t)[Y (t) - P_c(t)]ATc (t) + M(t), Y (t₀) - P_c(t₀) ≥ 0

выполняются при некоторых матрицах M(t) = M^T(t) ≥ 0. Тогда

∑

Y (t) - P_c(t) = Φ(t, t₀)[Y (t₀) - P_c(t₀)]Φ^T(t, t₀) +

Φ(i, t₀)M(i)Φ^T(i, t₀) ≥ 0,

i=t₀

где Φ(t, t₀)

- переходная матрица замкнутой системы. Следовательно,

P_c(t) ≤ Y (t) и E(P_c(t)) ⊆ E(Y (t)), т.е. состояние замкнутой системы находит-

ся внутри эллипсоида E(Y (t)), а значит, целевой выход находится внутри эл-

липсоида E_z(Q_z(t)), где Q_z(t) = [C(t) + D(t)Θ(t)]Y (t)[C(t) + D(t)Θ(t)]^T. То-

гда выполнение неравенства Q_z(t) ≤ Q(t), которое при Z(t) = Θ(t)Y (t) с по-

мощью леммы Шура приводится к третьему и четвертому неравенствам в

(4.5), обеспечит выполнение соответствующей цели управления. Второе нера-

венство в (4.5) согласно лемме 4.1 означает, что u(t) ∈ E(Q_u(t)). Таким обра-

зом, если неравенства (4.5) выполняются, то управление обеспечивает выпол-

нение цели. Теорема доказана.

СПИСОК ЛИТЕРАТУРЫ

Неймарк Ю.И. Математическое моделирование как наука и искусство. Нижний

Новгород: Изд-во Нижегород. уни-та, 2010.

Neimark Ju.I. Mathematical Models in Natural Science and Engineering. Verlag

Berlin Heidelberg: Springer, 2003.

Неймарк Ю.И. Динамические системы и управляемые процессы. М.: Наука,

1978.

Неймарк Ю.И. Робастная устойчивость и D-разбиение // АиТ. 1992. № 7.

С. 10-18.

Neimark Ju.I. Robust stability and D-partition // Autom. Remote Control. 1992.

V. 53. No. 7. P. 957-965.

Неймарк Ю.И. Робастная устойчивость по нелинейным параметрам // Диффе-

ренц. уравнения. 1992. № 12. С. 2185-2187.

Neimark Ju.I. Robust stability under nonlinear parameters // Differen. Equat. 1992.

V. 28. No. 12. P. 1829-1831.

Коган М.М., Неймарк Ю.И. Об оптимальности локально-оптимальных реше-

ний линейно-квадратичных задач управления и фильтрации // АиТ. 1992. № 4.

С. 101-110.

Kogan M.M., Neimark Ju.I. On Optimality of Locally-Optimal Solutions to Linear-

Quadratic Control and Filtering Problems // Autom. Remote Control. 1992. V. 53.

No. 4. P. 561-569.

Kogan M.M., Neimark Ju.I. Locally optimal adaptive control without persistent

excitation // Automatica. 1996. V. 32. No. 10. P. 1463-1467.

Булгаков Б.В. О накоплении возмущений в линейных колебательных системах

с постоянными параметрами // ДАН СССР. 1946. Т. 51. № 5. С. 339-342.

Schweppe F.C. Recursive State Estimation: Unknown but Bounded Errors and Sys-

tem Inputs // IEEE Trans. Autom. Control. 1968. V. 13. No. 1. P. 22-28.

10.

Bertsekas D.P., Rhodes I.P. On the Minimax Reachability of Target Sets and Target

Tubes // Automatica. 1971. V. 7. P. 233-247.

11.

Куржанский А.Б. Управление и наблюдение в условиях неопределенности. М.:

Наука, 1977.

12.

Черноусько Ф.Л. Оценивание фазового состояния динамических систем. М.:

Наука, 1988.

13.

Kurzhanski A.B., Valyi I. Ellipsoidal Calculus for Estimation and Control. Boston:

Birkhäuser, 1997.

14.

Kurzhanskiy A.A., Varaiya P. Reach Set Computation and Control Synthesis for

Discrete-Time Dynamical Systems with Disturbances // Automatica. 2011. V. 47.

P. 1414-1426.

15.

Kuntsevich V.M., Volosov V.V. Ellipsoidal and Interval Estimation of State Vectors

for Families of Linear and Nonlinear Discrete-Time Dynamic Systems // Cybernet.

Syst. Anal. 2015. V. 51. No. 1. P. 64-72.

16.

Filippova T.F. Ellipsoidal Estimates of Reachable Sets for Control Systems with

Nonlinear Terms // IFAC PapersOnLine. 2017. V. 50. No. 1. P. 15355-15360.

17.

Boyd S., El Ghaoui L., Feron E., Balakrishnan V. Linear Matrix Inequalities in

Systems and Control Theory. Philadelphia: SIAM, 1994.

18.

Chernousko F.L., Ovseevich A.I. Properties of the Optimal Ellipsoids Approximating

the Reachable Sets of Uncertain Systems// J. Optim. Theory Appl. 2004. V. 120.

No. 2. P. 223-246.

19.

Wang Z., Shen X., Zhu Y. On Equivalence of Major Relaxation Methods for Min-

imum Ellipsoid Covering Intersection of Ellipsoids // Automatica. 2019. V. 103.

P. 337-345.

20.

Баландин Д.В., Бирюков Р.С., Коган М.М. Оптимальное управление макси-

мальными уклонениями выходов линейной нестационарной системы на конеч-

ном интервале времени // АиТ. 2019. № 10. C. 37-61.

Balandin D.V., Biryukov R.S., Kogan M.M. Optimal Control of Maximum Output

Deviations of a Linear Time-Varying System on a Finite Horizon // Autom. Remote

Control. 2019. V. 80. No. 10. P. 1783-1802.

21.

Баландин Д.В., Бирюков Р.С., Коган М.М. Минимаксное управление уклонени-

ями выходов линейной дискретной нестационарной системы // АиТ. 2019. № 12.

С. 3-24.

Balandin D.V., Biryukov R.S., Kogan M.M. Minimax Control of Deviations for the

Outputs of a Linear Discrete Time-Varying System // Autom. Remote Control. 2019.

V. 80. No. 12. P. 345-359.

22.

Balandin D.V., Kogan M.M. Multi-Objective Generalized H₂ Control // Automat-

ica. 2019. V. 99. No. 1. P. 317-322.

23.

Balandin D.V., Biryukov R.S., Kogan M.M. Finite-Horizon Multi-Objective Gener-

alized H₂ Control with Transients // Automatica. 2019. V. 106. No. 8. P. 27-34.

24.

Wilson D.A. Convolution and Hankel Operator Norms for Linear Systems //IEEE

Trans. Autom. Control. 1989. V. 34. P. 94-97.

25.

Баландин Д.В., Бирюков Р.С., Коган М.М. Эллипсоидальные множества до-

стижимости линейных нестационарных систем в задачах управления и оцени-

вания // Дифференц. уравнения. 2019. Т. 55. № 11. С. 1485-1498.

26.

Boyd S., Vandenberghe L. Convex Optimization. Cambridge Univ. Press, 2004.

27.

Балакришнан А.В. Прикладной функциональный анализ. М.: Наука, 1980.

28.

Квакернаак Х., Сиван Р. Линейные оптимальные системы управления. М.: Мир,

1977.

29.

Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание. М.: Наука,

1977.

30.

Kailath T., Sayed A.N., Hassibi B. Linear Estimatiom. Upper Saddle River, New

Jersey: Prentice Hall, Inc., 2000.

31.

Nagpal K.M., Khargonekar P.P. Filtering and Smoothing in an H_∞ Setting // IEEE

Trans. Autom. Control. 1991. V. 36. No. 2. P. 152-166.

32.

Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.

Статья представлена к публикации членом редколлегии Б.Т. Поляком.

Поступила в редакцию 23.07.2019

После доработки 03.10.2019

Принята к публикации 30.01.2020