Автоматика и телемеханика, № 8, 2020

Н.В. БАРАБАШ (barabash@itmm.unn.ru)

(Волжский государственный университет водного транспорта, Нижний Новгород;

Нижегородский государственный университет им. Н.И. Лобачевского),

И.В. БЕЛЫХ, канд. физ.-мат. наук (ibelykh@gsu.edu)

(Государственный университет Джорджии, Атланта, США)

БИФУРКАЦИИ ХАОТИЧЕСКИХ АТТРАКТОРОВ

В КУСОЧНО-ГЛАДКОЙ СИСТЕМЕ ЛОРЕНЦЕВСКОГО ТИПА¹

Изучается динамика кусочно-гладкой системы дифференциальных

уравнений, для которой ранее было строго доказано существование стран-

ного аттрактора лоренцевского типа и получены бифуркационные меха-

низмы его рождения. В настоящей статье обсуждается вопрос о разру-

шении этого аттрактора за счет появления в его структуре скользящих

движений. Качественно-численными методами изучается сложная после-

довательность бифуркаций аттрактора, в результате которой в системе

остается глобально устойчивый предельный цикл. Показано, что основой

этой последовательности являются C-бифуркации и бифуркации много-

обходных гомоклинических траекторий.

Ключевые слова: динамическая система, бифуркации, предельный цикл,

скользящие движения, странный аттрактор, хаос.

DOI: 10.31857/S0005231020080036

1. Введение

Настоящая статья выполнена в русле одного из главных научных направ-

лений Ю.И. Неймарка бифуркационной теории динамических систем. Ши-

роко известный метод D-разбиений можно рассматривать как один из пер-

вых результатов Ю.И. Неймарка по теории бифуркаций корней характерис-

тических уравнений линеаризованных динамических систем. Другой значи-

мый результат это бифуркация рождения тора или сложного неблуждаю-

щего множества из периодического движения при смене его устойчивости.

Это хорошо известная специалистам бифуркация Неймарка-Сакера [1]. Тео-

рия кусочно-гладких (релейных) систем, начатая Ю.И. Неймарком в 50-60 гг.

XX в. [2, 3], продолжает успешно развиваться в настоящее время [4, 5]. На-

стоящую статью можно рассматривать как развитие теории бифуркаций в

кусочно-гладких динамических системах.

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проекты № 18-01-00556 и №18-31-20052), а также Национального научно-

го фонда США (проект DMS-1909924). Численные результаты получены при поддержке

Российского научного фонда (проект №19-12-00367).

Кусочно-линейные и кусочно-гладкие системы широко использовались в

теории динамических систем в различных контекстах и приложениях [4, 6-8].

Их потенциальное преимущество перед их нелинейными аналогами заключа-

ется в возможности получать явные решения в заданных областях фазового

пространства системы и “склеивать” решения на границах этих областей.

Широкий класс кусочно-гладких динамических систем [4-6] в настоящее

время широко используется в технике в качестве релейных, автоматических

систем управления и систем с переключениями [9-12].

Интересным примером такой кусочно-гладкой системы является биомеха-

ническая модель баланса пешехода, идущего по мосту [13], в которой пере-

ключения между двумя системами [14] соответствуют переносу веса пеше-

хода с одной ноги на другую. Траектория такой кусочно-гладкой системы

определяется двумя склеенными решениями интегрируемых подсистем, что

позволяет получить точные формы периодического движения пешехода [15].

Кусочно-гладкие динамические системы могут использоваться для

построения потоков, обладающих основными свойствами хаотических нели-

нейных систем и допускающих строгое аналитическое исследование. В недав-

ней статье [16] авторами был предложен новый подход построения кусочно-

гладких моделей, заменяющих нелинейные неинтегрируемые хаотические си-

стемы. Эти модели имеют качественно ту же бифуркационную структуру и

позволяют аналитически доказывать существование странных аттракторов

и их бифуркаций.

Этот подход был применен к известной системе Лоренца [17], вместо ко-

торой была построена кусочно-линейная система как ее простейший аналог.

Для этой системы авторам удалось провести строгое доказательство суще-

ствования сингулярно-гиперболического аттрактора и бифуркаций его рож-

дения. Полученные бифуркации и аттракторы качественно совпадают с би-

фуркационной картиной и структурой аттрактора самой системы Лоренца,

детально изученными качественно-численными методами [18-20]. Из числен-

ных результатов известно, что аттрактор Лоренца разрушается при потере

инвариантного слоения [19, 21] с последующими сложными бифуркациями.

В силу сложности сценарий разрушения аттрактора Лоренца теоретически

изучен слабо.

В настоящей статье рассматривается этот вопрос, т.е. бифуркационная

картина гибели сингулярно-гиперболического аттрактора, но не в системе

Лоренца, а в ее аналоге в модели из [16]. Это разрушение начинается с

разрушения инвариантного слоения и после бесконечной последовательности

бифуркаций заканчивается рождением единственного устойчивого предель-

ного цикла.

Статья устроена следующим образом. В разделе 2 дано описание пред-

ложенной кусочно-линейной модели, в разделе 3 приведена характеристи-

ка скользящих движений, в разделе 4 представлен основной результат [16],

в разделе 5 приведен качественно-численный анализ разрушения странного

аттрактора.

2. Описание модели

Рассматривается кусочно-линейная система, склеенная из трехмерных ли-

нейных подсистем A_s, A_l, и A_r

x = x,

A_s :

y = -αy,

(x, y, z) ∈ G_s,

Ż = -νz,

x = -λ(x + 1) + ω(z - b),

(1)

Al :

y = -δ(y + 1),

(x, y, z) ∈ G_l,

Ż = -ω(x + 1) - λ(z - b),

x = -λ(x - 1) - ω(z - b),

A_r :

y = -δ(y - 1),

(x, y, z) ∈ G_r,

Ż = ω(x - 1) - λ(z - b),

где α, δ, ν, ω, λ и b положительные параметры. Эти подсистемы определены

на следующем разбиении фазового пространства G_s, G_l, и G_r соответственно:

Gs : |x| < 1, y ∈ R¹, z < b,



x ≤ -1

при z ≤ b,

Gl :

x ≤ -1

при z > b и y ≥ 0,

(2)

x < 1 при z > b и y < 0,



x≥1

при z ≤ b,

Gr :

x≥1

при z > b и y < 0,

x > -1 при z > b и y ≥ 0.

Векторные поля подсистем A_s, A_l и A_r будем обозначать соответствен-

но F_s, F_l и F_r в виде системы

= F_i(X), где индекс i = (s,l,r) и вектор

X = (x,y,z).

Эта система моделирует известную систему Лоренца [17]. Она, как и систе-

ма Лоренца, имеет три состояния равновесия и инвариантность относительно

замены (x, y, z) → (-x, -y, z).

Линейная подсистема A_s управляет динамикой системы (1) в области G_s.

Эта система имеет седловое состояние равновесия O_s в начале координат,

поэтому будем называть G_s седловой областью. Подсистемы A_r,l определе-

ны в областях G_r,l и имеют симметричные равновесия e_r,l = {±1, ±1, b} со-

ответственно. Эти равновесия являются устойчивыми трехмерными фокуса-

ми в подсистемах A_r,l. В полной системе эти равновесия становятся склеен-

ными и поэтому могут менять устойчивость. Заметим, что линии склейки

w_l = {x = -1,z = b,y ∈ R¹} и w_r = {x = 1,z = b,y ∈ R¹} являются устойчи-

выми многообразиями фокусов e_l и e_r соответственно (см. рис. 1). Будем

называть G_r и G_l правой и левой фокусными областями.

Седловая область G_s ограничена справа и слева вертикальными полу-

плоскостями S₁ = {x = 1, y ∈ R¹, z < b} и S₂ = {x = -1, y ∈ R¹, z < b} (см.

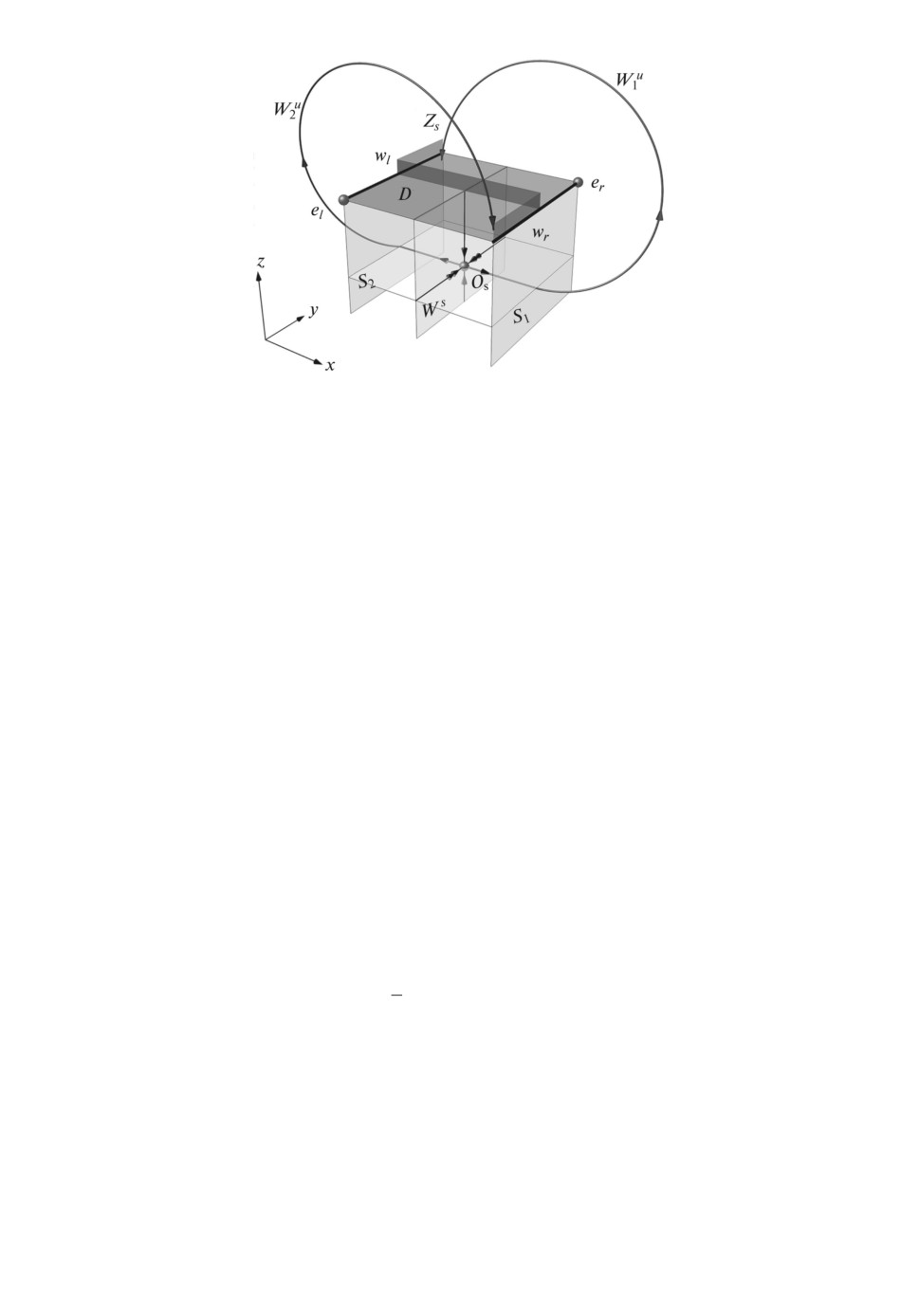
Рис. 1. Схема построения кусочно-линейной системы (1). Фазовое простран-

ство разделено на три области: G_s, G_l и G_r (не указаны на рисунке). Седловая

область G_s образована вертикальными полуплоскостями S_1,2 и горизонталь-

ной поверхностью D. Фокусные области G_l и G_r разделены седловой областью

и вертикальной Z-образной границей Z_s. Седло O_s имеет двумерное устойчи-

вое многообразие W^s и одномерное неустойчивое многообразие (W^u1 и W^u2 его

правая и левая ветви соответственно). Отрезки w_l и w_r принадлежат одно-

мерным устойчивым многообразиям фокусов e_l и e_r соответственно.

рис. 1). Область G_s также ограничена сверху частью плоскости D = {|x| ≤ 1,

y ∈ R¹, z = b} (темно-серая горизонтальная плоскость на рис. 1). Ниже плос-

кости D фокусные области G_l и G_r расположены слева и справа от вертикаль-

ных полуплоскостей S₂ и S₁ соответственно. Выше плоскости D фокусные

области разделены Z-образной границей Z_s (см. рис. 1).

Седло O_s имеет двумерное устойчивое многообразие, определенное в

седловой области как W^ssaddle = {x = 0, y ∈ R¹, z < b} (центральная верти-

кальная плоскость на рис. 1) и одномерное неустойчивое многообразие,

определенное в седловой области как W^u1saddle = {0 < x < 1, y = z = 0} и

W^u2saddle = {-1 < x < 0, y = z = 0}. Эти многообразия и их продолжения по

траекториям систем A_r,l в фокусных областях образуют глобальные много-

образия седла W^s, W^u1 и W^u2 седла O_s в полном фазовом пространстве систе-

мы (1).

Предполагается, что выполняется условие

(3)

< ν < 1 < α.

Часть неравенства (3) ν < 1 означает, что седловая величина равновесия O_s

положительна. В силу неравенства 1 < α плоскость Wlead = ((x,z) ∈ Gs,

y = 0) является частью ведущего многообразия, что аналогично системе Ло-

ренца.

3. Скользящие движения

Система (1) диссипативна, т.е. в ее фазовом пространстве существует по-

глощающая область G такая, что любая траектория с начальной точкой в

области R³ \ G попадает в область G и остается в ней навсегда. Эта область

задана неравенствами [16]



|y| ≤ 1,





0 ≤ z ≤ 2b при

|x| ≤ 1,

(4)



V_l ≤ b²

при x < -1,



V_r ≤ b²

при x > 1,

где V_l,r = (x ± 1)² + (z - b)². Очевидно, что в этой области находятся все тра-

ектории системы (1). Система (1) имеет две поверхности устойчивых сколь-

зящих движений S⁺¹ = {x = 1, z > b⁺ = b +^2λω , y < 0} и S⁺² = {x = -1,

z > b⁺ = b + 2λω , y > 0}. На поверхностях S⁺¹ и S⁺² векторное поле системы A_l

ориентировано в сторону увеличения x, а системы A_r в сторону уменьше-

ния x (векторные поля систем A_l и A_r “встречаются” на этих поверхностях).

Скользящие движения на этих поверхностях задаются двумерными систе-

мами, которые получаются по доопределению А.Ф. Филиппова [22], анало-

гичного одному из доопределений Ю.И. Неймарка [2]. Это доопределение в

рассматриваемом случае приобретает вид

(5)

= αF_r(X) + (1 - α)F_l

(X).

Здесь коэффициент α определен скалярным произведением

(6)

(αF_r(X) + (1 - α)F_l

(X), ▽s) = 0,

где градиент функции s(X), определяющей поверхность скользящих движе-

ний s(X) = 0, в рассматриваемом случае есть вектор ▽s(1, 0, 0). Из (1), (2),

(5), (6) получаем, что система скользящих движений имеет вид

λδ

y = -δy +

ω(z - b) - λ

(7)

λω

Ż = -ω - λ(z - b) -

ω(z - b) - λ

Из системы(7) получаем простую динамику скользящих движений. По-



скольку в (7) Ż

< 0, координата z уменьшается и любая траектория поки-

S⁺

1,2

дает S^+1,2 через линии срыва z = b⁺. В зависимости от параметров системы (1)

роль скользящих движений в динамике системы (1) разная. Рассмотрим два

основных случая.

4. Аттракторы без скользящих движений

В [16] доказано, что в области параметров

ω ln 2

δ>δ_cr =

(8)

√

)}

{λ(

b<b_cr =2

exp

arctg

+π

ω²

аттракторы системы (1) не содержат скользящих движений. При условиях (8)

строго доказано следующее утверждение [16].

e_l

e_r

O_s

Рис. 2. Аттрактор лоренцевского типа, существующий в системе (1) при зна-

чениях параметров b = 3,8, α = 2, ν = 0,75, δ = 0,588, ω = 2 и λ = 0,294 из

области (9). Траектории аттрактора склеены из траекторий седловой систе-

мы A_s (изображены черным) и траекторий фокусных систем A_l,r (изображены

серым).

Теорема 1

[16]. 1. В области параметров

3πλ

b_het = γ_het exp

≤ b < ν-1 exp

2ω

где γ_het(ν) - обратная функция функции ν = 1 +^{ln2-lnγln(γ-1)} , существует стран-

ный хаотический аттрактор лоренцевского типа, родившийся в результа-

те гетероклинической бифуркации при b = b_het и сосуществующий с двумя

устойчивыми фокусами e_l и e_r;

2. Поверхность

3πλ

b_AH = ν^-1 exp

2ω

соответствует бифуркации Андронова-Хопфа, при которой два симмет-

ричных седловых цикла влипают в устойчивые состояния равновесия e_l и e_r;

3. В области параметров

(9)

b_AH ≤ b ≤ b_cr

странный сингулярно-гиперболический аттрактор является единственным

аттрактором системы (1) (см. рис. 2).

5. Аттракторы, содержащие скользящие движения

При b > b_cr траектории аттрактора системы (1) могут попадать на по-

верхности скользящих движений. При этом любая периодическая орбита,

содержащая участок скользящих движений, становится устойчивой. Дело в

том, что неустойчивость периодических движений системы определена на-

правлением оси x (см. систему A_s в (1)). Ось x перпендикулярна плоско-

сти скользящих движений, вдоль которой траектории попадают на них не

асимптотически. Тем самым неустойчивость вдоль седловых орбит компен-

сируется суперустойчивостью скользящих плоскостей. Если же траектории

неблуждающего множества системы не попадают на поверхности скользя-

щих движений, то они продолжают оставаться седловыми, такими же, как и

при b < b_cr в случае гиперболического аттрактора. Возможность существова-

ния аттракторов, содержащих как устойчивые траектории со скользящими

движениями, так и седловые траектории, усложняет решение задачи о раз-

рушении странного аттрактора и приводит к необходимости использования

качественно-численных методов. При численном исследовании системы (1),

проводимом далее, обращаем внимание на следующие возможные эффекты.

1. Стабилизация седловых траекторий, попадающих на плоскости скользя-

щих движений, т.е. эффект появления устойчивых орбит. При малом откло-

нении параметра b от критического значения µ = 1 - b_cr/b > 0, µ ≪ 1, устой-

чивые орбиты имеют большие периоды, а их области притяжения (basins)

малы настолько, что их сложно найти при численном моделировании. Та-

ким образом, при малых µ > 0 аттрактор перестает быть гиперболическим и

становится так называемым квазистранным аттрактором [23].

2. Бифуркация рождения устойчивого цикла из гомоклинической орбиты

седла с положительной седловой величиной. Этот эффект является неожи-

данным, поскольку в случае гладких или даже кусочно-гладких непрерывных

систем цикл должен рождаться неустойчивым.

3. Возможность C-бифуркации [11], при которой из устойчивого предель-

ного цикла рождаются два симметричных устойчивых цикла того же пе-

риода, а сам цикл, покидая поверхность скользящих движений, становит-

ся седловым. В гладких системах аналогом такой бифуркации является би-

фуркация раздвоения коразмерности два (pitchfork bifurcation), происходя-

щая в симметричных системах, при которой из предельного цикла, теряюще-

го устойчивость через мультипликатор m = +1, рождаются два устойчивых

цикла того же периода. Далее для простоты такую C-бифуркацию в систе-

ме (1) будем называть бифуркацией раздвоения.

5.1. Бифуркации аттракторов, содержащих скользящие движения

Последовательность бифуркаций в области параметров b > b_cr, для точек

которой аттрактор содержит скользящие движения, удобнее рассматривать

при уменьшении параметра b, начиная с больших значений b ≈ 300.

На рис. 3 изображена бифуркационная диаграмма системы (1). При каж-

дом фиксированном значении параметра b по оси ординат указаны точки

пересечения установившихся движений системы с секущей плоскостью D.

Горизонтальные линии вблизи линий x = ±1 являются крайним следом пре-

дельных циклов.

На рис. 3,a бифуркационная диаграмма построена для всего интерва-

ла значений параметра b ∈ [0, 300]. При b > 283 на диаграмме существуют

только следы двухобходного глобально устойчивого предельного цикла (см.

рис. 4,a).

Вертикальная штриховая линия в точке b = 283 соответствует первой

C-бифуркации раздвоения цикла. В этой точке от крайних следов отходят

-1

143

283

-1

b_сr = 3,95

4,5

b_{k + 1}

b_k

5,5

Рис. 3. Бифуркационная диаграмма системы (1) при α = 2, ω = 2, δ = 0,588,

λ = 0,294. По оси ординат изображены точки пересечения установившихся

движений системы (1) с секущей плоскостью D.

две кривые. Вместе с горизонтальными линиями они соответствуют следам

двух устойчивых предельных циклов, родившихся в результате бифуркации

раздвоения (см. рис. 4,б).

Вертикальной штриховой линией в точке b = 143 отмечена первая гомо-

клиническая бифуркация, при которой два устойчивых цикла сливаются, по-

падая в линию (x = 0, |y| < 1, z = b) на устойчивом многообразии седла W^s,

и образуют гомоклиническую бабочку (см. рис. 4,в). Этому соответствует пе-

ресечение кривых в точке (b = 143, x = 0).

При дальнейшем уменьшении b гомоклническая бабочка разрушается

и рождается глобально устойчивый предельный цикл удвоенного периода

(см. рис. 4,г). Все четыре кривые бифуркационной диаграммы на интер-

вале b ∈ (29, 143) являются следом этого цикла до следующей бифуркации

раздвоения, наступающей при b = 29.

Рисунки 3,б и 3,в являются увеличенными фрагментами рис. 3,a. На

рис. 3,б изображена вторая пара бифуркаций “раздвоение (b = 29) - бифур-

кация гомоклинической бабочки (b = 21)”.

При дальнейшем уменьшении параметра b пары бифуркаций “раздвоение-

гомоклиническая бабочка” повторяются, удваивая период (обходность) устой-

w_l

e_l

e_r

e_l

e_r

e_l

w_r

e_l

O_s

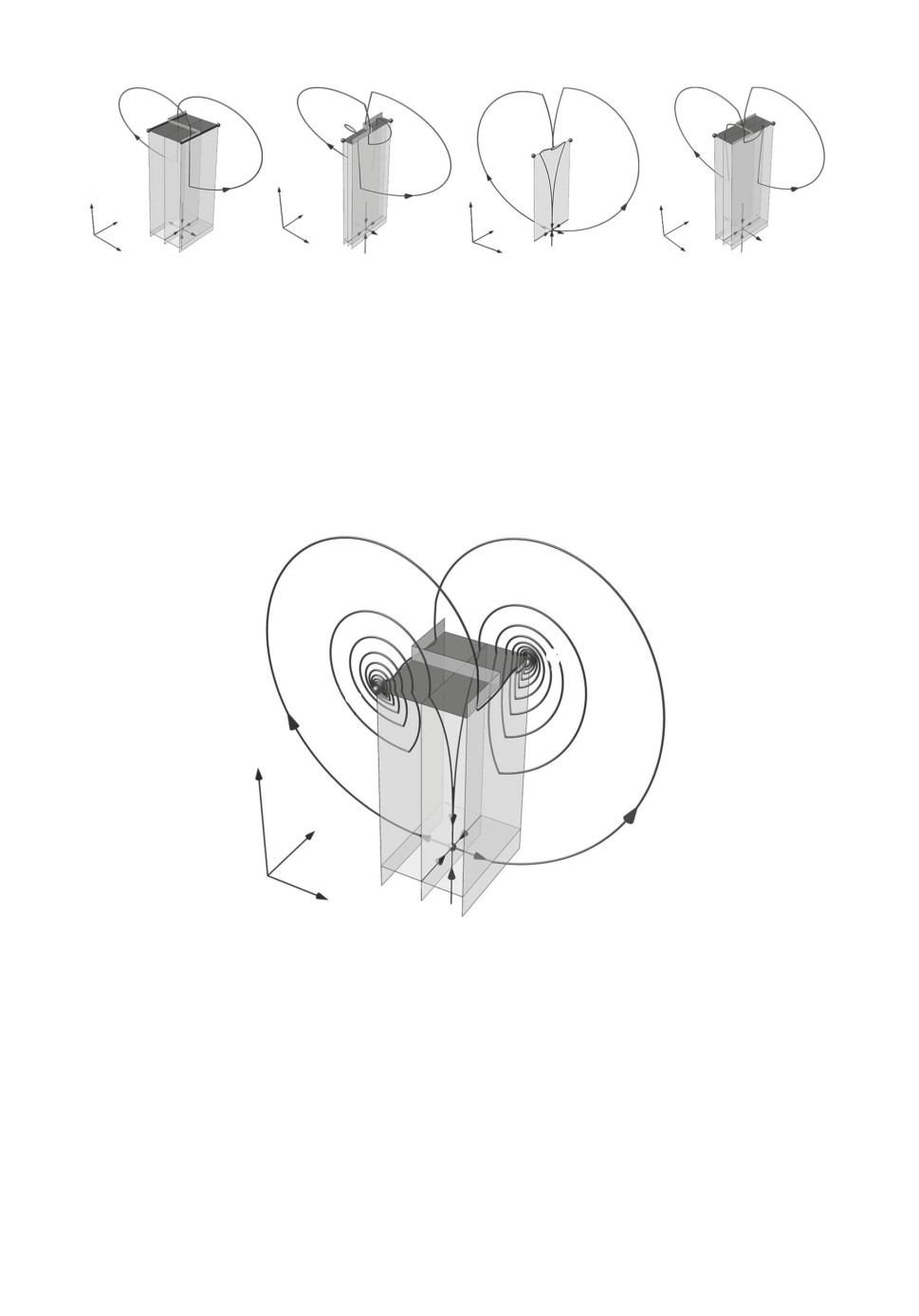
Рис. 4. Первая последовательность смены фазовых картин системы (1) при

уменьшении параметра b. a При b = 300 в системе существует двухобход-

ный глобально устойчивый предельный цикл, огибающий устойчивые одно-

мерные многообразия w_l,r фокусов e_l,r по одному разу. б При b = 270 со-

существуют два устойчивых предельных цикла того же периода. в При

b = 143,07 эти предельные циклы влипают в гомоклиническую бабочку и при

дальнейшем уменьшении параметра образуют глобально устойчивый предель-

ный цикл удвоенного периода. г Фазовый портрет этого четырехобходного

цикла при b = 40. Траектория цикла огибает каждое из многообразий w_l,r по

два раза. Остальные параметры: α = 2, ω = 2, δ = 0,588, λ = 0,294.

e_r

e_l

O_s

Рис. 5. Пример гомоклинической бабочки, образованной двумя симметричны-

ми многообходными гомоклиническими орбитами при b = 4,075. Остальные

параметры: α = 2, ω = 2, δ = 0,588, λ = 0,294.

чивых циклов (см. рис. 5). Эти пары накапливаются при b → b_cr, образуя

последовательность, которая служит скелетом бифуркационного множества.

Из рис. 3,в, видно, что каждый интервал (b_k+1, b_k), где b_k - предыдущая,

а b_k+1 - последующая бифуркации раздвоения, содержит хаотическое окно.

Бифуркационное множество в хаотических окнах усложняется с увеличени-

ем k. По-видимому, это связано с тем, что участки скользящих движений на

неблуждающих траекториях уменьшаются с ростом k, т.е. при приближении

к области существования странного аттрактора.

Область слева от вертикальной штриховой линии b_cr = 3,95 на рис. 3,в

соответствует сингулярно-гиперболическому аттрактору.

Следует отметить, что по известному сценарию перехода к хаосу для ло-

ренцеподобных гладких потоков с отрицательной седловой величиной [24, 25]

при увеличении бифуркационного параметра происходит удвоение периода

устойчивых предельных циклов через каскад бифуркаций гомоклинических

орбит.

Существенное отличие сценария, полученного в настоящей статье, состо-

ит в том, что у системы (1) седловая величина положительна. Однако цик-

лы, рождающиеся из гомоклинических орбит, в отличие от случая гладких

систем [26] устойчивы из-за наличия скользящих движений. Кроме того, в

рассматриваемом случае присутствуют окна хаотических движений наряду

с окнами устойчивых периодических орбит.

6. Заключение

В статье проведено качественно-численное исследование сложного би-

фуркационного множества, соответствующего разрушению сингулярно-

гиперболического аттрактора в кусочно-линейной системе, являющейся ана-

логом известной системы Лоренца. Это разрушение связано с тем, что в

структуре аттрактора появляются скользящие движения. Бифуркационное

множество представляет собой последовательность паттернов, сходящуюся к

критическому значению параметра, соответствующему началу разрушения

странного аттрактора. Основу бифуркационных паттернов составляют C-би-

фуркации, при которых происходят раздвоения многообходных предельных

циклов, и бифуркации многообходных гомоклинических орбит, приводящих

к рождению устойчивых предельных циклов с удвоенным периодом. Эти пат-

терны содержат хаотические окна, структура которых усложняется вдоль по-

следовательности. Нетривиальная задача строгого анализа, кратко описанно-

го в работе сложного бифуркационного перехода от устойчивого предельного

цикла к странному аттрактору, требует построения точечных отображений,

учитывающих скользящие движения, и выходит за рамки настоящей статьи.

СПИСОК ЛИТЕРАТУРЫ

1. Kuznetsov Y. Elements of Applied Bifurcation Theory. N.Y.: Springer, 2004.

2. Неймарк Ю.И. Метод точечных отображений в теории нелинейных колебаний.

М.: Наука, 1972.

3. Неймарк Ю.И. О скользящем режиме релейных систем автоматического регу-

лирования // АиТ. 1957. № 1. С. 27-33.

4. Champneys A.R., di Bernardo M. Piecewise Smooth Dynamical Systems // Schol-

arpedia. 2008. V. 3. No. 9. P. 4041.

5. di Bernardo M., Budd C.J., Champneys A.R., Kowalczyk P. Piecewise-smooth Dy-

namical Systems: Theory and Applications. London: Springer, 2008.

6. Andronov A.A., Vitt A.A., Khaikin S.E. Theory of Oscillations. M.: Fizmatgiz, 1959.

7. Zhusubaliyev Z.T., Mosekilde E. Bifurcations and Chaos in Piecewise-Smooth Dy-

namical Systems. Singapore: World Scientific, 2003.

Luo A.C.J., Chen L. Periodic Motions and Grazing in a Harmonically Forced, Piece-

wise, Linear Oscillator with Impacts // Chaos Soliton. Fract. 2005. V. 24. No. 2.

P. 567-578.

Gubar’ N.A. Investigation of a Piecewise Linear Dynamical System with Three Pa-

rameters // J. Appl. Math. Mech. 1961. V. 25. No. 6. P. 1011-1023.

10.

Matsumoto T., Chua L.O., Komoro M. Birth and Death of the Double Scroll //

Physica D. 1987. V. 24. No. 1-3. P. 97-124.

11.

di Bernardo M., Feigin M.I., Hogan S.J., Homer M.E. Local Analysis of C-Bifur-

cations in n-Dimensional Piecewise-Smooth Dynamical Systems // Chaos Soliton.

Fract. 1999. V. 10. No. 11. P. 1881-1908.

12.

Simpson D.J.W., Hogan S.J., Kuske R. Stochastic Regular Grazing Bifurcations //

SIAM J. Appl. Dyn. Syst. 2013. V. 12. No. 2. P. 533-559.

13.

Belykh I., Jeter R., Belykh V. Foot Force Models of Crowd Dynamics on a Wobbly

Bridge // Sci. Adv. 2017. V. 3. No. 11. P. e1701512.

14.

Macdonald J.H.G. Lateral Excitation of Bridges by Balancing Pedestrians // Proc.

Royal Society of London. A: Mathematical, Physical and Engineering Sciences. 2008.

V. 465. No. 1. P. 1055-1073.

15.

Belykh I.V., Jeter R., Belykh V.N. Bistable Gaits and Wobbling Induced by

Pedestrian-Bridge Interactions // Chaos: An Interdisciplinary J. Nonlinear Sci. 2016.

V. 26. No. 11. P. 116314.

16.

Belykh V.N., Barabash N.V., Belykh I.V. A Lorenz-type Attractor in a Piecewise-

Smooth System: Rigorous Results // Chaos: An Interdisciplinary J. Nonlinear Sci.

2019. V. 29. No. 10. P. 103108.

17.

Lorenz E. Deterministic Nonperiodic Flow // J. Atmos. Sci. 1963. V. 20. No. 2.

P. 130-141.

18.

Sparrow C. The Lorenz Equations; Bifurcations, Chaos and Strange Attractors. N.Y.:

Springer, 1982.

19.

Bykov V.V., Shilnikov A.L. On Boundaries of the Region of Existence of the Lorenz

Attractor // Selecta Math. Sovietica. 1992. V. 11. No. 4. P. 375-382.

20.

Doedel E.J., Krauskopf B., Osinga H.M. Global Bifurcations of the Lorenz Mani-

fold // Nonlinearity. 2006. V. 19. No. 12. P. 2947.

21.

Creaser J.L., Krauskopf B., Osinga H.M. Finding First Foliation Tangencies in the

Lorenz System // SIAM J. Appl. Dyn. Syst. 2017. V. 16. No. 4. P. 2127-2164.

22.

Filippov A.F. Differential Equations with Discontinuous Righthand sides. Dordrecht:

Kluwier Acad. Press, 1988.

23.

Белых В.Н. Странный аттрактор // Большая российская энциклопедия. 2016.

Т. 31. С. 285-286.

24.

Arneodo A., Coullet P., Tresser C. A Possible New Mechanism for the Onset of

Turbulence // Physics Lett. A. Elsevier Publ. 1981. V. 81. No. 4. P. 197-201.

25.

Lyubimov D.V., Zaks M.A. Two Mechanisms of the Transition to Chaos in Finite-

Dimensional Models of Convection // Physica D Nonlinear Phenomena. 1983. V. 8.

No. 1-2. P. 52-64.

26.

Шильников Л.П., Шильников А.Л., Тураев Д.В., Чуа Л. Методы качественной

теории в нелинейной динамике. Ч. 2. М.-Ижевск: НИЦ “Регулярная и хаотиче-

ская динамика”. Институт компьютерных исследований, 2009.

Статья представлена к публикации членом редколлегии Б.Т. Поляком.

Поступила в редакцию 23.07.2019

После доработки 18.10.2019

Принята к публикации 30.01.2020