Автоматика и телемеханика, № 8, 2020

(Нижегородский государственный архитектурно-строительный университет)

ОБОБЩЕННОЕ H₂-УПРАВЛЕНИЕ ЛИНЕЙНЫМ

НЕПРЕРЫВНО-ДИСКРЕТНЫМ ОБЪЕКТОМ

НА КОНЕЧНОМ ГОРИЗОНТЕ¹

На конечном горизонте рассматривается линейный непрерывно-дис-

кретный нестационарный объект, описываемый совокупностью диффе-

ренциальных и разностных уравнений. Вводится понятие обобщенной

H₂-нормы непрерывно-дискретного объекта как индуцированной нормы

линейного оператора, порожденного рассматриваемой системой. Получе-

на ее характеризация как в терминах разностных уравнений Ляпунова,

так и в терминах рекуррентных линейных матричных неравенств. Синте-

зированы дискретные нестационарные оптимальные законы управления,

в том числе и многокритериальные, при которых обобщенная H₂-норма

замкнутой системы принимает минимальное значение.

Ключевые слова: линейная нестационарная гибридная система, обобщен-

ная H₂-норма, оптимальное управление, многокритериальная задача.

DOI: 10.31857/S0005231020080048

1. Введение

Современные системы управления, как правило, реализуются в цифро-

вом виде, в то время как реальные объекты функционируют в непрерывном

времени. Подобное разделение приводит к тому, что регулятор использует

значения непрерывного сигнала, поступающего с объекта, лишь в дискрет-

ные моменты времени. По этой причине становится важной задача синтеза

дискретного регулятора, максимально полно учитывающего поведение объ-

екта в моменты времени между измерениями. Одним из показателей качества

функционирования системы управления является максимальное отклонение

целевого выхода системы от некоторого номинального значения по отноше-

нию к внешнему возмущению.

В [10] для непрерывных систем, а в [5] для дискретных, было введено по-

нятие обобщенной H₂-нормы, как максимальное отношение максимального

по времени значения евклидовой нормы выхода к L₂-норме неопределенного

внешнего возмущения системы. В [1, 9, 11] были получены условия существо-

вания оптимального регулятора по выходу на бесконечном горизонте как в

терминах уравнения Риккати, так и в терминах линейных матричных нера-

венств. В работах [2-4] для непрерывных и дискретных систем было введено

¹ Работа выполнена по теме государственного задания (№ 0729-2020-0055) при частич-

ной поддержке Российского фонда фундаментальных исследований (проекты №№ 18-41-

520002, 19-01-00289) и научно-образовательного математического центра “Математика тех-

нологий будущего”.

понятие максимального уклонения как естественное расширение обобщенной

H₂-нормы на системы с ненулевым начальным состоянием.

Для непрерывно-дискретных систем на бесконечном горизонте, описывае-

мых совокупностью дифференциальных и разностных уравнений, в [6-8] бы-

ли получены оценки обобщенной H₂-нормы и синтезированы законы управ-

ления, минимизирующие верхнюю оценку нормы, в терминах линейных мат-

ричных неравенств [7, 8] и в терминах дифференциальных уравнений Рикка-

ти [6].

В данной статье рассматривается непрерывно-дискретный объект с дис-

кретным целевым выходом на конечном горизонте при ненулевых начальных

условиях. Следуя работам [2-4, 10] вводится понятие обобщенной H₂-нормы

как индуцированной нормы линейного оператора, порожденного рассматри-

ваемой системой. Подобно тому как это делалось в работах [3, 10], получена

ее характеризация как в терминах разностных уравнений Ляпунова, так и

в терминах рекуррентных линейных матричных неравенств, что позволяет

синтезировать оптимальные законы управления.

2. Обобщенная H₂-норма непрерывно-дискретного объекта

Рассмотрим линейный непрерывно-дискретный нестационарный объект,

описываемый совокупностью дифференциальных и разностных уравнений

x = A_c(t)x + Δ_c(t)ξ_k + B_c(t)v, t_k ≤ t < t_k+1, k = 0,1,... ,N - 1,

ξ_k+1 = A_d,kξ_k + Δ_d,kx(t_k) + B_d,kw_k,

(1)

z_k = C_c,kx(t_k) + C_d,kξ_k,

где x ∈ Rnx и ξ_k ∈ Rnξ векторы состояния непрерывной и дискретной ча-

стей системы соответственно, v(t) ∈ Rnv

непрерывное внешнее возмуще-

ние кусочно-непрерывная справа вектор-функция, w_k ∈ Rnw дискретное

внешнее возмущение и z_k ∈ Rnz целевой выход. Будем считать, что

(

)

(

)

(

)

v∈L₂

[t₀, t_N ], Rnv

, w ={w_k}∈l₂

[0, N - 1], Rnw

, z ={z_k}∈l_∞

[0, N], Rnw

нормы в соответствующих пространствах определяются стандартным обра-

зом:

∑

(2)

∥v∥^2L

|v(t)|²²dt,

∥w∥² =_l

|w_k|²²,

∥z∥_∞ = max

|z_k|₂,

k=0,...,N

k=0

t₀

здесь через | · |₂ обозначена евклидова норма вектора. Кроме этого предпо-

ложим, что начальные условия x(t₀) = x₀ и ξ₀ в общем случае ненулевые и

неизвестны, а их влияние на поведение объекта интерпретируется как на-

чальное возмущение. Матричные функции A_c(t), B_c(t) и Δ_c(t) таковы, что

при выбранных начальных условиях и возмущениях решение системы на рас-

сматриваемом отрезке существует и единственно.

Система (1) порождает линейный оператор S вида

(

)

(

)

(

)

(3)

S :Rnx ×Rnξ ×L₂

[t₀, t_N ], Rnv

×l₂

[0, N - 1], Rnw

→l_∞

[0, N], Rnw

отображающий начальные состояния x₀, ξ₀ и внешние возмущения v, w в

целевой выход z. Определим норму элемента (x₀, ξ₀, v, w) формулой

√

(4)

= x^⊤0R^x1x₀ + ξ^⊤0R^-1ξξ₀ + ∥v∥^2L

+ ∥w∥² ,

l₂

где R_x = R^⊤x > 0 и R_ξ = R^⊤ξ > 0 весовые матрицы, отражающие относи-

тельную важность учета неопределенностей начальных условий и внешних

возмущений.

Определение. Обобщенной H₂-нормой непрерывно-дискретного объек-

та (1) назовем индуцированную норму оператора S, то есть

{

}

∥z∥_∞

(5)

∥S∥_∞/(R,2) = sup

: ∥(x₀, ξ₀, v, w)∥_(R,2) = 0

∥(x₀, ξ₀, v, w)∥_(R,2)

Перепишем соотношение (5) в развернутом виде:

max

|z_n|₂

n=0,...,N

(6)

∥S∥_∞/(R,2) = sup

(

)_1/2 ,

(x₀,ξ₀,v,w)

∫

∑

x^⊤0R^x1x₀ +ξ^⊤0R^-1ξξ₀ +

|v(t)|²²dt +

|w_k|²

t₀

k=0

где точная верхняя грань берется по всем таким наборам (x₀, ξ₀, v, w) для

которых знаменатель не обращается в ноль. Поскольку величина |z_n|₂ для

каждого n = 0, . . . , N зависит от внешних возмущений, определенных на от-

резке t₀ ≤ t ≤ t_n, то соотношение (6) можно переписать как

∥S∥_∞/(R,2) =

|z_n|₂

(7)

= max sup

(

)_1/2 ,

n=0,...,N (x₀,ξ₀,v,w)

∫

∑

x^⊤0R^x1x₀ + ξ^⊤0R^-1ξξ₀ +

|v(t)|²²dt +

|w_k|²

t₀

k=0

здесь точная верхняя грань берется, фактически, только по всем возмущени-

ям из отрезка t₀ ≤ t ≤ t_n. Таким образом, обобщенная H₂-норма объекта (1)

представляет собой максимум из максимальных относительных значений мо-

дуля целевого выхода. Заметим, что в частном случае, когда в системе (1) от-

сутствует непрерывная часть, то есть когда x(t) ≡ 0 и v(t) ≡ 0, то введенная

таким образом обобщенная H₂-норма совпадает с определенным в [3] макси-

мальным уклонением выхода дискретной системы.

Обозначим через Φ(t, s) фундаментальную матрицу Коши системы урав-

нений

Φ(t, s) = A_c(t)Φ(t, s),

Φ(s, s) = I,

и определим матрицы

∫

A_c,k = Φ(t_k+1,t_k),

Δ_c,k =

Φ(t_k+1, s)Δ_c(s)ds,

∫

Q_c,k =

Φ(t_k+1, s)B_c(s)B^⊤c(s)Φ^⊤(t_k+1, s)ds.

Справедливо утверждение.

Теорема 1. Обобщенная H₂-норма для непрерывно-дискретного объекта

(1) на заданном горизонте [t₀, t_N ] находится как

)

(

)

(8)

∥S∥_∞/(R,2) = max

λ^1/2max

C_kP_k

C^⊤k

C_k =

C_c,k, C_d,k

k=0,...,N

где через λ_max(·) обозначено максимальное собственное значение соответ-

ствующей матрицы, а P_k = P^⊤k ≥ 0 решение разностного уравнения Ля-

пунова

]

[A_c,k Δ_c,k

[Q_c,k

(9)

P_k+1

A_kP_k

A^⊤k +Qk,

A_k =

Q_k =

Δ_d,k A_d,k

B_d,kB^⊤

d,k

с начальными условиями P₀ = R = diag (R_x,R_ξ).

Доказательства этого и последующих утверждений содержатся в Прило-

жении. Отметим, что в частном случае, когда начальные состояния объек-

та (1) нулевые, для вычисления обобщенной H₂-нормы в рекуррентных урав-

нениях (9) необходимо взять в качестве начальных условий P₀ = 0. В другом

частном случае, когда внешние возмущения отсутствуют, а начальные со-

стояния неизвестны, обобщенная H₂-норма определяется соотношениями (8)

и (9), в которых следует положитьQk = 0.

Следующая теорема позволяет ответить на вопрос о наихудших начальных

условиях x^∗0, ξ^∗0 и внешних возмущениях v^∗, w^∗ для которых достигается (5).

Сразу отметим, что поскольку система (1) линейна, а обобщенная H₂-норма

представляет собой однородный функционал, то наихудшие начальные со-

стояния и внешние возмущения определяются неоднозначно, с точностью до

постоянного множителя.

Теорема 2. Если для непрерывно-дискретного объекта (1) на заданном

горизонте [t₀, t_N ] обобщенная H₂-норма равна γ^∗ и это значение достигает-

ся при k = k^∗, то наихудшие начальные состояния и внешние возмущения

определяются как

[

]

x^∗0

R^-1Ψ^⊤k∗_,0C⊤k∗e,

ξ^∗0

γ^∗

(10)

[

]

[

]

v^∗(t)

B^⊤c(t)Φ^⊤(t_k+1,t)x

C^⊤k∗

Ψ^⊤k∗,k+

w^∗k

γ^∗

B^⊤d,kξ

)

здесь через e = e_max

C_k∗Y_k

C^⊤k∗

обозначен нормированный собственный век-

тор матриц

C_k∗Y_k

C⊤k∗, соответствующий ее максимальному собствен-

ному числу, а через Ψ_i,j

переходная матрица дискретной системы

ζ_k

A_kζ_k, то есть

Ψ_0,0 = I, Ψ_i,j

A_i-1

A_i-2 ..

A_j, i ≥ j + 1.

Из теоремы 2 следует, что обобщенная H₂-норма на горизонте [t₀, t_N ] зави-

сит от значений, принимаемых возмущениями v^∗, w^∗ на отрезке t₀ ≤ t ≤ t_k∗ ,

и не зависит от значений вне этого отрезка.

Переформулируем теорему 1 в терминах линейных матричных неравенств,

символом ∗ обозначен соответствующий симметрический блок.

Теорема 3. Обобщенная H₂-норма для непрерывно-дискретного объ-

екта

(1) на заданном горизонте [t0, tN ] находится из решения задачи

∥S∥^2∞,2 = inf γ², при ограничениях, определяемых линейными матричными

неравенствами:

[

]

[

]

Y_k

∗

Y_l

∗

k = 0,...,N - 1,

(11)

≥ 0,

≥ 0, Y₀ ≥ R,

A_kY_k Y_k+1 -Qk

C_lY_l

γ²I

l = 0,...,N,

точная нижняя грань берется по переменной γ и симметрическим неотри-

цательно определенным матрицам Y₀, . . . , Y_N .

Доказательство теоремы 3 в настоящей работе опущено, поскольку дослов-

но повторяет основные шаги доказательства теоремы 2.2 из [3]. Также сде-

лаем замечания, аналогичные тем, что были сделаны к теореме 1. В случае,

если начальные состояния объекта (1) нулевые, для вычисления обобщенной

H₂-нормы в неравенствах (11) необходимо положить Y₀ ≥ 0, а в случае, ко-

гда внешние возмущения отсутствуют, а начальные состояния неизвестны, в

неравенствах (11) следует положитьQk = 0.

3. Синтез обобщенного H₂-управления

Рассмотрим линейный непрерывно-дискретный нестационарный объект с

управлением, описываемый совокупностью дифференциальных и разностных

уравнений

x = A_c(t)x + Δ_c(t)ξ_k + B_c(t)v + H_c(t)u(t),

ξ_k+1 = A_d,kξ_k + Δ_d,kx(t_k) + B_d,kw_k + H_d,ku(t_k),

(12)

z_k = C_c,kx(t_k) + C_d,kξ_k + D_ku(t_k),

t_k ≤ t < t_k+1, k = 0,... ,N - 1,

где u ∈ Rnu управление, а остальные переменные имеют тот же смысл,

что и ранее. Поставим задачу синтеза на конечном интервале времени [t₀, t_N ]

управления в виде нестационарной линейной обратной связи по состоянию

(13)

u(t) = u_k = Θ_c,kx(t_k) + Θ_d,kξ_k,

t_k ≤ t < t_k+1

k = 0,...,N - 1,

обеспечивающего минимальное значение обобщенной H₂-нормы замкнутой

системы.

Справедливо следующее утверждение.

Теорема 4. Параметры оптимального обобщенного H₂-регулятора ви-

да

(13) для)непрерывно-дискретного объекта

(12) находятся как

Θ_k =

(

Θ_c,k, Θ_d,k

= Z_kY ^-1k, где матрицы Y_k = Y ^⊤k ≥ 0 и Z_k являются решени-

ем задачи inf γ² при ограничениях, определяемых линейными матричными

неравенствами:

[

]

[

]

Y_k

⋆

Y_l

⋆

(14)

≥ 0,

≥ 0, Y₀

≥ R,

A_kY_k +HkZ_k Y_k+1 -Qk

C_lY_l + D_lZ_l γ²I

в которых k = 0, . . . , N - 1, l = 0, . . . , N и матрицыHk определены соотно-

шениями

[

]

∫

H_c,k

H_k =

H_c,k =

Φ(t_k+1, s)H_c(s)ds.

H_d,k

Предположим теперь, что объект управления имеет несколько целевых

выходов

x = A_c(t)x + Δ_c(t)ξ_k + B_c(t)v + H_c(t)u(t),

ξ_k+1 = A_d,kξ_k + Δ_d,kx(t_k) + B_d,kw_k + H_d,ku(t_k),

(15)

z^(j)k = C^(j)c,kx(t_k) + C^(j)d,kξ_k + D^(j)ku(t_k),

j = 1,...,m,

t_k ≤ t < t_k+1, k = 0,... ,N - 1,

и требуется синтезировать управление вида (13) при котором значения обоб-

щенной H₂-нормы по каждому целевому выходу замкнутой системы будут

минимальными. В общем случае указанные критерии являются противоречи-

выми, поэтому оптимальность следует понимать в смысле Парето. Обозначим

через Θ = {Θ1, . . . ,ΘN-1} матрицы обратной связи, а через γ_j (Θ) значение

обобщенной H₂-нормы j-го целевого выхода системы (15), замкнутой регуля-

тором Θ. Скажем, что регулятор Θ^∗ является оптимальным в смысле Парето,

если не существует другого регулятора Θ такого, что справедливы неравен-

ства γ_j(Θ) ≤ γ_j (Θ^∗), j = 1, . . . , m, в которых по крайней мере одно выполня-

ется строго. Необходимые условия оптимальности по Парето формулируются

следующим образом [1].

Теорема 5. Пусть (γ₁,...,γ_m) оптимальная по Парето точка в про-

странстве критериев и Θ_α минимум свертки Гермейера, скалярной функ-

ции вида

γ_j(Θ)

γ_j

(16)

G(Θ) = max

α_j =

j=1,...,m α_j

max

γ_j

j=1,...,m

Тогда точка Θ_α принадлежит множеству Парето и γ_j(Θ_α) = γ_j , j =

= 1, . . . , m.

В соответствии с теоремой 5, оптимальные по Парето решения в рассмат-

риваемой многокритериальной задаче следует искать среди оптимальных ре-

шений для свертки Гермейера. Применим теорему 3 к выражению (16), тогда:

)

(17)

G(Θ) = max

max

α^-1jλ^1/2max

C^(j)kY_k

C^(j)⊤k

j=1,...,m

k=0,...,N

здесь Y_k = Y^⊤k ≥ 0 - решения уравнения (9) для замкнутой системы. Представ-

ление (17) позволяет свести поиск оптимального решения для свертки Гер-

мейера к решению задачи выпуклого полуопределенного программирования.

Теорема 6. Параметры оптимальных по Парето обобщенных H₂-регу-

ляторов вида (13) для непрерывно-дискретного объекта (15) находятся как

Θ_α,k = Z_kY^-1k, где матрицы Y_k = Y^⊤k ≥ 0 и Z_k являются решением зада-

чи inf γ² при ограничениях, определяемых линейными матричными неравен-

ствами:

[

]

Y_k

⋆

≥ 0,

A_kY_k +HkZ_k Y_k+1 -Qk

(18)

[

]

Y_l

⋆

≥ 0,

Y₀ ≥ R,

C^(j)lY_l + D^(j)lZ_l α^2jγ²I

в которых k = 0, . . . , N - 1, l = 0, . . . , N и j = 1, . . . , m.

4. Пример

Рассмотрим механическую систему с одной степенью свободы, состоящую

из основания ¾1¿ и объекта ¾2¿, связанного с основанием через виброизоля-

тор (рис. 1). Математическая модель изоляции объекта от основания, совер-

шающего поступательное движение, описывается следующим дифференци-

альным уравнением:

∑

(19)

x = u + v + w_kδ(t - t_k),

x(0) = x₁₀,

x(0) = x₂₀,

k=0

где x координата защищаемого объекта, u управляющее силовое воздей-

ствие, порождаемое виброизолятором, v непрерывное внешнее воздействие,

с точностью до знака совпадающее с ускорением основания, и w_k дискрет-

ное внешнее возмущение, представляющее собой импульсы, приложенные к

основанию. Моменты времени t_k, k = 0, . . . , N - 1, в которые происходят уда-

ры по основанию, считаются заданными и образуют монотонно возрастаю-

щую последовательность.

Перепишем уравнение (19) в матрично-векторном виде (12). Для этого

определим переменную x₂ формулой

∑

x₂ = x -

w_kη(t - t_k),

k=0

x₁

v, w_k

Рис. 1. Схематическое изображение модели защиты от ударов и вибрации.

где через η(t) обозначена функция Хевисайда. Полагая теперь x = x₁ и вво-

дя дискретную переменную ξ_k, равную суммарному импульсу, сообщенному

основанию за время t_k+1, приходим к системе

x₁ = x₂ + ξ_k,

t_k ≤ t < t_k+1,

(20)

x₂ = u + v,

ξ_k+1 = ξ_k + w_k,

с начальными условиями x₁(0) = x₁₀, x₂(0) = x₂₀ и ξ₀ = 0.

Введем в рассмотрение два функционала, характеризующих качество виб-

роизоляции:



max

x

1(tk)

k=0,...,N

J₁(u) = sup

√

ζ^⊤0R ζ₀ + ∥v∥2L2 + ∥w∥²

l₂

(21)



max

u(t_k)

k=0,...,N

J₂(u) = sup

√

ζ^⊤0R ζ₀ + ∥v∥2L2 + ∥w∥²

l₂

здесь ζ₀ = column (x₁₀, x₂₀, ξ₀) и точная верхняя грань берется по всем началь-

ным условиям ζ₀ и внешним возмущениям v, w при которых знаменатель не

обращается в ноль. Нетрудно видеть, что функционал J₁ характеризует мак-

симальные смещения защищаемого тела относительно основания, а функцио-

нал J₂ определяет максимальное управляющее усилие. Введенные критерии

являются противоречивыми в том смысле, что чем меньше первый функцио-

нал, то есть чем меньше смещается тело, тем большее управляющее воздей-

ствие порождается изолятором, что соответствует большему значению вто-

рого функционала, и наоборот. Требуется синтезировать кусочно-постоянное

управление вида u_k = u(t_k) = θ_1,kx₁(t_k) + θ_2,kx₂(t_k) + θ_3,kξ_k при t_k ≤ t < t_k+1,

минимизирующее в смысле Парето оба критерия J₁ и J₂.

Для численного решения указанной задачи, положим R_x = 10I, R_ξ = 1,

N = 5 и рассмотрим два множества моментов времени, в которые происходят

удары по основанию: S₁ = {0; 2; 4; . . . ; 20} и S₂ = {0,5; 1,5; 2,0; 6,0; 10,0; 14,0;

18,0; 18,5; 19,5; 20,0}. Используя теорему 6 были синтезированы оптимальные

в смысле Парето регуляторыΘα,k и вычислены соответствующие им опти-

J₂

A₂

A₁

J₁

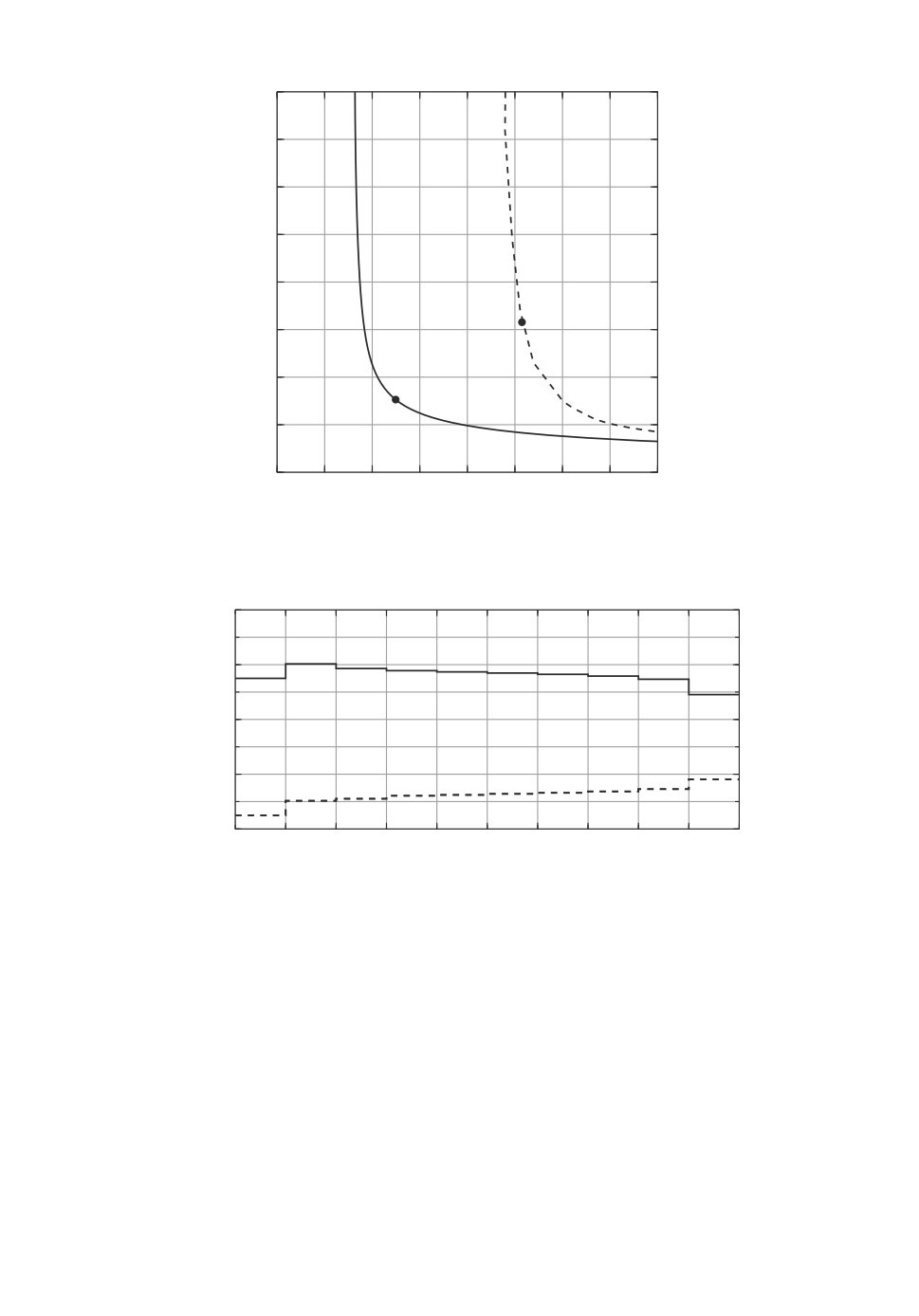
Рис. 2. Парето-фронт.

-0,2

q₁

q₂

-0,4

q₃

-0,6

-0,8

Рис. 3. Графики зависимостей от времени оптимальных по Парето коэффи-

циентов обратной связи.

мальные значения функционалов. На рис. 2 на плоскости критериев (J₁, J₂)

сплошной кривой изображен Парето-фронт для множества S₁, а пунктир-

ной для множества S₂. Точки A₁(2,493; 1,528) и A₂(5,148; 3,156) соответ-

ствуют параметру свертки α = 0,62. Для сравнения приведем значение перво-

го функционала в случае отсутствия управления: для множества S₁ получа-

ется J₁ = 65,167, а для S₂ J₁ = 67,021. Отметим следующую особенность,

замеченную при численных экспериментах: чем сильнее моменты времени t_k

¾отличаются¿ от равномерной сетки, тем сильнее Парето-фронт сдвигается

вправо. На рис. 3 приведены графики зависимости от времени оптимальных

по Парето коэффициентов обратной связиΘα,k, соответствующих точке A₁:

сплошная кривая соответствует коэффициенту θ_1,k, штриховая коэффици-

ентам θ_2,k и θ_3,k, которые, как оказалось при численных расчетах, совпадают.

5. Заключение

В работе для линейного непрерывно-дискретного нестационарного объек-

та с дискретным целевым выходом вводится понятие обобщенной H₂-нормы,

как индуцированной нормы линейного оператора, порожденного этим объек-

том. Показано, что эта характеристика есть максимальное отношения макси-

мального по времени значения евклидовой нормы выхода к смешанной норме

неизвестных начальных условий и внешних возмущений. Установлено, что

вычисление обобщенной H₂-нормы сводится к решению задачи выпуклого

полуопределенного программирования, это позволяет решить задачу синте-

за оптимальных законов управления, обеспечивающих минимально возмож-

ное значение обобщенной H₂-нормы замкнутой системы одного или несколь-

ких выходов. Эффективность предложенного подхода продемонстрирована

результатами численных экспериментов, проведенных для задачи активной

виброзащиты.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Рассмотрим оператор S^∗, двойствен-

ный к оператору (3)

(

)

(Π.1)

S^∗ : {z_k} →

x₀,ξ₀,v(t),{w_k}

здесь

z ∈l₁([0,N],Rⁿ),(x₀,ξ₀,v,w)∈ Rnx2×R2ξ×L2([t0,tN],Rnv)×l2([0,N - 1],Rnw).

Норма оператора S^∗ задается выражением

}



{(

)



S^∗

= sup

x₀,ξ₀,v,w

: ∥z∥l1 ≤ 1

(R,2)/1

(R,2)

и, согласно двойственности, справедливо следующее свойство:



(Π.2)

S

S^∗

∞/(E,2)

(E,2)/1

Таким образом, вместо вычисления нормы оператора S можно вычислять

норму двойственного оператора S^∗, что, как будет видно позднее, существен-

но проще.

Для определения выражения оператора S^∗, рассмотрим элемент

z ∈ l₁([0,N],Rⁿ), тогда

(Π.3)

〈z, Sy〉 = 〈S^∗z, y〉_(R,2),

где y = (x₀, ξ₀, v, w) и скалярное произведение, стоящее в левой части, опре-

деляется выражением:

∑

〈z, ζ〉 =

z^⊤kζ_k.

k=0

Скалярное произведение, стоящее в правой части, имеет вид

∫

∑

〈y₁, y₂〉_(R,2) = x^⊤0,1R^-1x x_0,2 + ξ^⊤0,1R^-1ξ ξ_0,2 +

w^⊤1,kw_2,k + v^⊤1(τ)v₂(τ)dτ,

k=0

t₀

и согласуется с определением нормы (4).

Перепишем систему (1) в полудискретной форме, последнее означает дис-

кретизацию только непрерывной переменной x, в то время как непрерывное

внешнее возмущение v остается неизменным, то есть

ζ_k+1

A_kζ_k + B_kω_k,

(Π.4)

z_k

C_kζ_k,

где ω_k = column (v(t), w_k ) и

(

)

B_k : L₂

[t_k, t_k+1), Rnv

×Rnw →Rnx+nξ



[

]

 t_k+1∫

(Π.5)

v(t)

→Φ(tk+1,τ)Bc(τ)v(τ)dτt

.

w_k

B_d,kw_k

Теперь, запишем замкнутое выражение, связывающее векторы

y = column(ζ₀,ω₀,...,ω_N-1) и

z = column(z₀,...,z_N). Для этого вос-

пользуемся соотношением (Π.4), тогда

(Π.6)

AB̃

здесь

)

(

)

C = diag

C₀

C₁,...

C_N

B = diag

I,B₀,...,B_N-1





···





A₀

···









A₁

A₀

A₁

···



.









A_N-1 ..

A₀

A_N-1 ..

A₁

A_N-1 ..

A₂

··· I

Таким образом, оператор S может быть представлен в виде S

B. Ис-

пользуя выражение (Π.3), легко увидеть, что двойственный оператор S^∗ мо-

жет быть записан как

(Π.7)

S^∗

B^∗

A^⊤C⊤,

(

)

гд

B^∗ = diag

R^-1,B^∗0,... ,B^∗N-1

[

]

[

]

(

)

B^⊤c(t)Φ^⊤(t_k+1,t)x

B^∗k : Rnx+nξ → L₂

[t_k, t_k+1), Rnv

→

× Rnw2 :

B^⊤d,kξ

Далее, с помощью представления (Π.7), нетрудно проверить справедли-

вость следующего выражения

∥S^∗z∥^2(R,2) = ∥S^∗z∥^2(R,2) = z^⊤

C^⊤z,

где

(

)

A^⊤,

Q = diag

R^-1,Q0,... ,QN-1

Поскольку матриц

C является блочно-диагональной, рассмотрим вспомога-

(

)

тельную блочно-диагональную матриц

Y = diag

Y₀,... ,Y_N

, имеющую те

же самые блоки на главной диагонали, что и матрица W . Блоки Y_k удовле-

творяют линейному рекуррентному уравнению

Y₀ = R^-1, Y_k+1

A_kY_k

A^⊤k +Qk,

совпадающему с уравнением (9) и, кроме того, справедливы следующие пре-

образования

}



{



²

S^∗

= sup

S^∗z

: ∥z∥l1 ≤ 1

(R,2)/1

(R,2)

{

}

(Π.8)

= sup

C^⊤z : ∥z∥l1 ≤ 1

{

}

)

= sup

C^⊤z : ∥z∥l1 ≤ 1

= max

λ_max

C_kY_k

C^⊤k

k=0,...,N

Последнее выражение совпадает с (8), что и завершает доказательство тео-

ремы

Доказательство теоремы 2. Для доказательства выражения (10),

предположим, что значение обобщенной H₂-нормы равно γ^∗ и достигается на

шаге k = k^∗. В этом случае существует элемент

z∗ = column (0, . . . , 0, z_k∗ , 0, . . . , 0),

∥z^∗∥l1 = 1

такой, что



γ^∗ =

S∗z^∗

(R,2)

)

Равенство ∥z^∗∥l1 = 1 означает, что z_k∗ = e_max

C_k∗Y_k

C⊤k∗

, здесь y^∗ = S^∗z^∗ =

= column (ζ^∗, ω^∗0, . . . , ω^∗N-1) это вектор, составленный из наихудших началь-

ных условий и внешних возмущений, кроме этого, ∥y^∗∥_(R,2) = γ^∗. Заметим,

что для вычисления y^∗ следует выбрать k^∗ столбец из матричного представ-

ления оператора S^∗:













R^-1

A^⊤0 ..

A⊤k∗

C⊤k∗z

C⊤k∗z_k∗

ζ^∗

k^∗

R^-1Ψ⊤k∗,

















ω^∗0



B₀

A^⊤1 ..

A^⊤k



C⊤k∗z_k∗





C^⊤k∗zk∗



B₀Ψ⊤k∗,































y∗ =















ω∗k∗









B_k

A⊤k∗

C⊤k∗z_k∗



C⊤k∗z_k∗







B_k∗Ψ⊤k∗,k























ω^∗

N-1

Наконец, чтобы получить выражение (10), нужно умножить вектор y^∗ на

1/γ^∗, поскольку в определении обобщенной H₂-нормы (5) вектор наихуд-

ших начальных условий и внешних возмущений удовлетворяет условию

∥y^∗∥_(R,2) = 1. Теорема 2 доказана.

Доказательство теоремы 4. Запишем уравнение системы (12), замк-

нутой обратной связью вида (13), тогда:

(

)

ζ_k+1 =

A_k +Hk Θ_k

ζ_k + B_kω_k,

(Π.9)

)

z_k =

C_k + D_k Θ_k

ζ_k.

Согласно теореме 3, обобщенная H₂-норма системы (Π.9) может быть вы-

числена как решение задачи (11), в которой матрицы

A_k

C_k следует за-

менить н

A_k +Hk Θ_k

C_k + D_k Θ_k соответственно. Вводя новые переменные

Z_k =ΘkY_k, приходим к неравенствам (14). Теорема 4 доказана.

Доказательство теоремы 6. Для доказательства теоремы заметим,

что равенство (17) может быть записано как

)

G(Θ) = max

max

α^-1jλ^1/2max

C^(j)kY_k

C^(j)⊤k

j=1,...,m

k=0,...,N

(

)

= max

max

λ^1/2max

α^-2j

C^(j)kY_kC(j)⊤k

j=1,...,m

k=0,...,N

следовательно, в неравенствах (14) достаточно заменить матриц

C_k иDk на

α^-1j

C^(j)k и α^-1j D_k, после чего получим неравенства (18). Теорема 6 доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Баландин Д.В., Коган М.М. Оптимальное по Парето обобщенное H₂-управление

и задачи виброзащиты // АиT. 2017. № 8. С. 76-90.

Balandin D.V., Kogan M.M. Pareto Optimal Generalized H₂-Control and Vibropro-

tection Problems // Autom. Remote Control. 2017. V. 78. No. 8. P. 1417-1429.

2. Баландин Д.В., Бирюков Р.С., Коган М.М. Оптимальное управление макси-

мальными уклонениями выходов линейной нестационарной системы на конеч-

ном интервале времени // АиТ. 2019. № 10. C. 37-61.

Balandin D.V., Biryukov R.S., Kogan M.M. Optimal Control of Maximum Output

Deviations of a Linear Time-Varying System on a Finite Horizon // Autom. Remote

Control. 2019. V. 80. No. 10. P. 1783-1802.

3. Баландин Д.В., Бирюков Р.С., Коган М.М. Оптимальное управление макси-

мальными уклонениями выходов линейной дискретной нестационарной систе-

мы // АиТ. 2019. № 12. С. 3-23.

Balandin D.V., Biryukov R.S., Kogan M.M. Minimax Control of Deviations for the

Outputs of a Linear Discrete Time-Varying System // Autom. Remote Control. 2019.

V. 80. No. 12. P. 2091-2107.

4. Balandin D.V., Biryukov R.S., Kogan M.M. Finite-Horizon Multi-Objective Gener-

alized H₂ Control with Transients // Automatica. 2019. V. 106. No. 8. P. 27-34.

5. Chellabonia V., Haddad W.M., Bernstein D.S., Wilson D.A. Induced convolution

operator norms for discrete-time linear systems // Proc. 38th IEEE Conference on

Decision and Control. 1999. P. 487-492.

6. Khargonekar P.P., Sivashankar N. H₂ optimal control for sampled-data systems //

Systems Control Lett. 1991. V. 17. No. 6. P. 425-436.

7. Kim J.H., Hagiwara T. Extensive theoretical/numerical comparative studies on H₂

and generalized H₂ norms in sampled-data systems // Int. J. Control. 2017. V. 90.

No. 11. P. 2538-2553.

8. Kim J.H., Hagiwara T. Upper/lower bounds of generalized H₂ norms in sampled-

data systems with convergence rate analysis and discretization viewpoint // Systems

Control Letters. 2017. V. 107. P. 28-35.

9. Rotea M.A. The generalized H₂ control problem // Automatica. 1993. V. 29. No. 2.

P. 373-385.

10. Wilson D.A. Convolution and Hankel Operator Norms for Linear Systems // IEEE

Trans. Autom. Control. 1989. V. 34. P. 94-97.

11. Wilson D.A., Nekoui M.A., Halikias G.D. An LQR weight selection approach to

the discrete generalized H₂ control problem // Int. J. Control. 1998. V. 71. No. 1.

P. 93-101.

Статья представлена к публикации членом редколлегии Б.Т. Поляком.

Поступила в редакцию 23.07.2019

После доработки 05.10.2019

Принята к публикации 30.01.2020