Автоматика и телемеханика, № 8, 2020

(Нижегородский государственный университет им. Н.И. Лобачевского)

ДИАГОНАЛЬНОЕ ОБОБЩЕНИЕ МЕТОДА DIRECT

НА ЗАДАЧИ С ОГРАНИЧЕНИЯМИ¹

Метод DIRECT решает задачи липшицевой глобальной оптимизации в

гиперинтервале при неограниченном диапазоне значений констант Лип-

шица. Предложено расширение принципов DIRECT на задачи с много-

экстремальными ограничениями при использовании в гиперинтервалах

сразу двух измерений функций на концах выбираемых главных диаго-

налей. Представлены вычислительные иллюстрации, включая решение

задачи с разрывами. Выполнен анализ сходимости.

Ключевые слова: глобальная оптимизация, липшицевы функции, метод

DIRECT, многоэкстремальные ограничения, функции с разрывами, двух-

точечная диагональная схема, вычислительные эксперименты.

DOI: 10.31857/S0005231020080073

1. Введение

Статья продолжает исследования, начатые в [1], и посвящена разработке

специального DIRECT-подобного метода условной глобальной оптимизации

для задач

(1)

Q^∗

= min Q(x), x ∈ X,

{

}

(2)

X =

x ∈ D = [a,b] ⊂ R^N : g(x) ≤ 0

где векторы a и b конечны, целевая функция Q и функция ограничения g

могут сложно зависеть от x и считаются многоэкстремальными. Конкрет-

ные требования на них будут указаны далее, но считаем, что минимум в

(1)-(2) существует в обычном или расширенном смысле согласно [1], где

под расширенной понимается трактовка (1)-(2) при X = ∅ как задачи ми-

нимизации невязки g(x) на D. Если ограничений неравенств в (2) несколь-

ко, то в (1)-(2) они заменяются одним ограничением с функцией вида

g(x) = max{g₁(x), . . . , g_m(x)}. Предполагается алгоритмическая форма зада-

ния функций и существенность времени их вычисления. Это делает оправ-

данным разработку для (1)-(2) методов, основанных на планировании новых

точек испытаний, исходя из принятых требований оптимальности к их раз-

мещению.

Потребность в таких методах возникает в различных областях, включая

разработку систем управления. Действительно, формальное применение со-

временных методов синтеза оптимальных регуляторов по заданным (как пра-

вило, линейным) целевым выходам (например, [2-6]) могут еще не полностью

удовлетворять конструктора-разработчика, так как его еще часто интересует

уменьшение или ограничение содержательных нелинейных показателей ка-

чества (таких как время окончательного вхождения откликов нелинейной

системы в желаемую окрестность входного задающего сигнала, величины

¹ Работа выполнена при поддержке научно-образовательного математического центра

“Математика технологий будущего”.

перерегулирований и т.п.). Оптимальная настройка таких критериев может

быть выполнена численно в форме решения задач вида (1)-(2) по оставшим-

ся свободным параметрам первичного алгоритма синтеза регулятора. Заме-

тим, что нелинейные критерии в таких задачах часто имеют разрывы либо

за счет эффекта бифуркаций, либо из-за самого вида критерия (например,

разрывы характерны для указанного выше критерия “времени вхождения”).

В [7] использование прямой численной оптимизации продемонстрировано на

модельном примере, причем методов локальной оптимизации оказалось недо-

статочно.

Применение к таким задачам различных методов липшицевой глобальной

оптимизации, использующих оценки констант Липшица по результатам изме-

рений функций (не претендуя на общность, укажем лишь несколько методов

из [8-12]), вызовет неограниченный рост этих оценок при появлении разрывов

в окрестностях глобальных минимумов. Это приведет к вырождению методов

в почти равномерный перебор.

Задачами указанного выше типа еще в период 1978-90 гг. занималась груп-

па в отделе Ю.И. Неймарка в НИИ Прикладной математики и кибернетики

при ГГУ (ныне ННГУ) им. Н.И. Лобачевского. Это были крупные хоздого-

ворные работы по заказу ряда предприятий. Для решения задач вида (1)-(2),

связанных с оптимальной настройкой следящих систем по 4-5 основным па-

раметрам, применялись методы условной глобальной оптимизации с адап-

тивными стохастическими моделями, разработанные в [13] для некоторых

подклассов кусочно-непрерывных функций. Методы основывались на общей

концепции, первоначально предложенной Ю.И. Неймарком в [14, гл. VIII, § 7],

первый вариант реализации которой представлен в [15]. Методы обладали

сходимостью за счет всюду плотного в пределе размещения точек испыта-

ний. Однако в [13] для этих методов были получены аналитические оценки

относительной плотности размещения испытаний, доказывающие существен-

ную неравномерность такого размещения. Недостатком этих методов явля-

лась невозможность их точной вычислительной реализации, а наличие лишь

приближенной.

Методы с несколько похожим поведением могут быть получены на осно-

ве совершенно другого подхода, лежащего в основе оригинального метода

DIRECT (от Dividing Rectangles), предложенного в [16] 1993 г. Этот метод,

хотя и относится к липшицевой оптимизации, в действительности применим

и к задачам с наличием разрывов. Исходная версия метода построена в [16]

для задач на гиперинтервале D без функциональных ограничений

(3)

f^∗ = f(x^∗) = minf(x), x ∈ D = [a,b] ⊂ R^N.

Целевая функция предполагается липшицевой с константой L^f = L. Однако

значение L считается неизвестным, не оценивается и может быть любым чис-

лом из диапазона [0, ∞). DIRECT принципиально отличается от других ме-

тодов липшицевой оптимизации именно отказом от возможного оценивания

и использования конкретных значений константы L. Он относится к компо-

нентным методам, использует адаптивное разбиение начального множества D

на компоненты-гиперинтервалы D_i = [aⁱ, bⁱ], в центральных точках cⁱ кото-

рых проводятся измерения функции f.

Кратко поясним принцип работы. При известном значении константы

Липшица L^f = L легко вычислить нижнюю оценку значений f для каждого

гиперинтервала с центром в cⁱ

f^-i(L) = f^-(L,D_i) = f_i - Ld_i/2, f_i = f(cⁱ),

где d_i = diam(D_i) = ∥bⁱ - aⁱ∥. В этом случае наиболее приоритетным для но-

вых измерений следует считать гиперинтервал D_t с наименьшим значением

нижней оценки функции. Поскольку в методе DIRECT значение L^f = L неиз-

вестно, он использует иное правило отбора делимых гиперинтервалов D_t. Оно

основано на двух принципах. Первый недоминируемость

{

}

(4)

∃L ∈ [0,∞) : f^-(L,D_t) = min f^-(L, Di) : i = 1, . . . , Mk

где M_k количество гиперинтервалов после k итераций, т.е. недоминируе-

мым является гиперинтервал, являющийся “лучшим” хотя бы при одном из

значений L. Второй достаточная улучшаемость достигнутого минималь-

ного значения целевой функции. Это значит, что хотя бы при некоторых

значениях L из (4) и заданных η_k > 0 должно выполняться условие

{

}

(5)

f^-(L,D_t) ≤ f^k∗ - η_k, f^k∗ = min f(xⁱ) : i = 1,...,nk

где xⁱ

точки выполненных измерений, n_k их число (в оригинальном

DIRECT всегда n_k = M_k).

Гиперинтервалы, удовлетворяющие условиям (4) и (5), называют потенци-

ально оптимальными. Именно такие гиперинтервалы DIRECT выделяет для

деления на очередной итерации. В [16] найдено простое геометрическое пред-

ставление, позволяющее легко находить множество гиперинтервалов D_t, удо-

влетворяющих (4)-(5). Если сопоставить гиперинтервалам D_i точки на плос-

кости (d/2, f) с координатами (d_i/2, f_i), где d_i = ∥bⁱ - aⁱ∥, f_i = f(cⁱ), и доба-

вить к ним точку (0, f^k∗-η_k), то множеству точек (d_t/2, f_t) потенциально опти-

мальных гиперинтервалов D_t соответствуют вершины правой-нижней части

границы выпуклой линейной оболочки множества всех точек (d_i/2, f_i), вклю-

чая дополнительную. Для вычислительно эффективного выделения (d_t/2, f_t)

и, следовательно, нахождения делимых гиперинтервалов D_t используют пра-

вило Грэхема [17].

Для дробления выбранных гиперинтервалов метод применяет схему их де-

ления на три равные части по большему ребру (см. описание в [18]). С исполь-

зованием центральной схемы измерений при делении одного D_t достаточно

провести только два новых измерения f(x) в центрах крайних из трех новых

гиперинтервалов, поскольку в центре среднего результат уже известен.

Заметим, что сама схема деления на три в рекурсивной реализации ис-

пользовалась в глобальной оптимизации для задач (1)-(2) и (3) значительно

раньше, еще в программной разработке Compromiss Solver ВЦ АН СССР

80-х гг. XX в. (предтече метода деления на три является метод деления на

два, который был опубликован в [19]).

К настоящему времени известны различные обобщения DIRECT. Обшир-

ная библиография приведена в [8]. Укажем на некоторые. Оригинальный

DIRECT относительно медленно уточняет найденные оценки решения, в [20]

предложена достаточно удачная локально-ориентированная модификация.

В [21] построен, а также описан в [8] более эффективный вариант метода [16]

для задач (3), работающий по диагональной схеме деления на три (в каждом

гиперинтервале проводится не одно, а два измерения на концах специаль-

но ориентируемых главных диагоналей, образующих вместе эффективную

диагональную кривую, построение которой было ранее предложено в [22]).

В [21] кроме двухточечной диагональной схемы измерений применен также

специальный механизм балансировки локальной и глобальной стратегий по-

иска за счет искусственных усечений множеств потенциально оптимальных

гиперинтервалов, что улучшило сходимость к глобальному решению. В [23]

получено нетривиальное обобщение метода DIRECT на задачи с вычислимой

липшицевой производной, константа Липшица которой неизвестна и может

изменяться на промежутке [0, ∞); метод построен для задач (3) с размер-

ностью N = 1. В [24] метод из [23] распространен на многомерные задачи с

использованием специальной нецентральной одноточечной схемы разбиения

множества D в задаче (3). Также в 2001 г. получен концептуально близкий к

DIRECT метод для задач (1)-(2) с несколькими ограничениями, второе из-

дание 2009 г. этой публикации приведено в [18]. Представленный в [18] метод

в отличие от [1] использует специально сконструированный на случай нали-

чия ограничений подход к выделению делимых гиперинтервалов. Принцип

их выделения существенно отличается от оригинального DIRECT.

Заметный интерес к DIRECT-подобным методам привел к проведению

в [25] представительного экспериментального сравнительного исследования

нескольких методов [16, 20, 21] этого семейства в сопоставлении с группой эв-

ристических методов, включая эволюционно-генетические алгоритмы. Тести-

рование проведено на задачах без функциональных ограничений размерности

N = 5, представляющих простой и сложный классы из 100 тестовых функ-

ций GKLS генератора (его описание приведено, например, в [8]). Результаты,

представленные в [25], показали, что при достаточно большом числе изме-

рений n_k решение с наибольшей надежностью обеспечивается именно диаго-

нальной реализацией DIRECT, представленной в [21], и особенно на классе

сложных тестовых задач. Это актуализирует разработку диагональной вер-

сии одноточечного варианта метода [1] в задачах с функциональными огра-

ничениями.

В [1] предложено два подхода к обобщению метода DIRECT на задачи с

ограничениями. Оба существенно отличаются от представленного в [18]. Пер-

вый подход сводит исходную задачу с ограничениями к последовательности

задач без ограничений с перестраиваемой целевой функцией. Второй основан

на непосредственном распространении принципов построения DIRECT на за-

дачи с ограничениями. В обоих подходах в [1] применена схема деления на

три с измерением функций в центральных точках (далее измерения функций

задачи называем испытанием). Данная статья обобщает второй из подходов,

предложенных в [1], на двухточечную диагональную схему измерений [22],

использованную в [21]. При этом испытания задачи в гиперинтервалах D_t

проводятся в двух точках a^t, b^t, расположенных на концах одной из главных

диагоналей. Ориентация этой диагонали определяется специальным образом

согласно безызбыточной стратегии разбиения, предложенной в [22] (описа-

на также в [8, 21]). Прежде чем перейти к формальной постановке задачи,

поясним основы подхода и терминологию, использованную в [1] и далее при-

меняемую.

Поскольку в задачах с ограничением (1)-(2) добавляется фактор допу-

стимости или недопустимости точек измерений, возможна ситуация пустоты

допустимого множества X. При X = ∅ целью является определение элемен-

тов x^∗ из множества X^∗ глобальных минимумов задачи. В случае пустоты

(X = ∅), следуя [1], неявно трактуем решение в расширенном смысле, как

определение глобального минимума x^∗ невязки в ограничениях (предполага-

ется что этот минимум существует):

g^∗ = g(x^∗) = ming(x), x ∈ D = [a,b] ⊂ R^N.

Множество таких минимумов по-прежнему обозначаем через X^∗.

Далее удобно трактовать эту задачу как задачу c добавленным функцио-

нальным ограничением g(x) ≤ 0, заданным фиктивной функцией g(x) ≡ -1.

Заметим, что в (1)-(2) при X = ∅ и наличии допустимых и недопустимых

подмножеств точек различия значений Q(x) на подмножествах с нарушением

ограничений не оказывают влияния на X^∗ множество глобальных мини-

мумов задачи. Однако наличие слишком малых значений Q в недопустимых

областях может существенно повлиять на процесс численного решения. По-

этому целевую функцию в (1) при X = ∅ целесообразно заменить функцией

вида

f (x) = max{Q(x); Q^∗ - ξ}, ξ ≥ 0.

Поскольку значение в условном глобальном минимуме Q^∗ неизвестно, за-

меним его текущей оценкой Q^∗k. В результате метод с учетом ограничений

далее будет применен не к решению задачи в форме (1)-(2), а к специально

модифицированной, возникающей из указанных выше замен

(6)

min f_k(x), x ∈ X_k,

{

}

(7)

X_k =

x ∈ D = [a,b] ⊂ R^N : g_k(x) ≤ 0

где k

номер итерации. Ее точный вид приведен в разделе 2. Чтобы не

усложнять обозначения, далее будем опускать индексы k у f_k и g_k, записывая

их как f и g. Предположения о функциях далее примем по отношению к

задаче (6)-(7). Они будут отличаться от требований в [1].

В [1] предположения о функциях следующие: f и g липшицевы в ев-

клидовой норме с неизвестными константами Липшица: L^f = L ∈ [0, ∞) и

L^g ∈ [0,αL) (где α > 0 введенный параметр класса задач). При неограни-

ченном L значение L^g также может быть сколько угодно большим. Принцип

потенциальной оптимальности при отборе делимых на итерации гиперинтер-

валов D_t в [1] заменен на модифицированную потенциальную оптимальность,

которая состоит в одновременном выполнении для D_t трех основных прин-

ципов.

Первый назовем принципом наименьшего нарушения, а именно: из множе-

ства D^k всех гиперинтервалов текущего разбиения выделим на итерации k со-

кращенное подмножествоDk гиперинтервалов, для которых выполнены тре-

бования:

∄D^′, D^′′ ∈Dk, что если с учетом измерений f^′ = f(c^′), f^′′ = f(c^′′) выполнено:

(8)

D^′ = D^′′, diam(D^′) = diam(D^′′), f^′ = f^′′, g^′ = g(c^′)>0, g^′′ = g(c^′′

)>0,

то g^′ = g^′′ и, кроме того, если гиперинтервал текущего разбиения D^′′ ∈Dk,

а D^′ ∈ Dk, то из выполнения для них условий (8) должно следовать неравен-

ство g^′ < g^′′.

Второй принцип модифицированной недоминируемости. К модифициро-

ванно недоминируемым отнесем все D_t ∈Dk, удовлетворяющие следующим

условиям

∃L ∈ [0,∞):

{

}

(9)

f^-(L,D_t) = min f^-(L,D_i) : D_i ∈Dk,∃L^g ∈ [0,αL] : g^-(L^g,D_i) ≤ 0 ,

(10)

∃L^g ∈ [0,αL] : g^-(L^g,D_t

) ≤ 0.

Очевидно, что эти условия прямое обобщение принципа недоминируемости

метода DIRECT, описанного, например, в [8].

Третий принцип достаточная улучшаемость. Пусть f^k∗ текущая оценка

минимального значения в (6)-(7) по результатам испытаний, тогда для D_t

изDk при некотором значении L, когда выполнены условия (9)-(10), должно

также для заданного η_k соблюдаться неравенство

(11)

f^-(L,D_t) ≤ f^k∗ - η_k, η_k

> 0.

Здесь нижние оценки функций имеют вид:

(12)

f^-i(L) = f^-(L,D_i) = f_i -Ld_i/2; g^-i(L^g) = g^-(L^g,D_i) = g_i -L^g d_i

/2.

В [1] предложен конструктивный алгоритм выделения гиперинтервалов D_t

с указанными свойствами (9)-(11). В примененной для этого технике суще-

ственно использована удобная структура нижней оценки значения ограни-

чения при центральном измерении из (12). Важным оказалось то, что знак

первого элемента g_i в g^-(L^g, D_i) однозначно определяет допустимость или

недопустимость измерения, выполненного в центре D_i.

В двухточечном диагональном обобщении

[21] стандартного метода

DIRECT (в задачах без ограничений) использован другой вид нижних оце-

нок функции f. В двухточечной схеме целевая функция f в D_i измерена

в двух точках aⁱ, bⁱ на концах выбранной главной диагонали D_i. Нижнюю

оценку функции f строим на этой диагонали. При обычных для DIRECT

предположениях о липшицевости f(x) с константой L^f = L ∈ [0, ∞) получим

минимальное значение оценки на диагонали

f^ai + f^bi

d_i

f^-i(L) = f^-(L,D_i) =

-L

Такой вид оценки не подходит для функции g(x) при наличии ограниче-

ний, если строить двухточечное обобщение метода из [1]. Действительно, в

оценке такого вида для g(x) первым элементом будет (g^ai + g^bi)/2. Очевид-

но, знак этой суммы однозначно не выделяет ситуации наличия допустимой

точки среди двух испытаний в aⁱ, bⁱ.

Поэтому в данной статье применен другой вид нижних оценок, вытекаю-

щий из измененных предположений относительно свойств f и g в задаче

(6)-(7). Поясним это на примере g(x). Пусть получены измерения g^ai, g^bi на

концах aⁱ, bⁱ главной диагонали длины d_i гиперинтервала D_i. Вычислим зна-

чение L^gi = |g^ai - g^bi|/d_i. Очевидно, что в D_i должно выполняться неравенство

L^g ≥ L^gi. Примем значение L^g для D_i в виде L^g = L^gi + ΔL^g, где ΔL^g будем

считать одинаковым для всех гиперинтервалов. Тогда нижняя оценка значе-

ний функции g на диагонали от aⁱ до bⁱ примет вид

g^ai + g^bi

d_i

g^-i(ΔL^g) = g^-(ΔL^g,D_i) =

- (L^gi + ΔL^g)di

= G_i - ΔL^g

;

(13)

ΔL^g ≥ 0,

где G_i = min{g^ai; g^bi}. При этом знак G_i однозначно определит наличие допу-

стимого испытания на концах используемой диагонали. Это позволит непо-

средственно обобщить результаты [1] на случай двухточечных диагональных

измерений.

2. Предварительные замечания и постановка задачи

2.1. Преобразование исходной задачи

Пусть выполнено k итераций некоторого метода и проведено n_k испыта-

ний (измерений функций задачи) в точках xⁱ ∈ D с сохранением в памяти

значений Q_i, g_i (i = 1, . . . , n_k). Определим рекордное значение Q^∗k в (1)-(2):

{

min{Q_i : g_i ≤ 0, i = 1, . . . , n_k}, если ∃ g_i ≤ 0,

(14)

Q^∗k =

+∞,

если ∀i = 1, . . . , n_k : g_i > 0.

Если еще не найдено ни одной допустимой точки, значение Q^∗k = +∞, и

с учетом расширенной трактовки решения выполним переход от решения

(1)-(2) к задаче поиска минимума невязки g(x) на D до тех пор, пока не

встретится первая допустимая точка. Для единообразного рассмотрения ал-

горитмов решения перейдем от исходной формы задачи (1)-(2) к ее изме-

ненному представлению в форме (6)-(7), где функции f_k(x) и g_k(x) имеют

вид:

{ max{Q(x);Q^∗

- ξ_k}, Q^∗k = +∞,

(15)

f_k(x) =

g(x),

Q^∗k = +∞;

{ g(x), Q^∗k = +∞,

(16)

g_k(x) =

-1, Q^∗k = +∞.

При проведении испытаний этой задачи в точках xⁱ вычисляются и со-

храняются значения Qⁱ и gⁱ исходной задачи, а величины вспомогательных

функций f_k(xⁱ) и g_k(xⁱ) восстанавливаются согласно (15), (16) по сохранив-

шимся в памяти результатам измерений исходных функций. Численный ме-

тод решает задачу (6)-(7), (15), (16), которая на итерациях сама изменяет

свою структуру в зависимости от рекордного значения (14). Такая форма

представления задачи удобна для построения метода. Текущее минимальное

значение вспомогательной целевой функции (15) обозначим

{

}

(17)

f^k∗ = min

f_k(xⁱ) : g_k(xⁱ) ≤ 0, i = 1,... ,n_k

Значение f^k∗ всегда конечно. Далее, как уже было указано выше, обычно

будем опускать у вспомогательных функций f_k и g_k нижний индекс k.

2.2. Использование безызбыточной диагональной стратегии разбиения

Поясним правила размещения точек испытаний при использовании безыз-

быточной диагональной стратегии разбиения [22] (см. также [8]). Перед нача-

лом поиска проводим два начальных испытания в вершинах a и b исходного

гиперинтервала D, соответствующих минимальным и максимальным значе-

ниям координат. В последующем каждый из делимых гиперинтервалов раз-

деляется на три равные части по первому из его больших ребер. У очередно-

го делимого гиперинтервала D_t перед делением всегда имеется пара вершин

a^t и b^t (назовем их активными), в которых испытания уже проведены. Эти

вершины лежат на одной из главных диагоналей (далее будем называть ее

активной). Эти диагонали могут иметь разные ориентации. Пусть r длина

делимого ребра, а e нормирова(ный в)ктор, направленный из вершины at

вдоль этого ребра так, чтобы e^⊤

b^t - a^t

> 0. Согласно [22] при делении D_t

выбираются две точки u и v, в которых могут проводиться новые испытания:

u=a^t +

r e;

v=b^t -

r e.

Три новых гиперинтервала порождаются из D_t по следующим парам ак-

тивных вершин (см. рис. 1): a^t и v, v и u, u и b^t.

В [22] показано, что при описанном способе выбора точек новых измерений

некоторые из них могут являться активными и для других смежных гипе-

ринтервалов (см. правую часть рис. 1). Поэтому в некоторых из новых точек

u или v испытания задачи могут быть уже проведены ранее и повторно их

D_t

b^t

a^t

D₃

D₂

-e

D₄

b^t

a^t

Рис. 1. Слева выбор новых точек измерений и ориентаций активных диа-

гоналей при делении на три выбранного гиперинтервала по безызбыточной

диагональной стратегии в R³; справа пример возможного разбиения на-

чального D в R²: при делении D₂ новая точка u совпала с точкой прежнего

испытания с номером 5.

выполнять не следует можно извлечь готовые результаты из памяти, эко-

номя на количестве испытаний. Быстрое выполнение операции поиска для

последующего извлечения обеспечено созданием специально организованной

структуры хранения результатов испытаний.

2.3. Новая модель поведения функций задачи и диагональное обобщение

DIRECT-подобного принципа отбора делимых гиперинтервалов

с учетом ограничений

{

}Mk

Пусть на итерации k имеется текущее разбиение D^k =

D^k

началь-

i i=1

ного множества D на гиперинтервалы D_i = D^ki, полученное по безызбыточ-

ной диагональной стратегии разбиения [8, 22]. В каждом D_i, в вершинах

aⁱ и bⁱ, оканчивающих активную диагональ, проведены испытания задачи.

Пусть f^ai = f(aⁱ), f^bi = f(bⁱ), g^ai = g(aⁱ), g^bi = g(bⁱ)

результаты испытаний.

Введем обозначения:



(18)

L_i = L^fi =

f^ai - f^bi /di, Lg

g^ai - g^bi /di.

Примем, что функции f и g, определяемые соотношениями (15) и (16),

липшицевы в D с нормой ∥·∥ и константами L^f = L и L^g, причем в гипер-

интервале D_i значения этих констант с использованием (18) представимы в

виде:

L = L_i + ΔL, L^g = L^gi + ΔL^g.

Приращения ΔL и ΔL^g неотрицательны и одинаковы для всех гиперинтер-

валов разбиения. Таким образом, гиперинтервалам разбиения назначаются

разные по величине минимально возможные значения констант и одинаковые

приращения к ним. Введем следующие предположения. Считаем, что прира-

щение ΔL неизвестно и его величина может быть сколь угодно большой, т.е.

ΔL ∈ [0,∞); значение ΔL^g также неизвестно, но ΔL^g ∈ [0,α ΔL], где α > 0

постоянный параметр метода. Заметим, что указанные выше предположения

применительно к функции f впервые были использованы и экспериментально

исследованы в [26] при построении методов для задач без ограничений в R¹.

Выполнив преобразования, аналогичные (13), получим следующий вид ми-

нимальных значений нижних оценок функций f и g на активных диагоналях

гиперинтервалов D_i:

f^-i(ΔL) = f^-(ΔL,D_i) = F_i - ΔLd_i/2,

(19)

g^-i(ΔL^g) = g^-(ΔL^g,D_i) = G_i - ΔL^g d_i/2,

{

}

{

}

(20)

;f^b

Fi = min

Gi = min gⁱ; gⁱ

Значения F_i и G_i из (20) назовем базовыми характеристиками функций

f и g на гиперинтервале D_i. Следует обратить внимание на то, что нижние

оценки (19), (20) двухточечной диагональной схемы отличаются от анало-

гичных оценок центральной схемы заменой прежних значений f_i, L, g_i, L^g

новыми F_i, ΔL, G_i, ΔL^g. Это позволяет доказать ряд фактов и разработать

алгоритмы, близкие к полученным в [1].

Введем необходимые определения.

Определение 1. Подмножеством гиперинтервалов с наименьшим на-

рушением (ограничений) назовем подмножествоDk множества всех гипер-

интервалов текущего разбиения D^k, в которое из каждой группы гиперин-

тервалов {D} ⊆ D^k одинакового диаметра, с одинаковыми значениями базо-

вых характеристик F и положительными значениями G базовых характе-

ристик ограничений включены только гиперинтервалы с наименьшим зна-

чением G в этой группе.

Проводимое сокращение D^k до подмножестваDk является значимым при

решении преобразованной задачи (6)-(7), когда уже обнаружены допустимые

точки, т.е. Q^∗k = +∞. Именно в этом случае в силу (15)-(16) может возни-

кать значительное количество гиперинтервалов D_i с одинаковыми значения-

ми F_i = Q^∗k - ξ_k и G_i > 0.

Определение 2. Гиперинтервал D_t ∈ D^k назовем модифицировано

недоминируемым на итерации k, если D_t ∈Dk и ∃ ΔL ∈ [0,∞) такое, что

для нижних оценок на активных диагоналях из (19) функций f_k(x), g_k(x) из

(15)-(16) выполнено:

f^-(ΔL,D_t) =

{

}

(21)

= min f^-(ΔL,D_i) : D_i ∈ Dk, ∃ ΔL^g ∈ [0,α ΔL] : g^-(ΔL^g,D_i) ≤ 0 ,

(22)

∃ ΔL^g ∈ [0,α ΔL] : g^-(ΔL^g,D_t

) ≤ 0.

Определение 3. Гиперинтервал D_t назовем модифицированно потен-

циально оптимальным (на итерации k), если он модифицированно недоми-

нируемый на этой итерации и хотя бы для некоторых ΔL, при которых

для него соблюдены требования (21)-(22), выполняется также условие до-

статочной улучшаемости с заданным η_k > 0 и f^k∗ из (17):

(23)

f^-(ΔL,D_t) ≤ f^k∗ - η_k.

Следуя [1], сформулируем простое утверждение, позволяющее записать

требования (21)-(22) в эквивалентной, но более простой форме.

Утверждение 1 (об эквивалентности). Условия (21)-(22) модифици-

рованной недоминируемости D_t ∈Dk в диапазоне ΔL ∈ [ΔL^′,ΔL^′′) эквива-

лентны следующим условиям: ∃ ΔL ∈ [ΔL^′, ΔL^′′) такое, что

{

}

f^-(ΔL,D_t) = min f^-(ΔL,D_i) : D_i ∈Dk,g^-(αΔL,D_i) ≤ 0 ;

(24)

g^-(αΔL,D_t) ≤ 0.

Доказательство утверждения приведено в Приложении.

Заметим, что по отношению к определению 2 утверждение применяем,

положив [ΔL^′, ΔL^′′) = [0, ∞).

Основная задача ставится следующим образом. Для получения диагональ-

ного варианта DIRECT-подобного метода условной глобальной оптимизации

требуется определить подходы к построению и структуру алгоритмов выде-

ления на итерации k подмножества (обозначим егоDk) всех модифициро-

ванно потенциально оптимальных гиперинтервалов с учетом упрощающего

утверждения 1. Также необходимо провести анализ сходимости построенно-

го метода и выполнить его экспериментальную апробацию. В данной статье

описаны указанные выше подходы к обработке информации в алгоритмах

формированияDk и их структура, выполнен анализ сходимости, а также

представлены вычислительные иллюстрации работы метода на двумерных

задачах. Детальное описание и аналитическое обоснование алгоритмов выде-

ленияDk, а также вычислительный эксперимент на задачах разных размер-

ностей не являются целью данной статьи, а составляют предмет отдельной

публикации.

3. О построении алгоритмов отбора делимых гиперинтервалов

при двухточечной диагональной схеме измерений

МножествоDk гиперинтервалов, делимых на текущей k-й итерации, яв-

ляется множеством всех модифицированно потенциально оптимальных гипе-

ринтервалов. Поясним правила их выделения и реализующие их алгоритмы,

используя иллюстративные примеры.

Заметим, что в обычном методе DIRECT для задач без ограничений от-

бор делимых гиперинтервалов происходит сравнением на плоскости (d/2, f)

их изображающих точек, где первая координата половина диаметра ги-

перинтервала, а вторая значение целевой функции в его центре. При на-

личии ограничений и использовании одноточечной центральной схемы ги-

перинтервалы D_i в [1] представлены трехмерными изображающими точками

(d_i/2, f_i, g_i), включающими результат вычисления функций f и g в центре D_i.

В рассматриваемой двухточечной схеме значения f_i, g_i в центральных точ-

ках заменим базовыми характеристиками этих функций F_i, G_i из (20). После

такой замены выделение искомого подмножестваDk может быть выполнено

по двухэтапной процедуре, похожей на описанную в [1].

Поясним характер возникающей при этом обработки накопленной по-

исковой информации. На первом этапе на множестве трехмерных точек

(d_i/2, F_i, G_i) выделим подмножества, соответствующие гиперинтервалам D^di

DL_d DL_d DL_d DL_d DL_d = +¥

fk*- x_k

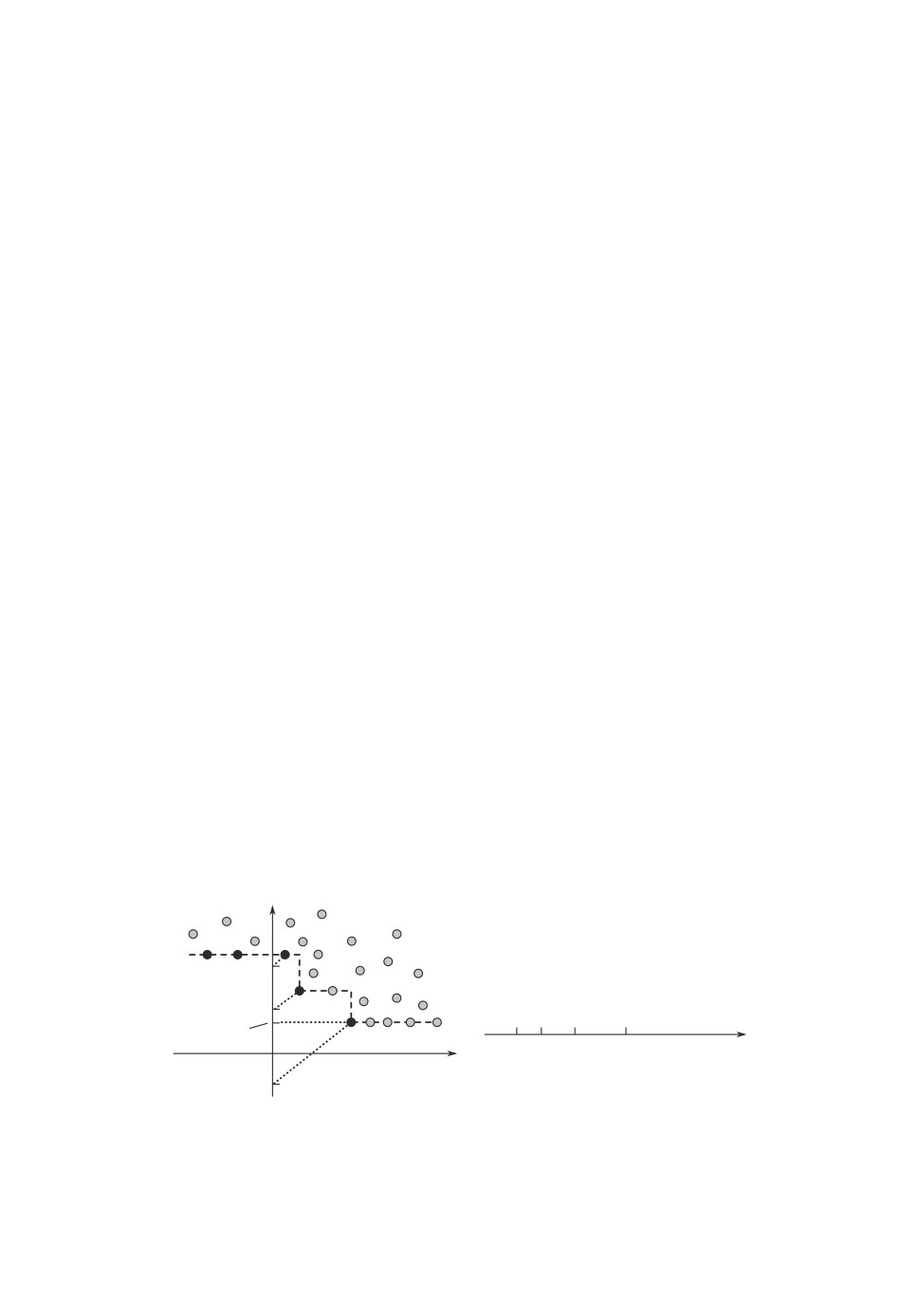
Рис. 2. Слева набор точек (G_j , F_j ), соответствующих d-слою гипер-

интервалов с diam(D_j ) = d, черные точки отвечают группам {Dds} ото-

бранных гиперинтервалов; справа порождаемые для {Dds} границы

диапазонов [ΔL^ds, ΔL^ds+1) приращений ΔL: значение s = 0 соответствует

точкам 1 и 2, s = 1, 2, 3 соответствуют точкам 3, 4, 5.

одинакового диаметра с d_i = d (назовем такие подмножества d-слоями).

В каждом d-слое выполним предварительный отбор гиперинтервалов за счет

сравнения соответствующих им точек на плоскости (G, F ) при выбранном d.

Сравнения выполним так, чтобы выделенные в результате отбора группы

гиперинтервалов (обозначим их {Dds}, s = 0, . . . , S(d)) удовлетворяли опре-

делениям 1 и 2, но только в пределах множества гиперинтервалов своего

d-слоя. Проводя рассуждения аналогично [1], но с учетом особенностей диа-

гональных испытаний, можно показать, что в достаточно общей ситуации,

представленной на рис. 2 слева, отобранными на плоскости (G, F ) будут точ-

ки, выделенные черным. Аналогично [1] для групп гиперинтервалов {Dds},

соответствующих выделенным точкам, наборы значений ΔL, при которых

дляDds в пределах d-слоя выполнены условия (21), (22), образуют диапа-

зоны вида [ΔL^ds, ΔL^ds+1), где при G_s ≤ 0 значение ΔL^ds = 0, а при G_s > 0

ΔL^ds = 2G_s/(αd). В последнем диапазоне ΔL^dS(d)+1 = +∞. Показанные на

рис. 2 наклонные точечные линии, имеют коэффициент наклона 1/α, где α

введенный ранее параметр класса функций ограничений. Прересечения этих

линий с осью F порождают указанные значения ΔL^ds, при которых впервые

выполняются условия неположительности g^-(α ΔL^ds,Dds) ≤ 0, а ординаты то-

чек пересечения совпадают с f^-(ΔL^ds,Dds). Легко видеть, что в каждом d-слое

будет существовать хотя бы одна точка, соответствующая группе отбираемых

гиперинтервалов.

В начале второго этапа происходит объединение множеств значений ΔL^ds

по всем d и по всем s с формированием общего упорядоченного ряда значений:

(25)

0 ≤ ΔL₁ < ΔL₂ < ... < ΔLmk < ΔLmk+1

= +∞.

Далее, при продолжении второго этапа обработки для каждого промежут-

ка [ΔL_j, ΔL_j+1) приращений ΔL выделяются для различных d-слоев из групп

{Dds}^S(d)s=0 отобранных гиперинтервалов те, для которых не пусто пересечение:

[ΔL_j , ΔL_j+1) ∩ [ΔL^ds, ΔL^ds+1) = ∅.

Обозначим множество таких гиперинтервалов черезOjk, а его элементы че-

резDjk. Каждое из множествOjk отдельно представим набором изображаю-

щих точек с координатами (d/2, F ).

Заметим, что аналогично геометрической интерпретации правил метода

DIRECT, минимальное значение нижней оценки функции f_k(x) на актив-

ной диагонали одного из гиперинтерваловDjk, соответствующего некоторой

изображающей точке (d/2, F ), можно получить как ординату пересечения с

осью F прямой, проведенной с коэффициентом наклона ΔL через эту изобра-

жающую точку. В оригинальном методе DIRECT сравнение гиперинтервалов

происходит по значениям аналогичных нижних оценок для целевой функ-

ции при условии, что диапазон изменения константы Липшица есть [0, +∞).

В рассматриваемом случае диапазон изменения ΔL ограничен промежутком

[ΔL_j, ΔL_j+1), что требует новых алгоритмов обработки. Их точное описание

и обоснование выходят за рамки данной статьи.

p²

p¹

p³

p⁸

p⁶

p⁵

f ^k- h_k

p⁷

p⁹

d/2

D^j

Рис. 3. Пример отбора в множество

гиперинтервалов, делимых на k-й ите-

O^j

рации, из множества

, сформированного для значений ΔL из [ΔL_j, ΔL_j+1);

O^j

если гиперинтервалам из

соответствует множество точек P^jk = {p¹, . . . , p⁹},

то отобранным для деления гиперинтервалам будут отвечать точки p⁹; p⁷; p⁴,

выделенные черным.

На полученном множестве точек эти алгоритмы должны проводить допол-

нительный отбор так, чтобы для гиперинтервалов, соответствующих остав-

шимся точкам, оказались выполнены определения 2 и 3, причем условия из

определения 2 должны выполняться для отобранных гиперинтервалов толь-

ко в пределах множестваOjk и только для значений ΔL из [ΔL_j, ΔL_j+1).

Пример отбора показан на рис. 3. Он иллюстрирует результат выделения

подмножестваDjk изOjk на конкретном примере. Вертикальные точечные

линии на рис. 3 соответствуют диаметрам возможных существующих d-слоев

после 9 итераций на примере исходного множества в виде некоторого четы-

рехмерного гиперинтервала. Границам промежутка [ΔL_j , ΔL_j+1) на рисунке

соответствуют коэффициенты наклона сплошных линий, проведенных через

точки. Наклонные штриховые линии отражают процесс отбора. Черным вы-

делены те изображающие точки, которым соответствуют гиперинтервалы,

отобранные в этом примере в множествоDjk для их последующего включе-

ния в полный наборDk гиперинтервалов, делимых на итерации k.

Повторяя процедуру выделенияDjk для j = 1, . . . , m_k и включая (с устра-

нением повторов) все отобранные таким образом гиперинтервалы в искомое

множествоDk, получим полный наборDk гиперинтервалов, делимых на ша-

ге. Нетрудно видеть, что полученноеDk совпадает со множеством всех мо-

дифицированно потенциально оптимальных на итерации k гиперинтервалов.

Лемма 1 (о наибольшем гиперинтервале). Построенное множество ги-

перинтерваловDk всегда содержит хотя бы один гиперинтервал наиболь-

шего диаметра из гиперинтервалов текущего разбиения D^k.

Лемма используется при доказательстве теоремы о сходимости в разделе 4.

Доказательства леммы и последующей теоремы приведены в Приложении.

4. Структурное описание диагонального метода с учетом ограничений,

анализ сходимости

4.1. Описание построенного метода

На каждой итерации метод должен выделить очередной наборDk дели-

мых гиперинтервалов D_t, реализуя принципы, предложенные в разделе 2.

Краткое описание структуры возникающей при этом обработки накопленной

поисковой информации приведено в разделе 3. Алгоритмы этой обработки

являются центральной частью построенного метода и в отличие от [1] учиты-

вают специфику двухточечных диагональных измерений в гиперинтервалах.

Из материала разделов 2 и 3 следует, что выполнение алгоритмов обработ-

ки зависит от значения ряда величин, а именно: η_k из условия (23); α

параметр, введенный в начале подраздела 2.3 при описании требований к

диапазону значений ΔL^g приращений константы Липшица функции огра-

ничения; а также ξ_k из (15). Значения η_k и ξ_k выберем пропорциональными

некоторой величине Δf_k, которая в [1] была названа базовым значением це-

левой функции решаемой задачи, а именно примем: η_k = Δf_kε; ξ_k = Δf_kδ.

Способ вычисления Δf_k предложен и подробно описан в [1, раздел 3] (в под-

разделе Новое базовое значение). Единственное отличие, применительно к

рассматриваемому диагональному варианту метода, состоит в том, что здесь

для вычисления Δf_k вместо набора измерений целевой функции в центрах

гиперинтервалов текущего разбиения используется набор имеющихся изме-

рений целевой функции f_k(x) из (15) на концах активных диагоналей этих

гиперинтервалов. При вычислении Δf_k каждое такое измерение учитывается

только один раз, хотя почти каждая точка измерения входит в несколько ги-

перинтервалов. Значение Δf_k содержательно можно трактовать как грубую

оценку разности f^µk - f^k∗, где f^k∗ определяется в (17), а f^µk значение, при

котором относительная мера множества точек {x ∈ D : f_k(x) ≤ f^µk} в D равна

заданной величине µ из интервала (0, 1). f^µk формируется в [1] приближенно

по результатам проведенных испытаний. Принятый в [1] алгоритм вычисле-

ния Δf_k предполагает задание еще одного параметра n, который определяет

пороговое число измерений. А именно если после очередной k-й итерации

число измерений n_k впервые превысит заданное n (обозначим этот номер k

черезk), то после этой итерации происходит обновление Δf_̃, и далее при

всех k >k используется Δf_k = Δf_̃

Таким образом, имеем набор параметров: µ, n, а также ε, α, δ. Параметры ε

и δ всегда неотрицательны и влияют на работу метода следующим образом.

Увеличение ε, как правило, увеличивает равномерность размещения точек

измерений, а его уменьшение увеличивает тенденцию к делению гиперинтер-

валов малого диаметра. Уменьшение δ, как правило, приводит к уменьшению

доли измерений в недопустимых областях, а его увеличение повышает долю

недопустимых измерений. Метод управляет этими тенденциями за счет ис-

пользования трех наборов значений ε, α, δ. Набор ε₀, α₀, δ₀ метод применяет

на первой стадии поиска, пока число измерений меньше заданного n, а далее

использует два других (ε₁, α₁, δ₁, либо ε₂, α₂, δ₂), попеременно применяя их

в зависимости от номера итерации k. Если k кратно дополнительному пара-

метру K, применяется первый набор, а если не кратно, второй. Значения

параметров двух последних наборов, как правило, выбираются так, чтобы

первый соответствовал стратегии уточнения найденных оценок решения, а

второй поиску в менее исследованных областях. Начальный набор должен

способствовать достаточной равномерности размещения начальных точек.

Одноточечный метод, построенный в [1], имеет маркировку ExDIR (от

DIRECT Extention), его двухточечное диагональное обобщение обозначим

как ExDIR-diag.

Поскольку DIRECT-подобные методы не оценивают константы Липшица,

останов по точности невозможен, поэтому указывают ресурс по количеству

испытаний.

Алгоритм 1 (принципиальное описание метода ExDIR-diag).

1. Задаем параметры µ, n, K, ε_s, α_s, δ_s, (s = 0, 1, 2) и n_max максимальное

количество испытаний.

2. Проводим два начальных испытания в вершинах a и b исходного гипе-

ринтервала D из (1), соответствующих минимальным и максимальным зна-

чениям координат, полагаем номер итерации k = 1, количество испытаний

n_k = 2 и множество гиперинтервалов D^k = {D}, количество гиперинтервалов

M_k = 1.

3. С учетом проведенных на k-й итерации испытаний обновляем Q^∗k из (14),

при необходимости корректируем текущий вид функций (15), (16) решае-

мой задачи (6)-(7). Если задача изменилась, пересчитываем значения функ-

ций f_k(x) и g_k(x) на концах aⁱ, bⁱ активных диагоналей всех гиперинтерва-

лов D_i текущего множества D^k гиперинтервалов. При этом функции исход-

ной задачи повторно не вычисляются, используются их ранее сохраненные в

памяти значения. При необходимости корректируем f^k∗ из (17) и x^∗k точ-

ку испытания, соответствующую значению f^k∗. Если одинаковое рекордное

значение f^k∗ наблюдается в точках нескольких испытаний, то в качестве x^∗k

принимаем последнее. Вычисляем базовое значение Δf_k согласно [1] с учетом

замечаний и описания, приведенного выше.

4. Если n_k ≥ n_max, то останавливаем поиск и выдаем значения Q^∗k, f^k∗,

x^∗k в качестве оценки решения. При n_k < n_max, в зависимости от превыше-

ния числом испытаний n_k порогового значения n и от кратности k значению

K выбираем, как описано выше, один из трех наборов значений ε_s, α_s, δ_s,

(s = 0, 1, 2) в качестве параметров ε, α, δ.

5. Выполняя двухэтапную обработку информации, структурно описанную

в разделе 3, из множества D^k всех гиперинтервалов разбиения выделяем под-

множествоDk всех модифицированно потенциально оптимальных.

6. Полагаем n_k+1 = n_k. Для каждого гиперинтервалаDkt изDk согласно

описанию из подраздела 2.2 определяем потенциальные точки новых испы-

таний u^t и v^t для его деления на три по большему ребру. Для каждой из

этих двух точек выполняем поиск в базе проведенных испытаний. В точках

u^t и v^t, не найденных в базе, проводим новые испытания, увеличивая при

этом счетчик n_k+1. Каждый гиперинтервалDkt разделяем на три по больше-

му ребру,Dkt исключаем из множества D^k, добавляем в него три новых гипе-

ринтервала. Полагаем M_k+1 = M_k + 2. Принимаем измененное множество D^k

в качестве D^k+1. Полагаем k = k + 1 и переходим к выполнению п. 3.

4.2. Анализ сходимости

Исследование сходимости метода ExDIR-diag проведем при более слабых

предположениях о свойствах функций задачи (1)-(2), чем было принято при

построении метода. Как и в [1], решение исходной задачи (1)-(2) понимаем

в расширенном смысле. А именно если в (2) допустимое множество X = ∅,

то предполагаем существование глобального минимума в (1)-(2), целью ре-

шения считаем определение элементов x^∗ из множества X^∗ глобальных ми-

нимумов задачи: X^∗ ⊆ X, x^∗ ∈ X^∗, Q(x^∗) = Q^∗. В случае пустоты допустимо-

го множества (X = ∅) неявно трактуем решение для (1)-(2) в расширенном

смысле как обеспечение минимума невязки в ограничениях, предполагая, что

минимум существует:

g^∗ = ming(x), x ∈ D = [a,b] ⊂ R^N.

При этом целью решения задачи (1)-(2) при X = ∅ является определение

элементов x^∗ из множества X^∗, которое в данном случае понимается как

множество глобальных минимумов g(x) на D: X^∗ ⊆ D, x^∗ ∈ X^∗, g(x^∗) = g^∗.

При анализе сходимости не будем предполагать липшицевость функций,

но наложим следующие дополнительные требования.

А. Значения функций Q и g ограничены на D.

В. При непустоте допустимого множества X для всякого решения x^∗ суще-

ствует открытое подмножество χ ⊂ X, замыкание которого χ содержит x^∗, а

функции Q и g непрерывны на этом замыкании. Если X = ∅, то для всякого

расширенного решения x^∗ существует открытое подмножество χ ⊂ D, замы-

кание которого χ содержит x^∗, а функция g непрерывна на этом замыкании.

С. Множество решений X^∗, понимаемое в обычном или расширенном ва-

рианте, замкнуто и является глобально устойчивым (по аналогии с термино-

логией [27]) в том смысле, что для любой минимизирующей последователь-

ности x_k, т.е. последовательности, удовлетворяющей при X = ∅ условиям

x_k ∈ X, Q(x_k) → Q^∗ при k → ∞, а при X = ∅ условиям x_k ∈ D, g(x_k) → g^∗

при k → ∞, выполняется требование ρ(x_k, X^∗) → 0, где

ρ(x_k, X^∗) = inf {∥x_k - x^∗∥ : x^∗ ∈ X^∗}.

Теорема 1 (о сходимости). Пусть для задачи с ограничениями неравен-

ствами (1)-(2), решение которой понимается в расширенном смысле, вы-

полняются требования А, В и С, тогда двухточечный диагональный метод

ExDIR-diag, расширяющий принципы метода DIRECT на задачи с ограниче-

ниями, порождает на множестве поиска D последовательность испыта-

ний со всюду плотным в пределе характером размещения, при этом все пре-

дельные точки последовательности оценок решения x^∗k принадлежат мно-

жеству решений X^∗.

Заметим, что всюду плотный характер размещения точек испытаний не

означает их равномерного расположения на множестве поиска D. Хотя для

DIRECT-подобных методов, в отличие от методов из [13], до сих пор не по-

лучено аналитических оценок относительной плотности размещения испы-

таний, приведенные в разделе 5 вычислительные иллюстрации показывают

существенно неравномерное распределение точек измерений в зависимости

от поведения функций Q и g задачи (1)-(2). При достаточно большом коли-

честве измерений наиболее высокая концентрация испытаний наблюдается в

окрестностях глобальных минимумов.

5. Вычислительные иллюстрации

В качестве вычислительных иллюстраций работы построенного двухто-

чечного диагонального метода ExDIR-diag приведем примеры размещения

испытаний на трех задачах с номерами № 1, № 3 и № 7 из тестового набо-

ра, использованного в [1]. Там же представлены постановки и описания этих

задач. Здесь укажем лишь общие характеристики: число ограничений нера-

венств m, число условных локальных минимумов n_loc, параметры глобально-

го минимума Q^∗ и x^∗, Q^o наименьшее значение в локальном минимуме, не

совпадающем с глобальным.

В задаче № 1 m = 3 и функции ограничений сильно разномасштабные,

n_loc = 5, Q^∗ = -1,48968, x^∗ = (0,94248;0,94526), Q^o = -1,0; в задаче №3

m = 1, n_loc = 8, Q^∗ = -0,81911, x^∗ = (1,30499;2,27249), Q^o = -0,81814, эта за-

дача характеризуется малым отличием в значениях глобального и следующе-

го по значению локального минимума (Q^o - Q^∗ = 0,00097).

Численные эксперименты проведены с использованием двух групп зна-

чений параметров, которые для удобства обозначены E1 и E3. Набор па-

раметров E1 включает: µ = 0,3, n = 100, K = 2; ε₀ = 0,5, α₀ = 1,0, δ₀ = 0,0;

ε₁ = 0,0001, α₁ = 0,5, δ₁ = 0,1; ε₂ = 0,1, α₂ = 2,0, δ₂ = 0,1. Набор E3 отлича-

ется изменением части параметров: ε₁ = 0,00001, α₁ = 0,5, δ₁ = 0,01; ε₂ = 0,1,

α₂ = 2,0, δ₂ = 0,01.

Представленные на рис. 4 и рис. 5 результаты тестирования соответствуют

следующей постановке эксперимента.

Для задачи вводим желаемую погрешность ǫ определения глобально ми-

нимального значения Q^∗. Вычисления проводим до первого испытания, в ре-

зультате которого текущая оценка Q^∗k значения Q^∗ окажется меньшей или

равной Q^∗ + ǫ. В этот момент определяем n^∗ количество проведенных испы-

таний, k^∗ номер итерации и M^∗ количество гиперинтервалов. Значения

n^∗, k^∗ и M^∗ указываем наряду с видами размещения испытаний. Допустимое

множество на всех рисунках выделено серым. Результаты рис. 4 показывают

размещения испытаний в одноточечном методе ExDIR из [1] в сравнениии с

его диагональным обобщением ExDIR-diag для задачи № 1. Использована

группа параметров E1. Размещение выглядит более рациональным у диаго-

нального варианта метода (на рисунке справа). Для достижения точности

ǫ = 0,002 по значению функции ему понадобилось провести n^∗ = 111 испы-

таний (выполнено k^∗ = 15 итераций, M^∗ = 157). У метода ExDIR испытаний

n^∗ = 219 за k^∗ = 43 итерации, M^∗ = n^∗. Число делимых в среднем на итера-

ции гиперинтервалов для ExDIR-diag оказалось примерно в два раза больше,

чем у ExDIR.

В задаче № 3 малое отличие значений глобального и следующего по глу-

бине локального минимума увеличивает число испытаний, необходимых для

определения глобального минимума с заданной точностью ǫ = 0,00051. Мето-

ду ExDIR потребовалось n^∗ = 577 испытаний (выполнена k^∗ = 61 итерация,

M^∗ = n^∗), а диагональному методу ExDIR-diag потребовалось n^∗ = 369 испы-

100

3,00

2,60

2,10

1,70

1,20

0,78

0,33

-0,33

-0,56

-1,00

0,44 0,89 1,30 1,80 2,20 2,70 3,10 3,60 4,00

0,44

0,89 1,30 1,80 2,20 2,70 3,10 3,60 4,00

Рис. 4. Размещение испытаний методами ExDIR (слева) и ExDIR-diag (справа)

в задаче № 1 до момента определения решения с погрешностью ǫ = 0,002.

6,3

5,6

4,9

4,2

3,5

2,8

2,1

1,4

0,7

1,4

2,1

2,8

3,5

4,2

4,9

5,6

6,3

0,7

1,4

2,1

2,8 3,5 4,2 4,9

5,6

6,3

Рис. 5. Размещение испытаний в ExDIR-diag до момента получения решения

с погрешностью ǫ = 0,00051 в задаче № 3 без разрыва (слева) и задаче № 7 с

разрывом.

таний (выполнено k^∗ = 30 итераций, M^∗ = 547). В обоих методах использова-

лась группа параметров E3. Размещение испытаний в диагональном методе

ExDIR-diag показано на рис. 5 слева.

Дополнительно на рис. 5 справа представлена задача № 7 из [1] для ил-

люстрации влияния разрывов на поведение метода. Она отличается от за-

дачи № 3 только добавленным разрывом в целевую функцию Q(x) вдоль

прямой x₂ = 2,3 за счет вычитания из Q(x) значения Δ = 1 на множестве

точек с x₂ ≤ 2,3. Линия разрыва проходит в непосредственной близости от

точки глобального минимума с x^∗2 = 2,27249. Общие характеристики зада-

101

чи № 7 отличаются от задачи № 3 лишь тем, что для нее Q^∗ = -1,81911 и

Q^o = -1,81814.

Поскольку метод ExDIR-diag не оценивает константы Липшица, то несмот-

ря на разрывы в областях концентрации точек не происходит вырождения

этого метода в равномерный перебор. Видно, что метод ExDIR-diag на за-

даче с разрывом сохраняет целесообразное поведение. В процессе решения

правильное распознавание области глобального минимума происходит доста-

точно быстро, однако наличие разрывов заметно замедляет уточнение най-

денного решения. В результате для достижения той же точности ǫ = 0,00051

методу потребовалось n^∗ = 707 испытаний (выполнено k^∗ = 53 итерации,

M^∗ = 1137). Вычисления проведены с группой параметров E1.

Следует отметить, что представленную в статье версию двухточечного

диагонального метода следует рассматривать как базовую, которую можно

использовать для его дальнейшего развития.

6. Заключение

Оригинальный метод DIRECT, построенный в [16] для решения задач

многоэкстремальной оптимизации без функциональных ограничений, при-

влекателен тем, что сохраняет способность поиска глобального экстремума

при наличии конечных (умеренной величины) разрывов целевой функции

в непосредственной близости от решений. Эта особенность связана со специ-

альными принципами отбора делимых гиперинтервалов, входящих в текущее

покрытие множества поиска. Эти принципы не используют оценок констант

Липшица, хотя липшицевость целевой функции (при неограниченности диа-

пазона возможных значений константы) предполагается.

В данной статье впервые предложено обобщение принципов DIRECT с уче-

том сразу двух дополнительных факторов: наличия функциональных ограни-

чений и использования испытаний функций в гиперинтервале не в одной цен-

тральной точке, а в двух на концах специально ориентируемых главных диа-

гоналей. Для одновременного учета пар измерений потребовалось изменить

традиционные для DIRECT предположения о свойствах функций решаемой

задачи. Введенные обобщенные принципы отбора можно рассматривать как

прямое развитие и расширение принципов построения метода DIRECT. В ста-

тье показана лишь структура двухэтапной обработки информации при отбо-

ре делимых гиперинтервалов. Детальное описание и обоснование алгоритмов

реализации обобщенных принципов требует отдельной публикации.

Проведенный анализ показывает, что сходимость оценок решения постро-

енного метода (как и в методе DIRECT) достигается за счет всюду плотного

в пределе размещения точек испытаний, но выполненная численная апроба-

ция демонстрирует существенную неравномерность их размещения с преиму-

щественной концентрацией в окрестностях решений, что определяет эффек-

тивность метода. Метод рассчитан на использование в прикладных задачах,

где значения функций определяются в результате затратных по времени вы-

числений, а сами функции могут иметь разрывы. Функции качества такого

вида могут возникать, например, в нелинейных задачах управления при оп-

тимальной настройке свободных параметров по численно рассчитываемым

для замкнутой системы дополнительным нелинейным критериям.

102

Построенная реализация метода является последовательной, но вычисле-

ния функций на наборе гиперинтервалов, выделенных для деления на оче-

редной итерации, можно выполнять параллельно.

ПРИЛОЖЕНИЕ

Доказательство утверждения 1. Если условия (24) выполнены

при некотором ΔL из указанного промежутка, то (21)-(22), очевидно, будут

справедливы при том же ΔL и при ΔL^g = α ΔL. Пусть теперь выполнены

(21)-(22) и для D_t нашлась соответствующая параΔL,ΔL^g. Но поскольку

g^-(ΔL^g,D_i) монотонно убывает с возрастанием ΔL^g, то (21)-(22) тем бо-

лее будут выполнены при значенияхΔL, ΔL^g = αΔL, что и требовалось.

Утверждение доказано.

Доказательство леммы 1. На первом этапе обработки поисковой ин-

формации на итерации k согласно описанию в разделе 3 в каждом d-слое

выделяется хотя бы один модифицированно недоминируемый гиперинтер-

вал

этого слоя. Последний из выделенных имеет связанный диапазон

[ΔL^ds, ΔL^ds+1) с наибольшим номером s = S_k(d), где ΔL^dS

= +∞. Это вер-

k(d)+1

но, в частности, и для d-слоя гиперинтервалов, имеющих на текущей k-й ите-

рации наибольший диаметр d = d^maxk.

Далее, при построении разбиения (25) оси приращений ΔL в последнем

промежутке [ΔL_j, ΔL_j+1) с номером j = m_k значение ΔLmk +1 = +∞. Это-

му промежутку соответствует множество гиперинтерваловOmkk^{,котороепо}

построению обязательно включает в себя хотя бы один гиперинтервал

d-слоя с d = d^maxk (т.е. максимального диаметра), соответствующий диапазо-

ну [ΔL^ds, ΔL^ds+1) значений ΔL с номером s = S_k(d^maxk). На плоскости срав-

нения (d/2, F ) при сопоставлении гиперинтервалов изOmkk^{этомугиперин-}

тервалу будет соответствовать самая правая точка в полученном множестве

точек Pmkk^{.Посколькусравнениепроисходитдляпромежутка[ΔL}mk^,+∞),

точка с наибольшим d = d^maxk при достаточно большом ΔL обязательно будет

доминировать остальные и для нее также выполнится условие (17). Следова-

тельно, гиперинтервал наибольшего диаметра будет включен в множествоDk

гиперинтервалов, делимых на итерации k. Лемма доказана.

Доказательство теоремы 1. В силу предположения о глобальной

устойчивости множества решений X^∗ (требование C), а также требований B

к структуре множества глобальных минимумов X^∗ и функциям задачи, для

доказательства теоремы достаточно обосновать всюду плотное в пределе раз-

мещение точек испытаний. Действительно, множество поиска D компактно.

При выполнении требований A и B всюду плотное в пределе размещение

испытаний приведет к появлению подпоследовательностей точек измерений,

сходящихся к каждому из решений x^∗. Каждое x^∗ принадлежит замыканию

некоторого открытого подмножества χ из X, если X = ∅, или из D в про-

тивном случае. При всюду плотном в пределе размещении испытаний сколь

угодно близко от x^∗ найдутся точки, являющиеся центрами открытых шаров,

включенных в χ. В каждом из таких шаров в какой-то момент метод разме-

стит точку испытания. Поэтому найдутся подпоследовательности допусти-

мых точек из подмножеств χ, сходящиеся к x^∗ при неограниченном возраста-

103

нии числа итераций. Функции Q, g или (при X = ∅) функция g непрерывны

на замыканиях χ. Таким образом, последовательность рекордных измере-

ний x^∗k будет минимизирующей и в силу требования C ее предельные точки

будут являться решениями задачи.

Остается обосновать всюду плотное в пределе размещение испытаний.

Приведем лишь схему рассуждения. Нужное поведение следует из леммы 1,

которая устанавливает, что в построенном методе на каждой итерации обяза-

тельно делится по крайней мере один из гиперинтервалов наибольшего диа-

метра. Поскольку деление гиперинтервалов происходит на три равные ча-

сти по наибольшему ребру, это обеспечивает строгое убывание диаметра с

некоторым коэффициентом, отделенным от единицы. Этих двух факторов

достаточно. Более подробное рассуждение можно построить аналогично до-

казательству теоремы 5.6 из [8] с учетом леммы 1. Теорема доказана.

СПИСОК ЛИТЕРАТУРЫ

Городецкий С.Ю. Несколько подходов к обобщению метода DIRECT на задачи

с функциональными ограничениями // Математическое моделирование. Опти-

мальное управление. 2013. № 6 (1). С. 189-215. Нижний Новгород: Вестн. Ни-

жегород. ун-та им. Н.И. Лобачевского.

Методы классической и современной теории автоматического управления: Учеб-

ник в 3-х т. Т. 2. Синтез регуляторов и теория оптимизации систем автоматиче-

ского управления / Под ред. Н.Е. Егупова. М.: Изд-во МГТУ им. Н.Э. Баумана,

2000.

Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных

матричных неравенств. М.: Физматлит, 2007.

Александров А.Г. Методы построения систем автоматического управления. М.:

Физматкнига, 2008.

Gershon E., Shaked U., Yaesh I. H_∞ Control and Estimation of State-multiplicative

Linear Systems. London: Springer, 2005.

Баландин Д.В., Коган М.М. Оптимальное по Парето обобщенное H₂-оптималь-

ное управление и задачи виброзащиты // АиТ. 2017. № 8. С. 76-90.

Balandin D.V., Kogan M.M. Pareto Optimal Generalized H₂-control and Vibropro-

tection Problems // Autom. Remote Control. 2017. V. 78. No. 8. P. 1417-1429.

Городецкий С.Ю., Сорокин А.С. Построение оптимальных регуляторов по нели-

нейным критериям качества на примере одной динамической системы // Мате-

матическое моделирование. Оптимальное управление. 2012. № 2 (1). С. 165-176.

Нижний Новгород: Вестн. Нижегород. ун-та им. Н.И. Лобачевского.

Сергеев Я.Д., Квасов Д.Е. Диагональные методы глобальной оптимизации. М.:

Физматлит, 2008.

Strongin R.G., Sergeyev Ya.D. Global optimization with non-convex constraints:

Sequential and parallel algorithms. Dordrecht: Kluwer Acad. Publishers, 2000.

10.

Евтушенко Ю.Г., Малкова В.У., Станевичюс А.А. Параллельный поиск гло-

бального экстремума функций многих переменных // Журн. вычисл. матем. и

матем. физ. 2009. Т. 49. № 2. С. 255-269.

11.

Стронгин Р.Г., Гергель В.П., Гришагин В.А., Баркалов К.А. Параллельные вы-

числения в задачах глобальной оптимизации / Предисл.: В.А. Садовничий. М.:

Изд-во МГУ, 2013.

104

12.

Городецкий С.Ю. Триангуляционные методы параболоидов в задачах многоэкс-

тремальной оптимизации с ограничениями для класса функций с липшицевыми

производными по направлениям // Математическое моделирование. Оптималь-

ное управление. 2012. № 1 (1). С. 144-155. Нижний Новгород: Вестн. Нижегород.

ун-та им. Н.И. Лобачевского.

13.

Городецкий С.Ю. Исследование процедур глобальной оптимизации с адаптив-

ными стохастическими моделями. Дисс. на соискание уч. степ. канд. физ.-мат.

наук. Горький: ГГУ, 1984.

14.

Неймарк Ю.И. Динамические системы и управляемые процессы. М.: Наука,

1978.

15.

Городецкий С.Ю., Неймарк Ю.И. О поисковых характеристиках алгоритма гло-

бальной оптимизации с адаптивной стохастической моделью // Пробл. случай-

ного поиска. Рига: Зинатне, 1981. С. 83-105.

16.

Jones D.R., Perttunen C.D., Stuckman B.E. Lipschitzian Optimization without the

Lipschitz Constant // J. Optim. Theory Appl. 1993. V. 79. No 1. P. 157-181.

17.

Препарата Ф.Ф., Шеймос М.И. Вычислительная геометрия. Введение. М.: Мир,

1989.

18.

Jones D.R. The DIRECT global optimization algorithm / Encyclopedia of opti-

mization. 7 Vols. 2nd revised and expanded ed., ed. by C.A. Floudas, P.M. Pardalos.

Springer, 2009. P. 725-735.

19.

Евтушенко Ю.Г., Ратькин В.А. Метод половинных делений для глобальной

оптимизации функций многих переменных // Изв. АНСССР. Технич. киберне-

тика. 1987. № 1. С. 119-127.

20.

Gablonsky J.M., Kelley C.T. A Locally-Biased from of the DIRECT Algorithm //

J. Global Optim. 2001. V. 21. No. 1. P. 27-37.

21.

Sergeyev Ya.D., Kvasov D.E. Global Search Based on Efficient Diagonal Partitions

and a Set of Lipschitz Constants // SIAM J. Optim. 2006. V. 16. No. 3. P. 910-937.

22.

Sergeyev Ya.D. An Efficient Strategy for Adaptive Partition of N-dimensional In-

tervals in the Framework of Diagonal Algorithms // J. Optim. Theory Appl. 2000.

V. 107. No. 1. P. 145-168.

23.

Sergeyev Ya.D., Kvasov D.E. A Univariate Global Search Working with a Set of

Lipschitz Constants for the First Derivative// Optimization Lettes. 2009. No. 3.

P. 303-318.

24.

Kvasov D.E., Sergeyev Ya.D. Lipschitz Gradients for Global Optimization in a

One-Point-Based Partitioning Scheme // J. Comput. Appl. Math. 2012. V. 236.

P. 4042-4054.

25.

Sergeyev Ya.D., Mukhametzhanov M.S., Kvasov D.E. On the Efficiency of Nature-

Inspired Metaheuristics in Expensive Global Optimization with Limited Budget //

Sci. Reports. 8, 453 (2018).

26.

Городецкий С.Ю. О новой модели поведения целевой функции для диагональ-

ной реализации DIRECT-подобных методов // Научное периодическое издание

CETERIS PARIBUS. М.: РИЦ ЭФИР, 2016. № 1. С. 4-16.

27.

Карманов В.Г. Математическое программирование: Уч. пос. М.: Физматлит,

2008.

Статья представлена к публикации членом редколлегии Б.Т. Поляком.

Поступила в редакцию 23.07.2019

После доработки 06.10.2019

Принята к публикации 30.01.2020

105