Автоматика и телемеханика, № 8, 2020

(Нижегородский государственный университет им. Н.И. Лобачевского)

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ВРАЩЕНИЯ

РОТОРНЫХ СИСТЕМ С ЖИДКОСТЬЮ¹

Изложен новый метод исследования устойчивости, в котором, в отли-

чие от традиционного метода D-разбиения, знание характеристического

уравнения не требуется. Метод эффективен в широком классе задач ди-

намики тел с полостями, содержащими жидкость.

Ключевые слова: роторная система, полость, содержащая вязкую жид-

кость, режим стационарного вращения, устойчивость и автоколебания.

DOI: 10.31857/S0005231020080085

1. Введение

И.А. Вышнеградский (1871-1876) обратился к задаче об устойчивости ре-

жима работы паровой машины, снабженной регулятором Уатта. В знамени-

той работе 1876 г. И.А. Вышнеградский впервые установил условия устойчи-

вости движения паровой машины, а также получил необходимые и достаточ-

ные условия отрицательности действительных частей корней алгебраическо-

го уравнения (полинома) третьей степени и дал геометрическую интерпрета-

цию этих условий в виде диаграмм Вышнеградского. Д.К. Максвелл в задаче,

близкой к той, которой занимался И.А. Вышнеградский, пришел к тем же ма-

тематическим требованиям отрицательности действительных частей корней

характеристического полинома (1868), но не сделал отчетливых инженерных

выводов. Критерий отрицательности действительных частей всех корней по-

линома n-й степени получил Раус (1877). А.М. Ляпунов в своей диссертации

(1892) дал математическое обоснование исследованиям устойчивости при по-

мощи линеаризованных уравнений. А. Стодола (1893) распространил линеа-

ризованную теорию И.А. Вышнеградского на непрямое регулирование и, не

зная о работах Д.К. Максвелла и Рауса, предложил А. Гурвицу задачу о на-

хождении критерия отрицательности действительных частей всех корней по-

линома n-й степени с действительными коэффициентами. А. Гурвиц нашел

решение этой задачи в изящной форме детерминантных неравенств (1895).

Заметим, что из условий Рауса-Гурвица следует положительность всех ко-

эффициентов полинома, корни которого располагаются в левой полуплоско-

сти. Но тогда, как было показано Льенаром и Шипаром (1914), количество

детерминантных неравенств сокращается почти вдвое, т.е. необходимые и до-

статочные условия отрицательности действительных частей всех корней по-

линома степени n с положительными коэффициентами записываются в виде

¹ Работа выполнена в порядке личной инициативы.

106

детерминантых неравенств

Δ_n-1 > 0, Δ_n-3 > 0,... ,

где Δ_k, k = 1, n определители из условий Гурвица [1].

В дальнейшем руководящим стимулом стало стремление дать в руки при-

кладников практически пригодные приемы исследования устойчивости. На

практике обычно речь идет не столько о том, что устойчива или неустойчива

данная система, сколько о таком подборе параметров системы, чтобы система

удовлетворяла ряду технических требований, оставаясь при этом устойчивой.

Фактически задача сводится к разбиению пространства параметров системы

на области устойчивости и неустойчивости. Существенным шагом в решении

этой задачи стало появление частотных критериев Найквиста (1932) и Ми-

хайлова (1938), новая трактовка критерия Найквиста и метод D-разбиения

Ю.И. Неймарка (1949) [2]. В методе D-разбиения рассматривается плоское

сечение пространства комплексных полиномов, точками которого являются

полиномы степени n, а их коэффициенты зависят либо от одного комплекс-

ного, либо от двух действительных параметров; значения параметров, таким

образом, принадлежат плоскости параметров. Поскольку корни полиномов

непрерывно зависят от их коэффициентов, то кривая на плоскости парамет-

ров (D-кривая), точкам которой соответствуют полиномы, имеющие хотя бы

один корень на мнимой оси, разбивает, в общем случае, плоскость параметров

на области с различной степенью неустойчивости, т.е. с различным числом

корней справа от мнимой оси. D-кривая, по сути, является отображением

мнимой оси плоскости корней полиномов на плоское сечение пространства

полиномов. Метод D-разбиения был обобщен на квазиполиномы и другие це-

лые функции, что позволило применять его к исследованию устойчивости

некоторых распределенных систем.

Идея построения отображения мнимой оси плоскости характеристических

чисел на плоское сечение пространства параметров оказалась очень плодо-

творной. Удалось построить области устойчивости в случае таких систем, для

которых само выписывание конечного уравнения для характеристических чи-

сел часто оказывается проблематичным. При этом оказалось, что рассмот-

рение всевозможных возмущенных движений излишне, а достаточно лишь

рассмотреть условия осуществимости возмущенных движений определенного

типа. Далее речь пойдет об устойчивости режимов стационарного вращения

роторных систем, содержащих жидкость. Именно для них при исследовании

устойчивости в линейном приближении удалось развить эффективный метод

[3, 4], в котором, в отличие от метода D-разбиения, знание характеристиче-

ского уравнения не требуется. В то же время исследование возмущенных

движений типа круговой прецессии позволяет с минимальными затратами

построить D-кривую и выделить области устойчивости.

Проиллюстрируем оригинальный метод исследования устойчивости на

примере задачи об устойчивости (в линейном приближении) стационарно-

го вращения цилиндра, частично заполненного вязкой несжимаемой жидко-

стью. Отличительная особенность рассматриваемой задачи состоит в том, что

скорость вращения тела, содержащего жидкость, поддерживается постоянной

за счет внешнего источника энергии, вследствие чего кинетическая энергия

107

содержащейся в полости жидкости может возрастать во времени благодаря

взаимодействию со стенками полости. Для таких задач представляет боль-

шую трудность использование методов, связанных с построением функции

Ляпунова.

2. Постановка задачи

Пусть круговой цилиндр радиуса a совершает стационарное вращение во-

круг своей оси (совпадающей с осью Oz неподвижной прямоугольной си-

стемы координат Oxyz), которая находится в вязкоупругом осесимметрич-

ном закреплении. Вязкая несжимаемая жидкость, частично заполняющая

цилиндр, при стационарном вращении расположена в слое постоянной тол-

щины h на боковой поверхности цилиндра и вращается вместе с ним как

твердое тело. Ограничимся рассмотрением задачи об устойчивости в линей-

ном приближении и в рамках плоской модели, т.е. в предположении, что точ-

ки цилиндра могут перемещаться лишь параллельно плоскости Oxy, а поле

скоростей жидкости имеет лишь x- и y-компоненты, которые, как и давление

жидкости, не зависят от z. Плоская модель применима, если осевые пере-

мещения цилиндра и угловое перемещение его оси пренебрежимо малы (на-

пример, ось цилиндра в подшипниках), а сам цилиндр достаточно длинный

(концевые эффекты несущественны). Система линеаризованных уравнений

плоской модели и граничных условий к ним, используемая в данной работе,

содержит:

1. Уравнения поступательного движения цилиндра параллельно плоскости

Oxy, линеаризованные вблизи состояния цилиндра при стационарном враще-

нии

Mx¨₀ +Hx˙₀ +Kx₀ =F_x,

(1)

y₀ + Hy˙₀ + Ky₀ = F_y,

где x₀, y₀ координаты точки пересечения оси цилиндра с плоскостью Oxy;

Fx, Fy компоненты силы, с которой жидкость действует на единицу дли-

ны цилиндра; M масса единицы длины цилиндра; H, K соответственно

коэффициенты демпфирования и жесткости закрепления оси цилиндра, де-

ленные на его длину;

2. Условие постоянства абсолютной угловой скорости вращения цилиндра

вокруг оси Oz: Ω = const;

3. Уравнения движения вязкой несжимаемой жидкости в плоскости Oxy,

линеаризованные вблизи стационарного квазитвердого вращения жидкости

вокруг оси Oz:

∂υ_j

∂

1 ∂p^′

+υ⁰

v_j + υ_γ

υ^0j = -

+ νΔυ_j,

∂t

^k∂x_k

∂x_γ

ρ ∂x_j

(2)

∂υ_j

= 0; υ⁰¹ = -Ωx₂; υ⁰² = Ωx₁;

∂x_j

4. Условие прилипания жидкости к поверхности цилиндра, условие непре-

рывности напряжений и кинематическое условие на свободной поверхности,

перенесенные в линейном приближении по отклонениям от состояния стацио-

108

нарного вращения на поверхности x² + y² = a² и x² + y² = (a - h)² соответ-

ственно:

υ₁ = x⁰¹ + Ω x⁰²; υ₂ = x⁰² - Ω x⁰¹,

x²¹ + x²² = a²,

σ^′ikn^0k = -ρΩ²bSn⁰ⁱ,

)

(∂υ_i

∂υ_k

σ^′ik = -p^′δ_ik + µ

∂x_k

∂x_i

(

)

∂S

∂

(3)

+ Ω -x₂

+x₁

S=υ_jn^0j; x²¹ +x²² =b²,

∂t

∂x₁

∂x₂

здесь n^0j внешняя нормаль к поверхности жидкости, S отклонение сво-

бодной поверхности жидкости от невозмущенной поверхности x² + y² = b² в

направлении нормали к ней;

5. Формулы, определяющие F_x, F_y через отклонения давления и компонент

поля скоростей жидкости от соответствующих величин при стационарном

квазитвердом вращении:

∫

Ω²a²

(4)

Fj = - σ^iknkdl + ρ

x^0j,

x²¹ + x²² = a².

Интеграл вычисляется по окружности x² + y² = a², dl элемент длины

дуги.

3. Свойства симметрии и круговая прецессия

Перечисленные уравнения и граничные условия линейны и однородны от-

носительно отклонений от состояния стационарного вращения цилиндра и

частично заполняющей его жидкости и обладают двумя очевидными свой-

ствами симметрии: а) инвариантны относительно сдвига начала отсчета вре-

мени, т.е. преобразования t^′ = t - t₀; б) инвариантны относительно поворота

системы координат вокруг Oz на угол^π2 , т.е. преобразования x^′ = y, y^′ = -x,

z^′ = z. В силу свойства симметрии а) система уравнений (1)-(4) допускает

частные решения, пропорциональные e^λt, где λ характеристическое число.

Будем считать стационарное вращение цилиндра с жидкостью устойчивым в

малом, если все λ имеют отрицательные действительные части, и неустойчи-

вым, если хотя бы одно λ имеет положительную действительную часть. Если

характеристические числа λ непрерывно зависят от параметров задачи, то

изменение степени неустойчивости в системе происходит при появлении мни-

мого λ = iω. При этом наряду с решением уравнений (1)-(4)

(

)

x^∗e_x + y^∗e_y,v^∗x(x,y)e_x + v^∗y(x,y)e_y,p^∗(x,y) e^iωt.

В силу свойства симметрии б) существует также решение

(

)

- y^∗e_x + x^∗e_y,-v^∗y(y,-x)e_x + v^∗x(y,-x)e_y,p^∗(y,-x) e^iωt,

109

где x^∗, y^∗

комплексные амплитуды компонент радиуса-вектора точки пе-

ресечения оси цилиндра с плоскостью Oxy; v^∗x, v^∗y, p^∗ комплексные ампли-

туды отклонений компонент поля скоростей и давления жидкости от соот-

ветствующих величин при стационарном квазитвердом вращении; e_x, e_y

орты координатных осей. Умножая первое из этих решений на i и склады-

вая со вторым, получим в силу линейности уравнений (1)-(4) частное ре-

шение, описывающее так называемую круговую прецессию цилиндра с жид-

костью, т.е. такое движение, в котором точка пересечения оси цилиндра с

плоскостью Oxy описывает окружность, а отклонения гидродинамических

элементов от стационарных значений изменяются во времени ∼ e^iωt. Обрат-

но: если при некоторых значениях параметров уравнения (1)-(4) допускают

решение типа круговой прецессии, то существует мнимое характеристическое

число λ. Таким образом, значения параметров, при которых происходит из-

менение степени неустойчивости в системе (существует хотя бы одно мнимое

характеристическое число), могут быть найдены из условия существования

круговой прецессии цилиндра с жидкостью. Приведенное соображение опре-

деляет ход решения задачи в данной статье. Именно сначала рассматрива-

ется гидродинамическая задача о движении вязкой несжимаемой жидкости,

частично заполняющей вращающийся цилиндр, совершающий круговую пре-

цессию. Затем вычисляется сила, с которой жидкость действует на вращаю-

щийся цилиндр в случае круговой прецессии. Далее, на основании получен-

ных выражений для гидродинамической силы из уравнений поступательного

движения цилиндра (1) находятся условия, при которых возможна круго-

вая прецессия. Эти условия в соответствии со сказанным выше определяют

границы областей с различной степенью неустойчивости в пространстве па-

раметров задачи.

4. Гидродинамическая задача

Пусть бесконечно длинный круговой цилиндр с внутренним радиусом а

вращается вокруг своей оси с угловой скоростью ω₀ и прецессирует с часто-

той ω таким образом, что его ось описывает цилиндрическую поверхность

радиуса ε (рис. 1). Абсолютная угловая скорость цилиндра Ω складывается

из угловой скорости собственного вращения цилиндра ω₀ и скорости прецес-

сии ω (Ω = ω₀ + ω).

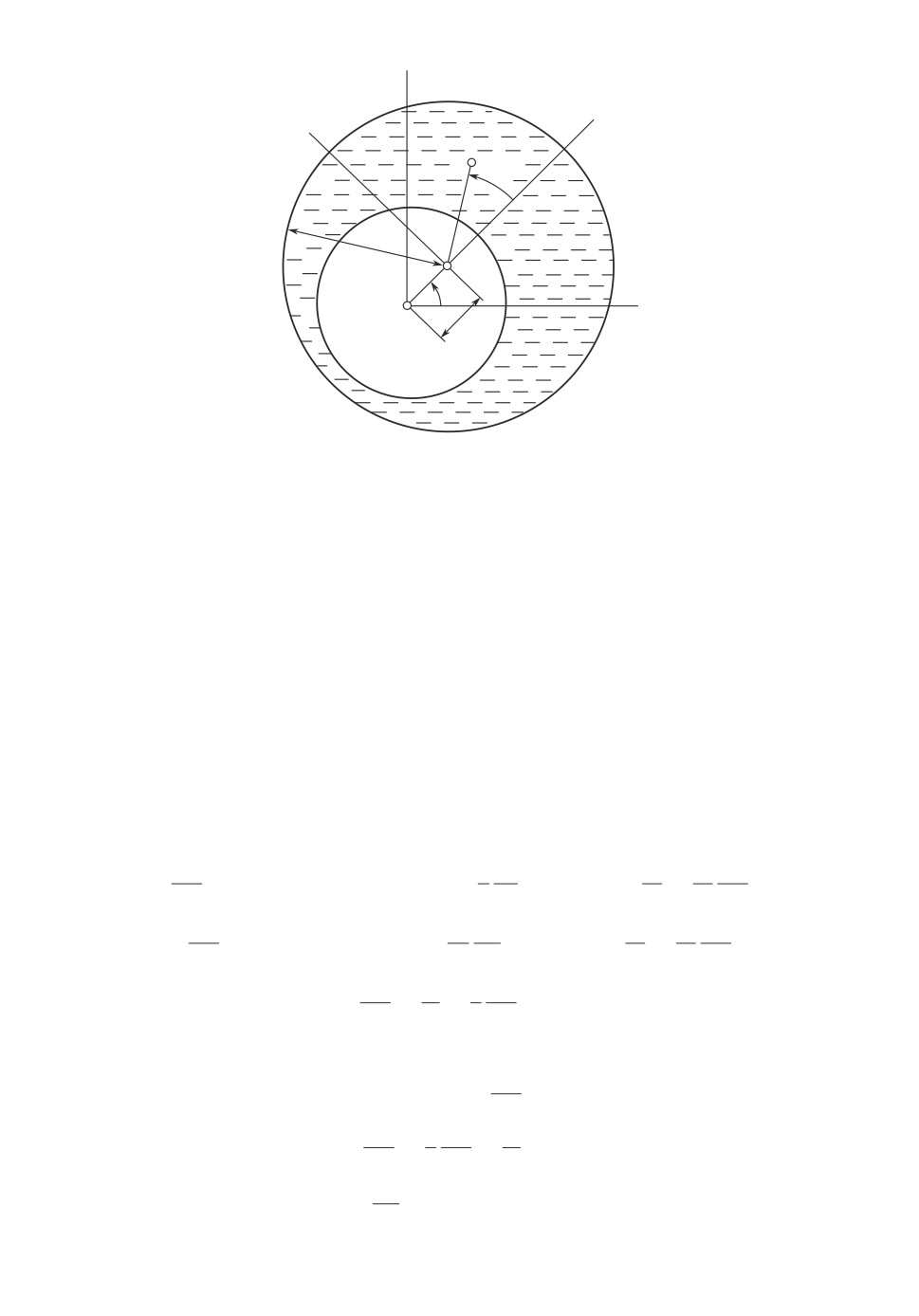
Выберем неинерциальную систему отсчета Oξη (см. рис. 1), жестко свя-

занную с так называемой линией центров, проходящей через центр прецес-

сии O₁ и центр сечения цилиндра O. Эта система поступательно двигается по

окружности радиуса ε со скоростью ωε и вращается вокруг оси цилиндра с

угловой скоростью ω. В пространстве отсчета Oξη введем полярную систему

координат r, ϕ с центром в точке O. В этой системе компоненты поля сил

инерции, действующих в пространстве отсчета Oξη на частицу единичной

массы, имеют вид:

f_r = ω²r + 2ωυ + ω²εcos φ,

(5)

f_φ = -2ωu - ω²

εsin φ.

Рассмотрим задачу о плоском движении вязкой несжимаемой жидкости,

частично заполняющей вращающийся цилиндр, в случае круговой прецес-

110

Рис. 1. Неинерциальная система отсчета Oξη.

сии с малым радиусом ε, при которой отклонения гидродинамических эле-

ментов от стационарных значений малы и в неподвижной системе отсчета

изменяются во времени ∼ e^iωt. Используя закон изменения энергии вязкой

жидкости, можно показать, что в случае круговой прецессии с малым радиу-

сом движение жидкости относительно системы отсчета Oξη установившееся,

т.е. не зависит от времени. Уравнения установившегося движения жидкости

относительно системы Oξη и граничные условия, линеаризованные вблизи

стационарного квазитвердого вращения жидкости вокруг оси цилиндра

(6)

u = 0, υ = ω₀r

записываются в виде:

(

)

∂u^′

1 ∂p

u^′

2 ∂υ^′

+ ν Δu^′ -

ω₀ ∂ϕ=Ω2r+ω2εcosϕ+2Ωυ′ -

ρ ∂ρ

r²

r² ∂ϕ

(

)

∂υ^′

1 ∂p

υ^′

2 ∂u^′

(7)

+ ν Δυ^′ -

ω₀ ∂ϕ=-ω2εsinϕ-2Ωu′ -

rρ ∂ϕ

r²

r² ∂ϕ

∂u^′

u^′

1 ∂υ^′

= 0,

∂r

r ∂ϕ

(8)

u^′ = 0, υ^′

= 0, r = a,

′

∂u

-p - ρΩ²rη + 2µ

= -p₀,

∂r

′

∂υ

1 ∂u^′

υ^′

(9)

= 0,

∂r

r ∂ϕ

∂η

ω₀ ∂ϕ=u′;r=a-h.

111

Здесь u^′, υ^′

малые отклонения компонент поля скоростей от (6), p

давление, ρ плотность, ν, µ кинематическая и динамическая вязкость

жидкости, r = a - h + η(ϕ) уравнение свободной поверхности жидкости,

p₀

давление на свободной поверхности. Введем потенциалы Ламба θ, ψ и

функцию χ

∂θ

1 ∂ψ

u^′ =

∂r

r ∂ϕ

1 ∂θ

∂ψ

υ^′ =

r ∂ϕ

∂r

χ=

Ω²r² + ω²εr cos ϕ - 2Ωψ + const

и запишем систему (7) в виде:

∂

1 ∂

∂

F +

G = 0,

F -

G = 0, Δθ = 0,

∂r

r ∂ϕ

∂r

∂θ

∂ψ

(10)

F =χ-

-ω₀

G = νΔψ + 2Ωθ - ω₀

∂ϕ

∂φ

Неоднозначностью в выборе потенциалов Ламба (калибровкой потенциа-

лов) можно распорядиться так, что (10) сведется к системе:

(11)

F = 0, G = 0, Δθ = 0.

Граничные условия (8) и (9) после введения потенциалов Ламба принима-

ют вид:

∂θ

1 ∂ψ

1 ∂θ

∂ψ

(12)

= 0,

= 0, r = a,

∂r

r ∂φ

∂r

)

(∂²θ

1 ∂ψ

1 ∂²ψ

p₀

2ν

-Ω²rη = -

∂r²

r² ∂φ

r ∂r∂φ

∂²ψ

∂θ

∂ψ

(13)

r²

- 2r

-r

= 0,

∂r²

∂r∂φ

∂φ²

∂φ

∂r

∂θ

1 ∂ψ

r = a - h.

ω₀ ∂φ=

∂r

r ∂φ

Уравнения (11) с граничными условиями (12), (13) содержат лишь следую-

щие размерные параметры: ω₀, Ω, ν, a, a - h, ε (параметр p₀ несуществен, так

как жидкость несжимаема). В силу линейности сформулированной краевой

задачи параметр ε войдет в решение в первой степени. Этим параметром

определяется лишь масштаб скорости движения жидкости, вызванного пре-

цессией цилиндра. Оставшиеся пять параметров образуют всего три незави-

112

симые безразмерные комбинации:

a-h

(14)

Ωa²

которые и будут критериями подобия в рассматриваемой задаче.

5. Вычисление гидродинамической силы

Перейдем к решению краевой задачи (11)-(13). Будем искать решение си-

стемы (11) в виде:

[

]

[

]

θ = 2Re Θ(r)eiφ ,

ψ = 2Re Ψ(r)eiφ ,

i² = -1.

Из третьего уравнения системы (11) найдем

[(

]

c₂ )

(15)

θ = 2Re c₁r +

eiφ ,

после чего второе уравнение сведется к виду

)

d²Ψ

1 dΨ

( iω₀

2Ω(

c₂ )

(16)

Ψ=-

c₁r +

dr²

r dr

r²

Интегрируя (16), получим

([

]

)

(

2Ω

c₂ )

ψ = 2Re

i c₁r +

+ c₃L₁(kr) + c₄M₁(kr) eiφ

ω₀

(17)

L₁ = e^-κaH⁽²⁾¹(kr), M₁ = e^κbH⁽¹⁾¹

(kr),

√

(

)

ω₀

|ω₀|

k=κ

κ=

b = a - h.

|ω₀|

2ν

где H^n1,2)(kr) функции Ганкеля.

Выражение для давления найдем из первого уравнения (11):

([

]

)

(

)

ω²εr

Ω²r²

(18)

= 2Re

-iω₀

c₁r +

e^iφ

- 2Ωψ +

+ C.

Радиальное отклонение свободной поверхности жидкости η(φ) ищем в виде

(19)

η(φ) = 2Re (η^∗e^iφ

Подставляя (15), (17)-(19) в граничные условия (12), (13), получим

систему линейных алгебраических уравнений относительно постоянных

113

c₁,c₂,c₃,c₄, выражения для η^∗ и аддитивной постоянной в (18):

3-τ

1+τ c₂

c₁ +

Z₁(ka) = 0,

1-τ

1-τa²

3-τ

1 + τ ic₂

ic₁ -

- kZ₀(ka) +

Z₁(ka) = 0,

1-τ

1-τ a²

(

)

1 + τ 4i

(20)

c₂ +

Z₀(kb) + k² -

Z₁

(kb) = 0,

1-τb³

b²

]

τ²(3 - τ)

[2 - 4τ + τ

ibc₁ +

(1 + τ)

c₂ -

(1 - τ)²

k²b²

)

1-τ

( 2τ - 1

1-τ

-2

Z₀(kb) +

Z₁(kb) = -

τ²Ωεb,

1-τ

k²b²

3-τ

1+τc₂

p₀

Ω²b

iω₀η^∗ =

c₁ +

Z₁(kb), C =

1-τ

1-τb²

где

(21)

τ =

Z_n(kr) = c₃L_n(kr) + c₄M_n

(kr),

L_n(kr) = e^-κaH⁽²⁾ⁿ(kr), M_n(kr) = e^κbH⁽¹⁾ⁿ(kr).

При выводе (20) были использованы известные формулы для производ-

ных от цилиндрических функций [5]. В ряде интересных случаев значение kr

(b ≤ r ≤ a) очень велико, что позволяет также использовать в (20) асимп-

тотические разложения для этих функций. Применение перенормированных

функций Ганкеля L_n(kr) и M_n(kr) оказывается при этом очень удобным.

После того как найдены постоянные c₁, c₂, c₃, c₄, краевая задача (11)-(13), в

принципе, решена. Обратимся к вычислению силы, с которой жидкость дей-

ствует на цилиндр. Интегрируя напряжения, приложенные к внутренней по-

верхности цилиндра, получим для компонент силы, действующей на единицу

его длины:

]

c₂

Fξ = 2πaρRe

ω²εa + 2i(Ω + ω)

(22)

Fη = -4πρ(Ω + ω)Re c2.

В случае когда частота прецесси ω → Ω, можно сравнительно просто вы-

разить c₂ из (20), воспользовавшись асимптотическими разложениями для

цилиндрических функций при малых значениях аргумента [5], и записать

(22) в виде:

Fξ = πρΩ²a²ε + O(ω0),

(

)

(23)

8πεµω₀(δ⁴

+ 1)

Fη =

+ O ω²⁰ln|ka| , δ =

δ⁴ - 1 - 2(δ⁴ + 1)lnδ

114

F_x*, F_h*

150

w/W

0,621

2,578

0,61

2,56

2,57

2,59

-150

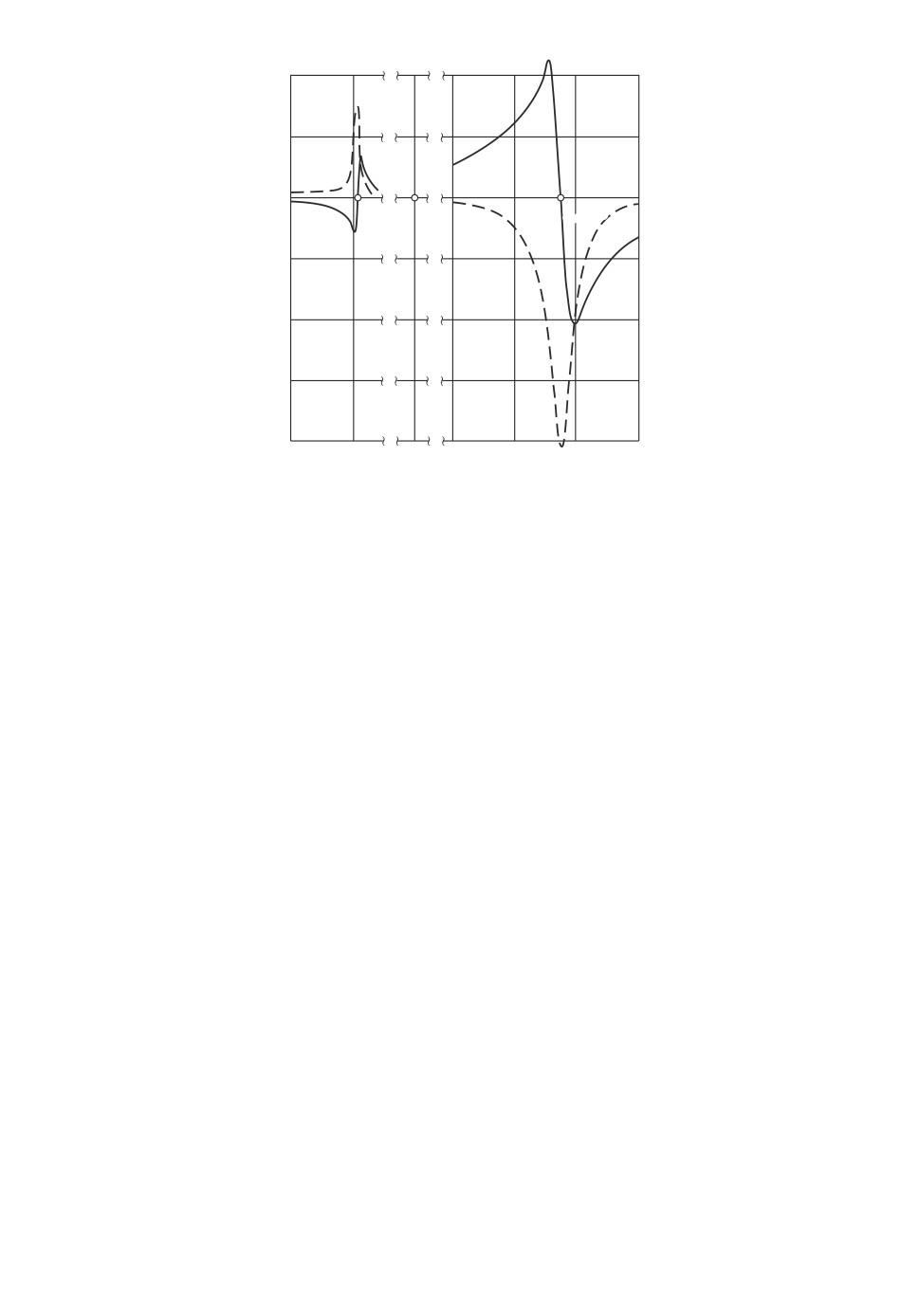
Рис. 2. Зависимости безразмерных компонент гидродинамической силы от па-

раметра τ.

Из выражений (23) видно, что в окрестности резонанса ω = Ω проекция

силы на линию центров F_ξ > 0, т.е. гидродинамическая сила стремится уве-

сти ось цилиндра от оси прецессии (на рис. 1 точка пересечения оси прецес-

сии плоскостью рисунка центр прецессии O₁). Далее, компонента силы F_η

может быть отлична от нуля только в случае вязкой жидкости. Знамена-

тель в выражении для F_η при 0 < δ < 1 положителен, следовательно, при

ω < Ω имеем F_η > 0, т.е. гидродинамическая сила стремится увеличить уг-

ловую скорость прецессии цилиндра, а при ω > Ω получаем, что F_η < 0 и

эффект действия силы обратный. Эти выводы согласуются с так называемой

концепцией вращающегося трения [6], распространенной в прикладных иссле-

дованиях. Отметим также, что момент гидродинамической силы (23) относи-

тельно оси цилиндра равен нулю. На рис. 2 изображены в качестве примера

зависимости безразмерных компонент гидродинамической силы F_ξ∗ = F_ξ /F⁰

(сплошные линии) и F_η∗ = F_η/F⁰ (штриховые линии) от ω/Ω, полученные

в соответствии с (20), (22) в случае δ = 0,5; ν/(Ωa²) = 10^-5. Масштаб силы

F⁰ = mω²ε, где m = πρ(a² - b²) масса жидкости, приходящаяся на еди-

ницу длины цилиндра. Зависимость силы от отношения частот имеет четко

выраженный резонансный характер, что обусловлено резонансным возбуж-

дением волн, распространяющихся по свободной поверхности вращающейся

жидкости, заполняющей цилиндр.

Сравнение результатов вычисления гидродинамической силы с силой, по-

лученной в рамках консервативной модели (µ = 0), показывает хорошее ко-

личественное совпадение ξ-компонент вне окрестностей резонансных значе-

ний ω/Ω. Вместе с этим в окрестностях резонансов, в отличие от того, что да-

ет консервативная модель, ξ-компонента гидродинамической силы конечна и

сравнима по величине с η-компонентой. Важно также отметить, что в окрест-

ностях резонансов, даже при весьма малых значениях параметра ν/(Ωa²) вол-

115

новое движение, вызванное прецессией цилиндра, всюду в жидкости сильно

отличается от того движения, которое дает консервативная модель.

6. Построение области устойчивости стационарного вращения

в плоскости параметров закрепления оси цилиндра

Подставим вычисленную гидродинамическую силу, действующую на еди-

ницу длины цилиндра, в уравнения движения цилиндра, положив в правых

частях (1):

Fx = Fξ cos(ωt) - Fη sin(ωt),

Fy = Fξ sin(ωt) + Fη cos(ωt).

Положив затем в (1) x₀ = ε cos ωt; y₀ = ε sin ωt , что соответствует круговой

прецессии с частотой ω и радиусом ε, получим соотношения, связывающие ω

и параметры задачи в случае круговой прецессии:

(24)

K^∗ -

τ² = F^∗ξτ², H^∗τ = F^∗ητ², K^∗ =

H_∗ =

mΩ²

mΩ

где K∗,H^∗

соответственно, безразмерные коэффициенты жесткости и

демпфирования закрепления оси цилиндра. Безразмерные компоненты си-

лы F^∗ξ, F^∗η зависят только от параметров (14). При фиксированных значе-

ниях этих параметров соотношения (24) задают в плоскости H^∗, K^∗ кри-

вую, точкам которой соответствуют такие значения параметров, при кото-

рых возможна круговая прецессия цилиндра. Эта кривая в соответствии со

сделанными выше замечаниями разбивает плоскость параметров закрепле-

ния оси цилиндра H^∗, K^∗ на области с различной степенью неустойчивости.

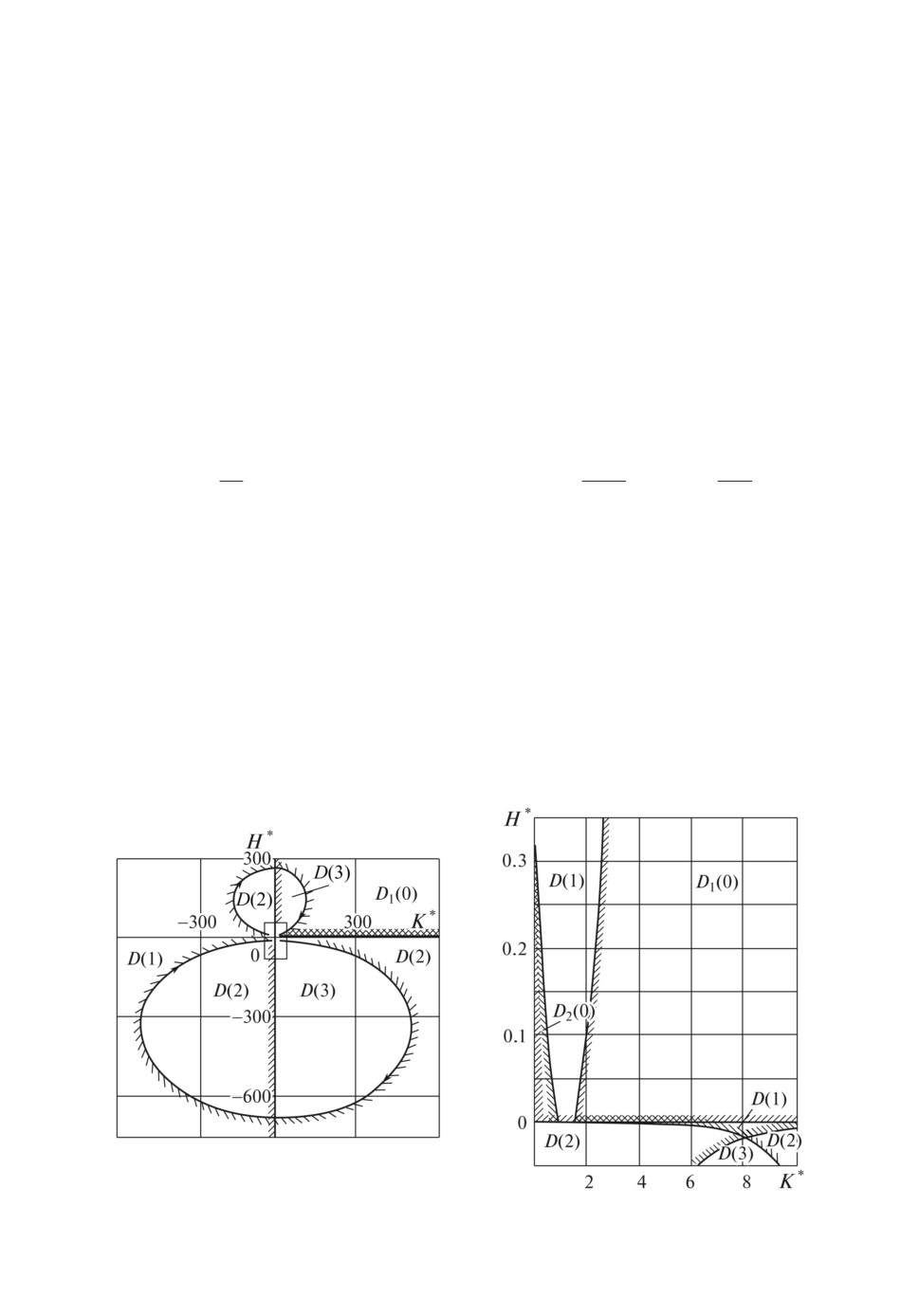
Следуя [2], будем называть ее D-кривой. На рис. 3 приведено разбиение плос-

кости H^∗, K^∗, осуществляемое D-кривой, в случае δ = 0,9, ν/(Ωa²) = 10^-6,

Рис. 3. D-кривая.

116

M/m = 1,68. Стрелкой вдоль D-кривой указано направление возрастания па-

раметра τ. D-кривая на рис. 3 образована регулярной ветвью, вдоль которой

параметр τ изменяется в интервале (-∞, +∞), и каждому значению парамет-

ра τ соответствует одна точка кривой и особой прямой K^∗ = 0, соответствую-

щей τ = 0. Наличие особой прямой вызвано тем, что при τ = 0 компоненты

гидродинамической силы обращаются в нуль.

D-кривую принято штриховать так, что переход в плоскости параметров

со штрихованной стороны кривой на нештрихованную соответствует увеличе-

нию степени неустойчивости. Штриховка может переходить с одной стороны

D-кривой на другую в тех точках, где нарушается однозначность отображе-

ния мнимой оси плоскости λ в точки D-кривой [2]. В рассматриваемой здесь

задаче штриховка D-кривой меняется в точке регулярной ветви, соответст-

вующей значению τ = 0, поскольку при этом значении τ нарушается одно-

значность вышеназванного отображения (точке τ = 0 на мнимой оси плоско-

сти λ соответствует особая прямая в плоскости параметров закрепления оси

цилиндра).

Область устойчивости всегда должна содержать точку, соответствующую

достаточно большим положительным значениям коэффициента демпфиро-

вания H^∗. Исходя из этого, на рис. 3 указана область с нулевой степенью

неустойчивости D₁(0). Указаны также области D(n) со степенью неустойчи-

вости n. Интересно отметить, что наряду с D₁(0) существует еще одна область

устойчивости D₂(0) в окрестности нулевых значений H^∗, K^∗ (разбиение

этой окрестности приведено в правой части рис. 3). Отметим также, что при

H^∗ = 0 точке на границе области устойчивости соответствует τ = 1, что со-

гласуется с известным результатом, установленным в [6] путем феноменоло-

гического введения сил внутреннего трения во вращающемся роторе.

7. Заключение

Предложенный метод исследования устойчивости был успешно применен

при решении ряда задач об устойчивости вращения роторных систем, содер-

жащих жидкость [7-12]. При этом одни задачи ставились впервые, а решение

других было, по сути дела, получено заново. Исследование поведения режи-

ма стационарного вращения цилиндра, частично заполненного вязкой несжи-

маемой жидкостью, вблизи границы области устойчивости в пространстве

параметров проведено в [13] впервые. Показано, что при переходе через эту

границу происходит бифуркация Андронова-Хопфа от режима стационар-

ного вращения рождается периодическое движение типа круговой прецессии.

В предложенном методе, в отличие от традиционного метода D-разбиения,

знание характеристического уравнения вообще не требуется. Более того, при

исследовании устойчивости достаточно ограничиться рассмотрением лишь

возмущений специального вида типа круговой прецессии. Последнее свя-

зано с учетом свойств симметрии уравнений движения рассматриваемой си-

стемы.

Выражаю благодарность Д.Н. Дерендяеву за помощь в оформлении ста-

тьи.

117

СПИСОК ЛИТЕРАТУРЫ

Гантмахер Ф.Р. Теория матриц. М.: Наука, 1967.

Неймарк Ю.И. Устойчивость линеаризованных систем. Л.: ЛКВВИА, 1949.

Дерендяев Н.В., Сандалов В.М. Об устойчивости стационарного вращения ци-

линдра, частично заполненного вязкой несжимаемой жидкостью // ПММ. 1982.

Т. 46. Вып. 4. С. 578-586.

Дерендяев Н.В., Сеняткин В.А. Условия устойчивости стационарного враще-

ния цилиндра, заполненного слоисто-неоднородной вязкой несжимаемой жид-

костью // ПМТФ. 1984. № 1. C. 34-44.

Ватсон Г.Н. Теория бесселевых функций. Ч. 1. М.: Изд-во иностр. лит., 1949.

Болотин В.В. Неконсервативные задачи теории упругой устойчивости. М.: Физ-

матгиз, 1961.

Дерендяев Н.В., Сандалов В.М. Устойчивость стационарного вращения ротора,

заполненного стратифицированной вязкой несжимаемой жидкостью // Маши-

новедение. 1986. № 1. С. 19-26.

Сандалов В.М. Динамическая неустойчивость турбомашин, обусловленная ра-

диальными зазорами в подшипниках скольжения и жидкостным наполнением

полостей роторов // Дисс. канд. физ.-мат. наук. Горький, 1983.

Сеняткин В.А. Неустойчивость роторных систем, обусловленная содержащейся

в них вязкой жидкостью // Дисс. канд. физ.-мат. наук. Горький, 1985.

10.

Солдатов И.Н. Устойчивость и автоколебания роторных систем, содержащих

проводящую вязкую жидкость в магнитном поле // Дисс. канд. физ.-мат. наук.

Нижний Новгород, 1994.

11.

Derendyaev N.V., Vostrukhov A.V., Soldatov I.N. Stability and Andronov-Hopf Bi-

furcation of Steady-State Motion of Rotor System Partly Filled with Liquid: Contin-

uous and Discrete Models // ASME. J. Appl. Mech. 2006. V. 73. No. 4. P. 580-589.

12.

Дерендяев Н.В. Устойчивость вращения роторных систем, содержащих жид-

кость. Нижний Новгород.: Изд-во Нижегород. гос ун-та, 2014.

13.

Дерендяев Н.В., Сандалов В.М., Солдатов И.Н. О рождении периодическо-

го движения в задаче об устойчивости стационарного вращения вертикально-

го ротора на гидродинамических подшипниках // Машиноведение. 1988. № 4.

C. 98-103.

Статья представлена к публикации членом редколлегии Б.Т. Поляком.

Поступила в редакцию 23.07.2019

После доработки 16.10.2019

Принята к публикации 30.01.2020

118