Автоматика и телемеханика, № 8, 2020

Ю.П. ЕМЕЛЬЯНОВА, канд. физ.-мат. наук (emelianovajulia@gmail.com)

(Арзамасский политехнический институт (филиал)

Нижегородского государственного технического

университета им. Р.Е. Алексеева)

CИНТЕЗ УПРАВЛЕНИЯ С ИТЕРАТИВНЫМ ОБУЧЕНИЕМ

ДЛЯ СИСТЕМ С ПЕРЕКЛЮЧЕНИЯМИ¹

В статье рассматриваются дискретные линейные системы с переклю-

чением параметров в повторяющемся режиме. Предлагается новый метод

синтеза управления с итеративным обучением. Метод основан на построе-

нии вспомогательной 2D-модели в форме дискретного повторяющегося

процесса, устойчивость которой гарантирует сходимость процесса обуче-

ния. Для получения условий устойчивости используется дивергентный

метод векторных функций Ляпунова. Вводится понятие среднего време-

ни ожидания относительно повторений. Приводится пример, демонстри-

рующий возможности и особенности нового метода.

Ключевые слова: управление с итеративным обучением, дискретные си-

стемы, системы с переключениями, повторяющиеся процессы, 2D-систе-

мы, устойчивость, диссипативность, векторная функция Ляпунова.

DOI: 10.31857/S0005231020080097

1. Введение

В современной теории управления под системами с переключениями обыч-

но понимают класс моделей динамических систем, состоящих из конечно-

го числа подсистем, из которых в текущий момент времени функциониру-

ет лишь одна, называемая активной подсистемой, при этом выбор актив-

ной подсистемы определяется некоторым логическим правилом. Простейшим

примером может служить многорежимная система, в которой подсистемы

интерпретируются как отдельные режимы этой системы. Обычно подсисте-

мы описываются индексированным множеством дифференциальных или раз-

ностных уравнений. Класс систем с переключениями интенсивно изучался в

последние десятилетия и продолжает активно изучаться, что мотивировано,

как многочисленными приложениями в технике, физике, биологии, экономи-

ке и других областях, так и открытыми в этом направлении теоретическими

задачами. Как и для других классов систем управления первоочередной ин-

терес здесь представляет развитие теории устойчивости и стабилизации, где

получен целый ряд интересных и важных результатов. Для первоначального

знакомства с этими результатами можно, в первую очередь, рекомендовать

монографию [1], обзорные статьи [2, 3] и недавние монографии [4, 5].

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 19-08-00528_а).

119

Начиная с 60-х годов прошлого века начала активно развиваться теория

2D систем. Ee появление мотивировали задачи обработки изображений и мно-

гомерных электрических цепей, где появились ставшие в настоящее время

классическими 2D модели Роессера и Форназини-Маркезини [6] и список ли-

тературы в [6]. Существенный всплеск развития теории 2D систем стимули-

ровали работы Аримото [7], в которых впервые было представлено теорети-

ческое обоснование алгоритмов управления с итеративным обучения (УИО)

для роботов, выполняющих повторяющиеся операции и выявлен естествен-

ный 2D характер процесса управления (он включает динамический процесс

на отдельном повторении и динамический процесс перехода от повторения

к повторению). Естественным описанием процессов УИО служат 2D моде-

ли в виде повторяющихся процессов [6, 8]. Теория повторяющихся процессов

успешно применялась к синтезу УИО в [9, 10], где были получены результаты,

подтвержденные экспериментально. В настоящее время теория и приложения

УИО продолжают интенсивно развиваться, им посвящены многочисленные

публикации. Для первоначального знакомства можно рекомендовать обзор-

ные статьи [11, 12]. Из недавних работ отметим [13], где УИО применяется

для высокоточного лазерного напыления металла и приводятся результаты

экспериментального подтверждения. Очень важным представляется приме-

нение УИО в медицинских роботах для реабилитации больных перенесших

инсульт. Известные разработки в этом направлении прошли клинические ис-

пытания [14, 15].

Повторяющиеся процессы с переключениями рассматривались в [16, 17].

Эти работы мотивированы задачей проката металла, где металлическая по-

лоска конечной длины приобретает желаемую форму проходя через систему

валков, так что выходная форма предыдущей группы валков является вход-

ной для следующей группы. В [16] такие системы моделировались линейны-

ми повторяющимися процессами с переключаемой динамикой. В обеих ци-

тированных статьях рассматриваются специальные правила переключения.

Конечными результатами этих исследований являются алгоритмы синтеза

закона управления, которые могут быть реализованы с использованием вы-

числений на основе линейных матричных неравенств.

Отметим ряд совсем недавних работ [18-21]. В статье [18] рассматривается

класс дискретных систем с переключениями, состоящих из линейной части

и статической нелинейности, удовлетворяющей ограничениям специального

вида. Вводятся определения экспоненциальной устойчивости и среднего вре-

мени ожидания и устанавливаются достаточные условия экспоненциальной

устойчивости с использованием методов общей и множественной 2D функции

Ляпунова соответственно. Полученные результаты далее применяются для

синтеза управления с итеративным обучением. В [19] предлагается управле-

ниe c итеративным обучением высокого порядка для линейных дискретных

систем с переключениями при различных начальных условия на повторени-

ях и воздействии ограниченных по норме возмущений. Дискретные линей-

ные системы с переключениями рассматривались также в [20] где начальные

условия на повторениях предполагались одинаковыми. Полученный здесь за-

кон управления с итеративным обучением предполагает доступность полного

вектора состояния и обеспечивает монотонную сходимость ошибки обучения.

120

В [21] рассматриваются системы состоящие из переключаемой непрерывной

линейной части и липшицевой нелинейности. Предложен адаптивный закон

управления с итеративным обучением, предполагающий доступность полного

вектора состояния. Во всех перечисленных работах эффективно используется

техника линейных матричных неравенств.

В данной работе рассматриваются линейные дискретные системы с пере-

ключениями. В отличие от цитированных и других известных работ доступ-

ным для измерения является только вектор выхода и закон управления с

итеративным обучением формируется на основе ошибки и оценки вектора

состояния. Предлагаемый подход развивает результаты авторов [22-25] для

систем с переключениями и его отличие от известных состоит в том, что он

эффективно использует оценки переменных состояния для улучшения харак-

теристик процесса обучения и открывает возможность синтеза нелинейных

законов управления, переключаемых в зависимости от достигнутой точности.

Дается пример, в котором рассматривается динамическая модель гибкого по-

воротного звена в повторяющемся режиме [26]. Получены переключаемые и

непереключаемые законы управления с итеративным обучением и приводит-

ся их сравнение.

2. Постановка задачи

Рассмотрим дискретную систему в повторяющемся режиме, описываемую

линейной моделью c переключениями

x_k(p + 1) = A(k)x_k(p) + B(k)u_k(p), (A(k),B(k)) ∈ F,

(2.1)

y_k(p) = Cx_k

(p), p ∈ [0, T - 1], k = 0, 1, . . . ,

где T число шагов на каждом повторении, x_k(p) ∈ Rnx вектор состояния,

y_k(p) ∈ Rny вектор выходных переменных, u_k(p) ∈ Rnu вектор управле-

ния, F = {(A₁, B₁), (A₂, B₂), . . . , (A_N , B_N )} множество пар матриц согласо-

ванных размеров.

Следуя понятиям, принятым в теории систем с переключениями [1], рас-

смотрим кусочно постоянное отображение множества неотрицательных це-

лых чисел Z⁺ → F. Такое отображение задается кусочно постоянной функ-

цией σ : Z⁺ → N = {1, . . . , N} так, что A(k) = A_σ(k) и B(k) = B_σ(k), k =

= 0, 1, 2

Функцию σ можно рассматривать как сигнал переключения относитель-

но повторений. Предположим, что переключения происходят в начале каж-

дого повторения и определим моменты переключения k₁, k₂, . . . как номера

повторений, на которых в системе (2.1) происходят переключения. Таким

образом, сигнал переключения определяет на каждом повторении k индекс

σ(k) = i ∈ N активной подсистемы, динамика которой описывается уравне-

ниями

x_k(p + 1) = A_ix_k(p) + B_iu_k(p), i ∈ N,

(2.2)

y_k(p) = Cx_k

(p), p ∈ [0, T - 1], k = 0, 1, . . .

121

Будем предполагать, что моменты переключений наблюдаемы и импульс-

ные эффекты отсутствуют, т.е. значение вектора состояния в момент пере-

ключения не меняется скачком, и остается неизменным.

Выходная переменная системы (2.1) на каждом повторении должна вос-

производить желаемую траекторию y_ref (p), 0 ≤ p ≤ T - 1. Для достижения

этой цели можно использовать управление с обратной связью. Обозначим че-

рез e_k(p) ошибку воспроизведения желаемой траектории на k-м повторении

(2.3)

e_k(p) = y_ref(p) - y_k

(p),

0 ≤ p ≤ T - 1.

Если начальные условия на каждом повторении одинаковы управление с об-

ратной связью будет обеспечивать одинаковую ошибку воспроизведения же-

лаемой траектории на всех шагах, причем может оказаться, что величина

этой ошибки не соответствует требованиям по точности. Поставим задачу

найти такую последовательность входных переменных u_k(p), k = 0, 1, . . . , ко-

торая обеспечивает достижение заданной точности воспроизведения профиля

за конечное число повторений k_fin и сохранение этой точности при дальней-

ших повторениях, т.е.

(2.4)

|e_k(p)| ≤ e^∗, k ≥ k_fin

0 ≤ p ≤ T - 1.

Для решения используем подход на основе управления с итеративным обу-

чением, при котором на очередном повторении входная переменная опреде-

ляется соотношением

(2.5)

u_k+1(p) = u_k(p) + Δu_k+1

(p),

где Δu_k+1(t) корректирующая поправка. Поставленная задача будет реше-

на, если эта поправка обеспечит выполнение условий,

(2.6)

lim

|e_k(p)| = 0, lim

|u_k(p) - u_∞

(p)| = 0,

0≤p≤T -1

k→∞

где u_∞(p) ограниченная переменная, обычно называемая обученным управ-

лением.

3. Дискретная 2D модель

Для формирования корректирующей поправки, следуя [25], будем исполь-

зовать ошибку обучения и оценку вектора состояния x_k(p), которая получа-

ется с помощью наблюдателя полного порядка.

(3.1)

x_k(p + 1) = A_ix_k(p) + B_iu_k(p) + F_i(y_k(p) - Cx_k

(p)), i ∈ N .

Введем в рассмотрение ошибку оценивания и приращения оценки и ошибки

оценивания

x_k(p) = x_k(p) - x_k(p),

(3.2)

ξ_k+1(p + 1) = x_k+1(p) - x_k(p),

122

тогда динамику системы с наблюдателем относительно приращений можно

описать уравнениями:

ξ_k+1(p + 1) = (A_i - F_iC

ξ_k+1(p),

(3.3)

ξ_k+1(p + 1) = F_i

ξ_k+1(p) + A_i

ξ_k+1(p) + B_iv_k+1(p),

e_k+1(p) = -CA_i

ξ_k+1(p)-CA_iξk+1(p)+ek(p)-CBivk+1(p), i∈N,

где

v_k+1(p) = Δu_k+1(p - 1).

Обозначим

[

]

[

]

Ai - FiC

η_k(p) =

ξ_k(p)^T

ξ_k(p)^T]^T, A_i11 =

B_i1 =

FiC

A_i

B_i

[

]

A_i12 =

A_i21 = [-CA_i

- CA_i], A₂₂ = I, B_i2 = -C_iB

и запишем (3.3) в виде стандартной модели дискретного повторяющегося про-

цесса [6]:

η_k+1(p + 1) = A_i11η_k+1(p) + A_i12e_k(p) + B_i1v_k+1(p),

(3.4)

e_k+1(p) = A_i12η_k+1(p) + A_i22e_k(p) + B_i2v_k+1

(p), i ∈ N .

Корректирующую поправку будем искать в виде закона обратной связи по

приращениям

(3.5)

Δu_k+1(p - 1) = v_k+1(p) = ϕ(η_k+1(p),e_k

(p)), ϕ(0, 0) = 0.

Если для всех 0 ≤ p ≤ T - 1 |e_k(p)| → 0 при k → ∞, то существует k_fin, при

котором выполняются условия (2.4). Таким образом, поставленная задача

будет решена, если найдется последовательность v_k(p), такая что

(3.6)

lim

|e_k(p)| = 0,

|u_∞

(p)| < ∞,

0 ≤ p ≤ T - 1,

k→∞

при условии, что норма ошибки ограничена сверху монотонно убывающей

функцией, где u_∞(p) = lim_k→∞ u_k(p). Ясно, что в этом случае существует k_fin,

начиная с которого будет выполнено условие (2.4).

4. Основные результаты

4.1. Условия устойчивости

Обозначим число переключений сигнала σ на интервале (k_s, k_f ) через

N_σ(k_f ,k_s) и введем в рассмотрение среднее время ожидания в соответствии

со следующим определением

123

Определение 1. Положительное число κ_a ∈ Z⁺ называется средним

временем ожидания для сигнала переключения относительно повторений σ,

если для некоторого N₀ ≥ 0

k_f - k_s

(4.1)

N_σ(k_f ,k_s) ≤ N₀ +

k_f ≥ k_s

≥ 0.

κ_a

Неравенство (4.1) означает, что в среднем число шагов между любыми дву-

мя последовательными переключениями на рассматриваемом интервале не

меньше чем κ_a.

Решение будем искать на основе развития теории устойчивости и дисси-

пативности повторяющихся процессов [22].

Определение 2

[22]. Система (3.4), (3.5) называется экспоненциаль-

но устойчивой, если существуют числа κ > 0 и 0 < ̺ < 1, такие что

(4.2)

|η_k(p)|² + |e_k(p)|² ≤ κ̺^k+p,

где ̺ не зависит от T .

Заметим, в случае выполнения (4.2) гарантируется указанная в предыду-

щем разделе ограниченность нормы ошибки монотонно убывающей функци-

ей, что, в свою очередь, обеспечивает достижение заданной точности.

Система (3.4), (3.5) в общем случае нелинейна. Универсальным методом

анализа устойчивости нелинейных систем является второй метод Ляпуно-

ва. Однако уравнения рассматриваемой системы не разрешены относительно

полных приращений переменных состояния, и применить этот метод непо-

средственно невозможно. Для преодоления этой трудности авторами разра-

ботан так называемый дивергентный метод векторных функций Ляпунова,

в котором, в отличие от классической версии, устойчивость устанавливается

на основе свойств дивергенции (дискретного аналога дивергенции) указанных

векторных функций. В рассматриваемом случае введем векторную функцию

Ляпунова так:

[

]

1(ηk+1(p))

(4.3)

V_i(η_k+1(p),e_k(p)) =

i∈N,

V_2i(e_k(p))

где V₁(x_k+1(p)) > 0, x_k+1(t) = 0, V_2i(e_k(p)) > 0, y_k(p) = 0, V₁(0) = 0, V_2i(0) = 0,

i ∈ N. Аналог дивергенции этой функции определим как

(4.4)

DV (η_k+1(p),y_k(p)) = Δ_pV₁(η_k+1(p)) + Δ_kV₂(e_k

(p)),

где Δ_pV₁(η_k+1(p)) = V₁(η_k+1(p + 1)) - V₁(η_k+1(p)), Δ_kV₂(e_k(p)) = V₂(e_k+1(p)) -

-V₂(e_k(p)).

Теорема 1. Дискретный повторяющийся процесс (3.4), (3.5) являет-

ся экспоненциально устойчивым для любого сигнала переключения относи-

тельно повторений σ со средним временем ожидания

)(

(

))_-1

(c₁

c₃

(4.5)

κ_a > ln

c₂

c₁

124

и произвольным N₀, если существует векторная функция (4.3) и положи-

тельные скаляры c₁, c₂ и c₃, такие что

(4.6)

c₁|η|² ≤ V₁(η) ≤ c₂|η|²,

(4.7)

c₁|e|² ≤ V_2i(e) ≤ c₂|e|²,

(

)

(4.8)

DV_i(η_k+1(p),e_k(p)) ≤ -c₃

|η_k+1(p)|² + |e_k(p)|²

Доказательство. Рассмотрим интервал

(0, k_f ) и обозначим через

N_σ = N_σ(k_f ,0) число переключений на этом интервале. Из неравенства (4.8)

следует

(

)

(4.9)

DV_σ(k)(η_k+1(p),e_k(p)) ≤ -c₃

|η_k+1(p)|² + |e_k(p)|²

Используя (4.6), (4.7) и (4.8), неравенство (4.9) можно переписать как

V₁(η_k+1(p + 1)) - V₁(η_k+1(p)) + V_2σ(k+1)(e_k+1(p)) - V_2σ(k)(e_k(p)) ≤

(4.10)

(

)

≤ -c₃

|η_k+1(p)|² + |e_k(p)|²

≤-

c₃ (V₁(η_k+1(p) + V_2σ(k)(e_k(p)))),

c₂

или

V₁(η_k+1(p + 1)) + V_2σ(k+1)(e_k+1(p)) ≤

(

(4.11)

)(

)

c₃

≤

V₁(η_k+1(p)) + V_2σ(k)(e_k(p))

c₂

Левая часть (4.11) является положительно определенной, следовательно 0 <

< 1 - c3c₂ < 1. Обозначим λ = 1 - c3 и перепишем (4.11) в виде2

V₁(η_k+1(p + 1)) ≤ λV₁(η_k+1(p)) + λV_2σ(k)(e_k(p)) - V_2σ(k+1)(e_k+1

(4.12)

(p)).

Решая неравенство (4.12) относительно V₁(x_k+1(p)) получим

V₁(η_k+1(p)) ≤ V₁(η_k+1(0))λ^p +

[

]

∑

(4.13)

λV_2σ(k)(e_k(h)) - V_2σ(k+1)(e_k+1(h)) λ^p-1-h.

h=0

∑_p-1

Обозначим H_k,σ(k)(p) =

V_2,σ(k)(e_k(p))λ^p-1-h, тогда из (4.13) следует что

h=0

(4.14)

H_k+1,σ(k+1)(p) ≤ λH_k,σ(k)(p) + λ^pV₁(η_k+1(0)) - V₁(η_k+1

(p)).

Пусть на некотором повторении k_n активный режим i переключается на ре-

жим j. Из условия (4.7) следует, что

(4.15)

V_2j(e) ≤ µV_2i

(e), i, j ∈ N ,

где µ =c2 ≥ 1. Решая неравенство (4.14) с учетом (4.15) получим_c

H_k,σ(k)(p) ≤ µNσ λ^kH_0,σ(0)(p) +

(

)

∑

(4.16)

+ µNσ λ^k-1-n λ^pV₁(η_n+1(0)) - V₁(η_n+1(p)) ,

n=0

125

или

∑

λ^k-1-nV₁(η_n+1(p)) +

λ^p-1-hV_2σ(k)(e_k(h)) ≤

n=0

h=0

∑

(4.17)

≤ µNσ λ^k-1-nV₁(η_n+1(p)) + λ^p-1-hV_2σ(k)(e_k(h)) ≤

n=0

h=0

(

)

∑

≤ µNσ λ^p λ^k-1-nV₁(η_n+1(0)) + λk

λ^p-1-hV_2,σ(0)(e₀(h))

n=0

h=0

Из неравенства (4.17) следует, что

∑

(4.18) λ^-(p-1)

λ^-nV₁(η_n+1

(p)) + λ^-(k-1)

λ^-hV_2σ(k)(e_k(h)) ≤

n=0

h=0

(

∑

≤ µNσ λ^-(k-1) λ^k-1-nV₁(η_n+1(0)) +

n=0

)

∑

+λ^-(p-1)

λ^p-1-hV_2,σ(0)(e₀(h))

h=0

По условию все повторения начинаются с одними и теми же начальными усло-

виями, следовательно V₁(η_n+1(0)) = 0. Кроме того, поскольку y_ref (p) ограни-

чена для всех p, то |e_o(p)|² = f(p) ≤ M_f . Тогда левую часть (4.18) можно

оценить следующим образом:

(

∑

(4.19) µNσ λ^-(k-1)

λ^k-1-nV₁(η_n+1(0)) +

n=0

)

∑

+λ^-(p-1)

λ^p-1-hV_2,σ(0)(e₀(h))

≤

h=0

∑

c₂M_f(λ^-T - 1)

≤µNσc₂M_f λ^-h ≤µNσ

=C_fµ^N

λ^-1 - 1

h=0

для всех k ≤ k_f и p ∈ [0, T ]. С учетом (4.19) из (4.18) следует

∑

(4.20)

C_fµNσ ≥ λ^-(p-1)

λ^p-1-hV₂(y₀(p)) ≥ c₁λ^-(k-1)λ^-(p-1)|η_k(p)|²,

h=0

∑

(4.21)

C_fµNσ ≥ λ^-(p-1)

λ^p-1-hV₂(y₀(h)) ≥ c₁λ^-(k-1)λ^-(p-1)|e_k(p - 1)|²

h=0

126

для всех k ≤ k_f и p ∈ [0, T ]. Полагая k = k_f с учетом (4.5) из (4.18)-(4.21)

получим

N₀

Cµ

|ηkf (p)|² + |e_k

(p)|² ≤

λkf +p0

c₁λ

для любых k_f и p ∈ [0, T ], где λ₀ = µκa1 = (c₂/c₁)κa1 < 1. Это доказывает

справедливость утверждения теоремы.

Из доказательства теоремы вытекает следующий результат.

Следствие 1. Дискретный повторяющийся процесс (3.4), (3.5) являет-

ся экспоненциально устойчивым для произвольного сигнала переключения

относительно повторений σ, если существует векторная функция

(4.22)

V (η_k+1(p), e_k(p)) = [V₁(η_k+1(p)) V₂(e_k(p))]^T

и положительные скаляры c₁,c₂, c₃, такие что

c₁|η|² ≤ V₁(η) ≤ c₂|η|²,

(4.23)

c₁|e|² ≤ V₂(e) ≤ c₂|e|²,

(

)

DV (η_k+1(p),e_k(p)) ≤ -c₃

|η_k+1(p)|² + |e_k(p)|²

4.2. Синтез на основе теории диссипативности

Введем в рассмотрение вспомогательный вектор

(4.24)

z_k+1(p) = C₁η_k+1(p) + C₂e_k(p) + Dv_k+1(p),

где C₁, C₂ и D постоянные матрицы согласованных размеров. Следуя [22]

введем следующее определение.

Определение 3. Дискретный повторяющийся процесс (3.4) называ-

ется экспоненциально диссипативным относительно входной переменной

v_k+1(t) и выходной переменной z_k+1(t), определенной в (4.24), если существу-

ют векторная функция (4.3) и положительные скаляры c₁, c₂ и c₃ такие,

что

c₁|η_k+1(p)|² ≤ V₁(η_k+1(p)) ≤ c₂|η_k+1(p)|²,

c₁|e_k(p)|² ≤ V_2i(e_k(p)) ≤ c₂|e_k(p)|²,

(

)

DV_i(η_k+1(t),e_k(t)) ≤ S_i(z_k+1(p),v_k+1(p)) - c₃

|η_k+1(t)|² + |e_k(t)|²

i∈N,

где S_i - скалярная функция, такая что S_i(0, 0) = 0.

В теории диссипативности по Виллемсу функции S_i и V_i называют-

ся функцией запаса и функцией накопления. Нетрудно видеть, что если

при некотором выборе z последовательность (3.5) удовлетворяет условию

S_i(z_k+1(p),v_k+1(p)) ≤ 0, i ∈ N, то система (3.4), (3.5) в соответствии с тео-

ремой 1 будет экспоненциально устойчива для любого сигнала переключения

127

относительно повторений σ со средним временем ожидания (4.5). Таким об-

разом, задача сводится к нахождению стабилизирующей тройки {V, z, v}.

Обозначим

[

]

[

]

[

]

A_i11

A_i12

B_i1

ζ_k+1(p) =^k+1(

A_i =

B_i =

i∈N.

e_k(p)

A_i21

A_i22

B_i2

Определим блочно-диагональную матрицу P_i = diag[P₁ P_2i] ≻ 0 как решение

неравенства Риккати

[

(4.25)

A^TiP_iA¯-(1-σ)P_i

A^TiP_i B_i

P_i B_i +R

]^-1 BTPiA¯i

+Q≼0, i∈N,

где 0 < σ < 1 - положительный скаляр, Q ≻ 0 и R ≻ 0 весовые матрицы.

Нетрудно видеть, что если система линейных матричных неравенств





(1 - σ)X_i

XA¯^T

X_i





(4.26)



A_iX_i X_i +BiR^-1 B^Ti

 ≽ 0, Xi ≻ 0, i ∈ N

X_i

Q^-1

разрешима относительно X_i = diag[X₁ X_2i] ≻ 0, то P_i = X^-1i, i ∈ N .

Следующая теорема предлагает одно из возможных множеств стабилизи-

рующих троек.

Теорема 2. Дискретный повторяющийся процесс (3.4) является экспо-

ненциально диссипативным с функцией запаса

(

S_i(v_k+1(p),z_k+1(p)) = z^Tk+1(p)

P_i B_i + R)-1 zk+1(p) +

(4.27)

[

]

+ 2z_k+1(p)^Tv_k+1(p) + v_k+1(p)^T

P_i B_i + R

v_k+1(p), i ∈ N

относительно входной переменной v_k+1(p) и выходной переменной

(4.28)

z_k+1(p) =BTiP_iA¯_iζ_k+1

(p), i ∈ N ,

где P_i = X^-1i, X_i = diag[X₁ X₂i] ≻ 0 i ∈ N ,

решение (4.25). Множество

последовательностей корректирующих поправок (3.5), обеспечивающих экс-

поненциальную устойчивость системы (3.4), (3.5) определяется соотноше-

нием

[

]_-1

(4.29)

v_k+1(p) = -

P_i B_i + R

PA¯_iΘ_i(ζ_k+1(p))ζ_k+1

(p), i ∈ N ,

где Θ(ζ) симметричная матричная функция, удовлетворяющая соотно-

шению

(4.30)

M_i - M_iΘ_i(ζ) - Θ_i(ζ)M_i + Θ_i(ζ)M_iΘ_i(ζ) - Q - (σ - µ)P_i

≺ 0, i ∈ N

для всех ζ ∈ R2nx+ny , где M_i

A^TiP_i B_i[BTiP_i B_i + R]^-1 B^TiP_iA¯_i, 0<µ<σ,

i∈N.

128

Доказательство. Выберем компоненты векторной функции накопле-

ния (4.3) в виде квадратичных форм:

V₁(η_k+1(p)) = η_k+1(p)^TP₁η_k+1(p), V_2i(e_k(p)) = e_k(p)^T(t)P₂e_k(p), i ∈ N,

где P₁ ≻ 0 и P₂ ≻ 0 диагональные блоки матрицы P , представляющей собой

решение (4.25). Вычисляя аналог дивергенции (4.3) вдоль траекторий (3.4),

получим, что

(4.31)

DV_i(η_k+1(p),e_k

(p)) =

(

)

[

]

^-1 BT

= ζ_k+1(p)^T

A^Ti

A_i -(1-σ)P_i

A^TiP_i B

P_i B_i +R

P_iA¯_i +Q ζ_k+1(p)+

[

]_-1

+ζ_k+1(p)^TA¯^TiP_i B

P_i B_i +R

P_iA¯_iζ_k+1(p)-ζ_k+1(p)^T(Q+σP_i)ζ_k+1(p)+

+ 2ζ_k+1(p)^TA¯Ti P_i B_iv_k+1(p) + v_k+1(p)^T BTi P_i B_iv_k+1(p) ≤

[

]_-1

≤ ζ_k+1(p)^TA¯Ti P_i B_i

P_i B_i +R

P_iA¯ζ_k+1(p)+2ζ_k+1(p)^TA¯^TiP_i B_iv_k+1(p) +

[

]

+ v_k+1(p)^T

P_i B_i + R

v_k+1(p) - ζ_k+1(p)^T(Q + σP_i)ζ_k+1(p), i ∈ N.

Из (4.31) следует, что (3.4) экспоненциально диссипативна относительно вход-

ной переменной v_k+1(p) и выходной переменной (4.28) с функцией запаса

(4.27). Из (4.31) также следует, что если последовательность (3.5) определя-

ется соотношением (4.29), то

(

)

DV_i(η_k+1(p),e_k(p)) ≤ -µλ_min(P_i)

|η_k+1(p)|² + |e_k(p)|²

и в соответствии с теоремой 1 система (4.29), (3.4) является экспоненциально

устойчивой для любого сигнала переключения относительно повторений σ со

средним временем ожидания (4.5). Теорема 2 доказана.

Замечание 1. Посколькуприращениеошибкиоценивани

ξ_k+1(p) недо-

ступно для формирования корректирующей поправки, матрица Θ_i всегда

должна иметь иметь вид Θ_i(ζ) = diag[0nx Θ_i1(ζ)]. В простейшем случае мат-

рица Θ_i1 может быть выбрана не зависящей от ζ и тогда, после того, как

матрица P_i найдена, условие (4.30) сводится к системе линейных матричных

неравенств, при этом теорема 2 дает линейную последовательность коррек-

тирующих поправок. В общем случае Θ_i(ζ) зависит от изменения ошибки

относительно повторений и можно пытаться уменьшать значения коэффи-

циентов корректирующих поправок после достижения требуемой точности

и, наоборот, увеличивать эти коэффициенты, когда ошибка велика, другими

словами, вводить адаптацию к величине ошибки. Такой подход позволит най-

ти разумный компромисс между скоростью обучения и энергозатратами на

управление. Наиболее просто это можно сделать за счет кусочно-постоянного

изменения Θ, в зависимости от достигнутой точности. Такое решение для си-

стем без переключений рассмотрено в [24].

4.3. Альтернативный подход

В ряде случаев представляет интерес построить управление без переклю-

чений. Здесь более эффективным представляется другой подход к решению.

129

Рассмотрим функцию Ляпунова (4.22) с компонентами

V₁(ξ_k+1(p)) = ξ^Tk+1(p)P₁ξ_k+1(p), V₂(e_k) = e^Tk (p)P₂e_k(p),

где P₁ ≻ 0 и P₂ ≻ 0. Закон коррекции будем искать в виде линейной обратной

связи по приращениям доступных для измерения переменных и по ошибке

(4.32)

v_k+1(p) = K₁

ξ_k+1(p) + K₂e_k(p) = KHζ_k+1(p),

где K = [K₁ K₂], H = [0 Inx+ny ]. Вычисляя дивергенцию (4.22) вдоль траек-

торий (3.4), (4.32) получим

(

)

(4.33)

DV = x^T

A^TciP_iA¯_ci - P

x, i ∈ N,

где





A_i - F_iC

P_i = diag[P₁ P_2i],

A_ci = F_iC

A_i + B_iK₁

B_iK₂

, i ∈ N .

−CA_i

-C(A_i + B_iK₁) I - CB_iK₂

Предположим, что матрицы P ≻ 0 и K удовлетворяют системе неравенств

(4.34)

A_i +BiKH)^T P

A_i

B_iKH) - P_i + Q + H^T K^T

RKH ≼ 0, i ∈ N,

где Q ≻ 0 и R ≻ 0 матрицы аналогичные весовым матрицам в теории

линейно-квадратичного регулятора. Поскольку выполняется (4.33) то соглас-

но следствию теоремы 1 система (3.4), (4.32) является экспоненциально устой-

чивой для произвольного сигнала переключения относительно повторений σ.

Неравенства (4.34) с помощью известной леммы о дополнении Шура сводятся

к линейным матричным неравенствам и уравнению относительно переменных

X = diag[P^-11 P^-12] , Y , Z





A_iX +BiY H)^T X (Y H)^T







A_iX +BiY H







≽ 0,



Q^-1



(4.35)

R^-1

X ≻ 0, HX = ZH, i ∈ N.

Если неравенства и уравнение (4.35) совместны, то K = [K₁ K₂] = Y Z^-1, по-

скольку, в силу структуры матрицы H, матрица Z является невырожденной.

5. Пример

Рассмотрим модель манипулятора с одним гибким звеном [26], функцио-

нирующего в повторяющемся режиме с постоянным периодом повторения.

Динамика движения манипулятора в пространстве состояний описывается

уравнениями

(5.1)

x_k(t) = A₀x_k(t)+B₀u_k(t), y_k(t) = Cx_k(t),

0≤t≤T_f

, k =0,1,2,... ,

130

y_ref, рад

1,6

1,4

1,2

1,0

0,8

0,6

0,4

0,2

100

150

200

250

300

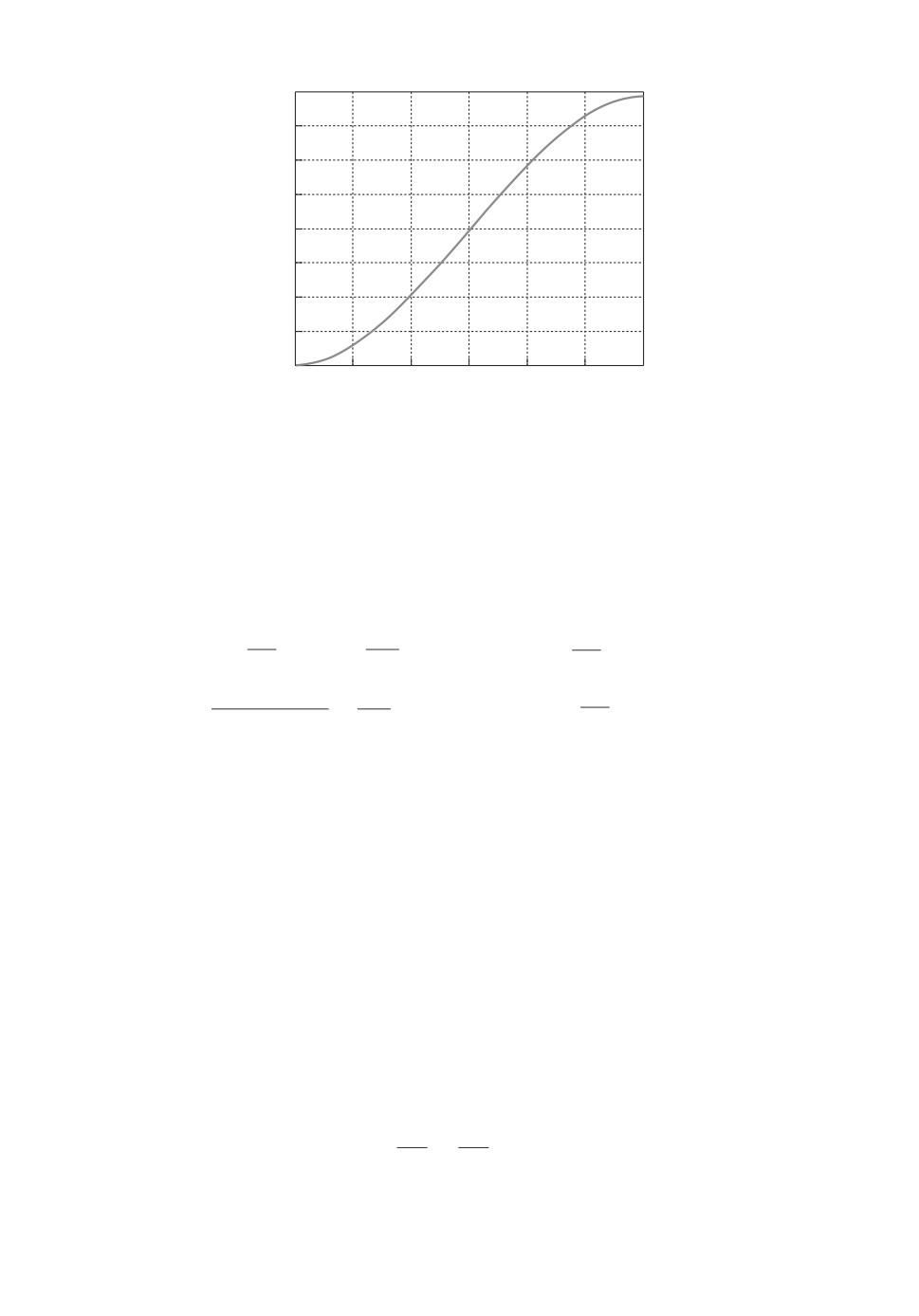
Рис. 1. Желаемая траектория изменения угла поворота вала сервомотора.

[

]_T

где x(t) = θ(t) α(t)

θ(t)

α(t)

, θ(t) угол поворота сервопривода, α(t)

угол отклонения гибкого звена,



































K_s

B_eq







A₀ =



,

B₀ =



,

C = [1

0] ,



J_eq





J_eq



















K_s(J_l + J_eq) B_eq

J_lJ_eq

J_eq

B_eq - коэффициент вязкого трения сервопривода, K_s - жесткость гибкого

звена, J_l - момент инерции гибкого звена относительно центра масс, J_eq -

момент инерции сервопривода. Движение гибкого звена происходит в гори-

зонтальной плоскости.

Задача состоит в том, чтобы найти алгоритм управления с итеративным

обучением, при котором выходная переменная y(t) = θ(t) воспроизводила бы

желаемую траекторию y_ref (t) с заданной точностью e^∗. Непосредственному

измерению доступен только угол θ.

Для расчетов и моделирования были приняты следующие номиналь-

ные значения параметров из [26]: B_eq = 0,004 Н·м/(рад/с), K_s = 1,3 Н·м/рад,

J_l = 0,0038 кг·м², J_eq = 2,08 · 10^-3 кг·м². Продолжительность цикла повторе-

ния T_f составляет 3 c, требуемая точность e^∗ = 0,5 град. = 0,00873 рад.

Желаемая траектория изменения выходной переменной описывается урав-

нением и представлена на рис. 1

πt

πt³

y_ref(t) =

t ∈ [0;T_f].

Предположим, что алгоритм управления реализуется на компьютере с пе-

риодом дискретности T_s = 0,01 c. Эквивалентная дискретная модель (5.1),

131

связывающая значения переменных в моменты 0, T_s, 2T_s, . . . запишется в

виде

(5.2)

x_k(p + 1) = Ax_k(p) + Bu_k(p), p = 0,1,... ,NTf

k = 0,1,2,...,

(

)

∫

где A = exp(A₀T_s), B =

exp(A₀τ)dτ B₀, NTf число периодов дискрет-

ности на отрезке [0, T_f ].

При начале работы манипулятора несколько первых повторений прохо-

дят без нагрузки для предварительной настройки, при этом значения па-

раметров соответствуют номинальным. После трех повторений манипуля-

тор нагружается, при этом J_l = 0,0076 кг · м², J_eq = 3,3 · 10^-3 кг · м². Исхо-

дя из физического смысла переменных состояния зададим весовые матрицы

Q = diag[10^-3I₈ 10⁶], R = 0,01. Рассматривая скачкообразное изменение на-

грузки на манипулятор как переключение, воспользуется результатами раз-

дела 4.3, которые удобны для сравнительного анализа. Обозначим матрицы

ненагруженного манипулятора через A₁, B₁ и матрицы нагруженного ма-

нипулятора A₂, B₂. Переключаемый алгоритм управления с итеративным

обучением имеет вид

x_k(p) = A_ix_k(p - 1) + B_iu_k(p - 1) + F_i(y_k(p - 1) - Cx_k(p - 1)),

{

если k < 3,

если k ≥ 3,

{

F₁ = [1,9199 - 1,8415 91,1151 - 84,9936]^T если k < 3,

Fi =

F₂ = [1,7575 - 1,7001 81,2812 - 78,3325]^T если k ≥ 3,

u_k(p) = u_k-1(p) + K₁ (x_k(p) - x_k-1(p)) + K_2i (y_ref(p) - y_k-1(p + 1)) ,

{

9,5140

если k < 3,

K₁ = [-31,0300 - 0,3018 - 0,4530 - 0,0444], K_2i =

27,1609

если k ≥ 3.

При использовании алгоритма без переключений

u_k(p) = u_k-1(p) + K₁ (x_k(p) - x_k-1(p)) + K₂ (y_ref(p) - y_k-1(p + 1)) ,

K₁ = [-28,1965 - 0,2408 - 0,4345 - 0,0395], K₂ = 12,8135.

В качестве меры точности воспроизведения желаемой траектории удобно вы-

брать среднеквадратическую ошибку обучения

∑

(5.3)

E(k) =

√

|e_k(p)|².

NTf

p=0

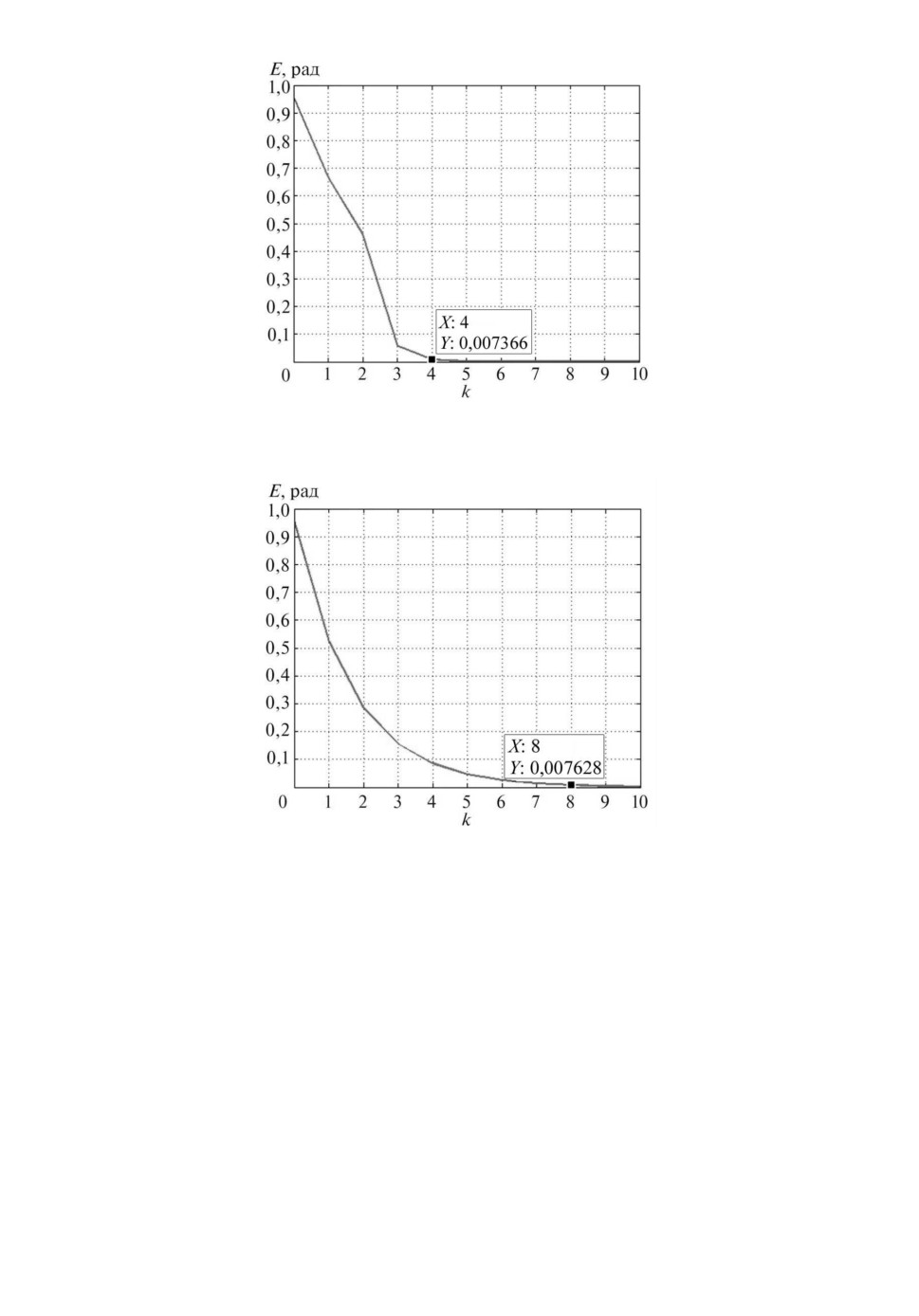
На рис. 2, 3 показано изменение среднеквадратической ошибки в зависимости

от числа повторений для управления с переключением и без переключения

соответственно.

132

Рис. 2. Изменение среднеквадратической ошибки в зависимости от числа по-

вторений для управления с переключением.

Рис. 3. Изменение среднеквадратической ошибки в зависимости от числа по-

вторений для управления без переключения.

Анализ полученных зависимостей показывает, что в случае управления с

переключением требуемая точность достигается сразу же после настроечных

повторений, в то время как в случае управления без переключений для дости-

жения нужной точности требуются дополнительные шаги в рабочем режиме,

что, очевидно, нежелательно.

6. Заключение

В данной работе предложен метод синтеза управления с итеративным обу-

чением с использованием наблюдателя состояния для систем с переключе-

ниями на основе теории 2D-систем в форме дискретных повторяющихся про-

цессов. Приведенный пример показывает, что в случае, когда переключения

133

наблюдаемы, управление с переключением позволяет ускорить сходимость

процесса обучения. Дальнейшее развитие исследований в данном направле-

нии авторы связывают с развитием теории для дифференциальных повто-

ряющихся процессов с переключениями и ее последующим применением к

задачам синтеза управления с итеративным обучением. Дальнейшего иссле-

дования требует вопрос выбора нелинейной функции Θ_i(ζ) в методе синтеза

на основе диссипативности (теорема 2 и замечание 1 к ней). Значительный

интерес представляют сетевые задачи управления с итеративным обучением,

где переключения являются естественной моделью изменений информацион-

ной структуры сети. Комбинация управления с итеративным обучением и

управления с обратной связью также представляет интересную задачу для

дальнейших исследований.

СПИСОК ЛИТЕРАТУРЫ

Liberzon D. Switching in Systems and Control. Boston, MA: Birkhäuser, 2003.

Shorten R., Wirth F., Mason O., Wulff K., King C. Stability criteria for switched

and hybrid systems // SIAM Review 2007. V. 49. P. 545-592.

Lin H., Antsaklis P.J. Stability and stabilizability of switched linear systems: A

survey of recent results // IEEE Transactions on Automatic Control. 2009. V. 54.

P. 308-321.

Sun Z., Ge S.S. Stability Theory of Switched Dynamical Systems. London: Springer-

Verlag, 2011.

Alwan M.S, Liu X. Theory of Hybrid Systems:Deterministic and Stochastic. Beijing:

Springer Nature Singapore Pte Ltd. and Higher Education Press, 2018.

Rogers E., Galkowski K., Owens D.H. Control Systems Theory and Applications for

Linear Repetitive Processes, ser. Lecture Notes in Control and Information Sciences.

V. 349. Berlin: Springer-Verlag, 2007.

Arimoto S., Kawamura S., Miyazaki F. Bettering operation of robots by learning //

J. Robotic Systems. 1984. V. 1. No. 2. P. 123-140.

Bolder J., Oomen T. Iterative learning control: A 2D system approach // Automat-

ica. 2016. V. 71. P. 247-253.

Hladowski L., Galkowski K., Cai Z., Rogers E., Freeman C.T., Lewin P.L. Ex-

perimentally supported 2D systems based iterative learning control law design for

error convergence and performance // Control Engineering Practice. 2010. V. 18.

P. 339-348.

10.

Paszke W., Rogers E., Galkowski K., Cai Z. Robust finite frequency range itera-

tive learning control design with experimental verification // Control Engineering

Practice. 2013. V. 23. P. 1310-1320.

11.

Bristow D.A., Tharayil M., Alleyne A. A survey of iterative learning control // IEEE

Control Systems Magazine. 2006. V. 26. No. 3. P. 96-114.

12.

Ahn H.-S., Chen Y.-Q., Moore K.L. Iterative learning control: Brief survey and

categorization // IEEE Transactions on Systems, Man and Cybernetics, Part C:

Applications and Reviews. 2007. V. 37. No. 6. P. 1099-1121.

13.

Sammons P.M., Gegel M.L., Bristow D.A., Landers R.G. Repetitive process con-

trol of additive manufacturing with application to laser metal deposition // IEEE

Transactions on Control Systems Technology. 2019. V. 27. No. 2. P. 566-575.

134

14.

Freeman C.T., Rogers E., Hughes A.-M., Burridge J.H., Meadmore K.L. Iterativel

learning control in health care: electrical stimulation and robotic-assisted upper-limb

stroke rehabilitation // IEEE Control Systems Magazine. 2012. 2012. V. 32. No. 1.

P. 18-43.

15.

Meadmore K.L., Exell T.A., Hallewell E., Hughes A.-M., Freeman C.T., Kutlu M.,

Benson V., Rogers E., Burridge J.H. The application of precisely controlled func-

tional electrical stimulation to the shoulder, elbow and wrist for upper limb stroke

rehabilitation: a feasibility study // J. Neuro Engineering Rehabil. 2014. V. 11.

No. 105. https://doi.org/10.1186/1743-0003-11-105.

16.

Bochniak J., Galkowski K., Rogers E. Multi-machine operations modelled and con-

trolled as switched linear repetitive processes // Int. J. Control. 2008. V. 81. P. 1549-

1567.

17.

Bochniak J., Galkowski K., Rogers E., Mehdi D., Bachelier O., Kummert A. Stabi-

lization of discrete linear repetitive processes with switched dynamics // Multidim.

Syst. Sign. Process. 2006. V. 17. P. 271-295.

18.

Shao Z., Xiang Z. Iterative learning control for non-linear switched discrete-time

systems // IET Control Theory Appl. 2017. V. 11. No. 6. P. 883-889.

19.

Shao Z., Duan Z. A High-order Iterative Learning Control for Discrete-time Linear

Switched Systems // Proc. 57th Annual Conference of the Society of Instrument and

Control Engineers of Japan (SICE). Nara, Japan. 2018. P. 354-361.

20.

Ouerfelli H., Ben Attia S., Salhi S. Switching-iterative learning control method for

discrete-time switching system // Int. J. Dynamics Control. 2018. V. 6. P. 1755-1766.

21.

Shao Z., Xiang Z. Adaptive iterative learning control for switched nonlinear

continuous-time systems // Int. J. Syst. Sci. 2019. V. 50. No. 5. P. 1028-1038.

22.

Pakshin P., Emelianova J., Emelianov M., Galkowski K., Rogers E. Dissipivity and

stabilization of nonlinear repetitive processes // Systems & Control Letters. 2016.

V. 91. P. 14-20.

23.

Pakshin P., Emelianova J., Galkowski K., Rogers E. Stabilization of two-dimensional

nonlinear systems described by Fornasini-Marchesini and Roesser models //SIAM

J. Control Optim. 2018. V. 56. P. 3848-3866.

24.

Pakshin P., Emelianova J., Emelianov M., Galkowski K., Rogers E. Passivity based

stabilization of repetitive processes and iterative learning control design // Systems

& Control Letters. 2018. V. 122. P. 101-108.

25.

Емельянова Ю.П., Пакшин П.В. Синтез управления с итеративным обучением

на основе наблюдателя состояния // АиТ. 2019. № 9. С. 9-24.

Emelianova J.P., Pakshin P.V. Iterative Learning Control Design Based on State

Observer // Autom. Remote Control. 2019. V. 80. No. 9. P. 1561-1573.

26.

Apkarian J., Karam P., Levis M. Workbook on Flexible Link Experiment for Mat-

lab/Simulink Users. Quanser, 2011.

Статья представлена к публикации членом редколлегии Б.Т. Поляком.

Поступила в редакцию 23.07.2019

После доработки 21.10.2019

Принята к публикации 30.01.2020

135