Автоматика и телемеханика, № 8, 2020

А.М. ФЕДОТКИН, канд. физ.-мат. наук (fandr@vmk.unn.ru),

Е.В. КУДРЯВЦЕВ (evgkudryavcev@gmail.com)

(Нижегородский государственный университет им. Н.И. Лобачевского)

ДИНАМИЧЕСКИЕ МОДЕЛИ НЕОДНОРОДНОГО ПОТОКА

ТРАНСПОРТА НА МАГИСТРАЛЯХ¹

Рассматривается кибернетический метод описания и анализа реальных

потоков, когда интервалы между последовательными моментами поступ-

ления требований являются статистически зависимыми и имеют разные

распределения. Предложены эвристические алгоритмы, которые позволя-

ют выделить в потоке два класса неоднородных требований. В качестве

описания предлагается использовать только интервалы между соседни-

ми требованиями первого класса и количество всех требований в каждом

таком интервале. Целесообразность предлагаемого описания продемон-

стрирована не только на примере транспортного потока движущихся ав-

томобилей на магистрали, но и при определении вероятностных законов

распределения реальных потоков другой физической природы.

Ключевые слова: неоднородные требования, управляющая кибернетиче-

ская система, уравнения Колмогорова, нелокальное описание, алгоритм

разбиения потока, статистические гипотезы, критерий Валлиса-Мура.

DOI: 10.31857/S0005231020080115

1. Введение

В теории массового обслуживания известно [1], что классическое описа-

ние входного потока систем массового обслуживания выполняется в виде

векторной случайной последовательности {(τ^′j , η^′j ); j = 1, 2, . . .}, в которой

через η^′j обозначено число поступивших требований в момент времени τ^′j

с номером j. Классическое описание входных потоков успешно применил

Ю.И. Неймарк для изучения динамики процесса управления транспортом

на перекрестке [2, 3]. Ю.И. Неймарк внес фундаментальный вклад в теорию

управления конфликтными пуассоновскими потоками в классе циклических

алгоритмов [4]. При классическом описании потоков предполагается незави-

симость и одинаковое распределение как величин τ^′j+1 - τ^′j, j = 1, 2, . . . , так и

независимость и одинаковое распределение величин η^′j , j = 1, 2, . . . Из-за уве-

личения интенсивности входных потоков в современных реальных системах

это предположение отсутствует [5]. Поэтому классический способ описания

входного потока для таких систем не является удобным, так как требует за-

дания сложных конечномерных распределений последовательности {(τ^′j, η^′j );

j = 1,2,...}. Задача остается сложной, если даже η^′j(ω) ≡ 1 при j = 1,2,...

В данной статье предлагается описание входного потока в виде последова-

тельности {(τ_i+1 - τ_i, χ_i); i = 0, 1, . . .}. Здесь {τ_i; i = 0, 1, . . .} строго возрас-

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 18-413-520005).

149

тающая последовательность случайных точек на оси времени Ot, и χ_i опре-

деляет случайное число требований на промежутке [τ_i, τ_i+1) или в группе с

номером i. Проблема заключается в том, чтобы по наблюдению за конеч-

ной реализацией случайной последовательности {(τ^′j, η^′j ); j = 1, 2, . . .} и по

алгоритму выбора последовательности {τ_i; i = 0, 1, . . .} найти распределение

последовательностей случайных интервалов {τ_i+1 - τ_i; i = 0, 1, . . .} и разме-

ров групп {χ_i; i = 0, 1, . . .} в некоторых классах вероятностных распределе-

ний, для которых ряд распределения или плотность можно выписать в явном

виде. В теории маркированных случайных потоков каждое требование пото-

ка отображается точкой или интервалом на оси времени Ot. В этом пред-

положении для определения распределения последовательности {τ_i+1 - τ_i;

i = 0,1,...} можно применять известные тестовые распределения, в том чис-

ле смещенные. Способ описания потока предполагает наблюдение только за

группами требований, а не за каждым требованием потока сложной веро-

ятностной структуры. Такой принцип описания потоков требований можно

назвать нелокальным [6, 7]. Поэтому необходимо предложить не только ме-

ханизм формирования каждой группы реального потока, но и на этом осно-

вании выбрать алгоритм выбора последовательности {τ_i; i = 0, 1, . . .}. В силу

этого определение и выбор тестовых распределений для последовательности

{χ_i; i = 0, 1, . . .} вызывает большие трудности.

Процесс образования величины χ_i группы с номером i потока рассматрива-

ется как функционирование по возможности простой управляющей системы

обслуживания [6, 7]. Это обстоятельство позволяет предложить адекватный

механизм образования группы (пачки) с номером i для сложного реального

потока. Интерпретация такого механизма образования группы дается на при-

мере потока пачек автомобилей на бесконечной или кольцевой магистрали с

однополосным движением, либо на магистрали с многополосным движением,

если рассматривать образование пачек только на одной из полос. При этом

в потоке будем различать требования с медленным движением и требования

с быстрым движением. Значит, в потоке имеется два класса (типа) требо-

ваний, что и означает их неоднородность. При многополосном движении с

возможностью перестроения интенсивность потока автомобилей с быстрым

движением для конкретной полосы изменяется за счет требований из дру-

гих полос, которые будут осуществлять обгон по этой полосе. В этом случае

следует предположить, что поток автомобилей с быстрым движением являет-

ся пуассоновским. Только требования с быстрым движением имеют возмож-

ность обгона требований с медленным движением. Предлагаемый в статье

подход дает возможность генерировать различные и неизвестные ранее за-

коны распределения реальных входных потоков, не используя предельные

теоремы теории вероятностей и математической статистики.

2. Представление механизма формирования потока

в виде процесса функционирования управляющей

кибернетической системы обслуживания

В статье предполагается существование основного вероятностного про-

странства (Ω, F, P(·)), которое является математической моделью изучаемого

случайного эксперимента E. Здесь Ω есть достоверный исход или множество

150

Cтратегия механизма

d₀

обслуживания

Медленная

машина

Входной поток

Очередь быстрых

Обслуживающее

Выходной поток

быстрых машин

машин

устройство

быстрых машин

(входной полюс)

(внешняя память)

(внутренняя память)

(выходной полюс)

Схема управляющей системы.

описаний всех элементарных исходов эксперимента E. Вероятностная функ-

ция P(A): F → [0, 1] задана на σ-алгебре F, элементами которой являются

наблюдаемые исходы A ⊂ Ω случайного эксперимента E. В некоторых случа-

ях не будем явно фиксировать символ ω как аргумент каких-либо функций.

При этом будем помнить о том, что все случайные события, случайные ве-

личины и случайные элементы рассматриваются на указанном пространстве

(Ω, F, P(·)). Типичным примером эксперимента E может служить процесс

движения разнотипных автомобилей на магистрали с однополосным движе-

нием или временной процесс прибытия автомобилей к стоп-линии некоторого

управляемого перекрестка.

Модель механизма формирования размера χ_i каждой транспортной пачки

реального потока неоднородных и точечных движущихся автомобилей будем

представлять в виде эволюции управляющей кибернетической системы обслу-

живания [6, 7] из некоторого класса. Для такой системы на рисунке представ-

лены следующие ее блоки: входной полюс, внешняя память, устройство δ по

переработке информации внешней памяти, внутренняя память, устройство δ₀

по переработке информации внутренней памяти и выходной полюс.

Рассмотрим математическое описание каждого из указанных блоков.

Входной полюс есть пуассоновский поток требований с быстрым движени-

ем. Интенсивность этого потока равна λ₀ > 0. Интенсивность λ^′ > 0 потока

из требований с медленным движением достаточно мала и такова, что рас-

стояние между любыми соседними требованиями с медленным движением

велико. Это обеспечивает восстановление пуассоновского потока требований

с быстрым движением после процесса обгона [8, 9]. Пусть здесь и далее сим-

вол o(Δt) обозначает неотрицательную бесконечно малую величину по срав-

нению с величиной Δt > 0 и пусть за промежуток времени [t, t + Δt) в оче-

редь из требований для обгона медленного требования поступает случайное

число ξ(ω; t, Δt) требований с быстрым движением. Тогда для пуассоновского

потока с параметром λ₀ при Δt → 0 хорошо известны следующие формулы:

P({ω : ξ(ω; t, Δt) = 0}) = 1 - λ₀Δt + o(Δt),

(1)

P({ω : ξ(ω; t, Δt) = 1}) = λ₀Δt - o(Δt),

P({ω : ξ(ω; t, Δt) ≥ 2}) = o(Δt).

Соотношение (1) является математическим описанием входного полюса.

151

По наблюдениям за реальными потоками оказалось, что каждое требова-

ние с быстрым движением догоняет требование с медленным движением и

поступает в некоторую очередь. При этом группа состоит из требований с

быстрым движением, которые ожидают возможности обгона, и обязательно

из требования с медленным движением. Возможны ситуации, когда размер

очереди равен нулю. В этом случае группа состоит только из требования с

медленным движением. Итак, физически внешняя память есть очередь из

требований с быстрым движением и единственного требования с медленным

движением. Если случайная величина χ(ω; t) ∈ {1, 2, . . .} измеряет число тре-

бований всех типов в группе в момент времени t ≥ 0, то случайный процесс

{χ(t): t ≥ 0} является математическим описанием блока внешней памяти.

Блок внутренней памяти отвечает за процесс обгона требований с быст-

рым движением требования с медленным движением. Каждое требование с

медленным движением можно интерпретировать как обслуживающий при-

бор для требований с быстрым движением. При этом под временем обслужи-

вания, естественно, понимается случайное время обгона. Для такого класса

систем не задается интегральная функция распределения случайного време-

ни обслуживания, так как времена обгона быстрыми машинами медленной

являются зависимыми случайными величинами и имеют различные законы

распределения. Более того, из реальных наблюдений нет возможности най-

ти статистические законы распределения указанных величин. Поэтому вме-

сто семейства многомерных интегральных функций распределения времен

обслуживания для такого рода систем удобно задавать так называемый по-

ток насыщения [6, 7] в виде семейства {κ(t, t₀): t ≥ 0, t₀ > 0} случайных ве-

личин. Здесь через κ(ω; t, t₀) обозначено случайное число требований с быст-

рым движением, которые могут обогнать требование с медленным движением

за промежуток времени [t, t + t₀). Тогда семейство случайных величин вида

{κ(t, t₀): t ≥ 0, t₀ > 0} определяет математическое описание блока внутрен-

ней памяти.

Так как в потоке не происходит потеря требований, то при Δt > 0 устрой-

ство δ по переработке информации внешней памяти можно математически

описать с помощью функционального соотношения

(2)

χ(ω; t + Δt) = χ(ω; t) + ξ(ω; t, Δt) - κ(ω; t, Δt).

В силу физического смысла величин χ(ω; t), ξ(ω; t, Δt), κ(ω; t, Δt) должно

выполняться соотношение 0 ≤ κ(ω; t, Δt) ≤ χ(ω; t) + ξ(ω; t, Δt) - 1. Отсюда с

учетом (2) получаем, что χ(ω; t + Δt) ≥ 1. Устройство δ по переработке внеш-

ней памяти реализует функциональный закон (2) отбора требований с быст-

рым движением из очереди для обгона требования с медленным движением.

Для процесса обгона в транспортном потоке механизм отбора естественно

должен происходить в порядке поступления (FIFO). Для потоков другой фи-

зической природы можно допустить другую дисциплину обслуживания, но

соотношение (2) есть условие модели и оно должно выполняться.

На практике распределение времени обслуживания (обгона) существенно

зависит от величины очереди из требований с быстрым движением. Вполне

естественно предположить, что при малых значениях Δt > 0 условные ве-

152

роятности событий, которые порождаются дискретной случайной величи-

ной κ(ω; t, Δt), определяются соотношениями

P({ω : κ(ω; t, Δt) = 0}|{ω : χ(ω; t) = m, ξ(ω; t, Δt) = 0}) = 1 - µ_m-1Δt + o(Δt),

P({ω : κ(ω; t, Δt) = 1}|{ω : χ(ω; t) = m, ξ(ω; t, Δt) = 0}) = µ_m-1Δt - o(Δt),

m = 2,...,q;

(3)

P({ω : κ(ω; t, Δt) = 0}|{ω : χ(ω; t) = m, ξ(ω; t, Δt) = 0}) = 1 - µ_qΔt + o(Δt),

P({ω : κ(ω; t, Δt) = 1}|{ω : χ(ω; t) = m, ξ(ω; t, Δt) = 0}) = µ_qΔt - o(Δt),

m = q + 1,q + 2,...

В (3) параметры µ^-11, µ^-12, . . . , µ^-1q-1 задают условное среднее время обго-

на, когда число требований всех типов в группе равно 2, 3, . . . , q соответ-

ственно. Здесь величина q > 1 заданное натуральное число. Аналогично

параметр µ^-1q в соотношении (3) определяет условное среднее время обго-

на, если транспортная пачка состоит из q + 1 и более требований. Парамет-

ры µ₁, µ₂, . . . , µ_q будем называть условными интенсивностями обгона. Таким

способом моделируется зависимость распределения времени обгона от числа

требований всех типов в очереди. Условные вероятности в (3) задают матема-

тическое описание блока δ₀ или устройства по переработке внутренней памя-

ти. Другими словами, соотношение (3) определяет изменение вероятностного

закона для обгона требований с быстрым движением.

В указанных предположениях относительно всех блоков управляющей си-

стемы обслуживания, которая моделирует процесс образования групп, тре-

буется найти нелокальное описание [6, 7] входного потока. При этом на вход-

ной поток неоднородных требований следует смотреть как на поток групп,

которые осуществляют перемещение. Следует иметь в виду, что каждое тре-

бование с медленным движением является источником образования очереди

движущихся требований. Соотношения типа (1), (2), (3) и управляющие па-

раметры λ₀, q, µ₁, µ₂, . . . , µ_q

это удобный способ задания класса матема-

тических моделей управляющих систем обслуживания. Это класс систем с

ожиданием, неограниченной очередью, одним прибором с переменной струк-

турой и с некоторой заданной стратегией механизма отбора требований.

Пусть величина Q(t, m) = P({ω : χ(ω, t) = m}) при фиксированных значе-

ниях t ≥ 0 и m = 1, 2, . . . Для вероятностей Q(t, m) в [10] получена бесконеч-

ная система линейных дифференциальных уравнений вида

dQ(t, 1)/dt = -λ₀Q(t, 1) + µ₁Q(t, 2),

dQ(t, m)/dt = λ₀Q(t, m - 1) - (λ₀ + µ_m-1)Q(t, m) + µ_mQ(t, m + 1),

(4)

m = 2,...,q;

dQ(t, m)/dt = λ₀Q(t, m - 1) - (λ₀ + µ_q)Q(t, m) + µ_qQ(t, m + 1),

m ≥ q + 1.

В [11] рассмотрены различные динамические системы, в том числе детер-

минированные и случайные. Для каждой задачи предложен метод описания

состояния системы и уравнения или соотношения, задающие динамику из-

менения состояния. Так, для одной из задач в качестве состояния динами-

ческой системы выбрано вероятностое распределение случайной величины.

153

При этом динамика изменения состояний системы может задаваться в ви-

де системы дифференциальных уравнений для вероятностого распределения.

Используя описанный подход для рассматриваемой задачи, состоянием бло-

ка внешней памяти в момент t является не конкретное значение случайной

величины χ(t) ∈ {1, 2, . . .}, а ее распределение (Q(t, 1), Q(t, 2), . . .). Соотноше-

ние (4) определяет функционирование динамической системы. В [10] доказа-

но, что эргодическое распределение lim_t→∞ Q(t, m) = Q(m), m ≥ 1, существу-

ет при λ₀ < µ_q. При q = 3 и обозначениях α = λ₀µ^-11, β = λ₀µ^-12, γ = λ₀µ^-13

получены формулы для эргодического распределения в виде

Q(1) = p = (1 + α + αβ/(1 - γ))^-1,

(5)

Q(2) = α(1 + α + αβ/(1 - γ))^-1,

Q(m) = αβγ^m-3(1 + α + αβ/(1 - γ))^-1, m ≥ 3.

Будем считать, что соотношение (5) является распределением случайного

числа χ(ω) требований в группе в установившемся режиме движения транс-

порта по магистрали. В этом случае каждая из случайных величин χ_i,

i = 1,2,..., имеет также распределение (5). Для случайной величины χ(ω)

получены математическое ожидание Mχ(ω) и дисперсия Dχ(ω) в следую-

щем виде:

(

))

Mχ(ω) = p

1 + 2α + αβ

1-γ

(1 - γ)²

[

(

)

Dχ(ω) = p² α + αβ

1-γ

(1 - γ)²

(1 - γ)³

(

)

(

)]

+α²β

+α²β²

(1 - γ)²

(1 - γ)³

(1 - γ)⁴

Сделаем одно важное замечание. При β = γ предельное распределение (5)

для числа χ(ω) требований всех типов в каждой группе входного пото-

ка совпадает с распределением Бартлетта [12]. Это возможно только при

µ₂ = µ₃ = ... = µ_q. Другими словами, среднее время обгона остается посто-

янным, если число требований всех типов в каждой группе равно 3, 4, . . .

Наконец, при α = β = γ распределение (5) совпадает с геометрическим рас-

пределением. Это возможно при µ₁ = µ₂ = . . . = µ_q, когда среднее время об-

гона не зависит от числа требований всех типов в каждой группе входного

потока. Свойства таких потоков подробно изучены в [9].

Для реальных потоков другой вероятностной структуры можно допустить

несколько иные соотношения (1), (2), (3) и управляющие параметры. Для

этого в следующем абзаце рассмотрим другой класс динамических моделей

неоднородных потоков.

Пусть условные интенсивности µ₁, µ₂, . . . , µ_q обгона в транспортном пото-

ке достаточно высоки и интенсивность λ₀ быстрых машин мала. Тогда бу-

дем наблюдать образование величины пачек не более целого числа N ≥ 2.

В этом случае χ(ω; t) ∈ {1, 2, . . . , N}. Если χ(ω; t) = N и на малом промежут-

ке [t, t + Δt) в группу поступает требование, то мгновенно происходит обгон и,

154

значит, в потоке не происходит потеря требований. В этих предположениях

для потока неоднородных требований имеет место соотношение (1), равен-

ство (2) при χ(ω; t) ∈ {1, 2, . . . , N} и соотношения

P({ω : κ(ω; t, Δt) = 0}|{ω : χ(ω; t) = m, ξ(ω; t, Δt) = 0}) = 1 - µ_m-1Δt + o(Δt),

P({ω : κ(ω; t, Δt) = 1}|{ω : χ(ω; t) = m, ξ(ω; t, Δt) = 0}) = µ_m-1Δt - o(Δt),

(6)

m = 2,...,N;

P({ω : κ(ω; t, Δt) = 1}|{ω : χ(ω; t) = N, ξ(ω; t, Δt) = 1}) = 1 - o(Δt).

Соотношения (6) задают математическое описание блока δ₀ или устройства

по переработке внутренней памяти в случае образования пачек величины не

более N. Динамическая модель механизма образования транспортной пач-

ки величины не более N была подробно изучена в [13]. В частности, для

вероятностей Q(t, m), m ∈ {1, 2, . . . , N}, в данной модели получена система

линейных дифференциальных уравнений

dQ(t, 1)/dt = -λ₀Q(t, 1) + µ₁Q(t, 2),

dQ(t, m)/dt = λ₀Q(t, m - 1) - (λ₀ + µ_m-1)Q(t, m) + µ_mQ(t, m + 1),

m = 2,...,N - 1;

dQ(t, N)/dt = λ₀Q(t, N - 1) - µ_N-1Q(t, N).

Данная система имеет решение при любых параметрах. Для эргодическо-

го распределения (Q(1), Q(2), . . . , Q(N)) при µ₃ = µ₄ = . . . = µ_N-1 получены

формулы

(

)_-1

Q(1) =

1 + α + αβ(1 - γ^N-2)/(1 - γ)

(

)_-1

Q(2) = α

1 + α + αβ(1 - γ^N-2)/(1 - γ)

(

)_-1

Q(m) = αβγ^m-3

1 + α + αβ(1 - γ^N-2)/(1 - γ)

m = 3,4,...,N.

3. Алгоритмы получения нелокального описания потоков

неоднородных требований

Ради сокращения записи в дальнейшем при η^′j(ω) ≡ 1 для всех j = 1, 2, . . .

обозначим τ^′j через θ_j. В этом случае θ_j определяет момент появления тре-

бования с номером j. В этом разделе по информации о конечной реализации

потока {θ_j ; j = 1, 2, . . .} предлагаются различные алгоритмы определения по-

следовательности {τ_i+1 - τ_i; i = 0, 1, . . .} такого типа, чтобы можно было счи-

тать ее элементы одинаково распределенными и независимыми случайными

величинами. Эффективность предложенных алгоритмов показана в разде-

ле 4 статьи. Приведем два алгоритма выделения моментов τ_i, i = 0, 1, . . .,

поступления первых требований групп из последовательных моментов θ_i,

i = 0,1,..., поступления всех требований.

Согласно первому алгоритму требования объединяются в группы по сле-

дующему принципу близости. Предположим, что θ₁ = 0. Это означает, что

начинаем наблюдать систему с момента прихода первого требования (этот

155

случай называется синхронным [8]). Зададим некоторый параметр близости

h₀ = const > 0 и коэффициенты 0 < a < 1 и b > 0. Тогда величины τ_i, i ≥ 0,

будут определяться из следующих соотношений:

{

}

τ_i = θki, k₀ = 0, k_i+1 = inf k: k > k_i,θ_k - θ_k-1 ≥ h_i

ak-ki-1

h_i+1 = h_iaki+1-ki-1b.

Если при некотором i ≥ 0 множество {k : k > k_i, θ_k - θ_k-1 ≥ h₀} окажется пу-

стым, то будем считать, что τ_i+1 = +∞. Заметим, что при таком разбиении

моменту τ_i, i ≥ 0, будет соответствовать поступление i-й группы требова-

ний, или i-й транспортной пачки. Длина каждой такой пачки будет равна

η_i = k_i+1 - k_i. Данный алгоритм подстраивается под интенсивность посту-

пающих требований, изменяя параметр близости требований h_i. Выбирая па-

раметры a и b, можно регулировать математическое ожидание размера груп-

пы.

Согласно второму алгоритму исходный поток делится на группы поэтап-

но. На этапе с номером m (m = 0, 1, . . .) будем получать векторную случай-

ную последовательность {(τ^mi, η^mi); i ≥ 0}, которую для краткости будем на-

зывать далее последовательностью (или потоком) m-го уровня. Как и рань-

ше, для любого m моменты τ^mi, i ≥ 0, совпадают с моментами поступлений

некоторых требований исходного потока в систему, т.е. τ^mi = θkm,i , k_m,i ≥ 1.

Далее, количество требований в i-й группе потока m-го уровня определяется

как η^mi = k_m,i+1 - k_m,i. Также введем величину δ^mi = θkm,i+1 - θkm,i+1-1, кото-

рая определяет интервал между i-й и (i + 1)-й пачками исходного процесса

при его нелокальном описании с помощью последовательности m-го уровня.

Параметрами данного способа являются натуральное число d и постоянные

величины h₀, h₁, удовлетворяющие соотношению 0 < h₀ < h₁. Итак, рекур-

рентные формулы для определения моментов τ^mi при m ≥ 0, i ≥ 0 имеют

следующий вид:

k_0,0 = 1,k_0,i+1 = inf {k: k > k_0,i,θ_k - θ_k-1 ≥ h₀} ,

{

}

s_m = inf

k: k ≥ 0,η^mk ≤ d,η^mk+1 ≤ d,δ^mk < h₁,η^mk = η^mk-1

{

τ^mi,i ≤ s_m,

τ^m+1i =

τ^mi+1,i > s_m.

Здесь полагается η^m-1 = 0 при любом m ≥ 0. Две группы из последователь-

ности предыдущего уровня объединяются, когда каждая из них содержит не

больше d требований, интервал между пачками меньше, чем h₁, а также раз-

мер первой группы в рассматриваемой паре совпадает с размером группы, ей

предшествующей. Отметим, что {ω : lim_m→∞ τ^mi существует} = Ω, поэтому,

определив τ_i = lim_m→∞ τ^mi и η_i = k_i+1 - k_i для любого i ≥ 0, получим нело-

кальное описание {(τ_i, η_i); i ≥ 0} исходного потока требований.

Получим оценку параметров распределения (5) для модели с неограничен-

ным размером группы. Пусть есть выборка x₁, x₂, . . . , x_n объема n реализа-

ций случайной величины χ. Обозначим через m_k число значений в выборке,

равных k (число пачек размера k). Неизвестные параметры α, β и γ будем

156

оценивать методом максимального правдоподобия [14, 15]. Для применения

данного метода удобно перейти от параметров α и β к новым параметрам p и

∑_∞

f, где p = Q(1) и f =

Q(k). В новых обозначениях выражения для Q(k),

k=3

k = 1,2,..., примут вид:

Q(1) = p,

Q(2) = 1 - f - p,

Q(k) = f(1 - γ)γ^k-3, k ≥ 3.

Функция правдоподобия равна

L(x₁, . . . , x_n, p, f, γ) = Q(x₁)Q(x₂) . . . Q(x_n) =

∏

(

)mk

= pm1(1 - f - p)m2

f (1 - γ)γ^k-3

k=3

Далее найдем натуральный логарифм функции правдоподобия

ln L(x₁, . . . , x_n, p, f, γ) = m₁ ln p + m₂ ln(1 - f - p) +

∑

(

)

(7)

+ m_k

ln f(1 - γ)γ^k-3

k=3

Согласно методу максимального правдоподобия необходимо найти аргумен-

ты функции, при которых она достигает максимума. Для этого приведем

систему уравнений правдоподобия





∂



ln L(x₁, . . . , x_n, p, f, γ) = 0,

∂p



∂

(8)

ln L(x₁, . . . , x_n, p, f, γ) = 0,

∂f



 ∂

ln L(x₁, . . . , x_n, p, f, γ) = 0.

∂γ

Используя соотношения (7) и (8), получим окончательную систему уравнений



m1

m₂



= 0,



1-f -p





m₂

∑

m_k

(9)

= 0,



1-f-p



k=3



∑

(

)



m₃

m_k

-

(k - 3)γ^k-4(1 - γ) - γ^k-3

1-γ

(1 - γ)γ^k-3

k=4

для нахождения оценок методом максимального правдоподобия. Решая си-

стему уравнений (9), получим оценки для параметров p, f и γ:

p^∗ = m₁/n,

f^∗ = (n - m₁ - m₂)/n,

∑

γ^∗

= (k - 3)m_k

(k - 2)m_k.

k=3

157

Данный результат является ожидаемым, так как p это вероятность полу-

чить группу из одной машины, а f из трех или более машин. Оценки для

исходных параметров α^∗, β^∗ и γ^∗ выражаются так:

1-f -p

α^∗ =

m₂ ,

m₁

∑

f (1 - γ)

n-m₁ -m₂

β^∗ =

m_k

(k - 2)m_k,

(10)

1-f-p

k=3

∑

γ^∗

= (k - 3)m_k

(k - 2)m_k.

k=3

4. Нелокальное описание реальных потоков

[16] было проведено исследование транспортного потока. По-

кажем эффективность предложенного подхода для анализа дан-

ных другой физической природы. Исследуем данные BC-pAug89.TL

(ftp://ita.ee.lbl.gov/html/contrib/BC.html)

[17]. В файле содержатся мо-

менты поступления и размеры пакетов в сети Ethernet. Общий объем

данных составляет 1 млн пакетов. Проанализируем моменты поступления

пакетов. Реализация {x₁, x₂, . . . x_V } объема V = 96 потока вида {θ_j+1 - θ_j;

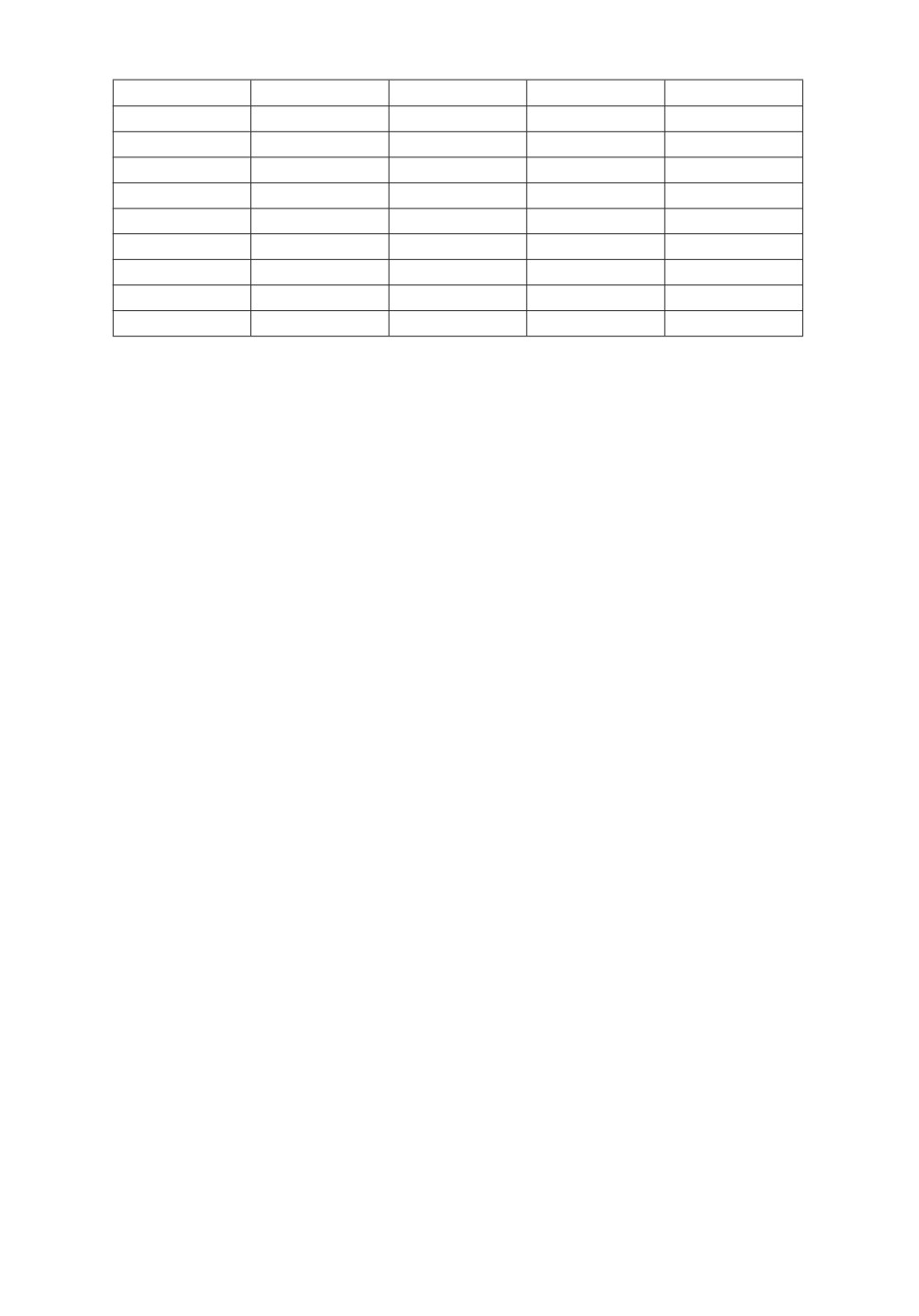
j = 1,2,...,V } приведена в табл. 1. В этой таблице по строкам приведены

значения интервалов между поступлениями пакетов.

Применяя фазово-частотный критерий Валлиса-Мура [9] о независимо-

сти и одинаковом распределении интервалов между соседними пакетами к

статистическим данным табл. 1, получаем значение статистики

Z(V, x₁, x₂, . . . , x_V ) =

[

]

Z₁(V,x₁,x₂,... ,x_V ) - (2V - 7)3^-1

× (90)^1/2 × (16V - 29)^-1/2

при V = 10000, равное 9,6221. Здесь функция Z₁(V, x₁, x₂, . . . , x_V ) определяет

так называемое число фаз по выборочным значениям x₁, x₂, . . . , x_V случай-

ных интервалов θ_i+1 - θ_i, i = 1, 2, . . . , V , и вычисляется следующим образом.

Таблица 1. Значения интервалов θ_i+1 - θ_i, i = 1, 2, . . . , 80

0,000168

0,002668

0,003964

0,002896

0,004036

0,00282

0,002712

0,001428

0,002268

0,000452

0,002604

0,001336

0,002148

0,000768

0,004236

0,002624

0,004056

0,00152

0,00128

0,001972

0,001952

0,001112

0,001824

0,001636

0,002536

0,002688

0,003984

0,002872

0,004132

0,002728

0,003968

0,002888

0,004116

0,002744

0,004008

0,002848

0,00416

0,00434

0,00392

0,00458

0,004008

0,004492

0,00392

0,00294

0,00408

0,00278

0,00396

0,002896

0,001104

0,002836

0,000712

0,002208

0,00084

0,003172

0,000088

0,002756

0,003932

0,002928

0,004128

0,002732

0,004056

0,0028

0,004016

0,002844

0,003324

0,00062

0,002912

0,000956

0,003688

0,00036

0,003496

0,001436

0,002592

0,002832

0,00128

0,002688

0,002892

0,001432

0,001956

0,000576

158

Для всех j = 1, 2, . . . , (V - 1) фиксируется знак разности x_j+1 - x_j. При

этом нулевые значения разностей не учитываются. Последовательность оди-

наковых знаков называют фазой. Далее вычисляют суммарное число плю-

совых и минусовых фаз, причем начальная и конечная фазы исключаются.

Тогда значение функции Z₁(V, x₁, x₂, . . . , x_V ) равно такому суммарному чис-

лу фаз. В случае справедливости выдвинутой гипотезы последовательность

случайных величин вида

{Z(V, θ₂ - θ₁, θ₃ - θ₂, . . . , θ_V+1 - θ_V ; V ≥ 30)}

сходится по распределению к стандартному нормальному закону. Порого-

вое значение на 5-процентном уровне значимости равно 1,96. Так как зна-

чение статистики Валлиса-Мура для данного потока удовлетворяет условию

9,6221 > 1,96, то согласно фазово-частотному критерию выдвинутую гипоте-

зу о независимости и одинаковом распределении интервалов между последо-

вательными пакетами следует отклонить.

По данным табл. 1 заметим, что интервалы имеют значительно отличаю-

щиеся длины. Так в первых 10000 наблюдений минимальный интервал имеет

длину 0,000064, а максимальный

0,11617. Данное поведение можно объяс-

нить образованием групп. Разобьем описанные данные на пачки с помощью

первого предложенного алгоритма. Подбирая управляющие параметры h₀,

a и b, можно разбить первоначальный поток объема V = 10000 на группы.

Например, при h₀ = 0,001, a = 0,96 и b = 1,44 получим N = 1009 значений

интервалов τ_i+1 - τ_i, где i = 0, 1, . . . , 1008 между группами, и последователь-

ность из 1009 значений для размеров χ₀, χ₁, . . . , χ₁₀₀₈ групп пакетов. Часть

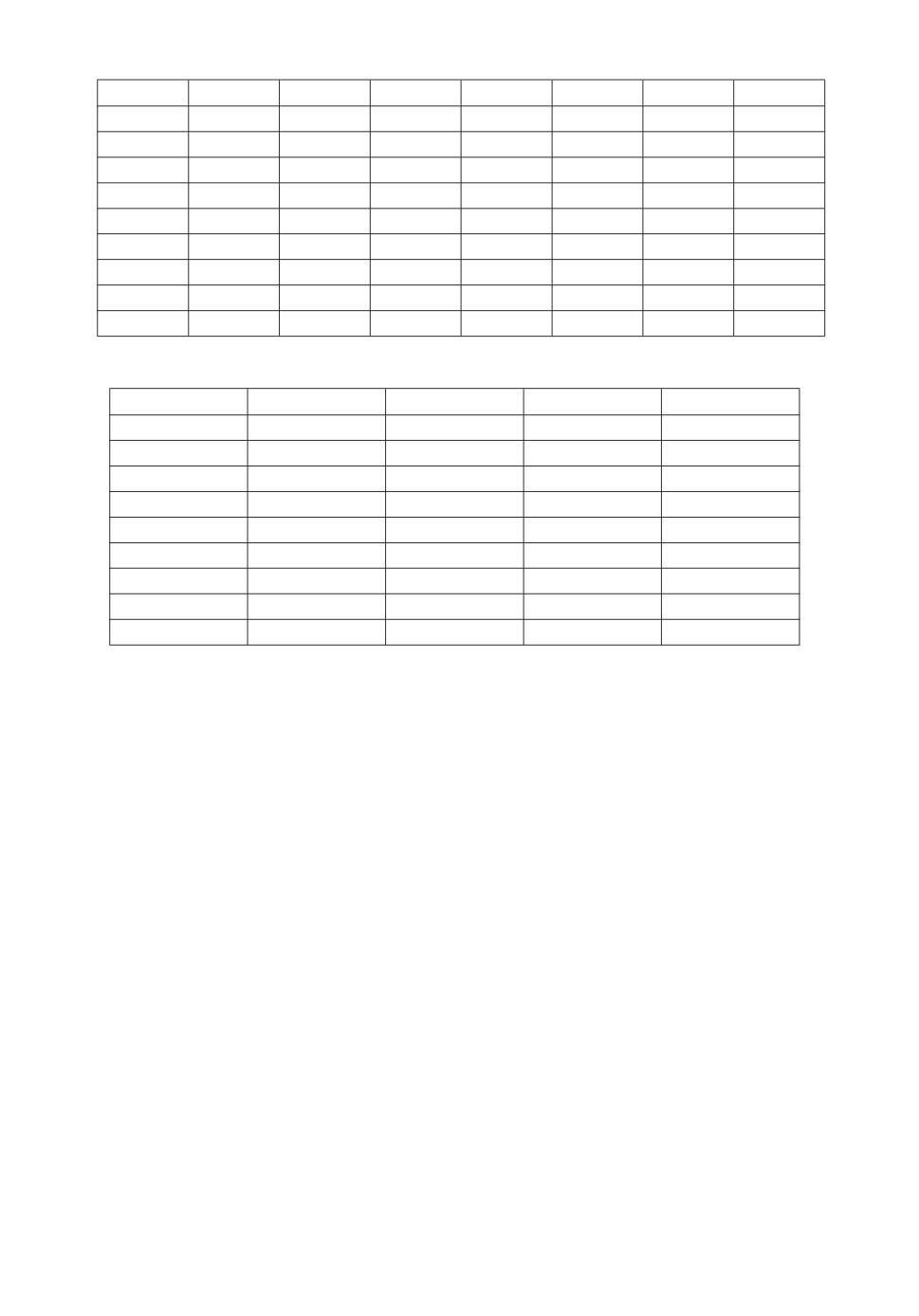
обработанных данных приведены в табл. 2.

Статистика Валлиса-Мура вида Z(1009, y₀, y₁, . . . , y₁₀₀₈) для временных

интервалов между первыми пакетами в группах равна 0,772. Значение

статистики Валлиса-Мура для этих интервалов удовлетворяет условию

|Z(1009, y₀, y₁, . . . , y₁₀₀₈)| = 0,772 < 1,96. Тогда согласно фазово-частотному

критерию [9] гипотеза о независимости и одинаковом распределении интерва-

лов между группами пакетов не отклоняется. С помощью формул (13) из [16]

при параметрах

s = 5, a₁ = min{y₀,y₁,...,y₁₀₀₈} +

+ (max{y₀, y₁, . . . , y₁₀₀₈} - min{y₀, y₁, . . . , y₁₀₀₈})/(6(s - 1)),

b₁ = (max{y₀,y₁,... ,y₁₀₀₈} - min{y₀,y₁,... ,y₁₀₀₈})/(s - 1)

получены следующие оценки для параметров смещенного экспоненциально-

го распределения h и σ: h^∗ = 0,0042 и σ^∗ = 0,0198. С помощью критерия хи-

квадрат проверим гипотезу о том, что последовательность {τ_i+1 - τ_i; i ≥ 0}

составлена из случайных величин, каждая из которых имеет смещенное экс-

поненциальное распределение. При N = 1009, s = 5, a₁ = 0,0075 и b₁ = 0,0343

из табл. 2 вычислим приближенное значение статистики хи-квадрат, рав-

ное 5,42. При двух степенях свободы и уровне значимости в 5 % пороговое

значение хи-квадрат распределения равно 5,991. Отсюда видно, что принятое

гипотетическое распределение для интервалов τ_i+1 - τ_i, i ≥ 0, между после-

довательными группами пакетов хорошо соответствует экспериментальным

данным из табл. 2. Таким образом, можно принять, что распределение ин-

159

Таблица 2. Значения (z_i, y_i) вектора (χ_i; τ_i+1 - τ_i), где i = 0, 1, . . . , 49

(2; 0,002836)

(1; 0,003964)

(1; 0,002896)

(1; 0,004036)

(10; 0,020772)

(2; 0,00668)

(10; 0,020504)

(10; 0,034464)

(10; 0,03902)

(10; 0,020544)

(12; 0,035004)

(25; 0,038748)

(1; 0,004)

(2; 0,00684)

(15; 0,02566)

(6; 0,0146)

(1; 0,012168)

(9; 0,027832)

(4; 0,040048)

(6; 0,034612)

(1; 0,02306)

(4; 0,039592)

(11; 0,071748)

(7; 0,08092)

(9; 0,05648)

(50; 0,110752)

(6; 0,013856)

(11; 0,030088)

(10; 0,031168)

(9; 0,02788)

(16; 0,042356)

(2; 0,007064)

(18; 0,041292)

(4; 0,013376)

(10; 0,022272)

(11; 0,034268)

(9; 0,020552)

(5; 0,0218)

(2; 0,026012)

(13; 0,034444)

(2; 0,014516)

(2; 0,02656)

(8; 0,083952)

(4; 0,057936)

(21; 0,12668)

(34; 0,076308)

(21; 0,024744)

(13; 0,015112)

(6; 0,010656)

(3; 0,006644)

тервалов между последовательными группами в наблюдаемом потоке имеет

вид

P({ω : τ_i+1 - τ_i < t}) = 1 - exp{-(t - 0,0042)/0,0198}, t > 0,0042;

P({ω : τ_i+1 - τ_i < t}) = 0, t ≤ 0,0042.

Статистика Валлиса-Мура Z(1009, z₀, z₁, . . . , z₁₀₀₈) для количества паке-

тов в группе равна 1,694 и удовлетворяет условию |Z(1009, z₀, z₁, . . . , z₁₀₀₈)| =

= 1,694 < 1,96. Значит, гипотеза о независимости и одинаковом распределе-

нии размеров групп не отклоняется. С помощью формулы (10) получены

оценки для α, β и γ: α^∗ = 0,864, β^∗ = 0,688, γ^∗ = 0,9042. При числе наблю-

дений N = 1009 и количестве разрядов r = 5 получим значение статистики

хи-квадрат, равное 2,9234. Это значение меньше 5 % порогового значения хи-

квадрат распределения с одной степенью свободы, равного 3,841. Таким обра-

зом, гипотеза о распределении вида (5) для количества требований в группе

не отвергается. Используя соотношения (5) и оценки α^∗, β^∗ и γ^∗, получим рас-

пределение для количества пакетов в группе следующего вида: Q(1) = 0,1238,

Q(2) = 0,107, Q(k) = 0,0736 × (0,9042)^k-3, k ≥ 3.

5. Получение дополнительных реализаций по одной выборке

При получении экспериментальных данных возможны ошибки или по-

грешности в полученных результатах. Это может быть связано с неточно-

стью измерительных приборов (систематическая ошибка) или с ошибками

наблюдателя (случайная ошибка). Необходимо проверить, могли ли ошиб-

ки получения данных значительно повлиять на результат анализа получен-

ной выборки. Предлагается алгоритм получения дополнительных реализа-

ций, близких к исходной. Если анализ измененных данных даст результат,

близкий результату анализа исходных данных, то можно считать, что воз-

можные неточности в данных не могли повлиять на выводы, сделанные по

исходной выборке.

Предположим, что наблюдатель получает данные с относительной погреш-

ностью, не превышающей величины δ. Обычно считают, что ошибка имеет

нормальное распределение. Тогда полученное измерение также имеет нор-

мальное распределение со средним, которое совпадает с реальным значени-

ем измеряемой величины. Для нормального распределения известно правило

160

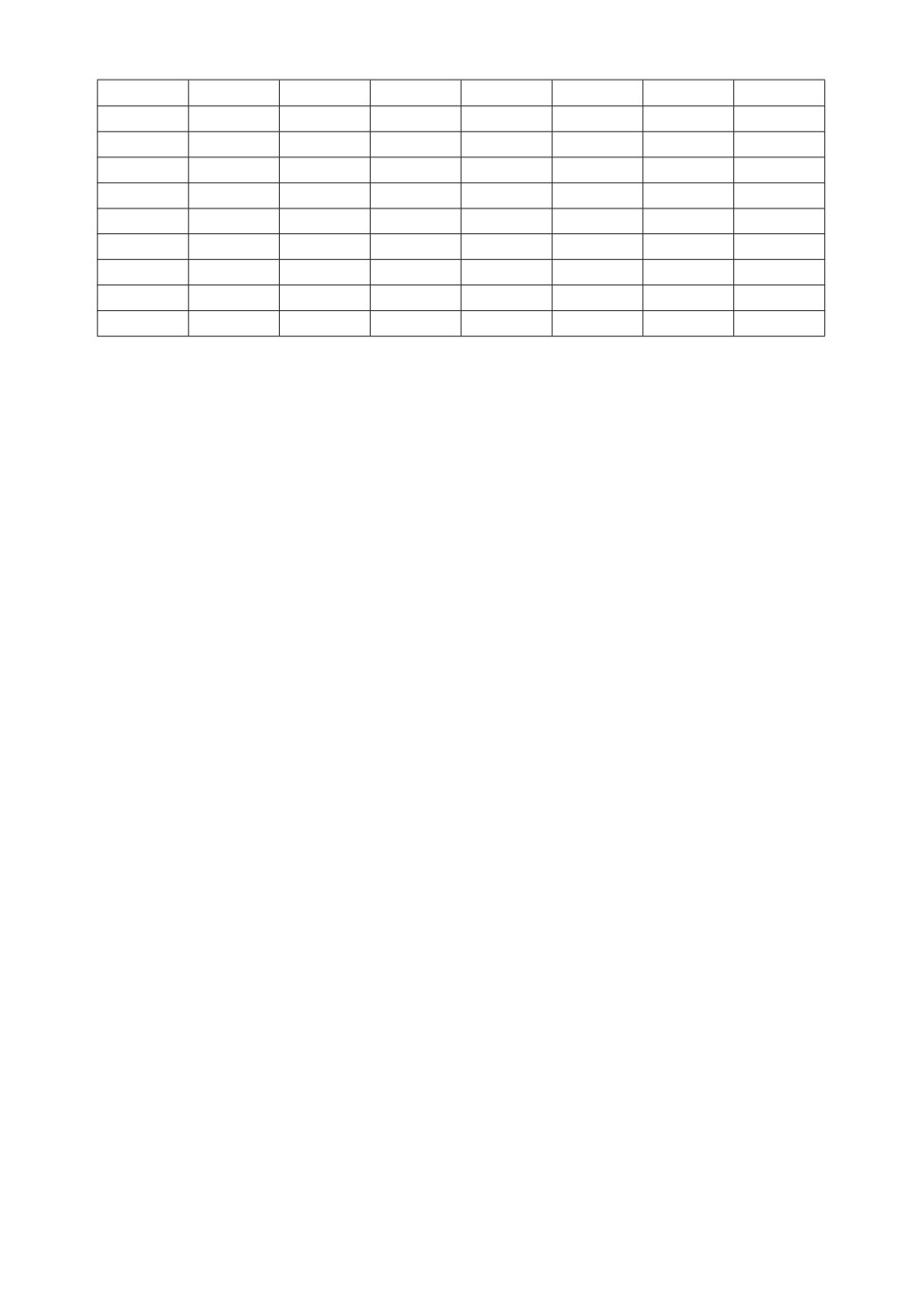
Таблица 3. Модифицированные данные θ_i+1 - θ_i, i = 1, 2, . . . , 80

0,000167

0,002651

0,003939

0,002877

0,004010

0,002802

0,002695

0,001419

0,002253

0,000449

0,002587

0,001327

0,002134

0,000763

0,004209

0,002607

0,004030

0,001510

0,001272

0,001959

0,001939

0,001105

0,001812

0,001625

0,002520

0,002671

0,003958

0,002854

0,004105

0,002710

0,003942

0,002869

0,004090

0,002726

0,003982

0,002830

0,004133

0,004312

0,003894

0,004551

0,003982

0,004463

0,003894

0,002921

0,004054

0,002762

0,003935

0,002877

0,001097

0,002818

0,000707

0,002194

0,000835

0,003152

0,000087

0,002738

0,003907

0,002909

0,004101

0,002714

0,004030

0,002782

0,003990

0,002825

0,003302

0,000616

0,002893

0,000950

0,003664

0,000358

0,003474

0,001427

0,002575

0,002814

0,001272

0,002671

0,002873

0,001423

0,001943

0,000572

Таблица 4. Значения (z_i, y_i) вектора (χ_i; τ_i+1 - τ_i), i = 0, 1, . . . , 49

(2; 0,002818)

(1; 0,003939)

(1; 0,002877)

(1; 0,00401)

(10; 0,020638)

(2; 0,006637)

(10; 0,020372)

(10; 0,034242)

(10; 0,038769)

(12; 0,027423)

(10; 0,027768)

(25; 0,038499)

(1; 0,003974)

(2; 0,006796)

(15; 0,025495)

(6; 0,014506)

(1; 0,01209)

(9; 0,027653)

(4; 0,039791)

(6; 0,03439)

(1; 0,022912)

(4; 0,039338)

(11; 0,071287)

(7; 0,0804)

(9; 0,056117)

(50; 0,11004)

(6; 0,013767)

(11; 0,029895)

(10; 0,030968)

(9; 0,027701)

(16; 0,042084)

(4; 0,01364)

(16; 0,034405)

(4; 0,01329)

(10; 0,022129)

(11; 0,034048)

(9; 0,02042)

(5; 0,02166)

(2; 0,025845)

(13; 0,034223)

(2; 0,014423)

(2; 0,026389)

(8; 0,083412)

(4; 0,057564)

(21; 0,125866)

(34; 0,075817)

(21; 0,024585)

(13; 0,015015)

(6; 0,010588)

(3; 0,006601)

“трех сигма”

почти все значения случайной величины находятся на рас-

стоянии не более величины 3σ от математического ожидания. Положим, что

число 3σ равно абсолютной погрешности δX, где X полученное измерение.

Получаем среднеквадратическое отклонение σ = δX/3. Таким образом, с по-

мощью исходной выборки {X₁, X₂, . . . , X_n} можно получить семейство выбо-

рок {Y₁, Y₂, . . . , Y_n}, где Y_i реализация случайной величины с нормальным

распределением N(X_i, (δX_i/3)²), i = 1, 2, . . . , n.

Применим описанный алгоритм получения дополнительных выборок к

данным, проанализированным в разделе 4. Пусть погрешность измерений не

превышает δ = 0,05. В табл. 3 приведена часть модифицированных данных.

Применяя фазово-частотный критерий Валлиса-Мура к статистическим

данным табл. 3, получаем значение статистики Z(10000, x₁, x₂, . . . , x₁₀₀₀₀) =

= 9,6221. Значение статистики для данного потока превышает пороговое зна-

чение 1,96. Тогда согласно фазово-частотному критерию выдвинутую гипоте-

зу о независимости и одинаковом распределении интервалов между пакетами

следует отклонить.

Применим к модифицированным данным первый алгоритм с теми же са-

мыми параметрами h₀ = 0,001, a = 0,96 и b = 1,44. Получим такое же число

N = 1009 групп, но объединены другие пакеты. Часть обработанных данных

приведена в табл. 4.

Статистика Валлиса-Мура Z(1009, y₀, y₁, . . . , y₁₀₀₈) = 0,323 для временных

интервалов между первыми пакетами в группах не превышает критического

161

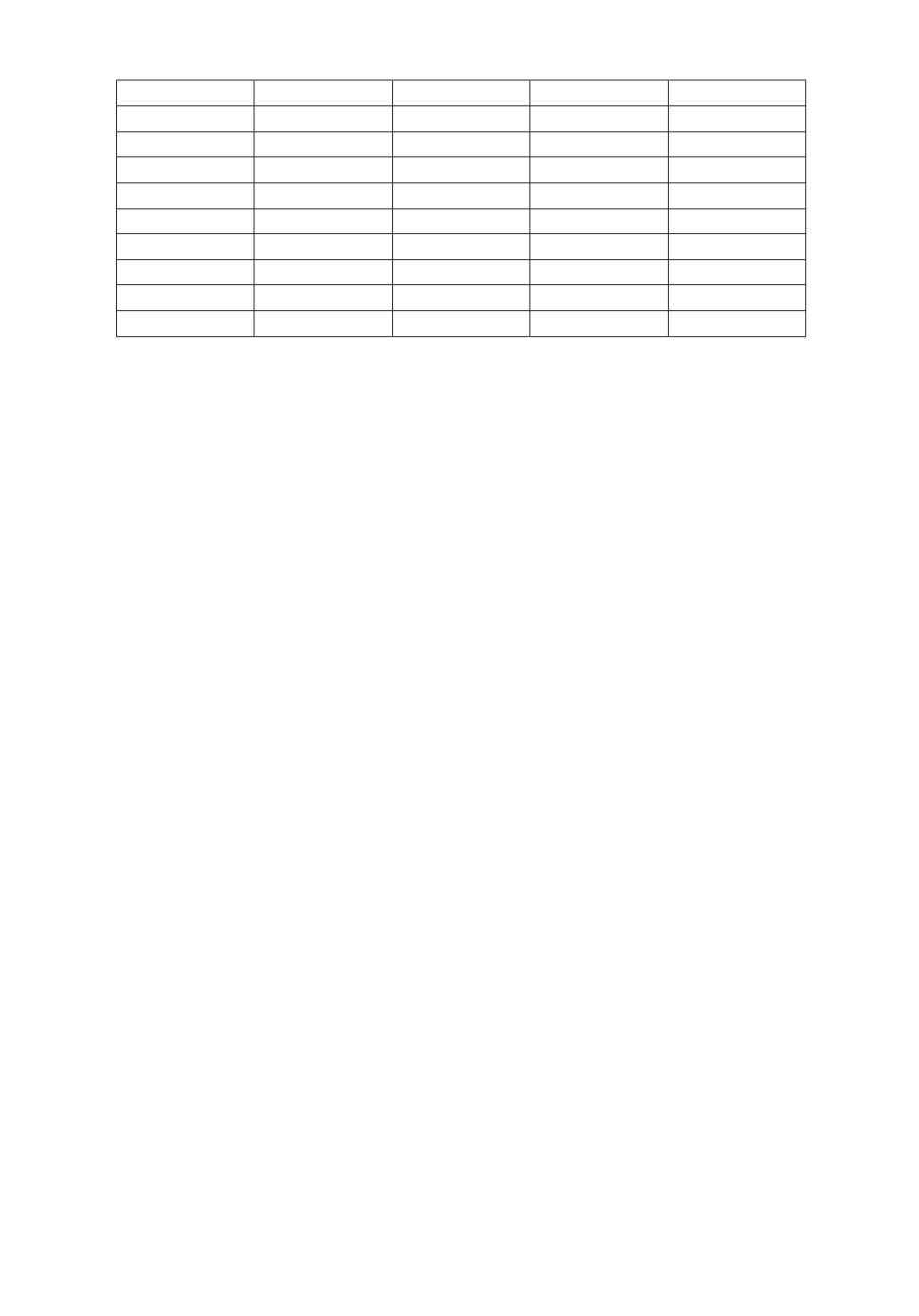
Таблица 5. Модифицированные данные θ_i+1 - θ_i, i = 1, 2, . . . , 80

0,000166

0,002640

0,003860

0,002907

0,004025

0,002755

0,002736

0,001445

0,002261

0,000461

0,002654

0,001366

0,002158

0,000761

0,004396

0,002666

0,004114

0,001551

0,001272

0,001915

0,001956

0,001099

0,001836

0,001592

0,002563

0,002676

0,003965

0,002880

0,004134

0,002743

0,004014

0,002914

0,004083

0,002679

0,004020

0,002826

0,004167

0,004390

0,003877

0,004458

0,004023

0,004402

0,003939

0,002845

0,004101

0,002749

0,004068

0,002869

0,001082

0,002811

0,000730

0,002202

0,000851

0,003130

0,000087

0,002800

0,003907

0,002911

0,004188

0,002751

0,004113

0,002819

0,003987

0,002797

0,003299

0,000619

0,002894

0,000955

0,003637

0,000355

0,003541

0,001436

0,002686

0,002906

0,001271

0,002718

0,002960

0,001462

0,001970

0,000575

уровня 1,96. Поэтому гипотеза о независимости и одинаковом распределении

интервалов между группами пакетов не отклоняется. Аналогичным способом

получены оценки для параметров смещенного экспоненциального распреде-

ления h и σ: h^∗ = 0,0041 и σ^∗ = 0,0197. Значение статистики хи-квадрат для

распределения интервалов равно 5,8864. Это значение не превышает 5-про-

центное пороговое значение распределения хи-квадрат, равное 5,991. Отсюда

следует, что гипотеза о смещенном экспоненциальном распределении интер-

валов между группами пакетов не отвергается.

Статистика Валлиса-Мура Z(1009, z₀, z₁, . . . , z₁₀₀₈) для количества паке-

тов в группе равна 1,684 и удовлетворяет условию |Z(1009, z₀, z₁, . . . , z₁₀₀₈)| <

< 1,96. Значит, гипотеза о независимости и одинаковом распределении раз-

меров групп не отклоняется. Аналогично с помощью формулы (10) получены

оценки для α, β и γ: α^∗ = 0,9024, β^∗ = 0,6675, γ^∗ = 0,9043. Значение стати-

стики хи-квадрат, равное 3,293, меньше 5 % порогового значения хи-квадрат

распределения с одной степенью свободы, равного 3,841. Таким образом, рас-

пределение вида (5) для количества требований в пачке хорошо описывает

данные. Получено распределение для количества пакетов в группе следую-

щего вида: Q(1) = 0,1219, Q(2) = 0,11, Q(k) = 0,0734 × (0,9043)^k-3, k ≥ 3.

Приведем также еще одну модифицированную выборку при случайном

колебании, не превышающем относительной погрешности δ = 0,05. В табл. 5

приведена часть модифицированных данных.

Применяя критерий Валлиса-Мура к модифицированным данным, полу-

чаем значение статистики Z(10000, x₁, x₂, . . . , x₁₀₀₀₀) = 9,343 > 1,96. Соглас-

но фазово-частотному критерию выдвинутую гипотезу о независимости и

одинаковом распределении интервалов между пакетами следует отклонить.

Обработаем модифицированные данные первым алгоритмом с параметра-

ми h₀ = 0,001, a = 0,96 и b = 1,44. Часть обработанных данных приведена

в табл. 6.

Гипотеза о независимости и одинаковом распределении интервалов меж-

ду группами пакетов не отклоняется, так как статистика Z(1009, y₀, y₁,

...,y₁₀₀₈) = 0,274 для временных интервалов между первыми пакетами в

группах не превышает критического уровня 1,96. Оценки для парамет-

ров смещенного экспоненциального распределения равны h^∗ = 0,0043 и

σ^∗ = 0,0194. Значение 5,647 статистики хи-квадрат для распределения ин-

162

Таблица 6. Значения (z_i, y_i) вектора (χ_i; τ_i+1 - τ_i), i = 0, 1, . . . , 49

(2; 0,002806)

(1; 0,00386)

(1; 0,002907)

(1; 0,004025)

(10; 0,020992)

(2; 0,00678)

(10; 0,020427)

(10; 0,03446)

(10; 0,038859)

(12; 0,027569)

(10; 0,027871)

(25; 0,039184)

(1; 0,004018)

(2; 0,006844)

(15; 0,02585)

(6; 0,014664)

(1; 0,012114)

(9; 0,027843)

(4; 0,039897)

(6; 0,03436)

(1; 0,023018)

(4; 0,040091)

(11; 0,071316)

(7; 0,080915)

(9; 0,056205)

(50; 0,110372)

(6; 0,013994)

(11; 0,030369)

(10; 0,031335)

(9; 0,027789)

(8; 0,022248)

(10; 0,027432)

(18; 0,04113)

(4; 0,013428)

(10; 0,022303)

(11; 0,034471)

(9; 0,020528)

(5; 0,021935)

(2; 0,026031)

(13; 0,034193)

(2; 0,014612)

(2; 0,026430)

(8; 0,083282)

(4; 0,05783)

(21; 0,126454)

(34; 0,07632)

(21; 0,024614)

(13; 0,015086)

(6; 0,010784)

(3; 0,006716)

тервалов не превышает 5-процентное пороговое значение распределения хи-

квадрат. Поэтому гипотеза о смещенном экспоненциальном распределении

интервалов между группами пакетов не отвергается.

Статистика Z(1009, z₀, z₁, . . . , z₁₀₀₈) = 0,7971 для количества пакетов в

группе не превышает критического уровня 1,96. Таким образом, гипотеза

о независимости и одинаковом распределении размеров групп не отклоня-

ется. Получены следующие оценки параметров распределения: α^∗ = 0,8281,

β^∗ = 0,6985, γ^∗ = 0,9044. Значение статистики хи-квадрат равно 3,124 и оно

меньше 5-процентного порогового значения, равного 3,841. Таким образом,

можно считать, что количество требований в пачке имеет распределение

вида (5). Итак, получаем распределение следующего вида: Q(1) = 0,1268,

Q(2) = 0,105, Q(k) = 0,0733 × (0,9044)^k-3, k ≥ 3.

6. Заключение

В статье описана модель неоднородного потока транспорта. Неоднород-

ность порождает зависимость и разное распределение интервалов между со-

седними требованиями. Таким образом, транспортный поток имеет сложную

вероятностную структуры. Предложено транспортный поток рассматривать

как поток групп (пачек) требований с определенным распределением размера

группы. Представить исходный поток в виде потока групп можно с помощью

одного из предложенных алгоритмов. Данный подход можно использовать

для изучения любого реального потока неоднородных требований.

При изучении реальных потоков часто для исследования доступна толь-

ко одна реализация данных. В статье предложен алгоритм получения до-

полнительных реализаций аналогичной вероятностной структуры. При этом

использование распределения Гаусса позволяет получить любое количество

дополнительных реализаций. Новые реализации можно исследовать теми же

методами, что и исходную. Полученные результаты оказались близкими к

результатам анализа исходных данных.

Итак, проведено численное исследование как исходных реальных данных,

так и модифицированных. Предложенные алгоритмы определения вероят-

ностной структуры потоков неоднородных требований показали свою эффек-

тивность.

163

СПИСОК ЛИТЕРАТУРЫ

Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. М.:

Наука, 1987.

Неймарк Ю.И., Федоткин М.А. О работе автомата, регулирующего уличное

движение на перекрестке // АиТ. 1966. № 3. Т. 27. C. 78-87.

Неймарк Ю.И., Федоткин М.А., Преображенская А.М. Работа автомата с об-

ратной связью, управляющего уличным движением на перекрестке // Изв. АН

СССР. Технич. кибернетика. 1968. № 5. C. 129-141.

Неймарк Ю.И. Динамические системы и управляемые процессы. М.: Наука,

1978.

Дрю Д. Теория транспортных потоков и управление ими. М.: Транспорт, 1972.

Федоткин М.А. Нелокальный способ задания управляемых случайных процес-

сов / Сб. научн. работ “Математические вопросы кибернетики”. М.: Физматлит,

1998. № 7. С. 333-344.

Федоткин М.А., Федоткин А.М. Анализ и оптимизация выходных процес-

сов при циклическом управлении конфликтными транспортными потоками

Гнеденко-Коваленко // АиТ. 2009. № 12. С. 92-108.

Fedotkin M.A., Fedotkin A.M. Analysis and Optimization of Output Processes of

Conflicting Gnedenko-Kovalenko Traffic Streams under Cyclic Control // Autom.

Remote Control. 2009. V. 70. P. 2024-2038.

https://doi.org/10.1134/S0005117909120108.

Haight F.A. Mathematical theories of traffic flow. N.Y.-London: Acad. press, 1963.

Федоткин М.А. Нетрадиционные проблемы математического моделирования

экспериментов. М.: Физматлит, 2018.

10.

Fedotkin M.A., Fedotkin A.M., Kudryavtsev E.V. Construction and Analysis of a

Mathematical Model of Spatial and Temporal Characteristics of Traffic Flows //

Autom. Control Comput. Sci. 2014. V. 48. No. 6. P. 358-367.

11.

Неймарк Ю.И. Метод точечных отображений в теории нелинейных колебаний.

М.: Наука, 1972.

12.

Федоткин М.А. Модели в теории вероятностей. М.: Физматлит, 2012.

13.

Fedotkin M.A., Rachinskaya M.A. Parameters Estimator of the Probabilistic Model

of Moving Batches Traffic Flow // Distributed Computer and Communication Net-

works. Ser. Communications in Computer and Inform. Sci. 2014. V. 279. P. 154-169.

14.

Федоткин М.А. Основы прикладной теории вероятностей и статистики. М.:

Высш. шк., 2006.

15.

Федоткин М.А. Лекции по анализу случайных явлений. М.: Физматлит, 2016.

16.

Fedotkin M.A., Fedotkin A.M., Kudryavtsev E.V. Nonlocal Description of the Time

Characteristic for Input Flows by Means of Observations // Autom. Control Comput.

Sci. 2015. V. 49. No. 1. P. 29-36.

17.

Fowler H.J., Leland W.E. Network Traffic Characteristics with Implications for

Broadband Network Congestion Management // IEEE J. Sel. Area. Comm. 1991.

No. 9(7). P. 1139-1149.

Статья представлена к публикации членом редколлегии Б.Т. Поляком.

Поступила в редакцию 23.07.2019

После доработки 26.10.2019

Принята к публикации 30.01.2020

164