Автоматика и телемеханика, № 8, 2020

М.И. БОЛОТОВ (maksim.bolotov@itmm.unn.ru)

(Нижегородский государственный университет им. Н.И. Лобачевского),

Л.А. СМИРНОВ, канд. физ.-мат. наук (smirnov_lev@appl.sci-nnov.ru)

(Нижегородский государственный университет им. Н.И. Лобачевского;

Институт прикладной физики РАН, Нижний Новгород),

Г.В. ОСИПОВ, д-р физ.-мат. наук (osipov@vmk.unn.ru)

(Нижегородский государственный университет им. Н.И. Лобачевского)

ФАЗОВОЕ УПРАВЛЕНИЕ ДИНАМИКОЙ СВЯЗАННЫХ РОТАТОРОВ¹

Исследована динамика вращательных движений в системе двух несим-

метрично связанных систем маятникового типа. Изучены механизмы по-

тери устойчивости синфазного вращательного движения. Проанализиро-

ван сценарий возникновения хаотической динамики в зависимости от зна-

чений управляющих параметров.

Ключевые слова: ротатор, фазовое управление, синхронизация, враща-

тельный режим, хаос.

DOI: 10.31857/S0005231020080127

1. Введение

Исследование коллективного поведения в сетях связанных элементов яв-

ляется одной из привлекательных и важных областей нелинейной динамики,

актуальных с точки зрения теории и приложений [1-4]. Известно, что даже

при слабой связи элементы ансамблей могут стремиться к достижению об-

щего ритма функционирования, т.е. к синхронизации [1]. Достаточно широ-

кий класс объектов, рассматриваемых в физике, радиотехнике, электронике

и других областях естествознания, могут быть описаны с помощью моделей

систем связанных маятников [5]. Несмотря на простоту этих моделей, они

используются не только для описания механических объектов [6], но и для

разнообразных процессов в молекулярной биологии [7-9], полупроводнико-

вых структурах [10] и т.д. Данная модель также может рассматриваться как

базовая при теоретических исследованиях связанных джозефсоновских кон-

тактов [11-13], а также систем фазовой синхронизации [3, 4, 14, 15].

2. Описание модели

В данной работе рассмотрено поведение ансамбля двух парциальных си-

стем фазовой синхронизации, соединенных параллельно через сигналы фа-

зовых рассогласований [3, 4]. Структурная схема ансамбля представлена на

рис. 1. Математическую модель системы двух таких объектов можно пред-

ставить в виде системы уравнений маятникового типа:

ϕ₁ + λϕ˙₁ + sin ϕ₁ = γ + κ₁ sin (ϕ₂ - ϕ₁),

(1)

ϕ₂ + λϕ˙₂ + sin ϕ₂ = γ + κ₂ sin (ϕ₁ - ϕ₂).

¹ Работа выполнена при финансовой поддержке Российского научного фонда, проект

№ 19-12-00367.

165

Рис. 1. Структурная схема пары систем фазовой синхронизации (СФС1

и СФС2), связанных параллельно через сигналы фазовых рассогласований

(ФД фазовый детектор).

Здесь λ коэффициент затухания сигнала, γ отношение начальной к мак-

симальной расстройке частот, κ₁, κ₂ параметры усиления сигнала, харак-

теризующие силу связи между системами.

Ансамбль двух симметрично связанных идентичных маятников был рас-

смотрен в [16]. Динамика неидентичных маятников (с различными величи-

нами γ) исследована в [17] . Заметим, что с помощью системы (1) возможно

описание поведения ансамбля глобально связанных ротаторов, в котором об-

разуются два кластера с различным числом взаимно синхронных элементов

(N₁ и N₂) [18]. В силу различных N₁ и N₂ связь между кластерами естествен-

ным образом является асимметричной.

Исследуем зависимость поведения системы (1) от степени асимметрично-

сти связи. Для этого представим систему (1) в виде

ϕ₁ + λϕ˙₁ + sin ϕ₁ = γ + K sin (ϕ₂ - ϕ₁),

(2)

ϕ₂ + λϕ˙₂ + sin ϕ₂ = γ + βK sin (ϕ₁ - ϕ₂),

где теперь K параметр связи, β параметр, характеризующий степень

асимметричности связи. Такой вид связи является дополнительным сред-

ством управления динамическими режимами, в том числе синхронными ре-

жимами в различного рода технических устройствах, например в системах

фазовой синхронизации [3, 4]. Как будет показано ниже, при определенном

выборе управляющих параметров в такой системе могут устанавливаться как

синфазные, так и несинфазные вращательные режимы.

3. Синфазный режим и его устойчивость

В системе (2) существует синфазное периодическое движение: координаты

совпадают друг с другом, т.е. ϕ₁(t) = ϕ₂(t) = φ_s(t). При этом φ_s(t) удовлетво-

ряет уравнению

φ_s +

φ_s + sinφ_s = γ.

Определим, при каких значениях управляющих параметров синфазный вра-

щательный режим системы (2) теряет устойчивость. Для этого линеаризуем

систему (2) относительно синфазного вращательного движения φ_s. Предста-

вим фазы ротаторов в виде

ϕ₁ = φ_s + δϕ₁,

ϕ₂ = φ_s + δϕ₂,

166

получим систему уравнений в вариациях

1 +

δϕ₁ + cos (φ_s)δϕ₁ = K(δϕ₂ - δϕ₁),

2 +

δϕ₂ + cos (φ_s)δϕ₂ = βK(δϕ₁ - δϕ₂).

Введем новую величину η = δϕ₂ - δϕ₁, представляющую собой расстройку

приращений фаз в окрестности φ_s, и получим относительно η дифференци-

альное уравнение

(3)

η+ λη + (cosφ_s

+ (1 + β)K)η = 0.

Подробный анализ уравнения (3) представлен в [16, 19], где показано, что

существует диапазон значений параметра K (K₁ < K < K₂), в котором имеет

место неустойчивость синфазного вращательного движения. Значения K₁, K₂

в рассматриваемом случае определяются выражением

]

√

[γ

1λ²

(λ⁴)

(4)

K_1,2 =

±2

1-γ² +

1+β λ²

2γ²

γ⁴

Внутри интервала ΔK = K₂ - K₁ возможно существование асинхронных пе-

риодических (разного периода) и хаотических движений. Из (4) следует, что

увеличение асимметрии связи приводит к уменьшению области неустойчиво-

сти синфазного режима. При этом интервал неустойчивости ΔK смещается

в область малых коэффициентов связи K.

4. Поиск регулярных вращательных режимов

Приведем описание численных методов, используемых для поиска регу-

лярных вращательных движений, существующих в базовой модели (2), и

определения их линейной устойчивости. Для начала отметим, что излагае-

мая ниже процедура является фактически модификацией схемы нахождения

замкнутых предельных циклов в нелинейных динамических системах и ис-

пользует методы, изложенные в [20]. Введем обозначение {ϕ_n(t)} здесь и

далее вектор-строка, где n = 1, 2. Основная идея этого метода заключает-

ся в следующем. Любой представитель {ϕ_n(t)}, искомого класса траекторий

характеризуется прежде всего своим периодом T (который, неизвестен и дол-

жен быть найден в конце вычислительной процедуры) и числом k, опреде-

ляющим то, сколько раз каждая составляющая из набора циклических коор-

динат {ϕ_n(t)} изменится на 2π за промежуток времени T . Основываясь на

этом, рассмотрим отображение {ϕ_n(0),ϕ˙_n(0)} → {ϕ_n(T ),ϕ˙_n(T )} и сконструи-

руем следующий вектор:

p(T, {ϕ_0n,ϕ˙_0n}) = {ϕ_n(T, {ϕ_0n,ϕ˙_0n}) - ϕ_0n - 2πk,ϕ˙_n(T, {ϕ_0n,ϕ˙_0n}) - ϕ˙_0n} ,

где {ϕ_n(t),ϕ˙_n(t)} решение системы (2) с начальными условиями {ϕ_0n,ϕ˙_0n},

т.е. {ϕ_n(0),ϕ˙_n(0)} = {ϕ_0n,ϕ˙_0n}.

Используя определенную подобным путем многомерную функцию

p(T, {ϕ_0n,ϕ˙_0n}), можно сформулировать условие, дающее возможность най-

ти {ϕ_n(t)} и T . Оно состоит в равенстве нулю всех компонент вектора

p(T, {ϕ_0n,ϕ˙_0n}). В итоге приходим к тому, что необходимо подобрать такие

167

значения T и {ϕ_n(t)}, которые позволят удовлетворить требованию

(5)

p(T, {ϕ_0n,ϕ˙_0n

}) = 0.

Другими словами можно сказать, что задача теперь состоит в поиске непо-

движной точки отображения {ϕ_n(0),ϕ˙_n(0)} → {ϕ_n(T ),ϕ˙_n(T )} с учетом цик-

личности {ϕ_n(t)} [20]. В силу инвариантности системы (2) относительно

трансляции во времени одну из величин {ϕ_0n} можно приравнять нулю без

потери общности и сделать тем самым количество неизвестных и число соот-

ношений в (3) одинаковым. Для отыскания корней совокупности уравнений

(3) целесообразно использовать метод Ньютона, так как он обладает высо-

кой эффективностью. Продолжая эти решения по параметру β в интервале

неустойчивости синфазного режима, можно проследить все семейство нетри-

виальных периодических движений и проанализировать их бифуркации.

Для изучения линейной устойчивости произвольных (2π-, 4π-, 8π- и т.д.)

периодических вращательных движений (с учетом цикличности) динамиче-

ской системы (2) введем малые возмущения δϕ_n(t): {ϕ_n(t) = φ_n(t) + δϕ_n(t)},

где φ_n(t) рассматриваемое периодическое движение. В результате процеду-

ры линеаризации получим следующие уравнения для возмущений {δϕ_n(t)}:

δϕ¨₁ + λδϕ˙₁ + cos(φ₁)δϕ₁ = K cos(φ₂ - φ₁)(δϕ₂ - δϕ₁),

δϕ¨₂ + λδϕ˙₂ + cos(φ₂)δϕ₂ = βK cos(φ₁ - φ₂)(δϕ₁ - δϕ₂).

Дальнейший анализ может быть проведен в рамках теории Флоке. Устой-

чивость рассматриваемых движений определяется спектром собственных

значений матрицы монодромии (оператора Флоке) M(T ), которая задается

выражением

{δϕ_n(T),δϕ˙_n(T)}^T = M {δϕ_n(0),δϕ˙_n(0)}^T .

Собственные значения µ_m (здесь и далее m = 1, 4 ) матрицы M(T ) являются

мультипликаторами Флоке, которые связаны с показателями Флоке q_m пери-

одического решения {φ_n(t)} соотношениями m = exp(iq_m). Таким образом,

для определения устойчивости каждого обсуждаемого движения достаточ-

но вычислить µ_m. Если |µ_m| ≤ 1 для всех m, тогда вращательный режим

линейно устойчив. Стоит отметить, что одно из собственных значений µ_m

всегда должно быть строго равным единице, так как {ϕ˙_n(t)} принадлежит

семейству периодических движений (с учетом цикличности). Следовательно,

появляется дополнительная возможность проверки того, что найденное с по-

мощью описанной выше процедуры решение {φ_n(t)} принадлежит обсуждае-

мому классу предельных вращений. Если хотя бы один из мультипликаторов

Флоке µ_m расположен на комплексной плоскости за пределами единичной

окружности, то вращательный режим является линейно неустойчивым.

5. Несинфазные регулярные и хаотические вращательные режимы

В результате численного моделирования в области параметров, где нет

устойчивости синфазного вращательного движения (см. выражение (4)), бы-

ли исследованы устанавливающиеся вращательные движения и их бифурка-

ции.

168

max(j_{1, 2})

2,25

(а)

(б)

(в)

2,00

1,75

1,50

(г)

(д)

(е)

1,0

0,5

10 b

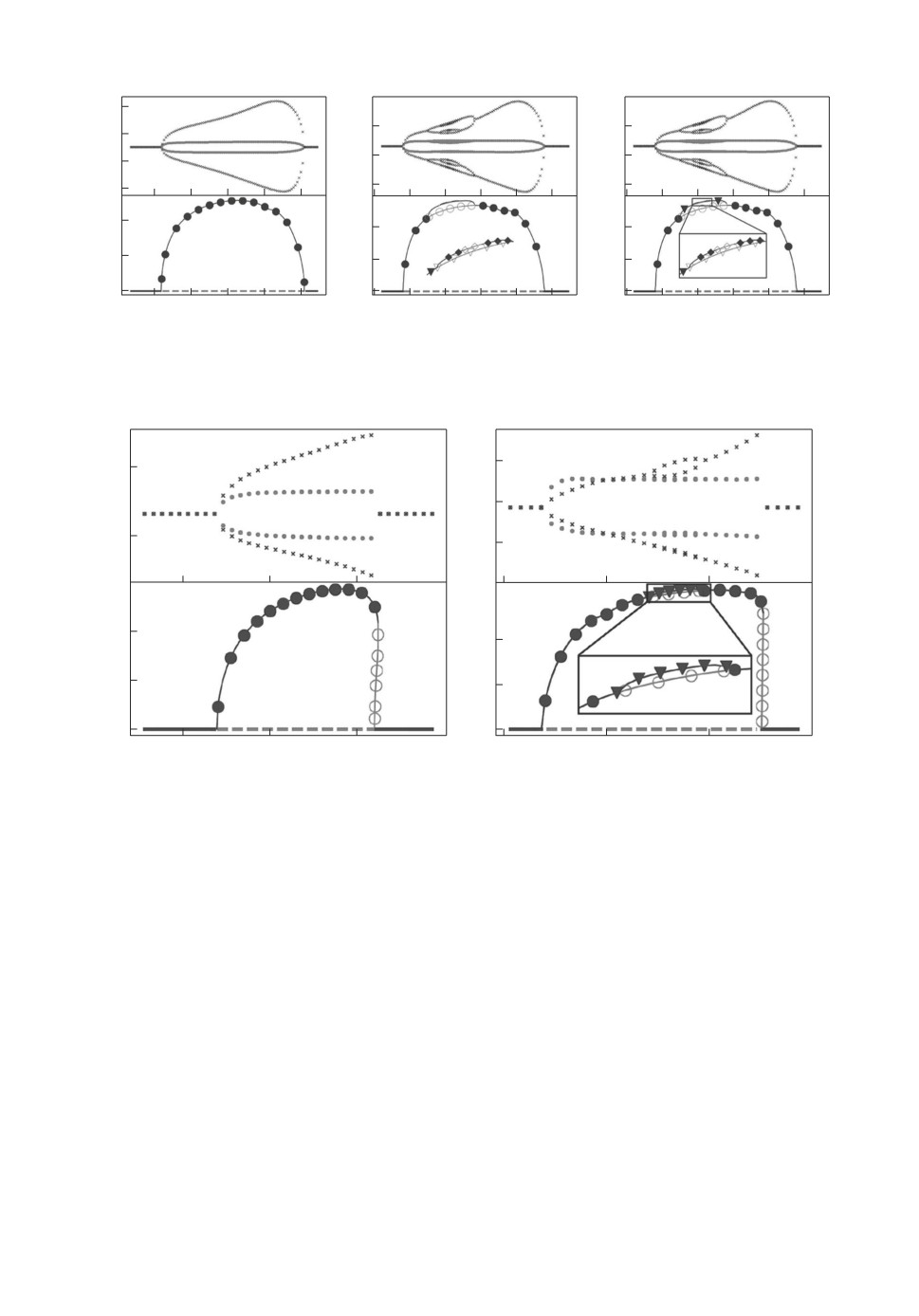
Рис. 2. а, б, в Локальные максимумы ϕ˙₁,ϕ˙₂. г, д, е Бифуркационные диа-

граммы вращательных режимов.

max(j_{1, 2})

(а)

(б)

2,25

2,5

2,00

2,0

1,75

(в)

(г)

1,0

0,5

Рис. 3. а, б Локальные максимумы ϕ˙₁,ϕ˙₂. в, г Бифуркационные диаграм-

мы вращательных режимов.

Для того чтобы характеризовать степень отклонения от синфазного режи-

ма, введем величину ξ = max

ϕ₁(t) -ϕ˙₂(t)|, где T

период вращательных

0<t<T

движений. Здесь и далее параметр внешнего воздействия выберем равным

γ = 0,97.

На рис. 2,а-2,в и рис. 3,а, 3,б изображены локальные максимумы мгно-

венных частот осцилляторов ϕ1(t) и ϕ2(t). Круглыми маркерами отмечены

значения max(ϕ˙₁(t)), крестообразными маркерами отмечены max(ϕ˙₂(t)). На

рис. 2,г-2,е и рис. 3,в, 3,г изображены зависимости параметра ξ от парамет-

ра β. Закрашенные маркеры соответствуют устойчивым вращательным дви-

жениям, полые маркеры неустойчивым. При этом круговыми, треуголь-

ными и четырехугольными маркерами показаны 4π-, 8π-, 16π-периодические

вращательные режимы соответственно. Линия без маркеров соответствует

синфазному 2π-периодическому вращательному режиму, сплошная устой-

чивому, пунктирная неустойчивому. Для K = 0,06, λ = 0,77 (рис. 2,а, 2,г)

при увеличении параметра β синфазное периодическое вращательное движе-

169

max(j_{1, 2})

j_{1, 2}(t)

2,2

(а)

2,00

(б)

2,1

1,75

2,0

1,50

1,9

1,25

1,8

1,00

1,7

0,75

1,6

0,50

1,5

0,25

1,4

2900

2920

2940

2960

2980

Рис. 4. а

Локальные максимумы ϕ˙₁,ϕ˙₂. б

Режим динамического хаоса

при β = 3,977.

max(j_{1, 2})

j_{1, 2}(t)

(а)

(б)

2,00

2,2

1,75

2,1

1,50

2,0

1,25

1,9

1,00

1,8

0,75

1,7

0,50

1,6

0,25

1,5

2900

2920

2940

2960

2980

Рис. 5. а

Локальные максимумы ϕ˙₁,ϕ˙₂. б

Режим динамического хаоса

при β = 1,25.

ние претерпевает бифуркацию удвоения периода при β ≈ 2,3. При этом из

устойчивого синфазного 2π-периодического движения рождается устойчивое

4π-периодическое движение, а 2π-периодическое движение теряет свою устой-

чивость. Затем при β ≈ 10,2 в результате обратной бифуркации удвоения

устойчивое 4π-периодическое движение сливается с неустойчивым синфаз-

ным 2π-периодическим движением, синфазное вращательное движение вновь

становится устойчивым. При λ = 0,8 (рис. 2,б , 2,д) теперь уже несинфаз-

ное 4π-периодическое движение претерпевает бифуркацию удвоения периода,

при этом рождается 8π-периодическое вращательное движение, а 4π-перио-

дическое движение теряет свою устойчивость. Далее при большем значении

параметра диссипации λ = 0,81 (рис. 2,в, 2,е) при увеличении параметра β

система претерпевает несколько бифуркаций удвоения периода, в результа-

те которых увеличивается количество неустойчивых вращательных движе-

170

ний. На рис. 4, 5 изображены локальные максимумы мгновенных частот

ϕ₁(t), ϕ2(t). Круглыми (крестообразными) маркерами отмечены значения

max(ϕ˙₁(t)) (max(ϕ˙₂(t))) (рис. 4,а, 5,a) и временные реализации

ϕ₁(t), ϕ2(t)

(рис. 4,б , 5,б ). Пунктирная линия

ϕ₁(t), сплошная линия

ϕ₂(t). При

λ = 0,816 (рис. 4) наблюдаем, что в результате каскада бифуркаций удвое-

ния периода появляется диапазон значений параметра β (3, 53 < β < 4, 53),

внутри которого в системе наблюдается режим динамического хаоса [21]. Те-

перь рассмотрим случай, когда K = 0,21 и λ = 0,6 (рис. 3,а, 3,в). В результа-

те бифуркации удвоения периода синфазное вращательное движение здесь

также теряет устойчивость при β ≈ 1,39. При этом рождается устойчивое

4π-периодическое движение, отличие которого от синфазного режима воз-

растает с увеличением параметра β. Однако при β > 3,22 система (2) вновь

возвращается к той ситуации, когда устанавливается состояние ϕ₁(t) = ϕ₂(t).

На бифуркационной диаграмме (рис. 3,в) видно, что такое изменение в по-

ведении модели (2) происходит резким образом при переходе через точку с

β = 3,22. Данный эффект жесткого исчезновения обусловлен существовани-

ем неустойчивого вращательного движения в интервале 3,199 < β < 3,24.

Чтобы проанализировать происходящие смены режимов, рассмотрим за-

висимость параметра ξ от параметра β (рис. 3,а, 3,в). Видно, что кроме устой-

чивых периодических движений, существует также неустойчивое несинфаз-

ное 4π-периодическое движение, которое рождается из синфазного неустой-

чивого 2π-периодического движения в результате субкритической бифурка-

ции удвоения периода (β ≈ 3,199), при этом синфазное 2π-периодическое дви-

жение вновь становится устойчивым. Далее при увеличении параметра β

устойчивое и неустойчивое 4π-периодические вращательные движения сли-

ваются и исчезают в результате седлоузловой бифуркации. При дальнейшем

увеличении параметра β в системе (2) возможен только синфазный враща-

тельный режим. Таким образом, в системе наблюдается эффект бистабильно-

сти вращательных режимов. При λ = 0,71 (рис. 3,б , 3,г) ситуация аналогична

предыдущему случаю: существует 4π-периодическое движение и происходит

бифуркация удвоения периода (β ≈ 1,38), в результате которой рождается

устойчивое 8π-периодическое движение, при этом 4π-периодическое движе-

ние теряет свою устойчивость. При λ = 0,779 (рис. 5) в результате каскада

бифуркаций удвоения периода появляется диапазон значений параметра β

(1,15 < β < 1,35), при которых в системе наблюдается режим динамического

хаоса.

На рис. 6 изображены карты вращательных режимов, показывающие тип

установившегося вращательного движения, реализующегося в системе в за-

висимости от параметров K и β. Рассмотрим случай λ = 0,67 (рис. 6,а), при

этом помимо синфазного вращательного движения в рассматриваемой об-

ласти параметров существует только устойчивый несинфазный 4π-периоди-

ческий вращательный режим. При увеличении λ до значения 0,73 (рис. 6,б )

кроме устойчивого 4π-вращательного режима, при некоторых K и β наблюда-

ется 8π-периодический несинфазный вращательный режим, при этом 4π-вра-

щательное движение теряет устойчивость. При λ = 0,82 (рис. 6,в) в системе

может наблюдаться режим динамического хаоса, возникающий в результате

каскада бифуркаций удвоения периода.

171

сhaos

0,20

0,15

0,20

0,10

0,20

0,10

Рис. 6. Тип вращательных периодических режимов в зависимости от значений

параметров K, β при γ = 0,97. а λ = 0,67, б λ = 0,73,в λ = 0,82.

Заметим, что при малых значениях параметра связи K неустойчивость

синфазного режима возникает при большем значении параметра асиммет-

ричности связи β.

6. Заключение

В работе рассмотрена вращательная динамика в связанных системах фа-

зовой синхронизации. Показано, что в системе с асимметричной связью су-

ществует область значений параметров, в которой синфазное вращательное

движение является неустойчивым, при этом реализуются несинфазные пе-

риодические и хаотические вращения. Аналитически получено, что увели-

чение асимметрии связи приводит к уменьшению области неустойчивости

синфазного режима ΔK = K₂ - K₁. При этом интервал неустойчивости ΔK

смещается в область малых коэффициентов связи K. Для возникновения

неустойчивости при малых значений параметра связи необходима большая

степень ее асимметричности.

Потеря устойчивости происходит в результате бифуркации удвоения пе-

риода (прямой и обратной). При обратной бифуркации удвоения периода в

системе наблюдается жесткий переход к несинфазному режиму. В случае

больших значений параметра затухания в результате каскада бифуркаций

удвоения периода возникают хаотические вращения.

Описаны численные методы, позволяющие находить и определять линей-

ную устойчивость регулярных вращательных режимов.

СПИСОК ЛИТЕРАТУРЫ

1. Pikovsky A., Rosenblum M., Kurths J. Synchronization. A Universal Concept in

Nonlinear Sciences. England: Cambridge Univer. Press, 2001.

2. Osipov G.V., Kurths J., Zhou Ch. Synchronization in Oscillatory Networks. Ger-

many: Springer Verlag, 2007.

172

Afraimovich V.S., Nekorkin V.I., Osipov G.V., Shalfeev V.D. Stability, Structures

and Chaos in Nonlinear Synchronization Networks. Singapore: World Sci., 1994.

Шалфеев В.Д., Матросов В.В. Нелинейная динамика систем фазовой синхро-

низации. Монография. Нижний Новгород: Изд-во Нижегород. госуниверситета,

2013.

Неймарк Ю.И. Математическое моделирование как наука и искусство. Учеб-

ник. - 2-е изд., испр. и доп. Нижний Новгород: Изд-во Нижегородского госуни-

верситета, 2010.

Kecik K., Warminski J. Dynamics of an Autoparametric Pendulum-Like System

with a Nonlinear Semiactive Suspension // Math. Probl. Engineer. 2011. V. 2011.

No. 451047. P. 1-15.

Yakushevich L.V. Nonlinear Physics of DNA. Germany: Wiley-VCH., 2004.

Homma S., Takeno S. A Coupled Base-Rotator Model for Structure and Dynamics of

DNA: Local Fluctuations in Helical Twist Angles and Topological Solitons // Progr.

Theoret. Physics. 1984. V. 72. No. 4. P. 679-693.

Takeno S., Homma S. Kinks and Breathers Associated with Collective Sugar Puck-

ering in DNA // Progr. Theoret. Physics. 1987. V. 77. No. 3. P. 548-562.

10.

Barone A., Paterno G. Physics and Applications of the Josephson Effect. United

States: John Wiley and Sons Inc., 1982.

11.

Ryu S., Yu W., Stroud D. Dynamics of an underdamped Josephson-junction lad-

der // Phys. Rev. E. 1996. V. 53. No. 3. P. 2190-2195.

12.

Qian M., Wang J.-Z. Transitions in two sinusoidally coupled Josephson junction

rotators // Ann. Physics. 2008. V. 323. No. 8. P. 1956-1962.

13.

Zheng Z., Hu B., Hu G. Spatiotemporal dynamics of discrete sine-Gordon lattices

with sinusoidal couplings // Phys. Rev. 1998. V. 57. No. 1. P. 1139-1144.

14.

Линдсей В. Системы синхронизации в связи и управлении / Под ред. Ю.Н. Ба-

каева, М.В. Капранове. М: Сов. радио, 1978.

15.

Системы фазовой синхронизации / Под ред. В.В. Шахгильдяна, Л.Н. Белюсти-

ной. М: Радио и связь, 1982.

16.

Smirnov L.A., Kryukov A.K., Osipov G.V., Kurths J. Bistability of rotational modes

in a system of coupled pendulums // Regul. Chaotic Dyn. 2016. V. 21. No. 7-8.

P. 849-861.

17.

Хрисанфова С.О., Кадина Е.Ю., Губина Е.В., Коган Л.В., Осипов Г.В. Динами-

ка системы двух нелинейно связанных маятников // Прикладная нелинейная

динамика. 2016. № 3. C. 4-20.

18.

Kemeth F.P., Haugland S.W., Krischer K. Cluster singularity: The unfolding of

clustering behavior in globally coupled Stuart-Landau oscillators // Chaos: An In-

terdisciplinary J. Nonlinear Sci. 2019. V. 29. No. 2. P. 023107.

19.

Bolotov M.I., Munyaev V.O., Kryukov A.K., et al. Variety of rotation modes in a

small chain of coupled pendulums // Chaos: An Interdisciplinary J. Nonlinear Sci.

2019. V. 29. No. 3. P. 033109.

20.

Неймарк Ю.И. Метод точеченых отображений в теории нелинейных колебаний.

М: Наука, 1972.

21.

Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания. М: Наука,

1987.

Статья представлена к публикации членом редколлегии Б.Т. Поляком.

Поступила в редакцию 23.07.2019

После доработки 18.10.2019

Принята к публикации 30.01.2020

173