Автоматика и телемеханика, № 9, 2020
© 2020 г. А. ЭРНАНДЕC (capricornale_1415@hotmail.com),
А.С. ПОЗНЯК, д-р техн. наук (apoznyak@ctrl.cinvestav.mx)
(Исследовательский центр CINVESTAV, Мехико, Мексика)
НЕЛИНЕЙНОЕ ПАРАМЕТРИЧЕСКОЕ ОЦЕНИВАНИЕ
ГАМИЛЬТОНОВЫХ СИСТЕМ: ЗАДАЧА ИДЕНТИФИКАЦИИ
КАК ЗАДАЧА СТАБИЛИЗАЦИИ1
В данной статье представлены две численные процедуры идентифика-
ции параметров гамильтоновых систем непрерывного времени. Предло-
женный подход использует свойства первых интегралов и их характери-
стики, позволяя рассматривать процесс параметрической идентификации
как стабилизацию производных первых интегралов. Эта идея реализует-
ся с помощью двух численных процедур, использующих дифференциатор
типа “супер-твист” для оценки производных обобщенных координат и им-
пульсов в реальном времени. Показана сходимость указанных процедур
идентификации и их применение для скалярного и векторного случаев.
Численные примеры демонстрируют хорошую работоспособность пред-
ложенных методов.
Ключевые слова: функция Гамильтона, первые интегралы, идентифика-
ция, стабилизация.
DOI: 10.31857/S0005231020090020
1. Введение
Идентификация систем это совокупность методов определения харак-
теристик математической модели системы по измерениям ее входов и выхо-
дов. Методы оценки параметров нелинейных систем зависят от структуры
модели и основаны либо на линейных, либо на нелинейных (по параметрам)
моделях. Выбор между этими двумя подходами часто диктуется исследуемым
процессом. Если известна структура дифференциального уравнения, описы-
вающего процесс, то алгоритмы оценивания параметров могут быть приме-
нены непосредственно для оценки неизвестных параметров. Когда априорной
информации не достаточно, и процесс рассматривается как черный ящик, то
стандартным подходом является описание оператора входа/выхода с помо-
щью подходящей модели представления, которая обычно выбирается нели-
нейной во входных и выходных переменных, но линейной по оцениваемым
параметрам. В этом случае для оценивания параметров обычно применяют-
ся различные варианты методов наименьших квадратов (МНК).
Применение МНК требует выполнения так называемого “условия постоян-
ного возбуждения”. Если неизвестные параметры, подлежащие оценке, участ-
вуют в описании модели в нелинейной форме, прямое применение такого
1 Работа выполнена при финансовой поддержке CONACYT-Mexico (грант № CB 2015-
251552-Y).
62
подхода приводит к глобальной многоэкстремальной оптимизационной за-
даче, решение которой может быть получено с помощью МНК или любого
другого градиентного метода (см. [1, 2]). Последние достижения в этой обла-
сти включают в себя комбинированный алгоритм сглаживания и оценивания
параметров [3, 5], который компенсирует неопределенную структуру модели
и внешние возмущения путем введения в модель изменяющихся во времени
параметров, и рекурсивный алгоритм, предполагающий повторное использо-
вание данных [6].
Гамильтоновы системы представляют собой особый класс консерватив-
ных нелинейных систем [7, 17], в которых отсутствует “потеря энергии”, а
некоторые функции координат и обобщенных импульсов поддерживаются
неизменными (первые интегралы) [8]. Эти консервативные свойства предо-
ставляют новые возможности для успешной параметрической идентифика-
ции неизвестных параметров, участвующих нелинейно в описании модели.
В данной работе реализован такой подход, предусматривающий использова-
ние двух новых процедур идентификации в непрерывном времени. Доказана
сходимость этих процедур, два численных примера иллюстрируют хорошую
работоспособность предлагаемого подхода.
1.1. Основные допущения и ограничения
Существует множество работ, посвященных идентификации линейных па-
раметров, но которые не могут быть реализованы для моделей, содержащих
нелинейные параметры. Как было уже отмечено выше, эта ситуация имеет
место из-за того, что многие модели систем основаны на динамике особо-
го вида: нелинейность параметров может спровоцировать сингулярность и
многоэкстремальность соответствующих оптимизационных задач. Основные
допущения, которые ограничивают класс гамильтоновых систем, рассматри-
ваемых в данной работе, могут быть сформулированы в следующем виде:
доступная (измеряемая в реальном времени) информация представляет
собой обобщенные координаты (q1, . . . , qn) и импульсы (p1, . . . , pn), но не их
производные;
специальное условие принадлежности “конусу”, о котором будет гово-
риться ниже, требуется для обеспечения работоспособности двух предло-
женных процедур идентификации; оно основано на так называемом условии
σ-стабилизации (локальной выпуклости).
1.2. Основные результаты
Основные результаты данной статьи состоят в следующем:
переформулирована задача параметрической идентификация для ши-
рокого класса гамильтоновых систем как задача стабилизации специальных
функций (первых интегралов), остающихся постоянными на траекториях си-
стем; их число не обязательно должно соответствовать полной системе неза-
висимых первых интегралов и может варьироваться от 1 до 2n;
применен наблюдатель типа “супер-твист” [9] для оценки соответствую-
щих производных состояний и обобщенных импульсов в реальном времени;
63
предложены две численные процедуры для реализации процедуры иден-
тификации: одинарная и двойная “сигнум-коррекция”;
проанализирована сходимость (асимптотическая и на конечном гори-
зонте) этих процедур;
приведены два численных примера, иллюстрирующие работоспособ-
ность предложенного подхода, где функции Гамильтона содержат неизвест-
ные параметры в нелинейном виде.
1.3. Структура работы
Структура работы выглядит следующим образом. Вторая часть, следую-
щая за Введением, представляет собой краткое описание лагранжева и га-
мильтонова формализма. В следующей части (третьей) дано определение
первых интегралов и приведены их возможные структуры. В четвертой части
представлена постановка задачи и кратко описан подход к решению пробле-
мы. В пятой части задача идентификации рассмотрена как стабилизация с
использованием методов оптимизации. Затем обсуждаются две предложен-
ные численные процедуры и их сходимость. Наконец, два примера числен-
ного моделирования, реализованных в MATLAB/SIMULINK ®, показывают
эффективность предложенных методов.
2. Гамильтонов формализм и постановка задачи
2.1. Лагранжев формализм
Описание динамических моделей для широкого класса электромеханиче-
ских систем задается классическим уравнением Лагранжа вида
d
∂
∂
(1)
L(q,
˙q,t) -
L (q,
˙q,t) = Qi,non-potential
(q,
˙q,t) , i = 1,n,
dt ∂
qi
∂qi
где q = (q1, . . . , qn)⊺ и
q=
q1,... ,
qn)⊺
вектора обобщенных координат и
скоростей, L(q,
q,t)
гладкая функция Лагранжа 2n + 1 переменных, задан-
ная в форме
(2)
L (q,
q,t) := T (q,
˙q,t) - V (q,t) .
Для “натуральных” механических систем T (q,
q,t)
кинетическая энер-
гия рассматриваемой системы, а V (q, t)
потенциальная энергия,
Qi,non-potential(q,
q,t)
обобщенная непотенциальная сила, действующая на
(
)
i-ую координату
i = 1,n
Ниже будет рассмотрен только класс консервативных систем, в которых
непотенциальные силы отсутствуют, т.е. для всех i = 1, n и всех t ≥ 0
Qi,non-potential (q,
˙q,t) = 0,
что обеспечивает выполнение равенства
d
∂
∂
(3)
L (q,
˙q,t) -
L (q,
˙q,t) = 0, i = 1,n.
dt ∂
qi
∂qi
64
Говоря о траектории системы, используем обозначения q(t) = (q1(t),
...,qn(t))⊺ и
q(t) = (q1(t),... ,
˙qn(t))⊺ векторы обобщенных координат и ско-
ростей как функции времени t ≥ 0.
2.2. Гамильтонов формализм
В соответствии с гамильтоновым подходом определим обобщенные им-
пульсы
∂
(4)
pi :=
L (q,
˙q,t) , i = 1,n,
qi
и функцию Гамильтона (преобразование Лежандра)
[
]
(5)
H (q, p, t) := p⊺
q-L(q,q,t)
,
q=˙q(q,p,t)
где вектор
q получен из условия (4) в предположении разрешимости этой
системы. Таким образом,
q=
˙q (q,p,t). Из уравнений (3) и (4) напрямую сле-
дует, что обобщенные координаты и импульсы удовлетворяют каноническим
уравнениям Гамильтона
∂
qi =
H (q, p, t) ,
∂pi
(6)
∂
pi = -
H (q,p,t) , i = 1,n.
∂qi
2.3. Неизвестные параметры динамических уравнений
Предположим, что и кинетическая энергия T (q,
˙q,t), и, вообще говоря,
потенциальная V (q, t) зависят от вектора неизвестных параметров α∗ ∈ Rr,
а именно
T =T(q,
˙q,t|α∗) , V = V (q,t|α∗),
причем подразумевается, что функция Лагранжа L (q,
˙q,t) (2) и соответст-
вующая функция Гамильтона H (q, p, t) (5) становятся зависящими также
от α∗, т.е.
L=L(q,
˙q,t|α∗), H = H (q,p,t|α∗).
Отметим, что на траектории системы переменные состояния, обобщенные ко-
ординаты и импульсы (и их производные), также зависят от этого неизвест-
ного параметра:
q = q (t|α∗),
q=
˙q (t|α∗), p = p (t|α∗) ,
p = p(t|α∗),
а уравнения (6) переходят в равенства
∂
˙qi (t|α∗) =
H (q (t|α∗) , p (t|α∗) , t|α∗) ,
∂pi
(7)
pi (t|α∗) = -∂ H (q (t|α∗),p(t|α∗),t|α∗).
∂qi
65
Замечание 1. Отметим, что ввиду равенства (4) могут возникнуть два
различных случая:
Случай 1: когда для всех i = 1, n
∂2
(8)
L (q (t|α∗) ,
) = 0,
∂α∗∂
qi
что влечет за собой независимость импульса p от α∗ и возможность оценить
его напрямую из (4), используя измерения q = q (t|α∗) и оценки производной
˙q (t|α∗).
Случай 2: когда по крайней мере для одного i = i0
∂2
(9)
L (q (t|α∗) ,
) = 0,
∂α∗
qi0
что требует использования специальной процедуры, которая в дальнейшем
будет названа p-адаптивным оцениванием.
2.4. Постановка задачи
Задача 1. Основываясь на онлайн-измерении координат q (t|α∗)
(предположим, что эти измерения точны, т.е. не содержат никакого шума
в измерениях), получить оценку векторного параметра α (t) ∈ Rr, которая
является асимптотически состоятельной, а именно, удовлетворяет
(10)
α (t) -→ α∗.
t→∞
Для успешного решения поставленной задачи, нужно получить онлайн-
оценки
˙q (t|α∗) , p (t|α∗) и
p(t|α∗), которые будут обозначены ниже как
˙q (t) ,
p(t) и̂p(t). Это можно сделать путем применения так называемого точного
дифференциатора, реализованного по схеме “супер-твист” [9].
Заметим, что вектор α∗ неизвестных параметров может участвовать в ка-
нонических уравнениях (7) нелинейным образом. Таким образом, во многих
случаях прямое применение метода наименьших квадратов (или его моди-
фикации) невозможно, что порождает новые задачи для исследователей и
инженеров: требуется разработать конкретные методы (численные процеду-
ры) для успешной идентификации неизвестного векторного параметра α∗.
3. Первые интегралы
3.1. Определение первых интегралов
Напомним, что функция f(t, q, p), которая принимает постоянное значение
на траекториях гамильтоновой системы (6), называется первым интегралом
системы. Класс первых интегралов характеризует следующее свойство [10].
Лемма 1. Функция f(t,q,p) является первым интегралом гамильтоно-
вой системы (6) с гамильтонианом H тогда и только тогда, когда
∂f(t,q,p)
(11)
+ [f, H] = 0,
∂t
66
где [f, H] называют скобками Пуассона и задают с помощью выражения
)
∑
(∂f ∂H
∂f ∂H
(12)
[f, H] :=
-
∂qi ∂pi
∂pi ∂qi
i=1
3.2. Характеристика первых интегралов путем исследования
гамильтоновой структуры
Проверяя выполнение свойства (11) (подставляя функции H в (11)),
несложно убедиться, что следующие функции являются первыми интегра-
лами:
1) если
∂H (q,p)
(13)
= 0, то H = const,
∂t
t
2) если
H = H(f(q1,...,qm,p1,...,pm),qm+1,pm+1,...,qn,pn,t),
(14)
то f(q1, . . . , qm, p1, . . . , pm) = const,
t
3) если
H = H(ϕ1(q1,p1),...,ϕn(qn,pn),t),
(15)
то ϕi(qi, pi) = const, i = 1, n ,
t
4) если
H = H(ϕj(...ϕ2(ϕ1(q1,p1),q2,p2)...),qj+1,pj+1,...,qn,pn,t),
(16)
то ϕk(. . . ϕ2(ϕ1(q1, p1), q2, p2) . . . , qk, pk) = const, k = 1, j ,
t
5) если
n fi(qi,pi)
H =i=1n
,
∑
(17)
ϕi(qi, pi)
i=1
то fi(qi, pi) - Hϕi(qi, pi) = const, i = 1, n,
t
6) если
n αifi(qi,pi)
(18)
H = φ(t)i=1n
, то fi(qi, pi) = const,
i = 1,n.
t
∑ βifi(qi,pi)
i=1
67
4. Задача идентификации как задача стабилизации
4.1. Производная первого интеграла
Неизвестные параметры, вообще говоря, входят аналитически в каждый
первый интеграл f(t, q, p|α), поэтому нужно помнить, что измеренные или
оцененные траектории зависят от реальных значений неизвестного α∗, т.е.
q = q (t|α∗) и p = p(t|α∗). Это означает, что
(19)
f (t, q (t|α∗) , p (t|α∗) |α) = const, если α = α∗.
t
Другими словами, для идентификации неизвестного параметра α ∈ Rr при-
дется использовать свойство (19), рассматривая параметр α как управляю-
щее (корректирующее) воздействие, которое будет выбрано для стабилизации
функции f(t, q (t|α∗) , p (t|α∗) |α).
Это требование можно выразить в виде
d
(20)
σ (t,α) :=
f (t, q (t|α∗) , p (t|α∗) |α) ≡ 0, если α = α∗.
dt
Таким образом, выполнение условия стабилизации (19) можно интерпрети-
ровать как построение управляющего воздействия u ∈ Rr, обеспечивающего
σ-стабилизацию
(21)
σ (t, u) = 0
для любого t ≥ 0.
4.2. Мотивирующий пример
Для иллюстрации свойства (20) рассмотрим стандартный маятник, дина-
мика которого описана уравнением
p
(22)
q=
,
p = -mgα∗ sin(q) + (να∗)2 sin(q)cos(q), α∗
>0
α∗2
(r = n = 1) с гамильтонианом
2
p
1
(23)
H(q, p|α∗) =
+ mgα∗(1 - cos(q)) -
(να∗)2 sin2
(q).
2α∗2
2
Отметим, что неизвестный параметр α∗ входит в это уравнение нелинейно.
Следуя (20) и обозначая для простоты q∗ = q (t|α∗) и p∗ = p (t|α∗), определим
∗
[
]
p
σ (t, u) =
p∗ +
mgusin (q∗) - (νu)2 sin (q∗)cos (q∗)
q∗ =
u2
∗
p
∂H
[
] ∂H
=-
+
mgusin (q∗) - (νu)2 sin (q∗) cos(q∗)
=
u2 ∂q
∂p
∗
[
(
)
]
p
=-
mgusin (q∗) -
νu2
sin (q∗) cos (q∗)
+
u2
68
[
]p∗
+
mgusin (q∗) - (νu)2 sin(q∗)cos (q∗)
=
u2
∗2
(u2 -α
)[
(
)
]
=p∗
mg sin (q∗)(α∗ + u) -
α∗2 + u2
ν2 sin(q∗) cos(q∗)
α∗2u2
Когда u = α∗, имеем σ (t, α∗) = 0. Для иллюстрации зависимости σ(t, u) от u
для различных t ≥ 0 рассмотрим ситуацию, когда α∗ = 0,5, m = 1, g = 9,82 и
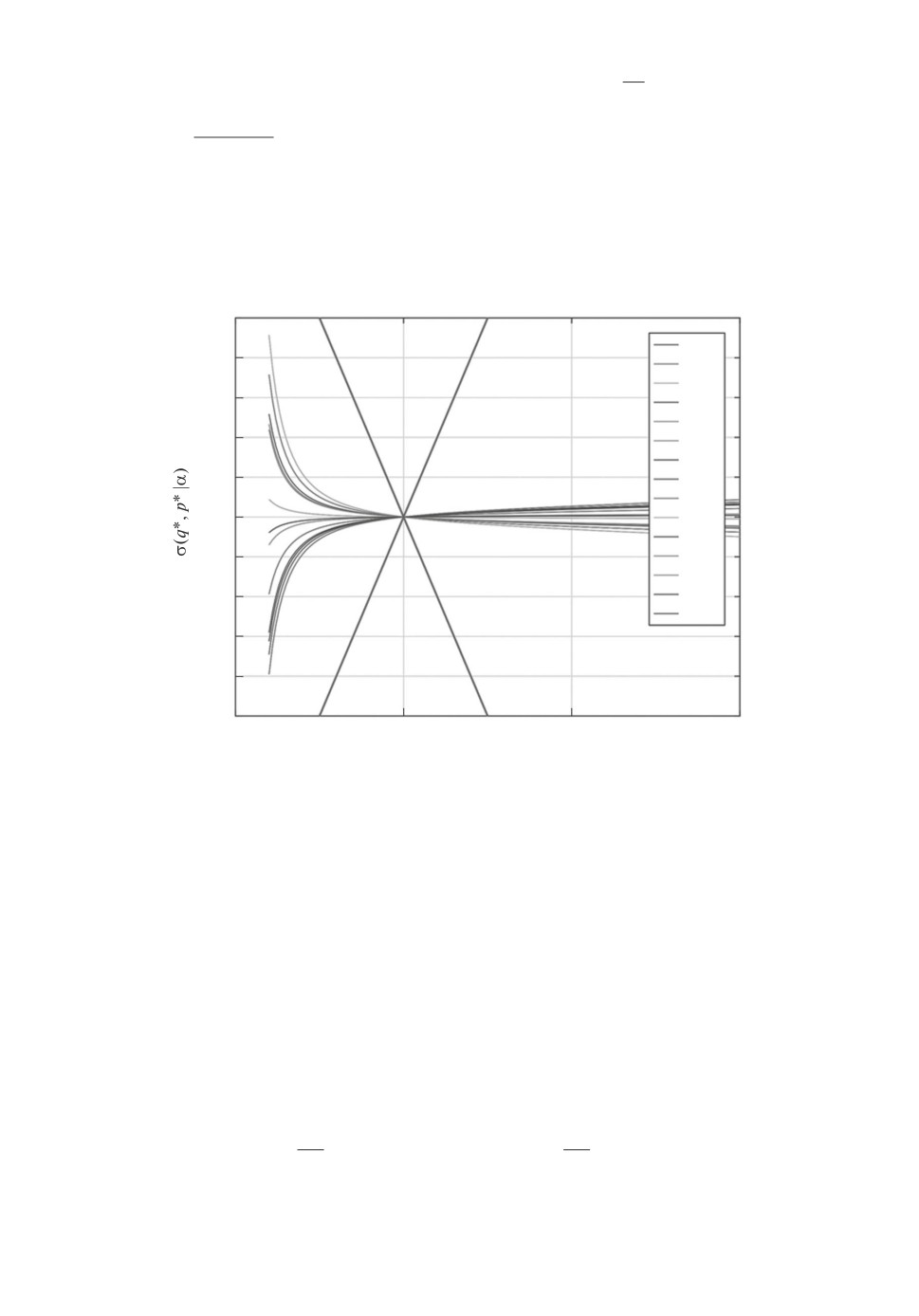
ν = 1. График соответствующей функции σ(t,u) показан на рис. 1 для раз-
личных значений t = tk (k = 1, 2, . . .).
2500
t = 2
2000
t = 4
C
t = 6
1500
t = 8
t = 10
1000
t = 12
t = 14
500
t = 16
t = 18
0
t = 20
t = 22
-500
t = 24
t = 26
-1000
t = 28
t = 30
-1500
C
-2000
-2500
0
0,5
1,0
1,6
a
Рис. 1. График σ(t, u).
Отметим, что все кривые на рисунке лежат за пределами конуса C.
5. Задача идентификации как задача оптимизации
5.1. Дифференциальные оптимизаторы
Условие (21), которое нужно реализовать, также может быть представлено
в виде следующей задачи оптимизации:
(24)
|σ (t, α)| → min
α
для всех t ≥ 0 или, другими словами,
∂
∂
0=
|σ (t, α)| = sign (σ (t, α))
σ (t, α) .
∂α
∂α
Рассмотрим следующие численные дифференциальные процедуры (оптими-
заторы) [15, 16]:
69
1) Процедура 1 (использование одной сигнум-функции):
∂
(25)
α (t) = -γ (t) sign (σ (t, α (t)))
σ (t,α(t)) ;
∂α
2) Процедура 2 (использование двух сигнум-функций):
(
)
∂
(26)
α(t) = -γ (t)sign(σ (t,α (t))) sign
σ (t, α (t))
∂α
В обеих процедурах функция усиления γ (t) удовлетворяет предположе-
нию
∫∞
(27)
γ (t) ≥ 0,
γ (t)dt = ∞.
t=0
5.2. Наблюдатель типа “супер-твист” для оценивания
˙q (t|α∗) иp (t|α∗)
Сначала отметим, что, если ∂f/∂t ≡ 0 в (20), то
[
]⊺
[
]⊺
∂
∂
σ (t, α (t)) =
f (t, α (t))
˙q (t|α∗) +
f (t,α (t))
p(t|α∗),
∂q
∂p
в результате имеем
[
]⊺
[
]⊺
∂
∂
∂
∂
∂
σ (t, α (t)) =
f (t, α (t))
˙q (t|α∗) +
f (t, α (t))
p(t|α∗).
∂α
∂α
∂q
∂α
∂p
∂
Несложно заметить, что получена функция
σ (t, α (t)), которая использу-
∂α
ется в обеих процедурах (25) и (26). Для нахождения ее значения необхо-
димо знать вектор-функции
˙q (t|α∗) и p (t|α∗) , или, если первое невозможно,
использовать их онлайн-оценкиq (t) и̂p (t) . Эти оценки можно получать в
реальном времени, применяя следующий “супер-твист” алгоритм [9, 11]:
для случая 1 (8):
(
)
{
x2 (t)
q(t|α∗) - βsign(q(t) - q(t|α∗)),
(28)
=
˙q (t|α∗)
x2 (t) - θ||q(t|α∗) - q(t)||1/2sign(q(t) - q(t|α∗)),
(
)
{
x2 (t)
p(t) - βsign(p(t) - p(t)),
(29)
=
p(t)
x2 (t) - θ||p(t) - p(t)||1/2sign(p(t) - p(t)),
для случая 2 (9) p-адаптивная оценка:
(
)
{
x2 (t)
q(t|α∗) - βsign(q(t) - q(t|α∗)),
(30)
=
˙q (t|α∗)
x2 (t) - θ||q(t|α∗) - q(t)||1/2sign(q(t) - q(t|α∗)),
70
(
)
{
x2 (t)
p(t|α (t)) - βsign(p(t|α (t)) - p(t|α (t))),
(31)
=
p(t|α(t))
x2(t)-θ||p(t|α(t))- p(t|α(t))||1/2sign(p(t|α(t))-p(t|α(t))),
где параметры дифференциаторов θ и β удовлетворяют условиям [28, 29, 30,
31]
β > 5L, θ2 ∈ {32L,8[β - L]},
{
}
max sup|
˙q(t|α∗)|; sup| p(t|α∗)|
≤ L,
t
t
если производные обобщенных координат и импульсов ограничены на всей
числовой оси времени.
Замечание 2. Заметим,чтооценкиq (t) и̂p(t) сходятся за конечное вре-
мя к реальным значениям
˙q (t|α∗) и p (t|α∗), если в онлайн-измерениях q(t|α∗)
и p(t|α∗) нет шума и возмущений.
5.3. Анализ сходимости процедуры оптимизации
Следующая теорема представляет собой достаточные условия работоспо-
собности предлагаемых процедур идентификации (25)-(26). Зададим функ-
цию Ляпунова V (α) в виде
1
(32)
V (α) :=
∥α - α∗∥2 .
2
Теорема 1. Предположим, что
1. Условие (27) выполнено при ограниченных γ(t).
2. Для всех t ≥ 0 и всех α ∈ Rr специальное условие принадлежности “ко-
нусу” выполнено
∂
sign (σ (t, α)) (α - α∗)⊺
[σ (t,α)] ≥ ρVκ (α) , ρ > 0,
∂α
где κ ∈ (0, 1].
Тогда
процедура (25) обеспечивает асимптотическую сходимость
α (t) -→ α∗,
t→∞
процедура (26) при γ(t) = const > 0 и κ = 0,5 обеспечивает сходимость
за конечное время, а именно, для всех t > treach α (t) = α∗, где
√
||α(0) - α∗||
(33)
treach :=
2
γρ
71
Доказательство. Из (32) следует, что
V (α (t)) = (α (t) - α∗)⊺ α (t) =
∂
= -γ (t)sign (σ (t,α (t)))(α(t) - α∗)⊺
[σ (t, α (t))] .
∂α
По условиям этой теоремы
(34)
V (α (t)) ≤ -γ (t) ρVκ
(α(t)).
Принимая κ = 1 для процедуры (25) и учитывая предположение (27), полу-
чаем
t
∫
V (α(t)) ≤ V (α (0)) exp-ρ γ (τ)dτ -→ 0,
t→∞
τ=0
что влечет за собой α(t) -→ α∗. Если же κ = 0,5 и γ = const > 0, то для
t→∞
процедуры (26) имеем
√
(35)
V (α (t)) ≤ -γρ
V (α (t)),
что влечет
√
||α(t) - α∗||
√
1
0≤
V (α (t)) =
√
≤
V (α(0)) -
γρt
2
2
и
γρ
||α(t) - α∗|| ≤ ||α(0) - α∗|| -
√ t
2
и приводит к выполнению условия (33).
6. Численное моделирование
Пример 1 (наклонная плоскость). Рассмотрим простую механическую
систему, представленную на рис. 2.
j
m
r
q
M
x
Рис. 2. Наклонная плоскость.
72
Q(q, r)
´106
2,0
1,5
1,0
0,5
06
8
4
6
4
r
2
2
q
0
Рис. 3. Функция Q(θ, r).
Кинетическая энергия этой системы задана в виде
1
3
T (x, ϕ, x,ϕ˙) =
(M + m) ˙x2 - mr ˙xϕ˙ cos(θ) +
mr2ϕ˙2,
2
4
а потенциальная энергия равна
V (x, ϕ, t) = -gmϕr sin(θ).
Соответствующая функция Лагранжа имеет вид
1
3
L(x, ϕ, x,ϕ˙) =
(M + m) ˙x2 - mr ˙xϕ˙ cos(θ) +
mr2ϕ˙
2 + gmϕr sin(θ),
2
4
а уравнения Эйлера-Лагранжа заданы как
f1(θ,r,t) := (M + m)x(t) - mrϕ (t) cos(θ) = 0,
3
f2(θ,r,t) := -mrx(t)cos(θ) +
mr2
ϕ(t) - gmr sin(θ) = 0.
2
Для численного моделирования выберем M = 0,1, m = 1 и g = 9,81. Для при-
менения МНК для оценки двух параметров θ и r, зададим функцию затрат
в виде
∫
[
]
(36)
Q(θ, r) =
f21(θ,r,t) + f22(θ,r,t)
dt.
t=0
График этой функции Q(θ, r) приведен на рис. 3, где каждый может увидеть
разные локальные экстремумы. Соответствующий гамильтониан задан в виде
r cos(θ)
2(m + M)p2ϕ + 3mp2xr2 + 4mpϕpx
(37)
H(q(t), p(t)) =
− gmϕr sin(θ),
2mr2(m + 3M + 2m sin2(θ))
73
16 000
14 000
H(q,
p|a*)
12 000
H(q,
p|a)
10 000
8000
6000
4000
2000
0
-2000
0
1
2
3
4
5
6
7
8
9
10
t(s)
Рис. 4. H(q, p|α∗) и H(q, p|α).
Оценки q
1,5
q*
1,0
q M1
0,5
q M2
0
-0,5
0
1
2
3
4
5
6
7
8
9
10
t(s)
Оценки r
1,5
r*
1,0
r M1
0,5
r M2
0
-0,5
0
1
2
3
4
5
6
7
8
9
10
t(s)
Рис. 5. α-сходимость.
[
]
[
]
π
который получен с учетом первого интеграла и α∗ =
θ r
=
2
. Как
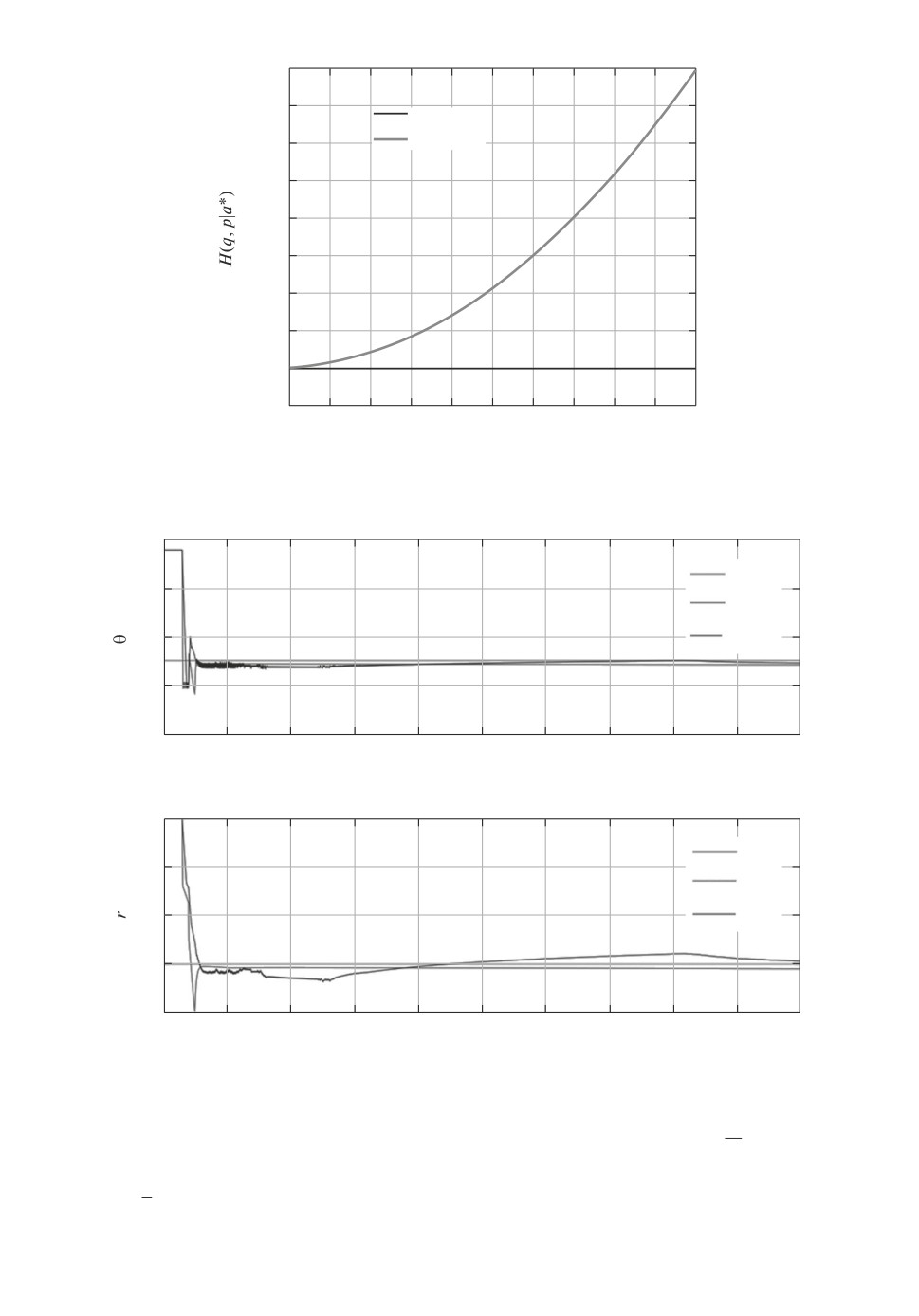
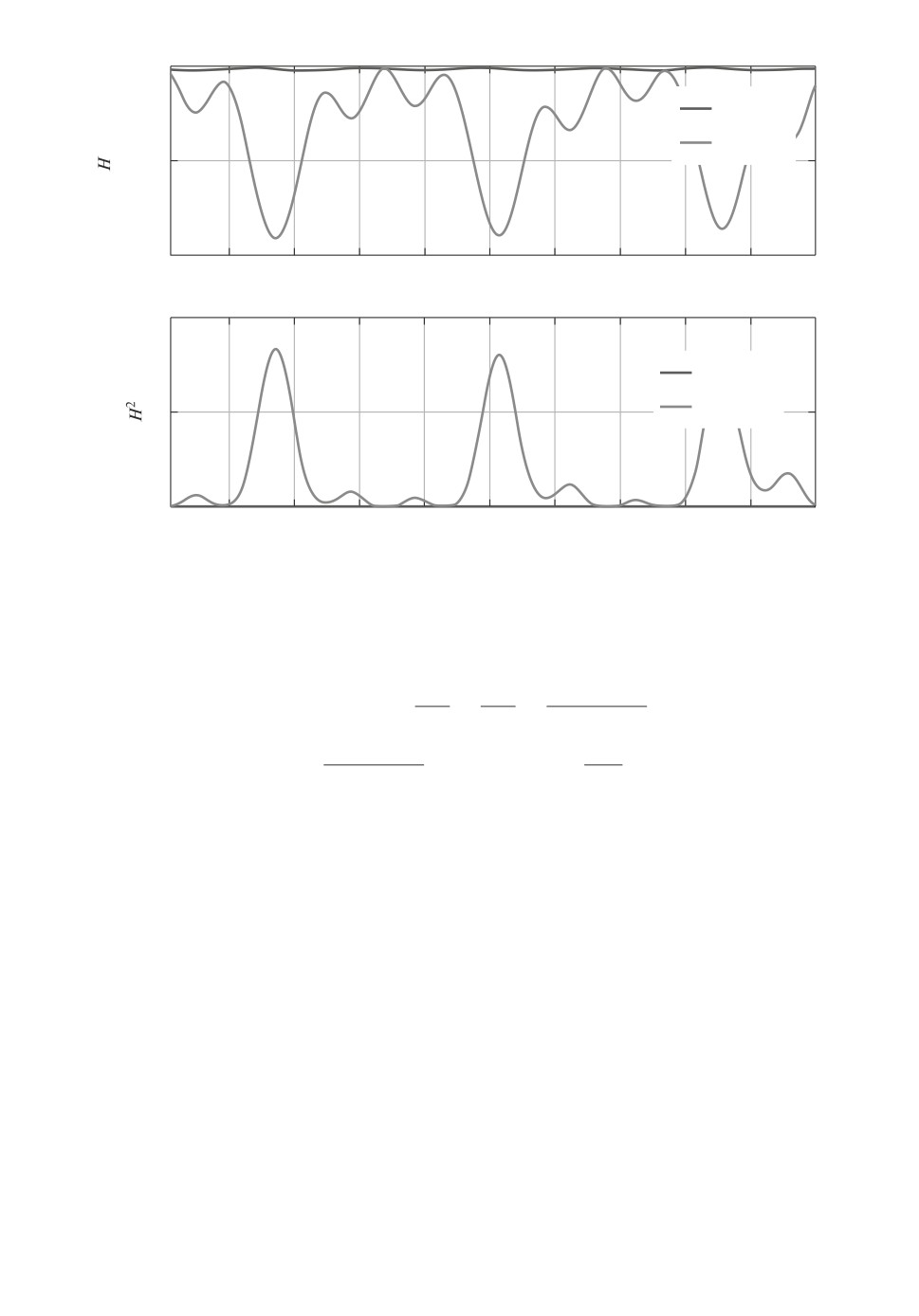
12
видно на рис. 4, H(q(t), p(t)|α∗) = const, а H(q(t), p(t)|α) с “неправильным”
t
α=[π3
5 ] осциллирует по времени. Этот результат подтверждает тот факт,
что стабилизация H(q(t), p(t)|α) имеет смысл и соответствует идентификации
74
Процедура 1
50
0
-50
-100
-150
0
1
2
3
4
5
6
7
8
9
10
t(s)
Процедура 2
100
0
-100
-200
0
1
2
3
4
5
6
7
8
9
10
t(s)
Рис. 6. Гамильтониан.
точного значения параметра α∗. Используя процедуры (25)-(26), получим
процесс идентификации, представленный на рис. 5.
В данных экспериментах γ(t) была задана в виде
γ/η,
если t ∈ [0, t0) ,
(38)
γ(t) =
γ
,
если t ≥ t0.
η(t - t0 + 1)
Для процедуры (25) были использованы γ = 1, γ = 15 и η = 1000, а для про-
цедуры (26) были взяты значения γ = 20 и η = 1. Динамика изменения га-
мильтониана (23) показана на рис. 6.
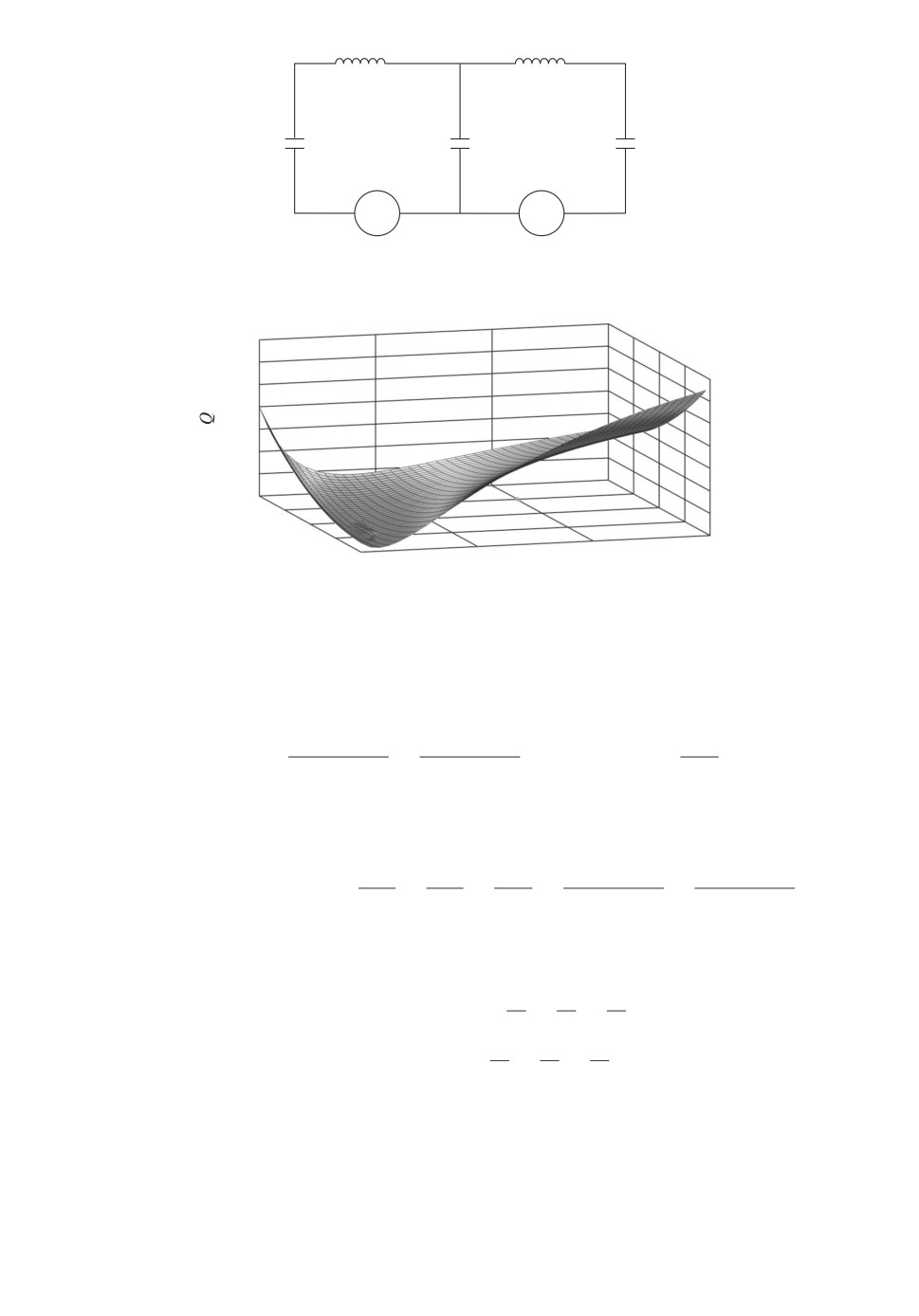
Пример 2 (электрическая цепь). Рассмотрим электрическую цепь, пока-
занную на рис. 7. Кинетическая энергия задана в виде
q21L1
q22L2
T (q,
˙q,t) =
+
,
2
2
75
L1
L2
C1
C0
C2
~
~
E1(t)
E2(t)
Рис. 7. Электрическая цепь.
7000
6000
5000
4000
3000
2000
1000
0
6
5
4
L1
3
2,0
1,5
20,5
1,0
c0
Рис. 8. Функция Q(c0, L1).
а потенциальная энергия - выражением
(c0 + c1)q21
(c0 + c2)q22
q1q2
V (q, t) =
+
-e1q1 - e2q2 -
2c0c1
2c0c2
c0
Тогда, получим следующую функцию Лагранжа L = T - V :
q21L1
q22L2
q1q2
(c0 + c1)q21
(c0 + c2)q22
L(q,
q,t) = e1q1 + e2q2
+
+
-
-
2
2
c0
2c0c1
2c0c2
Соответствующие уравнения Эйлера-Лагранжа имеют вид
q1
q1
q2
f1(c0,L1,t) := q1L1 - e1 +
+
-
= 0,
c0
c1
c0
q2
q2
q1
f2(c0,t) := q2L2 - e2 +
+
-
= 0.
c0
c2
c0
Для проведения численного моделирования были выбраны следующие зна-
чения: L2 = 7, c1 = 0,5 и c2 = 2,2. Для использования МНК снова зададим
функцию затрат вида (36), которая будет минимизирована с помощью под-
ходящего выбора двух параметров c0, L1. График функции Q(c0, L1) показан
на рис. 8, видно, что функция имеет несколько экстремумов.
76
0
H(q, p|c
*
H(q, p|c)
-5000
-10 000
5
10
15
20
25
30
35
40
45
50
t(s)
´107
10
H 2(q, p|c
*
H 2(q, p|c)
5
0
5
10
15
20
25
30
35
40
45
50
t(s)
Рис. 9. H(q, p|α∗) и H(q, p|α).
Соответствующий гамильтониан представлен в виде
p1
p2
(c0 + c1)q21
H(q(t), p(t), t) =
+
+
+
2L1
2L2
2c0c1
(39)
(c0 + c2)q22
q1q2
+
-e1q1 - e2q2 -
2c0c2
c0
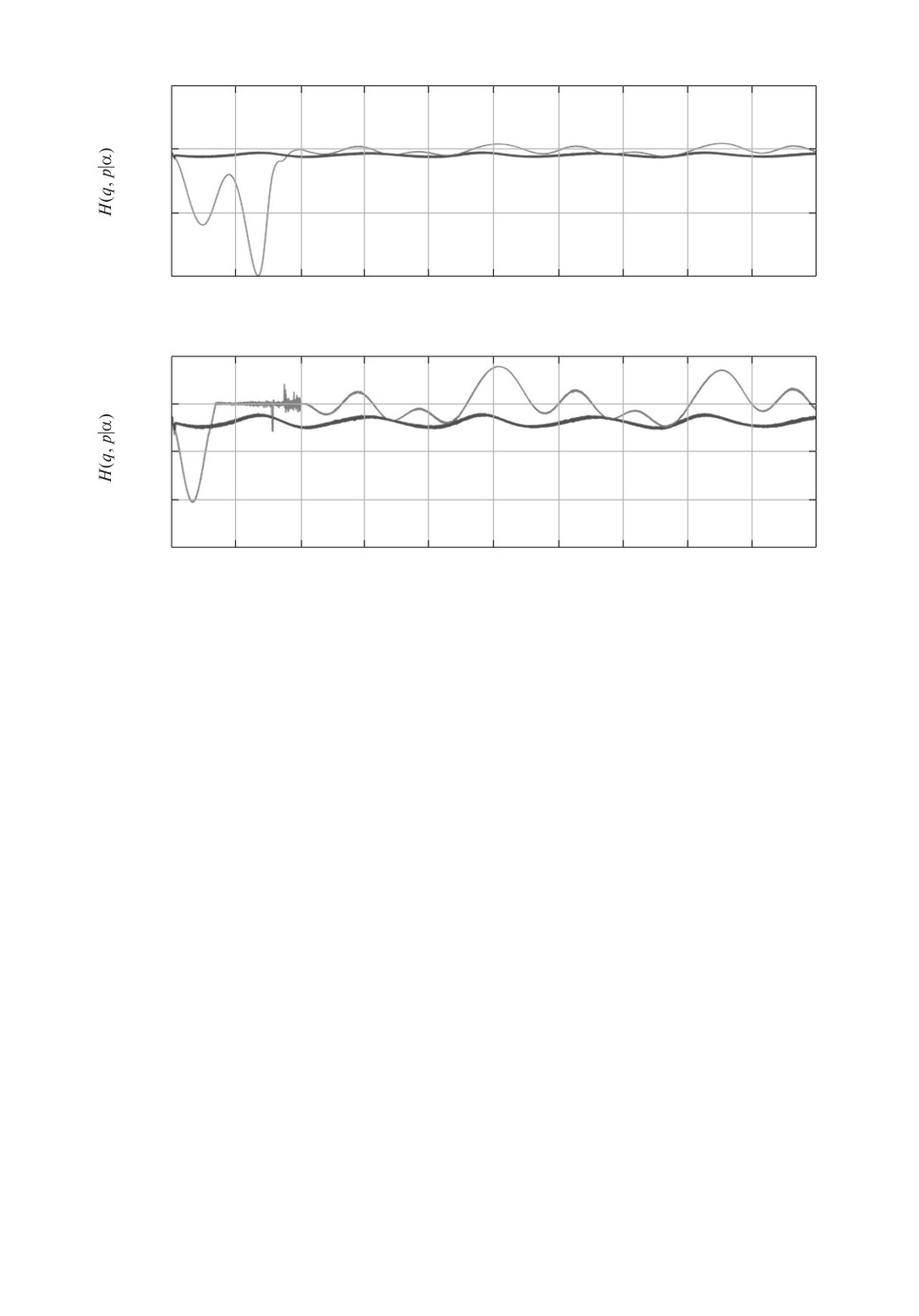
Фактич[ски он с]овп[дает с ]ервым интегралом при реальных значениях α =
=α∗ =
c0
L1
=
1,5
5
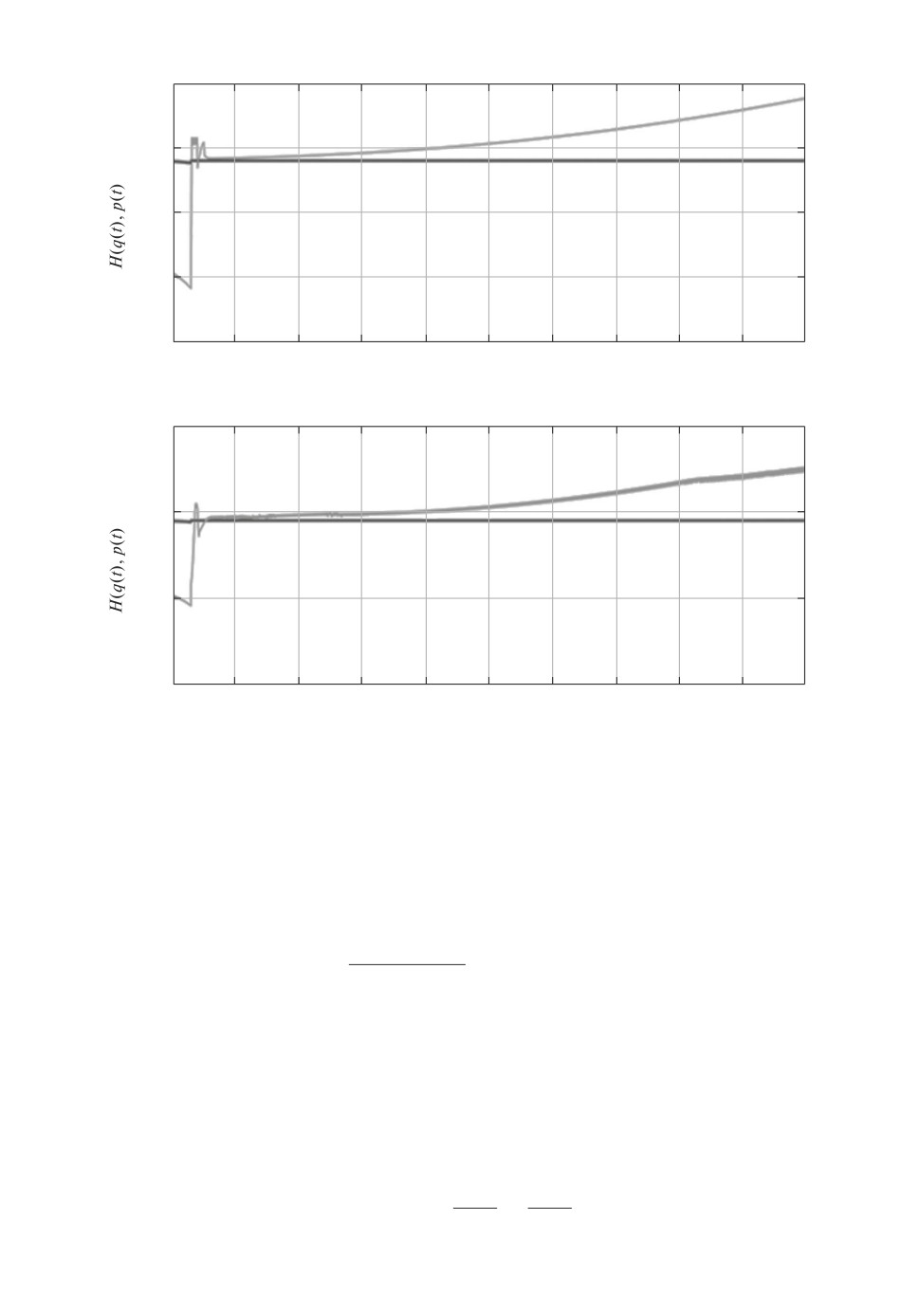
. Как видно, на рис. 9 H(q(t), p(t)|α∗) = const,
t
а H(q(t),p(t)|α) при α = [ 3
2 ] осциллирует со временем, что подтвержда-
ет предположение о необходимости идентификации неизвестного вектора α∗
путем решения задачи стабилизации H(q(t), p(t)|α).
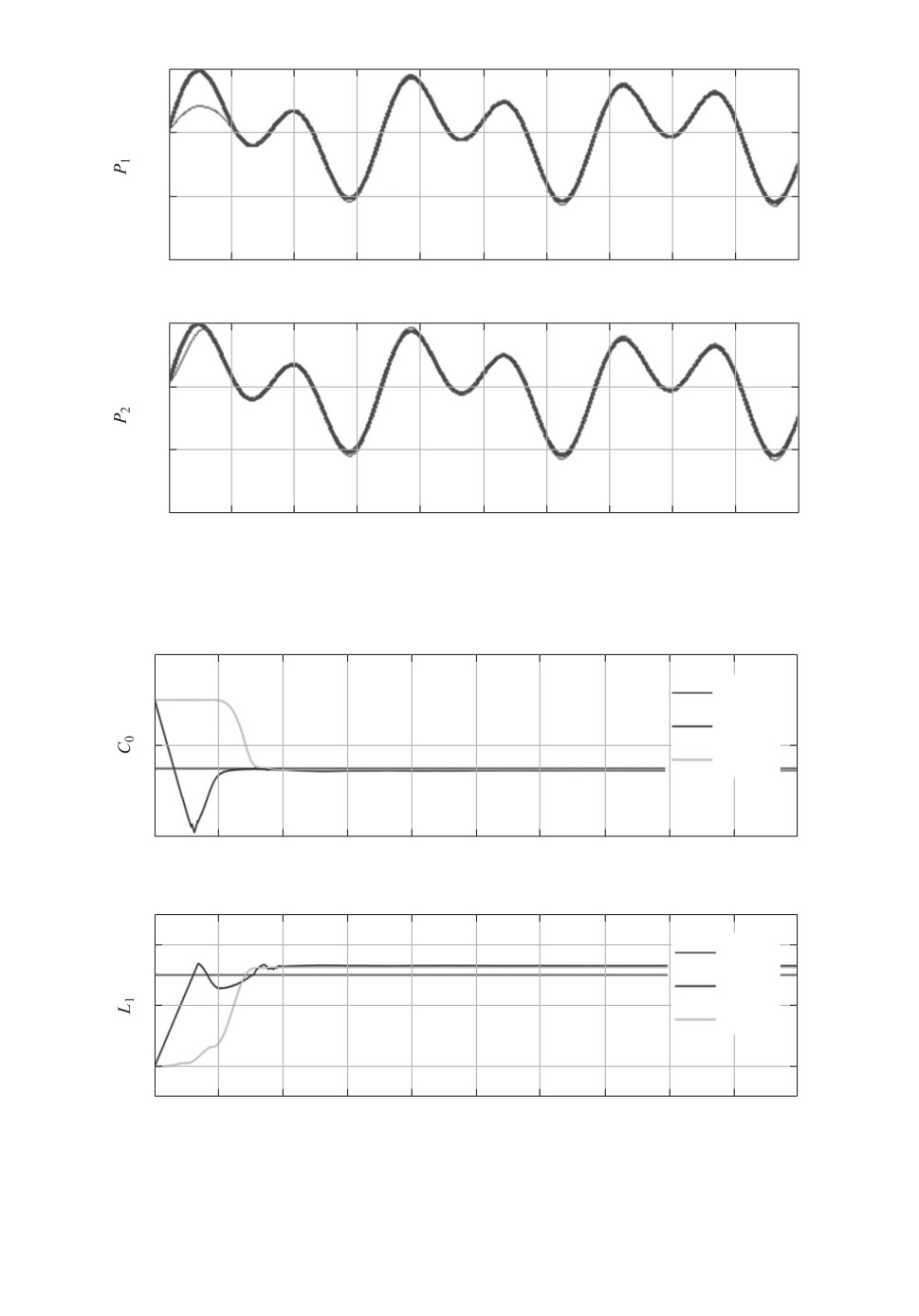
В этом случае имеем дело со случаем 2, когда обобщенный импульс за-
висит от неизвестного параметра. т.е. p = p(t, α∗). Таким образом, используя
p-адаптивную оценку (31), можно увидеть, что p(t, α(t)) быстро сходится к
p(t, α∗) (см. рис. 10).
Применяя процедуры (25), (26), получим процесс идентификации, пока-
занный на рис. 11.
Для данного примера были использованы γ = 0,00000148 для процеду-
ры (25), а для процедуры (26) γ = 2 и тот же вид γ(t) (38). Динамика
гамильтониана (39) представлена на рис. 12.
Как видно из примеров, численное моделирование динамических систем,
которые нелинейно содержат неизвестные параметры в описании, показывает
77
200
0
-200
-400
0
5
10
15
20
25
30
35
40
45
50
t(s)
200
0
-200
-400
0
5
10
15
20
25
30
35
40
45
50
t(s)
Рис. 10. p(t, α(t)).
Идентификация C0
4
C0*
C0 M1
2
2
C0 M
0
5
10
15
20
25
30
35
40
45
50
t(s)
Идентификация L1
6
L1*
L1 M1
4
L1 M2
2
0
5
10
15
20
25
30
35
40
45
50
t(s)
Рис. 11. α-сходимость.
78
Динамика гамильтониана H(q, p|a): процедура 1
2000
0
-2000
-4000
0
5
10
15
20
25
30
35
40
45
50
t(s)
Динамика гамильтониана H(q, p|a): процедура 2
500
0
-500
-1000
-1500
0
5
10
15
20
25
30
35
40
45
50
t(s)
Рис. 12. Гамильтониан.
хорошую работоспособность предложенного подхода в то время, как МНК
практически не работает, застревая в точках локальных экстремумов.
Замечание 3. Предложенный подход может быть эффективно приме-
нен к большому классу физических моделей, где рассматривается движение
релятивистских частиц в электромагнитных полях, так как в этих системах
отсутствуют непотенциальные силы, а следовательно, их можно отнести к
классу консервативных систем, допускающих применение формализма Га-
мильтона.
7. Выводы
• В настоящей работе предложен подход для параметрической идентифика-
ции, основанный на первых интегралах гамильтоновой системы.
• Этот подход требует онлайн-измерений соответствующих обобщенных ко-
ординат и применения наблюдателя типа “супер-твист” для оценки их про-
изводных и обобщенных импульсов.
• Численное моделирование процедур “стабилизации” (25) и (26) иллюстри-
рует работоспособность предложенного подхода.
СПИСОК ЛИТЕРАТУРЫ
1. Astrom, K.J. and Eykhoff, P., System Identification-A Survey, Automatica, 1971,
vol. 7, no. 2, pp. 123-162.
79
2.
Seinfeld, J.H., Nonlinear Estimation Theory Industrial & Engineering Chemistry.
1970. V. 62. No. 1. P. 32-42.
3.
Billings S.A. Identification of nonlinear systems-a survey // IEE Proc. D (Control
Theory and Applications). 1980. V. 127(6). P. 272-285.
4.
Bard J. Nonlinear parameter estimation. Academic Press. New York and London.
1974.
5.
Leal D.J., Georgantzis G., Roberts P.D. Parameter estimation in uncertain models
of nonlinear dynamic systems // Electron. Lett. 1977. V. 14. No. 22. P. 718-720.
6.
Lawrence P.J., Rogers G.J. Recursive identification for system models of transfer
function type // IFAC Proc. Darmstadt. 1979. V. 12. No. 8. P. 283-288.
7.
Kenneth R.M., Glen R.H., Dan O. Introduction to Hamiltonian Dynamical Systems
and N-Body Problem. Second Edition. Springer Nature Switzerland AG, 2017.
8.
Primera J.R., Sanchez M., Romero M., Sierraalta A., Ruette F. Analysis of paramet-
ric functionals in semiempirical approaches using simulation techniques // Journal
of Molecular Structure: THEOCHEM. 1999. V. 469. P. 177-190.
9.
Levant A. Robust exact differentiation via sliding mode technique // Automatica.
1998. V. 34. No. 3. P. 379-384.
10.
Гантмахер Ф.Р. Лекции по аналитической механике. М.: Наука, 1966.
11.
Shtessel Yu., Edwards C., Fridman L., Levant A. Sliding Mode Control and Obser-
vation. Birkhauser. New York. 2014.
12.
Noel J., Kerschen C. Nonlinear system identification in structural dynamics: 10 more
years of progress // Mechanical Systems and Signal Processing. 2017. V. 83. P. 2-35.
13.
Kerschen G., Worden K., Vakakis A., Golinval J.-C. Past, present and future of
nonlinear system identification in structural dynamics // Mechanical Systems and
Signal Processing. 2006. V. 20. No. 3. P. 505-592.
14.
Norton J. An Introduction to Identification // Academy Press London. 1986.
15.
Поляк Б.Т. Введение в оптимизацию. М.: Наука. 1983.
16.
Poznyak A. Advanced Mathematical Tools for Automatic Control Engineers: Deter-
ministic Systems. Elsevier. Amsterdam-NY. 2008. V. 1.
17.
Reyhanoglu M., van der Schaft A., McClamroch N.H., Kolmanovsky I. Dynamics
and control of a class of underactuated mechanical systems // IEEE Transactions
on Automatic Control. 1999. V. 44. No. 9. P. 1663-1671.
Статья представлена к публикации членом редколлегии А.В. Назиным.
Поступила в редакцию 30.01.2020
После доработки 20.05.20209
Принята к публикации 25.05.2020
80