Автоматика и телемеханика, № 9, 2020

(agassi.melikov@gmail.com)

(Институт систем управления НАН Азербайджана, Баку),

С.Г. АЛИЕВА, канд. техн. наук (s@aliyeva.info)

(Бакинский государственный университет),

М.О. ШАХМАЛЫЕВ (mamed.shahmaliyev@gmail.com)

(Институт систем управления НАН Азербайджана, Баку)

МЕТОДЫ РАСЧЕТА СИСТЕМЫ C МГНОВЕННОЙ

ОБРАТНОЙ СВЯЗЬЮ И ПЕРЕМЕННОЙ ИНТЕНСИВНОСТЬЮ

ВХОДЯЩЕГО ПОТОКА

Изучена марковская модель системы обслуживания с одним сервером

и мгновенной обратной связью. После завершения обслуживания часть

вызовов согласно схеме Бернулли либо покидают систему, либо мгновен-

но возвращается для получения повторного обслуживания, при этом для

повторного обслуживания потребуется положительное (случайное) время

переключения сервера. Интенсивность входящего потока зависит от со-

стояния сервера, который может быть в рабочем режиме или в режиме

переключения. Найдено условие эргодичности соответствующей двумер-

ной цепи Маркова и предложены три метода для ее исследования: метод

производящих функций, метод спектрального расширения и метод фазо-

вого укрупнения состояний. Приводятся результаты численных экспери-

ментов.

Ключевые слова: система обслуживания, мгновенная обратная связь, ме-

тод расчета.

DOI: 10.31857/S0005231020090056

1. Введение

В последние годы системы массового обслуживания (СМО) с обратной

связью все больше привлекают внимание исследователей. Это объясняет-

ся тем, что учет эффекта обратной связи позволяет повысить адекватность

изучаемых моделей к реальной ситуации, где получившие один раз обслужи-

вание заявки могут потребовать повторного обслуживания по целому ряду

различных причин. Так, например, в коммуникационных сетях ошибочно пе-

реданные данные передаются повторно. Другим примером служат производ-

ственные системы, где бракованные детали требуют повторной обработки.

Третьим примером могут быть современные сервисные интеграторы, в кото-

рых получивший один раз качественное обслуживание клиент может еще раз

обратиться для обслуживания именно к ним.

В классе СМО с обратной связью различают системы с мгновенной и от-

сроченной (задерживающей) обратной связью. История исследования этих

систем берет свое начало от пионерских работ Такача [1, 2]. После опубли-

кования указанных работ подобные системы некоторое время не привлекали

105

внимания исследователей СМО, исследования в этом направлении получили

интенсивное продолжение лишь в последние два десятилетия. Здесь наряду

с прочими следует отметить работы [3-13]. Подробный обзор работ можно

найти в [12, 13], и поэтому здесь не будем останавливаться на изложении из-

вестных фактов.

В указанных выше работах, как правило, предполагается, что сервер мо-

жет мгновенно начинать обслуживание заявки, которая требует повторного

обслуживания. Вместе с тем это предположение зачастую плохо соотносится

с действительностью. На практике зачастую для начала процесса обслужива-

ния заявок указанного типа потребуется некоторое время “разогрева” сервера,

т.е. время переключения сервера для обслуживания этих заявок является по-

ложительной случайной величиной (с.в.). Подобные ситуации, как правило,

наблюдаются в производственных системах, где для обработки бракованной

детали потребуется некоторое время переналадки сервера.

Здесь изучается модель СМО с одним сервером и мгновенной обратной

связью, в которой время переключения сервера для повторного обслужива-

ния является положительной с.в. Изучаются модели с неограниченной об-

щей очередью для первичных заявок и заявок, которые требуют повторного

обслуживания. Предлагаются и сравниваются три метода расчета характе-

ристик модели: метод производящих функций, метод спектрального расши-

рения [14, 15] и метод фазового укрупнения состояний многомерных цепей

Маркова (ЦМ) [12, 13].

Отметим, что при соответствующем изменении термина “переключение

сервера” получаются модели систем: а) с прогулками сервера, где незави-

симо от длины очереди вызовов прогулки могут быть осуществлены после

каждого акта обслуживания; б) с ненадежным сервером, где поломки сер-

вера возможны лишь в моменты завершения обслуживания вызовов. Полу-

ченные в данной работе результаты могут быть использованы и для анализа

указанных систем.

2. Описание модели системы и постановка задачи

Рассматривается система обслуживания с одним сервером и неограничен-

ным числом мест для ожидания. На вход системы извне поступает пуас-

соновский поток первичных вызовов. Времена обслуживания этих вызовов

являются независимыми и одинаково распределенными (н.о.р.) с.в. и имеют

общую показательную функцию распределения со средним µ^-1. После завер-

шения процесса обслуживания вызовы независимо друг от друга и согласно

схеме Бернулли либо с вероятностью σ мгновенно требуют повторного об-

служивания, либо с дополнительной вероятностью 1 - σ покидают систему.

Времена обслуживания повторных вызовов также являются н.о.р. с.в. с тем

же средним µ^-1.

Для начала процесса обслуживания вызовов, которые требуют повторного

обслуживания, требуется некоторое положительное случайное время (время

переключения сервера), которое имеет показательную функцию распределе-

ния со средним θ^-1. Иными словами, в любой момент времени сервер может

находиться в одном из двух состояний: в рабочем режиме или в режиме пе-

106

реключения. Считается, что не допускается прерывать время переключения

сервера. При этом вызов, который требует повторного обслуживания, из-за

запрета на прерывание переключения сервера остается на нем.

Первичные вызовы имеют информацию о статусе сервера, т.е. если сервер

находится в режиме переключения, то интенсивность p-вызовов равна λ₀,

иначе она равна λ₁.

Считается, что случайные процессы поступления вызовов, их обслужива-

ния и времена переключения сервера являются не зависимыми друг от друга.

Требуется найти совместное распределение числа вызовов в системе и со-

стояние сервера (задача А), а также среднее число вызовов в системе и про-

изводительность системы, т.е. интенсивность потока обслуженных вызовов,

выходящих из системы (задача В).

3. Метод производящих функций

Состояние системы в произвольный момент времени определяется двумер-

ным вектором (n, k), где n число вызовов в системе, k состояние сервера,

т.е.

{

0, если сервер находится в режиме переключения,

1, если сервер находится в рабочем режиме.

Работа системы описывается двумерной ЦМ со следующим пространством

состояний:

⋃

(3.1)

E=E₀

E_n,

n=1

где E₀ = {(0, 1)}, E_n = {(n, 0) , (n, 1)}, n = 1, 2, . . .

l₁

0, 1

1, 1

2, 1

3, 1

m(1 - s)

l₀

1, 0

2, 0

3, 0

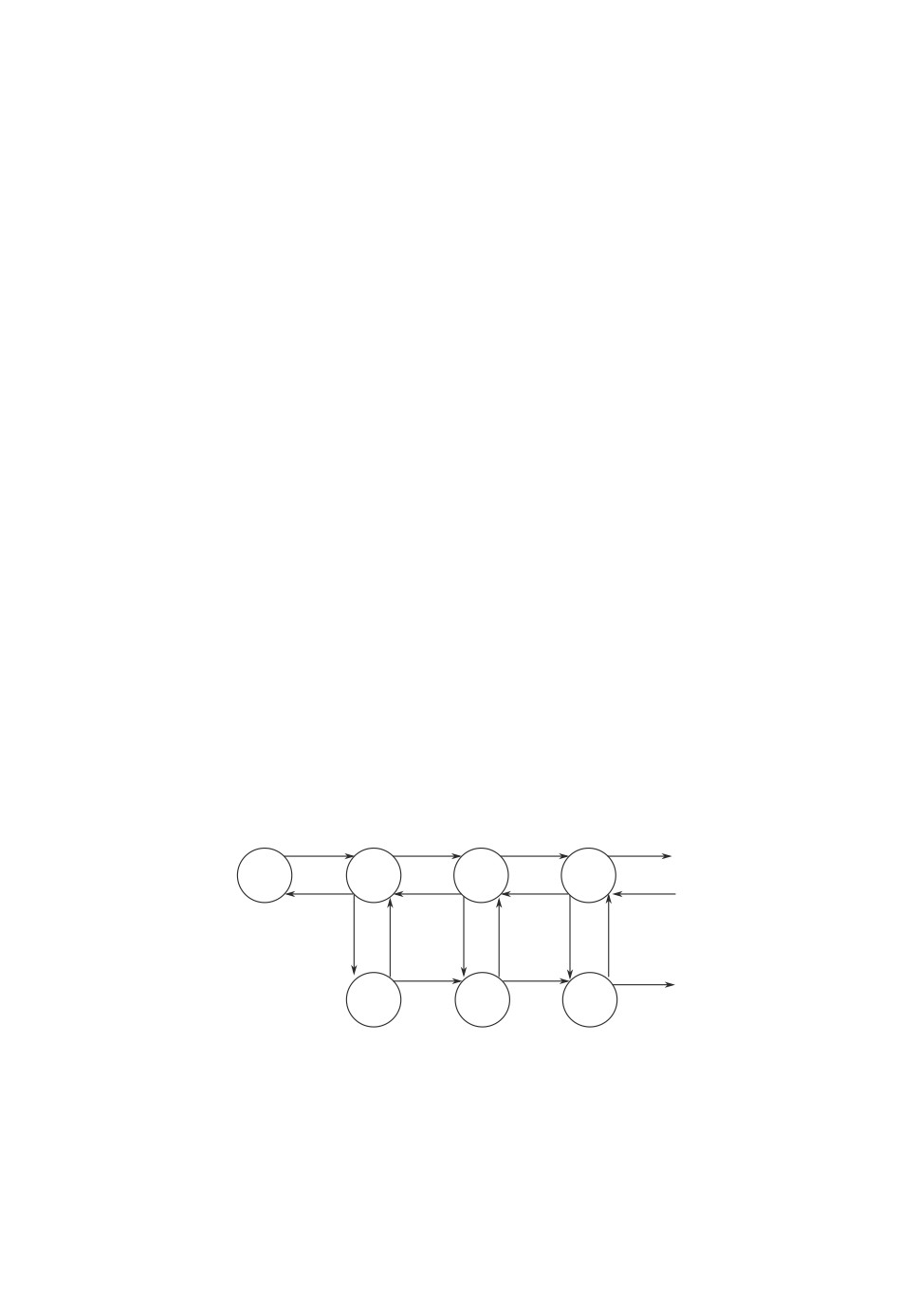
Рис. 1. Граф переходов.

Интенсивность перехода из состояния (n, k) в состояние (n^′, k^′) обозначим

через q((n, k), (n^′, k^′)). Эти величины определяются как (см. рис. 1):

(3.2)

q ((n, 1) , (n + 1, 1)) = λ₁;

(3.3)

q ((n, 1) , (n - 1, 1)) = µ (1 - σ) , n > 0;

107

(3.4)

((n, 1) , (n, 0)) = µσ, n > 0;

(3.5)

q ((n,0) ,(n,1)) = θ;

(3.6)

q ((n, 0) , (n + 1, 0)) = λ₀.

Пусть p(n, k) обозначает стационарную вероятность состояния (n, k) ∈ E

(условие эргодичности устанавливается ниже). Эти величины удовлетворяют

следующей бесконечной системе уравнений равновесия (СУР):

(3.7)

λ₁

p (0, 1) = µ (1 - σ) p (1, 1) ;

Для случаев n ≥ 1:

(3.8)

(λ₁ + µ) p (n, 1) = µ (1 - σ) p (n + 1, 1) + λ₁

p (n - 1, 1) + θp (n, 0) ;

(3.9)

(λ₀

+ θ)p(1,0) = µσp(1,1) ;

Для случаев n ≥ 2:

(3.10)

(λ₀ + θ) p (n, 0) = λ₀

p (n - 1, 0) + µσp (n, 1) .

Введем следующие производящие функции:

∑

P_k (z) =

p (n, k) zⁿ, k = 0, 1,

n=k

{

0, если k = 1,

где k =

1, если k = 0.

Из (3.8) имеем

(

)

-λ₁z² + (λ₁ + µ)z - µ(1 - σ)

P₁ (z) - θzP₀ (z) =

(3.11)

= ((λ₁ + µ) z - µ (1 - σ)) p (0, 1) - µ (1 - σ) zp (1, 1) .

С учетом (3.7) из (3.11) получаем

(

)

-λ₁z² + (λ₁ + µ)z - µ(1 - σ)

P₁ (z) - θzP₀ (z) =

(3.12)

= µ(z - 1 + σ)p(0,1).

Аналогичным образом из уравнений (3.9) и (3.10) имеем

(3.13)

-µσP₁ (z) + (θ + λ₀ (1 - z))P₀

(z) = -µσp (0, 1) .

Из (3.13) получаем

(3.14)

P₁ (z) = p(0,1) + a(z) P₀

(z) ,

где

a (z) =

(-λ₀z + λ₀ + θ) .

µσ

108

С учетом (3.12) из (3.14) получаем

λ₁z² - λ₁z

(3.15)

P₀ (z) =

p (0, 1) ,

a(z) b(z) - θz

где

b (z) = -λ₁z² + (λ₁ + µ) z - µ (1 - σ) .

Из (3.14) и (3.15) имеем

(

)

λ₁z² - λ₁z

(3.16)

P₁ (z) =

1 + a(z)

p (0, 1) .

a (z) b (z) - θz

Для нахождения неизвестной величины p(0, 1) используем следующее

условие: lim

(P₀ (z) + P₁ (z)) = 1. При вычислении пределов получается

z→1

неопределенность вида⁰⁰ , и согласно правилу Лопиталя находим, что

(

)_-1

λ₁ (θ + µσ)

(3.17)

p (0, 1) =

θµ(1 - σ) - λ₁θ - λ₀µσ

Замечание 1. При выводе формулы (3.17) находим следующее необхо-

димое условие эргодичности системы:

(3.18)

λ₁θ + λ₀

µσ < θµ(1 - σ) .

Далее, при выполнении условия эргодичности (3.18) условные средние

значения числа вызовов в системе, когда сервер находится в рабочем ре-

жиме (L₁) и в режиме переключения (L₀), а также безусловное значение

среднего числа вызовов в системе (L) определяются как

(3.19)

L₁ = P^′1 (1) , L₀ = P^′0 (1) , L = L₁P₁ (1) + L₀P₀

(1) .

Производительность системы вычисляется следующим образом:

(3.20)

Λ = µ(1 - σ)(P₁

(1) - p (0, 1)) .

Ввиду очевидности получения и громоздкости явный вид формул (3.19)

и (3.20) здесь не приводится (лишь отметим, что для его получения правило

Лопиталя применяется 2 раза).

Таким образом, метод производящих функций позволяет решить задачу В,

но не позволяет решить задачу А.

4. Метод спектрального расширения

Применение метода спектрального расширения [14, 15] позволяет решить

обе задачи, А и В. Поскольку этот метод подробно описан в указанных рабо-

тах, то здесь описываются лишь его основные этапы.

109

Вводятся следующие матрицы:

A элементы этой матрицы определяют одношаговые вертикальные пе-

реходы между состояниями (см. рис. 1), т.е.

)

(

)

( 0

q ((n, 0) , (n, 1))

;

q ((n,1) ,(n,0))

µσ

B элементы этой матрицы определяют одношаговые горизонтальные

переходы вправо (см. рис. 1), т.е.

(

)

(

)

q ((n, 0) , (n + 1, 0))

λ₀

q ((n, 1) , (n + 1, 1))

λ₁

)

(

)

( 0 0

B₀ =

;

q (n, 1) , (n + 1, 1)

λ₁

C элементы этой матрицы определяют одношаговые горизонтальные

переходы влево (см. рис. 1), т.е.

)

( 0 0

C =

q ((n,1) ,(n - 1,1))

µ (1 - σ)

Считается, что A₀ и C₀ являются нулевыми матрицами. На базе указанных

выше матриц определяются диагональные матрицы D^A, D^B и D^C , в кото-

рых элементы главных диагоналей равны сумме элементов соответствующих

строк матриц A, B и C, т.е.

(

)

(

)

(

)

λ₀

D^A =

D^B =

D^C =

µσ

λ₁

µ(1 - σ)

Балансовые уравнения для вероятностей состояний из однородной части

графа (см. рис. 1) с учетом введенных матриц записывается так:

(

)

(4.1)

v_n

D^A + D^B + D^C

=v_n-1B + v_nA + v_n+1C, n ≥ 1,

где

v_n = (p(n,0) ,p(n,1)), n ≥ 1.

Уравнения (4.1) представляются в виде матрично-разностных уравнений

второго порядка с постоянными коэффициентами:

(4.2)

v_nQ₀ + v_n+1Q₁ + v_n+2Q₂

= 0, n ≥ 1,

где

(

)

Q₀ = B, Q₁ = A -

D^A + D^B + D^C

Q₂ = C.

110

Характеристический матричный полином уравнения (4.2) имеет следую-

щий вид:

(4.3)

Q (η) = Q₀ + Q₁η + Q₂η².

Далее собственные значения η₀, η₁ и соответствующие им левые собствен-

ные векторы ψ = (ψ₀ (k) , ψ₁ (k)), k = 0, 1, матрицы Q (η) определяются из

следующих уравнений:

(4.4)

det (Q (η)) = 0,

(4.5)

ψQ(η) = 0,

где правая часть уравнения (4.5) является нулевой вектор-строкой.

В указанных выше работах разработаны эффективные алгоритмы реше-

ния уравнений (4.4) и (4.5). После нахождения решений уравнений (4.4) и

(4.5) вероятности состояний определяются как

(4.6)

p (n, k) = a₀ψ₀ (k) ηⁿ⁰ + a₁ψ₁ (k) ηⁿ¹

n = 0,1,...; k = 0,1,

где a₀, a₁ являются параметрами, которые определяются с помощью балан-

совых уравнений для вероятностей состояний из неоднородной части графа

(способ их нахождения также подробно описан в [14, 15]).

С помощью данного метода можно найти необходимое и достаточное усло-

вие эргодичности системы. Формулируется оно следующим образом [16]: цепь

Маркова является эргодической тогда и только тогда, когда в однородной ча-

сти графа суммарные интенсивности переходов вправо должны быть меньше,

чем суммарные интенсивности переходов влево, т.е. требуется выполнение

условия

(4.7)

vBe < vCe,

где e = (1, 1)^T, и v = (ν₀, ν₁) представляет собой вектор вероятностей состоя-

ний ЦМ с двумя состояниями и инфинетизимальным генератором A, т.е.

ν₀ =^µσθ+µσ , ν₁ =^θθ+µσ . Тогда из (4.7) получаем условие эргодичности, кото-

рое совпадает с условием (3.18).

Условные средние значения числа вызовов в системе, когда сервер нахо-

дится в рабочем режиме (L₁) и в режиме переключения (L₀), определяются

как

∑

(4.8)

L₁ = np(n,1) ; L₀ =

np (n,0) .

n=1

Безусловное значение среднего числа вызовов в системе (L) определяется

как

∑

(4.9)

L=L₁

p (n, 1) + L₀

p (n, 0) .

n=0

n=1

Производительность системы вычисляется так:

∑

(4.10)

Λ = µ(1 - σ)

p (n, 1) .

n=1

111

5. Метод фазового укрупнения

Хотя метод спектрального расширения позволяет решить обе задачи А

и В, иногда при определенных значениях исходных данных системы появля-

ются проблемы вычислительной неустойчивости. Ниже рассматривается при-

менение метода фазового укрупнения состояний двумерных ЦМ [12, 13] для

решения поставленных задач А и В. Он корректно может быть применен для

систем, в которых время переключения сервера существенно меньше, чем ин-

тервалы между поступлениями вызовов, т.е. предполагается, что имеет место

соотношение θ ≫ max (λ₀, λ₁). При выполнении этого условия интенсивности

переходов внутри классов E_n (см. (3.1) и рис. 1) существенно больше, чем

интенсивности переходов между состояниями из разных классов.

Согласно алгоритму метода фазового укрупнения состояний двумерных

ЦМ, каждый класс E_n, n = 0, 1, 2, . . . представляется в виде одного укруп-

ненного состояния < n >, n = 0, 1, 2, . . . При этом класс E₀ содержит лишь

одно состояние (0, 1), а каждый класс E_n, n > 0 содержит два состояния (n, 1)

и (n, 1).

Вероятности состояний внутри классов E_n, n = 0, 1, 2, . . . обозначаются че-

рез ρ_n (k), k = 0, 1. Поскольку класс E₀ содержит лишь одно состояние (0, 1),

то имеем ρ₀ (1) = 1.

Интенсивности переходов между состояниями класса E_n, n > 0 определя-

ются из (3.4) и (3.5), т.е. вероятности состояний внутри каждого класса E_n,

n > 0 не зависят от индекса n и вычисляются как

µσ

(5.1)

ρ_n (0) =

ρ_n (1) =

θ + µσ

Замечание 2. Поскольку вероятности состояний внутри классов E_n,

n = 0,1,2,... , ρn (k), k = 0,1, не зависят от индекса n (см. (5.1)), то далее

у этих величин индекс опускается.

С учетом (5.1) находим, что интенсивности переходов между укрупненны-

ми состояниями < n >, n = 0, 1, 2, . . . определяются следующим образом:

(5.2)

q (< 0 >,< 1 >) = λ₁.

Для случаев n > 0

(5.3)

q (< n >,< n + 1 >) = λ

;

q (< n >, < n - 1 >) = µ.

Здесьλ =

(λ₁θ + λ₀µσ), µ =^θθ+µσ µ (1 - σ) .

θ+µσ

Из соотношений (5.2) и (5.3) заключаем, что укрупненная модель опи-

сывается бесконечным процессом размножения

гибели с переменными

параметрами. Условием эргодичности этого процесса являетсяλ < µ или

λ₁θ + λ₀µσ < θµ(1 - σ).

Замечание 3. Полученное здесь условие эргодичности полностью сов-

падает с условием (3.18), найденным выше с помощью метода производящих

функций. Там трудно было дать интерпретацию этого условия. Здесь, одна-

ко, можно дать его вероятностную интерпретацию. Когда сервер находится в

112

рабочем режиме, интенсивность поступления вызовов равна λ₁ρ (1), а когда

сервер находится в режиме переключения, эта величина равна λ₀ρ (0). Иными

словами,λ представляет собой суммарную интенсивность поступления вызо-

вов при различных режимах работы сервера. Вызовы обслуживаются лишь

тогда, когда сервер находится в рабочем режиме, т.е. интенсивность обслужи-

вания равна µ (1 - σ) ρ (1). Следовательно, условие эргодичности (3.18) имеет

простую вероятностную интерпретацию: суммарная интенсивность поступле-

ния вызовов при различных режимах работы сервера должна быть меньше,

чем интенсивность обслуживания.

Из соотношений (5.2) и (5.3) вычисляются вероятности укрупненных со-

стояний π (< n >), n ≥ 0:

)_n

(˜

λ₁

(5.4)

π (< n >) =

π (< 0 >) , n ≥ 1,

где

(

)_-1

λ₁

π (< 0 >) =

α=

λ1-α

С учетом (5.1)-(5.4) находим приближенные значения вероятностей со-

стояний исходной ЦМ:

(5.5)

p (0, 1) = π (< 0 >) ;

(5.6)

p(n, 0) = ρ (0) π (< n >) ;

(5.7)

p(n, 1) = ρ (1) π (< n >) .

Приближенные значения (ПЗ) характеристики (4.8)-(4.10) определяются

как

∑

θ λ₁

(5.8)

L₁ ≈ np(n,1) = ρ(1)

nπ (< n >) =

π (< 0 >) ;

θ + µσ λ (1 - α)2

n=1

∑

µσ λ₁

(5.9)

L₀ ≈ np(n,0) = ρ(0)

nπ (< n >) =

π (< 0 >) ;

θ + µσ λ (1 - α)2

n=1

µσ

(5.10)

L≈

L₁ +

L₀.

θ + µσ

∑

(5.11)

Λ ≈ µ(1 - σ) ρ_n

(1) π (< n >) = µ (1 - σ) ρ (1) (1 - π (< 0 >)) .

n=1

6. Численные результаты

Далее приводятся результаты расчета вероятностей состояний и харак-

теристик изучаемой системы с помощью предложенных методов. Очевидно,

что с методологической точки зрения, а также по времени выполнения ме-

тод спектрального расширения и метод фазового укрупнения существенно

113

выигрывают перед методом производящих функций. Метод фазового укруп-

нения позволяет приближенно решить поставленные задачи А и В, при этом

он существенно выигрывает у метода спектрального расширения в части реа-

лизации, так как этим методом удается решить указанные задачи с помощью

простых формул.

Основная цель проведения вычислительных экспериментов сводится к

оценке точности результатов, полученных с помощью метода фазового укруп-

нения, а также к определению области его применения в зависимости от ис-

ходных параметров конкретной системы. При этом точные значения (ТЗ)

вероятностей состояний и характеристик системы вычисляются с помощью

метода спектрального расширения.

Точность вычисления вероятностей состояний оценивается с помощью

двух норм подобия: подобия косинуса (∥N∥₁) и максимума разностей меж-

ду точными и приближенными значениями этих величин (∥N∥₂), т.е.

∑

p (n, k) p(n, k)

(n,k)∈E

(6.1)

∥N∥₁ =

(

)1^;

∑

(p(n,k))²

(n,k)∈E

(6.2)

∥N∥₂ = max

|p (n, k) - p(n, k)| .

(n,k)∈E

Отметим, что подобие косинуса, как правило, применяется для оценки

близости ориентации векторов, а не для оценки их длины. Однако здесь это

применение правомерно, так как согласно условию

∑

p(n,k) =

p(n, k) = 1

(n,k)∈E

конечные точки этих векторов находятся в одной гиперплоскости.

Некоторые результаты численных экспериментов, в которых имеет место

соотношение θ ≫ max (λ₀, λ₁), показаны в табл. 1 (поскольку рассматрива-

ется проблема определения точности вычисления вероятностей состояний и

характеристик системы, а не характер их поведения относительно исходных

данных, то результаты численных экспериментов представлены в виде таб-

лицы. Кроме того, в проводимых экспериментах зачастую точные и прибли-

женные значения характеристик отличаются друг от друга в четвертом знаке

после запятой. Именно с такой точностью и проводились вычисления). Здесь

и далее принято, что σ = 0,2. Из таблицы видно, что точные и приближенные

значения вероятностей состояний почти совпадают, так как норма подобия

косинуса почти всегда равна единице и максимум разностей между точными

и приближенными значениями является достаточно малой величиной. Более

того, в этих экспериментах характеристики L₀ и L₁ также вычисляются с

очень высокой точностью. Так, относительная погрешность (ОП) вычисле-

ния характеристики L₀ в наихудшем случае не превышает 0,1 % (т.е. почти

совпадает с точными значениями) и ОП при вычислении характеристики L₁

не превышает 4 %.

114

Таблица 1. Результаты численных экспериментов для системы, в которой удовле-

творяется условие θ ≫ max(λ₀, λ₁)

L₁

L₀

(µ, θ)

(λ₀, λ₁)

∥N∥₁

∥N∥₂

ТЗ

ПЗ ОП ТЗ

ПЗ ОП

(50,

75)

(3, 5)

0,0006

0,1436

0,0004

0,0198

0,0191

0,0338

(4, 10)

0,0012

0,3329

0,3327

0,0007

0,0461

0,0444

0,0385

(5, 15)

0,99

0,0018

0,5972

0,5966

0,0011

0,0829

0,0795

0,0400

(55,

75)

(3, 5)

0,0006

0,1289

0,1288

0,0004

0,0196

0,0189

0,0342

(4, 10)

0,0013

0,2936

0,2934

0,0007

0,0448

0,0430

0,0396

(5, 15)

0,99

0,0019

0,5141

0,5135

0,0011

0,0786

0,0753

0,0421

(60,

75)

(3, 5)

0,0006

0,1169

0,1168

0,0004

0,0194

0,0187

0,0346

(4, 10)

0,0013

0,2626

0,2624

0,0007

0,0438

0,0420

0,0405

(5, 15)

0,99

0,0020

0,4513

0,4508

0,0011

0,0754

0,0721

0,0438

(50,

80)

(3, 5)

0,0005

0,1436

0,1435

0,0004

0,0185

0,0179

0,0318

(4, 10)

0,0011

0,3330

0,3327

0,0006

0,0432

0,0416

0,0361

(5, 15)

0,0016

0,5973

0,5967

0,0010

0,0775

0,0746

0,0376

(55,

80)

(3, 5)

0,0005

0,1288

0,0004

0,0183

0,0177

0,0322

(4, 10)

0,0011

0,2936

0,2935

0,0006

0,0419

0,0403

0,0372

(5, 15)

0,0017

0,5142

0,5137

0,0010

0,0736

0,0706

0,0396

(60,

80)

(3, 5)

0,0005

0,1168

0,0004

0,0181

0,0175

0,0325

(4, 10)

0,0011

0,2626

0,2625

0,0006

0,0409

0,0394

0,0381

(5, 15)

0,0018

0,4515

0,4510

0,0010

0,0706

0,0677

0,0412

(50,

85)

(3, 5)

0,0004

0,1435

0,0003

0,0174

0,0169

0,0300

(4, 10)

0,0010

0,3330

0,3328

0,0006

0,0405

0,0391

0,0341

(5, 15)

0,0015

0,5974

0,5969

0,0009

0,0728

0,0702

0,0355

(55,

85)

(3, 5)

0,0004

0,1288

0,1287

0,0003

0,0172

0,0167

0,0303

(4, 10)

0,0010

0,2936

0,2935

0,0006

0,0394

0,0380

0,0351

(5, 15)

0,0015

0,5144

0,5139

0,0009

0,0691

0,0665

0,0373

(60,

85)

(3, 5)

0,0004

0,1168

0,1167

0,0003

0,0170

0,0165

0,0306

(4, 10)

0,0010

0,2626

0,2625

0,0006

0,0384

0,0371

0,0359

(5, 15)

0,0016

0,4516

0,4512

0,0009

0,0663

0,0637

0,0389

Интересными являются результаты численных экспериментов, в которых

не выполняется соотношение θ ≫ max (λ₀, λ₁). Соответствующие результаты

показаны в табл. 2, откуда видно, что в этих экспериментах точные и при-

ближенные значения вероятностей состояний также вычисляются с высокой

точностью. Здесь однако при вычислении характеристик L₀ и L₁ имеются

большие погрешности. Так, при вычислении характеристики L₀ относитель-

ная погрешность в наихудшем случае составляет почти 28 %, а эта же ве-

личина при вычислении характеристики L₁ достигает 45 %. Эти результа-

ты доказывают, что принятое условие θ ≫ max (λ₀, λ₁) является важным для

корректного применения метода фазового укрупнения состояний.

В связи с приведенными выше результатами численных экспериментов ин-

терес представляет изучение зависимостей значений указанных выше норм

подобия (6.1) и (6.2) относительно изменения параметра θ. Некоторые резуль-

115

Таблица 2. Результаты численных экспериментов для системы, в которой не удо-

влетворяется условие θ ≫ max (λ₀, λ₁)

L₁

L₀

(µ, θ)

(λ₀, λ₁)

∥N∥₁

∥N∥₂

ТЗ

ПЗ ОП ТЗ

ПЗ ОП

(50, 4)

(3, 5)

0,99

0,0818

0,1843

0,1616

0,1233

0,6692

0,4040

0,3962

(4, 10)

0,97

0,1136

0,4545

0,3636

0,2000

1,5909

0,9091

0,4286

(5, 15)

0,94

0,1002

1,0269

0,7385

0,2809

3,2885

1,8462

0,4386

(55, 4)

(3, 5)

0,99

0,0832

0,1649

0,1445

0,1233

0,6617

0,3975

0,3993

(4, 10)

0,96

0,1188

0,3953

0,3162

0,2000

1,5415

0,8696

0,4359

(5, 15)

0,94

0,1111

0,8417

0,6053

0,2809

3,0359

1,6646

0,4517

(60, 4)

(3, 5)

0,99

0,0843

0,1491

0,1307

0,1233

0,6556

0,3922

0,4019

(4, 10)

0,96

0,1231

0,3497

0,2797

0,2000

1,5035

0,8392

0,4419

(5, 15)

0,94

0,1202

0,7131

0,5128

0,2809

2,8606

1,5385

0,4622

(50, 7)

(3, 5)

0,99

0,0384

0,1589

0,1519

0,0439

0,2984

0,2171

0,2727

(4, 10)

0,99

0,0649

0,3668

0,3391

0,0755

0,6920

0,4844

0,3000

(5, 15)

0,98

0,0734

0,6979

0,6189

0,1131

1,2789

0,8842

0,3086

(55, 7)

(3, 5)

0,99

0,0390

0,1424

0,1361

0,0439

0,2951

0,2139

0,2753

(4, 10)

0,99

0,0674

0,3214

0,2971

0,0755

0,6731

0,4669

0,3063

(5, 15)

0,98

0,0790

0,5894

0,5228

0,1131

1,2082

0,8215

0,3201

(60, 7)

(3, 5)

0,99

0,0394

0,1289

0,1233

0,0439

0,2925

0,2113

0,2774

(4, 10)

0,99

0,0694

0,2860

0,2644

0,0755

0,6584

0,4533

0,3115

(5, 15)

0,98

0,0837

0,5102

0,4524

0,1131

1,1565

0,7756

0,3293

(50, 10)

(3, 5)

0,99

0,0220

0,1522

0,1488

0,0220

0,1879

0,1488

0,2079

(4, 10)

0,99

0,0404

0,3478

0,3344

0,0385

0,4348

0,3344

0,2308

(5, 15)

0,99

0,0500

0,6375

0,6000

0,0588

0,7875

0,6000

0,2381

(55, 10)

(3, 5)

0,99

0,0223

0,1364

0,1334

0,0220

0,1857

0,1467

0,2101

(4, 10)

0,99

0,0418

0,3055

0,2938

0,0385

0,4230

0,3231

0,2361

(5, 15)

0,99

0,0534

0,5426

0,5106

0,0588

0,7468

0,5617

0,2479

(60, 10)

(3, 5)

0,99

0,0226

0,1236

0,1209

0,0220

0,1840

0,1450

0,2118

(4, 10)

0,99

0,0430

0,2724

0,2619

0,0385

0,4138

0,3143

0,2405

(5, 15)

0,99

0,0562

0,4722

0,4444

0,0588

0,7167

0,5333

0,2558

таты этих исследований показаны на рис. 2, где исходные данные выбраны

так: µ = 50, λ₀ = 5, λ₁ = 10. Из этих графиков видно, что с ростом значе-

ний параметра θ норма подобия (6.1) систематически растет и приближается

к единице, а норма подобия (6.2) систематически убывает и приближается

к нулю. Эти результаты были вполне ожидаемыми, так как с ростом зна-

чений параметра θ увеличиваются интенсивности переходов между состоя-

ниями внутри классов E_n, n ≥ 0 и тем самым уменьшаются интенсивности

переходов между состояниями из разных классов (см. рис. 1).

Предложенные простые формулы позволяют изучить поведение характе-

ристик системы (3.19) и (3.20) относительно любых параметров. Для кон-

кретности изложения на рис. 3 показано поведение указанных характеристик

относительно параметра θ. Эти результаты также были ожидаемыми, т.е. с

ростом параметра θ увеличивается доля времени пребывания сервера в рабо-

116

Рис. 2. Зависимость норм подобия (6.1) (а) и (6.2) (б) от параметра θ.

0,4

s = 0,2

0,3

s = 0,3

0,2

0,1

20 q

9,2

9,0

8,8

s = 0,2

s = 0,3

8,5

20 q

Рис. 3. Зависимость характеристик (3.19) (а) и (3.20) (б) от параметра θ.

чем режиме, тем самым уменьшается среднее число вызовов в системе (см.

рис. 3,а) и увеличивается производительность системы (см. рис. 3,б ). При

этом с ростом вероятности мгновенного повторения обслуживания (т.е. σ)

увеличивается среднее число вызовов в системе (см. рис. 3,а) и одновремен-

но уменьшается производительность системы (см. рис. 3,б ). Действительно, с

ростом указанной вероятности увеличивается доля времени пребывания сер-

вера в режиме переключения (при котором не производится обслуживание

117

вызовов), тем самым увеличивается среднее число вызовов в системе и, сле-

довательно, уменьшается ее производительность.

7. Заключение

В работе изучается модель системы обслуживания с одним сервером,

неограниченным числом мест для ожидания и мгновенной обратной связью.

После завершения обслуживания часть вызовов согласно схеме Бернулли

либо покидает систему, либо мгновенно требует повторного обслуживания.

Для начала процесса повторного обслуживания вызовов серверу потребует-

ся некоторое случайное время переключения, которое имеет показательную

функцию распределения. Считается, что когда сервер находится в статусе пе-

реключения, он не может осуществлять обслуживание вызовов. При этом не

допускается прерывание периода переключения. Интенсивность поступления

вызовов зависит от статуса сервера.

Показано, что математической моделью изучаемой системы является дву-

мерная ЦМ с бесконечномерным пространством состояний. Найдено условие

эргодичности модели и предложены три метода исследования соответствую-

щей двумерной ЦМ: метод производящих функций, метод спектрального рас-

ширения и метод фазового укрупнения состояний двухмерных ЦМ. Первые

два из них являются точными методами, а третий приближенный. С по-

мощью численных экспериментов показана высокая точность разработанных

приближенных формул для решения поставленной задачи.

СПИСОК ЛИТЕРАТУРЫ

1. Takacs L. A single-server queue with feedback // Bell Syst. Tech. J. 1963. V. 42.

P. 505-519.

2. Takacs L. A queuing model with feedback // Oper. Res. 1977. V. 11. P. 345-354.

3. Назаров А.А., Моисеева С.П., Морозова А.С. Исследования СМО с повторным

обслуживанием и неограниченным числом обслуживающих приборов методом

предельной декомпозиции // Выч. технол. 2008. Т. 13. Вып. 5. С. 88-92.

4. Dudin A.N., Kazimirsky A.V., Klimenok V.I., et.al. The queuing model MAP/PH/

1/N with feedback operating in a Markovian random environment // Austrian J.

Stat. 2005. V. 34. Iss. 2. P. 101-110.

5. Krishnamoorthy A., Manjunath A.S. On queues with priority determined by feed-

back // Calcutta Stat. Assos. Bul. 2018. V. 70. Iss. 1. P. 33-56.

6. Boxma O.J., Yechiali U. An M/G/1 queue with multiple types of feedback and gated

vacations // J. Appl. Probab. 1997. V. 34. Iss. 3. P. 773-784.

7. Choi B.D., Kim B. M/G/1 queueing system with fixed feedback policy // The

ANZIAM J. 2002. V. 44. Iss. 2. P. 283-297.

8. Choi B.D., Kim B., Choi S.H. An M/G/1 queue with multiple types of feedback,

gated vacations and FCFS policy // Comput. & Oper. Res. 2003. V. 30. Iss. 9.

P. 1289-1309.

9. Krishna Kumar B., Madheswari S.P., Vijayakumar A. The M/G/1 retrial queue

with feedback and starting failures // Appl. Math. Model. 2002. V. 26. Iss. 11.

P. 1057-1075.

118

10. Krishna Kumar B., Rukmani R., Thangaraj V. On multiserver feedback retrial queue

with finite buffer // Appl. Math. Model. 2009. V. 33. Iss. 4. P. 2062-2083.

11. Krishna Kumar B., Vijayalakshmi G., Krishnamoorthy A., et.al. A single server

feedback retrial queue with collisions // Comput. & Oper. Res. 2010. V. 37. Iss. 7.

P. 1247-1255.

12. Koroliuk V.S., Melikov A.Z., Ponomarenko L.A., et.al. Methods for analysis of multi-

channel queuing models with instantaneous and delayed feedbacks // Cyber. Syst.

Anal. 2016. V. 52. Iss. 1. P. 58-70.

13. Melikov A.Z., Aliyeva S.H., Sztrik J. Analysis of queuing system MMPP/M/ K/K

with delayed feedback // Mathematics. 2019. V. 7. 1128. 14 p.

doi:10.3390/math7111128

14. Mitrani I., Chakka R. Spectral expansion solution for a class of Markov models:

application and comparison with the matrix-geometric method // Perform. Eval.

1995. V. 23. P. 241-260.

15. Chakka R. Spectral expansion solution for some finite capacity queues // Oper. Res.

1998. V. 79. P. 27-44.

16. Neuts M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Ap-

proach. Baltimore: John Hopkins Univer. Press, 1981. 332 р.

Статья представлена к публикации членом редколлегии В.М. Вишневским.

Поступила в редакцию 09.12.2019

После доработки 02.03.2020

Принята к публикации 25.05.2020

119