Автоматика и телемеханика, № 9, 2020
© 2020 г. М.И. ГЕРАСЬКИН, д-р экон. наук (innovation@ssau.ru)
(Самарский национальный исследовательский университет
имени академика С.П. Королева)
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ РАВНОВЕСИЙ
В НЕЛИНЕЙНОЙ МОДЕЛИ ОЛИГОПОЛИИ ШТАКЕЛЬБЕРГА
НА ОСНОВЕ ЛИНЕАРИЗАЦИИ
Рассматривается теоретико-игровая проблема выбора оптимальных
стратегий агентов рынка олигополии при линейной функции спроса и
нелинейных функциях издержек агентов. Доказаны необходимые условия
существования решения системы нелинейных уравнений, включающих в
себя степенные функции. На основе разложения степенных функций в
ряды Тейлора проведена линеаризация системы уравнений оптимальных
реакций агентов. В результате линеаризованная система зависит от век-
тора параметров линеаризации, а расчет игровых равновесий сводится к
подбору неподвижных точек нелинейных отображений. Исследованы от-
клонения значений приближенного равновесия от точного решения. Вы-
ведены аналитические формулы расчета равновесий в игре олигополистов
для произвольного уровня лидерства по Штакельбергу. Анализ дуопо-
лии и триполии показал, что равновесие в игре является следствием двух
факторов: во-первых, вогнутость функции издержек агента, т.е положи-
тельный эффект расширения масштаба, ведет росту его выигрыша по
сравнению с агентами, имеющими выпуклые функции издержек, т.е от-
рицательный эффект расширения масштаба; во-вторых, выигрыш агента
повышается, если он является лидером, однако преимущество окружения
по типу функции издержек снижает воздействие второго фактора.
Ключевые слова: олигополия, игра Штакельберга, степенная функция из-
держек, многоуровневое лидерство, линеаризация.
DOI: 10.31857/S0005231020090068
1. Введение
Линейная модель выбора оптимальных действий агентов рынка олигопо-
лии, в которой обратная функция спроса и функции издержек агентов яв-
ляются линейными, широко использовалась [1-5] для анализа равновесий
в игре олигополистов, поскольку эта модель допускает простое аналитиче-
ское решение в виде равновесия Курно-Нэша [6, 7]. Нелинейная модель вы-
бора оптимальных действий, в которой обратная функция спроса линейная,
а функции издержек агентов являются нелинейными, использовалась реже
[8-11], так как не позволяет найти аналитическое решение. В этом случае
особенные вычислительные трудности возникают при анализе игры агентов
с лидером (лидерами) по Штакельбергу [12] первого и последующих уров-
ней [13, 14], поскольку для нахождения предположительных вариаций [15]
необходимо решать системы нелинейных уравнений на каждом уровне и для
каждого агента. Формы таких систем уравнений получены [16] для лидеров
по Штакельбергу первого и второго уровня, однако равновесия были рас-
считаны численными методами. Формулы предположительных вариаций в
120
явном виде [17] позволяют анализировать характер их изменения при вариа-
циях действий агентов, что необходимо для вычисления равновесий при на-
личии лидеров по Штакельбергу второго и более высоких уровней, а ограни-
чение [17] на модуль суммы предположительных вариаций позволяет оценить
диапазоны возможных равновесий.
В данной статье ставится задача поиска аналитического решения равнове-
сий Курно-Нэша в нелинейной модели олигополии для произвольного уровня
лидерства.
2. Методология
Рассмотрим следующую нелинейную модель рынка олигополии. Пусть
агенты выбирают действия исходя из максимума своих функций полезности
(прибыли)
(1)
Πi (Q,Qi) = P (Q)Qi - Ci (Qi) , Qi
≥ 0, i ∈ N = {1, . . . , n}
при линейной функции цены спроса на товар от суммарного объема предло-
жения всех агентов рынка
∑
(2)
P (Q) = a - bQ, a > 0, b > 0, Q = Qi,
i∈N
и нелинейных (степенных) функциях издержек агентов
(3)
∈ (0, 2) , i ∈ N,
Ci (Qi) = CFi + BiQβii, CFi > 0, Bi > 0, βi
где Qi, Πi
действие (объем выпуска) и функция полезности (прибыль)
i-го агента; N
множество агентов рынка; n количество агентов, т.е.
количество элементов множества N; P , Q равновесная цена и суммар-
ный объем рынка; CFi, Bi, βi коэффициенты функций издержек агентов,
CFi интерпретируется как постоянные издержки; a, b коэффициенты об-
ратной функции спроса. Степенная функция издержек (3) в диапазоне ко-
эффициентов βi ∈ (0, 2) обобщает два типа агентов: агент с положительным
эффектом расширения масштаба описывается вогнутой функцией издержек
при 0 < βi < 1, агент с отрицательным эффектом выпуклой функцией при
1 < βi < 2.
Модели выбора оптимальных (символ ¾∗¿) действий агентов с учетом
условий (1)-(3) запишем в виде
{
}
(4)
Q∗i = arg maxΠi(Q,Qi) = arg max
(a - bQ)Qi - CFi - BiQβi
,
i∈N.
i
Qi≥0
Qi≥0
Равновесие Нэша в системе (4) представляет собой вектор оптимальных
действий агентов при выбранных действиях окружения и определяется пу-
тем решения системы уравнений реакций следующего типа (при некотором
известном векторе предположительных вариаций):
∂Πi (Qi,xij)
(5)
= 0, i, j ∈ N,
∂Qi
121
где xij = Q′
предположительная вариация в уравнении реакции i-го аген-
jQi
та, т.е. предполагаемое изменение выпуска j-го агента в ответ на единичный
прирост выпуска i-го агента. Поскольку согласно модели (4) оптимумы аген-
тов зависят не только от собственного действия i-го агента Qi, но и от дей-
ствий окружения через Q, то последняя зависимость представлена в систе-
ме (5) как функция полезности Πi (Qi, xij ) от вектора предположительных
вариаций, характеризующих влияние действий окружения на изменение Q.
Стратегическая игра Γ есть кортеж множества агентов, множества страте-
гий агентов, множества функций полезности (прибыли) агентов и множества
уровней лидерства
(6)
Γ = 〈N,{Qi,i ∈ N},{Πi
,i ∈ N},G〉,
где G = (M0, M1, . . . , ML) множество уровней лидерства агентов; L ко-
личество уровней лидерства агентов; Mr (r = 0, . . . , L) множества агентов;
M0
множество ведомых агентов; Mr (r = 1, . . . , L) множество лидеров
r-го уровня.
В дальнейшем подмножество агентов окружения i-го агента, имеющих
один и тот же уровень лидерства, обозначено символом M = {l ∈ N\i}, число
элементов этого множества обозначено символом m = n - 1.
Уровни лидерства определяются следующим образом. Нулевой уровень,
соответствующий ведомому η0-му агенту, имеет место, если в η0-м уравнении
системы (5) полагается x0η0j=0∀j∈N\η0,гдеверхнийиндекспредположи-
тельной вариации обозначает уровень лидерства r. Первый уровень лидер-
ства η1-го агента возникает, если в η1-м уравнении системы (5) вариации x1η1j
вычисляются дифференцированием по Qη1 остальных (N - 1) уравнений (5),
в которых полагается x0ij = 0 ∀j ∈ N\i. Произвольный r-й уровень лидерства
ηr-го агента возникает, если в ηr-м уравнении системы (5) вариации xrηrjвы-
числяются дифференцированием по Qηr остальных (N - 1) уравнений (5), в
которых полагается xij = xr-1ij ∀j ∈ N\i.
Решения игры (6) на r-м уровне лидерства i-го агента для модели выбора
действий (4) были получены [16] в виде системы (5) уравнений равновесия
Нэша:
∑
(7)
Fri = a - bQ - bQi 1 +
xr
ij
-BiβiQβi-1i = 0, Qi
> 0, i ∈ N,
j∈N\i
при условии
(8)
ui - Sri
< 0, i ∈ N,
с учетом следующих обозначений:
βi-2
∑
Biβi (βi - 1) Q
i
(8a)
ui = -2 -
,
Sri =
xril
,
i∈N,
b
l∈N\i
122
где ui (•), i ∈ N,
непрерывные и дифференцируемые по Qi функции, ха-
рактеризующие влияние нелинейности функций издержек агентов на унимо-
дальность функции полезности i-го агента (при ui = -2 система (3) является
линейной); Sri величина суммы предположительных вариаций i-го агента
относительно действий окружения на r-м уровне лидерства; Fri (•), i ∈ N,
непрерывные и дифференцируемые по Qi функции.
По сравнению с линейной моделью, для которой условие (8) имеет вид
-2 - Sri < 0, i ∈ N, в нелинейной модели (4) функция полезности агента мо-
жет быть неунимодальной не только вследствие влияния действий окруже-
ния, т.е. ситуаций, когда Sri < -2, но и в результате положительного эффекта
расширения масштаба функции издержек агента. Поэтому введем предполо-
жение о том, что темп снижения предельных издержек при возрастающей
отдаче от масштаба (т.е. βi < 1) не может быть больше темпа снижения цены
при увеличении объема предложения
(8b)
MC′
=Biβi |βi - 1| Qβi-2i < b ∀βi
< 1,
iQi
где MCi = C′iQi = BiβiQβi-1i предельные издержки i-го агента. Предполо-
жение (8b) гарантирует выполнение условия (8), если не выполнено условие
|Sri| < 1, так как |ui| > 1 при условии (8b).
В дальнейшем символом ¾∗¿ обозначены оптимальные действий агентов
как решения системы уравнений (7).
Поставим задачу нахождения приближенного решения системы (7) в яв-
ном виде при некотором известном векторе предположительных вариаций,
соответствующем заданному множеству уровней лидерства G.
3. Результаты
Система нелинейных уравнений (7) не имеет аналитического решения, по-
этому проведем линеаризацию уравнений (7), которая позволяет свести ре-
шение к подбору неподвижных точек нелинейных отображений относительно
параметров линеаризации. Линеаризация основана на следующем утвержде-
нии, доказательство которого приведено в Приложении.
Утверждение 1. Система (7) имеет решение Q∗ = {Q∗i,i ∈ N}, если
выполняются условие (8) и следующие условия:
Qi ≤ Q∗i ≤ Qmax,
|xji| = |ui - Sri| ,
{
(9a)
> 0 при |xr
| < |ui - Sri |,
ji
Fri (κj)
∀i, j ∈ N,
< 0 при |xrji| > |ui - Sri|,
где
∑
(
)
a
BjβjQm
ax
κj =
-
Qk - Qmax - Qmax
1+Srj
-
,
b
b
k∈N\(i,j)
(
)
a-MCmin
Qmax =
,
MCmin = min
BiβiQβi-1
,
i
b
i∈N
123
∑
Fi (κj) = a - bQmax +
Qk + κj - bκj (1 + Sri) - Biβiκβi-1j,
k∈N\(i,j)
1
2-βj
Qj = Bj(j |βj -)|
при βj < 1,
Qj = 0
при βj > 1.
b
2+Sr
j
Если система (7) имеет решение, то уравнения
∑
Fri = â -bq -bqi 1 +
xr
- Biβiνβi-1i -
ij
(9b)
j∈N\i
- Biβi (βi - 1) νβi-2i(qi - νi) = 0, i ∈ N
∑
относительно неизвестных qi =Qi
∈ (0, 1) при q =
qi с коэффициента-
Q
max
i∈N
ми
(9c)
â = Qmaxa,
b = Q2maxb,
,
i∈N
Bi = QβimaxBi
имеют решенияQ∗i, отклонения которых ΔQ∗i = Q∗i -Q∗i от точного реше-
ния Q∗i при условиях |qi - νi| < ri, νi < qi, i ∈ N не превышают по модулю
значения
2
(qi -νi)
|uimax + 2| |βi - 2| Ωβi-3i
(9d)
|ΔQ∗|≤ξi, ξi=Qmax
,
i∈N,
i
2
i-2
2-(uimax +2) νβ
+Smax
i
причем
(9e)
lim
|ΔQ∗i
| = 0, i ∈ N,
r→0
где
Ωi = νi + θi (qi - νi), θi,νi ∈ (0,1), ri ∈ (0,Ωi), uimax = ui (Qmax),
(
)2 (
)-1
m
1-ε
ε
ε
Smax =
,
υmax =
2-
1-
,
m-1-υmax
m
2
2
ε≪1
малое положительное число, m ≥ 2 количество агентов окруже-
ния i-го агента.
Условия (9а) в случае дуополии (n = 2) допускают следующую геометри-
ческую интерпретацию: построим численно по уравнению (7) второго агента
линию реакции Q∗2 (Q1), а линию реакции первого агента Q2 (Q∗1) постро-
им, выразив Q2 из уравнения (7) первого агента. Тогда первое условие (9а)
устанавливает интервалы монотонного убывания этих реакций, второе усло-
вие (9а) обеспечивает различие их угловых коэффициентов, т.е. наличие точ-
ки пересечения реакций, а третье условие (9а) требует, чтобы точка пересе-
чения принадлежала интервалам монотонности.
124
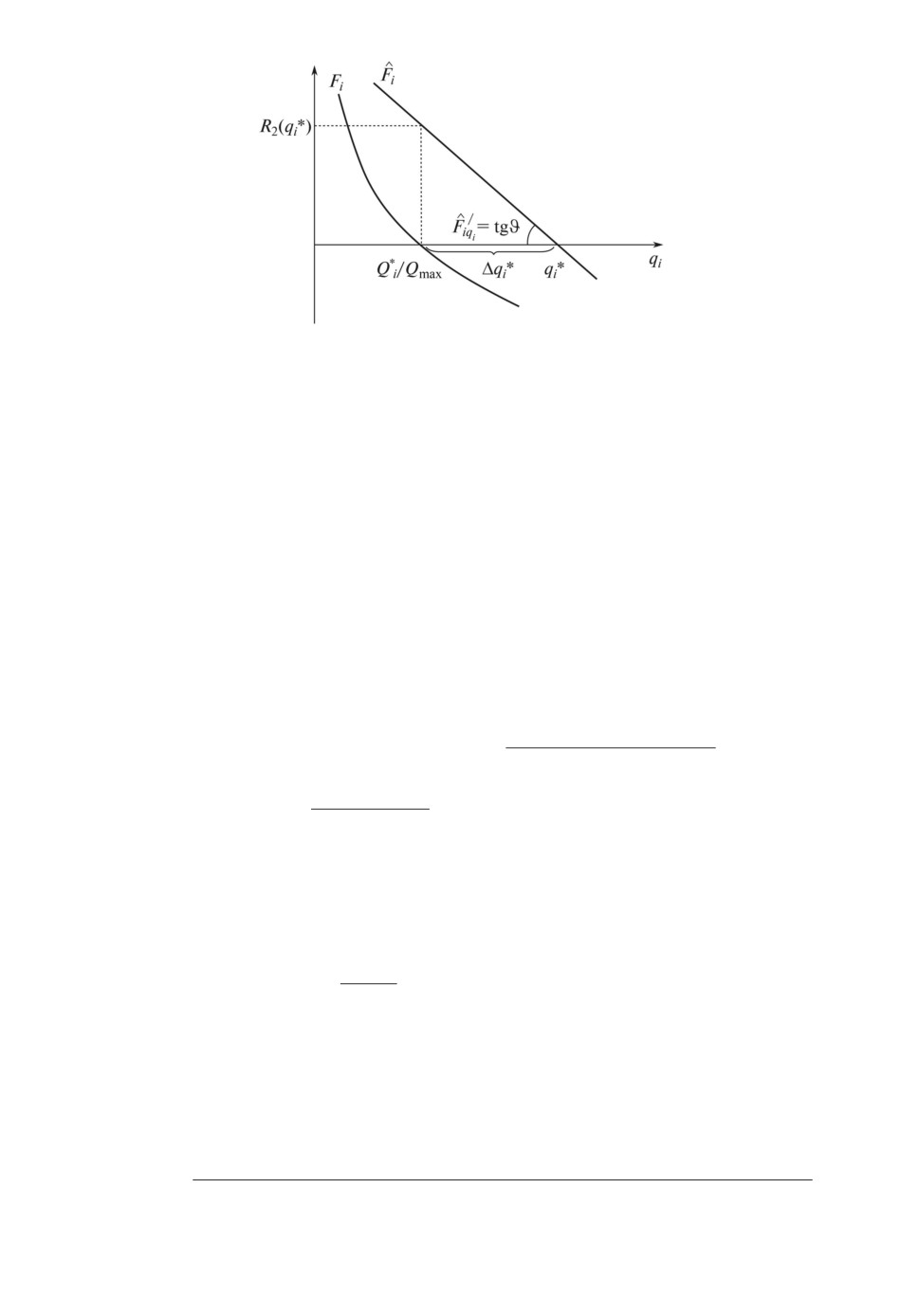
Рис. 1. Графический анализ погрешности линеаризации.
Условия (9d), (9e) показывают, что корректный подбор параметров νi
с учетом |qi - νi| < ri и νi < qi при заданном малом положительном числе
ri ∈ (0,Ωi) позволяет достичь необходимой точности решения системы (7).
Существование параметров νi, удовлетворяющих этим условиям, доказано
ниже, в утверждении 2.
Графический анализ отклонения (9d) решения q∗i системы (9b) от точного
решения Q∗i системы (7) показан на рис. 1.
На основе результатов утверждения 1 систему уравнений (7) после линеа-
ризации можно привести к более компактному виду, для которого легко полу-
чить общее решение, что сформулировано в виде следующего утверждения.
Утверждение 2. Уравнения (9b) сводятся к виду
βi-1
â - Biβi (2 - βi)νi
δiqi + q-i = αi, i ∈ N, αi =
,
b
(10a)
∑
Biβi (βi - 1)
δri = 2 +
νβi-2i + Sri, Sri =
xrik,
b
k∈N\i
∑
где q-i =
qk
сумма действий окружения i-го агента; если выполня-
k∈N\i
ются условия
∑
1
(10b)
= -1 ∧ δrj
= 1 ∀j ∈ N,
δrj
-1
j=1
то система (10а) имеет единственное решение и корни вычисляются по
следующим формулам:
[
]
[
]
(
∏
∑
∏
(
)
∑
∏
(
)
αi
δrj -1
+
δrγ -1
-
αj
δrγ -1
j=1\i
j=1\i γ=1\j,i
j=1\i
γ=1\i,j
(10c) q∗i =
(
∏
∑
∏ (
)
δrj
-1
+
δrγ - 1
j=1
j=1 γ=1\j
125
Для решения (10с) существует набор параметров ν∗i, при котором выпол-
няются следующие условия утверждения 1 :
|qi - ν∗i| < ri, Ωi = ν∗i + θi (qi - ν∗i) , θi, ν∗i ∈ (0, 1) ,
(10d)
ri ∈ (0,Ωi), ν∗i < qi, i ∈ N,
если для всех i ∈ N
)
a
(10e)
n<
+uimax, θi ∈
(ri -ν∗i,1
при ri > ν∗i.
bQmax
ri
В частных практически важных случаях формула (10с) имеет следующий
вид:
αiδrj - αj
q∗i =
,
i = j = 1,2
при n = 2,
δr1δr2 - 1
(
)
(10f)
∏
∑
∏
∑
αi
δrj - 1
-
αjδrγ +
αj
j=1\i
j=1\i γ=1\i
j=1\i
q∗i =
при n = 3.
δr1δr2δr3 - δr1 - δr2 - δr3 + 2
Таким образом, решение системы уравнений (7) сведено к задаче поис-
ка неподвижной точки отображения qi (νi) = νi, заданного формулами (10c),
причем существование этой неподвижной точки доказано при условиях (10е).
Подбор параметров линеаризации ν∗i, удовлетворяющих условиям (10d), осу-
ществляется эвристически, путем последовательного вычисления равновесий
по формулам (10c) и проверки условий (10d).
Сравнение формул (8а) и (10а) показывает, что в случае выполнения усло-
вия (9e) имеет место равенство1 δri = - (ui - Sri). Поэтому выполнение усло-
вий (8), (9а) существования решения системы (7) не гарантирует выполнение
условия (10b) и наоборот. Следовательно, применение формул (10c) должно
сопровождаться проверкой условий (8), (9а).
Решение (10f) для случая дуополии допускает сравнение с известным рав-
новесием Курно [18] при линейных функциях издержек. В этом случае βi = 1,
а параметр Bi имеет смысл предельных издержек агентов, поэтому из фор-
мул (10а) с учетом формул (9с) следует, что
â-Bi
a-Bi
αi =
=
,
δi = 2,
b
bQmax
следовательно, из формулы (10f) при n = 2 получим
2(a - Bi) - (a - Bj)
q∗i =
,
i, j = 1, 2,
3bQmax
а в случае равенства параметров типа агентов, т.е. Bi = Bj = B, отсюда сле-
дует формула равновесного выпуска агентов Курно q∗i =a-B3bQ
⇒Q∗i =a-B3b,
max
идентичная формуле [18].
1 Поскольку подстановка из (9с)
b = Q2maxb, Bi = QmiaxBi в формулу δi (10а) в случае
(
βi
)βi-2
maxBiβi(βi-1)
Qi
qi = νi и qi =QiQ
приводит к формуле δri = 2+Q
+Sri = -ui+Si.
max
Q2maxb
Qmax
126
4. Численные эксперименты
На точность линеаризации нелинейных уравнений реакции (7) в виде (9b)
влияет характер функций Fri и их близость к функция
Fri в достаточно ши-
роком диапазоне значений параметров рынка a, b и параметров типов аген-
тов Bi, βi, i ∈ N. Поскольку b = 0, то допустимо представление функций (7) в
(
)
∑
следующем виде: Fri =a
-Q-Qi 1+j∈N\ixr
b
ij
- Bib βiQii-1. Анализ [19]
телекоммуникационных компаний РФ показал, что у всех фирм наблюдается
положительный эффект расширения масштаба, т.е. βi < 1, коэффициент из-
держек Bi ∈ (1, 3), если Qi ∈ (0, 500) млрд мин, параметр функции спроса a≈
≈Bi, параметр b = 0,0009 руб./мин. Поэтому будем рассматривать соотноше-
ние, далее называемое коэффициентом спроса и издержек, σ =Bib≈b ≈1000
как параметр функции Fri, а при моделировании отрицательного эффек-
та масштаба в связи с отсутствием эмпирических данных примем σ =ab и
Bi
= kσ, k < 1. Также в качестве параметра этой функции рассмотрим сум-
b
му предположительных вариаций в функции Fri i-го агента Sri. Отметим,
что было получено [17] следующее ограничение на сумму предположитель-
ных вариаций: |Sri| <mm-1-υ , где υ < 1 ∀m ≥ 2, причем если для всех аген-
тов имеет место убывающая отдача от расширения масштаба, т.е. βi > 1
∀i ∈ N, то данное ограничение более жесткое: |Sri| < 1 ∀m ≥ 1. Поэтому иссле-
дуем трехпараметрическую функцию Fri = σ - Q - Qi (1 + Sri) - kσβiQβi-1i,
{
1 ∀βi < 1,
k=
в диапазоне Qi ∈ (100, Qmax) , Qmax = 500 млрд мин при
0,3 ∀βi > 1
различных значениях параметров σ, βi, Sri.
Аналогично проведем моделирование линеаризованных функций (9b), ко-
торые представим в виде
∑
Bi
Bi
â
Fri =
- q - qi 1 +
xr
-
βiνβi-1i -
βi (βi - 1) νβi-2i (qi - νi).
ij
b
b
b
j∈N\i
С учетом (9c) коэффициенты этих функций вычисляются по формулам
Bi
â
Qmaxa
a
QmiaxBi
=
=
= σQ-1max,
=
= kσQβi-2max .
b
Q2maxb
Qmaxb
b
Q2maxb
Поэтому вместо функци
Fri исследуем функцию
[
]
F∼i = σQ-1max - q - qi (1 + Sri) - kσQβi-2maxβi νβi-1i + (βi - 1) νβi-2i (qi - νi)
при Qmax = 500 и различных значениях параметров σ, βi, Sri, причем ось абс-
цисс переведем в единицы измерения Qi = qiQmax.
Исследуем адекватность оценки линеаризации (9b) по формуле (9d), для
чего сравним фактическое отклонение решения линеаризованной системы
равнений (b) от точного решения системы (7), вычисленное по формуле
∗
ΔQ∗iфакт=
Q∗i -Q
, и оценку максимального отклонения ξi, вычисленную
i
127
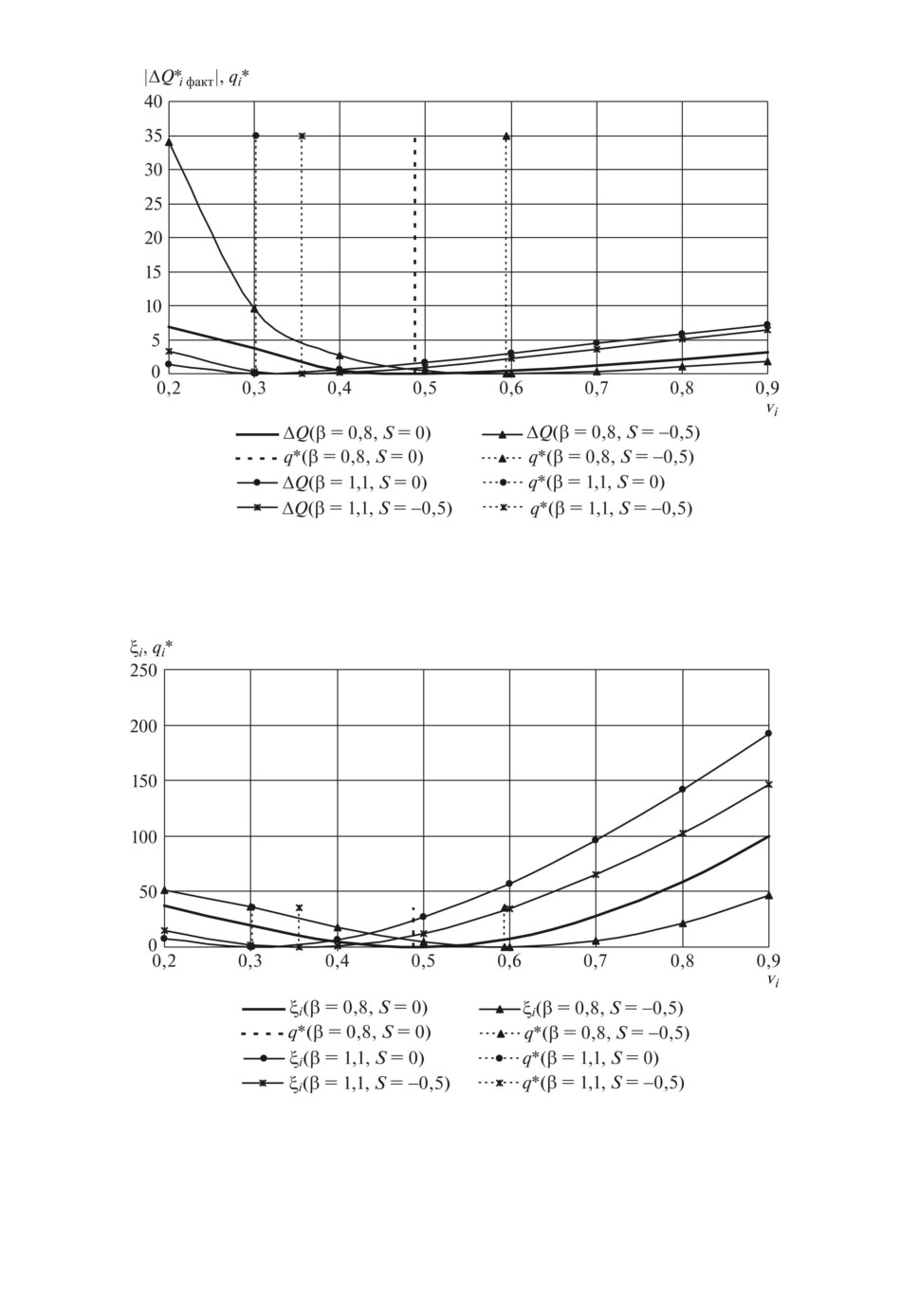
Рис. 2. Фактическое отклонение |ΔQ∗iфакт| решения линеаризованной системы
от точного решения и точное решение q∗i при n = 2, σ = 1000.
Рис. 3. Максимальное отклонение ξi решения линеаризованной системы от
точного решения и точное решение q∗i при n = 2, σ = 1000.
128
по формуле (9d). При моделировании отклонения ξi используем двухпара-
метрическую функцию (8) в виде
βi-2
Biβi (βi - 1) Q
i
ui = -2 -
= -2 - kσβi (βi - 1) Qβi-2i
b
при различных значениях σ, βi.
На рис. 2, 3 в зависимости от параметра линеаризации νi показаны от-
клонения |ΔQ∗iфакт| и ξi, а также точное решение q∗i для случая дуополии
(т.е. при n = 2) при коэффициенте спроса и издержек, равном σ = 1000, для
случая однотипных агентов (т.е. β = βi ∀i ∈ N) при различных типах эф-
фекта расширения масштаба (β < 1 и β > 1) и различных значениях суммы
предположительных вариаций (Sri = 0 и Sri = -0,5). На рис. 4, 5 отклонения
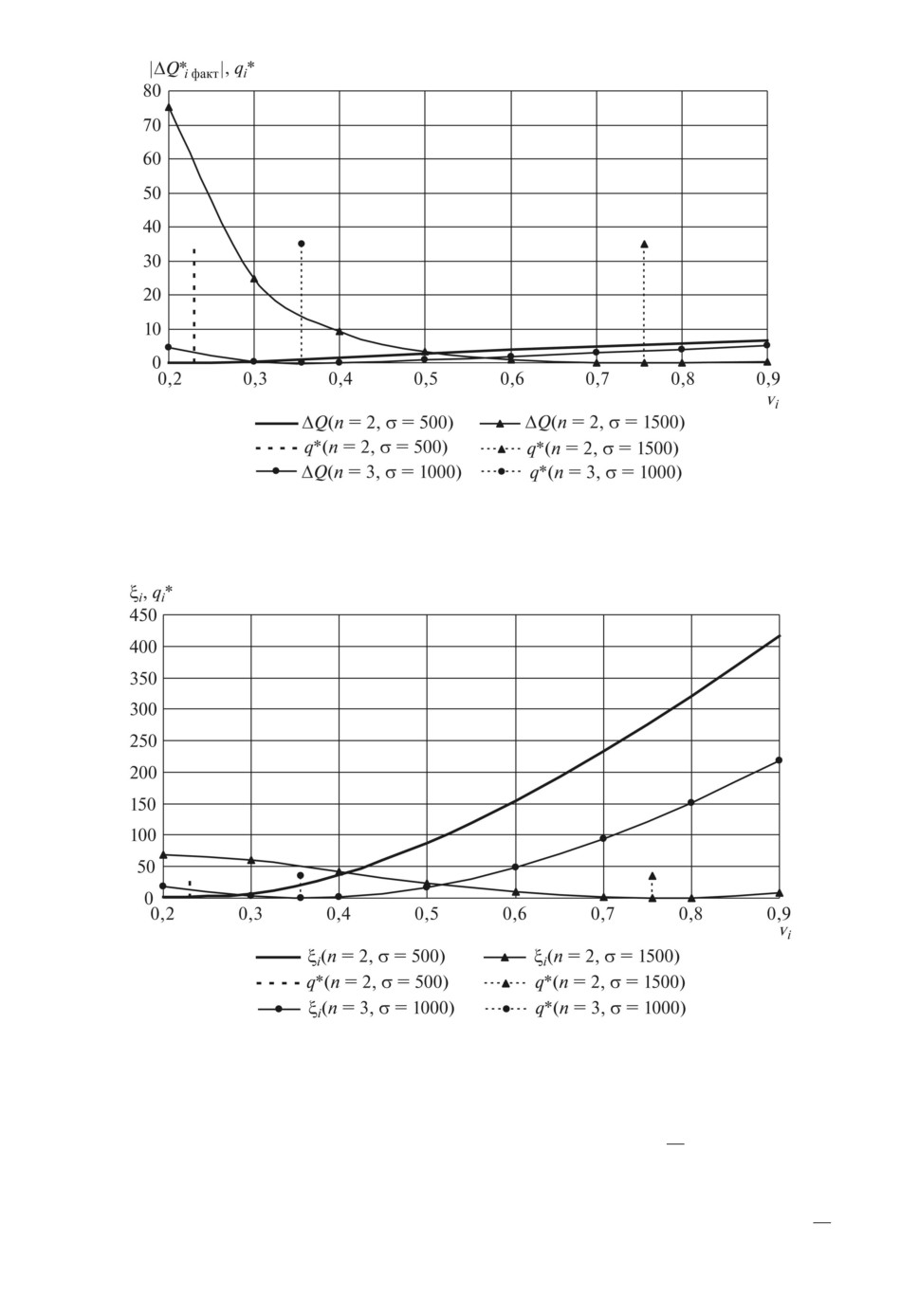
показаны для дуополии и триполии (т.е. при n = 2, 3) при положительном
эффекте расширения масштаба (β < 1) и нулевой сумме предположительных
вариаций для различных значений коэффициента спроса и издержек σ.
Во всех случаях видно, что |ΔQ∗iфакт| < ξi, т.е. фактическая точность ли-
неаризации существенно превышает предельную оценку, так как для нагляд-
ности высоты линий q∗i на обоих рисунках одинаковы. Кроме того, видно,
что отклонения |ΔQ∗iфакт| и ξi практически совпадают и достигают наимень-
ших значений, близких к нулю, при νi = q∗i, что подтверждает выполнение
условий (10d), т.е. возможность нахождения достаточно точного решения си-
стемы (7) по линеаризованной системе (9b).
На рис. 6 в зависимости от действия каждого из агентов Qi при значе-
нии параметра линеаризации νi = q∗i показаны сплошными линиями функции
оптимальных реакций Fi и пунктирными линиями линеаризованные функ-
ции F∼i для случая дуополии (т.е. при n = 2) при коэффициенте спроса и
издержек, равном σ = 1000; графики иллюстрируют точность совпадения ре-
шения уравнений (7) и (9b), т.е. совпадения точек пересечения этих функций
с осью абсцисс.
Проведем анализ чувствительности решения системы линеаризованных
уравнений (10а), вычисленных по формулам (10d), к изменениям парамет-
ров рынка и типа агентов. С использованием коэффициента спроса и издер-
жек σ, формулы коэффициентов системы (10а) имеют вид трехпараметриче-
ских функций
βi-1
â
Biβ2iνi
αi =
-
= σQ-1max - kσQβi-2max β2i νβi-1i,
b
b
δi = 2 + kσQβi-2maxβi (βi - 1) νβi-2i + Sri
при различных значениях параметров σ, βi, Sri.
Рассмотрим случай дуополии, когда функция издержек первого агента
имеет положительный эффект расширения масштаба, а именно β1 = 0,8, а
у второго агента может быть положительный или отрицательный эффект.
Опишем эти констелляции с помощью переменного соотношения параметров
типа агентовβ2β1 приβ1=0,8:еслиβ2 <1,25,товторойагентимеетположи-1
129
Рис. 4. Фактическое отклонение |ΔQ∗iфакт| решения линеаризованной системы
от точного решения и точное решение q∗i при β = 0,8, Sri = 0.
Рис. 5. Максимальное отклонение ξi решения линеаризованной системы от
точного решения и точное решение q∗i при β = 0,8, Sri = 0.
тельный эффект расширения масштаба, т.е. β2 < 1; еслиβ2 > 1,25, то вто-β
1
рой агент имеет отрицательный эффект расширения масштаба, т.е. β2 > 1.
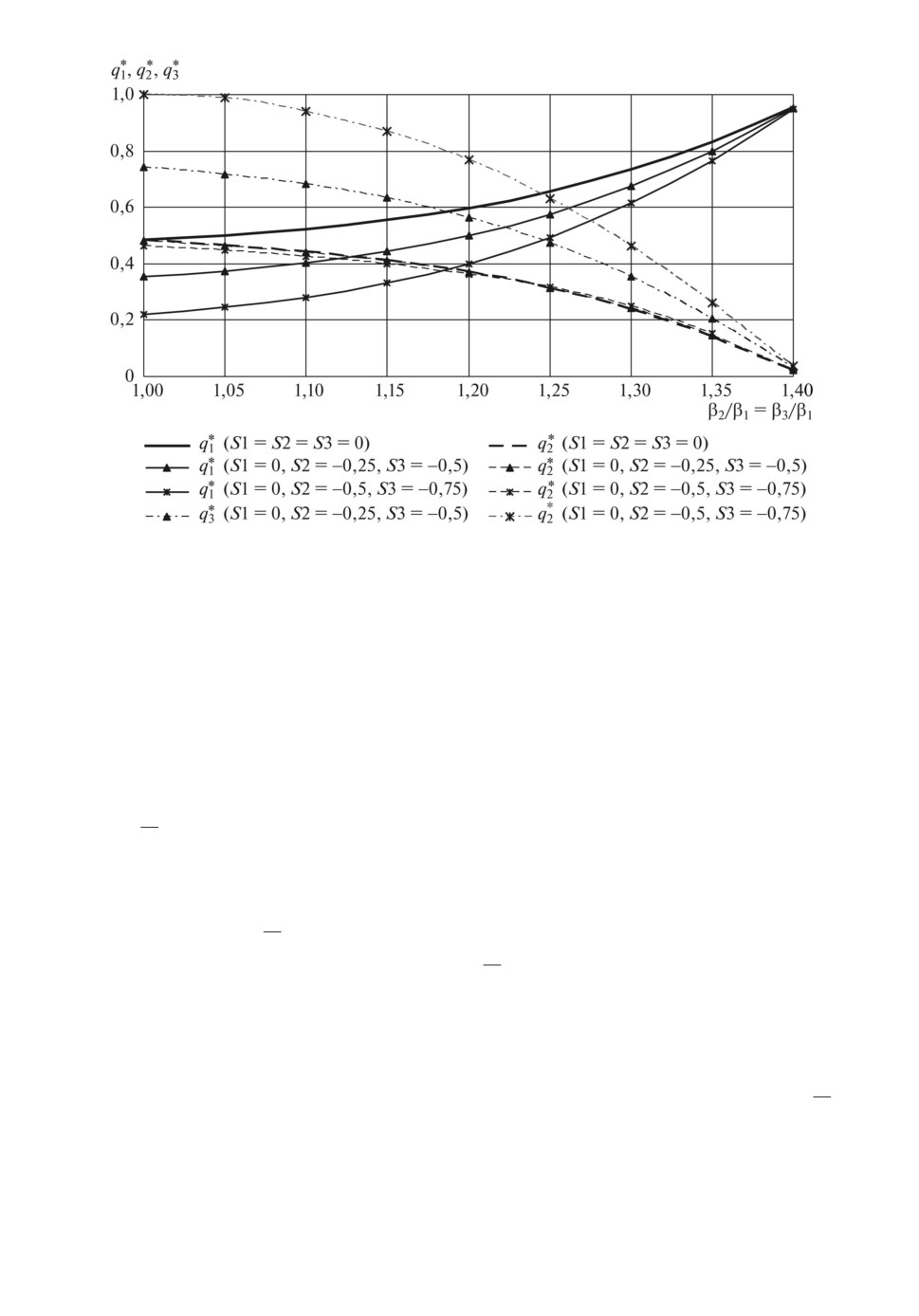
На рис. 7 изображены зависимости равновесных значений действий агентов
q∗1,q∗2 в дуополии как функции от соотношения параметров типа агентовβ2 .β
1
130
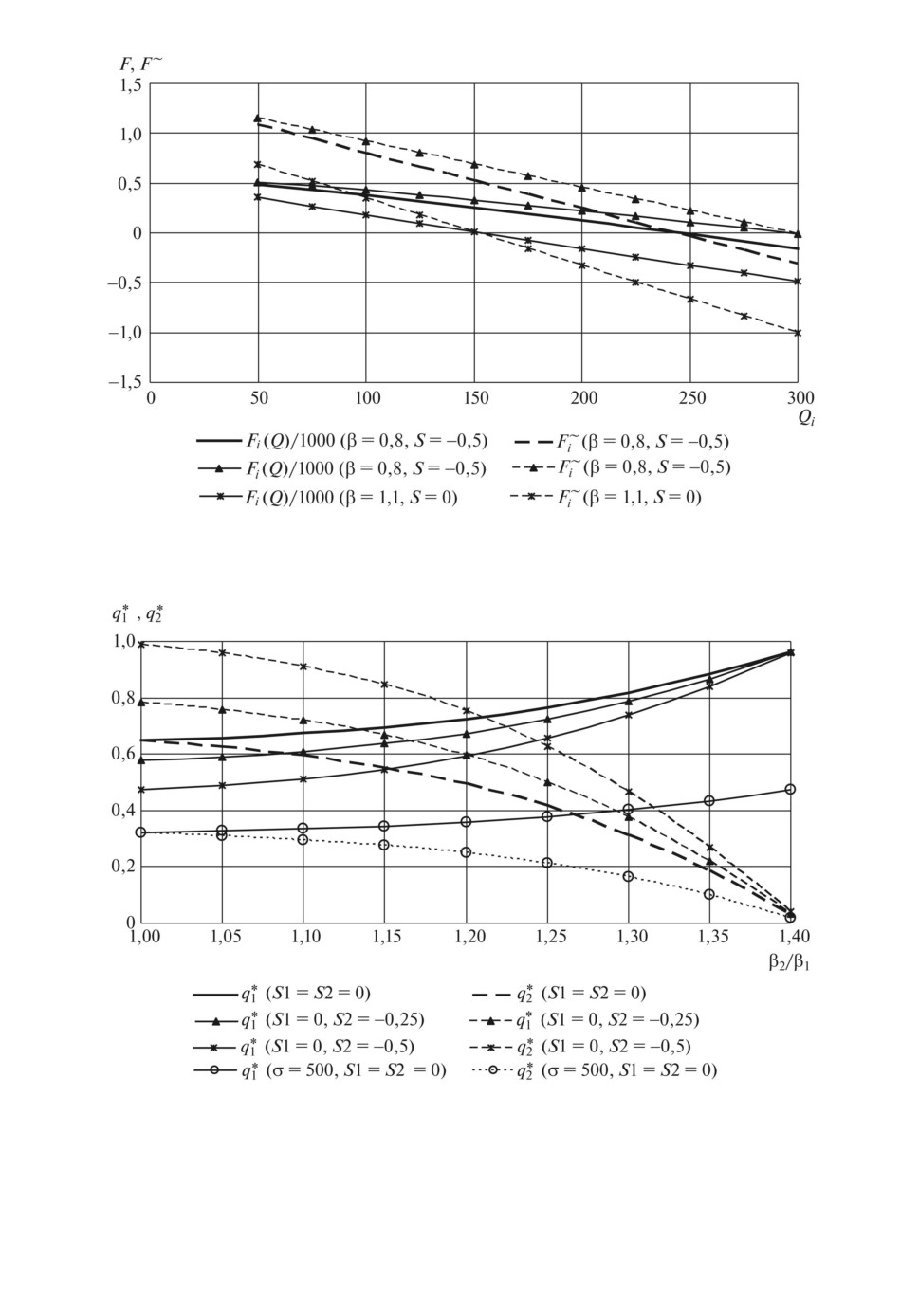
Рис. 6. Функция оптимальной реакции Fi и линеаризованная функция F∼i при
n = 2, σ = 1000 для νi = q∗i .
Рис. 7. Зависимости равновесных относительных действий в дуополии от соот-
ношений параметров типа агентов при n = 2, σ = 1000, Qmax = 500, β1 = 0,8,
k = 0,2.
131
Рис. 8. Зависимости равновесных относительных действий в триполии от соот-
ношений параметров типа агентов при n = 3, σ = 1000, Qmax = 500, β1 = 0,8,
k = 0,2.
Все графики построены при значении коэффициента спроса и издержек, рав-
ного σ = 1000, за исключением равновесия при σ = 500, которое иллюстриру-
ет влияние этого параметра. Базой сравнения является случай агентов Курно
при нулевых предположительных вариациях (S1 = S2 = 0), в котором влия-
ние изменения параметра типа второго агента вполне объяснимо: равновес-
ные действия первого агента увеличиваются, а второго уменьшаются с ро-
стомβ2 , что обусловлено относительным опережением прироста издержекβ
1
второго агента. Далее, показано влияние лидерства по Штакельбергу второ-
го агента, т.е. увеличения модуля предположительной вариации этого аген-
та (S2 = -0,25; S2 = -0,5; S2 = -0,75), которое выражается в том, что при
малых значенияхβ2 равновесные действия второго агента существенно пре-β
1
вышают действия первого, однако приβ2β1 >1,25(т.е.β2>1)первыйагент
вновь выигрывает в равновесии. Наконец, влияние изменения коэффициента
спроса и издержек до σ = 500 вызывает одновременный сдвиг равновесных
действий агентов в сторону уменьшения.
На рис. 8 представлены зависимости равновесных значений действий аген-
тов в триполии как функции от соотношения параметров типа агентовβi ,β
1
i = 2,3 при β1 = 0,8, т.е. параметры типа второго и третьего агентов оди-
наковы. Поэтому в случае S1 = S2 = S3 = 0 графики q∗2 и q∗3 совпадают и
характер влияния относительного изменения параметров функций издержек
этих агентов по сравнению с первым агентом аналогичен случаю дуополии:
равновесные действия первого агента увеличиваются, а второго и третьего
132
уменьшаются с ростомβi . Далее рассмотрены ситуации, в которых первыйβ
1
агент считается ведомым, второй агент лидером по Штакельбергу, а тре-
тий лидером по Штакельбергу более высокого уровня, т.е. при S1 = 0 имеет
место S2 = -0,25; S2 = -0,5 и S3 = -0,5; S3 = -0,75 соответственно. В ре-
зультате лидеры получают преимущество в равновесии до тех пор, пока их
функции издержек характеризуются положительным эффектом масштаба,
т.е.βiβ1 <1,25,авслучаеβi >1,25равновесныедействияпервогоагентаста-1
новятся больше, чем действия лидеров.
5. Заключение
Процессы, протекающие в экономических и технических системах, зача-
стую нелинейны, поэтому нелинейные модели описывают их наиболее точно.
Однако системы нелинейных уравнений, которые описывают оптимальные
действия агентов в многоагентных системах, не имеют аналитического ре-
шения, что затрудняет исследование таких систем в случае, если одни их
состояния зависят от других состояний, например при анализе динамики си-
стем. В игре олигополии эта сложность возникает при анализе лидерства по
Штакельбергу различных уровней, когда равновесие на данном уровне вы-
числяется в зависимости от равновесия на предшествующем уровне.
В статье рассмотрен первый этап разрешения этой проблемы, состоящий
в редукции системы нелинейных уравнений оптимальных реакций агентов
к системе линейных уравнений, зависящих от вектора параметров линеари-
зации. Для линеаризованной системы получено аналитическое решение как
функция этих параметров. В результате расчет игровых равновесий сводится
к подбору неподвижных точек нелинейных отображений. На этом этапе под-
бор параметров линеаризации осуществлялся эвристически, что тем не менее
позволило получить решения игры с удовлетворительной точностью.
Моделирование равновесий для достаточно широкого спектра параметров
состояния агентов подтвердило удовлетворительную точность линеаризации,
а также продемонстрировало возможности данного подхода в задачах анали-
за влияния изменения параметров состояния на результирующее равновесие
в игре.
Исследование позволило сделать следующие выводы. В игре олигополи-
стов преимущество одного агента по типу функции издержек, т.е. наличие
положительного эффекта расширения масштаба, ведет к повышению выиг-
рыша этого агента по сравнению с выигрышами окружения. Лидерство по
Штакельбергу одного из агентов также способствует повышению его выиг-
рыша по сравнению с выигрышами окружения, однако преимущество других
агентов по типу функции издержек корректирует влияние этого фактора.
Развитие исследований видится, во-первых, в нахождении замкнутой фор-
мы решения линеаризованной системы уравнений на основе процедуры вы-
числения неподвижных точек нелинейных отображений; во-вторых, в направ-
лении применения разработанных расчетных методик к проблеме вычисле-
ния равновесий на реальных рынках, например рынке телекоммуникаций,
при различных уровнях лидерства агентов с целью оценки их фактических
133
уровней путем сравнения с реальными состояниями. Результаты также ак-
туальны в связи с увеличением количества агентов свыше трех, например
на российском рынке телекоммуникаций, что приводит к усложнению анали-
за их взаимодействий. Наряду с этим, результаты могут быть использованы
при анализе игр на других рынках, а именно на рынках розничной продажи
электроэнергии [23-25], поскольку возможность анализа нелинейных систем
обеспечивает более точные оценки результатов.
ПРИЛОЖЕНИЕ
Доказательство утверждения 1. Проведем нормализацию векто-
ра действий агентов из условия qi ∈ (0, 1), которому удовлетворяет следующая
формула:
Qi
(Π.1)
qi =
,
i∈N, Qmax >Qi
,
i∈N.
Qmax
(
)
определено из формулы
Значение Qmax =a-MCminb,MCmin=mini∈N BiQiβi-1
объема рынка олигополии при бесконечно большом количестве фирм [18].
Коэффициенты уравнений (7) для нормализованного вектора действий най-
дем из условия равенства критерия (1) при векторах действий qi, i ∈ N и Qi,
i∈N:
(
)
(Π.2)
,
i∈N.
â - bq qi - CFi -Biqβii = (a - bQ) Qi - CF i - BiQii
Подставив в это выражение (П.1) и сравнив коэффициенты при одинаковых
степенях вектора действий, получим формулы (9c). Следовательно, (7) мож-
но записать в виде
∑
(Π.3)
Fi = â -bq -bqi1 +
xr
- Biβiqβi-1i
= 0, i ∈ N.
ij
j∈N\i
Нелинейный компонент уравнений (П.3) есть функция f(qi) =Biβiqβi-1i.
В окрестности числа νi, такого что νi ∈ (0, 1), νi < qi, разложение этой функ-
ции в ряд Тейлора имеет вид
f′′ (νi)
f (qi) = f (νi) + f′ (νi)(qi - νi) +
(qi - νi)2 +
2!
Если существует такое число Ωi = νi + θi (qi - νi), что νi < Ωi < qi, иначе го-
воря θ ∈ (0, 1), то этот ряд имеет остаточный член формулы Тейлора в форме
Лагранжа [20], вычисляемый по следующей формуле:
k
∏
1
Ωβi
i
(Π.4)
Rk (qi) =
f(k) (Ωi)(qi - νi)k =(qi -νi)
Biβi
(βi
− j) .
k!
k!
Ωk+1
i
j=1
134
Ряд сходится, если |qi - νi| < ri и lim
) = 0, поэтому зададим ма-
Rk (qi
k→∞
лое число ri, такое что 0 < ri < Ωi, и при этом покажем существование
предела последовательности остаточных членов. Поскольку ri ∈ (0, Ωi), то
k
∏k
Ωi > qi - νi, значит,(qi-νi)
> (qi-νi)k+1
, и k!=
j, j ≥ |βi - j|, значит,
Ωki
Ωk+1i
j=1
∏k
∏k+1
j=1
|βi-j|
|βi-j|
∏k
> ∏1
k+1
. Поэтому lim
Rk (qi) = 0, значит, ряд Тейлора с оста-
j=1
j
j=1
j
k→∞
точным членом (П.4) сходится к функции f (qi) =Biβiqβi-1i.
С учетом только первого члена ряда разложение функции f (qi) имеет вид
f (qi) =Biβiνβi-1i + Biβi (βi - 1) νβi-2i (qi - νi). Поэтому (П.3) можно предста-
вить в виде (9b). Остаточный член (П.4) при этом равен
2
(qi - νi)
(Π.5)
R2 (qi) =
Biβi (βi - 1) (βi - 2) Ωβi-3i.
2
Оценим погрешность замены решения системы (7) на решение систе-
мы (9b). Функции Fi, описывающие левые части уравнений (7), в окрестности
локального максимума критерия (1) являются убывающими по Qi, посколь-
ку F′iQi = ui - Sri < 0 выполняется при условии (8). Функци
Fi левых частей
уравнений (9b) также убывающие, поскольку неравенство
(Π.6)
F′iq
= -2b - bSri - Biβi (βi - 1) νβi-2i
<0
i
выполняется при условии (8). В (П.6) учтено, что согласно
[17]
∂Sri =∂q
i
= ∂Qi∂i ∂
qi
Как видно из рис. 1, отклонение решения q∗i системы (9b) от точного ре-
шения Q∗i системы (7), приведенного по нормализации (П.1) к единицам из-
мерения Qi, т.е. отклонение ΔQ∗i = Q∗i -Q∗i, равно
|R2 (q∗i)|
(Π.7)
|ΔQ∗i| = Qmax
F′
iqi
С учетом коэффициентов, вычисленных по формулам (9c), выражение (П.6)
имеет вид
F′iq
=
i
= -2Q2maxb - Q2maxbSri - QβimaxBiβi (βi - 1)
i
(
)
Biβi (βi - 1)
= -bQ2max
2+Sri +
Qβi-2maxνβi-2
i
b
[
]
Это выражение с учетом (8a) равн
F′iqi = -bQ2max
2-(uimax +2)νβi-2i+Sr
,
i
где uimax = ui (Qmax). Подставим это выражение, а также (П.5) в (П.7), по-
135
лучим
2
(qi - νi)
BiQmiaxβi |βi - 1| |βi - 2| Ωii-3
|ΔQ∗|=Qmax
=
i
2
i-2
bQ2max
2 - (uimax + 2) νβ
+Sri
i
(qi - νi)2
|uimax + 2| |βi - 2| Ωβi-3i
=Qmax
.
2
i-2
2 - (uimax + 2) νβ
+Sri
i
m
Было показано [17], что выполняется ограничение |Sri| < Smax =
,
m-1-υmax
2
где υmax =ψmax(√√ψmax)
, ψmax ≈ 1, ψmax < 1, m количество агентов окру-
m
ψmax
жения i-го агента, m ≥ 2, тогда, приняв ψmax = 1 - ε, где 0 < ε ≪ 1, получим
(
)2 (
)-1
приближенно υmax ≈1-εm
2-ε2
1-ε2
. Поэтому в общем можно запи-
сать следующее ограничение:
2
(qi - νi)
|uimax + 2| |βi - 2| Ωβi-3i
|ΔQ∗|≤Qmax
.
i
2
i-2
2 - (uimax + 2) νβ
+Smax
i
Поскольку uimax есть ограниченная величина по (8а), Smax также ограни-
ченная величина [17] при m ≥ 2, поэтому если ri → 0, то |qi - νi| → 0, значит,
lim
|ΔQ∗i| = 0.
r→0
Исследуем проблему существования решения системы уравнений (7). Рас-
смотрим следующую систему уравнений, решение которой, очевидно, такое
же, как и системы (7):
∑
fri = -Fri = -a + bQ + bQi 1 +
xr
ij
+BiβiQβi-1i = 0,
(Π.8)
j∈N\i
Qi > 0, i ∈ N.
Используем условия, сформулированные в теореме 3 [21] для вектор-функ-
ции fr = {fri, i ∈ N} (в дальнейшем индекс r опущен): если матрица Якоби{}
системы (7) J = f′
, i, j ∈ N имеет диагональное преобладание, т.е.
iQj
∑
(Π.9)
f′
-
f′iQ
> 0, i ∈ N,
iQi
j
j=1,j=i
то система (П.8) имеет единственное решение.
(
)
Поскольку f′iQi = -b (ui - Si), f′iQj
=b
1+Sr/
и в [17] показано, что
iQj
∂Sri
lim
= 0, поэтому при достаточно больших Qi матрица Якоби Jn n-го по-
∂Qj
Qj→∞
рядка для системы (П.8) имеет вид
-b(u1 - S1)
b
b
b
-b(u2 - S2) ...
b
Jn =
=
b
b
-b(un - Sn)
136
-g1
1
1
1
-g2
1
=b
,
1
1
-gn
где gi = ui - Si < 0, i ∈ N согласно (8). Обратная матрица J-1n существует,
если определитель матрицы Якоби ΔJN = 0; этот определитель [17] вычис-
ляется по формуле
∏
∑
∏
ΔJn = b
(-gi - 1) +
(gi - 1).
i=1
γ=1 j=1\γ
∑
1
Поэтому условие ΔJn = 0 равносильноi∈Ng
=1 и gi =0
∀i ∈ N
i+1
(см. [17]). В этом случае условие (П.9) имеет вид -gi - (n - 1) > 0, i ∈ N,
откуда следует, что
(Π.10)
n < |ui - Sri
| + 1, i ∈ N.
Отметим, что условия теорем 1, 2 [21] для системы (7) не выполняют-
ся (а именно, не выполняется условие различных знаков производных F′iQi
и F′
), поэтому нельзя гарантировать существования неотрицательного ре-
iQj
шения; этот вопрос рассматривался в [22].
Однако условие (П.10) не является необходимым, т.е. если оно не выполня-
ется, система (7) может иметь решение. Сформулируем необходимое условие
существования решения системы (7), базируясь на геометрическом смысле
решения как точки пересечения линий оптимальных реакций в случае n = 2.
Предположим, что существуют функци
Fi, полученные путем выражения
из уравнений (7) действий i-го агента от действий окружения (обозначено
символом ¾-i¿), т.е. функции оптимальных реакций Qi
Fi (Q-i), и введем
функции отклонений реакций i-го и j-го агентов вида Gij (Qi, Qj )
Fi
F-1ij,
гд
F-1ij обратная функция дл
Fj , полученная выражением Qi из Fj . Если
решение {Q∗i, i ∈ N} системы (7) существует, то
(
)
(Π.11)
Gij
Q∗i,Q∗j
= 0 ∀i,j ∈ N.
(
)′
Поскольку
F-1ij
= ui - Si, причем xji < 0 соглас-
F′iQj =∂Qi∂j =xji,
Qj
но [17] и ui - Si < 0 согласно (8), то функци
Fi
F-1ij являются монотонно
убывающими по Qj в интервале, на котором выполняются указанные усло-
вия. Поэтому при данном Q∗i функции Gij (Q∗i, Qj) являются монотонно воз-
растающими (или убывающими при альтернативно возможной форме Gij =
=
F-1ij
Fi) по Qj на интервале
( Qj,Qmax), т.е.
(
)′
G′ijQ
=
F′iQ
-
F-1ij
> 0,
j
j
Qj
137
если выполнено условие |xji| < |ui - Si| (или |xji| > |ui -Si| при Gij
F-1ij
Fi).
Иначе говоря условие монотонности функции Gij имеет вид
(Π.12)
|xji| = |ui - Si
|.
Граница интервалаQj вычисляется из условия (8) с учетом (8а) по следую-
щей формуле:
1
2-βj
Qj = Bj(j |βj -)|
при βj < 1,
Qj = 0
при βj > 1.
b
2+Sr
j
[
]
Монотонная функция ограничена на замкнутом интервале Aj =
Qj,Qmax
,
т.е. по теореме Вейерштрасса
m ≤ Gij (Q∗i,Qj) ≤ M, где m = inf
Gij , M = sup Gij .
Qj∈Aj
Qj∈Aj
Отсюда следует, что при условии (П.11) m ≤ 0 ≤ M. При этом по теореме
Больцано-Коши о промежуточном значении имеемQj ≤ Q∗j ≤ Qmax, следо-
вательно, совместное выполнение (П.12) и 0 ≤Qj ≤ Qmax есть необходимое
(
)
условие для (П.11) на интервале
Qj,Qmax
Это условие является также достаточным, если, кроме того, m и M имеют
противоположные знаки, т.е.
(
)
(Π.13)
Gij
Q∗i,Qj
Gij (Qi, Qmax
) < 0,
поскольку при (П.12) функция Gij монотонна, а с учетом (П.13) интервал
монотонности включает в себя точку Gij (Q∗i, Qj) = 0. Выведем удобную для
проверки форму условия (П.13): выражени
F-1ij для уравнений системы (7)
имеет вид
∑
BjβjQβj-1j
a
(Π.14)
F-1ij = Qi =
-
Qk - Qj - bQj (1 + Sj) -
b
b
k∈N\(i,j)
Поскольку условия (П.13) должны выполняться при всех значениях дей-
ствий, то рассмотрим случай, когда действия всех агентов, кроме i-го и j-го,
равныQk; поэтому из выражения (П.14) следует
∑
a
ax
F-1ij (Qmax) ≡ κj =
-
Qk - Qmax - Qmax (1 + Sj) -BjβjQm
b
b
k∈N\(i,j)
(
)
(Qj)<
(Qj),т.е.G
Пусть
Fi
F-1ij
ij
Q∗i,Qj
< 0; тогда в силу монотонно-
го убывани
Fi (Qj) условие
Fi (Qmax)
F-1ij (Qmax), т.е. Gij (Q∗i,Qmax) > 0,
138
выполняется при |xji| < |ui - Si|. Подставим в i-е уравнение системы (7)
Qj = Qmax иQk, получим
∑
Fi (κi) = a - bQmax +
Qk + κi - bκi (1 + Si) - Biβiκβi-1i = 0,
k∈N\(i,j)
где символом κi обозначено решение этого уравнения. Поскольку функ-
ции Fi являются монотонно убывающими при условии (8), то из неравенства
Fi (κj) > 0 следует κj < κi, и наоборот. Следовательно, условие (П.13) мож-
но представить в виде: если Fi (κj) > 0 и |xji| < |ui - Si| для всех i, j ∈ N, то
m и M имеют противоположные знаки.
■
Доказательство утверждения 2. Из уравнений (9а) следует, что
∑
â - bq-i - bqi -bqi 1 +
xr
- Biβiνβi-1i -Biβi (βi - 1) νβi-2iqi +
ij
j∈N\i
+ Biβi (βi - 1) νβi-2iνi = 0,
∑
Biβi (βi - 1)
-b 2 +
νβi-2i +
xr
qi -bq-i + â -Biβiνβi-1i +
ij
b
j∈N\i
+ Biβi (βi - 1) νβi-1i = 0,
∑
Biβi (βi - 1)
-b 2 +
νβi-2i +
xr
ij
qi -bq-i + â -Biβi (2 - βi) νβi-1i = 0,
b
j∈N\i
βi-1
∑
Biβi (βi - 1)
2+
νβi-2i +
xr
qi + q-i -â-Biβi (2-βi)νi
= 0,
ij
b
b
j∈N\i
поэтому можно записать (10а).
Система (10а) решается методом Крамера. Используем материалы прило-
жения статьи [17]. Левые части системы (10а) аналогичны системе (П.2) из
[17], поэтому главный определитель имеет вид
∏
∑
∏
Δ = (δj - 1) +
(δγ - 1).
j=1
j=1 γ=1\j
Условие существования решения системы (10а) определяется по теореме Кра-
мера [20]: система имеет единственное решение, если главный определитель
Δ = 0. Из формулы главного определителя следует, что
∑
Δ
1
=1+
при δj - 1 = 0 ∀j ∈ N,
∑
δj - 1
(δj - 1)
j=1
j=1
139
поэтому решение системы (10а) существует, если
∑
1
= -1 ∧ δj - 1 = 0 ∀j ∈ N.
δj
-1
j=1
Вспомогательный определитель системы (10а), соответствующий i-й неиз-
вестной, вычисляется путем следующих преобразований: 1) из i-й строки вы-
носится множитель αi, 2) в i-м столбце создаются нули, 3) определитель раз-
лагается по элементам i-го столбца с понижением порядка, 4) полученный
определитель последовательно разлагается на суммы определителей по каж-
дой строке, 5) в этом разложении определители, имеющие одинаковые стро-
ки (столбцы), равны нулю, а остальные определители соответствуют либо
главному определителю, либо вспомогательному определителю системы (П.2)
из [17]. Эти преобразования (например, при i = 2) имеют вид
α1
α1
α1
δ1
1
δ1 -
0
1-
δ1
α1
1
α
α2
α2
2
Δ2 =
1
α2
1
=α2
1
1
1
=α2
1
1
1
=
α3
α3
α3
1
α3
δ3
1
δ3
1-
0
δ3 -
α2
α2
α2
α1
α1
δ1 -
1-
δ1
1
δ1
1
1
α2
α2
α3
α1
1
=α2
=α2
α3
α3
-
-
1
+
1
δ3
α2 α2
1
1
α2 α2
δ3
1-
δ3 -
α2
α2
1
α3 α3
1
+
α2Δ-2 - α3 (δ1 - 1) - α1 (δ2 - 1) ,
1
1
=
α2 α2
где Δ-i главный определитель системы (10а) без i-го уравнения и без i-й
неизвестной. Для вспомогательного определителя системы четвертого поряд-
ка (например, при i = 1) эти преобразования имеют вид
1
1
1
1
α2
α2
α2
α1
1
1
1
0
δ2 -
1-
1-
α1
α1
α
1
α2
δ2
1
1
Δ1 =
=α1
α3
α3
α3
=
α3
1
δ3
1
0
1-
δ3 -
1-
α1
α1
α1
α4
1
1
δ4
α4
α4
α4
1-
1-
δ4 -
0
α1
α1
α1
α2
α2
α2
δ2 -
1-
1-
α1
α1
α
1
δ2
1
1
α3
α3
α3
=α1
1-
δ3 -
1-
=α1
1
δ3
1
-
α1
α1
α1
1
1
δ4
α4
α4
α4
1-
1-
δ4 -
α1
α1
α1
δ2
1
1
δ2
1
1
δ2
1
1
α4
α3
α3
α4
-α1
1
δ3
1
-α1
1
1
1
+α1
1
1
1
-
α1
α1
α1 α1
1
1
1
1
1
δ4
1
1
1
140
1
1
1
1
1
1
α2
α2
α4
=
-α1
1
δ3
1
+α1
1
δ3
1
α1
α1 α1
1
1
δ4
1
1
1
= α1Δ-1 - α2 (δ3 - 1) (δ4 - 1) - α3 (δ2 - 1) (δ4 - 1) - α4 (δ2 - 1) (δ3 - 1) .
Обобщение этих выражений для системы произвольного порядка по индук-
ции приводит к формуле
∑
∏
Δi = αiΔ-i -
αj
(δγ - 1),
j=1\i
γ=1\i,j
что позволяет записать формулу (10b).
Покажем, в каких случаях для корней (10с) выполняются условия (10d),
т.е.
|qi - νi| < ri, Ωi = νi + θi (qi - νi) , θi, νi ∈ (0, 1) ,
(Π.15)
ri ∈ (0,Ωi), νi < qi, i ∈ N.
Условия
|qi - νi| < ri и νi < qi совместно выполняются, если для кор-
ней (10с) существует функция Gi = q∗i (νi) - νi, причем Gi ∈ (0, ri) на интер-
вале νi ∈ (0, 1). В этом случае условие ri ∈ (0, Ωi) выполняется, если Ωi =
1 > θi > ri-νi. Отме-r
= νi + θi (q∗i - νi) > ri, т.е. θi >r∗−νiqii > rirνii,значит,
i
тим, что в последнем неравенстве для малых значений νi возможен случай
ri - νi < 0, поэтому в этом случае условие (П.15) выполняется при любом
θi ∈ (0,1).
Поскольку функция Gi непрерывна при условии
(10b), то усло-
вие Gi ∈ (0, ri) выполняется, если на интервале νi ∈ (0, 1) функция Gi имеет
хотя бы один ноль. В дальнейшем индекс i опущен, поскольку условия (П.15)
должны выполняться для всех i ∈ N, поэтому из (10с) следует, что
(
)
n-2
α
χn-1 + (n - 1) χn-2
- (n - 1) αχ
α
q∗ =
=
,
где χ = δ - 1.
χn + nχn-1
χ+n
Исследуем функцию Gi на границах интервала ν ∈ (0, 1), для чего найдем
пределы справа (при ν → 0 + 0) коэффициентов α (ν) , δ (ν):
{
µ1
при β > 1,
lim
α=
ν→0+0
−∞ при β < 1,
a
{
где µ1 =
∞ при β > 1,
bQ
max
lim
δ=
ν→0+0
−∞ при β < 1,
Поэтому lim
q∗ = 0, значит, lim G = -0, т.е. при ν → 0 справа функция
ν→0+0
ν→0+0
G → 0 снизу, или G(ν → 0 + 0) < 0. Найдем пределы слева (при ν → 1 - 0)
коэффициентов α (ν) , δ (ν):
â - Biβi (2 - βi)
a
β
a
lim
α=
=
+
(umax + 2) ≈
,
ν→1-0
b
bQmax
β-1
bQmax
141
поскольку согласно (8а) lim (ui + 2) = 0;
Q→Qmax
Biβi (βi - 1)
lim
δ=2+
+ Sri = -(umax - Sri ) > 0
ν→1-0
b
согласно (8). Поэтому
a
1
lim
q∗ =
;
ν→1-0
bQmax - (umax - Sri) - 1 + n
так как согласно [17] |Sri| ≤ 1, то
a
1
lim
q∗ ≥
;
ν→1-0
bQmax -umax + n
это число будет больше единицы, т.е.
lim G = +0,
ν→1-0
при условии
a
1
a
>1⇒n<
+umax.
bQmax -umax + n
bQmax
Поскольку на интервале νi ∈ (0, 1) функция Gi меняет знак, то по теореме
Коши [20] она имеет хотя бы один нуль.
■
СПИСОК ЛИТЕРАТУРЫ
1. Karmarkar U.S., Rajaram K. Aggregate Production Planning for Process Industries
under Oligopolistic Competition // Eur. J. Oper. Res. 2012. No. 223 (3). P. 680-689.
2. Ledvina A., Sigar R. Oligopoly Games under Asymmetric Costs and an Application
to Energy Production // Math. Financ. Econom. 2012. No. 6 (4). P. 261-293.
3. Currarini S., Marini M.A. Sequential Play and Cartel Stability in Сournot
Oligopoly // Appl. Math. Sci. 2013. No. 7 (1-4). Р. 197-200.
4. Vasin A. Game-theoretic Study of Electricity Market Mechanisms // Procedia Com-
put. Sci. 2014. No. 31. Р. 124-132.
5. Sun F., Liu B., Hou F., Gui L., Chen J. Cournot Equilibrium in the Mobile Virtual
Network Operator Oriented Oligopoly Offloading Market // 2016 IEEE Int. Conf.
Communicat., ICC 2016. No. 7511340.
6. Nash J. Non-cooperative Games // Ann. Math. 1951. No. 54. P. 286-295.
7. Cournot A.A. Researches into the Mathematical Principles of the Theory of Wealth.
London: Hafner, 1960. (Original 1838).
8. Naimzada A.K., Sbragia L. Oligopoly Games with Nonlinear Demand and Cost Func-
tions: Two Boundedly Rational Adjustment Processes // Chaos. Solit. Fractal. 2006.
No. 29 (3). P. 707-722.
9. Askar S., Alnowibet K. Nonlinear Oligopolistic Game with Isoelastic Demand Func-
tion: Rationality and Local Monopolistic Approximation // Chaos. Solit. Fractal.
2016. No. 84. P. 15-22.
142
10.
Naimzada A., Tramontana F. Two Different Routes to Complex Dynamics in an
Heterogeneous Triopoly Game // J. Differ. Equat. Appl. 2015. No. 21 (7). P. 553-563.
11.
Cavalli F., Naimzada A., Tramontana F. Nonlinear Dynamics and Global Analysis
of a Geterogeneous Cournot Duopoly with a Local Monopolistic Approach Versus
a Gradient Rule with Endogenous Reactivity // Commun. Nonlinear Sci. Numer.
Simulat. 2015. No. 23 (1-3). P. 245-262.
12.
Stackelberg H. Market Structure and Equilibrium: 1st Edition. Translation into En-
glish, Bazin: Urch & Hill, Springer, 2011. (Original 1934.)
13.
Chong J.-K., Ho T.-H., Camerer C. A Generalized Cognitive Hierarchy Model of
Games // Games Econom. Behavior. 2016. No. 99. Р. 257-274.
14.
Berger U., De Silva H., Fellner-Rцhling G. Cognitive Hierarchies in the Minimizer
Game // J. Econom. Behavior Organizat. 2016. No. 130. Р. 337-348.
15.
Bowley A.L. The Mathematical Groundwork of Economics. Oxford: Oxford Univers.
Press, 1924.
16.
Geras’kin M.I., Chkhartishvili A.G. Game-Theoretic Models of an Oligopoly Market
with Nonlinear Agent Cost Functions // Autom. Remote Control. 2017. V. 78. No. 9.
P. 1631-1650.
17.
Гераськин М.И. Свойства предположительных вариаций в нелинейной модели
олигополии Штакельберга // АиТ. 2020. № 6. С. 105-130.
Geras’kin M.I. The Properties of Conjectural Variations in the Nonlinear Stackelberg
Oligopoly Model // Autom. Remote Control. 2020. Vol. 81. No. 6. P. 1051-1072.
18.
Intriligator M.D. Mathematical Optimization and Economic Theory. Englewood
Cliffs: Prentice Hall, 1971.
19.
Geras’kin M.I. Modeling Reflexion in the Non-Linear Model of the Stakelberg Three-
Agent Oligopoly for the Russian Telecommunication Market // Autom. Remote Con-
trol. 2018. V. 79. No. 5. Р. 841-859.
20.
Korn A., Korn M. Mathematical Handbook for Scientists and Engineers. Definitions,
Theorems and Formulas for References and Review. New York: McGraw-Hill, 1968.
21.
Яковлев М.Н. Неотрицательные решения систем нелинейных (в частности, раз-
ностных) уравнений // Тр. МИАН СССР. 1968. T. 96. С. 111-116.
22.
Geras’kin M.I., Chkhartishvili A.G. Analysis of Game-Theoretic Models of an
Oligopoly Market under Constrains on the Capacity and Competitiveness of
Agents // Autom. Remote Control. 2017. V. 78. No. 11. P. 2025-2038.
23.
Aizenberg N., Stashkevich E., Voropai N. Forming Rate Options for Various Types of
Consumers in the Retail Electricity Market by Solving the Adverse Selection Prob-
lem // Int. J. Public Administrat. 2019. No. 42(15-16). Р. 1349-1362.
24.
Paccagnan D., Kamgarpour M., Lygeros J. On Aggregative and Mean Field Games
with Aapplications to Electricity Markets // 2016 Eur. Control Conf., ECC 2016.
2017. No. 7810286. Р. 196-201.
25.
Prosvirkin N., Blinova E., Gerasimov K. Multicriteria Optimization Model of the
Interaction of Elements when Managing Network Integrated Structures // Espacios.
2019. No. 40(40). Р. 1-10.
Статья представлена к публикации членом редколлегии М.В. Губко.
Поступила в редакцию 23.09.2019
После доработки 27.12.2019
Принята к публикации 30.01.2020
143