Автоматика и телемеханика, № 1, 2021
Робастное, адаптивное и сетевое
управление
© 2021 г. А.А. АРДЕНТОВ, канд. техн. наук (aaa@pereslavl.ru),
А.П. МАШТАКОВ, канд. техн. наук (alexey.mashtakov@gmail.com)
(Институт программных систем им. А.К. Айламазяна РАН,
Переславль-Залесский)
УПРАВЛЕНИЕ МОБИЛЬНЫМ РОБОТОМ С ПРИЦЕПОМ
НА ОСНОВЕ НИЛЬПОТЕНТНОЙ АППРОКСИМАЦИИ1
Рассматривается кинематическая модель мобильного робота с при-
цепом, движущегося по однородной плоскости. Робот может двигаться
вперед-назад и вращаться на месте. Для рассматриваемой модели ставит-
ся задача оптимального управления: требуется перевести систему “робот
с прицепом” из произвольно заданной начальной конфигурации в произ-
вольно заданную конечную конфигурацию так, чтобы величина манев-
ра была минимальна. Под маневром понимается функционал, задающий
компромисс между линейным и угловым перемещением робота. В за-
висимости от способа сцепки прицепа с роботом такая задача соответ-
ствует двухпараметрическому семейству задач оптимального управления
в 4-мерном пространстве с 2-мерным управлением.
Предлагается метод нильпотентной аппроксимации для приближенно-
го решения задачи. Разработан ряд итерационных алгоритмов и про-
грамм, успешно решающих поставленную задачу в идеальном случае
при условии отсутствия фазовых ограничений. На основе этих алгорит-
мов предлагается специализированный алгоритм перепарковки, решаю-
щий частный случай задачи, когда начальное и конечное положение ро-
бота совпадают, и учитывающий фазовое ограничение на угол поворота
прицепа, возникающее в реальных системах.
Ключевые слова: робот с прицепом, кинематическая модель, оптимальное
управление, нильпотентная аппроксимация, субриманова задача.
DOI: 10.31857/S0005231021010050
1. Введение
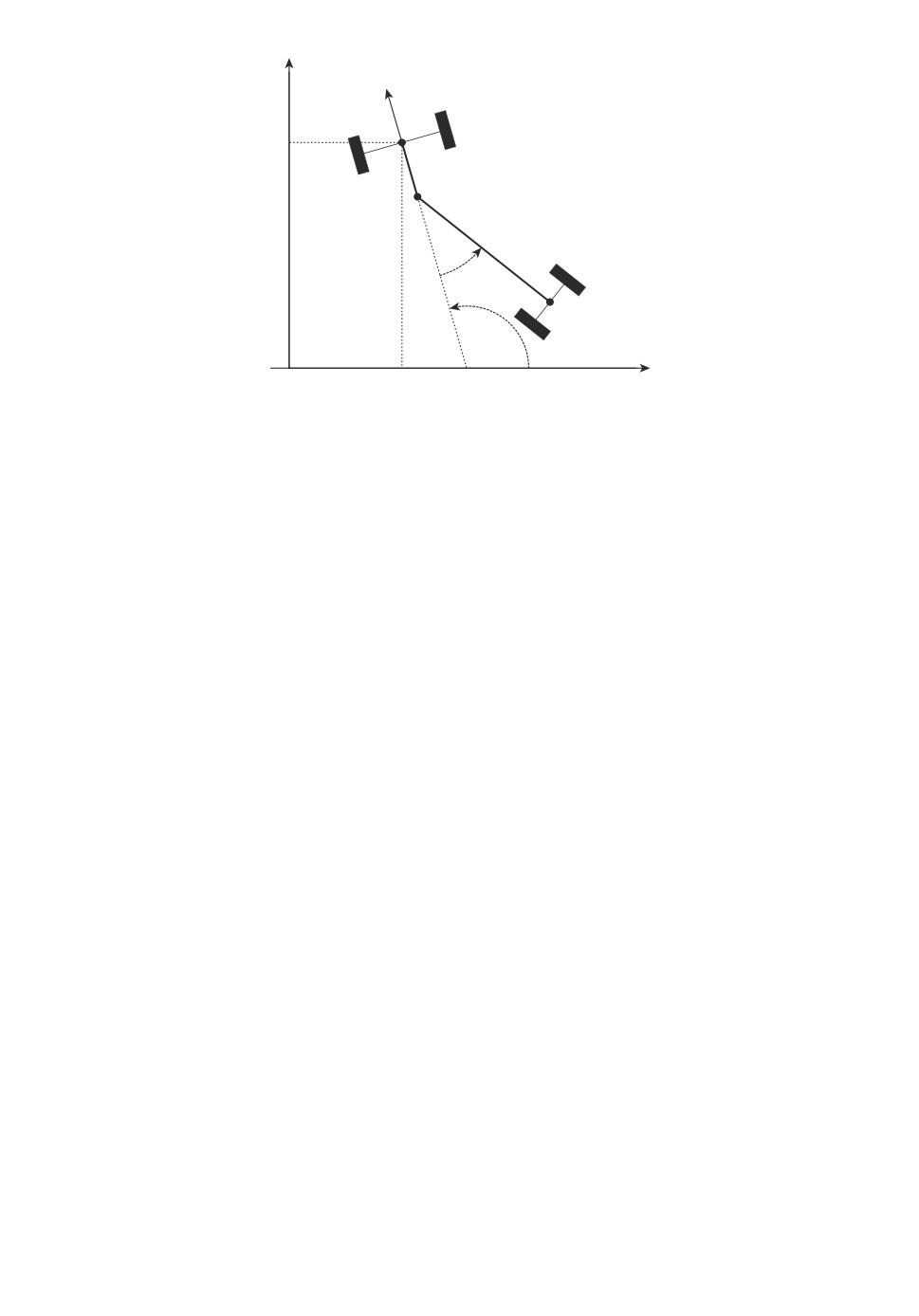
Рассмотрим мобильный колесный робот с прицепом, движущийся по го-
ризонтальной плоскости. Сила трения колес, масса и форма робота и при-
цепа в расчет не берутся. Под роботом будем понимать ведущую колесную
пару с центром в точке (x, y) ∈ R2x,y и углом θ ∈ S1θ, задающим направление
движения колес относительно оси абсцисс. Под прицепом понимается пассив-
ная колесная пара, которая сцепливается с ведущей в некоторой точке, см.
1 Исследование выполнено за счет гранта Российского научного фонда (проект № 17-
11-01387-П) в Институте программных систем им. А.К. Айламазяна РАН.
95
y
lr
lt
j
q
0
x
Рис. 1. Модель мобильного колесного робота с прицепом и ее параметры.
рис. 1. Положение прицепа определяется углом ϕ ∈ S1ϕ ориентации относи-
тельно робота. Таким образом, положение робота с прицепом задается точкой
q = (x,y,θ,ϕ) в пространстве M = R2x,y × S1θ × S1ϕ. Параметры lr ≥ 0, lt > lr
задают расстояния от точки сцепки до центра робота и до центра прицепа,
определяя конфигурацию сцепки робота с прицепом.
Кинематическая модель задается дифференциальной системой, возникаю-
щей, см. [1], из неголономного ограничения на движение без проскальзывания
колес робота и прицепа. В данной статье продолжается начатое в [2] изуче-
ние модели. Предлагается метод приближенного решения задачи управления
системой “робот с прицепом”, основанный на построении нильпотентной ап-
проксимации более простой системы, сохраняющей важные свойства ис-
ходной системы. Подобный метод применялся в [3] для управления системой
“робот с двумя прицепами”.
Рассматривается задача парковки робота с прицепом, формализуемая как
двухточечная граничная задача управления, см. [4], в пространстве состоя-
ний M. По заданным граничным условиям требуется найти удовлетворяю-
щую им траекторию q(t) ∈ M, t ∈ [0,t1], допустимую в смысле неголономных
ограничений (т.е. удовлетворяющую дифференциальной системе) и миними-
зирующую заданный функционал, определяющий взвешенную цену за угло-
вое и линейное перемещение робота.
Задача управления неголономными системами широко известна в робото-
технике [1]. Кинематические модели разнообразных мобильных роботов опи-
сываются управляемыми системами вида
∑
(1)
˙q = uiXi(q), q ∈ M, dimM = n ≥ k,
ui
∈ R,
i=1
где Xi гладкие векторные поля на многообразии M.
Решение задачи для систем (1) общего вида неизвестно. Удовлетворитель-
ное решение имеется лишь для систем специального вида. Одним из наиболее
эффективных считается дифференциально-геометрический подход [5, 6].
96
В [7, 8] исследовано использование тригонометрических управлений для
неголономных систем определенного рода: класс систем, которые могут быть
преобразованы в цепную форму. Благодаря специальной форме, существует
простое тригонометрическое управление, изменяющее определенный набор
координат, в то время как другие координаты остаются неизменными. В [9]
предложено использовать тригонометрические управления для перемещения
системы в целевое состояние одновременно по всем координатам для систем
с двумерным управлением. Кроме того, они показали, как для достижения
этой цели могут быть использованы полиномиальные управления. В [10] по-
казано, что кусочно-постоянные управления доставляют точное решение за-
дачи управления системами в цепной форме. Техника приведения системы
к цепной форме описана в [8, 11]. Заметим, что системы общего положения
и, в частности, систему, возникающую в рассматриваемой задаче управления
роботом с прицепом, нельзя привести к цепной форме, однако метод нильпо-
тентизации [12], описанный далее, порождает систему в цепной форме.
В исключительных случаях для управляемых систем можно найти точный
закон оптимального управления (в смысле минимума заданного функционала
качества). Одним из возможных подходов к решению задачи оптимального
управления системами, линейными по управлению, с фиксированным вре-
менем является метод, разработанный в [13]. Метод основан на разложении
функции управления в ряд Фурье и отбрасывании слагаемых выше некоторо-
го порядка N. Решение новой конечномерной задачи сходится к решению ис-
ходной задачи при N, стремящимся к бесконечности [13]. Найденное решение
называется близким к оптимальному. Задачу оптимального управления мож-
но также решать с помощью инвариантных геометрических методов [6, 14],
развитых при решении задач оптимального управления на группах Ли. Чис-
ленное решение для систем, моделирующих различные типы мобильных ро-
ботов на плоскости и в пространстве, предложено в [15].
Один из классов управляемых систем, допускающих точное решение, за-
дается нильпотентными системами. Напомним, что управляемая система яв-
ляется нильпотентной, если скобки Ли управляемых векторных полей обну-
ляются, начиная со скобок некоторой длины. Метод управления нильпотент-
ными системами был представлен в [16]. Он основан на возможности пере-
мещения в направлении произвольно заданной голономной кривой (априори
не удовлетворяющей неголономному ограничению (1)) на основе формулы
Кэмпбелла-Хаусдорфа-Бэйкера-Дынкина. Благодаря этому, становится воз-
можным вычисление допустимых кусочно-постоянных управлений, перево-
дящих неголономную систему точно в конечное состояние.
В [17] А. Беллаиш с соавторами разработали технику нильпотентизации,
которую впоследствии применили к задаче управления неголономными си-
стемами. В [18] показано, как перевести любую управляемую систему в кано-
ническую форму, соответствующую нильпотентной аппроксимирующей си-
стеме в специальной треугольной форме, позволяющей искать тригономет-
рические управления.
Представленное в данной статье решение задачи оптимального управле-
ния также опирается на нильпотентизацию исходной системы и основано на
построении итерационного процесса, на каждой итерации которого решает-
97
ся задача оптимального управления приближенной системой. Итоговый за-
кон управления формируется последовательным применением найденных на
каждой итерации управлений. Будем называть такое управление субопти-
мальным.
Статья имеет следующую структуру. В разделе 2 приводится постановка
задачи 1, а именно задачи оптимального управления роботом с прицепом без
фазовых ограничений. В разделе 3 при помощи алгоритма 1 устанавливается
связь между рассматриваемой задачей 1 и более простой задачей (опреде-
ляемой полиномиальной системой (10)), так называемой нильпотентной суб-
римановой задачей на группе Энгеля [19]1, которая доставляет нелинейную
аппроксимацию исходной задачи. В теореме описывается замена координат
между этими задачами. Для решения нильпотентной задачи используется ги-
бридный алгоритм 2. Приводится сравнение известных оптимальных реше-
ний с найденными субоптимальными траекториями для близких граничных
точек. В разделе 4 уточняется, как построить субоптимальное решение зада-
чи 1 (без фазовых ограничений) в ситуации общего положения (для далеких
граничных точек) с помощью алгоритма 3. Раздел 5 посвящен программной
реализации представленных алгоритмов. Ставится задача 2 (с ограничени-
ем на угол поворота прицепа), а также приводятся несколько примеров ее
решения с помощью модифицированного алгоритма 3. В разделе 6 рассмат-
ривается частный случай задачи с ограничением перепарковка прицепа.
Для решения этой задачи разработан специализированный алгоритм, проте-
стированный на регулярной сетке значений для угла прицепа и соотноше-
ния длин плеч робота lr, lt. Результаты тестирования приведены в таблице.
В Приложение вынесены определения основных терминов, используемых в
работе.
2. Постановка задачи оптимального управления
Задача 1 (без ограничений). Задана управляемая система
(
)
(
)
(2)
˙q=u1X1q
+u2X2
q
,
(3)
q = (x,y,θ,ϕ) ∈ M = R2x,y × S1θ × S1ϕ, (u1,u2) ∈ R2.
Здесь q, x, y, θ, ϕ, u1, u2 по умолчанию зависят от параметра времени
t ∈ [0,t1]; управления u1, u2
вещественнозначные кусочно-непрерывные
функции, задающие линейную и угловую скорость движения робота с цен-
тром в точке (x, y); а векторные поля при управлениях имеют следующий
вид:
(
)
sin ϕ
X1(q) = cos θ,sinθ,0,-
,
lt
(4)
(
)
lr cosϕ
X2(q) =
0, 0, 1, -
-1
lt
1 Правила умножения на группе приведены в [20], см. главу 15.
98
Для некоторого заданного µ > 0 требуется найти кривую q(t), t ∈ [0, t1], с
заданными граничными значениями в двух точках
(
)
(
)
(5)
q(0) = q0 =
x0,y0,θ0,ϕ0
,
q(t1) = q1 =
x1,y1,θ1,ϕ1
,
удовлетворяющую системе (2)-(5) и имеющую минимальное значение функ-
ционала
∫t1
√
(6)
J =
u21(t) + µ2u22
(t) dt,
0
где коэффициент µ задает компромисс между линейным и угловым переме-
щением.
Замечание 1. Система (2)-(4) имеет следующую симметрию (растяже-
ние):
(
)
(
)
δµ :
x,y,θ,ϕ,lt,lr,u1,u2
→
µx,µy,θ,ϕ,µlt,µlr,µu1,u2
Поэтому минимизация (6) равносильна минимизации субримановой дли-
ны [21]
t1
∫
√
(7)
u21(t) + u22
(t) dt
0
с пересчитанными граничными значениями и параметрами сцепки робота и
прицепа.
Замечание 2. Инвариантность задачи 1 относительно параллельных
переносов и поворотов в плоскости R2xy позволяет без ограничения общно-
сти фиксировать q0 = (0, 0, 0, ϕ0).
Вычислим следующие коммутаторы (скобки Ли):
(
)
lr + lt cos ϕ
X3(q) = [X1,X2](q) = sin θ,- cos θ,0,-
,
l2
t
(
)
[
]
lt + lr cos ϕ
X4(q) =
X1,[X1,X2]
(q) =
0, 0, 0, -
l3
t
Из теоремы Рашевского-Чжоу [14] следует, что система (2)-(5) вполне управ-
ляема, так как в силу начального допущения lt > lr ≥ 0 выполнено условие
lt + lr cosϕ
(8)
det(X1, X2, X3, X4) = -
= 0.
l3
t
Задача 1 соответствует двухпараметрическому семейству субримановых
задач, а именно задач оптимального управления с линейной по управлению
системой (2), где в качестве критерия оптимальности выступает минимум
субримановой длины (7). Решение любой такой задачи с определенными зна-
чениями параметров lr, lt является открытой проблемой. Цель данной ра-
боты разработать общую схему построения приближенного решения для
всего семейства задач.
99
3. Решение локальной задачи
Локальное приближение управляемой системы другой, более простой си-
стемой широко используется в теории управления. Обычно в качестве ло-
кальной аппроксимации используется линеаризация управляемой системы.
Однако для линейных по управлению систем (2) линеаризация дает слишком
грубое приближение. Так как размерность управления меньше размерности
состояния, то линеаризация не может быть вполне управляемой. Это следует
из теоремы Рашевского-Чжоу [14].
В случае (2)-(4) линеаризация имеет вид
˙q = u1X01(q) + u2X02(q),
(
)
sin ϕ0
X01(q) =
1, 0, 0, -
,
lt
(
)
lr cos ϕ0
X02(q) =
0, 0, 1, -1 -
lt
Легко проверить, что [X01, X02](q) = (0, 0, 0, 0), поэтому линеаризация неуправ-
ляема.
Естественную замену линейной аппроксимации в этом случае доставляет
нильпотентная аппроксимация наиболее простая система, сохраняющая
свойство полной управляемости. Для системы (2)-(3) она задается управляе-
мой системой вида
(9)
q = u1 X1(q) + u2 X2(q),
q∈ R4, (u1,u2) ∈ R2,
X2
гдеX1,
векторные поля приближающей системы, см. подробнее в При-
ложении.
Нильпотентная аппроксимация строится по системе (2), записанной в при-
вилегированных координатах (см. определение 6 в Приложении), таким обра-
зом, что векторные поля
Xi аппроксимирующей системы определяют ниль-
потентную алгебру Ли, т.е. для некоторого N ∈ N выполнено
[
[
]]
Xi
,
Xi
,...,[Xi
,
Xi
], . . .
= 0, ∀i1, . . . , iN+1 ∈ {1, 2}.
1
2
N
N+1
В частности, для системы (2)-(4) обнуляются коммутаторы выше 3 порядка
(N = 3):
[
[
]]
Xi,
Xj,[X1,X2]
= 0,
∀i, j ∈ {1, 2}.
Замечание 3. В отличие от линейной аппроксимации нильпотентная
аппроксимация сохраняет такой важный инвариант, как вектор роста, см.
определение 1 в Приложении. Для системы (2)-(3) общего положения в точ-
ке общего положения вектор роста равен (2, 3, 4), т.е. векторные поля X1, X2,
X3 = [X1,X2], X4 = [X1,X3] (либо X4 = [X2,X3]) формируют базис касатель-
ного пространства TqM в каждой точке q ∈ M. В частности, это выполнено
для системы “робот с прицепом” (2)-(4).
100
Понятие нильпотентной аппроксимации управляемых систем было впер-
вые введено Ж. Стефани [22] и независимо развито А.А. Аграчевым, А.В. Са-
рычевым [23] и Х. Хермсом [24]. В данной работе использован алгоритм вы-
числения нильпотентной аппроксимации, предложенный А. Беллаишем [25],
конкретизированный для систем (2)-(3) и дополненный переходом в систе-
му координат, в которой нильпотентная аппроксимация имеет канонический
вид (10).
Замечание 4. Касательное пространство к субриманову многообразию
само является субримановым многообразием. Его можно определить как мет-
рическое пространство, используя определение Громова [26]. Более того, оно
имеет алгебраическую структуру нильпотентной группы Ли. Ключевое на-
блюдение состоит в том, что структура TqM похожа на структуру веще-
ственного векторного пространства, только группа является не абелевой, а
нильпотентной.
3.1. Вычисление нильпотентной аппроксимации
Предложенный А. Беллаишем [25] способ построения нильпотентной ап-
проксимации в привилегированных координатах конкретизируется для си-
стем с вектором роста (2, 3, 4) в следующем алгоритме 1. В нем получено
явное выражение векторных полей аппроксимирующей системы в канони-
ческих привилегированных координатах, позволяющих искать оптимальное
управление для нильпотентной аппроксимации.
Алгоритм 1. Замена координат τ = Φ ◦ A, приводящая систему (2)-(3)
к каноническому виду, строится следующим образом:
1. Через исходные координаты q вычисляются привилегированные коор-
динаты q:
)
1(
(
)2
(
)2
A : q= g(q) -
0, 0, 0, σ1
g1(q)
+ 2σ2g1(q)g2(q) + σ3
g2(q)
,
2
где g(q) = (g1(q), . . . , g4(q)) = Γ-1(q - q0), а Γ
это 4 × 4 матрица, со-
ставленная из элементов Γij, определяемых соотношением Xj (q0) =
∑4
∂
=
Γij
|q0 , при этом коэффициенты σi вычисляются по форму-
i=1
∂qi
лам
(
)
(
)
(
)
σ1 = X1
X1(g4)
(q0), σ2 = X1
X2(g4)
(q0), σ3 = X2
X2(g4)
(q0).
При такой замене q0 переходит в начало координат 0 = (0, 0, 0, 0), а век-
торные поля Xi переходят в поля
Xi = A∗Xi, формирующие привиле-
гированный базис.
2. С использованием разложения векторных полейXi(q) в ряд Маклорена
строится нильпотентная аппроксимация в координатах q:
q =u1 X1(q) + u2 X2(q),
q∈ R4, (u1,u2) ∈ R2,
∑
∂ X3i
Xi =X1i(0)∂q1 +X2i(0)∂q2 +
(0) qk∂q3 +
∂qk
k=1
(
)
2
∑
∂ X4i
1
∂2 X4i
∂2 X4i
+
(0)q3 +
(0)q2k +
(0)q1 q2
∂q4 .
∂q3
2
∂q2k
∂q1∂q2
k=1
101
3. Вычисляется замена переменных Φ : q → q : q = eT4 X4 ◦ · · · ◦ eT1 X1 (0),
где параметры Ti ≥ 0 находятся из условия q = eT4 X4 ◦ · · · ◦ eT1 X1 (0), для
перехода от привилегированных координат q в координаты q, в которых
нильпотентная аппроксимация имеет канонический вид:
q1 = u1,
q2 = u2,
(10)
1
q∈R4,
q3 =
(q1u2 - q2u1),
2
˙q4 =1(q21 + q22)u2,
2
т.е. векторные поля
X1,
X2 имеют вид
(
)
(
q2
q1 )
q21 + q22
X1 = 1, 0, -
,
,
X2 =
0, 1, 0,
2
2
2
Теорема. Для системы (2)-(4) отображение τ имеет вид
1
q1 = x,
q2 = θ,
q3 =
xθ-y,
2
(
((
)
(
)
(
)
(
))
q4 = lt
l2r + 2
θ3 + 6θ x
x-lr
+6y
2lr - x
- 12l2t
ϕ-ϕ0 +θ
+
(
)
(
)
+ sin(ϕ0) -3x
l2rθ2 + 4l2t
- 6lrl2tθ2 + x3
+
(
((
)
(
)
)
(
))
(11)
+ cos(ϕ0) lrθ
l2r + 2
θ2 + 2l2t
θ2 - 6
+ 9x2
+ 12y
l2t - lrx
(
)
+ 3lt cos(2ϕ0) l2rθ3 + 2lrθx - 2xy
+
(
)
(
)
(
)
+ 3lt sin(2ϕ0) -l2rθ2 + lrθ
θx + 2y
+x2
- xsin(3ϕ0) x2 - 3l2rθ2
+
)
(
))∕(
(
)
+ lrθ cos(3ϕ0) l2rθ2 - 3x2
12
lr cos(ϕ0) + lt
Доказательство. Вычислим коммутаторы
(
)
(
)
lr + lt cos ϕ
lt + lr cosϕ
X3 = sin θ,- cosθ,0,-
,
X4 =
0, 0, 0, -
l2t
l3
t
Заметим, что в силу (8) система векторных полей
Xi образуют в каждой
точке базис. Вычислим коэффициенты σi:
0
lt cos ϕ0 sin ϕ
lrlt sin2 ϕ0
σ1 = -
,
σ2 =
,
σ3 = lrlt sin ϕ0.
lt + lr cos ϕ0
lt + lr cos ϕ0
Известно [28], что любые две нильпотентные системы с вектором роста
(2, 3, 4) диффеоморфны. Замена переменных, переводящая одну такую си-
стему в другую, строится следующим образом. Пусть
X1,X2
векторные
102
поля первой, а
X1,X2
векторные поля второй нильпотентной системы с
вектором роста (2, 3, 4). Вычислив коммутаторы
X3,X4 и
X3,X4, можно по-
строить диффеоморфизм, переводящий поля
Xi в окрестности точки q0 в
поляXi в окрестности q0:
Φ:O(q0)→O(q0), Φ∗
Xi) =Xi.
Определим отображения F и G как композицию потоков векторных полей
Xi и
Xi соответственно за время Ti:
F (T1, . . . , T4) = eT4 X4 ◦ · · · ◦ eT1 X1 (q0),
G(T1, . . . , T4) = eT4 X4 ◦ · · · ◦ eT1 X1 (q0).
Тогда искомый диффеоморфизм имеет вид Φ = G ◦ F-1.
Применим пункты 2) и 3) алгоритма 1 к точке q0 = (0, 0, 0, ϕ0). Прямые
вычисления и элементарные упрощения приводят к замене переменных (11)
для перехода в канонические привилегированные координаты.
3.2. Поиск корней для нильпотентной задачи
Алгоритм 1 позволяет отыскать приближенное решение задачи 1 как ре-
шение нильпотентной субримановой задачи на группе Энгеля, заданной зада-
чей оптимального управления дифференциальной системой (10) с критерием
качества минимумом функционала субримановой длины (7). Эта задача
активно исследуется в последние годы [19, 29-32], ее оптимальный синтез
описан в [30]. В общем случае задача сведена к решению четырехмерной си-
стемы алгебраических уравнений в эллиптических функциях Якоби sn, cn, dn
и эллиптических интегралах I и II рода (F и E). Левая часть этой системы
определяется из параметризации экстремальных траекторий, заданной с по-
мощью так называемого экспоненциального отображения
Exp(u1,u2,k,α) =
(
)
=
q1(u1,u2,k,α),
q2(u1,u2,k,α),q3(u1,u2,k,α),q4(u1,u2,k,α)
Явные выражения вычисляются непосредственно из формул, приведенных
в [19]. Правая часть системы определяется конечной точкой
q(t1) = q1 =
= (q11, q12, q13, q14). Кроме того, имеющаяся в задаче симметрия растяжения по
параметру α позволяет избавиться от него и редуцировать систему до трех-
мерной. В результате для решения задачи в общем случае q11 q13 = 0 необходи-
мо решить трехмерную систему следующего вида:
q2(u1,u2,k,1)
q12
=
,
q1(u1,u2,k,1)
q1
1
q3(u1,u2,k,1)
q13
(
)2 =
,
(12)
(q11)2
q1(u1,u2,k,1)
q4(u1,u2,k,1)
q14
(
)3 =
q1(u1,u2,k,1)
(q11)3
103
При этом искомый вектор (u1, u2, k) единственен и лежит в некотором под-
множестве ограниченного множества (0, π) × (0, 2π) × (0, 1). Соответствую-
щие подмножества подробно описаны в [30]. Для поиска корня (u1, u2, k) си-
стемы (12) с фиксированной правой частью использовались различные из-
вестные численные методы, такие как метод Ньютона и метод хорд. Так как
система (12) задается неэлементарными функциями, то для сходимости стан-
дартных методов необходимы начальные приближения, близкие к искомому
корню. Использование стохастических методов в комбинации с мультистар-
том не дает требуемого эффекта. Поэтому для приближенного решения си-
стемы (12) разработан следующий алгоритм.
Алгоритм 2 (гибридный). Рассматривается система алгебраических
уравнений Q(ν) = Q1, имеющая единственное решение ν ∈ Ω ⊂ Rn при каж-
дом значении Q1 ∈ Ξ ⊂ Rn. Гибридный алгоритм численного поиска решения
с некоторой точностью ǫe > 0 и некоторыми константами m1, m2 ∈ N состоит
из следующих шагов:
1. Задаются множества Ωj ⊂ Ω, j = 0, 1, каждое из которых состоит из
дискретного набора случайных точек νji , i = 1, . . . , m1.
2. Из каждого множества Ωj, j = 0, 1, выбирается точка, имеющая наи-
меньшую невязку de(ν) = (Q(ν) - Q1)w(Q(ν) - Q1)T , где w ∈ Rn×n
матрица весовых коэффициентов. Обозначим соответствующие точки:
νj = arg min
de(νji).
νj∈Ωj
i
3. На выбранных точках ν0, ν1 запускается метод хорд [33] для решения
системы Q(ν) = Q1. Результатом вычисления является точка ν2.
4. Для i = 1, . . . , m2 - 1 итеративно запускается метод Ньютона [33] для
модифицированной системы Q(ν) =Q1+(m2-i)Q(νi+1)m
с начальным при-
2-i+1
ближением ν = νi+1. Результатом является точка νi+2, которая подается
в качестве начального приближения для следующей итерации. После
выполнения m2 - 1 итераций получается точка νm2+1. Если при этом
соответствующая невязка достаточно мала de(νm2+1) < ǫe, то искомый
корень найден: ν = νm2+1 является приближенным решением исходной
системы Q(ν) = Q1. Иначе перейдем к п. 1) алгоритма и повторим все
шаги заново, пока нужная точность не будет достигнута.
Замечание 5. Алгоритм 2 был реализован в программной системе Wol-
fram Mathematica для решения системы уравнений (12), п(и этом выбр)
на диагональная матрица весовых коэффициентов w = diag
q11,(q11)2,(q11)3
Программа находит вектор ν = (u1, u2, k). При этом возможны два общих
случая ν ∈ N1 ∪ N2, которые определяют формулы для оптимального управ-
ления и соответствующей кривой q(t) [19].
3.3. Построение управления для исходной задачи
Итак, предложен алгоритм 1, который позволяет локально свести задачу 1
к нильпотентной субримановой задаче на группе Энгеля. Чтобы построить
оптимальное управление в нильпотентной задаче в общем случае использу-
ется алгоритм 2 для решения системы алгебраических уравнений (12). Полу-
104
ченный корень ν = (u1, u2, k) ∈ Nc, c ∈ {1, 2}, определяет искомое управление
следующим образом:
• вычисляются параметры p1 = F (u1, k), p2 = F (u2, k) и
α =q1(u1,u2,k,1)|q1(u1,u2,k,1)|
, где F - нормальный эллиптический интеграл
q11|q11|
Лежандра I рода; параметр k задает модуль эллиптического интеграла;
• параметры t1, φ0 определяются с помощью выражений [19]
2p1
p2 - p1
c=1
⇒ t1=
√
, φ0 =
√
,
|α|
|α|
2kp1
k(p2 - p1)
c=2
⇒ t1=
√
, φ0 =
√
;
|α|
|α|
• оптимальное управление определяется следующими формулами:
)
2k sign α
(√
(√
)
u1 = -
sn
|α|(φ0 + t), k dn
|α|(φ0 + t), k
,
c=1
⇒
µ
(
(√
))
u2 = -sign α 1 - 2dn2
|α|(φ0 + t), k
;
(√
)
(√
)
(13)
2sign α
|α|(φ0 + t)
|α|(φ0 + t)
u1 = ∓
sn
,k cn
,k
,
µ
k
k
c=2
⇒
(
(√
))
|α|(φ0 + t)
u2 = -sign α
1 - 2cn2
,k
,
k
где функции sn, cn и dn суть эллиптический синус, эллиптический косинус
и дельта амплитуда.
3.4. Сравнение с оптимальными решениями
Задача 1 в общем случае не решена, однако известны оптимальные
(в смысле минимума функционала (7)) управления для парковки робота
(без прицепа), см. [34-36]. Соответствующая субриманова задача вкладывает-
ся в задачу 1: взяв оптимальные управления (u1(t), u2(t)), t ∈ [0, t1] для робо-
та (без прицепа) и подставив их в систему (2), можно ее численно проинтегри-
ровать при фиксированных значениях ϕ0, lr, lt и получить траекторию q(t),
t ∈ [0,t1], приходящую в точку q1 = q(t1). Заметим, что эта траектория будет
оптимальна в задаче 1 при µ = 1.
Этот класс оптимальных траекторий был использован для сравнения с
найденными в данной работе субоптимальными траекториями, построенны-
ми методом нильпотентной аппроксимации. Для этого получившиеся значе-
ния q1 = (x1, y1, θ1, ϕ1) подставлялись в формулу (11) для вычисления конеч-
ной точки q1 в нильпотентной задаче. С использованием алгоритма 2 нахо-
дились соответствующие значения корня ν, определяющего искомое управле-
ние по формулам (13). Наконец интегрированием системы (2) с полученным
управлением вычислялось субоптимальное решение для задачи 1.
Для сравнения полученных решений введем следующую меру близости
между конечной точкой и точкой на найденной субоптимальной траектории:
105
(
)
((
)2
(
)2
(
)2
d
q(t), q1
:=
x(t) - x1
+
y(t) - y1
+
θ(t) - θ1
+
)
(
)2
1
θ(t) - θ
ϕ(t) - ϕ1
+
ϕ(t) - ϕ1
+ 4l2r sin2
+ 4l2t sin2
2
2
Дополнительно будем выбирать конечное время T на субоптимальной траек-
тории
(
)
(14)
T = argmind
q(t), q1
t
Замечание 6. При выборе натуральной параметризации u21 + u22 ≡ 1
при µ = 1 имеем J = t1 для оптимального решения и J = T для субопти-
мального.
-0,2
0,2
0,4
q
y -0,9
-0,6
-0,3
-0,4
x
-0,15
-0,30
-0,8
-0,45
-1,2
j
(
)
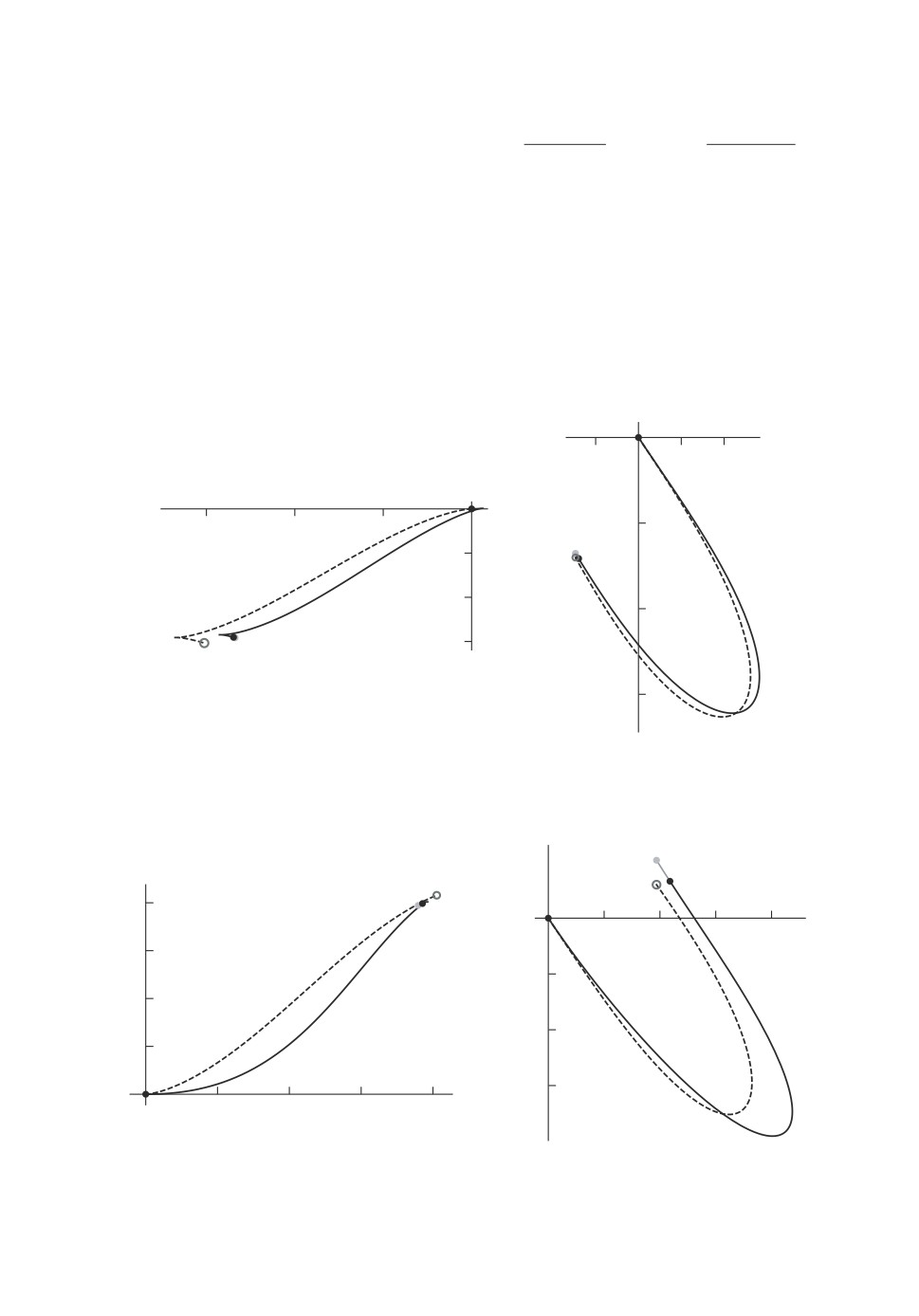
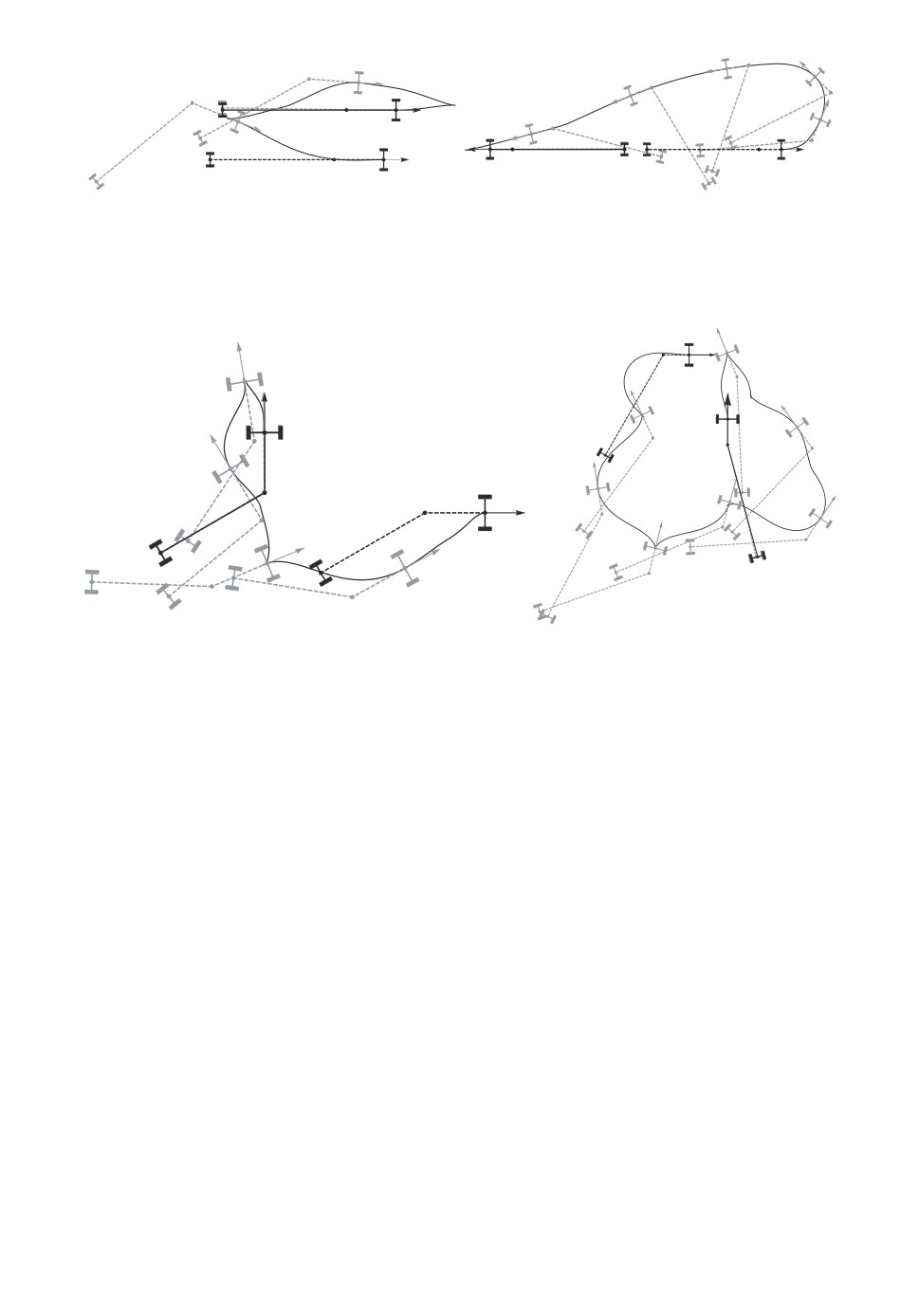
Рис. 2. q1 = (-0,90724; -0,45537; -0,29433; -0,5608), точность d
q(T ), q1
=
= 0,1025, для оптимального решения J = 2 (для субоптимального J =
= 1,975927).
y
0,8
0,2
0,4
0,6
0,8 q
0,6
-0,2
0,4
-0,4
0,2
-0,6
0,3
0,6
0,9
1,2 x
j
(
)
Рис. 3. q1 = (1,21571; 0,831468; 0,387799; 0,119918), точность d
q(T ), q1
=
= 0,08905, для оптимального решения J = 2 (для субоптимального J =
= 2,10794).
106
y
j
2,5
1,5
2,0
1,0
1,5
1,0
0,5
0,5
-0,3
0,3
0,6
0,9 x
-1,5
-1,0
-0,5
q
(
)
Рис. 4. q1 = (-0,18761; 1,74623; -0,178081; 2,12067), точность d
q(T ), q1
=
= 0,50614, для оптимального решения J = 4 (для субоптимального J =
= 3,51347).
На рис. 2-4 приведено сравнение найденных траекторий: пунктирной ли-
нией обозначено оптимальное решение, сплошной линией субоптимальное,
серая окружность малого размера задает конечную точку q1, серая точка
соответствует исходной конечной точке на субоптимальном решении, черная
точка есть q(T ), вычисленное по формуле (14). Рисунки 2, 3 с малым вре-
менем t1 = 2 показывают достаточно близкое соответствие между оптималь-
ным и субоптимальным решением, однако как видно из рис. 4 при достаточ-
но большом t1 такое соответствие нарушается. Поэтому возникает необходи-
мость в создании алгоритма глобального решения.
4. Общая схема решения: сведение к серии локальных задач
На основе алгоритма 1, приближенно решающего задачу 1 локально, раз-
работан глобальный алгоритм для общего случая далеких граничных точек
q0, q1.
Алгоритм 3. Рассмотрим задачу управления (2)-(5), в которой условие
попадания траектории q(t) в конечную точку q(t1) = q1 заменено на условие
(
)
попадания в некоторую ǫ-окрестность точки q1, т.е. d
q(t1), q1
< ǫ.
Пусть m3 ∈ N некоторая константа, тогда субоптимальное управление
рассматриваемой задачи строится следующим образом.
1. Воспользуемся алгоритмом 1 и вычислим точку q1 с помощью форму-
лы (11) для q = q1. С помощью алгоритма 2 находим корень ν1 систе-
мы (12) и по формулам (13) строим управление. Далее, подставив его
в систему (2)-(5) и проинтегрировав полученные выражения численно,
получаем траекторию q0(t), t ∈ [0, t01] с начальным условием q0(0) = q0.
(
)
2. Если расстояние d0 = d
q0(t01),q1
< ǫ, то траектория q0(t), t ∈ [0,t01], до-
ставляет приближенное решение с требуемой точностью. Иначе отрезок
[0, t01] делится на m3 одинаковых частей. После чего последовательно за-
107
j
y
2,5
1,5
2,0
1,0
1,5
1,0
0,5
0,5
-0,3
0,3 x
-1,5
-1,0
-0,5
q
(
)
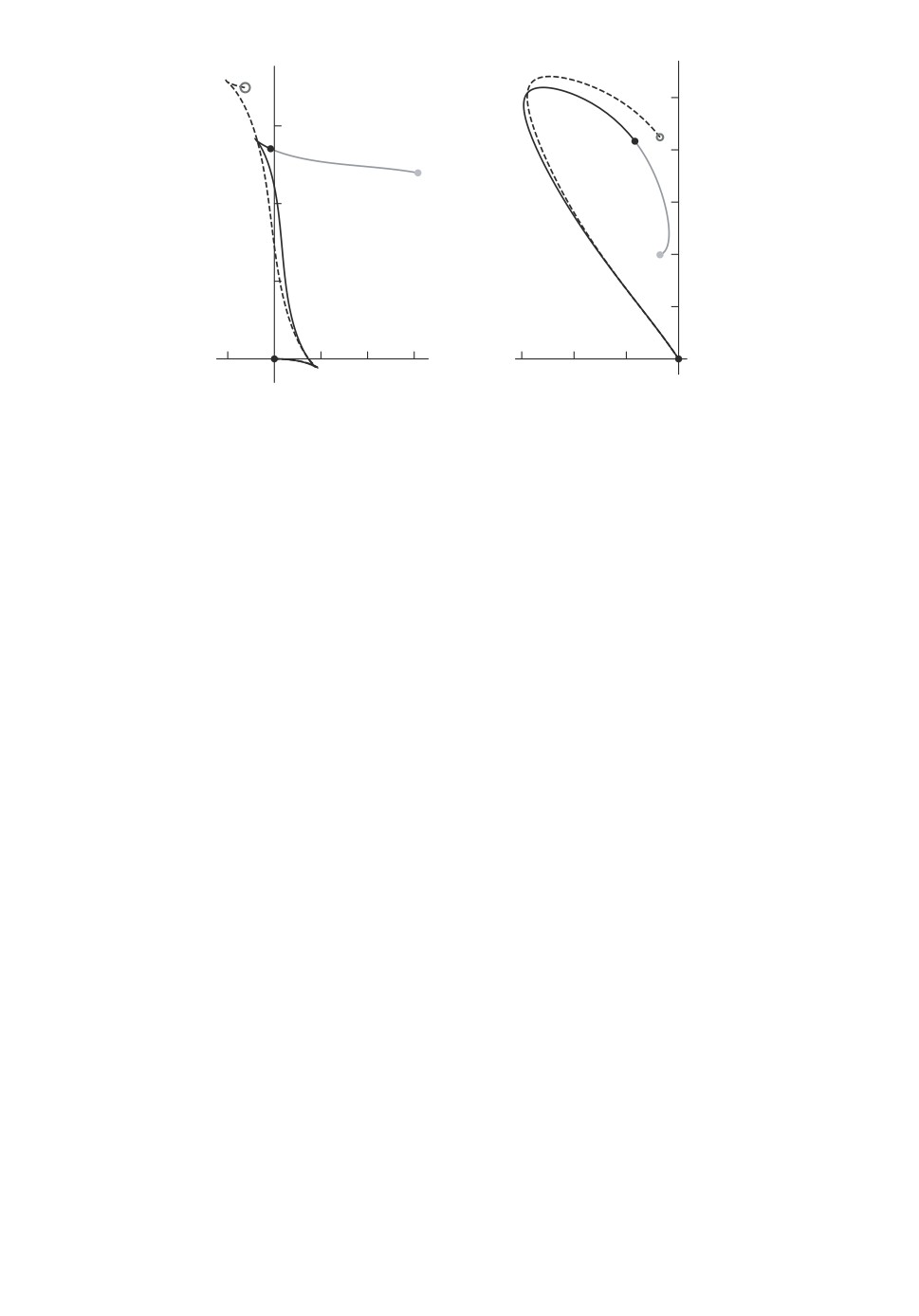
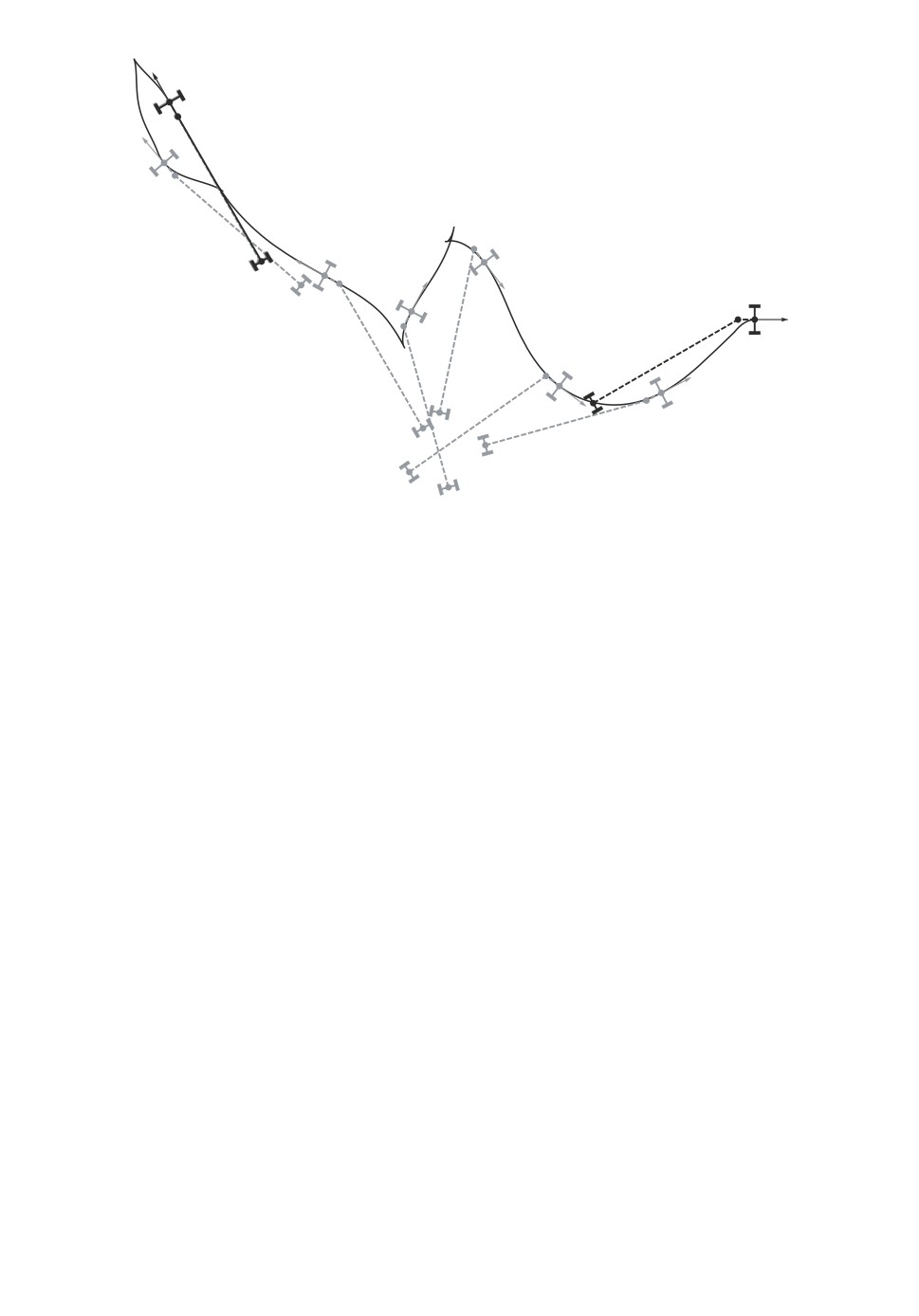
Рис. 5. q1 = (-0,18761; 1,74623; -0,178081; 2,12067), точность d
q(t1), q1
=
= 0,02739, для оптимального решения J = 4 (для субоптимального J =
= 3,9688).
(
)
it01
пускается вычисление нильпотентных аппроксимаций в точках q0
,
m3
i = 1,...,m3, как это сделано в первом пункте для точки q0. Обозна-
чим соответствующие траектории через qi(t), t ∈ [0, ti1], для которых вы-
(
)
it01
полнено начальное условие qi(0) = q0
, и соответствующие расстоя-
m3
(
)
ния через di = d
qi(ti1),q1
. Затем выбирается номер j = arg min di и
i=0...m3
процедура, описанная в данном пункте, применяется уже для траекто-
рии qj(t), t ∈ [0, tj1].
На рис. 5 приведен пример улучшения решения с помощью алгоритма 3,
черная точка на траектории соответствует некоторой промежуточной точ-
ке qi(0), в которой была вычислена дополнительная аппроксимация. Как вид-
но из рисунка, в этом случае достаточно одной дополнительной итерации,
чтобы получить приемлемую близость оптимального и субоптимального ре-
шений.
5. Программная реализация и примеры работы алгоритма для парковки
В среде Wolfram Mathematica разработаны программы построения суб-
оптимального управления для приближенного решения задачи 1 на основе
нильпотентной аппроксимации. Программы по входным данным lr, lt, ϕ0, x1,
y1, θ1, ϕ1, ǫ строят функции управления u1, u2 и соответствующую траекто-
рию движения робота с прицепом q(t), выходящую из точки q0 = (0, 0, 0, ϕ0)
и приходящую в ǫ-окрестность точки q1 = (x1, y1, θ1, ϕ1).
Программа парковки была протестирована для различных конфигураций
робота 0 ≤ lr < lt. В результате тестирования оказалось, что для большин-
ства тестов программа строит управление, при котором имеет место эффект
складного ножа (от англ. jackknifing [37]), означающий столкновение робота с
прицепом. На практике такие решения не допустимы, поэтому дополнительно
108
Рис. 6. Пример парковки. Слев(: (lt, lr) ) (10, 4), x1 = 1, y1 = 4, θ1 = ϕ1 = ϕ0 =
= 0, ϕmax = π/2 c µ = 0,15 и d
q(t1), q1
= 0,061644. Справа: (lt, lr) = (10, 2),
(
)
x1 = -26, θ1 = π, y1 = ϕ1 = ϕ0 = 0, ϕmax = 3π/4 c µ = 0,05 и d
q(t1), q1
=
= 0,0264575.
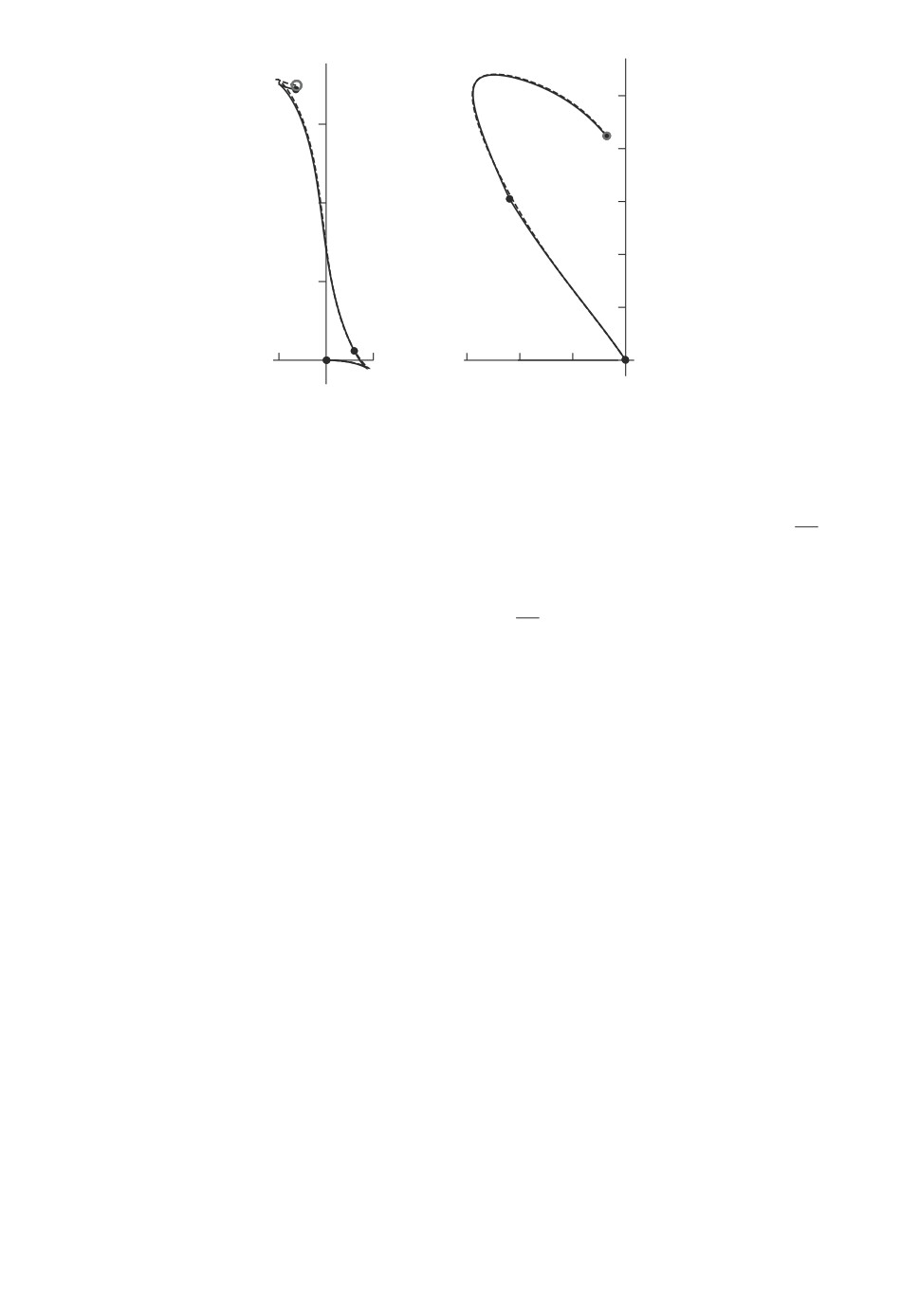
Рис. 7. Пример парковки. Слева: (lt, lr) = (6, 3(, x1 = -)11, y1 = 4, θ1 = π/2,
ϕ1 = -π/3, ϕ0 = π/6, ϕmax = 3π/4 c µ = 0,5 и d
q(t1), q1
= 0,057446. Справа:
(lt, lr) = (9, 2( x1 = 3,)y1 = -5, θ1 = π/2, ϕ1 = π/12, ϕ0 = π/3, ϕmax = 3π/4 c
µ = 0,512 и d
q(t1), q1
= 0,046904.
была рассмотрена следующая задача, учитывающая естественное ограниче-
ние на угол поворота прицепа.
Задача 2 (с ограничениями). Дана система “робот с прицепом” (2)-(4).
Задано следующее ограничение на угол поворота прицепа:
(15)
|ϕ(t)| ≤ ϕmax
< π.
(
)
Требуется найти кривую q(t) =
x(t), y(t), θ(t), ϕ(t)
, удовлетворяющую гра-
ничным условиям (5) и минимизирующую функционал качества (6).
Для решения задачи 2 использовалась естественная модификация алго-
ритма 3, в которой соответствующие траектории qi(t), i = 0, 1, . . . , строятся
на урезанном интервале t ∈ [0, ti1], ti1 ≤ ti1, на котором выполнено условие (15).
В программной реализации параметр µ считается свободн (м, его з)ачение
подбирается в начале работы программы так, что невязка d
q0(t01),q1
имеет
наименьшее значение. На рис. 6-8 представлено несколько примеров пар-
ковки с помощью разработанной программы. Черным пунктиром обозначено
начальное положение робота; требуемое конечное положение обозначено чер-
ным сплошным цветом; черная линия соответствует траектории движения
109
Рис. 8. Пример парковки: (lt, lr) = ((0, 1), x1 )= -35, y1 = 13, θ1 = 2π/3, ϕ1 = 0,
ϕ0 = π/6, ϕmax = 3π/4 c µ = 0,5 и d
q(t1), q1
= 0,042426.
робота, построенной с помощью программы; серым пунктиром обозначены
некоторые промежуточные состояния робота с прицепом вдоль построенной
траектории (в том числе конечное состояние). Отметим, что задача 1 до сих
пор остается открытой, а существующие методы решения задачи управле-
ния (2)-(5) не учитывают критерий оптимальности (6). Сравнение найден-
ных траекторий парковки с траекториями, полученными другими методами,
требует отдельного исследования. Известные методы решения [37, 38] зада-
чи управления (2)-(5) нацелены в основном на учет фазовых ограничений
в плоскости (x, y), которые зачастую и определяют искомую траекторию.
А именно, в плоскости (x, y) ищется так называемая голономная траекто-
рия, соединяющая граничные значения (5) без учета неголономных ограни-
чений, представленных дифференциальной системой (2). Затем на постро-
енной голономной траектории выделяется набор промежуточных значений
и с помощью различных локальных методов ищется неголономная траекто-
рия, соединяющая близкие друг к другу промежуточные значения. В си-
туации общего положения такой подход приводит к решению с большой
величиной маневра.
Далее рассматривается частный случай задачи 2, в котором начальное и
конечное положение робота совпадают.
6. Тестирование алгоритма перепарковки прицепа
На основе общего алгоритма парковки был разработан специальный алго-
ритм для перепарковки прицепа, т.е. для случая парковки с условием x1 =
= y1 = θ1 = 0. Конечная точка для нильпотентной аппроксимации перепар-
110
ковки в каноническом виде вычисляется по формуле
(
)
l3t(ϕ1 - ϕ0)
q1 =
0, 0, 0,
lt + lr cos ϕ1
Этот случай интересен тем, что для нильпотентной задачи в каждую точ-
ку такого вида приходит однопараметрическое семейство оптимальных тра-
екторий (в отличие от ситуации общего положения, в котором существует
лишь единственное оптимальное решение) эластик, имеющих форму вось-
мерки (лемнискаты Бернулли). Вместе с вариацией по параметру µ в этом
случае имеется двухпараметрическое семейство нильпотентных аппроксима-
ций, среди которых возможно отыскать то решение, которое переводит ис-
ходную систему из начального положения в конечное достаточно точно и
которое удовлетворяет фазовому ограничению (15). Решение такой задачи с
помощью алгоритма 3 находится в виде траектории q0(t) без рассмотрения
траекторий qi(t), i = 1, . . . , m3.
Заметим, что выбор масштаба позволяет без ограничения общности за-
фиксировать значение lt > 0 произвольным образом.
В программной системе Wolfram Mathematica разработана программа,
к(торая с)троит решение задачи перепарковки q(t), t ∈ [0, t1] с точностью
d
q(t1), q1
< 1/10 и дополнительным условием на максимальный угол при-
цепа
max |ϕ(t)| - ϕmax < 1/10.
t∈[0,t1]
Программа для поиска подходящего решения использует стандартные функ-
ции программной системы ParametricNDSolveValue и FindMinimum.
Рассмотрен следующий набор тестов. Пусть lt = 10, а lr = 0,12 , 1,32 , . . . , 5.
Зададим максимальный угол ϕmax = 3π/4, а также сетку для угла прицепа
ϕ0,ϕ1 ∈ Φ = {πi/12 | i ∈ {-6,... ,6}} ,
ϕ0 = ϕ1.
Обозначим траекторию, которую строит программа по параметрам lr, ϕ0, ϕ1,
через
q(lr,ϕ0,ϕ1)(t), t ∈ [0,t1]
(формально значение t1 также зависит от lr, ϕ0, ϕ1, далее будем это подразу-
мевать).
Определим максимальную погрешность
(
)
dΦ(lr) = max
d
,
q(lr,ϕ0,ϕ1)(t1), q1
ϕ0,ϕ1∈Φ
а также максимальное отклонение от максимального угла:
(
)
maxΦ(lr) = max
max
,
|ϕ(lr ,ϕ0,ϕ1)(t)| - ϕmax
ϕ0,ϕ1∈Φ
t∈[0,t1]
где ϕ(lr ,ϕ0,ϕ1)(t)
соответствующая компонента траектории q(lr ,ϕ0,ϕ1)(t).
111
Тестирование перепарковки прицепа
lr
0
1/2
1
3/2
2
5/2
3
7/2
4
9/2
5
dΦ
0,027
0,028
0,027
0,03
0,078
0,03
0,026
0,03
0,038
0,071
0,058
maxΦ
0
0
0
0
0
0
0
0
0,059
0,085
0,038
В таблице приведены результаты тестирования в виде максимальной по-
грешности и максимального отклонения от ϕmax.
Проведенное тестирование показало, что при любых lt > 2lr и ϕ0, ϕ1 ∈
∈ [-π/2, π/2] найдется нильпотентная аппроксимация, позволяющая переве-
сти робота со связкой (lt, lr) из состояния (0, 0, 0, ϕ0) в состояние (0, 0, 0, ϕ1)
с погрешностью dΦ(lr) < 1/10 и максимальным абсолютным значением уг-
ла поворота прицепа 3π/4 + 1/10. Для конкретных значений (lt, lr), которые
вычисляются из реальной модели робота, можно разработать более точный
специализированный алгоритм перепарковки.
Известно решение для субримановой задачи, описывающей оптимальное
управление роботом без прицепа [34-36]. Соответствующая субриманова дли-
на доставляет нижнюю грань для субримановой длины (7) в задаче, рассмат-
риваемой в данной работе. При этом случай перепарковки позволяет описать
верхнюю грань для субримановой длины (7), что поможет при дальнейшем
анализе рассматриваемой задачи.
7. Заключение
В данной работе рассмотрена задача управления мобильным роботом с
прицепом, движущимся по плоскости. Получены следующие основные новые
результаты:
• предложен алгоритм построения нильпотентной аппроксимации для си-
стемы “робот с прицепом” в канонических координатах (алгоритм 1);
• в явном виде найдена замена переменных, приводящая нильпотентную ап-
проксимацию к каноническому виду (теорема); при этом замена оптималь-
ного управления нильпотентной аппроксимацией системы “робот с прице-
пом” сводится к нильпотентной задаче на группе Энгеля;
• разработан гибридный алгоритм и программа решения системы алгебраи-
ческих уравнений, определяющие оптимальное управление в нильпотент-
ной субримановой задаче на группе Энгеля (алгоритм 2);
• разработан алгоритм и программа глобального решения задачи парковки
робота с прицепом без ограничений на фазовые переменные (алгоритм 3);
• на основе разработанных алгоритмов созданы специализированный алго-
ритм и программа перепарковки, решающие частный случай задачи и учи-
тывающие фазовое ограничение на угол поворота прицепа.
Для поиска оптимального управления в нильпотентной субримановой за-
даче используется алгоритм 2 для решения системы из трех уравнений, зави-
сящих от эллиптических интегралов первого и второго рода. Следует отме-
тить, что при введении фазовых ограничений на угол прицепа, могут возник-
нуть случаи, когда глобальный алгоритм 3, модифицированный для решения
112
задачи 2 с ограничением, требует слишком много итераций. Для устране-
ния этой проблемы перспективным направлением представляется разработка
алгоритма, использующего нильпотентную аппроксимацию в субримановом
случае только для перепарковки прицепа: сначала робот с прицепом пере-
водится в конечное положение без учета прицепа при движении только впе-
ред (например, вдоль пути машины Дубинса, состоящего из комбинации дуг
окружностей и отрезков прямых [39], либо вдоль эластики Эйлера [40]), а
затем переводит прицеп в нужное положение с помощью алгоритма пере-
парковки. В дальнейшем планируется сравнение предложенных алгоритмов
согласно критерию (6) и апробация разработанных программ для управления
реальной моделью робота в рамках решения задачи 2 с ограничением на угол
поворота прицепа исходя из конкретной модели робота.
В данной статье подразумевается, что у робота есть возможность зада-
вать произвольную скорость приводных колес и соответственно свою ли-
нейную и угловую скорость. Математическая модель, учитывающая огра-
ничение на скорости колес робота естественным образом приводит к по-
нятию субфинслеровой структуры на M. Соответствующая субфинслерова
задача по определению задается системой (2)-(5) с минимизацией време-
ни t1 → min (или длины траектории на плоскости (x, y)) и ограничением
управления на некоторое выпуклое множество (u1, u2) ∈ Ω ⊂ R2 [41]. Заме-
тим, что рассматриваемая задача 1 эквивалента субфинслеровой задаче при
Ω = Ωµ := {(u1,u2) ∈ R2 | u21 + µ2u22 ≤ 1}. В общем субфинслеровом случае
множество Ω определяется исходя из конкретной модели, например случай,
когда Ω есть выпуклый многоугольник (четырехугольник), представляет со-
бой важный подкласс субфинслеровых задач, в котором оптимальное управ-
ление, как правило, кусочно-постоянно.
В завершение отметим, что предложенные алгоритм 1 и теорему можно
использовать не только для приближения субримановых задач, т.е. задач без
ограничения на управление и с минимизацией субримановой длины (7), но и
для более общего класса субфинслеровых задач.
Авторы благодарны проф. Ю.Л. Сачкову за ценные замечания и поддерж-
ку на протяжении всего исследования задачи.
ПРИЛОЖЕНИЕ
Пусть M гладкое многообразие размерности dim M = n.
Обозначим через TqM касательное пространство к M в точке q ∈ M.
Пусть на M задано семейство F = {X1, X2} из двух гладких векторных по-
лей X1, X2 ∈ Vec (M), удовлетворяющих условию полного ранга, т.е. для ко-
торых выполнено
LieqF = TqM,
∀q ∈ M,
где LieqF обозначает алгебру Ли, порождаемую системой F в точке q
(
LieqF = span
X1(q), X2(q), [X1,X2](q),
)
...,[Xi,[...,[X1,X2]...]](q) | Xi ∈ F
113
Здесь квадратные скобки обозначают коммутатор (скобку Ли) векторных по-
лей
(
√
√
√
√
)
d
[X1, X2](q) =
e-
tX2 ◦ e-
tX1 ◦ e
tX2 ◦ e
tX1 (q)
∈ Vec(M),
dt
t=0
где через etXi (q) обозначен поток векторного поля Xi ∈ Vec (M) из точки q ∈
∈ M за время t, т.е. решение задачи Коши γ(t) = Xi(γ(t)), γ(0) = q.
Обозначим через Ls(q), s ∈ N, векторные пространства, порождаемые зна-
чениями в точке q скобок Ли полей X1, X2 длины ≤ s, (сами поля Xi скобки
длины 1):
(
)
L1(q) = span
X1(q),X2(q)
,
(
)
L2(q) = span
L1(q) + [L1,L1](q)
,
(
)
Ls(q) = span
Ls-1(q) + [L1,Ls-1](q)
Условие полного ранга гарантирует, что для любой точки q ∈ M существу-
ет наименьшее целое число r = r(q) такое, что dim Lr(q) = n. Другими сло-
вами, система F задает распределение в касательном пространстве с флагом
(Π.1)
L1(q) ⊆ L2(q) ⊆ ... ⊆ Lr-1(q) ⊂ Lr(q) = Tq
M.
Определение 1. Вектором роста системы F в точке q называется
вектор
(
)
dim L1(q), . . . , dim Lr(q)
Зафиксируем размерность dim M = 4 и рассмотрим управляемую систему
(
)
(
)
(Π.2)
˙q=u1X1q
+u2X2
q
,
где траектория q = q(t) ∈ M, t ≥ 0 кусочно-гладкая кривая, управления
u1, u2
вещественнозначные кусочно-непрерывные функции, а гладкие век-
торные поля X1, X2 ∈ Vec (M) образуют систему с вектором роста (2, 3, 4):
span(X1(q),X2(q),[X1,X2](q),[X1,[X1,X2]](q)) = TqM,
∀q ∈ M.
Далее для системы (Π.2) будет описана конструкция нильпотентной ап-
проксимации в некотором смысле простейшей системы с вектором роста
(2, 3, 4), траектории которой локально приближают траектории исходной си-
стемы. Под простейшей понимается следующее свойство: векторные поля
приближенной системы образуют нильпотентную алгебру Ли, все скобки Ли
которой обнуляются начиная с третьего порядка. Такая приближенная систе-
ма наиболее легко строится в специальных координатах, описывающих пере-
мещение системы в направлениях базовых векторных полей и их коммута-
торов так называемых привилегированных координатах. Перед описанием
самой конструкции введем несколько определений, см. подробнее в [27].
114
Определение 2. Заменой координат для системы (Π.2) называется
диффеоморфизм σ : M → M : q → σ(q). Дифференциал этой замены обозна-
чим через σ∗ : TqM → Tσ(q)M : Xi → σ∗(Xi), i = 1, . . . , 4.
Определение 3. Для системы (Π.2) порядком дифференциального
оператора X в точке q0 называется такое ми{имальное число s ∈ N, что
для любой функции σ, имеющей порядок p = min
p∈N |Xk1...Xkp(σ)(q0)= 0,
}
kj ∈ {1,2}
, все производные порядка s + p вдоль полей X1, X2 от X(σ) об-
нуляются в этой точке:
Xk1 ... Xks+pX(σ)(q0) = 0, kj ∈ {1,2}.
Определение 4. Система локальных координат
q= (q1,..., q4) на(
)
M с центром в точке q0, определяемая заменой
q1(q),... , q4(q)
=
(
)
=
σ1(q),... ,σ4(q)
, называется линейно адаптированной в точке q0, если
дифференциалы dq1,... ,dq4 образуют базис T∗q0 M, адаптированный к флагу
∂
{0} = L0(q0) ⊂ L1(q0) ⊂ L2(q0) ⊂ L3(q0), т.е. Li(q0) = span(∂∂˜q
|q0 ,... ,
|q0 ),
1
∂qi
i = 1,2,3. При этом порядком координаты qi в точке q0 называется ми-
нимальное число p ∈ N, такое что все производные порядка p вдоль по-
лей Xkj от σi обнуляются в этой точке: Xk1 . . . Xkp (σi)(q0) = 0, kj ∈ {1, 2},
где Xkj (f) = 〈∇f, Xkj 〉 обозначает производную функции f по направлению
поля Xkj , оператор 〈, 〉 скалярное произведение, а ∇ взятие градиента.
Определение 5. Для системы (Π.2), записанной в линейно адаптиро-
ванных координатах q, весом координаты qi называется наименьшее число
ωi ∈ N такое, что Lωi(q0) не обнуляется тождественно.
Определение 6. Система локальных координат q= (q1,..., q4) с цен-
тром в точке q0 называется привилегированной для системы (Π.2), если
выполнено
• (q1,..., q4) линейно адаптированы в точке q0;
• порядок координаты qi в точке q0 равен весу ωi.
Теперь, когда даны все необходимые определения, опишем конструкцию
нильпотентной аппроксимации. Нильпотентная аппроксимация для систе-
мы (Π.2) строится в пространстве R4 следующим образом:
1) система (Π.2) записывается в привилегированных координатах q
(Π.3)
q = u1X1(q) + u2X2(q),
q∈ M, (u1,u2) ∈ R2;
2) векторные поля Xi(q) раскладываются в ряд Маклорена с последующей
группировкой слагаемых одинакового порядка
Xi(q) = X(-1)i(q) + X(0)i(q) + X(1)i(q) + X(2)i(q) + ... ;
3) отбрасываются слагаемые начиная с нулевого порядка, и оставшиеся
слагаемые порядка -1 формируют базисные векторные поля
Xi(q) =
= X(-1)i(q) приближенной системы нильпотентной аппроксимации
(Π.4)
q = u1 X1(q) + u2 X2(q),
q∈ R4, (u1,u2) ∈ R2.
115
Нильпотентная аппроксимация (Π.4) для исходной системы (Π.3) обладает
следующими ключевыми свойствами:
1) все коммутаторы порядка ≥ 3 векторных полейX1,X2 равны нулю;
2) вектор роста системы (Π.4) равен (2, 3, 4);
3) под действием управлений u1(t), u2(t) траектория q(t) системы (Π.4)
локально (при малых t > 0) приближает траекторию q(t) системы (Π.3).
В главе 8 книги Р. Монтогомери [21] объясняется связь между исходной
системой и ее нильпотентизацией (нильпотентной аппроксимацией), она дана
теоремой Громова-Митчелла (8.4.1). Оценка на близость траекторий приве-
дена в разделе 8.7. Более детально с конструкцией нильпотентной аппрок-
симации можно познакомиться в работе Беллаиша [25]. Раздел 7 посвящен
оценкам на расстояния, в частности см. Утверждение 7.29 о близости траек-
торий исходной и приближающей систем.
Замечание 7. В общем случае dimM = n, для исходной q(t) = (q1(t),
..., qn(t)) и приближающей траекторий q(t) = (q1(t),..., qn(t)) в привилеги-
рованных координатах, выходящих из одной точки, выполнена локальная
оценка |qi(t) - qi(t)| ≤ Ctwi+1, где C константа, wi вес координаты qi (сте-
пень неголономности в направлении qi, которая вычисляется как наименьшая
глубина флага распределения (Π.1), не обнуляющая i-е направление).
В данной работе для траекторий q(t) и q(t) систем (Π.3) и (Π.4) выполнена
оценка
|qi(t) - qi(t)| ≤ Ctwi+1, w = (1,1,2,3),
где C константа, определяемая видом векторных полей Xi и начальной
точкой q0.
СПИСОК ЛИТЕРАТУРЫ
1. Laumond J.-P. Nonholonomic Motion Planning for Mobile Robots. Tutorial notes.
LAAS-CNRS. Toulouse, 1998.
2. Ardentov A.A. Controlling of a Mobile Robot with a Trailer and Its Nilpotent Ap-
proximation // Regular. Chaot. Dynam. 2016. V. 21. No. 7-8. P. 775-791.
3. Маштаков А.П. Алгоритмическое и программное обеспечение решения кон-
структивной задачи управления неголономными пятимерными системами //
Программные системы: теория и приложения. 2012. T. 3. № 1(10). С. 3-29.
4. Красовский Н.Н. Теория управления движением. М.: Наука, 1968.
5. Chitour Y., Jean F., Long R. A Global Steering Method for Nonholonomic Sys-
tems // J. Differ. Equat. 2013. V. 254. P. 1903-1956.
6. Kushner A.G., Lychagin V.V., Rubtsov V.N. Contact Geometry and Nonlinear Dif-
ferential Equations. Cambridge: Cambridge University Press, 2007.
7. Murray R.M., Sastry S. Steering Nonholonomic Systems Using Sinusoids // IEEE
Int. Conf. on Decision and Control. 1990. P. 2097-2101.
8. Murray R.M. Robotic Control and Nonholonomic Motion Planning // PhD Thesis.
Memorandum No. UCB/ERL M90/117. University of California. Berkeley. 1990.
9. Tilbury D., Murray R., Sastry S. Trajectory Generation for the n-Trailer Problem
Using Goursat Normal Form // IEEE TAC. 1995. V. 40. No. 5. P. 802-819.
116
10.
Monaco S., Norman-Cyrot D. On Carnot-Caratheodory Metrics // J. Differ. Geom-
etry. 1985. V. 21. P. 35-45.
11.
Murray R.M. Nilpotent Bases for a Class on Nonintegrable Distributions with Appli-
cations to Trajectory Generation for Nonholonomic Systems // Math. Control Signal
Syst. University of California. Berkeley, 1990.
12.
Venditelli M., Oriolo G., Jea F., Laumond J.P. Nonhomogeneous Nilpotent Approx-
imations for Nonholonomic Systems with Singularities // Transact. Autom. Control.
2004. V. 49. No. 2. P. 261-266.
13.
Fernandes C., Gurvits L., Li Z.X. A Variational Approach to Optimal Nonholonomic
Motion Planning // IEEE ICRA. Sacramento. 1991. P. 680-685.
14.
Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.: Физматлит,
2005.
15.
Duits R., Meesters S.P.L., Mirebeau J.M., Portegies J.M. Optimal Paths for Variants
of the 2D and 3D Reeds-Shepp Car with Applications in Image Analysis // J. Math.
Imaging and Vision. 2018. V. 60. No. 6. P. 816-848.
16.
Lafferriere G., Sussmann H.J. A Differential Geometric Approach to Motion Plan-
ning. Nonholonomic Motion Planing. 1992. Editors: Zexiang Li, J.F. Canny.
17.
Bellaiche A., Laumond J. P., Chyba M. Canonical Nilpotent Approximation of Con-
trol Systems: Application to Nonholonomic Motion Planning. 32nd IEEE CDC. 1993.
18.
Bellaiche A., Laumond J.P., Riser J.J. Nilpotent Infinetisimal Approximations to a
Control Lie Algebra // IFAC NCSDS. Bordeaux. 1992. P. 174-181.
19.
Ардентов А.А., Сачков Ю.Л. Экстремальные траектории в нильпотентной суб-
римановой задаче на группе Энгеля // Матем. сб. 2011. Т. 202. № 11. С. 31-54.
20.
Сачков Ю.Л. Управляемость и симметрии инвариантных систем на группах Ли
и однородных пространствах. М.: Физматлит, 2007.
21.
Montgomery R. A Tour of Sub-Riemannian Geometries, Their Geodesics and Appli-
cations. Vol. 91 of Mathematical Surveys and Monographs. 2002.
22.
Stefani G. Polynomial Approximations to Control Systems and Local Controllabil-
ity // Proc. 24th. I.E.E.E. Conference on Decision and Control. Ft. Lauderdale. Fla.
1985. P. 33-38.
23.
Аграчев А.А., Сарычев А.В. Фильтрация алгебры Ли векторных полей и ниль-
потентная аппроксимация управляемых систем // ДАН СССР. 1987. Т. 295.
С. 777-781.
24.
Hermes H. Nilpotent and High-Order Approximations of Vector Fields Systems //
SIAM. 1991. V. 33. P. 238-264.
25.
Bellaiche A. The Tangent Space in Sub-Riemannian Geometry // Sub-Riemannian
Geometry. Birkhauser. Basel. P. 1-78.
26.
Gromov, M. (avec J. Lafontaine, P. Pansu), Structures métriques pour les variétés
riemanniennes / Textes Mathématiques. Paris: CEDIC/Fernand Nathan. 1981.
27.
Jean F. Control of Nonholonomic Systems: from Sub-Riemannian Geometry to Mo-
tion Planning. Springer, 2014.
28.
Sachkov Yu.L. Symmetries of Flat Rank Two Distributions and Sub-Riemannian
Structures // Transact. Amer. Math. Soc. 2004. V. 356. P. 457-494.
29.
Ardentov A.A., Sachkov Yu.L. Conjugate Points in Nilpotent Sub-Riemannian Prob-
lem on the Engel Group // JMS. 2013. V. 195. No. 3. P. 369-390.
30.
Ardentov A.A., Sachkov Yu.L. Cut Time in Sub-Riemannian Problem on Engel
Group // ESAIM: COCV. 2015. V. 21. No. 4. P. 958-988.
117
31.
Ardentov A.A., Sachkov Yu. L. Maxwell Strata and Cut Locus in Sub-Riemannian
Problem on Engel Group // RCD. 2017. V. 22. No. 8. P. 909-936.
32.
Ардентов А.А., Сачков Ю.Л. Множество разреза в субримановой задаче на
группе Энгеля // ДАН. 2018. Т. 478. № 6. С. 623-626.
33.
Уиттекер Ю.Т., Ватсон Дж.Н. Курс современного анализа. М.: УРСС, 2002.
34.
Moiseev I., Sachkov Yu.L. Maxwell Strata in Sub-Riemannian Problem on the Group
of Motions of a Plane // ESAIM: Control, Optimisation and Calculus of Variations.
2010. V. 16. P. 380-399.
35.
Sachkov Yu.L. Conjugate and Cut Time in the Sub-Riemannian Problem on the
Group of Motions of a Plane // ESAIM: Control, Optimisation and Calculus of
Variations. 2010. V. 16. P. 1018-1039.
36.
Sachkov Yu.L. Cut Locus and Optimal Synthesis in the Sub-Riemannian Problem
on the Group Of Motions of a Plane // ESAIM: Control, Optimisation and Calculus
of Variations. 2011. V. 17. P. 293-321.
37.
David J., Manivannan P.V. Control of Truck-Trailer Mobile Robots: A Survey //
Intelligent Service Robotics. 2014. V. 7. No. 4. P. 245-258.
38.
Lamiraux F., Sekhavat S., Laumond J.-P. Motion Planning and Control for Hilare
Pulling a Trailer // IEEE Transact. Robot. Autom. 1999. V. 15. No. 4. P. 640-652.
39.
Dubins L.E. On Curves of Minimal Length with a Constraint on Average Curvature,
and with Prescribed Initial and Terminal Positions and Tangents // Amer. J. Math.
1957. V. 79. No. 3. P. 497-516.
40.
Ardentov A.A., Karavaev Y.L., Yefremov K.S. Euler Elasticas for Optimal Control of
the Motion of Mobile Wheeled Robots: the Problem of Experimental Realization //
RCD. 2019. V. 24. No. 3. P. 312-328.
41.
Локуциевский Л.В. Выпуклая тригонометрия с приложениями к субфинслеро-
вой геометрии // Матем. сб. 2019. Т. 210. № 8. С. 120-148.
Статья представлена к публикации членом редколлегии Л.Б. Рапопортом.
Поступила в редакцию 13.10.2019
После доработки 14.05.2020
Принята к публикации 09.07.2020
118