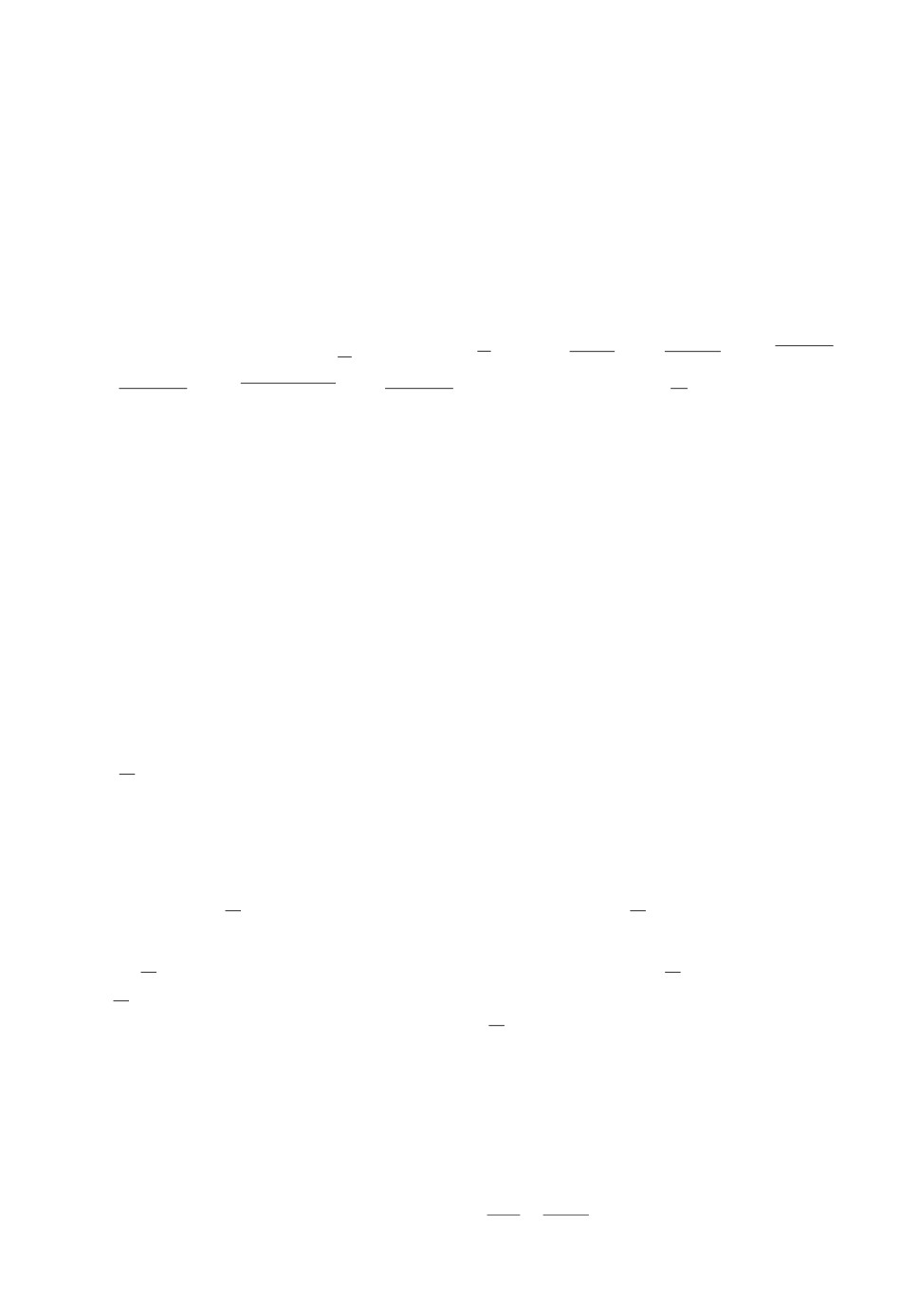Автоматика и телемеханика, № 1, 2021

Управление в социально-экономических

системах

А.В. НАУМОВ, д-р физ.-мат. наук (naumovav@mail.ru)

(Московский авиационный институт)

О ЗАДАЧЕ УВЕЛИЧЕНИЯ ПРОПУСКНОЙ СПОСОБНОСТИ

ЖЕЛЕЗНОДОРОЖНОЙ СТАНЦИИ¹

Рассматривается задача увеличения пропускной способности железно-

дорожной станции с учетом некоторого базового расписания движения

по станции. С этой целью определяются время и маршрут для каждого

дополнительного поезда путем решения набора задач смешанного цело-

численного линейного программирования. Предлагается схема по учету

влияния случайных задержек в движении поездов на возможность их

пропуска через железнодорожную станцию. Приводятся результаты чис-

ленного эксперимента.

Ключевые слова: железнодорожная станция, пропускная способность,

граф, смешанное целочисленное линейное программирование.

DOI: 10.31857/S0005231021010074

1. Введение

В рамках национальных проектов развития Российской Федерации пред-

полагается увеличение количества перевозимых грузов, в частности с исполь-

зованием железной дороги. Для увеличения количества перевозимых грузов

возможны два пути: расширение действующей и строительство новой желез-

нодорожной инфраструктуры и увеличение эффективности использования

действующей инфраструктуры. Первый путь предполагает большие матери-

альные затраты, длителен по времени и может быть осуществлен вследствие

дороговизны только на некотором относительно небольшом участке желез-

нодорожной сети. Второй же путь существенно дешевле и может быть мас-

штабирован в пределах всей Российской Федерации. Для увеличения эффек-

тивности действующей инфраструктуры необходимо, в частности, увеличить

количество поездов, обращающихся по железнодорожным перегонам. Однако

увеличение интенсивности движения на железнодорожных перегонах невоз-

можно без оценки пропускной способности станции и оптимизации движения

на ней, что составляет предмет настоящей статьи.

В то же время большая часть математических постановок задач, посвя-

щенных увеличению пропускной способности, как правило, касаются состав-

¹ Работа выполнена при поддержке Российского фонда фундаментальных исследований

(проект № 20-07-00046 А).

131

ления оптимального расписания движения поездов по железнодорожным пе-

регонам [1-4], оптимальной подвязки локомотивов к поездам [5-9], назначе-

нию “технологического окна” - времени, в течение которого прекращается

движение поездов по отдельным железнодорожным путям для производства

ремонтно-строительных работ - на железнодорожных перегонах [10-13]. Мо-

делированию движения на станции и его оптимизации уделяется меньше вни-

мания. Среди российских публикаций, посвященных данной проблематике,

выделим [14, 15]. В [14] была представлена задача по оптимизации движения

маневровых составов по станции с целью исполнения всех маневровых работ в

рамках оценки вероятности бокового столкновения на станции между манев-

ровыми составами и пассажирскими/грузовыми поездами. В [15] изучалась

задача назначения “технологического окна” на железнодорожной станции на

основе различных критериев. Отметим, что большая часть исследований по

моделированию и оптимизации движения на станции отражена в зарубеж-

ных публикациях. В [16] представлен подробный обзор исследований, посвя-

щенных оценке и оптимизации пропускной споcобности станции, на начало

2000-x гг. В [16] выделено несколько подходов для оценки пропускной спо-

собности: использование некоторых аналитических формул, которые могут

использоваться в качестве начального приближения для оценки пропускной

способности; подход, основанный на оптимизации расписания движения в ко-

тором предполагается встраивать новые поезда в действующее, возможно пу-

стое, расписание; имитационное моделирование. Наиболее близок настоящей

статье подход, основанный на оптимизации расписания. Среди публикаций,

посвященных оптимизационному подходу, выделим [17, 18]. В [17] ставилась

задача по поиску циклического, т.е. повторяющегося через некоторый проме-

жуток времени, расписания в части времени движения по перегонам и вре-

мени нахождения на станции. Рассматривалась однопутная однонаправлен-

ная железнодорожная сеть, учитывались различные технологические огра-

ничения, в том числе количество станционных путей на железнодорожных

станциях. Критерием оптимизации выступала взвешенная сумма из длины

цикла и суммарного времени поездов в пути. Таким образом, в [17] использо-

валась пропускная способность станции, которая неявно оптимизировалась.

В [18] рассматривалась наиболее близкая настоящей статье постановка зада-

чи. В этой статье исследовалась задача по назначению платформы прибытия

поездов на станцию и выбору маршрутов движения связанных с этими по-

ездами отцепляющихся и прицепляющихся вагонов. Авторы [18] отметили

среди недостатков своей работы то, что оптимизация по выбору маршрута

движения из одной точки входа-выхода со станции до платформы не про-

водится, при этом возможность движения для других поездов по всему же-

лезнодорожному пути из этого маршрута полностью исключается, хотя по

некоторым участкам пути из этого маршрута движение безопасно. Данный

недостаток обуславливается тем, что авторы [18] не используют графовую

структуру станции, а используют лишь маршруты, которые в [18], по сути,

представляют пару: платформа-точка входа-выхода со станции. В настоящей

статье эти недостатки отсутствуют.

В настоящей статье рассматривается задача по увеличению пропуск-

ной способности железнодорожной станции. Станция представляется в ви-

132

де неориентированного нагруженного графа. Имеется некоторое базовое рас-

писание движения поездов, позволяющее определить свободность дуг гра-

фа станции для движения. Ставится задача по поиску времени и маршрута

движения дополнительных поездов по станции с учетом возможности сто-

янки поезда на станции, а также смены поездных локомотивов. Эта задача

формулируется в виде набора задач смешанного целочисленного линейного

программирования. Если существует решение в хотя бы одной задаче из это-

го набора, то рассматриваемый поезд может быть пропущен через станцию.

Подобная процедура по “встраиванию” новых поездов в действующее рас-

писание проводится для каждого поезда, который планируется пропустить

через станцию в порядке приоритетности этих поездов.

2. Основные обозначения и предположения

Пусть имеется неориентированный граф станции G =< V, E >, где V -

множество вершин (стрелочных переводов, стыков между рельсами и точек

входа и выхода со станции (границ станции)), а E - множество ребер (желез-

нодорожных путей), соединяющих данные вершины. Также задана функция

D : E → R₊, характеризующая длину ребра. Пусть количество ребер в гра-

фе G равно m. Пронумеровав ребра графа G от единицы до m, составим но-

вый граф G^′ =< V^′, E^′ >, множеством вершин V^′ которого являются номера

ребер графа G, т.е. V^′ = {1, 2, . . . , m}. Множество ребер E^′ включает в себя

ребра между вершинами из V^′, если эти вершины являются смежными реб-

рами в графе G. На элементах множества V^′ введем функцию D^′ : V^′ → R₊,

характеризующую “вес” вершин в графе G^′, т.е. длину соответствующих ре-

бер в графе G.

Пусть на станции имеется некоторое базовое расписание движения пас-

сажирских поездов и некоторое расписание маневровых работ. Метода-

ми из [14] можно составить совместное расписание движения пассажир-

ских поездов и маневровых составов и таким образом составить функцию

F : V ^′ × R¹⁺ → {0,1}:





0, ребро (графа G) с номером j свободно

F (j, t)=

для движения в момент времени t,

 1 иначе,

характеризующую занятость ребра железнодорожной станции для движения

в момент времени t от некоторого момента отсчета, например начала суток.

Пусть t_макс - момент времени, не позднее которого осуществляется движение

на станции в планируемый период, например конец суток.

Пусть требуется пропустить через станцию пассажирский/грузовой поезд

из перечня дополнительных поездов со следующими характеристиками:

• время (начиная от некоторого момента отсчета) прибытия t_приб;

• минимальное время стоянки на станции Δ_ост;

• длина поездного локомотива d_л;

• общая длина поезда d_п;

• средняя скорость движения поезда/поездного локомотива по станции v_ср.

133

Пусть L - количество возможных маршрутов пропуска поезда, а J =

= {j₁, j₂, . . . , j_L} - множество возможных маршрутов пропуска поезда. Про-

извольный маршрут j_l = {j_1,l, j_2,l, . . . , jKl,l} из множества J характеризуется

величиной K_l - количеством дуг на этом маршруте - и представляет собой

конечный набор номеров попарно смежных ребер из графа G, являющихся

вершинами графа G^′, т.е. j_k,l ∈ V^′, k = 1, K_l, и имеется ребро в графе G^′ меж-

ду вершинами с номерами j_k,l и j_k+1,l, k = 1, K_l - 1, l = 1, L. Отметим, что

множество J является конечным в силу того, что пассажирский/грузовой

поезд не может менять направление своего движения без смены локомотива.

Смена же локомотива не может происходить в произвольной точке желез-

нодорожной станции, а только в местах, где поезд может останавливаться.

Пусть для каждого маршрута j_l, l = 1, L, из множества J задано ребро оста-

новки - место, где поезд может останавливаться. Пусть для маршрута j_l такое

ребро находится на S_l по порядку месте.

Отметим, что в силу “плечей обслуживания”

определенных участков

железнодорожной сети, обслуживаемых тем или иным локомотивным депо,

на железнодорожной станции может осуществляться смена поездного локо-

мотива пассажирского/грузового поезда. В случае когда требуется смена по-

ездного локомотива, к каждому маршруту j_l из множества J должны быть

дополнительно указаны множества J^отцl и J^прицl, которые состоят из маршру-

тов следования по станции отцепляющегося (старого) поездного локомотива

и прицепляющегося (нового) поездного локомотива, т.е.

{

}

{

}

J^отцl = j^отц1,l,j^отц2,l,... ,jKот

J^прицl = j^приц1,l,j^приц2,l,... ,jKпри

где K^отцl - количество возможных маршрутов следования отцепляющегося

локомотива, а K^прицl - количество возможных маршрутов следования при-

цепляющегося локомотива при условии, что поезд проследует станцию по

маршруту j_l из множества J. Произвольные элементы j^отцˆp,l, j^{приц˜p,l} из мно-

жеств J^отцl и J^прицl соответственно имеют вид

{

}

{

}

j^отцˆp,l = j^{отц1,ˆp,l},j^{отц2,ˆp,l},... ,j^отцˆ

j^{приц˜p,l} = j^{приц1,˜p,l},j^{приц2,˜p,l},... ,j^приц

K_p,l,p,l

K_˜

p,l,p,l

где j^отцˆ

∈V^′, j^приц˜

∈ V ^′ иKp,l - количество дуг, которые проследует отцеп-

k,p,l

ляющийся локомотив, выбрав маршрут j^отцˆp,l, аKp,l - количество дуг, которые

проследует прицепляющийся локомотив, выбрав маршрут j^{приц˜p,l}, l = 1, L, p =

= 1, K^отцl, p = 1, K^прицl, k = 1, K_p,l, k = 1, K_p,l. Имеется ребро в графе G^′ меж-

ду вершинами с номерами j^отцˆ

иj^отцˆ

p= 1,K^отцl, k = 1, Kp,l - 1, а также

k,p,l

k+1,p,l

с номерами j^приц˜

и j^приц˜

k= 1,Kp,l - 1, p = 1,K^прицl, l = 1,L. Следует от-

k,p,l

k+1,p,l

метить, что также имеют место равенства:

j^{отц1,ˆp,l} = j_S

j^приц˜

= jSl,l,

l,l,

K_p,l,p,l

l = 1,L, p= 1,K^отцl, p= 1,K^прицl, так как первое ребро движения старого ло-

комотива и последнее ребро движения нового локомотива должно совпадать с

134

местом остановки. Также далее будем рассматривать только такие маршруты

старого локомотива, которые не содержат повторяющихся ребер. Аналогич-

ное ограничение наложим и на маршруты нового локомотива.

Поскольку движение между железнодорожными станциями осуществляет-

ся только по определенным железнодорожным путям в определенные проме-

жутки времени по “подниткам”, будем предполагать, что выехать за границы

станции пассажирский/грузовой поезд, используя маршрут j_l, может толь-

ко в один из промежутков [t^нач1,l, t^кон1,l], [t^нач2,l, t^кон2,l], . . . , [t^начT,l, t^конT,l]. Заметим, что

момент пересечения границ со станции может выбираться именно из набора

промежутков, а не набора точек вследствие того, что внутри одной “поднит-

ки” возможны различные режимы ведения поезда.

3. Математическая модель движения по станции

Построим математическую модель движения пассажирского/грузового

поезда по маршруту j_l из множества J с отцепляющимся локомотивом, сле-

дующим по маршруту j^отцˆp,l из множества J^отцl, с прицепляющимся локомоти-

вом, следующим по маршруту j^{приц˜p,l} из множества J^прицl, с выходом поезда

за границы станции в промежуток времени [t^начq,l, t^конq,l], т.е. зафиксируем па-

раметры l, p, p, q.

Для этой цели сформируем множество T_j, состоящее из левой и правой

границ интервалов времени, когда ребро с номером j свободно для движения

поезда в рамках действующего расписания. С помощью множества T_j выде-

лим моменты времени, в которые ребро с номером j свободно. Упорядочим

элементы множества T_j по возрастанию, составим из них вектор τ_j, Пусть

dim τ_j = 2I_j ,

где I_j - количество промежутков времени, когда ребро с номером j свободно

для движения.

Введем новые переменные δ^ik,l, равные единице, если движение по ребру

с номером j_k,l будет осуществляться поездом в промежуток времени между

τ^2i-1j

и τ^2ij

, и равные нулю, если движение по ребру с номером j_k,l в про-

k,l

межуток времени между τ^2i-1j

иτ^2ij

не осуществляется, k = 1, K_l, i = 1, Ijk,l .

k,l

Также введем переменныеδiˆ

, равные единице, если движение по ребру

k,p,l

с номером j^отц будет осуществляться старым локомотивом в промежуток_ˆ

k,p,l

времени между τ^2i-1j

и τ²ⁱ

, и равные нулю, если движение по ребру с но-

j_ˆ

k,p,l

мером j^отцˆ

в промежуток времени между τ^2i-1j

и τ²ⁱ не осуществляется,_j

k,p,l

k= 1,Kp,l, i = 1,I_j

. Аналогичным образом введем переменныеδi˜

, рав-

k,p,l

ные единице, если движение по ребру с номером j^приц будет осуществляться_˜

k,p,l

новым локомотивом в промежуток времени между τ^2i-1j

и τ²ⁱ

, и равные

j_˜k,˜p,l

k,p,l

нулю, если движение по ребру с номером j^приц˜

в промежуток времени между

k,p,l

τ^2i-1j

и τ^2ij

не осуществляется,k = 1,Kp,l - 1, i = 1, I

j_˜k,˜p,l

k,p,l

135

Пусть t_k,l - время, когда голова поезда проехала полностью ребро с но-

мером j_k,l, k = 1, K_l, а t_0,l = t_приб. Пусть также t_ˆk,ˆp,l - время, когда голова

старого локомотива проехала полностью ребро с номером j^отцˆ,

k= 1,Kp,l, и

k,p,l

t˜k,˜p,l - время, когда голова нового локомотива проехала полностью ребро с

номером j^приц˜, k = 1, Kp,l - 1. Также введем переменную t0,p,l - время, когда

k,p,l

голова нового локомотива появилась в пределах станции.

Вначале запишем множество ограничений в решаемой задаче. Поскольку

ребро j_k,l имеет длину D^′(j_k,l), а поезд имеет скорость движения v_ср, то вре-

мя проезда поездом ребра с номером j_k,l не может быть меньшеD′(jk,l) , что_v

ср

запишем в виде

D^′(j_k,l)

(1)

t_k,l - t_k-1,l ≥

k = 1,...,S_l - 1,S_l + 1,...,K_l.

v_ср

Время нахождения поезда на ребре остановки jSl,l не должно быть меньше,

чем минимальное время стоянки Δ_ост и время пересчения ребра остановки

D^′(jSl,l)

(2)

tSl,l - tS_l-1,l ≥ 2

+Δ_ост.

v_ср

Отметим, что коэффициент 2 перед дробью в последней формуле вызван тем,

что если поезд меняет направление своего движения, то ребро остановки он

пересекает дважды. Так как движение поезда осуществляется только в про-

межутки свободности ребра, то на каждом ребре из своего маршрута поезд

должен находиться исключительно в промежуток свободности этого ребра

для движения:

I_jk,l

∑

(3)

δ^ik,l = 1, k = 1,K_l,

i=1

(

)

d_п

(4)

t_k,l ≤ δ^ik,l τ^2ij

+ (1 - δ^ik,l)t_макс, k = 1, K_l, i = 1, I_j

k,l

v_ср

(5)

t_k-1,l ≥ δ^ik,lτ^2i-1j

k = 1,K_l, i = 1,Ijk,l.

k,l

Прокомментируем ограничения (3)-(5). Ограничение (3) гарантирует, что по-

езд будет занимать k-е по порядку ребро из маршрута j_l в один промежу-

ток свободности, k = 1, K_l. Если переменная δ^ik,l будет равна нулю, то огра-

ничения (4)-(5) выполнятся автоматически, если же переменная δ^ik,l равна

единице, то получится, что хвост поезда пересечет k-е по порядку ребро из

маршрута j_l не позднее окончания промежутка свободности с номером i для

этого ребра, при этом голова поезда попадает на k-е по порядку ребро из

маршрута j_l не ранее начала промежутка свободности с номером i, k = 1, K_l,

i = 1,Ijk,l. Так как выезд поезда со станции может быть осуществлен только

в промежуток времени [tначq,l , tконq,l ], введем ограничение

(6)

t^начq,l ≤ t_K

≤t^конq,l.

l,l

136

Время пересечения первого по порядку следования ребра отцепляющего-

ся поездного локомотива не может быть раньше момента остановки поезда,

поэтому введем ограничение

D^′(jSl,l)

(7)

t_1,ˆp,l ≥ t_S

l-1,l +

v_ср

Аналогично ограничениям (1), (3)-(5) на движение поезда по станции нало-

жим следующие ограничения на движение отцепляющегося поездного локо-

мотива по всем ребрам в его маршруте следования за исключением ребра

остановки поезда:

(

)

отц

D^′ j

k,p,l

(8)

tˆk,ˆp,l -tˆk-1,ˆp,l ≥

k= 2,Kp,l,

v_ср

I_jˆ

∑ˆδ

(9)

= 1,

k= 2,Kp,l,

k,p,l

i=1

(

)

(

)

d_л

(10)

tˆk,ˆp,l ≤δ

τ²

j_ˆ

+ 1-δ

t_макс,

k = 2, Kp,l,

i = 1,I

j_ˆ

k,p,l

v_ср

i-1

(11)

τ²

k= 2,Kp,l,

i = 1,I

j_ˆ

tˆk-1,ˆp,l ≥δ

j_ˆ

k,p,l

Поскольку первое по порядку следования ребро отцепляющегося поездного

локомотива совпадает с ребром остановки поезда, то отцепляющийся поезд-

ной локомотив должен занимать это ребро в тот же промежуток свободности,

что и поезд

(

)

(

)

d_л

(12)

t_1,ˆp,l ≤ δ

τ²

+ 1-δ

t_макс,

i = 1,IjS

S_l,l

j_Sl,l

S_l,l

v_ср

l,l

Введем теперь ограничения на движение прицепляющегося локомотива по

станции:

(

)

приц

D^′

j_˜

k,p,l

(13)

t˜k,˜p,l -t˜k-1,˜p,l ≥

k= 1,Kp,l

− 1,

v_ср

I_j˜

∑˜δ

(14)

= 1,

k= 1,Kp,l

− 1,

k,p,l

i=1

(

)

(

)

d_л

t˜k,˜p,l ≤δ

τ²

+ 1-δ

t_макс,

k,p,l

j_˜k,˜p,l

k,p,l

v_ср

(15)

k= 1,Kp,l - 1,

i = 1,I

j_˜k,˜p,l

i-1

(16)

t˜k-1,˜p,l ≥δ

τ²

k= 1,Kp,l - 1,

i = 1,I

j_˜k,˜p,l

k,p,l

j_˜k,˜p,l

137

Ограничения (13)-(16) идентичны ограничениям (1), (3)-(5). Так как время

пересечения головой поезда ребра остановки составляет tSl,l, а прицепляю-

щийся локомотив после прицепки вместе с поездом мог поехать в обратную

своему первоначальному движению сторону и таким образом проехать ребро

остановки дважды, то, чтобы гарантированно успеть осуществить прицепку,

введем ограничение

D^′(jSl,l)

(17)

tK^{приц˜p,l}-1,p,l ≤ tSl,l^-2

v_ср

Прицепка нового локомотива не может быть осуществлена ранее, чем старый

локомотив полностью пересечет ребро остановки, поэтому введем ограниче-

ние

(18)

tK^{приц˜p,l}-1,p,l ≥t1,p,l +dл .

v_ср

Теперь введем ограничения на безопасность движения, а именно исклю-

чим возможные столкновения между поездом, старым и новым локомоти-

вами. Для этого предварительно отметим, что k-е по порядку следования

ребро из своего маршрута поезд занимает в промежуток [t_k-1,l, t_k,l + d_п/v_ср],

старый локомотивk-е ребро по порядку следования из своего маршрута -

в промежуток [t_ˆk-1,ˆp,l, t_ˆk,ˆp,l + d_л/v_ср], новый локомотивk-е ребро по поряд-

ку следования из своего маршрута - в промежуток [t_˜k-1,˜p,l, t_˜k,˜p,l + d_л/v_ср].

Сформируем множестваK = ∅,K = ∅, K = ∅. Вначале исключим возмож-

ность столкновений между поездом и локомотивами. Для этого для каждого

ребра следования j_k,l, кроме ребра остановки jSl,l, из маршрута поезда jl

проверяются равенства

(19)

j_k,l ∩ j^отцˆp,l

=∅

(20)

j_k,l ∩ j^{приц˜p,l}

= ∅.

Если оба равенства выполняются, то никаких дополнительных ограничений

вводить не нужно. Если не выполняется равенство (19), то определяется по-

рядковый номер n_k ребра из маршрута следования старого локомотива, ко-

торое совпадает с ребром j_k,l. Во множествоK добавляется номер k. Далее

вводятся бинарные переменные α_k

β_k с целью наложения ограничений:

(21)

t_k,l + d_п/v_ср - t_n

k-1,p,l ≥-(1-αk^)tмакс^,

(22)

t_k-1,l - (t_n

β_k)t_макс,

k,p,l +dл^/vср^)≤(1

(23)

α_k

β_k

≥ 1.

Ограничения (21)-(23) гарантируют, что либо поезд раньше полностью пере-

сечет k-е по порядку следования ребро из своего маршрута, нежели старый

138

локомотив на него заедет, либо старый локомотив быстрее пересечет k-е по

порядку следования ребро из маршрута поезда, нежели последний на него

заедет.

Если не выполняется равенство (20), то определяется порядковый номер ñ_k

ребра из маршрута следования нового локомотива, которое совпадает с реб-

ром j_k,l. Во множество

K добавляется номер k. Далее вводятся бинарные

переменные α_k

β_k с целью наложения ограничений:

(24)

t_k,l + d_п/v_ср - t_ñ

k-1,p,l ≥-(1-αk^)tмакс^,

(25)

t_k-1,l - (t_ñ

β_k)t_макс,

k,p,l +dл^/vср^)≤(1

(26)

α_k

β_k

≥ 1,

которые идентичны ограничениям (21)-(23).

Теперь исключим возможные столкновения старого и нового локомотивов.

Для этого для каждого ребра следования j^отцˆ, кроме ребра остановки jSl,l,

k,p,l

из маршрута старого локомотива j^отцˆp,l проверяется равенство

(27)

j^отцˆ

∩j^{приц˜p,l}

= ∅.

k,p,l

Если равенство (27) выполняется, то никаких дополнительных ограничений

не вводится. В противном случае определяется порядковый номер n_ˆk ребра из

маршрута следования нового локомотива, которое совпадает с ребром j^отц ._ˆ

k,p,l

Во множество K добавляется номерk. Далее вводятся бинарные переменные

α_ˆk и β_ˆk с целью наложения ограничений:

(28)

tˆk,l + dл/vср -tn_ˆ-1,p,l ≥ -(1 - αk)tмакс,

(29)

tˆk-1,l - (tn_ˆk,p,l + dл/vср) ≤ (1 - βˆk)tмакс,

(30)

α_ˆk + β_ˆk

≥ 1.

Ограничения (28)-(30) идентичны ограничениям (21)-(23).

δi

Учитывая бинарность переменных δ^ik,l,δ

, k = 1,K_l, i = 1,Ijk,l,

k,p,l

k= 1,Kp,l,

ˆi = 1,Ijˆ

k= 1,Kp,l - 1,

˜i = 1,j

по определению, введем

k,p,l

ограничения:

(31)

δ^ik,l ∈ {0,1}, k = 1,K_l, i = 1,I_j

k,l

(32)

∈ {0, 1},

k= 1,Kp,l,

i = 1,I

j_ˆ

k,p,l

(33)

∈ {0, 1},

k= 1,Kp,l - 1,

i = 1,I

j_˜k,˜p,l

k,p,l

Также по определению

(34)

α_k′ ∈ {0,1},

β_k′ ∈ {0,1}, k^′ ∈K,

(35)

α_k′′ ∈ {0,1},

β_k′′ ∈ {0,1}, k^′′ ∈K,

(36)

α_k′′′ ∈ {0,1}, β_k′′′ ∈ {0,1}, k^′′′

∈ K.

139

4. Постановка задачи

Для максимизации прибыли от перевозок людей/грузов следует увеличи-

вать объемы перевозок, что можно осуществить, максимально эффективно

используя станционные ресурсы. Для этой цели следует максимально быстро

освобождать станционные пути, поэтому в качестве критерия оптимизации

выберем минимизацию времени нахождения поезда на станции. Таким обра-

зом, задача оптимизации имеет вид

(37)

tKl,l

→ min,

в которой оптимизируемыми переменными выступают δ^ik,l,δ

, t_k,l,

k,p,l

tˆk,ˆp,l,t0,p,l,t˜k,˜p,l,

α_k′, αk′′ , αk′′′,

β_k′,

β_k′′ , β_k′′′, k = 1,K_l, i = 1,Ijk,l,k = 1,Kp,l,

i = 1,Ijˆ

k= 1,Kp,l - 1,

˜i = 1,j

, k^′ ∈

K, k^′′ ∈K, k^′′′ ∈ K.

k,p,l

Заметим, что задача (37) с ограничениями (1)-(36) является задачей сме-

шанного целочисленного линейного программирования и может быть решена,

например, в пакете Matlab или CPLEX, а также VNS-методом [19], доказав-

шим свою эффективность на ряде практических примеров.

Решение задачи (37) при ограничениях (1)-(36) позволяет определить вре-

мена движения пассажирского/грузового поезда, старого и нового локомо-

тивов по станции при некотором зафиксированном маршруте их движения.

Выберем теперь наилучший маршрут следования пассажирского/грузового

поезда, старого и нового локомотивов с целью наискорейшего выхода пас-

сажирского/грузового поезда за пределы станции. Пусть решение в задаче

(37) с ограничениями (1)-(36) существует и оптимальное значение критерия

равно t^{∗l,ˆp,˜p,q} С использованием этой переменной введем





t^{∗l,ˆp,˜p,q}, решение в задаче (37) с ограничениями (1)-(36)

существует,



+∞ иначе.

Для решения общей задачи поиска маршрута и времени движения поезда и

поездных локомотивов по станции надо определить

T^∗ = min

min

min_приц

min

T_l,p,p,q.

l=1,...,L

p=1,...,K^отц

p=1,...,K_l

q=1,...,T

Если T^∗ конечно, то надо найти l, p, p, q, при которых T_l,p,p,q будет рав-

но T^∗, и использовать полученные времена и маршруты движения поезда и

локомотивов. В противном случае, когда T^∗ бесконечно, поезд пропустить по

станции невозможно. Подобная процедура по “встраиванию” новых поездов

в действующее расписание проводится для каждого поезда, который плани-

руется пропустить через станцию в порядке приоритетности этих поездов.

Отметим, что если не требуется смена поездных локомотивов, то следует

решать задачу

tKl,l →

min

δ^ik,l,t_k,l,k=1,K_l,i=1,I_jk,l

140

при ограничениях (1)-(6), (31). Отметим, что полученная задача практически

совпадает с задачей поиска маршрута и времени движения маневрового со-

става по станции из [14]. Отличием представленной постановки от постановки

из [14] является то, что в [14] маневровый состав, по сути, представлялся ма-

териальной точкой, а в настоящей статье у поезда и локомотивов есть длина.

Также в [14] не предполагалась остановка длительностью не меньше заданной

маневрового состава на некотором пути.

Для учета влияния случайных задержек поездов на возможность пропуска

дополнительных поездов через станцию возможны два способа. Первый спо-

соб заключается в непосредственном использовании апостериорных расписа-

ний, получающихся по результату функционирования станции в день недели,

в который предполагается “вставка” дополнительных поездов. Второй способ

заключается в статистическом моделировании. Для второго пути необходимо

исключить из базового расписания (т.е. из функции F (j, t)) задерживающие-

ся поезда, методом Монте-Карло получить их времена прибытия на станцию

и далее по указанной в настоящей статье процедуре осуществить процеду-

ру вставки в оставшееся от базового расписание задерживающихся поездов.

После этого методами из [14] следует пересчитать расписание маневровых

работ. Закон распределения задержек можно оценить, исходя из апостери-

орных расписаний из первого способа, либо экспертным путем. Для каждой

реализации расписания, сформированного с учетом задержек, производит-

ся процедура “вставки” дополнительных поездов. Отметим, что предложен-

ная схема позволяет не только оценить возможность (вероятность) пропус-

ка некоторого поезда из перечня дополнительных поездов, но и проверить

устойчивость базового расписания на возможность его исполнения с учетом

задержек.

Заметим, что задача по поиску оптимального маршрута движения допол-

нительного поезда и поездных локомотивов через станцию может быть рас-

параллелена. А именно для различных l, p, p, q задача (37) с ограничениями

(1)-(36) может быть решена на различных ядрах процессора/на различных

компьютерах. При этом сами маршруты движения по станции могут быть

определены заранее с использованием теории графов. Это позволяет сокра-

тить время поиска оптимального маршрута движения дополнительного по-

езда и поездных локомотивов через станцию.

5. Пример

Пусть через станцию, часть схемы которой приведена на рисунке, требует-

ся пропустить поезд длиной d_п = 250 м со временем прибытия 7:30 (отсчиты-

вая время от начала суток, получим, что t_приб = 27000 с), минимальным вре-

менем стоянки 30 мин (Δ_ост = 1800 с), единственным промежутком выхода

со станции 8:10-8:20 (t^нач1,1 = 29400 с, t^кон1,1 = 30000 с). Пусть средняя скорость

движения по станции v_ср составляет 5 м/c, а длина поездных локомотивов d_л

равна 30 м. Пусть зафиксировано некоторое базовое расписание движения,

а t_макс = 86400 с. Приведем промежутки свободности для некоторых ребер

станции с 7:00 до 9:00. Предварительно отметим, что схема рассматривае-

мой станции и промежутки свободности ребер практически повторяют схему

141

N22

176

N92

174

236

238

244

N12

144

148

154

164

168

192

T220

220

230

242

240

158

228

152

150

156

162

166

172

196

194

218

216

2161 2162

156

T170

180

170

198

208

214

140

178

182

200

210

2163

145

160

158

N42

186

212

T142

142

N52

202

Схема станции.

и промежутки свободности ребер пассажирского парка станции Челябинск-

Главный.

Пусть поезд возможно пропустить только по одному маршруту, т.е. L = 1

и J = {j₁}, причем

j₁ = {1,2,3,4,5,6,7, 8, 9, 10, 9, 8, 7,6,5,4,11,12, 13,14,15},

а ребром остановки выступает ребро с номером 10, которое по порядку деся-

тое, т.е. S₁ = 10, а K₁ = 21. Также предположим, что множества возможных

маршрутов старого J^отц1 и нового J^приц1 локомотивов для маршрута j₁ состоят

из одного элемента, т.е. K^отц1 = 1, K^приц1 = 1, J^отц1 = {j^отц1,1}, J^приц1 = {j^приц1,1}.

Пусть также

jотц1,1 = {10,21,20,16,17,18,19,6,5,4,3,2,1},

j^приц1,1 = {1,2,3,4,5,6,7,8, 9, 10},

т.е.

K_1,1 = 13,

K_1,1 = 10.

Для краткости изложения не приведены остальные промежутки свобод-

ности (до 7:00 и после 9:00), участвующие в расчете, которых насчитывает-

ся 535. Однако и по промежуткам, представленным в таблице, заметно, что

за короткий промежуток времени вручную крайне затруднительно отыскать

времена движения по станции поезда, а также старого и нового локомотивов.

Решая задачу (37) с ограничениями (1)-(36) в пакете CPLEX, получим

расписание движения поезда

1[27000 - 27067] → 2[27017 - 27101,2] → 3[27051,2 - 27116,8] →

→ 4[27066,8 - 27141] → 5[27091 - 27152,4] → 6[27102,4 - 27160,6] →

→ 7[27110,6 - 27172,6] → 8[27122,6 - 27196] → 9[27146 - 27213,4] →

→ 10[27163,4 - 29271] → 9[29221 - 29288,4] → 8[29238,4 - 29311,8] →

→ 7[29261,8 - 29323,8] → 6[29273,8 - 29332] → 5[29282 - 29343,4] →

→ 4[29293,4 - 29367,6] → 11[29317,6 - 29383,2] → 12[29333,2 - 29387,6] →

→ 13[29337,6 - 29403,2] → 14[29353,2 - 29442,6] → 15[29392,6 - 29450],

где слева от квадратных скобок записан номер пересекаемого поездом ребра,

а справа - соответствующий промежуток занятости. Отметим, что для полу-

чения времени пересечения головой поезда k-го по порядку ребра в маршру-

те, нужно взять левую границу промежутка занятости для k + 1 по порядку

ребра, k = 1, 20.

142

где указание знака вопроса в промежутке занятности ребра № 10 вызвано

тем, что априори неизвестно, где именно на ребре остановки поезд осуществит

стоянку.

Расписание движения нового локомотива имеет вид

1[28857,6 - 28880,6] → 2[28874,6 - 28914,8] → 3[28908,8 - 28930,4] →

→ 4[28924,4 - 28954,6] → 5[28948,6 - 28966] → 6[28960 - 28974,2] →

→ 7[28968,2 - 28986,2] → 8[28980,2 - 29009,6] →

→ 9[29003,6 - 29027] → 10[29021-?],

где указание знака вопроса в промежутке занятности ребра № 10 вызвано

тем, что априори неизвестно, где именно на ребре остановки поезд осуществит

стоянку.

Результаты численного эксперимента были получены с помощью матема-

тического пакета ILOG CPLEX на персональном компьютере (Intel Core i5

4690, 3.5 GHz, 8 GB DDR3 RAM). Расчеты заняли менее 1 секунды, что поз-

воляет сделать вывод о применимости предлагаемого подхода на практике,

когда имеется несколько маршрутов движения поезда и несколько маршру-

тов старого и нового локомотивов.

6. Заключение

В настоящей статье рассмотрена задача по увеличению пропускной спо-

собности станции. Для этой цели в виде задачи смешанного целочисленного

линейного программирования сформулирована задача по вставке в действую-

щее базовое расписание некоторого дополнительного поезда, у которого воз-

можна смена поездных локомотивов. Предложена схема по учету влияния

случайных задержек в движении поездов на возможность их пропуска через

железнодорожную станцию.

СПИСОК ЛИТЕРАТУРЫ

1. Cordeau J.-F., Toth P., Vigo D. A Survey of Optimization Models for Train Routing

and Scheduling // Transp. Sci. 1998. V. 32. No. 4. P. 380-404.

2. Kroon L., Maroti G., et al. Stochastic Improvement of Cyclic Railway Timetables //

Transp. Res. Part B: Method. 2008. V. 42. No. 6 P. 553-570.

3. Лазарев А.А., Мусатова Е.Г. Целочисленные постановки задачи формирования

железнодорожных составов и расписания их движения // Управление большими

системами. 2012. № 38. С. 161-169.

4. Зиндер Я.А., Лазарев А.А. и др. Построение расписаний двухстороннего движе-

ния на однопутной железной дороге с разъездом // АиТ. 2018. № 3. С. 144-166.

Zinder Y., Lazarev A.A., et al. Scheduling the Two-Way Traffic on a Single-Track

Railway with a Siding // Autom. Remote Control. 2018. V. 79. No. 3. P. 506-523.

5. Ziarati K., Soumis F., et al. Locomotive Assignment with Heterogeneous Consists

at CN North America // Eur. J. Oper. Res. 1997. No. 97. P. 281-292.

6. Ahuja R.K., Liu J., et al. Solving Real-Life Locomotive-Scheduling Problems //

Transp. Sci. 2005. V. 39. No. 4. P. 503-517.

145

Буянов М.В., Иванов С.В. и др. Развитие математической модели управления

грузоперевозками на участке железнодорожной сети с учетом случайных фак-

торов // Информатика и ее применения. 2017. Т. 11. № 4. С. 85-93.

Буянов М.В., Наумов А.В. Оптимизация функционирования подвижного соста-

ва при организации грузовых перевозок на участке железнодорожной сети //

АиТ. 2018. № 9. С. 143-158.

Buyanov M.V., Naumov A.V. Optimizing the Operation of Rolling Stock in Or-

ganizing Cargo Transportation at a Railway Network Segment // Autom. Remote

Control. 2018. V. 79. No. 9. P. 1661-1672.

Powell W.B., Simao H.P., Bouzaiene-Ayari B. Approximate Dynamic Programming

in Transportation and Logistics: a Unified Framework // Eur. J. Transp. Logist. 2012.

No. 1. P. 237-284.

10.

Albrecht A.R., Panton D.M., Lee D.H. Rescheduling Rail Networks with Mainte-

nance Disruptions Using Problem Space Search // Comput. Oper. Res. 2013. V. 40.

No. 3. P. 703-712.

11.

Forsgren M., Aronsson M., Gestrelius S. Maintaining Tracks and Traffic Flow at the

Same Time // J. Rail Transp. Plan. & Management. 2013. V. 3. No. 3. P. 111-123.

12.

Liden T., Joborn M. An Optimization Model for Integrated Planning of Railway

Traffic and Network Maintenance // Transp. Res. Part C: Emerging Tech. 2017.

No. 74. P. 327-347.

13.

Гайнанов Д.Н., Игнатов А.Н. и др. О задаче назначения “технологического ок-

на” на участках железнодорожной сети // АиТ. 2020. № 6. С. 3-16.

Gainanov D.N., Ignatov A.N., et al. On Track Procession Assignment Problem at the

Railway Network Sections // Autom. Remote Control. 2020. V. 81. No. 6. P. 967-977.

14.

Босов А.В., Игнатов А.Н., Наумов А.В. Модель передвижения поездов и ма-

невровых локомотивов на железнодорожной станции в приложении к оценке и

анализу вероятности бокового столкновения // Информатика и ее применения.

2018. Т. 12. № 3. C. 107-114.

15.

Ignatov A.N., Naumov A.V. On time selection for track possession assignment at

the railway station // Bull. of the South Ural State University. Ser. Math. Model.

Progr. Comp. Soft. 2019. V. 12. No. 3. P. 5-16.

16.

Abril M., Barber F., et al. An Assessment of Railway Capacity // Transp. Res.

Part E: Logistics and Transp. Rev. 2008. V. 44. No. 5. P. 774-806.

17.

Petering M.E.H., Heydar M., Bergmann D.R. Mixed-Integer Programming for Rail-

way Capacity Analysis and Cyclic, Combined Train Timetabling and Platforming //

Transp. Sci. 2016. V. 50. No. 3. P. 892-909.

18.

Sels P., Vansteenwegen P., et al. The Train Platforming Problem: The Infrastructure

Management Company Perspective // Transp. Res. Part B: Methodological. 2014.

V. 61. P. 55-72.

19.

Hansen P., Mladenovic N., et al. Variable Neighborhood Search in Handbook of

Metaheuristics. Eds., by Gendreau M., Potvin J.-Y. 2010. P. 61-86.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 23.02.2020

После доработки 10.06.2020

Принята к публикации 09.07.2020

146