Автоматика и телемеханика, № 10, 2021
© 2021 г. Л.Г. АФРАЙМОВИЧ, д-р физ.-мат. наук (levafraimovich@gmail.com),
М.Д. ЕМЕЛИН (makcum888e@mail.ru)
(Нижегородский государственный университет)
ЭВРИСТИЧЕСКИЕ СТРАТЕГИИ КОМБИНИРОВАНИЯ РЕШЕНИЙ
ТРЕХИНДЕКСНОЙ АКСИАЛЬНОЙ ЗАДАЧИ О НАЗНАЧЕНИЯХ
Рассматривается NP-трудная целочисленная трехиндексная аксиаль-
ная задача о назначениях. Исследуются стратегии комбинирования допу-
стимых решений задачи. Такое комбинирование может быть применено
в качестве дополнения к эвристическим или приближенным алгоритмам
решения вместо общепринятого шага выбора рекорда среди найденных
допустимых решений. Приводятся результаты вычислительных экспери-
ментов, демонстрирующие перспективность предложенного подхода.
Ключевые слова: аксиальная задача о назначениях, многоиндексная за-
дача, приближенные алгоритмы.
DOI: 10.31857/S0005231021100020
1. Введение
Многоиндексные аксиальные задачи о назначениях возникают при реше-
нии множества прикладных задач [1-3]. Обзор результатов анализа подклас-
сов многоиндексных задач о назначениях приведен в [1]. Класс трехиндекс-
ных аксиальных задач о назначениях является NP-трудным [4]. В [5] доказано
отсутствие полиномиальных ε-приближенных алгоритмов решения трехин-
дексной аксиальной задачи о назначениях (здесь ε - произвольная констан-
та), в противном случае P = NP.
Известны приближенные и эвристические алгоритмы решения NP-труд-
ной аксиальной задачи о назначениях [2, 5-10]. Такие алгоритмы, как пра-
вило, позволяют строить серию допустимых решений задачи. Далее на фи-
нальном шаге таких алгоритмов общепринятым подходом является выбор
рекорда среди построенных допустимых решений. В качестве улучшения фи-
нального шага выбора рекорда Л.Г. Афраймович и М.Д. Емелин предлагают
решение задачи оптимального комбинирования найденных допустимых ре-
шений. Ранее в [11] был построен алгоритм оптимального комбинирования
пары допустимых решений, обладающий линейной сложностью. В данной
статье исследуется проблема комбинирования в случае произвольного числа
решений.
Далее статья построена следующим образом. В разделе 2 приводится по-
становка трехиндексной аксиальной задачи о назначениях и ставится задача
комбинирования допустимых решений. В разделе 3 исследуется задача ком-
бинирования допустимых решений и описываются эвристические стратегии
комбинирования. В разделе 4 приводятся результаты вычислительных экспе-
риментов.
6
2. Постановка задачи
Пусть I, J, K - непересекающиеся множества индексов, I ∩ J = ∅, I ∩ K =
= ∅, J ∩ K = ∅ и |I| = |J| = |K| = n; cijk, i ∈ I, j ∈ J, k ∈ K - трехиндексная
матрица стоимостей; xijk, i ∈ I, j ∈ J, k ∈ K - трехиндексная матрица неиз-
вестных. Тогда трехиндексная аксиальная задача о назначениях ставится как
следующая задача целочисленного линейного программирования:
∑∑
(1)
xijk
= 1, k ∈ K,
i∈I j∈J
∑∑
(2)
xijk
= 1, j ∈ J,
i∈I k∈K
∑∑
(3)
xijk
= 1, i ∈ I,
j∈J k∈K
(4)
xijk
∈ {0, 1} , i ∈ I, j ∈ J, k ∈ K,
∑∑∑
(5)
cijkxijk
→ min .
i∈I j∈J k∈K
Далее пусть задано множество W ⊆ I × J × K, которое определяет подмно-
жество разрешенных назначений. Тогда рассмотрим задачу (1)-(4), (6), (5)
(6)
xijk
= 0, (i, j, k) ∈ W.
Для удобства изложения задачу (1)-(4), (6), (5) для заданного множества W
будем обозначать через Z (W ) . Очевидно, задача (1)-(5) соответствует задаче
Z (I × J × K).
В общем случае задача Z (W ) является NP-трудной [1]. Более того, про-
блема проверки совместности системы (1)-(4), (6) для произвольного множе-
ства W является NP-полной [1]. Будем рассматривать такие множества W ,
которые соответствуют набору назначений некоторых допустимых решений
задачи (1)-(5).
Введем вспомогательные обозначения. Пусть x - допустимое решение си-
стемы ограничений (1)-(4). Тогда через W (x) обозначим следующее множе-
ство разрешенных назначений:
W (x) = {(i, j, k)| xijk = 1, i ∈ I, j ∈ J, k ∈ K}.
Для удобства через C (x) обозначим значение критерия, соответствующего∑∑∑
решению x, C (x) =i∈Ij∈Jk∈K cijkxijk. Пусть x1, x2, . . . , xm - произ-
вольные допустимые решения системы ограничений (1)-(4). Тогда обозначим
(
)
⋃m
W
x1,x2,... ,xm
=
W (xt). Через Sm обозначим множество перестано-
t=1
вок размера m.
Пусть x1, x2, . . . , xm - некоторые допустимые решения системы ограни-
чений (1)-(4), найденные известными приближенными или эвристическими
7
методами решения аксиальной задачи о назначениях (1)-(5). Общепринятым
подходом является выбор рекорда среди данных допустимых решений на фи-
нальном шаге алгоритма: C′ = mint=1,m C(xt). В качестве улучшения финаль-
ного шага выбора рекорда предлагается решение задачи Z(W (x1, x2, . . . , xm)),
т.е. выбор рекорда предлагается заменить на поиск решения, скомбинирован-
ного из компонент известных допустимых решений.
3. Исследования задачи комбинирования решений
Для случая m = 2 в [11] был разработан полиномиальный алгоритм реше-
(
)
ния задачи Z(W
x1,x2,... ,xm
). Вопрос построения алгоритма для случая
m > 2 является открытым.
Покажем, что решение задачи комбинирования m > 2 допустимых реше-
(
)
ний Z(W
x1,x2,... ,xm)
в общем случае не может быть сведено к последо-
вательному комбинированию пар допустимых решений. В качестве базового
алгоритма последовательного комбинирования пар допустимых решений рас-
смотрим следующий алгоритм.
Алгоритм 1. Последовательное комбинирование пар допустимых реше-
ний.
Вход: Исходные допустимые решения x1,x2,...,xm и перестановка p ∈
∈Sm.
Шаг 1. y1 является решением задачи Z (W (xp1,xp2)).
(
(
))
Шаг 2. yt является решением задачи Z
W
yt-1,xpt+1
, t = 2,m - 1.
Выход: ym-1.
Замечание. На шагах 1 и 2 алгоритма 1 применяется алгоритм опти-
мального комбинирования пар решений (случай m = 2), предложенный в
[11].
Теорема. Алгоритм
1
не является алгоритмом решения задачи
(
(
))
Z
W
x1,x2,... ,xm
при m > 2.
Доказательство. Для доказательства данной теоремы приведем
контрпример. Пусть n = 3, m = 3,
1
2
2
2
2
2
2
2
2
c= 2 2 2
212
222
,
2
2
2
2
2
2
2
2
1
1
0
0
0
0
0
0
0
0
000
001
,
x1 = 0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
x2 = 0
0
0
010
000
,
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
000
000
.
x3 = 1
0
0
0
0
0
0
0
0
0
0
1
8
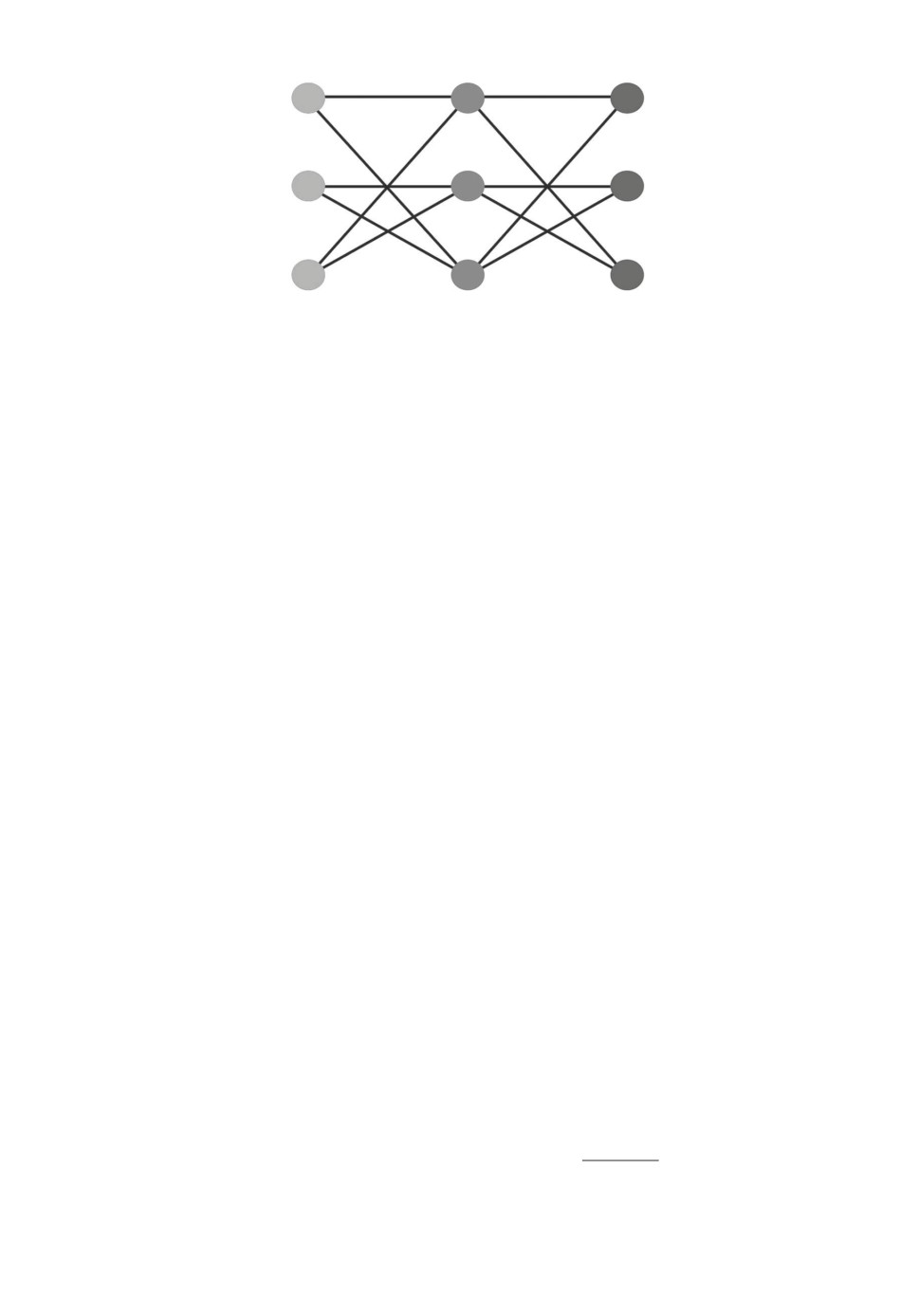
I
J
K
1
2
3
Рисунок.
Несложно увидеь, что граф G = (V, A), где V = {I ∪ J ∪ K}, A =
{
(
)}
=
(i, j) , (i, k) , (j, k)
(i,j,k)∈W
xl1 ,xl2
, l1 = l2, l1,l2 ∈ {1,2,3}, имеет од-
ну компоненту связности (на рисунке в качестве примера приведен граф,
построенный для l1 = 1, l2 = 2).
(
(
))
Отсюда согласно [11] решением задачи Z
W
xl1 ,xl2
является xl1 или xl2 .
Следовательно, при применении алгоритма 1 комбинирования решений x1,
x2, x3 с произвольной перестановкой p ∈ S3 получим на выходе одно из этих
(
)
решений. При этом оптимальным решением задачи Z(W
x1,x2,x3
) является
1
0
0
0
0
0
0
0
0
x∗ = 0
0
0
010
000
,
0
0
0
0
0
0
0
0
1
в котором тройка (1, 1, 1) выбрана из решения x1, тройка (2, 2, 2) из x2,
(
)
(
)
(
)
тройка (3, 3, 3) из x3. И выполняется условие C
x1
=C
x2
=C
x3
=
= 5 > 3 = C (x∗). Теорема доказана.
По причине отсутствия на данный момент известного эффективного ал-
(
)
горитма решения задачи Z(W
x1,x2,... ,xm
) при m > 2 в данной статье
предлагается ряд эвристических стратегий решения данной задачи, основан-
ных на последовательном комбинировании пар решений. Согласно теореме
данные стратегии не гарантируют построение оптимального решения, одна-
ко на численных задачах предложенные стратегии показывают улучшение
результатов по сравнению с общепринятым выбором рекорда.
Предлагаются следующие эвристические стратегии комбинирования реше-
ний:
Стратегия 1.
Применить алгоритм 1 к решениям x1, x2, . . . , xm со случайной переста-
новкой p ∈ Sm. Полученное алгоритмом 1 решение выбрать в качестве вы-
ходного.
Стратегия 2.
Применить алгоритм 1 к решениям x1, x2, . . . , xm с перестановкой p ∈ Sm,
удовлетворяющей свойству C (xpi ) ≤ C (xpi+1 ), i = 1, m - 1, т.е. решения упо-
рядочены в порядке неубывания критерия. Полученное алгоритмом 1 реше-
ние выбрать в качестве выходного.
9
Стратегия 3.
Применить алгоритм 1 к решениям x1, x2, . . . , xm с перестановкой p ∈ Sm,
удовлетворяющей свойству C (xpi ) ≤ C (xpi+1 ), i = 1, m - 1. Обозначим полу-
ченное алгоритмом 1 решение через y1.
Получить k решений yt, t = 2, k + 1, следующим способом. Для каж-
дого t = 2, k + 1 создать перестановку p ∈ Sm, удовлетворяющую свойству
⌊m⌋
C (xpi) ≤ C (xpi+1), i = 1,m - 1, выбрать случайным образом d =
элемен-
2
тов перестановки и случайно поменять их местами. Применить алгоритм 1
к решениям x1, x2, . . . , xm с перестановкой p ∈ Sm. Полученное решение обо-
значим через yt.
Применить алгоритм 1 к решениям y1, y2, . . . , yk+1 с тождественной пере-
становкой e = (1, 2, . . . , k + 1). Полученное алгоритмом 1 решение выбрать в
качестве выходного.
4. Вычислительный эксперимент
По аналогии с [12] построим тестовый набор c матрицами стоимостей,
элементы которых сгенерированы с целочисленными значениями, равномер-
но распределенными в интервале [0, 300]. Будем строить серии эксперимен-
тов с задачами размерности n ∈ {10, 11, . . . , 19}, в каждой серии построим
M = 10 задач. Для каждой из тестовых задач случайным образом сгенериру-
ем m = n3 допустимых решений, к каждому из которых применим алгоритм
локальной оптимизации, предложенный в [6]. Полученные допустимые реше-
ния задачи (1)-(5) обозначим через xt, t = 1, m. Тогда рекорд среди получен-
ных решений обозначим C′ = mint=1,m C(xt). Далее применим разработанные
стратегии оптимального комбинирования решений к полученным локально
оптимальным решениям и обозначим значения критерия, соответствующего
решению, полученному с использованием стратегии s, через Cs, s = 1, 3. На-
конец, через C∗ обозначим оптимальное значение критерия исходной задачи.
Будем сравнивать отклонение от оптимума рекорда среди локально оптими-
зированных случайных решений и отклонение от оптимума среди локально
Таблица
∗
∗
∗
∗
· 100%
10
10
3,195
2,399
2,399
1,478
11
10
8,883
7,413
6,332
4,274
12
10
15,054
14,185
14,185
10,923
13
10
24,319
24,319
24,319
22,010
14
10
41,210
34,207
34,387
23,276
15
10
54,856
47,248
52,372
46,553
16
10
72,872
69,792
70,677
69,473
17
10
68,145
68,145
59,684
51,387
18
10
87,201
81,402
82,272
66,769
19
10
100,464
88,211
90,114
81,358
10
оптимальных случайных решений, к которым применили соответствующие
разработанные стратегии комбинирования. Для серии экспериментов будем
оценивать среднее отклонение в серии. Полученные результаты приведены в
таблице.
Таким образом, среднее отклонение для C′ по всем сериям составляет
47,620 %, для C1 составляет 43,732 %, для C2 составляет 43,674 %, для C3
составляет 37,750 %.
5. Заключение
В литературе известны приближенные и эвристические алгоритмы реше-
ния NP-трудной аксиальной задачи о назначениях. Такие алгоритмы, как
правило, позволяют строить серию допустимых решений задачи. На финаль-
ном шаге таких алгоритмов общепринятым является выбор рекорда среди
построенных допустимых решений. В качестве улучшения финального шага
выбора рекорда Л.Г. Афраймович и М.Д. Емелин предложили решение зада-
чи оптимального комбинирования найденных m допустимых решений. Для
случая m = 2 ранее был разработан эффективный алгоритм решения. В дан-
ной статье было показано, что решение задачи комбинирования при m > 2 в
общем случае не сводится к последовательному комбинированию пар допу-
стимых решений. Тем не менее предложенные эвристические стратегии по-
следовательного комбинирования пар решений для случая m > 2 позволяют
получить улучшение результатов по сравнению с общепринятой стратегией
выбора рекорда. Построение эффективного алгоритма оптимального комби-
нирования при m > 2 остается открытой проблемой.
СПИСОК ЛИТЕРАТУРЫ
1. Spieksma F.C.R. Multi Index Assignment Problems. Complexity, Approximation,
Applications / P.M. Pardalos, L.S. Pitsoulis (Eds.). Nonlinear Assignment Problems:
Algorithms and Applications. Dordrecht: Kluwer Acad. Publishers, 2000. P. 1-11.
2. Афраймович Л.Г. Эвристический метод решения целочисленных декомпозици-
онных многоиндексных задач // АиТ. 2014. № 8. С. 3-18.
Afraimovich L.G. A Heuristic Method for Solving Integer-Valued Decompositional
Multiindex Problems // Autom. Remote Control. 2014. V. 75. No. 8. P. 1357-1368.
3. Афраймович Л.Г., Прилуцкий М.Х. Многоиндексные задачи оптимального пла-
нирования производства // АиТ. 2010. № 10. С. 148-155.
Afraimovich L.G., Prilutskii M.Kh. Multiindex Optimal Production Planning Prob-
lems // Autom. Remote Control. 2010. V. 71. No. 10. P. 2145-2151.
4. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.:
Мир, 1982.
5. Crama Y., Spieksma F.C.R. Approximation Algorithms for Three-Dimensional As-
signment Problems with Triangle Inequalities // Eur. J. Oper. Res. 1992. V. 60.
P. 273-279.
6. Huang G., Lim A. A Hybrid Genetic Algorithm for the Three-Index Assignment
Problem // Eur. J. Oper. Res. 2006. V. 172. P. 249-257.
11
7. Karapetyan D., Gutin D. A New Approach to Population Sizing for Memetic Algo-
rithms: A Case Study for the Multidimensional Assignment Problem // Evolutionary
Computation. 2011. V. 19. No. 3. P. 345-371.
8. Медведев С.Н., Медведева О.А. Адаптивный алгоритм решения аксиальной
трехиндексной задачи о назначениях // АиТ. 2019. № 4. С. 156-172.
Medvedev S.N., Medvedeva O.A. An Adaptive Algorithm for Solving the Axial
Three-Index Assignment Problem // Autom. Remote Control. 2019. V. 80. No. 4.
P. 718-732.
9. Gabrovšek B., Novak T., Povh J., Rupnik Poklukar D.,
Žerovnik J. Multiple Hun-
garian Method for k-Assignment Problem // Mathematics. 2020. V. 8. 2050.
10. Гимади Э.Х., Коркишко Н.М. Об одном алгоритме решения трехиндексной акси-
альной задачи о назначениях на одноциклических подстановках // Дискретный
анализ и исследование операций. Сер. 1. 2003. Т. 10. № 2. С. 56-65.
11. Афраймович Л.Г., Емелин М.Д. Комбинирование решений аксиальной задачи о
назначениях // АиТ. 2021. (принято к печати)
12. Balas E., Saltzman M.J. An Algorithm for the Three-Index Assignment Problem //
Oper. Res. 1991. V. 39. No. 1. P. 150-161.
Статья представлена к публикации членом редколлегии А.А. Лазаревым.
Поступила в редакцию 20.01.2021
После доработки 01.06.2021
Принята к публикации 30.06.2021
12