Автоматика и телемеханика, № 10, 2021

(ООО “Мобайл парк ИТ”, Химки),

Е.В. ДЮКОВА, д-р физ.-мат. наук (edjukova@mail.ru)

(ФИЦ “Информатика и управление” РАН, Москва)

ПОИСК ЧАСТЫХ ЭЛЕМЕНТОВ ПРОИЗВЕДЕНИЯ

ЧАСТИЧНЫХ ПОРЯДКОВ С ИСПОЛЬЗОВАНИЕМ

ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ¹

Рассматриваются вопросы анализа данных c элементами из декартово-

го произведения конечных частично упорядоченных множеств. Для эф-

фективного поиска частых элементов, порождаемых всеми возможными

вариантами бинаризации исходных небинарных данных, используется мо-

дификация классического FP-дерева (Frequent Pattern Tree). Сокращение

временных затрат достигается за счет использования параллельных вы-

числений на основе технологии CUDA (Compute Unified Device Architec-

ture). Приводятся результаты тестирования построенных параллельных

процедур синтеза искомых частых элементов на модельных и реальных

данных.

Ключевые слова: декартовое произведение частичных порядков, база дан-

ных, частый элемент, FP-дерево, пороговое FP-дерево, параллельные вы-

числения, технология CUDA.

DOI: 10.31857/S0005231021100032

1. Введение

Задача поиска частых элементов в данных востребована для ряда при-

кладных областей, среди которых следует выделить нахождение ассоциатив-

ных правил в базах данных и машинное обучение. Приведем классическую

постановку рассматриваемой задачи для наиболее исследованного случая, а

именно для случая бинарных данных [1].

Дано некоторое множество P, элементы которого называются атрибутами,

и дана некоторая совокупность D подмножеств множества P (не обязательно

различных), называемая базой данных. Подмножества множества P называ-

ются наборами атрибутов, а те из них, которые содержатся в D, называются

транзакциями. Набор атрибутов Z называется s-частым, если отношение

числа транзакций, содержащих Z, к числу всех транзакций не менее s. Тре-

буется найти все s-частые наборы атрибутов.

Среди алгоритмов поиска частых наборов атрибутов в бинарных данных

наиболее известными являются алгоритмы Apriori, Eclat, FP-Growth, SaM,

RElim, LCM, DepthProject ([2-9]). Рассматриваемый в настоящей статье ал-

горитм FP-Growth ([2, 5]) делает предобработку бинарной базы данных, бла-

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фунда-

ментальных исследований (проект № 19-01-00430-а).

годаря которой поиск частых наборов атрибутов сводится к анализу компакт-

ной древовидной структуры, называемой Frequent Pattern Tree или FP-дере-

вом. В результате алгоритм FP-Growth имеет в ряде случаев преимущество

перед другими алгоритмами, например, позволяет избежать слишком затрат-

ной процедуры поиска решений, характерной для алгоритмов Apriori [2] и

DepthProject [9].

В случае небинарных данных каждый атрибут имеет некоторое множество

числовых значений, вместо наборов атрибутов рассматриваются наборы их

значений и, как правило, задача сводится к бинарному случаю путем задания

для каждого небинарного атрибута некоторого числа (порога), позволяющего

перекодировать исходные небинарные данные в бинарные [10, 11].

На практике возникает необходимость нахождения зависимостей в частич-

но упорядоченных данных. В [12] рассмотрена задача поиска ассоциативных

правил в данных, представленных в виде декартового произведения частич-

ных порядков, и в связи с этим введено понятие s-частого элемента для мно-

жества P = P₁ × . . . × P_n при условии, что P₁, . . . , P_n - конечные частично

упорядоченные числовые множества.

На множестве P устанавливается частичный порядок. Считается, что эле-

мент y = (y₁, . . . , y_n) ∈ P следует за элементом x = (x₁, . . . , x_n) ∈ P , если y_i

следует за x_i при i = 1, . . . , n (запись x ≼ y). Элементы x, y ∈ P называются

сравнимыми, если один из этих элементов следует за другим, иначе x и y

называются несравнимыми.

Предполагается, что каждое множество (атрибут) P_i содержит наимень-

ший элемент, т.е. такой элемент l_i, для которого выполнено l_i ≼ x_i для лю-

бого x_i ∈ P_i. Элемент x_i ∈ P_i называется существенным значением элемента

x = (x₁,...,x_i,...,x_n) ∈ P, если x_i = l_i. Допускается, что база D не содержит

l = (l₁,...,l_n).

В случае бинарных данных P_i = {0, 1}, i = 1, . . . , n, и в P_i установлен по-

рядок 0 ≼ 1, 0 = 1 (здесь l_i = 0, i = 1, . . . , n).

Пусть x ∈ P , x = l и S_D (x) - число транзакций y в D таких, что x ≼ y.

Элемент x называется s-частым, если S_D (x) / |D| ≥ s, иначе x называется

s-нечастым (здесь и далее |D| - число транзакций в базе D). Заметим, что ес-

ли x ≼ y, то S_D (x) ≥ S_D (y) . Элемент x называется максимальным s-частым

элементом, если S_D (x) / |D| ≥ s и S_D (y) / |D| < s для любого y, такого что

x ≼ y, x = y (т.е. из условия x ≼ y, x = y следует, что y - s-нечастый элемент

в P).

В [13-15] рассмотрены вопросы бинаризации множества P = P₁ × . . . × P_n.

Для каждого множества P_i, i ∈ {1, . . . , n} , строится множество “значимых

порогов” Q_i ⊆ P_i. Каждый набор порогов H = {p₁, . . . , p_n}, в котором p_i ∈ Q_i

при i = 1, . . . , n, порождает произведение бинарных частичных порядков P^H .

Частые элементы множества P^H названы пороговыми частыми элементами.

Поставлена задача перечисления максимальных пороговых частых элемен-

тов, порождаемых всеми возможными вариантами бинарной перекодировки.

Заметим, что находить частые элементы, не являющиеся максимальными,

неэффективно как по времени, так и по памяти. Для решения поставленной

задачи предложен подход, основанный на построении порогового FP-дерева

(TFP-дерева).

Модель TFP-дерева является модификацией модели классического бинар-

ного FP-дерева [2, 5]. В TFP-дереве для каждого небинарного атрибута P_i

строится так называемая полная вершина, содержащая информацию о воз-

можных вариантах бинаризации этого атрибута. При спуске из полной вер-

шины строится либо новая полная вершина, либо корневая вершина класси-

ческого бинарного FP-дерева. Бинарное FP-дерево строится тогда, когда в

текущей ветви все значения небинарных атрибутов перекодированы в бинар-

ные значения.

В реальных задачах может формироваться большое число значимых на-

боров порогов и для поиска максимальных пороговых частых элементов с

использованием TFP-дерева требуются существенные вычислительные ре-

сурсы. В настоящей статье с целью ускорения процедуры поиска искомых

частых элементов разработаны параллельные алгоритмы на основе техноло-

гии CUDA [16, 17], позволяющей выполнить операции, не требующие боль-

ших временных затрат на центральном процессоре, а все сложные операции

на графическом процессоре (GPU). Реализованы две схемы распараллелива-

ния: блочная и одиночная. В блочной схеме множество всех “значимых” набо-

ров порогов H_D разбивается на непересекающиеся подмножества, каждое из

которых подается на отдельный вычислительный блок GPU для синтеза мак-

симальных пороговых частых элементов. При одиночном распараллеливании

для нахождения максимальных пороговых частых элементов, порождаемых

набором порогов из H_D, используется один вычислительный блок GPU.

В разделе 2 введены основные понятия. В разделе 3 описана процедура

построения TFP-дерева. В разделах 4 и 5 дано описание алгоритмов поис-

ка максимальных пороговых частых элементов в TFP-дереве на основе па-

раллельных вычислений с использованием технологии CUDA и приведены

результаты тестирования этих алгоритмов на модельных данных и на реаль-

ных задачах из репозитория UCI [18].

2. Основные понятия

Рассмотрим случай небинарных данных. Задачу поиска частых элементов

в произведении частичных небинарных порядков P сведем к бинарному слу-

чаю путем задания набора порогов H = {p₁, . . . , p_n} , в котором p_i ∈ P_i при

i = 1,...,n, p_i = l_i. В каждом элементе x = (x₁,...,x_n) множества P заменим

значение x_i, i ∈ 1, . . . , n, на 1, если p_i ≼ x_i, и заменим на 0 в противном слу-

чае. В результате такой кодировки получаем вместо множества P множество

P^H = P^H1 × ... × P^Hn, где P^Hi = {0,1}, i ∈ {1,... ,n}, и в каждом P^Hi установ-

лен порядок 0 ≼ 1, 0 = 1. Вместо базы данных D получаем базу данных D_H .

Порогу p, p ∈ P_i, поставим в соответствие элемент ϕ_i (p) = (x₁, . . . , x_n)

из P , в котором x_i = p и x_j = l_i при j = i. Тогда порог p называется зна-

чимым, если S_D (ϕ_i (p)) ≥ s, т.е. элемент ϕ_i (p) является s-частым в P. Пред-

полагается, что каждое P_i имеет хотя бы один значимый порог.

Набор порогов H = (p₁, . . . , p_n) называется значимым, если для любого

i ∈ {1,...,n} порог p_i - значимый. Для бинарной перекодировки будем вы-

бирать только значимые наборы порогов.

Набор порогов (p₁, . . . , p_n) , в котором для каждого p_i, i ∈ {1, . . . , n}, вы-

полняется условие S_D (ϕ_i (p_i)) = maxp∈Pi S_D (ϕ_i (p)), называется оптималь-

ным значимым. Оптимальный значимый набор порогов позволяет находить

наибольшее число пороговых частых элементов.

Ставится задача нахождения всех максимальных пороговых частых эле-

ментов, которые порождаются всеми значимыми наборами порогов. В силу

большого числа s-частых элементов имеет смысл искать и хранить только те

из них, которые являются максимальными.

Рассматриваются три способа решения поставленной задачи. Первый спо-

соб основан на последовательном поиске значимых наборов порогов и синтезе

для каждого такого набора соответствующего бинарного FP-дерева. Второй

способ основан на нахождении искомых элементов в TFP-дереве. Третий спо-

соб основан на параллельном поиске частых элементов в TFP-дереве с при-

менением технологии CUDA. Результаты экспериментального сравнения по

скорости счета указанных подходов приводятся в разделе 5.

3. Синтез порогового FP-дерева (TFP-дерева) и пороговых частых

элементов произведения частичных небинарных порядков

Отметим, что описание варианта FP-дерева для произведения бинарных

частичных порядков (далее бинарного FP-дерева) приведено в [14].

Введем обозначения: a_ri, r ∈ {1, . . . , m}, i ∈ {1, . . . , n}, - значение атрибута

P_i для транзакции S_r в базе D; X - множество небинарных атрибутов в D;

H - набор вида (1,...,1) длины n; H_D - множество всех значимых наборов

порогов. Не ограничивая общности, можно считать, что каждый небинарный

атрибут имеет хотя бы один значимый порог.

Опишем алгоритм синтеза TFP-дерева. Данный алгоритм является рекур-

сивным. Положим на первом шаге D^′ = D,X = X,Ĥ = H, H_D = ∅. Далее

на каждом шаге рекурсии осуществляется следующая последовательность

действий 1-3.

1. Если

X= ∅, то осуществляется переход к 3, иначе осуществляется 2.

2. Выбирается атрибут P_i ∈X с множеством значимых порогов Q_i и созда-

ется полная вершина с меткой (P_i, Q_i). Далее осуществляется ветвление

из вершины (P_i, Q_i) по каждому порогу p ∈ Q_i. Для порога p строится

одна дуга и создается база D_p путем бинарной перекодировки атрибу-

та P_i в текущей для данной ветви базе D^′ по правилу: a_ri = 1, если

p ≼ a_ri, иначе a_ri = 0. Полагается D^′ = D_p,X =X\{P_i}, в набореĤ ко-

ордината с номером i заменяется на p и осуществляется рекурсивный

переход к 1.

{

}

3. Полагается H_D = H_D∪

, и для набора пороговĤ строится бинарное

FP-дерево. Рекурсия останавливается.

После построения TFP-дерева для каждого построенного значимого набо-

ра порогов осуществляется поиск максимальных пороговых s-частых элемен-

тов.

Пусть H₁ = {p₁, . . . , p_n} и H₂ = {q₁, . . . , q_n} - два значимых набора порогов

таких, что p_t = q_t для некоторого t ∈ {1, . . . , n} и p_i = q_i, i = t, i ∈ {1, . . . , n}.

Пусть W (H₁) - множество пороговых s-частых элементов в PH1 , W (H₂) -

множество пороговых s-частых элементов в PH2 . Имеют место приводимые

далее утверждения 1 и 2.

Утверждение 1. Если S_D(ϕt (q_t)) ≤ S_D(ϕ_t(p_t)), то W(H₂) ⊆ W(H₁).

Доказательство. Пусть S_D(ϕt (q_t)) ≤ S_D(ϕ_t(p_t)). Покажем, что

W (H₂) ⊆ W (H₁). Возьмем произвольный элемент x = (x₁, . . . , x_n) из W (H₂).

Заметим, что наборы H₁ и H₂ отличаются друг от друга по значению толь-

ко одного порога с индексом t, поэтому база DH1 отличается от базы DH2

только по атрибуту с номером t. Тем самым если x_t = 0, то x будет также

s-частым элементом и в PH1 по построению базы DH1 . Если же x_t = 0, то из

условия S_D(ϕ_t (q_t)) ≤ S_D(ϕ_t(p_t)) получаем, что в DH1 содержится не меньше

транзакций, чем в DH2 , следующих за элементом x. Тем самым элемент x

также принадлежит и множеству W (H₁). Утверждение 1 доказано.

Пусть W_t(H₁) - множество пороговых s-частых элементов в PH1 , в кото-

рых значение атрибута с индексом t равно нулю, W_t(H₂) - множество поро-

говых s-частых элементов в PH2 , в которых значение атрибута с индексом t

равно нулю.

Утверждение 2. Если S_D(ϕt (q_t)) ≤ S_D(ϕ_t(p_t)), то W_t(H₂) = Wt (H₁).

Доказательство. Пусть SD (ϕt (q_t)) ≤ SD (ϕt (p_t)). Покажем, что

W_t(H₂) = W_t (H₁) . Возьмем произвольный элемент x = (x₁,... ,x_n) из

W_t(H₁). Заметим, что наборы H₁ и H₂ отличаются друг от друга по значению

только одного порога с индексом t, поэтому база DH1 отличается от базы DH2

только по атрибуту с номером t. Из x_t = 0 и S_D(ϕ_t (q_t)) ≤ S_D(ϕ_t(p_t)) получа-

ем, что в базе DH2 найдется s |DH2 | транзакций, следующих за элементом x.

Тем самым элемент x также принадлежит и множеству W_t(H₂). Аналогично

рассматривается обратная ситуация, когда элемент x принадлежит W_t (H₂).

Утверждение 2 доказано.

Применяя утверждения 1 и 2, процесс поиска всех максимальных поро-

говых s-частых элементов с использованием TFP-дерева можно существен-

но ускорить. С этой целью в каждом Q_i, i ∈ {1, . . . , n}, пороги упорядочи-

ваются по убыванию значения величины S_D (ϕ_i (p)), p ∈ Q_i, и ветвление из

полной вершины (P_i, Q_i) осуществляется в соответствии с выбранным поряд-

ком. Множество H_D упорядочивается в порядке построения его элементов.

Нетрудно видеть, что в таком случае в H_D первым по порядку будет опти-

мальный значимый набор порогов H_opt (раздел 2).

Пусть F_max(H), H ∈ H_D, - множество максимальных пороговых s-частых

элементов для набора порогов H; F (H_D) - множество пар вида (F_max(H), H),

H ∈ H_D. Для поиска требуемых частых элементов применяются процедуры

AllMaxSets и MaxSets, результатом работы которых является соответственно

построение множества F (H_D) и пары (F_max(H), H), H = H_opt.

На первом шаге процедура AllMaxSets по FP-дереву, построенному

для H_opt, классическим способом, находит множество F_max(H_opt) и пару

(F_max(H_opt), H_opt) добавляет в F (H_D) (первоначально F (H_D) = ∅). Далее

процедура AllMaxSets осуществляет построение множества F (H_D) путем по-

следовательного вызова процедуры MaxSets для каждого H ∈ H_D, H = H_opt

(в порядке следования наборов в H_D).

На вход процедуры MaxSets подаются набор порогов H = {q₁, . . . , q_n}, мно-

жество F_max(H) = ∅ и текущее множество (последовательность) F (H_D). На

выходе из MaxSets пара (F_max(H), H) добавляется в F (H_D). В процедуре

MaxSets осуществляется следующая последовательность действий 1-3.

1. В последовательности F (H_D) среди пар (F_max(H^′), H^′), H^′ = H, H^′ =

= {p₁, . . . , p_n}, S_D(ϕ_i (q_i)) ≤ S_D(ϕ_i(p_i)), i ∈ {1, . . . , n}, ищутся пары с ми-

нимальным числом неравенств S_D(ϕ_i (q_i)) < S_D(ϕ_i(p_i)). Среди этих пар

берется пара (F_max(H^∗), H^∗) с максимальным номером и создается мно-

жество T (H^∗) индексов i, для каждого из которых при H^′ = H^∗ верно

указанное выше строгое неравенство. Далее осуществляется переход к 2.

2. Просматриваются элементы из F_max (H^∗) . Элемент A из F_max (H^∗) , в ко-

тором значения атрибутов с индексами из T (H^∗) равны 0, добавляется в

Fmax(H), иначе осуществляется переход к 3. После просмотра всех элемен-

тов в F_max(H^∗) построение множества F_max(H) заканчивается и осуществ-

ляется выход из процедуры MaxSets.

3. Пусть M(A) - множество различных элементов из P^H , каждое из которых

получается из A заменой одного элемента 1 на элемент 0. Если A - s-час-

тый элемент в D_H и A ∈ F_max(H), то элемент A добавляется в F_max(H).

Если же A - s-нечастый элемент в D_H и |A| > 2, то действие 3 осуществ-

ляется для каждого элемента из M(A). Во всех других случаях элемент A

не добавляется в F_max(H).

Следует заметить, что в связи с особенностью построения TFP-дерева на

первом шаге работы процедуры MaxSets всегда найдется хотя бы одна пара

(F_max(H^∗), H^∗). Дело в том, что спуск из полной вершины осуществляется

последовательно начиная с рассмотрения наиболее значимого порога.

4. Поиск пороговых частых элементов на базе TFP-дерева

и технологии параллельных вычислений CUDA

В случае больших данных для построения пороговых частых элементов

произведения частичных порядков требуются существенные вычислительные

ресурсы. В данном разделе с целью уменьшения временных затрат при поиске

искомых элементов реализованы параллельные схемы вычислений на основе

применения технологии параллельных вычислений CUDA (Compute Unified

Device Architecture), которая позволяет использовать графический процессор

[16, 17].

Графический процессор (GPU) состоит из однородных вычислительных

элементов (мультипроцессоров) с общей памятью. Каждый мультипроцессор

способен исполнять параллельно тысячи вычислительных “нитей”. Нити мо-

гут быть сгруппированы в вычислительные потоки, имеющие общий кэш и

быструю разделяемую память для обмена данными между нитями потока.

Вычислительные потоки также могут быть сгруппированы в вычислительные

блоки для лучшего распараллеливания вычислений. Применение вычислений

на GPU наиболее эффективно в решении задач, в которых число арифмети-

ческих операций велико по сравнению с операциями над памятью.

Далее описаны два параллельных алгоритма поиска максимальных по-

роговых частых элементов произведения частичных порядков: PTFP-tree и

DPTFP-tree. В алгоритме PTFP-tree реализована одиночная схема распа-

раллеливания, а в алгоритме DPTFP-tree применена блочная схема. В каче-

стве базового алгоритма поиска максимальных пороговых частых элементов

предлагается алгоритм, описанный в разделе 3. В этом алгоритме наиболее

существенное время требуется для работы процедуры AllMaxSets. Поэтому

в разработанных параллельных алгоритмах данные вычисления полностью

перенесены на GPU.

В алгоритме PTFP-tree реализована процедура MaxSetsGPU, осуществ-

ляющая построение множества F_max(H), H ∈ H_D, H = H_opt, на GPU. На вход

MaxSetsGPU подаются исходная база данных D, значение уровня поддерж-

ки s, число вычислительных нитей z, набор порогов H = {q₁, . . . , q_n}, множе-

ство F_max(H) = ∅ и пара (F_max(H^∗), H^∗) = (F_max(H_opt), H_opt). На выходе из

MaxSetsGPU пара (F_max(H), H) добавляется в F (H_D).

В процедуре MaxSetsGPU выполняются следующие действия 1-3.

1. Просматриваются элементы из F_max(H^∗), H^∗ = {p₁, . . . , p_n}. Если для

A ∈ F_max(H^∗), A = {a₁,...,a_n}, найдется t ∈ {1,...,n} такое, что a_t = 1,

p_t = q_t, то осуществляется переход к 2. В противном случае элемент A

добавляется в F_max(H). Данная проверка элемента A выполняется парал-

лельно z вычислительными нитями GPU. После просмотра всех элементов

в F_max(H^∗) происходит переход к 3, после которого построение множества

Fmax(H) заканчивается и осуществляется выход из процедуры MaxSets-

GPU.

2. Пусть M(A) - множество различных элементов из P^H , каждое из которых

получается из A заменой одного элемента 1 на элемент 0. Если A - s-час-

тый элемент в D_H и A ∈ F_max(H), то элемент A добавляется в F_max(H).

Если же A - s-нечастый элемент в D_H и |A| > 2, то действие 2 осуществ-

ляется для каждого элемента из M(A). Во всех других случаях элемент A

не добавляется в F_max(H).

3. Из множества F_max(H) удаляются элементы, которые предшествуют дру-

гим элементам из F_max(H). Данный блок выполняется параллельно z вы-

числительными нитями GPU.

В алгоритме DPTFP-tree в отличие от алгоритма PTFP-tree построение

множества F_max(H) осуществляется параллельно для всех H ∈ H_D, H = H_opt.

Для этого создается |H_D| - 1 вычислительных потоков, в каждом из кото-

рых вызывается процедура MaxSetsGPU. Также для лучшей загрузки муль-

типроцессоров GPU в алгоритме DPTFP-tree в действиях 1 и 2 процедуры

MaxSetsGPU активно применяется динамический параллелизм (возможность

динамически порождать внутри потока новые вычислительные потоки без

возврата к коду, исполняемому на CPU [16]).

Дополнительное отличие состоит в том, что каждый вычислительный по-

ток “сообщает” свой результат всем вычислительным потокам, которые на-

ходятся в очереди на выполнение, и те из них, которые запустятся далее,

перед каждым вызовом процедуры MaxSetsGPU действуют следующим об-

разом. Среди пар (F_max(H^′), H^′), H^′ = H, H^′ = {p₁, . . . , p_n}, H = {q₁, . . . , q_n},

S_D (ϕ_i (q_i)) ≤ S_D (ϕ_i (p_i)) , i ∈ {1,... ,n}, множества F(H_D) ищутся пары с ми-

нимальным числом неравенств S_D (ϕ_i (q_i)) < S_D (ϕ_i (p_i)) , i ∈ {1, . . . , n}, из ко-

торых выбирается пара (F_max(H^∗), H^∗) с максимальным номером. Поиск па-

ры (F_max(H^∗), H^∗) полностью выполняется на GPU с применением динами-

ческого параллелизма.

5. Результаты численных экспериментов на реальных и модельных данных

Выполнены эксперименты на случайных модельных данных, содержащих

как бинарные атрибуты, так и небинарные целочисленные атрибуты. Число

небинарных атрибутов составляло 10 % от общего числа атрибутов. Значение

бинарного атрибута в транзакции полагалось равным 0 с вероятностью v,

v ∈ [0,5;0,9], и равным 1 с вероятностью 1 - v. Число v выбиралось с примене-

нием датчика случайных чисел. Значения небинарного атрибута выбирались

из интервала [0; 9] с равной вероятностью. Число транзакций m изменялось

от 60 до 1 800 000, число атрибутов n изменялось от 30 до 40. Максимальные

пороговые s-частые элементы искались при s = 0,3. Время счета измерялось

в миллисекундах.

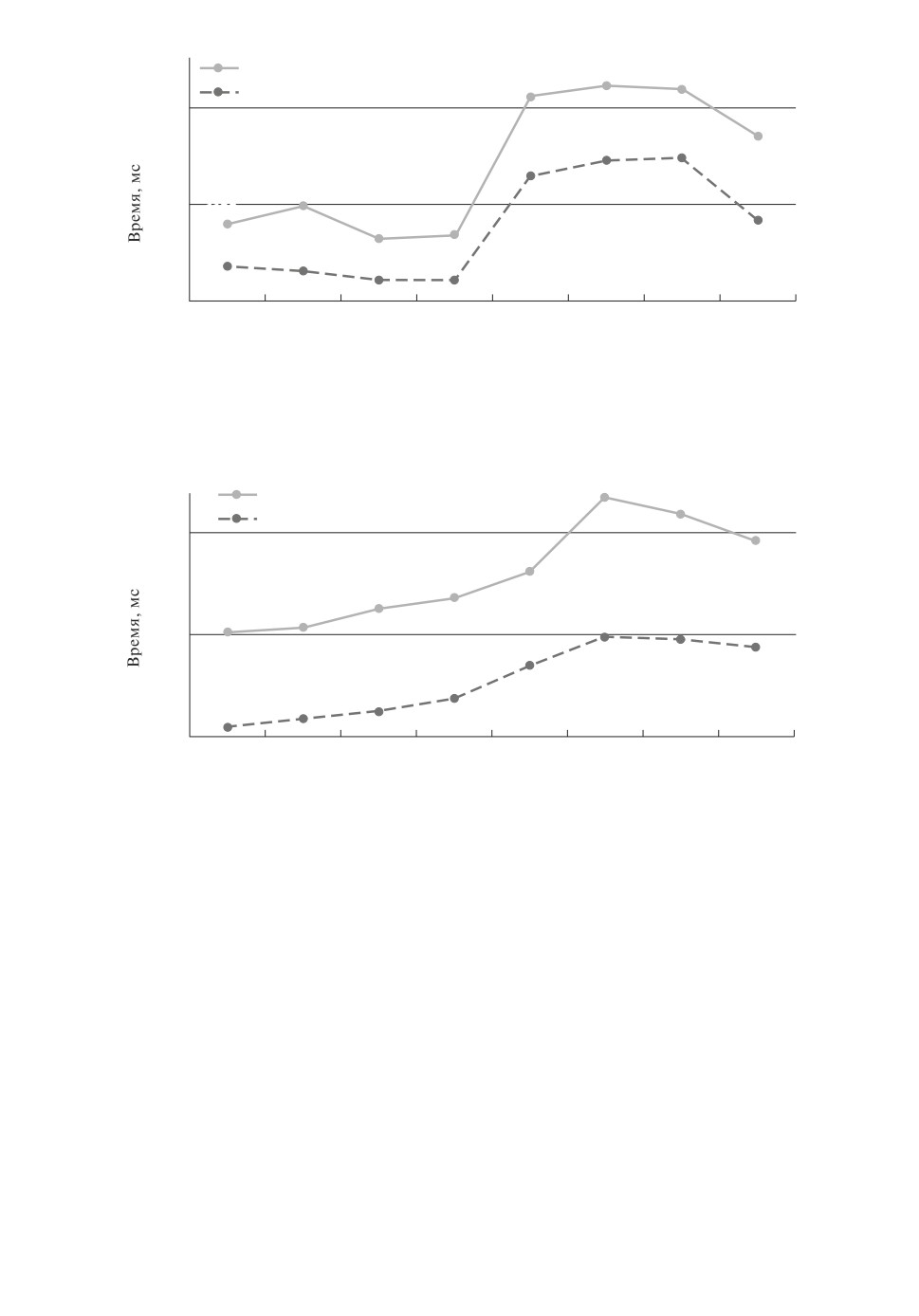
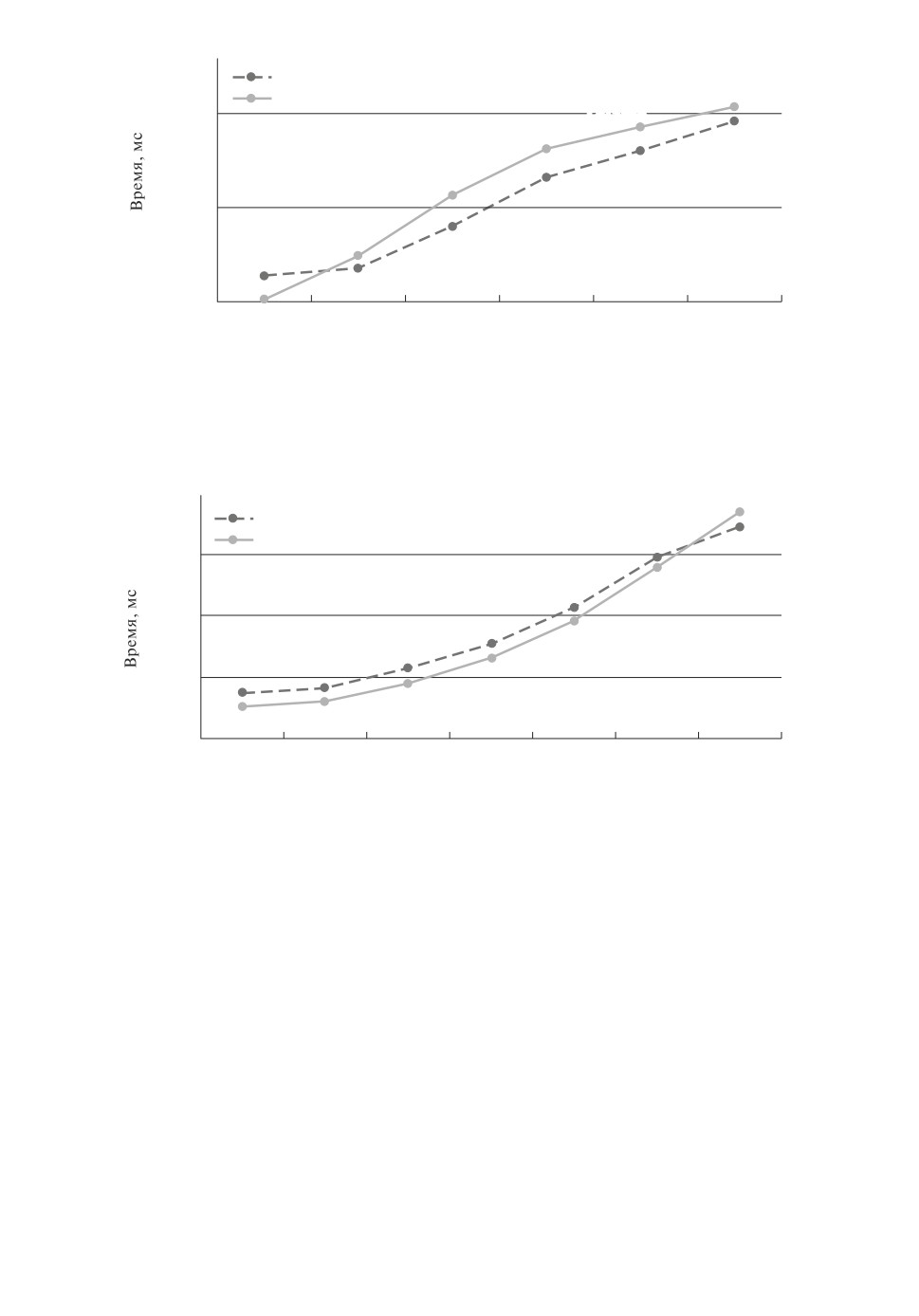
На рис. 1-4 приведено время поиска всех максимальных пороговых s-час-

тых элементов алгоритмом FP-tree, основанным на последовательном синтезе

для каждого значимого набора порогов классического бинарного FP-дере-

ва, алгоритмом TFP-tree, основанным на построении TFP-дерева, и парал-

лельными алгоритмами, описанными в разделе 4. Для каждого алгоритма

приведено среднее время поиска при анализе 20 случайных баз данных раз-

мера m × n. Дополнительно указаны число значимых наборов порогов |H_D|

и число найденных максимальных пороговых s-частых элементов |F_D| . На

рис. 4 представлены результаты работы алгоритмов DPTFP-tree и TFP-tree

при числе небинарных атрибутов k, равном 1, . . . , 7.

Из полученных результатов можно сделать следующие выводы.

Более быстрым из двух разработанных параллельных алгоритмов являет-

ся алгоритм DPTFP-tree (рис. 1). При n = 40 алгоритм DPTFP-tree в среднем

в 6 раз работает быстрее алгоритма PTFP-tree.

Алгоритм TFP-tree работает существенно быстрее алгоритма FP-tree. На-

пример, при n = 40 время счета TFP-tree в 20-40 раз меньше времени счета

FP-tree (рис. 2). Этот вывод ранее был получен в [13-15].

При большом числе транзакций (более 30 000 транзакций) и относитель-

но небольшом числе значимых наборов порогов (не более 2500) алгоритм

DPTFP-tree работает быстрее алгоритма TFP-tree в среднем в четыре раза

(рис. 3). Заметим, что при n = 40, m ∈ {100, 200, 300} время счета TFP-tree

меньше времени счета DPTFP-tree в 3-10 раз (рис. 1-2) за счет того, что

копирование данных между GPU и CPU занимает слишком большое время.

PTFP-tree

30 366

644

DPTFP-tree

23 173

18 000

9098

5169

5384

1741

3530

1800

1129

795

870

1238

408

364

297

295

180

mxn

60 ´ 30

100 ´ 30

200 ´ 30

300 ´ 30

60 ´ 40

100 ´ 40

200 ´ 40

300 ´ 40

|H_D|

252

343

252

343

1260

2058

1512

|F_D|

9266

8570

8208

7397

60 483

100 686

73 988

27 866

Рис. 1. Зависимость времени поиска максимальных пороговых s-частых эле-

ментов параллельными алгоритмами от размерности базы данных.

57908

FP-tree

33 724

TFP-tree

13 676

18 000

4853

2033

1426

645

549

517

396

600

215

mxn 60 ´ 30

100 ´ 30

200 ´ 30

300 ´ 30

60 ´ 40

100 ´ 40

200 ´ 40

300 ´ 40

|H_D|

252

343

252

343

1260

2058

1512

|F_D|

9266

8570

8208

7397

60 483

100 686

73 988

27 866

Рис. 2. Зависимость времени поиска максимальных пороговых s-частых эле-

ментов последовательными алгоритмами от размерности базы данных.

При большом числе значимых наборов порогов (более 600 000) и неболь-

шой размерности базы данных (n = 40, m = 300) алгоритм DPTFP-tree ра-

ботает быстрее алгоритма TFP-tree в среднем в три раза (рис. 4).

Тестирование алгоритмов DPTFP-tree и TFP-tree также осуществлялось

на 7 реальных задачах из репозитория UCI [18]: Stone Flakes (задача № 1),

Cloud (задача № 2), Wine Quality White (задача № 3), Clickstream data for

online shopping (задача № 4), Wholesale customers (задача № 5), Adult (зада-

ча № 6), Heart Disease (задача № 7).

В таблице представлены результаты счета для задач 1-7. В задачах 4-7 ва-

рьировались параметры: s (значение уровня поддержки) и h (максимальное

число значимых порогов для небинарного атрибута). При отсутствии ограни-

чения на значение параметра h в соответствующей ячейке таблицы поставлен

DPTFP-tree

4 815 668

TFP-tree

3 500 000

1 813 618

631566

2 353 156

561015

64 202

158 602

35 000

3375

14 419

1238

396

1846

350

mxn

300 ´ 40

3000 ´ 40

30 000 ´ 40

300 000 ´ 40

900 000 ´ 40

1 800 000 ´ 40

|H_D|

1512

1764

2401

1764

|F_D|

27 866

18 795

27 875

29 288

28 268

38 275

Рис. 3. Зависимость времени поиска максимальных пороговых s-частых эле-

ментов от m и при n = 40.

23 587247

DPTFP-tree

PTFP-tree

9 013

7897241

1 000 000

18 492

378 606

10 000

1238

6673

195

396

100

mxn

300 ´ 40

|H_D|

252

1512

10 584

86 436

691 488

|F_D|

399

3771

27 866

229 951

2 217 292

22 897 938

Рис. 4. Зависимость времени поиска максимальных пороговых s-частых эле-

ментов от числа небинарных атрибутов k при n = 40 и m = 300.

знак^∗. Для наглядности результатов счета приведены значения величины r,

равной (-t_G/t_C ), если t_G > t_C , иначе равной t_C /t_G, где t_C - время работы

алгоритма TFP-tree, t_G - время работы алгоритма DPTFP-tree. Серым цве-

том выделены значения величины r в случае, когда достигается ускорение

алгоритма DPTFP-tree относительно алгоритма TFP-tree.

Из результатов, представленных в таблице, следует, что при большом чис-

ле значимых наборов порогов и при большом числе транзакций алгоритм

DPTFP-tree до 3,6 раз работает быстрее алгоритма TFP-tree. На задачах

с небольшим числом транзакций или с небольшим числом значимых набо-

ров порогов алгоритм DPTFP-tree до 2,3 раз работает медленнее алгоритма

TFP-tree.

Эффективность алгоритмов TFP-tree и DPTFP-tree на реальных задачах

Описание задачи

|H_D|

|F_D|

TFP-tree, с DPTFP-tree, с

№ m×n

s h

79 ×8

84672

695634

119

167

-1,4

2048 ×10

786432

22740

6400

3,6

4898 ×12

354294

4520

1609

2,8

165474 ×12

768

2501

2,9

165474 ×12

20300

103052

1159

372

3,1

165474 ×12

216384

1 511248

16442

4884

3,4

440 ×8

46656

-1,2

440 ×8

117649

180

186

-1,0

440 ×8

262144

1087

864

1,3

32560 ×15

42090

186900

504

398

1,3

32560 ×15

48990

220480

548

496

1,1

32560 ×15

55890

254532

840

588

1,4

303 ×14

15488

94696

-1,5

303 ×14

29282

123022

-2,3

303 ×14

197568

787141

727

1230

-1,7

Таким образом, показана целесообразность применения в случае данных

большого размера параллельного поиска максимальных пороговых s-частых

элементов, осуществляемого на базе TFP-дерева и технологии CUDA. Уста-

новлено, что время счета заметно снижается при использовании динамиче-

ского параллелизма в вычислениях на графическом ускорителе GPU.

6. Заключение

Рассмотрена актуальная задача логического анализа данных - задача по-

иска (максимальных) пороговых частых элементов произведения частичных

порядков. Для ее решения на основе использования TFP-дерева (порогового

FP-дерева) и технологии CUDA (Compute Unified Device Architecture) по-

строены и исследованы параллельные алгоритмы. Конструкция TFP-дерева

является модификацией конструкции классического бинарного FP-дерева на

случай небинарных данных и ранее была предложена в [13-15].

Приведены результаты тестирования построенных алгоритмов на модель-

ных и реальных данных. Показано, что в случае больших данных исполь-

зование TFP-дерева заметно снижает время синтеза искомых частых эле-

ментов по сравнению с их последовательным поиском на базе классического

FP-дерева, и установлена целесообразность применения технологии CUDA

для решения поставленной задачи.

СПИСОК ЛИТЕРАТУРЫ

1. Agrawal R., Imielinski T., Swami A. Mining Association Rules between Sets of Items

in Large Databases // Proc. 1993 ACM SIGMOD Int. Conf. on Management of Data.

1993. P. 207-216.

Aggarwal C., Jiawei H. Frequent Pattern Mining. Springer, 2014.

Agrawal R., Srikant R. Fast Algorithms for Mining Association Rules in Large

Databases // VLDB Conf. 1994. P. 487-499.

Zaki M.J. Scalable Algorithms for Association Mining // IEEE Trans. Knowledge

and Data Engineering. 2000. V. 12. No. 3. P. 372-390.

Han J., Pei H., Yin Y. Mining Frequent Patterns without Candidate Generation //

Proc. Conf. on the Management of Data (SIGMOD’00, Dallas, TX). 2000. P. 1-12.

Borgelt C., Wang X. SaM: A Split and Merge Algorithm for Fuzzy Frequent Item

Set Mining // IFSA/EUSFLAT Conf. 2009. P. 968-973.

Borgelt C. Keeping Things Simple: Finding Frequent Item Sets by Recursive Elimi-

nation // OSDM. 2005. P. 66-70.

Takeaki U., Masashi K., Hiroki A. LCM ver. 2: Efficient Mining Algorithms for

Frequent/Closed/Maximal Itemsets // FIMI ’04. 2004.

Agrawal R., Aggarwal C., Prasad V. Depth First Generation of Long Patterns //

KDD ’00: Proc. 6th ACM SIGKDD Int. Conf. on Knowledge discovery and data

mining. 2000. P. 108-118.

10.

Imberman S.P., Domanski B. Finding Association Rules from Quantitative Data

Using Data Booleanization // AMCIS Proc. 2001. P. 369-375.

11.

Angiulli F., Ianni G., Palopoli L. On the Complexity of Inducing Categorical and

Quantitative Association Rules // Theoretical Comput. Sci. 2004. V. 314. No. 1.

P. 217-249.

12.

Elbassioni K.M. On Finding Minimal Infrequent Elements in Multi-dimensional Data

Defined over Partially Ordered Sets // arXiv:1411.2275. 2014.

13.

Генрихов И.Е., Дюкова Е.В. О поиске ассоциативных правил в небинарных дан-

ных // 19-я Всеросс. конф. с междунар. участием “Математические методы рас-

познавания образов”. М.: РАН, 2019. С. 15-19.

14.

Генрихов И.Е., Дюкова Е.В. Поиск частых элементов произведения частичных

порядков и ассоциативные правила // Информационные технологии и нанотех-

нологии (ИТНТ-2020). Сб. тр. по матер. VI Междунар. конф. и молодежной

школы (Самара, 26-29 мая). Самара: Изд-во Самар. ун-та, 2020. Том 4. Науки

о данных. С. 620-629.

15.

Genrikhov I.E., Djukova E.V. Finding Frequent Elements for a Product of Partial

Orders and Association Rules // Int. Conf. on Information Technology and Nano-

technology (ITNT), Samara, Russia. 2020. P. 1-5.

16.

Боресков А.В., Харламов А.А., Марковский Н.Д. Параллельные вычисления на

GPU. Архитектура и программная модель CUDA. М.: Изд-во Моск. ун-та, 2012.

17.

Cheng J., Grossman M., McKercher T. Professional CUDA C Programming. N.Y.:

Wrox, 2014.

18.

Lichman M. UCI Machine Learning Repository. Irvine, CA: University of California,

School of Information and Computer Science. 2013. http://archive.ics.uci.edu/ml.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 24.01.2021

После доработки 05.04.2021

Принята к публикации 30.06.2021