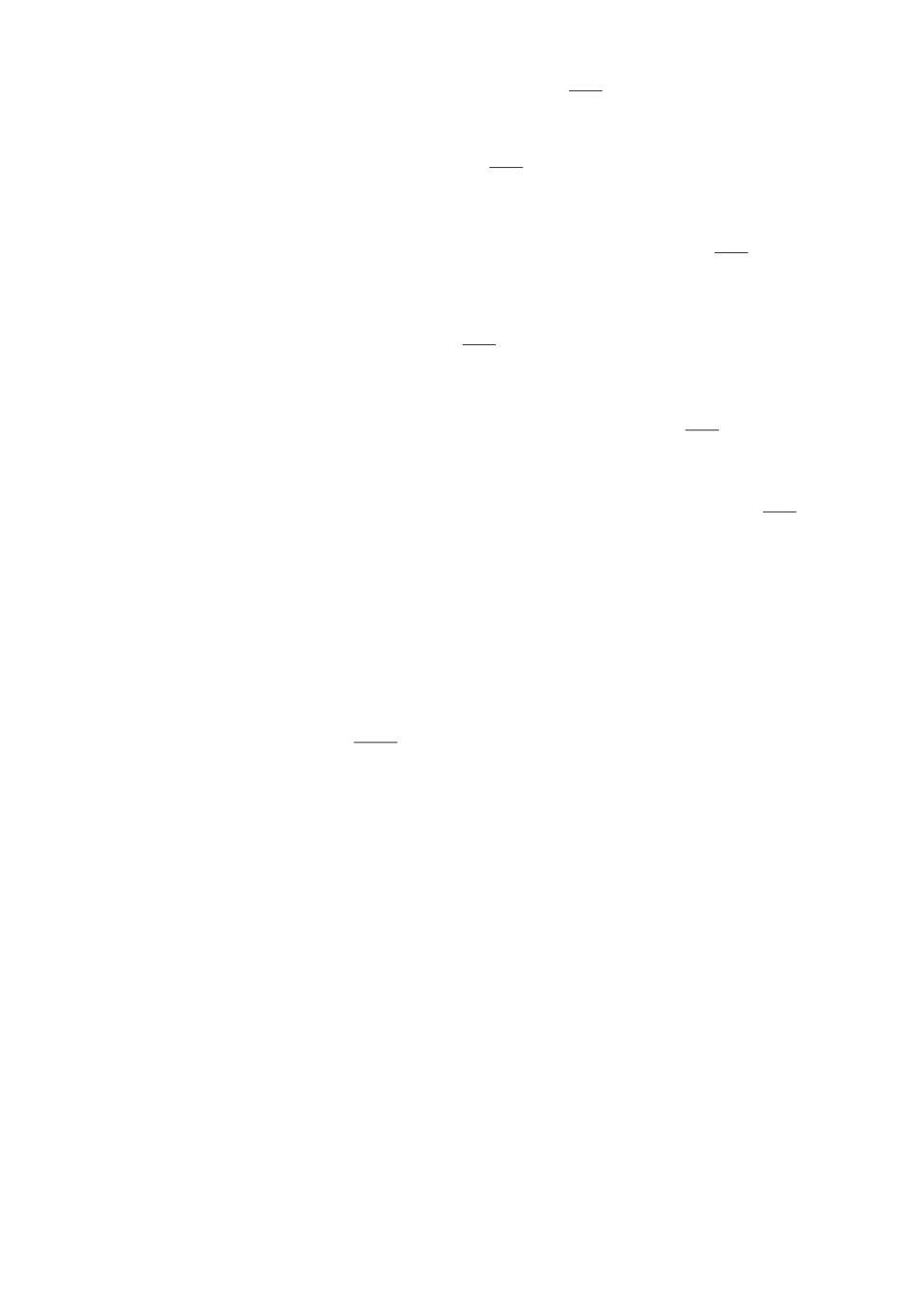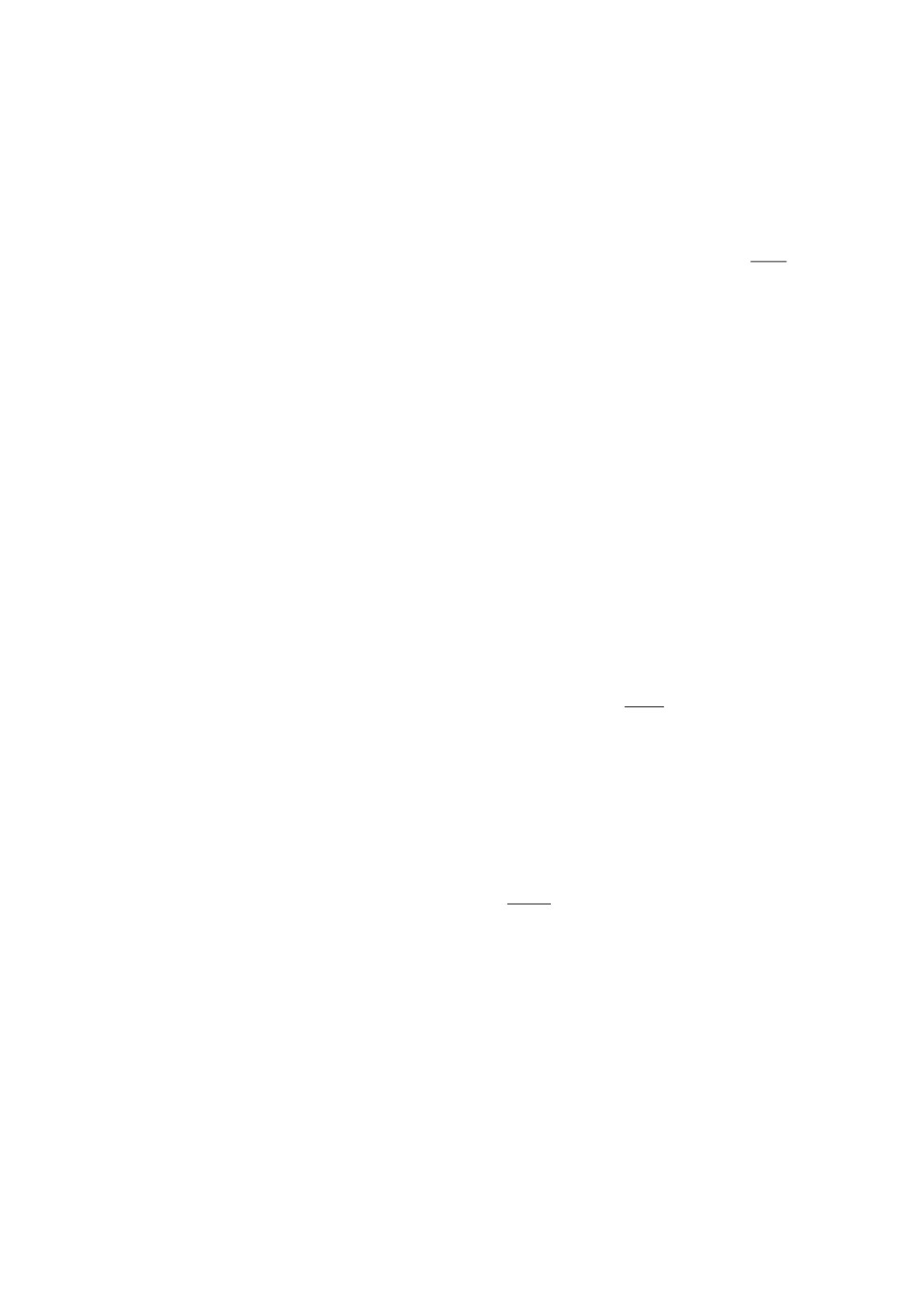Автоматика и телемеханика, № 10, 2021

М.Г. КОЗЛОВА, канд. физ.-мат. наук (art-inf@mail.ru),

В.А. ЛУКЬЯНЕНКО, канд. физ.-мат. наук (art-inf@yandex.ru)

(Крымский федеральный университет им. В.И. Вернадского, Симферополь)

ПСЕВДОБУЛЕВЫЕ МОДЕЛИ УСЛОВНОЙ ОПТИМИЗАЦИИ

ДЛЯ КЛАССА ЗАДАЧ МНОГИХ КОММИВОЯЖЕРОВ

Рассматриваются знаниеориентированные модели, задачи и алгоритмы

построения маршрутов в сложных сетях агентами-коммивояжерами. Фор-

мализация приводит к моделям псевдобулевой дискретной оптимизации с

ограничениями, учитывающими специфику задачи многих коммивояже-

ров. Рассмотрен класс задач, который представим в виде псевдобулевых

оптимизационных моделей с сепарабельными целевыми функциями (мо-

нотонные, линейные) и ограничениями в виде дизъюнктивных нормаль-

ных форм (ДНФ). Показана возможность приближенного синтеза ДНФ

ограничений на основе прецедентной информации. Приведена методоло-

гия, теоретические положения и алгоритмы решения такого класса задач.

Показано, что решение задач маршрутизации может базироваться на при-

менении многоагентного подхода в сочетании с кластеризацией исходной

задачи, алгоритмах псевдобулевой оптимизации с дизъюнктивными огра-

ничениями и метаэвристиках.

Ключевые слова: многоагентные задачи коммивояжера, модели псевдобу-

левой условной оптимизации с дизъюнктивными ограничениями, метаэв-

ристики.

DOI: 10.31857/S0005231021100044

1. Введение

Прикладная теория задач маршрутизации на сложных сетях (типа многих

агентов-коммивояжеров) базируется на точных решениях выделенных клас-

сов задач с полиномиальными алгоритмами решения, использовании прибли-

женных алгоритмов решения (например, с гарантированной функционально-

стью) и декомпозиции (кластеризации) исходной задачи, т.е. сведения к за-

дачам меньшей размерности и уточняющих преобразованиях для возврата

к исходной задаче. Важным в этом процессе является учет всей имеющейся

информации, знаний, фактов и прецедентов как для построения иерархии мо-

делей (извлечение моделей), так и для разработки практических алгоритмов

решения [1-10].

Разнообразие алгоритмов также связано с наличием априорных знаний о

решении или структуре сети, прецедентным характером знаний и требова-

ниями к точности решения. Рационально использование как точных, так и

приближенных алгоритмов и их композиций. Заметим, что задачи приклад-

ной маршрутизации возникают в сочетании с другими известными задачами:

задача о ранце, распределение ресурсов, кластеризации, максимального раз-

реза, покрытия и т.п.

Многоагентные системы с роевым интеллектом используются для реше-

ния сложных задач дискретной оптимизации, которые нельзя эффективно

решать классическими алгоритмами. Агентная модель для сложной сети

задачи типа многих коммивояжеров (Multiple Traveling Salesman Problem,

mTSP) становится интеллектуализированной системой, определяющей эври-

стические алгоритмы поиска оптимального решения реактивными агентами

(следующих заложенным в них правилам).

Синтез многоагентных систем (МАС) искусственного интеллекта (ИИ) по

частичной, прецедентной, априорной информации базируется на результатах

наблюдения за поведением МАС на основе накопленной информации в ви-

де [6]: “. . . вектора состояния, значения качества функционирования системы,

бинарного индикатора допустимости этого состояния”. Для МАС маршрути-

зации типа mT SP используется модель скалярной псевдобулевой условной

оптимизации с ограничениями в виде дизъюнктивной нормальной формы

(ДНФ). Такие модели естественным образом учитывают линейные ограни-

чения по прохождению вершин сети, декларативные требования, требования

предшествования, обязательного прохождения выделенного множества дуг и

другую прецедентную информацию.

Псевдобулевые оптимизационные модели с сепарабельными целевыми

функциями и ДНФ ограничениями, имеющими ограниченную постоянной ве-

личиной длину, являются полиномиально разрешимыми. Представляют ин-

терес классы задач, которые приведены или легко приводятся к форме с

ДНФ ограничениями, так как в общем случае такие приведения являются

экспоненциальными. Синтез модели с ДНФ ограничениями из данных мож-

но осуществлять приближенно, и сложность такой аппроксимации оказыва-

ется полиномиальной. В [6] показано, что число конъюнкций в извлеченной

ДНФ не превышает числа примеров в исходной прецедентной информации.

При этом указывается, что для построения ДНФ ограничений целесообраз-

но использовать решающие деревья. В случае монотонности и линейности

частично заданной целевой функции в публикациях В.И. Донского [3, 6] и

М.Г. Козловой [7, 8] предложены алгоритмы решения задач псевдобулевой

скалярной оптимизации при наличии неполной, прецедентной начальной ин-

формации. Идея этого подхода будет применена для решения многоагентных

задач типа многих коммивояжеров.

В настоящей статье приводится часть проекта, представленного в декабре

2020 г. на Международной конференции “Интеллектуализация обработки ин-

формации” [2]. Исторические аспекты по задачам коммивояжера, их обобще-

ниям, точным и приближенным алгоритмам решения можно найти в [11-13].

В [14] показано применение композиции алгоритмов: модификация генетиче-

ского алгоритма, муравьиный, роевой (пчелиной колонии), имитации отжи-

га. Предложен и реализован обобщенный алгоритм, в котором исходной сети

ставится в соответствие более простая сеть (сеть облета). Алгоритм инспи-

рирован рядом актуальных прикладных задач: задачей планирования много-

дневных туристических маршрутов на инфраструктурной сети достоприме-

чательностей Крыма и задачей доставки ресурсов агентами-коммивояжерами

по территории Ялты в условиях чрезвычайных ситуаций (ЧС). Численный

эксперимент проведен для задачи маршрутизации по карте ГИС для го-

родской инфраструктуры. Реализованы алгоритмы кластеризации, в кото-

рых первоначально пройденные маршруты уточняются с помощью алгорит-

мов 2-opt, имитации отжига и других метаэвристик [14].

В данной статье выделено важное направление - построение МАС mT SP

на базе моделей псевдобулевой оптимизации с дизъюнктивными ограниче-

ниями.

2. Предварительные сведения. Задачи псевдобулевой оптимизации

Оптимизационные задачи с булевыми переменными имеют широкие при-

ложения [1, 3, 15]. В связи с задачами маршрутизации на графах особый инте-

рес представляют задачи псевдобулевой оптимизации. Достаточно подробно

такие задачи исследовались в [16, 17], где разработаны методы решения в слу-

чае аналитически заданных моделей псевдобулевой оптимизации. В [18] псев-

добулевые функции рассматриваются как отображения из семейства подмно-

жеств конечного исходного множества действительных чисел. Оптимизация

на графах в классе псевдобулевых функций представлена в [19, 20]. Базовые

результаты содержатся в [21, 22].

Введем обозначения:

Bⁿ = {0,1}ⁿ

единичный n-мерный куб, P₂(n) = {F : Bⁿ → {0, 1}}

класс функций алгебры логики (ФАЛ), зависящих от n переменных, x =

= (x₁, x₂, . . . , x_n) ∈ Bⁿ.

Функция вида f : Bⁿ → R, где R - множество действительных чисел, на-

зывается псевдобулевой [1, 3, 18]. Для обозначения класса таких функций

будем использовать обозначение P S₂(n), а для обозначения класса линей-

ных псевдобулевых функций LP S₂(n). Функции из P S₂(n) определены на

множестве вершин единичного n-мерного куба Bⁿ и могут принимать веще-

ственные значения.

Задача вида

(1)

extr f(x),

x∈Ω⊆Bⁿ, f ∈PS₂

(n),

называется задачей псевдобулевой оптимизации.

Введем характеристическую функцию множества ограничений Ω:

{

x ∈ Ω;

FΩ(x) =

x ∈ Bⁿ\Ω.

Задачу (1) можно представить в эквивалентной форме:

(2)

extr f(x), F_Ω(x) = 1, f ∈ P S₂(n), F_Ω ∈ P₂(n),

x∈Bⁿ,

где P₂(n) - класс функций алгебры логики от n переменных.

⋁_m

Пусть D_F

= j=1^Kj^{-любаядизъюнктивнаянормальнаяформафунк-}

ции F_Ω(x); тогда задача, эквивалентная задачам (1) и (2), имеет вид:

(3)

extr f(x), DFΩ (x) = 1,

x∈Bⁿ.

Задача (3) называется задачей псевдобулевой оптимизации с дизъюнктив-

ным ограничением, и форму ее представления называют канонической.

Определение 1. Переменная x_i называется существенной для f ∈

∈PS₂(n), если найдется такой набор значений переменных α₁,...,α_i-1,

α_i+1,... ,α_n, что f(α₁,... ,α_i-1,0,α_i+1,... ,α_n) = f(α₁,... ,α_i-1,1,α_i+1,

...,α_n). В противном случае переменная называется фиктивной.

Определение 2. Псевдобулевые функции f₁ и f₂ называются равными,

если функция f₂ может быть получена из f₁ путем введения или удаления

фиктивных переменных.

Каноническая форма псевдобулевой функции f аналогична совершенной

дизъюнктивной нормальной форме в P₂(n) и имеет вид

∑

f (x₁, . . . , x_n) =

(4)

a_σxσ11 · ... · xii · ... · xnn,

σ∈Bⁿ

где

{

x, σ = 1,

σ = (σ₁,...,σ_n), σ_i ∈ {0,1}, i = 1,n, a_σ ∈ R, x^σ =

x, σ = 0.

Каждая псевдобулевая функция может быть представлена в полиноми-

альной форме над полем действительных чисел

k_f

∑

(5)

f (x₁, . . . , x_n) =

c_jxj1 · ... ·xjr

+ c₀, c_j ∈ R, j = 1,... ,k_f.

j=1

Задача псевдобулевой оптимизации в форме слабых неравенств имеет вид:

extr f(x₁, . . . , x_n), g_j (x₁, . . . , x_n) ≤ 0, j = 1, 2, . . . , m,

(6)

(x₁, . . . , x_n) ∈ Bⁿ, f, g_j ∈ P S₂(n).

Определение 3. Две формы представления оптимизационной задачи

называются эквивалентными, если множества их решений совпадают.

Теорема 1[4].Для любой задачи псевдобулевой оптимизации в форме(1)

существует эквивалентная форма представления

(7)

extr f(x), h(x) ≤ 0,

x∈Bⁿ,

с единственным ограничением в виде нестрогого неравенства, где f,h ∈

∈PS₂(n) есть некоторые полиномы.

Полиномиальное представление для функции f ∈ P S₂(n) существует все-

гда.

Теорема 2

[4]. Любая задача оптимизации псевдобулевой функции с

ограничениями, определяющими непустое множество допустимых реше-

ний Ω задачи (1), может быть представлена в эквивалентной форме с

дизъюнктивным условием (3).

Доказательство теоремы 2 следует из существования эквивалентной фор-

мы задачи с характеристическими функциями на наборе допустимых значе-

ний F_Ω(x) и полноты представления ФАЛ в виде дизъюнктивных нормаль-

ных форм.

Определение 4. Представление задач произвольного класса Z в фор-

ме F называется полным в Z, если любая задача этого класса может быть

представлена в форме F.

Из данного определения следует, что представление задач условной опти-

мизации псевдобулевой функции в форме с дизъюнктивным условием явля-

ется полным.

Область допустимых решений задачи (3) и эквивалентной ей задачи (1)

может быть представлена в виде:

⋃

Ω= NKj,

j=1

где NKj - интервал ранга r_j , соответствующий элементарной конъюнкции

K_j = xσj1j₁ & ... &xjjrj , что приводит к еще одной эквивалентной форме задачиrj

(1):

(8)

extr

f(x).

1≤j≤m

x∈N_Kj

Действительно, учитывая, что область допустимых решений есть объеди-

нение интервалов NKj , j = 1, m, легко убедиться, что экстремальное решение

задачи можно определить путем его выбора из предварительно найденных

допустимых решений, являющихся экстремальными в интервалах NKj .

Рассмотрим основные алгоритмы решения задач псевдобулевой оптими-

зации. Пусть дана задача псевдобулевой оптимизации с линейной целевой

функцией

∑

⋁

(9)

max c_ix_i,

K_j(x) = 1,

x∈Bⁿ,

i=1

j=1

где K_j (x) = xσj1j₁ & . . . &xjjrj , j = 1, m. Приведем к эквивалентной форме:rj

∑

⋃

(10)

max c_ix_i,

x∈ NKj,

i=1

j=1

Рис. 1. Схема решения задачи.

где NKj - интервал в Bⁿ, соответствующий конъюнкции K_j; интервал NKj

определяется набором значений {j₁, . . . , jrj } (направление) и множеством

{σj1 , . . . , σ

} (код интервала).

jrj

Решение (10) сводится к решению задачи

∑

(11)

max

c_ix_i,

1≤j≤m

x∈N_Kj

i=1

которое в свою очередь требует решения m задач вида:

∑

(12)

max

c_ix_i,

x : (xj1 = σj1)&...&(xjrj = σ

jrj

i=1

Задача (12) решается следующим образом: допустимыми являются толь-

ко те булевы наборы x, у которых зафиксированы координаты xj1 = σj1 ,

...,xjrj =σ

, а остальные могут иметь любые значения из множе-

jrj

ства {0, 1}. Свободные переменные (вне множества номеров {j₁, . . . , jrj })

можно назначать единичными или нулевыми в зависимости от значения c_i,

i ∈ {1,2,...,n}\{j₁,...,jrj} - коэффициентов целевой функции. Экстремаль-

ные решения x^∗ задачи (12) будут определяться формулой [23]:

{

i ∈ {j₁,...,jrj},

(13)

x^∗i =

ϕ(c_i), i ∈ {j₁, . . . , jrj },

где



 1, c_i > 0,

ϕ(c_i) =

c_i < 0,



α,

c_i = 0,

α - любое значение из {0,1}. В случае когда все c_i = 0, задача (12) имеет

единственное решение, а исходная задача (11) - не более m решений.

На каждом интервале NKj при вычислении x^∗i согласно (13) просматрива-

ется n значений, а интервалов всего m, поэтому сложность решения O(mn).

Так как любую задачу псевдобулевой оптимизации можно представить в

эквивалентной форме с ДНФ ограничением, то это справедливо и для за-

дач с линейной целевой функцией. Следовательно, решение любой линейной

задачи (в том числе задачи коммивояжера) можно осуществлять по схеме,

представленной на рис. 1.

Теорема 3

[4]. Если задача условной оптимизации линейной псевдобу-

левой функции с ограничениями-неравенствами приводится к эквивалент-

ной форме с дизъюнктивным ограничением за число шагов, ограниченное

полиномом от размерности задачи, то она разрешима за полиномиальное

время.

3. Псевдобулевая модель задачи коммивояжера

Рассмотрим задачу коммивояжера, формализованную в виде модели ли-

нейной псевдобулевой условной оптимизации с неотрицательными коэффи-

циентами (c_ij ≥ 0) целевой функции:

∑

(14)

c_ijx_ij

→ min,

i=1 j=1

∑

(15)

x_ij = 1,

x_ij

= 1, i, j = 1, n,

i=1

j=1

(16)

u_i - u_j + nx_ij

≤ n - 1, i,j = 2,n, i = j.

Здесь u_i

произвольные действительные числа (в частности, им мо-

жет соответствовать нумерация вершин, по которым проходит коммивоя-

жер). Ограничения

(16) препятствуют образованию подциклов. Чтобы

упростить выкладки, будем использовать обозначение двухиндексных ве-

личин через одноиндексные:

x = (x₁,x₂,...,x_N) = (x₁₁,x₁₂,...,x_nn) ∈ B^N,

c = (c₁,c₂,...,c_N) = (c₁₁,c₁₂,...,c_nn), где N = n². Ограничениям можно по-

ставить в соответствие функции F_j (x) ∈ P₂(N), j = 1, M, где M - число огра-

ничений. Можно в x использовать и другую нумерацию элементов: x_ij , i, j =

= 1, n.

Определение 5. Вершина α ∈ Bⁿ называется верхним нулем моно-

тонной функции алгебры логики f(x), если f(α) = 0 и для всякой вершин

из α

β следует, что f

β) = 1 [24].

Лемма 1. Если







∑

x_ij = 1,

x_ij = 1, i,j = 1,n, u_i - u_j + nx_ij ≤ n - 1, i = j

⇔





j=1

i=1

⇔ {F_j(x) = 0} ,

то F_j - монотонные функции алгебры логики (ФАЛ) и задачу (14)-(16)

можно записать в виде

⋁

(17)

(c, x) → min, F₀(x) =

(x) = 0,

j=1

где c = (c₁₁, c₁₂, . . . , c_nn), (c, x) - скалярное произведение, F₀(x) - монотонная

ФАЛ.

Доказательство. Покажем монотонность функций F_j(x). Пусть

β∈B^N такие, что α

β, т.е. α_ij ≤ βij ∀i, j = 1, n. Тогда



∑

S(α) =

α_ij - 1,

α_ij - 1, i,j = 1,n,



j=1

i=1





u_i - u_j + nα_ij - (n - 1), i,j = 2,n

≤





∑

β_ij - 1, i,j = 1,n,

≤βij -1,

j=1

i=1





u_i - u_j + nβ_ij - (n - 1), i,j = 2,n

= S

β).



Неравенства выполняются покомпонентно в силу α_ij ≤ β_ij ∀i, j = 1, n.

По условию леммы (S(α) ≤ 0) ⇔ (F_j (α) = 0), (S

β)≤0)⇔(F_j

β) = 0).

Учитывая, что S(α) ≼ S

β), имеем (F_j (α) = 1) ⇒ (F_j

β) = 1), поэтому

Fj (α) ≤ Fj

β). Следовательно, F_j (x) - монотонная ФАЛ.

⋁_M

Функция F₀(x) =

Fj (x) является монотонной. Это следует из того,

j=1

что класс монотонных ФАЛ является замкнутым и содержит дизъюнкцию.

Функция F₀(x) равна нулю тогда и только тогда, когда выполняются все

⋁_M

ограничения (14)-(16), так как дизъюнкция

Fj (x) равна нулю только

j=1

при F_j (x) = 0 для всех j = 1, M. Лемма 1 доказана.

{

Отсюда следует, что если область допустимых решений Ω =

x∈B^N :

}

F₀(x) = 0

= ∅, то решением задачи является верхний ноль функций F₀(x).

Задача (17) сводится к задаче расшифровки монотонной ФАЛ или к поиску

ее верхних нулей [4].

Псевдобулевая задача линейного программирования (17)

{

}

(18)

min(c, x), Ω =

x∈B^N : F₀(x)=0 ,

x∈Ω

с ДНФ ограничениями позволяет учитывать знания о решении задачи ком-

мивояжера, которые представимы в ДНФ форме. Например, если необхо-

димо включить прохождение дуг x_kl и x_pm, тогда к ограничениям добав-

ляется условие (x_kl - 1) ∨ (x_pm - 1) = 0. Если, наоборот, не включать, то

x_kl ∨ x_pm = 0 [25].

Полученный формализм позволяет учитывать знания о модели и решени-

ях, использовать их в теоретических обоснованиях и конкретных алгоритмах

решения.

4. Модели псевдобулевой условной оптимизации с дизъюнктивными

ограничениями для задачи многих коммивояжеров

Задаче многих коммивояжеров (mT SP ) с общими интересами соответ-

ствует одна целевая функция, выражающая минимум общего расстояния,

как и в задаче для одного коммивояжера. Ограничения линейные. Задача

приводится к задаче псевдобулевой оптимизации с дизъюнктивными ограни-

чениями.

При большой размерности задачи (сложность сети) условной псевдобу-

левой оптимизации с ДНФ ограничениями применять полиномиальные ал-

горитмы, предназначенные для такого класса задач, может быть нерацио-

нально. Требуется упрощение задачи (применение приближенных, эвристи-

ческих методов) с помощью отсечения излишних вариантов перебора на ос-

нове имеющихся знаний. Прежде всего снижение сложности (размерности)

достигается с помощью кластеризации сети. При этом количество агентов,

количество депо и их расположение, количество кластеров может быть зада-

но, искомо или быть произвольным.

Следуя идеологии сведéния исходной задачи к нескольким задачам мень-

шей размерности, рассмотрим следующий подход к решению задачи марш-

рутизации для многих агентов. Пусть m = 2 (два агента).

Алгоритм решения задачи для двух коммивояжеров (AmTSP).

Вход: сеть S = (G, C), G = (U, V ), n = |V |, U - множество дуг,

C - матрица расстояний (весов); информация о структуре сети.

Выход: маршруты коммивояжеров, длина общего маршрута.

1: Провести кластеризацию сети: S = S₁ ∪ S₂, G = G₁ ∪ G₂, V = V₁ ∪ V₂

(V₁ ∩ V₂ = ∅).

2: На сетях S₁, S₂ сформировать задачи коммивояжеров,

выписать все основные и дополнительные ограничения.

3: Трансформировать задачи коммивояжеров к задачам псевдобулевой

оптимизации с ДНФ ограничениями.

4: Найти решения задач с ДНФ ограничениями.

5: Провести локальные преобразования, обмениваясь вершинами множеств

V₁,V₂. Добавление вершины приводит к изменению ДНФ ограничений

(добавление интервалов конъюнкций).

Алгоритм остается полиномиальным.

6: Выбрать лучший вариант (или провести заданное число итераций).

7: Получить решение исходной задачи.

Каждый шаг алгоритма AmT SP конкретизируется в зависимости от

структуры (сложности) исходной сети и всей имеющейся информации (зна-

ний).

Задача каждого коммивояжера на выделенном кластере является задачей

скалярной псевдобулевой условной оптимизации, т.е. может быть представ-

лена в канонической форме с дизъюнктивными ограничениями (9):







∑∑

⋁



(19) min

f_k(x) = (c^k, x) =

c^kijx_ij,

= 1, k = 1, m



xσj1j1&...&xjjrjrj



i=1 j=1

j=1

Каноническая модель является исчерпывающей в своем классе в силу

полноты. Левая часть ограничения (19) является ДНФ характеристической

функции множества Ω^k-ограничений искомой задачи на k-м кластере, в ко-

торой может быть учтена дополнительная информация о структуре кластера

и искомого решения (запреты, предписания и др.).

В случае общих интересов модель будет однокритериальной:

∑

⋁

(20)

min f₀(x) = min f_k(x),

= 1.

xσj1j₁ & ... &xjjrj

k=1

j=1

Процессом выбора решения будем называть поиск такого набора значений

α∈B^N, признаковых предикатов, чтобы (одновременно или по отдельности):

обращался в единицу один или несколько целевых предикатов;

достигала экстремального значения несколько (или одна в однокрите-

риальной постановке) псевдобулевых функций f_k, k = 1, m.

Единственное ограничение канонической модели (20) в виде ДНФ харак-

теристического множества ограничений задает И/ИЛИ граф, которому соот-

ветствует логическая система продукций. Существование логической систе-

мы продукций (ЛСП)

xσj1j₁ & ... &xjjrj → gj,rj

g_j → g₀, j = 1,M,

позволяет выводить целевой факт g₀ = “ x

допустимое решение”. Граф

И/ИЛИ ограничения канонической модели задачи mT SP является трехъ-

ярусным. Любой граф ЛСП, не имеющий циклов, может быть сведен к трехъ-

ярусному и представлен в виде ДНФ. Отсюда следует, что соответствующая

база знаний (БЗ) системы построения допустимого решения mT SP должна

удовлетворять следующим требованиям:

1) решения mT SP должны удовлетворять ограничениям задачи, следова-

тельно, ЛСП должна обеспечивать возможность вывода целевых предикатов,

соответствующих этим ограничениям;

2) группа ограничений, которые должны выполняться одновременно, за-

даются вершиной типа “И”, связывающей эти ограничения вместе.

Заметим, что ДНФ ограничение может быть получено с помощью обуче-

ния по прецедентной (эмпирической) информации [6, 7]. Для синтеза ДНФ

по заданным ЛСП можно использовать D- и DS-алгоритмы [3], реализую-

щие соответственно стратегии “сверху вниз” и “снизу вверх”, т.е. реализуется

синтез областей допустимости решений в знаниеориентированных продук-

ционных системах моделей псевдобулевой условной оптимизации, соответ-

ствующих mT SP (в этих же публикациях можно найти оценки сложности

алгоритмов).

Вопрос полноты знаний об ограничениях в БЗ задачи коммивояжера яв-

ляется важным и рассматривается самостоятельно в теории знаниеориенти-

рованных систем.

Уточним шаги 4, 5 алгоритма AmT SP с точки зрения преодоления неопре-

деленности (для m = 2, аналогичная ситуация для m > 2). Задачи псевдобу-

левой оптимизации для каждого кластера имеют вид:

min f₁(x) = min(c¹, x), F₁(x) = 0,

min f₂(x) = min(c², x), F₂(x) = 0,

(21)

c^k = (c^k11,c^k12,... ,c^knn) ≡ (c^k1,c^k2,... ,c^kj,... ,c^kN ),

x ∈ B^N, N = n², F_k(x) ∈ P₂(N), k = 1,2.

В том случае, когда кластеры определены единственным образом, а це-

левые функции и ограничения заданы точно, решение полученных задач

на кластерах сводится к расшифровке монотонной функции алгебры логи-

ки (или к поиску ее верхних нулей). В более общем случае модели mT SP

получены как неполное представление исходной задачи mT SP : когда в ре-

зультате кластеризации (или при другом сведении и задаче меньшей раз-

мерности) при исследовании линейной модели не удалось получить полную

информацию о ее ограничениях. Но по доказанному выше F_j (x) являются

монотонными функциями алгебры логики.

Будем предполагать, что существуют множества

{

}

{

}

x∈B^N :F_k(x)=1 ;

(22)

{

}

{

}

x∈B^N :f_k(x)=0 ;

x ∈ B^N : f_k(x) = 1 , k = 1,2.

С позиции первого коммивояжера (k = 1) F_k(x) функция, определяю-

щая допустимые решения, задана частично с помощью указания множеств

(прецедентов или фактов), т.е. заданы некоторые частич-

ные функции алгебры логики f_k, k = 1, 2.

Пусть Φ_k множество монотонных функций алгебры логики из P₂(n),

и значение “1” на множе-

, а Z_k(Φ_k) множество всех верхних нулей всех функций из Φ_k.

Непротиворечивым решением задач (21) называется такой набор

z∗k ∈

∈Z_k(Φ_k), что

∑

z^∗j = min

c^kjz_j.

z∈Z_k(Φ_k )

j=1

Не теряя общности, можно считать, что булевы переменные упорядочены

так, что c^k1 > . . . > c^kN . Это легко выполнить для любой исходной задачи.

Теорема 4. Функция fk ∈P₂(N), не являющаяся константой, монотон-

на тогда и только тогда, когда для любых пар вершин x, y∈ B^N таких, что

f_k(x) = 1, f_k(y) = 0, найдется переменная с номером i ∈ {1,2,... ,N} такая,

что x_i = 1, y_i = 0.

Доказательство.

Необходимость. Докажем необходимость методом от противного. Пусть

f_k ∈ P₂(N) не константа, монотонна и не существует переменной с номером

i∈{1,2,...,N} такой, что x_i = 1, y_i = 0, т.е. x_i ≤ y_i, i = 1,N. Тогда x ≼ y, но

f_k(x) > f_k(y), что противоречит условию монотонности функции f_k.

Достаточность. Рассмотрим три множества пар наборов x, y ∈ B^N :

W_k1 = {(x, y) : f_k(x) = 1, f_k(y) = 0};

W_k2 = {(x, y) : f_k(x) = 0, f_k(y) = 1};

W_k3 = {(x, y) : f_k(x) = f_k(y)}.

Пусть x ∈ W_k1. Тогда f_k(x) > f_k(y) и по условию теоремы 4 найдется такой

индекс i, что x_i > y_i. Следовательно, либо x ≻ y, либо наборы x и y - несрав-

нимы. Для всех сравнимых наборов из W_k1 имеем: x ≻ y и f_k(x) > f_k(y).

Аналогично проверяется выполнение условия монотонности функции f_k

на множества W_k2.

Пусть x ∈ W_k3, тогда f_k(x) = f_k(y), в том числе всегда, когда x ≼ y. Учи-

тывая, что объединение W_k1 ∪ W_k2 ∪ W_k3 содержит любую пару вершин ку-

ба B^N , получаем, что f_k - монотонная функция: если x ≼ y, то f_k(x) ≤ f_k(y).

Теорема 4 доказана.

На основании теоремы 4 можно сделать следующий вывод. Если во мно-

частичной функции алгебры логики f_k найдутся та-

, что не существует переменной с номером

i ∈ {1,...,N}, для которой α_i < β_i, то f_k не может быть доопределена моно-

тонной функцией.

Пусть частичная функция f_k доопределена монотонной функцией ϕ_k.

, следовательно, любой набор

, но N^kj не

должен покрываться

Класс монотонных функций ϕ_k, доопределяющих f_k, обозначим Φ_k ⊂ M_k.

Функции класса Φ_k определяют множество:

{

}

Φk = gk ∈ P2(N) : gk(x) = ϕk(x), ϕk ∈ Φk

Любая функция может быть представлена сокращенной дизъюнктивной

нормальной формой (ДНФ) так, что может быть указан набор максимальных

произвольной

функции g_k ∈ Φ_k и соответствующую ему элементарную конъюнкцию L =

= xi1& ... &xir. Вхождение переменных в простую импликанту только с

инверсиями доказывается с учетом монотонности функции g_k(x). Набор

α ∈ N^kL является допустимым решением, и в этом наборе αi1 = 0,...,αir = 0.

Среди всех наборов

α ∈ N^kL наибольшее значение целевой функции бу-

дет достигаться на наборе, в котором α_j = 1 для всех j из множества

{1, 2, . . . , N} \ {i₁, i₂, . . . , i_r}. Назовем такой набор экстремальным.

Если теперь для каждой простой импликанты всех функций из множе-

ства Φ_k выбрать экстремальный набор, то в полученном множестве будут

содержаться все непротиворечивые решения задачи.

Различные доопределения функц{и f_k функц}ями ϕk ∈ Φk отличаются

∪Mfk

, поэтому простые импли-

канты различных функций g_k из Φ_k могут отличаться рангом. Экстремаль-

ная постановка задачи требует из всех простых импликант всех функций

g_k ∈ Φ_k выделить кратчайшие. Для построения таких простых импликант с

инверсиями, необходимыми для любых доопределений, можно использовать

следующий алгоритм.

Алгоритм построения простых импликант.

выписать конъюнктивную нормальную фор-

му (КНФ) K_k(α), каждая дизъюнкция которой состоит из переменных x_i

(с инверсиями), таких, что α_i < β_i для одного из наборо

; КНФ



K_k(α) будет содержать m^k1 =

 дизъюнкций число наборов в мно-

2: В полученных КНФ K_k(α₁), . . . , K_k(α_mk

| (число наборов

), раскрыть скобки и выполнить операции поглощения, получая ДНФ

D₁,... ,D_mk .

3: Записать ДНФ D₁ ∨ . . . ∨ Dm0 и выполнить все возможные операции по-

глощения. Будет получена ДНФ D(Φ_k).

, являющиеся частью исходной информации в за-

даче (21) и содержащие m^k0 + m^k1 двоичных наборов, можно рассматривать

как стандартную обучающую информацию задачи Z_k распознавания: в обу-

чающей таблице T^k

относятся к классу K^k1

m^k0m^k1

к классу K^k2 недопустимых

решений.

Обозначим через A^kz = A^kz(T_mk

m^k ,x)алгоритмраспознаванияклассапро-1

извольного набора x ∈ B^N \T_mk

m^k1 ;пустьAZ∗ корректныйалгоритм:

{

(

)

1, x ∈ Kk2 = Bn\Ωk,

A^k∗z T_mk

m^k1

0, x ∈ Kk1 = Ωk, k = 1,2.

Очевидно, что если информация в T_mkmk1 достовернаиалгоритмAz∗ от-

носит экстремальный набор x^∗, являющийся непротиворечивым решением

задачи (21), к классу K^k1 = Ω_k, то x^∗ является решением задачи

∑

min c^kix_i/x ∈ Ω_k.

i=1

Пусть алгоритм A^kz экстремальный в некотором классе алгоритмов рас-

познавания или построен с применением корректирующих (алгебраических)

методов, т.е. является в некотором смысле наилучшим для решения задачи

Z_k(T_mk

m^k ,x).1

Подход к решению mT SP как задачи линейного псевдобулевого програм-

мирования с частично заданными ограничениями с применением алгоритмов

распознавания образов состоит в следующем:

1) при помощи алгоритма находится множество экстремальных наборов

ℵ^k = {x^∗} для задачи (21)-(22);

(

)

}

к классу K₁; ℵ^kA ⊆ ℵ^k; ℵ^kA =

x^∗ ∈ ℵ^k : A T_mk

,x^∗

=0 ;

m^k

3) если ℵ^kA = 0, то входящий в него экстремальный набор, которому со-

ответствует наибольшее значение целевой функции, объявляется решением

задачи;

∪ℵ^k,

и повторяется п. 1, внутри которого обеспечивается проверка монотонности,

обеспечивающая линейность модели.

множества экстремальных

наборов ℵ^k равносильно переопределению для некоторых функций алгебры

логики верхних нулей единицами.

Линейность задачи mT SP позволила эффективно “сузить” область поиска

решения, что обеспечивается указанным алгоритмом (см. [9] по сужающим

запросам).

5. Многокритериальные задачи многих коммивояжеров,

представленные в канонической форме

Пусть задача mT SP сводится к многокритериальной псевдобулевой опти-

мизации с дизъюнктивным ограничением:



min f₁(x), min f₂(x), . . . , min f_m(x),





σ_jr

mxσj1

(23)

&...&x

= 1,

j₁



jrj

 j=1

f_k ∈ LPS₂(N), k = 1,m,

x∈B^N.

Отметим, что задачи псевдобулевой оптимизации возникают как результат

синтеза моделей mT SP на основе индуктивного обобщения или построения

логического описания области дедуктивной выводимости в системах, осно-

ванных на знаниях.

Необходимо найти паретовское множество P задачи (23), его логическое

описание в виде дизъюнктивной нормальной формы и подходов к выбору

решения x^∗ ∈ P. Для этого используем необходимое условие принадлежности

точки множеству Парето и принцип ветвей и границ.

В задаче mT SP учитывается информация о распределении весов дуг. Вы-

бор прохождения тех или иных дуг для коммивояжера зависит от среднего

значения веса дуги, дисперсии (при большой дисперсии преобладают дуги с

большими весами). Если в матрице весов вычесть среднее значение веса, по-

лучим новую матрицу весов с положительными и отрицательными значения-

ми. Такие матрицы появляются в процессе реализации некоторых алгорит-

мов T SP . Поэтому необходимое условие принадлежности точки множеству

Парето учитывает знаки коэффициентов c^kj, j = 1, N , N = n², k = 1, m.

Рассмотрим необходимое условие принадлежности точки множеству Па-

рето в задаче безусловной оптимизации.

Обозначим через P_i множество номеров переменных, имеющих положи-

тельный, а через N_i множество номеров переменных, имеющих отрица-

тельный коэффициент в линейной функции f_i, i = 1, m. Пусть

P₀ = P₁ ∩ P₂ ∩ ... ∩ P_m, N₀ = N₁ ∩ N₂ ∩ ... ∩ N_m.

Лемма 2. Если для задачи безусловной многокритериальной оптимиза-

ции mT SP

{

min f₁(x), min f₂(x), . . . , min f_m(x),

(24)

x ∈ B^N, f₁,...,f_m ∈ LPS₂(N),

множества P₀ и N₀ непусты и точка x^∗ является паретовской, то она

удовлетворяет уравнению

(

)(

)

(25)

x_i

& x_i

= 1.

i∈P₀

i∈N₀

Доказательство. Пусть α любая точка, удовлетворяющая уравне-

нию (25). Тогда найдется такое i, что α_i = 0 при i ∈ P₁ ∩ P₂ ∩ . . . ∩ P_m или

α_i = 1 при i ∈ N₁ ∩ N₂ ∩ ... ∩ N_m. Заменяя α_i на α_i, получим точку α^′ такую,

что f₁(α^′) < f₁(α), f₂(α^′) < f₂(α), . . . , f_m(α^′) < f_m(α) и тогда α не является

паретовской точкой. Лемма 2 доказана.

Замечание 2. Если P₀ = ∅ и N₀ = ∅, то необходимыми условиями эф-

фективности точки x^∗ в задаче (24) являются &

x_i = 1 и & x_i = 1. Если

i∈P₀

i∈N₀

P₀ = ∅ и N₀ = ∅, то необходимым условием эффективности точки x^∗ в зада-

че (24) является & x_i = 1. Если P₀ = ∅ и N₀ = ∅, то необходимым условием

i∈P₀

эффективности точки x^∗ в задаче (24) является & x_i = 1.

i∈N₀

Определение 6. Нижней векторной оценкой допустимого множе-

ства X называется вектор

(

)

minf1(x), minf2(x), ... , minfm(x)

x∈X

Определение 7. Вектор (a₁,a₂,...,a_m) мажорируется вектором

(b₁, b₂, . . . , b_m), если a_j ≤ b_j для всех j = 1, m, причем хотя бы для одного j

выполняется строго неравенство a_j < b_j .

Определение 8. Рекордом называется вектор значений скалярных

критериев в некоторой допустимой точке γ, который не мажорируется

никаким другим имеющимся рекордом или нижней векторной оценкой, по-

лученной для какого-либо подмножества допустимого множества решений.

Будем использовать метод ветвей и границ (см. [3, 8] для данного класса

задач). Ветвление будем осуществлять путем фиксации значений 0 и 1 пере-

менных x_i, i = 1, N . На каждом шаге ветвления будет происходить измель-

чение множества B^N и порождение подмножеств-интервалов, подлежащих

исследованию.

Интервал подлежит исключению из рассмотрения в следующих случаях:

а) существует рекорд, мажорирующий верхнюю векторную оценку этого

интервала;

б) известен другой интервал, нижняя векторная оценка которого мажори-

рует верхнюю векторную оценку этого интервала. Интервал подлежит ветв-

лению, если он не подлежит исключению и его верхняя векторная оценка

отличается от нижней. Выбор переменной и интервала, подлежащего ветвле-

нию, является эвристическим элементом метода и будет рассмотрен далее.

Рассмотрим задачу (24) с добавлением дизъюнктивных ограничений.

Теорема 5. Пусть в задаче (24) существует непустое множество Па-

рето P, и к данной задаче добавляется ограничение x ∈ Ω; Ω = ∅; Ω ⊂ B^N,

Ω = B^N. Для полученной задачи множество P ∩ Ω, если оно не пусто, бу-

дет состоять только из паретовских точек.

Доказательство. Пусть x∗ ∈{P ∩ Ω}. Тогда x∗ ∈P и не мажорируется

ни одной точкой из B^N и, тем более, ни одной точкой из P ∩ Ω, а так как

x₂

x₃

H(26, 26)

L(1, 1)

x₁

x₂

H(1, 26)

H(26, 25)

L(0, 1)

L(25, 0)

x₄

x₃

f(1, 1)

R₁(0, 26) R₂(26, 0) R₃(25, 25)

Рис. 2. Начальное дерево.

Рис. 3. Результат решения задачи.

x^∗ ∈ Ω, то она является допустимой. Таким образом, x^∗ немажорируемая

допустимая точка, следовательно, является паретовской. Теорема 5 доказана.

Условие (25) не является достаточным. В этом можно убедиться, рассмот-

рев следующий упрощенный пример:



 min f1(x) = -25x1 - x2 + x3 + x4;

min f₂(x) = x₁ - x₂ + x₃ - 25x₄;



x∈B^N.

Очевидно, что P₁ ∩ P₂ = {2}; N₁ ∩ N₂ = {3}. Условие (25) принимает вид:

x₂x₃ = 1. Этому условию удовлетворяет точк

β = (0,1,0,0), но она не па-

ретовская: взяв точку γ = (1, 1, 0, 1), убеждаемся, что -25 = f₁(γ) < f₁

β) =

= -1, -25 = f₂(γ) < f₂

β) = -1.

Найдем множество Парето в задаче безусловной многокритериальной оп-

тимизации. Используем необходимое условие, которому должны удовлетво-

рять эффективные точки: x₂x₃ = 1. Начальное дерево представлено на рис. 2.

Знак “∅” указывает на отсутствие эффективных точек в интервале, соот-

ветствующем ветви; знак “?” на необходимость дальнейшего ветвления.

Обозначим через H(y₁, y₂) вектор верхних и через L(y₁, y₂) вектор нижних

достижимых оценок функций f₁, f₂, R(α, β) рекорд.

Результат решения задачи представлен на рис. 3.

Знак “×” указывает на отсечение интервала.

Множество Парето состоит из трех точек {0101, 1100, 1101}, являющих-{

⋁

ся рекордными (R₁, R₂, R₃), и имеет логическое описание: P =

x: x₁x₂x₃

}

⋁

x₂x₃x₄ = 1

Замечание 3. Условие x ∈ P ∩ Ω, как следует из теоремы 5, является

достаточным для того, чтобы точка x была паретовской в задаче с ограни-

чением x ∈ Ω при P ∩ Ω = ∅. Однако это условие не является необходимым.

Действительно, в задаче



 min f1(x) = -25x1 - x2 + x3 + x4;

min f₂(x) = x₁ - x₂ + x₃ - 25x₄;



x ∈ Ω = {x : x₁x₂ = 1} ⊂ B^N

паретовскими являются точки {0100, 0101} со значениями векторов критери-

ев (-1, -1) и (0, -26) соответственно, причем точка {0100} не принадлежит

множеству P ∩ Ω.

Рассмотрим варианты выбора интервалов и переменных для ветвления.

От последовательности выбора интервалов и переменных для ветвления

зависит скорость нахождения решения задачи. Стратегии ветвления являют-

ся эвристиками, например (возможны другие):

1) разбиению по переменной с номером i подвергается тот интервал мно-

жества допустимых решений, конъюнкция которого не содержит литерала

переменной с номером i, и изменение этой переменной с единицы на нуль

обеспечивает одновременное уменьшение как можно большего числа скаляр-

ных критериев;

2) разбиению подвергается тот интервал, для которого является макси-

мальной следующая мера различия между верхней H = (h₁, . . . , h_m) и ниж-

ней L = (l₁, . . . , l_m) его векторными оценками:

(

)

h_j - l_j

D(H, L) = min

1≤j≤m M_j - µ_j

где M_j = max_x∈Ωf_j(x); µ_j = min_x∈Ωf_j(x); M_j - µ_j > 0, поскольку в против-

ном случае критерий f_j может быть исключен из рассмотрения.

Можно привести пример задачи многокритериальной псевдобулевой оп-

тимизации, для которой процесс принятия решения по изложенному методу

будет близок к полному перебору. В расчете на такие ситуации возможен

приближенный подход к решению, суть которого состоит в следующем.

Пусть заданы значения ε₁, . . . , ε_m ∈ R⁺. Будем говорить, что два векто-

ра (a₁, a₂, . . . , a_m) и (b₁, b₂, . . . , b_m) являются

ε-равными, если |a_i - b_i| ≤ ε_i,

i = 1,m.

Если верхняя и нижняя векторные оценки некоторого интервала, получен-

ного при ветвлении, ε-равны, то такой интервал называется ε-интервалом.

Если нижняя векторная оценка некоторого ε-интервала мажорируется ре-

кордом или нижней векторной оценкой другого интервала, то такой ε-интер-

вал подлежит исключению.

Совокупность немажорируемых ε-интервалов вместе с рекордами дает

приближение к искомому паретовскому множеству. Логическое описание па-

ретовского множества P получается обратным проходом по ветвям деревьев

ветвлений, листья которых соответствуют немажорируемым элементам.

Таким образом, предложены методы решения многоэкстремальных задач,

представленных в канонической форме. Показано, как использование метода

ветвей и границ решения таких задач позволяет строить логическое описание

паретовского множества.

6. Заключение

В статье представлен класс задач для многих коммивояжеров, который

приведен или достаточно просто приводится к моделям псевдобулевой услов-

ной оптимизации с ограничениями в виде дизъюнктивных нормальных форм.

Предложен алгоритм, основанный на кластеризации графа, согласно которо-

му на каждом кластере решаются задачи для одного коммивояжера, пред-

ставленные в канонической форме скалярной псевдобулевой оптимизации и

дизъюнктивными ограничениями. Указывается на возможность формирова-

ния ДНФ ограничений с помощью обучения по прецедентной информации,

а тем самым синтез областей допустимости решений в продукционных си-

стемах моделей псевдобулевой оптимизации, соответствующих mT SP . Пред-

ложен подход с частично заданными ограничениями, основанный на при-

менении алгоритмов распознавания образов. Методика распространяется на

многокритериальный случай задач mT SP .

Прикладные аспекты применения полученных результатов требуют учета

всех компонент задачи mT SP в сложных сетях.

Разработка приближенных алгоритмов выбора маршрутов в сложных се-

тях может быть связана с учетом знаний о свойствах структуры сети, ее слож-

ности, наличием ограничений, предписаний, условий достижимости, числа

агентов-коммивояжеров.

Необходимо будет учитывать специфику задач маршрутизации в сложных

сетях, которая, в отличие от классической теории графов, связана с рядом

уникальных задач: о нахождении метрических характеристик сложных сетей;

поиск минимального (максимального) среднего пути в сети; коэффициентов

кластеризации; изучения информационных потоков в сети; выявление кри-

тичных мест в сети; определения кластеров; выявление блоков, компонент,

мостов, точек сочленения (перемычек).

Методология разработки алгоритма решения задач маршрутизации может

быть основана на формировании по исходной сложной сети более простой (от-

носительно реализации алгоритмов маршрутизации) по своей структуре сети.

Построение рациональных решений mT SP на сетях большой размерности

реализуется по схеме алгоритма AmT SP для m коммивояжеров. В случае

разных интересов агентов приходим к многокритериальной задаче псевдо-

булевой оптимизации с дизъюнктивными ограничениями. Здесь возможны

игровые модели.

Дальнейшие исследования также связаны с обучением агентов-коммивоя-

жеров, их автономностью и организацией обмена прецедентной информацией

между агентами (системами управления). При этом в многоагентной системе

(МАС) mT SP должны сочетаться задачи выбора решения; управления; рас-

пределения ресурсов; синтеза сети (вершин-источников ресурсов); устойчиво-

сти сети в зависимости от удаления вершины, дуги или некоторого маршрута;

кластеризации сети в зависимости от изменяющихся условий; обмена инфор-

мацией между агентами; потоковые задачи; задачи прокладки кратчайших

путей и замкнутых маршрутов.

СПИСОК ЛИТЕРАТУРЫ

Антамошкин А.А., Масич И.С. Поисковые алгоритмы псевдобулевой оптими-

зации // Системы управления, связи и безопасности. 2016. № 1. С. 103-145.

Германчук М.С., Козлова М.Г., Лукьяненко В.А. Знаниеориентированные моде-

ли маршрутизации многих коммивояжеров // Интеллектуализация обработки

информации // Тез. докл. 13-й Междунар. конф., Москва, 2020. С. 352-355.

Донской В.И., Башта А.И. Дискретные модели принятия решений при непол-

ной информации. Симферополь: Таврия, 1992.

Донской В.И. Задачи псевдобулевой оптимизации с дизъюнктивным ограниче-

нием // Журн. выч. матем. и матем. физ. 1994. № 4. С. 461-472.

Donskoy V., Perekhod I. Multiple Criteria Models with the Linear Pseudoboolean

Functions and Disjunctive Restrictions / Fandel G., Gal T. (eds). Multiple Criteria

Decision Making. Lecture Notes in Economics and Mathematical Systems. V. 448.

Berlin-Heidelberg: Springer, 1997. https://doi.org/10.1007/978-3-642-59132-7_2

Donskoy V.I. A Synthesis of Pseudo-Boolean Empirical Models by Precedential In-

formation // Bulletin SUSU MMCS. 2018. V. 11. No. 2. P. 96-107.

Козлова М.Г. Знаниеориентированные модели принятия решений // Ученые за-

писки СГУ. 1998. № 7 (46). С. 76-83.

Козлова М.Г. Многокритериальные модели принятия решений с линейными

псевдобулевыми функциями и дизъюнктивным ограничением // Искусственный

интеллект. 2000. № 2. С. 67-73.

Козлова М.Г. Синтез сужающих запросов // Динамические системы. 2000.

Вып. 16. С. 208-211.

10.

Масич И.С. Поисковые алгоритмы условной оптимизации: монография. Крас-

ноярск: СибГАУ. 2013.

11.

Меламед И.И., Сергеев С.И., Сигал И.Х. Задача коммивояжера. Вопросы тео-

рии // АиТ. 1989. № 9. С. 3-33.

Melamed I.I., Sergeev S.I., Sigal I.K. The Traveling Salesman Problem. Issues in

Theory // Autom. Remote Control. 1989. V. 50. No. 9. P. 1147-1173.

12.

Меламед И.И., Сергеев С.И., Сигал И.Х. Задача коммивояжера. Точные мето-

ды // АиТ. 1989. № 10. С. 3-29.

Melamed I.I., Sergeev S.I., Sigal I.K. The Traveling Salesman Problem. Exact Meth-

ods // Autom. Remote Control. 1989. V. 50. No. 10. P. 1303-1324.

13.

Меламед И.И., Сергеев С.И., Сигал И.Х. Задача коммивояжера. Приближенные

алгоритмы // АиТ. 1989. № 11. С. 3-26.

Melamed I.I., Sergeev S.I., Sigal I.K. The Traveling Salesman Problem. Approximate

Algorithms // Autom. Remote Control. 1989. V. 50. No. 11. P. 1459-1479.

14.

Германчук М.С., Лемтюжникова Д.В., Лукьяненко В.А. Метаэвристические

алгоритмы для многоагентных задач маршрутизации // Проблемы управления.

2020. Т. 6. С. 3-13.

15.

Grama Y., Hammer P.L. Boolean Functions: Theory, Algorithms and Applications. -

N.Y.: Cambridge Universuty Press, 2011.

16. Hammer P.L., Rudeanu S. Boolean Methods in Operations Research and Related

Areas. Berlin-Heidelberg-N.Y.: Springer-Verlag, 1968.

17. Foldes S., Hammer P.L. Disjunctive and Cojunctive Normal Forms of Pseudo-

Boolean Functions // Descrete Appl. Math. 2000. No. 107. P. 1-26.

18. Boros E., Hammer P.L. Pseudo-Boolean Optimization // Descrete Appl. Math.

2002. No. 123. P. 155-225.

19. Hammer P.L. Pseudo-Boolean Remarks on Balanced Graphs // Int. series of Nu-

merical Math. 1977. No. 36. P. 69-78.

20. Ebenegger Ch., Hammer P.L., de Werra D. Pseudo-Boolean Functions and Stability

of Graphs // Annals of Descrete Math. 1984. No. 19. P. 83-97.

21. Журавлев Ю.И. О локальных алгоритмах над дизъюнктивными нормальными

формами // Докл. АН СССР. 1979. Т. 245. № 2. С. 289-292.

22. Журавлев Ю.И., Коган А.Ю. Реализация булевых функций с малым числом

нулей дизъюнктивными нормальными формами и смежные задачи // Докл.

АН СССР. 1985. Т. 285. № 4. С. 795-799.

23. Hammer P.L., Rudeanu S. Pseudo-Boolean Methods for Bivalent Programming //

Lecture Notes in Math. Sept. 2-7, 1966.

24. Сапоженко А.А. О поиске максимального верхнего нуля монотонных функций

на ранжированных множествах // Журн. выч. матем. и матем. физ. 1991. Т. 31.

№ 12. С. 1871-1884.

25. Германчук М.С., Козлова М.Г., Лукьяненко В.А. Задачи практической марш-

рутизации // Анализ, моделирование, управление, развитие социально-эконо-

мических систем. Сб. науч. тр. XI Междунар. школы-симпозиума АМУР, 2017.

С. 116-120.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 24.01.2021

После доработки 16.03.2021

Принята к публикации 30.06.2021