Автоматика и телемеханика, № 10, 2021

M. АЛКУСА, канд. физ.-мат. наук (mohammad.alkousa@phystech.edu),

А.В. ГАСНИКОВ, д-р физ.-мат. наук (gasnikov.av@mipt.ru)

(Московский физико-технический институт, Долгопрудный;

Институт проблем передачи информации им. А. А. Харкевича РАН, Москва)

О РЕШЕНИИ ВЫПУКЛЫХ MIN-MIN ЗАДАЧ

С ГЛАДКОСТЬЮ И СИЛЬНОЙ ВЫПУКЛОСТЬЮ

ПО ОДНОЙ ИЗ ГРУПП ПЕРЕМЕННЫХ

И МАЛОЙ РАЗМЕРНОСТЬЮ ДРУГОЙ¹

Статья посвящена некоторым подходам к решению выпуклых задач

вида min-min с гладкостью и сильной выпуклостью только по одной из

двух групп переменных. Показано, что предложенные подходы, основан-

ные на методе Вайды, быстром градиентном методе и ускоренном гра-

диентном методе с редукцией дисперсии, имеют линейную сходимость.

Для решения внешней задачи предлагается использовать методы Вайды,

для решения внутренней (гладкой и сильно выпуклой) быстрый гради-

ентный метод. Ввиду важности для приложений в машинном обучении

отдельно рассмотрен случай, когда целевая функция является суммой

большого числа функций. В этом случае вместо быстрого градиентного

метода используется ускоренный градиентный метод с редукцией диспер-

сии. Приведены результаты численных экспериментов, иллюстрирующие

преимущества предложенных процедур для задачи логистической регрес-

сии, в которой есть априорное распределение на одну из двух групп пе-

ременных.

Ключевые слова: выпуклая оптимизация, метод секущей плоскости, ме-

тод Вайды, редукция дисперсии, быстрый градиентный метод, логисти-

ческая регрессия.

DOI: 10.31857/S0005231021100068

1. Введение

Одним из основных направлений исследований численных методов выпук-

лой оптимизации в последнее десятилетие стало повсеместное распростране-

ние конструкции ускорения обычного градиентного метода, предложенной

в 1983 г. Ю.Е. Нестеровым [1], на различные другие численные методы опти-

мизации. За последние 15 лет ускоренный метод был успешно перенесен на

гладкие задачи условной выпуклой оптимизации, на задачи со структурой

¹ Работа выполнена при поддержке Министерства науки и высшего образования Рос-

сийской Федерации (госзадание) № 075-00337-20-03, номер проекта 0714-2020-0005. Работа

А.В. Гасникова была также частично поддержана Российским фондом фундаментальных

исследований (проект № 18-29-03071 мк).

(в частности, так называемые композитные задачи), безградиентные и рандо-

мизированные методы (например, ускоренный градиентный метод с редукци-

ей дисперсии для задач минимизации суммы функций [2]). Также ускорение

было успешно перенесено на методы, использующие старшие производные.

Детали и более подробный обзор публикаций можно найти в [3].

Задачи оптимизации вида min-max и седловые задачи широко изучались в

литературе из-за их широкого спектра приложений в статистике, машинном

обучении, компьютерной графике, теории игр и других областях. В послед-

нее время многие исследователи активно работают над темой ускоренных

методов решения этих задач, учитывающих их структуру: [4-8] и это лишь

некоторые из последних публикаций. В некоторых приложениях существует

задача, аналогичная задаче min-max, которая остается в значительной сте-

пени неизученной это задача вида min-min:

(1)

min

F (x, y),

x∈Qx

y∈Qy

где Q_x ⊂ R^d, Q_y ⊂ Rⁿ непустые компактные выпуклые множества, размер-

ность d относительно небольшая (d ≪ n), функция F (x, y) выпуклая по со-

вокупности переменных, а также L-гладкая и µ-сильно выпуклая по y. Под

L-гладкостью по y понимается свойство

∥∇_yF (x, y) - ∇_yF (x, y^′)∥₂ ≤ L∥y - y^′∥₂

∀x ∈ Q_x, y,y^′ ∈ Q_y.

Такая постановка возникает, например, при поиске равновесий в транспорт-

ных сетях [9]. В машинном обучении задачи такого типа соответствуют слу-

чаю, когда регуляризация применяется к одной из двух групп параметров

модели (отсюда сильная выпуклость только по одной группе переменных из

двух). Например, когда в датасете большая группа признаков являются раз-

реженными, то регуляризация может использоваться только для весов моде-

ли, соответствующих этим признакам. В качестве еще одного примера можно

привести логистическую регрессию, в которой есть априорное распределение

на часть параметров. Задаче min-min посвящено несколько публикаций, сре-

ди которых [10-12]. Например, в [10] авторы предложили новые алгоритмы

для задач min-max, шаги которых настраиваются автоматически, но предло-

женные методы также применяются и к задачам min-min.

В данной статье рассматриваются два подхода к решению задачи (1),

имеющие линейную скорость сходимости. Предлагается свести рассматривае-

мую задачу к совокупности вспомогательных задач (внутренней и внешней).

Внешняя задача (минимизация по x) решается методом Вайды (метод секу-

щей плоскости) [13, 14].

В случае когда целевая функция F простая, т.е. не является суммой боль-

шого количества функций, внутренняя задача (минимизация по y) решается

быстрым градиентным методом для задач сильно выпуклой оптимизации.

В результате такого подхода приближенное решение задачи (1) может быть(

√

)

достигнуто за

O (d) вычислений ∂_xF

O d

вычислений ∇_yF , см. тео-

рему 5. Здесь и далее

O(·) = O(·) с точностью до небольшой степени лога-

рифмического множителя, обычно эта степень равна единице или двум.

Оптимизация суммы большого количества функций в течение последних

нескольких лет является предметом интенсивных исследований из-за широ-

кого спектра приложений в машинном обучении, статистике, обработке изоб-

ражений и других математических и инженерных приложениях. Поэтому

отдельно рассматривается случай, когда целевая функция F представляет

собой сумму (или среднее арифметическое) большого числа m функций, в

котором использование быстрого градиентного метода для задач сильно вы-

пуклой оптимизации потребовало бы вычисления градиентов m слагаемых

на каждом шаге, что может занимать много времени. Вместо этого пред-

лагаем использовать ускоренный градиентный метод с редукцией диспер-

сии [2, 15], который также имеет линейную сходимость. В результате такого

подхода решение задачи может быть достигнуто з

O (md) вычислений ∂_xF

(

√

)

и з

O md + d

вычислений ∇_yF , см. теорему 6.

Используя два предложенных подхода, получаем линейную скорость схо-

димости для задачи min-min (1). Отметим, что гладкость и сильная выпук-

лость требуются только по одной из двух групп переменных.

Статья состоит из 5 разделов и Приложения. В разделе 2 приводятся ис-

пользуемые алгоритмы и их сложность, а именно: быстрый градиентный ме-

тод, метод Вайды (метод секущей плоскости) и метод ускоренного градиент-

ного спуска с редукцией дисперсии. В разделе 3 формулируется постанов-

ка задачи и приводятся подходы к рассматриваемой задаче для различных

случаев целевой функции, в одном из которых целевая функция является

суммой или средним арифметическим большого числа функций. В разделе 4

приводятся результаты вычислительных экспериментов и сравнение скоро-

сти работы предложенных подходов. Отметим, что полные доказательства

теорем 4, 5, 6 и вспомогательного утверждения 1 приводятся в Приложении.

2. Используемые алгоритмы

Приведем алгоритмы, используемые в предлагаемых в статье подходах к

решению задачи (1). Сначала приводится быстрый градиентный метод, затем

метод Вайды (метод секущей плоскости) и, наконец, ускоренный градиент-

ный метод с редукцией дисперсии.

2.1. Быстрый градиентный метод

В [16] предложен адаптивный алгоритм для решения задачи оптимизации

(2)

f (y) → min ,

y∈Qy

где Q_y ⊂ Rⁿ непустое компактное выпуклое множество, f L-гладкая вы-

пуклая функция. Этот алгоритм, получивший название быстрого градиент-

ного метода, позволяет ускорить сходимость обычного градиентного спуска

(₁

)

(₁

)

с O

до O

, где N

количество итерации алгоритма. Быстрый гра-

N²

диентный метод (не адаптивный вариант) приведен далее как алгоритм 1.

Алгоритм 1. Быстрый градиентный метод [16].

Вход: Количество шагов N, начальная точка y⁰ ∈ Q_y, параметр L > 0.

0-шаг: z⁰ := y⁰, u⁰ := y⁰, α₀ := 0, A₀ := 0.

2: for k = 0, 1, . . . , N - 1 do

Находим наибольший корень α_k+1 такой, что A_k + α_k+1 = Lα^2k+1,

A_k+1 := A_k + α_k+1,

α_k+1u^k + A_kyk

z^k+1 :=

A_k+1

{

}

D (

)

u^k+1 := arg min

α_k+1

∇f z^k+1

,y-z^k+1

∥y - u^k∥²

y∈Qy

y^k

α_k+1u^k+1 + A_k

y^k+1 :=

A_k+1

8: end for

Выход: y^N .

Следующая теорема дает оценку сложности (скорости сходимости) алго-

ритма 1.

Теорема 1

[16]. Пусть функция f : Q_y → R является L-гладкой и вы-

пуклой, тогда алгоритм 1 возвращает такую точку y^N , что

(

)

8LR

y^N

- f(y_∗) ≤

(N + 1)²

где y_∗

решение задачи (2), R² =¹²∥y⁰ - y_∗∥²².

Опишем далее технику рестартов (перезапусков) быстрого градиентного

метода (алгоритм 1) для случая µ-сильно выпуклой функции.

Ввиду µ-сильной выпуклости f имеем

∥z - y∥²² ≤ f(z) - (f(y) + 〈∇f(y), z - y〉) ≤

∥z - y∥²²

∀y,z ∈ Q_y.

Тогда после N₁ итераций алгоритма 1 с учетом теоремы 1 получаем

(

)

4L∥y⁰ - y_∗∥²²

(3)

∥yN1 - y_∗∥²² ≤ f

yN1

- f (y_∗) ≤

N²

отсюда

∥yN1 - y_∗∥²² ≤

∥y⁰ - y_∗∥²².

µN²

⌈

√

⌉

Поэтому, выбирая N₁ =

, где ⌈·⌉

округление вверх, получим

∥yN1 - y_∗∥²² ≤

∥y⁰ - y_∗∥²².

После этого выберем для алгоритма 1 в качестве точки старта yN1 , снова

сделаем N₁ итераций и т.д. Для достижения приемлемого качества решения

можно выбрать количество рестартов алгоритма 1 (параметр p алгоритма 2)

следующим образом:

)⌉

⌈1

(µR

В таком случае общее число итераций алгоритма 2 будет

⌈

√

⌉

)⌉

⌈1

(µR

N =

т.е.

(√

)

))

(µR

(4)

N =O

Алгоритм 2. Быстрый градиентный метод для задач сильно выпуклой

оптимизации, рестарты алгоритма 1.

(

)⌉

⌈1

µR²

Вход: начальная точка y⁰ ∈ Q_y, L > 0, число рестартов p =

1: for j = 1, . . . , p do

⌈

√L⌉

Выполнить N_j =

итераций алгоритма 1,

y⁰ := yNj .

4: end for

Выход: ŷ := yNp .

2.2. Метод Вайды

Метод Вайды (метод секущей плоскости) был предложен Вайдой в [13, 14]

для решения условной задачи оптимизации

(5)

f (x) → min ,

x∈Qx

где Q_x ⊂ R^d выпуклое компактное множество с непустой внутренностью, а

целевая функция f, определенная на Q_x, непрерывна и выпукла.

Пусть P = {x ∈ R^d : Ax ≥ b} ограниченный d-мерный многогранник,

где A ∈ R^m×d и b ∈ R^m. Логарифмический барьер множества P определяется

как

∑ (

)

Barr(x) = - log a^⊤x-bi

i=1

где a^⊤i i-я строка матрицы A. Гессиан H(x) функции Barr(x) равен

∑

a_ia^⊤i

H(x) =

(

)₂ .

a^⊤ix - b_i

i=1

Матрица H(x) положительно определена для всех x из внутренности P . Во-

люметрический барьер (volumetric barrier) V определяется как

V(x) =

log (det (H(x))) ,

где det (H(x)) обозначает детерминант H(x). Будем называть точку миниму-

ма функции V на P волюметрическим центром множества P .

Обозначим

a^⊤i (H(x))^-1 a_i

(6)

σ_i(x) =

(

)₂

1 ≤ i ≤ m,

a^⊤ix - b_i

тогда градиент волюметрического барьера V может быть записан как

∑

a_i

∇V(x) = -

σ_i(x)

a_i⊤x - b_i

i=1

Пусть Q(x) определяется как

∑

a_ia^⊤i

Q(x) =

σ_i(x)(

)₂ .

a^⊤ix - b_i

i=1

Заметим, что Q(x) положительно определена на внутренности P , а также

Q(x) является хорошим приближением гессиана функции V(x), т.е. ∇²V(x).

Метод Вайды производит последовательность пар (A_k, b_k) ∈ R^m×d × R^m

таких, что соответствующие многогранники содержат решение. В качестве

начального многогранника, задаваемого парой (A₀, b₀), обычно берется сим-

плекс (алгоритм может начинать с любого выпуклого ограниченного n-мерно-

го многогранника, для которого легко вычислить волюметрический центр

например, с n-прямоугольника).

Параметром алгоритма является небольшое число γ ≤ 0,006, смысл кото-

рого более подробно раскрывается в книге [17]. Пусть x_k (k ≥ 0) обозначает

волюметрический центр многогранника, заданного парой (A_k, b_k), и пусть для

него вычислены величины {σ_i(x_k)}_1≤i≤m (см. (6)). Следующий многогранник

(A_k+1, b_k+1) получается из текущего в результате либо присоединения, либо

удаления ограничения:

1) Если для некоторого i ∈ {1, . . . , m} выполняется σ_i(x_k) = min

σ_j(x_k

1≤j≤m

< γ, тогда (A_k+1,b_k+1) получается исключением i-й строки из (A_k,b_k);(

)

2) иначе если min

σ_j(x_k) ≥ γ оракул, вызванный в текущей точ-

1≤j≤m

{

ке x_k, возвращает вектор c_k такой, что f(x) ≤ f(x_k) ∀x ∈ z ∈ Q_x :

}

:c^⊤kz ≥ c^⊤kxk , т.е. ck ∈ -∂f(xk). Выберем βk ∈ R таким, что

c^⊤k (H(x_k))^-1 c_k

(

)₂

√γ.

x^⊤kc_k - β_k

Определим (A_k+1, b_k+1) добавлением строки (c_k, β_k) к (A_k, b_k).

Волюметрический барьер V_k является самосогласованной функцией, поэтому

может быть эффективно минимизирован методом Ньютона. Достаточно од-

ного шага метода Ньютона для V_k, сделанного из x_k-1. Подробности и анализ

метода Вайды можно найти в [13, 14, 17].

Следующая теорема дает оценку сложности алгоритма Вайды.

Теорема 2. Пусть B_ρ и B_R некоторые евклидовы шары радиусов ρ

и R соответственно такие, что B_ρ⊆Q_x⊆B_R, и пусть число B > 0 таково,

что |f(x) - f(x^′)| ≤ B ∀x, x^′ ∈ Q_x. Тогда метод Вайды находит ε-решение(

)

задачи (5) за O d log^dBR

шагов.

ρε

Замечание 1. Как показано в [18], метод Вайды можно использовать с

неточным субградиентом без накопления ошибки.

Замечание 2. Помимо вычисления субградиента, в стоимость итерации

метода Вайды входит стоимость обращения матрицы размера d×d и решения

системы линейных уравнений.

2.3. Ускоренный градиентный метод с редукцией дисперсии

Рассмотрим задачу

(7)

f (y) → min ,

y∈Qy

где Q_y ⊆ Rⁿ замкнутое выпуклое множество, а целевая функция f пред-

ставляет собой сумму (или среднее арифметическое) большого числа m глад-

∑_m

ких выпуклых функций f_i, т.е. f(y) =¹

f_i(y). При решении (7) с по-

m i=1

мощью быстрого градиентного метода для задач сильно выпуклой оптими-

зации (алгоритм 2) потребуется вычислять градиент m функций на каждой

итерации, что очень дорого. Поэтому предпочтительнее вместо алгоритма 2

использовать рандомизированный градиентный метод, а именно ускоренный

градиентный метод с редукцией дисперсии, также называемый Varag [2, 15].

Приведенный далее алгоритм 3 представляет собой ускоренный градиентный

метод с редукцией дисперсии (Varag) для гладкой сильно выпуклой задачи

оптимизации конечной суммы (7). Этот алгоритм был предложен Г. Ланом

и др. в [15].

Предположим, что для каждого i ∈ {1, . . . , m}, существует L_i > 0 такое,

что

∥∇f_i(y) - ∇f_i(z)∥₂ ≤ L_i∥y - z∥₂

∀y,z ∈ Q_y.

∑_m

Ясно, что f имеет липшицев градиент с константой не более L :=¹

L_i.

m i=1

Предположим также, что целевая функция f сильно выпуклая с константой

µ > 0, т.е.

f (z) ≥ f(y) + 〈∇f(y), z - y〉 +

∥y - z∥₂

∀y,z ∈ Q_y.

Определение 1. Случайный вектор y, принимающий значения из Q_y,

называется стохастическим ε-решением задачи (7), если E[f(y) - f(y_∗)] ≤

≤ ε, где y_∗ точное решение задачи (7).

Алгоритм Varag содержит вложенные циклы внешний и внутренний

(индексируемые переменными s и t соответственно). На каждой итерации

внешнего цикла вычисляется полный градиент ∇f(y) в точке y, который за-

тем используется во внутреннем цикле для определения оценок градиента G_t.

Каждая итерация внутреннего цикла требует информацию о градиенте толь-

ко одного случайно выбранного слагаемого fit и содержит три основные по-

следовательности: {y_t}, {y_t} и {y_t}.

Обозначим s₀ := ⌊log₂ m⌋ + 1, где ⌊·⌋ округление вниз. Параметры ал-

горитма 3 {q₁, . . . , q_m}, {θ_t}, {α_s}, {γ_s}, {p_s} и {T_s} описываются следующим

образом:

∑_m

• Вероятности q_i =

L_i ∀i ∈ {1,... ,m};

L_i

i=1

√

12L

• Веса {θ_t} при 1 ≤ s ≤ s₀ или s₀ < s ≤ s₀ +

- 4, m < ^3L4µ равны

mµ



γ_s



(α_s + p_s) ,

1 ≤ t ≤ T_s - 1,

α_s

(8)

θ_t =



γ_s ,

t=T_s.

α_s

В остальных случаях они равны

{ Γt-1 - (1 - αs - ps) Γt, 1 ≤ t ≤ Ts - 1,

(9)

θ_t =

Γ_t-1,

t=T_s,

где Γ_t = (1 + µγ_s)^t;

• Параметры {T_s}, {γ_s} и {p_s} определяются как

{

2s-1, s ≤ s

(10)

T_s =

γ_s =

, p_s =

;

Ts0, s > s₀,

3Lα_s

• Наконец,





s≤s₀,



(11)

α_s =

{

{√

}}



mµ

 max

,min

, s>s₀.

s-s₀ +4

Алгоритм 3. Ускоренный градиентный метод с редукцией дисперсии

(Varag) [15].

Вход: y⁰ ∈ Q_y, {T_s}, {γ_s}, {α_s}, {p_s}, {θ_t} и распределение вероятностей

{q₁, . . . , q_m} на {1, . . . , m}.

y⁰ := y⁰.

2: for s = 1, 2, . . . , do

y := y^s-1, g := ∇f(y).

y₀ := y^s-1, y0 = y, T := Ts.

for t = 1, 2, . . . , T do

Выбрать i_t ∈ {1, . . . , m} случайным образом согласно {q₁, . . . , q_m}.

:= (1 + µγ_s(1 - α_s))[(1+µγs)(1-αs -ps)yt-1 +αsy^t-1 +(1+µγs)ps y].

(

)

Gt :=

∇fit y

- ∇fit(y)

+ g.

(qitm)

{

}

(

)

y_t := arg min

γ_s

〈G_t, y〉 +

∥y_t - y∥²

∥y_t-1 - y∥²

y∈Qy

10:

yt := (1 - αs - ps) yt-1 + αsyt + ps y.

11:

end for

∑

12:

y^s := y_T , y^s :=

∑

(θ_ty_t).

θt t=1

t=1

13: end for

Следующий результат дает оценку сложности алгоритма 3.

Теорема 3

[15]. Если параметры алгоритма 3 {θ_t}, {α_s}, {γ_s}, {ps}

и {T_s} заданы согласно формулам (8), (9), (10) и (11), то общее количество

вычислений градиентов функций f_i, выполняемых алгоритмом 3 для нахож-

дения стохастического ε-решения задачи (7), ограничено



{

}



D₀



O mlog

m≥

или m ≥



4µ



{

}

√



mD₀

D₀

(12)

N :=

O mlogm +

≤



4µ



{

}



√mL

D₀/ε

D₀

 O mlogm +

log

, m<

≤

3L/4µ

4µ

(

)

где D₀ = 2

f (y⁰) - f(y_∗)

+^3L2∥y⁰ - y_∗∥²², где y_∗ решение задачи (7).

(

√

)

Заметим, что оценку (12) можно записать как N

O m+

, где

O(·) = O(·) с точностью до логарифмического множителя по m, L, µ, ε и D₀.

3. Постановка задачи и полученные результаты

Рассмотрим задачу

(13)

min

F (x, y),

x∈Qx

y∈Qy

где Q_x ⊂ R^d, Q_y ⊂ Rⁿ непустые компактные выпуклые множества, раз-

мерность d относительно небольшая (d ≪ n), функция F (x, y) выпуклая

по совокупности переменных, а также L-гладкая и µ-сильно выпуклая по y.

Под L-гладкостью по y понимается свойство

∥∇_yF (x, y) - ∇_yF (x, y^′)∥₂ ≤ L∥y - y^′∥₂

∀x ∈ Q_x, y,y^′ ∈ Q_y.

Введем функцию

(14)

f (x) = min

F (x, y).

y∈Qy

Задачу (13) можно переписать в виде

(15)

f (x) → min .

x∈Qx

При решении (15) некоторым итерационным методом необходимо на каждом

его шаге решать вспомогательную задачу (14), чтобы приближенно находить

субградиент ∂f(x). Обратимся к следующему определению.

Определение 2 ([19], с. 123). Пусть δ ≥ 0, Q_x ⊆ R^d выпуклое мно-

жество, f : Q_x → R выпуклая функция. Вектор g ∈ R^d называется δ-суб-

градиентом f в точке x^′ ∈ Q_x, если

f (x) ≥ f(x^′) + 〈g, x - x^′〉 - δ

∀x ∈ Q_x.

Множество δ-субградиентов f в точке x^′ обозначается ∂_δf(x^′).

Обозначим D := maxy,z∈Qy ∥y - z∥₂, y(x) := arg miny∈Qy F (x, y). Следую-

щая теорема говорит о том, как вычислить δ-субградиент функции f(x), при-

ближенно решая вспомогательную задачу (15).

Теорема 4. Пусть найден такой y ∈ Q_x, что F(x, y) - f(x) ≤ ε, тогда

(

)

√ 2ε

∂_xF(x, y) ∈ ∂_δf(x), δ =

LD + ∥∇_yF (x,y(x))∥₂

Эта теорема непосредственно следует из двух утверждений.

Утверждение 1. Пусть g : Q_y → R

L-гладкая µ-сильно выпуклая

функция, точка y ∈ Q_y такова, что g(y) - g(y_∗) ≤ ε, тогда

√ 2ε

max

〈∇g(y), y - y〉 ≤ δ, δ = (LD + ∥∇g (y_∗)∥₂)

y∈Qy

где y_∗ = arg miny∈Qy g(y).

Утверждение 2 ([20], с. 12). Пусть найден такой y ∈ Q_y, что

max 〈∇_yF (x, y), y - y〉 ≤ δ,

y∈Qy

тогда ∂_xF(x, y) ∈ ∂_δf(x).

Интуитивно теорема 4 говорит о том, что, решив вспомогательную зада-

чу (14) достаточно точно, получим хорошее приближение субградиента ∂f(x),

которое может быть использовано для решения внешней задачи (15). На этой

идее основан предлагаемый подход к решению (13).

Подход 1 (основной случай). Внешняя задача (15) решается методом Вай-

ды. Вспомогательная задача (14) решается быстрым градиентным методом

для задач сильно выпуклой оптимизации (алгоритм 2).

Теорема 5. Подход 1 позволяет получить ε-решение задачи (13) после(

√

)

O (d) вычислений ∂_xF и обращений матриц размера d×d, а такж

O d

вычислений ∇_yF .

Замечание 3. Обращение матриц появляется в сложности предлагаемо-

го подхода из-за того, что оно производится на каждом шаге метода Вайды.

3.1. Минимизация суммы большого числа функций

Пусть в задаче (13)

∑

(16)

F (x, y) =

(x, y),

i=1

где функции F_i являются выпуклыми по совокупности переменных и L_i-глад-

кими по y, а F является µ-сильно выпуклой по y. Из этого следует, что F яв-

ляется выпуклой по совокупности переменных и гладкой по y с константой

∑_m

гладкости не более L :=¹

L_i.

m i=1

Подход 2 (сумма функций). Внешняя задача (15) решается методом Вай-

ды. Вспомогательная задача (14) решается ускоренным градиентным мето-

дом с редукцией дисперсии (алгоритм 3).

Теорема 6. Подход2позволяетполучитьε-решениезадачи(13)з

O(md)

(

√

)

вычислений ∂_xF_i

O (d) обращений матриц размера d × d

O dm + d

вычислений ∇_yF_i.

4. Эксперименты

Рассмотрим модель логистической регрессии для задачи бинарной класси-

фикации. Ошибка модели с параметрами w на обучающем объекте с вектором

признаков z, принадлежащем классу t ∈ {-1, 1}, записывается как

(

)

ℓ_z(w) = log

1+e^-t〈w,z〉

10 000

20 000

30 000

40 000

50 000

60 000

Количество вычислений Ñ_yF_i

20 000

40 000

60 000

80 000

Количество вычислений Ñ_yF_i

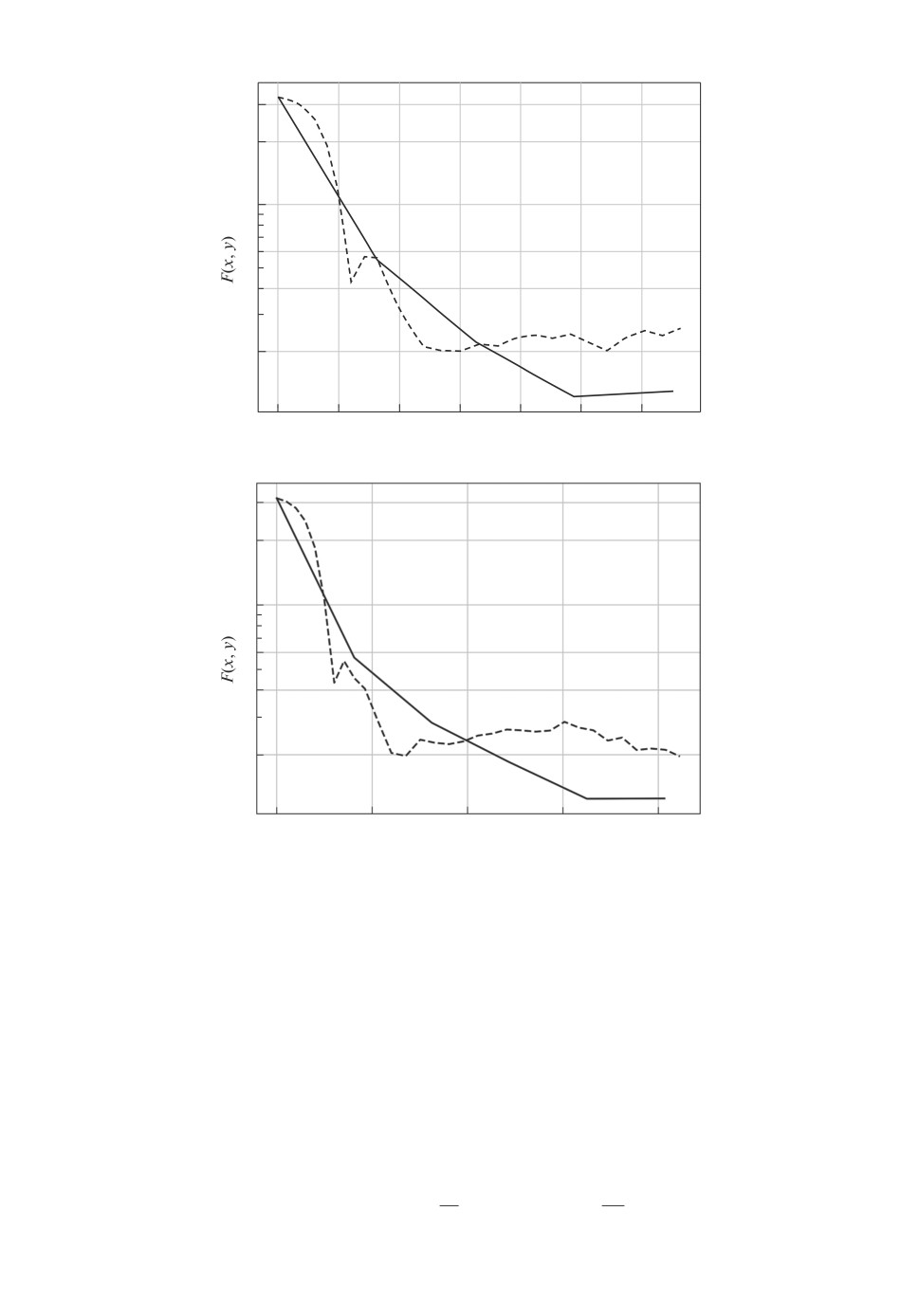
Рис. 1. а и б соответствуют размерностям d = 20 и d = 30 соответственно.

Графики 1 и 2 показывают сходимость предлагаемого подхода и метода Varag

соответственно.

Пусть параметры модели состоят из двух групп: w = (x, y), x ∈ R^d, y ∈ Rⁿ,

причем для группы y задано гауссовское априорное распределение:

(

)

y∼N

0, σ²I_n

где I_n единичная матрица размера n. Максимизация апостериорной веро-

ятности приведет (см. [21], § 4.5.1) к задаче

{

}

∑

(17)

min

F (x, y) :=

ℓzi(x,y) +

∥y∥²

x∈Qx

y∈Qy

σ²

i=1

где в качестве Q_x и Q_y можно взять евклидовы шары достаточно большого

радиуса.

Будем решать задачу (17) при помощи подхода 2 и сравним его работу

с работой метода Varag (алгоритм 3). Заметим, что эта задача не является

сильно выпуклой по совокупности переменных. Для такой постановки можно

использовать Varag, задавая параметры θ_t по формуле (8), а все остальные па-

раметры по формулам для сильно выпуклого случая, положив µ = 0, см. [15].(

)

√

mD₀

При этом стохастическое ε-решение будет найдено за O

+ mlogm

(

)

вычислений градиентов функций F_i, где D₀ = 2

F (x⁰, y⁰) - F (x_∗, y_∗)

+^3L2∥(x⁰,y⁰) - (x_∗,y_∗)∥²², (x_∗,y_∗)

решение задачи (17). Эта сублинейная

оценка уступает предлагаемому в статье подходу, см. теорему 2.

Для экспериментов использовался датасет madelon, представленный

2000 объектов, имеющих 500 признаков. Был выбран небольшой коэффици-

ент регуляризации

= 0,005 и проведены эксперименты для двух размер-

σ²

ностей d, равных 20 и 30.

На рис. 1 отражены результаты эксперимента. По оси x откладывается

количество вычислений градиентов ∇_yF_i, которое для Varag совпадает с ко-

личеством вычислений ∇_xF_i. Отметим, что предложенный подход требует

меньше вычислений ∇_xF_i, поскольку они выполняются только во внешнем

цикле. Так, график 1 на рис. 1,а соответствует четырем итерациям внешнего

цикла (т.е. 8000 вычислений ∇_xF_i), а график 1 на рис. 1,б пяти итераци-

ям (т.е. 10 000 вычислений ∇_xF_i). В данном эксперименте подход 2 позволил

достичь меньших значений целевой функции.

Исходный код и результаты экспериментов могут быть найдены в репози-

тории https://github.com/egorgladin/min_min.

5. Заключение

В статье рассмотрена задача вида min-min:

(18)

min

F (x, y),

x∈Qx

y∈Qy

где Q_x ⊂ R^d, Q_y ⊂ Rⁿ непустые компактные выпуклые множества, размер-

ность d относительно небольшая (d ≪ n), функция F (x, y) выпуклая по

совокупности переменных, а также L-гладкая и µ-сильно выпуклая по y.

Предложено два подхода к решению задачи (18), в которых она сводит-

ся к совокупности вспомогательных задач (внутренней и внешней). Внешняя

задача (минимизация по x) решается методом Вайды, а внутренняя (мини-

мизация по y) быстрым градиентным методом для задач сильно выпуклой

оптимизации или, если минимизируется сумма большого количества функ-

ций, ускоренным градиентным методом с редукцией дисперсии. Это позволя-

ет достигать приближенного решения задачи (18) з

O (d) вычислений ∂_xF

(

√

)

O d

вычислений ∇_yF , см. теорему 5. Для сравнения, если бы за-

дача (18) была гладкой по совокупности переменных, то ее решение при

ис(ользов)нии только быстрого градиентного метода имело бы сложность

√

O LR2

, где R

расстояние от начального приближения до решения.

В случае суммы с m слагаемыми решение задачи может быть достигнуто(

√

)

за

O (md) вычислений ∂_xF и з

O md + d

вычислений ∇_yF , см. тео-

рему 6.

Проведен численный эксперимент, в котором один из предлагаемых подхо-

дов применен к задаче логистической регрессии с регуляризацией, применяе-

мой к одной из двух групп параметров модели. По сравнению с алгоритмом

Varag, предложенный подход достиг меньших значений функции при мень-

шем числе вызовов оракулов.

Отметим также, что если функция F (x, y)

µ-сильно выпуклая по

совокупности переменных, то функция g(y) = minx∈Qx F (x, y) также будет

µ-сильно выпуклая. Более того, все это можно сформулировать в терминах

(δ, µ, L)-оракула (см. [3] и цитированную там литературу). При µ = 0 это

сделано в [20], при µ > 0 доказательство практически дословно повторяет

утверждения 1 и 3 из [20] (см. также [9]). Приведенное наблюдение позволяет

обоснованно (с теоретической проработкой) использовать для решения внут-

ренней задачи метод Вайды, а для решения внешней задачи использовать,

например, быстрый градиентный метод. Однако такой подход будет предпо-

чтительнее рассмотренного в данной статье только при весьма специальных

(как правило, трудно выполнимых) условиях [5].

ПРИЛОЖЕНИЕ

Доказательство утверждения 1. Рассмотрим произвольный y ∈Q_y

(Π.1)

〈∇g(y), y - y〉 = 〈∇g(y) - ∇g(y_∗), y - y〉 + 〈∇g(y_∗

), y - y〉 .

Оценим сверху первое слагаемое, используя неравенство Коши-Буняковского

и определение липшицевости градиента:

〈∇g(y) - ∇g(y_∗), y - y〉 ≤ ∥∇g(y) - ∇g(y_∗)∥₂ ∥y - y∥₂ ≤

(Π.2)

≤L∥y-y_∗∥₂∥y-y∥₂.

Из сильной выпуклости следует, что

g(y) ≥ g(y_∗) + 〈∇g(y_∗), y - y_∗〉 +

∥y-y_∗∥²².

Воспользовавшись неравенствами g(y) - g(y_∗) ≤ ε и 〈∇g(y_∗), y - y_∗〉 ≥ 0 ∀y ∈

∈ Q_y, получим

√

2ε

(Π.2)

2ε

(Π.3)

∥y-y_∗∥₂ ≤

=⇒ 〈∇g(y) - ∇g(y_∗), y - y〉 ≤ L ∥y - y∥₂

Теперь оценим сверху второе слагаемое в (Π.1)

〈∇g(y_∗), y - y〉 = 〈∇g(y_∗), y - y_∗〉 + 〈∇g(y_∗), y_∗ - y〉 .

Снова воспользовавшись критерием оптимальности точки y_∗ и неравенством

Коши-Буняковского, получим

(Π.3)

√ 2ε

〈∇g(y_∗), y - y〉 ≤ ∥∇g(y_∗)∥₂∥y - y_∗∥₂

≤ ∥∇g(y_∗)∥₂

Объединив верхние оценки для обоих слагаемых, получим

√

2ε

〈∇g(y), y - y〉 ≤ (L ∥y - y∥₂ + ∥∇g(y_∗)∥₂)

откуда следует доказываемое утверждение 1.

Доказательство теоремы 4. Зафиксировав x∈Q_x, применим утверж-

дение 1 к функции g(y) := F (x, y) и утверждение 2. Теорема 4 доказана.

Доказательство теоремы 5. Согласно (4) алгоритм 2 сходится ли-

нейно, поэтому можно считать, что вспомогательная задача miny∈Qy F (x, y)

(√

)

решается сколь угодно точно за врем

. Согласно теореме 4 это позво-

ляет использовать δ-субградиент, где δ убывает со скоростью геометрической

прогрессии. Для внешней задачи используется метод Вайды, который также

сходится линейно и имеет сложност

O (d). Таким образом, для решения за-

дачи (13) достаточно

O (d) вычислений ∂_xF и обращений матриц размера

(

√

)

d×d, атакж

O d

вычислений ∇_yF . Теорема 5 доказана.

Доказательство теоремы 6. Согласно теореме 3 Varag сходится ли-

нейно, поэтому можно считать, что вспомогательная задача miny∈Qy F (x, y)

(

√

)

решается сколь угодно точно за врем

O m+

. Согласно теореме 4 это

позволяет использовать δ-субградиент, где δ убывает со скоростью геометри-

ческой прогрессии. Для внешней задачи используется метод Вайды, который

также сходится линейно и имеет сложность

O (d) итераций. На каждой его

итерации необходимо вычислять субградиенты всех m слагаемых ∂_xF_i. Та-

ким образом, для решения задачи достаточн

O (md) вычислений ∂_xF_i

O (d)

(

√

)

обращений матриц размера d × d

O dm + d

вычислений ∇_yF_i. Тео-

рема 6 доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Нестеров Ю.Е. Метод минимизации выпуклых функций со скоростью сходимо-

сти O(1/k²) // Докл. АН СССР. 1983. Т. 269. № 3. С. 543-547.

2. Lan G. First-order and Stochastic Optimization Methods for Machine Learning. At-

lanta: Springer, 2020.

3. Гасников А.В. Современные численные методы оптимизации. Метод универ-

сального градиентного спуска. М.: МЦНМО, 2020.

4. Alkousa M.S., Dvinskikh D.M., Stonyakin F.S., Gasnikov A.V., Kovalev D. Accel-

erated Methods for Saddle Point Problems // Comput. Math. Math. Phys. 2020.

V. 60. No. 11. P. 1787-1809.

Gladin E., Kuruzov I., Stonyakin F., Pasechnyuk D., Alkousa M., Gasnikov A. Solv-

ing strongly convex-concave composite saddle point problems with a small dimension

of one of the variables. https://arxiv.org/pdf/2010.02280.pdf

Tianyi L., Chi J., Michael I.J. Near-Optimal Algorithms for Minimax Optimization.

https://arxiv.org/pdf/2002.02417v5.pdf

Yuanhao W., Jian L. Improved Algorithms for Convex-Concave Minimax Optimiza-

tion. https://arxiv.org/pdf/2006.06359.pdf

Zhongruo Wang, Krishnakumar Balasubramanian, Shiqian Ma, Meisam Razaviyayn.

Zeroth-Order Algorithms for Nonconvex Minimax Problems with Improved Com-

plexities. https://arxiv.org/pdf/2001.07819.pdf

Гасников А.В., Гасникова Е.В. Модели равновесного распределения транспорт-

ных потоков в больших сетях. Уч. пос. М.: МФТИ, 2020.

10.

Bolte J., Glaudin L., Pauwels E., Serrurier M. A Hölderian backtracking method

for min-max and min-min problems. https://arxiv.org/pdf/2007.08810.pdf

11.

Jungers M., Trélat E., Abou-Kandil H. Min-Max and Min-Min Stackelberg Strategies

with Closed-Loop Information Structure // J. Dynamical and Control Syst. Springer

Verlag, 2011. No. 17 (3). P. 387-425.

12.

Konur D., Farhangi H. Set-based Min-max and Min-min Robustness for Multi-

objective Robust Optimization // Proc. 2017 Industrial and Systems Engineering

Research Conf. K. Coperich, E. Cudney, H. Nembhard, eds.

13.

Vaidya P.M. A New Algorithm for Minimizing Convex Functions over Convex Sets //

Foundations of Computer Science, 1989. 30th Annual Sympos. 1989. P. 338-343.

14.

Vaidya P.M. A new algorithm for minimizing convex functions over convex sets //

Mathematical Programming 73. Springer, 1996. P. 291-341.

15.

Lan G., Zhize Li, Yi Zhou. A unified variance-reduced accelerated gradient method

for convex optimization // 33rd Conf. on Neural Information Processing Systems

(NeurIPS 2019). Vancouver, Canada. https://arxiv.org/pdf/1905.12412.pdf

16.

Tyurin A.I., Gasnikov A.V. Fast Gradient Descent Method for Convex Optimization

Problems with an Oracle That Generates a (δ, L)-model of a Function in a Requested

Point // Comput. Math. Math. Phys. 2019. V. 59. No. 7. P. 1137-1150.

17.

Bubeck S. Convex Optimization: Algorithms and Complexity // Foundations and

Trends in Machine Learning. 2015. V. 8. No. 3-4. P. 231-357.

18.

Gladin E., Sadiev A., Gasnikov A., Stonyakin F., Dvurechensky P., Beznosikov A.,

Alkousa M. Solving smooth min-min and min-max problems by mixed oracle algo-

rithms. https://arxiv.org/pdf/2103.00434.pdf

19.

Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983.

20.

Гасников А.В., Двуреченский П.Е., Камзолов Д.И., Нестеров Ю.Е., Спокой-

ный В.Г., Стецюк П.И., Суворикова А.Л., Чернов А.В. Поиск равновесий в мно-

гостадийных транспортных моделях // Тр. Московского физико-технического

института. 2015. № 7.4 (28).

21.

Bishop C. Pattern recognition and machine learning. Springer, 2006.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 28.01.2021

После доработки 26.04.2021

Принята к публикации 30.06.2021