Автоматика и телемеханика, № 10, 2021

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ЭФФЕКТИВНЫЙ АЛГОРИТМ ТУПИКОВЫХ УПРАВЛЕНИЙ

ДЛЯ РЕШЕНИЯ ЗАДАЧ КОМБИНАТОРНОЙ ОПТИМИЗАЦИИ

Предлагается алгоритм тупиковых управлений, предназначенный для

точного решения NP-трудных задач комбинаторной оптимизации. Эф-

фективность алгоритма демонстрируется на примерах решения задачи

разбиения на равные части и задачи об одномерном рюкзаке. В статье

также показано, что применение идеи тупиковых управлений при реали-

зации метода динамического программирования позволяет значительно

сократить на каждом шаге оптимизации число переменных состояний за-

дачи. Проведен сравнительный анализ предлагаемого метода с известны-

ми алгоритмами решения этих задач.

Ключевые слова: тупиковое управление, функция Беллмана, алгоритм,

задача разбиения, задача о рюкзаке.

DOI: 10.31857/S000523102110007X

1. Введение

В настоящее время на практике получили распространение два основных

оптимальных метода решения задач комбинаторной оптимизации, к которым

относится задача об одномерном рюкзаке (0-1 knapsack problem) и сводящая-

ся к ней задача разбиения на равные части (set-partition problem), а именно:

метод ветвей и границ в рамках статичной модели, когда параметры задачи

не меняются во времени, и различные модификации метода динамического

программирования [1-3]. Подробный обзор различных методов и алгоритмов,

разработанных для решения задачи о рюкзаке, изложены в [4].

Наряду с модификациями метода динамического программирования для

решения задачи о рюкзаке применяются и приближенные алгоритмы, в част-

ности жадный алгоритм и аппроксимационный алгоритм, подробно изложен-

ные в [2, с. 448-478; 5, с. 417-424] соответственно.

Комбинированные эвристические алгоритмы для задачи о рюкзаке по-

дробно изложены в [6]. В [7-9] представлен графический подход к решению

задачи разбиения на равные части и задачи об одномерном рюкзаке.

Несмотря на то что данные задачи относятся к классу NP-трудных, в по-

следнее время в большом количестве научных публикаций появляются новые

алгоритмы для задачи о ранце в виде как точных алгоритмов, так и прибли-

женных, включая и эвристические алгоритмы, обладающие различной вре-

менной трудоемкостью [10-12].

Рассмотрим математические постановки задач комбинаторной оптимиза-

ции.

1. Задача разбиения на равные части (partition) состоит в следующем:

задано множество целых чисел B = {b₁, . . . , b_n}. Требуется разбить множе-

ство B на два непересекающихся подмножества B₁ и B₂ так, чтобы миними-

зировать значение:



∑



(1)

b_j -

b_j

→ min .



b_j∈B₁

b_j∈B₂

2. Задача об одномерном рюкзаке (0-1 knapsack). В общем виде вербаль-

ная постановка задачи сводится к следующему: из заданного множества

предметов, характеризующихся для j-го предмета “ценностью” p_j и “весом

(объемом)” w_j, требуется отобрать такое число предметов, чтобы получить

максимальную суммарную ценность при одновременном соблюдении ограни-

чения b на суммарный вес или объем.

Математическую постановку целочисленной задачи представим в виде за-

дачи булевого линейного программирования:



∑



f (x₁, . . . , x_n) =

p_jx_j → max ,



x₁,..., xn

j=1

(2)

∑



jxj ≤ b, xj ∈ {0, 1} , j = 1,2,... ,n.

 w

j=1

∑_n

Когда p_j = w_j = b, j = 1, n, и b =¹

b_j, то задачи (1) и (2) являются

j=1

эквивалентными.

Идея тупиковых управлений взята из задачи минимизации и получения

сокращенной (тупиковой) дизъюнктивной нормальной формы (ДНФ) [13],

представляющей собой произвольную дизъюнкцию элементарных конъюнк-

ций логических функций булевой алгебры, которую нельзя упростить. По

аналогии с ДНФ допустимое управление, в котором замена произвольной ну-

левой компоненты в булевском векторе на единицу приводит к нарушению

ресурсных ограничений, в задаче о ранце будем называть тупиковым.

В данной статье предлагается новый оптимальный алгоритм тупиковых

управлений, который по своей эффективности на данный момент превосходит

опубликованные алгоритмы для решения задачи разбиения на равные части

и задачи об одномерном рюкзаке.

Кроме того, предлагаемый алгоритм может быть применим в задачах вы-

полнения комплекса взаимосвязанных работ, математическая постановка ко-

торых представлена на динамических управляемых моделях [14]. В статье

демонстрируется применение тупиковых управлений при решении задачи о

рюкзаке методом динамического программирования.

2. Алгоритм тупиковых управлений

Рассмотрим шаги а л г о р и т м а тупиковых управлений более подробно.

Шаг 1. Упорядочение номеров предметов в порядке убывания весов. Не

умаляя общности, будем предполагать, что для любого предмета справедливо

неравенство:

w_j ≤ b ∀j = 1,n.

Построение тупиковых управлений начинается с упорядочения номеров

предметов в порядке убывания весов (объемов):

wj1 ≥ ... ≥ wjk ≥ ... ≥ wjn.

Пусть u_k ≡ xjk ∈ {0, 1} - переменная управления, принимающая значение

единица, если k-й предмет по порядку помещается в рюкзак, и нулевое зна-

чение в противном случае. В связи с перенумерацией переменных математи-

ческая постановка задачи о рюкзаке сводится к нахождению такого вектора

управления u = (u₁, . . . , u_n), который доставляет максимум целевой функ-

ции:

∑

(3)

f (u) =

p_ku_k → max

u₁,..., un

k=1

при условии

∑

(4)

w_ku_k ≤ b, u_k

∈ {0, 1} , k = 1, 2, . . . , n.

k=1

Очевидно, что задача (3)-(4) эквивалентна задаче (2).

Шаг 2. Построение тупиковых управлений. В первое тупиковое управ-

ление включаем первый предмет, который соответствует управлению u₁ = 1,

если он не нарушает ограничения (4), т.е. выполняется неравенство: w₁u₁ ≤ b,

в противном случае полагаем u₁ = 0. Точно так же поступаем со вторым, тре-

тьим и так далее по порядку и с n-м предметом в соответствии с формулой:





∑



1, если

u_iw_i ≤ b;



i=1

(5)

u_k =



∑



 0, если

u_iw_i > b,

i=1

последовательно для k = 1, 2, . . . , n.

В результате получим первое тупиковое управление, состоящее из нулей и

единиц

(

)

(6)

u₁ = u⁽¹⁾¹,u⁽¹⁾²,... ,u⁽¹⁾

Построенному вектору управления u₁ (6) соответствует некоторое двоич-

ное число

(7)

ξ₁

= (11010..1..01001) ,

где единицы стоят в тех разрядах, номера которых совпадают с номерами

предметов, включенных в управление u₁ (6). Замена любого нуля единицей

делает это управление недопустимым по ограничению (4).

С помощью первого тупикового управления построим второе. Для этого

найдем самый младший разряд числа ξ₁, в котором записан ноль. Во всех

разрядах справа от него вместо единиц записываем нули. В полученном дво-

ичном числе первую справа единицу перенесем на один разряд вправо. Ес-

ли полученное управление недопустимо по ограничению (4), то эту единицу

сдвигаем еще на один разряд вправо до тех пор, пока управление не окажется

допустимым.

Далее в разряды справа от этой единицы помещаем единицы по тому же

правилу (5), что и при построении числа ξ₁ (7). В результате получаем дво-

ичное число ξ₂ < ξ₁. Этому числу соответствует тупиковое управление u₂ =(

)

= u⁽²⁾¹,u⁽²⁾²,... ,un2)

. Точно таким же образом из тупикового управления u₂

строится тупиковое управление u₃, которому соответствует двоичное число

ξ₃ < ξ₂ < ξ₁ и т.д. В результате получаем множество тупиковых управлений

{ (

)

}

(8)

U =

u_l = u^(l)1,... ,u^(l)k,... ,u^(l)

|l = 1,2,...,N

которому соответствует упорядочение двоичных чисел:

ξ_N < ξ_N-1 < ... < ξ₃ < ξ₂ < ξ₁.

Описанная процедура дает возможность получить все тупиковые управ-

ления, удовлетворяющие ограничению (4).

Шаг 3. Вычисление оптимального тупикового управления. Для каждо-

го тупикового управления u_l, l = 1, N , находим значение целевой функцией

f (u_l) (3).

За оптимальное управление принимаем тупиковое u_∗ ∈ U (8), обеспечи-

вающее максимальное значение целевой функции f (u) (3):

(

)

u_∗ = (u^∗1,... ,u^∗k,... ,u^∗n) = arg maxf u(l)1,... ,u(l)k,... ,u(l)

u_l∈U

Обоснование изложенного алгоритма решения задачи о рюкзаке базиру-

ется на следующих теоремах.

Теорема 1 (о существовании оптимального решения). Среди всех ту-

пиковых управлений из множества U (8) найдется по крайней мере одно

тупиковое управление, обеспечивающее максимум целевой функции задачи

о рюкзаке (3)-(4).

Доказательство. Пусть u_∗ - оптимальное тупиковое управление, яв-

ляющееся решением задачи (3)-(4). Предположим обратное, что u_∗ не явля-

ется оптимальным и тупиковым управлением, т.е. u_∗ ∈ U (8). Дополним его

до тупикового u₀ ∈ U (8).

Это значит, что найдется предмет, который войдет в рюкзак, и значение

целевой функции при этом увеличится на величину ценности этого предмета.

При этом для целевой функции f (u) (3) будет выполняться неравенство, т.е.

f (u₀) > f (u_∗) .

Получили противоречие с тем, что нашлось решение u₀ лучшее, чем u_∗.

Следовательно, предположение u_∗ не верно, что и требовалось доказать. Тео-

рема 1 доказана.

От исходной прямой задачи (3)-(4) максимизации ценности рюкзака пе-

рейдем к двойственной задаче минимизации остатка веса (объема) рюкзака

по критерию:

∑

(9)

g (u_l) = b -

w_ku^(l)k → min,

u_l∈U

k=1

который равносилен максимизации суммы весов предметов, помещаемых в

рюкзак.

Очевидно, что для функции g (u_l) (9) должно выполняться неравенство

∑

(10)

g (u_l) = b -

w_ku^(l)k

≥ 0 ∀ l = 1,2,...,N,

k=1

где b - объем (вес) рюкзака, w_k - вес k-го предмета управления u_l ∈ U (8).

При этом имеет место следующее утверждение.

Теорема 2 (о связи прямой и двойственной задач). Пусть

(

)

(

)

u_f = u^(f)1,... ,u^(f)k,... ,u^(f)j

u_g = u^(g)1,... ,u^(g)k,... ,u^(g)

оптимальные решения прямой f (u_l) (3)-(4) и двойственной g (u_l) (9)-(10)

задач соответственно.

Тогда для весов предметов, помещаемых в рюкзак, справедливо неравен-

ство

∑

(11)

w_ku^(f)k ≤

w_ku^(g)k.

k=1

Доказательство. Пусть

{

}

(12)

U_min =

u_g ∈ U (8) | u_g = arg min

g (u_l)

u_l∈U

подмножество множества U (8) тупиковых управлений, на которых крите-

рий g (u_l) (9) достигает минимального значения, которое не всегда совпадает

с точной нижней гранью U (8), а именно: inf g (u_l) = 0, u_l ∈ U (8).

Очевидно, что если оптимальные решения прямой f (u_l) (3)-(4) задачи

u_f ∈ U_min (12) , то неравенство (11) выполняется как равенство.

Покажем, что если u_f ∈ U_min (12), то неравенство (11) выполняется как

строгое. Действительно, в соответствии с определением минимума целевой

функции [5] должно выполняться неравенство

g (u_g) < g (u_f ) ∀ u_f ∈ U_min

(12) ,

т.е.

∑

b- w_ku^(g)k <b- w_ku^(f)k ⇒ w_ku^(g)k >

w_ku^(f)k.

k=1

Отсюда следует справедливость неравенства (11), что и требовалось дока-

зать. Теорема 2 доказана.

3. Метод динамического программирования с тупиковыми управлениями

на примере решения задачи о рюкзаке в прямом времени

Используя основную идею динамического программирования [1], сведем

решение задачи (3)-(4), поставленной на статичной математической модели,

к задаче оптимизации управляемой динамической системы, решение которой

сводится к следующим этапам.

1. Этап инвариантного погружения. Для этого вложим задачу о рюкзаке

в семейство задач той же природы, в результате чего получим управляемую

систему в прямом времени:









∑

(13)

Z =

Z_k : max

p_ju_j,

w_ju_j ≤ s_k, k = 1,n



u₁,...,u



^k j=1

j=1

где u_k ∈ {0, 1} - управление на k-м шаге оптимизации, s_k - переменная со-

стояния, характеризующая остаточный вес рюкзака.

Множество допустимых значений переменной состояния s_k управляемой

системы (13) для u_k-го управления будем обозначать через S_k, являющееся

подмножеством множества числовых значений параметров S = {0, 1, . . . , b},

связанным с семейством задач (13). Исходная задача очевидным образом вхо-

дит в рассматриваемое семейство, если в (13) положить k = n и s_n = b. По-

скольку из семейства задач выделяется исходная задача, то семейство задач Z

(13) реализует принцип инвариантного погружения в прямом времени.

Пусть на первом шаге k = 1 осуществляется выбор переменной управле-

ния u₁ при некотором выборе переменных u₂, u₃, . . . , u_n таком, что

∑

s₁ = b - w_ju_j,

j=2

где 0 ≤ s₁ ≤ b.

Величина s₁ характеризует тот остаток общего ресурса b, который можно

использовать при выборе u₁. Перейдя ко второму шагу, а затем и к третьему и

далее к k-му шагу, будем рассматривать остаток общего ресурса b на k-м шаге

как s_k состояние процесса выбора управления u_k управляемой системы (13).

Из ресурсных ограничений

∑

(14)

0≤ w_ju_j ≤s_k

k = 1,n,

j=1

имеем:

а) параметры состояния управляемой системы на k-м шаге оптимизации







∑



(15)

S_k = s_k =

w_ju_j |u_j ∈ {0,1} , k = 1,... ,n





j=k+1

где s₀ = 0 начальное состояние на первом шаге k = 1,

s_n = b конечное состояние на последнем шаге k = n;

б) уравнения состояний в прямом времени

s_k-1 = s_k - w_ku_k,

связывающие переменные состояний функций Р. Беллмана на шагах оптими-

зации k - 1 и k-м.

Множества значений функции Беллмана на k-м шаге оптимизации пред-

ставим в виде

(16)

S_k = {s_k,s_k

+ 1, . . . , b} ,

где минимальное значение переменной состояния s_k ∈ S_k (15) определяется

из условия:







∑



(17)

s_k = min

w_ju_j

u_k+1,...,un





j=k+1

причем c учетом неравенства (14) переменные управления u_k+1, . . . , u_n долж-

ны удовлетворять соотношению (5).

Поскольку для любых переменных u_k+1, . . . , u_n и не обязательно тупико-

∑_n

вых на k-м шаге справедливо неравенство

w_ju_j ≤

w_j, то ми-

j=k+1

нимальное значение переменной состояния s_k ∈ S_k (15) для задач большой

размерности можно определять и из условия:















∑



s_k = min

b-

w_j



u_k+1,...,un 





j=k+1

Множество допустимых управлений k-го шага представим в виде:

{



[s_k ]},

U (s_k) = u_k ∈ {0, 1}0≤uk ≤

w_k

[

]

s_k

где

- целая часть числаsk ._w

w_k

Отсюда под действием управления u_k система, находящаяся в состоянии

s_k-1, перейдет в состояние s_k. Показатель эффективности k-го шага опреде-

лим как f_k = p_ku_k.

Заключаем, что задача (3)-(4) поставлена как задача динамического про-

граммирования оптимизации управляемой системы.

2. Этап построения рекуррентных функциональных уравнения Р. Беллма-

на. На решениях задач Z (13) определим функцию Беллмана от k переменных

управления u₁, . . . , u_k в виде

∑

(18)

B_k(s_k) = max

p_ju_j

k = 1, 2,...,n,

u₁,...,u

^k j=1

с областью определения S_k (16), характеризующую суммарную ценность рюк-

зака от первогого шага до k-го шага.

Так как вычисление последовательности функций Беллмана B_k(s_k) (18)

происходит в направлении возрастания дискретного аргумента k (идет слева

направо: 1, 2, . . . ), то для k-го шага имеем рекуррентное уравнение Беллмана

в прямом времени в виде:

(19)

B_k (s_k) = m[ax

)} ,

]{pkuk + Bk-1 (sk - wkuk

u_k≤

которое удовлетворяет начальному условию

B₁ (s_k) = ma[

]p1u1.

0≤u₁≤^s1

Выбрав на k-м шаге некоторое произвольное управление u_k, система из со-

стояния s_k-1 придет в состояние s_k. Так как в оптимальном решении задач Z

(13) должно быть либо 0, либо 1, то уравнения (19) запишутся в виде

}

{ p

u_k = 1

B_k (s_k) = ma[

k = 1,2,...,n.

^] Bk-1 (s_k-1), u_k = 0

0≤u_k≤^sk

Таким образом, для любого значения s_k ∈ S_k определение величины B_k(s_k)

сводится к простейшей задаче оптимизации сравнению двух чисел, началь-

ное условие при этом для начального шага k = 1 запишется в виде:

}

{ p1, u1 = 1

B₁ (s₁) = ma[

]

0, u₁ = 0

0≤u₁≤^s1

Дойдя до k = n, определим оптимальное значение целевой функции

B_n(s_n), совпадающей со значением целевой функции исходной задачи.

3. Этап решения рекуррентных функциональных уравнений. На данном

этапе алгоритмом обратной прогонки, дойдя до k = n шага, определим оп-

тимальное значение функции B_n (s_n), s_n ∈ S_n, совпадающей со значением

целевой функции исходной задачи (3)-(4). Из условия B_n (s_n) = f_n (u^∗n) +

+Bn-1 (s_n - w_nu^∗n) имеем оптимальное управление u^∗n = u∗n (s_n).

Далее последовательно на каждом шаге для k = n, n-1, . . . , 1, определяем

оптимальные управления:

B_n (s_n) → u^∗n = u^∗n (s_n) → s_n-1 = s_n - w_nu^∗n;

B_k (s_k) → u^∗k = u^∗k (s_k) → s_k-1 = s_k - w_ku^∗k;

B₁ (s₁) → u^∗1 = u^∗1 (s₁) .

Тогда в конце работы пошаговой процедуры получим оптимальное управ-

ление

(20)

u_∗ = (u^∗1,... ,u^∗n

Необходимо заметить, что если на каждом шаге запоминать вектор управ-

ления вида u (k) = (u₁, . . . , u_k) , k = 1, n, то на последнем шаге сразу можно

выделить оптимальное решение u^∗ (20).

4. Сравнительная оценка эффективности алгоритма

Для оценки эффективности алгоритма сравним его трудоемкость с тради-

ционными методами решения задачи о рюкзаке. Продемонстрируем работу

алгоритма на примерах решения задачи разбиения и задачи о рюкзаке.

Пример 1. На данных примера из [9, с. 320-323] решим задачу разбие-

ния. Пусть числа множества B = {100, 70, 50, 20}, пронумерованы по невоз-

растанию, n = 4. Сведем задачу разбиения (1) к эквивалентной задаче о рюк-

заке (3), что можно представить в виде

f (u₁,u₂,u₃,u₄) = 100u₁ + 70u₂ + 50u₃ + 20u₄ → max ,

u₁,...,u₄

100u₁ + 70u₂ + 50u₃ + 20u₄ ≤ 120,

∑₄

где b =¹

b_j = 120.

j=1

Выполнив шаги 2 и 3 алгоритма, тупиковые управления и соответствую-

щие им значения целевой функции представим в виде табл. 1.

В результате, построив четыре тупиковых управления, получаем два оп-

тимальных решения:

B₁ = {b₁,b₄} = {100,20}, B₂ = {b₂,b₃} = {70,50};

B₁ = {b₂,b₃} = {70,50}, B₂ = {b₁,b₄} = {100,20}.

Таблица 1

U u₁ u₂ u₃ u₄ f (u_l)

u₁

120

u₂

120

u₃

u₄

Таблица 2

U u₁ u₂ u₃ u₄ f (u_l)

u₁

u₂

u₃

u₄

Как видно из табл. 1, понадобилось всего лишь четыре тупиковых управле-

ния, чтобы найти точное оптимальное решение. Для решения данной задачи

разбиения графическим алгоритмом понадобилось рассмотреть семь точек

(см. [9, с. 322]), а для алгоритма тупиковых управлений потребовалось по-

строить всего лишь четыре управления (см. табл. 1).

Пример 2. Продемонстрируем работу алгоритма при решении задачи о

рюкзаке на данных примера из [9, с. 326-333].

Постановку исходной задачи представим с учетом убывания весов пред-

метов в виде





f (u) = 3u₁ + 6u₂ + 7u₃ + 5u₄ → max ,

u₁,...,u₄

7u₁ + 5u₂ + 3u₃ + 2u₄ ≤ 9,



u_j ∈ {0,1} , j = 1,2,3,4.

Выполнив шаги 2 и 3 алгоритма, тупиковые управления и соответствую-

щие им значения целевой функции представим в виде табл. 2.

Построив четыре тупиковых управления, получаем оптимальное решение:

u_∗ = u₂ = (0,1,1,0) ,

где

u₁ = x₄ = 0, u₂ = x₃ = 1, u₃ = x₂ = 1, u₄ = x₁ = 0.

Для решения данной задачи о рюкзаке графический алгоритм вычисляет

только 14 элементов [9, с. 333], в то же время для алгоритма тупиковых управ-

лений потребовалось построить всего лишь четыре управления (см. табл. 2).

Пример 3. Рассмотрим задачу о рюкзаке вместимостью b = 10 для мно-

жества из 7 предметов, т.е. J₀ = {1, 2, 3, 4, 5, 6, 7}, вес и стоимость которых

представлены в табл. 3 (исходные данные взяты из [15, с. 437]).

Таблица 3. Исходные данные задачи о рюкзаке

w_j

p_j

299

159

221

137

157

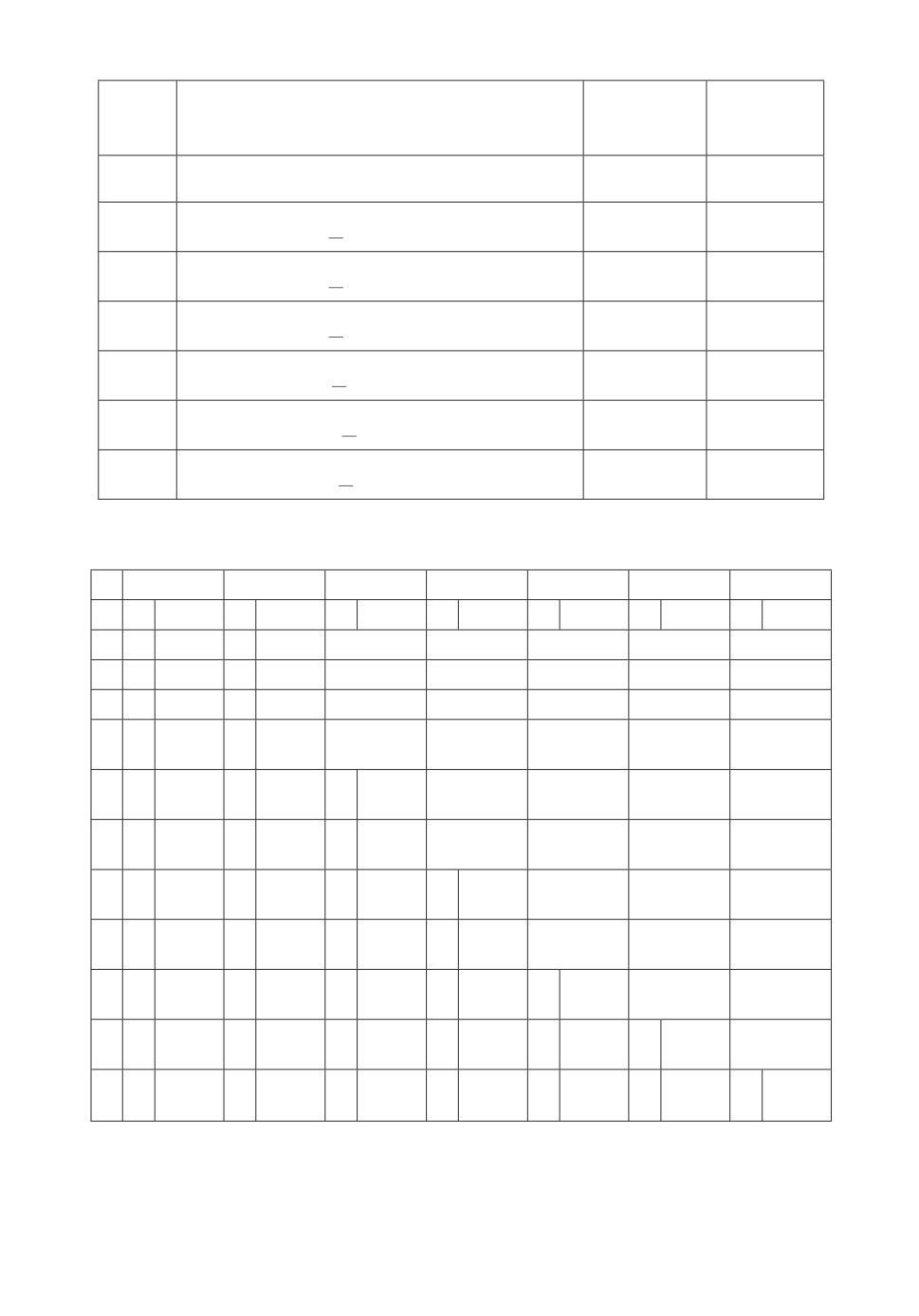
Таблица 4. Результаты решения методом тупиковых управлений

(

)

ξ_l - значение в десятичной

u_l = u^(l)1, . . . , u^(l)7

∑ w_ku_k

f (u_l)

системе счисления

k=1

1110010

114

752

1110001

113

768

1101010

106

730

1101001

105

746

1100110

102

750

1100101

101

766

1100011

682

1011100

752

1011011

757

1010111

777

1001111

755

0111110

747

0111101

763

0111011

679

0110111

699

0101111

677

0011111

615

1. Решение псевдополиномиальным алгоритмом динамического програм-

мирования ДП-III. Результатом решения является подмножество

(21)

J_∗

= {1, 2, 3, 6, 7} ,

∑

где p =j∈J∗ p_j = 777.

При этом алгоритм проходит через построение 91 пары (J, p), где J ⊂ J₀.

(

)

Трудоемкость данного алгоритма O

n²p

, где p - значение оптимальной

стоимости [15, с. 436].

2. Решение задачи о рюкзаке методом тупиковых управлений. Упорядочим

номера предметов в порядке убывания весов (объемов)

w11 > w42 > w33 ≥ w54 ≥ w75 > w26 ≥ w67 ,

где w11 = 4, w42 = 3, w33 = 2, w54 = 2, w75 = 2, w26 = 1, w67 = 1.

Пусть u_k ∈ {0, 1} - переменная управления, принимающая значение еди-

ница, если k-й предмет по порядку помещается в рюкзак, и нулевое значение

в противном случае. Тогда постановку задачи о ранце представим в виде:

299u₁ + 221u₂ + 159u₃ + 137u₄ + 157u₅ + 73u₆ + 89u₇ → max

N(b)

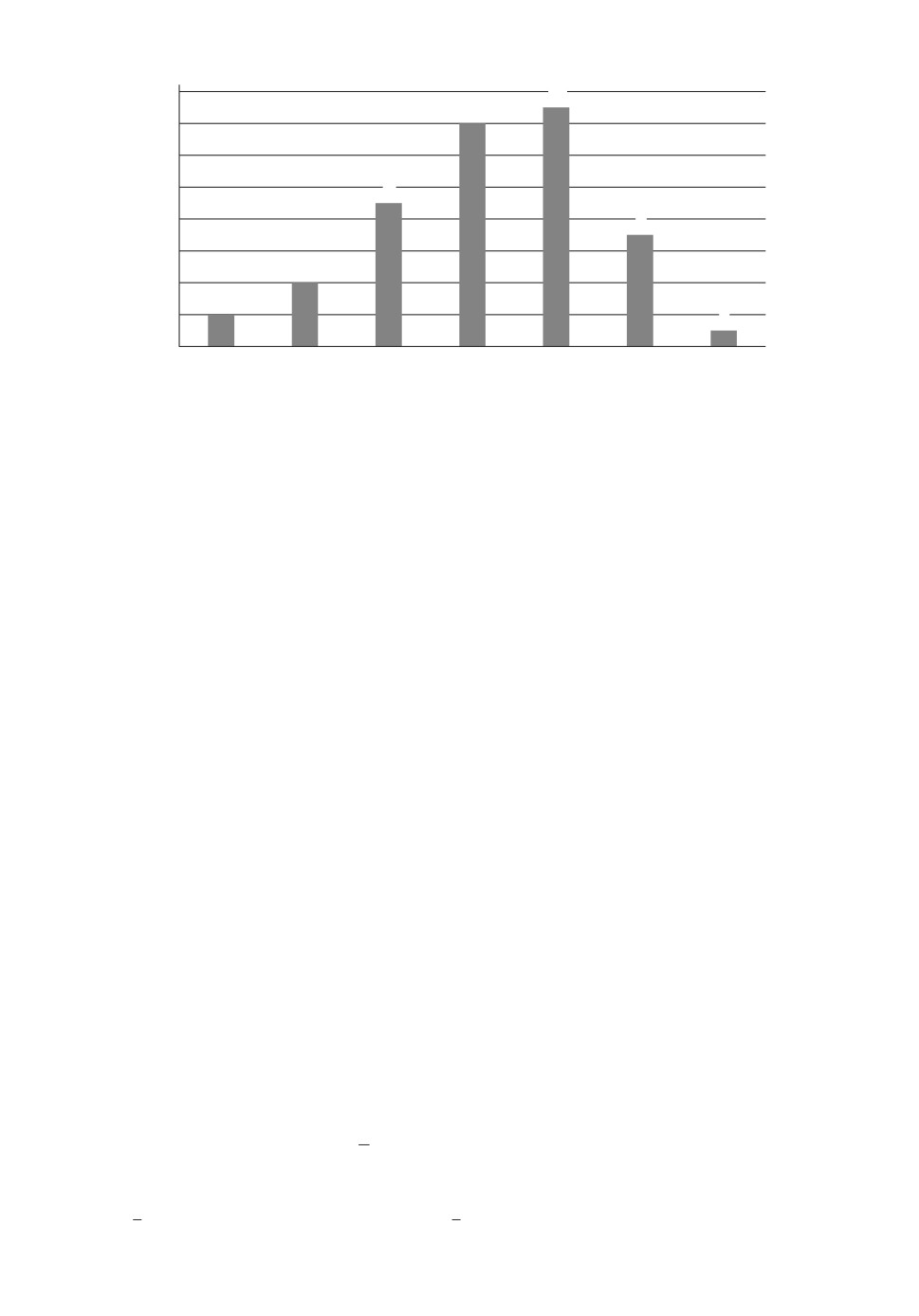
Зависимость числа тупиковых управлений от веса рюкзака.

при ограничениях

4u₁ + 3u₂ + 2u₃ + 2u₄ + 2u₅ + 1u₆ + 1u₇ ≤ 10.

Построенные тупиковые управления и ценность предметов, попадающих

в рюкзак, представлены в табл. 4.

Решением задачи является тупиковое управление u₁₀ = (1010111), которое

совпадает с решением J_∗ (21) в исходных обозначениях с величиной ценности

рюкзака:

∑

p_j = 299 + 159 + 157 + 73 + 89 = 777.

j∈J∗

Возникает вопрос о зависимости числа тупиковых управлений от веса рюк-

зака. Можно предположить, что максимальное число тупиковых управлений

будет приходить на вес рюкзака, равный примерно половине суммы весов

всех предметов.

На рисунке приведен график зависимости числа тупиковых управлений

N (b) от веса b рюкзака для исходных данных из табл. 3, где величина веса

(объема) рюкзака определялась по формуле

∑

b_k =

w_j, k = 1,2,... ,7;

1 ≤ w₁ ≤ w₂ ≤ ... ≤ w₇ ≤ 4.

j=1

Из рисунка видно, что максимальное число тупиковых управлений прихо-

дится на вес рюкзака, равный не менее половины суммы весов всех предме-

тов, и убывает, когда вес рюкзака возрастает, т.е.





∑

1

w_j ≤ b < w_j,

j=1

[

]

∑_n

где

w_j

- целая часть числа ¹

w_j.

j=1

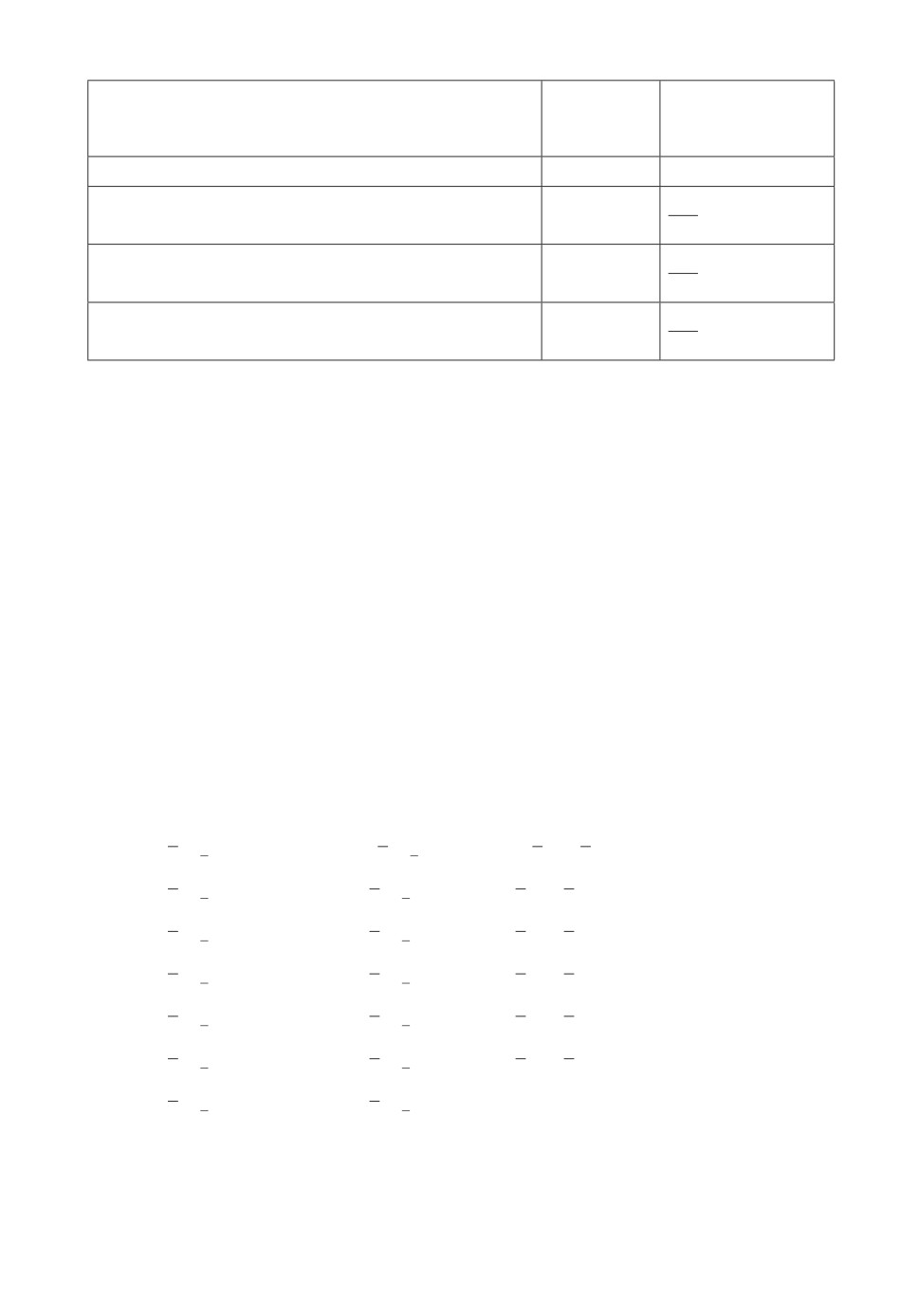
Таблица 5. Рекуррентные функциональные уравнения Р. Беллмана

Тупиковое

Множество

Номер

Функция Р. Беллмана B₁(s₁)

управление

состояний

шага k

u_l

S_k(u_l)

B₁ (s₁) = max

299u₁, s₁ ∈ S₁

0111110

0 ÷ 10

0≤u₁≤[s1/4]

B₂ (s₂) = max

{221u₂ + B₁ (s₂ - 3u₂)}

0011111

2 ÷ 10

0≤u₂≤[^s23 ]

B₃ (s₃) = max

{159u₃ + B₂ (s₃ - 2u₃)}

0001111

4 ÷ 10

0≤u₃≤[^s32 ]

B₄ (s₄) = max

{137u₄ + B₃ (s₄ - 2u₄)}

0000111

6 ÷ 10

0≤u₄≤[^s42 ]

B₅ (s₅) = max

{157u₅ + B₄ (s₅ - 2u₅)}

0000011

8 ÷ 10

0≤u₅≤[^s52 ]

B₆ (s₆) = max

{73u₆ + B₅ (s₆ - u₆)}

0000001

0≤u₆≤[^s61 ]

B₇ (s₇) = max

{89u₇ + B₇ (s₇ - u₇)}

0000001

0≤u₇≤[^s72 ]

Таблица 6. Результаты расчетов функций Р. Беллмана в прямом времени

k Шаг 1

Шаг 2

Шаг 3

Шаг 4

Шаг 5

Шаг 6

Шаг 7

s_k u1 B1(s1) u2 B2(s2) u3 B3(s3) u4 B4(s4) u5 B5(s5)

u6 B6(s6) u7 B7(s7)

–

221

299

380

299

458

299

458

520

299

520

299

520

595

615

299

520

679

657

677

688

679

299

520

679

752

750

777

В этом случае можно предположить, что мощность |U| множества тупи-

ковых U (8), как правило, значительно меньше числа bn, т.е. |U| ≤ cn, где

c > 0, поэтому трудоемкость алгоритма можно оценить как O(n).

Таблица 7. Результаты сравнений методов решения задачи о рюкзаке

Число

Процент

Метод решения

прямых

от полного

вычислений

перебора

Полный перебор

128

100%

Метод динамического программирования ДП III

× 100% ≈ 71%

128

Метод динамического программирования с ТУ

× 100% ≈ 30%

128

Метод тупиковых управлений

× 100% ≈ 13%

128

Представляет интерес нахождение функциональной зависимости числа ту-

пиковых управлений от веса рюкзака. Данную проблему, хотя бы для частных

случаев, автор предлагает исследовать читателю.

3. Решение задачи методом динамического программирования с тупико-

вым управлением. Расчет значений функций Беллмана ведется по всем до-

пустимым u_k от начала к концу, k = 1, 2, . . . , 7.

Исходное дискретное множество области значений функции Р. Беллмана

S₀ = {0,1,2,... ,10}. В табл. 5 сведены функции Р. Беллмана на каждом шаге

оптимизации и множество состояний в зависимости от тупиковых управлений

рекуррентных функциональных уравнений Р. Беллмана.

Результаты расчетов B_k (s_k) представлены в табл. 6, где оптимальное

управление выделено подчеркиванием (в скобках после значения функции

Р. Беллмана текущего шага указано значение переменной состояния предше-

ствующей функции Р. Беллмана).

Алгоритмом обратной прогонки находим оптимальное управление:

B₇ (s₇)|s7=10=777→u7 (s7⁾|s₇=10^=1→s6^=s7-1u7 =10-1=9;

B₆ (s₆)|s6=9=688→u6 (s6⁾|s₆=9^=1→s5^=s6-1u6 =9-1=8;

B₅ (s₅)|s5=8=615→u5 (s5⁾|s₅=8^=1→s4^=s5-2u5 =8-2=6;

B₄ (s₄)|s4=6=458→u4 (s4⁾|s₄=6^=0→s3^=s4-2u4 =6-0=6;

B₃ (s₃)|s3=6=458→u3 (s3⁾|s₅=6^=1→s2^=s3-2u3 =6-2=4;

B₂ (s₂)|s2=4=299→u2 (s2⁾|s₂=4^=0→s1^=s2-3u2 =4-0=4;

B₁ (s₁)|s1=4=299→u1 (s1⁾|s₁=4^=1.

(

)

Отсюда u_∗ =

u^∗1,u^∗2,u^∗3,u^∗4,u^∗5,u^∗6,u^∗7

= (1010111), что соответствует в исход-

ных обозначениях решению J_∗ (21). Сравнительный анализ по трудоемкости

методов решений задачи о рюкзаке представлен в табл. 7.

Из табл. 7 следует, что применение тупиковых управлений оказалось эф-

фективнее в⁹¹¹⁷ ≈ 5,3 раза, чем алгоритм ДП III [2, 16], и в³⁸¹⁷ ≈ 2,2 раза, чем

метод динамического программирования с тупиковым управлением.

Традиционно считается, что временная сложность метода динамического

программирования линейна по числу этапов, что является его достоинством.

Если число состояний на каждом шаге ограничено константой b, то времен-

ная сложность для задачи распределения ресурсов с небулевским управле-

(

)

нием может быть оценена как O

b²n

[5]. Временная сложность алгоритма с

булевским управлением обычно не превышает величины O(nb) [8]. Покажем,

что если определять множество допустимых состояний k-го шага по форму-

ле S_k (16), то временную сложность вычислений можно оценить как O(n)

за n шагов алгоритма.

Теорема 3 (о трудоемкости метода динамического программирования

с тупиковым управлением). Пусть нижняя граница переменной состоя-

ния s_k ∈ S_k (15) на k-м шаге определяется по формуле s_k (17), тогда вре-

менная сложность алгоритма динамического программирования с тупико-

вым управлением решения задачи о рюкзаке в прямом времени будет удо-

влетворять неравенству

∑

(22)

|S_k

| ≤ cn,

0 < c < b,

k=1

что равносильно оценке временной сложности как O(n), где |S_k| - число

состояний на k-м шаге оптимизации.

Доказательство. Поскольку для переменной состояний на k-м шаге

выполняется неравенство

∑

s_k = b -

w_ju_j ≥ 0,

j=k+1

то для любых (тупиковых) управлений

u(k) = (u_k, u_k+1, . . . , u_n) и

u(k + 1) = (u_k+1, u_k+2, . . . , u_n)

справедливо неравенство

∑

b= w_j ≥...≥ w_ju_j ≥

w_ju_j ≥ ... ≥ w_n > 0

∀k = 1,n - 1,

j=1

j=k

j=k+1

т.е.

b ≥ |S₁| ≥ |S₂| ≥ ... ≥ |S_n| = 1.

Отсюда следуют справедливость неравенства (22) и оценка временной слож-

ности O(n). Теорема 3 доказана.

5. Заключение

В статье рассмотрен эффективный алгоритм тупиковых управлений для

решения задач комбинаторной оптимизации, относящийся к классу точных

оптимальных алгоритмов с временной сложностью O(n). В [8, 9] показано,

что графический алгоритм решения задач комбинаторной оптимизации об-

ладает временной сложностью O(n), однако при этом, как показано в приме-

рах 1 и 2, алгоритм тупиковых управлений оказался более эффективным. По

своей эффективности, на данный момент, алгоритм тупиковых управлений

превосходит известные алгоритмы, включая алгоритм Balsub, представлен-

ный в [4].

Также показано, что применение идеи тупиковых управлений при реали-

зации метода динамического программирования позволяет значительно со-

кратить на каждом шаге оптимизации число переменных состояний задачи.

Достоинствами метода тупиковых управлений являются его вычислительная

простота и более высокое быстродействие по сравнению с известными алго-

ритмами, что позволяет решать с его помощью характерные для практики

задачи большой размерности.

СПИСОК ЛИТЕРАТУРЫ

Беллман Р. Динамическое программирование. М.: Мир, 1960.

Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и ана-

лиз. М.: Издательский дом “Вильямс”, 2013.

Pisinger D. A Minimal Algorithm for the 0-1 Knapsack Problem // University of

Copenhagen. Oper. Res. 1997. V. 46. No. 5. P. 758-767.

Kellerer H., Pferschy U., Pisinger D. Knapsack Problems. Springer Science. Business

Media, 2010.

Корнеенко В.П. Методы оптимизации. М.: Высш. шк., 2007.

Сигал И.Х., Иванова А.П. Введение в прикладное дискретное программирова-

ние: модели и вычислительные алгоритмы. М.: Физматлит, 2002.

Гафаров Е.Р., Долгий А., Лазарев А.А., Вернер Ф. Новый эффективный алго-

ритм решения задачи об инвестициях // АиТ. 2016. № 9. С. 150-166.

Gafarov E.R., Dolgui A., Lazarev A.A., et al. A New Effective Dynamic Program

for an Investment Optimization Problem // Autom. Remote Control. 2016. V. 77.

No. 9. P. 1633-1648. https://doi.org/10.1134/S0005117916090101

Лазарев А.А. Графический подход к решению задач комбинаторной оптимиза-

ции // АиТ. 2007. № 4. С. 13-23.

Лазарев А.А. Теория расписаний. Методы и алгоритмы. М.: ИПУ РАН, 2019.

10.

Bretthauer K.M., Shetty B. The Nonlinear Knapsack Problem - Algorithms and

applications // Eur. J. Oper. Res. 2002. V. 138. Iss. 3. P. 459-472.

11.

Riedhammer K., Gillick D., Favre B., Hakkani-Tür D. Packing the Meeting Sum-

marization Knapsack // Proc. Interspeech. Brisbane, Australia, 2008.

12.

Robson J.M. Finding a Maximum Independent set in Time O(2n/4) // Technical

Report 1251-01, LaBRI, Universitte de Bodeaux I, 2001.

13.

Яблонский С.В. Введение в дискретную математику. М.: Наука, 1986.

14. Korneenko V.P., Nazyuta S.V., Chursin A.A. System for Uncertainty Factors Ac-

counting When Optimizing and Choosing Effective Options for Network Work

Schedules on a Dynamic Model with Dead-End Controls / IOP Conference Series:

Earth and Environmental Science // Proc. Int. Science and Technology Conf. on

Earth Science. Vladivostok, Russian: IOP Publishing Ltd, 2021. Sci. 666 062129.

https://doi.org/10.1088/1755-1315/666/6/062129.

15. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и

сложность. М.: Мир, 1985.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 20.01.2020

После доработки 17.03.2021

Принята к публикации 30.06.2021