Автоматика и телемеханика, № 10, 2021
© 2021 г. А.А. ЛАЗАРЕВ, д-р. физ.-мат. наук (jobmath@mail.ru),
Д.В. ЛЕМТЮЖНИКОВА, канд. физ.-мат. наук (darabbt@gmail.com)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва),
А.А. ТЮНЯТКИН (andtun@yandex.ru)
(Московский государственный университет им. М.В. Ломоносова)
МЕТРИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ ДЛЯ ЗАДАЧИ
МИНИМИЗАЦИИ МАКСИМАЛЬНОГО ВРЕМЕННÓГО
СМЕЩЕНИЯ ДЛЯ ОДНОГО ПРИБОРА1
Статья основана на использовании методов непрерывной математики
в дискретных задачах. Рассматриваются три новых подхода к решению
задач теории расписаний: метрический, интерполяционный и комбини-
рованный метрическая интерполяция. Метрическая интерполяция яв-
ляется объединением двух других и совмещает в себе их преимущества.
Каждый из этих подходов позволяет сокращать время решения соответ-
ствующих задач и вычислять значения гарантированной абсолютной по-
грешности целевой функции.
Ключевые слова: теория расписаний, метрический подход, интерполяция,
аппроксимация, дискретная оптимизация.
DOI: 10.31857/S0005231021100081
1. Введение
Подавляющее большинство задач теории расписаний NP-трудны [1]. Для
решения таких задач часто используются быстрые алгоритмы, производи-
тельность которых сильно зависит от входных данных. Предлагается новый
подход нахождения приближенных решений задач теории расписаний мет-
рическая интерполяция. Данный метод это комбинация двух различных
подходов, интерполяционного и метрического [1, 2], благодаря совместному
использованию которых возможно:
1) использовать приближенное значение целевой функции как начальное
решение для итерационных методов;
2) аппроксимировать решение задачи теории расписаний, используя неко-
торый класс полиномиально разрешимых примеров (при его существовании);
3) аппроксимировать значение целевой функции задачи даже при отсут-
ствии полиномиально разрешимых примеров, используя интерполяционный
подход.
Следует сразу отметить, что метрическая интерполяция подход, кото-
рый используется для ускорения работы уже существующих алгоритмов ре-
шения задач теории расписаний. В связке с рассматриваемым подходом могут
1 Работа выполнена при частичной финансовой поддержке Российского фонда фунда-
ментальных исследований (проект № 20-58-S52006).
93
быть использованы алгоритмы решения задач теории расписаний, рассмот-
ренные, например, в [1, 3, 4]. Для работы со случайными данными могут
быть использованы алгоритмы и методы из [5], а метрическая интерполяция
ускоряет их выполнение при обработке трудных случаев.
Поскольку интерполяционный подход работает лишь со значениями це-
левой функции, с его помощью можно составлять и расписания многоста-
дийных систем, решая задачи, например, алгоритмами из [6]. Метрический
подход можно использовать для этой цели при небольшой модификации, рас-
смотренной в [2].
Для определенности, в данной статье рассматривается решение задачи ми-
нимизации максимального временнóго смещения 1|rj |Lmax с помощью двой-
ственного алгоритма [7] и трех подходов, которые упомянуты выше.
2. Задача минимизации максимального временнóго смещения
для одного прибора
2.1. Постановка задачи минимизации максимального временнóго смещения
В задаче 1|rj |Lmax, которую будем рассматривать, задано множество из
n требований N = {1, . . . , n}. Для каждого требования j заданы: время по-
ступления rj , длительность выполнения pj и директивный срок dj [1]. Под
расписанием π будем подразумевать некоторую перестановку требований
множества N. Введем время завершения требования j при расписании π:
{
}
(1)
Cj(π) = max
rj, max Ck(π)
+pj.
π
(k→j)π
Здесь (k → j)π требования, которые выполняются перед работой j при
расписании π.
Таким образом, задача минимизации максимального временнóго смещения
состоит в нахождении такого расписания π0, при котором целевая функция
принимает минимальное значение:
(2)
Lmax(π0) = min
max
{Cj (π) - dj
}.
π
j=1,...,n
Данная задача является NP-трудной в сильном смысле [8].
2.2. Пространство примеров размерности n
Рассмотрим пример A, который состоит из n заявок. Такой пример можно
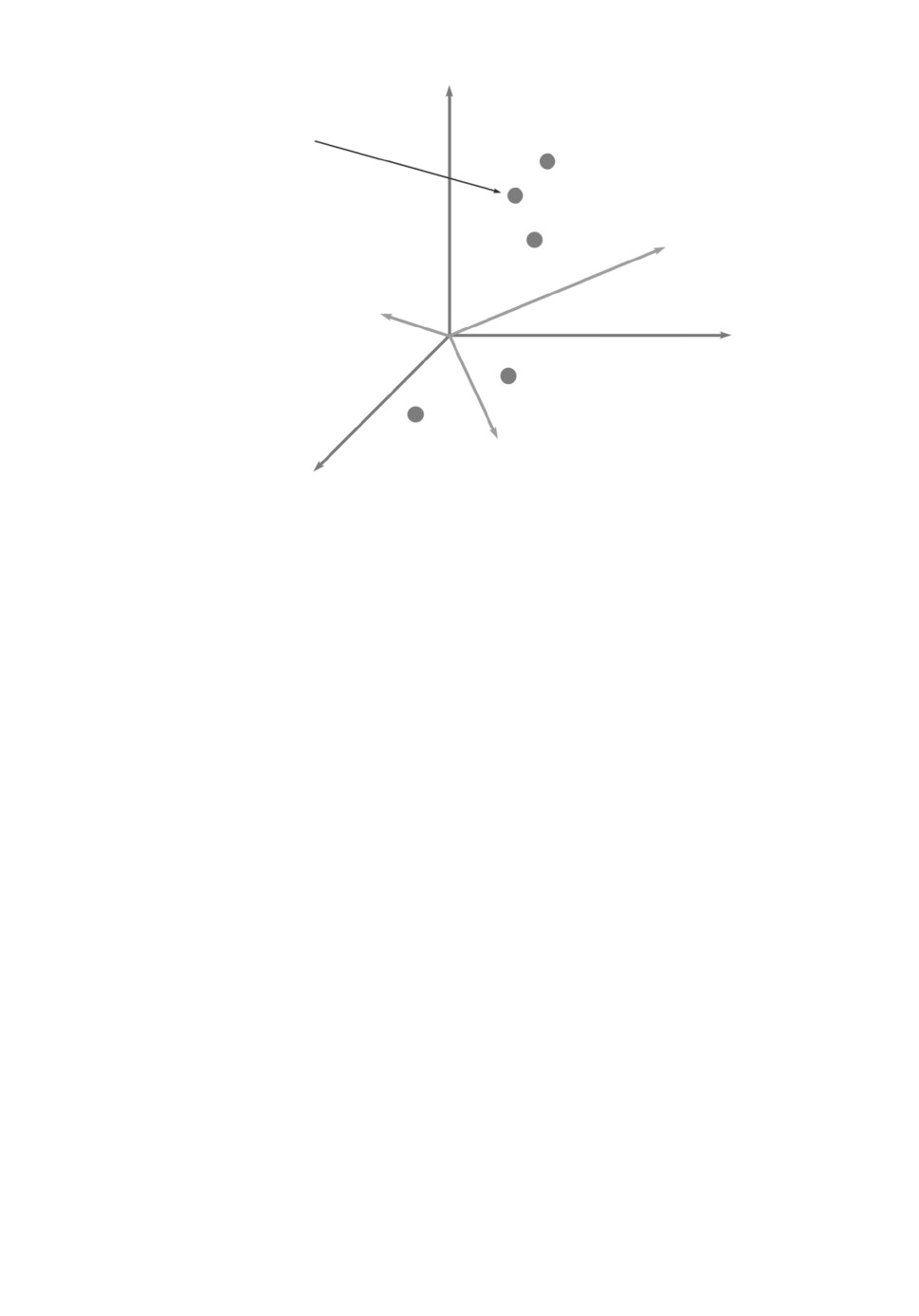
представить точкой в 3n-мерном пространстве с координатами A(r1, r2, . . . ,
rn,p1,p2,... ,pn,d1,d2,... ,dn). Для наглядности будем записывать эти коор-
динаты в виде матрицы 3 × n:
r1
r2
... rn
p1
.
p2
... pn
d1
d2
... dn
94
r1
æ
r1
r2
rn
ö
ç
p1
p2
pn
÷
ç
d1
d2
dn
÷
è
ø
rn
dn
p1
pn
d1
Рис. 1. 3n-мерное пространство примеров размерности n.
Далее в работе будем рассматривать каждый пример как точку в 3n-мер-
ном пространстве примеров, состоящих из n требований (см. рис. 1). А само
это пространство будем называть пространством примеров размерности n.
Более подробно о пространстве примеров размерности n см. [9].
3. Метрический подход
3.1. Идея подхода
В этом разделе представлены основы метрического подхода, который был
предложен и описан более подробно в [1, 2].
Во введенном пространстве примеров размерности n зададим метрику.
Определение 1. Метрикой для произвольных примеров A и B называ-
ется функция ρ(A,B), удовлетворяющая свойствам:
(3)
ρ(A, B) ≥ 0;
(4)
ρ(A, B) = 0 ⇔ A = B;
(5)
ρ(A, B) = ρ(B, A);
(6)
ρ(A, C) ≤ ρ(A, B) + ρ(B, C) для всех A, B, C;
(7)
ρ(A, B) = ρd(A, B) + ρr(A, B) + ρp
(A, B);
{
}
{
}
(8)
ρd(A,B) = max
dAj - dBj
- min
dAj - dBj
;
j∈N
j∈N
{
}
{
}
(9)
ρr(A,B) = max
rAj - rBj
- min
rAj - rBj
;
j∈N
j∈N
∑
(
)
(10)
ρp(A,B) =
|pAj - pBj|
j∈N
95
Использование расписания
для примера А
B
А
P-точка
P-область
Поиск ближайшей точки B
O
Рис. 2. Метрический подход.
Можно доказать, что если решить задачу 1|rj |Lmax для примера B и полу-
чить оптимальное расписание πB, можно оценить погрешность при исполь-
зовании расписания πB в качестве решения той же задачи для исходного
примера A.
Теорема 1. Пусть πB приближенное решение примера B, удовлетво-
ряющего LBmax(πB ) - LBmax(πB) ≤ δB. Тогда
(11)
0 ≤ LAmax(πB) - LAmax(πA) ≤ ρ(A,B) + δB.
Доказательство теоремы 1 приведено в [1, 2].
Согласно этой теореме, получается, что при принадлежности примера B
некоторой полиномиально разрешимой области можно поступить следующим
образом: решить пример B (за полиномиальное время), использовать полу-
ченное расписание для примера A и оценить погрешность, вычислив значение
метрики ρ(A, B).
Качественно опишем алгоритм решения задачи 1|rj |Lmax при помощи мет-
рического подхода. Будем обозначать через LAmax(π) значения целевой функ-
ции для примера A при расписании π.
Алгоритм 1 (метрический подход).
1) Найти пример B из полиномиально разрешимой области, наиболее близ-
кий к A по метрике ρ(A, B);
2) найти оптимальное расписание πB для примера B;
3) применить расписание πB к исходному примеру A;
4) оценить погрешность согласно теореме 1: 0 ≤ LAmax(πB) - LAmax(πA) ≤
≤ ρ(A, B).
На рис. 2 проиллюстрирована работа алгоритма 1.
Остается лишь поставить задачу нахождения примера B, наиболее близ-
кого к исходному примеру A по метрике ρ(A, B).
96
3.2. Поиск ближайшего полиномиально разрешимого примера
Рассмотрим множество точек, которые соответствуют полиномиально раз-
решимым примерам задачи. В пространстве примеров это множество задает-
ся следующей системой неравенств:
(12)
XR+YP +ZD≤H,
где R = (r1, . . . , rn)Т, P = (p1, . . . , pn)Т (pj ≥ 0 для всех j ∈ N), D =
= (d1, . . . , dn)Т и X, Y , Z
некоторые матрицы размерности k × n; а H =
= (h1, . . . , hk)Т является k-мерным вектором, где верхний индекс Т обознача-
ет транспонирование.
Решив эту систему, сможем построить многомерный конус в пространстве
примеров, все точки которого полиномиально разрешимы [9]. Например, в
случае значений Y = 0, Z = 0 и произвольной матрицы X решением системы
будет множество примеров Джексона [10].
Тогда в классе примеров (12) определим пример B с минимальным значе-
нием метрики ρ(A, B) относительно исходного примера A, решив следующую
задачу линейного программирования [9]:
∑
(xd - yd + xr - yr) +
xpj -→ min,
j∈N
yd ≤ dAj - dBj ≤ xd
∀j ∈N,
yr ≤ rAj - rBj
≤xr
∀j ∈N,
(13)
-xpj ≤ pAj - pBj ≤ xpj
∀j ∈N,
0≤xpj
∀j ∈N,
XRB +YPB +ZDB ≤H.
После решения этой подзадачи остается лишь найти расписание для ис-
ходного примера, пользуясь алгоритмом 1.
Более подробно про метрический подход, классы полиномиально разре-
шимых примеров и задачи линейного программирования для этих классов
см. [1, 2, 9].
3.3. Оценка сложности алгоритма
Сложность решения задачи с помощью метрического подхода напрямую
зависит от трудоемкости алгоритма, используемого для решения примера из
полиномиальной области. Для класса полиномиально разрешимых примеров
Джексона [10], например, сложность алгоритма будет порядка O(n log n) без
учета трудоемкости решения задачи (13).
97
4. Интерполяционный подход
4.1. Преобразования в пространстве примеров размерности n
Определение 2. Преобразованием r′j = αrj называется такое преобра-
r1
r2
... rn
зование, которое ставит в соответствие примеруp1 p2 . . . pn при-
d1
d2
... dn
αr1
αr2
... αrn
мер p1
p2
pn
, где α - произвольное неотрицательное число: α ∈
d1
d2
dn
∈ R, α ≥ 0.
Аналогично определяются преобразования p′j = αpj и d′j = αdj .
Теорема 2. Все точки, полученные в результате какого-либо из преоб-
разований r′j = αrj , p′j = αpj или d′j = αdj , лежат на одной прямой в про-
странстве примеров размерности n.
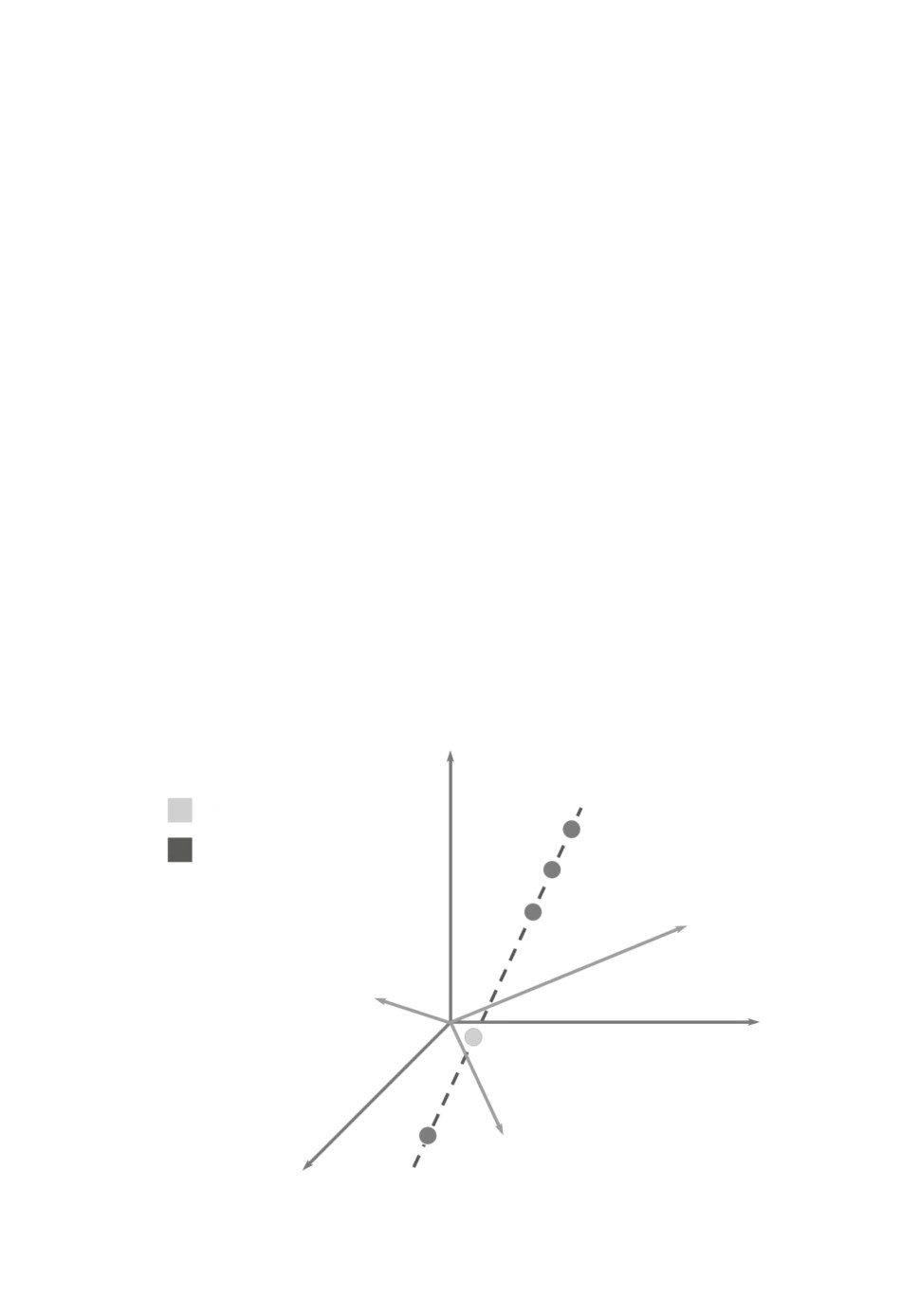
Из теоремы 2 следует, что любые точки, полученные в результате какого-
либо из предложенных преобразований исходного примера, лежат на одной
прямой в этом 3n-мерном пространстве, причем эта прямая содержит и ис-
ходный пример (при α = 1). Иллюстрация к этому утверждению приведена
на рис. 3. Доказательство теоремы 2 приведено в Приложении 1.
r1
Исходный пример
Производные примеры
rn
dn
p1
pn
d1
Рис. 3. Иллюстрация к теореме 2.
98
4.2. Идея подхода
Рассмотрим алгоритм решения задачи 1|rj |Lmax при помощи интерполя-
ционного подхода. Для определенности будем использовать преобразование
r′j = αrj, а также интерполяцию Лагранжа [11].
Интерполяционный полином Лагранжа задается следующей формулой:
∏
(x - xi)
∑
(14)
Lm(x) =
i=k∏
f (xk
),
(x - xj )
k=0
j=k
где xk, k = 1, . . . , m - узлы интерполяции, значения целевой функции в ко-
торых соответственно равны f(xk), причем x = xj.
Кроме того, в [11] показано, как оценить погрешность интерполяции функ-
ции по m узлам с учетом, что x = x1 = . . . = xm:
Rm(x) = f(x) - Lm(x) =
(
∏
f (x)
=
(x - xi)
+
(x - x1)(x - x2) . . . (x - xm)
i=1,...,m
(15)
f (x1)
+
+...
(x1 - x)(x1 - x2) . . . (x1 - xm)
)
f (xm)
...+
(xm - x)(xm - x1) . . . (xm - xm-1)
Таким образом, качественный вид алгоритма интерполяционного подхода
будет следующим:
Алгоритм 2 (интерполяционный подход).
1) Определить множество m численных значений αi;
2) для каждого αi получить i-й производный пример Ai путем преобра-
зования r′j = αrj (см. определение 2) исходного примера с коэффициентом
α=αi;
3) для каждого i-го производного примера Ai решить соответствующую
задачу и вычислить значение целевой функции;
4) зная значения целевых функций производных примеров, оценить зна-
чение целевой функции исходного примера, используя (14);
5) оценить погрешность аппроксимации целевой функции по формуле (15),
т.е. задать в этой формуле xi = αi и x = 1.
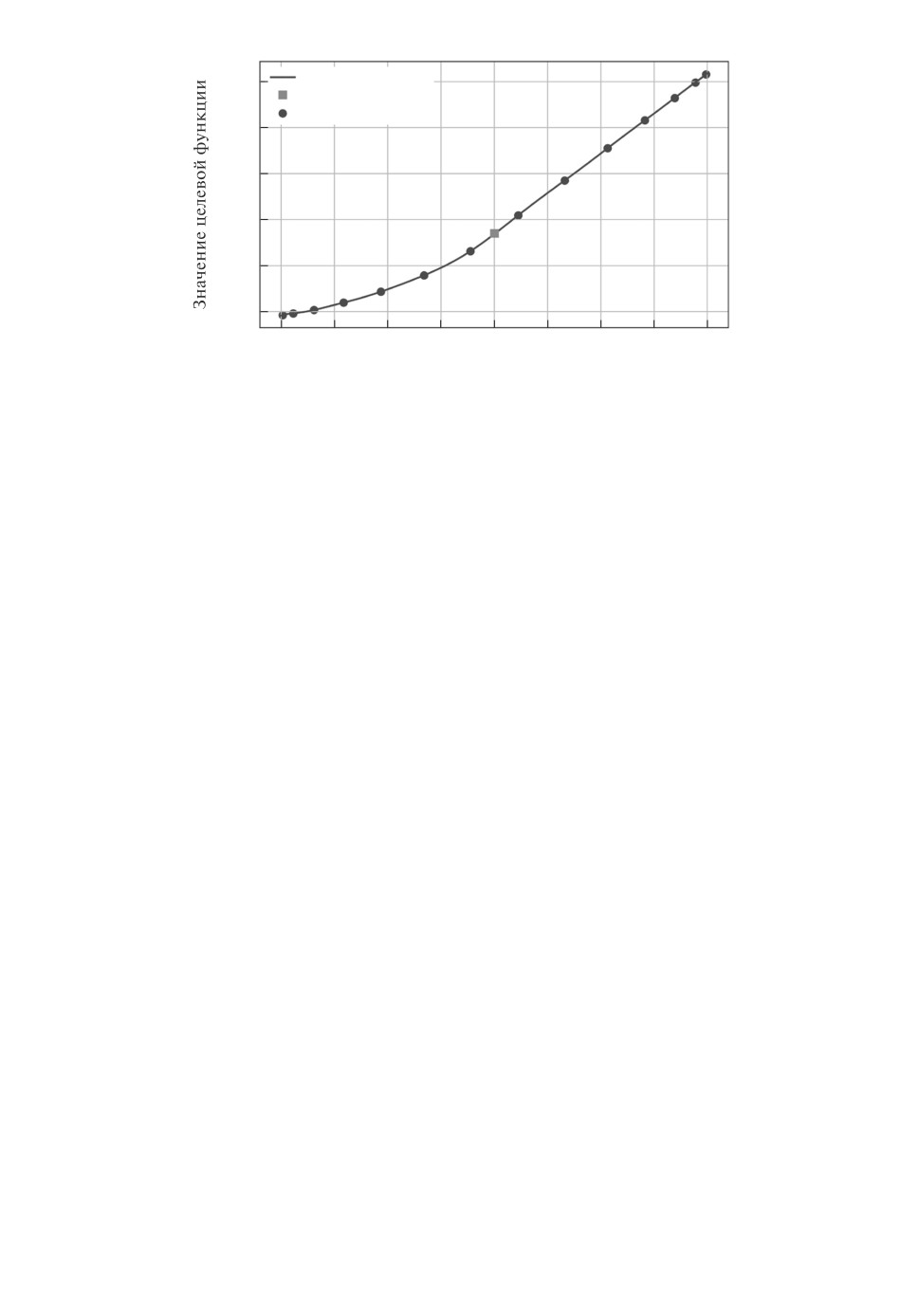
Для наглядного объяснения принципа работы алгоритма приведен гра-
фик на рис. 4. По оси x отложены значения αi, по оси y значения целевой
функции. Темные точки производные примеры используются как уз-
лы интерполяции, по ним и строится интерполяционная кривая. Затем для
α = 1, т.е. в точке, соответствующей исходному примеру, вычисляется значе-
ние интерполирующего полинома Lm(x), которое и является аппроксимацией
значения целевой функции исходного примера.
99
-400
Интерполяция
Реальн. знач.
Эксперимент
-600
-800
-1000
-1200
-1400
0
0,25
0,50
0,75
1,00
1,25
1,50
1,75
2,00
Коэффициент a
Рис. 4. Иллюстрация к алгоритму 2.
4.3. Модификации алгоритма
Акцентируем внимание на том, что преобразование r′j = αrj , т.е. домно-
жение всех параметров r исходного примера на некоторый коэффициент α,
является лишь одним из возможных преобразований и приводится здесь в
качестве примера.
Полученные в результате какого-либо из преобразований точки можно ре-
шить некоторым полиномиальным в среднем алгоритмом (например, двой-
ственным [7]), который долго работает над решением исходного примера, но,
как показали эксперименты, решит производные примеры за полиномиальное
в среднем время.
Стоит также подчеркнуть, что представленный алгоритм отличается гиб-
костью: можно использовать любые алгоритмы решения производных при-
меров, а также различные методы интерполяции.
Например, по принципу оптимального выбора узлов интерполирования
[11] рекомендуется выбирать эти узлы с помощью многочленов Чебышева.
При большом количестве узлов интерполирования рекомендуется исполь-
зовать кусочно-полиномиальную интерполяцию ввиду неравномерной сходи-
мости интерполяционных полиномов Лагранжа [11].
В численных экспериментах, параметры которых будут указаны в табл. 1,
а результаты в табл. 2, 3, для решения примеров использовался двойствен-
ный алгоритм [7], а для интерполяции значений целевой функции методы
Лагранжа и Чебышева.
4.4. Оценка сложности алгоритма
Время выполнения алгоритма будет наиболее низким при следующей мо-
дификации: необходимо задать некоторый лимит времени вычислений τ и
при итерации через множество значений αi, как только время вычисления
примера Ai превышает τ, сразу переходить к примеру Ai+1. Благодаря такой
модификации, время работы алгоритма гарантированно не будет превышать
значения mτ, где m количество всех производных примеров.
100
Таким образом, при использовании алгоритма решения задач с помощью
интерполяционного подхода возможно заранее оценить максимальное время
работы алгоритма.
5. Метод метрической интерполяции
Метрическая интерполяция
комбинированный метод, совмещающий
в себе оба предыдущих. Введем его для общего случая, не опираясь на кон-
кретные задачи и алгоритмы их решения.
Алгоритм 3 (метод метрической интерполяции).
1) На вход подается исходный пример A, принадлежащий классу примеров
некоторой задачи теории расписаний;
2) при наличии полиномиально разрешимого класса примеров рассмат-
риваемой задачи с помощью алгоритма 1 находится некоторый пример B с
минимальным расстоянием до исходного примера A по метрике ρ(A, B);
3) по теореме 1 оценивается погрешность метрического подхода;
4) с помощью некоторого заранее выбранного преобразования заполняется
множество производных примеров Ai;
5) проводится интерполяция значений целевой функции для производных
примеров согласно алгоритму 2;
6) для производного решенного примера Ai с наиболее близким к исход-
ному примеру A значением целевой функции составляется оптимальное рас-
писание πAi ;
7) по теореме 1 оценивается расстояние по метрике ρ(A, Ai) между приме-
рами, а значит, и погрешность аппроксимации;
8) получив окрестность, содержащую точное решение, используем най-
денную точку этой окрестности в качестве начального значения для других
точных алгоритмов.
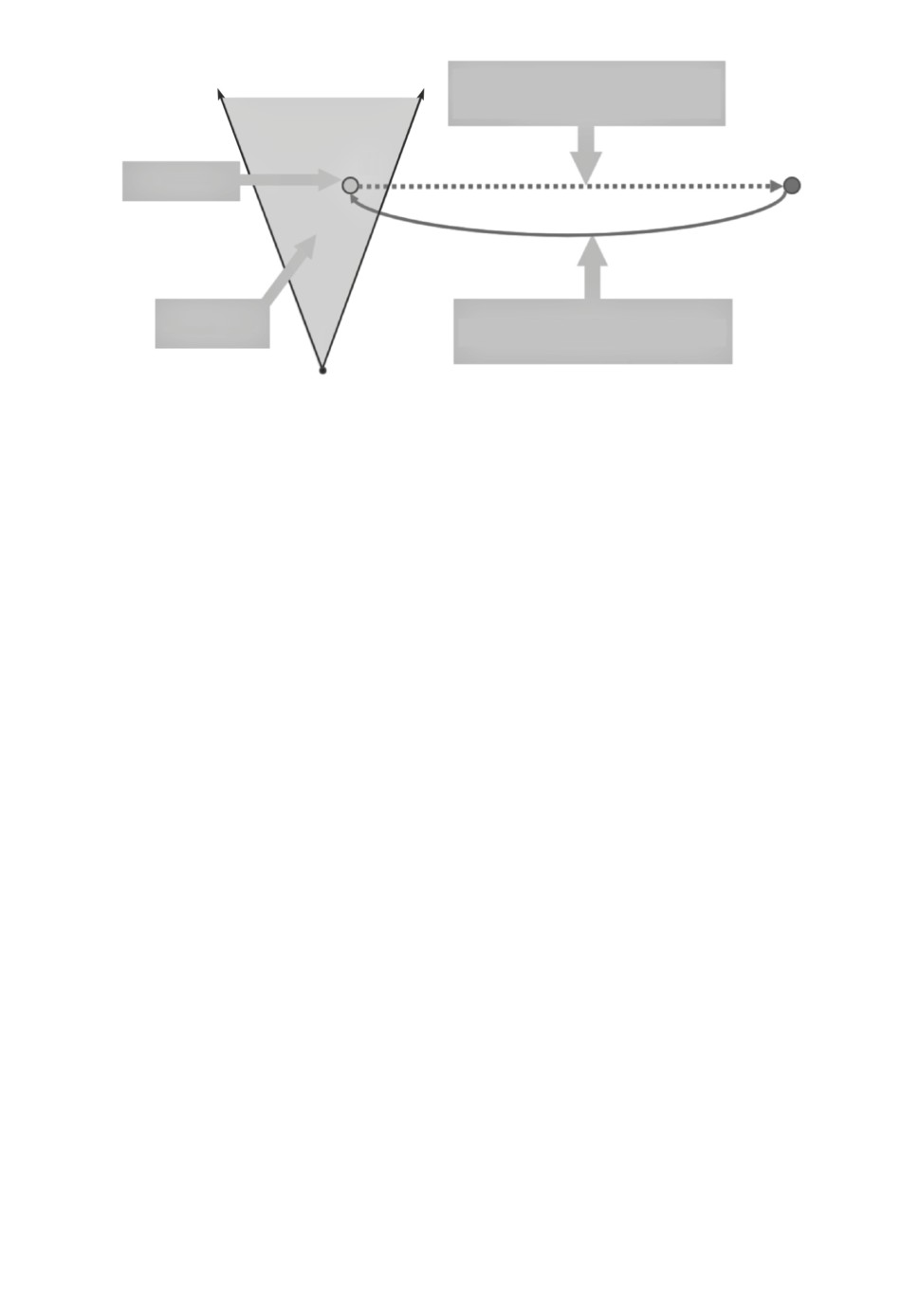
Схема алгоритма 3 приведена на рис. 5.
Построение
решения
P-область
Исходный
пример
Точные методы
Оценка ЦФ
Интерполяция
Построение
решения
Метрический подход
Интерполяционный подход
Рис. 5. Схема алгоритма 3.
101
6. Пример решения задачи
r1
r2
r3
1) Дан пример A =p1
p2
p3.
d1
d2
d3
2) Воспользуемся для определенности классом L полиномиально разреши-
мых примеров Лазарева [1, 2, 9]. Решив задачу (13), найдем пример B ∈ L,
принадлежащий классу L, с минимальной метрикой ρ(A, B).
3) Решим пример B двойственным алгоритмом [7]. Из теоремы 1 следует
оценка погрешности этого решения: она не превосходит ρ(A, B).
0·r1
0·r2
0·r3
4) Рассмотрим два производных примера: A0 =
p1
p2
p3
, Aξ =
d1
d2
d3
ξ·r1
ξ·r2
ξ·r3
=
p1
p2
p3
,ξ≫max(r1 + p1,r2 + p2,r3 + p3). Пример A0 поли-
d1
d2
d3
номиально разрешимый случай Джексона [10], решаемый очевидным перебо-
ром: подставляя на первое место расписания любую из работ, все остальные
работы упорядочиваем в порядке возрастания директивных сроков. Пример
Aξ случай, в котором момент поступления следующей работы превосхо-
дит продолжительность предыдущей. Оптимальное расписание составляется
сортировкой требований по возрастанию времен поступления rj.
5) Вычислим оптимальные значения целевой функции Lmax(π∗0) и Lmax(π∗ξ)
для примеров A0 и Aξ соответственно. Используя (14) и (15), получим оценку
целевой функции исходного примера Lmax(π∗) и погрешность этой оценки.
7. Результаты экспериментов
7.1. Метрический подход
В численных экспериментах с метрическим подходом подсчитывались три
параметра:
1) µ процент примеров, для которых алгоритм нашел оптимальное ре-
шение;
2) βav средняя относительная погрешность значения целевой функции;
3) βmax
максимальная относительная погрешность значения целевой
функции.
Погрешность определяется относительно оптимального значения целевой
функции тестового примера. Перечисленные параметры рассчитываются по
следующим формулам:
K
∑
Lmax(πi) - Lmax(π∗)
(16)
βav =
· 100%;
Lmax(π∗)
i=1
}
{Lmax(πi) - Lmax(π∗)
(17)
βmax = max
· 100%
;
i=1,...,K
Lmax(π∗)
K∗ · 100%
(18)
µ=
K
102
m
100
80
60
Хогевен
Лазарев
40
Шраге
20
01
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 n
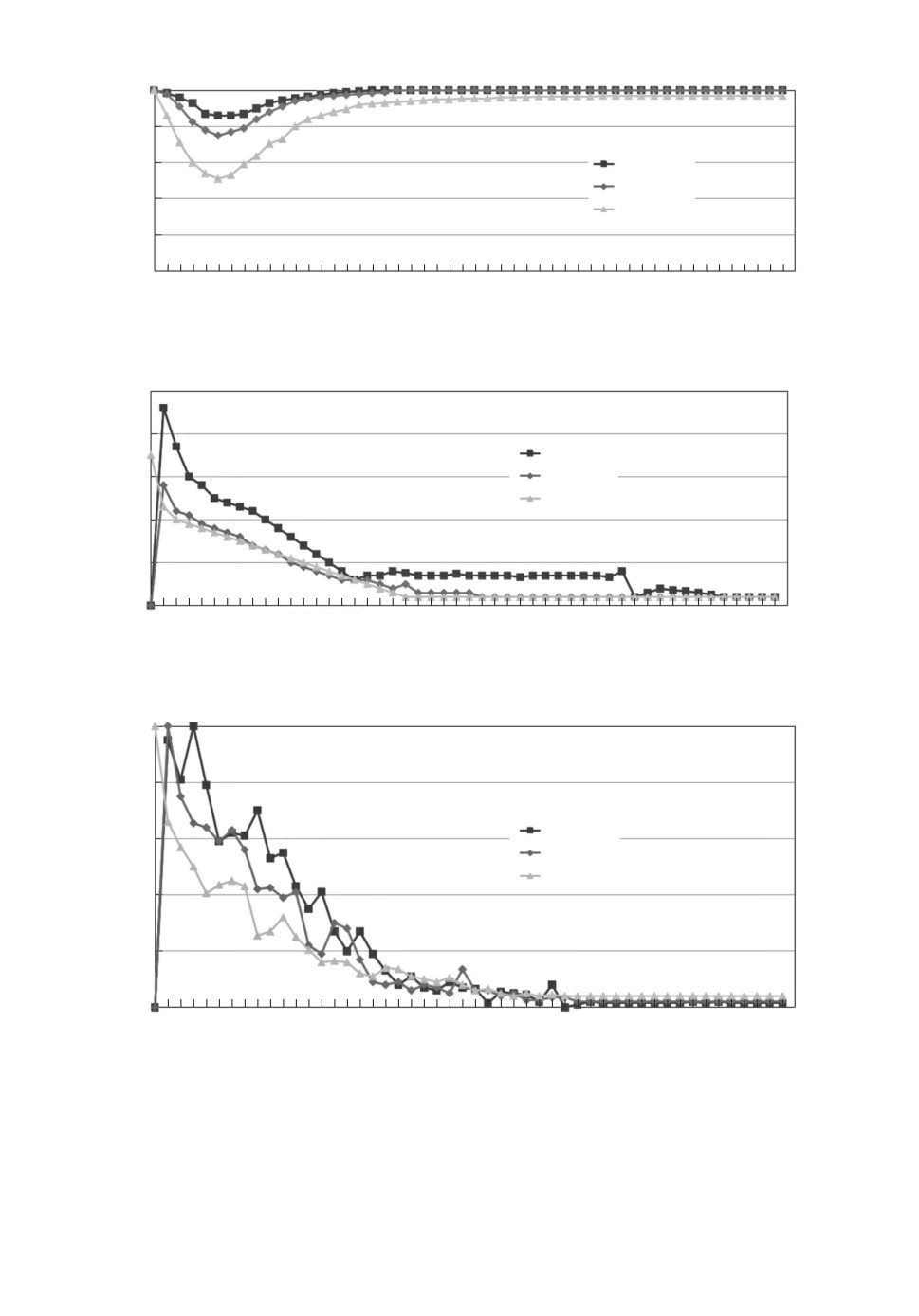
Рис. 6. График зависимости значения µ от количества требований в примере.
bav
25
20
Хогевен
15
Лазарев
Шраге
10
5
01
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 n
Рис. 7. График зависимости значения βav от количества требований в примере.
bmax
100
80
Хогевен
60
Лазарев
Шраге
40
20
01
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 n
Рис. 8. График зависимости значения βmax от количества требований в примере.
Здесь K - количество сгенерированных примеров,K - количество приме-
ров, для которых решение, полученное алгоритмом, не было оптимальным
( K = K - K∗), πi и π∗i - найденное алгоритмом расписание и оптимальное
расписание для i-го сгенерированного примера, решенного неоптимально, а
K∗ - количество тестовых примеров, оптимально решаемых алгоритмом.
103
Результаты экспериментов приведены на графиках рис. 6-8.
Три класса примеров (Хогевена, Лазарева и Шраге), указанные на гра-
фиках, - это разновидности областей полиномиально разрешимых примеров,
на которые проецировался исходный пример в ходе проведения эксперимента.
Выбор множества полиномиально разрешимых примеров рассмотрен подроб-
нее в [9].
Подробнее о метрическом подходе, полиномиально разрешимых классах
примеров, методике проведения экспериментов и их результатах см. [2].
7.2. Интерполяционный подход
На численных экспериментах с интерполяционным подходом стоит оста-
новиться подробнее, поскольку их результаты представляются впервые.
В табл. 1 приведена основная информация о методике проведения этих экс-
периментов.
Cто простых примеров, каждый из 10 требований, были сгенерированы.
Критерий простоты время решения каждого такого примера двойственным
алгоритмом [7] не должно превышать 1 секунду. Это множество примеров ис-
пользовалось во всех последующих экспериментах, чтобы иметь возможность
сравнивать результаты. Простота этих примеров способ ускорить вычис-
ления.
На приведенных графиках рис. 9, 10 представлены экспериментальные ре-
зультаты для одного из этих примеров с использованием двух методов интер-
поляции: Лагранжа и Чебышева [11, 15]. Коэффициент α изменялся в диапа-
зоне α ∈ [0; 2] с шагом 0,1. Таким образом, для интерполяции использовалось
20 точек, а затем 21-я, соответствующая исходному примеру, также отобра-
жалась на графике для сравнения аппроксимации с действительностью.
Обозначения следующие: значение целевой функции исходного примера
показано серым квадратом, узлы и кривая интерполяции отображены темно-
серым. Визуально оценить точность метода можно, сравнивая положение
серого квадрата (реальное значение целевой функции) относительно темно-
серой кривой (аппроксимированное значение).
Таблица 1. Основная информация о методике проведения экспериментов с интер-
поляционным подходом
Операционная система
Windows 10
ЦП
Intel core i3
Оперативная память
4 Гб
Язык программирования
Python 3.6 [12]
Среда программирования
Jupyter Notebook [12]
Основная библиотека для вычислений numpy [13]
Библиотека для построения графиков matplotlib/pyplot [14]
Способ генерации rj
ri = ri-1 + Xi; Xi h exp(λ); λ = 0,01
Способ генерации pj
pj h N(µ, σ); µ = 100, σ = 40
Способ генерации dj
dj = rj + E[pj]
104
0
Интерполяция
-200
Реальн. знач.
Эксперимент
-400
-600
-800
-1000
-1200
-1400
0
0,25
0,50
0,75
1,00
1,25
1,50
1,75
2,00
Коэффициент a
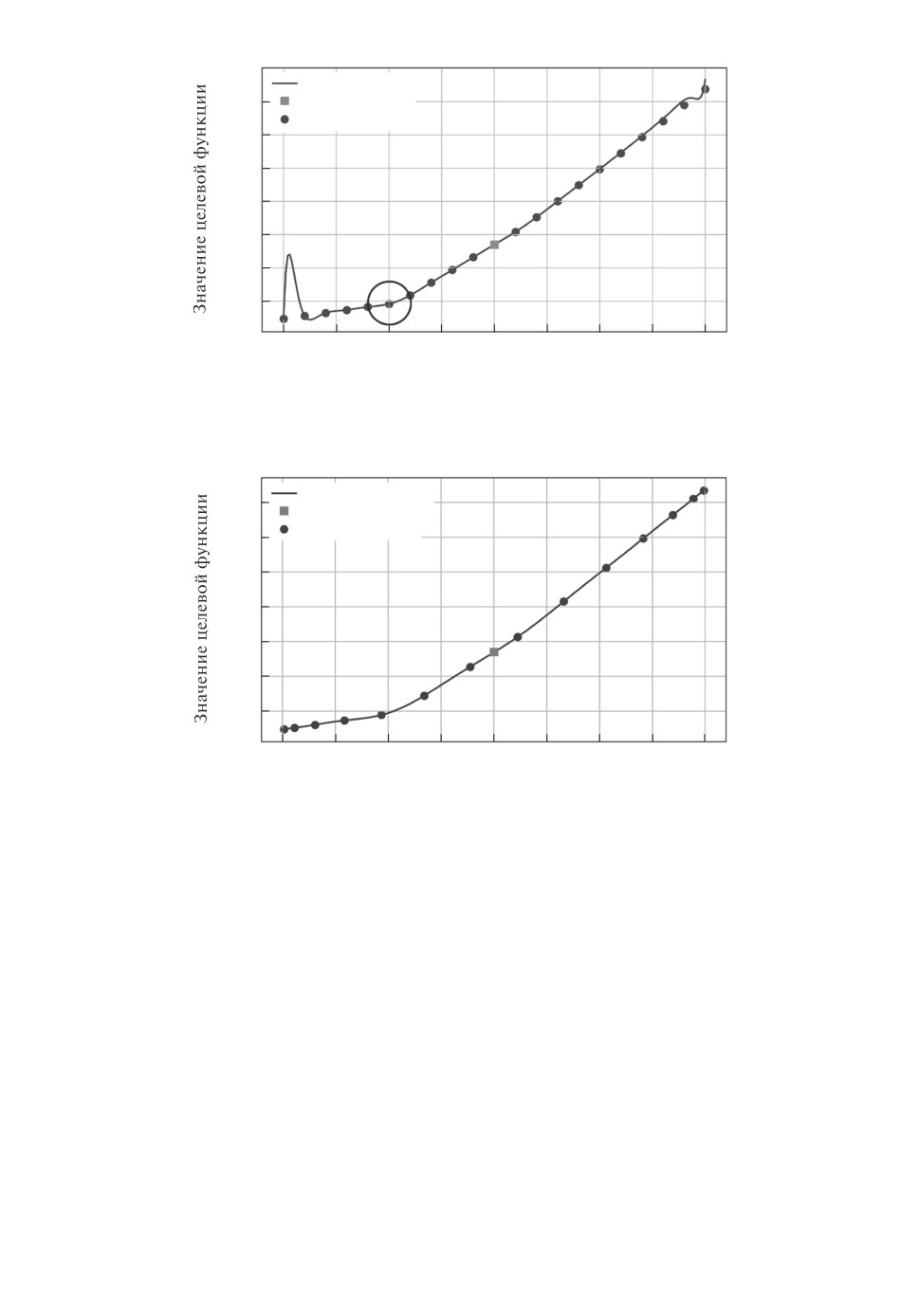
Рис. 9. Результаты эксперимента для преобразования r′j = αrj с использова-
нием интерполяции Лагранжа.
Интерполяция
-200
Реальн. знач.
Эксперимент
-400
-600
-800
-1000
-1200
-1400
0
0,25
0,50
0,75
1,00
1,25
1,50
1,75
2,00
Коэффициент a
Рис. 10. Результаты эксперимента для преобразования r′j = αrj с использова-
нием интерполяции Чебышева.
На графике рис. 9 рассмотрим точку перегиба, соответствующую значе-
нию α = 0,5 - она помещена в круг. Тем не менее оптимальные расписания в
точках α = 0,4, 0,5, 0,6 одинаковы. Таким образом, наличие точки перегиба
не означает изменение оптимального порядка расстановки требований.
При использовании в рассматриваемой задаче метода Лагранжа характер-
ны всплески по краям отрезка интерполяции. Возможная причина этого
большое количество узлов интерполяции [11], однако это явление требует
дальнейшего исследования.
При использовании интерполяции Чебышева такие всплески не характер-
ны (см. график рис. 10). Несмотря на это, у метода Чебышева есть свой недо-
статок - невозможно выбирать узлы интерполяции произвольным образом.
Узлы интерполяции строго выбираются при помощи многочленов Чебыше-
ва [15].
105
Таблица 2. Таблица результатов экспериментов для интерполяции Лагранжа
Величина
Значение
Формула
Lmax(i) - LTmax(i)
Максимальный модуль ошибки, %
287,66
max
100%
·
i∈N
LTmax(i)
Lmax(i) - LTmax(i)
Минимальный модуль ошибки, %
0,00
min
100%
·
i∈N
LTmax(i)
∑
1
Lmax(i) - LTmax(i)
Средний модуль ошибки, %
5,48
100%
·
n
LTmax(i)
i∈N
)
1
∑
(Lmax(i) - LTmax(i)
Среднее значение ошибки, %
3,73
· 100%
n
LTmax(i)
i∈N
Таблица 3. Таблица результатов экспериментов для интерполяции Чебышева
Величина
Значение
Формула
Lmax(i) - LTmax(i)
Максимальный модуль ошибки, %
137,32
max
100%
·
i∈N
LTmax(i)
Lmax(i) - LTmax(i)
Минимальный модуль ошибки, %
0,00
min
100%
·
i∈N
LTmax(i)
1
∑
Lmax(i) - LTmax(i)
Средний модуль ошибки, %
1,93
100%
·
n
LTmax(i)
i∈N
)
1
∑
(Lmax(i) - LTmax(i)
Среднее значение ошибки, %
0,28
· 100%
n
LTmax(i)
i∈N
В табл. 2 и 3 представлены результаты численных экспериментов со всеми
стами сгенерированными примерами при использовании преобразования r′j =
= αrj и обоих методов интерполяции.
Обозначения следующие: LTmax(i) - реальное значение целевой функции
i-го примера, Lmax(i) - аппроксимированное значение целевой функции i-го
примера; N - множество n различных примеров.
8. Заключение
В статье рассмотрен метрический подход [2] к решению задач теории рас-
писаний. Кроме того, представлен новый интерполяционный метод, при-
ведены результаты численных экспериментов. Также представлена идея ком-
бинированного подхода метрической интерполяции как способа объеди-
нения двух предыдущих методов.
Перечисленные подходы отличаются универсальностью и гибкостью, а
экспериментальные результаты подтверждают также и их высокую точность,
позволяющую использовать рассмотренные подходы для решения широкого
круга задач теории расписаний.
106
ПРИЛОЖЕНИЕ
Доказательство теоремы 2. Задача ставится следующим образом:
пусть выбраы три произвоных неотрицательных числа αA, αB, αC и за-
r1
r2
... rn
.Доказать,чтоврассмотренномвыше3n-мер-
дан примерp1 p2 . . . pn
d1
d2
... dn
ном пространстве примеры
αAr1
αAr2
... αArn
(A),
p1
p2
pn
d1
d2
dn
αBr1
αBr2
... αBrn
p1
p2
pn
(B),
d1
d2
dn
αCr1
αCr2
... αCrn
p1
p2
pn
(C)
d1
d2
dn
лежат на одной прямой. В силу произвольности выбора значений αA . . . αC
это утверждение будет означать, что исходный пример лежит на той же пря-
мой, что и примеры (A)-(C).
Таким образом, решение задачи докажет, что любые точки, полученные
в результате преобразования r′j = αrj исходного примера, лежат на одной
прямой в 3n-мерном пространстве, причем эта прямая содержит и исходный
пример.
Рассмотрим некоторое 3n-мерное пространство и три точки на нем:
A(xA1 . . . xA3n), B(xB1 . . . xB3n), C(xC1 . . . xC3n). Каноническое уравнение прямой
(AB) имеет вид [16]:
x1 - xA1
x2 - xA2
x3n - xA3n
(Π.1)
=
=...=
xB1 - xA1
xB2 - xA2
xB3n - xA
3n
Тогда критерий того, что точка С лежит на прямой (AB):
xC1 - xA1
xC2 - xA2
xC3n - xA3n
(Π.2)
=
=...=
xB1 - xA1
xB2 - xA2
xB3n - xA
3n
В рассматриваемой задаче анализируется расположение трех точек:
αAr1
αAr2
... αArn
(A),
p1
p2
pn
d1
d2
dn
αBr1
αBr2
... αBrn
(B),
p1
p2
pn
d1
d2
dn
107
αCr1
αCr2
... αCrn
p1
p2
pn
(C).
d1
d2
dn
Заметим, что координаты p1, p2, . . . , pn, d1, d2, . . . dn у всех трех точек оди-
наковы. Тогда критерий (Π.2) в приложении к рассматриваемой задаче при-
мет вид
αCr1 - αAr1
αCr2 - αAr2
αCrn - αArn
(Π.3)
=
=...=
αBr1 - αAr1
αBr2 - αAr2
αBrn - αArn
Преобразуем его:
r1(αC - αA)
r2(αC - αA)
rn(αC - αA)
(Π.4)
=
=...=
r1(αB - αA)
r2(αB - αA)
rn(αB - αA)
И после сокращения получим тождество
αC - αA
αC - αA
(Π.5)
=
αB - αA
αB - αA
Таким образом, критерий (Π.2) выполняется при любых αA, αB, αC . То
есть любые три точки, полученные в результате преобразования r′j = αrj ис-
ходного примера, лежат на одной прямой в 3n-мерном пространстве.
Преобразования p′j = βpj и d′j = γdj вводятся и доказываются аналогично.
Так же как и в случае с r′j = αrj , полученные в результате этих преобразова-
ний примеры лежат на одной прямой в 3n-мерном пространстве, содержащей
и исходный пример.
Теорема 2 доказана.
СПИСОК ЛИТЕРАТУРЫ
1. Лазарев А.А. Теория расписаний. Методы и алгоритмы. М.: ИПУ РАН, 2019.
2. Lazarev A.A., Lemtyuzhnikova D.V., Werner F. A metric approach for schedul-
ing problems with minimizing the maximum penalty // Appl. Math. Modell. 2021.
No. 89. P. 1163-1176.
3. Tanaev V.S., Gordon V.S., Shfransky Y.M. Scheduling theory: single-stage systems
Dordrecht, The Netherlands: Kluwer Academic Publishers, 1994.
4. Brucker P. Scheduling algorithms. Berlin: Springer, 1995.
5. Sotskov Y.N., Werner F. (Editors). Sequencing and Scheduling with Inaccurate Data.
New York, USA: Nova Science Publishers, Inc., 2014.
6. Tanaev V.S., Sotskov Y.N., Strusevich V.A. Scheduling theory: multi-stage systems.
Dordrecht, The Netherlands: Kluwer Academic Publishers, 1994.
7. Lazarev A.A., Pravdivets N., Werner F. On the Dual and Inverse Problems of
Scheduling Jobs to Minimize the Maximum Penalty // Mathematics. 2020. V. 8.
No. 7. P. 1131.
108
8. Lenstra J.K., Rinnooy Kan A.H.G., Brucker P. Complexity of machine scheduling
problems // Annals of discrete mathematics. Elsevier, 1977. V. 1. P. 343-362.
9. Lazarev A.A., Lemtyuzhnikova D.V., Pravdivets N.A., Werner F. Polynomially Solv-
able Subcases for the Approximate Solution of Multi-machine Scheduling Prob-
lems // Communications in Computer and Information Science (Advances in Op-
timization and Applications, 11th International Conference, OPTIMA 2020). 2021.
No. 1340. P. 211-223.
10. Jackson J.R. Scheduling a production line to minimize maximum tardiness. Los
Angeles, CA: University of California, 1955.
11. Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для вузов. М.:
Наука. Гл. ред. физ-мат. лит., 1989.
12. Kluyver T., Ragan-Kelley B., Perez F., et.all. Jupyter Notebooks
a publish-
ing format for reproducible computational workflows. Netherlands: InELPUB, 2016.
P. 87-90.
13. Harris C.R., Millman K.J., van der Walt S.J., et al. Array programming with
NumPy // Nature. 2020. V. 585. No. 7825. P. 357-362.
14. Hunter J.D. Matplotlib: A 2D Graphics Environment // Computing in Science &
Engineering. 2007. V. 9. No. 3. P. 90-95.
15. Rivlin T.J. Chebyshev polynomials. Courier Dover Publications, 2020.
16. Розенфельд Б.А. Многомерные пространства. М.: Рипол Классик, 2013.
Статья представлена к публикации членом редколлегии А.А. Галяевым.
Поступила в редакцию 20.01.2021
После доработки 25.05.2021
Принята к публикации 30.06.2021
109