Автоматика и телемеханика, № 10, 2021
© 2021 г. А.С. МАНДЕЛЬ, д-р техн. наук (almandel@yandex.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва),
В.А. ЛАПТИН (straqker@bk.ru)
(Московский государственный университет им. М.В. Ломоносова)
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ СИСТЕМАМИ
МАССОВОГО ОБСЛУЖИВАНИЯ С ПЕРЕКЛЮЧЕНИЕМ
КАНАЛОВ ОБСЛУЖИВАНИЯ
Рассматривается задача оптимизации работы системы массового обслу-
живания, в которой число рабочих каналов обслуживания может управ-
ляемо изменяться в моменты контроля, отстоящие друг от друга на фик-
сированный временной шаг. Предполагается, что при переходе от шага
к шагу интенсивность простейшего входящего потока изменяется в соот-
ветствии с некоторой однородной марковской цепью. Критерием выбора
стратегии переключения каналов обслуживания является минимум сум-
марных средних затрат на многошаговом периоде планирования. Выяв-
лена параметрическая структура оптимальной стратегии переключения
каналов обслуживания.
Ключевые слова: управляемые системы массового обслуживания, марков-
ский входящий поток, оптимизация, стратегии переключения каналов,
параметризация стратегий.
DOI: 10.31857/S0005231021100093
1. Введение
Интерес к управляемым системам массового обслуживания (СМО) вос-
ходит к 70-м гг. XX в., когда была опубликована серия работ В.В. Рыкова.
Отметим его фундаментальную публикацию [1], в которой приведена доста-
точно общая постановка задачи управления СМО и предложены подходы
к ее решению. Оригинальным вкладом в теорию управляемых СМО стало
исследование Ю.И. Неймарка [2], в котором изучались так называемые кон-
фликтные системы, см. также развивающую эти результаты применительно
к СМО публикацию [3].
К концу 80-х гг. интерес к управляемым системам массового обслужива-
ния заметно вырос в связи с тем, что возник, начал и продолжает бурно
развиваться такой класс прикладных систем как вычислительные и инфор-
мационные сети и опирающиеся на них системы связи. Именно поэтому ос-
новные усилия специалистов в области теории массового обслуживания ока-
зались направленными на решение задач управления, связанных именно с
такими прикладными системами. Среди постановок задач и исследуемых мо-
делей как у нас в стране, так и за ее рубежами рассматривались прежде всего
110
модели, в которых в качестве критериев выступали различные характеристи-
ки времен реакции на запрос [4], значения пропускных способностей [5, 6] и
энергетической эффективности [7]. При этом решались вопросы оптимизации
параметров [5, 7] и структуры этих систем [4, 6]. На эти темы имеется весьма
значительное число публикаций, см., например, обзор [8].
В отличие от упомянутых работ в настоящей статье рассматривается за-
дача оптимизации функционирования управляемой СМО по критерию ми-
нимума суммарных средних затрат за счет включения дополнительных или
отключения лишних каналов обслуживания. Соответствующие модели весь-
ма удобны для описания процессов, которые характерны для различных си-
стем социально-экономической природы, включая производственно-торговые
комплексы, системы продажи различного рода билетов, бронирования мест в
гостиницах и многие другие. Настоящая статья развивает и обобщает поста-
новки задач и методы их решения, которые были рассмотрены в предыдущих
публикациях авторов настоящей статьи [9-14].
2. Постановка и алгоритм решения задачи
2.1. Содержательная постановка задачи
Рассматривается СМО с параллельно работающими каналами обслужи-
вания, структурная схема которой представлена на рис. 1. При этом помимо
работающих каналов обслуживания, которые на рис. 1 названы основными,
имеются и резервные каналы обслуживания. В некоторые моменты времени
(назовем их моментами контроля) любое доступное число резервных кана-
лов может быть переведено в статус основных (включение) так же, как и
любое число имеющихся основных каналов может быть переведено в статус
резервных (выключение). Система рассматривается на конечном интервале
времени периоде планирования продолжительности T = Nτ, где τ - дли-
тельность промежутка времени между соседними моментами контроля. Этот
промежуток будет называться шагом. Таким образом, рассматриваемая СМО
является системой с периодическим контролем, когда в равноудаленные мо-
менты контроля можно включать дополнительные или отключать лишние
1
Основные устройства
обслуживания
Очередь
2
Входящий поток
требований
m1
1
Резервные устройства
обслуживания
2
m2
Рис. 1. Структурная схема исследуемой управляемой СМО.
111
каналы обслуживания. В предположении, что СМО должна выполнить все
поступающие в нее требования, требуется минимизировать суммарные сред-
ние затраты на функционирование СМО в периоде планирования [0, T ]. На
каждом шаге в перечень затрат включаются затраты на содержание и экс-
плуатацию основных и резервных каналов обслуживания, затраты на реше-
ния о включении или отключении каналов (затраты на переключения) и за-
траты СМО на требования, пребывающие в очереди. При этом считается, что
в СМО поступает простейший входящий поток, интенсивность которого λ(t)
на протяжении шага постоянна, а в моменты контроля претерпевает скачко-
образные изменения, принимая конечное число k значений λi из дискретного
множества Λ = {λi, i ∈ 1, k}.
2.2. Математическая постановка и решение задачи
Итак, рассматривается СМО, в которой число рабочих каналов обслужи-
вания является управляемой величиной и может быть изменено в периоди-
чески (с шагом, равным единице) расположенные на оси времени моменты
контроля за состоянием СМО. Задана матрица вероятностей перехода соот-
ветствующей однородной марковской цепи P = ∥pij ∥, где pij вероятность
перехода (в момент контроля) от интенсивности λi, i ∈ 1, k, на предыдущем
шаге к интенсивности λj , j ∈ 1, k, на следующем шаге.
Если на данном шаге интенсивность входящего потока равна λi, а интен-
сивность обслуживания на одном рабочем канале составляет µ, то, чтобы в
рассматриваемой СМО на данном шаге мог установиться стационарный в ве-
роятностном смысле режим функционирования, число основных рабочих ка-
налов u в СМО должно выбираться, чтобы удовлетворять неравенству [4, 15]:
]
[λi
(1)
u ≥ uкрит(λi) = ui =
+ 1,
µ
где через [•] обозначена целая часть числа.
Рассмотрим состояние СМО в момент контроля за n шагов длительно-
сти τ до конца периода планирования. Будем считать, что в начальный мо-
мент времени случайная интенсивность входящего потока приняла на этом
шаге значение λi, к этому моменту в системе имелось m основных каналов
обслуживания и принимается решение о том, что в СМО должно работать
u основных каналов обслуживания.
Запишем выражение для суммарных средних затрат C(1)(λi, m, u) на пер-
вом шаге процесса управления (стартующем за n шагов до конца периода
планирования), считая, что затраты на эксплуатацию резервных устройств
обслуживания равны нулю. В силу сделанных выше замечаний эти затраты
могут быть представлены в виде
C(1)(λi,m,u) = Cэкспл(u) + Cочереди(λi,u) + Cпереключ(λi
(2)
,m,u).
112
В (2) Cэкспл(u) - это одношаговые затраты на эксплуатацию u основных
устройств (Cэкспл(u) = c1u, где c1 - цена эксплуатации основного устройства
обслуживания на протяжении одного шага); Cочереди(λi, u) - одношаговые
затраты на очередь в стационарном режиме, которые будем считать пропор-
циональными средней длине очередиLочереди(λi, u) как функции от интен-
сивности входящего потока λi и управляющего решения о числе u основных
каналов; Cпереключ(λi, m, u) - затраты на переключения, которые зависят от
интенсивности входящего потока λi, от начального (до выполнения операции
переключения) числа основных каналов m и от управляющего решения о
числе основных каналов u. Будем считать, что эта компонента затрат может
быть представлена в виде
A1,
если u > m;
(3)
Cпереключ =
0,
если u = m;
A2 + c2(m - u),
если u < m,
где A1 - фиксированная цена принятия решения о подключении новых рабо-
чих устройств (“включение”), A2 - это фиксированная цена принятия реше-
ния об отключении новых рабочих устройств (“выключение”), а c2 - стоимость
отключения одного рабочего устройства обслуживания (c1 > c2). В форму-
ле (2) осталось конкретизировать только значение Cочереди(λi, u). Будем счи-
тать, что пребывание каждого требования в очереди на протяжении одно-
го шага обходится в сумму d, т.е. Cочереди(λi, u) = dLочереди(λi, u). Пользуясь
классическими результатами [4, 15], можно записать:
[
]-1
∑
(uρi)k
(uρi)u
(uρi)uρi
(4)
Lочереди =
+
,
k!
u!(1 - ρi)
u!(1 - ρi)2
k=1
где ρi =λiuµ.
Собираясь воспользоваться для решения проблемы методом дискретно-
го динамического программирования, введем следующий промежуточный
функционал, а именно функционал C∗n(λi, m), описывающий минимально воз-
можное (т.е. при использовании еще не найденной оптимальной стратегии
переключения каналов) значение средних суммарных затрат на последних
n шагах процесса управления, когда в начале первого шага текущее число
основных рабочих каналов равно m, а интенсивность простейшего входящего
потока принимает значение λi. В этих обозначениях окончательное решение
проблемы переключений на протяжении всего периода планирования будет
описываться по уровню минимально возможных средних затрат величиной
C∗N(λ,m), где λ и m - текущие значения интенсивности входящего потока и
числа основных каналов обслуживания, с которых стартует СМО в периоде
планирования [0, T ].
Теперь нетрудно записать систему уравнений дискретного динамическо-
го программирования, которая и является решением проблемы управления
113
процессом переключения каналов:
(5)
C∗1(λi,m) = min C(1)(λi
,m,u),
u≥ui
∑
(6)
C∗n(λi,m) = min
C(1)(λi,m,u) + α
pijC∗n-1(λj,u)
,
n ∈ 2,N,
u≥ui
j=1
где значение ui задается формулой (1), значение C(1)(λi, m, u) - формулой (2),
i ∈ 1,k, а α - коэффициент дисконтирования, 0 ≤ α ≤ 1.
Преобразуем уравнения
(5) и
(6), введя вспомогательные функции
Gвключ(λi, u), Gвы)ключ(λi, u), Gвключ(λi, u), Gвы)ключ(λi, u):
(7)
G(1)включ(λi, u) = uc1 + dLочереди(λi
, u),
(8)
G(1)выключ(λi, u) = u(c1 - c2) + dLочереди(λi
, u),
∑
G(n)включ(λi, u) = uc1 + dLочереди(λi, u) + α
pijC∗n-1(λj
(9)
, u), n = 2, 3, . . . ,
j=1
∑
G(n)выключ(λi, u) = u(c1 - c2) + dLочереди(λi, u) + α
pijC∗n-1(λj,u),
(10)
j=1
n = 2,3,...
Теперь уравнения (5) и (6) можно переписать в единообразном виде:
(11)
C∗n(λi
,m) =
A1 + min
Gв
ключ(λi, u),
u≥ui
−c1m + min
Gвключ(λi, m),
= min
n ∈ 1,N.
A2 + min
Gвы)ключ(λi, u),
u≥ui
(c1 - c2)m + min
-
Gвы)ключ(λi,m),
Поясним запись уравнений дискретного динамического программирова-
ния (5)-(6) в форме (11). Очевидно, что появление нижних индексов “включ”
и “выключ” в функциях с общим обозначением G соответствует принятию
решений о включении дополнительных резервных каналов или, наоборот, от-
ключении части рабочих каналов. Решениям о включении и выключении со-
ответствуют первая (включение) и третья (выключение) строки в крайней
правой части формулы (11). В то же время вторая и четвертая строки в
крайней правой части формулы (11) отвечают за принятие решений об от-
казе от каких-либо переключений. При этом сама оптимальная стратегия в
новой переформулированной записи уравнений (11) пока еще не определена.
114
Прежде чем перейти к обсуждению решений уравнений (5)-(6) или (11),
отметим, что поставленная задача в “близорукой” постановке (n = 1), которая
сводится к решению задачи минимизации (2), подробно исследовалась в [13],
где обсуждение опиралось на качественное использование аналогий с мате-
матическими задачами теории управления запасами и производством [16].
Опора на эту аналогию, в конечном счете, привела к тому, что для управляе-
мых СМО удалось в несколько видоизмененной форме воспроизвести неко-
торые классические свойства стратегий оптимального управления запасами,
например их параметрический характер (наличие двух критических уров-
ней R и r). При этом упомянутые аналогии выстраивались между задачами
управления запасами с непрерывными переменными состояния, тогда как
рассматриваемые задачи теории массового обслуживания по одной из пере-
менных (значение интенсивности входящего потока) являются дискретными.
Чтобы восполнить этот пробел, в разделе 3 настоящей статьи приводятся
некоторые развивающие известные и новые результаты по математическим
инструментам изучения “похожих” на выпуклые дискретных задач оптими-
зации.
3. A-выпуклость в дискретных задачах оптимизации
Рассматривается функция g(i) от переменной i, принимающей значения из
ряда натуральных чисел (i = 1, 2, 3, . . . ). Напомним несколько известных по-
нятий, которые тщательно изучены для случая вещественных (непрерывных)
переменных и функций, а для случая дискретных переменных используются
несколько реже.
Определение 1. Функция g(i) называется выпуклой (вниз), если для
всех натуральных чисел i и j
(12)
g(i + j) - g(i) - Δ(1)
g(i) × j ≥ 0,
где Δ(1)g(i) - первая разность функции g(i) в точке i : Δ(1)g(i) = g(i)-g(i-1).
Необходимым и достаточным условием выпуклости (вниз) функции яв-
ляется выполнение неравенства Δ(2)g(i) ≥ 0, где Δ(2)g(i) - вторая разность
функции g(i) в точке i. Действительно, пусть j из определения 1 равно едини-
це, тогда формула (11) записывается как Δ(1)g(i + 1) ≥ Δ(1)g(i), т.е. первая
разность g(i) оказывается монотонно возрастающей функцией, т.е. Δ(2)g(i) ≥
≥ 0. Аналогично доказывается и достаточность.
Определение 2. Функция g(i) называется A-выпуклой1 (A ≥ 0), если
для всех натуральных чисел i и j:
(13)
A + g(i + j) - g(i) - Δ(1)
g(i) × j ≥ 0.
1 Понятие A-выпуклости было предложено Г. Скарфом [17] для анализа свойств оп-
тимальных стратегий принятия решений (управления) в задачах логистики запасов при
наличии фиксированных цен поставки, не зависящих от размера поставки, с добавлением
к ним сумм, обусловленных размером партии поставки.
115
Для функций от дискретных переменных сохраняются все свойства A-вы-
пуклых функций, подмеченные Гербертом Скарфом [8], а именно:
Свойство 1. Если функция g(i) является A-выпуклой, то при любом
натуральном j функция g(i + j) также A-выпукла.
Свойство 2. Если функция g1(i) является A1-выпуклой, а функция
g2(i)
A2-выпуклой, то при любых θ1,θ2 > 0 функция g(i) = θ1g1(i)+θ2g2(i)
также является (θ1A1 + θ2A2)-выпуклой.
Свойство 3. Если функция g(i) является A1-выпуклой, то она и A2-вы-
пукла для любого A2 > A1.
Свойство 4. Пусть i - случайная величина с распределением {pi}k1, pi >
∑k
> 0,
pi = 1, и пусть функция g(i) является A-выпуклой. Тогда функция
i=1
∑k
α
pig(i), где α ≥ 0, также A-выпукла.
i=1
Отметим, что доказательство устанавливаемых в разделе 4 настоящей ста-
тьи фактов опирается на аналогию между задачами теории управления за-
пасами и задачами теории массового обслуживания. Первичный анализ этих
аналогий был выполнен в публикации [16], в которой была рассмотрена зада-
ча управления запасами, названная авторами “фантазийной”2. Тем не менее
нельзя не признать, что для рассматриваемого класса задач (как “фанта-
зийной” из теории управления запасами3, так и задачи о переключении ка-
налов), была продемонстрирована некоторая неготовность, неприспособлен-
ность существующих теории оптимизации и теории выпуклости к решению
этих задач. Дело в том, что в при математическом описании рассматриваемо-
го класса задач используется не одно, а два разных видения оптимальности
(критерия оптимальности). Говоря на языке, адекватном рассматриваемому
в данной статье классу задач, это оптимальность при включении каналов
(при подаче заказов в теории управления запасами), если перемещаться по
оси целочисленной переменной u слева-направо, и оптимальность при от-
ключении каналов (возвращении товара в теории управления запасами), если
перемещаться по оси переменной u справа-налево. Используем это замечание,
чтобы сформулировать новые определения.
Определение 3. Функция g(i) называется A-выпуклой слева (A ≥ 0) в
интервале (-∞,s], если для некоторого натурального числа s, которое об-
ладает тем свойством, что оно находится правее точки абсолютного ми-
нимума функции g(i), и для всех натуральных чисел i и j, удовлетворяющих
неравенствам i,i + j ≤ s, справедливо неравенство (13).
Определение 4. Функция g(i) называется A-выпуклой справа (A ≥ 0)
в интервале [p,∞), если для некоторого натурального числа p, которое об-
ладает тем свойством, что оно находится левее точки абсолютного мини-
2 Фантастическим в [16] было предположение о том, что склад может не только подавать
заказы на пополнение запасов, но и возвращать товар его поставщикам.
3 В настоящее время подвергнутый критике на ряде семинаров термин “фантазийная
задача” заменен на новый
“задача управления запасами с возвратами”.
116
мума функции g(i), и для всех натуральных чисел i и j, удовлетворяющих
неравенствам p ≤ i,i + j, справедливо неравенство (13).
4. Исследование свойств оптимальных стратегий переключения каналов
Чтобы воспользоваться введенными выше понятиями A-выпуклости, а
также A-выпуклости слева и справа для выявления свойств оптимальной
стратегии переключения каналов, убедимся в том, что для введенных выше
функционалов (5), (6) и (11) эти свойства имеют место. Рассмотрим сначала
“близорукий” случай, когда число шагов n = 1.
4.1. Свойства “близоруких” стратегий переключения каналов
Рассмотрим одношаговую задачу переключения каналов, которая пред-
ставляет собой задачу, описываемую уравнением (5) или уравнением (11)
при n = 1. В этом случае целевой функционал состоит в минимизации функ-
ции (7) при включении каналов или функции (8) при выключении каналов.
В обоих случаях эти функционалы представляют собой сумму возрастающей
линейной функции от назначаемого к включению числа каналов u и взве-
шенной с коэффициентом d средней длины очередиLочереди(λi, u). Изучим
свойства характеристикиLочереди(λi, u) как функции переменной u.
Из чисто вероятностных соображений следует, что функцияLочереди(λi, u),
как функция от u, является монотонно убывающей функцией u, при этом та-
кой, что скорость этого убывания с ростом u также монотонно убывает. При
этом очевидно, что для любого значения λi предел limu→∞ Lочереди(λi, u) = 0,
и вполне понятно, что по мере роста числа каналов от минимально возмож-
ного значения ui величинаLочереди(λi, u) уменьшается, причем с ростом u
это сокращение средней длины очередиLочереди(λi, u) само становится все
меньше, поскольку введение еще одного дополнительного рабочего канала на
фоне большего числа рабочих каналов привносит выигрыш, ¾доля¿ которо-
го 1/(u + 1) постоянно снижается. Однако оказывается, что строгое доказа-
тельство этого факта требует довольно утомительных выкладок (по крайней
мере авторам статьи не удалось технически упростить соответствующие до-
казательства).
Изменим обозначения, сняв индекс i состояния СМО и заменив величи-
ну ρi из формулы (4) величиной ρ0 = λ/µ. В результате формула (4) приоб-
ретет вид
[
]-1
∑
(ρo)k
(ρ0)u
(ρ0)u+1
(14)
Lочереди(λ,u) =
+
k!
(u - 1)!(u - ρ0)
(u - 1)!(u - ρ0)2
k=1
При u - 1 ≥ uкрит(λ) = u = [ρ0] + 1 рассмотрим первую разность функции
Lочереди(λi,u), как функции от u:
(15)
ΔLочереди(λ,u) =Lочереди(λ,u) -Lочереди
(λ, u - 1).
117
Утверждение 1. При u - 1 ≥ uкрит(λ) = u = [ρ0] + 1 подсчитываемая
по формуле (15) первая разностьLочереди(λ,u) отрицательна.
Доказательство. Используя формулы (14) и (15) и опуская промежу-
точные выкладки, запишем:
ΔLочереди(λ,u) =
[
]-1
∑
(ρo)k
(ρ0)u
(ρ0)u+1
=
+
-
k!
(u - 1)!(u - ρ0)
(u - 1)!(u - ρ0)2
k=1
[
]-1
∑
(ρo)k
(ρ0)u
(ρ0)u
-
+
=
k!
(u - 2)!(u - 1 - ρ0)
(u - 2)!(u - 1 - ρ0)2
k=1
[
∑
(ρ0)k
= -C1(ρ0,u) + C2(ρ0,u)
ρ0(u - 1 - ρ0)2 - (u - 1)(u - ρ0)2
k!
k=1
В последнем выражении величины C1(ρ0, u) и C2(ρ0, u) положительны, а
для множителя в квадратных скобках можно записать:
ρ0(u - 1 - ρ0)2 - (u - 1)(u - ρ0)2 < ρ0(u - ρ0)2 - (u - 1)(u - ρ0)2 =
= (ρ0 - u + 1)(u - ρ0)2 < 0.
Последнее неравенство записано в силу первого условия в утверждении 1.
Из этих выкладок следует утверждение 1.
Введем вторую разность функцииLочереди(λ, u), как функция от u:
Δ(2) Lочереди(λ,u) = ΔLочереди(λ,u) - ΔLочереди
(16)
(λ, u - 1) =
= Lочереди(λ,u) - 2Lочереди(λ,u - 1) -Lочереди(λ,u - 2).
Выполнив аналогичные выкладки, можно доказать следующее утвержде-
ние.
Утверждение 2. При u - 2 ≥ uкрит(λ) = u = [ρ0] + 1 рассчитываемая
по формуле (16) вторая разность функцииLочереди(λ,u) положительна.
Из утверждений 1 и 2 следует, что средняя длина очередиLочереди(λ, u)
является выпуклой вниз функцией переменной u. Из последнего утвержде-
ния и свойств 2 и 3 вытекает, что функции Gвключ(λ, u) из формулы (7) и
Gвы)ключ(λ, u) из формулы (8) выпуклы вниз. Последнее в силу формул (5)
и (11) и по аналогии с рассуждениями при доказательстве факта A-выпукло-
сти в главе 7 монографии [18], казалось бы, должно было привести к выводу
о том, что функция C∗1(λ, m) является A-выпуклой. Однако такой вывод ока-
зывается поспешным, поскольку структура функции C∗1(λ, m) более сложна,
чем те конструкции, которые были рассмотрены в классической публикации
по теории управления запасами и производством [17]: она “склеена” из функ-
ции средних затрат при включении дополнительных рабочих каналов (че-
рез функцию Gвключ(λ, u)) и функции средних затрат при отключении части
118
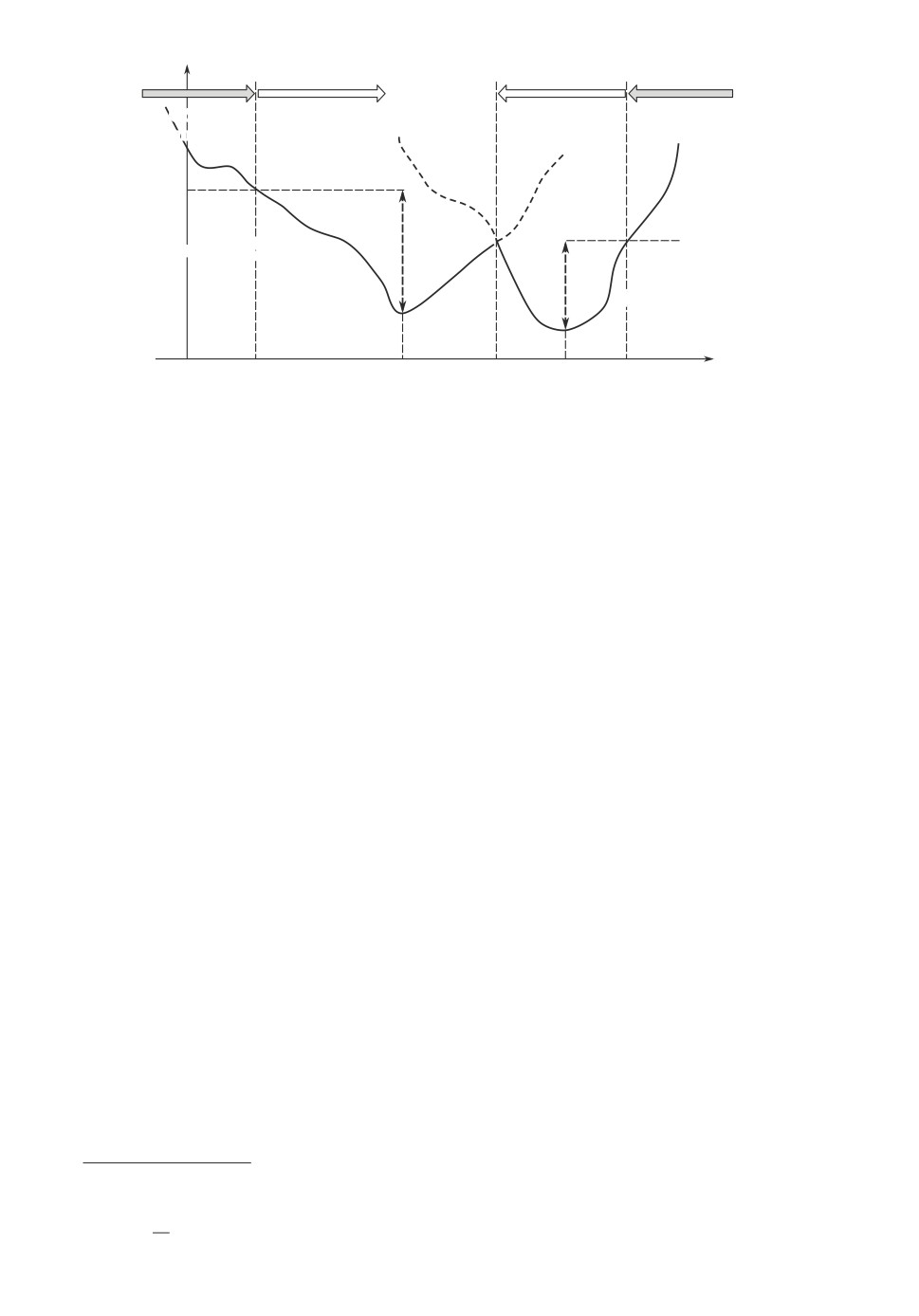
С*(l, m)
Область
бездействия
Область
Область
включения
выключения
(1)
A1
Функция G
вк
люч
(
l, u)
A2
Ф
ункция G(1)ключ (
l, u)
(1)
(1)
(2)
r1
R1
s
R1
r1(2)
m
Рис. 2. Вид функции C∗1(λ, m).
рабочих каналов (через функцию Gвы)ключ(λ, u)). Чтобы окончательно разо-
браться в характере этой “склейки”, выделим точки абсолютных минимумов
функций Gвключ(λ, u) и Gвы)ключ(λ, u), обозначив их через R11) и R12) соот-
ветственно. Из формул (7) и (8) очевидно, что R(1)1 < R(2)1. Таким образом, в
силу формулы (11) для случая n = 1 график функции C∗1(λ, m) может быть
представлен таким, как это показано на рис. 2.
Из рис. 2 видно, что в силу упорядочения точек абсолютных минимумов
R(1)1 и R(2)1 функций Gвключ(λ, u) и Gвы)ключ(λ, u) существует точка s пересече-
ния соответствующих фрагментов графиков (пунктиром на рис. 2 показаны
нереализуемые части графиков). Эта точка играет роль точки s и, одновре-
менно, точки p из определений 3 и 4. Таким образом, становится понятным,
что до точки s функция C∗1(λ, m) является A1-выпуклой слева, а после точ-
ки s A2-выпуклой справа. Тогда, следуя логике формирования оптималь-
ных двухуровневых стратегий в теории управления запасами [17, 18], опти-
мальное правило переключения каналов может быть формализовано в виде:
R(1)1, если m ≤ r(1)1(включение),
(17)
m,
если r(1)1 < m ≤ r(2)1,
u=
R(2)1,
если m ≥ r(2)1(отключение).
При этом параметры r(1)1 и r(2)1 в формуле (17)4 представляют собой реше-
ния следующих уравнений (см. рис. 2):
(18)
A1 + G(1)включ(λ,R(1)1) = G(1)включ(λ,r(1)1) для r(1)1 < R(1)1,
(19)
A2 + G(1)выключ(λ,R(2)1) = G(1)выключ(λ,r(2)1) для r(2)1 < R(2)1.
4 Применение формулы (17) связано с некоторыми оговорками, суть которых заклю-
чается в том, что в некоторых случаях, перечисленных в [13], параметр R(2)1,i назначается
равным ui. Имеются и другие нюансы.
119
Осталось заметить, что, на самом деле, четыре параметра “близорукой”
стратегии управления запасами должны быть снабжены индексом i состоя-
ния, в котором СМО находится на первом шаге, т.е. фактически их надо
обозначать как r(1)1,i, R(1)1,i, r(2)1,i и R(2)1,i, рассчитывая эти параметры для всех
i ∈ 1,k.
4.2. Многошаговые динамические задачи о переключении каналов
Вернемся к решению многошаговой задачи управления переключениями
каналов, которая описывается уравнениями (5)-(6) или (11). В этом случае
функции Gвключ(λ, u) и Gвы)ключ(λ, u) уступают место функциям Gв
ключ(λ, u)
и Gвы)ключ(λ,u), n = 2,3,..., задаваемым формулами (9) и (10). Повторим
запись целевого функционала в уравнении (6):
∑
C∗n(λi,m) = min
C(1)(λi,m,u) + α
pijC∗n-1(λj,u)
u≥ui
j=1
Выражение в фигурных скобках в правой части этого уравнения, независимо
от того, какая альтернатива оценивается (включение или отключение), со-
∑l
держит не меняющийся при смене альтернативы член α
pijC∗n-1(λj,u).
j=1
Одношаговый добавок C(1)(λi, m, u), являющийся, как показано в подразде-
ле 4.1, выпуклой вниз функцией от u, наоборот, варьирует при смене альтер-
нативы. Из этого можно сделать вывод, что есть все основания считать, что
выражение в фигурных скобках в правой части формулы (6) (также двухва-
риантное) является одновременно A1-выпуклым слева и A2-выпуклым спра-
ва. Вопрос только в том, как будут упорядочены точки абсолютного миниму-
ма функций Gвключ(λ, u) и Gвы)ключ(λ, u), которые обозначим как R(1)n,i и R(2)n,i.
Утверждение 3. Для любого n справедливо неравенство R(1)n,i < R(2)n,i.
Доказательство. Используя формулы (9) и (10), которые можно пе-
реписать в виде
G(n)включ(λ, u) = uc1 + β(n)(λi, u) и G(n)выключ(λ, u) = u(c1 - c2) + β(n)(λi, u),
устанавливаем искомое неравенство для любого n.
Теперь выскажем предположение математической индукции о том, что это
для любого номера n функции Gвключ(λ, u) и Cn(λ, m) являются A1-выпук-
лыми слева и A2-выпуклыми справа. Дальнейшее продвижение заключается
в том, что следует установить факт A1-выпуклости слева и A2-выпуклости
справа функции Gвключ(λ, u). Тогда из уравнения (11) и утверждения 3 бу-
дет следовать, что A1-выпуклой слева и A2-выпуклой справа будет функция
C∗n+1(λ,m). В свою очередь из факта A1-выпуклости слева и A2-выпуклости
справа функции Gвключ(λ, u) вытекает (по аналогии с подразделом 4.1), что
120
оптимальная стратегия переключения каналов будет определяться правилом:
R(1)n+1,i, если m ≤ r(1)n+1,i (включение),
(20)
m,
если r(1)n+1,i < m ≤ r(2)n+1,i,
u=
R(2)n+1,i, если m ≥ r(2)n+1,i (отключение).
При этом параметры r(1)n+1,i и r(2)n+1,i в формуле (20) представляют собой
решения следующих уравнений (см. рис. 2):
(21)
A1 + G(n+1)включ(λ,R(1)n+1,i) = G(n+1)включ(λ,r(1)n+1,i) для r(1)n+1,i < R(1)n+1,i,
(22)
A2 + G(n+1)выключ(λ,R(2)n+1,i) = G(n+1)выключ(λ,r(2)n+1,i) для r(2)n+1,i < R(2)n+1,i.
Нетрудно видеть, что доказательство сформулированного выше утвержде-
ния математической индукции идейно повторяет доказательство аналогично-
го утверждения (для двухуровневых стратегий) в теории управления запаса-
ми [18] с поправкой на дискретность и отмеченную выше альтернативность
(включение и выключение каналов) целевого функционала.
Как отмечалось выше, немаловажным фактом, который позволяет не опа-
саться “подводных камней” в форме скользящих режимов, является упорядо-
чение точек абсолютного минимума альтернативных функционалов в форме
неравенств R(1)n,i < R(2)n,i, n ∈ 1, N , i ∈ 1, k.
5. Заключение
Рассмотрена многошаговая задача оптимального переключения каналов
в многолинейной системе массового обслуживания. Исследованы стратегии
переключения каналов в дискретном времени при Марковском описании про-
цесса изменения интенсивности входящего потока. Критерием для выбора
стратегий переключения является минимизация суммарных средних затрат
на многошаговом периоде планирования. Предполагается, что процедура пе-
реключения (включения или отключения) каналов приводит к расходам, ко-
торые состоят из фиксированных платежей и затрат, величина которых за-
висит от числа включаемых или отключаемых рабочих каналов. Доказано,
что оптимальные стратегии переключения каналов оказываются параметри-
ческими и на каждом шаге оптимальное решение задачи о переключениях
зависит только от четырех характеристических параметров. Указаны спосо-
бы расчета этих параметров.
СПИСОК ЛИТЕРАТУРЫ
1. Рыков В.В. Управляемые системы массового обслуживания // Теория вероят-
ностей. Математическая статистика. Теоретическая кибернетика. 1975. Т. 12.
С. 43-153.
2. Неймарк Ю.И. Динамические системы и управляемые процессы. М.: Наука,
1978.
121
3.
Голышева Н.М., Федоткин М.А. Циклическое управление конфликтными пото-
ками в условиях гибели и рождения очередей критических размеров // АиТ.
1990. № 4. С. 68-75.
Golysheva N.M., Fedotkin M.M. A Conflict Flows Cyclic Control in Conditions of
Critical Queues Deaths and Births // Autom. Remote Control. 1990. V. 51. No. 4.
Р. 479-484.
4.
Вишневский В.М. Теоретические основы проектирования компьютерных сетей.
М.: Техносфера, 2003.
5.
Захаров П.П. Разработка автоматизированного программного комплекса для ис-
следования качества и эффективности функционирования моделей технических
систем и управляемых систем массового обслуживания. Дисс. канд. техн. наук.
М.: МИЭМ, 2006.
6.
Ivanov R., Mukhtarov A., Pershin O. A Problem of Optimal Location of Given
Set of Base Stations in Wireless Networks with Linear Topology // Distributed
Computer and Communication Networks. 22nd Int. Conf., DCCN 2019, Moscow,
Russia, September 23-27, 2019, Revised Selected Papers. Springer, 2019. P. 53-64.
7.
Галинина О.С., Андреев С.Д., Кучерявый Е.А. Оптимальное управление мощ-
ностью передачи устройства в гетерогенных сетях связи. // Матер. 21-й Между-
нар. науч. конф. “Распределенные компьютерные и телекоммуникационные се-
ти: управление, вычисление, связь” (DCCN-2018, Москва). М.: ИПУ РАН, 2018.
C. 79-83.
8.
Вишневский В.М., Дудин А.Н. Системы массового обслуживания с коррелиро-
ванными входными потоками и их применение для моделирования телекомму-
никационных сетей // АиТ. 2017. № 8. С. 3-59.
Vishnevskii V.M., Dudin A.N. Queueing Systems with Correlated Arrival Flows and
Their Applications to Nodeling Telecommunication Networks
// Autom. Remote
Control. 2017. V. 74. No. 8. Р. 1361-1403.
9.
Mandel А. Econometric Models of Controllable Multiple Queuing Systems // Proc.
18th Int. Conf. “Distributed Computer and Communication Networks” (DCCN 2015,
Moscow, Russia). Geneva: Springer, 2016. P. 296-304.
10.
Мандель А.С., Барладян И.И., Токмакова А.Б. Многолинейная СМО с измене-
нием числа рабочих каналов: стационарный случай. Ч. 1 // Материалы 18-й
Международной научной конференции “Распределенные компьютерные и теле-
коммуникационные сети: управление, вычисление, связь” (DCCN-2015, Москва).
М.: ИПУ РАН, 2015. С. 345-354.
11.
Мандель А.С., Махукова В.В. Многолинейная СМО с изменением числа рабочих
каналов: нестационарный случай. Ч. 2 // Матер. 18-й Междунар. науч. конф.
“Распределенные компьютерные и телекоммуникационные сети: управление, вы-
числение, связь” (DCCN-2015, Москва). М.: ИПУ РАН, 2015. С. 355-361.
12.
Mandel A., Bakulin K. Models of Controllable Multiple Queuing Systems for Channel
Switching Myopic Strategies // Proc. 20th Int. Conf. “Distributed Computer and
Communication Networks” (DCCN 2017, Moscow, Russia). М.: Техносфера, 2017.
С. 534-542.
13.
Mandel А., Laptin V. Myopic Channel Switching Strategies for Stationary Mode:
Threshold Calculation Algorithms / Vishnevskiy V., Kozyrev D. (eds). Distributed
Computer and Communication Networks. DCCN 2018. Communications in Com-
puter and Information Science. V. 919. Geneva: Springer, 2018.
122
14. Mandel А., Laptin V. Channel Switching Threshold Strategies for Multichannel Con-
trollable Queuing Systems // Communications in Computer and Information Science.
2020. V. 1337. P. 259-270. link.springer.com/chapter
15. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. М.:
Наука, 1966.
16. Mandel А., Granin S. Investigation of Analogies between the Problems of Inven-
tory Control and the Problems of the Controllable Queuing Systems // Proc. 2018
Eleventh Int. Conf. “Management of large-scale system development” (MLSD’2018).
17. Arrow K., Karlin S., Scarf H. Studies in the Mathematical Theory of Inventory and
Production. Stanford University Press, 1958.
18. Хедли Дж., Уайтин Т. Анализ систем управления запасами. М.: Наука, 1969.
Статья представлена к публикации членом редколлегии А.А. Лазаревым.
Поступила в редакцию 20.01.2021
После доработки 20.03.2021
Принята к публикации 30.06.2021
123