Автоматика и телемеханика, № 10, 2021

(Институт математики и информатики Московского

педагогического государственного университета;

Московский физико-технический институт)

ОБ ОДНОМ РОБАСТНОМ ПОДХОДЕ К ПОИСКУ

ЦЕНТРОВ КЛАСТЕРОВ¹

Предложен новый подход к построению алгоритмов кластеризации

k-means, в котором вместо евклидова расстояния используется расстоя-

ние Махаланобиса. Подход основан на минимизации дифференцируемых

оценок среднего значения, нечувствительных к выбросам. На иллюстра-

тивных примерах убедительно показана возможность устойчивости пред-

ложенного алгоритма по отношению к большим объемам выбросов в дан-

ных.

Ключевые слова: центр кластера, робастное среднее, расстояние Маха-

ланобиса, итеративное перевзвешивание, робастный алгоритм.

DOI: 10.31857/S0005231021100111

1. Введение

Задача кластеризации одна из классических задач машинного обучения.

В основе одного классического подхода для разбиения конечного множества

точек на кластеры лежит процедура поиска центров кластеров. Центр класте-

ра это точка, от которой сумма обобщенных расстояний до всех его точек

минимальна. Разбиение на кластеры осуществляется по простому правилу:

точка относится к тому кластеру, до центра которого расстояние минималь-

но. Формально это можно выразить следующим образом.

2. Классическая постановка задачи

{

}

Пусть U ⊂ Rⁿ открытое множество, X =

x₁,... ,x_N

⊂ U конечное

множество, которое требуется разбить на K кластеров. Пусть d: U × U →

→ R₊ функция обобщенного расстояния между точками из U. Она об-

ладает свойствами, которые достаточны для того, чтобы следующая задача

минимизации

∑

c∗ = arg min d(x_j , c)

c∈S j=1

¹ Работа выполнена при поддержке Российского фонда фундаментальных исследований

(проект №18-01-00050).

140

для поиска центра произвольного кластера C ⊂ U имела решение. Точное

формальное определение функции d можно найти в [1].

Если заданы центры кластеров c₁, . . . , c_K , то произвольная точка x будет

относиться к кластеру с центром c_t (1 ≤ t ≤ K), если

d(x, c_t) = min

d(x, c_j ).

1≤j≤K

Задачу поиска центров кластеров можно сформулировать как задачу мини-

мизации

(1)

c∗1, . . . , c^∗K = arg min Q(c₁, . . . , c_K

c₁,...,c_K

где

∑

(2)

Q(c₁, . . . , c_K ) =

ν_k min

d(x_k, c_j

1≤j≤K

k=1

величина ν_k ≥ 0 соответствует значимости k-й точки, ν₁ + . . . + ν_N = 1.

3. Постановка задачи с выпуклыми функциями среднего по Колмогорову

В [1] рассматривается более общая постановка задачи, в которой наряду

с функцией min в формуле (2) используются выпуклые функции среднего

по Колмогорову:







∑



h_s(x_j)

Ghs^(x1^,...,xK^)=hs-1

K



j=1

где h_s : R₊ → R₊ непрерывно-дифференцируемая строго монотонно убы-

вающая неотрицательная биективная функция. При этом

lim

x_j.

Ghs^(x1^,...,xK^)=min

s→∞

j=1,...,K

Например:

}

(

)

1) G_e-sx (x₁, . . . , x_K ) = -

e-sx1 + ... + e-sxK

;

)_-1/s

(

)

2) G_x-s (x₁, . . . , x_K ) =

x^-s1 + ... + x^-sK

Целевая функция (2) принимает вид:

∑

(

)

(3)

Q(c₁, . . . , c_K ) =

ν_kGhs

d(x_k, c₁), . . . , d(x_k, c_K )

k=1

141

Градиенты целевой функции Q принимают вид:

∂Q

∑

∂d(x_k, c_j )

ν_kv_jk(c₁,... ,c_K)

∂c_j

k=1

где

h^′s(d(x_k,c_j))

v_jk(c₁,... ,c_K) =

(

)).

h^′s

Ghs

d(x_k, c₁), . . . , d(x_k, c_K )

В случае Gh∞ = min

{

1, если d(x, cj) = min

d(x, c_t),

t=1,...,K

v_jk(c₁,... ,c_K) =

иначе.

Алгоритм SKM.

Для поиска центров в [1] предложен алгоритм SKM (Smooth k-Means) и

при определенных условиях доказана его сходимость к решению задачи ми-

нимизации (3).

procedure SKM(X, {ν₁, . . . , ν_N }, {c⁰¹, . . . , c^0K })

t←0

repeat

for all j = 1, . . . , K do

ν^tjk = ν_kv_k(c^t1,... ,c^tK),

∑

ν^tjk

ct+1j ← arg min

ν^tjkd(x_k,c), где ν^tjk =

ν^tj1 + ··· + ν^tjN

k=1

end for

t←t+1

until значения целевой функции не стабилизируются

return c^t1, . . . , c^tK

end

Если d - Евклидово расстояние, а G - min, то SKM представляет собой

алгоритм KMeans. В [1] показано, что SKM обобщает хорошо известные ал-

горитмы кластеризации, такие как FCM [2], EM [3], DA [4], Bergman Soft

Clustering [5].

3.1. Вариант алгоритма SKM для расстояния Махаланобиса

Рассмотрим случай, когда

d(x, c, S) = ln |S| + (x - c)^′S^-1(x - c)

регуляризованный квадрат расстояния Махаланобиса с ковариационной

матрицей S.² Поэтому кроме центров кластеров необходимо искать ковариа-

ционные матрицы, ассоциированные с ними. Целевая функция записывается

(

{

})

² d(x,c, S) = - ln

|S|^-1/2 exp

-¹(x - c)′S-1(x - c)

142

в виде

∑

(

)

(4)

Q(c₁, . . . , c_K ; S₁, . . . , S_K ) =

ν_kGhs

d(x_k, c₁, S₁), . . . , d(x_k, c_K , S_K )

k=1

Чтобы избежать вырождения, добавим дополнительное условие |S| = 1. При

фиксированных значениях S₁, . . . , S_K центры находятся при помощи алго-

ритма SKM вида:

procedure SKM_M1(X, {ν₁, . . . , ν_N }, {c¹, . . . , c^K };{S₁, . . . , S_K })

t←0

repeat

for all j = 1, . . . , K do

ν^tjk = ν_kv_k(c^t1,... ,c^tK;S₁,... ,S_K),

∑

ν^tjk

ct+1j ←

ν^tjkx_k, где ν^tjk =

ν^tj1 + ··· + ν^tjN

k=1

end for

t←t+1

until значения целевой функции не стабилизируются

return c₁, . . . , c_K

end

При фиксированных значениях c₁, . . . , c_K ковариационные матрицы мож-

но найти при помощи следующего алгоритма:

procedure SKM_M2(X, {ν₁, . . . , ν_N }, {S¹, . . . , S^K };{c₁, . . . , c_K })

t←0

repeat

for all j = 1, . . . , K do

ν^tjk = ν_kv_k(c₁,... ,c_K;S^t1,... ,S^tK),

∑

S^t+1j ←

ν^tjk(x_k - c_j)^′(x_k - c_j), где

k=1

ν^tjk

ν^tjk =

ν^tj1 + ··· + ν^tjN

end for

t←t+1

until значения целевой функции не стабилизируются

return c^t1, . . . , c^tK

end

143

Для поиска центров и ковариационных матриц применяется метод альтер-

нативных направлений:

procedure SKM_M(X, {ν₁, . . . , ν_N }, {c¹, . . . , c^K }, {S¹, . . . , S^K })

s←0

repeat

cs+11, . . . , c^s+1K← SKM_M1(X, {ν₁, . . . , ν_N }, {c¹, . . . , c^K }; {S¹, . . . , S^K })

S^s+11,... ,S^s+1K← SKM_M2(X,{ν₁,... ,ν_N},{S¹,... ,S^K};{c¹⁺¹,... ,c^K+1})

s←s+1

until значения целевой функции не стабилизируются

return (c^s1, . . . , c^sK ),(S^s1, . . . , S^sK )

end

4. Проблема выбросов

Алгоритм SKM_MM хорошо справляется с задачей поиска центров кла-

стеров и ковариационных матриц расстояний Махаланобиса, ассоцииро-

ванных с ними, до тех пор, пока в эмпирическом распределении значе-

(

)

ний {D₁(x₁), . . . , D_N (x_N )}, где D_k(x) = Ghs

d(x_k, c₁, S₁), . . . , d(x_k, c_K , S_K )

не появятся выбросы.

К выбросам можно отнести те данные, которые совершенно (или в доста-

точно большой степени) не соответствуют модели распределения точек. Их

присутствие приводит к искажению положений центров кластеров.

Можно указать две основные причины появления выбросов:

• часть данных (<50 %) содержит существенные ошибки или неустранимые

искажения;

• часть данных (<50 %) подчиняется другому закону распределения, основ-

ная часть (>50 %).

В таких случаях среднее взвешенное среднее арифметическое может сохра-

нять свою устойчивость по отношению к выбросам, если веса точек ν_k, соот-

ветствующих выбросам, достаточно малы, чтобы предотвратить их влияние

на величину оценки эмпирического среднего. Но на практике изначально веса

примеров, как правило, неизвестны, а поиск значений весов примеров, спо-

собных подавить влияние выбросов, является задачей, сопоставимой по труд-

ности с задачей идентификации самих выбросов. Поэтому естественный вы-

ход из такой ситуации это использование оценок среднего значения, кото-

рые нечувствительны к выбросам. Например, медиана, квантили, усеченные

средние арифметические, винзоризированные средние. Но проблема состоит

в том, что частные производные таких оценок среднего значения имеют син-

гулярные свойства, что создает неустранимое препятствие для применения

градиентных алгоритмов минимизации, которые используются при построе-

нии алгоритмов SKM, SKM_M1, SKM_M2 и SKM_M.

В данной статье для преодоления проблемы выбросов предлагается расши-

рить принцип разбиения на кластеры. Для этого в определении (3) целевой

144

функции Q будем использовать непрерывно-дифференцируемые усредняю-

щие агрегирующие функции, устойчивые к выбросам, вместо взвешенного

среднего арифметического. Теперь

(5)

Q(c₁, . . . , c_K ) = M{D(x₁; c₁, . . . , c_N ), . . . , D(x_N ; c₁, . . . , c_N

)},

где M{z₁, . . . , z_N } дифференцируемая усредняющая агрегирующая функ-

ция, нечувствительная к определенной доле выбросов в {z₁, . . . , z_N },

D(x_k; c₁, . . . , c_N ) = min

d(x_k, c_j )

1≤j≤K

или

(

)

D(x_k; c₁, . . . , c_N ) = Ghs

d(x_k, c₁), . . . , d(x_k, c_K )

Это позволяет расширить описанный выше подход для построения робастных

алгоритмов кластеризации.

Для случая расстояний Махаланобиса

Q(c₁, . . . , c_K ; S₁, . . . , S_K ) =

= M{D(x₁;c₁,...,c_K;S₁,...,S_K),...,D(x₁;c₁,...,c_K;S₁,...,S_K)}.

Если M среднее арифметическое, то получим задачу, эквивалентную задаче

минимизации (2) и (3).

Далее рассмотрим некоторые способы построения дифференцируемых

усредняющих агрегирующих функций, нечувствительных к определенной до-

ле выбросов.

4.1. Оценки среднего, нечувствительные к выбросам

Оценки среднего, нечувствительные к выбросам, можно построить

несколькими способами.

Первый способ основан на приближении медианы на базе М-средних [6, 7].

Определим М-среднее как решение следующей задачи [8]:

∑

M_ρ{r₁,... ,r_m} = arg min

ρ(r_j - s).

j=1

Если ρ(r) строго выпуклая функция и ρ(0) = 0, то M_ρ усредняющая

агрегирующая функция [9, 10].

Если существует ρ^′′(r), то

∂M_ρ

ρ^′′(r_j - r)

∂r_j

ρ^′′(r₁ - r) + ... + ρ^′′(r_m - r)

где r = M_ρ{r₁, . . . , r_m}.

145

Второй способ основан на применении цензурированного среднего ариф-

метического, в котором пороговое значение оценивается при помощи сгла-

женного варианта α-квантиля:

∑

(6)

WM_ρ,α{z₁,... ,z_N} =

min{z_k, zρα,},

k=1

где ρ_α(r) - функция, при которой Mρα выступает в качестве приближения

медианы,



αρ(r),

если r > 0,



)

(7)

ρ_α(r) =

αρ(0₊) + (1 - α)ρ(0₊)

если r = 0,

2



(1 - α)ρ(r),

если r < 0,

является функцией, для которой Mρα {z₁, . . . , z_N } выступает в качестве при-

ближения α-квантиля.

Частные производные имеют вид

)

∂WMρα

m ∂Mρα

[z_k < zρα ] +

∂z_k

N ∂z_k

где m - число значений z_k ≥ zρα . В обоих случаях^∂M∂z

≥0и^∂M∂z

+...+^∂M = 1._∂z

Алгоритм SRKM.

Рассмотрим обобщение путем замены взвешенного среднего арифметиче-

ского в (2) и (3) на дифференцируемые оценки среднего M, определенные

выше.

Градиент Q по c_j (1 ≤ j ≤ K) имеет вид

∑

∂Q

∂d

ν_k(c₁,... ,c_N )v_jk(c₁,... ,c_N )

∂c_j

k=1

где

∂M_ρ{r₁,... ,r_N }

ν_k(c₁,... ,c_N ) =

r_k = D(x_k;c₁,... ,c_N ).

∂r_k

Для минимизации (5) запишем алгоритм SRKM (Smooth Robust k-Means) -

обобщение алгоритма SKM.

procedure SRKM({x₁, . . . , x_N }, {c⁰¹, . . . , c^0K })

t←0

repeat

ν^tk = ν_k(c^t1,... ,c^tK)

ct+11, . . . , c^t+1K← SKM(X, {ν^t1, . . . , ν_N }, {c^t1, . . . , c^tK })

t←t+1

until значения целевой функции не стабилизируются

return c^t1, . . . , c^tK

end

146

Алгоритм SRKM можно рассматривать как робастный вариант алгоритма

SKM.

В случае применения расстояния Махаланобиса получим вариант SRKM

с применением метода альтернативных направлений для поиска центров и

ковариационных матриц.

procedure SRKM_M({x₁, . . . , x_N }, {c¹, . . . , c^K },{S¹, . . . , S^K })

s←0

repeat

ν^sk = ν_k(c^s1,... ,c^sK)

cs+11, . . . , c^s+1K← SKM_M1(X, {ν¹, . . . , ν^N }, {c¹, . . . , c^K }, {S¹, . . . , S^K })

S^s+11,... ,S^s+1K← SKM_M2(X,{ν¹,... ,ν^N },{c¹⁺¹,... ,c^K+1},{S¹,... ,S^K})

s←s+1

until значения целевой функции не стабилизируются

return (c^s1, . . . , c^sK ),(S^s1, . . . , S^sK )

end

Нетрудно видеть, что алгоритм SRKM отличается от SKM тем, что на

каждом шаге s вычисляются веса точек ν^s1, . . . , ν^sN как частные производ-

ные дифференцируемой робастной оценки среднего значения от минималь-

ных расстояний от точек до ближайшего кластера, вычисляемых при помощи

min или Ghs .

Алгоритм SRKM_M является робастным вариантом SKM_M, которые

представляют собой варианты алгоритмов SRKM и SRKM соответственно,

когда используется расстояние Махаланобиса d(x, c, S), в котором учитыва-

ется ковариационная матрица, с помощью которой может учитываться эл-

липсоидальная форма распределения точек в кластере. В прилагаемых далее

иллюстративных примерах применяется расстояние Махаланобиса.

5. Иллюстративные примеры

Для иллюстрациии возможностей алгоритма SRKM-M рассмотрим ряд

примеров. Они наглядно демонстрируют его способность находить центры,

которые лежат достаточно близко к настоящим центрам кластеров в услови-

ях, когда данные содержат выбросы или когда ищутся центры не всех кла-

стеров, а лишь некоторой части из них. Если в первом случае причиной сме-

щения найденных центров являются выбросы, то во втором случае причиной

смещения являются избыточные кластеры.

Пример 1. В этом примере сравнивается п√менение алгоритмов SKM_M

и SRKM_M с M-средним Mρα,ε, где ρ_ε(r) =

ε² + r², ε = 10^-3, для поиска

центров трех кластеров. Здесь расстояние d - Евклидово. Точки искусственно

сгенерированного набора данных принадлежат трем кластерам с несиммет-

ричным распределением расстояний точек кластера от своего центра, которое

имеет эллипсоидную форму с центром в одном из фокусов, плотность рас-

пределения убывает по мере удаления от фокуса. Все кластеры содержат по

147

SRKM-M

SKM-M

Центр

Фокус

-20

-40

100

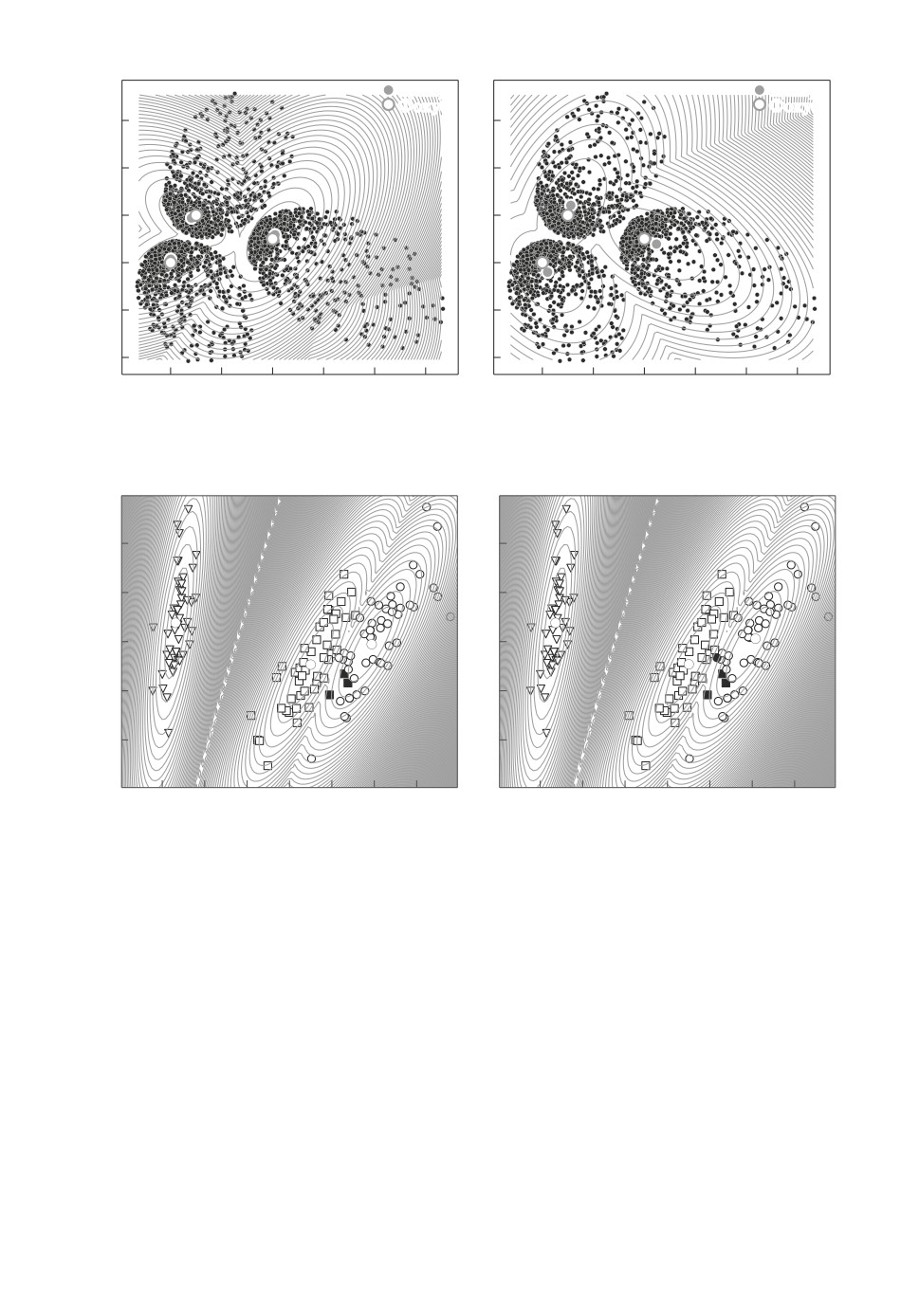
Рис. 1. Применение алгоритмов SKM_M и SRKM-M в примере 1.

SRKM-M

SKM-M

1.0

0.5

-0.5

-1.0

-3

-2

-1

-3

-2

-1

Рис. 2. Применение алгоритма SRKM_M и SKM_M в примере 2.

1000 точек. Метод SKM_M выдает центры кластеров, смещенные в направ-

лении противоположного фокуса. Робастный алгоритм SRKM_M с α = 0,4

позволяет найти центры, которые расположены вблизи фокусов, в то время

как алгоритм SKM_M находит центры, которые более удалены от настоя-

щих фокусов эллипсов. Это достигается за счет того, что основная масса то-

чек сосредоточена около фокусов эллипсов. Поиск фокусов эллипсов можно

искать по той части точек, которые как раз находятся около фокусов. Ро-

бастный алгоритм обеспечивает возможность нахождения центра множества

точек, расположенных вблизи фокусов, не испытывая существенного влия-

ния со стороны более удаленных от фокусов точек. Результаты представлены

на рис. 1.

Пример 2. Расcмотрим классический набор данных iris. Как правило,

он используется для задач классификации. Попытаемся идентифицировать

148

Робастный алгоритм

Классический алгоритм

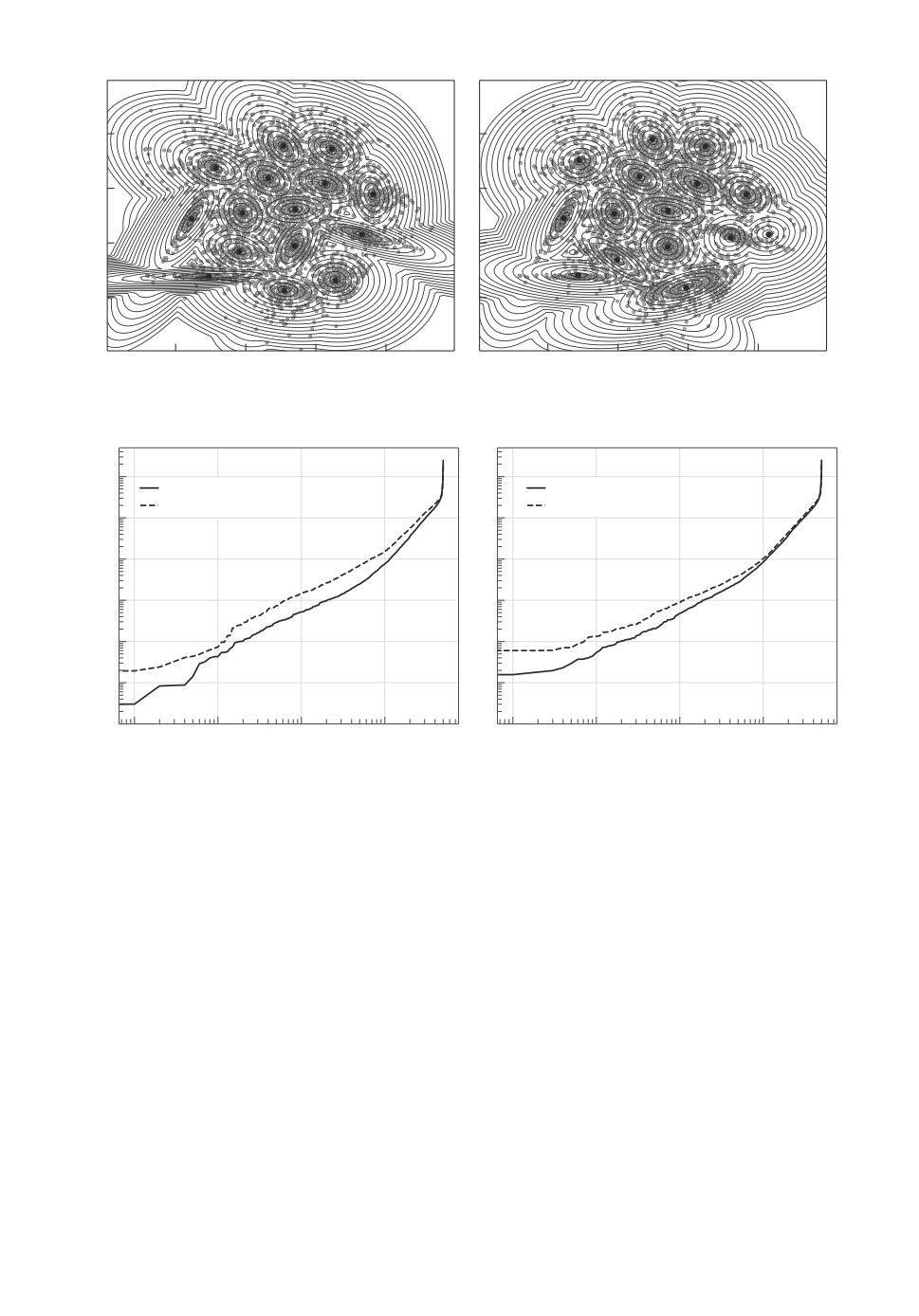
Рис. 3. S4: Результаты алгоритмов SRKM_M и SKM_M из примера 3.

10⁰

Robust (S)

Regular (S)

10^-1

10^-2

10^-3

10^-4

10^-5

10^-6

10⁰

10¹

10²

10³

10⁰

10¹

10²

10³

Рис. 4. S4: Распределение расстояний до центра ближайшего кластера для

алгоритмов SRKM_M (слева) и SKM_M (справа) из примера 3.

классы при помощи кластеризации, используя расстояния Махаланобиса вме-

сто Евклидового. На рис. 1 представлен результат кластеризации при помощи

алгоритмов SRKM_M и SKM_M. При помощи алгоритма SRKM_M можно

получить разбиение, которое отличается от заданного в 3 точках из 150. При

помощи алгоритма SKM_M можно получить разбиение, которое отличается

от заданного в 4 точках из 150. Хотя преимущество минимальное, но с учетом

того что наилучшие надежные алгоритмы классификации по данным набора

iris как раз дают 98 % точности и выше, то это можно считать хорошим ре-

зультатом. Он показывает, что с применением предложенного здесь подхода

на основе реалистичного набора признаков можно получать разбиения, ко-

торые практически соответствуют естественной классификации. Результаты

представлены на рис. 2.

Пример 3. Рассмотрим наборы данных S3-S4 из [11, 12]. Они содержат

5000 точек, 15 кластеров. Среди наборов данных S1-S4 [12] в S4 наблюдается

149

наибольшая вариация в распределении точек на плоскости, что затрудняет

поиск центров кластеров. Именно поэтому он представляет наибольший инте-

рес. Для сравнения приведем результаты применения алгоритмов SRKM_M

и SKM_M. На рис. 3 представлены результаты кластеризации для S4. Рису-

нок 4 иллюстрирует зазоры между распределением расстояний от точкек до

ближайшего к ним кластера. Применение робастного варианта алгоритмов

показывает уменьшение значений расстояний. Он также наглядно иллюстри-

рует увеличение этого зазора при применении алгоритма SRKM_M.

6. Заключение

Применение дифференциуемых оценок среднего значения, нечувствитель-

ных к выбросам, позволило построить новые робастные процедуры поиска

центров кластеров SRKM и SRKM_M, которые обобщают SKM и SKM_M,

позволяя использовать широкий спектр методов поиска среднего значения

как для четкого, так и для нечеткого отнесения точек к кластерам. Предло-

женный метод и алгоритмы SRKM и SRKM_M наследуют структуру ал-

горитмов SKM и SKM_M, однако отличаются методом расчета весов точек.

Особенность предложенного подхода состоит в том, что веса точек вычис-

ляются как значения частных производных дифференцируемой робастной

оценки среднего значения от минимальных расстояний от точек до ближай-

шего кластера, вычисляемых при помощи min или Ghs . В результате веса

точек убывают с ростом модуля разности между соответствующим аргумен-

том робастной усредняющей агрегирующей функции и величиной среднего

значения. Наибольшие значения весов соответствуют точкам, которые соот-

ветствуют аргументам усредняющей агрегирующей функции, которые нахо-

дятся вблизи величины среднего значения. Это объясняет, почему предло-

женный подход способен преодолевать влияние выбросов. Приведенные ил-

люстративные примеры убедительно показывают устойчивость предложен-

ных алгоритмов по отношению к относительно большим объемам выбросов.

СПИСОК ЛИТЕРАТУРЫ

1. Teboulle M. A Unified Continuous Optimization Framework for Center-Based Clus-

tering Method // J. Machine Learning Research. 2007. No. 8. P. 65-102.

2. Bezdek J.C. Pattern Recognition with Fuzzy Objective Function Algorithms. N.Y.:

Plenum Press, 1981.

3. Duda R.O., Hart P.E., Stork D.G. Pattern Classification. John Wiley & Sons, Inc.,

2-nd edition. 2001.

4. Rose K.A, Gurewitz E., Fox C.G. Deterministic annealing approach to clustering //

Pattern Recognition Letters. 1990. V. 11. No. 9. P. 589-594.

5. Banerjee A., Merugu S., Dhillon I.S., Ghosh J. Clustering with Bregman Diver-

gences // J. Machine Learning Research. 2005. No. 6. P. 1705-1749.

6. Mesiar R., Komornikova M., Kolesarova A., Calvo T. Aggregation functions: A

revision / H. Bustince, F. Herrera, J. Montero, eds., Fuzzy Sets and Their Extensions:

Representation, Aggregation and Models. Berlin-Heidelberg: Springer, 2008.

150

7. Grabich M., Marichal J.-L., Pap E. Aggregation Functions. Series: Encyclopedia of

Mathematics and its Applications. No. 127. Cambridge University Press, 2009.

8. Шибзухов З.М. О принципе минимизации эмпирического риска на основе усред-

няющих агрегирующих функций // Докл. РАН. 2017. Т. 476. № 5. С. 495-499.

9. Calvo T., Beliakov G. Aggregation functions based on penalties // Fuzzy Sets and

Systems. 2010. V. 161. No. 10. P. 1420-1436.

10. Beliakov G., Sola H., Calvo T. Practical Guide to Averaging Functions. Springer,

2016.

11. Franti P., Sieranoja S. K-means Properties on Six Clustering Benchmark Datasets //

Applied Intelligence. 2018. V. 48. No. 12. P. 4743-4759.

12. Clustering Basic Benchmark. http://cs.joensuu.fi/sipu/datasets/

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 24.01.2021

После доработки 26.04.2021

Принята к публикации 30.06.2021

151