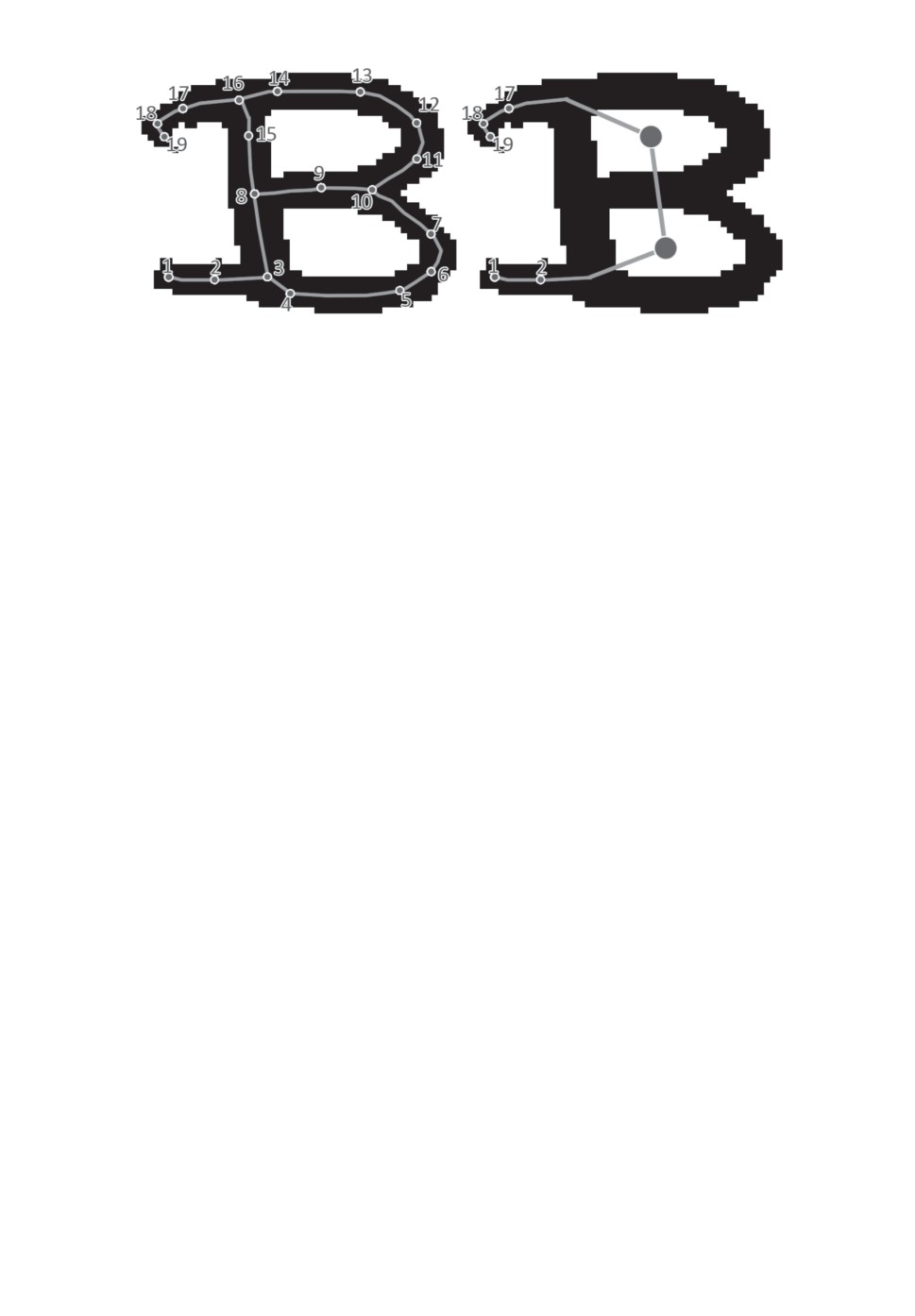Автоматика и телемеханика, № 11, 2021

Тематический выпуск¹

Л.М. МЕСТЕЦКИЙ, д-р техн. наук (mestlm@mail.ru)

(Московский государственный университет им. М.В. Ломоносова)

СКЕЛЕТ СИМВОЛА КАК МОДЕЛЬ СЛЕДА ПЕРА ДЛЯ

РАСПОЗНАВАНИЯ ПО ВОССТАНОВЛЕННОЙ ТРАЕКТОРИИ²

Статья посвящена исследованию задачи распознавания рукописного

текста и сведению задачи распознавания по изображению текста к задаче

распознавания по следу пера при его написании. Предложен метод, осно-

ванный на использовании медиального представления, восстанавливаю-

щий след пера по изображению рукописного текста. Предложено обосно-

вание метода на основе экспериментального исследования распознавания

символов по их изображению, по восстановленному и по истинному следу

пера.

Ключевые слова: глубокое обучение, сверточные нейронные сети, рекур-

рентные нейронные сети, скелет, распознавание символов, распознавание

рукописного текста.

DOI: 10.31857/S0005231021110015

1. Введение

Одной из активно исследуемых задач компьютерного зрения является рас-

познавание рукописного текста. Эта задача находит множество практических

применений, от автоматической обработки документов до работы с архива-

ми. Методы, использующиеся для решения этой задачи, можно разделить на

два подхода: offline-распознавание и online-распознавание.

Offline-распознавание рукописного текста представляет собой распознава-

ние по изображению. На практике эта задача встречается чаще всего, и спо-

собы ее решения достаточно разнообразны: от классических алгоритмов ком-

пьютерного зрения с выделением векторов признаков и последующей клас-

сификацией до использования искусственных нейронных сетей со сверточ-

ной архитектурой, популярность которых начала быстро расти после того,

как в 2012 г. сеть AlexNet [1] превзошла конкурирующие методы. В данный

момент нейронные сети превосходят альтернативные методы во многих за-

дачах компьютерного зрения. Классические методы распознавания изобра-

жений отличаются разнообразием применяемых дескрипторов: здесь могут

¹ Статьи с 3 стр. по 147 стр. являются окончанием тематического выпуска № 10, 2021.

² Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 20-01-00664).

использоваться дескрипторы LBP [2], SIFT [3], SURF [4], HOG [5] и многие

другие. Пример подборки классических методов, использующихся для задачи

распознавания рукописного текста, можно увидеть в публикации [6], где на

примере распознавания индийского письма деванагари исследуются различ-

ные классификаторы, оперирующие на гистограмме ориентированных гра-

диентов изображения. Одно из первых применений сверточных нейронных

сетей для задачи распознавания символов описывается в [7].

Online-распознавание представляет собой распознавание следа пера в мо-

мент написания текста. Так как такой след имеет вид последовательности ко-

ординат пера, рекуррентные нейронные сети часто применяются в решении

этой задачи, пример использования таких сетей для решения задачи распо-

знавания китайских рукописных символов можно увидеть в [8]. Такая зада-

ча зачастую проще в решении, чем задача offline-распознавания из-за мень-

шей размерности данных, но основным ограничением этого подхода являет-

ся необходимость наличия данных о траектории, что требует использования

оборудования для записи данных и существенно ограничивает возможность

применять этот подход на практике. Во многих задачах запись следа пера мо-

жет отсутствовать, тогда для распознавания доступны только изображения

текста.

Цель данной статьи заключается в попытке свести задачу распознавания

рукописных символов по их изображению (offline-распознавания) к задаче

распознавания по траектории пера (online-распознавания) посредством по-

строения по изображению символа возможной траектории пера при его на-

чертании. Такое сведение позволит применять методы online-распознавания

ко многим задачам распознавания текста, что позволит пользоваться пре-

имуществами этой группы методов: они не накладывают таких требований

на объем обучающей коллекции и могут оказываться более эффективными.

Для реконструкции следа пера используется представление символа в виде

графовой модели, что позволяет рассматривать также возможность реше-

ния задачи с использованием графовых нейронных сетей, которые успешно

применяются для детектирования [9] и распознавания различных объектов.

Однако первые эксперименты [10] с применением простейших графовых ней-

ронных сетей для распознавания рукописных символов показали отсутствие

заметного преимущества таких моделей по сравнению со сверточными ней-

ронными сетями, обрабатывающими изображение.

2. Восстановление следа пера

Основная идея предложенного подхода заключается в том, что для симво-

ла строится его модель в формате геометрического графа. Вершины графа

близки к положениям пера в определенные моменты при начертании сим-

вола, а ребра между вершинами соответствуют отрезкам траектории пера.

Полная траектория пера будет представлять собой набор маршрутов в этом

графе, где каждый маршрут соответствует куску траектории, написанному

без отрыва пера.

2.1. Построение медиального представления

В качестве основы для графа, моделирующего положения пера, исполь-

зуется медиальное представление (скелет) символа на изображении, впервые

описанное в [11]. Введем несколько ключевых понятий, также использовав-

шихся в [10, 12].

Определение 1. Скелетом (медиальным представлением) называет-

ся множество центров всех вписанных кругов фигуры [13, раздел 2.4].

В медиальном представлении фигуры сложной формы обычно присутству-

ет множество коротких “шумовых” ветвей, которые могут быть исключены

без существенных потерь информации, необходимой для распознавания, а их

наличие, наоборот, затрудняет обработку.

Определение 2. Стрижкой скелета или его регуляризацией называ-

ется процесс исключения из скелета ветвей, вклад которых в образование

формы объекта незначителен [13, 14, глава 10].

В предложенном алгоритме применятся метод стрижки, подробно описан-

ный в [13, раздел 10.3]. Медиальное представление является множеством то-

чек, соединенных отрезками прямых линий и парабол [13, раздел 7.1], но при-

менительно к данной задаче его можно приблизить неориентированным гео-

метрическим графом S = (V ; E). Потери при приближении кусков парабол

прямолинейными ребрами незначительны из-за малой длины ребер графа.

Построение модели производится по алгоритму, подробно описанному в [13].

После бинаризации изображения связные области на его бинарном представ-

лении аппроксимируются многоугольниками [13, главы 5-6], после чего на

этих многоугольниках строится морфологическая модель [13, главы 7-10].

Пример выхода алгоритма после регуляризации показан на рис. 1.

Предлагаемый подход основан на предположении, что скелет изображения

символа может использоваться в качестве модели следа пера при написании

Рис. 1. Медиальное представление символа (буква “g”).

этого символа. В большинстве случаев вершины скелетного графа располо-

жены в точках, близких к середине штриха, и существенные отклонения от

этого возможны только в случае сильного шума на краях штриха, не дающего

точно построить модель, или же существенного перекрытия близко располо-

женных штрихов, вызывающего визуальное слияние нескольких штрихов в

один. Поэтому задача восстановления траектории пера (одной из возможных)

сводится к построению маршрута (последовательности инцидентных вершин

и ребер с возможными повторами) или множества в скелетном графе, в кото-

рые в совокупности должны входить все ребра графа. Предложенный алго-

ритм строит маршрут для каждой связной компоненты графа без разбиения

на пересекающиеся штрихи. Таким образом, восстанавливается возможная

траектория начертания “без отрыва пера”. В силу архитектуры рекуррент-

ной нейронной сети, используемой в дальнейшем для распознавания, данные

о ребрах не подаются на вход этой сети. Поэтому вместо полного маршру-

та достаточно сохранять только соответствующую ему последовательность

вершин, что и будет являться выводом полного алгоритма.

В общей сложности предложенный в статье алгоритм, сводящий задачу

offline-распознавания к задаче online-распознавания, состоит из следующих

этапов:

1. Построение медиального представления символа в формате геометри-

ческого графа;

2. Конструирование вспомогательного графа (далее — метаграфа) по ис-

ходному графу;

3. Обход метаграфа;

4. Построение обхода скелетного графа на основе обхода его метаграфа;

5. Генерализация построенного маршрута посредством удаления близко

расположенных вершин и ребер.

2.2. Построение вспомогательного графа

Ребра исходного скелетного графа моделируют фрагменты траектории пе-

ра, и обход этих фрагментов определяется направлением движения пера на

данном участке. Для последовательности смежных вершин (расположенных

на штрихе) степени 2 (не развилок и не терминальных) направление обхода

определяется только выбором направления движения пера по всей последо-

вательности. Неоднозначность построения маршрута возникает на развилках

(т.е. в вершинах степени 3), а отдельным источником неоднозначности явля-

ется проблема обхода цикла, так как при обходе требуется обойти все ребра

цикла, при этом минимизировав количество повторов. Для облегчения задачи

такого обхода графа на его основе строится новый вспомогательный граф.

Определение 3. Метаграфом исходного графа называется вспомога-

тельный граф, где каждому циклу из минимального базиса циклов исходного

графа ставится в соответствие единственная вершина. Метаграф стро-

ится по алгоритму 1.

Определение 4. Вершина V₁ исходного графа соответствует вер-

шине V₂

его метаграфа, если выполняется одно из следующих усло-

вий:

1. V₁ входит в один цикл исходного графа, которому при построении вер-

шин метаграфа ставится в соответствие V₂. В этом случае одной вер-

шине исходного графа может соответствовать несколько вершин метагра-

фа и, наоборот, каждой вершине метаграфа, поставленной в соответствие

какому-либо циклу, соответствуют все вершины, входящие в этот цикл;

2. V₁ не входит ни в один цикл исходного графа, а V₂ ставится ей в со-

ответствие при построении вершин метаграфа. В этом случае соответ-

ствие имеет взаимно однозначный характер: каждой такой вершине соот-

ветствует ровно одна вершина на другом графе.

Алгоритм 1 (построение метаграфа).

Выделение в исходном графе минимального базиса циклов, т.е. мно-

жества циклов, являющегося базисом пространства циклов для графа

(любой цикл графа можно представить как комбинацию циклов из это-

го множества), имеющего при этом минимальную суммарную длину.

II.

Построение вершин:

1. Если вершина не входит ни в один из циклов, она переходит в мета-

граф напрямую, т.е. в метаграф добавляется одна новая вершина,

которая ставится в соответствие этой исходной вершине;

2. Для каждого цикла из базиса в метаграф добавляется ровно одна

новая вершина, которая ставится в соответствие этому циклу.

III.

Построение ребер:

1. Если обе вершины ребра исходного графа не входят ни в один из

циклов, это ребро переходит в метаграф напрямую, т.е. между со-

ответствующими им вершинами проводится ребро той же длины;

2. Если одна вершина ребра не входит ни в один из циклов, а вторая

входит в один или несколько циклов, то в метаграф добавляют-

ся ребра той же длины, соединяющие вершину, соответствюющую

первой вершине, с каждой из вершин, соответствующих этим цик-

лам;

3. Если обе вершины ребра входят в разные циклы графа (но само

ребро не является частью цикла), то в метаграф добавляется ребро

той же длины, которое соединяет две вершины метаграфа, соответ-

ствующие этим циклам;

4. Если два цикла исходного графа имеют хотя бы одну общую вер-

шину, то в метаграф добавляется ребро нулевой длины, которое

соединяет вершины, соответствующие этим циклам;

5. Берется минимальное остовное дерево получившегося графа.

Построение метаграфа по этому алгоритму однозначно, если однозначен

выбор минимального базиса циклов исходного графа. Это всегда выполня-

ется для скелета плоской фигуры, где длина ребра определяется как ев-

клидово расстояние между его концами, и вероятность наличия циклов с

Ц2

Ц1

Рис. 2. Пример скелетного графа и его метаграфа.

равной длиной мала. Пример построения этого вспомогательного графа по-

казан на рис. 2, где для символа из тестового набора показан его скелет-

ный граф (большинство вершин не показано в целях удобства восприятия)

и соответствующий ему метаграф. В этом примере каждый цикл исходного

графа превращается в вершину (Ц1 и Ц2) метаграфа, причем вершина Ц1

метаграфа соответствует вершинам 3-10 исходного графа, а вершина Ц2 —

вершинам 8-16. Так как циклы могут иметь общие вершины, получающийся

на предпоследнем шаге алгоритма 1 граф не обязательно будет являться де-

ревом. При взятии его остовного дерева в качестве метаграфа ни одно ребро,

соответствующее ребру исходного графа, не будет потеряно, так как циклы в

метаграфе возникают только в результате применения правил III, п. 2 и III,

п. 4 из алгоритма построения метаграфа.

2.3. Обход метаграфа

Так как целью восстановления траектории является ее пригодность для

распознавания, соответствие реальной траектории не требуется, но желатель-

но. В качестве эвристического критерия для качественной траектории можно

предложить минимизацию повторных проходов через ребра графа. Для гра-

фа в виде дерева это достигается посредством рекурсивного обхода поддере-

вьев от наименее глубокого до наиболее глубокого. Этот метод может быть

применен для обхода метаграфа, на основе которого уже строится маршрут

в исходном графе.

Первый обход метаграфа и его разметка производятся по алгоритму 2.

Алгоритм 2 (обход метаграфа).

I. Выбор начальной вершины:

1. В исходном графе строится список всех вершин степени 1 (конец

штриха);

2. Если список пуст (вершин степени 1 в графе нет), то рассматрива-

ются все вершины графа;

3. Для каждой вершины из списка считается ее сумма координат S =

=x+y;

4. Выбирается вершина N₀ из списка с минимальной суммой S;

5. Если на шаге 2 рассматривались все вершины графа, то в исход-

ный граф добавляется новая вспомогательная вершина N с теми

же значениями координат, что и N₀, соединенная ребром длины 0 с

вершиной N₀. В метаграф добавляется соответствующая ей верши-

на с теми же координатами, аналогично соединенная с вершиной,

соответствующей N₀. В противном случае N = N₀;

6. Вершина N называется стартовой.

II. Обход метаграфа:

1. Метаграф рассматривается как дерево с корнем в вершине N, ко-

торая выбирается в качестве текущей вершины;

2. Повторять следующие шаги:

— Если у текущей вершины есть дочерние вершины, не поме-

ченные как обойденные, спуститься в одну из них, выбран-

ную произвольно (назначить ее текущей вершиной);

— Иначе, если текущая вершина является терминальной, при-

своить ей значение глубины d = 1, пометить ее как обойден-

ную и подняться в родительскую вершину;

— Иначе (если у текущей вершины есть дочерние вершины, но

все помечены как обойденные) присвоить ей значение глуби-

ны d = max(d_child) + 1, где d_child - множество меток глубины

ее дочерних вершин; пометить ее как обойденную. Если теку-

щая вершина совпадает с вершиной N (обойден весь граф),

завершить алгоритм, иначе подняться в родительскую вер-

шину.

Разберем приведенный алгоритм на примере графа с рис. 2. Обход начи-

нается с вершины 17. Метаграф данного графа имеет линейную структуру,

что существенно упрощает обход. В качестве стартовой выбирается верши-

на 19. Алгоритм последовательно спускается в вершину 1 и присваивает ей

глубину 1, после чего возвращается, помечая глубину остальных вершин (вер-

шина 2 будет иметь значение 2, вершина Ц1 - значение 3 и т.д.).

2.4. Обход графа

После первого обхода метаграфа производится второй обход, во время ко-

торого в соответствии с алгоритмом 3 строится трасса.

Определение 5. Трассой в графе называется последовательность вер-

шин графа, соответствующая последовательности вершин в некотором

маршруте, в который входят все ребра и вершины данного графа. Трасса,

которая строится данным алгоритмом, соответствует возможной после-

довательности положений пера при написании символа.

Алгоритм 3 (обход графа).

1. Если текущая вершина не соответствует никакому из циклов исходного

графа, то занести ее в трассу и спуститься в еще не обойденную дочернюю

вершину с минимальной глубиной.

2. Если текущая вершина соответствует какому-либо циклу исходного гра-

фа, то выбрать финальную вершину, где будет производиться выход из цик-

ла. Эта вершина соответствует дочерней вершине с максимальной глубиной.

Также выбрать направление обхода цикла. Двигаться по соответствующему

циклу исходного графа, занося в трассу пройденные вершины, от точки вхо-

да (из предыдущей вершины) до ближайшей точки выхода, соответствующей

еще не обойденной вершине метаграфа и не совпадающей с финальной вер-

шиной выхода. Если не обойдена только финальная вершина, то двигаться

по циклу, занося пройденные вершины в трассу, до этой вершины.

3. Если дочерних вершин нет (вершина является листом дерева) или все

они уже обойдены, то занести текущую вершину в трассу и вернуться на

уровень вверх. Для вершины, соответствующей циклу исходного графа, это

означает движение по циклу до точки изначального входа в цикл (как и

ранее, с занесением в трассу всех пройденных вершин).

Ни одно ребро исходного графа не будет потеряно при таком обходе, так

как обход покрывает все вершины и ребра метаграфа. Каждому ребру исход-

ного графа, не входящему ни в какой из циклов, соответствует ребро мета-

графа (при выделении остовного дерева на последнем этапе построения ме-

таграфа из него исключаются только дубликаты ребер и те ребра, которые

не имеют аналогов на исходном графе). Ребра же, которые входят в циклы

исходного графа, обходятся при рассмотрении вершины, соответствующей

этому циклу в метаграфе. Такой обход позволяет по метаграфу построить

трассу в исходном графе.

Помимо минимизации возвратов и повторных проходов, сортировка дочер-

них вершин на глубине соответствует специфике задачи: так как короткие

ответвления будут обходиться в первую очередь, метод применим не толь-

ко для построения обхода в отдельных символах, но и для более длинных

элементов рукописного текста (слитно написанных слов).

На риc. 2 обход исходного графа начинается с вершины 19 и продолжается

до прихода в вершину 16, которая соответствует вершине Ц2 метаграфа. При

выборе обхода против часовой стрелки алгоритм выбирает точку выхода в

вершине 8, после чего последовательно обходит вершины цикла 15, 8, 9, 10,

11 и далее до возврата в вершину 16. Далее производится переход в вершину 8

через вершину 15 и обход цикла Ц1: точка выхода находится в вершине 3, и

алгоритм обходит цикл в следующем порядке: 3, 4, . . . , 7, 10, 9, 8, 3, после

чего обход цикла завершается и обходятся вершины 2 и 1. Итоговая трасса

будет иметь вид [19, 18, 17, 16, 15, 8, 9, 10, 11, 12, 13, 14, 16, 15, 8, 3, 4, 5, 6,

7, 10, 9, 8, 3, 2, 1].

2.5. Генерализация трассы

В местах большой кривизны штрихов текста его скелетный граф будет

иметь большое количество вершин, расположенных близко одна к другой.

В трассе, получающейся при обходе такого скелета, также будет много близ-

ко расположенных вершин, идущих подряд. Объединение таких вершин (или

исключение из трассы лишних вершин) позволяет существенно уменьшить

объем входных данных без существенных потерь важной информации, опи-

сывающей форму символа. Это облегчает обучение классификатора при ре-

шении задачи распознавания по траектории. Прореживание трассы произво-

дится в соответствии с алгоритмом 4.

Алгоритм 4 (прореживание трассы).

I. Вершины начинают рассматриваться со второй вершины трассы (так

как трасса строится таким образом, что она всегда начинается в терми-

нальной вершине).

II. Для вершины проверяются следующие критерии:

1. Вершина имеет степень 2;

2. Предыдущая или следующая вершина последовательности тоже

имеет степень 2;

3. Расстояние от рассматриваемой вершины до обеих вершин, рассмот-

ренных на предыдущем шаге, не превышает порогового значения.

III. В случае выполнения всех трех критериев вершина удаляется из после-

довательности.

IV. Рассмотрение переходит к следующей вершине.

В результате всех вышеописанных действий из скелетного графа получает-

ся трасса, последовательность его вершин. Эта последовательность объявля-

ется реконструированным следом пера (одним из возможных) при написании

рассматриваемого рукописного символа или слова.

3. Распознавание символов

Пригодность восстановленной траектории пера для распознавания руко-

писного символа по нему обосновывается посредством экспериментального

исследования работы алгоритма распознавания на этой восстановленной тра-

ектории и сравнения с результатами распознавания по реальной траектории.

Сведение задачи offline-распознавания к задаче online-распознавания обосно-

вывается также посредством экспериментального исследования и сравнением

качества распознавания символов при помощи предложенных алгоритмов и

при помощи традиционных методов offline-распознавания.

Для распознавания символов на основе восстановленной траектории при-

менялся алгоритм, описанный в [15] и основанный на архитектуре двунаправ-

ленной рекуррентной нейронной сети, которая состояла из 24 управляемых

рекуррентных блоков [16]. Рекуррентная нейронная сеть представляет собой

вариант искусственной нейронной сети, предназначенной для работы с дан-

ными, имеющими формат последовательности. Структурный элемент такой

сети, называемый рекуррентным блоком (управляемый рекуррентный блок

представляет собой один из типов таких блоков), выводит два значения: вы-

вод рекуррентного блока и скрытое состояние, а на вход принимает также

два значения: текущий элемент последовательности и скрытое состояние с

обработки предыдущего элемента последовательности. Размерность каждого

блока определяет размерность скрытых состояний.

y₀

y₁

y₂

y_i

s₀

s_i

X₀

X₁

X₂

X_i

Рис. 3. Двунаправленная рекуррентная нейронная сеть.

Двунаправленная рекуррентная нейронная сеть представляет собой две

схожие рекуррентные нейронные сети, которые обрабатывают последователь-

ность в двух противоположных направлениях. Выход этих сетей объединяет-

ся для получения итогового результата. Схема такой сети показана на рис. 3,

на котором A обозначает рекуррентный блок, x - элементы последователь-

ности, S - скрытые состояния, y - вывод для каждого элемента, i - длина

последовательности. Итоговый вывод нейронной сети для всей последова-

тельности получается из y₀ и y_i.

Предобучение модели в данном случае не проводилось; обучающая и тесто-

вая выборки имели соотношение размеров 4 к 1. Обучающая выборка также

была расширена посредством случайных сдвигов точек исходных последова-

тельностей.

Для сравнения с алгоритмом offline-распознавания использовалась свер-

точная нейронная сеть VGG16 [17], предобученная на базе ImageNet. Раз-

биение на обучающую и тестовую выборки проводилось также в соотноше-

нии 4 к 1.

4. Экспериментальное исследование

4.1. Малый объем данных

Первый эксперимент проводился на коллекции данных, представленной

в [15]. Эта коллекция данных представляет собой траектории пера, записан-

ные с помощью сенсорного контроллера. Набор данных состоит из семи клас-

сов и содержит по 100 примеров для каждого класса.

Для получения изображений символов для offline-распознавания эти тра-

ектории были растеризованы, дальше предложенный алгоритм работал с эти-

ми изображениями без использования данных о реальной траектории пера.

Примеры растеризованных изображений показаны на рис. 4.

Результаты экспериментального исследования

Метод

Точность

RNN-True

0,93

RNN-Offline

0,87

VGG

0,60

Рис. 4. Примеры символов, класс “А”.

Результаты экспериментального исследования приведены в таблице. Ме-

тодам присвоены следующие обозначения:

RNN-True — рекуррентная нейронная сеть, которая была обучена на истин-

ной траектории пера;

RNN-Offline — рекуррентная нейронная сеть, которая была обучена на вос-

становленной предложенным алгоритмом траектории;

VGG — сверточная сеть VGG16, предобученная на ImageNet и дообученная

на изображениях из набора.

Видно, что предложенный метод отстает от online-распознавания по ис-

тинным траекториям, что достаточно предсказуемо, но при этом его точ-

ность заметно превосходит точность метода offline-распознавания. Сверточ-

ная сеть VGG16 оказалась неспособна обучиться на такой выборке, в отличие

от рекуррентной модели.

4.2. Большой объем данных

Второй эксперимент проводился на коллекции данных EMNIST [18],

представляющем собой преобразованный набор данных NIST Special

Database 19 [19]: по сравнению с оригинальным набором данных размер изоб-

ражений уменьшен, а сами изображения из бинаризованных переведены в от-

тенки серого. Следует отметить, что предложенный алгоритм, основанный на

построении морфологического скелета и восстановлении траектории, устой-

чив к вышеописанным преобразованиям, так как один из этапов алгоритма

включает в себя (повторную) бинаризацию изображения, координаты узлов

скелетного графа являются дробными числами, а алгоритм обхода инвари-

антен к сдвигу и масштабированию координат узлов графа.

Основными трудностями для обучения сверточных нейронных сетей на на-

боре EMNIST является высокое число классов (10 цифр, 26 прописных букв

латинского алфавита и 26 строчных, итого 62 класса), повышенная схожесть

отдельных классов между собой (в частности, для некоторых букв строч-

ные и прописные написания практически идентичны друг другу), а также

несбалансированность классов в наборе. В связи с этим многие исследова-

тели упрощают постановку задачи, объединяя часть классов между собой.

В [20] набор данных был сокращен до 47 классов, итоговый размер обучаю-

щей выборки составил 112 800 изображений, а тестовой— 18 800 изображений.

На получившемся наборе искусственная сверточная сеть показала точность

классификации, равную 81%.

Предложенный алгоритм проверялся на всех классах набора без их объ-

единения и балансирования. Несмотря на простоту предложенной рекуррент-

ной модели, она показала точность классификации, равную 74%, что сопо-

ставимо с точностью сверточной модели, решавшей более простую задачу.

Большая часть ошибок алгоритма связана именно с межклассовым сход-

ством, те символы, которые не имеют аналогов со сходным написанием, рас-

познаются с высокой точностью.

5. Заключение

Предложен метод сведения задачи offline-распознавания рукописных сим-

волов к задаче online-распознавания, проиллюстрированный посредством ис-

пользования рекуррентной искусственой нейронной сети для распознавания

на двух коллекциях данных. При малом количестве обучающих примеров мо-

дель показала способность к обучению на данных, получаемых предложен-

ным алгоритмом, в отличие от сверточной модели, существенно отставшей

по точности.

На большом наборе данных алгоритм показал способность к обучению

и классификации несмотря на сложность набора данных, в связи с которой

большинство работ, использующих этот набор, оперируют упрощенными дан-

ными с объединенными классами. С учетом повышенной сложности задачи,

показанная алгоритмом точность сопоставима с методами, основанными на

сверточных аналогах.

Дальнейшие направления развития этого исследования могут включать в

себя эксперименты с совершенствованием способов восстановления траекто-

рии пера, а также эксперименты на различных данных, например слитных

последовательностях символов.

СПИСОК ЛИТЕРАТУРЫ

1. Krizhevsky A., Sutskever I., Hinton G.E. Imagenet Classification with Deep

cCnvolutional Neural Networks // Advances in neural information processing

systems. 2012. P. 1097-1105.

2. Ojala T., Pietikainen M., Hardwood D. A Comparative Study of Texture Measures

with Classification Based on Feature Distributions // Pattern Recognition. 1996.

V. 29. No. 1. P. 51-59.

3. Lowe D.G. Distinctive image features from scale-invariant keypoints // Inte. J. of

Computer Vision. 2004. V. 16. No. 2. P. 91-110.

4. Bay H., Ess A., Tuytelaars T., Van Gool L. SURF: Speeded up Robust Features //

Computer Vision and Image Understanding. 2008. V. 110. No. 3. P. 346-359.

5. Dalal N., Triggs B. Histograms of Oriented Gradients for Human Detection // IEEE

Computer Society Conf. on Computer Vision and Pattern Recognition (CVPR 2005).

2005. V. 1. P. 886-893.

6. Pal U., Wakabayashi T., Kimura F. Comparative Study of Devnagari Handwritten

Character Recognition Using Different Feature and Classifiers // 2009 10th Int. Conf.

on Document Analysis and Recognition. 2009. P. 1111-1115.

Ciresan D.C., Meie, U., Gambardella L.M., Schmidhuber J. Convolutional Neural

Network Committees for Handwritten Character Classification // 2011 Int. Conf. on

Document Analysis and Recognition. 2011. P. 1115-1139.

Zhang X.Y., Yin F., Zhang Y.M., Liu C.L., Bengio Y. Drawing and Recognizing

Chinese Characters with Recurrent Neural Network // IEEE Trans. Pattern Analysis

and Machine Intelligence. 2017. V. 40. No. 4. P. 849-862.

Захаров А.А., Баринов А.Е., Жизняков А.Л., Титов В.С. Поиск объектов на

изображениях с использованием структурного дескриптора на основе графов //

Компьютерная оптика. 2018. Т. 42. № 2. С. 283-290.

10.

Ломов Н.А., Арсеев С.П. Нейронные сети для распознавания формы по ме-

диальному представлению // Тр. Междунар. конф. по компьютерной графике

и зрению “Графикон”. ФГУ “Федеральный исследовательский центр Институт

прикладной математики им. М.В. Келдыша РАН”. 2018. № 28. С. 218-221.

11.

Blum H.A. A Transformation for Extracting New Descriptors of Shape // Proc.

Sympos. Models for the Perception of Speech and Visual Form. 1967. V. 4. P. 362-

380.

12.

Арсеев С.П., Местецкий Л.М. Распознавание рукописного текста по восстанов-

ленному следу пера с помощью медиального представления // Информационные

технологии и нанотехнологии (ИТНТ-2020). 2020. С. 683-689.

13.

Местецкий Л.М. Непрерывная морфология бинарных изображений: фигуры,

скелеты, циркуляры. М.: Физматлит, 2009.

14.

Shaked D., Bruckstein A.M. Pruning Medial Axes // Computer Vision and Image

Understanding. 1998. V. 69. No. 2. P. 156-189.

15.

Fischer T. “Online Handwritten Character Recognition with capacitive sensors”

project

// Online: https://github.com/tobiasfshr/online-handwritten-character-

recognition-capacitive-sensors. 2018.

16.

Chung J., Gulcehre C., Cho KH., Bengio Y. Empirical Evaluation of Gated

Recurrent Neural Networks on Sequence Modeling

// arXiv preprint.

2014.

arXiv:1412.3555.

17.

Simonyan K., Zisserman A. Very Deep Convolutional Networks for Large-scale

Image Recognition // arXiv preprint. 2014. arXiv:1409.1556.

18.

Cohen G., Afshar S., Tapson J., Van Schaik A. EMNIST: Extending MNIST to

Handwritten Letters // 2017 Int. Joint Conf. on Neural Networks (IJCNN). 2017.

P. 2921-2926.

19.

Grother P., Hanaoka K. NIST Special Database 19 Hhandprinted Forms and

Characters 2nd Edition // National Institute of Standards and Technology, Tech.

Rep. Online: http://www.nist.gov/srd/upload/nistsd19.pdf. 2016.

20.

Neftci E.O., Augustine C., Paul S., Detorakis G. Event-driven Random Back-

propagation: Enabling Neuromorphic Deep Learning Machines // Frontiers in

Neuroscience. 2017. V. 11. P. 324.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 20.01.2021

После доработки 15.06.2021

Принята к публикации 30.06.2021