Автоматика и телемеханика, № 11, 2021

(Московский физико-технический институт),

В.В. СТРИЖОВ, д-р физ.-мат. наук (strijov@phystech.edu)

(Вычислительный центр им. А.А. Дородницына ФИЦ ИУ РАН, Москва)

БАЙЕСОВСКАЯ ДИСТИЛЛЯЦИЯ МОДЕЛЕЙ

ГЛУБОКОГО ОБУЧЕНИЯ¹

Исследуется проблема понижения сложности аппроксимирующих мо-

делей. Рассматриваются методы, основанные на дистилляции моделей

глубокого обучения. Вводятся понятия учителя и ученика. Предполагает-

ся, что модель ученика имеет меньшее число параметров, чем модель учи-

теля. Предлагается байесовский подход к выбору модели ученика. Пред-

ложен метод назначения априорного распределения параметров ученика

на основе апостериорного распределения параметров модели учителя. Так

как пространства параметров учителя и ученика не совпадают, предла-

гается механизм приведения пространства параметров модели учителя

к пространству параметров модели ученика путем изменения структуры

модели учителя. Проводится теоретический анализ предложенного меха-

низма приведения. Вычислительный эксперимент проводился на синтети-

ческих и реальных данных. В качестве реальных данных рассматривается

выборка FashionMNIST.

Ключевые слова: выбор модели, байесовский вывод, дистилляция модели,

локальные преобразования, преобразования вероятностных пространств.

DOI: 10.31857/S0005231021110027

1. Введение

Исследуется проблема снижения числа обучаемых параметров моделей ма-

шинного обучения. Примерами моделей с избыточным числом параметров

являются AlexNet [1], VGGNet [2], ResNet [3], BERT [4, 5], mT5 [6], GPT3 [7]

и др. В табл. 1 приводится число параметров моделей глубокого обучения,

которое с годами растет. Это влечет снижение интерпретируемости моделей.

Данная проблема рассматривается в специальном классе задач по состяза-

тельным атакам (adversarial attack) [8]. Большое число параметров требу-

ет значительных вычислительных ресурсов. Из-за этого данные модели не

¹ Настоящая статья содержит результаты проекта Математические методы интеллекту-

ального анализа больших данных, выполняемого в рамках реализации Программы Центра

компетенций Национальной технологической инициативы “Центр хранения и анализа боль-

ших данных”, поддерживаемого Министерством науки и высшего образования Российской

Федерации по Договору МГУ им. М.В. Ломоносова с Фондом поддержки проектов Нацио-

нальной технологической инициативы от 11.12.2018 №13/1251/2018. Работа выполнена при

поддержке Российского фонда фундаментальных исследований (проекты № 19-07-01155,

№ 19-07-00875).

Таблица 1. Число параметров в моделях машинного обучения

Название

AlexNet VGGNet ResNet BERT mT5 GPT3

Год

2012

2014

2015

2018

2020

Тип данных

изобра- изобра- изобра- текст текст текст

жение жение жение

Число параметров, млрд

0,06

0,13

0,06

0,34

175

могут быть использованы в мобильных устройствах. Для снижения числа

параметров предложен метод дистилляции модели [9-11]. Дистиллируемая

модель с большим числом параметров называется учителем, а модель, по-

лучаемая путем дистилляции, называется учеником. При оптимизации па-

раметров модели ученика используется модель учителя с фиксированными

параметрами.

Определение 1. Дистилляция модели — снижение сложности моде-

ли путем выбора модели в множестве более простых моделей на основе

параметров и ответов более сложной фиксированной модели.

Идея дистилляции предложена Дж.Е. Хинтоном и В.Н. Вапником [9-11].

В их публикациях предлагалось использовать ответы учителя в качестве це-

левой переменной для обучения модели ученика. Поставлен ряд эксперимен-

тов, в которых проводилась дистилляция моделей для задачи классифика-

ции машинного обучения. Базовый эксперимент на выборке MNIST [12] пока-

зал результативную дистилляцию избыточно сложной нейросетевой модели

в нейросетевую модель меньшей сложности. Проводился эксперимент по ди-

стилляции ансамбля моделей в одну модель для решения задачи распознания

речи. В [9] проведен эксперимент по обучению экспертных моделей на осно-

ве одной модели с большим числом параметров при помощи предложенного

метода дистилляции на ответах учителя.

В [13] предложен метод передачи селективности нейронов (neuron

selectivity transfer), основанный на минимизации специальной функции по-

терь. Метод основан на вычислении функции максимального среднего от-

клонения (maximum mean discrepancy) между выходами всех слоев модели

учителя и ученика. Вычислительный эксперимент показал эффективность

данного метода для задачи классификации изображений на примере выбо-

рок CIFAR [14] и ImageNet [15].

В данной статье предлагаются методы, основанные на байесовском выводе.

В качестве априорного распределения параметров модели ученика предлага-

ется использовать апостериорное распределение параметров модели учите-

ля. Решается задача приведения пространства параметров модели учителя к

пространству параметров модели ученика. Авторы предлагают подход, осно-

ванный на последовательном приведении пространства параметров модели

учителя.

Определение 2. Структура модели — множество структурных па-

раметров модели, которые задают вид суперпозиции.

Определение 3. Приведение параметрических моделей — изменение

структуры модели (одной или нескольких моделей), в результате которого

векторы параметров различных моделей лежат в одном пространстве.

В результате приведения параметры модели учителя и модели ученика ле-

жат в одном пространстве. Как следствие, в качестве априорного распреде-

ления параметров модели ученика выбирается апостериорное распределение

параметров модели учителя. В данной статье в качестве параметрических

моделей рассматривается полносвязная нейронная сеть. В качестве струк-

турных параметров модели выбраны число слоев, а также размер каждого

скрытого слоя.

В рамках предложенного метода приведения параметрических моделей не

оговорен выбор порядка на множестве параметров модели учителя. Для это-

го предлагается упорядочивать параметры модели учителя на основе их зна-

чимости [16]. Первый нейрон является наиболее значимым, а последний ней-

рон — наименее значимым. Порядок задается на основе отношения плотности

распределения упорядочиваемого параметра к плотности распределения па-

раметра в нуле [17] или на основе метода Белсли [18]. В рамках данной статьи

порядок на параметрах задается случайный образом.

В рамках вычислительного эксперимента проводится теоретический ана-

лиз. Предложенный метод дистилляции анализируется на примере синтети-

ческой выборки, а также на реальной выборке FashionMnist [19].

2. Постановка задачи дистилляции

Задана выборка

(1)

D = {(x_i,y_i)}mi=1 ,

x_i ∈ Rⁿ, y_i

∈ Y,

где x_i, y_i — признаковое описание и целевая переменная i-го объекта, чис-

ло объектов в обучающей выборке обозначается m. Матрица признаковых

[

]_T

описаний обозначается X =

x^T1,... ,xTm

, а вектор целевых переменных обо-

значается y = [y₁, . . . , y_m]. Размер признакового описания объектов обознача-

ется n. Множество Y = {1, . . . , K} для задачи классификации, где K число

классов, множество Y = R для задачи регрессии.

Задана модель учителя в виде суперпозиций линейных и нелинейных пре-

образований:

(

)

= σ ◦ U_Tσ ◦ UT-1 ◦ ...U₂σ ◦ U₁x,

где T — число слоев модели учителя, σ — функция активации, а U_t обозна-

чает матрицу линейного преобразования. Матрицы U соединяются в вектор

параметров u модели учителя f:

(

)

(2)

u = vec

U_T ,UT-1,... ,U₁

где vec — операция векторизации соединенных матриц. Каждая матрица U_t

имеет размер n_t × nt-1, где n₀ = n, а n_T = 1 для задачи регрессии и n_T = K

для задачи классификации на K классов. Число параметров N_tr учителя f

∑

(3)

N_tr =

n_tnt-1.

t=1

Для построения вектора параметров u задается полный порядок на элементах

матриц U_t. Для полносвязанной нейронной сети вводится естественный поря-

док, индуцированный номером слоя t, номером нейрона и номером элемента

вектора параметров нейрона: выбирается матрица U_t, строка этой матрицы

и элемент строки.

Например, для модели учителя в задаче регрессии:

(

)

(4)

=σ◦U₃σ◦U₂σ◦U₁x

вектор параметров u принимает вид

[

u = u1,11,... ,u1,n1,... ,un1,¹¹,...,un1,n1,u1,12,... ,u1,n12,...

]

... ,un2,¹²,... ,un2,n12,u3,1,... ,u3,n2

Пусть для вектора параметров u учителя f известно апостериорное распре-

(

)

деление параметров p

u|D

На основе выборки D и апостериорного распределения параметров учи-

теля f требуется выбрать модель ученика из параметрического семейства

функций:

(

)

= σ ◦ W_Lσ ◦ ... ◦ W₁x, W_l ∈ Rnl×nl-1,

где L — число слоев модели ученика. Число параметров N_st модели ученика g

вычисляется аналогично выражению (3). Вектор параметров модели учени-

ка w строится аналогичным образом (2). Модель g задается своим вектором

параметров w. Следовательно, задача выбора модели g эквивалентна задаче

оптимизации вектора параметров w ∈ RNst .

Параметры ŵ ∈ RNst оптимизируются при помощи вариационного вывода

на основе совместного правдоподобия модели и данных:

∫

(

)

(

)

(

)

(

)

(5)

D,A

= log p

D|A

= log

D|w

w|A

dw,

w∈R^Nst

(

)

где p

w|A

— априорное распределение вектора параметров модели учени-

ка, A обозначает гиперпараметры априорного распределения. Взятие инте-

грала (5) является вычислительно сложной задачей. В качестве приближен-

ного решения используется вариационный подход [17, 18]. Для этого задается

(

)

вариационное распределение параметров модели ученика q

w|μ, Ψ

, которое

(

)

аппроксимирует неизвестное апостериорное распределение p

w|D

(

)

(

)

w|μ, Ψ

≈p

w|D

где оптимальные гиперпараметры распределения μ иΨ требуется найти вме-

сте с оптимальными параметрами ŵ, решив оптимизационную задачу:

(

)

(

))

∑

(

)

(6)

ŵ, μ,Ψ = arg min

D_KL

w|μ, Ψ

||p

w|A

- log p

y_i|x_i,w

μ,Ψ,w

i=1

где D_KL обозначает расстояние Кульбака-Лейблера между вариационным

(

)

(

)

распределением q

w|μ, Ψ

и априорным распределением p

w|A

. Второе сла-

(

)

гаемое формулы (6) является логарифмом правдоподобия log p

y_i|x_i,w

объ-

екта (x_i, y_i) ∈ D выборки (1). Выражение (6) не учитывает параметры учите-

ля f. Для использования информации о распределении параметров учителя

(

)

предлагается рассмотреть параметры априорного распределения p

w|A

как

(

)

функцию от апостериорного распределения учителя p

u|D

3. Построение априорного распределения ученика

Апостериорное распределение параметров модели учителя предполагается

нормальным:

(

)

(

)

(7)

u|D

m, Ψ

где m и Ψ — гиперпараметры этого распределения. На основе гиперпарамет-

(

)

ров m и Ψ требуется задать параметры A априорного распределения p

w|A

Когда структура моделей учителя и ученика задается числом слоев и разме-

ром этих слоев, возможны следующие варианты: 1) число слоев и размер

каждого слоя совпадают; 2) число слоев совпадает, а размеры слоев разли-

чаются; 3) не совпадает число слоев.

3.1. Учитель и ученик имеют одну структуру

Рассмотрим следующие условия:

1) число слоев модели ученика равняется числу слоев модели учителя

L=T;

2) размеры соответствующих слоев совпадают, другими словами, для

всех t, l, таких что t = l, выполняется n_l = n_t, где n_t обозначает размер

t-го слоя учителя, а n_l — размер l-го слоя ученика.

В случае выполнения этих условий априорное распределение параметров

модели ученика приравнивается к апостериорному распределению парамет-

(

)

(

)

ров учителя p

w|A

u|D

3.2. Удаление нейрона в слое учителя

Приведем структуру модели учителя к структуре модели ученика соглас-

но определению 3 при помощи последовательных преобразований вектора

параметров u. Рассмотрим преобразование

(

)

t,u

:RNtr →RNtr-2nt

вектора u, которое описывает удаление одного нейрона из t-го слоя учите-

(

)

ля. Обозначим новый вектор параметров υ = φ

t,u

, а элементы вектора,

которые были удалены, — через υ. Заметим, что векторы υ и υ являются

случайными величинами.

Теорема 1. Пусть выполняются следующие условия:

(

)

1) апостериорное распределение p

u|D

параметров модели учителя яв-

ляется нормальным распределением (7);

2) число слоев модели учителя равняется числу слоев модели ученика

T = L;

3) размеры соответствующих слоев не совпадают, другими словами, для

всех t, l, таких что t = l, выполняется n_t ≤ n_l.

(

)

Тогда апостериорное распределение параметров модели учителя p

υ|D

также является нормальным.

(

)

Доказательство. Не уменьшая общности, пусть φ

t,u

удаляет j-й ней-

рон в t-м слое, что является удалением j-й строки матрицы U_t. Заметим,

что удаление j-й строки матрицы U_t влечет удаление j-й компоненты векто-

ра zt+1, где

zt = σ ◦ Ut-1σ ◦ . . . U2σ ◦ U1x.

Удаление j-й компоненты вектора zt+1 эквивалентно занулению j-го столб-

ца матрицы Ut+1. Заметим, что тогда предсказание модели не зависит от

параметров j-й строки матрицы U_t, а поэтому данными параметрами также

можно пренебречь.

Найдем распределение вектора υ. Для поиска распределения вектора па-

раметров после зануления j-го столбца матрицы Ut+1 воспользуемся форму-

лой условной вероятности p(ν1|D,ν1 = 0), а для удаления j-й строки матри-

(

)

цы U_t воспользуемся маргинализацией распределения p

ν₁|D,ν₁ = 0

. Обо-

значим зануляемые параметры модели через ν₁, а удаляемые параметры —

через ν₂. Также обозначим все параметры, которые не были занулены, че-

рез ν₁ = [υ^T, ν^T2]. Итоговое распределение параметров принимает вид:

∫

(

)

(

)

υ|D

= p

ν₁|D,ν₁ = 0

dν₂.

ν₂

Из свойств нормального распределения следует, что распределение

(

)

(8)

ν₁|D,ν₁ = 0

также является нормальным распределением с параметрами μ, Ξ:

μ = mν1 + Ψν1,ν₁Ψν11,ν₁ (0 - mν1) ,

Ξ = Ψν1,ν₁ - Ψν₁,ν₁Ψν11,ν₁Ψν1,ν1,

где введенные обозначения mν1 , mν1 соответствуют подвектору вектора m,

который относится к параметрам ν₁ и ν₁ соответственно. Ковариационная

матрица Ψν1,ν₁ обозначает подматрицу матрицы Ψ, которая соответствует

ковариационной матрицей между параметрами ν₁ и ν₁.

(

)

Распределение p

υ|D

найдем при помощи маргинализации распределе-

ния (8) по параметрам ν₂. Используя свойства нормального распределения,

получаем распределение

(

)

(

)

(9)

υ|D

μ_υ,Ξ_υ,υ

где μ_υ обозначает подвектор вектора μ, который относится к вектору пара-

метров υ, а матрица Ξ_υ,υ является подматрицей матрицы Ξ, которая отно-

сится к вектору параметров υ. Теорема 1 доказана.

Теорема 1 задает апостериорное распределение параметров (9) после за-

нуления нейронов в модели нейросети — учителя. Заметим, что аналогич-

ным образом можно удалить сразу подмножество нейронов в рамках одного

слоя. В случае если число нейронов отличается в нескольких слоях модели

нейросети учителя, то выполняются последовательно применения отображе-

(

)

ния φ

t,u

для каждого t-го слоя.

3.3. Удаление слоя учителя

Приведем структуру модели учителя к модели ученика согласно определе-

нию 3 при помощи последовательных преобразований вектора параметров u.

Рассмотрим преобразование

(

)

t,u

:RNtr →RNtr-ntnt-1

вектора u, которое описывает удаление одного t-го слоя. Обозначим новый

(

)

вектор параметров υ = ψ

t,u

, а элементы вектора, которые были удале-

ны, — через υ.

Теорема 2. Пусть выполняются следующие условия:

(

)

1) апостериорное распределение параметров p

u|D

модели учителя яв-

ляется нормальным распределением (7);

2) соответствующие размеры слоев совпадают, n_t = nt-1, т.е. матри-

ца U_t является квадратной;

3) функция активации удовлетворяет свойству идемпотентности

σ◦σ=σ.

Тогда апостериорное распределение также описывается нормальным рас-

пределением с плотностью распределения

(

)

(

)

(10)

υ|D

m_υ + Ψ_υ,υΨ-1¯υ,¯υ (i - υ) ,Ψ_υ,υ - Ψ_υ,υΨ-1¯υ,¯υΨ_υ,υ

где вектор i задается как

i = [1,0,...,0,0,1,...,0,0,0,1,... ,0,0,...,1]^T.

Доказательство. Рассмотрим структуру нейронной сети с T слоями и

T + 1 слоем. Не уменьшая общности, для удаления рассматривается t-й слой,

для которого выполняются условия этой теоремы. Заметим, что если t-й слой

нейронной сети с T + 1 слоем приравнять к единичной матрице, то он будет

эквивалентным архитектуре с T слоями:

f =σ◦UT+1σ◦U_T ...σ◦U_tσ◦...U₂σ◦U₁ =

= σ ◦ UT+1σ ◦ U_T ...σ ◦ Iσ ◦ ...U₂σ ◦ U₁ =

=σ◦UT+1σ◦U_T ...σ◦σ◦...U₂σ◦U₁ =

=σ◦UT+1σ◦U_T ...σ◦...U₂σ◦U₁.

Получаем, что удаление t-го слоя нейросети эквивалентно приравниванию

матрицы параметров t-го слоя к единичной матрице. Распределение пара-

метров после приравнивания к единичной матрице вычисляется при помощи

условного распределения. В силу общих свойств нормального распределения

условное распределение также является нормальным распределением с па-

раметрами μ, Ξ :

μ = m_υ + Ψ_υ,υΨ-1¯υ,¯υ (i - υ),

Ξ=Ψ_υ,υ -Ψ_υ,υΨ-1¯υ,¯υΨ_υ,υ,

где вектор m_υ является подвектором вектора m соответствующей парамет-

рам υ, а матрица Ψ_υ,υ является подматрицей ковариационной матрицы Ψ,

соответствующей векторам параметров υ и υ. Теорема 2 доказана.

Теорема 2 задает апостериорное распределение (10) параметров после уда-

(

)

ления слоя нейросети. Полученное распределение p

υ|D

является оценкой

апостериорного распределения модели без одного слоя.

3.4. Выполнение последовательных преобразований

Преобразования φ, ψ приводят пространство параметров учителя f к про-

странству параметров ученика g. После приведения параметрических моде-

лей получаем, что параметры модели учителя и модели ученика принадлежат

одному семейству 3.1.

4. Вычислительный эксперимент

Вычислительный эксперимент анализирует предложенный метод дистил-

ляции на основе апостериорного распределения параметров модели учителя.

4.1. Синтетические данные

Проанализируем модель на синтетической выборке. Выборка построена

следующим образом:

[

(

)]

[

(

)]

w_j : w_j ∼ N

0, 1

X =

x_ij : x_ij ∼ N

0, 1

n×1

m×n

[

(

)]

y= y_i :y_i ∼N

xTiw,β

m×1

1,00

0,75

0,50

0,25

2500

5000

7500

10 000

2500

5000

7500

10 000

Итерации

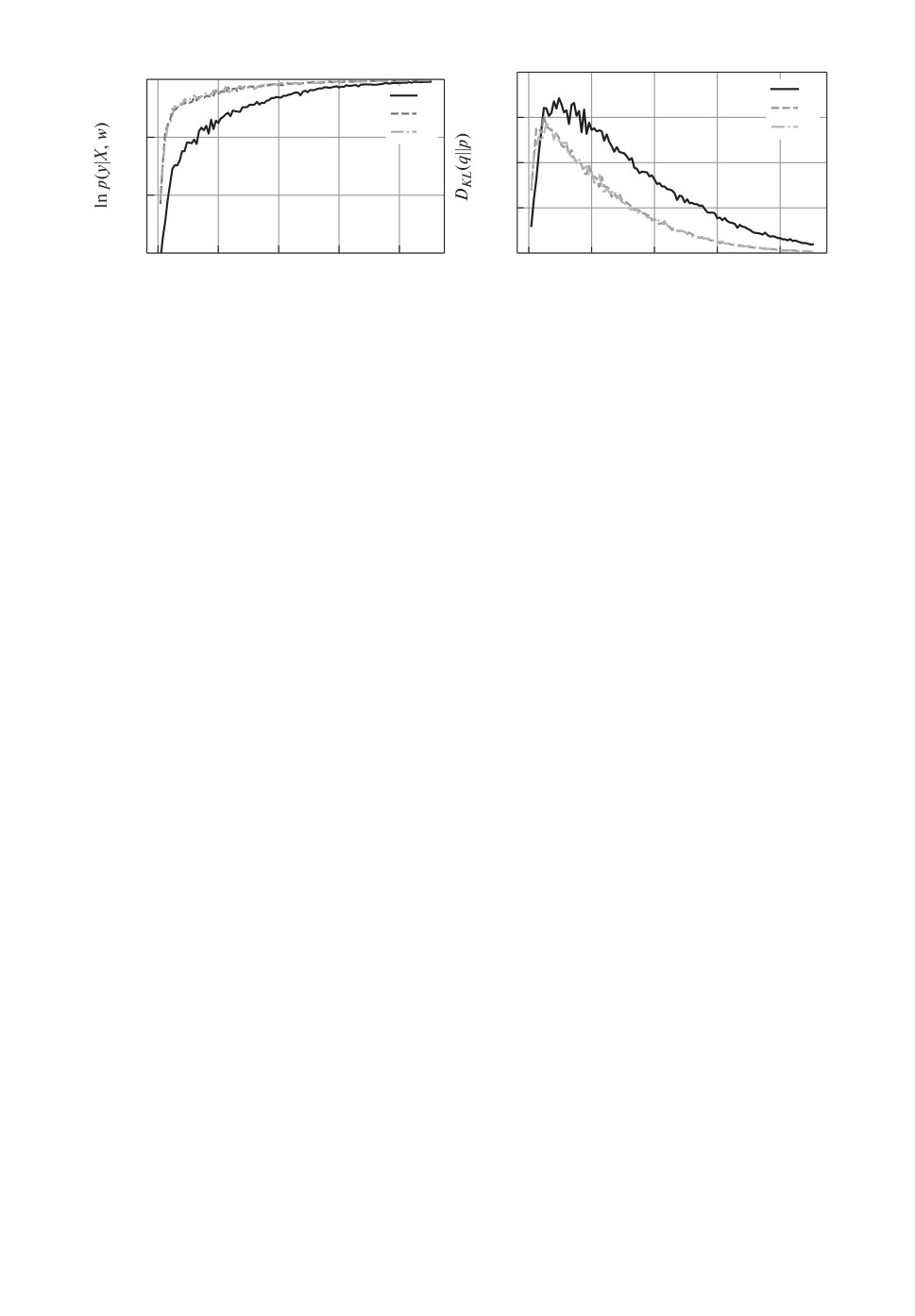
Рис. 1. Структура (11) модели ученика g. Слева: правдоподобие выборки в за-

висимости от номера итерации при обучении. Справа: дивергенция Кульбака-

Лейблера между вариационным и априорным распределениями параметров

модели.

где β = 0,1 — уровень шума в данных. В эксперименте число признаков n =

= 10, для обучения и тестирования было сгенерировано m_train = 900 и m_test =

= 124 объекта.

В качестве модели учителя рассматривалась модель — многослойный пер-

цептрон с двумя скрытыми слоями (4). Матрицы линейных преобразований

имеют размер:

U₁ ∈ R100×10, U₂ ∈ R50×100, U₃ ∈ R1×50.

В качестве функции активации была выбрана функция активации ReLu. Мо-

дель учителя предварительно обучена на основе вариационного вывода (6),

где в качестве априорного распределения параметров выбрано стандартное

нормальное распределение.

В качестве модели ученика были выбраны две конфигурации. Первая кон-

фигурация получается путем удаления нейронов в модели учителя:

(

)

(11)

=σ◦W₃σ◦W₂σ◦W₁

где σ является нелинейной функцией активации, а матрицы линейных пре-

образований имеют размер:

W₁ ∈ R10×10, W₂ ∈ R10×10, W₃ ∈ R1×10.

В качестве функции активации была выбрана функция активации ReLu.

На рис. 1 сравниваются модели ученика со структурой (11). Представ-

лено сравнение разных моделей: модель без дистилляции (график 1 ), где

в качестве априорного распределения выбирается стандартное нормальное

распределение; модель с частичной дистилляцией (график 2 ), где в качестве

среднего значения параметров выбираются параметры согласно (9), а кова-

риационная матрица была приравнена к единичной матрице; модель с пол-

ной дистилляцией (график 3 ) согласно (9). Видно, что модели ученика, где

в качестве априорного распределения выбраны распределения, основанные

0,8

0,6

0,4

0,2

2500

5000

7500

10000

2500

5000

7500

10 000

Итерации

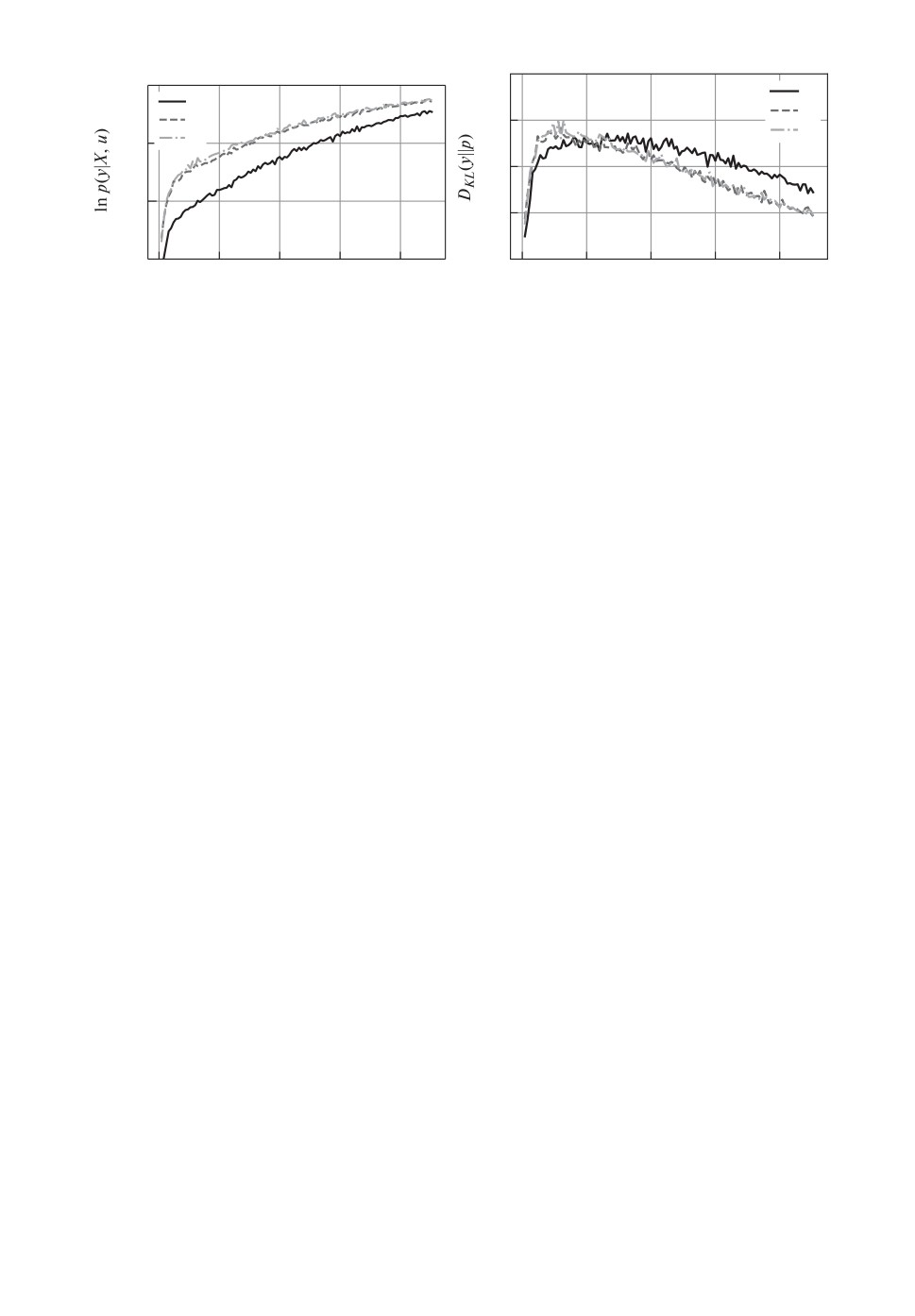
Рис. 2. Структура (12) модели ученика g. Слева: правдоподобие выборки в за-

висимости от номера итерации при обучении. Справа: дивергенция Кульбака-

Лейблера между вариационным и априорным распределениями параметров

модели.

на апостериорном распределении учителя, имеют большее правдоподобие,

чем модель, где в качестве априорного распределения выбрано стандартное

нормальное. Также заметим, что использование параметра среднего из апо-

стериорного распределения дает основной вклад при дистилляции, так как

качество моделей без дистилляции и с полной дистилляцией совпадает.

Вторая конфигурация получается путем удаления слоя модели учителя:

(

)

(12)

=σ◦W₂σ◦W₁

где σ является нелинейной функцией активации, а матрицы линейных пре-

образований имеют размер:

W₁ ∈ R50×10, W₂ ∈ R1×50.

В качестве функции активации была выбрана функция активации ReLu.

На рис. 2 сравниваются модели ученика со структурой (12). Аналогично

рис. 1 на рис. 2 представлено сравнение модели без дистилляции (график 1 ,

модели с дистилляцией параметра среднего значение (график 2 ) и модели

с полной дистилляцией (график 3 ). В рамках данного эксперимента по ди-

стилляции модели учителя в модель ученика с меньшим числом парамет-

ров получены результаты, которые подтверждают, что задание априорного

распределения параметров ученика позволяет улучшить число итераций при

выборе оптимальных параметров модели ученика.

4.2. Выборка FashionMnist

В рамках данного эксперимента проводился анализ байесовского подхода

к дистилляции на реальных данных. В качестве реальных данных выбрана

выборка FashionMnist [19], которая является задачей классификации изобра-

жений на 10 классов.

В качестве модели учителя рассматривалась модель многослойный пер-

цептрон с двумя скрытыми слоями (4). Матрицы линейных преобразований

0,20

0,5

0,15

1,0

0,10

1,5

0,05

2,0

5000

10 000

15000

5000

10 000

15 000

Итерации

Рис. 3. Слева: правдоподобие выборки в зависимости от номера итерации при

обучении. Справа: дивергенция Кульбака-Лейблера между вариационным и

априорным распределениями параметров модели.

имеют размер:

U₁ ∈ R800×784, U₂ ∈ R50×800, U₃ ∈ R10×50.

В качестве функции активации была выбрана функция активации ReLu. Мо-

дель учителя предварительно обучена на основе вариационного вывода (6),

где в качестве априорного распределения параметров выбрано стандартное

нормальное распределение.

В качестве модели ученика были выбрана конфигурация с одним скрытым

слоем (12), где матрицы линейных преобразований имеют размер:

W₁ ∈ R50×784, W₂ ∈ R50×10.

В качестве функции активации была выбрана функция активации ReLu.

На рис. 3 сравниваются модели ученика с разными априорными распреде-

лениями параметров. Аналогично синтетическому эксперименту модель, где

в качестве априорного распределения использовалось стандартное нормаль-

ное распределение, сравнивалась с моделью, где параметры распределения

определялись на основе формулы (10). Видно, что у моделей с заданием апри-

орного распределения на основе апостериорного распределения параметров

учителя правдоподобие выборки выше, чем у модели, где в качестве априор-

ного распределения выбрано стандартное нормальное распределение.

В табл. 2 представлен результат вычислительного эксперимента. Для чис-

ленного сравнения качества моделей выбрана разность площадей графика

(

)

y|X, u

между моделью без дистилляции и моделями с частичной дистил-

ляцией и полной дистилляцией соответственно:

∑

(

)

(

)

(13)

S= p

y|X, uss

-p

y|X, usds

где uss, usds обозначают параметры модели ученика и модели дистиллирован-

ного ученика после s-й итерации оптимизационного процесса. Заметим, что

площадь S имеет знак: чем большее положительное число, тем дистиллиро-

ванная модель лучше, чем модель, построенная без учителя. Если площадь S

Таблица 2. Сводная таблица результатов вычислительного эксперимента

Модель

ученика

Учитель

ученика без

с частичной

с полной

дистилляции

дистилляцией дистилляцией

Эксперимент на синтетической выборке (удаление нейрона)

Структура

[10, 100, 50, 1]

[10, 10, 10, 1]

Число параметров

6050

210

Разность

16559

16864

площадей S

Эксперимент на синтетической выборке (удаление слоя)

Структура

[10, 100, 50, 1]

[10, 50, 1]

Число параметров

6050

550

Разность

23310

25506

площадей S

Эксперимент на выборке FashionMnist

Структура

[784, 800, 50, 10]

[784, 50, 10]

Число параметров

667700

39700

Разность

1165

1145

площадей S

принимает отрицательное значение, то, значит, модель без дистилляции яв-

ляется лучше, чем модель с дистилляцией. В рамках вычислительного экс-

перимента видно, что площадь S под графиками принимает положительные

значения, т.е. модели ученика, полученные при помощи дистилляции, явля-

ются лучше, чем модель ученика без дистилляции.

Код вычислительного эксперимента доступен по ссылке

https://github.com/andriygav/BayesianDistilation.

5. Заключение

В данной статье проанализирована байесовская дистилляция модели учи-

теля в модель ученика на основе вариационного вывода. В рамках данной

статьи дистилляция основывается на задании априорного распределения па-

раметров модели ученика. Априорное распределение параметров модели уче-

ника задается на основе апостериорного распределения параметров модели

учителя. Механизм преобразования структуры модели учителя в структуру

модели ученика представлен в теореме 1 и теореме 2.

Теорема 1 описывает механизм приведения пространства параметров мо-

дели учителя к пространству параметров модели ученика в случае, если чис-

ло слоев совпадает, но размер слоев различается. Теорема 2 описывает меха-

низм приведения пространства параметров модели учителя к пространству

параметров модели ученика в случае, если число слоев различается.

В вычислительном эксперименте сравнивается модель ученика, которая

обучена без использования распределения параметров учителя, и модель уче-

ника, где в качестве априорного распределения параметров выбрано апо-

стериорное распределение параметров модели учителя после приведения.

В табл. 2 показано, что модели ученика с заданием априорного распределе-

ния параметров на основе апостериорного распределения параметров учите-

ля сходятся быстрее, что подтверждается положительным значением метри-

ки (13), которая введена для численного сравнения модели без дистилляции

с дистиллированной моделью.

СПИСОК ЛИТЕРАТУРЫ

Krizhevsky A., Sutskever I., Hinton G. ImageNet Classification with Depp

Convolutional Neural Networks // Proc. 25th Int. Conf. on Neural Information

Procescing Systems. 2012. V. 1. P. 1097-1105.

Simonyan K., Zisserman A. Very Deep Convolutional Networks for Large-Scale

Image Recognition // Int. Conf. on Learning Representations. San Diego. 2015.

He K., Ren S., Sun J., Zhang X. Deep Residual Learning for Image Recognition //

Proc. IEEE Conf. on Computer Vision and Pattern Recognition. Las Vegas. 2016.

P. 770-778.

Devlin J., Chang M., Lee K., Toutanova K. BERT: Pre-training of Deep Bidirectional

Transformers for Language Understanding // Proc. 2019 Conf. North American

Chapter of the Association for Computational Linguistics: Human Language

Technologies. Minnesota. 2019. V. 1. P. 4171-4186.

Vaswani A., Gomez A., Jones L., Kaiser L., Parmar N., Polosukhin I., Shazeer N.,

Uszkoreit J. Attention Is All You Need // In Advances in Neural Information

Processing Systems. 2017. V. 5. P. 6000-6010.

Al-Rfou R., Barua A., Constant N., Kale M., Raffel C., Roberts A., Siddhant A.,

Xue L. mT5: A Massively Multilingual Pre-trained Text-to-text Transformer //

Proc. 2021 Conf. North American Chapter of the Association for Computational

Linguistics: Human Language Technologies. 2021. P. 483-498.

Brown T., et al. GPT3: Language Models are Few-Shot Learners // Advances in

Neural Information Processing Systems. 2020. V. 33. P. 1877-1901.

Zheng T., Liu X., Qin Z., Ren K. Adversarial Attacks and Defenses in Deep

Learning // Engineering. 2020. V. 6. P. 346-360.

Hinton G., Dean J., Vinyals O. Distilling the Knowledge in a Neural Network //

NIPS Deep Learning and Representation Learning Workshop. 2015.

10.

Vapnik V., Izmailov R. Learning Using Privileged Information: Similarity Control

and Knowledge Transfer // J. of Machine Learning Research. 2015. V. 16. P. 2023-

2049.

11.

Lopez-Paz D., Bottou L., Scholkopf B., Vapnik V. Unifying Distillation and

Privileged Information // Int. Conf. on Learning Representations. Puerto Rico. 2016.

12.

Burges C., Cortes C., LeCun Y. The MNIST dataset of handwritten digits. 1998.

http://yann.lecun.com/exdb/mnist/index.html

13.

Huang Z., Naiyan W. Like What You Like: Knowledge Distill via Neuron Selectivity

Transfer // arXiv:1707.01219. 2017.

14.

Hinton G., Krizhevsky A., Nair V. CIFAR-10 (Canadian Institute for Advanced

Research) // http://www.cs.toronto.edu/ kriz/cifar.html

15.

Deng J., et al. Imagenet: A Large-scale Hierarchical Image Database // Proc. IEEE

Conf. on Computer Vision and Pattern Recognition. Miami. 2009. P. 248-255.