Автоматика и телемеханика, № 11, 2021

А.А. ЛАЗАРЕВ, д-р физ.-мат. наук (jobmath@mail.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ОПТИМИЗАЦИЯ РЕКУРСИВНОГО КОНВЕЙЕРА СВЕДЕНИЕМ

К ЗАДАЧЕ УДОВЛЕТВОРЕНИЯ ОГРАНИЧЕНИЙ¹

Рассматривается задача оптимизации расписания рекурсивного кон-

вейера. Для этого вводится определение конвейера, описываемого связ-

ным ациклическим графом, каждая вершина которого представляет со-

бой операцию или функцию управления, ассоциированную с соответст-

вующей рекурсивной функцией из некоторого конечного набора. Каж-

дая рекурсивная функция определяет отношение предшествования опе-

рации конвейера. Рассматривается решение задачи минимизации времени

выполнения заказа конвейером на конечном множестве возобновляемых

ресурсов. Решение осуществляется сведением к задаче удовлетворения

ограничений.

Ключевые слова: теория расписаний, балансировка конвейера, flow-shop

задачи, задача удовлетворения ограничений.

DOI: 10.31857/S0005231021110052

1. Введение

Задачи RCPSP (Resource-Constrained Project Scheduling Problem) являют-

ся одними из основных в теории расписаний. В задачах RCPSP задано множе-

ство заказов, которые необходимо обслужить на конечном множестве машин

(далее по тексту ресурсов). Заказ тождественен множеству упорядоченных

операций и характеризуется временем выполнения. Необходимо минимизи-

ровать время выполнения заказов на множестве распределений ресурсов по

операциям. Данного вида задачи актуальны и для конвейерных систем [1].

Работы, которые рассматривают методы балансировки сборочного конвейе-

ра и планирования ресурсов на этапе проектирования конвейера, приведены

в [2]. В [3] приводятся комплексный обзор и анализ различных методов про-

ектирования и планирования конвейерных систем. Большинство работ по-

священо балансировке сборочного конвейера (ALB). Для ALB модели пред-

ложены методы поиска оптимальных решений с использованием линейного

программирования [4, 5] и целочисленного программирования [6]. Из совре-

менных работ по оптимизации планирования ресурсов для типовых задач

теории расписаний представляют интерес работы [7-10].

Важно отметить две особенности постановки таких задач.

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 20-58-S52006).

p₁₁ = 1

p₂₂ = 2

{m1}

{m2, m3}

{m3, m4}

p₂₃ = 2

p₃₃ = 2

p₃₄ = 2

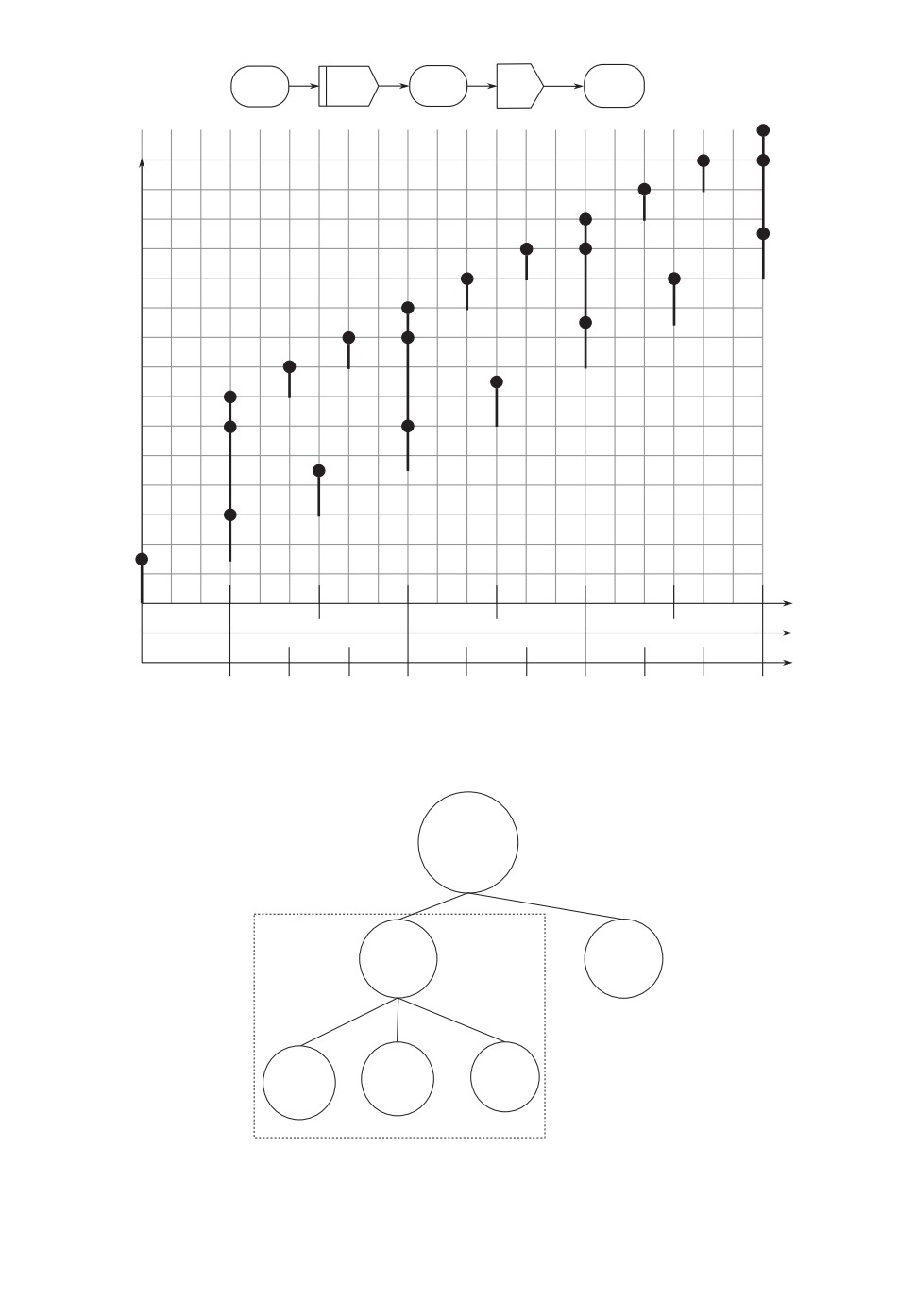
Рис. 1. Пример двух методов распределения ресурсов конвейера.

Первая состоит в том, что ресурсы распределяются до процесса выполне-

ния заказа и на весь процесс выполнения. Это приводит к тому, что каждый

ресурс закреплен за какой-либо одной операцией, даже если он может потен-

циально использоваться несколькими операциями. Однако можно показать

на примере, что “перебрасывание ресурса” с одной операции на другую может

привести к построению более эффективного расписания. На рис. 1,а показана

модель конвейера из трех последовательно выполняемых операций. Под опе-

рациями в фигурных скобках указаны потенциально используемые ресурсы

из множества {m1, m2, m3, m4}. На рис. 1,б указаны длительности операций

при использовании различных ресурсов. Первый индекс — номер операции,

второй индекс — номер ресурса. На рис. 1,в и 1,г показаны временные диа-

граммы выполнения операций для семи заказов. По оси абсцис номер заказа,

по оси ординат время. Отрезок с индексом i, j определяет временной интер-

вал выполнения i-й операции с использованием j-го ресурса для k-го заказа.

На рис. 1,г показана оптимальная диаграмма с закреплением ресурса за опе-

рацией на все время выполнения заказов, а на рис. 1,в диаграмма с распре-

делением ресурсов без закрепления за операциями. Из сравнения диаграмм

видно преимущество по времени второго метода.

Вторая особенность состоит в использовании ограниченного набора отно-

шений предшествования. Это отношение предшествования между операция-

ми и определяемое с помощью предиката and.

В данной статье предлагается решение, преодолевающее оба эти ограни-

чения. Рассматривается распределение ресурсов с возможностью использо-

вания одного ресурса несколькими операциями и с расширением отношений

предшествования с помощью рекурсивных функций. Задачи Удовлетворения

Ограничений (ЗУО) и методы Constraint Programming [11-13] наряду с про-

чим используются для решения задач теории расписаний. В данной работе

рассматривается решение задачи RCPSP сведением ее к ЗУО применительно

к конвейерам, описываемым рекурсивными функциями [14]. Время выполне-

ния операции i зависит от используемого ресурса j, т.е. равно p_ij. Примеры

описания возможностей и применения таких конвейеров приведены в [15].

Статья имеет следующую структуру. В разделе 2 приведено определение

рекурсивного конвейера. Подробно описаны рекурсивные функции. В разде-

ле 3 приведены примеры рекурсивных конвейеров. В разделе 4 описывается

определение ЗУО и задача распределения ресурсов конвейера формулиру-

ется как ЗУО. Раздел 5 является заключением, в котором рассматривается

проблема сложности алгоритма решения поставленной в статье ЗУО.

2. Определение конвейера

Модель и свойства рекурсивного конвейера подробно рассмотрены в

[14, 16]. Однако они описаны в предположении, что за каждой операцией

закреплен свой ресурс на время выполнения всех заказов. В данном разделе

определение рекурсивных функций конвейера дано с учетом распределения

ресурса для каждой пары (операция, заказ).

Модель конвейера представляет собой связный ациклический ориентиро-

ванный граф G = (V, A) с единственной конечной вершиной. V - множество

вершин графа и n - количество вершин. A - множество дуг графа, упоря-

доченных пар вида (v, w), где v, w ∈ V . Вершины графа помечены номерами

из множества I = {1, . . . , n} таким образом, что первые n₀ (1 ≤ n₀ < n) вер-

шин являются начальными, а вершина n конечной. Графическое изображение

вершин и дуг графа представлено на рис. 2. Здесь i, j, j₁, j₂ - номера опера-

ций (вершин), k - номер заказа, p_i,j - время выполнения i-й операции при

использовании j-го ресурса и q_i - коэффициент мультиплицирования или ре-

Рис. 2. Графическая нотация операций и спусковых функций конвейера.

дуцирования. Каждая вершина графа может иметь одну входную дугу (см.

рис. 2 варианты б,в,г,е) или две (см. рис. 2 варианты д,ж) в зависимости от

типа вершины. На множестве номеров вершин графа определены функции

предшествования pred, pred1, pred2 : I → I.

Функция pred(i) определена для вершины, имеющей одну предшествую-

щую вершину и вычисляет номер j вершины графа такой, что (j, i) ∈ A.

Следующие две функции определены для вершин, имеющих две предше-

ствующие вершины, условно вершина 1 и вершина 2:

pred1(i) - вычисляет номер j₁ вершины 1 графа такой, что существует

дуга (j₁, i) ∈ A;

pred2(i) - вычисляет номер j₂ вершины 2 графа такой, что существует

дуга (j₂, i) ∈ A.

Каждая вершина графа может соответствовать операции или спусковой

функции. Операции ассоциированы с производственными операциями. Спус-

ковые функции определяют отношения временного предшествования опера-

ций. Вершины графа помечены с помощью отображения

type : I → E, где E = {bop,op,and,mul,red,get1,get2,put}

на множество из восьми элементов. Каждая константа множества E обо-

значает тип вершины графа, а вершина имеет соответствующую графи-

ческую нотацию (рис. 2). Конвейер использует множество ресурсов M =

= {m₁, . . . , m_r}. Каждая операция i потенциально может использовать ре-

сурсы из некоторого множества D_i ⊆ M. Для каждого 1 ≤ i ≤ n определим

переменную x_ik на множестве D_i. Если x_ik = m_j, то операция i при выпол-

нении k-го заказа использует ресурс m_j ∈ D_i. Время выполнения операции

равно p_ij и является константой. В каждый момент времени каждый ресурс

может использоваться только одной операцией. Прерывания операций запре-

щены.

Спусковые функции ресурсы не потребляют, и время их выполнения рав-

но 0.

Расписание выполнения операций строится с помощью рекурсивных функ-

ций R : I × K × M → T , где K-конечное множество номеров заказов, а

T -время.

Например, рекурсивная функция

t(i, k) = r₁(t(i, k - 1), t(j, k), p_il)

или

t(i, k) = r₂(t(i, k - 1), t(j₁, k), t(j₂, k), p_il),

где j = pred(i), j₁ = pred1(i), j₂ = pred2(i), вычисляет время завершения об-

работки i-й операцией k-го заказа при k ∈ K исходя из времени завершения

ею обработки (k - 1)-го заказа и из времен завершения обработки k-го заказа

предшествующими операциями. Рекурсивные функции имеют два аргумента:

i - номер операции (номер вершины графа) и k - номер заказа. Для каждого

типа вершины, т.е. элемента множества E, своя рекурсивная функция.

Рекурсивная функция t(i, k), вычисляемая по формуле (1), обеспечивает

суперпозицию рекурсивных функций, соответствующих вершинам графа, и

является обращением к одной из них в соответствии с типом вершины.

⎧

⎪

bop(i, k), если type(i) = bop;

⎪

op(i, k),

если type(i) = op;

⎪

and(i,k),

если type(i) = and;

⎨

mul(i,k), если type(i) = mul;

(1)

t(i, k) =

⎪

red(i, k), если type(i) = red;

⎪

get1(i, k), если type(i) = get1;

⎪

get2(i, k), если type(i) = get2;

⎩

put(i,k), если type(i) = put.

Вычисление времени завершения выполнения k-го заказа конвейером осу-

ществляется обращением к рекурсивной функции t(n, k).

Далее описываются все виды вершин: их назначение, тип и соответствую-

щая типу рекурсивная функция.

1. Начальная производственная операция (см. bop рис. 2,а) с номером 1 ≤

≤ i ≤ n₀ характеризуется временем выполнения k-го заказа p_ij, если операция

использует ресурс m_j (x_ik = m_j). Время завершения выполнения данной опе-

рацией k-го заказа определяется как время завершения выполнения (k-1)-го

заказа плюс время выполнения операции p_ij . Если операция при выполнении

k-го и (k-1)-го заказа использует разные ресурсы, то времена их выполнений

совмещаются. Время выполнения нулевого заказа равно p_ij .

(2) bop(i, k) :

⎧

⎪

p_ij,

⎪

если (x_ik = m_j )&(k = 0);

а)

⎨

bop(i, k - 1) + p_ij,

bop =

⎪

если (x_ik = xi,k-1)&(x_ik = m_j)&(k > 0);

б)

⎪

op(i, k - 1) + p_ij - p_il,

⎩ b

если (x_ik = xi,k-1)&(xi,k-1 = m_l)&(x_ik = m_j)&(k > 0).

в)

2. Не начальная производственная операция (см. op рис. 2,б ) с номе-

ром n₀ < i характеризуется временем выполнения p_ij, если используется ре-

сурс m_j. Время завершения выполнения данной операцией k-го заказа опре-

деляется как максимум времен: завершения выполнения данной операцией

(k - 1)-го заказа и завершения выполнения предшествующей ей операцией

k-го заказа и плюс время выполнения операции p_ij. При этом начала выпол-

нений i-й операцией k-го и (k-1)-го заказов совмещаются, если для выполне-

ния используются разные ресурсы. Время выполнения нулевого заказа равно

времени выполнения нулевого заказа предшествующей операцией плюс p_ij.

(3) op(i, k) :

⎧

⎪

t(pred(i), k) + p_ij, если (x_ik = m_j)&(k = 0);

а)

⎪

t(pred(i), k) + p_ij,

⎪

если (t(pred(i), k) ≥ t(i, k - 1))&(x_ik = m_j)&(k > 0);

б)

⎪

⎨

t(pred(i), k) + p_ij,

op =

если (t(pred(i), k) < t(i, k - 1))&

⎪

&(x_ik = xi,k-1)&(x_ik = m_j)&(k > 0);

в)

⎪

t(i, k - 1) + p_ij,

⎪

сли (t(pred(i), k) < t(i, k - 1))&

⎩ е

&(x_ik = xi,k-1)&(x_ik = m_j)&(k > 0).

г)

3. Спусковая функция and (см. and рис. 2,д) вычисляет время завершения

выполнения k-го заказа для двух предшествующих операций.

(4)

and(i,k) : and = max(t(pred1(i),k),t(pred2(i),k)).

4. Спусковая функция мультиплицирования (см. mul рис. 2,в) для каждо-

го времени завершения предшествующей ей операции вычисляет q_i времен

завершения операции i. Это означает, что на одно выполнение предшествую-

щей i операции осуществляется q_i (q_i ≥ 1) выполнений операции i.

(5)

mul(i,k) : mul = t(pred(i),⌊k/q_i

⌋),

где ⌊x⌋ обозначает целую часть x.

5. Спусковая функция редуцирования (см. red рис. 2,г) является обратной

по отношению к функции мультиплицирования и вычисляет время заверше-

ния выполнения очередной партии из q_i (q_i ≥ 1) заказов.

(6)

red(i, k) : red = t(pred(i), (k + 1)q_i

− 1).

6. Спусковая функция раздачи (см. get рис. 2,е) имитирует разделение

конвейерных операций на два потока. Для пользователя она выступает как

одна функция, а в реализации она разбивается на две (условно верхнюю и

нижнюю) см. рис. 2,з. Для верхнего варианта спусковая функция get1 вычис-

ляет времена завершений четных заказов, т.е. t(i, 0) = t(p, 0), t(i, 1) = t(p, 2),

t(i, 2) = t(p, 4), . . .

(7)

get1(i, k) : get1 = t(pred(i), 2k), k ≥ 0.

Для нижнего вычисляет времена завершения выполнения нечетных заказов,

т.е. t(j, 0) = t(p, 1), t(j, 1) = t(p, 3), t(j, 2) = t(p, 5), . . .

(8)

get2(i, k) : get2 = t(pred(i), 2k + 1), k ≥ 0.

7. Спусковая функция приема (см. put рис. 2,ж) является обратной

по отношению к функции раздачи и имитирует слияние двух конвейеров

в один. Проще всего это пояснить последовательностью значений t(i, k):

t(i, 0) = t(p, 0), t(i, 1) = t(q, 0), t(i, 2) = t(p, 1), t(i, 3) = t(q, 1), t(i, 4) = t(p, 2),

t(i, 5) = t(q, 2), . . .

⎧

⎪

t(pred1(i), k),

⎪

если k = 0;

⎨

max(put(i, k - 1), t(pred2(i), k/2)),

(9)

put(i,k) : put =

⎪

если (k mod 2 = 0)&(k > 0);

⎪

ax(put(i, k - 1), t(pred1(i), (k - 1)/2)),

⎩^m

если k mod 2 = 1.

Здесь x mod y - вычисление остатка от деления x на y.

На рис. 3 представлен пример графа конвейера и соответствующей супер-

позиции рекурсивных функций для случая, когда каждой операции выделен

один ресурс на все время процесса. В реальности такой граф не строится, он

является результатом процесса вычисления рекурсивной функции t(i, k).

Время начала функционирования конвейера полагается равным 0.

В предлагаемой модели интерпретация операций и спусковой функции and

не отличается от таковых в теории расписаний. Остальной набор спусковых

функций выработан практикой, на основе построения моделей и является

двумя парами прямых и обратных функций (mul-red и get-put). Возможно

построение новых функций, расширяющих отношение предшествования.

Рис. 3. Пример графа конвейера (сверху) и соответствующего графа суперпо-

зиции рекурсивных функций (снизу).

3. Примеры моделей

Примеры некоторых моделей конвейеров для различных приложений опи-

саны в [15]. В данной статье приведем дополнительные примеры рекурсивных

конвейеров. Перед тем как привести примеры, отметим, что временная диа-

грамма должна составляться для каждой операции отдельно, это ненаглядно

p = 1

p = px

and

q = pa_i

s = s + q

i = i + 1

s = a₀

i = 0

s = s + q

q = pa_i

s = s + q

q = pa_i

p = px

i = i + 1

s = s + q

q = pa_i

p = px

i = i + 1

q = pa_i

p = px

i = i + 1

p = px

i = i + 1

s = a₀

p = 1

i = 0

Рис. 4. Пример модели вычислительного конвейера и временной диаграммы.

и громоздко, диаграммы будут совмещены в одной. По оси абсцисс будут от-

ложены номера заказов, а по оси ординат время. Некоторые отрезки времени

при таком совмещении в одной диаграмме будут сливаться. Чтобы этого не

происходило, отрезки, имеющие по оси абсцис значение k, будут размещаться

в интервале между делениями k и (k + 1).

Пример 1. На рис. 4 представлена модель конвейера, вычисляющего по-

лином

p=a₀ +a₁x¹ +a₂x² +a₃x³ +a₄x⁴,

и соответствующая временная диаграмма в предположении, что каждая опе-

рация выполняется своим процессором. Времена выполнения всех операций

равны 1.

Пример 2. Прежде чем рассмотреть второй пример, разберем вспомога-

тельный. На рис. 5 представлен пример конвейера и его временной диаграм-

мы. Конвейер состоит из трех операций, функции редуцирования с коэффи-

циентом 2 и функции мультиплицирования с коэффициентом 3. На диаграм-

ме видно, что все операции выполняются с разной кратностью, но процесс

является конвейерным. Чтобы понять, что такой конвейер может иметь ме-

сто на практике, рассмотрим пример конвейерной сборки некоторого изделия,

которое имеет структуру, представленную на рис. 6. Особенность сборки со-

стоит в том, что узел 2 и узел 3 собираются в отдаленном от основной сборки

месте. Поэтому на месте собирается партия из q2 узлов, которая потом пе-

ревозится на склад основного производства. Аналогично узел 3 собирается

в другом отдаленном месте и перевозится партиями по q3 узлов. Требуется

составить расписание: производства узлов, хранения на складе, перевозки и

сборки основного изделия как единого конвейерного процесса. Пример мо-

дели такого процесса приведен на рис. 7. Суть ее в том, что узел 2 по мере

конвейерной сборки накапливается на складе в количестве q2 и потом эта

партия доставляется на место основной сборки. Конвейерность этого про-

цесса позволяет описывать функции редуцирования и мультиплицирования.

Аналогично для узла 3.

4. Постановка задачи

В данном разделе рассматривается рекурсивный конвейер, представлен-

ный в виде ациклического связного графа, для которого необходимо рас-

пределением ресурсов минимизировать время выполнения^k заказов, где^k -

некоторая константа. Данная RCPSP задача сводится к минимизации функ-

ции t(n,k) для заданного^k на конечном множестве ресурсов M. Опишем

формулировку постановки ЗУО для дискретных переменных с конечными

множествами значений.

В теории ЗУО [11] представляет собой четверку (V, D, R, C),

где V = {x₁, . . . , x_n} - множество переменных,

D = {D₁,...,D_n} - множество доменов переменных,

R - множество отношений различной арности над областями D,

C = {C₁,...,C_m} - множество ограничений, связывающих множество

значений переменных из V посредством отношений из R.

Решением ЗУО является нахождение таких значений всех переменных

множества V , которые удовлетворяют всем ограничениям. Решений ЗУО мо-

жет быть одно или несколько.

ЗУО может быть представлена в виде сети ограничений. Было бы есте-

ственно в качестве такой сети взять граф модели конвейера, в котором вер-

шине соответствует некоторая операция. Однако в связи с тем, что операция i

выполняется k раз при наличии k заказов и в каждом случае может использо-

ваться некоторый ресурс m_i, с операцией связано некоторое множество ресур-

сов. Чтобы избежать этой ситуации, сгенерируем из исходного графа модели

для заданного^k развернутый граф, в котором каждой вершине соответствует

пара (номер операции, номер заказа) и сохраняются отношения предшество-

вания. Построение такого графа возможно для любой модели конвейера и не

представляет сложности. Простые примеры таких графов представлены на

рис. 8. Сверху представлен исходный граф модели, а ниже граф для конкрет-

ного значения^k. Вершины графов помечены соответствующими рекурсивны-

ми функциями и ассоциируются с конкретными операциями и заказами. Если

исходный граф имеет n вершин (операций), то новый граф имеет nk вершин.

Легко показать, что развернутый граф так же является ациклическим. Оче-

видно, что в этом случае каждой вершине соответствует один ресурс, если

вершина соответствует операции (тип вершины bop или op). В остальных

случаях, когда вершина соответствует спусковой функции, ресурс не исполь-

зуется. Для отражения этого факта в задаче дополним множество ресурсов

нулевым элементом M = {m₀, m₁, . . . , m_r}.

Перенумеруем вершины развернутого графа некоторым способом. Пусть

I^′ = {1,... ,n^′}, n^′ = nk, - множество новых номеров. Будем считать по умол-

чанию, что i^′ ∈ I^′ обозначает номер вершины нового графа и существуют

отображения ψ : I^′ → I и ϕ : I^′ → K. Если в исходном графе существует пред-

шествование по i, то в развернутом графе существует как предшествование

по i, так и по k. Определим эти две функции. Функция pk : I^′ → I^′ вычис-

ляет предшествующую по k вершину, т.е. если i^′′ = pk(i^′), то ψ(i^′) = ψ(i^′′), а

ϕ(i^′′) = ϕ(i^′) - 1. Функция pi : I^′ → I^′ вычисляет предшествующую по i вер-

шину, т.е. если i^′′ = pi(i^′), то ψ(i^′′) = pred(ψ(i^′)), а ϕ(i^′′) = ϕ(i^′). Далее для

упрощения записи в выражениях будут использоваться обе нумерации: сквоз-

ная со штрихом и двухкоординатная (i, k) без штриха в предположении, что

i^′ → (i,k), i = ψ(i^′) и k = ϕ(i^′).

Перенесем приведенную постановку ЗУО в рассматриваемую область тео-

рии расписаний.

Четверка объектов ЗУО будет определена следующим образом:

1) V = {x₁, . . . x_n′ } - множество дискретных переменных и для каждой из

них определено множество значений.

2) D_i′ = D_i - домен переменной x_i′ , связанный с соответствующей i-й вер-

шиной исходного графа, т.е. i^′ → (i, k). При этом следует иметь в виду, что

для каждой вершины i^′ - спусковой функции соответствующие перемен-

ные x_i′ будут определены на доменах D_i = {m₀}, содержащих один нулевой

ресурс. Данный факт существенно сокращает пространство поиска.

3) R ⊆ (D₁ × D₂ × . . . × D_n′ ).

4) C - множество ограничений, которое делится на несколько групп.

Множество ограничений представляет собой в основном множество рекур-

сивных функций производных от рекурсивных функций операций. Модифи-

кации вызваны переходом к развернутому графу и связанной с этим заме-

ной переменных. Данные функции порождают ограничения, обусловленные

допустимыми расписаниями для каждой операции конвейера при некотором

заданном распределении ресурсов для пар (операция, заказ). Последнее усло-

вие проверяет допустимость расписания с точки зрения того, чтобы ресурс в

некоторый момент времени не использовался двумя операциями.

1-я группа — это множество унарных ограничений, определенных для на-

чальных операций (1 ≤ i ≤ n₀) и построенных на основе функции (2).

⎧

⎪pij,

⎪

если (x_i′ = m_j)&(k = 0);

⎪

⎨

bop(i, k - 1) + p_ij ,

bop(i, k) =

если (x_i′ = xpk(i′₎)&(x_i′ = m_j)&(0 < k ≤^k);

⎪

⎪bop(i, k - 1) - pij + pil,

⎩

если (x_i′ = xpk(i′₎)&(x_i′ = m_l)&(xpk(i′₎ = m_j)&(0 < k ≤^k).

2-я группа — это множество бинарных ограничений, определенных для пары

вершин графа, соединенных дугой и построенных на основе функций (3),

(5)-(8).

⎧

⎪t(pred(i), k) + pij,

⎪

если (type(i) = op)&

⎪

&(x_i′ = m_j)&(k = 0);

⎪

⎪t(pred(i), k) + pij,

⎪

если (type(i) = op)&(t(pred(i), k) ≥ t(i, k - 1)&

⎪

⎨

&(x_i′ = m_j)&(0 < k ≤^k);

op(i, k) =

⎪t(pred(i), k) + pij,

⎪

если (type(i) = op)&(t(pred(i), k) < t(i, k - 1)&

⎪

&(x_i′ = xpk(i′₎)&(x_i′ = m_j )&(0 < k ≤^k);

⎪

t(i, k - 1) + p_ij,

⎪

если (type(i) = op)&(t(pred(i), k) < t(i, k - 1)&

⎪

⎩

&(x_i′ = xpk(i′₎)&(x_i′ = m_j )&(0 < k ≤^k).

mul(i,k) = t(pred(i),⌊k/q_i⌋), если (type(i) = mul)&(0 ≤ k ≤^k);

red(i, k) = t(pred(i), (k + 1)q_i - 1), если (type(i) = red)&(0 ≤ k ≤^k);

get1(i, k) = t(pred(i), 2k),

если (type(i) = get1)&(k mod 2 = 0)&(0 ≤ k ≤^k);

get2(i, k) = t(pred(i), 2k + 1),

если (type(i) = get2)&(k mod 2 = 1)&(0 ≤ k ≤^k).

3-я группа

— это множество ограничений, определенных для тройки вер-

шин графа и построенных в соответствии с функциями (4) и (9).

and(i,k) = max(t(pred1(i),k),t(pred2(i),k)), если (type(i) = and).

⎧

⎪

t(pred1(i), k),

⎪

если (type(i) = put)&(k = 0);

⎪

max(put(i, k - 1), t(pred2(i), k/2)),

⎨

если (type(i) = put)&

put(i,k) =

⎪

&(k mod 2 = 0)&(0 < k ≤^k);

⎪

max(put(i, k - 1), t(pred1(i), (k - 1)/2)),

⎪

если (type(i) = put)

⎩

&(k mod 2 = 1)&(0 < k ≤^k).

4-я группа ограничений относится к ограничениям типа all-different. Она

отображает тот факт, что использование ресурса в каждый момент вре-

мени возможно не более чем одной операцией. Введем следующие обозна-

чения:

τ_i′ = (tbi′ ,tei′ ) обозначает интервал времени от tbi′ до tei′ (tbi′ ≤ tei′), в течение

которого выполняется i-й операцией k-й заказ (i = ψ(i^′), k = ϕ(i^′)) и ис-

пользуется некоторый ресурс m_j . Операция ∩ принимает значение истины,

если временные отрезки пересекаются.

{

true, если (tbi′ < tei′′ ≤ tei′ ) or (tbi′ ≤ tbi′′ < tei′ );

τ_i′ ∩ τ_i′′ =

f alse, otherwise.

В этих определениях глобальное ограничение будет выглядеть следующим

образом:

∀i^′∀i^′′ (1 ≤ i^′,i^′′ ≤ n^′)&(i^′ = i^′′)&(τ_i′ ∩ τ_i′′) ⊢

⊢ ((type(i^′) = bop)&(type(i^′) = op)) ∨

∨(type(i^′′) = bop)&(type(i^′′) = op)) ∨

∨(x_i′ = x_i′′ ).

Cмысл условия в том, что если интервалы двух разных вершин i^′ и i^′′ пере-

секаются, то либо хотя бы одна из них соответствует спусковой функции,

либо они используют разные ресурсы.

Решением ЗУО будет нахождение таких значений переменных x_i′ , при ко-

торых все перечисленные условия будут удовлетворены, и очевидно, что в

данной постановке ЗУО всегда будет иметь некоторое решение. Для любого

допустимого распределения ресурсов можно построить расписание. В ста-

тье требуется оптимальное расписание. Пусть T_opt - время выполнения оп-

тимального расписания. Будем полагать, что решение квазиоптимальное с

точностью до некоторой, наперед заданной величины Δ, если найденное ре-

шение T такое, что T - T_opt ≤ Δ. Вычисление квазиоптимального значения

времени выполнения расписания можно осуществить с помощью следующего

известного алгоритма:

1) Выбрать некоторое множество значений V , равное V₀.

Вычислить значение T_max = t(n^′,k) для V₀.

Положить T_min = 0.

2) Если T_max - T_min ≤ Δ, то задача решена и T_max является решением, а со-

ответствующее данному решению множество V является искомым рас-

пределением ресурсов.

3) Вычислить значение T = T_min + (T_max - T_min)/2.

4) Ввести в ЗУО дополнительное ограничение: t(n^′,k) ≤ T .

5) Если ЗУО с дополнительным условием не будет иметь решение, то по-

ложить T_min = T и перейти к п. 3.

6) Если ЗУО с дополнительным условием будет иметь решение, то поло-

жить T_max = T и перейти к п. 2.

Конец алгоритма.

Найденное значение T_max является квазиминимальным, но квазиопти-

мальность этого значения следует доказать. Суть проблемы состоит в том,

что рекурсивные функции на локальном уровне строят оптимальное расписа-

ние (реализуют жадный алгоритм), и следует доказать, что при фиксирован-

ном распределении ресурсов локальная оптимизация является и глобальной.

Утверждение 1. Для любого допустимого значения V = {x₁,...,x_n′}

рекурсивная функция t(i,k) вычисляет одно из оптимальных значений для

1≤i≤n и 0≤k≤^k.

Доказательство осуществим методом математической индукции.

Для системности изложения напомним формулировку принципа матема-

тической индукции. Некоторое утверждение P (i), зависящее от натурального

параметра i, считается доказанным, если:

1) установлено, что P (1) верно;

2) для любого 1 ≤ i < n^′ из предположения, что P (i) верно, следует, что

P (i + 1) верно.

Применим данный метод к развернутому графу. Из теории графов из-

вестно [17], что ациклический граф является строго частично упорядочен-

ным. Существуют алгоритмы построения для строго частично упорядоченно-

го графа некоторого линейного порядка. Неформально линейный порядок —

это когда все вершины графа расположены в строку и все дуги направлены

слева направо. Пример построения линейного порядка из строго частичного

показан на рис. 9, где а) — это исходный ациклический граф, а б ) — один

из возможных линейных порядков. В данной статье устроит любой такой ал-

горитм с условием, что первые n₀ вершин исходного графа так и останутся

первыми, хотя можно и в другом порядке, а вершина n останется последней.

При вычислении рекурсивной функции в соответствии с линейным порядком

ее аргументы уже будут вычислены.

Метод математической индукции применим следующим образом.

Шаг 1. Исходя из определения рекурсивного конвейера и способа упо-

рядочивания вершин исходного графа очевидно, что все начальные вершины

Рис. 9. Пример линейного порядка графа.

исходного графа являются операциями (не функциями) и являются производ-

ными для начальных вершин развернутого графа. Если в исходном графе n₀

начальных вершин, то и в развернутом графе тоже n₀ начальных вершин и

для каждой начальной вершины i в исходном графе существует вершина (0, i)

в развернутом графе, которой не предшествует никакая другая вершина. Ес-

ли 1 ≤ i ≤ n₀ - некоторая начальная вершина исходного графа, то i^′ такая,

что ψ(i^′) = i и ϕ(i^′) = 0 является начальной вершиной развернутого графа.

Таким образом, для каждой начальной вершины i^′ → (i, k) развернутого

графа справедливы следующие утверждения:

type(i) = bop,

1 ≤ ψ(i^′) ≤ n₀ и ϕ(i^′) = 0, т.е.

(1 ≤ i ≤ n₀)&(k = 0).

В этом случае в соответствии с функцией (1)

t(i, 0) = bop(i, 0) = p_ij, если x_i′ = m_j.

Таким образом, для конкретного значения x_i′ значение t(i, 0) единственно

и, следовательно, оно оптимально. Утверждение верно. Поскольку данное

утверждение верно для любой из n₀ начальных операций, далее эти варианты

рассматривать не будем.

Шаг 2. Допустим, что для вершины любого номера n₀ < i^′ < n^′ утвержде-

ние верно. Докажем, что в этом случае оно верно и для вершины с номером

i′′ = i′ + 1. В соответствии с (1) возможны 8 вариантов.

Рассмотрим варианты 1 и 2, когда

type(i^′′) = bop и

type(i^′′) = op.

Вариант 1. Выполняется начальная операция над ненулевым заказом, т.е.

i′′ → (i, k) и (1 ≤ i ≤ n0)&(k > 0). Если xi′′ = xpk(i′′), то операция i при выпол-

нении k-го и (k - 1)-го заказов использует один ресурс.

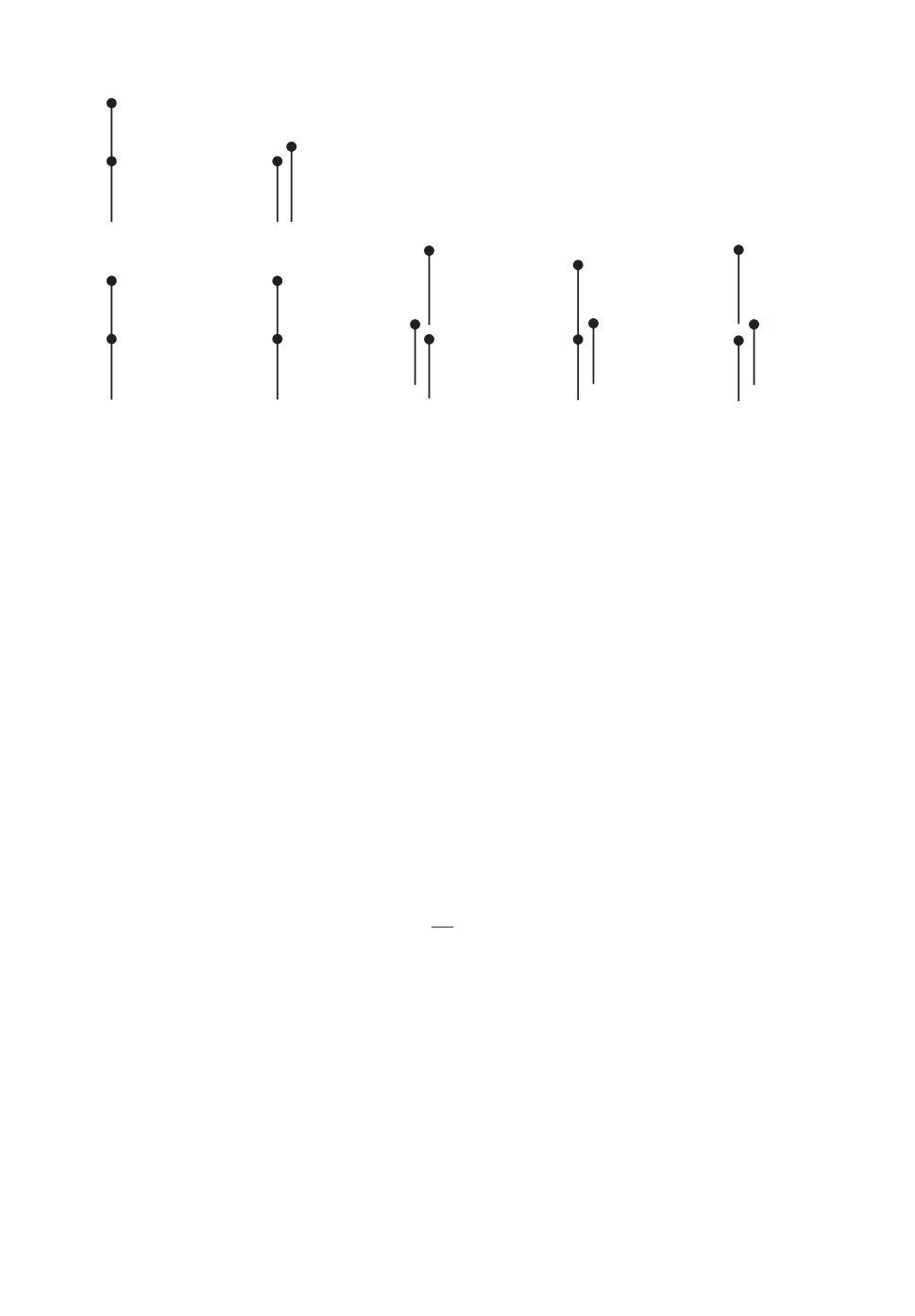
В этом случае время завершения вычисляется по формуле (2,a) (диаграм-

ма на рис. 10,а). Если же используются разные ресурсы, то выполнение опе-

рации i можно осуществить одновременно над заказами (k - 1) и k. Завер-

шение выполнения вычисляется по формуле (2,б) (диаграмма на рис. 10,б ).

Длительности операций могут не совпадать. Учитывая, что время выполне-

i ''

(i, k)

i ''

(i, k

pk(i '')

i ''

(i, 1)

pi(i '')

pk(i '')

(i, 0)

pk(i '')

pi(i '')

Рис. 10. Варианты фрагментов временных диаграмм.

ния операцией i (k - 1)-го заказа оптимально, время выполнения i k-го заказа

также оптимально. Вариант рассмотрен.

Вариант 2. В этом случае выполняется неначальная операция. Если k =

= 0, то время завершения вычисляется по формуле (3,a). Если k > 0, то время

завершения вычисляется по вариантам (3,б)-(3,г). Соответствующие приме-

ры временных диаграмм приведены на рис. 10,c-e. Во всех вариантах новое

расписание с добавлением вершины i^′′ будет оптимальным, если предшест-

вующее расписание было оптимальным.

Варианты 3-8. Во всех данных вариантах вершины соответствуют спус-

ковым функциям. В этом случае не производится распределение ресурсов

и итоговое расписание строится единственным возможным способом исходя

из отношения временного предшествования, определяемого соответствующей

рекурсивной функцией.

Утверждение доказано.

Временная сложность алгоритма равна

)

( (

∏

T₀

O log₂

|D_i |

i=1

где T₀ - значение времени выполнения расписания для некоторого произ-

вольного множества значений V₀, Δ - некоторая наперед заданная константа

точности вычисления результата, а | D_i |= 1 для спусковых функций.

5. Заключение

В данной статье осуществлена теоретическая постановка задачи. Впервые

для исследования конвейерной модели используется такой инструмент, как

Constraint Programming. Применение данного метода на практике является

дальнейшим направлением работы авторов статьи.

В настоящее время существует большое количество коммерческих и сво-

бодного использования систем программирования в ограничениях. Обзор та-

ких систем можно посмотреть в [2].

Изучение вычислительной сложности решения ЗУО представляется фун-

даментальной проблемой. В [18] было показано, что класс всех ЗУО является

NP-трудным, так что вряд ли существуют эффективные (полиномиальные)

алгоритмы общего назначения для решения всех видов ЗУО. Классы легко

разрешимых ЗУО, которые могут быть решены за полиномиальное время,

обычно описываются или деревьями и древовидными графовыми структура-

ми [19, 20], или определенной комбинацией алгебраических операторов [21].

Рассматриваемая в статье задача базируется на дереве ограничений (исход-

ный ациклический граф и расщиренный граф), что внушает оптимизм по по-

воду существования эффективного алгоритма решения поставленной задачи.

Построение расписания для конвейера вычислением суперпозиции рекурсив-

ных функций предполагает для решения ЗУО вариант поиска с возвратами

(backtracking) в различных модификациях [2]. Важно отметить, что введение

в модель конвейера спусковых функций нисколько не увеличивает алгорит-

мическую сложность решения задачи.

Использование данного метода дает два важных преимущества.

Первое. Метод оптимизации рекурсивного конвейера, рассмотренный в

статье [22], сводится к задаче целочисленного линейного программирования и

рассматривает строго определенный набор рекурсивных функций. Введение

новых функций требует дополнительного рассмотрения корректности при-

менения метода. Подход, используемый в данной статье, хотя и рассматри-

вает конкретный набор функций, однако никаких ограничений, кроме вы-

числимости, к ним не предъявляет. Это позволяет вводить в рассмотрение

новые рекурсивные функции без обсуждения вопроса корректности приме-

нения метода.

Второе. Предложенный метод позволяет распределять ресурсы без их за-

крепления за отдельными операциями. Данный подход увеличивает размер-

ность задачи, но открывает возможности для построения более эффективного

расписания.

СПИСОК ЛИТЕРАТУРЫ

1. Лазарев А.А., Гафаров Е.Р. Теория расписаний. Задачи и алгоритмы. М.: Изд-

во МГУ, 2011.

2. Rekiek B., Dolgui A., Delchambre A., Bratcu A. State of art of optimization methods

for assembly line design // Annual Reviews in Control. 2002. V. 26. P. 163-174.

3. Ghosh S., Gagnon R.J. A comprehensive literature review and analysis of the design,

balancing and scheduling of assembly systems // Int. J. Product. Res. 1989. V. 26.

No. 4. P. 637-0670.

4. Helgeson W.B., Salveson M.E., Smith W.W. How to balance an assembly line /

Technical Report, Carr Press. 1954. New Caraan, Conn.

5. Bowman E.H. Assembly line balancing by linear programming // Oper. Res. 1960.

No. 8(3). P. 3850-389.

Salveson M.E. The assembly line balancing problem // J. Indust. Engineer. 1955.

No. 6. P. 18-25.

Neumann K., Schwindt C., Zimmermann J. Recent results on resource-constrained

project scheduling with time windows: Models, solution methods, and applications //

Central Eur. J. Oper. Res. 2002. V. 10. 2. P. 113-148.

Drexl A., Kimms A. Optimization guided lower and upper bounds for the resource

investment problem // J. Oper. Res. Society. 2001. V. 52. No. 3. P. 340-351.

Ranjbar M., Kianfar F., Shadrokh S. Solving the resource availability cost problem in

project scheduling by path relinking and genetic algorithm // Applied Mathematics

and Computation. 2008. V. 196. No. 2. P. 879-888.

10.

Yamashita D.S., Armentano V.A., Laguna M. Robust optimization models for

project scheduling with resource availability cost // Journal of Scheduling. 2007.

V. 10. No. 1. P. 67-76.

11.

Щербина О.А. Удовлетворение ограничений и программирование в ограничени-

ях// Интеллектуальные системы. 2011. Т. 15. № 1-4. С. 53-170.

12.

Apt K.R. Principles of Constraint Programming. New York: Cambridge University

Press, 2003.

13.

Нариньяни А.С., Седреева Г.О., Седреев С.В., Фролов С.А. TimeEX/Windows -

новое поколение недоопределенной технологии календарного планирования /

Проблемы представления и обработки не полностью определенных знаний. Под

ред. И.Е. Швецова. Москва; Новосибирск, 1996. С. 101-116.

14.

Куприянов Б.В. Рекурсивные конвейерные процессы - основные свойства и ха-

рактеристики // Экономика, статистика и информатика. Вестн. УМО. 2015. № 1.

С. 163-170.

15.

Куприянов Б.В. Применение модели конвейерных процессов рекурсивного ти-

па для решения прикладных задач // Экономика, статистика и информатика.

Вестник УМО. 2014. № 5. С. 170-179.

16.

Куприянов Б.В. Метод эффективного анализа модели рекурсивного конвейер-

ного процесса // АиТ. 2017. № 3. С. 63-79.

Kupriyanov B.V. Method of Efficient Analysis of the Recursive Conveyor Process

Models // Autom. Remote Control. 2017. V. 78. No. 3. P. 435-449.

17.

Оре О. Теория графов. М.: Наука, 1980.

18.

Mackworth A.K. Consistency in networks of relations // Artificial Intelligence. 1977.

V. 8. No. 1. P. 99-118.

19.

Dechter R., Pearl J. Tree clustering for constraint networks // Artificial Intelligence.

1989. V. 38. No. 3. P. 353-366.

20.

Freuder E.C. Backtrack-free and backtrack-bounded search / Search in Artificial

Intelligence / L. Kanal, V. Kumar (eds.). Springer-Verlag, 1988. P. 343-369.

21.

Jeavons P.G., Cohen D.A., Gyssens M. Closure properties of constraints // Journal

of ACM. 1997. V. 44. P. 527-548.

22.

Куприянов Б.В. Оценка и оптимизация производительности рекурсивного кон-

вейера // АиТ. 2020. № 5. С. 6-25.

Kupriyanov B.V. Estimation and Optimization of the Efficiency of a Recursive

Conveyor // Autom. Remote Control. 2020. V. 81. P. 775-790.

Статья представлена к публикации членом редколлегии А.А. Галяевым.

Поступила в редакцию 25.01.2021

После доработки 21.06.2021

Принята к публикации 30.06.2021