Автоматика и телемеханика, № 11, 2021
© 2021 г. А.А. САРАТОВ, канд. тех. наук (sapfor58@.gmail.com)
(ООО “Интерактивные системы автоматизации проектирования”, Тула)
ЖАДНЫЙ АЛГОРИТМ РЕШЕНИЯ КЛАССИЧЕСКОЙ NP-ТРУДНОЙ
ЗАДАЧИ ТЕОРИИ РАСПИСАНИЙ МИНИМИЗАЦИИ
СУММАРНОГО ЗАПАЗДЫВАНИЯ
Представлен эффективный метод решения классической NP-трудной
задачи теории расписаний для одного прибора минимизации суммарно-
го запаздывания 1||
∑Tj. Предлагается алгоритм решения задачи, осно-
ванный на декомпозиции исходной задачи на подзадачи своевременного
обслуживания каждого из требований и размещении в конец расписаний
тех из них, прирост запаздывания которых в наибольшей степени компен-
сируется сокращением запаздываний п(ред)шествующих требований. Тру-
доемкость алгоритма не превышает O
n2
операций, где n - количество
требований.
Ключевые слова: теория расписаний, один прибор, минимизация суммар-
ного запаздывания, жадные алгоритмы.
DOI: 10.31857/S0005231021110064
Рассматривается классическая NP-трудная в обычном смысле задача тео-
рии расписания, в которой необходимо обслужить множество требований
N = {1,...,,n} на одном приборе [1]. Прерывания при обслуживании и об-
служивание более одного требования в любой момент времени запрещены.
Для требования j ∈ N заданы продолжительность обслуживания pj > 0 и
директивный срок окончания обслуживания dj. Все требования поступают
на обслуживание одновременно в момент времени t0, с которого прибор го-
тов начать обслуживание этих требований. Расписание обслуживания требо-
ваний строится с момента времени t0 и однозначно задается перестановкой
элементов множества N.
Требуется построить расписание π∗ обслуживания требований множе-
ства N , при котором достигается минимум функции
∑
F (π) =
max {0, cj (π) - dj },
j=1
где cj (π) - момент завершения обслуживания требования j при расписа-
нии π. Пусть π = (j1, . . . , jn), тогда cj1 (π) = t0 + pj1 и cjk (π) = cjk-1 + pjk для
k = 2,3,...,n.
Величина Tj(π) = max {0, cj (π) - dj } называется запаздыванием требова-
ния j при расписании π, a F (π) - суммарным запаздыванием требований
при расписании π. Если обслуживание требования i предшествует обслужи-
ванию требования j, то для этого будем использовать запись (i → j)π. Если
94
обслуживание требования i переносится на более ранний или поздний срок,
то будем называть это смещением влево или вправо.
К настоящему времени опубликовано большое число работ, посвященных
подходам к решению данной задачи [1, 2]. Все предложенные решения не
позволяют получить точное решение задачи за приемлемое для практиче-
ского использования время. Здесь предлагается метод синтеза оптимально-
го расписания, основанный на декомпозиции исходной задачи на подзадачи
своевременного обслуживания каждого из требований и размещении в конец
расписаний тех из них, прирост запаздывания которых в наибольшей степени
компенсируется сокращением запаздываний предшествующих требований.
Поскольку в оптимальном расписании π∗ любое перемещение требования j
и любая парная перестановка требований i, j не могут привести к уменьше-
нию F (π), то для всех i, j ∈ π∗ должно выполняться условие:
⎧
⎧
⎪
∑
⎪
∑
⎪
(π) ≥
(π), j > i
⎪
⎨
∇
j
∇
i
⎨∇Tij (π) ≥
∇Tv(π), pi > pj
i=j+1
v=i+1
(1)
∧
⎪
∑
⎪
∑
⎪
⎪
⎩∇T′′j(π) ≤
∇
(π), j < i
⎩∇Tji(π) ≤
(π), pi < pj,
i
∇
v
i=j-k
v=i+1
где
∇
j
(π)∇T′′j(π) — изменение запаздывания требования j при перемещении j
в очереди на k позиций соответственно вправо и влево;
∑j+k
(π) — суммарное уменьшение запаздывания требований i =
j+1 ∇
i
= {j + 1, . . . , j + k} ∈ N при их перемещении в очереди на k позиций влево;
{
[ (
)]
∑
∑
∑
(2)
∇
i
(π) =
max 0, t0 +
pm - di
-
j+1
j+1
m=0
[ (
)]}
∑
−max 0, t0 +
pm - pj - di
;
m=0
∑j-1
(π)
— суммарное увеличение запаздывания требований i =
j-k∇
i
= {j - k, . . . , j - 1} ∈ N при их перемещении в очереди на k позиций вправо;
{
[ (
)]
∑
∑
∑
(3)
(π) =
max 0, t0 +
pm + pj - di
-
∇
i
j-k
j-k
m=0
[ (
)]}
∑
−max 0, t0 +
pm - di
;
m=0
∇Tij(π) — увеличение запаздывания требования i при замещении j ;
∇Tji(π) — уменьшение запаздывания требования j при замещении i;
95
∑j-1
— суммарное уменьшение запаздывания требований v =
i+1 ∇Tv(π)
= {i + 1, . . . , j - 1} при перестановке требований i, j и pi > pj ;
∑j-1
(π) — суммарное увеличение запаздывания требований v =
i+1 ∇
v
= {i + 1, . . . , j - 1} при перестановке требований i, j и pi < pj .
Множества перемещаемых требований формул (2), (3) будем называть ча-
стичными расписаниями π∧ и π∧∧;
π∧ = {j + 1,... ,j + k} ∈ N, π∧∧ = {j - k,... ,j - 1} ∈ N.
Выражение (1) при k = 1, . . . , n - 1, является эффективным инструментом
(
)
оценки оптимальности построенного расписания, ибо вычисляется за 0
n2
операций.
Для обеспечения эффективного процесса синтеза π∗ на основе фор-
мулы (1) необходим быстрый алгоритм формирования частичных распи-
саний π∧ и π∧∧, эквивалентных по соотношению суммарных смещений
∑i+k
∑i-1
(π) ,
(π) с суммарными смещениями в расписании π∗. Та-
i+1 ∇
i
i-k ∇
i
кая эквивалентность может быть достигнута в частичных расписаниях π∧,
π∧∧, отвечающих (1) при k = 1. Истинность выражения (1) при k = 1 от-
ражает известный факт, что в оптимальном расписании перестановка двух
смежных требований не может уменьшить их суммарного запаздывания и яв-
ляется необходимым условием для проверки оптимальности π∗. Очередность
обслуживания требований j ∈ π∧ определяется соотношениями их парамет-
ров dj , pj, поэтому расписания, отвечающие условию (1) при k = 1, будем
называть локально оптимальными.
Рассмотрим метод построения расписания π∗ начиная от последнего тре-
бования к первому, используя процедуры формирования π∧.
Алгоритм А построения π∧ имеет вид.
1. Принимаем время старта t = t0.
2. Моделируем попарно перестановки требований i → j, j → i и вычис-
ляем сумму∇Tij = Ti(π) + Tj (π). Если при i → j суммарное смещение
меньше, чем при j → i, то i помечается, как приоритетное требование i∗
и продолжает участвовать в перестановках, а j исключается. Если сум-
марные смещения для i → j и j → i равны, то помечается требование с
меньшим dj .
3. Исключаем i∗ из N и помещаем в N∗, добавляя список справа.
4. Принимаем время старта t = t0 + pi.
5. Повторяем шаги 2-4, пока N = ∅.
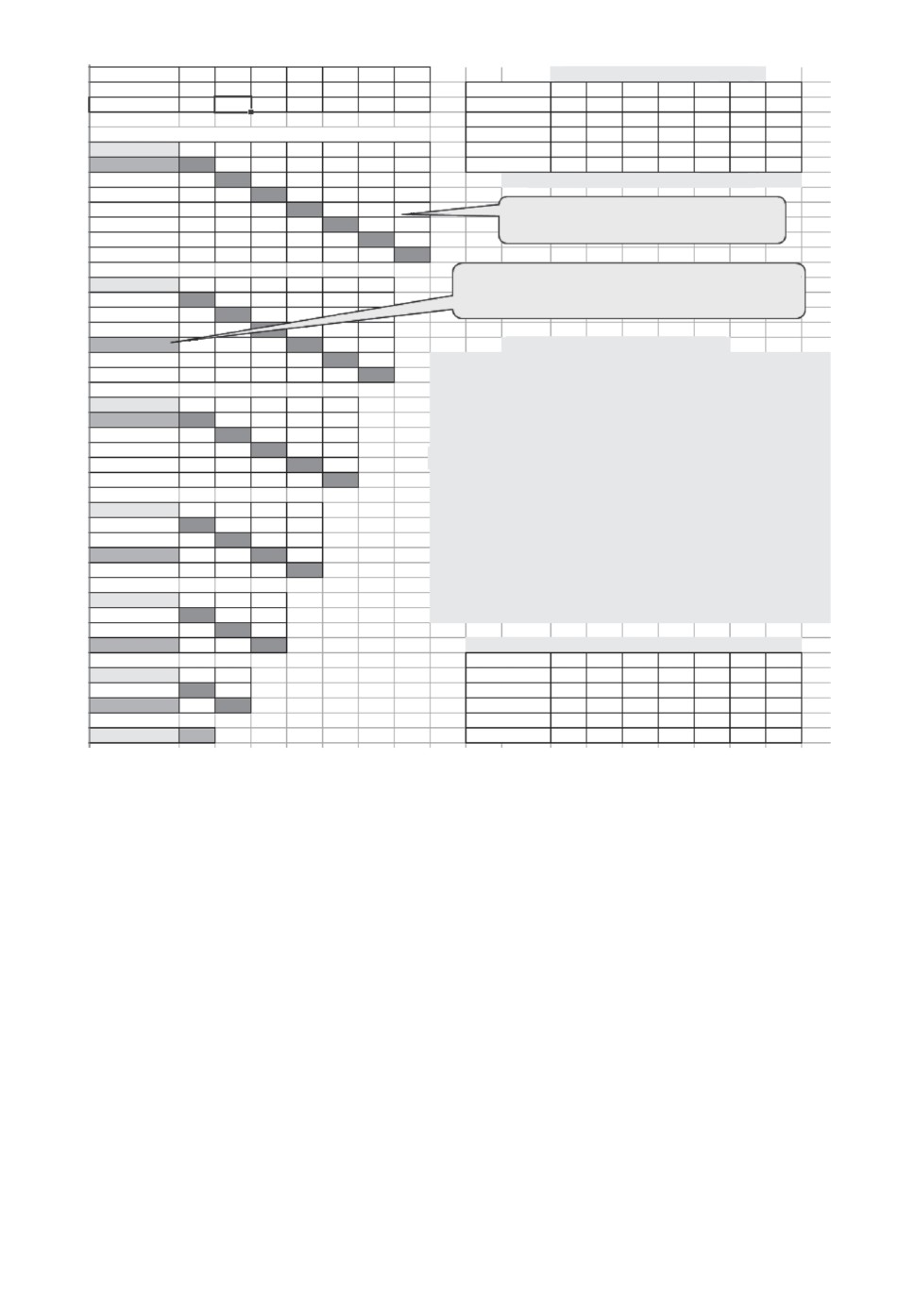
Для канонических DL примеров [1] алгоритм А достаточен для синтеза оп-
тимального расписания. Рассмотрим работу алгоритма А на одном из таких
примеров (рис. 1).
В канонических LG расписаниях [1] первые n/2 - 1 требований не опазды-
вают, и при построении таких расписаний можно использовать соотношения
прироста запаздываний от перемещения требований вправо с уменьшением
суммарных запаздываний требований, перемещаемых влево на освоившиеся
места (2).
96
Работы
D1
D2
D3
D4
D5
D6
D7
Результат полного перебора
Директ. сроки
17,2
17,6
51,4
51,6
18,0
35,7
36,7
Работы
D1
D5
D2
D6
D7
D4
D3
Длительность
17,2
17,1
16,9
16,8
0,9
0,9
0,9
Длительность
17,2
0,9
17,1
0,9
0,9
16,8
16,9
Директ. сроки
17,2
18,0
17,6
35,7
36,7
51,6
51,4
Циклограмма синтеза расписания
Момент старта
0,0
17,2
18,1
35,2
36,1
37,0
53,8
1. T = 0
D1
D2
D3
D4
D5
D6
D7
Момент оконч.
17,2
18,1
35,2
36,1
37,0
53,8
70,7
D1
0,0
17,1
16,9
16,8
0,9
0,9
0,9
Смещение
0,0
0,1
17,6
0,4
0,3
2,2
19,3
D2
16,7
16,4
16,3
0,4
0,4
0,4
Просчитано 5040 вариантов. Результат = 39,9
D3
0
0
0
0
0
0
D4
0
0
0
0
0
0
Матрица смещений требований при
D5
0,1
0
0
0
0
0
попарных перестановках
D6
0
0
0
0
0
0
D7
0
0
0
0
0
0
2. T = 17,2
D2
D3
D4
D5
D6
D7
На каждом шаге выбираем работу, которая имеет
D2
16,9
16,8
0,9
0,9
0,9
нибольший прирост смещения
D3
0
0
0
0
D4
0
0
0
0
0
D5
17,1
16,9
16,8
0,9
0,9
Алгоритм синтеза расписания
D6
0
0
0
0
0
1. Принимаем время старта Т = То.
D7
0
0
0
0
0
2. Моделируем попарно перестановки работ Di Dj и
3. T = 18,1
D2
D3
D4
D6
D7
вычисляем прирост Cij задержки Dj при старте Di в
D2
16,9
16,8
0,9
0,9
момент Т. Результат заносим в матрицу.
D3
0,7
0,4
0
0
3. Выбираем работу Di, которая имеет наибольший
D4
0
0
0
0
D6
0
0
0
0
прирост задержки при перестановке.
D7
0
0
0
0
4. Исключаем Di из списка не распределенных работ D и
помещаем в список распределенных работ D', добавляя
4. T = 35,2
D3
D4
D6
D7
D3
16,8
0,9
0,9
список справа.
D4
16,9
0,9
0,9
5. Принимаем время старта T = T + Ri,
D6
16,9
16,8
0,9
где Ri длительность работы Di
D7
16,3
16,8
0,3
6. Повторяем 2 5, пока в D не останется одна работа Di
5. T = 36,1
D3
D4
D7
7. Помещаем Di в D', добавляя список справа.
D3
16,8
0,9
D4
16,9
0,9
D7
16,9
16,8
Результат расчет
Работы
D1
D5
D2
D6
D7
D4
D3
6. T = 37
D3
D4
Длительность
17,2
0,9
17,1
0,9
0,9
16,8
16,9
D3
16,8
Директ. сроки
17,2
18,0
17,6
35,7
36,7
51,6
51,4
D4
16,9
Момент старта
0
17,2
18,1
35,2
36,1
37,0
53,8
Момент оконч.
17,2
18,1
35,2
36,1
37,0
53,8
70,7
6. T = 53,8
D3
Смещение
0
0,1
17,6
0,4
0,3
2,2
19,3
Рис. 1. Решение канонического DL-примера.
Обозначим как πj расписание, состоящее из π∧ и следующего за ним тре-
бования j , а суммарное запаздывание требований πj — как F (πj).
Если принять условие (1) достаточным для проверки оптимальности π∧,
то в расписании πj = (π∧, j) с минимальным суммарным смещением F (πj)
требование j ∈ πj будет последним в оптимальном расписании π∗. Исходя из
этого, алгоритм построения π∗ имеет вид:
1. Для каждого требования j формируем расписание πj = (π∧, j), в кото-
ром j размещается в конце очереди, а остальные работы упорядочены
согласно алгоритму А. Вычисляем суммарные смещения F (π).
2. Выбираем расписание πj = (π∧, j) с минимальным F (π).
3. Исключаем j из N и помещаем в список последних требований N∗ ∈ π∗,
добавляя список слева.
4. Повторяем шаги 1, 2, 3, пока в N останутся только успевающие работы.
5. Объединяем N и N∗.
6. Конец.
97
1
02
03
05
04
01
7
01
04
05
03
p
20,00
18,10
16,00
18,00
20,10
p
20,10
18,00
16,00
18,10
d
52,25
53,70
54,25
53,75
52,10
d
52,10
53,75
54,25
53,70
t
0
20,00
38,10
54,10
72,10
t
0
20,10
38,10
54,10
t'
20,00
38,10
54,10
72,10
92,20
t'
20,10
38,10
54,10
72,20
T
0
0
0
18,35
40,10
58,45
T
0
0
0
18,50
18,50
2
01
03
05
04
02
8
01
03
05
04
p
20,10
18,10
16,00
18,00
20,00
p
20,10
18,10
16,00
18,00
d
52,10
53,70
54,25
53,75
52,25
d
52,10
53,70
54,25
53,75
t
0
20,10
38,20
54,20
72,20
t
0
20,10
38,20
54,20
t'
20,10
38,20
54,20
72,20
92,20
t'
20,10
38,20
54,20
72,20
T
0
0
0
18,45
39.95
58,40
T
0
0
0
18,45
18,45
3
D1
D2
D5
D4
D3
9
D1
D3
D4
D5
p
20,10
20,00
16,00
18,00
18,10
p
20,10
18,10
18,00
16,00
d
52,10
52,25
54,25
53,75
53,70
d
52,10
53,70
53,75
54,25
t
0,00
20,10
40,10
56,10
74,10
t
0,00
20,10
38,20
56,20
t'
20,10
40,10
56,10
74,10
92,20
t'
20,10
38,20
56,20
72,20
T
0,00
0,00
1,85
20,35
38,50
60,70
T
0,00
0,00
2,45
17,95
20,40
4
D1
D2
D5
D3
D4
10
D3
D5
D1
p
20,10
20,00
16,00
18,10
18,00
p
18,10
16,00
20,10
d
52,10
52,25
54,25
53,70
53,75
d
53,70
54,25
52,10
t
0,00
20,10
40,10
56,10
74,20
t
0,00
18,10
34,10
t'
20,10
40,10
56,10
74,20
92,20
t'
18,10
34,10
54,20
T
0,00
0,00
1,85
20,50
38,45
60,80
T
0,00
0,00
2,10
2,10
5
D1
D2
D4
D3
D4
11
D1
D5
D3
p
20,10
20,00
18,00
18,10
16,00
p
20,10
16,00
18,10
d
52,10
52,25
53,75
53,70
54,25
d
52,10
54,25
53,70
t
0,00
20,10
40,10
58,10
76,20
t
0,00
20,10
36,10
t'
20,10
40,10
58,10
76,20
92,20
t'
20,10
36,10
54,20
T
0,00
0,00
4,35
22,50
37,95
64,80
T
0,00
0,00
0,50
0,50
6
D3
D4
D5
D1
12
D1
D3
D5
p
18,10
18,00
16,00
20,10
p
20,10
18,10
16,00
d
53,70
53,75
54,25
52,10
d
52,10
53,70
54,25
t
0,00
18,10
36,10
52,10
t
0,00
20,10
38,20
t'
18,10
36,10
52,10
72,20
t'
20,10
38,20
54,20
T
0,00
0,00
0,00
20,10
20,10
T
0,00
0,00
0,00
0,00
Итог
D1
D3
D5
D4
D2
p
20,10
18,10
16,00
18,00
20,00
d
52,10
53,70
54,25
53,75
52,25
t
0,00
20,10
38,20
54,20
72,20
t'
20,10
38,20
54,20
72,20
92,20
T
0,00
0,00
0,00
18,45
39,95
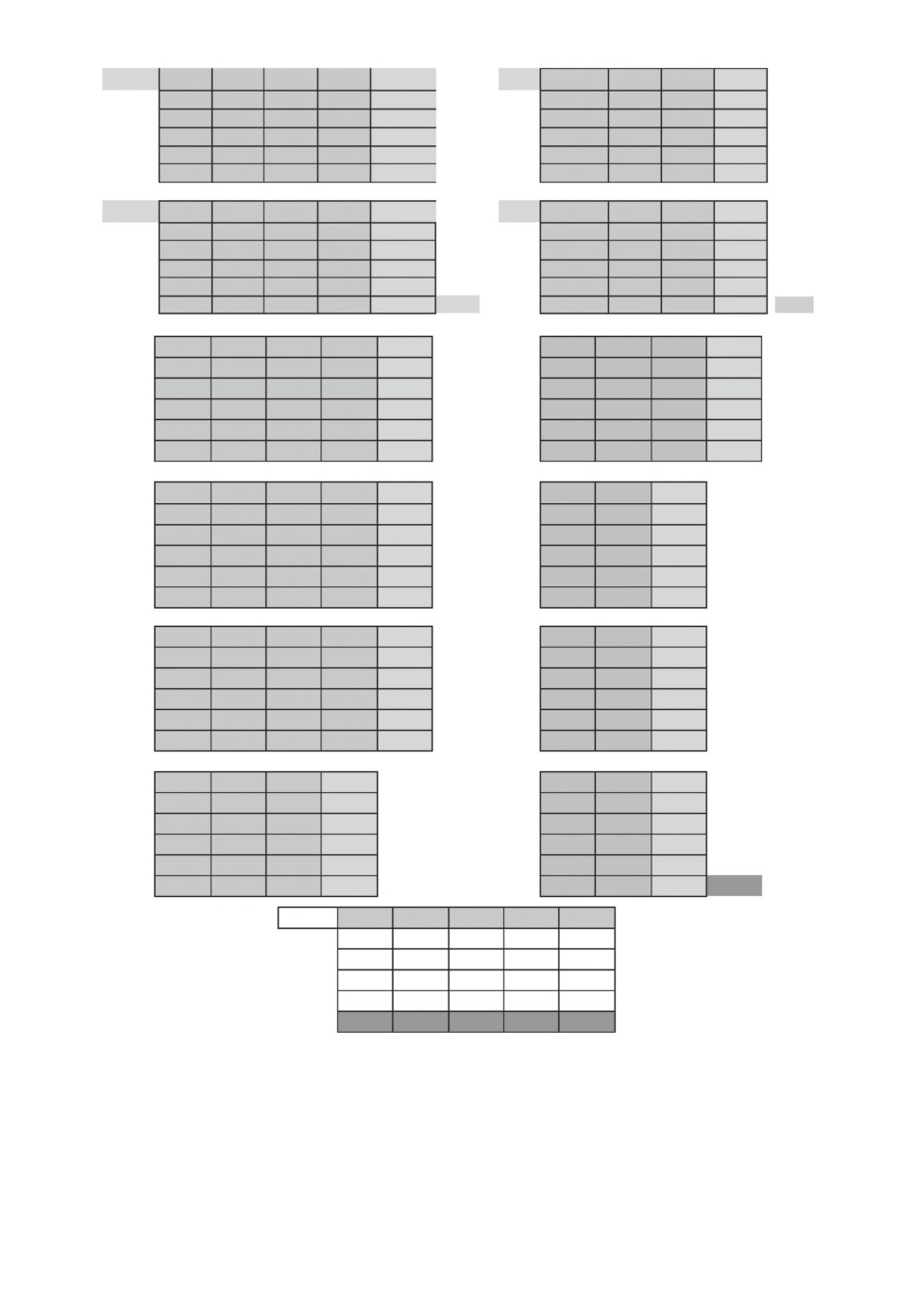
Рис. 2. Синтез оптимального расписания для LG примера.
Рассмотрим пример. Пусть имеется 5 требований N = {D1, D2, D3, D4, D5
}
с параметрами: p1 = 20,1, p2 = 20, p3 = 18,1, p4 = 18, p5 = 16, d1 = 52,1,
d2 = 52,25, d3 = 53,7, d4 = 53,75, d5 = 54,25. Необходимо составить расписа-
ние с минимальным суммарным запаздыванием (Ti) требований. Процедура
синтеза расписания (рис. 2) будет включать 12 шагов:
98
1. Переносим D1 в конец расписания, а остальные требования выстраива-
ем по результатам перестановок i → j, j → i (алгоритм А). Вычисляем
суммарное запаздывание T = T4 + T1 = 18,35 + 40,1 = 58,45.
2. Выполняем п. 1 для D2, . . . , D5 (шаги 2, . . . , 5).
3. Выбираем требование (D2), с наименьшим T = 58,4, и переносим D2
из N в N∗.
4. Выполняем пп. 1-3 для N = {D1, D3, D4, D5} (шаги 6, . . . , 9). Перено-
сим D4 из N в N∗.
5. Выполняем пп. 1-3 для N = {D1, D3, D5} (шаги 10, . . . , 12). Перено-
сим D5 из N в N∗.
6. Оставшиеся требования N = {D1, D3} имеют T = 0. Переносим D1, D3
из N в N∗.
7. Конец.
Полученное расписание N∗ = {D1, D3, D5, D4, D2} имеет минимальное
суммарное запаздывание T = T1 + T3 + T5 + T4 + T2 = 18,45 + 39,95 = 58,4.
Испытания предложенного метода проводились на канонических DL и LG
примерах с количеством требований от 5 до 26. Во всех случаях были полу-
чены оптимальные решения.
СПИСОК ЛИТЕРАТУРЫ
1. Лазарев А.А., Гафаров Е.Р. Теория расписаний. Задачи и алгоритмы. М.: Изд-во
МГУ, 2011, 222 с.
2. Лазарев А.А., Архипов Д.И. Оценка абсолютной погрешности и полиномиаль-
ной разрешимости для классической NP-трудной задачи теории расписаний //
Доклады АН. 2018. Т. 480. № 5. С. 523—527.
3. Саратов А.А. Согласование производственных циклов методом взаимных штра-
фов // Автоматизация процессов управления. 2019. № 1. C. 66-73.
Статья представлена к публикации членом редколлегии А.А. Лазаревым.
Поступила в редакцию 27.01.2021
После доработки 28.05.2021
Принята к публикации 30.06.2021
99