Автоматика и телемеханика, № 12, 2021
Обзоры
© 2021 г. O.В. ЧЕРНОЯРОВ, д-р физ.-мат. наук (o_v_ch@mail.ru)
(Национальный исследовательский университет “МЭИ”, Москва;
Национальный исследовательский Томский государственный университет;
Майкопский государственный технологический университет),
С. ДАШЯН, д-р физ.-мат. наук (serguei.dachian@univ-lille.fr)
(Университет Лилля, Лилль, Франция;
Национальный исследовательский Томский государственный университет),
Ю.А. КУТОЯНЦ, д-р физ.-мат. наук (yury.kutoyants@univ-lemans.fr)
(Университет Ле Мана, Ле Ман, Франция;
Национальный исследовательский Томский государственный университет),
А.В. ЗЮЛЬКОВ, канд. физ.-мат. наук (avzz888@yandex.ru)
(Воронежский государственный университет)
ОБ ОШИБКАХ ОЦЕНИВАНИЯ В ОПТИЧЕСКОЙ СВЯЗИ И ЛОКАЦИИ1
Рассматривается несколько задач оценки параметров по наблюдениям
неоднородных пуассоновских процессов, возникающих в различных прак-
тических приложениях оптической связи и локации. Функция интенсив-
ности наблюдаемого процесса складывается из периодического сигнала,
зависящего от неизвестного параметра и постоянной интенсивности шума.
Описывается асимптотическое поведение оценок максимального правдо-
подобия и байесовских оценок в случаях фазовой и частотной модуля-
ции сигналов. Особое внимание уделяется сигналам разной регулярно-
сти (гладкие, непрерывные, но не дифференциируемые и типа разлад-
ки). Численное моделирование иллюстрирует представленные результа-
ты. Работа является обзором результатов по поведению оценок в случаях
частотной и фазовой модуляций сигналов разной регулярности.
Ключевые слова: оценка параметров, неоднородные процессы Пуассона,
фазовая и частотная модуляции, ОМП и байесовские оценки, асимптоти-
ческие свойства.
DOI: 10.31857/S0005231021120035
1. Введение
Во многих практических задачах, связанных с управлением стохастиче-
скими системами, необходимо анализировать случайные потоки событий, воз-
действующие на систему или являющиеся результатом ее работы. Эти потоки
присутствуют в информационнo-вычислительных сетях, в радиотехнических
системах и системах связи. Такие задачи, как правило, требуют контроля за
1 Исследование выполнено при финансовой поддержке Российского фонда фундамен-
тальных исследований в рамках научного проекта № 20-11-50024.
8
изменением свойств наблюдаемого потока. Причем при изучении подобных
объектов естественные предположения об ординарности и отсутствии после-
действия во многих случаях приводят к наиболее распространенной модели
потока — нестационарному пуассоновскому точечному потоку и к его про-
стейшему варианту — периодически нестационарному пуассоновскому пото-
ку. Подобные потоки (процессы) используются в различных стохастических
системах и при реализации задач управления в качестве моделей:
• в теории телетрафика для описания нагрузки, обладающей естественной
(например суточной) периодичностью;
• для описания входных потоков в цифровых сетях интегрального обслужи-
вания (ISDN) — SPP и ММР-потоки [1, 2];
• для анализа характеристик распределенного мультиагентного управления
в “сложных сетевых системах” [3];
• в задачах приема слабых оптических сигналов [4];
• потоков истинных и ложных целей в задачах управления радиолокаци-
онными наблюдениями (обзор пространства, формирование диаграмм на-
правленности антенн и т.д.);
• при измерении Допплер эффекта в различных прикладных задачах, на-
пример в астрономии (красное смещение) [5], радарах [6], медицине [7],
задачах локализации [8-10].
Выше использованы обозначения: ISDN (Integrated Services Digital Net-
work) — цифровые сети интегрального обслуживания (ЦСИО); SPP (Switched
Poisson Process) — поток, в котором интервалы поступления стационарного
пуассоновского потока одной интенсивности альтернируют с интервалами по-
ступления стационарного пуассоновского потока другой интенсивности; MMP
(Markov modulated Poisson process) — ММР-поток (см. в [2]).
Причем во всех рассматриваемых задачах для адекватного описания
нестационарностей необходимо использовать различные модели, а также в
той или иной мере контролировать изменение свойств наблюдаемого потока.
Имеются две базовые модели случайных процессов с непрерывным време-
нем, которые обычно используются в задачах передачи информации: одна —
это модель наблюдений сигнала в белом гауссовском шуме
(1)
dXt = S (ϑ,t)dt + σdWt, X0
= 0,
0≤t≤T,
где S (ϑ, t) — передаваемый сигнал, несущий информацию ϑ, σ — уровень
шума и Wt — винеровский процесс, производная которого и есть белый шум.
Вторая модель — это неоднородный процесс Пуассона, функция интенсив-
ности которого зависит от неизвестного параметра ϑ (информации). Первая
модель хорошо изучена в статистической радиотехнике, а вторая модель изу-
чена существенно меньше. В этой работе описываются ошибки оценивания
при передачи информации в рамках второй модели.
Рассмотрим задачу передачи информации ϑ с помощью сигнала S (ϑ, t)
через канал Пуассона с шумом интенсивности λ0 > 0 (dark current, т.е.
9
темновой ток). Предположим, что оптический сигнал (неоднородный пуас-
соновский процесс) имеет функцию интенсивности S (ϑ, t), 0 ≤ t ≤ T , где
S (ϑ, t) — периодическая функция времени t. Следовательно, наблюдения
XT = (Xt, 0 ≤ t ≤ T) являются пуассоновским (считающим) процессом с
функцией интенсивности
(2)
λ (ϑ, t) = S (ϑ, t) + λ0
,
0≤t≤T.
Цель — оценить ϑ по наблюдениям XT и описать свойства оценок в асимпто-
тике больших выборок (T → ∞). Это известная модель наблюдений в опти-
ческих системах связи (см., например, [4, 11-13] с соответствующими лите-
ратурными ссылками). Будем рассматривать два типа модуляции (фазовую
и частотную) и три типа регулярности сигналов: гладкий, непрерывный (но
не дифференцируемый) и разрывный. Авторов интересует предел распреде-
ления оценок во всех этих ситуациях. Особое внимание уделяется изучению
среднеквадратических ошибок
2
(3)
Eϑ
ϑT - ϑ2 =σ
(1 + o(1)),
T -→ ∞,
Tm
где
ϑT — некоторая оценка параметра ϑ. Здесь σ2 > 0 — предельная дис-
персия этой оценки, а значение m > 0 (определяющее скорость сходимости)
зависит от регулярности функции S (ϑ, t) относительно ϑ. Для простоты изло-
жения предполагаем, что неизвестный параметр одномерный: ϑ ∈ Θ = (α, β),
где α и β конечны.
В качестве оценок будем использовать оценку максимального правдоподо-
бия (ОМП) и байесовские оценки (БО). Предполагаем, что λ0 > 0 и семейство
функций S (·, t) ≥ 0 равномерно ограничено по ϑ. Тогда меры, соответствую-
щие разным значения ϑ, эквивалентны, и функция отношения правдоподобия
(ОП) (см. [14]) имеет вид
⎧
⎫
∫
T
(
)
∫
T
⎨
⎬
(
)
S (ϑ, t)
L
ϑ,XT
= exp
ln
1+
dXt -
S (ϑ, t) dt
,
ϑ ∈ Θ.
⎩
λ0
⎭
0
0
Оценки вводятся по обычным формулам. В частности, ОМ
ϑT является
решением уравнения
(
)
(
)
(4)
L
ϑT ,XT
= sup L
ϑ,XT
,
ϑ∈Θ
а Б
ϑT для квадратичной функции потерь и априорной плотности p (ϑ),
ϑ ∈ Θ, записывается как отношение двух интегралов
∫
(
)
ϑp (ϑ)L
ϑ,XT
dϑ
(5)
ϑT =∫
p(ϑ)L(ϑ,XT )dϑ
Θ
10
В этой работе всегда предполагаем, что функция p (ϑ), ϑ ∈ Θ, положительна
и непрерывна на Θ.
Функцию ОП и асимптотику T → ∞ иногда удобно записать в немного
другой форме. Предположим, что функция S (ϑ, t) периодическая с периодом
τ > 0. Если T = nτ, где τ не зависит от ϑ и n → ∞, тогда можно разрезать
траекторию Xnτ на n периодов
Xnτ = X(n) = (X1,... ,Xn),
Xj = (Xj (s), 0 ≤ s ≤ τ) ,
где Xj (s) = Xs+(j-1)τ - X(j-1)τ , j = 1, . . . , n, — независимые одинаково рас-
пределенные процессы Пуассона. Функцию ОП в этом случае можно записать
следующим образом:
⎧
⎫
∫
τ
(
)
∫
τ
(
)
⎨∑
⎬
S (ϑ, s)
L ϑ,X(n)
= exp
ln
1+
dXj (s) - n
S (ϑ,s)ds
=
⎩
λ
0
⎭
j=1 0
0
⎧
⎫
(
)
∫
τ
⎨∫τ
⎬
S (ϑ,t)
= exp
ln
1+
dYn (t) - n
S (ϑ, t) dt
=
⎩
λ0
⎭
0
0
= L(ϑ,Y n),
где введен случайный процесс Yn = (Yn (s) , 0 ≤ s ≤ τ), который определя-
ется равенством
∑
Yn (s) =
Xj (s),
0≤s≤τ.
j=1
Пуассоновский процесс Yn (·) имеет функцию интенсивности
(6)
λn (ϑ,t) = nS (ϑ,t) + nλ0
,
0≤t≤τ.
В данной работе рассматриваются два типа модуляции: фазовая и частотная.
В случае фазовой модуляции ϑ ∈ (α, β), 0 < α < β < τ, функция интенсив-
ности (2) неоднородного пуассоновского процесса XT — это
λ (ϑ, t) = S (t - ϑ) + λ0,
0≤t≤T,
где S (t) — τ-периодическая функция. Здесь период τ не зависит от ϑ и сведе-
ние XT к n независимым одинаково распределенным пуассоновским процес-
сам: XT -→ Xnτ , а также к процессу Пуассона большой интенсивности (6):
XT -→ Yn является возможными. Это означает, что модели наблюдений XT ,
Xnτ и Yn эквивалентны.
В случае частотной модуляции функция интенсивности (2) наблюдения
XT — это
λ(ϑ,t) = S (ϑt) + λ0,
0≤t≤T.
11
Если функция S (t) τ-периодическая, то период функции интенсивности
λ (ϑ, t) равенτϑ , т.е. зависит от ϑ, и сведения XT -→ Xnτ и XT -→ Yn
невозможны, потому что значение ϑ неизвестно.
В данной работе описываются свойства ОМП и БО в случаях как фазовой
(S (t - ϑ) , 0 ≤ t ≤ T), так и частотной (S (ϑt), 0 ≤ t ≤ T) модуляций в
ситуациях различных типов регулярности функции S (t).
Задача оценки частоты периодического сигнала занимает специальное ме-
сто в статистической радиотехнике. Частотная модуляция имеет ряд пре-
имуществ при передаче информации. Измерение частоты также важно при
использовании эффекта Допплера в различных моделях наблюдений. Мате-
матически строгое описание свойств ОМП и БО впервые было дано в [15],
где была рассмотрена модель (1) наблюдений “сигнал в белом гауссовском
шуме”.
Здесь не рассматривается случай амплитудной модуляции, скажем,
λ(ϑ,t) = ϑf (t) + λ0,
0≤t≤T,
где f (·) ≥ 0 — τ-периодическая функция. Заметим, что ОМ
ϑT даже в этом
случае не имеет явного выражения и является решением уравнения ОП
∫
T
∫
T
f (t)
dXt -
f (t) dt = 0,
ϑ ∈ Θ.
ϑf (t) + λ
0
0
0
Скорость сходимости и предельное распределение ОМП хорошо известны
(см., например, [16])
∫
τ
(
)
(
)
√
f (t)2
T
ϑT
−ϑ
=⇒ N 0, I (ϑ)-1 , I (ϑ) =1
dt.
τ
ϑf (t) + λ0
0
Чтобы проиллюстрировать регулярность/сингулярность сигнала, введем
функцию
tκ
(7)
S (t) = 2
l{0≤t≤δ} + 21l{δ<t≤τ},
δ
где δ > 0 мало по отношению к τ. Регулярность статистического экспери-
мента полностью определяется значением параметра κ. Заметим, что все эти
типы сингулярностей в случае независимых одинаково распределенных слу-
чайных величин описаны в [17].
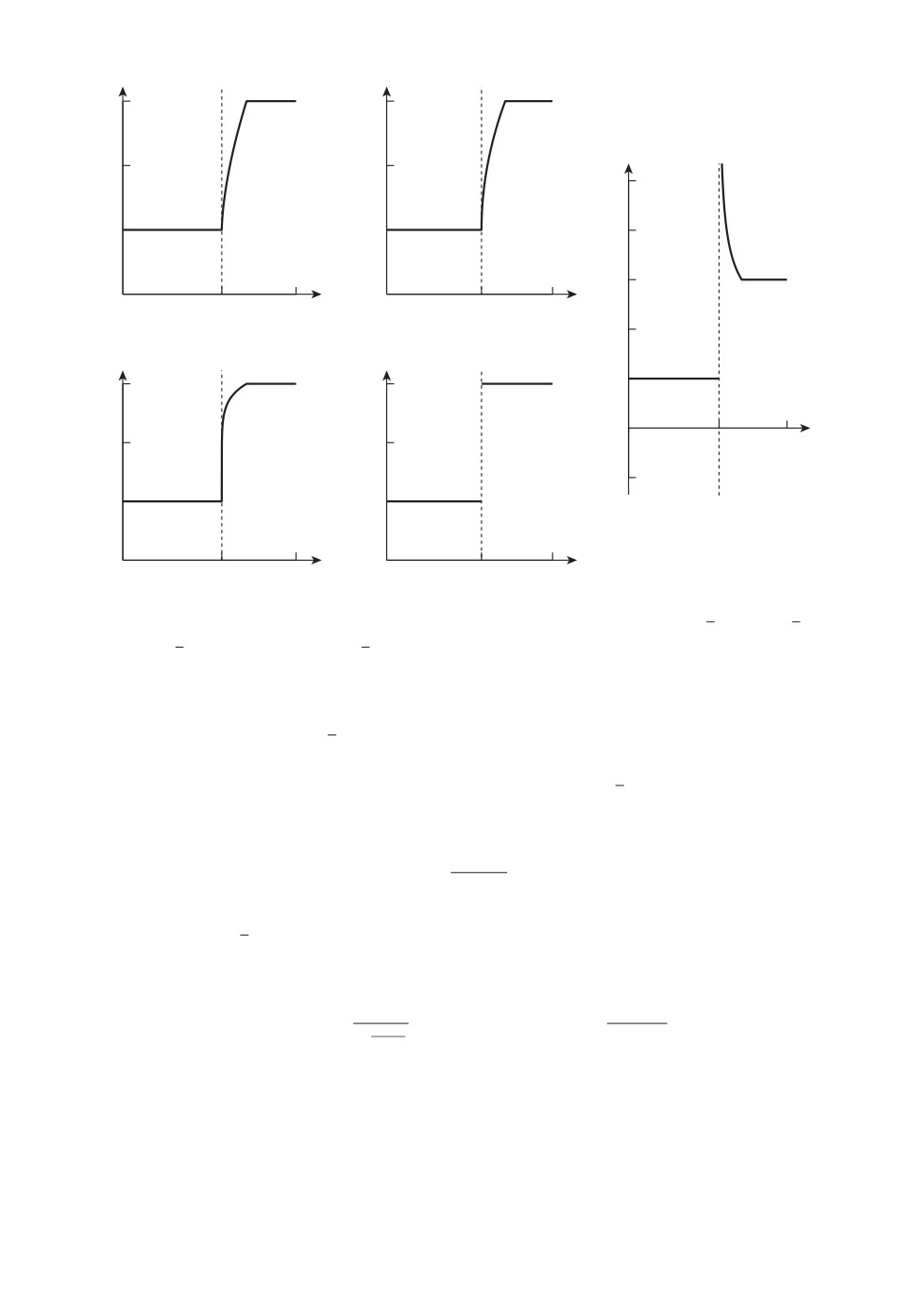
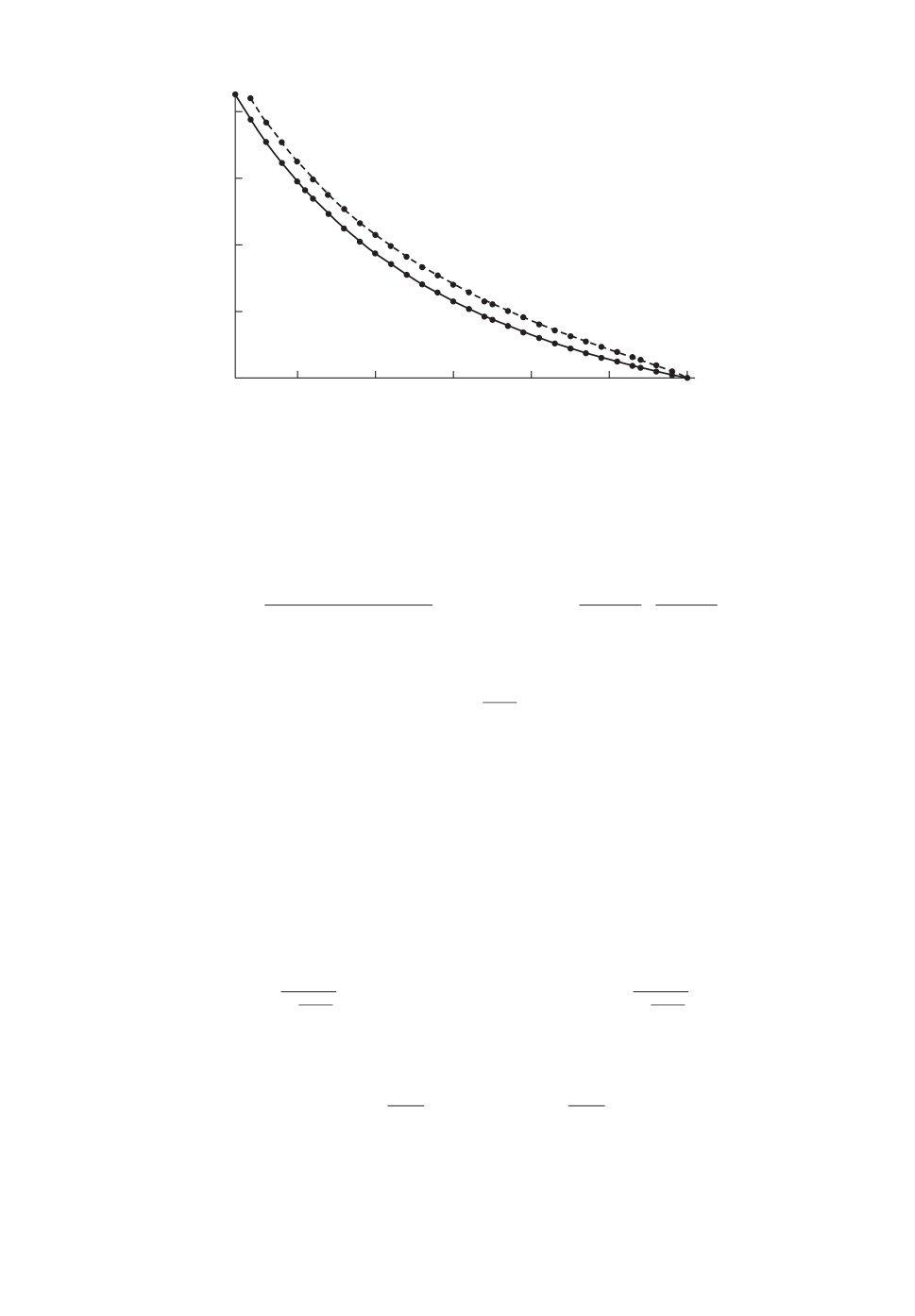
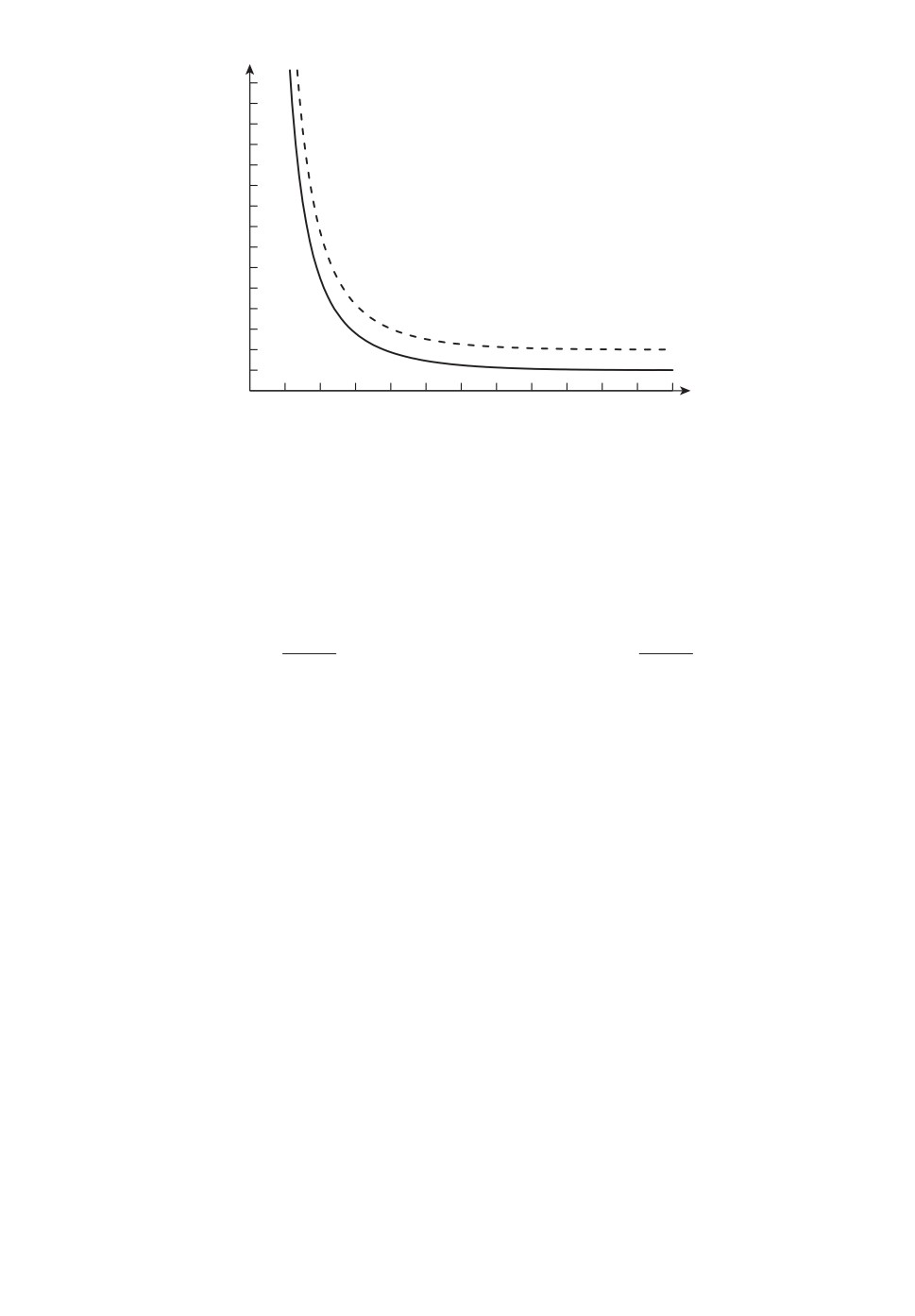
Графики функции
λ(ϑ,t) = S (t - ϑ) + 1,
0≤t≤τ
для различных значений κ показаны на рис. 1.
12
a
б
3
3
д
2
2
5
1
1
4
3
0
0
2
в
г
1
3
3
2
2
0
1
1
1
0
0
Рис. 1. Примеры сигналов с функциями интенсивности (7): a) κ =58 , б ) κ =12 ,
в) κ = 18, г) κ = 0, д) κ = -38.
Кратко опишем зависимость между κ и m в (3). Детали будут даны позже
в этой работе. Если κ >12 (случай а), то имеем регулярную статистическую
задачу оценивания с конечной информацией Фишера, и скоростям сходимо-
сти ОМП и БО в (3) соответствует m = 1. Если κ =12 (случай б ), то снова
имеем регулярный статистический эксперимент и
2
Eϑ
ϑT - ϑ2 =σ
(1 + o(1)).
T ln T
(
)
Если κ ∈
0,12
(случай в), то имеем особенность типа касп (cusp type
singularity), и скорость сходимости этих оценок
2
2
Eϑ
ϑT - ϑ2 =σ
(1 + o (1)) ,
1<
< 2.
2
2κ+1
2κ + 1
T
Таким образом m = 2/(2κ + 1). Заметим, что термин cusp используется в ста-
тистике для описания этого типа сингулярности после работы [18].
Ситуация когда сигнал разрывный (случай г) соответствует известной мо-
дели разладки (change-point). Здесь κ = 0 и функция интенсивности равна
λ (ϑ, t) = 21l{t≥ϑ} + 1,
0≤t≤τ,
13
а скорость сходимости
2
Eϑ
ϑT - ϑ2 =σ
(1 + o(1)) .
T2
Наконец, ситуация когда κ ∈ (-1, 0) (случай д) соответствует сингулярно-
сти типа взрыва (∞-type singularity). Свойства БО для особенностей этого
типа изучались в [19]. Заметим, что скорость сходимости в этом случае
2
Eϑ
ϑT - ϑ2 =σ
(1 + o (1)) .
2
T
κ+1
Так как функция интенсивности не ограничена, то этот тип сингулярности
не обсуждается в данной работе.
Представленное исследование охватывает в основном собственные резуль-
таты авторов, что позволяет ограничить объем рукописи.
Отметим, что многие результаты для моделей пуассоновских процессов,
представленные в этом обзоре, есть прямые аналоги результатов, полученных
для моделей независимых одинаково распределенных случайных величин,
описанных в [17].
2. Методика исследования
Свойства ОМП (4) и БО (5) изучаются с привлечением общих результа-
тов Ибрагимова и Хасьминского [17]. Метод, разработанный этими авторами,
довольно универсален и позволяет изучать ОМП и БО как в регулярном слу-
чае, так и в сингулярных ситуациях. Основная идея этого метода может быть
описана следующим образом. Предположим, что истинное значение равно
ϑ0 ∈ (α,β) и у нас есть функция ϕT → 0 такая, что нормализованная функ-
ция отношения правдоподобия
(
)
)
T
L
ϑ0 + ϕT u,X
(α-ϑ0
β-ϑ0
ZT (u) =
,
u∈UT =
,
L (ϑ0, XT )
ϕT
ϕT
сходится к некоторому невырожденному случайному процессу Z (u), u ∈ R.
Обратите внимание, что UT ↗ R. Асимптотические распределения нормиро-
ванных разностей
)
)
(ˆϑ
(˜
T - ϑ0
ϑT - ϑ0
Pϑ0
<x
и
Pϑ0
<x
ϕT
ϕT
можно получить из этой сходимости, используя следующие соотношения.
14
Для ОМП имеем
(
(
)
)
Pϑ0
ϕ-1T
ϑT - ϑ0
<x
=
{
}
(
)
(
)
T
=Pϑ0
sup
L
ϑ,XT
> sup L
ϑ,X
=
ϕ-1T(ϑ-ϑ0)<x
ϕ-1T(ϑ-ϑ0)≥x
{
(
)
(
)
}
L
ϑ,XT
L
ϑ,XT
=Pϑ0
sup
> sup
=
)
L (ϑ0, XT )
ϕ-1T(ϑ-ϑ0)<x L(ϑ0,XT
ϕ-1T(ϑ-ϑ0)≥x
(8)
{
(
)
(
)}
L
ϑ0 + ϕT u,XT
L
ϑ0 + ϕT u,XT
=Pϑ0
sup
> sup
=
u<x
L (ϑ0, XT )
u≥x
L (ϑ0, XT )
{
}
=Pϑ0
sup
ZT (u) > sup ZT (u)
-→
u<x,u∈UT
u≥x,u∈UT
{
}
(
)
-→ Pϑ0
supZ (u) > supZ (u)
=Pϑ0
ζ <x
,
u<x
u≥x
где сделана замена переменной ϑ = ϑ0 + ϕT u и обозначено чере
ζ решение
уравнения
(9)
Z
ζ) = sup
Z(u).
u∈R
Следовательно, для ОМ
ϑT получена сходимость
)
(ˆ
(
)
ϑT - ϑ0
(10)
Pϑ0
<x
-→ Pϑ0
ζ <x
ϕT
Для БО имеем (с той же заменой θu = ϑ0 + ϕT u):
∫
(
)
∫
(
)
θp (θ)L
θ,XT
dθ
up (θu) L
θu,XT
du
UT
ϑT =∫
=ϑ0 +ϕT
∫
=
p (θ) L (θ, XT ) dθ
p(θu) L(θu,XT )du
Θ
UT
∫
∫
up (θu)L(θu,XT )
du
up (θu) ZT (u) du
L(θ0,XT )
UT
=ϑ0 +ϕT∫T
=ϑ0 +ϕT
∫
p (θu) ZT (u) du
p (θu) L(θu,XT )
du
UT
UT
L(θ0,XT )
Следовательно,
∫
∫
ϑ
up (θu) ZT (u) du
uZ (u) du
T - ϑ0
(11)
= ∫UT
∫
= ζ,
ϕT
p (θu) ZT
(u) du
Z (u) du
UT
R
и для БО получена сходимость
)
(˜
(
)
ϑT - ϑ0
(12)
Pϑ0
<x
-→ Pϑ0
ζ <x
ϕT
15
Видим, что предельные распределения ОМП и БО задаются случайными
величинам
ζ
ζ, определяемыми соотношениями (9) и (11).
Отметим, что различным типам модуляции (фазовая, частотная) и регу-
лярности/сингулярности соответствуют различные скорости ϕT и различные
ζ
ζ.
Покажем, как этот подход работает в простейшем гладком случае и при
фазовой модуляции, т.е. λ (ϑ, t) = S (t - ϑ) + λ0, где сигнал S (·) дважды
непрерывно дифференцируемый, τ-периодический и λ0 > 0. Используя фор-
мулу Тейлора и полагая ϕT = T-1/2, можно написать (ниже T = nτ, Xj (s) =
=Xs+τ(j-1) -Xτ(j-1),j =1,...,n,и ϑu =ϑ0
√
)
T
u
L(ϑ0 +
√
,XT)
T
ln ZT (u) =
=
L(ϑ0,XT )
∫T
(
)
∫
T
S (t - ϑu)
=
ln
1+
dXt - (S (t - ϑu) - S (t - ϑ0)) dt =
λ(ϑ0,s)
0
0
∫
τ
(
)
∑
S (s - ϑu)
=
ln
1+
[dXj (s) - λ (ϑ0, s) ds] -
S (s - ϑ0) + λ0
j=1 0
∫τ
(
(
))
S (s - ϑu)
-n
S (s - ϑu) - S (s - ϑ0) - λ (ϑ0, s) ln
1+
ds =
λ (ϑ0, s)
0
∫τ
∫
τ
∑
u
S (s - ϑ0)
u2
S (s - ϑ0)2
=-
dπj (s) -
ds + o(1) =
√nτ
λ (ϑ0, s)
2τ
λ(ϑ0,s)
j=1 0
0
2
(
)
u
= uΔT
ϑ0,XT
-
I (ϑ0) + o (1) .
2
Здесь точка означает дифференцирование по θ, использованы разложения
(
)
Тейлора ln (1 + εf (s)) = εf (s) + O
ε2
(
)
и ln (1 + εf (s)) = εf (s) -ε22f(s)2 +
+O
ε3
, обозначено dπj (s) = dXj (s) - λ (ϑ0, s) ds и положено
∫
τ
(
)
∑
1
S (t - ϑ0)
ΔT
ϑ0,XT
=-
dπj (t) ,
√nτ
S (t - ϑ0) + λ0
j=1 0
τ
∫
1
S (t)2
I (ϑ0) =
dt.
τ
S (t) + λ0
0
По центральной предельной теореме
∫
τ
(
)
1
S (s)
ΔT
ϑ0,XT
=⇒ Δ (ϑ0) =
√
dWs ∼ N (0,I(ϑ0)) .
√τ
S (s) + λ0
0
16
Здесь Ws, 0 ≤ s ≤ τ, — это стандартный винеровский процесс. Конечно, ин-
формация Фишера I (ϑ0) не зависит от ϑ0, но сохраним это обозначение, по-
тому что в общем случае эта зависимость имеется.
Следовательно
{
}
(
)
u2
ZT (u) = exp uΔT
ϑ0,XT
-
I(ϑ0) + o(1)
=⇒
2
(13)
{
}
u2
=⇒ Z (u) = exp uΔ (ϑ0) -
I (ϑ0)
2
Семейства мер, соответствующие наблюдениям с отношениями правдопо-
добия, удовлетворяющими (13), называются локально асимптотически нор-
мальными (ЛАН), а соответствующие статистические эксперименты счита-
ются регулярными.
Случайную величин
ζ получаем следующим образом:
(
)
∂ ln Z (u)
Δ(ϑ0)
=Δ(ϑ0)
ζI(ϑ0) = 0,
ζ =
∼ N 0,I(ϑ0)-1
∂u
I (ϑ0)
u=ζ
Отсюда согласно (10) получаем асимптотическую нормальность ОМП:
√
(
)
(
)
T
ϑT - ϑ0
=
ζ ∼N
0, I (ϑ0)-1
Для предел
ζ БО имеем представление (11) с данным процессом Z (·).
Можем написать (ниже Δ = Δ (ϑ0), I = I (ϑ0) иΔ = I-1Δ)
2
]
]2
u
I [
Δ2
I [
Δ2
ln Z (u) = uΔ -
I=-
u2 - 2uΔ +Δ2 +
=-
u-Δ
+
2
2
2I
2
2I
Следовательно,
∫
∫
2
I
uZ (u) du = eΔ
2I
ue- 2
[u-Δ]2 du =
R
R
∫
(
)
∫
2
=e
2I
u - Δ e-2[u-Δ]2du + Δe2I
e-2 [u-Δ]2 du =
R
R
∫
= Δ Z (u)du,
R
потому что
∫
ve-2v2dv = 0.
R
17
Таким образом, получаем
∫
(
)
uZ (u) du
ζ =∫R
= Δ=Δ(ϑ0)
∼ N 0,I(ϑ0)-1 ,
Z (u) du
I (ϑ0)
R
и в соответствии с (12)
√
(
)
(
)
T
ϑT - ϑ0
=⇒ N 0, I (ϑ0)-1
Представленные выше вычисления не являются доказательством асимптоти-
ческой нормальности и приведены для объяснения общего метода в регуляр-
ном случае. Настоящие доказательства включают в себя множество техниче-
ских деталей, которые здесь не обсуждаются (см. [16, 17]).
В нерегулярных случаях (случаи сингулярности типа касп и разладки)
нормировки ϕT и предельные процессы Z (·) разные, но соотношения (8)-(12)
всегда действительны и позволяют описывать предельное поведение ОМП и
БО и в этих случаях тоже.
Предельное отношение правдоподобия Z (·) в этих трех случаях (гладкий,
касп и разладка) имеет существенно разные аналитические свойства. Чтобы
проиллюстрировать возможные численные трудности в расчете ОМП, вклю-
чим в эту работу графики реализаций Z (·).
Во всех рассматриваемых ниже задачах нас интересует построение асимп-
тотически эффективных оценок.
В отличие от регулярного случая в сингулярных моделях нет нижней гра-
ницы Крамера-Рао для определения асимптотически эффективных оценок.
Будем использовать минимаксный подход, чтобы ввести нижние границы на
среднеквадратические ошибки всех оцено
ϑT , а затем определим асимпто-
тически эффективные оценки как оценки, которые достигают эти границы.
Нижняя граница имеет вид
(14)
lim lim sup ϕ-2TEϑ
ϑT - ϑ|2 ≥ Eϑ0
ζ|2.
ν→0T→∞ |ϑ-ϑ0|<ν
Назовем оценку ϑ∗T асимптотически эффективной, если для нее в этом
неравенстве имеет место равенство для всех ϑ0 ∈ Θ, а точнее, если имеем
(15)
lim
lim sup ϕ-2TEϑ|ϑ∗T - ϑ|2 = Eϑ0
ζ|2
ν→0
T→∞ |ϑ-ϑ0|<ν
для всех ϑ0 ∈ Θ.
Нижнюю оценку (14) можно получить следующим образом. Предполо-
жим, что уже доказаны сходимость (12) и сходимость моментов
ϕ-2TEϑ
ϑT - ϑ|2 -→ Eϑ
ζ|2,
18
где D (ϑ) = Eϑ
ζ|2 — непрерывная функция от ϑ ∈ Θ. Зафиксировав некото-
рые ϑ0 ∈ Θ и ν > 0, можно написать
∫
sup ϕ-2TEϑ
ϑT - ϑ|2 ≥ ϕ-2T
Eϑ
ϑT - ϑ|2pν (ϑ)dϑ ≥
|ϑ-ϑ0|<ν
ϑ0-ν
∫
≥ϕ-2T
Eϑ
ϑp,T - ϑ|2pν (ϑ) dϑ -→
ϑ0-ν
∫
-→ Eϑ
ζ|2pν (ϑ)dϑ
ϑ0-ν
при T → ∞. Здесь введена положительная непрерывная плотность pν (ϑ),
ϑ∈Θν, где Θν =(ϑ0 -ν,ϑ0 +ν), и обозначена чере
ϑp,T БО, соответствую-
щая этой плотности. Используя непрерывность функции Dν (ϑ) = Eϑ
ζ|2, по-
лучаем последний предел (при ν → 0):
∫
∫
Eϑ
ζ|2pν (ϑ)dϑ =
Dν (ϑ) pν (ϑ)dϑ -→ Eϑ0
ζ|2.
ϑ0-ν
ϑ0-ν
Напомним, что в гладком случае получаем известную нижнюю границу
Гаека-Ле Кама [20]
lim lim sup ϕ-2TEϑ
ϑT - ϑ|2 ≥ I(ϑ0)-1 .
ν→0T→∞ |ϑ-ϑ0|<ν
Более общие результаты и подробное доказательство см. в [17].
3. Фазовая модуляция
Рассмотрим задачу оценки ϑ по наблюдениям XT пуассоновского процесса
функции интенсивности
λ (ϑ, t) = S (t - ϑ) + λ0,
0 ≤ t ≤ T = nτ,
где S (t) — τ-периодическая функция, а интенсивность шума λ0 > 0.
3.1. Гладкий случай
Предположим, что функция S (·) ≥ 0 двукратно непрерывно дифферен-
цируема и тождественно не равна нулю. Напомним, что информация Фише-
ра I (ϑ) для этой модели наблюдений имеет вид [21]
τ
∫
1
S (t)2
I(ϑ) =
dt.
τ
S (t) + λ0
0
19
Тогда имеет место нижняя оценка Гаека-Ле Кама на среднеквадратиче-
ские ошибки всех оцено
ϑT :
lim lim sup T Eϑ
ϑT - ϑ|2 ≥ I(ϑ0)-1 .
ν→0T→∞ |ϑ-ϑ0|<ν
Назовем оценку ϑ∗T асимптотически эффективной, если для нее в этом нера-
венстве имеет место равенство для всех ϑ0 ∈ Θ.
Предложение 1. ОМ
ϑT и Б
ϑT равномерно на компактах K ⊂ Θ
состоятельны, асимптотически нормальны:
√
(
)
(
)
√
(
)
T
ϑT - ϑ0
=
ζ ∼N
0, I (ϑ0)-1 ,
T
ϑT - ϑ0
=
ζ,
имеем сходимость моментов: для всех p > 0
p
p
T
2Eϑ0
ϑT - ϑ0|p -→ Eϑ0
ζ|p,
T
2Eϑ0
ϑT - ϑ0|p -→ Eϑ0
ζ|p,
и обе оценки асимптотически эффективны.
Доказательство см. в [16, 22].
Пример 1. Предположим, что S (t - ϑ) = a2 [1 + cos(t - ϑ)], где a > 0.
Функция S (·) периодична с периодом τ = 2π и T = 2πn. Информация Фи-
шера имеет вид (см. [21])
[
√
]
a
λ0
I (ϑ0) =
1 + 2q - 2
q+q2 ,
q=
2
2
Пример 2. Предположим, что S (t - ϑ) = bexp[acos(t - ϑ)], где a,b > 0.
Функция S (·) периодична с периодом τ = 2π и T = 2πn. Информация Фи-
шера имеет вид (см. [21])
I (ϑ0) = ab I′0 (a),
где I′0 (a) — производная модифицированной функции Бесселя
2π
∫
1
I0 (a) =
eacosydy.
2π
0
В случае многомерного параметра аналогичный результат получен в [21,
23].
Пример 3. Отметим, что существование двух непрерывных ограничен-
ных на [0, τ] производных — это достаточное условие. Можно показать, что
есть регулярные модели с неограниченной первой производной. Если
λ (ϑ, t) = a |t - ϑ|κ + λ0,
0≤t≤τ,
где a > 0 и κ > 1/2, то имеем регулярный (гладки √ случай с конечной ин-
формацией Фишера и скорость сходимости оценок
T (случай а на рис. 1).
Интересно отметить, что если κ = 1/2 (случай б на рис. 1), то имеем регу-
лярный эксперимент (семейство ЛАН с представлением (13)), но ОМП и БО
асимптотически нормальны со скоростью ϕT = (T ln T )-1/2.
Для модели (1) аналогичный результат получен в [15].
20
3.2. Случай сингулярности типа касп
Предположим, что функция интенсивности наблюдаемого процесса имеет
вид
λ (ϑ, t) = S (t - ϑ) + λ0,
0≤t≤T,
где сигнал S (t - ϑ) является τ-периодическим и может быть записан на пер-
вом периоде как S (t - ϑ) = ψ (t - ϑ) g (t - ϑ), где t ∈ [0, τ], а функция пере-
хода ψ(·) задается формулой
(
)
κ
1
y
(16)
ψ (y) =
1 + sgn(y)
l{|y|≤δ} +
1l{y>δ}.
2
δ
Здесь κ ∈ (0, 1/2) и постоянная δ > 0 известны, а функция g (·) непрерывно
дифференцируема. Кроме того, предполагаем, что g(y) > 0 для y ∈ (-δ, τ∗)
и g(y) = 0 для y ≥ τ∗, где δ < τ∗ < τ - δ, и что множество Θ = (α,β) с
δ<α<β <τ-τ∗.
Заметим, что S (t - ϑ) = 0 для t ∈ [0, ϑ - δ] и что S (t - ϑ) = g (t - ϑ) для
t ≥ ϑ + δ и, следовательно, в частности, S (t - ϑ) = 0 для t ∈ [ϑ + τ∗,τ]. Сле-
довательно, сигнал может быть периодически продолжен на интервал [0, T ],
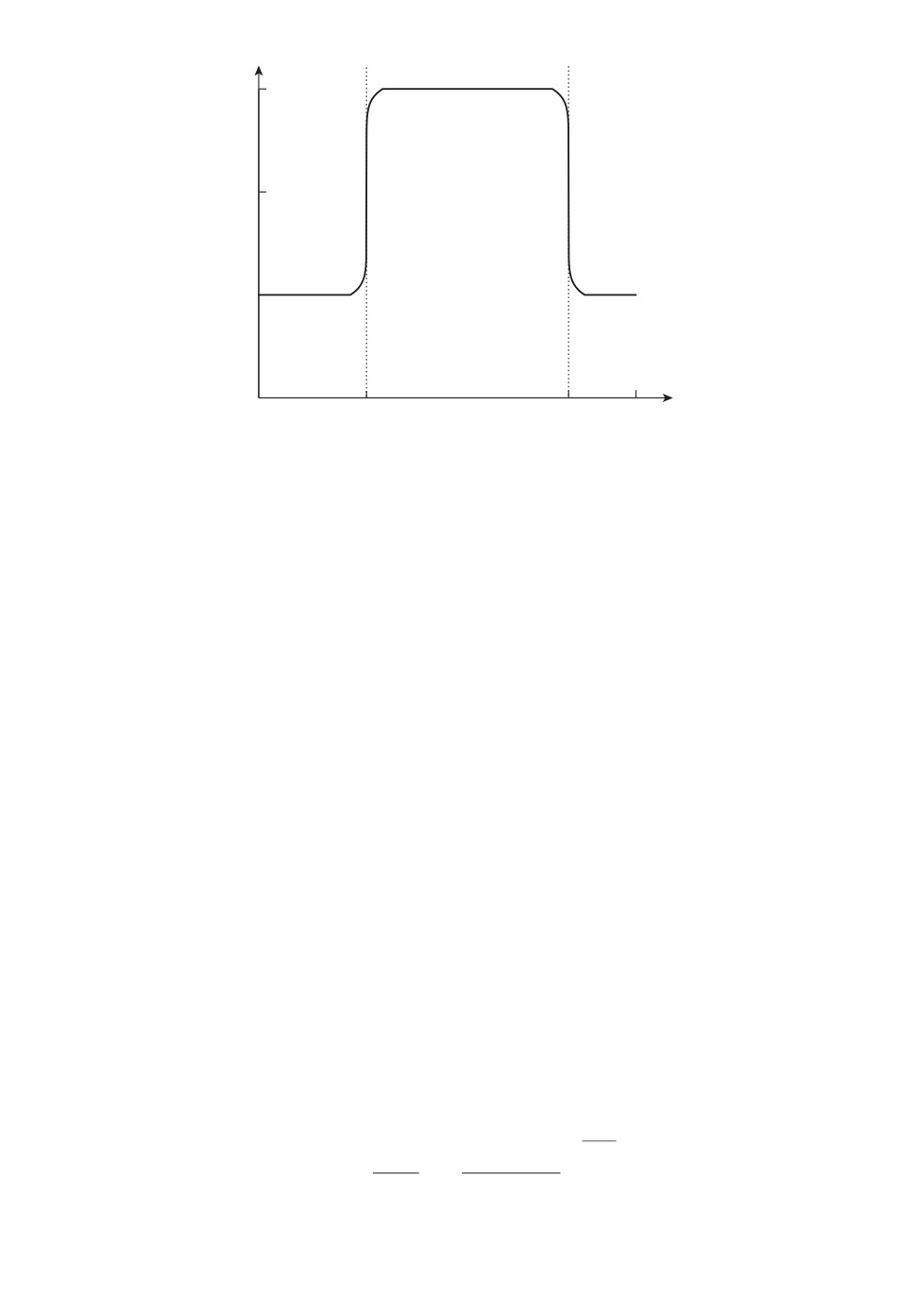
и функция ψ (·) описывает фронт сигнала. График такой функции интенсив-
ности λ (ϑ, t) приведен на рис. 2.
Поскольку κ ∈ (0, 1/2), информация Фишера I (ϑ0) = ∞, и, следовательно,
имеем сингулярный статистический эксперимент.
Кратко объясним, почему рассматриваем сигналы с сингулярностью ти-
па касп как альтернативу хорошо известным сигналам разрывного типа.
Функция интенсивности неоднородного пуассоновского процесса (сигнала)
S (t) в передатчике (источнике сигнала) соответствует вариации электри-
ческого тока. В начале излучения по законам физики ток не может иметь
3
2
1
0
Рис. 2. Пример функции интенсивности с сигналом типа касп.
21
скачка, и фронт сигнала скорее должен быть описан сильно возрастающей,
но непрерывной функцией. В зависимости от параметров электрической це-
пи это увеличение можно рассматривать как имеющее конечную (медлен-
ное увеличение) или бесконечную (быстрое увеличение) информацию Фи-
шера. По нашему мнению, модель с непрерывным сигналом, но бесконеч-
ной информацией Фишера лучше подходит для описания так называемой
“модели разладки”.
Исследование оценок для моделей наблюдений независимых одинаково
распределенных случайных величин с плотностью, имеющей сингулярность
типа касп, началось с работы [18]. Отметим, что исчерпывающее описание
свойств оценок параметров плотностей, имеющих широкий класс сингуляр-
ностей, включающих и сингулярности типа касп, приведено в [17]. Затем ис-
следовались модели нелинейной регрессии [24-27]. Непараметрическое оцени-
вание в модели регрессии изучалось в [28]. Для моделей наблюдений с непре-
рывным временем и сингулярностями типа касп свойства оценок изучались
в следующих работах: неоднородные процессы Пуассона [29], эргодические
диффузионные процессы [30, 31], диффузионные процессы с малой диффу-
зией [32], детерминированный сигнал в белом гауссовском шуме [33]. Модели
с касп сингулярностями использованы в [10, 34] в задачах локализации ис-
точников на плоскости.
Введем следующие обозначения.
1) WH (u), u ∈ R, — стандартное дробное броуновское движение (fBm) с
параметром Херста H = κ + 1/2 ∈ (0, 1), т.е. гауссовский процесс с ну-
левым средним и ковариационной функцией
[
]
1
EWH (u1) WH (u2) =
|u1|2H + |u2|2H - |u1 - u2|2H
2
2) Z (·) — случайный процесс
{
}
2κ+1
(17)
Z (u) = exp Wκ+2 (u) - |u|
,
u ∈ R.
2
3)
ζ
ζκ и
ζ
ζκ — случайные величины, определяемые соотношения-
ми (9) и (11) соответственно с Z (·), см. (17).
4) Интеграл
∫
[
]2
(18)
Q(κ) =
sgn (v - 1) |v - 1|κ - sgn (v) |v|κ
dv
R
и постоянная
(
) 1
g2(0)Q(κ)
2κ+1
γκ,τ =
2τ(g(0) + 2λ0)
22
2,0
2
0
1,5
2
4
1,0
6
8
0,5
10
0
12
10
5
0
5
10
10
5
0
5
10
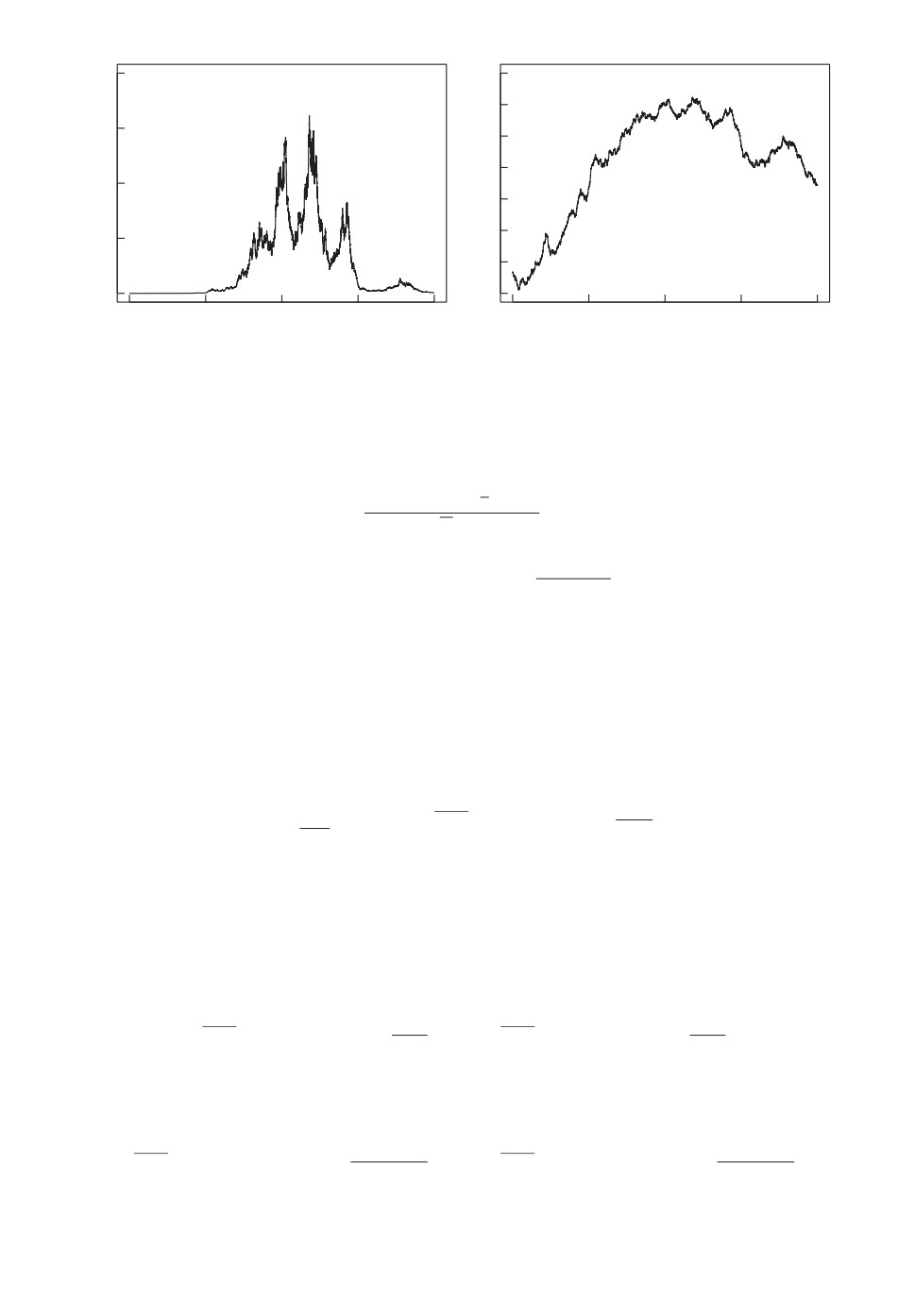
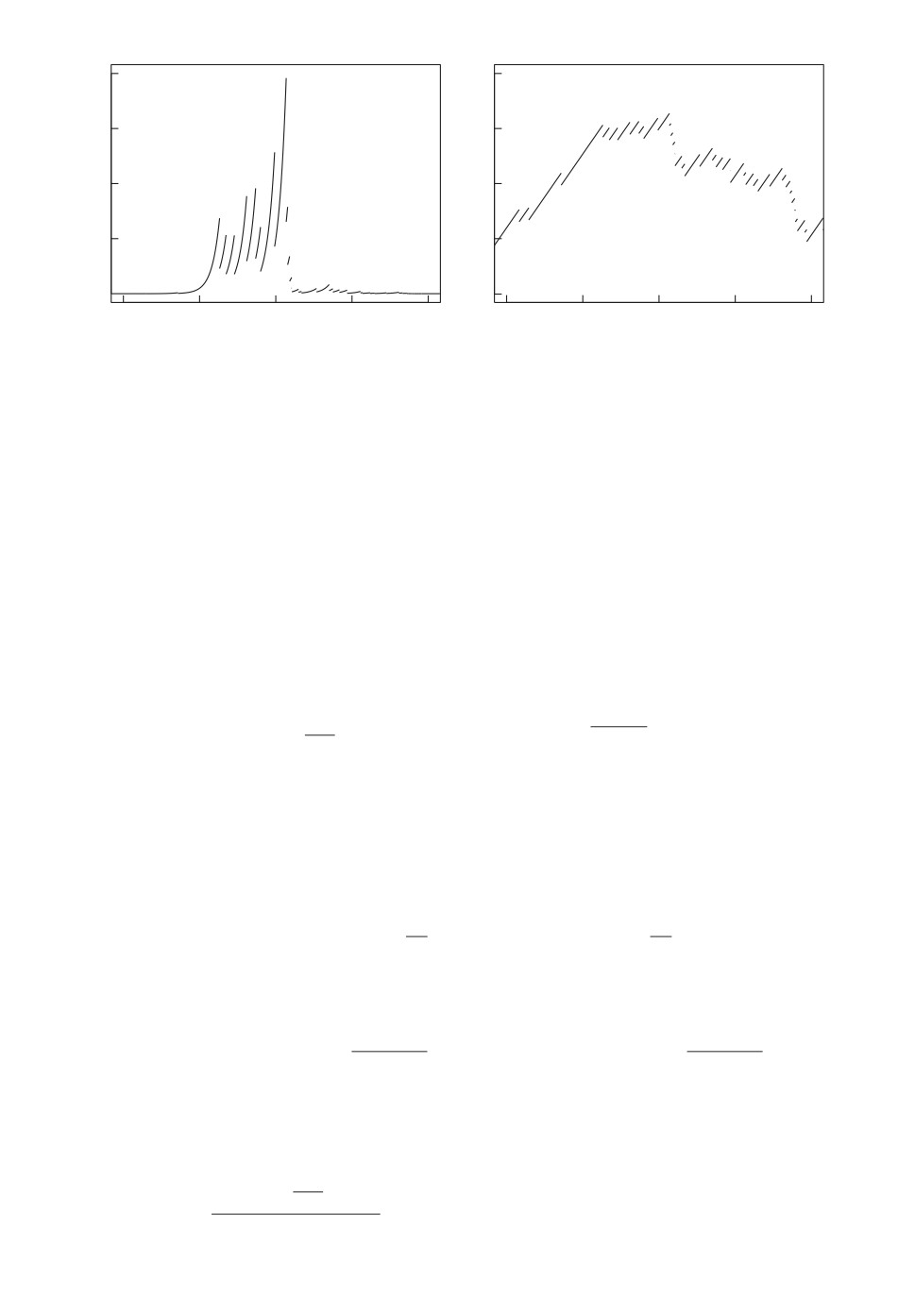
Рис. 3. Примеры реализаций Z(·) (слева) и ln Z(·) (справа) в случае сингуляр-
ности типа касп с κ = 0,1.
Отметим, что Q (κ) допускает представления
(
)
1
Γ(1 + κ) Γ
-κ
2
Q (κ) =
[1 + cos (πκ)] =
22κ-1
√π (2κ
+ 1)
(19)
[
]
1
= 2B (κ + 1, κ + 1)
+1 ,
cos (πκ)
где через Γ (·) и B (·, ·) обозначены гамма и бета функции соответственно
(см. раздел VI.4 в [17]). Единственност
ϑρ доказана в [35].
Примеры реализаций предельного процесса ОП Z(·) и процесса ln Z(·) по-
казаны на рис. 3.
Первый результат — это нижняя граница рисков всех оцено
ϑT :
2
ζ2κ
lim lim sup
T
2κ+1 Eϑ
ϑT - ϑ|2 ≥
γ2κ,τ
ν→0T→∞ |ϑ-ϑ0|<ν
Как обычно, называем оценку ϑ∗T асимптотически эффективной, если для
нее в этом неравенстве имеет место равенство для всех ϑ0 ∈ Θ.
Предложение 2. ОМ
ϑT и Б
ϑT равномерно на компактах K ⊂ Θ
состоятельны, имеют разные предельные распределения:
(
)
(
)
1
ζκ
1
ζκ
T
2κ+1
ϑT - ϑ0
=⇒
,
T
2κ+1
ϑT - ϑ0
=⇒
,
γκ,τ
γκ,τ
моменты сходятся: для всех p > 0
p
Eϑ0
ζκ|p
p
Eϑ0
ζκ|p
T 2κ+1 Eϑ0
ϑT - ϑ0|p -→
,
T 2κ+1 Eϑ0
ϑT - ϑ0|p -→
,
γκ,τ
γκ
,τ
и БО асимптотически эффективны.
23
log(Var)
4
3
2
1
0,5
0,6
0,7
0,8
0,9
1,0
H
Рис. 4. Графики ln σ2∗ (H - 1/2) ≥ ln σ2∗ (H - 1/2).
Доказательство см. в [29]. Нормализованная функция ОП в этой задаче
имеет вид
(
)
)
T
L
ϑ0 + ϕT u,X
(α-ϑ0
β-ϑ0
ZT (u) =
,
u∈UT =
,
,
L (ϑ0, XT )
ϕT
ϕT
где
(
)-1
1
2κ+1
ϕT = γκ,τ T
Имеет место сходимость
ZT (·) =⇒ Z (·),
и поэтому процесс Z(·) является пределом процесса отношения правдоподо-
бия. Следовательно, свойства ОМП и БО следуют согласно соотношениям (8)
и (11) соответственно.
Среднеквадратичные ошибки ОМП и БО следующие:
σ2 (κ)
σ2 (κ)
Eϑ0
ϑT - ϑ0|2 =
(1 + o(1)), Eϑ0
ϑT - ϑ0|2 =
(1 + o (1)) ,
2
2
T
2κ+1
T
2κ+1
где
ζ2κ
ζ2κ
σ2 (κ) =
,
σ2 (κ) =
γ2κ,τ
γ2κ,τ
Интересно сравнить предельные среднеквадратические ошибки σ2 (κ) и
σ2 (κ) ОМП и БО соответственно. Параметр Херста H = κ+1/2 ∈ (1/2,1), где
κ ∈ (0,1/2), и аналитические выражения для значений σ2 (κ) = σ2 (H - 1/2) и
24
3
2
1
0
ϑ
+ *
Рис. 5. Функция интенсивности примера 4.
σ2 (κ) = σ2 (H - 1/2) неизвестны. Значения σ2∗ (κ) =
ζ2κ и σ2∗ (κ) =
ζ2κ были
рассчитаны путем численного моделирования в [36] для значений H ∈ [0,4, 1]
и представлены (в логарифмическом масштабе) на рис. 4. Значение H = 1
(κ = 1/2) соответствует регулярному случаю, когда предельные среднеквад-
ратические ошибки ОМП и БО совпадают.
Приведенные выше результаты можно обобщить на случай, когда сигнал
имеет K точек сингулярности типа касп на интервале [0, τ]. Точнее, пред-
положим, что есть K ≥ 1 точек 0 = τ1 < τ2 < · · · < τK < τ - 2δ, таких что
τk+1 - τk > 2δ, и что τ-периодический сигнал S (t - ϑ) можно записать на
первом периоде t ∈ [0, τ] в виде
∑
S (t - ϑ) =
ψ(t - τk - ϑ) gk(t - τk - ϑ),
k=1
где функции gk(·) непрерывно дифференцируемы, а функция ψ(·) задается
формулой (16). Предполагаем, что gk(y) = 0 для y ∈ (τk -δ, τ∗) и gk(y) = 0 для
y ≥ τ∗, где τK + δ < τ∗ < τ - δ, и множество Θ = (α,β) с δ < α < β < τ - τ∗ .
Заметим, что S (t - ϑ) = 0 для t ∈ [0, ϑ - δ] и для t ∈ [ϑ + τ∗, τ], и таким
образом, сигнал может быть периодически продолжен на интервал [0, T ].
Заметим также, что если фронт k-го сигнала описывается функцией ψ (·)
(и gk (·) ≥ 0) или функцией -ψ (·) (и gk (·) ≤ 0), тогда все вышеприведенные
результаты остаются верными с единственным отличием, что константа γκ,τ
теперь задана формулой
(
) 1
K
2κ+1
∑
Q(κ)
g2k(0)
γκ,τ =
4τ
S(τk) + λ0
k=1
25
3
2
1
0
ϑ
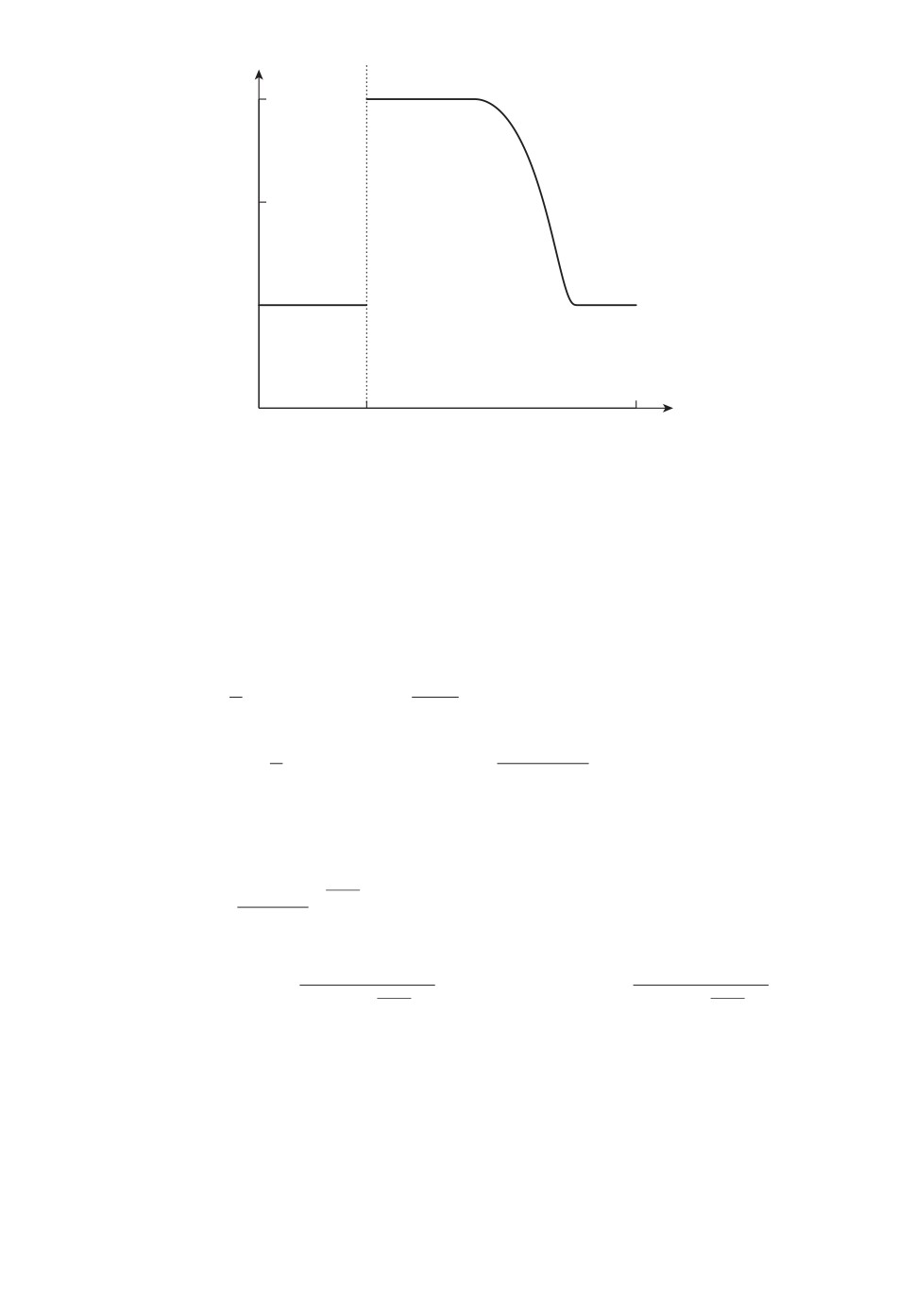
Рис. 6. Пример функции интенсивности сигнала с разладкой в ϑ.
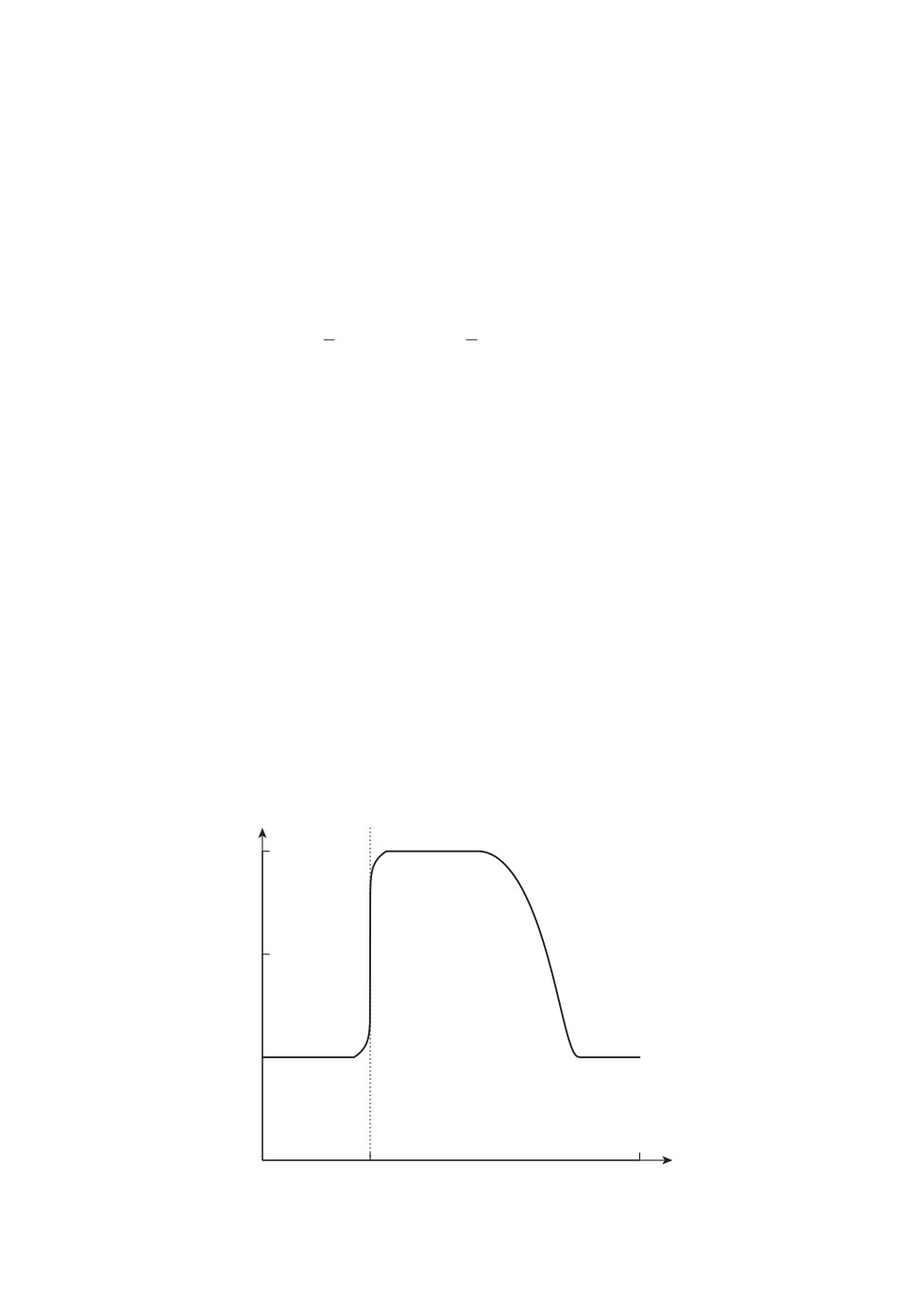
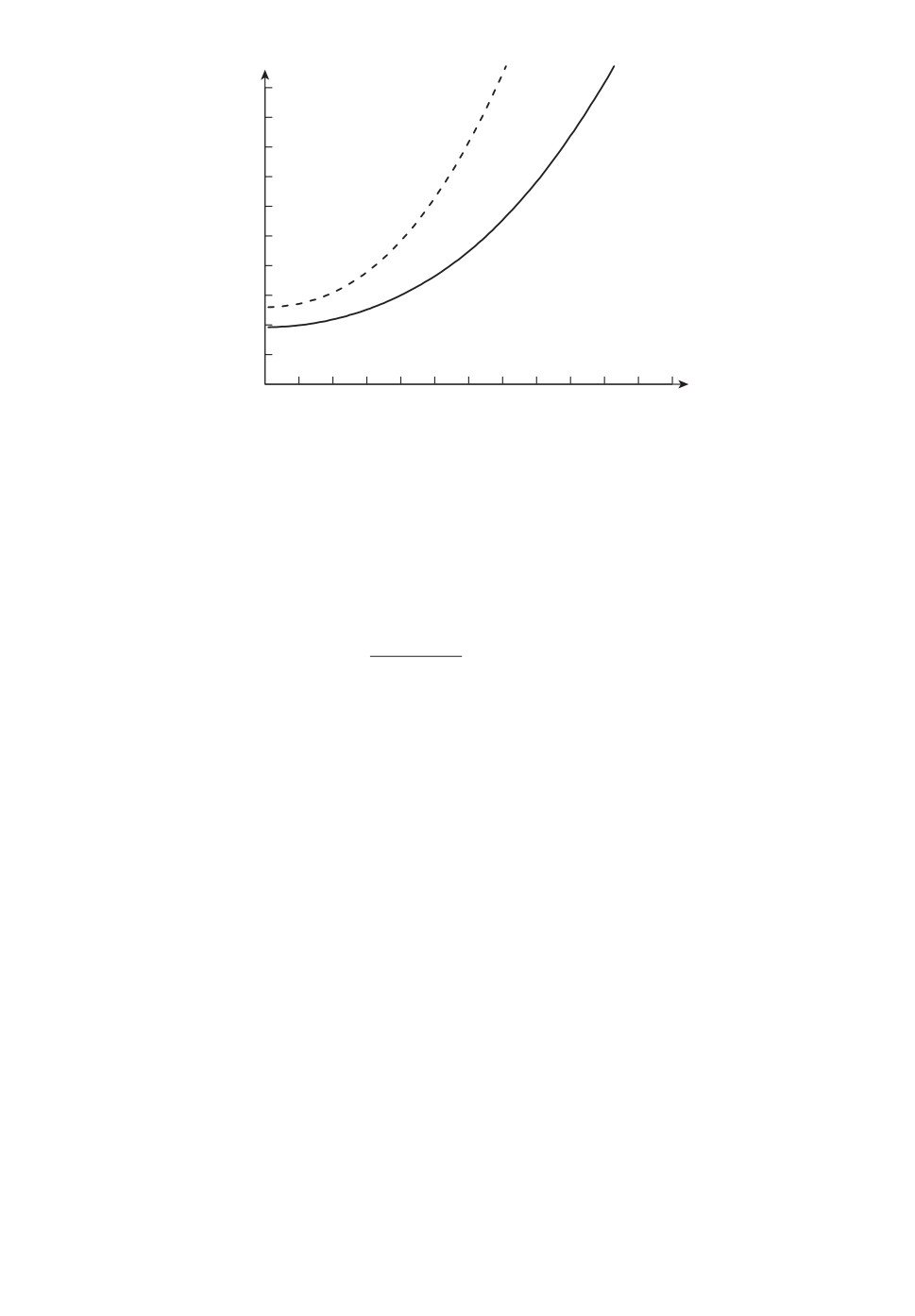
Пример 4. Рассмотрим случай импульсного сигнала конечной длитель-
ности с особенностями типа касп в начале и в конце:
λ (ϑ, t) = S (t - ϑ) + λ0,
0≤t≤T,
где S (t - ϑ) является τ-периодическим сигналом, заданным для t ∈ [0, τ]
формулой
(
)
λ
t-ϑκ
S (t - ϑ) =
1 + sgn(t - ϑ)
l{|t-ϑ|<δ} + λ
1l{ϑ+δ≤t≤τ∗+ϑ-δ} +
2
δ
(
)
λ
t-τ∗ - ϑκ
+
1 - sgn(t - τ∗ - ϑ)
l{|t-τ∗-ϑ|<δ}.
2
δ
Здесь 2δ < τ∗ < τ - 2δ, и множество Θ = (α, β) с δ < α < β < τ - τ∗ - δ. Гра-
фик такой функции интенсивности λ (ϑ, t) приведен на рис. 5.
Асимптотическое поведение ОМП и БО в этой модели дается в предложе-
(
)
1
λ2Q(κ)
нии 2 с γκ,τ =
2κ+1 . В частности, их среднеквадратические ошибки
τ (2λ0+λ)
имеют вид
ζ2κ (1 + o(1))
ζ2κ (1 + o(1))
Eϑ0
ϑT - ϑ0|2 =
,
Eϑ0
ϑT - ϑ0|2 =
2
2
γ2κ,τ T
2κ+1
γ2κ,τ T
2κ+1
Обзор результатов для моделей с касп сингулярностями см. в [37].
3.3. Случай разладки
Рассмотрим проблему оценки точки разладки. Наблюдаем неоднородный
периодический пуассоновский процесс XT = (Xt, 0 ≤ t ≤ T ) с функцией ин-
тенсивности
λ (ϑ, t) = S (t - ϑ) + λ0,
0≤t≤T,
26
где на первом периоде
S (y) = h(y) + g (y)
1l{0≤y≤τ∗}.
Здесь h (·) и g (·) — τ-периодические непрерывно дифференцируемые неотри-
цательные функции, причем g (0) > 0 и g (τ∗) = 0. Неизвестный параметр —
ϑ ∈ (α,β), 0 < α < β < τ - τ∗. Конечно, предполагаем, что τ∗ < τ. Пример та-
кой функции интенсивности λ (ϑ, t) приведен на рис. 6.
Поскольку период τ известен, можем без ограничения общности предпо-
ложить, что T = nτ, и привести исходную модель к модели неоднородного
пуассоновского процесса Yn = (Yn (t) , 0 ≤ t ≤ τ) с интенсивностью
λn (ϑ,t) = nS (t - ϑ) + nλ0,
0≤t≤τ.
(
)
Справедливо равенство L
ϑ,XT
= L(ϑ,Y n), и поэтому лог-ОП можно за-
писать следующим образом:
∫τ
∫
τ
(S (t - ϑ) + λ0)
ln L (ϑ, Yn) =
ln
dYn (t) - n
[S (t - ϑ) - h (t - ϑ)] dt =
h(t - ϑ) + λ0
0
0
∫
(
)
∫
g (t - ϑ)
=
ln
1+
dYn (t) - n
g (t - ϑ) dt =
h (t - ϑ) + λ0
ϑ
ϑ
∫
(
)
∫
τ∗
g (t - ϑ)
=
ln
1+
dYn (t) - n
g (t) dt.
h (t - ϑ) + λ0
ϑ
0
Поскольку функция ОП L (ϑ, Yn), ϑ ∈ Θ, разрывная, ОМ
ϑT определяется
уравнением
(
)
(
)
max L
ϑT +,XT ),L
ϑT -,XT )
= sup L
ϑ,XT
ϑ∈Θ
(
)
Здесь L
ϑ±,XT
— правый и левый пределы ОП в точке ϑ соответственно.
БО определяется соотношением (5).
Положим ρ = lng(0)+h(0)+λ0 и введем предельный процесс отношения прав-h(0)+λ
0
доподобия
⎧
{
(
)
}
u
⎪
⎨exp
-ρx+
+u
,
u ≥ 0,
1-e-ρ
(20)
Z (u) =
{
(
)
}
⎪
u
⎩exp ρx-
-
+u
,
u < 0,
eρ - 1
где x±(·) — два независимых пуассоновских процесса единичной интенсивно-
сти.
27
4
5
3
0
2
5
1
10
0
15
20
10
0
10
20
20
10
0
10
20
Рис. 7. Примеры реализаций Z(·) (слева) и ln Z(·) (справа) в случае ρ = ln 3.
Примеры реализаций предельного процесса Z(·) и процесса ln Z(·) показа-
ны на рис. 7.
Предельные распределения ОМП и БО даны с помощью случайных вели-
чи
ζ
ζρ
ζ
ζρ, которые определяются соотношениями
(
)
(21)
max Z
ζρ+),Z
ζρ-)
= sup
Z (u)
u∈R
и (11) соответственно, где Z (·) задано уравнением (20).
Имеем следующую нижнюю границу (15) на среднеквадратические ошиб-
ки всех оценок:
2
E
ζρ|
lim lim sup
T2Eϑ
ϑT - ϑ|2 ≥
,
γ2τ
ν→0T→∞ |ϑ-ϑ0|<ν
где γτ = τ-1g(0), и называем оценку ϑ∗T асимптотически эффективной, если
для нее в этом неравенстве имеет место равенство для всех ϑ0 ∈ Θ.
Предложение 3. ОМ
ϑT и Б
ϑT равномерно на компактах K ⊂ Θ
состоятельны, имеют разные предельные распределения:
(
)
(
)
ζρ
ζρ
T
ϑT - ϑ0
=⇒
,
T
ϑT - ϑ0
=⇒
,
γτ
γτ
моменты сходятся: для всех p > 0
p
Eϑ0
ζρ|
Eϑ0
ζρ|p
TpEϑ0
ϑT - ϑ0|p -→
,
TpEϑ0
ϑT - ϑ0|p -→
,
γτ
γτ
и БО асимптотически эффективны.
Доказательство см. в [16]. Доказывается, что нормированное ОП
(
)
u
L ϑ0 +γτ
,XT
T
ZT (u) =
,
u ∈ UT = (γτT (α - ϑ0),γτT (β - ϑ0))
L (ϑ0, XT )
28
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
11
12
Рис. 8. Графики E|ζρ|2 (пунктирная линия) и E|ζρ|2 (сплошная линия).
сходится:
ZT (·) =⇒ Z (·),
и для среднеквадратических ошибок получаем представления
Eϑ0
ϑT - ϑ02 =σ2(ρ)
(1 + o(1)), Eϑ0
ϑT - ϑ02 =σ2(ρ)
(1 + o(1)).
T2
T2
Здесь также интересно сравнить предельные среднеквадратические ошиб-
ки ОМП и БО. Аналитические выражения для σ2 (ρ) = γ-2τE
ζρ|2 и σ2 (ρ) =
=γ-2τE
ζρ|2 неизвестны. Исследованию случайной величины
ζρ посвяще-
но несколько работ. Распределения случайных величин supu≥0 Z (u) и
supu≤0 Z (u) описаны в [38-40]. Распределения положениий точек максимума
на отрицательной и на положительной полуосях изучены (по отдельности)
в [41]. Распределение положения глобальной точки максимум
ζρ получено
в [42, 43]. Точную экспоненциальную асимптотику больших уклонений дл
ζρ
можно найти в [44].
Значения E
ζρ|2 и E
ζρ|2 получены численным моделированием в [45]. Гра-
фики E
ζρ|2 и E
ζρ|2 представлены на рис. 8. Заметим, что при больших зна-
чениях ρ предельная ошибка ОМП в два раза больше, чем у БО.
При малых значениях ρ удобнее проследить кривые ρ2E
ζρ|2
и ρ2E
ζρ|2
(см. рис. 9). Объяснение пределов этих кривых при ρ → 0 можно найти в [45].
Рассмотрим несколько обобщений.
Пример 5. Предположим, что сигнал S (t) имеет K скачков на один пе-
риод в точках 0 < τ1 < τ2 < · · · < τK < τ, скажем,
∑
S (t) =
hk-1 (t)
l{τk-1≤t<τk}.
k=1
29
100
90
80
70
60
50
40
30
20
10
0
1
2
3
4
5
6
7
8
9
10
11
12
Рис. 9. Графики ρ2E|ζρ|2 (пунктирная линия) и ρ2E|ζρ|2 (сплошная линия).
Здесь τ0 = 0 и τK+1 = τ. Функции hk (·) такие, что δk = hk-1 (τk-)-hk (τk+) =
= 0 для всех k = 1,...,K. Так как сигнал S (·) является τ-периодической
функцией, предполагаем, что h0 (0) = hK (τ). Обозначим: h-k-1 = hk-1 (τk-),
h+k = hk (τk+),
-
∑
h
+λ0
k-1
ρk = ln
,
δΣ = δk
+
h
+λ0
k
k=1
и введем предельное ОП
⎧
{
}
⎪
∑
(
)
⎪
⎨exp
ρkx+k
(h+k + λ0)u
-δΣu
,
u ≥ 0,
k=1
Z (u) =
{
}
⎪
∑
(
)
⎪
⎩exp
-ρkx-k
-(h-k-1 + λ0)u
-δΣu
,
u < 0.
k=1
Здесь x±k(·), k = 1, . . . , K, — независимые пуассоновские процессы единичной
интенсивности.
Для описания асимптотических свойств ОМ
ϑT и Б
ϑT вводим слу-
чайные величин
ζ
ζΣ
ζ
ζΣ соотношениями (21) и (11) соответственно.
Теперь если предположим, что δΣ = 0, то предложение 3 справедливо и для
оцено
ϑT
ϑT с соответствующими обозначениями. Следовательно,
(
)
(
)
T
ϑT - ϑ0
=⇒
ζΣ,
T
ϑT - ϑ0
=⇒
ζΣ.
Заметим, что здесь немного другая нормализация.
Пример 6. Рассмотрим частный случай примера 5, где K = 2, но δΣ = 0.
Предположим, что имеется прямоугольный импульсный сигнал известной ко-
30
3
2
1
0
ϑ
+ *
τ
Рис. 10. Функция интенсивности примера 6.
4
5
0
3
5
2
10
1
15
0
20
10
5
0
5
10
10
5
0
5
10
Рис. 11. Примеры реализаций Z(·) (слева) и ln Z(·) (справа) в случае ρ = ln 3.
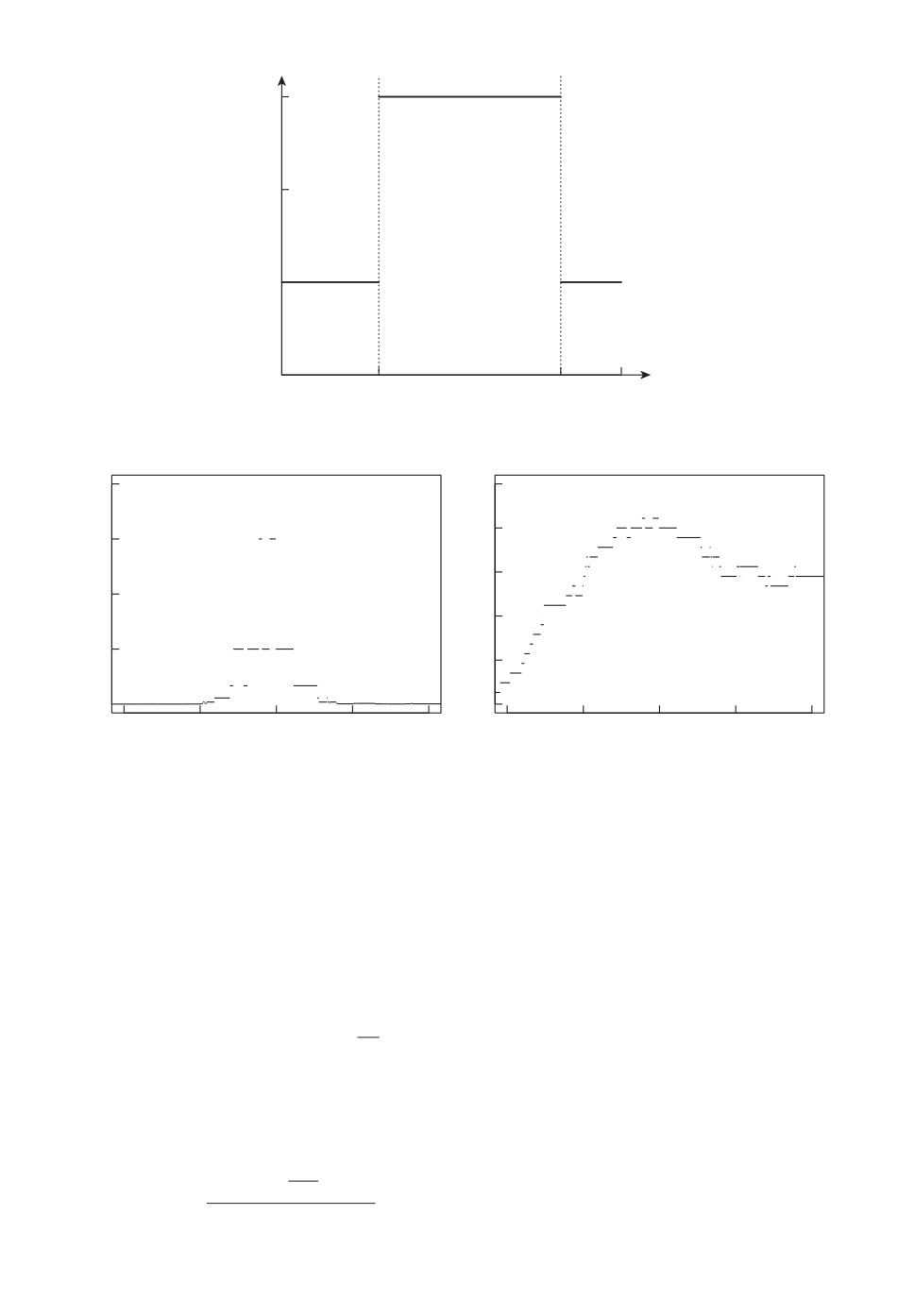
нечной продолжительности τ∗. Это соответствует функции интенсивности
λ(t - ϑ) = λ
1l{ϑ≤t≤ϑ+τ∗} + λ0,
0≤t≤τ,
на первом периоде, где λ > 0 (см. рис. 10).
Предполагаем, что 0 < α < ϑ < β < τ - τ∗ и T = nτ. Функцию ОП в этой
задаче можно записать следующим образом:
{
(
)
}
(
)
λ
L
ϑ,XT
= exp ln
1+
[YT (ϑ + τ∗) - YT (ϑ)] - nτ∗
,
ϑ ∈ (α,β),
λ0
∑n
[
]
где Yn (t) =
Xt+τ(j-1) - Xτ(j-1)
. Введем нормализующую функцию
j=1
ϕT = (γτ T )-1, где γτ = λ/τ и соответствующий нормализованный процесс ОП
(
)
u
L ϑ0 +γτ
,XT
T
ZT (u) =
,
u ∈ UT = (γτT (α - ϑ0),γτT (β - ϑ0)).
L (ϑ0, XT )
31
Тогда можно показать, что конечномерные распределения ZT (·) сходятся к
конечномерным распределениям предельного процесса Z (·)
⎧
{
[
(
)
(
)]}
⎪
u
u
⎨exp
-ρ x+
-x+
,
u ≥ 0,
1
2
1-e-ρ
eρ - 1
Z (u) =
{ [
(
)
(
)]}
⎪
u
u
⎩expρx-
-
-x-
-
,
u < 0,
1
2
eρ - 1
1-e-ρ
где ρ = lnλ+λ0λ0 ,аx1(·),x2(·)—четыренезависимыхпуассоновскихпроцес-
са единичной интенсивности. Примеры реализаций процессов Z(·) и ln Z(·)
показаны на рис. 11.
Заметим, что имеется существенная разница между этим предельным про-
цессом и другими предельными процессами в этой статье. Множество то-
че
ζρ, удовлетворяющих уравнению
Z
ζρ) = sup Z (u),
u∈R
не является одноэлементным (это интервал со случайными концами или даже
конечное объединение таких интервалов). Следовательно, асимптотика ОМП
ϑT требует специального исследования. Для Б
ϑT этой проблемы нет, и
имеем предел
∫
(
)
uZ (u) du
γτ T
ϑT - ϑ0
=
ζρ =∫R
,
Z (u) du
R
а сходимость моментов следует из общих рассуждений, аналогичных приве-
денным выше в доказательстве предложения 2:
2
ζρ|
Eϑ0
ϑT - ϑ02 =E
(1 + o (1)) .
γ2τT2
Пример 7. Рассмотрим случай нескольких точек разладки на одном пе-
риоде. Предположим, что функция интенсивности τ-периодического пуассо-
новского процесса XT на первом периоде равна
∑[
]
λ (ϑ, t) =
hk (t - ϑk)
+λ0,
0≤t≤τ,
l{t<ϑk} + gk (t - ϑk)1l{t≥ϑk}
k=1
где ϑ = (ϑ1, . . . , ϑK ) ∈ Θ ⊂ [0, τ]K . Следовательно, надо оценить K точек раз-
ладки 0 < ϑ1 < ϑ2 < . . . < ϑK < τ по наблюдениям неоднородного пуассонов-
ского процесса XT = (Xt, 0 ≤ t ≤ T ) с такой функцией интенсивности. Пред-
полагаем, что функции hk (·) и gk (·) и множество Θ удовлетворяют условиям,
обеспечивающим идентифицируемость модели.
ОМ
ϑT определяется уравнением вида (21), где правый и левый пределы
рассчитываются в каждой компоненте. БО определяется как отношение (11).
32
Случайное поле предельного отношения правдоподобия равно
∏
Z (u) = Zk (uk) ,
u∈RK,
k=1
где
⎧
{
)
}
⎪
(hk +λ0
⎨exp ln
x+
((gk + λ0) uk) - (hk - gk) uk
,
uk ≥ 0,
k
gk + λ0
Zk (uk) =
{
)
}
⎪
(gk +λ0
⎩expln
x-
(- (hk + λ0) uk) - (hk - gk) uk
,
uk < 0.
k
hk + λ0
Здесь hk = hk(τk), gk = gk(τk), а x±k(·), k = 1, . . . , K, — независимые пуассо-
новские процессы единичной интенсивности.
Введем случайные вектор
ζ =
ζ1,...
ζK)
ζ =
ζ1,...
ζK) независимых
случайных величин, определяемых соотношениями
∫
(
)
ukZk (uk)duk
max Zk
ζk+),Zk
ζk-)
= sup Zk (v) ,
∫
,
v∈R
Zk (uk) duk
R
где k = 1, . . . , K. Используя метод Ибрагимова-Хасьминского [17], можно
проверить сходимость
(
)
T
ϑT - ϑ
=⇒
ζ,
TpEϑ
ϑT - ϑ∥p -→ τpEϑ
ζ∥p.
Здесь ∥·∥ - евклидово расстояние в RK . Доказательство аналогичных преде-
лов для ОМП
(
)
T
ϑT - ϑ
=⇒
ζ,
TpEϑ
ϑT - ϑ∥p -→ τpEϑ
ζ∥p
является более сложной задачей, и ее решение пока неизвестно.
Для модели (1) аналогичный результат получен в [46]. Другой подход к ис-
следованию моделей процессов Пуассона с разладкой в интенсивности развит
в [47].
4. Частотная модуляция
Теперь рассмотрим практически те же модели с той лишь разницей, что
используется частотная модуляция. Наблюдаемый неоднородный пуассонов-
ский процесс XT = (Xt, 0 ≤ t ≤ T ) имеет функцию интенсивности
λ(ϑ,t) = S (ϑt) + λ0,
0≤t≤T,
где сигнал S (t), t ≥ 0, является τ-периодической функцией. Частота ϑ ∈
∈ Θ = (α,β), 0 < α < β, а интенсивность шума (dark current) λ0 > 0. Таким
образом, функция λ (ϑ, t) периодическая с периодом τϑ = ϑ/τ. Поскольку ϑ
33
неизвестно, нельзя заменить XT на n = T/τϑ независимых одинаково рас-
пределенных пуассоновских процессов, как это было сделано в предыдущем
разделе.
Ниже описываются свойства ОМ
ϑT и Б
ϑT , определяемых соотноше-
ниями
∫
ϑp (ϑ)L(ϑ,XT )dϑ
L
ϑT ,XT ) = sup L(ϑ,XT ),
ϑT =∫Θ
,
ϑ∈Θ
p (ϑ) L(ϑ, XT )dϑ
Θ
где функция ОП равна
⎧
⎫
∫
T
(
)
∫
T
⎨
⎬
S (ϑt)
L(ϑ, XT) = exp
ln
1+
dXt -
S (ϑt) dt
,
ϑ ∈ Θ.
⎩
λ0
⎭
0
0
Как и прежде, рассмотрим три типа регулярности/сингулярности моделей:
гладкие модели, модели типа касп и модели разладки.
4.1. Гладкий случай
Предположим, что функция S (·) ≥ 0 дважды непрерывно дифференци-
руема и тождественно не равна нулю. Информацию Фишера запишем сле-
дующим образом:
∫
T
∫
T
∫
τ
λ(ϑ,t)2
t2S′ (ϑt)2
T3
S′ (t)2
dt =
dt =
dt(1 + o(1)).
λ (ϑ, t)
S (ϑt) + λ0
3τ
S (t) + λ0
0
0
0
Точка означает производную по ϑ, а штрих — производную по аргументу
функции. Здесь S′ (ϑt) = S′ (y)|y=ϑt. Поэтому для этой модели наблюдений
можно положить
τ
∫
1
S′ (t)2
I (ϑ) =
dt.
3τ
S (t) + λ0
0
Нижняя граница (Гаека-Ле Кама) на среднеквадратические ошибки всех оце-
но
ϑT имеет вид
lim lim sup T3Eϑ
ϑT - ϑ|2 ≥ I(ϑ0)-1 .
ν→0T→∞ |ϑ-ϑ0|<ν
Как обычно, называем оценку ϑ∗T асимптотически эффективной, если для нее
в этом неравенстве имеет место равенство для всех ϑ0 ∈ Θ.
Предложение 4. ОМ
ϑT и Б
ϑT равномерно на компактах K ⊂ Θ
состоятельны, асимптотически нормальны:
(
)
(
)
(
)
T3/2
ϑT - ϑ0
=
ζ ∼N
0, I (ϑ0)-1 ,
T3/2
ϑT - ϑ0
=
ζ,
34
имеет место сходимость моментов: для всех p > 0
3p
3p
T
2 Eϑ0
ϑT - ϑ0|p -→ Eϑ0
ζ|p,
T
2 Eϑ0
ϑT - ϑ0|p -→ Eϑ0
ζ|p,
и обе оценки асимптотически эффективны.
Доказательства см. в [21, 22]. Нормализующая функция может быть выбрана
как ϕT = T-3/2, и предельное отношение правдоподобия имеет вид
{
}
u2
Z (u) = exp uΔ (ϑ0) -
I (ϑ0)
,
u ∈ R, Δ(ϑ0) ∼ N (0,I(ϑ0)).
2
Для среднеквадратических ошибок имеем
-1
I (ϑ0)
I (ϑ0)-1
Eϑ0
ϑT - ϑ0|2 =
(1 + o(1)), Eϑ0
ϑT - ϑ0|2 =
(1 + o (1)) .
T3
T3
Пример 8. Предположим, что S (ϑt) = a2 [1 + cos(ϑt)], где a > 0. Функ-
ция S (·) периодическая с периодом τ = 2π/ϑ. Информация Фишера равна
(см. [21])
[
√
]
a
λ0
I (ϑ0) =
1 + 2q - 2
q+q2 ,
q=
6
2
Пример 9. Предположим, что S (ϑt) = bexp[acos(ϑt)], где a,b > 0.
Функция S (·) периодическая с периодом τ = 2π/ϑ. Информация Фишера рав-
на (см. [21])
ab
I(ϑ0) =
I′0 (a),
3
где I′0 (a) — производная модифицированной функции Бесселя.
ОМП является асимптотически эффективной, но ее построение связано
с определенными техническими трудностями, поэтому представляет инте-
рес построение вычислительно существенно более простых оценок с теми же
асимптотическими свойствами. Такое построение предложено в [48] в случае
частотной модуляции для модели (1). Аналогичная конструкция может быть
реализована и в случае пуассоновских наблюдений.
Заметим, что задача оценки частоты изучалась также в [49, 50]. В ряде
работ рассматриваются задачи непараметрической оценки частоты и формы
периодического сигналам, см., например, [51] и ссылки там.
4.2. Случай сингулярности типа касп
Предположим, что функция интенсивности наблюдаемого процесса равна
λ(ϑ,t) = S (ϑt) + λ0,
0≤t≤T,
35
где функция S (·) является τ-периодической и может быть записана на первом
периоде как S (y) = ψ (y) g (y), где y ∈ [0, τ] и функция ψ(·) задана формулой
(
)
1
y-μκ
ψ (y) =
1 + sgn(y - μ)
l{|y-μ|<δ} +
1l{y≥μ+δ}.
2
δ
Здесь κ ∈ (0, 1/2), постоянная δ > 0 известна, μ ∈ (δ, τ - δ) и функция g (·)
непрерывно дифференцируема. Более того, предполагаем, что g(y) > 0 для
y ∈ (μ - δ,τ∗) и g(y) = 0 для y ≥ τ∗, где μ + δ < τ∗ < τ. Как и ранее, множе-
ство Θ = (α, β) с 0 < α < β.
Заметим, что S (y) = 0 для y ∈ [0, μ - δ] и что S (y) = g (y) для y ≥ μ + δ,
и, следовательно, S (y) = 0 для t ∈ [τ∗, τ]. Таким образом, сигнал можно пе-
риодически продолжить, а функция ψ (·) описывает фронт сигнала. Также
заметим, что поскольку κ ∈ (0, 1/2), статистический эксперимент сингуляр-
ный.
Напомним некоторые обозначения, введенные в разделе 3.2. А именно вве-
дем случайные величин
ζ
ζκ
ζ
ζκ соотношениями (9) и (11) соответ-
ственно, используя случайный процесс
{
}
2κ+1
Z (u) = exp Wκ+2 (u) - |u|
,
u ∈ R.
2
Здесь WH (·), как и раньше, обозначает дробное броуновское движение с па-
раметром Херста H = κ +12 . Напомним также интеграл Q(κ), определенный
ранее в (18)-(19). Пример реализации процесса Z(·) приведен на рис. 3.
Введем постоянную
(
) 1
2κ+1
g2(μ)Q(κ)
γκ,τ =
4τ(g(μ) + 2λ0)(κ + 1)
Первый результат — это нижняя граница рисков всех оцено
ϑT :
4(κ+1)
ζ2κ
lim lim sup
T 2κ+1
Eϑ
ϑT - ϑ|2 ≥
γ2κ,τ
ν→0T→∞ |ϑ-ϑ0|<ν
Как обычно, называем оценку ϑ∗T асимптотически эффективной, если для нее
в этом неравенстве имеет место равенство для всех ϑ0 ∈ Θ.
Предложение 5. ОМ
ϑT и Б
ϑT равномерно на компактах K ⊂ Θ
состоятельны, имеют разные предельные распределения:
(
)
(
)
2(κ+1)
ζκ
2(κ+1)
ζκ
T 2κ+1
ϑT - ϑ0
=⇒
,
T 2κ+1
ϑT - ϑ0
=⇒
,
γκ,τ
γκ,τ
моменты сходятся: для всех p > 0
2p(κ+1)
Eϑ0
ζκ|p
2p(κ+1)
Eϑ0
ζκ|p
T 2κ+1
Eϑ0
ϑT - ϑ0|p -→
,
T 2κ+1
Eϑ0
ϑT - ϑ0|p -→
,
γκ,τ
γκ
,τ
и БО асимптотически эффективны.
36
Доказательство следует тем же этапам, что и доказательство аналогичного
результата в [29]. Нормализованная функция ОП в этой задаче имеет вид
(
)
)
T
L
ϑ0 + ϕT u,X
(α-ϑ0
β-ϑ0
ZT (u) =
,
u∈UT =
,
,
L (ϑ0, XT )
ϕT
ϕT
(
)-1
2(κ+1)
где нормирующая функция ϕT = γκ,τ T 2κ+1
. Устанавливаем сходимость
ZT (·) =⇒ Z (·),
и поэтому процесс Z(·) является процессом предельного отношения прав-
доподобия этой модели. Следовательно, свойства ОМП и БО описываются
соотношениями (8) и (11) соответственно.
Среднеквадратичные ошибки ОМП и БО имеют вид
σ2 (κ)
σ2 (κ)
Eϑ0
ϑT - ϑ0|2 =
(1 + o (1)) , Eϑ0
ϑT - ϑ0|2 =
(1 + o(1)) ,
4(κ+1)
4(κ+1)
T 2κ+1
T 2κ+1
где
2
E
ζκ|
E
ζκ|2
σ2 (κ) =
,
σ2 (κ) =
γ2κ,τ
γ2κ,τ
Как и в разделе 3.2, предложение 5 можно обобщить на случай, когда функ-
ция S (·) имеет несколько точек сингулярности на интервале [0, τ].
Пример 10. Рассмотрим случай импульсного сигнала конечной длитель-
ности с особенностями типа касп в начале и в конце сигнала:
λ(ϑ,t) = S (ϑt) + λ0,
0≤t≤T,
где S (y) является τ-периодической функцией, заданной для y ∈ [0, τ] фор-
мулой
(
)
1
y-μκ
S (y) =
1 + sgn(y - μ)
l{|y-μ|<δ} +
1l{μ+δ≤y≤τ∗-δ} +
2
δ
(
)
1
y-τ∗κ
+
1 - sgn(y - τ∗)
1l{|y-τ∗|<δ}.
2
δ
Здесь δ < μ < τ - 3δ и μ + 2δ < τ∗ < τ - δ.
Асимптотическое поведение ОМП и БО в этой модели дается в предложе-
(
)
1
Q(κ)
нии 5 с γκ,τ =
2κ+1 .
2τ(2λ0+1)(κ+1)
37
4.3. Случай разладки
Перейдем к проблеме оценки момента разладки. Функция интенсивности
наблюдаемого неоднородного пуассоновского процесса XT = (Xt, 0 ≤ t ≤ T )
имеет вид
λ(ϑ,t) = S (ϑt) + λ0,
0≤t≤T,
где ϑ ∈ (α, β), 0 < α < β, а функция S (·) является τ-периодической. На пер-
вом периоде она имеет представление
S (t) = h(t) + g (t)
1l{μ≤t≤μ+τ∗},
0≤t<τ,
где h (·) и g (·) — τ-периодические непрерывно дифференцируемые функции,
удовлетворяющие условиям h (·) > 0, g (μ) > 0, g (μ + τ∗) = 0, 0 < τ∗ < τ - μ.
Имеем
τ
S (ϑt) = h (ϑt) + g (ϑt)
1l{μ≤ϑt≤μ+τ∗},
0≤t<τϑ ≡
ϑ
Функции h (·), g (·) и параметры μ > 0, τ∗ предполагаются известными.
Лог-ОП может быть записан следующим образом:
∫
T
∫
T
(
)
(S (ϑt) + λ0)
ln L
ϑ,XT
=
ln
dXt -
[S (ϑt) - h (ϑt)] dt =
h(ϑt) + λ0
0
0
∫ϑT
)
∫
(S (v) + λ0
1
=
ln
dXv
-
[S (v) - h (v)] dv =
h(v) + λ0
ϑ
ϑ
0
0
∫
τk
)
∫
τk
∑
∑
(S (v) + λ
0
=
ln
dX
v
-
[S (v) - h (v)] dv +
ϑ
h(v) + λ0
ϑ
k=1τ(k-1)
k=1τ(k-1)
τT
)
∫
(S (v) + λ0
1
+
ln
dXv
-
[S (v) - h(v)] dv =
h(v) + λ0
ϑ
ϑ
τnϑ
τnϑ
∫
(
)
∑
g (s)
=
ln
1+
dXk (ϑ,s)(1 + o(1)) -
h(s) + λ0
k=1
μ
∫
T
-
g (s) ds (1 + o (1)) .
τ
μ
38
[ϑT
]
Здесь были использованы следующие обозначения: nϑ =
(целая часть)
τ
и Xk (ϑ, s) = Xs+τ(k-1) - Xτ(k-1) .
ϑ
ϑ
(
)
Напомним, что функция ОП L
ϑ,XT
, ϑ ∈ Θ разрывная, поэтому ОМП
ϑT определяется уравнением
(
)
(
)
max L
ϑT +,XT ),L
ϑT -,XT )
= sup L
ϑ,XT
ϑ∈Θ
БО определяется соотношением (5).
Положим
g (μ)
h(μ) + g (μ) + λ0
γτ =
,
ρ = ln
2τ
h(μ) + λ0
и введем процесс предельного отношения правдоподобия
⎧
{
(
)
}
⎪
v
⎨exp ρx+
-v
,
v ≥ 0,
eρ - 1
(22)
Z (v) =
{
(
)
}
⎪
v
⎩exp
-ρx-
-
-v
,
v < 0,
1-e-ρ
где x±(·) представляют собой два независимых пуассоновских процесса еди-
ничной интенсивности. Заметим, что до замены переменной v = -u этот про-
цесс аналогичен процессу (20), который был в случае фазовой модуляции (см.
раздел 3.3 и риc. 7).
Предельные распределения ОМП и БО даны с помощью случайных вели-
чи
ζ
ζρ
ζ
ζρ, определяемых соотношениями
(
)
max Z
ζρ+),Z
ζρ-)
= sup Z (u)
u∈R
и (11) соответственно, где Z (·) задано в (22).
Нижняя граница для среднеквадратических ошибок всех оценок имеет вид
2
E
ζρ|
lim lim sup
T4Eϑ
ϑT - ϑ|2 ≥
,
γ2τ
ν→0T→∞ |ϑ-ϑ0|<ν
и называем оценку ϑ∗T асимптотически эффективной, если для нее в этом
неравенстве имеет место равенство для всех ϑ0 ∈ Θ.
Предложение 6. ОМ
ϑT и Б
ϑT равномерно на компактах K ⊂ Θ
состоятельны, имеют разные предельные распределения:
(
)
(
)
ζρ
T2
ϑT - ϑ0
=⇒
,
T2
ϑT - ϑ0
=⇒
ζρ ,
γτ
γτ
моменты сходятся: для всех p > 0
p
Eϑ0
ζρ|
Eϑ0
ζρ|p
T2pEϑ0
ϑT - ϑ0|p -→
,
T2pEϑ0
ϑT - ϑ0|p -→
,
γτ
γτ
и БО асимптотически эффективны.
39
Доказательство см. в [16]. Нормированное ОП определяем соотношением
(
)
u
L ϑ0 +γ
,XT
τT2
(
)
ZT (u) =
,
u∈UT =
γT2 (α - ϑ0) ,γτT2 (β - ϑ0)
,
L(ϑ0,XT )
и проверяем сходимость
ZT (·) =⇒ Z (·).
Для среднеквадратических ошибок получаем выражения
σ2 (ρ)
σ2 (ρ)
Eϑ0
ϑT - ϑ0|2 =
(1 + o(1)), Eϑ0
ϑT - ϑ0|2 =
(1 + o (1)) ,
T4
T4
где σ2 (ρ) = γ-2τEϑ0
ζρ|2 и σ2 (ρ) = γ-2τEϑ0
ζρ|2. Результаты численных вычис-
лений значений Eϑ0
ζρ|2 и Eϑ0
ζρ|2 приведены на рис. 8 и 9 в разделе 3.3.
Свойства ОМП частоты разрывного сигнала модели (1) описаны в [16] (см.
утверждение 2.4.2). Сходные свойства эта оценка имеет и для более общей
модели диффузионного процесса с разрывным периодическим сносом [52].
5. Численное моделирование
Значения ошибок, представленные на рис. 4, 8 и 9, соответствуют пре-
дельной модели (T = ∞). Интересно посмотреть, как среднеквадратические
ошибки
(
)2
σ2
Eϑ0
ϑT - ϑ0
=
(1 + o (1))
Tm
сходятся к своим предельным значениям σ2. Скорость этой сходимости мож-
но увидеть по результатам численного моделирования, приведенным ниже.
Рассмотрим функции интенсивности:
гладкий случай (фаза и частота)
λPS (ϑ,t) = cos2 (2π (t - ϑ)) + 1,
0≤t≤T,
λFS (ϑ,t) = cos2 (2πϑt) + 1,
0≤t≤T,
случай сингулярности типа касп (фаза и частота)
λPC (ϑ,t) = f (t - ϑ) + 1,
0≤t≤τ,
λFC (ϑ,t) = f (ϑt) + 1,
0≤t≤τ,
где на первом периоде
[
]
1
2t+δκ
f (t) =
1 + sgn(2t + δ)
1l{-δ≤t≤0} -
2
δ
[
]
1
2t-δκ
-
1 + sgn(2t - δ)
1l{0≤t≤δ},
2
δ
40
V
V
3
3
2
103
103
1
2
104
104
1
105
105
106
106
7
107
10
1
5
10
50 100
N
1
5
10
50
N
Рис. 12. Результаты симуляций в случаях фазовой (левая часть) и частотной
(правая часть) модуляций.
V
1
V
1
V
1
2
2
103
103
103
2
104
104
104
105
105
105
106
106
106
7
7
10
107
10
1
5
10
50 100
N
1
5
10
50 100 N
1
5
10
50 100 N
Рис. 13. Результаты симуляций в гладком случае (левая часть), в случае син-
гулярности типа касп (центральная часть) и в случае разладки (правая часть).
случай разладки (фаза и частота)
λPD (ϑ,t) = f (t - ϑ) + 1,
0≤t≤τ,
λPD (ϑ,t) = f (ϑt) + 1,
0≤t≤τ,
где на первом периоде
f (t) =
1l{t≥μ} + 1,
0≤t≤τ.
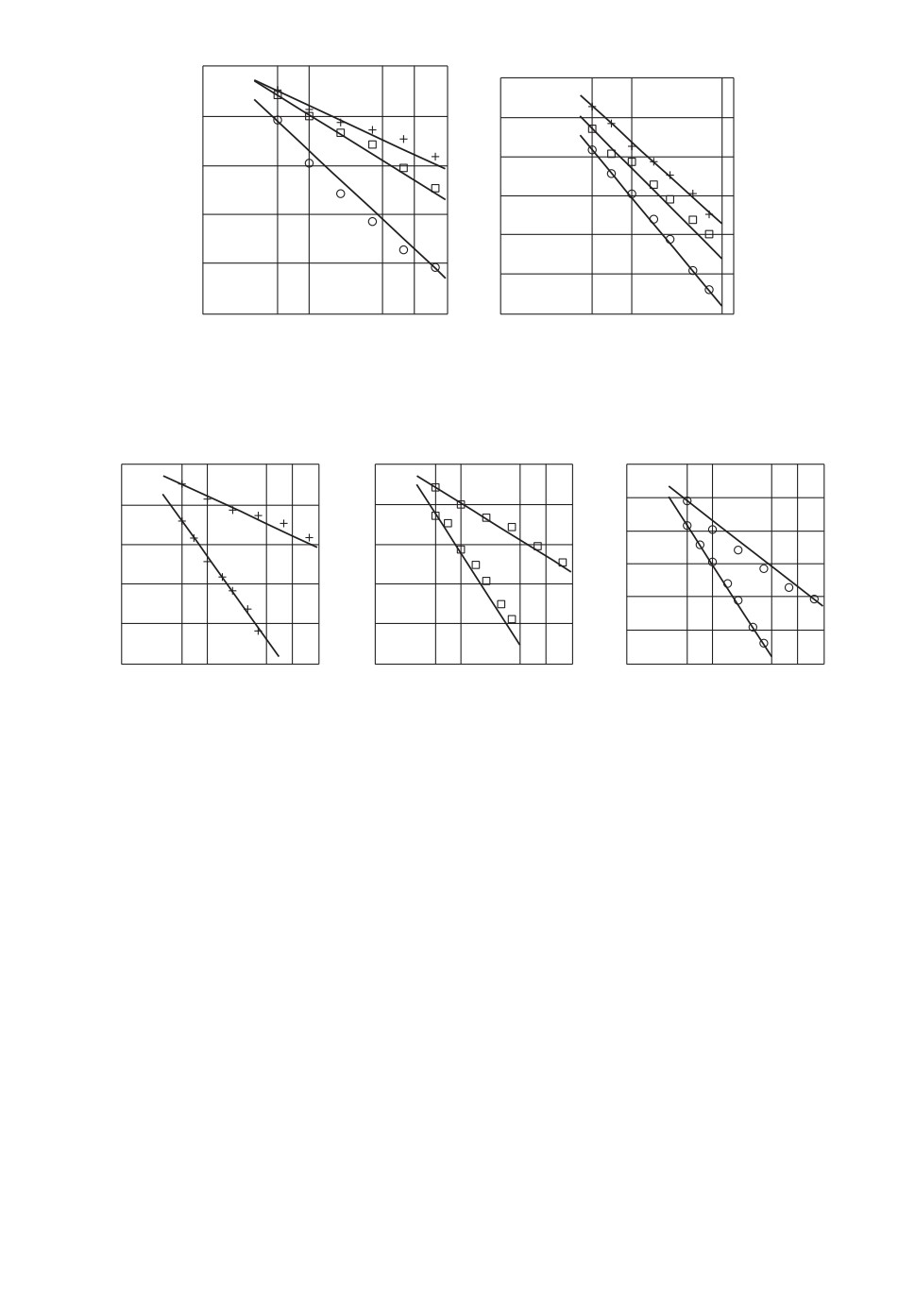
Результаты численной симуляции
(
)2
V (T) = ln Eϑ0
ϑT - ϑ0
= ln σ2 - m ln T
в случаях фазовой и частотной модуляций представлены на рис. 12 и 13.
Используем обозначения: + (гладкий случай), □ (случай сингулярности типа
касп) и ◦ (случай разладки).
41
6. Выбор модели
Как видим, существует большое разнообразие скоростей сходимости оши-
бок в зависимости от аналитических свойств сигналов и типа модуляции.
Поэтому естественно рассмотреть следующий вопрос:
Как выбрать функцию интенсивности и оценку, обеспечивающие мини-
мально возможную ошибку оценки параметра? В частности, какова опти-
мальная скорость сходимости среднеквадратической ошибки?
Напомним, что в статистике обычно приводится модель наблюдений и про-
блема состоит в том, чтобы идентифицировать эту модель оптимальным об-
разом. Здесь утверждение отличается, и можно выбрать и модель, и оценку,
которые обеспечат лучшую ошибку.
Таким образом, рассматриваем задачу, которая в некотором смысле яв-
ляется обратной. Предположим, что можно выбрать любую интенсивность
λ(ϑ, t), которую хотим, и цель состоит в том, чтобы найти такую функцию
λ (ϑ, t), ϑ ∈ Θ = (0, 1) и t ∈ [0, T ], и такую оценку ϑ⋆T , что скорость убыва-
ния погрешности оценивания является наилучшей. Конечно, надо наложить
некоторые ограничения на “энергию сигнала” (терминология, пришедшая из
теории связи), поскольку если допустить λ (·) → ∞, то можно будет получить
любую скорость.
Зафиксируем некоторое число L > 0 и введем класс функций интенсивно-
сти, ограниченных этой константой:
F (L) = {λ(·) :
0 ≤ λ(ϑ,t) ≤ L, 0 ≤ t ≤ T}.
Имеется следующий результат:
{
}
)
TL
inf
inf sup
Eλ,ϑ
ϑT - ϑ
2 = exp
-
(1 + o(1))
λ∈F(L)
ϑT ϑ∈Θ
6
На самом деле, здесь представлено два разных результата.
Первый — это нижняя граница на среднеквадратический риск при любом
выборе интенсивности из этого класса и любой оценк
ϑT :
{
}
)
TL
inf supEλ,ϑ
ϑT - ϑ
2 ≥ exp
-
(1 + o(1))
λ∈F(L)ϑ∈Θ
6
Второй результат — это выбор такой интенсивности λ∗ (·) и построение такой
оценки ϑ∗T , что эта граница достигается:
{
}
TL
sup
Eλ∗,ϑ (ϑT - ϑ)2 ≤ exp -
(1 + o(1))
ϑ∈Θ
6
Доказательства, приведенные в [53, 54], существенно опираются на вычисле-
ние пропускной способности пуассоновского канала (см. [13, 55, 56]).
42
7. Обсуждения
Представленные выше результаты показывают, что порядок ошибки силь-
но зависит от свойств регулярности передаваемого сигнала. Заметим, что
важно изучить ситуации, в которых предполагаемая регулярность сигнала и
реальная регулярность разные. Например, статистик предполагает, что сиг-
нал имеет сингулярность типа разладки, и строит ОМП на основе этого пред-
положения, но реальный сигнал сглажен и функция интенсивности имеет ко-
нечную информацию Фишера. Тем самым имеем ошибку в определении ре-
гулярности. Тогда ОМП сходится к значению ϑ∗, которое минимизирует рас-
стояние Кульбака-Лейблера, и скорость сходимости среднеквадратической
ошибки существенно отличается от предполагаемой. Например, если имеем
фазовую модуляцию и ожидаем скорость Eϑ0
ϑT - ϑ0)2 ∼ T-2, то реальная
скорость ошибки ОМП будет Eϑ0
ϑT - ϑ∗)2 ∼ T-2/3. Среднеквадратичные
ошибки ОМП при различных типах ошибок в типе регулярности сигналов
изучались в [33, 57], где исследовалась модель “сигнал в белом гауссовском
шуме” (1). Подобное исследование может быть интересно также и в случае
пуассоновских процессов.
СПИСОК ЛИТЕРАТУРЫ
1.
Вишневский В.М., Дудин А.Н. Системы массового обслуживания с коррелиро-
ванными входными потоками и их применение для моделирования телекомму-
никационных сетей // АиТ. 2017. № 8. С. 3-59.
Vishnevskii V.M., Dudin A.N. Queueing Systems with Correlated Arrival Flows and
Their Applications to Modeling Telecommunication Networks // Autom. Remote
Control. 2017. V. 78. No. 8. P. 1361-1403.
2.
Назаров А.А., Любина Т.В. Немарковская динамическая RQ-система с входя-
щим MMP-потоком заявок // АиТ. 2013. № 7. С. 89-101.
Nazarov A.A., Lyubina T.V. The Non-Markov Dynamic RQ System with the
Incoming MMP Flow of Requests // Autom. Remote Control. 2013. V. 74. No. 7.
P. 1132-1143.
3.
Проскурников А.В., Фрадков А.Л. Задачи и методы сетевого управления // АиТ.
2016. № 10. С. 3-39.
Proskurnikov A.V., Fradkov A.L. Problems and Methods of Network Control //
Autom. Remote Control. 2016. V. 77. No. 10. P. 1711-1740.
4.
Rao M.M. Optical Communication. Hyderabad: Universities Press, 2001.
5.
Karttunen H., Kröger P., Oja H., Poutanene M., Donner K.J. (Ed’s) Fundamental
Astronomy. New York: Springer, 2017.
6.
Chen V.C. The Micro-Doppler Effect in Radar. 2nd ed. Boston: Artech House
Publishers, 2019.
7.
Breyer B. Physcal Principles of the Doppler Effect and Its Applicatio in Medecine //
Color Doppler, 3D and 4D Ultrasound in Gynecology, Infertility and Obstetrics
(Kupesic S. Ed.). Jaypee Brothers Medical Publishers, 2011. P. 1-11.
8.
Zekavat S.A.R., Buehrer R.M. (Ed’s) Handbook of Position Location: Theory,
Practice and Advances. 2nd ed. Hoboken: Jhon Wiley and Sons, 2019.
43
9.
Chernoyarov O.V., Kutoyants Yu.A. Poisson Source Localization on the Plane.
Smooth Case // Metrika. 2020. V. 83. No. 4. P. 411-435.
10.
Chernoyarov O.V., Dachian S., Kutoyants Yu.A. Poisson Source Localization on the
Plane. Cusp Case // Annals of the Institute of Statistical Mathematics. 2020. V. 72.
No. 5. P. 1137-1157.
11.
Bandyopdhyay M.N. Optical Communication and Networks. Prentice Hall of India
Private, 2014.
12.
Bar-David I. Communication under the Poisson Regime // IEEE Trans. Information
Theory. 1969. V. IT-15. No. 1. P. 31-37.
13.
Wyner A.D. Capacity and Error Exponent for the Direct Detection Photon
Channel — Parts I and II // IEEE Trans. Inform. Theory. 1988. V. IT-34. P. 1449-
1471.
14.
Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов. М.: Наука, 1974.
Liptser R.S., Shiryaev A.N. Statistics of Random Processes. Berlin: Springer, 2001.
15.
Ибрагимов И.А., Хасьминский Р.З. Оценка параметра сигнала в гауссовском
белом шуме // Пробл. передачи информ. 1974. Т. 10. № 1. С. 39-59.
Ibragimov I.A., Khasminskii R.Z. Estimation of a Signal Parameter in Gaussian
White Noise // Problems Inform. Transmission. 1974. V. 10. No. 1. P. 31-46.
16.
Kutoyants Yu.A. Parameter Estimation for Stochastic Processes. Berlin:
Heldermann, 1984.
17.
Ибрагимов И.А., Хасьминский Р.З. Асимптотическая теория оценивания. М.:
Наука, 1979.
Ibragimov I.A., Khasminskii R.Z. Statistical Estimation. Asymptotic Theory. New
York: Springer, 1981.
18.
Prakasa Rao B.L.S. Estimation of the Location of the Cusp of a Continuous
Density // Ann. Math. Statist. 1968. V. 39. No. 1. P. 76-87.
19.
Dachian S. Estimation of the Location of a 0-type or ∞-type Singularity by Poisson
Observations // Statistics: A Journal of Theoretical and Applied Statistics. 2011.
V. 45. No. 5. P. 509-523.
20.
Hajek J. Local Asymptotic Minimax and Admissibility in Estimation // Proceedings
of the Sixth Berkeley Symposium on Mathematical Statistics and Probability. 1972.
V. 1. P. 175-194.
21.
Kutoyants Yu.A. Statistical Inference for Spatial Poisson Processes. New York:
Springer, 1998.
22.
Kutoyants Yu.A. Parameter Estimation of Intensity of Inhomogeneous Poisson
Processes // Probl. Contr. Inform. Theory. 1979. V. 8. P. 137-149.
23.
Kutoyants Yu.A. Multidimensional Parameter Estimation of Intensity of Inhomo-
geneous Poisson Processes // Probl. Contr. Inform. Theory. 1982. V. 11. P. 325-334.
24.
Prakasa Rao B.L.S. Asymptotic Theory of Least Squares Estimator in a Nonregular
Nonlinear Regression Model // Statist. and Probab. Lett. 1985. V. 3. No. 1. P. 15-18.
25.
Prakasa Rao B.L.S. Estimation of Cusp in Nonregular Nonlinear Regression Mo-
dels // Journal of Multivariate Analysis. 2004. V. 88. No. 2. P. 243-251.
26.
Döring M. Asymmetric Cusp Estimation in Regression Models // Statistics: A
Journal of Theoretical and Applied Statistics. 2015. V. 49. No. 6. P. 1279-1297.
27.
Döring M., Jensen U. Smooth Change Point Estimation in Regression Models with
Random Design // Ann. Inst. Stat. Math. 2015. V. 67. P. 595-619.
44
28.
Raimondo M. Minimax Estimation of Sharp Change Points // The Annals of
Statistics. 1998. V. 26. No. 4. P. 1379-1397.
29.
Dachian S. Estimation of Cusp Location by Poisson Observations // Statist.
Inference Stoch. Processes. 2003. V. 6. No. 1. P. 1-14.
30.
Dachian S., Kutoyants Yu.A. On Cusp Estimation of Ergodic Diffusion Process //
J. Stat. Plann. Infer. 2003. V. 117. P. 153-166.
31.
Fujii T. An Extension of Cusp Estimation Problem in Ergodic Diffusion Processes //
Statistics and Probability Letters. 2010. V. 80. No. 9-10. P. 779-783.
32.
Kutoyants Yu.A. On Cusp Location Estimation for Perturbed Dynamical Systems //
Scand. J. Statist. 2019. V. 46. P. 1206-1226.
33.
Chernoyarov O.V., Dachian S., Kutoyants Yu.A. On Parameter Estimation for Cusp-
type Signals // Annals of the Institute of Statistical Mathematics. 2018. V. 70. No. 1.
P. 39-62.
34.
Kutoyants Yu.A. On Localization of Source by Hidden Gaussian Processes with Small
Noise // Annals of the Institute of Statistical Mathematics. 2021. V. 73. No. 4.
P. 671-702.
35.
Pflug G.C. A Statistically Important Gaussian Process // Stochastic Processes and
their Applications. 1982. V. 13. P. 45-47.
36.
Новиков А.А., Кордзахия Н.Е., Линг Т. О моментах оценок Питмена: cлучай
дробного броуновского движения // Теория вероятн. и ее примен. 2013. Т. 58.
№ 4. С. 695-710.
Novikov A.A., Kordzakhia N.E., Ling T. On Moments of Pitman Estimators: the
Case of Fractional Brownian Motion // Theory Probab. Appl. 2014. V. 58. No. 4.
P. 601-614.
37.
Dachian S., Kordzakhia N., Kutoyants Yu.A., Novikov A. Estimation of Cusp
Location of Stochastic Processes: A Survey // Stat. Inference Stoch. Process. 2018.
V. 21. No. 2. P. 345-362.
38.
Pyke R. The Supremum and Infimum of the Poisson Process // Ann. Math. Statist.
1959. V. 30. P. 568-576.
39.
Скороход А.В. Случайные процессы с независимыми приращениями. М.: Наука,
1964.
Skorohod A.V. Random Processes with Independent Increments. Dordrecht: Kluwer,
1991.
40.
Shorack G.R., Wellner J.A. Empirical Processes with Applications to Statistics. New
York: John Wiley and Sons, 1986.
41.
Pflug G.C. On an Argmax-Distribution Connected to the Poisson Process //
Proceedings of the Fifth Prague Conference on Asymtotic Statistics (Mandl P.,
Huskova M. Ed’s). 1993. P. 123-130.
42.
Мосягин В.Е., Швемлер Н.А. Распределение момента максимума разности двух
пуассоновских процессов с отрицательным линейным сносом // Сиб. электрон.
матем. изв. 2016. Т. 13. С. 1229-1248.
Mosyagin V.E., Shvemler N.A. Distribution of the Time of Attaining the Maximum
for the Difference of the Two Poisson’s Processes with Negative Linear Drift (in
Russian) // Sib. Elektron. Mat. Izv. 2016. V. 13. P. 1229-1248.
43.
Мосягин В.Е., Швемлер Н.А. Локальные свойства предельного распределения
статистической оценки точки разрыва плотности // Сиб. электрон. матем. изв.
2017. Т. 14. С. 1307-1316.
45
Mosyagin V.E., Shvemler N.A. Local Properties of the Limiting Distribution of the
Statistical Estimator for Jump Point of a Density (in Russian) // Sib. Elektron. Mat.
Izv. 2017. V. 14. P. 1307-1316.
44.
Мосягин В.Е. Асимптотика распределения момента достижения максимума тра-
екторией процесса Пуассона со сносом и изломом // Теория вероятн. и ее при-
мен. 2021. Т. 66. № 1. С. 94-109.
Mosyagin V.E. Asymptotics for the Distribution of the Time of Attaining the
Maximum for a Trajectory of a Poisson Process with Drift and Break // Theory
Probab. Appl. 2021. V. 66. No. 1.
45.
Dachian S. On Limit Likelihood Ratio Processes of some Change-Point Type
Statistical Models // J. Stat. Plan. Inference. 2010. V. 140. P. 2682-2692.
46.
Ибрагимов И.А., Хасьминский Р.З. Оценка параметра разрывного сигнала в
белом гауссовском шуме // Пробл. передачи информ. 1975. Т. 11. № 3. С. 31-43.
Ibragimov I.A., Khasminskii R.Z. Parameter Estimation for a Discontinuous Signal
in White Gaussian Noise // Problems Inform. Transmission. 1975. V. 11. No. 3.
P. 203-212.
47.
Галун С.А., Трифонов А.П. Обнаружение и оценка момента изменения интен-
сивности пуассоновского потока // АиТ. 1982. № 6. С. 95-105.
Galun S.A., Trifonov A.P. Detection and Estimation of the Time when the Poisson
Flow Intensity Changes // Autom. Remote Control. 1982. V. 43. No. 6. P. 782-790.
48.
Голубев Г.К. Фишеровский метод накопления в задаче оценивания частоты //
Зап. научн. сем. ЛОМИ. 1981. Т. 108. С. 22-44.
Golubev G.K. Fisher’s Method of Scoring in the Problem of Frequency Estimation //
Journal of Soviet Mathematics. 1984. V. 25. No. 3. P. 1125-1139.
49.
Helstrom C. Estimation of Modulation Frequency of a Light Beam // Optical Space
Communication; Proceedings of an MIT-NASA Workshop held at Williams College,
Williamstown, MA, August 4-17, 1968 (Kennedy R.S., Karp S. Ed’s). Appendix E.
1968.
50.
Vere-Jones D. On the Estimation of Frequency in Point-Process Data // J. Appl.
Probab. 1982. V. 19(A). P. 383-394.
51.
Hall P., Reimann J., Rice J. Nonparametric Estimation of a Periodic Function //
Biometrika. 2000. V. 87. No. 3. P. 545-557.
52.
Хепфнер Р., Кутоянц Ю.А. Об оценивании частоты периодического эргодиче-
ского диффузионного процесса // Пробл. передачи информ. 2012. Т. 48. № 2.
С. 48-64.
Hopfner R., Kutoyants Yu.A. On Frequency Estimation for a Periodic Ergodic
Diffusion Process // Problems Inform. Transmission. 2012. V. 48. No. 2. P. 127-
141.
53.
Бурнашев М.В., Кутоянц Ю.А. О границе сферической упаковки, пропускной
способности и о подобных результатах для пуассоновского канала // Пробл.
передачи информ. 1999. Т. 35. № 2. С. 3-22.
Burnashev M.V., Kutoyants Yu.A. On the Sphere-Packing Bound, Capacity, and
Similar Results for Poisson Channels // Problems Inform. Transmission. 1999. V. 35.
No. 2. P. 95-111.
54.
Burnashev M.V., Kutoyants Yu.A. On Minimal α-Mean Error Parameter Trans-
mission over Poisson Channel // IEEE Transactions on Information Theory. 2001.
V. IT-47. No. 6. P. 2505-2515.
46
55. Кабанов Ю.М. Пропускная способность канала пуассоновского типа // Теория
вероятн. и ее примен. 1978. Т. 23. № 1. С. 148-153.
Kabanov Yu.M. The Capacity of a Poisson Type Channel // Theory Probab. Appl.
1978. V. 23. No. 1. P. 143-147.
56. Davis M.H.A. Capacity and Cutoff Rate for Poisson-type Channels // IEEE Trans.
Inform. Theory. 1978. V. IT-26. No. 6. P. 710-715.
57. Chernoyarov O.V., Kutoyants Yu.A., Trifonov A.P. On Misspecifications in Regu-
larity and Properties of Estimators // Electron. J. Statist. 2018. V. 12. No 1.
P. 80-106.
Статья представлена к публикации членом редколлегии Е.Я.Рубиновичем.
Поступила в редакцию 16.06.2021
После доработки 01.07.2021
Принята к публикации 05.08.2021
47